Spatial and temporal coordination of traction forces in one-dimensional cell migration

ABSTRACT

Migration of a fibroblast along a collagen fiber can be regarded as cell locomotion in one-dimension (1D). In this process, a cell protrudes forward, forms a new adhesion, produces traction forces, and releases its rear adhesion in order to advance itself along a path. However, how a cell coordinates its adhesion formation, traction forces, and rear release in 1D migration is unclear. Here, we studied fibroblasts migrating along a line of microposts. We found that when the front of a cell protruded onto a new micropost, the traction force produced at its front increased steadily, but did so without a temporal correlation in the force at its rear. Instead, the force at the front coordinated with a decrease in force at the micropost behind the front. A similar correlation in traction forces also occurred at the rear of a cell, where a decrease in force due to adhesion detachment corresponded to an increase in force at the micropost ahead of the rear. Analysis with a bio-chemo-mechanical model for traction forces and adhesion dynamics indicated that the observed relationship between traction forces at the front and back of a cell is possible only when cellular elasticity is lower than the elasticity of the cellular environment.

Introduction

Migration is an important cell function in wound healing, immune response, embryonic development, and cancer metastasis.¹ Cell migration consists of 4 distinct processes – protrusion at the front edge, formation of new adhesions, generation of traction forces, and detachment of adhesions at the rear.² A frontal towing model has been proposed to describe the role of traction forces in cell migration,³ in which forces at the front of a cell are thought to pull the body of a cell forward and cause dragging forces at its rear. These dragging forces are believed to contribute to the detachment of adhesions at its rear so a cell can advance.^4-8 Studies focused on measuring traction forces during cell migration have been insightful to understand the process.^3,9-14 However, to the best of our knowledge, a correlation between adhesion formation, traction forces, and adhesion detachment has not been verified. Likely, this effort has been difficult because adhesion formation and detachment can occur simultaneously and at multiple locations under a cell, which makes it difficult to conduct a spatial and temporal analysis of a cell's traction forces at all of its adhesions.

In this study, we used arrays of microposts that were stamped with lines of fibronectin in order to confine the migration of fibroblasts along a single line of microposts. This arrangement ensured that at any given time, a cell could form one new adhesion at its leading edge, and likewise, could release one adhesion at its rear. Previously, one-dimensional (1D) patterns like these have been used to control cell migration and have found that patterned cells move with similar speed and morphology as they would on matrix fibrils in vivo.^15,16 Accordingly, induction of 1D migration has been actively used to study chemo- and haptotactic cell migration¹⁷ and cancer cell invasion behavior.¹⁸ An advantage of 1D patterning, in combination with microposts, is that it simplifies the spatial configuration of its adhesions, cytoskeleton, and traction forces, allowing us to test the frontal towing model in 1D.

We compared the results of these experiments with a mathematical model that encompasses many of the bio-chemo-mechanical aspects of traction forces during cell migration. Mathematical models have proven to be useful in understanding and predicting the mechanisms that underlie cell migration.¹⁹ A simple model has been used to predict a biphasic relationship between migration speed and adhesion strength.²⁰ Since then, other migration models have attempted to capture the fluctuations in cell shape,²¹ signal transduction,²² or migration speed.^20,23,24 Recently, we developed a mathematical model that is able to simulate the traction forces produced by cells migrating on arrays of micropost.²⁵ This model is based upon a bio-chemical-mechanical model for cell contraction,²⁶ which is governed by a set of fundamental and coupled relationships: a triggered activation signal, stress fiber assembly, and a force-velocity relationship. Here, we have added aspects of cellular viscoelasticity and focal adhesion strength to this model in order to make comparisons with our 1D migration studies.

Here, we show that there is not a spatiotemporal correlation between the onset of force at the front of a cell and adhesion detachment at the rear during 1D cell migration. Rather, we show that there is a local, inverse correlation between the traction force measured at the front micropost and the force measured at the micropost immediately adjacent to it. As the force at the micropost at the front of the cell increases, the force at its adjacent micropost decreases and there are insignificant changes in the forces at the other microposts. Likewise, prior to adhesion detachment at the rear, we show that the traction force at the rear micropost weakens while the traction force at the micropost adjacent to the rear increases. Furthermore, we find that the bio-chemical-mechanical model is able to suitably resemble these experimental findings if the elasticity of a cell is assumed to be low. Taken together, these results indicate a new aspect of cell migration in 1D that involves a local regulation of traction forces at the front and at the rear of a cell that are not apparently synchronized with one another.

Results

One-dimensional migration on microposts

To investigate the traction forces produced by 3T3 fibroblasts migrating in 1D, we printed lines of fibronectin onto arrays of microposts and measured the traction forces produced by individual cells with time-lapse microscopy (Fig. 1A and B, Supplemental Movie S1). Within 4 hours of seeding the cells onto the microposts, we observed that the cells adopted elongated shapes and attached to 10–20 microposts. After approximately 8 hours, we observed that the cells began to migrate across the lines of microposts. At this time, we imaged the cells using time-lapse microscopy and observed that the cells migrated on the microposts at an average velocity of 11.6 ± 6.5 μm/hr (mean ± SD, 17 cells), which is statistically similar to the speed measured for cells migrating in 1D on flat PDMS substrates (11.0 ± 5.0 μm/hr, 36 cells, p > 0.7, Fig. S1). These videos also revealed that the leading edge of a cell on microposts advances in a more step-wise manner than those on the flat PDMS substrates (Fig. S2). However, the geometric center of a cell migrating on microposts moved in a smooth manner and closely matched that of a cell migrating on a flat PDMS surface (Fig. S2 B, E).

Figure 1.

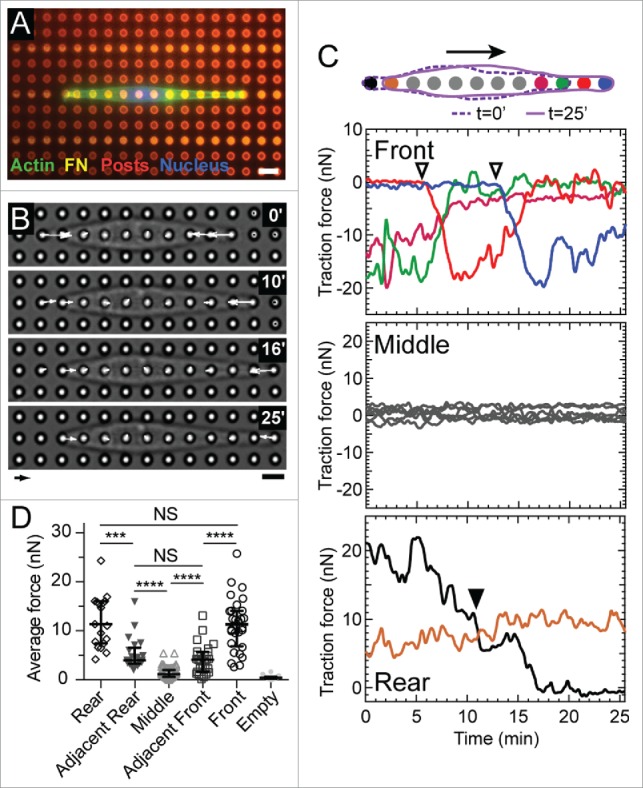
Cell migration on microposts in 1D. (A) Fluorescent image of a representative 3T3 cell stained for actin (green) and its nucleus (blue). The cell is confined to migrate along a row of microposts (red) that have been printed with a line-pattern of fibronectin (magenta). Scale bar: 6 μm. (B) Phase contrast images of a representative migrating cell and its corresponding traction forces. Arrow scale: 10 nN, bar scale: 6 μm. (C) Traces of traction forces over time at each micropost for the representative cell. The color of each trace is illustrated in the accompanying diagram. (Top) Forces at the front of the cell increased when a new adhesion was formed (open inverted triangles). As the force at the front of the cell increases, the force at the micropost adjacent to it decreases. (Middle) Forces at the middle of a cell had an average value of zero within a range of ±5 nN. (Bottom) Force at the rear of the cell decreased steadily over time and did not correlate with the forces at the leading edge. When the cell detached from a rear micropost (▾), the force at its adjacent micropost (brown) increased. (D) Average forces at microposts at the front, adjacent to the front, middle, adjacent to the rear, and rear of migrating cells (M = 15, N = 165 where M indicates the number of experiments and N is the total number of force measurements). The empty posts indicate the posts unoccupied by a cell, the forces of which thus indicate the force resolution of the micropost array. **** p < 0.0001, *** p < 0.001, NS: p > 0.05.

Traction forces in 1D cell migration

For a typical cell migrating along a line of microposts (Fig. 1B), the force measured at the front micropost followed a consistent pattern: when a new adhesion formed at the leading edge, the force at the front micropost rose steadily to a peak value of 10–20 nN within 5–10 min (Fig. 1C, top panel). Following this peak, the force at the front micropost decayed until it reached a value that was below the resolution of the microposts. We refer to this rise in force at the front micropost as “frontal contraction.” This decrease in force following frontal contraction was found to coincide with an increase in force at the micropost adjacent to the front micropost (Fig. 1C, top panel). The changes in traction forces at the front and adjacent microposts did not coincide with changes in the forces at the middle of the cell, which fluctuated about an average of zero for the entirety of the study (Fig. 1C, middle panel). During cell release at the rear of the cell, the traction force measured at the rear micropost decreased steadily until detachment occurred (Fig. 1C, bottom panel).

Over the course of these events, we analyzed the average traction forces at the front, middle, and rear microposts. Specifically, we calculated the average force at the front micropost during the period of time between initial membrane attachment at the first micropost and subsequent membrane attachment at the next micropost. Likewise, we calculated the average force at the rear micropost during the period of time between the release at the rear micropost and the release at the next micropost. Quantifying the average force for each region revealed that the forces at the front and rear microposts were significantly larger than those measured at the middle microposts (p < 0.0001, Fig. 1D). Moreover, the forces at the front and rear microposts were statistically similar to each other (p = 0.28). The forces at the microposts adjacent to the front and rear were statistically similar to each other (p = 0.24), were lower than the forces at the front or rear microposts (p < 0.001), and were larger than the forces at the middle microposts (p < 0.0001). We also analyzed the maximum forces and observed a spatial relationship for the magnitudes that was similar to the average forces: the highest forces were at the front and rear and the lowest forces were at the middle (Fig. S3). These results indicate that a cell migrating in 1D has a symmetric spatial distribution of traction forces. The spatial distribution of traction forces in 1D is different than that in 2D, where traction forces are larger on average at the front of a cell and smaller at its rear.^3,10

Frontal contraction does not coincide with rear release

One aspect of the frontal towing model is that traction forces at the front of a cell lead to detachment at its rear, which we refer to as “rear release”.^5,6,27 To examine this aspect in 1D, we quantified the time between frontal contraction and rear release, i.e. the time between the events of peak force at the front micropost and cell detachment from the rear micropost. A histogram of this data shows that these 2 events occurred up to 75 minutes from one another (Fig. 2A). There were no peaks or trends in the data, indicating that that rear release is likely to be temporally independent from frontal contraction. In addition, 12 frontal contraction events were not followed by a release event within the analysis period of 75 minutes, so this data is not shown in the histogram. Taken together, these data support our hypothesis that rear release does not temporally correlate with frontal contraction.

Figure 2.

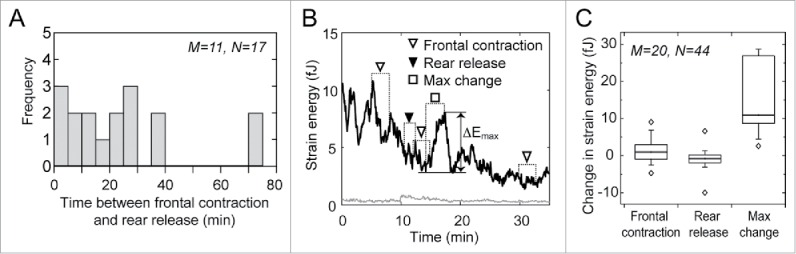
Front contraction does not coincide with sudden rear release. (A) Histogram of the time between front contraction and subsequent rear release. (B) Strain energy in the microposts due to the contractile work of the representative cell shown in Fig. 1. Open inverted triangles show the time period (dotted lines) from membrane attachment to the time when force at the front micropost reached its peak. A filled inverted triangle indicates the 2-min period after membrane detachment at the rear. The maximum change in the strain energy (ΔE_max) is indicated by an open square, which does not correspond with a new adhesion or rear release. The changes in strain energy during frontal contractions were negative or negligibly small and were significantly smaller than ΔE_max. (C) Box-plot of the change in strain energy during front contraction and rear release as compared to the maximum change (ΔE_max). The change in strain energy during front contraction was significantly larger than zero (p < 0.05), but also significantly less than the average maximum change in strain energy (p < 0.001). The average change in strain energy during rear release was statistically similar to zero (p = 0.156) and significantly less than the maximum change (p < 0.001). Here, M indicates the number of cells and N shows the number of analyzed events.

Frontal contraction does not affect overall contractility

Previous migration studies have suggested that the cytoskeletal tension generated in a cell is transmitted to the focal adhesions in a cell via the network of actin filaments. This tension is thought to cause rear release when the strength of the local adhesion is weaker than the applied traction force.^3,28 A rise in cytoskeletal tension in a cell would be reflected in the contractile work produced by the cell, which should increase up until the point of rear release and decrease immediately thereafter. Here, we examined the contractile work of a migrating cell by measuring changes in the strain energy of the microposts.²⁵ During three frontal contraction events (for the cell shown in Fig. 1B), we found that strain energy either decreased (first open triangle) or increased slightly (second and third open triangles). However, these changes were much smaller than the maximum changes in strain energy recorded during the observation period, which occurred neither during frontal contraction nor rear release (ΔE_max in Fig. 2B). By analyzing the migration of 20 cells, we found that the change in strain energy during frontal contraction on average, was positive (p < 0.05, Fig. 2C), but its magnitude was 10-fold smaller than the maximum change in strain energy (Fig. 2C). We also found that rear release did not cause a change in strain energy that was statistically greater than zero (Fig. 2B, C), nor did it temporally coincide with a large decrease in strain energy (filled inverted triangle in Fig. 2B). Therefore, these findings suggest that frontal contraction does not correspond with an increase in the overall contractility of a cell, nor does rear release correspond with a significant increase or decrease in its contractility.

Traction force dynamics during frontal contraction

Since a network of actin filaments connect individual focal adhesions to one another, we examined whether frontal contraction affects the traction forces at the other microposts beneath a cell. Phase-contrast images revealed that the traction force at the front micropost began to rise to a measurable level for nearly 20 sec after the cell membrane was first observed to encounter a micropost (Fig. 3A). This force then rose monotonically for 5–10 min until it reached its peak level (Fig. 3B, blue curve). As it rose, the force measured at the micropost immediately adjacent to it decreased (Fig. 3B, red curve). None of the other microposts beneath the cell showed any measureable changes in force during frontal contraction (Fig. 3B, gray curves). Examining these changes in force from 29 events that were measured for 11 cells (Fig. S4), we determined that the decrease in force at the adjacent micropost was statistically larger than zero (p < 0.05), while the change in force at the middle or rear microposts were statistically equivalent to zero (Fig. 3D). In instances where a migrating cell elongated but did not have rear release within 75 minutes of observation, there was an increase in the force at the front micropost that was accompanied by a decrease in force at the micropost adjacent to it (Fig. S5 B and C). By analyzing the contractile work of migrating cells, e.g. Figure 2B and Fig. S5 D, we determined that frontal contraction had a negligible increase in a cell's contractile work (Fig. S5 E). Thus, these findings indicates that frontal contraction during 1D migration has an local and inverse effect on the traction forces at adjacent adhesions and does not appear to transmit cytoskeletal tension to adhesions at the middle or rear of a cell.

Figure 3.

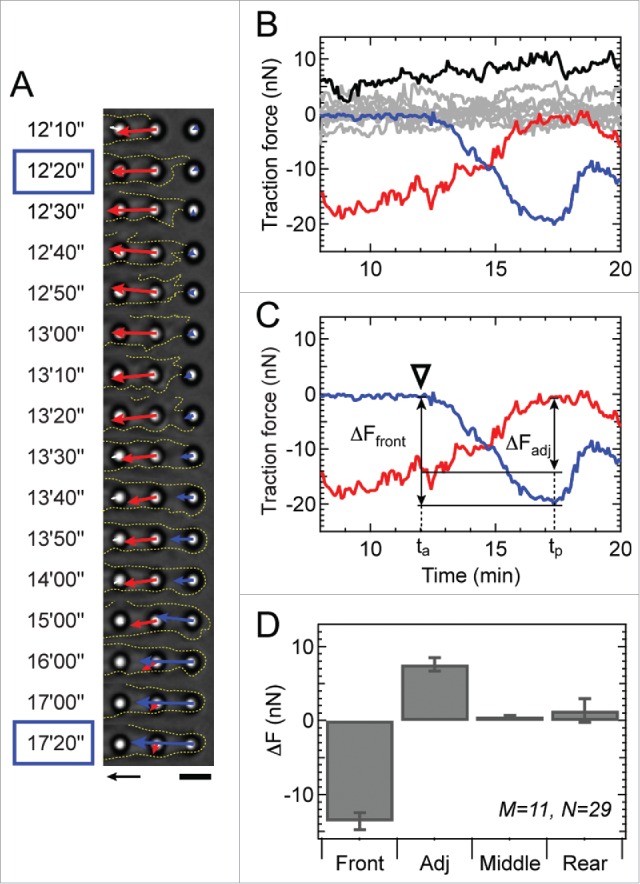
Frontal contraction coincides with a decrease in force at the adjacent micropost. (A) Phase contrast images showing the movement of the cell membrane (outlined by yellow dotted line) as it attaches to a micropost at 12′20″ and develops maximal force (blue arrow) at 17′20.” Note that the force of the adjacent micropost (red arrow) begins to decrease over time after 12′10.” Arrow scale: 10 nN, Bar scale: 5 μm. (B) Traction forces of all microposts under a cell during frontal contraction at the front micropost (blue). Traction forces measured at the adjacent, middle and rear regions of the cell are shown in red, gray, and black, respectively. (C) The change in force at each micropost (ΔF_front for the front micropost and ΔF_adj for the adjacent micropost) was quantified based on 2 time points, t_a and t_p. Adhesion time t_a denotes when the membrane attaches to a micropost and peak time t_p denotes when the force at the new micropost reaches its peak value as indicated in panel A with blue boxes. (D) The change in force at the cell's front, adjacent, middle, and rear microposts. The change in force at the adjacent micropost was significantly greater than zero (p < 0.00001), whereas the change in force at the rear was statistically zero (p = 0.865). The change in force at the middle microposts was not statistically larger than zero (p = 0.017), but its mean was very low (<5%) compared to the change in force at the adjacent micropost. Here, M indicates the number of analyzed cells and N shows the number of events.

Traction force dynamics during rear release

Rear release was examined by quantifying the traction forces produced by a migrating cell during membrane detachment using phase contrast microscopy (Supplemental Movie S2). Prior to rear release, we noted that the force measured at the rear micropost decreased rapidly, until it fell to a value below the resolution limit (t_br in Fig. 4A and C). We noted the time at which the membrane was no longer observed to be attached to the micropost (t_ar in Fig. 4A and C). There may still be a membrane tether attached to the micropost after t_ar, but it was not visibly detected in our experiments. The time between t_br and t_ar was on average 20 ± 12 sec. In the time between t_br and t_ar, we observed a rapid loss of force at the rear micropost that coincided with an increase in force at its adjacent micropost (Fig. 4B and C). After t_ar, the force at the adjacent micropost was observed to rise steadily over time. We quantified the changes in force at all of the microposts under a cell during rear release (see Fig. 4C, where ΔF_rear denotes the reduction in force at the rear micropost and ΔF_adj denotes the rise in force at the adjacent micropost). Data from 21 events and 13 cells indicate that there was an inverse correlation between the magnitude of force measured at the rear and adjacent microposts (Fig. S6). The traction forces at the middle and front microposts did not exhibit a significant change during rear release (Fig. 4D). Together, these results suggest that prior to rear release, there is a rapid relaxation of force at the rear of a migrating cell that is transferred to the adjacent adhesion and not to the other adhesions at the middle or front of a cell.

Figure 4.

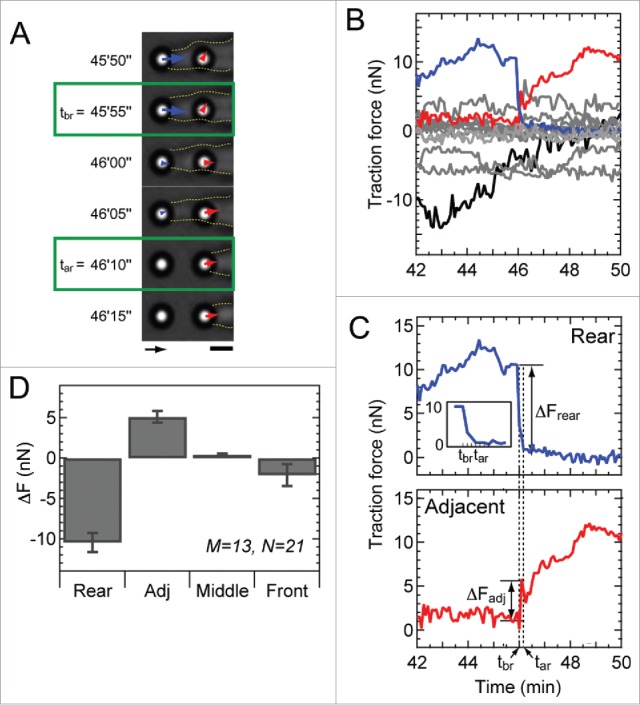
Rear release coincides with a rise in force at the adjacent micropost. (A) Phase contrast images showing the movement of the cell membrane (yellow dotted line) during rear release. Green boxes indicate the time t_br after which the force at the rear micropost (blue arrow) begins to decrease toward zero, as well as the time t_ar when the membrane visibly detaches from the micropost. Arrow scale: 10 nN, bar scale: 3 μm. (B) Plot of traction forces at the rear (blue), adjacent to the rear (red), middle (gray) and front microposts (black) over time. (C) Plot of traction forces at the rear (top) and adjacent micropost (bottom) as shown in panel B. Changes in force (ΔF_rear for the rear micropost and ΔF_adj for the adjacent micropost) were measured in reference to the 2 time points: t_br and t_ar, shown in panel A. (D) Change in force at the rear, adjacent, middle, and front microposts. Although the changes in force at the adjacent, middle, and rear microposts were all significantly larger than zero (p < 0.01), the changes in force within the middle and rear regions of the cell were much smaller than that at the adjacent micropost (p < 0.00001). M represents the number of analyzed cells, whereas N shows the number of events.

Computational simulations of frontal contraction and rear release

To better understand our experimental results, we used a bio-chemo-mechanical model for traction forces during cell migration (Fig. S7 and S8, Supplemental Note 1). The model was calibrated using our experimental measurements of traction forces and strain energy for non-migrating cells (Fig. S9, Table S1, Supplemental Note 2).

During frontal contraction, we observed an inverse correlation between the force at the front micropost and at the adjacent micropost. Since a cell's elasticity is likely to determine the transfer of tension between adhesions, we investigated the effect of cellular elasticity in our simulations. We studied values for k_c = 1 or 100 nN/μm. From these values, one can estimate the elastic modulus of a cell by E = 4 k_c L / π D,² where D is the cylindrical diameter of a cell, which is assumed to be approximately equal to the width of a micropost (D = 3 μm) and L is the center-to-center spacing between the microposts (L = 6 μm). From this approach, a cell with an elasticity of 1 nN/μm corresponds to an elastic modulus of 0.85 kPa, while an elasticity of 100 nN/μm corresponds to 85 kPa. For stiff cells (100 nN/μm), the results of these simulations showed that frontal contraction significantly changed the forces at the front and adjacent microposts (Fig. 5A) and also caused a significant change in force at the rear and within the middle region of the cell (Fig. 5B and C), which is contrary to our migration experiments. However, our simulations of frontal contraction for soft cells (1 nN/μm) has better agreement with our experiments for they demonstrated an inverse relationship between the change in force at the front and adjacent microposts (Fig. 5D) and negligible changes in the forces at the middle and rear microposts (Fig. 5E and F).

Figure 5.

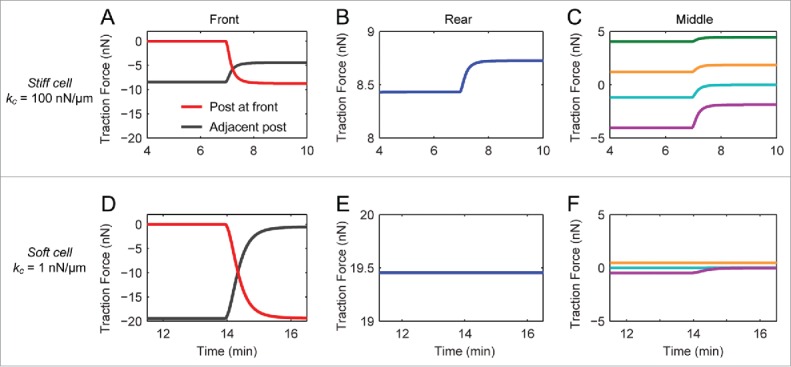
Simulated traction forces during front contraction using the bio-chemo-mechanical model for cell migration. (A,D) The traction forces for cells with high (k_c = 100 nN/μm, A) and low cellular elasticity (k_c = 1 nN/μm, D), at the front (red) and adjacent microposts (black). (B,E) Traction forces at the rear for cells with high (B) and low (D) elasticity. (C,F) Traction forces at the middle microposts for cells with high (C) and low (F) elasticity. Note that there is a significant change in force at the middle and rear microposts in the case of high k_c, whereas there are negligible changes in force for microposts at the middle and rear in the case of low k_c.

During rear release, we observed a loss of force at the rear micropost that was accompanied by an increase in force at the adjacent micropost. To study these observations, we simulated an adhesion release event for a cell migrating along a line of microposts (Fig. 6). As was done for simulations of frontal contraction, the effect of a cell's elasticity on its traction forces was investigated. These simulations showed that, if a cell was assumed to be stiff, rear release resulted in an inverse relationship between the change in traction forces at the rear and adjacent microposts (Fig. 6A), as well as a change in the forces at the middle and front microposts (Fig. 6B and C). For simulations with soft cells, the change in force at the rear of the cell affected the force at the adjacent micropost (Fig. 6D), but there was little effect on the forces at the middle or front microposts (Fig. 6E and F). These results for cell elasticity during rear release, along with simulation of frontal contraction (Fig. 5), suggest that a cell's elasticity during migration is at least one order of magnitude lower than the elasticity of the substrate.

Figure 6.

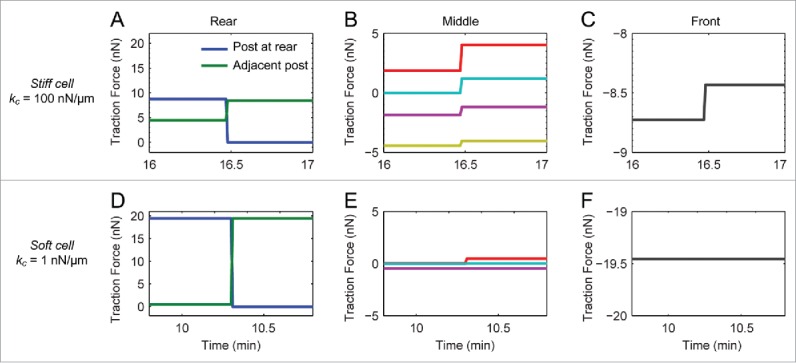
Cell elasticity affects the spatiotemporal distribution of traction forces during rear release. (A,D) Traction forces at the rear part for in the cases of high (k_c = 100 nN/μm, A) and low (k_c = 1 nN/μm, D) cellular elasticity with a force at the rear (blue) and adjacent micropost (green). (B,E) Traction forces at the microposts in the middle for cells with high (C) and low (F) elasticity. (C,F) Traction forces at the microposts at the front for cells with high (C) and low (F) elasticity. Note that there is a significant change in force at the middle and front microposts in the case of high k_c, whereas there are negligible changes in the forces at the middle or front in the case of low k_c.

Discussion

Cell migration is a process of protrusion, adhesion, contraction, and rear release.² There has been speculation that, during migration, cellular contraction leads to rear detachment.^6,27 The frontal towing model supports this hypothesis,^3,29,30 with the idea that the front edge of a cell pulls on the rest of a cell's body during contraction, resulting in the retraction of the rear adhesion. However, the results of our experimental and computational studies for 1D cell migration indicate that contraction does not necessarily lead to rear release, as previously held.⁵ Instead, we suggest that focal adhesion disassembly regulates the release at the rear in a manner that is independent of cytoskeletal contraction. One possible explanation is that adhesion disassembly is induced by microtubule regrowth,³¹ which is independent of RhoA and Rac1 activity, but depends on molecules that play an important role in endocytosis.³²

Upon comparing our experimental and computational analysis, we deduced that a migrating cell has an elasticity that is much lower than that of its underlying substrate, e.g., k_c = 1 nN/μm and k_s = 38 nN/um. Using atomic force microscopy (AFM), a previous study found that the elasticity of fibroblasts is equal to or lower than the elasticity of their substrate.³³ Likewise, Dictyostelium discoideum were measured using AFM and found to have an elasticity that was much lower than that of its agarose substrate.³⁴ Furthermore, upon injecting microspheres into the cytoplasm of migrating 3T3 fibroblasts, Kole et al. found that the elasticity of the cytoplasm was very soft (2 to 33 Pa) in comparison to the stiffness of the cover glass substrate (∼3 GPa).³⁵ Here, it is important to point out that the stiffness of a cell in our study is modeled as a spring between adjacent microposts, its mechanical role is to resist to the compression due to a stress fiber (Fig. S7). Thus, cell components other than stress fibers, e.g. the cytosol, microtubules, intermediate filaments, and nucleus, are expected to contribute to the ‘passive’ stiffness of a cell. Due to this reason, the traction forces were found to be lower for stiff cells (100 nN/μm) than for soft cells (1 nN/μm) in our simulations (Figs. 5 and 6) because a greater portion of the compression was counterbalanced by the passive stiffness of the cell.

Taken together, our experimental and computational studies indicate that cells migrating in 1D exert traction forces during frontal contraction that are not correlated with those produced at the rear of the cell. Likewise, the change in forces measured during rear retraction has only a local effect on the traction forces measured at the middle or front of a cell. These results suggest that frontal contraction may not be the main driver for rear retraction as proposed in the frontal towing model. Instead, our model suggests that contractile forces support the assembly of stress fibers and adhesions, via stabilizing molecular bonds in them. Why migrating cells in 1D have different spatiotemporal patterns in traction forces than cells in 2D, which was modeled as frontal-towing model, has yet to be answered.³⁶ A recent study has shown that cells in 1D have both longer adhesions and more adhesion-to-cytoskeleton coupling.³⁷ Our speculation is that a cell in 1D may have a concentrated amount of stress fibers on its ventral side during adaptation its cytoskeletal structures to a 1D environment. This accumulation of stress fibers likely ensures that there are a large bundle of stress fibers connecting between adjacent focal adhesions, which is how a cell is represented in our mechanical model. In addition, a cell in a 1D configuration may remove heterogeneities like dorsal, transverse and ventral stress fibers and reduce the effect of nuclear-to-cytoskeletal linkages, both of which have been shown to play different roles in 2D cell migration.^38,39 In conclusion, our results reveal a distinct mechanism by which traction forces are regulated during 1D cell migration, which can also shed light on how cells regulate their traction forces when migrating along matrix fibers in 3D.

Materials and methods

Cell culture

NIH 3T3 fibroblasts were cultured in DMEM (Lonza), supplemented with 10% bovine serum (Gibco), 100 U/ml penicillin, 0.1 mg/ml streptomycin, and 2 mM L-glutamine. Cells were seeded onto microposts arrays and incubated at 37°C in 5% CO₂. To prevent cell proliferation, 5 μg/ml of mitomycin-C (Sigma Aldrich) was added to the culture media.⁴⁰

Micropost arrays

Arrays of polydimethylsiloxane (PDMS) (Sylgard 184; Dow-Corning, Midland, MI) microposts were fabricated in via soft lithography, as previously described.⁴¹ The microposts used for these studies were 2.1 μm in diameter, 5.6 μm in height, and had a center-to-center spacing of 6 μm. The PDMS microposts were baked for 3 h at 110°C. Fibronectin (50 μg/ml, BD Bioscience) was micro-contact printed onto the tips of the microposts using PDMS stamps that had a pattern of lines that were 6 μm wide and spaced 12 μm apart (edge-to-edge). To ensure robust printing of this pattern, we used stamp-off technique in which fibronectin is patterned first on a flat PDMS stamp and then stamped on the micropost tips.⁴² Briefly, flat stamps were prepared via soft lithography with 30:1 base-to-crosslinker ratio against a 4-inch flat wafer. Patterned PDMS stamps were prepared with 20:1 ratio against line-patterned SU-8 so that the PDMS stamps have 12 μm-wide protruded parts with 6 μm of indented spacing. Fibronectin solution was adsorbed on a full surface of the flat PDMS stamps for 1 hour. The flat stamps were washed with PBS and dried with nitrogen. We activated the surface of the bare patterned stamps with UV-ozone for 7 minutes and placed the patterned stamps onto the flat stamps for 5 seconds in order to remove the protein within the regions between the line patterns (6 μm wide with 12 μm spacing). The flat stamp was then used for stamping fibronectin onto the array of microposts. The remaining surfaces of the microposts were fluorescently labeled with 5 µg/ml of bovine serum albumin conjugated with Alexa Fluor 594 (Invitrogen, A13101) for 1 hr and blocked with 0.2% Pluronic F-127 (BASF, Mount Olive, NJ) for 30 min to restrict additional protein adsorption.

Live cell microscopy

Time-lapse image sequences of individual migrating cells on the microposts were acquired with an inverted bright-field microscope (Ti-E, Nikon) with a 40×, 1.4 NA, Plan Apo phase objective lens (Nikon). An environmental control chamber equipped with a heating unit (In Vivo Scientific) and CO₂ controller (In Vivo Scientific) were used to maintain the cells at 37°C and 5% CO₂ throughout the imaging process. Bright-field images were acquired at 5-second intervals using a CCD camera (Clara, Andor). Prior to recording, a fluorescent image of the microposts was taken at a focal plane corresponding to the base of the microposts in order to determine their original, unloaded positions. To account for lateral drift during live-cell imaging, each frame of the time-lapse video was registered to the first frame, based upon the positions of unoccupied microposts.

We analyzed cells that advanced at least 4 microposts in the forward direction during the imaging period and that exhibited at least one detachment event at the rear of the cell during this period. During our experiments, we did observe cells that extended in both the front and the rear directions, i.e., elongation or spreading (15% of all cells observed), those that changed migration direction (20%) or those that did not migrate (40%), all of which we excluded for the analyses in our study, leaving 25% of cells that fit for our criteria as a migrating cell. A total 11 independent experiments were performed, from which total 15 cells were used to obtain the experimental data shown in Figures 1–4.

Traction force analysis

Bright-field time-lapse image sequences were analyzed using a custom-written code in MATLAB (Mathworks). Specifically, the deflection of a micropost was calculated as the difference between the centroid of a micropost in the bright-field image and its corresponding centroid in the fluorescent image taken at the base of the microposts. The centroids of the microposts were located using Gaussian fits on the bright-field image of each frame of the captured video.⁴³ The deflection (δ) of each micropost was then used to calculate the traction force (F) produced by the cell according to: F = k_p δ = 3πd⁴Eδ/64h³ where k_p = 38 nN/μm is the spring constant for each micropost, d is its diameter (2.1 μm), h is its height (5.6 μm), and E is the elastic modulus of PDMS (2.5 MPa). We chose this post dimensions and PDMS's material property so that the final spring constant (38 nN/μm) is in intermediate range, according to our previous study.⁴⁴ The contractile work of a migrating cell was determined by calculating the strain energy in the microposts according to: ${\displaystyle {\sum }_j^N\mathrm{½}{k}_p{\text{δ}}_j^2}$ where N is the number of microposts on which a cell is attached at any given time.

As previously described,⁴⁴ the dimensions of the mic-roposts were measured using a scanning electron microscope (FEI Sirion), and the elastic modulus of PDMS dog-bone samples was measured using an Instron 5585H tensile test according to ASTM standard D412. We analyzed the fluctuations in the position of the tips of the microposts that had no cells attached to them. By measuring the fluctuations of these empty microposts, we determined that the resolution limit for measuring traction forces was 0.7 ± 0.4 nN.

Immunofluorescence

After culturing the cells on top of the microposts for 14 hours, the samples were fixed with 4% paraformaldehyde (EMD Chemicals) in PBS. The samples were permeabilized in 0.1% Triton X-100 for 5 min and blocked with 10% goat serum for 1 hr (Gibco). Following this, the samples were incubated with Hoechst 33242 (Invitrogen), Alexa Fluor 488-conjugated phalloidin (Invitrogen), and imaged on an inverted fluorescence microscope (Ti-E, Nikon) using a 40×, 1.4 NA, oil immersion objective (Nikon).

Statistical methods

For spatial analysis of the traction forces, the microposts on which a cell was attached were divided into 3 groups: front, middle, and rear. Front denotes the leading micropost in the direction of migration, rear denotes the micropost at the opposite end, middle denotes all of the others microposts under a cell. Student's t-test was used to compare the means for each group or to compare with zero.

Bio-chemo-mechanical model

We previously developed a model to predict the traction forces produced by a cell migrating on arrays of microposts.²⁵ Briefly, the model represents the cell as a material with passive elasticity that contracts by myosin-based force generation. The formation of a new adhesion at the front of a cell triggers an activation signal that causes the generation of myosin-based forces. Specifically, the activation signal drives the assembly of stress fibers within a local region of a cell. Myosin-based forces are assumed to be isometric and the magnitude of force is determined by the assembly level of the stress fibers in the local region. A process of adhesion assembly at the front and disassembly at the rear is added to the model, where the rate of adhesion assembly is tension-dependent and the rate of adhesion disassembly is constant. Theoretical justification, mathematical equations, and the specific algorithms used to simulate the model are described in Supplemental Note 1, Fig. S7 and Fig. S8. Previous validation efforts for the bio-chemo-mechanical model are summarized in Supplemental Note 3.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.

Acknowledgements

We thank M. Driscoll, A. Veress, G. Odell and T. Daniel for helpful discussions and advice.

Supporting citations

References (45–75) appear in the Supporting Material.

Funding

This work was supported by National Science Foundation CAREER Award.