Numerical Modeling of Experimental Human Fibrous Cap Delamination

Abstract

Fibrous cap delamination is a critical process during the rupture of atherosclerotic plaque, which often leads to severe life-threatening clinical consequences such as myocardial infarction or stroke. In this study a finite element modeling and simulation approach is presented that enables the study of fibrous cap delamination experiments for the purpose of understanding the fibrous cap delamination process. A cohesive zone model (CZM) approach is applied to simulate delamination of the fibrous cap from the underlying plaque tissue. A viscoelastic anisotropic (VA) model for the bulk arterial material behavior is extended from existing studies so that the hysteresis phenomenon observed in the fibrous cap delamination experiments can be captured. A finite element model is developed for the fibrous cap delamination experiments, in which arterial layers (including the fibrous cap and the underlying plaque tissue) are represented by solid elements based on the VA model and the fibrous cap-underlying plaque tissue interface is characterized by interfacial CZM elements. In the CZM, the delamination process is governed by an exponential traction-separation law which utilizes critical energy release rates obtained directly from the fibrous cap delamination experiments. A set of VA model parameter values and CZM parameter values is determined based on values suggested in the literature and through matching simulation predictions of the load vs. load-point displacement curve with one set of experimental measurements. Using this set of parameter values, simulation predictions for other sets of experimental measurements are obtained and good agreement between simulation predictions and experimental measurements is observed. Results of this study demonstrate the applicability of the viscoelastic anisotropic model and the CZM approach for the simulation of diseased arterial tissue failure processes.

1. Introduction

Atherosclerotic plaque rupture is a serious complication of advanced atherosclerosis, often leading to life-threatening clinical consequences such as myocardial infarction (heart attack) or stroke (Assemat and Hourigan, 2013; Badimon and Vilahur, 2014; Schwartz et al., 2007). Roughly 75% of all myocardial infarctions originate from plaque rupture and approximately 1.1 million people are affected in the USA per year (Virmani, 2007).The American Heart Association has developed a method to predict future costs of cardiovascular disease, which includes coronary heart disease and stroke; associated costs are estimated to increase from $172 billion in 2010 to $276 billion in 2030 (Heidenreich et al., 2011). These forecasts illustrate the magnitude of the clinical problems resulting from arterial tissue failures and the importance of improving our basic understanding of the arterial failure processes. A full understanding of plaque rupture will provide a solid basis for medical advances in intervention and prevention of this life-threatening event.

Plaque rupture is, in essence, a mechanical failure phenomenon, often in the form of fibrous cap separation (delamination) from the underlying tissue. Fibrous cap failure typically occurs at one of two locations. One location is at the center of the plaque, where the fibrous cap may be very thin and prone to rupture under large deformations and stress concentrations. Another is at the shoulder region, where the interface between the fibrous cap and the underlying plaque tissue is located (Jensen et al., 2006; Loree et al., 1992), which is prone to delaminate along the interface. This type of failure occurs, for example, when the atherosclerotic plaque experiences large expansion under balloon angioplasty or stenting, possibly caused by stress concentration along the interface due to mismatch in mechanical properties (Badel et al., 2014; Kolodgie et al., 2007; Li et al., 2008). For example, fibrous cap delamination at the shoulder region during balloon angioplasty has been demonstrated by intravascular ultrasound in vivo (Honye et al., 1992). At the site of stress concentration, mechanical damage is expected to initiate and accumulate, leading to delamination when the damage reaches a critical level. In general, the subsequent delamination growth may contain Mode I (opening mode, caused by an opening force) and Mode II (shearing mode, caused by a shearing force) components.

In order to understand and eventually predict the fibrous cap delamination phenomenon, delamination experiments on human carotid artery endarterectomy specimens have been carried out at the University of South Carolina. These experiments enable the study of the adhesive strength of the interface between the fibrous cap and the underlying plaque tissue. Through multiple cycles of loading, delamination, and unloading of the fibrous cap in an experiment, measurements of the load-displacement curve through the cycles contain important information such as the critical energy release rate during delamination and provide opportunities to develop and validate modeling and simulation approaches for understanding and predicting fibrous cap delamination events in human atherosclerosis. To this end, in the current study a finite element based numerical approach has been developed to model and simulate the fibrous cap delamination experiments. It is noted that the modeling and simulation approach developed in this study is formulated so that it is applicable to mixed-mode fibrous cap delamination events in which both the opening and shearing modes can occur. To the authors’ knowledge, simulations of fibrous cap delamination events have not been reported in the literature.

2. Materials and methods

In the current study, the Holzapfel-Gasser-Ogden (HGO) model (Gasser et al., 2006) was initially considered to provide a hyper-elastic constitutive law for the bulk material behavior of all arterial layers (including the fibrous cap and the underlying plaque tissue). The HGO model is commonly employed for arterial walls. It treats each artery layer as a fiber-reinforced material with the fibers symmetrically disposed with respect to the circumferential direction of the artery. However, this model was not able to capture the hysteresis behavior observed in the load-displacement curves obtained from the fibrous cap delamination experiments, because there is no viscoelastic component in the HGO model. To extend the HGO model, a viscoelasticity formulation developed by Holzapfel (Holzapfel, 2000a) was adopted in the current study to incorporate a viscoelastic component into the HGO model, leading to a viscoelastic anisotropic (VA) model, which is used in the current study.

To capture the material separation (delamination) process along the interface between the fibrous cap and the underlying plaque tissue, the cohesive zone model (CZM) approach is employed in the current study. The CZM approach has been shown to be an effective way of modeling separation failure processes in composite materials, including debonding and delamination across interfaces (Turon et al., 2006). This approach has also been applied in limited cases to the study of material separation failure in arteries (Ferrara and Pandolfi, 2010; Gasser and Holzapfel, 2006; Gasser and Holzapfel, 2007; Leng et al., 2015a; Leng et al., 2015b). In the current study, an exponential traction-separation law is adopted for the CZM, which utilizes the critical energy release rates obtained directly from the fibrous cap delamination experiments.

Both the VA model and the CZM are implemented in the general-purpose finite element code ABAQUS (ABAQUS, 2013) via user subroutines, which enables the finite element simulations of the fibrous cap delamination experiments. In order to make the simulations possible, one challenge in the current study is the determination of the material parameter values for both the VA model and the CZM model, which are not readily available from the literature. To overcome this difficulty, in the current study a set of parameter values is determined based on limited values suggested in the literature and through matching simulation predictions of the load vs. load-point displacement curve with one set of measurements from the fibrous cap delamination experiments, which involves multiple loading-delamination-unloading cycles (cycle #1, cycle #2, etc.) of the fibrous cap. This set of experimental measurements for determining the material model parameter values is taken from the load-displacement curve for cycle #1 and from the loading phase of the curve for cycle #2 (see later in Fig. 8a). Once the set of parameter values is determined, it is kept intact and used to enable simulations of subsequent loading-delamination-unloading cycles, so that comparisons of the simulation predictions of the load-displacement curves with experimental measurements for the subsequent cycles provide a validation of the parameter values and of the CZM-based finite element modeling and simulation approach for understanding fibrous cap delamination phenomena in arterial failure processes.

Fig.8.

The simulation-predicted load-displacement curves of nine loading-delamination-unloading cycles are compared with the measured curves: (a) the load-displacement curves and (b) relative error vs. displacement curves for cycles #1, #2 and #3 for sample FC1; (c) load-displacement curves and (d) relative error vs. displacement curves for cycles #4, #5 and #6 for sample FC1; (e) the load-displacement curves and (f) relative error vs. displacement curves of cycles #1, #2 and #3 for sample FC2.

The remaining sections of this paper are as follows. In Section 2.1 and Section 2.2, the material models for the bulk material behavior of arterial layers and the interfacial behavior of the interface between the fibrous cap and the underlying plaque tissue for the human carotid artery are described, respectively. In Section 2.3, relevant experimental details are provided. In Section 2.4, modeling and simulation details are given. In Section 3, simulation predictions are compared with and validated by experimental measurements. Finally in Section 5, the main findings and conclusions are summarized.

2.1 Bulk material model

To describe the mechanical behavior of diseased arterial materials such as atherosclerotic plaque and fibrous cap, a viscoelastic, anisotropic material model extended from the HGO model (Gasser et al., 2006) (which does not have a viscoelastic component) is proposed, so that the hysteresis behavior seen in the loading-delamination-unloading data from the fibrous cap delamination experiments can be captured.

Following a practice reported in the literature (e.g. Holzapfel et al. 2005), to pre-condition the fibrous cap in order to remove its viscoelastic behavior during a subsequent delamination experiment, the fibrous cap was loaded and unloaded successively by being pulled forward and backward 15 times with large deformation before the start of a fibrous cap delamination experiment.

However, the underlying plaque tissue did not undergo preconditioning during fibrous cap delamination, because the position of deformed plaque tissue changed as the delamination front moved forward during the experiment. Therefore, the viscoelastic anisotropic model is applied to the underlying plaque tissue and to the media layer next to the plaque tissue, but not to the fibrous cap (which instead is represented by the HGO model).

For convenience of easy reference, the HGO model, its extension to include a viscoelastic component, and some associated concepts are briefly described below.

2.1.1 Anisotropic hyperelastic model: Holzapfel-Gasser-Ogden (HGO) model

The HGO model (Gasser et al., 2006) assumes that the mean orientation of collagen fibers lies parallel to the arterial wall (as shown in Fig.1), thus neglecting the out-of-plane component. A Helmholtz free energy function Ψ(C̅, H₁, H₂) which is defined per unit reference volume in a decoupled form is expressed as:

$$\Psi (\mathit{C},{\mathit{H}}_1,{\mathit{H}}_2)={\Psi }_{\mathit{\text{vol}}}(J)+\overline{\Psi }(\overline{\mathit{C}},{\mathit{H}}_1,{\mathit{H}}_2)$$ (1)

In the above equation, C is the right Cauchy-Green strain tensor, and C̅ denotes a modified version of C, $\overline{\mathit{C}}=\overline{{\mathit{F}}^T}\overline{\mathit{F}}$ with F̅ = J^−1/3F, where F is the deformation gradient, and J = det(F). The volumetric part, Ψ_vol(J), as given in (ABAQUS, 2013) is

$${\Psi }_{\mathit{\text{vol}}}(J)=\frac{1}{D}(\frac{J^2-1}{2}-\text{ln }J)$$ (2)

Where $\frac{1}{D}$ is analogous to the bulk modulus of the material.

Fig.1.

Arterial tube with helicoidal arrangement of two families of fibers in cylindrical and rectangular coordinate systems. The two direction vectors a₀₁ and a₀₂ are tangent to the fiber directions and 2γ is the angle between a₀₁ and a₀₂.

The potential Ψ̅(C̅, H₁, H₂) can be represented by a superposition of an isochoric potential Ψ̅_g(C̅) for the non-collagenous ground-matrix (indicated by subscript ‘g’), which accounts for the material behavior with no fibers, and two transversely isochoric potentials Ψ̅_f1 and Ψ̅_f2, which represent the two families of collagen fibers (with subscript ‘f’), respectively. Hence, the free-energy function Ψ̅ is expressed as

$$\overline{\Psi }(\overline{\mathit{C}},{\mathit{H}}_1,{\mathit{H}}_2)={\overline{\Psi }}_g(\overline{\mathit{C}})+[{\overline{\Psi }}_{f1}(\overline{\mathit{C}},{\mathit{H}}_1({\mathit{a}}_{01},\mathrm{\kappa }))+{\overline{\Psi }}_{f2}(\overline{\mathit{C}},{\mathit{H}}_2({\mathit{a}}_{02},\mathrm{\kappa }))]$$ (3)

In the above, H₁, H₂ are two structure tensors depending on the direction vectors a₀₁ and a₀₂

$${\mathit{H}}_1({\mathit{a}}_{01},\mathrm{\kappa })=\mathrm{\kappa }\mathit{I}+(1-3\mathrm{\kappa })({\mathit{a}}_{01}\otimes {\mathit{a}}_{01})$$ (4)

$${\mathit{H}}_2({\mathit{a}}_{02},\mathrm{\kappa })=\mathrm{\kappa }\mathit{I}+(1-3\mathrm{\kappa })({\mathit{a}}_{02}\otimes {\mathit{a}}_{02})$$ (5)

where I is the identity tensor; κ is the dispersion parameter, which characterizes the dispersion of the two families of fibers along the two mean distributed directions, and 0 ≤ κ ≤ 1/3; the collagen fibers of one family of fibers are parallel to each other when κ = 0, whereas the fibers distribute isotropically when κ = 1/3. The two vectors a₀₁ and a₀₂ have the following matrix forms in a rectangular coordinate system (as shown in Fig.1):

$$[{\mathit{a}}_{01}]=\left[\begin{array}{c}\hfill \mathit{\text{cos}}\gamma \hfill \\ \hfill \mathit{\text{sin}}\gamma \hfill \\ \hfill 0\hfill \end{array}\right],[{\mathit{a}}_{02}]=\left[\begin{array}{c}\hfill \mathit{\text{cos}}\gamma \hfill \\ \hfill -\mathit{\text{sin}}\gamma \hfill \\ \hfill 0\hfill \end{array}\right]$$ (6)

where γ represents the angle between the mean fiber orientation of one family of fibers and the circumferential direction of the artery, as shown in Fig.1.

An incompressible isotropic Neo-Hookean model has been used to denote the response of the non-collagenous ground-matrix. Thus,

$${\overline{\Psi }}_g(\overline{\mathit{C}})=\frac{\mu }{2}({Ī}_1-3)$$ (7)

In the above, Ī₁ = tr(C̅) denotes the first invariant of C̅, and μ is the neo-Hookean parameter, which characterizes the shear modulus of the material without fibers. The mechanical behavior of the two families of collagen fibers is represented by the following transversely isotropic free-energy functions

$${\overline{\Psi }}_{f1}(\overline{\mathit{C}},{\mathit{H}}_1({\mathit{a}}_{01},\kappa ))=\frac{k_1}{2k_2}[e^{k_2{[\text{tr}({\mathit{H}}_1\overline{\mathit{C}})-1]}^2}-1]$$ (8)

$${\overline{\Psi }}_{f2}(\overline{\mathit{C}},{\mathit{H}}_2({\mathit{a}}_{02},\kappa ))=\frac{k_1}{2k_2}[e^{k_2{[\text{tr}({\mathit{H}}_2\overline{\mathit{C}})-1]}^2}-1]$$ (9)

$$\text{tr}({\mathit{H}}_1\overline{\mathit{C}})=\kappa {Ī}_1+(1-3\kappa ){Ī}_{41};\text{ tr}({\mathit{H}}_2\overline{\mathit{C}})=\kappa {Ī}_1+(1-3\kappa ){Ī}_{42}$$ (10)

where Ī₄₁ = a₀₁ · C̅a₀₁ and Ī₄₂ = a₀₂ · C̅a₀₂ are tensor invariants equal to the square of the stretch in the directions of a₀₁ and a₀₂, respectively. Finally, according to relations (7), (8) and (9), we obtain

$$\overline{\Psi }(\overline{\mathit{C}},{\mathit{H}}_1,{\mathit{H}}_2)=\frac{\mu }{2}({Ī}_1-3)+\frac{k_1}{2k_2}[e^{k_2{[\kappa {Ī}_1+(1-3\kappa ){Ī}_{41}-1]}^2}-1]+\frac{k_1}{2k_2}[e^{k_2{[\kappa {Ī}_1+(1-3\kappa ){Ī}_{42}-1]}^2}-1]$$ (11)

Note that constitutive parameter k₁ is related to the relative stiffness of the fibers, which is determined from mechanical tests of arterial tissues; and k₂ is a dimensionless stiffness parameter.

2.1.2 Stress tensors

To prepare for the introduction of a viscoelastic anisotropic material model by extending the HGO model with the addition of a viscoelastic component, in the following the superscript “∞” will be used to signify stress quantities derived from the HGO model. In particular, the second Piola-Kirchhoff stress can be derived from the Clausius-Planck inequality and given by:

$${\mathit{S}}^{\infty }={\mathit{S}}_{\mathit{\text{vol}}}^{\infty }+{\mathit{S}}_{\mathit{\text{iso}}}^{\infty }$$ (12)

$${\mathit{S}}^{\infty }=2\frac{\partial \Psi (\mathit{C},{\mathit{H}}_1,{\mathit{H}}_2)}{\partial \mathit{C}},{\mathit{S}}_{\mathit{\text{vol}}}^{\infty }=2\frac{\partial {\Psi }_{\mathit{\text{vol}}}(J)}{\partial \mathit{C}},{\mathit{S}}_{\mathit{\text{iso}}}^{\infty }=2\frac{\partial \overline{\Psi }(\overline{\mathit{C}},{\mathit{H}}_1,{\mathit{H}}_2)}{\partial \mathit{C}}$$ (13)

The partial derivative of local volume ratio J and the modified right Cauchy-Green tensor C̅ to C are obtained by using the chain rule:

$$\frac{\partial J}{\partial \mathit{C}}=\frac{1}{2}J{\mathit{C}}^{-1},\hspace{1em}\frac{\partial \overline{\mathit{C}}}{\partial \mathit{C}}=J^{-2/3}(𝕀-\frac{1}{3}\mathit{C}\otimes {\mathit{C}}^{-1})$$ (14)

In the above, 𝕀 is the fourth order identity tensor, which has the form below in indicial notation (Holzapfel, 2000a)

$${(𝕀)}_{\mathrm{I}\mathrm{J}\mathrm{K}\mathrm{L}}=\frac{{\delta }_{IK}{\delta }_{JL}+{\delta }_{IL}{\delta }_{JK}}{2}$$ (15)

where δ_IK is the Kronecker delta.

With the associated property in the first equation in (14), the volumetric part of the second Piola-Kirchhoff stress has the form:

$${\mathit{S}}_{\mathit{\text{vol}}}^{\infty }=2\frac{\partial {\Psi }_{\mathit{\text{vol}}}(J)}{\partial \mathit{C}}=pJ{\mathit{C}}^{-1}$$ (16)

Where p is the hydrostatic pressure (Holzapfel, 2000b)

$$p=\frac{d{\Psi }_{\mathit{\text{vol}}}(J)}{dJ}=\frac{1}{D}(J-\frac{1}{J})$$ (17)

According to the second equation in (14), the isochoric part of the ground matrix of the arterial material is expressed as:

$${\mathit{S}}_g^{\infty }=2\frac{\partial {\overline{\Psi }}_g(\overline{\mathit{C}})}{\partial \mathit{C}}=J^{-2/3}\mathbb{P}:\mathrm{\mu }\mathit{I}$$ (18)

where ℙ is the projection tensor which has the form:

$$\mathbb{P}=𝕀-\frac{1}{3}{\mathit{C}}^{-1}\otimes \mathit{C}$$ (19)

With the associated property in the second equation in (14), the isochoric part used to describe the behavior of the two families of fibers is given by

$${\mathit{S}}_{fi}^{\infty }=2\frac{\partial {\overline{\Psi }}_{fi}}{\partial \mathit{C}}=J^{-2/3}\mathbb{P}:2k_1{e}^{{k_2{Ē}_i}^2}{Ē}_i{\mathit{H}}_i$$ (20)

where E̅_i (i = 1, 2) are the structure strain invariants and h̅_i (i = 1, 2) are the modified structure tensors which can be expressed by

$${Ē}_i=\text{tr}{\overline{\mathit{h}}}_i-1$$ (21)

$${\overline{\mathit{h}}}_i=\kappa \overline{\mathit{b}}+(1-3\kappa )({\mathit{ā}}_i\otimes {\mathit{ā}}_i)$$ (22)

where b̅ denotes the modified left Cauchy-Green strain tensor, $\overline{\mathit{b}}=\overline{\mathit{F}}\overline{{\mathit{F}}^T}$; ā_i = F̅a_0i (i = 1, 2) represents the push-forward of a_0i through tensor F̅.

Considering the relations (16), (18) and (20), the second Piola-Kirchhoff stress can be written as (Holzapfel, 2000a):

$${\mathit{S}}^{\infty }={\mathit{S}}_{\mathit{\text{vol}}}^{\infty }+{\mathit{S}}_{\mathit{\text{iso}}}^{\infty }={\mathit{S}}_{\mathit{\text{vol}}}^{\infty }+{\mathit{S}}_g^{\infty }+{\sum }_{i=1}^2{\mathit{S}}_{fi}^{\infty }=pJ{\mathit{C}}^{-1}+J^{-2/3}\mathbb{P}:\mathrm{\mu }\mathit{I}+{\sum }_{i=1}^2[J^{-2/3}\mathbb{P}:(2{\mathrm{k}}_1{\mathrm{e}}^{{{\mathrm{k}}_2{Ē}_i}^2}{Ē}_i{\mathit{H}}_i\left)\right]$$ (23)

2.1.3 Elasticity tensors

It is noted that the derivation of the elasticity tensors for the hyperelastic constitutive law of the HGO model is important for its implementation in the general-purpose finite element code ABAQUS (ABAQUS, 2013) via its user subroutine option. The closed-form elasticity tensor ℂ are defined through $ℂ=2\frac{\partial {\mathit{S}}^{\infty }}{\partial \mathit{C}}$, which can be determined by following the process described in (Holzapfel, 2000a), and is denoted in the decoupled form below:

$${ℂ}^{\infty }={ℂ}_{\mathit{\text{vol}}}^{\infty }+{ℂ}_{\mathit{\text{iso}}}^{\infty }$$ (24)

$${ℂ}_{\mathit{\text{iso}}}^{\infty }={\overline{ℂ}}_g^{\infty }+{\overline{ℂ}}_f^{\infty }$$ (25)

In the current study, the volumetric part ${ℂ}_{\mathit{\text{vol}}}^{\infty }$ and the isochoric part ${ℂ}_{\mathit{\text{iso}}}^{\infty }$ of the elasticity tensor (the tangent modulus tensor) are obtained using the approximate expressions (A.6) described in Appendix A.

2.1.4 Viscoelastic anisotropic (VA) model

In the current study, a Viscoelastic Anisotropic (VA) model for arterial materials is extended from the HGO model (Gasser et al., 2006) by introducing a viscoelastic component into the HGO model. This is done by employing a viscoelasticity formulation developed by Holzapfel (Holzapfel, 2000a). According to this formulation, a VA model can be built upon the HGO model by adding a strain-energy function term in Eq. (1). This additional term represents the dissipative potential responsible for the viscoelastic contribution. Based on this formulation, the second Piola-Kirchhoff stress tensor of the AV model S_n+1 at time t_n+1 can be written as:

$${\mathit{S}}_{n+1}={({\mathit{S}}_{\mathit{\text{vol}}}^{\infty }+{\mathit{S}}_{\mathit{\text{iso}}}^{\infty }+{\sum }_{\alpha =1}^m{\mathit{Q}}_{\alpha })}_{n+1}$$ (26)

Where the superscript “∞” denotes the equilibrium condition when the time approaches infinity. The first and second terms with the superscript “∞” in Eq. (26) are contributions from the HGO model (see Eq. (12)), and the third term in Eq. (26) describes the viscoelastic contribution to the stress state.

The non-equilibrium stress tensor Q_{α n+1} at time t_n+1 is expressed as

$${\mathit{Q}}_{\alpha n+1}={\mathit{\mathscr{H}}}_{\alpha n}+{\beta }_{\alpha }\mathit{\text{ exp }}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }}){\left({\mathit{S}}_{\mathit{\text{iso}}}^{\infty }\right)}_{n+1}$$ (27)

where the history term is defined as:

$${\mathit{\mathscr{H}}}_{\alpha n}=\mathit{\text{exp }}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }})\left[\text{exp }\right(-\frac{\mathrm{\Delta }t}{2T_{\alpha }}){\mathit{Q}}_{\alpha n}-{\beta }_{\alpha }{\left({\mathit{S}}_{\mathit{\text{iso}}}^{\infty }\right)}_n]$$ (28)

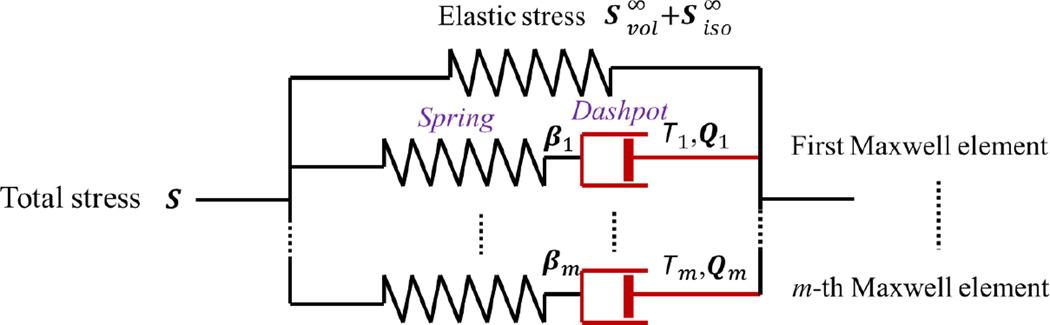
In the above equations, Δt is the time increment from time t_n to t_n+1; T_α (α = 1, …, m) is the relaxation time β_α and is a non-dimensional parameter. The viscoelastic parameters T_α and β_α (α = 1, …, m) correspond to the parameters in a generalized Maxwell model for one-dimensional viscoelasticity (Rajesh, 2000) with m Maxwell elements (see Fig. 2).

Fig. 2.

Schematic model of a viscoelastic material (Rajesh, 2000).

The corresponding viscous part (ℂ_vis)_n+1 of the elasticity tensor at time t_n+1 is

$${({ℂ}_{\mathit{\text{vis}}})}_{n+1}={({ℂ}_{\mathit{\text{iso}}}^{\infty })}_{n+1}{\sum }_{\alpha =1}^m{\beta }_{\alpha }\mathit{\text{ exp }}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }})$$ (29)

And the total elasticity tensor at time t_n+1 is

$${(ℂ)}_{n+1}={[{ℂ}_{\mathit{\text{vol}}}^{\infty }+\{1+{\sum }_{\alpha =1}^m{\beta }_{\alpha }\mathit{\text{ exp }}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }})\left\}{ℂ}_{\mathit{\text{iso}}}^{\infty }\right]}_{n+1}$$ (30)

Table 1 below provides a concise summary of the procedure and associated quantities involved in the VA model for implementation in ABAQUS via a user material subroutine.

Table 1.

Summary of the procedure for creating an efficient user material subroutine implemented in ABAQUS

The deformation gradient of solid elements is provided at the beginning of each increment, F

A unimodular distortional part of F, F̄ = J−1/3F, J = detF

Modified counterparts of Cauchy-Green tensors b, b̄ = F̄F̄T

Structure tensors$${\mathit{H}}_i=\kappa \mathit{I}+(1-3\kappa )({\mathit{a}}_{0i}\otimes {\mathit{a}}_{0i})$$ $${\overline{\mathit{h}}}_i=\kappa \overline{\mathit{b}}+(1-3\kappa )({\mathit{ā}}_i\otimes {\mathit{ā}}_i),{\mathit{ā}}_i=\overline{\mathit{F}}{\mathit{a}}_{0i}$$

Structure strain invariants $${Ē}_i=\text{tr}{\overline{\mathit{h}}}_i-1=\text{tr}\left(\kappa \overline{\mathit{b}}\right)+(1-3\kappa )\text{tr}({\mathit{ā}}_i\otimes {\mathit{ā}}_i)-1$$

Stress tensor $${\mathit{S}}_g^{\infty }=J^{-2/3}\mathrm{\mathbb{P}}:\mu \mathit{I},\hspace{1em}{\mathit{S}}_{fi}^{\infty }=J^{-2/3}\mathbb{P}:2k_1{e}^{k_2{Ē}_i^2}{Ē}_i{\mathit{H}}_i,\hspace{1em}{\mathit{S}}_{\mathit{\text{vol}}}^{\infty }=pJ{\mathit{C}}^{-1}$$ $${\mathit{S}}_{\mathit{\text{iso}}}^{\infty }={\mathit{S}}_g^{\infty }+{\mathrm{\Sigma }}_{i=1}^2{\mathit{S}}_{fi}^{\infty }$$ $$\mathbb{P}=𝕀-\frac{1}{3}{\mathit{C}}^{-1}\otimes \mathit{C}$$

The second Piola-Kirchhoff stress tensor Sn+1 at time tn+1 $${\mathit{S}}_{n+1}={({\mathit{S}}_{\mathit{\text{vol}}}^{\infty }+{\mathit{S}}_{\mathit{\text{iso}}}^{\infty }+\sum _{\alpha =1}^m{\mathit{Q}}_{\alpha })}_{n+1}$$

The Cauchy stress tensor σn+1 at time tn+1 $${\mathit{\sigma }}_{n+1}={(J^{-1}\mathit{F}\mathit{S}{\mathit{F}}^T)}_{n+1}$$

The current non-equilibrium stress tensor Q α n+1 at time tn+1 $${\mathit{Q}}_{\alpha n+1}={𝓗}_{\alpha n}+{\beta }_{\alpha }\mathit{\text{ exp}}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }}){({\mathit{S}}_{\mathit{\text{iso}}}^{\infty })}_{n+1}$$ where the history term is defined as: $${𝓗}_{\alpha n}=\mathit{\text{exp}}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }})\left[\mathit{\text{exp}}\right(-\frac{\mathrm{\Delta }t}{2T_{\alpha }}){\mathit{Q}}_{\alpha n}-{\beta }_{\alpha }{({\mathit{S}}_{\mathit{\text{iso}}}^{\infty })}_n]$$

The viscous part (ℂvis)n+1 of the elasticity tensor at time tn+1is $${({ℂ}_{\mathit{\text{vis}}})}_{n+1}={({ℂ}_{\mathit{\text{iso}}}^{\infty })}_{n+1}\sum _{\alpha =1}^m{\beta }_{\alpha }\mathit{\text{ exp}}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }})$$

The elastic tensor at time tn+1is $${(ℂ)}_{n+1}={[{ℂ}_{\mathit{\text{vol}}}^{\infty }+\{1+\sum _{\alpha =1}^m{\beta }_{\alpha }\mathit{\text{ exp}}(-\frac{\mathrm{\Delta }t}{2T_{\alpha }})\left\}{ℂ}_{\mathit{\text{iso}}}^{\infty }\right]}_{n+1}$$

In the current study, finite element simulation results show that it is sufficient to use only one viscoelastic term (i.e. m=1 in Eq. (26) and subsequent equations) in the VA model to capture the essential hysteresis behavior observed in the fibrous cap delamination experiments (additional terms do not improve the results significantly). Thus, the only viscoelastic parameters involved in the simulations described subsequently are T₁ and β₁.

The nonlinear static analysis option in ABAQUS/Standard (ABAQUS, 2013) with implicit time integration was employed to carry out the fibrous cap delamination simulations. The tangential modulus tensor that is implemented in this study in the ABAQUS user UMAT subroutine can be found in Appendix A.

2.2 Interfacial Cohesive Zone Model

An irreversible exponential cohesive zone model (CZM) is adopted to represent the behavior of the delamination interface. In this CZM, the free energy potential (φ) per unit (undeformed) cohesive surface is expressed as (Ortiz and Pandolfi, 1999; Roy and Dodds, 2001; Siegmund and Needleman, 1997):

$$\phi =e{\sigma }_c{\delta }_c[1-(1+\frac{\delta }{{\delta }_c})\mathit{\text{ exp}}(-\frac{\delta }{{\delta }_c})]$$ (31)

where e = exp(1) ≈ 2.71828 and σ_c denotes the cohesive strength of the material; δ_c is the maximum effective displacement t = σ_c at and δ is the displacement jump across the cohesive surfaces. Considering the loading conditions, the cohesive traction is given by:

$$t=\frac{\partial \phi }{\partial \delta }=e{\sigma }_c\frac{\delta }{{\delta }_c}\mathit{\text{exp}}(-\frac{\delta }{{\delta }_c})$$ (32)

For the unloading process, the traction follows

$$t=\left(\frac{t_{\mathit{\text{max}}}}{{\delta }_{\mathit{\text{max}}}}\right)\delta \text{ if }\delta <{\delta }_{\mathit{\text{max}}}\text{ or }\dot{\delta }<0$$

$$t=K\delta \text{ if }\delta <0$$ (33)

where K is the coefficient of resistance against the penetration of the delaminated surfaces. The effective displacement jump is expressed as:

$$\delta =\sqrt{{\lambda }^2{\delta }_s^2+{\delta }_n^2}$$ (34)

where δ_n is the normal displacement jump, and δ_s is the sliding displacement jump across the cohesive surfaces, given by

$${\delta }_s=\sqrt{{\delta }_{s1}^2+{\delta }_{s2}^2}$$ (35)

where δ_s1 and δ_s2 denote the in-plane and out-of-plane components of the sliding displacement (δ_s) across the cohesive surfaces, and λ is a scalar parameter introduced to assign different weights to the opening and sliding displacement jumps.

The critical energy release rate of the cohesive surface follows the form:

$$G_c=e{\sigma }_c{\delta }_c$$ (36)

For the purposes of expressing the irreversible response, a damage parameter has been introduced to represent the damage of the cohesive surfaces under loading and unloading conditions:

$$d=\frac{\phi ({\delta }_{\mathit{\text{max}}})}{G_c}$$ (37)

The damage parameter d ranges from 0 to 1, where 0 corresponds to the state of no damage and 1 to the fully damaged state in which the cohesive surfaces are fully separated. Fig. 3 illustrates the loading and unloading processes of the exponential cohesive traction-separation law, in which damage will initiate and accumulate when the effective displacement jump δ becomes larger than zero. For unloading at point A or B (as shown in Fig. 3) the traction-separation relation will follow line AO or BO, because permanent has damage occurs at point A and B.

Fig. 3.

Normalized traction vs. effective displacement jump curve in the irreversible exponential cohesive zone model.

The exponential CZM is implemented in the current study through a user UEL subroutine in ABAQUS (ABAQUS, 2013).

2.3 Experimental Details

2.3.1 Human fibrous cap delamination experiments

The current study is focused on numerical modeling and simulation of fibrous cap delamination experiments performed on human carotid artery plaque specimens obtained from endarterectomies. The experiments are similar to the mouse plaque and human media-intima delamination experiments reported in the literature (Wang et al., 2013; Wang et al., 2014; Wang et al., 2011).

Six fresh carotid endarterectomy samples were obtained at the time of surgery from six patients, and one specimen from each sample was successfully prepared, leading to a total of six fibrous cap (FC) delamination experiments.

The fresh carotid endarterectomy samples were sliced transversely into segments 5–7 mm in width. Each ring-shaped segment was opened with fine scissors on the side opposite the plaque.

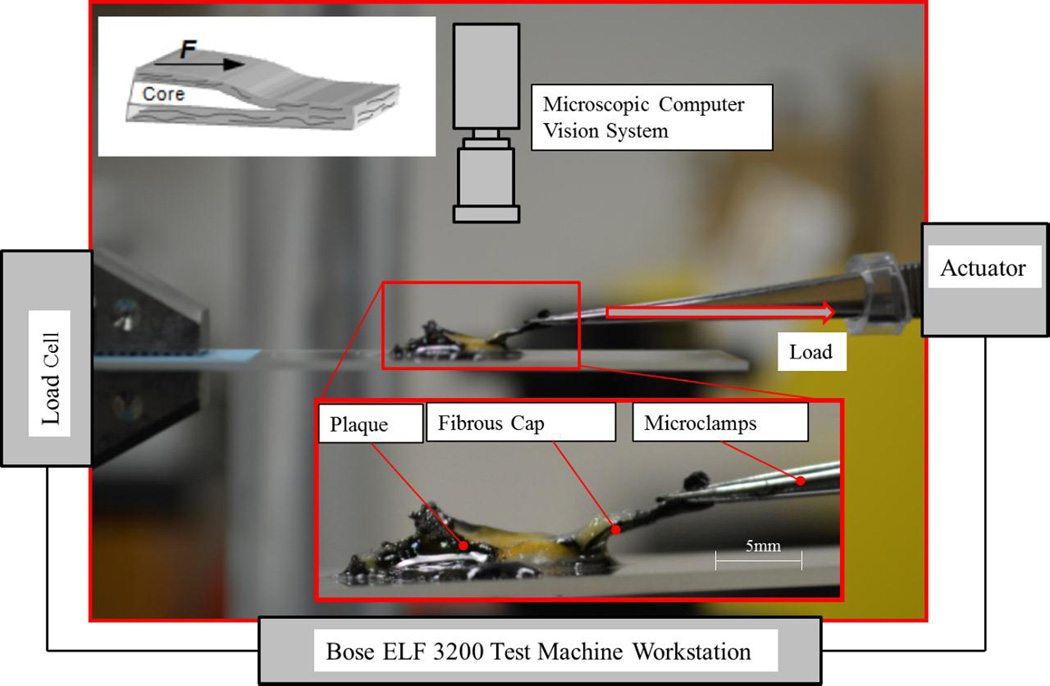
At the start of an experiment, a longitudinal cut was made at one plaque shoulder. At this edge, a scalpel was used to carefully introduce a small initial delamination between the fibrous cap and the underlying plaque tissue. A micro-clamp was used to grip the free edge of the cap, as shown in Fig. 4.The medial face of the carotid artery was glued with DermaBond to a glass plate connected to the load cell of a Bose ELF 3200 test system for load data recording. The delaminated tissue tab on the lateral edge of the fibrous cap was gripped by a pair of micro-clamps connected to the Bose ELF 3200 actuator, which controls the sequential loading-delamination-unloading cycles. For each experiment, a load vs. load-point displacement curve with multiple loading-delamination-unloading cycles was obtained. The delamination process was recorded by a microscopic computer vision system which was placed at a fixed distance above the specimen. After the experiment, the specimen was prepared for histological analysis, which showed that fibrous cap delamination took place between the fibrous cap and the underlying plaque tissue, as shown in Fig. 5.

Fig.4.

Fibrous cap delamination experiments: experimental setup (scale bar=5 mm).

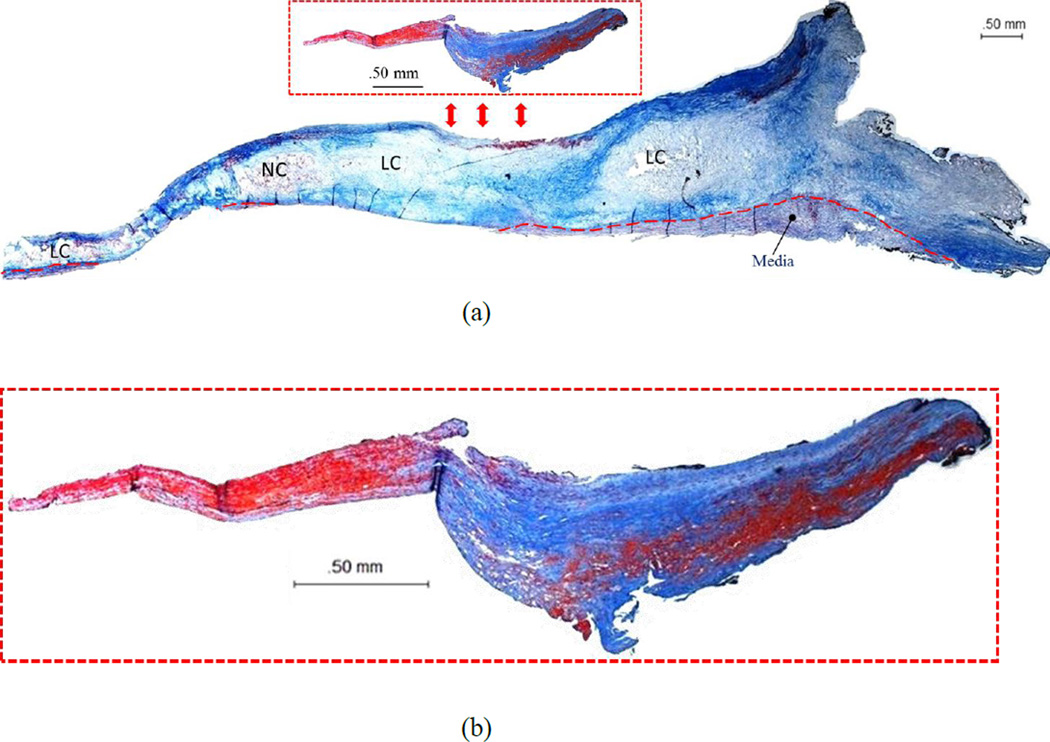
Fig. 5.

Histological images of the fibrous cap delamination surfaces after Masson’s Trichrome staining: (a) a longitudinal section of a completely delaminated specimen, including a partial media and the tissues of atherosclerotic plaque and fibrous cap; (b) a fibrous cap delaminated from the underlying plaque tissue. In these images, the collagen is stained blue, the nuclei are stained purple-black, and the smooth muscle cells (SMCs) are stained red. (Lipid rich core and necrotic core are identified by LC and NC labels, respectively)

2.3.2 Histological images

Two histological images of paraffin sections of the human fibrous cap delamination specimen stained with Masson’s Trichrome are shown in Fig. 5. The double-headed arrows show the delamination surface (Fig. 5a). It is noted that part of the media layer remained on the glass plate after the fibrous cap was peeled off because of the adhesion of the glue. The boundary of the remaining part of the media in the specimen is marked by red dotted lines, as shown in Fig. 5a.

According to Tong et al. (Tong et al., 2011), because the fibrous cap was delaminated along the circumferential direction where the tearing strength is lower than that along the axial direction, the delaminated surface appears smooth when the delamination occurs along the interface between the fibrous cap and the underlying plaque tissue.

2.4 Modeling and Simulation

Although six fibrous cap delamination experiments were performed, at the time of the experiments the focus was on the experimental determination of the critical strain energy release rate, not on the reconstruction of the specimen geometry. As a result, sufficient images of the specimen geometry were taken only for two of the six specimens. These two specimens are labeled samples FC1 and FC2 and are utilized in the modeling and simulation effort.

The geometric models of these two specimens were reconstructed from the images recorded at the start of the experiments. Since the geometry reconstruction procedure is the same for both samples, the specimen geometry model is described in detail below for sample FC1 only.

Further, since the subsequent modeling and simulation procedure is also the same for both samples, it is described in detail below also for sample FC1 only.

2.4.1 Finite Element Model

Through a Boolean operation, the shape of the specimen created according to an image of the side view (as shown in Fig. 6a) was merged with the shape created from an image of the top view (as shown in Fig. 6b). The delamination area was measured directly from the available experimental images recorded by the microscopic vision system during a delamination experiment. The area to be delaminated is marked in red in Fig. 6c. The resulting three-dimensional (3D) FE model based on the geometric model is shown in Fig. 6d (the edge portion (tab) of the initial delaminated fibrous cap away from the delamination front was not included in the FE model because it does not affect the stress state along the delamination front, and its exclusion improves computational efficiency).

Fig. 6.

Representative experimental images of the fibrous cap delamination specimen: (a) a front view of the specimen and the finite element (FE) model; (b) a top view of the specimen and the FE model; (c) the delamination area and the area for simulation predictions are marked by red color (the delamination direction is along the X axis); (d) the FE model based on the geometric model reconstructed from the images.

It is noted that the geometric model and the subsequent FE model are not perfect due to approximations and uncertainties inherent in the recorded images and from the shape reconstruction process. Thus, approximation errors in the geometric model are expected to affect the accuracy of the FE simulation results and their agreement with experimental measurements. The effect of geometry approximation was studied in an earlier paper on a related topic (Leng et al. 2015a) in which a sensitivity analysis was performed about the effects of geometric approximations on simulation predictions.

The FE mesh is generated using ABAQUS (ABAQUS, 2013). The media and plaque regions are meshed with 6,302 eight-node brick elements, C3D8H, while the cohesive interface is meshed with 255 zero thickness eight-node 3D user-defined elements which are placed along the delamination path starting from the initial delamination front to the end of the fibrous cap. The global size of the element for the media and plaque is 0.5 mm and the cohesive element size is 0.1 mm. The CZM can be implemented for simulating interfacial material separation events with a high computational efficiency when the delamination path is known in advance or pre-defined. In the current study, the delamination path was known from experimental observations and thus was pre-defined at the beginning of simulations.

2.4.2 Boundary Conditions

The human carotid artery plaque specimens were obtained from endarterectomies, which contain part of the media layer along with the fibrous cap and the underlying plaque tissue from the carotid artery. At the beginning of an experiment, the bottom media surface of the specimen was glued with DermaBond to a glass plate. Therefore, in the finite element model the boundary condition for the bottom surface of the specimen was taken to be that all nodes on the bottom surface were fixed so that they could not move in any direction.

The delaminated tissue tab on the lateral edge of the fibrous cap was gripped by a pair of microclamps which were translated with a certain displacement parallel to the glass plate, as shown in Fig. 4. Thus, in the finite element model, nodes at the lateral edge of the fibrous cap were given a displacement boundary condition in which the displacement parallel to the glass plate followed the experimentally recorded loading-delamination-unloading cycle values. The displacement loading rate in the experiments was 0.05 mm/s.

Except for the fixed bottom surface and the lateral edge of the fibrous cap where displacement loading was applied, all other surfaces of the finite element model were given a traction-free boundary condition.

2.4.3 Parameter Value Identification

The parameter values for the bulk arterial material models and for the CZM were obtained through a numerical identification procedure (Chen et al., 2013; Leng et al., 2015b) that matches simulation predictions of the overall load vs. load-point displacement curve with experimental measurements. Since the material models used for the simulation involved many parameters and only a limited number of experimental data were available, a fully automated inverse procedure (Chen et al., 2014) was not adopted (hence a manual procedure was used) and not all parameter values were determined from the numerical identification procedure. A subset of the material model parameter values were taken from the literature (or assigned simple values when literature data were not available) and were used as input for the identification procedure. The material model parameter values for the media were taken from the study by Cilla et al. (Cilla et al., 2012) (see Table 2); the value for the parameter D in eq. (2) was taken to be 10⁻⁴ (Holzapfel et al., 2002) (see Table 2); and the values for K and λ for the CZM were assigned assumed values (see Table 3) that were simple but meaningful.

Table 2.

HGO and VA material model parameter values

	μ (kPa)	D (kPa−1)	k1 (kPa)	k2	κ	γ (degree)	T1 (s)	β1
Media	1.4†	1E-4*	206.16†	58.55†	0.29†	28.35†	5.8§	10§
Plaque	49.45§	1E-4*	23.7§	2630§	0.226§	30§	2.06§	20§
Fibrous cap	21.89§	1E-4*	93.63§	7957§	0.226§	17.22§	-	-

^†from reference (Cilla et al., 2012);

^§from parameter value identification;

^*from reference (Holzapfel et al., 2002)

Table 3.

CZM parameter values

CZM parameters	Gc (N/mm)	σc (MPa)	K (N/mm3)	λ
Cycles 1–3 (group 1)	0.23Ξ	0.42§	10Θ	1Θ
Cycles 4–6 (group 2)	0.294Ξ	0.42§	10Θ	1Θ

^Ξfrom experimental measurement;

^§from parameter value identification;

^Θassumed for simplicity

The experimental load vs. load-point displacement curve for the first loading-delamination-unloading cycle and for the loading phase of the second loading-delamination-unloading cycle (shown in Fig. 8) were used as input data for the identification procedure to determine the remaining material model parameter values. Material model parameter values from the literature (e.g. the material model parameter values for the fibrous cap for human carotid arteries (Balzani et al., 2012; Kiousis et al., 2009) and for the plaque for human carotid arteries (Sommer and Holzapfel, 2012)) were also used as reference values. For CZM parameters, the ultimate tensile stress σ_c was acquired through matching simulation predictions with the experimental measurements using the delamination phase of the load-displacement curve for loading-delamination-unloading cycle #1, and the value for the critical energy release rate G_c was taken to be the mean measured value from the fibrous cap experiments averaged over three loading-delamination-unloading cycles for each delamination group (e.g. cycles 1 to 3 for group 1 and cycles 4 to 6 for group 2).

In the numerical identification process, the HGO and VA material model parameter values and CZM parameter values were considered “acceptable” when the root mean square error (Holzapfel et al., 2005; Zhou et al., 2015; Zhou et al., 2014) satisfies

$$\mathrm{E}=\frac{\sqrt{\frac{{\chi }^2}{N-M}}}{F_{\mathit{\text{avg}}}}<0.2,\text{ with }{\chi }^2={\sum }_{i=1}^N\left[{(F_{\mathit{\text{exp}}}-F_{\mathit{\text{sim}}})}_i^2\right]$$ (50)

where F_sim is the reaction force from simulations and F_exp is the experimentally measured force; F_avg is the sum of all experimentally measured forces for each data point divided by the number of data points; N is the number of data points on the load-displacement curve that were used in the parameter value identification procedure; and M is the number of parameters whose values were determined from the identification procedure.

A set of HGO and VA material model parameter values is shown in Table 2, which were obtained when the root mean square error defined in Eq. (50) was E = 0.152 with N=183 and M = 15.

A set of CZM parameter values is shown in Table 3 (this set is from the same error function in Eq. (50)). It is noted that, although simple values for K and λ were assumed, they are relevant and meaningful. The value of 10 N/mm³ for K is sufficiently large so that artificial compliance from the cohesive interface can be prevented (a different but sufficiently large value will not change the outcome of the simulation). In the absence of experimental data, the value of 1 for the mode mixity parameter λ implies the choice that Mode I and Mode II components have the same significance in the delamination process.

2.4.4 Mesh Convergence analysis

A mesh convergence study was performed in order to ensure that the finite element mesh is sufficiently refined to produce converged solutions.

Since mesh generation in this study was done by controlling the number of divisions along geometric lines, mesh refinements were done by doubling the number of divisions along the lines, which may lead to more or fewer elements than required for strict mesh refinement (in which each brick element is cut into eight elements and each cohesive element is divided into four elements), depending on the complexity of the geometry and the software used for the mesh refinement.

In the current study, Mesh 1 has 6,302 brick (C3D8H) elements and 255 interfacial cohesive elements, and 9,098 nodes. Mesh 2 is refined from mesh 1 so that the element size in mesh 2 is half of that in mesh 1 along x, y and z directions. Mesh 2 has 50,012 brick elements and 1,030 interfacial cohesive elements, and 60,605 nodes. During the mesh refinements, the cohesive element size is dictated by the bulk element size along the delamination path. Specifically, the cohesive element size is 0.1 mm and 0.05 mm, respectively, in the two meshes.

We observed that, from Mesh 1 to Mesh 2, there is little change in the predicted load-displacement curves (see Fig. 7b). The corresponding variation of the relative error (the percent difference between the predicted loads from Mesh 1 and Mesh 2) with displacement is shown in Fig. 7c. This relative error is greater than 5% only when the predicted reaction load has a small magnitude (below 0.05 N), in which case the large error is mostly due to division by a small value. The average relative percent error for all data points is 3.3%. Overall, Mesh 1 gives well converged predictions, and thus subsequent simulation results are derived from Mesh 1.

Fig. 7.

(a) Mesh 1 and Mesh 2 (a refinement of Mesh 1) of the 3D finite element model ; (b) the predicted load-displacement curves for three loading cycles using the two meshes; (c) relative percept error in the reaction load vs. displacement between Mesh 2 and Mesh 1 (M2/M1) for three loading cycles.

3. Results

3.1 Fibrous cap delamination test results

Fibrous cap (FC) delamination tests were performed on six specimens. Test results include the load-displacement curves for multiple loading-delamination-unloading cycles for each test, and the critical energy release rate values calculated from these curves.

Test results show that there is a large inter-plaque and inter-sample variability, although the trends in the load-displacement curves are similar. The values of the critical energy release rate G_c (see Table 4.) acquired from the delamination tests show a mean value of 0.254 N/mm and a large standard deviation of ±0.15 N/mm.

Table 4.

Critical energy release rate values from fibrous cap delamination tests

	Critical energy release rate Gc (N/mm)
Specimen	FC1	FC2	FC3	FC4	FC5	FC6
Cycles 1–3	0.23	0.24	0.695	0.132	0.217	0.229
Cycles 4–6	0.294	0.199	—	—	—	0.167
Cycles 7–9	—	—	—	—	—	0.133

Typical load-displacement curves from these tests are presented in the next section when simulation predictions are compared with experimental data for samples FC1 and FC2.

3.2 Prediction and Validation

In the previous section, a finite element model was developed for the fibrous cap delamination experiments and the parameter values for the bulk material models and for the CZM were identified. In this section, simulation predictions of the mechanical response of the specimen during the experiments are discussed. The focus is placed on the prediction of the load vs. load-point displacement curve since it allows for a direct comparison with experimental measurements, which can serve as a validation of the CZM based modeling/simulation approach for fibrous cap delamination events.

It is worth pointing out that, since the load-displacement curve for the first loading-delamination-unloading cycle and for the loading phase of the second loading-delamination-unloading cycle have been utilized in identifying the material parameter values, they will not be used to validate the simulation predictions. However, comparisons of the predicted and measured load-displacement curves for the first loading-delamination-unloading cycle and for the loading phase of the second loading-delamination-unloading cycle do provide useful information about the level of errors introduced in the geometry of the specimen and in determining the material parameter values, which serves as a good reference for assessing the level of agreement between simulation predictions and experimental measurements for subsequent loading-delamination-unloading cycles.

Simulation results are presented for two fibrous cap samples, FC1 and FC2. For sample FC1, simulation predictions of the load-displacement curve for cycles #1, #2 and #3 are shown in Fig. 8a and those for cycles #4, #5 and #6 are shown in Fig. 8c. For sample FC2, simulation predictions for sample FC2 for cycles #1, #2 and #3 are shown in Fig. 8e.

It is noted that, due to inter-sample variability (the test results and model parameter values are patient-specific), the material parameter values for sample FC1 cannot be transferred to sample FC2. As such, key material parameter values for sample FC2 are determined from the test results of FC2 according to the same procedure as the one used for FC1. The parameter values for FC2 that are different from those for FC1 are: γ = 58.35° (media), μ = 11.45 kPa (plaque), γ = 60° (plaque), T₁ = 9.06s (plaque), μ = 11.89 kPa (fibrous cap), and G_c = 0.24 N/mm (CZM). All remaining parameter values for FC2 are taken to be the same as those for FC1.

The relative error vs. displacement curves for the comparisons of simulation predictions with experimental measurements are shown in Figs. 8b, 8d and 8f. Relative percent errors for the loading and unloading phases are large (above 10%) when the magnitude of the load is small (0.145 N for FC1 and 0.285 N for FC2). Factors that may contribute to these large errors are discussed in Section 4. However, relative errors for the rest of the loading and unloading curves as well as for the delamination phases are below 10%. It can be seen that overall the simulation predictions match well with the experimental data. The unloading phase of cycle#1 and the loading phase of cycle #2 from FC1, which describe the first hysteresis loop between cycles #1 and #2, show good match between predictions and measurements. The agreement between predictions and measurements for the subsequent hysteresis loops is similar to that for the first loop.

The von Mises stress contours in the specimen when the loading was at three typical points during the 3rd loading-delamination-unloading cycle are shown in Fig. 9. The values of stress contours in the area near the delamination front shown in the zoomed-in views in Figs. 9(a), (b) and (c) are correlated with the loading levels in the load-displacement curve. Taking the loading level for Fig. 9(b) as an example, the highest stress is located behind the delamination front in the delaminated cap, which is consistent with the corresponding effective traction level as shown in Fig. 9d, where the maximum effective traction t = 0.42 MPa occurs behind the delamination front.

Fig. 9.

von Mises stress contours at three typical points during loading-delamination-unloading cycle #3: (a) at point 1 in the loading phase; (b) at point 2 in the delamination phase; (c) at point 3 in the unloading phase; (d) the effective traction contours in the cohesive elements at point 2; (e) the cohesive damage parameter contours in the cohesive elements at point 2.

It can be seen from Fig.9d that the interfacial cohesive elements are stretched and the effective traction contours in the cohesive elements enclosed by the black dotted line reveal the stiffening and softening portions of the interfacial separation process during delamination propagation, as shown more clearly in the zoomed-in view of the insert. In Fig. 9d, the initial crack tip represents the delamination front at the beginning of cycle #1, the delamination tip indicates the delamination front at the end of the delamination phase of cycle #3 (a point where the cohesive traction is zero and the cohesive damage parameter d = 1), and the cohesive zone tip shows the point where the traction equals the maximum value (t = 0.42 MPa). The cohesive elements are completely separated when the damage parameter d = 1(as shown in Fig. 9e) and also the effective traction t is approximately equal to zero (as shown in Fig. 9d). The traction-separation curve and the damage-separation curve are shown in the zoomed-in views in the inserts of Figs.9d and Fig.9e, respectively.

4. Discussion

There are two regions where the predictions have the largest differences from the measurements. One is when the load is small, and the other is during the delamination phase. The differences between the simulation predictions and experimental results may be due to several simplifications, approximations and uncertainties.

First, there are the approximations for the geometries of the delamination path and the specimen surfaces. The geometry of the diseased artery specimen is complex and many of the small features (e.g. the depressions on the uneven delaminated surface) were not modeled. The shape of the fibrous cap is not regular and has a zigzag boundary along the circumferential direction.

Second, the local components of the atherosclerotic plaque (e.g. the lipid core and calcified tissue) were assigned the same material properties due to the lack of sufficient experimental data. The lipid core and the calcified tissues are distributed randomly in the plaque with different volumes (as shown in Fig. 5). The heterogeneous distribution of strong materials (e.g., calcified tissue and collagen fibers) and weak materials (e.g., lipid core) is expected to lead to material property variations throughout the specimen, which can largely influence the local mechanical response and hence alter the load-displacement curve.

Third, to reduce experimental data noise, the critical energy release rate data for cycles #1, #2 and #3 were averaged and the resulting mean value was set to be the input value for the critical energy release rate in the simulations for cycles #1, #2 and #3. The same was done for cycles #4, #5 and #6. In reality, the critical energy release rate is observed experimentally to vary along the delamination path and from cycle to cycle, and the measured values oscillate in a certain range (Tong et al., 2011; Wang et al., 2014). This gross approximation is expected to affect agreement between predicted and measured load-displacement curve during the delamination phase of a loading cycle.

Fourth, the material parameter values used for the HGO and VA models may not be the best values to describe the complex bulk mechanical response. There were many unknown parameter values involved and the available experimental data were limited, and compromises were made in the numerical identification procedure for determining the parameter values. As a result, the parameter values determined through the identification process mentioned in section 2.4.3 may not be the only choice or the best choice for the specimen.

Furthermore, the differences between predictions and measurements seen in the first hysteresis loop of the load-displacement curve, which was used for parameter value identification, suggest that features not captured in the current study (e.g. local material variations due to heterogeneous tissue distribution) may be an important factor that affects the accuracy of the results when the viscoelastic material model is implemented.

Considering the various simplifications, approximations and uncertainties involved in the simulations, which are unavoidable in this study due to the lack of available data, it can be said that the simulation predictions can capture, both qualitatively and quantitatively, the main features of the load-displacement curve, and that the overall good agreement between predictions and measurements provides a meaningful validation of the CZM based modeling and simulation approach for fibrous cap delamination events.

5. Conclusions

In the current study a cohesive zone model-based computational approach for modeling and simulating fibrous cap delamination events was developed and applied successfully to fibrous cap delamination experiments performed on human carotid artery endarterectomy specimens. A 3D finite element model was built based on a 3D specimen geometry reconstructed from recorded images of the specimen.

The bulk material behavior of the arterial layers (including the fibrous cap and the underlying plaque tissue) was represented by the HGO anisotropic hyperelastic constitutive model and a viscoelastic extension of the model proposed in the current study that allows for capture of the hysteresis behavior exhibited in the load-displacement curve over loading-delamination-unloading cycles. The behavior of the interface between the fibrous cap and the underlying plaque was characterized by an exponential cohesive zone model, which governs the traction-separation relationship and the interfacial failure process.

A numerical procedure for identifying material model parameter values was developed, in which measured load and load-point displacement data for the first loading-delamination-unloading cycle and for the loading phase of the second loading-delamination-unloading cycle were used as input to an inverse analysis. The identified parameter values were then applied in the simulations to predict the load-displacement response for the subsequent loading-delamination-unloading cycles of the fibrous cap delamination experiments.

Comparisons of simulation predictions of the load-displacement curve with experimental measurements reveal that the simulation predictions were able to capture the essential features of the load-displacement curve from the fibrous cap delamination experiments and show reasonably good quantitative agreement with experimental measurements. The results of this study provide a validation for the proposed CZM based approach for modeling and simulating fibrous cap delamination events.

Appendix A

In the simulations of the fibrous cap delamination experiments, the finite element equations are nonlinear and are solved using the Newton-Raphson iteration procedure. The simulations were carried out using the general-purpose code ABAQUS which allows for the implementation of the viscoelastic anisotropic material model (see Section 2.1) via a user UMAT subroutine. This appendix provides the expressions for an approximation of the tangent modulus tensor (Sun et al., 2008) that is needed in the user subroutine. Some relevant concepts involved below have been defined in Section 2.1.

The Jaumann rate can be expressed as

$$\begin{array}{c}\hfill \mathbf{\nabla }\hfill \\ \hfill \mathit{\tau }\hfill \end{array}=\dot{\mathit{\tau }}-\mathit{W}\mathit{\tau }-\mathit{\tau }{\mathit{W}}^T={ℂ}^{\mathit{\tau }J}:\mathit{D}$$ (A.1)

where ℂ^τJ is the tangent modulus tensor for the Jaumann rate of the Kirchhoff stress tensor τ = FS^∞F^T; W and D are the spin tensor and rate of deformation gradient tensor, which constitute the antisymmetric and symmetric parts of the spatial velocity gradient tensor, respectively (Sun et al., 2008).

The linearized incremental form of the Jaumann rate is given by

$$\mathrm{\Delta }\mathit{\tau }-\mathrm{\Delta }\mathit{W}\mathit{\tau }-\mathit{\tau }\mathrm{\Delta }{\mathit{W}}^T={ℂ}^{\tau J}:\mathrm{\Delta }\mathit{D}$$ (A.2)

where

$$\mathrm{\Delta }\mathit{W}=\frac{1}{2}(\mathrm{\Delta }\mathit{F}{\mathit{F}}^{-1}-{(\mathrm{\Delta }\mathit{F}{\mathit{F}}^{-1})}^T)$$ (A.3)

$$\mathrm{\Delta }\mathit{D}=\frac{1}{2}(\mathrm{\Delta }\mathit{F}{\mathit{F}}^{-1}+{(\mathrm{\Delta }\mathit{F}{\mathit{F}}^{-1})}^T)$$

A perturbation of the deformation gradient tensor can be written as

$$\mathrm{\Delta }{\mathit{F}}^{ij}=\frac{\epsilon }{2}({\mathit{e}}_i\otimes {\mathit{e}}_j\mathit{F}+{\mathit{e}}_j\otimes {\mathit{e}}_i\mathit{F})$$ (A.4)

where ε is a small perturbation parameter, and e_i, i = 1,2,3 represents the unit vectors in the spatial description.

An approximation of the tangential modulus tensor is acquired through the application of symmetry properties:

$${ℂ}^{\mathit{\tau }{J}^{ij}}\approx \frac{1}{\epsilon }[\mathit{\tau }({\hat{\mathit{F}}}^{ij})-\mathit{\tau }(\mathit{F})]$$ (A.5)

where F̂^ij = F + ΔF^ij is the perturbed deformation gradient tensor.

The tangential modulus tensor utilized in the ABAQUS user subroutine has the expression

$${ℂ}^{m{J}^{ij}}\approx \frac{1}{J\epsilon }[\mathit{\tau }({\hat{\mathit{F}}}^{ij})-\mathit{\tau }(\mathit{F})]$$ (A.6)

Detailed derivations can be found in reference (Sun et al., 2008).