Performance of protein-structure predictions with the physics-based UNRES force field in CASP11

Abstract

Summary: Participating as the Cornell-Gdansk group, we have used our physics-based coarse-grained UNited RESidue (UNRES) force field to predict protein structure in the 11th Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction (CASP11). Our methodology involved extensive multiplexed replica exchange simulations of the target proteins with a recently improved UNRES force field to provide better reproductions of the local structures of polypeptide chains. All simulations were started from fully extended polypeptide chains, and no external information was included in the simulation process except for weak restraints on secondary structure to enable us to finish each prediction within the allowed 3-week time window. Because of simplified UNRES representation of polypeptide chains, use of enhanced sampling methods, code optimization and parallelization and sufficient computational resources, we were able to treat, for the first time, all 55 human prediction targets with sizes from 44 to 595 amino acid residues, the average size being 251 residues. Complete structures of six single-domain proteins were predicted accurately, with the highest accuracy being attained for the T0769, for which the CαRMSD was 3.8 Å for 97 residues of the experimental structure. Correct structures were also predicted for 13 domains of multi-domain proteins with accuracy comparable to that of the best template-based modeling methods. With further improvements of the UNRES force field that are now underway, our physics-based coarse-grained approach to protein-structure prediction will eventually reach global prediction capacity and, consequently, reliability in simulating protein structure and dynamics that are important in biochemical processes.

Availability and Implementation: Freely available on the web at http://www.unres.pl/.

Contact: has5@cornell.edu

1 Introduction

Template-based and other knowledge-based methods are currently used routinely for the modeling of unknown protein structures. However, despite tremendous advancement in the field (Dill and MacCallum, 2012) the quality of the resulting structures depends strongly on the similarity of the target protein sequences to those in the Protein Data Bank (PDB). If even a small section of the sequence has weak similarity to those of PDB proteins, the uncertainty of the prediction increases dramatically. Therefore, advantage is taken of our coarse-grained procedure, UNited RESidue (UNRES), which performs successfully with comparable accuracy as that of homology modeling. The latter performs better than UNRES only when there is a good template in the PDB. However, when no such templates exist, homology modeling is not superior to UNRES. For that reason, for the proteins for which there are no good templates in the databases, the de novo methods, not using knowledge-based information, are superior to the template-based modeling (TBM) methods.

In the physics-based approaches, the prediction candidates are selected from the basin(s) with the lowest free energy and, consequently, such methods involve large-scale molecular dynamics (MD) simulations which enable us to perform extensive walks in the conformational space [e.g. replica-exchange Monte Carlo (Hansmann and Okamoto, 1993; Hansmann, 1997; Kolinski and Skolnick, 2004; Latek and Kolinski, 2008), replica-exchange molecular dynamics (REMD) (Mitsutake et al., 2003; Pande et al., 2003; Czaplewski et al., 2009) or the multiplexed REMD (MREMD) application (Rhee and Pande, 2003)]. Such simulations are very expensive to perform with all-atom representations even for small proteins and even with the use of the most powerful supercomputers available because of too large discrepancy between the MD time step (1–10 fs) and the time-scale of protein folding (microseconds for the fastest folders to seconds; Kubelka et al., 2004).

Use of dedicated supercomputers such as ANTON (Shaw et al., 2008) helps to overcome some of the limitations, but the access to such machines is restricted, and the size or the effective time-scale of the simulation is limited to 200 amino acid residues and microseconds, respectively (Sanbonmatsu et al., 2005; Lindorff-Larsen et al., 2011, 2012). Owing to the elimination of the fast-moving degrees of freedom (Khalili et al., 2005; Liwo et al., 2005), using the coarse-grained approaches, enables us to extend both the time-scale (by about 3–4 orders of magnitude) and the size-scale of simulations. Thus, the main advantage of coarse-grained models, with properly designed knowledge-based potentials such as CABS (Jamroz et al., 2013; Kurcinski et al., 2015) and Primo (Kar et al., 2013) or physics-based potentials such as Martini (Monticelli et al., 2008; Goga et al., 2015) and UNRES (Liwo et al., 2014; Mozolewska et al., 2015) that can locate native-like structures (not necessarily with perfect experimental-quality resolution) in free Monte Carlo or MD simulations, is the ability to simulate the dynamics of the relatively large systems in reasonable time-scale (Ingólfsson et al., 2014). However, the development of coarse-grained force fields is much more difficult than that of all-atom force fields because the effective energy function originates from the potential of mean force of the system, in which the insignificant degrees of freedom have been integrated out, and additional terms, like multibody potentials, are necessary to compensate for the missing effects (Liwo et al., 2001; Ayton et al., 2007)

In our laboratory, we have been developing the UNRES force field (Liwo et al., 1993, 1997, 2014) which uses a coarse-grained representation of polypeptide chains. Our physics-based approach to protein-structure prediction, that uses the UNRES force field, performed reasonably well in biannual CASP Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction, exercises to obtain fold topology, e.g. for targets T0061, T0063 and T0079 in CASP3 (Lee et al., 1999, 2000), T0102 in CASP4 (Liwo et al., 2011), T0129 and T0149 in CASP5, T0215, T0223, T0230 and T0281 in CASP6 (Ołdziej et al., 2005), T0534, T0537 and T0578 in CASP9 (Liwo et al., 2011) and T0644, T0663, T0668 and T0740 in CASP10 (He et al., 2013; Khoury et al., 2014). However, because the UNRES predictions are generally of medium-resolution quality, which is remarkably lower than those for TBM targets, UNRES was featured only for new-fold targets (proteins with unique orientation of the local structure) and for targets with new types of domain packing.

In the CASP10 experiment, two UNRES-based predictions made only by the Cornell-Gdansk group, and by one other group with additional participants, were featured by the assessors (He et al., 2013). The first one was a two-domain target T0663 (treated by the Cornell-Gdansk group) (He et al., 2013), and the second one was T0740 (treated by the wfCPUNK group within the WeFold initiative) (Khoury et al., 2014); in the second prediction exercise, UNRES was supplemented with contact-prediction restraints. In the CASP10 experiment, we proved that the UNRES force field is a very good tool to predict the orientation of the domains for the 2-fold symmetry target T0663 (He et al., 2013) that was further confirmed by post-CASP tests with use of restraints within the domains, but not between them (Krupa et al., 2015).

In the past CASP experiments, we were not able to predict all of the human-prediction targets within the 3-week time-window from the target announcement to the submission deadline, because of limited manpower and computer resources. CASP11 was the first exercise in which the Cornell-Gdansk group was able to perform simulations for every human-prediction target using our physics-based approach, treating all 55 human-prediction targets, varying in size from 44 (for target T0797) to 595 amino acid residues (for target T0793), with the average size being 251 residues. These targets represented all structural classes. We used the newest version of the UNRES force field supplemented with energy terms corresponding to the coupling between backbone-local and sidechain-local conformational states (Krupa et al., 2013; Sieradzan et al., 2015).

2 Materials and methods

2.1 UNRES representation of polypeptide chain

We used the UNRES (Liwo et al., 1993, 2001, 2004, 2007, 2008, 2011, 2014) coarse-grained physics-based force field to perform calculations, which provides a 4 order-of-magnitude speed-up compared with all-atom calculations. In the UNRES model, a polypeptide chain is represented by a sequence of C^α atoms with united peptide groups (p), each of which is placed between two consecutive C^αs, and united side chains (SC) (represented by ellipsoids of revolution), which are attached to the C^α atoms. Only the SC and p centers are interaction sites; the C^α-carbon atoms serve only to define the geometry of a chain (Fig. 1).

Fig. 1.

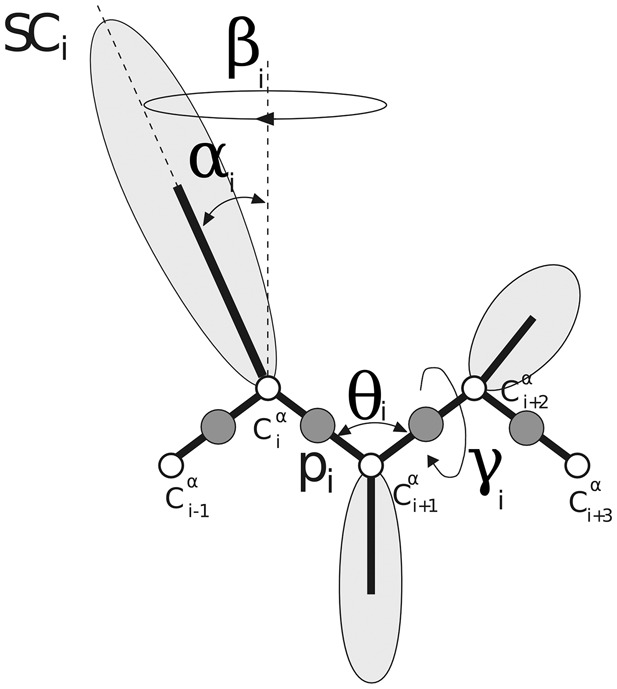
The UNRES model of polypeptide chains. The interaction sites are united peptide groups (p, represented by dark spheres), each located halfway between two consecutive α-carbon (C^α) atoms (represented by white spheres), and side-chains (SC, represented by ellipsoids with different dimensions) that are attached to the corresponding C^αs, which define backbone geometry and are not the interaction centers. The equilibrium length of a C^α…C^α virtual bond is 3.8 Å for the trans and 2.8 Å for the cis peptide group, respectively. For the $i$th residue, the virtual-bond angle ${\theta }_i$, virtual-bond-dihedral angle ${\gamma }_i$, and the polar angles ${\alpha }_i$ and ${\beta }_i$ are also indicated in the figure

The UNRES force field originates from the potential of mean force of a protein in an aqueous environment, which has been expanded into a cluster-cumulant series to provide an implementable effective energy function. This energy function is given by Equation (1):

$$U=\mathrm{ }{w}_{SC}\sum _{i<j}{U}_{{SC}_i{SC}_j}+w_{{SC}_p}\sum _{i\ne j}{U}_{{SC}_i{p}_j}+w_{pp}^{VDW}\sum _{i<j-1}{U}_{p_i{p}_j}^{VDW}+w_{pp}^{el}{f}_2\left(T\right)\sum _{i<j-1}{U}_{p_i{p}_j}^{el}+w_{tor}{f}_2\left(T\right)\sum _{i<j-1}{U}_{tor}\left({\gamma }_i\right)+w_{tord}{f}_3\left(T\right)\sum _i{U}_{tord}\left({\gamma }_i,\mathrm{ }{\gamma }_{i+1}\right)+w_b\sum _i{U}_b\left({\theta }_i\right)+w_{rot}\sum _i{U}_{rot}\left({\alpha }_{{SC}_i},{\beta }_{{SC}_i}\right)+w_{bond}\sum _i{U}_{bond}\left(d_i\right)+w_{corr}^{\left(3\right)}{f}_3\left(T\right)U_{corr}^{\left(3\right)}+w_{corr}^{\left(4\right)}{f}_4\left(T\right)U_{corr}^{\left(4\right)}+w_{turn}^{\left(3\right)}{f}_3\left(T\right)U_{turn}^{\left(3\right)}+w_{turn}^{\left(4\right)}{f}_4\left(T\right)U_{turn}^{\left(4\right)}+w_{ssbond}\sum _{nss}{U}_{ssbond}\left(d_{ss}\right)+w_{SC-corr}{f}_2\left(T\right)\sum _{m=1}^3\sum _i{U}_{SC-corr}\left({\tau }_i^{\left(m\right)}\right)$$ (1)

where the U’s are energy terms,${\theta }_i$ is the backbone virtual-bond angle between three consecutive C^α atoms, γ_i is the backbone virtual-bond-dihedral angle (defined by four consecutive C^αs), α_i and β_i are the angles defining the location of the center of the united SC of residue $i$ (Fig. 1) with respect to the ${\mathrm{C}}_{i-1}^{\alpha }$, ${\mathrm{C}}_i^{\alpha }$ and ${\mathrm{C}}_{i+1}^{\alpha }$ plane, $d_i$ is the length of the $i$th virtual bond, which is either a C^α…C^α virtual bond or C^α…SC virtual bond, $d_{ss}$ is the distance between the SCs of two cysteine residues, and the angles ${\tau }^{(1\hspace{0.17em}-\hspace{0.17em}3)}$ are the SC…C^α…C^α…C^α ${(\tau }^{\left(1\right)})$, C^α…C^α…C^α…SC ${(\tau }^{\left(2\right)})$ and SC…C^α…C^α…SC ${(\tau }^{\left(3\right)})$, respectively. Each energy term is multiplied by an appropriate weight, ${\omega }_x$, and the terms corresponding to factors of order higher than 1 are additionally multiplied by the respective temperature factors which were introduced in our earlier work (Liwo et al., 2007) and which reflect the dependence of the first generalized-cumulant term in those factors on temperature, as discussed in Liwo et al. (2007) and Shen et al. (2009). The factors $f_n$ are defined by Equation (2):

$$f_n\left(T\right)=\frac{\ln \left[\mathrm{e}\mathrm{x}\mathrm{p}\left(1\right)+\mathrm{e}\mathrm{x}\mathrm{p}\left(-1\right)\right]}{\mathrm{l}\mathrm{n}\left\{\mathrm{e}\mathrm{x}\mathrm{p}\left[{\left(\frac{T}{T_0}\right)}^{n-1}\right]+\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{T}{T_0}\right)}^{n-1}\right]\right\}}$$ (2)

where

$$T_0=300 \mathrm{K}.$$

The term $U_{{SC}_i{SC}_j}$ represents the mean free energy of the hydrophobic (hydrophilic) interactions between the SCs, which implicitly contain the contributions from the interactions of the SC with the solvent. The term $U_{{SC}_i{p}_j}$ denotes the excluded-volume potential of the side-chain–peptide-group interactions. The peptide-group interaction potential is split into two parts: the Lennard-Jones interaction energy between peptide-group centers ($U_{p_i{p}_j}^{VDW}$) and the average electrostatic energy between peptide-group dipoles ($U_{p_i{p}_j}^{el}$); the second of these terms accounts for the tendency to form backbone hydrogen bonds between peptide groups $p_i$ and $p_j$. The terms $U_{tor}$, $U_{tord}$, $U_b$, $U_{rot}$ and $U_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}}$ are the virtual-bond-dihedral angle torsional terms, virtual-bond dihedral angle double-torsional terms, virtual-bond angle bending terms, side-chain rotamer and virtual-bond-deformation terms; these terms account for the local properties of the polypeptide chain. The terms ${\mathrm{U}}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^{\left(m\right)}$ represent correlation or multibody contributions from the coupling between backbone-local and backbone-electrostatic interactions, and the terms ${\mathrm{U}}_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}}^{\left(m\right)}$ are correlation contributions involving m consecutive peptide groups; they are, therefore, termed turn contributions. The multibody terms are indispensable for reproduction of regular α-helical and β-sheet structures (Kolinski and Skolnick, 1992; Liwo et al., 1998, 2001). ${\mathrm{U}}_{ssbond}$ is the disulfide bond formation potential calculated over all possible permutations of disulfide bonds (nss). The $U_{SC-corr}$ terms are new knowledge- and physics-based side-chain backbone correlation potentials (Krupa et al., 2013; Sieradzan et al., 2015) recently introduced to the UNRES force field, which improved the correctness of secondary-structure and loop modeling with the UNRES force field.

2.2 Structure prediction procedure

For ab initio protein structure prediction with UNRES, we developed a detailed procedure which is summarized in Figure 2, which was strictly adhered to by all predictors of the Cornell-Gdansk group during CASP11 and involves no subjective selection of any prediction candidate. Owing to semi-automatic generation of input files, all the simulations were run in repeatable and unified way in constant conditions for all human targets. Contrary to the TBM methods, as a result the UNRES prediction procedure provides dynamics and thermodynamics of the investigated proteins, which is not possible from homology modeling.

Fig. 2.

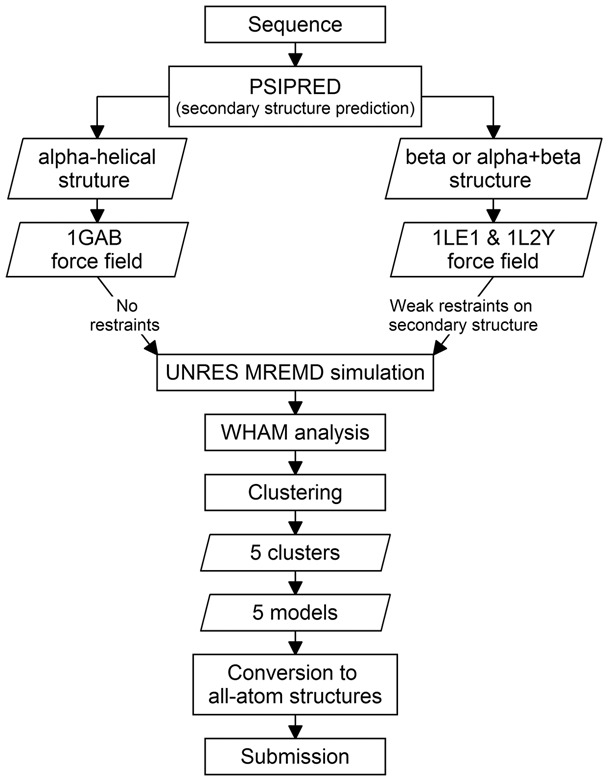
The basic steps of the procedure used during the CASP11 exercise by the Cornell-Gdansk group to predict structures of proteins. See Section 2.2 for details

For each target, the first step of the procedure is to predict its secondary structure by using PSIPRED (Jones, 1999; McGuffin et al., 2000; Buchan et al., 2013) to determine whether the protein contains only α-helical structure or both α- and/or β-structure. If the target is recognized to contain only α-helical structure, the force field originally parametrized with the 1GAB (α-helical) protein (Liwo et al., 2007) is used; otherwise, the force field parametrized with two mini-proteins: the tryptophan cage (α-helical, PDB code 1L2Y) and the tryptophan zipper (β-sheet, PDB code 1LE1) (He et al., 2009) is used. No restraints are imposed, for α-helical structures whereas, for the β and α + β targets, weak restraints are imposed on the virtual-bond-dihedral angle γ (Fig. 1), based on the results of secondary-structure predictions, to speed-up the calculations. The restraints have the form of a flat-bottom quartic function:

$$U_{restr}=\left\{\begin{array}{l}\frac{1}{4}k{\left({\gamma }_{-}-\gamma \right)}^4\\ 0\\ \frac{1}{4}k{\left(\gamma -{\gamma }_{+}\right)}^4\end{array}\mathrm{ }\begin{array}{l}\mathrm{i}\mathrm{f}\mathrm{ }\gamma <\mathrm{ }{\gamma }_{-},\\ \mathrm{i}\mathrm{f}\mathrm{ }{\gamma }_{-}\le \gamma \le {\gamma }_{+}\\ \mathrm{i}\mathrm{f}\mathrm{ }\gamma <\mathrm{ }{\gamma }_{+}\end{array}\right.$$ (3)

where $k=0.01$ kcal/(mol × rad⁴), ${\gamma }_{-}$= 30°, ${\gamma }_{+}$= 70° for the α- and ${\gamma }_{-}$= 140°, ${\gamma }_{+}$= 220° for the β-structure, which are typical ranges of the torsional angle γ observed for these types of structures.

As follows from Figure 2, in CASP11 we used two versions of the UNRES force field, one referred to as the ‘1GAB’ force field, parameterized with the 1GAB α-helical protein and is good for simulating proteins with α-helical structure (Liwo et al., 2007) and another one, referred to as ‘1LE1 & 1L2Y’, parameterized with the tryptophan-cage and tryptophan-zipper mini proteins, which is a general-purpose force field but gives lower resolution of the produced models (He et al., 2009). As can be seen from Figure 2, the selection of the appropriate force field depended on the results of secondary-structure prediction with PSIPRED.

In the second step of the procedure, MREMD simulations (Rhee and Pande, 2003; Liwo et al., 2008) with UNRES are carried out, using our implementation of MREMD to this force field (Czaplewski et al., 2009). Each of the MREMD simulations is run at 32 temperatures (250, 255, 260, 265, 270, 275, 280, 285, 290, 295, 300, 305, 310, 315, 320, 325, 330, 335, 340, 345, 350, 360, 380, 390, 400, 410, 420, 430, 440, 460, 480, and 500 K) with two trajectories per temperature, providing a total of 64 trajectories. Typically, 20 000 000 MD steps at time intervals of 4.89 fs are run for each trajectory, which provides about 0.1 μs formal time and 1 ms real time per trajectory, given the time-scale extension of UNRES (Khalili et al., 2005; Liwo et al., 2005). Replicas are exchanged every 20 000 MD time steps. Running MREMD in a wide range of temperatures enables us to explore the conformational space more exhaustively than in canonical MD simulations. Moreover, MREMD simulation runs are efficiently parallelizable, in the UNRES force field energy and force calculations, reaching up to 75% efficiency with over 4000 CPUs (Liwo et al., 2008; Liwo and Ołdziej, 2010). Also, as mentioned above, weak secondary-structure restraints were added to the energy function; their inclusion speeded up the simulations by a factor of about 2, which enabled us to cut the length of each trajectory to fulfill the time window of predictions. Because the secondary-structure-prediction methods included in PSIPRED are accurate, the chance of model deterioration because of wrong secondary-structure restraints is small.

In the third step, the results of MREMD simulations are processed with the Weighted Histogram Analysis Method (WHAM) (Kumar et al., 1992), which was implemented in UNRES in our earlier work (Liwo et al., 2007), to determine the statistical weights of each of the generated conformations at any desired temperature and to compute the thermodynamics properties. The last 100 snapshots from each trajectory (corresponding to the last 2 000 000 MD steps; 12 800 structures in total) are subjected to WHAM and a cluster analysis. The heat-capacity profile is determined, and the temperature 10 K below the major heat-capacity peak (corresponding to the folding transition) is selected for further analysis. Ward’s minimum-variance clustering (Spath, 1980), using thermodynamic information obtained by WHAM analysis, is subsequently carried out at this temperature to partition the whole ensemble into five clusters, which are the basis for selecting the five candidate models. Thanks to the temperature dependence of the UNRES force field, calculated thermodynamic properties are used in the cluster procedure in addition to the distance measurements, and the free energy, instead of the potential energy, is taken into consideration (Liwo et al., 2007).

The conformations of the respective clusters are weighted with the statistical weights calculated by using WHAM, and the clusters are ranked from the largest (rank 1) to the least probable (rank 5) based on the sum of the statistical weights (Liwo et al., 2007). For each cluster, the mean conformation is determined (by weighting the coordinates of each conformation with the weights determined by WHAM) and the conformation of this cluster centroid which has the lowest C^α RMSD from the average structure is selected as the candidate coarse-grained model. It should be noted that this feature of our approach makes it fully physics-based because not only a physics-based coarse-grained force field is used but also model selection is based on the thermodynamic hypothesis (Anfinsen, 1973) according to which the native structure is an ensemble with the lowest free energy below the folding-transition temperature and not just has the lowest-potential energy, which makes a conformation dominant only at 0 K.

In the last step, the five candidate coarse-grained models determined in the previous step are converted to all-atom structures by using the PULCHRA (Rotkiewicz and Skolnick, 2008) (conversion of the C^α trace to all-atom backbone) and SCWRL(Wang et al., 2008) (optimization of side-chain conformations), which are more efficient than the previously used software (Kaźmierkiewicz et al., 2002a,b). These all-atom models are submitted to CASP.

As an example for target T0765 53 000 000 steps of the MREMD simulation were carried out. The last 12 800 structures were used in WHAM analysis to determine the statistical weights of conformations and to compute the thermodynamic properties. According to the CASP rules, only five structures could be submitted for evaluation; so the subset of the 1807 structures with the statistical weights corresponding to the temperature of 300 K was clustered into five groups (see Fig. 2), each containing 572, 533, 353, 219 and 130 structures. From each of the clusters, only one representative structure (cluster centroid) was chosen and submitted for evaluation.

The procedure used by us in CASP11 differs by several aspects from those used in CASP10 (He et al., 2013) and in previous CASP experiments (Liwo et al., 1999; Ołdziej et al., 2005). First, owing to improved parallelization and code optimization performed lately, as well as access to larger supercomputer resources, we were able to treat all CASP11 targets released for human prediction instead of selecting only those which were judged not to be TBM targets. Second, the new $U_{SC-corr}$ potentials were introduced which improve the quality of the local structure (Sieradzan et al., 2015). Third, model selection was automatized and made fully objective by dissecting the population of conformations (weighted by probabilities) into five clusters and selecting the average structure from each cluster. No ‘inspection by eye’ was involved in model selection.

3 Results and discussion

3.1 General performance of the UNRES force field

As in the last CASP exercises, the CASP11 targets were divided by the assessors into two major post-CASP categories (Kinch et al., 2015) upon the conclusion of the CASP exercise. Category 1 consisted of the TBM targets for which structures of highly homologous proteins existed in the PDB (Berman, 2000) during the course of the exercise. Category 2 consisted of the free-modeling (FM) targets, for which no homologous proteins could be found in the PDB or they were very difficult to select.

The first group of successful predictions with use of the UNRES force field consisted of whole structures of targets, which were predicted with high accuracy with the UNRES force field during CASP11: T0765_D1 (TBM), T0769_D1 (TBM), T0797 (TBM), T0803_D1 (TBM), T0816_D1 (TBM) and T0855_D1 (FM). All of those but T0855 turned out to be TBM targets and TBM methods yielded more accurate models; for T0855, our approach resulted in models which are among the best models submitted to CASP (Fig. 9). An example of the well-predicted TBM target is T0769 whose Global Distance Test (GDT) (Zemla et al., 1999) plots of our group and the other groups are shown in Figure 3A. For targets which were not handled by template-based approaches, UNRES predicted the general fold or part of the fold and its predictions ranked higher. Example GDT plots for T0771_D1 are shown in Figure 3B.

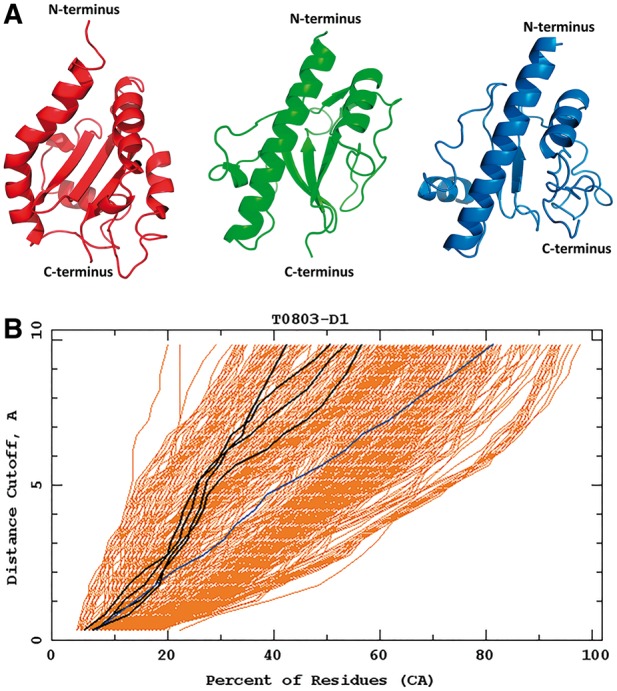
Fig. 9.

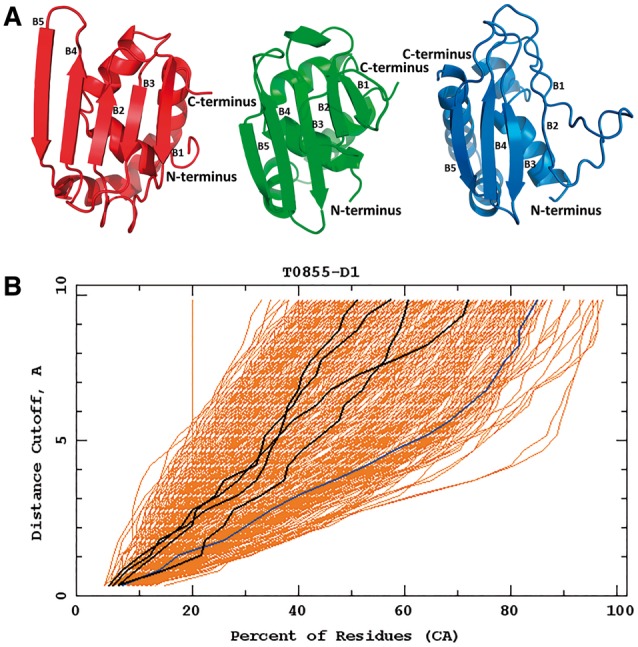
Top: the best Cornell-Gdansk model (model 3) of the target T0855 (left structure), the experimental structure (center structure; PDB code: 2MQD) and the best Zhang model (model 1; right structure); B1-B5 indicates the order of β-strands according to the experimental structure. Bottom: the GDT plots for this target (dark lines: Cornell-Gdansk models; brighter lines: other group models)

Fig. 3.

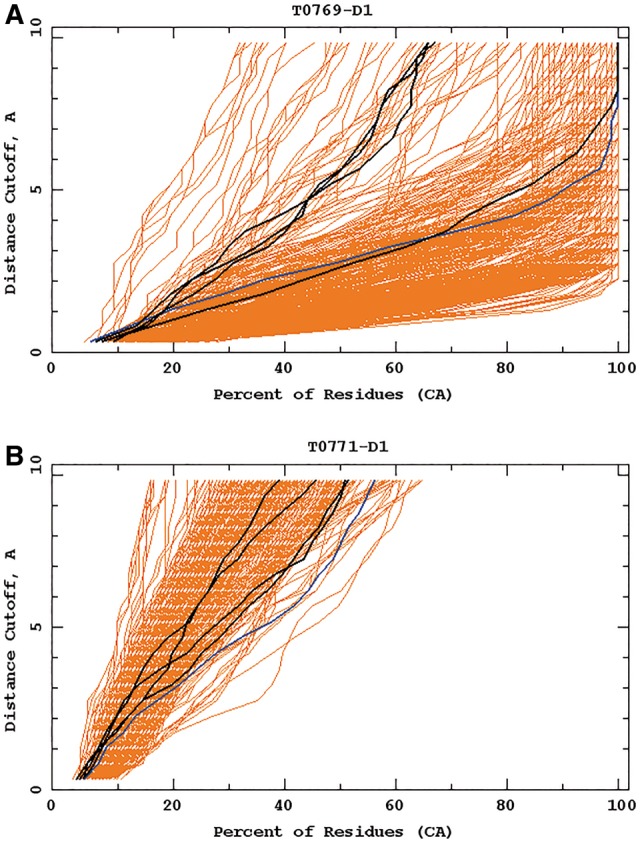
Example GDT-TS plots for targets T0769_D1 (A) and T0771_D1 (B). Cornell-Gdansk models are marked by dark lines and those corresponding to other groups' models are marked by brighter lines. The diagrams were taken from the official CASP11 website at http://www.predictioncenter.org/casp11 (Color version of this figure is available at Bioinformatics online.)

The second group of the successful predictions with UNRES consists of the targets for which the structures of only individual domains were predicted with remarkably good accuracy compared with TBM and other methods; these were T0761 (TBM), T0771_D1 (FM), T0775_D2 (FM), D3 (FM), and D4 (FM), T0785_D1 (FM), T0793_D2 (TBM), T0793_D5 (FM), T0799_D2 (TBM) and D3 (TBM), T0820_D1 (FM) and D2 (TBM), and T0834_D2 (FM). Although full convergence of MREMD simulations was not achieved for multi-domain proteins (T0775, T0793 and T0799) because of the strictly restricted time window for predictions, our models of their domains are very good. In Figure 4, the GDT-TS (Global Distance Test - Total Score) values and RMSDs from the experimental structure of the best models from the Cornell-Gdansk group are compared with the best predictions over all groups participating in CASP11 and with those of the Zhang group, which generally performed best in the CASP11 experiment (Yang et al., 2015) (Fig. 4). As shown, in 11 of 18 cases, the Cornell-Gdansk models are of comparable or better quality than Zhang models; namely T0761, T0763_D1, T0771_D1, T0775_D2, T0775_D4, T0785_D1, T0793_D2, T0793_D5, T0799_D2, T0834_D2, T0855_D1.

Fig. 4.

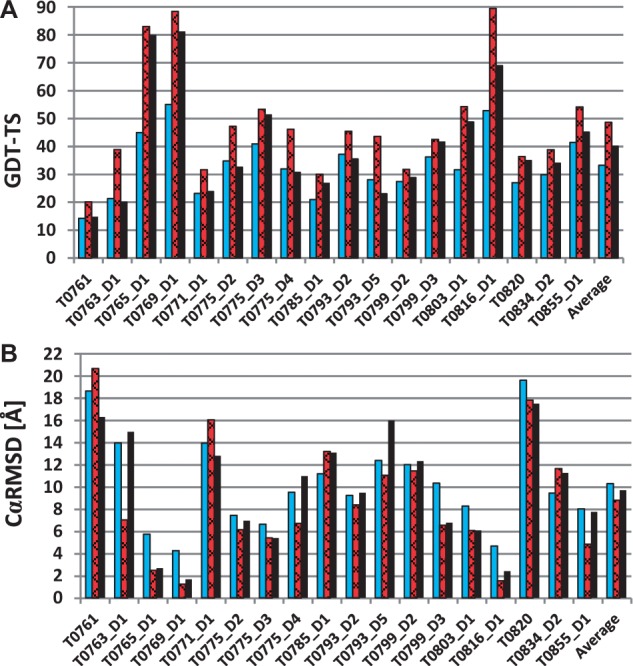
Summary of the official CASP11 assessment for the best predictions of the Cornell-Gdansk group. The GDT-TS values (A) and CαRMSD (B) for the best Cornell-Gdansk predictions (bright bars), the overall best predictions (slanted bars), the best predictions by the Zhang group (black bars), which achieved the best overall performance in CASP11 (Color version of this figure is available at Bioinformatics online.)

Due to the coarse-grained representation of the UNRES force field and the imperfect rebuilding of the all-atom chain, the GDT scores are inferior for very small distance cutoffs (up to 1–1.5 Å) compared with the TBM methods. However, in most cases, the UNRES force field performs very well in higher values of the distance cutoff (from 5–6 to 10 Å), correctly predicting the overall topology of the proteins. The differences between many of the predicted and the experimental structures are in the loops and other weakly defined regions, because in the UNRES force field such elements are highly flexible and submitted models are only the average states of such elements.

In the next section, some of the UNRES successful predictions are described briefly and compared with the best performing TBM group in the CASP 11 experiment.

3.2 Examples of specific successful predictions

T0765 is a 128 amino acid residue target, from which only the structure of the fragment 33-108 was solved experimentally and used in the official CASP assessment. These resulting 76 residues form two α-helices and four antiparallel β-sheets. Our model 2 of this target contains all the secondary structure elements and their relative orientation, and its RMSD from the experimental structure is 5.75 Å (Fig. 5). The only differences between model 2 and the experimental structure occur in the N-terminal part of the protein and in the first loop, which regions are defined with a lower accuracy in the crystal structure, presumably because of their flexibility. As can be seen in Figure 5, the Cornell-Gdansk structure is as comparable quality to the best Zhang model.

Fig. 5.

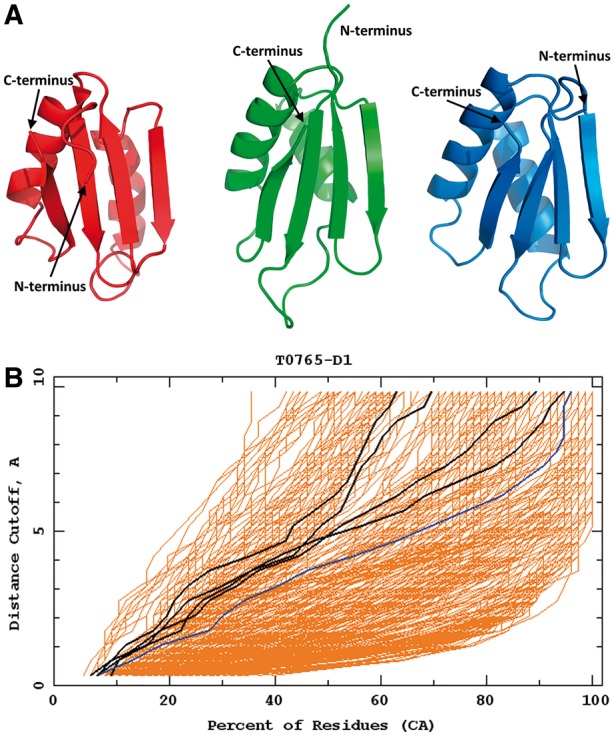
Top: the best Cornell-Gdansk model of target T0765 (model 2; left structure), the experimental structure (center structure; PDB code: 4PWU) and the best Zhang model (model 2; right structure). Bottom: the GDT plots for this target (dark lines: Cornell-Gdansk models; brighter lines: other group models) (Color version of this figure is available at Bioinformatics online.)

T0769 is a 128 amino acid residue target, from which only the section 1–97 was subjected to official CASP analysis, due to the presence of a long, histidine-rich unfolded fragment at the C-terminus of the experimental structure (not shown in Fig. 6).

Fig. 6.

The best Cornell-Gdansk model (model 5) of target T0769 (left structure), the experimental structure (center structure; PDB code: 2MQ8) and the best Zhang model (model 1; right structure). The GDT-TS plot for this target are shown in Figure 3A (Color version of this figure is available at Bioinformatics online.)

The experimental structure of the 1–97-residue section contains two long α-helical fragments and four antiparallel β-sheets. Our model 5 of this target is very close to the experimental structure with RMSD equal to 3.77 Å and all secondary-structure elements are correctly oriented in space (Fig. 6). The only noticeable difference is in the placement of the small fourth β-strand, which is slightly separated from the other three strands, because of the unfolded C-terminus. Contrary to the Cornell-Gdansk model, whose β-sheets are slightly too straight, the best Zhang model β-sheets are slightly too bent; the only other differences in both models are in the loop fragments.

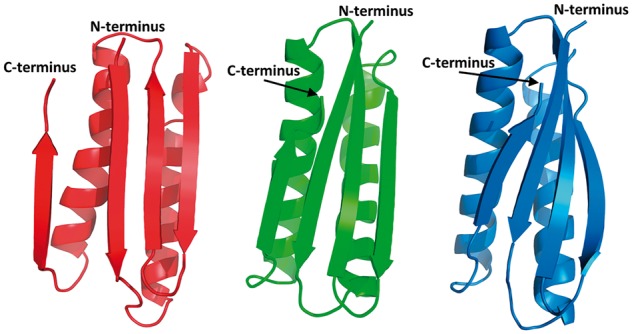
For T0803 (a 139-residue α + β-protein), we predicted a general fold correctly but the details of the structure of the secondary-structure elements differ from those of the experimental structure, as shown in Figure 7 in which our model 3 is compared with the experimental structure. The N-terminal α-helix in our model 3 is bent, as opposed to the experimental structure in which it is straight, the core three-stranded antiparallel β-sheet is packed parallel to the motif composed of two α-helices and the N- and C-terminal sections form short α-helices and are not disordered as in the experimental structure, due to the highly disordered and flexible structure of the large part of the protein (Fig. 7). The overall C^α-RMSD from the experimental structure is 8.30 Å. The best Zhang model has perfectly predicted two helices with orientation, which are too bent and separated in the Cornell-Gdansk model, but the β-strands in the Zhang model are of worse quality.

Fig. 7.

Top: the best Cornell-Gdansk model (model 3) of target T0803 (left structure), the experimental structure (center structure; PDB code: 4OGM) and the best Zhang model (model 2; right structure). Bottom: the GDT plots for this target (dark line: Cornell-Gdansk models; brighter lines: other group models) (Color version of this figure is available at Bioinformatics online.)

Target T0816 is a small 68-residue protein formed by four α-helices. In our model 2, the helices are packed correctly but the second α-helix is broken, as opposed to the experimental structure and the best Zhang model (Fig. 8). The overall C^α RMSD of the Cornell-Gdansk model from the experimental structure is 4.69 Å.

Fig. 8.

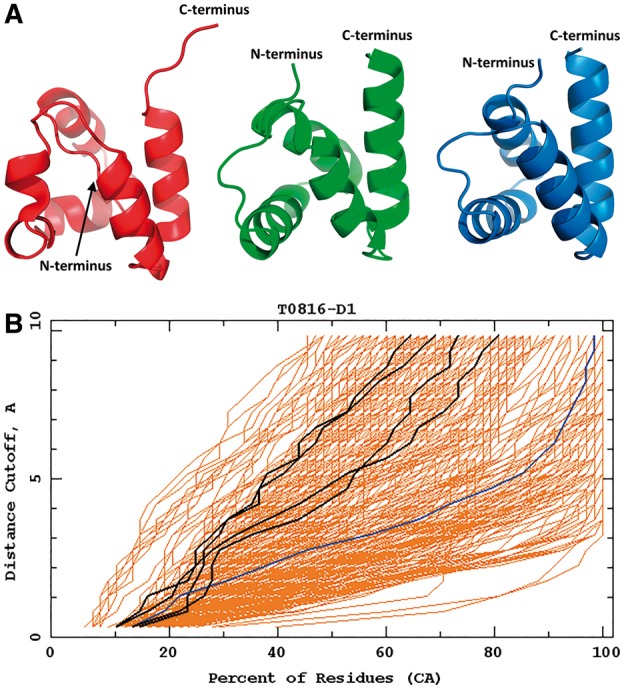
  Top: the best Cornell-Gdansk model (model 2) of target T0816 (left structure), the experimental structure (center structure; PDB code: 5A1Q) and the best Zhang model (model 3; right structure). Bottom: the GDT plots for this target (dark lines: Cornell-Gdansk models; brighter lines: other group models) (Color version of this figure is available at Bioinformatics online.)

Target T0855 (an FM target) is the last regular human target assessed in the CASP11 experiment. T0855 is a medium size 115-residue protein, the structure of which consists of four short α-helices and five antiparallel β-sheets. The C^α RMSD of our model 3 from the experimental structure is 8.05 Å but the overall fold of the model matches the experimental structure (Fig. 9).

The main difference between the experimental structure and the predicted model 3 are misplaced second and third β-strands (Fig. 9). The misplaced β-strands also caused a slight shift of the third and fourth α-helices. However, it should be noted that the quality of our model 3 is comparable to those obtained by approaches that use knowledge-based input. In particular, the orientation of the particular fragments inside the protein is mostly correct. The structure of the FM target T0855 predicted by the Cornell-Gdansk group is an example, when the de novo method can be superior to the TBM methods. The Cornell-Gdansk group predicted both the structure of the secondary elements and their orientation better than the best TBM group, Zhang, whose best model β-strand 1 is wrongly predicted and the orientation of the α-helices is incorrect, resulting in the improper orientation of the C-terminus.

4 Conclusion

Knowledge-based methods, in particular the template-based methods and methods with mixed approaches for the prediction of protein structure, are at present more successful than the physics-based approaches. However, as demonstrated by the recent CASP exercises, new proteins whose structures cannot be predicted with these approaches continue to emerge. Moreover, the physics-based methods are the only ones with which to study protein dynamics and large-scale conformational changes, which are crucial in the functioning of the machinery of life and, further, to study the mechanisms of diseases and to help design effective therapies. In this regard, assessment of the capability of the physics-based methods to predict protein structures enables us to assess their applicability in the simulations of biochemical processes.

The Cornell-Gdansk group was the only group in the CASP11 experiment that used only molecular-dynamics simulations without any knowledge-based information (except for weak secondary-structure restraints, which were necessary in order to accomplish the predictions within the strict 3-week time window), and which carried out all human-prediction targets and achieved satisfactory results. Moreover, the applied prediction procedure was also physics based because mean structures from the conformational ensembles with the lowest free energy, rather than the lowest-energy conformations, were selected as candidate predictions. With our physics-based approach, we achieved good predictions of complete structures of six medium-sized single-domain proteins and the structures of 13 complete protein domains and the general fold of the large multi-domain proteins. The best prediction in terms of RMSD was achieved for the TBM target T0769 (the C^α-RMSD from the experimental structure being 3.8 Å over the 97 residues). However, the optimum character of the UNRES force field can be seen from the prediction of the small FM target T0855, which is an example of the situation, in which, due to the lack of good homologous proteins in the database, the structure prediction with the TBM methods is not as good as that with the superior UNRES force field. UNRES force field managed to achieve comparable results to the most of the TBM methods also for other ‘FM’ targets and domains, such as T0763-D1, T0771-D1, T0775-D2, T0793-D2, T0820-D1 and T0834-D2. It is also remarkable that, in CASP11, there is only a small difference between the ranking of our ‘model 1's’ and our best models indicating that the UNRES force field, supplemented with the recently introduced terms corresponding to the coupling of the backbone- and side-chain-local interactions (Krupa et al., 2013; Sieradzan et al., 2015), enables us to select the most native-like predictions out of the five models more accurately than the previous version of the force field used in CASP10.

The better overall performance of our approach in CASP11 compared with previous CASP exercises was achieved because of recent addition of the new potentials coupling the backbone-local and side-chain-local conformational states. This improvement enables us to predict more folds and rank the models better. Nevertheless, the results show that, even though UNRES predicts a large number of folds correctly and the accuracy of a few targets is comparable with the best TBM methods, especially for the TBM targets, the predicted structures have higher RMSDs from the experimental structures compared with those predicted by TBM methods.

To improve the capacity of UNRES to predict new folds and to improve the accuracy of predictions, at present, we are working on the calibration of the force field, which is aimed at the refinement of the energy-term weights of the parameters of the expressions for the energy terms in Equation (1). For this purpose, we have recently developed a new method for force-field calibration (Zaborowski et al., 2015), which is based on the maximum-likelihood approach (Seber and Wild, 1989). A very early variant of the UNRES force field optimized with the use of this approach was already used in CASP11 for a very limited number of 12 targets. The performance of this variant of UNRES will be described in a separate paper (A.K. Sieradzan et al., unpublished data). Full optimization of UNRES is now being carried out with the maximum-likelihood approach, and the first results demonstrate that it improves the capability of finding the folds and to rank the models and the accuracy of the predicted structures (Zaborowski et al., 2015). Because the simulations could not be run to achieve full convergence for the largest targets during CASP11, work is also being carried out in our laboratory to optimize and improve the parallel efficiency of the UNRES code for use with the optimized force field. It can be anticipated that these improvements will constitute yet another important step toward accurate prediction of protein structure without the use of any database information and, consequently, simulations of important biochemical processes with a great degree of reliability.