Patient Prognosis from Vital Sign Time Series: Combining Convolutional Neural Networks with a Dynamical Systems Approach

Abstract

In this work, we propose a stacked switching vector-autoregressive (SVAR)-CNN architecture to model the changing dynamics in physiological time series for patient prognosis. The SVAR-layer extracts dynamical features (or modes) from the time-series, which are then fed into the CNN-layer to extract higher-level features representative of transition patterns among the dynamical modes. We evaluate our approach using 8-hours of minute-by-minute mean arterial blood pressure (BP) from over 450 patients in the MIMIC-II database. We modeled the time-series using a third-order SVAR process with 20 modes, resulting in first-level dynamical features of size 20×480 per patient. A fully connected CNN is then used to learn hierarchical features from these inputs, and to predict hospital mortality. The combined CNN/SVAR approach using BP time-series achieved a median and interquartile-range AUC of 0.74 [0.69, 0.75], significantly outperforming CNN-alone (0.54 [0.46, 0.59]), and SVAR-alone with logistic regression (0.69 [0.65, 0.72]). Our results indicate that including an SVAR layer improves the ability of CNNs to classify nonlinear and nonstationary time-series.

1. INTRODUCTION

Subtle dynamical patterns in physiological time-series, often difficult to observe with the bare eye, may contain important information about the pathophysiological state of patients and their long-term outcomes. We present an approach to physiological time-series analysis that simultaneously models the underlying dynamical systems using a switching vector autoregressive (SVAR) model, and the high-level transition patterns among the dynamical modes using Convolutional Neural Networks (CNNs). CNNs have been shown recently to produce state-of-the-art performance in image classification tasks [1]. This success is largely attributed to their ability to exploit hierarchical structures for feature learning. However, direct application of CNNs to physiological time-series have been limited due to the presence of underlying physiological control systems, capable of exhibiting rich dynamical patterns at multiple time-scales.

In previous work, we adopted a SVAR process framework to discover the shared dynamic behaviors exhibited in HR/BP time series of a patient cohort [2]. We used the proportion of time a patient spents in each of the dynamic modes (“mode proportions” from now on) to construct a feature vector for predicting a patient's underlying “state of health”. However, this feature does not capture the high-level transition dynamic among the dynamical mode. To address this limitation, we propose a stacked SVAR-CNN architecture. The SVAR-layer extracts dynamical features (or modes) from the time-series, which are then fed into the CNN-layer to extract higher-level features representative of transition patterns among the dynamical modes. We evaluated our approach using minute-by-minute mean arterial blood pressure (BP) of 453 ICU patients during their first 24 hours in the ICU from the Multi-parameter Intelligent Monitoring in Intensive Care (MIMIC) II database [3].

2. Materials and Methods

This section describes the utilized dataset, as well as the SVAR and CNN architectures used to learn high-level features in the multivariate time-series of vital signs.

2.1. Dataset

Minute-by-minute mean arterial blood pressure (MAP) measurements of MIMIC II [3] adult ICU patients during the first 24 hours of their ICU stays were extracted. The analysis in this paper was restricted to 453 patients with day 1 SAPS-I scores [4] and with at least 8 hours of blood pressure data during the first 24 hours after ICU admission. Hospital mortality of this cohort is 14%. The data set contains over 9,000 hours of minute-by-minute heart rate and invasive mean arterial blood pressure measurements (over 20 hours per patient on average) from 453 adult patients collected during the first 24 hours in the ICU. Time series were detrended, and Gaussian noise was used to fill in the missing or invalid values. The median age of this cohort was 69 with an inter-quartile range of (57, 79). 59% of the patients were male. Approximately 15% (67 out of 453) of patients in this cohort died in the hospital.

2.2. Switching Vector Autoregressive Modeling of Cohort Time Series

Our approach to discovery of shared dynamics among patients was based on the SVAR model [2, 5], which assumes there exists a library of possible dynamic behaviors or modes; a set of multivariate autoregressive model parameters ${\{A_p^{\left(k\right)},p=1\cdots P\}}_{k=1}^K,{\left\{Q^{\left(k\right)}\right\}}_{k=1}^K$, where K is the number of dynamic modes. For each mode k, $A_p^{\left(k\right)}$, p = 1 ··· P are the AR coefficient matrices (corresponding to each of the P lags) and Q^(k) is the corresponding noise covariance matrix. Let y_t be the observation at time t, and z_t be an indicator variable indicating the active dynamic mode at time t. Following these definitions, a SVAR model is defined by:

$$y_t=\sum _{p=1}^P{A}_p^{\left(z_t\right)}{y}_{t-p}+Q^{\left(z_t\right)}.$$ (1)

A collection of related time series can be modeled as switching between these dynamic behaviors which describe a locally coherent linear model that persist over a segment of time. We modeled minute-by-minute MAP time series as a switching AR(3) process with 20 dynamic modes as in [2]. Patients were divided into 10 training/test sets. Ten switching VAR models were learned, one for each training set. The mode assignment of time series for patients in the test set was inferred based on the model learned from the corresponding training set.

2.3. Convolutional Neural Networks

Convolutional neural networks are a particular formulation of deep neural networks that were first developed for the automatic classification of handwritten digits in images [6]. Deep neural networks [7] are a class of models which consist of a hierarchy of latent representations distributed across numerous simple units or neurons. Although each level in the hierarchy is a simple transformation from the previous layer, having many units spanning multiple layers results in a very rich latent representation that has proven to facilitate complex tasks. Convolutional networks leverage the spatio-temporal structure of the data they model by applying a spatial or temporal convolution of the model parameters over the input to compute the following layer. Recently, such networks have achieved state of the art results on image classification [1, 8] and text understanding [9,10] tasks.

The latent or hidden representation H = {h₁, ..., h_t} resulting from a convolutional layer in such a network is computed by convolving a parameterized weight matrix W over the input Z = {z₁, ..., z_t} followed by an elementwise non-linearity g(·) i.e. H = g(W * Z). This is typically repeated for multiple layers and that are followed by a final classification layer.

2.4. Combining SVAR and Convolutional Neural Network

We modeled the time-series using a third-order SVAR process with 20 modes as described above. We then used the SVAR state marginals from the final 8 hours of the minute-by-minute BP from each patient (during their first days in the ICU) as input to the CNN, resulting in first-level dynamical features of size 20×480 per patient. As a pre-processing step, we ordered rows of the state marginal matrix based on the modes’ odds ratios for hospital mortality (from logistic regression using the training set) so that modes with similar mortality risk share location proximity in the CNN input image space. A one-layer fully connected CNN is then used to learn hierarchical features from these inputs, and to predict hospital mortality.

As a comparison, we also use the SVAR model to learn a time-series specific transition matrix among the dynamic modes, and use the learned patient-specific transition matrix (20×20) as an input to CNN. This feature does not capture the specific time of a transition, but includes information regarding the frequency of transitions from one dynamical model to another, and will allow us to assess the relative importance of transient versus global transition features of the dynamics.

The CNN kernel size is 20×20 with 12 hidden units. In each of the 10-fold, the training set was further divided into 70%/30% training and validation set: the 70% training set was used to build 30 different CNN models using 30 different random initializations; for each initialization, we use a 5-fold validation procedure (i.e. validate the performance of the learned CNN model using 5 different subsets of the validation set) to select the best CNN model for actual inference on the test set; the CNN model with the highest mean AUC from the 5-fold validation was used to do prediction on the actual test set.

3. RESULTS

3.1. State Marginals from SVAR

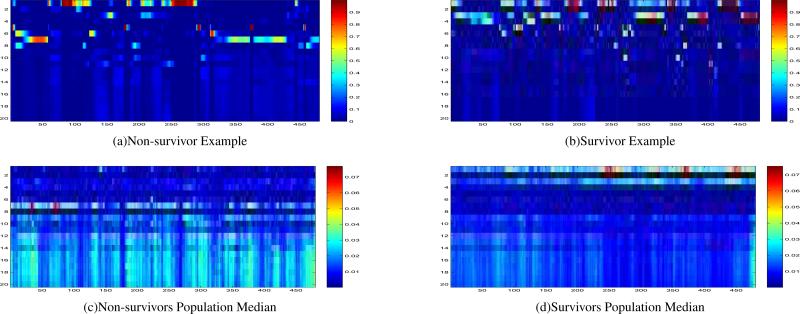
Figure 1 shows example dynamic modes state marginal probabilities over 8 hours (20×480) for survivors vs. non-survivors. (Top 4 rows are low-risk modes; the remaining modes are high-risk modes.) We used univariate logistic regression analysis to test the association between the proportion of time patients spent in each dynamic mode (20 in total) and the outcome (hospital mortality). The odds ratios from the association analysis were then used to sort the dynamic modes.

Figure 1.

Dynamic modes state marginal probabilities over 8 hours (20×480): a comparison of the non-survivors vs. the survivors. Each patient was represented by a 20×480 state marginals. The x-axis represents the time (in minutes), and the y-axis is the probability of belonging to different dynamic modes (20 in total). The rows were ordered based on the modes’ odds ratios in ascending order, as in Table 2 (see Appendix). Low risk modes (odds ratios < 1) are on the top (rows 1 - 4), and higher risk modes (odds ratios > 1) are on the bottom (after row 5).

Table 2 in the Appendix shows the 20 discovered SVAR dynamic modes (from one fold), listed in the order of their associations with hospital mortality. The same ordering is used to construct a CNN input-image from SVAR state marginals: rows of the state marginals appear in the same order as the corresponding dynamic modes appear in Table 2. For each mode, we report its p value, and odds ratios (OR, with 95% confidence interval) in mortality risks as per 10% increase in mode proportions. Modes are listed in ascending order based on their odds ratios. Note that the low-risk modes are on the top four rows; the remaining modes are higher-risk modes with odds ratios greater than one. Table shows the order of the dynamic modes in the state marginal probabilities (20×480) input matrix to CNN.

3.2. Prediction Performance

Table 1 summarized the AUCs from 10-fold cross validation. Applying CNN-alone on the raw BP time series achieved an AUC of 0.54 [0.46, 0.59]. Applying logistic regression on SVAR mode proportion alone achieved an AUC of 0.69 [0.65, 0.72]. As a baseline comparison, an existing acuity metric SAPS-I, using 14 different physiological/lab measurements gave an AUC of 0.65 [0.59, 0.71].

Table 1.

Performance of Mortality Predictors. LR - logistic regression. MP - mode proportion.

	AUC	(IQR)
SAPS I	0.65	(0.59, 0.71)
BP Raw Samples + CNN	0.54	(0.46, 0.59)
SVAR Trans. Matrix + CNN	0.67	(0.63, 0.69)
SVAR BP Dynamics MP + LR	0.69	(0.65, 0.72)
SVAR BP Dynamics + CNN	0.74	(0.69, 0.75)

The best performance was achieved by combining CNN/SVAR using SVAR generated state marginals from BP time-series as an input to CNN, achieving a median and interquartile-range AUC of 0.74 [0.69, 0.75]. Using SVAR learned patient-specific transition matrix among dynamic modes as an input to CNN achieved a median AUC of 0.67 [0.63, 0.69].

4. DISCUSSION and CONCLUSIONS

We have presented a framework that combines switching state space models with convolutional neural networks for time series classification. Our approach uses the inferred state marginals of hidden variables from SVAR as inputs to convolutional neural network for a supervised learning task. Our approach simultaneously models the underlying dynamics of physiological time series using a switching state-space model, and the high-level transition patterns among the states using convolutional neural networks. We have compared several different approaches of modeling physiological time series for outcome prediction using CNN, SVAR, and a stacked SVAR/CNN approach. The stacked CNN/SVAR architecture using state marginals achieves the best performance, outperforming both stand-alone SVAR and CNN in prediction performance. Our results indicate that including an SVAR layer significantly improves the ability of CNNs to classify nonlinear and nonstationary time-series. The proposed approach is particularly useful when dealing with small datasets, since the expectation-maximization algorithm used to learn the SVAR features [5] is less likely to overfit to the data, compared to a supervised backpropagation based algorithm directly applied to the CNN on the raw time-series. Finally, a switching state space model allows for incorporating models of the underlying physiological processes that generate the observed time series, and provides a level of interpretability not achievable by the standard deep learning algorithms.

Appendix: Discovered SVAR Dynamic Modes

Table 2.

Discovered dynamic modes and their association with hospital mortality.

	Mode	p-val	OR (95% CI)
1	11	0.0001	0.61 (0.47 0.78)
2	17	0.5665	0.70 (0.21 2.35)
3	15	0.0244	0.71 (0.53 0.96)
4	2	0.7395	0.90 (0.48 1.67)
5	20	0.8908	1.02 (0.78 1.34)
6	8	0.7981	1.22 (0.27 5.58)
7	13	0.0000	1.44 (1.22 1.71)
8	9	0.3519	1.58 (0.60 4.16)
9	18	0.1881	2.28 (0.67 7.76)
10	7	0.3372	2.80 (0.34 22.95)
11	10	0.1997	4.08 (0.48 35.04)
12	4	0.0677	9.18 (0.85 98.97)
13	16	0.0633	9.56 (0.88 103.45)
14	19	0.0577	11.34 (0.92 139.10)
15	6	0.0339	14.36 (1.23 168.33)
16	12	0.0311	16.38 (1.29 208.20)
17	3	0.0282	16.88 (1.35 210.84)
18	14	0.0205	18.62 (1.57 220.83)
19	5	0.0226	19.81 (1.52 258.17)
20	1	0.0120	23.41 (2.00 274.21)