Summary
Protein-peptide interactions play an important role in many cellular processes. In silico prediction of protein-peptide complex structure is highly desirable for mechanistic investigation of these processes and for therapeutic design. However, predicting all-atom structures of protein-peptide complexes without any knowledge about the peptide binding site and the bound peptide conformation remains a big challenge. Here, we present a docking-based method for predicting protein-peptide complex structures, referred to as MDockPeP, which starts with the peptide sequence and globally docks the all-atom, flexible peptide onto the protein structure. MDockPeP was tested on the peptiDB benchmarking database, using both bound and unbound protein structures. The results show that MDockPeP successfully generated near-native peptide binding modes in 95.0% of the bound docking cases and in 92.2% of the unbound docking cases, respectively. The performance is significantly better than other existing docking methods. MDockPeP is computationally efficient and suitable for large-scale applications.
Graphical Abstract
eTOC Blurb
MDockPeP, developed by Yan et al., is a molecular docking method for protein-peptide complex structure prediction. MDockPeP starts with the peptide sequence and globally docks the all-atom, flexible peptide onto the protein structure with no need for a priori knowledge about the binding site.
2 Introduction
Up to 40% of protein-protein interactions are estimated to be mediated by short peptides, which are involved in a variety of cellular processes such as signal transduction, immune responses and transcriptional regulation (Petsalaki and Russell, 2008). Peptides are also attractive candidates for drug development (Wells and McClendon, 2007; Craik et al., 2013; Fosgerau and Hoffmann, 2015). Therefore, studying protein-peptide interactions is of great significance for mechanistic investigation of many biological processes and for development of peptide therapeutics. However, there are only a limited number of protein-peptide complex structures in the Protein Data Bank (PDB) (Berman et al., 2000), because of the difficulties and cost for determining such structures by X-ray crystallography and NMR spectroscopy. By contrast, in silico methods provide a much cheaper and faster alternative. Numerous efforts have been devoted to predicting protein-peptide interactions, ranging from the prediction of peptide binding sites (Singh and Raghava, 2001, 2003; Petsalaki et al., 2009; Trabuco et al., 2012; Lavi et al., 2013; Saladin et al., 2014; Yan and Zou, 2015) to the much more challenging prediction of protein-peptide complex structures (Verschueren et al., 2013; Lee et al., 2015; Hetényi and van der Spoel, 2002; Niv and Weinstein, 2005; Liu et al., 2004; Huang and Wong, 2009; Dagliyan et al., 2011; Antes, 2010; Raveh et al., 2011, 2010; Trellet et al., 2013; Kurcinski et al., 2015; Blaszczyk et al., 2016; Schindler et al., 2015; Ben-Shimon and Niv, 2015).
The existing methods for predicting protein-peptide complex structures can be roughly classified into three categories: template-based modeling (Verschueren et al., 2013; Lee et al., 2015), molecular docking (Hetényi and van der Spoel, 2002; Liu et al., 2004; Raveh et al., 2011, 2010; Trellet et al., 2013; Kurcinski et al., 2015; Blaszczyk et al., 2016; Schindler et al., 2015) and molecular dynamics (MD) simulation (Niv and Weinstein, 2005; Huang and Wong, 2009; Dagliyan et al., 2011; Antes, 2010; Ben-Shimon and Niv, 2015). Template-based modeling is computationally efficient. However, due to the very limited number of protein-peptide complexes in the PDB, a high-quality template is often unavailable. MD simulation is the most rigorous method, which uses physically-based force field parameters to simulate the dynamics of the protein-peptide complex to reach a state of equilibrium. However, the extremely intensive computational requirement hinders large-scale applications of this kind of methods. Molecular docking, which employs simplified scoring functions and (fully or partially) restricts the protein structure to reduce the computational time, is the most commonly-used method for protein-peptide complex structure prediction. Yet, most docking studies before Year 2010 focused either on very short peptides (fewer than 5 amino acids) (Hetényi and van der Spoel, 2002) or on specific systems (Liu et al., 2004; Niv and Weinstein, 2005). Recently, a few docking methods have been developed for longer peptides (i.e., 5 to 15 amino acids) (Raveh et al., 2011, 2010; Trellet et al., 2013; Kurcinski et al., 2015; Blaszczyk et al., 2016; Schindler et al., 2015). For example, the FlexPepDock ab initio (Raveh et al., 2011) flexibly docks the coarse-grained model of a peptide to a protein by sampling peptide backbone conformations and rigid-body orientations in the given binding site; the generated coarse-grained protein-peptide complexes are then converted to all-atom models through all-atom refinement. This method is computationally expensive and takes about 24 hours on a cluster of 120 processors for each prediction (Raveh et al., 2011). HADDOCK (Trellet et al., 2013) rigidly docks three pregenerated peptide conformers (extended, alpha-helix, and polyproline-II) to the given peptide binding site; the top 400 rigid complexes are flexibly refined by using simulated annealing in the torsional angle space followed by MD simulations in explicit solvent (Trellet et al., 2013). An improved method, pepATTRACT (Schindler et al., 2015), rigidly docks the same three peptide conformers onto the whole surface of the protein, followed by the refinements of the top 1000 generated complex structures with a flexible interface refinement method and then MD simulations in implicit solvent (Schindler et al., 2015). Similar to HADDOCK, pepATTRACT is time-consuming because of the MD-based refinement step for a large number of complex structures. CABS-dock (Kurcinski et al., 2015; Blaszczyk et al., 2016) flexibly docks the coarse-grained model of the peptide; the secondary structure of the peptide is either provided by the user or predicted by PSI-PRED (McGuffin et al., 2000), a secondary structure prediction tool for proteins. CABS-dock is computational efficient, and a typical run takes about 3 hours on the CABS-server. However, the secondary structure of the bound peptide is often unknown, and it is unclear whether the protein-based PSI-PRED is suitable for predicting secondary structures of bound peptides. In summary, to our best knowledge, the existing global docking methods are restricted either by the time-consuming MD-based refinements or by the inaccurate coarsegrained models. A docking strategy with a good balance between the accuracy and the computational efficiency is highly desired.
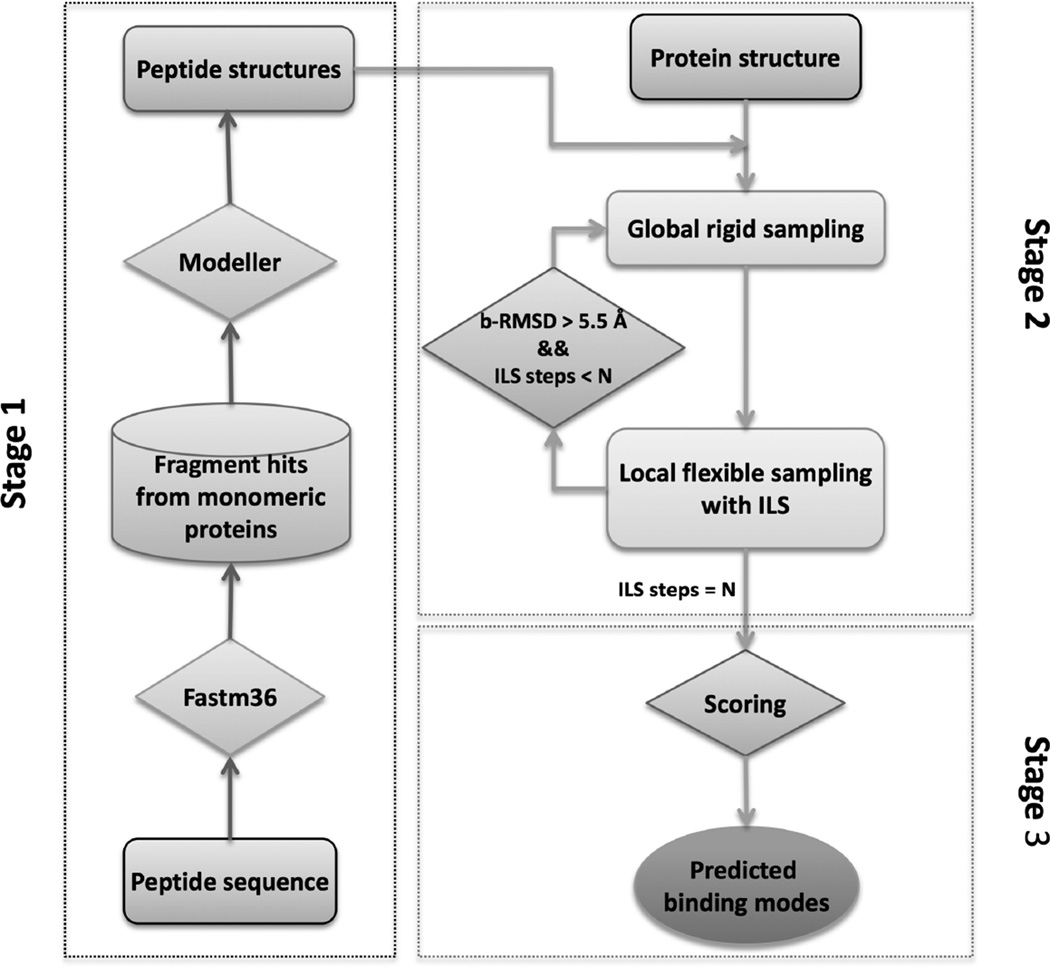
Here, we present an all-atom and blind docking strategy for protein-peptide complex structure prediction. The method, referred to as MDockPeP, requires only the peptide sequence and the 3D structure of the protein. MDockPeP consists of three stages. In Stage 1, peptide conformers are constructed. In Stage 2, putative protein-peptide binding modes are globally sampled on the whole surface of the protein. In Stage 3, the sampled binding modes are scored and ranked. The flowchart of MDockPeP is summarized in Figure 1.
Figure 1.
The flowchart for MDockPeP.
Specifically, given the sequence of a peptide and the 3D structure of a protein, the conformations of the peptide are modeled based on the template fragments of monomeric proteins that have similar sequences. This modeling effort is based on 1) the argument that peptide binding is similar to protein folding except that the peptide is not covalently connected to the protein (Kippen et al., 1994; Zhang et al., 1997), and 2) the finding that peptide binding interfaces share striking similarities to the folds in single protein chains (Vanhee et al., 2009). Up to 3 non-redundant peptide conformers are kept, and each conformer is individually docked to the whole surface of the protein. During each docking process, to reduce the configurational space for sampling, a restrictive sampling approach is employed that effectively integrates global rigid sampling and local flexible sampling, eliminating the binding modes in which their peptide conformations are significantly different from the initially modeled peptide conformations (with backbone root-mean-square deviation (bRMSD) larger than 5.5 Å). The resulting binding modes based on different starting peptide conformers are combined, followed by scoring and ranking with our statistical potential-based scoring function, ITScorePeP. ITScorePeP is derived based on the crystal structures of protein-peptide complexes, using our previous iterative approach (Huang and Zou, 2006, 2008, 2011, 2014).
In the present study, MDockPeP has been systematically assessed on the peptiDB benchmarking database (London et al., 2010; Trellet et al., 2013), using both bound and unbound protein structures. In the stage of peptide modeling, for 95.1% of the cases, at least one of the top three models produced a prediction with a RMSD < 4.0Å. In the sampling stage, our sampling method produced near-native peptide binding modes (high or medium quality based on ligand RMSD (Lrms) for 95.0% of the bound docking cases (i.e., using bound protein structures), and 92.2% of the unbound docking cases (i.e., using unbound protein structures). In the scoring stage, at least one near-native peptide binding mode was ranked among the top 10 predictions (or the top 100 predictions) for 54.0% (81.0%) of the bound docking cases, and for 37.5% (59.4%) of the unbound docking cases. Compared with the existing methods for protein-peptide complex structure prediction, MDockPeP is computationally efficient and performs very well particularly on sampling near-native binding modes. Each docking calculation normally takes a few hours on a computational node of 24 processors. The details of the methods and results are described in the following sections.
3 Results
3.1 The criteria for assessment
The method of peptide structure modeling was evaluated by calculating both backbone RMSD (bRMSD) and heavy-atom RMSD (hRMSD) between the constructed peptide structures and the corresponding bound peptide structures in the peptiDB database. The sampling and scoring methods are assessed in terms of the three parameters defined by CAPRI for protein-protein and protein-peptide docking analysis (Méndez et al., 2003), ligand RMSD (Lrms), interface RMSD (Irms) and fraction of native contact (fnc). Notably, Lrms and Irms have been used in previous studies on protein-peptide docking assessment (Raveh et al., 2011, 2010; Trellet et al., 2013; Kurcinski et al., 2015; Blaszczyk et al., 2016; Schindler et al., 2015). However, these two parameters cannot reflect the side chain quality of the predicted peptide binding modes. In addition, the RMSD values are often dependent on the structural sizes (Irving et al., 2001). Therefore, in this work, besides Lrms and Irms, the fraction of native contacts (fnc) was also employed for peptide binding mode assessment. Lrms was calculated based on the backbone atoms of the peptide between the predicted binding mode and the native binding mode after the optimal superimposition of the protein structures. The unbound protein structure was matched onto the bound protein structure using the MatchMaker tool of UCSF Chimera (Pettersen et al., 2004). Irms was calculated based on the backbone atoms of the interface residues that are within 10.0Å of its binding partner. The interface residues were defined based on the experimental structure of the protein-peptide complex. fnc is the fraction of the correctly identified residue contacts between the protein and the peptide. A pair of residues were defined as a contact if any two heavy atoms in the two residues are within 5.0Å. The criteria for assessment are summarized in Table 1.
Table 1.
The criteria for the assessment of the predicted protein-peptide complex structures.
| Parameters | High quality | Medium quality | Low quality |
|---|---|---|---|
| Lrms | Lrms ≤ 3.0Å | 3.0Å < Lrms ≤ 5.5Å | Lrms > 5.5Å |
| Irms | Irms ≤ 1.0Å | 1.0Å < Irms ≤ 2.0Å | Irms > 2.0Å |
| fnc | fnc ≥ 80% | 50% ≤ fnc < 80% | fnc < 50% |
3.2 The Construction of the Initial Peptide Conformers
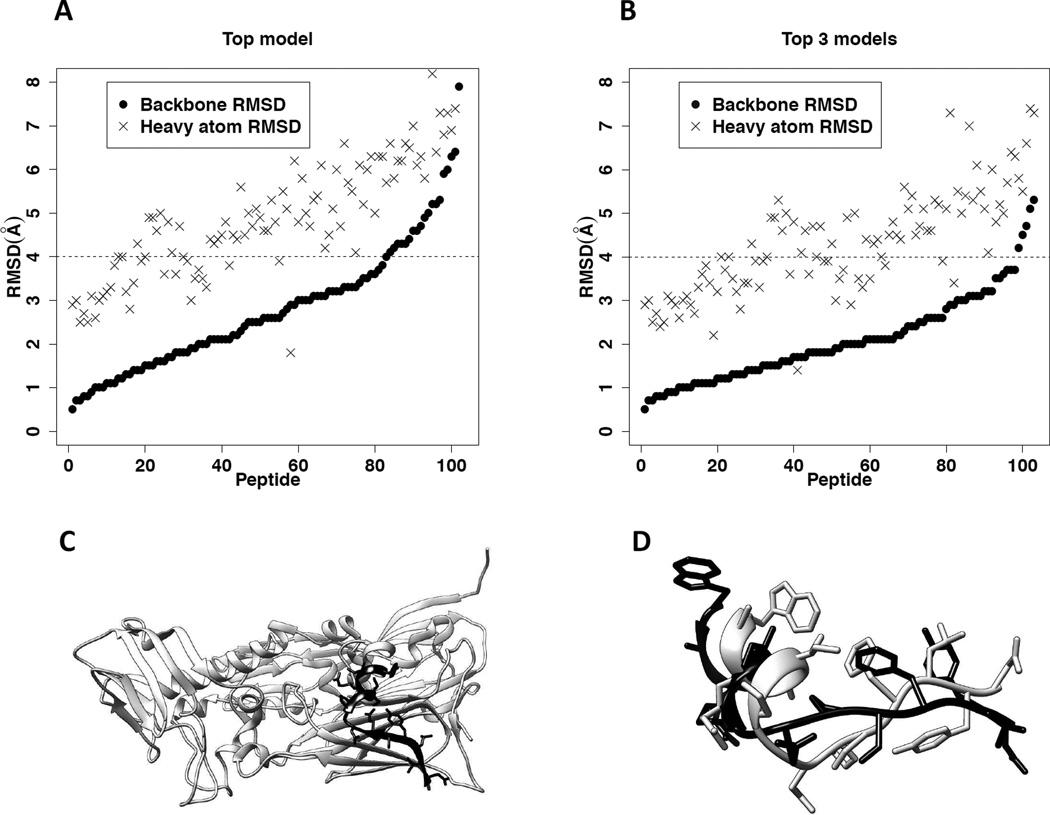
The 3D structures of the 103 peptides in the peptiDB database were constructed based on their sequences. Figure 2A shows bRMSD and hRMSD between the top model (i.e., the peptide conformer built based on the template with the highest sequence similarity to the query peptide) and the corresponding experimental bound structure for each peptide, and Figure 2B shows bRMSD and hRMSD of the best conformer (i.e., the conformer with the lowest bRMSD) among the top 3 models for each peptide. For 79.6% of the 103 peptides, bRMSD of the top model was below 4.0Å. The median value of the bRMSD for all the peptides equals 2.6Å. In 95.1% of the cases, bRMSD of the best peptide conformer among the top 3 models was below 4.0Å; the median value of bRMSD for all the cases was 1.9Å. The median values of hRMSD for the top model and top 3 models were 4.8Å and 4.3Å, respectively. Remarkably, in all the 103 cases, bRMSD of the best conformer among the top 3 peptide models was below 5.3 Å compared to the corresponding experimental bound peptide structure, as shown in Table S2.
Figure 2.
Modeling peptide conformers based on the template fragments of monomeric proteins for 103 bound peptides in peptiDB. Also see Table S2. A. The distributions of bRMSD and hRMSD between the top modeled conformer and the corresponding bound peptide structure for the 103 peptides. The horizontal axis shows individual peptide (ranging from 1 to 103). The black dashed line represents 4.0Å in bRMSD, the defined threshold for a successful prediction of the peptide conformation. B. The distributions of bRMSD and hRMSD between the best modeled conformer (i.e., the conformer with the lowest bRMSD) in the top 3 models and the corresponding bound peptide structure for the 103 peptides. C. The top template (amino acids 450 – 463 in PDB entry 3SAM, chain A) for the bound peptide in the protein-peptide complex 2BBA. The protein 3SAM is shown in ribbon diagram and colored light gray. The template fragment is highlighted in black, with their side chains displayed in stick mode. D. The superimposed top modeled peptide conformer and its corresponding bound peptide structure in pdb entry 2BBA. The modeled peptide structure is colored black, and the bound peptide structure is colored light gray.
It is also noticed that our peptide modeling method was more accurate on modeling backbone conformations than on side chain conformations (see Figure 2A and Figure 2B), probably because the side chains of the template protein fragments are more sensitive to the surrounding environment than the backbone atoms. For this reason, bRMSD rather than hRMSD was used in this study to control the switch between global rigid sampling and local flexible sampling.
For example, Figure 2C shows the top template used in our prediction (amino acids 450 – 463 in PDB entry 3SAM, chain A) for the bound peptide in the protein-peptide complex 2BBA. The backbone of the template fragment in 3SAM is displayed in ribbon representation (colored black), and its side chains are displayed in stick mode. The sequence similarity and sequence identity between the template fragment and the peptide are 78.6% and 50.0%, respectively. Figure 2D shows the superimposition between the modeled peptide conformer (black) and the corresponding experimental bound structure (light gray). bRMSD and hRMSD between the modeled conformer and the experimental bound structure are 3.1Å and 6.1Å, respectively.
3.3 The Sampling of the Peptide Binding Modes
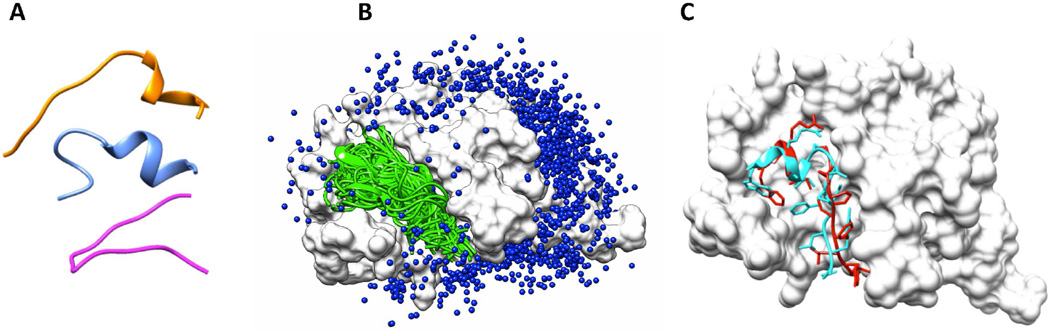
As described in the EXPERIMENTAL PROCEDURES section, the top three modeled peptide conformers are individually docked to the whole protein by switching between global rigid sampling and local flexible sampling. Taking the protein-peptide complex 2BBA as an example, Figure 3A shows the three initial conformations of this 14-mer peptide to be used for docking. Putative peptide binding modes are sampled over the whole surface of the bound protein structure, as shown in Figure 3B. The binding modes with Lrms < 5.5Å are displayed in ribbon diagram and the remaining modes are represented by the 7th alpha carbon atom of the peptide. Figure 3C shows a comparison between the best sampled binding mode (colored red) and the native binding mode (cyan). This mode is considered to be high quality for Lrms (2.97Å), and medium quality for Irms (1.20Å) and fnc (67.3%), respectively.
Figure 3.
An example of binding mode sampling. A. The three modeled peptide conformers based on the sequence of the peptide from the protein-peptide complex 2BBA. B. The sampled peptide binding modes on the whole surface of protein from complex 2BBA. The high-quality and medium-quality binding modes (Lrms < 5.5Å) are shown in ribbon and colored cyan. The low-quality binding modes are represented by the 7th Cα atom of the peptide and colored blue. C. The comparison between the best sampled binding mode (with Lrms = 2.97Å) and the native binding mode. The native binding mode is colored cyan and the sampled binding mode is colored red. Three representative failed cases are shown in Figure S2.
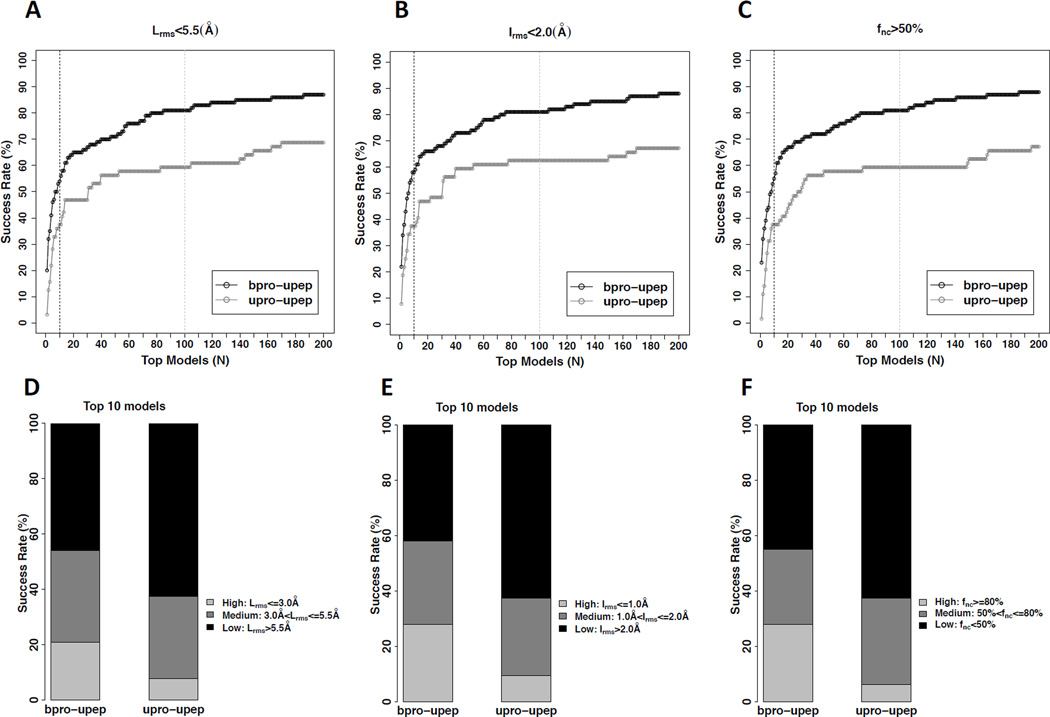
Our sampling strategy was systematically assessed using the 100 bound docking cases (i.e., bound protein and unbound peptide, denoted as bpro-upep) and 64 unbound docking cases (i.e., unbound protein and unbound peptide, denoted as upro-upep) in peptiDB. The sampled peptide binding modes were evaluated using Lrms, Irms and fnc, respectively (see Tables S3–S5). Figure 4A shows the success rates of peptide binding mode sampling for bound docking (bproupep) and unbound docking (upro-upep), using different values of Lrms as the respective thresholds for successful predictions. For each docking calculation, the binding mode sampling was defined to be a success if the Lrms of at least one sampled mode was less than the threshold value. MDockPeP successfully generated high-quality binding modes for 78.0% of the bound docking cases and medium-quality binding modes for 17.0% of the bound docking cases. Thus, the total success rate (high quality + medium quality) of peptide binding mode sampling is 95.0% for bound docking (bpro-upep). Remarkably, for the more challenging unbound docking cases in which the unbound protein structures were used, a high success rate (92.2%) was also achieved. The success rates for generation of high-quality binding modes and for generation of medium-quality binding modes were 59.4% and 32.8%, respectively, as shown in Figure 4B.
Figure 4.
The performance of binding mode sampling for both the bound docking cases and the unbound docking cases in peptiDB. Also see Tables S3–S5, Figure S1, and Figure S3. A. The success rates of peptide binding mode sampling using different values of Lrms as the thresholds for the bound docking cases (bpro-upep) and the unbound docking cases (upro-upep), respectively. Lrms = 3.0Å is considered as the threshold for the high-quality sampled binding mode, shown in the black dashed line. Lrms = 5.5Å is considered as the threshold for the medium-quality sampled binding mode, shown in the light gray dashed line. B. The performance of peptide binding mode sampling based on the criterion of Lrms for the bound docking cases and unbound docking cases, respectively. C. The relationship between the bRMSD of the best peptide conformer and the Lrms of the best sampled binding mode for the bound docking cases. The threshold for the effective peptide modeling (bRMSD = 4.0Å) is shown in the black vertical dashed line. The thresholds for the high-quality sampled binding mode (Lrms=3.0Å) and the medium-quality sampled binding mode (Lrms = 5.5Å) are shown in horizontal dashed lines and colored black and light gray, respectively. D. The relationship between the bRMSD of the best peptide conformer and the Lrms of the best sampled binding mode for the unbound docking cases.
The sampling performance based on Irms and fnc are plotted in Figure S1. If Irms was used for the evaluation of the success rates, MDockPeP generated near-native binding modes for 94.0% of the bound docking cases (77.0% for high quality, and 17.0% for medium quality), and for 85.9% of the unbound docking cases (high quality: 46.9%; medium quality: 39.0%). If fnc was used as the criterion, MDockPeP achieved a total success rate of 96% for the bound docking cases (high quality: 77%; medium quality: 19%) and 95.3% for the unbound docking cases (high quality: 40.6%; medium quality: 54.7%).
In summary, comparable success rates for both bound docking and unbound docking were achieved when different criteria (Lrms, Irms and fnc) were employed. Therefore, Lrms would be used as the primary criterion for the following analyses.
When Lrms was set as the criterion, MDockPeP failed to yield near-native binding modes (i.e., Lrms < 5.5Å) for 5 bound docking cases, 1YUC, 2A3I, 2FGR, 2O4J, and 2P0W. Interestingly, the proteins in 1YUC, 2A3I, and 2O4J belong to the same superfamily (i.e., nuclear receptors) and the bound peptides share the LXXLL binding motif (L is leucine and X stands for any residues). The protein-peptide interaction is mainly contributed by the interactions between the three leucine residues in the peptide and a small hydro phobic region on the protein surface. Relatively few contacts in these crystal structures could be the reason for the sampling failures. A similar reason could be responsible for the failure of 2FGR. For the case of 2P0W, the lowest Lrms of the sampled models was 6.7Å. The challenge on sampling in this case resulted from the facts that the number of residues in the peptide was 15 and that the lowest bRMSD of the initial peptide conformers was 4.2Å. The sampled modes with the lowest Lrms for 2A3I, 2FGR and 2P0W, are shown in Figure S2. It is noted that 2A3I was selected as a representative of the aforementioned three failed nuclear receptors.
Furthermore, the relationship between bRMSD of the best modeled peptide conformer and Lrms of the best sampled binding mode (the mode with the lowest Lrms) are plotted in Figure 4C and Figure 4D for bound docking and unbound docking, respectively. As seen in both panels, bRMSD and Lrms show very weak correlations, with the Pearson correlation coefficients of 0.197 (for bpro-upep) and 0.094 (for upro-upep), respectively. Encouragingly, in several cases, modeling of the peptide structures failed to generate high-quality conformers (bRMSD < 4.0Å), however, our sampling method still successfully produced medium-quality or even high-quality peptide binding modes (based on the Lrms criterion). The dependency of the sampling performance on the peptide size is also studied in Figure S3. Specifically, panel A and panel B in Figure S3 show the distribution of the Lrms of the best sampled binding mode as a function of the peptide length for the bound docking cases and the unbound docking cases, respectively; panel C and panel D show the distribution of the fnc of the best sampled binding mode (the mode with the highest fnc) as a function of the peptide length for the bound docking cases and the unbound docking cases, respectively. As we can see from Figure S3, the two metrics produce consistent result. Overall speaking, it is more difficult to generate high quality modes for long peptides. The finding is reasonable, because long peptides typically contain many rotatable bonds and thus require large configuration spaces for sampling.
3.4 Rescoring of the Sampled Peptide Binding Modes
The sampled peptide binding modes were ranked by the scoring function ITScorePeP as described in EXPERIMENTAL PROCEDURES. For any two modes with Lrms<4.0Å, only the mode with the lower score was kept. The success rates based on the Lrms, Irms, and fnc criteria, respectively, are plotted in Figure 5. Panels 5A–C show the rates for successfully ranking at least one near-native (i.e., medium-quality or high-quality) mode among the top N models, with respective to each criterion. Noticeably, bound docking (bpro-upep) achieved high success rates, namely, over 80% for all the three criteria when top 100 models were considered. The success rate decreased to around 60% for more challenging cases, unbound docking (upro-upep). The scoring results for considering only the top 10 models for each protein-peptide complex are shown in panels 5D–F. If using the criterion of Lrms, MDockPeP successfully predicted at least one near-native binding mode in the top 10 models for 54.0% of the bound docking cases (high quality: 21.0%; medium quality: 33.0%), and 37.5% of the unbound docking cases (high quality: 7.8%; medium quality: 29.7%), as shown in Figure 5D. Figure 5E and 5F show similar performances with the Irms criterion and the fnc criterion, respectively.
Figure 5.
The performance of of ranking the sampled peptide binding modes for both the bound docking cases and the unbound docking cases in peptiDB. Also see Tables S3–S5 and Figure S5. A. The success rates of ranking at least one near-native (i.e., medium-quality or high-quality) mode based on Lrms among the top N models for the bound docking cases (bpro-upep) and the unbound docking cases (upro-upep), respectively. The black dashed line and the light gray dashed line correspond to N = 10 and N = 100, respectively. B. The success rates based on Irms among the top N models for the bound docking cases (bpro-upep) and unbound docking cases (upro-upep), respectively. C. The success rates of ranking at least one near-native mode based on fnc among the top N models for the bound docking cases (bpro-upep) and unbound docking cases (upro-upep), respectively. D. The scoring performance using the top 10 modes based on the criterion of Lrms for the bound docking cases (bpro-upep) and unbound docking cases (uproupep), respectively. E. The scoring performance using the top 10 modes based on the criterion of Irms for the bound docking cases (bpro-upep) and unbound docking cases (upro-upep), respectively. F. The scoring performance using the top 10 modes based on the criterion of fnc for the bound docking cases (bpro-upep) and unbound docking cases (upro-upep), respectively.
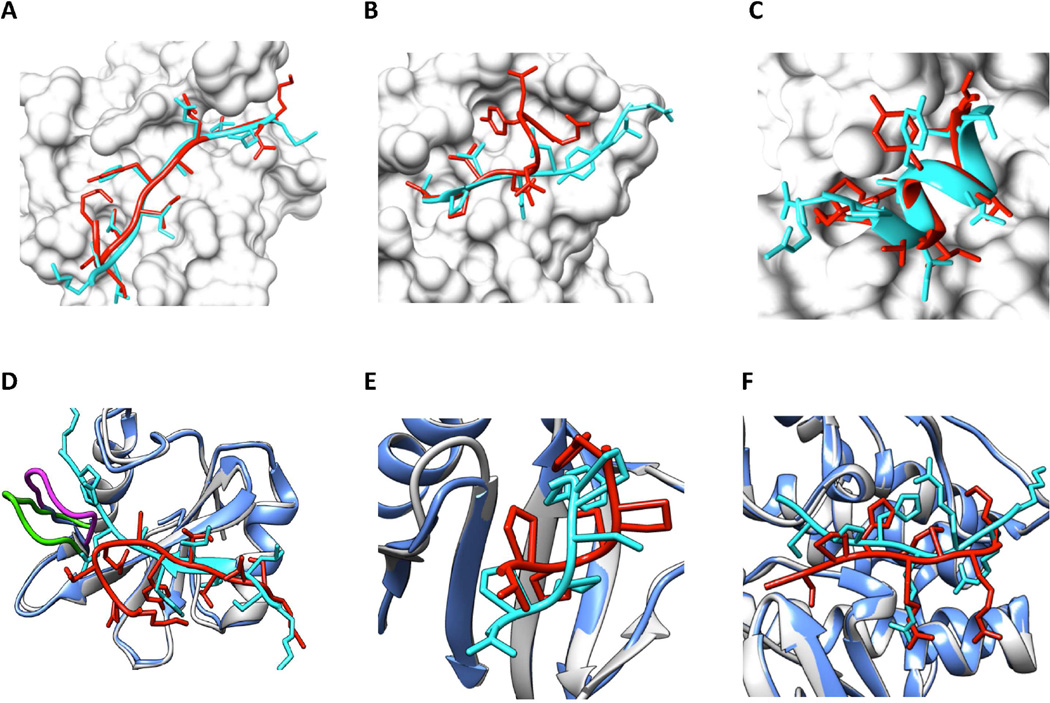
Figure 6 presents six examples for bound docking cases (A–C) and unbound docking cases (D–F). The experimental peptide bound structures are colored cyan, and the predicted peptide binding modes are colored red. The proteins in the bound docking cases (A–C) are represented by their molecular surfaces. For each unbound docking case (D–F), the unbound protein structure (shown in ribbon and colored light blue) is matched to the bound protein structure (shown in ribbon and colored light gray) using the MatchMaker tool of UCSF Chimera. Panel A shows a high-quality prediction of 1D4T (being ranked #1), with Lrms = 2.38Å, Irms = 0.89Å and fnc = 91.2%. Panel B shows a medium-quality model of 1MFG (#12), with Lrms=5.10Å, Irms = 1.81Å and fnc = 76.5%. Interestingly, in panel C for 1YMT, the predicted model (#4) is assessed with different qualities if different criteria are used. This peptide binding mode is considered as medium quality with the Irms criterion (1.11Å), but high quality for the Lrms criterion (2.52Å) and the fnc criterion (87.5%), respectively.
Figure 6.
Six examples for bound docking cases (A–C) and unbound docking cases (D–F). The experimental peptide bound structures are colored cyan, and the predicted peptide binding modes are colored red. Proteins in the bound docking cases (A–C) are represented by the surface and colored light gray. For each unbound docking case (D–F), the unbound protein structure (shown in ribbon and colored light blue) is matched to the bound protein structure (shown in ribbon and colored light gray) using UCSF Chimera’s MatchMaker tool. Also see Figure S4. A. The #1 predicted mode of 1D4T with Lrms = 2.38Å, Irms = 0.89Å and fnc = 91.2%. B. The #12 predicted mode of 1MFG with Lrms = 5.10Å, Irms = 1.81Å and fnc = 76.5%. C. The #4 predicted mode of 1YMT with Lrms = 2.52Å, Irms = 1.11Å and fnc = 87.5%. D. The #1 predicted mode of 1D4T (using the unbound protein structure: 1D1Z:C) with Lrms = 7.68Å, Irms = 2.89Å and fnc = 49.1%. E. The #2 predicted mode of 1DDV (using the unbound protein structure: 1I2H:A) with Lrms = 3.59Å, Irms = 1.23Å and fnc = 50.0%. F. The #6 predicted mode of 2C3I (using the unbound protein structure: 2J2I:B) with Lrms = 3.97Å, Irms = 1.15Å and fnc = 57.5%.
Figure 6D shows the top predicted binding mode for the protein-peptide complex 1D4T when the unbound protein structure (1D1Z:C) was used. This prediction is a low-quality model, with Lrms = 7.68Å, Irms = 2.89Å and fnc = 49.1%. The failure results from a large conformational change of a loop in the binding site (colored green for the bound protein and magenta for the unbound protein). Still, our predicted binding mode successfully captures the interactions exhibited in the experimental complex structure that are not near this loop. Panel E shows the 2nd ranked binding mode calculated with the unbound protein structure, 1I2H:A, of the protein-peptide complex 1DDV. This mode is a medium-quality prediction, with Lrms = 3.59Å, Irms = 1.23Å and fnc = 50.0%. Panel F shows the 6th ranked binding mode, using the unbound protein structure, 2J2I:B, for the protein-peptide complex 2C3I. This model is medium quality, with Lrms = 3.97Å, Irms = 1.15Å and fnc = 57.5%. The “score vs Lrms” relationships for these six examples are plotted in Figure S4.
4 Discussion
MDockPeP is an effective integration of peptide modeling and flexible docking. Based on the fact that the structure of the bound peptide can often be estimated by our peptide modeling method, the peptide conformation during flexible sampling is restricted to be close to the modeled peptide conformer (with bRMSD<5.5Å) by switching between global rigid sampling and local flexible sampling. The restriction of the peptide conformations significantly reduces the configuration space for docking, allowing flexible sampling of the peptide binding modes over the whole surface of the protein at the all-atom level. This strategy can be generalized to other docking studies such as protein-nucleic acid docking.
It is notable that only up to 3 peptide conformations are used for docking in MDockPeP. There are two reasons. First, at least one of these 3 conformations is not very far from the bound peptide conformation. Specifically, for 95.1% of the test cases, at least one of the top three models produced a prediction with bRMSD<4.0Å. Second, our docking procedure allows for peptide conformational flexibility (with bRMSD from the initially modeled peptide conformations up to 5.5Å).
It is also noticed that in the sampling stage (Stage 2) the Vina scoring function was used for scoring, whereas ITscorePeP is only used in the rescoring/ranking stage (Stage 3). ITScorePeP is different from our published statistical potential-based scoring functions in two aspects. First, the training set for ITScorePeP was changed to the flexible decoys that were sampled through our integrated global/flexible docking method for the protein-peptide complexes. Previously, the training sets were rigid decoys, for protein-ligand complexes (Huang and Zou, 2006), protein-protein complexes (Huang and Zou, 2008) or protein-RNA complexes (Huang and Zou, 2014), respectively. Second, the intramolecular energy of the peptide was included, in addition to the inter-molecular energy, due to the large peptide flexibility.
Unlike FlexPepDock and HADDOCK, MDockPeP does not require any knowledge about the peptide binding site. Certainly, the performance of MDockPeP will be improved if the binding site is specified. Figure S5 shows the scoring results that were re-calculated by keeping only the sampled binding modes having at least one heavy atom within 6.0 Å from the geometric center of the native binding mode. The success rates for the top 10 predictions were improved by 10% on average. However, in practice, it is usually difficult to define the boundary of the peptide binding site for docking. Even if a few residues on the protein are known to be involved in binding, the boundary may remain unclear because a peptide often binds to a protein in an extended conformation, forming a slender and tortuous interface that is challenging to predict a priori. Therefore, global docking is a big advantage of MDockPeP.
Compared with pepATTRACT, MDockPeP is more computationally efficient and easier to use. pepATTRACT consists of three stages of sampling including MD simulation-based refinement for 1000 protein-peptide complex models; this refinement stage typically takes 16 hours on a GPU unit (Schindler et al., 2015). MDockPeP involves only one sampling stage, which generally takes several hours on a computational node of 24 processors.
MDockPeP requires slightly more powerful computational resource than CABS-dock, however, CABS-dock samples the peptide binding modes based on coarse-grained peptide models (i.e., no side chains). The side chains of the anchor residues in a peptide play an important role in protein-peptide association. Furthermore, CABS-dock requires the secondary structure of the bound peptide for docking; if not known, the peptide secondary structure is predicted using PSI-PRED (Kurcinski et al., 2015; Blaszczyk et al., 2016). It is unclear whether PSI-PRED, a protein secondary structure prediction tool can be directly used for the secondary structure prediction for the bound peptide.
The sampling effectiveness of HADDOCK, CABS-dock and MDockPeP were assessed using similar databases that were prepared based on peptiDB. Although these databases are slightly different because of a few technical concerns (see EXPERIMENTAL PROCEDURES), they overlap for more than 95% of the cases. Specifically, using 97 bound docking cases and 62 unbound docking cases, HADDOCK generated near-native binding modes for 79.4% of the bound docking cases (high quality: 23.7%; medium quality: 55.7%), and 69.4% for unbound docking cases (high quality: 16.1%; medium quality: 53.3%), based on the Irms criterion (Trellet et al., 2013). CABS-dock generated near-native binding modes for 84% of the 103 bound docking cases (high quality: 50%; medium quality: 34%), and 85% of the 68 unbound docking cases (high quality: 35%; medium quality 50%), assessed with the Lrms criterion (Kurcinski et al., 2015; Blaszczyk et al., 2016), pepATTRACT was evaluated using the 103 bound docking cases and 80 unbound docking cases from a modified version of peptiDB. With the Irms criterion, pepATTRACT yielded near-native binding modes for 70% of the cases (high quality: 20%; medium: quality 50%). For the 62 unbound docking cases that overlap with the test set of HADDOCK, the corresponding success rate was 73%(Schindler et al., 2015). Compared with HADDOCK, CABS-dock and pep-ATTRACT, MDockPeP showed a much better performance. For the 100 bound docking cases and 64 unbound docking cases, based on the Lrms criterion, MDockPeP generated near-native binding modes for 95.0% of the bound docking cases (high quality: 78.0%; medium quality: 17.0%), and for 92.2% of the unbound docking cases (high quality: 59.4%; medium quality: 32.8%). Based on the Irms criterion, the success rates were 94% for the bound docking cases (high quality: 77.0%; medium quality: 17.0%), and 85.9% for the unbound docking cases (high: 46.9%; medium: 39.0%).
The direct comparisons of the scoring performances among MDockPeP, HADDOCK and pep-ATTRACT are difficult, because HADDOCK and pepATTRACT use cluster-based ranking (Trellet et al., 2013; Schindler et al., 2015). Here, the scoring performances on the top 10 predictions were compared between MDockPeP and CABS-dock. Specifically, using the Lrms criterion, CABS-dock predicted near-native modes among the top 10 models for 53% of the 103 bound docking cases (high quality: 13%; medium quality 40%), and 37% of the 68 unbound docking cases (high quality: 10%; medium quality 27%) (Kurcinski et al., 2015). MDockPeP achieved a slightly better performance than CABS-dock, with 54.0% for the 100 bound docking cases (high quality: 21.0%; medium quality: 33.0%), and 37.5% for the 64 unbound docking cases (high quality: 7.8% and medium quality: 29.7%). Furthermore, unlike CABS-dock, which provides only a few scoring modes because these modes correspond to the centroids of the clusters from K-means clustering, MDockPeP ranks modes based on ITScorePeP, which can output many ranked modes. For example, if the top 100 modes were considered, the success rates of MDockPeP increased to 81.0% and 59.4% for the bound docking cases and unbound docking cases, respectively. These modes can be further refined and re-scored by computationally intensive methods such as MD simulations.
5 Conclusion
We have developed a blind docking method for protein-peptide complex structure prediction, referred to as MDockPeP. MDockPeP requires the sequence of a peptide and the 3D structure of a protein. Starting with the given peptide sequence, MDockPeP globally searches for all-atom, flexible peptide binding modes. The method consists of three stages: (1) Modeling peptide conformers based on the sequence; (2) Sampling flexible peptide binding modes on the whole protein surface; (3) Ranking the sampled binding modes according to their energy scores based on the iterative knowledge-based scoring functions (ITScorePeP). MDockPeP was extensively tested on both bound docking cases and unbound docking cases. Compared with the existing methods for protein-peptide complex structure prediction, MDockPeP is computationally efficient and performed very well particularly on sampling near-native binding modes. MDockPeP can be used as a standing-alone tool for protein-peptide complex structure prediction or as an initial-stage sampling tool for protein-peptide structure refinement programs.
6 Experimental Procedures
6.1 The Construction of the Peptide Conformers
The non-redundant protein database provided by MODELLER (Webb and Sali, 2014) (pdb 95.pir.gz, updated on September 17, 2015) is used for template search for a given peptide sequence. Specifically, proteins with sequence lengths ≤ 50 are removed from the database in order to ensure that the template is a protein fragment rather than a peptide. Next, fastm36 (Mackey et al., 2002) is employed to scan the protein database to search for fragments with high sequence similarity to the query peptide. The E-value cutoff is set to 10000 to warrant sufficient fragment hits. The sequence similarity and sequence identity between the query peptide and each fragment hit are then calculated using the global sequence alignment program, EMBOSS Needle (Rice et al., 2000). Fragments with sequence identities lower than 50% are discarded. The remaining fragments are re-ranked by the sequence similarity. The fragments with the same sequence similarity are ordered according to their sequence identities. The resulting global alignments are used as the input for MODELLER to construct peptide conformers based on the structures of the template fragments. The generated peptide models are clustered with a bRMSD cutoff. Namely, for any two peptide conformers with their bRMSD smaller than the specified cutoff, only the peptide conformer having a higher sequence similarity with its template fragment is kept. The cutoff is set to 3.0Å if the peptide sequence length is shorter than 11, and to 4.0Å otherwise. The top 3 peptide conformers are saved for docking.
In a few cases, the program outputs fewer than 3 peptide conformers because of clustering. In summary, up to 3 peptide conformers are used as the input for the next sampling stage.
6.2 The Global, Flexible Sampling of the Peptide Binding Modes
Up to 3 peptide conformers built from Stage 1 are independently docked onto the whole surface of the protein, using a protocol modified from the protein-ligand docking software AutoDock Vina (Trott and Olson, 2010). AutoDock Vina cannot be directly applied to protein-peptide docking, because peptides normally contain many more rotatable bonds than typical ligand molecules and because Vina’s scoring function (Vina score) is not sufficiently accurate to distinguish the native binding modes from nonnative binding modes for even short peptides (Rentzsch and Renard, 2015). Therefore, in our docking protocol, instead of docking the peptide to a local pocket of the protein and exporting only a few top binding modes ranked by Vina score, each initial peptide conformer is docked to the whole protein by switching between global rigid sampling and local flexible sampling. Up to 20,000 modes ranked by Vina score are outputted as the putative binding modes. The respective modes generated from the 3 initial peptide conformers are then combined for further scoring and ranking. The details of this sampling procedure are described as follows.
6.2.1 The basic settings for AutoDock Vina
1. The protein and the peptide
The protein is treated as a rigid molecule. The peptide is set as a flexible molecule and the torsion tree is built with AutoDockTools using the default parameters (Morris et al., 2009). Given a peptide conformer with n rotatable bonds, a peptide binding mode is uniquely determined by n+6 variables: {x, y, z, ψ, θ, φ}, which determine the location and orientation of the peptide, and {χ1, χ2, …, χn}, which determine the conformation of the peptide. The bond angles and bond lengths are fixed during docking calculations.
2. The grid box
The center of the grid box is set to ((xmin + xmax)/2, (ymin + ymax)/2, (zmin + zmax)/2). The box dimensions are set to {xmax − xmin + 40, ymax − ymin + 40, zmax − zmin + 40}. Here, {xmin, xmax, ymin, ymax, zmin, zmax} represent the minimum and maximum values of the atomic coordinates of the protein in the three dimensions, respectively. The grid box covers the whole protein structure and an extension of 20 Å in each dimension so as to also cover the peptide.
3. The exhaustiveness
The value of exhaustiveness is set to 500 for protein-peptide docking, namely, each docking calculation contains 500 independent runs. For each run, the number of steps (N) for the iterated local search (ILS) global optimizer (Baxter, 1981) is determined by the number of torsional angles n and the number of movable atoms m. The default parameters of AutoDock Vina are used in this study:
| (1) |
6.2.2 The sampling procedure
Each independent docking run is performed based on a protocol modified from AutoDock Vina. The details are described as follows.
1. Rigid sampling
The initial peptide conformer is rigidly docked onto the whole surface of the protein by randomly generating up to 100,000 orientations, with each orientation characterized by {x, y, z, ψ, θ, φ}. Specifically, the positional variables {x, y, z} are randomly and equally sampled in the grid box, and the Euler angles ψ, θ, φ are randomly and equally sampled in the angular space. Among these 100, 000 randomly sampled binding modes, the mode with the lowest Vina score is saved as the initial mode for flexible sampling in the next step.
2. Flexible sampling
In this step, starting with the binding mode generated from rigid docking, flexible sampling is performed by successively searching the configuration space of the peptide, {x, y, z, ψ, θ, φ, χ1, χ2, …, χn}, using the ILS global optimizer in AutoDock Vina guided by Vina score. When each configurational change is accepted, the peptide conformation is compared with the initial peptide conformation. If bRMSD is larger than 5.5Å, the peptide conformation is restored to the initial peptide conformation and Step 1 (rigid sampling) is repeated. Otherwise, the ILS-based flexible sampling is continued until this run is completed (i.e., when the number of ILS steps reaches N). Up to top 20,000 non-redundant modes ranked by Vina score are kept for each run. Here, the definition of non-redundancy is that for any two modes with heavy atom RMSD (hRMSD) less than 2.0Å, only the mode with a more negative score is kept.
To restrict the amount of peptide conformational change generated in each flexible sampling step, if the operation is to rotate a rotatable bond, the torsional angle of this bond is set to within 30° around the corresponding value in the initial peptide conformation. This restriction does not prevent other peptide torsional angles from large changes, because the local refinement algorithm of AutoDock Vina can dramatically change the peptide torsional angles.
3. Merging the results
The binding modes generated from different docking runs are merged. For any two modes with hRMSD < 2.0Å, only the mode with a more negative Vina score is kept. Up to 20, 000 merged binding modes based on each initial peptide conformation are kept for rescoring.
6.3 The rescoring of the sampled binding modes
The sampled modes based on up to 3 initial peptide conformations are merged, resulting in up to 60, 000 putative binding modes. These putative binding modes are then rescored with ITScorePeP, based on the following equation:
| (2) |
Here, Einter stands for the inter-energy score, which equals the sum of the atomic pairwise potentials between the protein and the peptide. Eintra stands for the intra-energy score of the peptide, which is the sum of the atomic pairwise potentials among the non-neighboring residues in the peptide. i and j represent the atom types of an atom pair. A total of 20 atom types are defined by classifying the atoms in the standard 20 amino acids based on their covalent connections (see Table 1 in (Huang and Zou, 2011)). r is the distance between the atom pair. rcut is the cutoff distance for atomic pairwise interactions, which is set to 8.0Å. uij(r) is the statistical potential for atom pair ij at distance r. The statistical potentials are symmetric for atom pairs, namely, uij(r) equals uji(r) The details of the derivation of ITScorePeP are described in the Appendix.
6.4 The peptiDB benchmarking database
Our docking strategy was assessed using the protein-peptide benchmarking database, peptiDB. This database was originally developed by Schueler-Furman and co-workers (London et al., 2010) and was later updated by Bonvin and colleagues (Trellet et al., 2013). The database consists of 103 non-redundant protein-peptide complexes. Among them, unbound protein structures are available for 69 complexes. Following these authors’ definition, a bound protein structure refers to the conformation of the protein bound with the specified peptide. An unbound protein structure refers to the conformation of the same protein in the absence of a peptide.
All the peptides in the peptiDB database (a total of 103) were used to assess our method on construction of initial peptide structures. However, for the assessment of our docking and scoring methods, three bound cases that are inappropriate for blind docking (1H6W, 1SFI, and 2D5W) were removed from the database. Specifically, 1H6W and 2D5W were discarded because their peptide binding sites are inaccessible. 1SFI was discarded because its bound peptide is cyclic. Thus, the unbound protein structure of 1SFI (i.e., 1UTN chain A) was also removed. (It is noted that 1H6W and 2D5W do not have unboud protein structures in the database.) In addition, four unbound protein structures were removed from the database in our docking study. Specifically, the unbound protein structure 1JWT for the protein-peptide complex 1VZQ was removed because the pdb file of 1JWT contains problematic coordinates. The unbound protein structure 3NSQ for 2P1T was removed because the C-terminus of this protein experiences a huge conformational change, switching from being far apart from the binding site (in 3NSQ) to being part of the binding site in the bound structure. The unbound protein structures 2YQL and 1QBH of 2PUY and 3D9T, respectively, were removed because 2YQL and 1QBH are NMR structures. In summary, a total of 100 bound cases and 64 unbound cases were used to assess our sampling strategy and scoring function.
Because our statistical potential-based scoring function requires a training set of protein-peptide structures, a 3-fold cross-validation was used to assess the scoring function in order to avoid overlap between the training set and the test set. Specifically, the above 100 bound cases were randomly grouped into three subsets and listed in Table S1. Any two of these three subsets were combined into a training set, and the remaining subset was treated as a test set (Efron and Stein, 1981).
Highlights.
MDockPeP docks the all-atom, flexible peptide onto the whole protein.
MDockPeP requires only the peptide sequence and the protein structure.
MDockPeP achieves significantly better performance than other existing docking methods.
It is suitable for large-scale applications.
Acknowledgments
This work is supported by NSF CAREER Award DBI-0953839 and the NIH R01GM109980 (XZ). The computations were performed on the high performance computing infrastructure supported by NSF CNS-1429294 (PI: Chi-Ren Shyu) and the HPC resources supported by the University of Missouri Bioinformatics Consortium (UMBC).
Appendix
9.1 The derivation of ITScorePeP
The main idea for deriving ITScorePeP is to iteratively adjust the pairwise statistical potentials by comparing the observed pair distribution functions calculated from the native binding modes and the predicted pair distribution functions calculated from the decoys (including the native binding modes) for each iterative step, with each decoy carrying a Boltzmann weight calculated based on the statistical potentials of the current step. The iteration is terminated when the native binding mode of every complex has the lowest score compared with its decoys. The idea is described by the following equation:
| (3) |
Here, is the pairwise statistical potential of atom pair ij in the k-th step, and is the updated interaction potential in the next step. λ is a parameter that controls the speed of convergence and is set to 0.5 in the present study.
Given a set of initial potentials , the potentials are updated based on the above equation until all the native binding modes have the lowest scores compared with their decoys. Here, the energy score associated with a putative binding mode is calculated by
| (4) |
To account for the fluctuations in the pairwise potentials caused by sparse data and inaccuracies in the atomic coordinates of the experimental structures, the final potentials for the i-th bin in distance are smoothed by the weighted average of 1 : 2 : 4 : 2 : 1 of the potentials from bins (i − 2) to (i + 2).
9.2 The calculation of and
is calculated from the experimental protein-peptide complex structures by the following equation:
| (5) |
where is the number density of atom pair ij in a spherical shell of radius r − Δr/2 to r + Δr/2, and is the number density in a reference sphere with a radius of Rmax. Here, the bin size Δr is set as 0.1Å, and the radius of the reference sphere Rmax is set as 10Å. The atomic pair densities and are calculated as:
| (6) |
where M is the number of protein-peptide complexes in the training set, and is the number of atom pair ij in the spherical shell for the m-th experimental protein-peptide complex structure. V(Rmax) equals , which is the volume of the reference sphere. equals which is the total number of atom pair ij in the reference sphere for the m-th experimental protein-peptide complex. To reduce the local correlation effects of covalent bonds, the atom pairs between residue l and residue l + m of the peptide are not counted if m < 5. The atom pairs within a protein structure are not counted, because the protein structure is fixed in the present study. To ensure sufficient statistics, the interactions between atom pairs with fewer than 400 occurrences (i.e., ) are ignored.
The initial potential is set as the combination of the potential mean force ωij(r) and the van der Waals (VDW) potential νij(r):
where ωij(r) equals , and νij(r) is the Lennard-Jones 6–12 potential with the VDW radii taken from the AMBER force field. The well depth of νij(r) is set to three times of the corresponding value given in the AMBER force field to make the potential minima of νij(r) and ωij(r) comparable. The maximum potential for is set to 10.0 in the present study to provide clash penalty at short distances.
9.3 The calculation of
is calculated from the protein-peptide decoys by the following equation:
| (8) |
where and are the predicted number densities of atom pair ij in the spherical shell (with radius r and thickness Δr) and in the reference sphere (with radius Rmax), respectively. and are calculated as the Boltzmann-weighted pair frequencies over different binding modes in the k-th iterative cycle:
| (9) |
where and are the numbers of atom pair ij in the spherical shell and in the reference sphere for the l-th mode of the m-th complex, respectively. Lm is the total number of modes for the m-th complex. is the probability for the m-th complex to occupy the l-th state calculated with the potentials in the k-th step based on the Boltzmann distribution:
| (10) |
where β = 1/KBT. β is set to 1 in this study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Contributions
C.Y., X.X and X.Z. conducted the experiments. C.Y., X.X and X.Z. designed the experiments and wrote the paper.
References
- Antes I. Dynadock: A new molecular dynamics-based algorithm for protein–peptide docking including receptor flexibility. Proteins. 2010;78:1084–1104. doi: 10.1002/prot.22629. [DOI] [PubMed] [Google Scholar]
- Baxter J. Local optima avoidance in depot location. J. Oper. Res. Soc. 1981;32:815–819. [Google Scholar]
- Ben-Shimon A, Niv MY. Anchordock: blind and flexible anchor-driven peptide docking. Structure. 2015;23:929–940. doi: 10.1016/j.str.2015.03.010. [DOI] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat T, Weissig H, Shindyalov IN, Bourne PE. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaszczyk M, Kurcinski M, Kouza M, Wieteska L, Debinski A, Kolinski A, Kmiecik S. Modeling of protein–peptide interactions using the cabs-dock web server for binding site search and flexible docking. Methods. 2016;93:72–83. doi: 10.1016/j.ymeth.2015.07.004. [DOI] [PubMed] [Google Scholar]
- Craik DJ, Fairlie DP, Liras S, Price D. The future of peptide-based drugs. Chem Biol Drug Des. 2013;81:136–147. doi: 10.1111/cbdd.12055. [DOI] [PubMed] [Google Scholar]
- Dagliyan O, Proctor EA, D’Auria KM, Ding F, Dokholyan NV. Structural and dynamic determinants of protein-peptide recognition. Structure. 2011;19:1837–1845. doi: 10.1016/j.str.2011.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Stein C. The jackknife estimate of variance. Ann. Stat. 1981;9:586–596. [Google Scholar]
- Fosgerau K, Hoffmann T. Peptide therapeutics: current status and future directions. Drug Discovery Today. 2015;20:122–128. doi: 10.1016/j.drudis.2014.10.003. [DOI] [PubMed] [Google Scholar]
- Hetényi C, van der Spoel D. Efficient docking of peptides to proteins without prior knowledge of the binding site. Protein Sci. 2002;11:1729–1737. doi: 10.1110/ps.0202302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S-Y, Zou X. An iterative knowledge-based scoring function to predict protein–ligand interactions: I. derivation of interaction potentials. J. Comput. Chem. 2006;27:1866–1875. doi: 10.1002/jcc.20504. [DOI] [PubMed] [Google Scholar]
- Huang S-Y, Zou X. An iterative knowledge-based scoring function for protein–protein recognition. Proteins. 2008;72:557–579. doi: 10.1002/prot.21949. [DOI] [PubMed] [Google Scholar]
- Huang S-Y, Zou X. Statistical mechanics-based method to extract atomic distance-dependent potentials from protein structures. Proteins. 2011;79:2648–2661. doi: 10.1002/prot.23086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S-Y, Zou X. A knowledge-based scoring function for protein-rna interactions derived from a statistical mechanics-based iterative method. Nucleic Acids Res. 2014;42:e55–e55. doi: 10.1093/nar/gku077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z, Wong CF. Docking flexible peptide to flexible protein by molecular dynamics using two implicit-solvent models: an evaluation in protein kinase and phosphatase systems. J. Phys. Chem. B. 2009;113:14343–14354. doi: 10.1021/jp907375b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irving JA, Whisstock JC, Lesk AM. Protein structural alignments and functional genomics. Proteins. 2001;42:378–382. doi: 10.1002/1097-0134(20010215)42:3<378::aid-prot70>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Kippen AD, Sancho J, Fersht AR. Folding of barnase in parts. Biochemistry. 1994;33:3778–3786. doi: 10.1021/bi00178a039. [DOI] [PubMed] [Google Scholar]
- Kurcinski M, Jamroz M, Blaszczyk M, Kolinski A, Kmiecik S. Cabs-dock web server for the flexible docking of peptides to proteins without prior knowledge of the binding site. Nucleic Acids Res. 2015;43:W419–W424. doi: 10.1093/nar/gkv456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavi A, Ngan CH, Movshovitz-Attias D, Bohnuud T, Yueh C, Beglov D, Schueler-Furman O, Kozakov D. Detection of peptide-binding sites on protein surfaces: The first step toward the modeling and targeting of peptide-mediated interactions. Proteins. 2013;81:2096–2105. doi: 10.1002/prot.24422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Heo L, Lee MS, Seok C. Galaxypepdock: a protein–peptide docking tool based on interaction similarity and energy optimization. Nucleic Acids Res. 2015;43:W431–w435. doi: 10.1093/nar/gkv495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Dominy BN, Shakhnovich EI. Structural mining: self-consistent design on flexible protein-peptide docking and transferable binding affinity potential. J. Am. Chem. Soc. 2004;126:8515–8528. doi: 10.1021/ja032018q. [DOI] [PubMed] [Google Scholar]
- London N, Movshovitz-Attias D, Schueler-Furman O. The structural basis of peptide- protein binding strategies. Structure. 2010;18:188–199. doi: 10.1016/j.str.2009.11.012. [DOI] [PubMed] [Google Scholar]
- Mackey AJ, Haystead TA, Pearson WR. Getting more from less algorithms for rapid protein identification with multiple short peptide sequences. Mol. Cell. Proteomics. 2002;1:139–147. doi: 10.1074/mcp.m100004-mcp200. [DOI] [PubMed] [Google Scholar]
- McGuffin LJ, Bryson K, Jones DT. The psipred protein structure prediction server. Bioinformatics. 2000;16:404–405. doi: 10.1093/bioinformatics/16.4.404. [DOI] [PubMed] [Google Scholar]
- Méndez R, Leplae R, De Maria L, Wodak SJ. Assessment of blind predictions of protein–protein interactions: current status of docking methods. Proteins. 2003;52:51–67. doi: 10.1002/prot.10393. [DOI] [PubMed] [Google Scholar]
- Morris GM, Huey R, Lindstrom W, Sanner MF, Belew RK, Goodsell DS, Olson AJ. Autodock4 and autodocktools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niv MY, Weinstein H. A flexible docking procedure for the exploration of peptide binding selectivity to known structures and homology models of pdz domains. J. Am. Chem. Soc. 2005;127:14072–14079. doi: 10.1021/ja054195s. [DOI] [PubMed] [Google Scholar]
- Petsalaki E, Russell RB. Peptide-mediated interactions in biological systems: new discoveries and applications. Curr. Opin. Biotechnol. 2008;19:344–350. doi: 10.1016/j.copbio.2008.06.004. [DOI] [PubMed] [Google Scholar]
- Petsalaki E, Stark A, García-Urdiales E, Russell RB. Accurate prediction of peptide binding sites on protein surfaces. PLoS Comput. Biol. 2009;5:e1000335. doi: 10.1371/journal.pcbi.1000335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimeraa visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Raveh B, London N, Schueler-Furman O. Sub-angstrom modeling of complexes between flexible peptides and globular proteins. Proteins. 2010;78:2029–2040. doi: 10.1002/prot.22716. [DOI] [PubMed] [Google Scholar]
- Raveh B, London N, Zimmerman L, Schueler-Furman O. Rosetta flexpepdock ab-initio: simultaneous folding, docking and refinement of peptides onto their receptors. PLOS ONE. 2011;6:e18934. doi: 10.1371/journal.pone.0018934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rentzsch R, Renard BY. Docking small peptides remains a great challenge: an assessment using autodock vina. Brief. Bioinform. 2015;16:1045–1056. doi: 10.1093/bib/bbv008. [DOI] [PubMed] [Google Scholar]
- Rice P, Longden I, Bleasby A, et al. Emboss: the european molecular biology open software suite. Trends Genet. 2000;16:276–277. doi: 10.1016/s0168-9525(00)02024-2. [DOI] [PubMed] [Google Scholar]
- Saladin A, Rey J, Thévenet P, Zacharias M, Moroy G, Tufféry P. Pepsitefinder: a tool for the blind identification of peptide binding sites on protein surfaces. Nucleic Acids Res. 2014;42:W221–W226. doi: 10.1093/nar/gku404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindler CE, de Vries SJ, Zacharias M. Fully blind peptide-protein docking with pepattract. Structure. 2015;23:1507–1515. doi: 10.1016/j.str.2015.05.021. [DOI] [PubMed] [Google Scholar]
- Singh H, Raghava G. Propred: prediction of hla-dr binding sites. Bioinformatics. 2001;17:1236–1237. doi: 10.1093/bioinformatics/17.12.1236. [DOI] [PubMed] [Google Scholar]
- Singh H, Raghava G. Propred1: prediction of promiscuous mhc class-i binding sites. Bioinformatics. 2003;19:1009–1014. doi: 10.1093/bioinformatics/btg108. [DOI] [PubMed] [Google Scholar]
- Trabuco LG, Lise S, Petsalaki E, Russell RB. Pepsite: prediction of peptide-binding sites from protein surfaces. Nucleic Acids Res. 2012;40:W423–w427. doi: 10.1093/nar/gks398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trellet M, Melquiond AS, Bonvin AM. A unified conformational selection and induced fit approach to protein-peptide docking. PLOS ONE. 2013;8:e58769. doi: 10.1371/journal.pone.0058769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trott O, Olson AJ. Autodock vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010;31:455–461. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanhee P, Stricher F, Baeten L, Verschueren E, Lenaerts T, Serrano L, Rousseau F, Schymkowitz J. Protein-peptide interactions adopt the same structural motifs as monomeric protein folds. Structure. 2009;17:1128–1136. doi: 10.1016/j.str.2009.06.013. [DOI] [PubMed] [Google Scholar]
- Verschueren E, Vanhee P, Rousseau F, Schymkowitz J, Serrano L. Protein-peptide complex prediction through fragment interaction patterns. Structure. 2013;21:789–797. doi: 10.1016/j.str.2013.02.023. [DOI] [PubMed] [Google Scholar]
- Webb B, Sali A. Comparative protein structure modeling using modeller. Curr Protoc Bioinformatics. 2014 doi: 10.1002/0471250953.bi0506s47. [DOI] [PubMed] [Google Scholar]
- Wells JA, McClendon CL. Reaching for high-hanging fruit in drug discovery at protein–protein interfaces. Nature. 2007;450:1001–1009. doi: 10.1038/nature06526. [DOI] [PubMed] [Google Scholar]
- Yan C, Zou X. Predicting peptide binding sites on protein surfaces by clustering chemical interactions. J. Comput. Chem. 2015;36:49–61. doi: 10.1002/jcc.23771. [DOI] [PubMed] [Google Scholar]
- Zhang C, Cornette JL, Delisi C. Consistency in structural energetics of protein folding and peptide recognition. Protein Sci. 1997;6:1057–1064. doi: 10.1002/pro.5560060512. [DOI] [PMC free article] [PubMed] [Google Scholar]