Population Pharmacokinetic and Pharmacodynamic Modeling Analysis of GCC‐4401C, a Novel Direct Factor Xa Inhibitor, in Healthy Volunteers

Abstract

GCC‐4401C, an orally active direct factor Xa inhibitor that is similar to rivaroxaban, is currently under development for venous thromboembolic disease (VTE). The purpose of this study was to characterize the pharmacokinetics (PKs) and pharmacodynamics (PDs) of GCC‐4401C by population modeling analysis and to predict proper dosage regimens compared to rivaroxaban using data from two phase I clinical studies. Plasma GCC‐4401C concentrations over time were best described by a two‐compartment linear model and body weight was associated with central volume of distribution. Relevant PD markers generally changed in a dose‐dependent manner and were described well with sigmoid, simple maximum effect, or linear models. GCC‐4401C was absorbed more rapidly than rivaroxaban. Comparisons based on simulations of PD marker changes over time suggest that 20 mg and 40 mg of GCC‐4401C administered under fasted status are comparable to 10 mg and 20 mg of rivaroxaban under fed status.

Venous thromboembolic disease (VTE), including deep vein thrombosis and pulmonary embolism, is common, with incidence rates of nearly 1–2 cases per 1,000 people in the general population.1, 2 Patients with deep vein thrombosis and/or pulmonary embolism have increased morbidity and mortality, and survival after the disease is worse than expected.3, 4, 5 Standard management of VTE uses intravenous or subcutaneous low‐molecular‐weight heparin (LMWH) followed by long‐term treatment with vitamin K antagonists (VKAs).6 VKAs are effective for VTE, but their use is complicated by a narrow therapeutic window and drug interactions, requiring frequent prothrombin time (PT) monitoring and dose adjustments, as well as parenteral administration.6 Non‐VKA oral anticoagulants have been developed providing similar or improved efficacy and safety with convenience of oral administration,7 and are recommended by some guidelines.8, 9 Rivaroxaban, a direct inhibitor of coagulation factor Xa, is the most representative example of Non‐VKA oral anticoagulants.10, 11, 12 It reaches peak plasma concentration (C_max) levels 2–4 hours following oral administration, and shows dose‐dependent bioavailability. Although the bioavailability of rivaroxaban is high (80–100%), independent of food up to 10 mg, bioavailability decreases at >10 mg under fasting status, which is maintained high when the drugs are taken with food, as reported that mean area under concentration time curve and C_max of rivaroxaban increase by 39% and 76% with food, respectively.13

GCC‐4401C is a novel, oral, direct factor Xa inhibitor intended for use in the prevention and treatment of VTE, which is currently under development. It is a novel molecule with the formula (S)−5‐chloro‐N‐((3‐(4‐(5,6‐dihydro‐1,2,4‐triazin‐1(4H)‐yl)phenyl)−2‐oxooxazolidin‐5‐yl)methyl)thiophene‐2‐carboxamide methanesulfonate (US patent No. 8,178,525), which is similar to rivaroxaban in structure (Supplementary Figure S1). In a human mass balance study, GCC‐4401C was the predominant circulating compound in plasma accounting for 58.4% of the high performance radioactive fractions recovered. The proposed major metabolic routes of GCC‐4401C in humans are oxidation and dehydrogenation by cytochrome P450, 2D6, 3A4, and others (unpublished data). The primary pharmacodynamic (PD) activity of GCC‐4401C showed dose‐dependent inhibition of human factor Xa with prolonged PT and activated partial thromboplastin time (aPTT). GCC‐4401C showed equipotent anticoagulant activity to rivaroxaban. In a rat arteriovenous shunt model, GCC4401C and rivaroxaban reduced thrombus formation and showed similar dose‐response pattern, whereas ED50s (dose corresponding to 50% of maximal effect) of both compounds were 5 mg/kg (unpublished data).

A first‐in‐human single‐ascending dose (SAD) study and a single and multiple‐ascending dose (S&MAD) study for GCC‐4401C were conducted to evaluate PD of GCC‐4401C and compare with rivaroxaban, as well as tolerability and pharmacokinetics (PKs). The SAD study evaluated plasma and urine PKs of GCC‐4401C, and the S&MAD study compared GCC‐4401C to rivaroxaban. For PD evaluation, PT, aPTT, coagulation factor X (CFX) assay, coagulation factor X chromogenic activity assay (FXCAA), ecarin‐stimulated thrombin activity (ESTA), LMWH, antifactor Xa (AFX) assay, and antithrombin III (AT III) activity were measured.14, 15, 16 The aims of our current population analyses were to characterize the PK/PD of GCC‐4401C and predict the proper dosage regimens compared to rivaroxaban.

MATERIALS AND METHODS

Subjects and study design

PK and PD data for this analysis were from two phase I studies for healthy male subjects, “A Phase I, Randomized, Double‐blind, Placebo‐controlled, Single Ascending Dose Study Evaluating the Safety, Tolerability, and Pharmacokinetics of Orally Administered GCC‐4401C in Healthy Subjects” (ClnicalTrials.gov Identifier No. NCT01651234), and “A Phase I, Randomized, Double‐blind, Placebo‐controlled, Single and Multiple Sequential Ascending Dose Study Evaluating the Safety, Tolerability, Pharmacokinetics, and Pharmacodynamics of Orally Administered GCC‐4401C in Healthy Males” (ClnicalTrials.gov Identifier No. NCT01954238).

The first study was a SAD study in 48 subjects with six dose groups (2.5, 5, 10, 20, 40, and 80 mg) of eight subjects for each group. In each dose group, six subjects received GCC‐4401C and two received placebo after overnight fasting. Serial blood samples for plasma GCC‐4401C concentrations, CFX activity, AT III activity, ESTA, PT in international normalized ratio (INR), PT in seconds, aPTT, and LMWH, AFX assays were drawn from pre‐dose through 48 hours after dosing. Serial urine amounts and concentrations of GCC‐4401C were also measured in the 10‐, 20‐, 40‐, and 80‐mg groups.

The second study was an S&MAD study in 46 subjects with five dose groups (10, 20, 40, 60, and 80 mg). In each dose group, six subjects received GCC‐4401C after overnight fasting on day 1 and days 3 through 9, whereas two subjects received placebo on the same schedule. An additional six subjects in the 20‐mg group were administered 20 mg of rivaroxaban 30 minutes after a standard breakfast, as recommended. Serial blood samples for plasma GCC‐4401C or rivaroxaban concentrations and CFX activity, AFX activity, FXCAA, PT in INR, PT in seconds, and aPTT were drawn on days 1 and 9, respectively.

The two studies were in full accordance with the Declaration of Helsinki, International Conference on Harmonization of Technical Requirements for Registration of Pharmaceuticals for Human Use–Good Clinical Practice guidelines. The clinical study protocols, amendments, informed consent documents, and any other appropriate study‐related documents were reviewed and approved by an independent ethics committee/institutional review board. All subjects provided written informed consent before screening tests.

Measurement of GCC‐4401C and PD markers

In the SAD study, blood samples were obtained for measurement of GCC‐4401C concentrations at 0 (pre‐dose), 0.25, 0.5, 1, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 12, 16, 24, and 48 hours post‐dose. Urine samples were also collected at 0 (pre‐dose), 0–4, 4–8, 8–12, 12–24, and 24–48 hours post‐dose. Blood samples for PD were collected at the same time as PK samples. In the S&MAD study, blood samples were obtained for measurement of GCC‐4401C concentrations at 0 (pre‐dose), 0.5, 1, 1.5, 2, 3, 4, 6, 8, 12, 24, and 48 hours post‐dose on days 1 and 9, with additional pre‐dose samples on days 5 through 8. Blood samples for PD were collected at the same times, except for samples on days 5 through 8.

The measurement of GCC‐4401C concentration in plasma and urine samples from the SAD study was performed by ABC Laboratories (Columbia, MO), and from the S&MAD study by Tandem Laboratory (Princeton, NJ) using validated, high‐performance liquid chromatography/tandem mass spectrometric methods.

PD markers were measured by validated methods. Specifically, FXCAA, AFX, and LMWH were measured at Mayo Medical Laboratories (Wilmington, MA). In FXCAA, the subject's plasma factor X was activated in the presence of calcium by Russell's viper venom, the activator. The activated factor X then hydrolyzed a chromogenic substrate (S2337), releasing a chromophore (paranitroaniline), which was detected by monitoring light absorbance at 405 nm.17 The factor Xa inhibitor assay consists of measuring the difference in factor X activity (PT assay) before and after incubation of a mixture of normal plasma and the patient's plasma for 1 hour at 37°C. If the inhibitor screen was positive for an inhibitor of factor X, the inhibitor was quantitated by the Bethesda assay.18 In LMWH assay, residual free factor Xa was measured in plasma by chromogenic substrate assay after addition of bovine AT III and factor Xa, which forms an inactive factor Xa‐AT III‐heparin complex.18

PK and PD modeling analysis of GCC‐4401C

PK and PD analyses were conducted using pooled data from the SAD and S&MAD studies. A total of 1,401 GCC‐4401C plasma concentrations (576 from the SAD study, and 825 from the S&MAD study), 120 GCC‐4401C urine concentrations, and 168 rivaroxaban plasma concentrations from the S&MAD study were used for PK analysis. PK and PD analysis was conducted by nonlinear mixed effect modeling using NONMEM version 7.2 (ICON Development Solutions, Ellicott City, MD), and data processing and plotting were performed using R program version 3.0.1. NONMEM subroutines ADVAN6 and FOCE (first order conditional estimation) with the INTERACTION method were used.

Compartmental linear and nonlinear plasma PK models were assessed, based on statistical criteria, and graphical goodness of fits. Plasma and urine PK data were modeled simultaneously. For urine PK, concentration and volume of each urine sample collected in prespecified time intervals were used in the modeling, in which urine volume was used as the scaling factor for the conversion of the concentration into the amount in NONMEM.

PD data were sequentially modeled using individual PK parameter estimates. Plasma and urine PK for GCC‐4401C was modeled first, and then PD was modeled using individual empirical maximum a posteriori probability Bayes PK parameter estimates as inputs. For PD analysis, linear, log‐linear, simple maximum effect (E_max), and sigmoid E_max models were tested for each of CFX, FXCAA, AFX, PT in INR, PT in seconds, aPTT, AT III activity, ESTA, and LMWH. Baseline PD values of each endpoint were used as such in each model without parameterization. To describe the potential time delay in PD, ligand‐receptor association‐dissociation models were tested, as well as direct effect models that assume no time delay.

The parameters for a specific subject were described by Eq. (1):

$$P_i=P_{TV}\times \exp ({\eta }_i)$$ (1)

where P_TV is the typical value of the parameter and η_i is a normally distributed variable with zero mean.

Interoccasional variability (IOV) was considered for the unexplained differences in PK parameters among each period during multiple doses of GCC‐4401C and rivaroxaban within an individual. We tested the statistical significance of IOV with the following equation:

$$\eta ={\eta }_{IIV}+{\eta }_{IOV1}* \left(1-\text{OCC}\right) +{\eta }_{IOV2}* \text{OCC} \dots +{\eta }_{IOVn}* \text{OCC}$$ (2)

where η_IIV is a random variable for unexplained interindividual variability (IIV), η_IOV1, η_IOV2, and η_IOVn are random variables for unexplained IOVs for each period of multiple dosing, and OCC is an indicator variable for each period, which is 0 in each corresponding period and 1 in other periods.

After construction of base models without any covariates other than dose, age, body weight, height, race, and study effect were tested to investigate whether they significantly improved the PK and PD models. Covariate effects were incorporated and tested as proportional, linear, exponential, or power function in the models.

The residual error was described by the proportional error model for the PK model and additive model for the PD model, as described by Eqs. (3) and (4), respectively:

$$DV=IPRED+IPRED*{\epsilon }_1$$ (3)

$$DV=IPRED+{\epsilon }_2$$ (4)

where dependent variable (DV) is observed PK or PD values, individual predicted value (IPRED) is individual predictions for PK and PD values, and ε₁ and ε₂ are zero‐mean normally distributed variables.

Final PK and PK/PD models were selected, guided by a graphical assessment of optimum fit properties and statistical significance criteria. A likelihood ratio test was used to discriminate between hierarchic models at P ≤ 0.05, based on the fact that the distribution of −2 log likelihood of the models follows an approximately χ2 distribution. Standard diagnostic plots, including the observed values of the dependent variable vs. the population predicted values or the individual predicted values and the individual predicted vs. the individual weighted residuals were used for the diagnosis of optimum fit capabilities. A 95% prediction interval constructed by 1,000 replicates of the model predictions and real observed data were compared by visual predictive check (VPC) plots. For GCC‐4401C, prediction corrected VPCs, standardized to dose at 40 mg, were drawn for PK and PD models.18 VPCs for the urine PK model were conducted by simulating the cumulative amount of GCC‐4401C and then comparing the simulated and observed values.

Monte‐Carlo simulation for PK and PD of GCC‐4401C and rivaroxaban

Using the PK and PD models constructed in this study, Monte‐Carlo simulations for plasma concentrations and PD markers over time for various dosing regimens of GCC‐4401C or rivaroxaban were conducted. The purpose of the simulations was to compare the PK and PD between various dosing regimens of GCC‐4401C and treatment regimens of rivaroxaban (10 or 20 mg/day) and to explore the optimal dosing regimens for GCC‐4401C.

Monte‐Carlo simulation was performed using NONMEM version 7.2, and IIV, IOV, and residual variability were used as sources of random variables, as appropriate in the Monte‐Carlo simulation. The simulation results were visualized in time‐series plots using R version 3.01.

RESULTS

Demographics of subjects included in the PK/PD analysis

A total of 94 subjects participated in the two phase I studies, and all the data were included in this PK/PD analysis (Table 1). Most of the subjects were white (n = 41.0; 43.6%) or African American (n = 40.0; 42.6%), with mean (±SD) age of 30.3 (± 8.6) years, and mean weight of 76.6 (± 9.7) kg. There was no significant demographic difference between the two phase I studies.

Table 1.

Baseline demographic characteristics of subjects included in the PK/PD analysis

Characteristics	Single‐dose trial (n = 48)	Single and multiple dose trial (n = 46)	Total (n = 94)
Race
White	25	16	41
African American	19	21	40
Asian	3	5	8
Other	1	4	5
Age, y	30.1 ± 10.3	30.5 ± 6.5	30.3 ± 8.6
Weight, kg	75.6 ± 9.8	77.6 ± 9.6	76.6 ± 9.7
Height, cm	174.4 ± 5.9	178.7 ± 6.8	176.5 ± 6.7

Plasma and urine PK modeling analysis

After single or multiple oral administrations of GCC‐4401C in a fasted status, plasma concentrations generally increased in a dose‐dependent manner (Figure 1). Plasma GCC‐4401C concentrations over time were best described by a two‐compartment linear model. The analysis results are summarized in Table 2. Inclusion of D₁ (duration of zero order absorption) and ALAG₁ (delay in the onset of absorption) of NONMEM version 7.2 with their IOVs in the PK model significantly improved the fit. IOVs for D₁ and ALAG₁ in the model were implemented in every inter‐dose interval, during which plasma were drawn for PK and the period after the last dose. However, the data did not allow the PK model to estimate unexplained IIV and IOV for D₁ and ALAG₁ separately. Therefore, random effect parameters reflecting combined IIV and IOV (IIV + IOV) were estimated. The average steady‐state volume of distribution of GCC‐4401C was estimated to be 81.5 L. V_c (55.6 L) was larger than V_p (25.9 L) in the base model.

Figure 1.

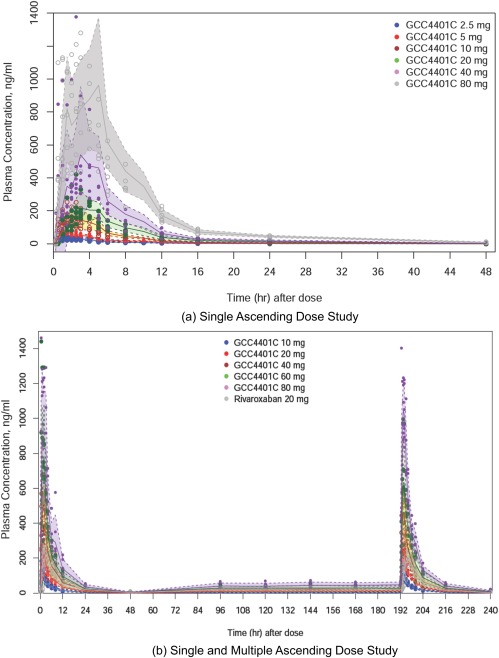
Plasma concentration‐time profiles of single ascending dose trial and single and multiple ascending dose trial.

Table 2.

Population pharmacokinetic parameter estimates for GCC4401C and Rivaroxaban

Parameter	Estimates	RSE %	95% CI
(a) Plasma and urine GCC4401C from both the SAD and S&MAD studies
Ka, 1/h	3.50	19.7	2.15–4.85
IIVKa (CV, %)	0.97 (128.0)	35.2	0.30–1.64
ALAG1, h	0.20	11.1	0.16–0.24
IIV + IOVALAG1 (CV, %)	0.14 (38.8)	37.2	0.038–0.242
D1, h	0.395	10.5	0.314–0.476
IIV + IOVD1 (CV, %)	1.49 (185.4)	35.0	0.47–2.51
Vc,[Link] L	55.7	5.8	49.4–62.0
Θ for WT and Vc[Link]	0.67	50.2	0.01–1.32
IIVVc (CV, %)	0.09 (30.5)	39.9	0.02–0.16
Vp, L	27.8	7.0	24.0–31.6
IIVVp (CV, %)	0.11 (33.8)	26.2	0.05–0.16
Q, L/h	2.99	4.8	2.71–3.27
CLNR, L/h	11.2	3.8	10.4–12.0
IIVCLNR (CV, %)	0.046 (21.7)	30.4	0.019–0.073
CLR, L/h	0.78	9.7	0.63–0.93
IIVCLR (CV, %)	0.052 (23.2)	68.8	−0.002–0.123
IMAXc	0.88	7.5	0.75–1.00
IC50,c ng/mL	166.0	37.1	45.3–286.7
Assayd	0.82	4.6	0.74–0.89
ε (proportional), plasmae	0.20	3.0	0.19–0.20
ε (proportional), urinee	0.28	10.1	0.22–0.33
(b) Plasma rivaroxaban from the S&MAD study
Ka, 1/h	2.24	79.9	−1.27–5.75
IIVKa (CV, %)	3.3 (503.1)	45.3	0.37–6.17
D1, h	1.07	40.9	0.21–1.93
IIV + IOVD1 (CV, %)	0.13 (144.8)	48.6	0.05–2.21
γ	1.34	25.2	0.68–2.00
Vc, L	58.4	9.1	48.0–68.8
IIVVc (CV, %)	0.01 (10.0)	104.1	−0.01–0.03
Vp, L	24.4	14.2	17.6–31.2
IIVVp (CV, %)	0.06 (25.7)	37.1	0.02–0.11
Q, L/h	3.49	27.8	1.59–5.39
CL, L/h	10.1	5.5	9.0–11.2
IIVCL (%)	0.015 (12.3)	41.7	0.003–0.027
ε (proportional)e	0.28	5.4	0.25–0.30

ALAG1, delay in absorption; CI, confidence interval; CL, clearance; CLNR, nonrenal clearance; CLR, renal clearance; CV, %, % coefficient of variation (CV) calculated by CV (%)=sqrt(exp(omega)−1))*100; D₁, duration of zero‐order absorption; IIV, interindividual variability; IMAX, Maximum inhibition which is between 0 and 1; IOV, interoccasional variability, variance (% coefficient of variation (CV), calculated by CV (%)=sqrt(exp(omega)−1))*100; Ka, absorption rate constant; Q, intercompartmental clearance; RSE, relative standard error (standard error divided by the parameter estimate); S&MAD, single and multiple ascending dose; SAD, single ascending dose; V_c, central volume of distribution; V_p, peripheral volume of distribution; WT, weight; γ, shape parameter in Weibull‐type absorption model.

^aV_c is a typical V_c in people of 75 kg in body weight. ^bΘ for WT and V_c represents the covariate effect of body weight (WT) normalized in 75 kg on the V_c expressed as a power function in the form of $Typical Vc={Vc\left(75\right)*(WT/75) }^{\Theta }$, where V_c (75) is a typical V_c in people of 75 kg in body weight. ^cIn this PK model, non‐renal clearance (CLNR) of GCC4401C is empirically described to decrease with the increase of the doses by inhibitory maximum effect model. IMAX and IC50 constitute the model, which are maximum inhibition of the GCC4401C clearance, and IC50 is the GCC4401C concentration at half‐maximum inhibition. ^dAssay in this model represents the relative accuracy in the plasma GCC4401C measurements between SAD and S&MAD studies. 0.82 in this result means that the plasma GCC4401C concentrations measured in the SAD/MAD study are lower by about 18% on average compared to those of SAD study. ^e ε (proportional) is represented as SDs.

Body weight (WT) was associated with V_c in the plasma PK analysis for GCC‐4401C as follows:

$$Typical Vc={Vc\left(75\right)*\left(\frac{WT}{75}\right)}^{\Theta }$$ (5)

where V_c (75) is the typical V_c in people weighing 75 kg and $\Theta$ represents the covariate effect of WT normalized to 75 kg on V_c.

The plasma and urine PK modeling analysis results from the SAD study suggested that most GCC‐4401C was eliminated by non‐renal routes, with renal clearance (CLR) and nonrenal clearance (CLNR) of 0.82 and 12.0 L/hr, respectively. Renal elimination of GCC‐4401C was found to be limited in high doses. These phenomena were empirically described by applying inhibitory E_max model between plasma GCC‐4401C and CLR as the following Eq. (6):

$$\text{CLR} = \text{BCLR} * \left(1 - \text{IMAX}*{\mathrm{C}}_{\mathrm{p}}/\left({\mathrm{C}}_{\mathrm{p}}+{ \text{IC}}_{50}\right)\right)$$ (6)

where CLR is renal clearance, BCLR is baseline CLR, IMAX is maximum inhibition which is between 0 and 1, IC₅₀ is the plasma GCC‐4401C concentration at half‐maximum inhibition, and C_p is plasma GCC‐4401C concentration.

When different scaling factors (S2) were applied to the SAD and S&MAD studies as following in NONMEM, the PK model was significantly improved (ΔMOFV: −21.037), which might be ascribed to the differences in the accuracy of the bioanalytical method for drug concentration measurements between the two studies.

$$\mathrm{S}2 = \text{Vc}/1000$$ (7)

$$\text{IF}\left(\text{STUDY}.\text{EQ}.2\right) \mathrm{S}2 = \left(\text{Vc}/1000\right)/\text{THETA}\left(10\right)$$ (8)

where, Vc is the central volume of distribution, EQ means “equal to,” study 2 indicates the S&MAD study, and THETA(10) is the parameter for the relative difference in assay accuracy of the S&MAD study compared to the SAD study.

However, other difference between the two studies as well as the difference in assay accuracy might have been reflected in the difference in the scaling factors between the two studies. We also implemented different residual errors between the two phase I studies in the model to explore the potential difference in the precision of the bioanalytical method, with no improvement of the model.

For rivaroxaban, a two‐compartment, linear model best described the PK in fed status (Table 2). The absorption process was described by a Weibull model with mixed first and zero order absorption. Inclusion of IOV in the D₁ parameter also improved the model fit. However, IOV and IIV could not be separately estimated, and the lumped variances of IOV and IIV for D₁ were estimated. Disposition PK parameters were similar between GCC‐4401C and rivaroxaban, with slightly larger steady‐state volume of distribution and total clearance in GCC‐4401C. Basic goodness‐of‐fit plots (Supplementary Figure S2) and model prediction vs. observed concentration plots (Figure 2) indicate that the final PK models reasonably describe the PK of both compounds. Potential underprediction of the model was observed in the prediction‐corrected VPC plot standardized to dose at 40 mg for a single dose PK of GCC‐4401C (Figure 2 a, left column), which was not definite for multiple dose PK of GCC‐4401C (Figure 2 a, right column). In the VPC for urine PK model for GCC‐4401C, there was overestimation of interindividual difference. The plots for confidence interval VPC with percentiles were presented in Supplementary Figure S3 for more detailed information.

Figure 2.

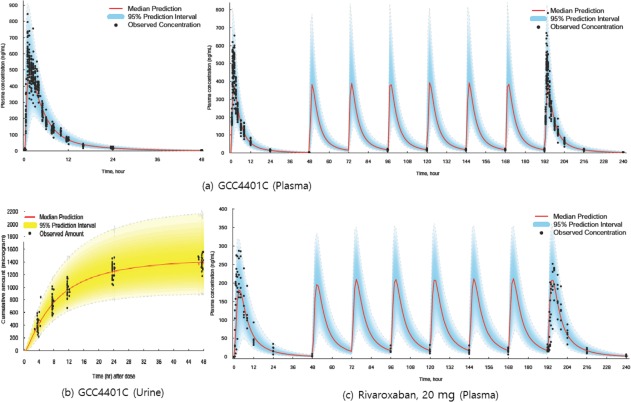
Model prediction versus observed concentration plots for pharmacokinetic models of GCC‐4401C and rivaroxaban. (a) Plasma GCC‐4401C concentrations over time on single oral dose (left column), and on single and multiple doses (right column). (b) Cumulative GCC‐4401C amount over time excreted in urine. (c) Plasma rivaroxaban concentrations over time on single and multiple doses at 20 mg. The shaded area represents the 95% prediction interval, and the solid red line represents the median prediction. Plots for plasma GCC‐4401C (a) and urine GCC‐4401C (b) are standardized ones to dose at 40 mg (prediction‐corrected visual predictive check).

PK‐PD modeling analysis

The PD modeling results for GCC‐4401C and rivaroxaban are displayed in Table 3. Plot between plasma drug concentrations vs. PD endpoints suggested no counterclockwise hysteresis (not shown), and modeling results also suggested no time delay since ligand‐receptor association‐dissociation models used to describe potential time delays were not superior in describing the PK/PD data, compared to the direct effect models assuming no time delay, therefore used in the final PK/PD models for all the PD markers evaluated in this study. ETA shrinkage of major PK parameters would be important in this sequential PK‐PD modeling using individual PK parameter estimates, and were ∼0.93–22.5% in the current final PK model.19 PD markers changed generally in a dose‐dependent manner, but this was not definite in ESTA and AT III. All of the PD markers were described well with sigmoid, simple (inhibitory) E_max, or linear models, except for ESTA. The PD models adopted in this analysis did not describe the ESTA data well because the PD models basically describe the monotonically increasing or decreasing values by doses, whereas the changes in observed ESTA values with ascending doses of GCC‐4401C were not definite. Inclusion of IOV improved the model fit for some PD markers. However, in some parameters for PD markers, combined variances of IOV and IIV were estimated, because IOVs were not estimated separately from IIVs. Some PD parameters were different between the SAD and S&MAD studies, which might be partially ascribed to study difference. The final PD models predicted the observed PD values well, as some of them are shown in Figure 3.

Table 3.

Population pharmacodynamic parameter estimates

Parameter	Estimates	RSE %	95% CI
(a) Coagulation factor X
GCC4401C from the SAD and S&MAD studies: Sigmoid Emax model
Emax, %	81.2	11.3	63.2–99.2
IIVEmax (CV, %)	0.10 (33.1)	48.5	0.01–0.20
EC50, ng/mL	2880.0	34.1	957.2–4802.8
IIVEC50 (%)	0.98 (129.4)	39.0	0.23–1.74
γSAD	1.07	14.3	0.77–1.37
γSAD/MAD	0.60	11.7	0.46–0.74
IIVγ (CV, %)	0.24 (51.8)	32.7	0.09–0.39
IOVγ (CV, %)	0.09 (30.1)	35.3	0.03–0.15
ε (additive), %	3.94	22.5	2.20–5.68
ε (proportional)e	0.06	12.9	0.04–0.07
Rivaroxaban from the S&MAD study (Sigmoid Emax model)
Emax, %	42.9	19.0	26.9–58.9
EC50, ng/mL	194.0	27.4	99.9–288.1
IIVEC50 (CV, %)	0.33 (62.1)	117.8	−0.43–1.08
IOVEC50 (CV, %)	0.25 (52.9)	155.5	−0.51–1.00
γ	0.90	21.3	0.53–1.28
ε (proportional)e	0.06	6.9	0.05–0.06
(b) Factor X chromogenic activity assay
GCC4401C from the S&MAD study (Sigmoid Emax model)
Emax, %	99.8	7.3	85.5–114.1
IIVEmax (CV, %)	0.01 (11.3)	52.1	0–0.03
EC50, ng/mL	420.0	16.4	284.8–555.2
IIV + IOVEC50 (%)	0.08 (129.4)	42.1	0.01–0.15
γ	0.90	7.5	0.76–1.03
IIVγ (CV, %)	0.06 (25.7)	44.9	0.01–0.12
ε (additive), %	3.03	34.7	0.97–5.1
ε (proportional)e	0.06	18.3	0.04–0.08
Rivaroxaban from the S&MAD study (Simple Emax model)
Emax, %	112.0	3.2	104.9–119.1
EC50, ng/mL	126.0	13.1	93.7–158.3
IIVEC50 (CV, %)	0.07 (26.9)	62.9	−0.02–0.16
IOVEC50 (CV, %)	0.01 (8.2)	90.1	−0.01–0.02
ε (additive), %	3.89	15.0	2.75–5.03
ε (proportional)e	0.05	33.2	0.02–0.08
(c) Antifactor Xa activity
GCC4401C from the S&MAD study (Sigmoid Emax model)
Emax, IU/mL	3.24	21.3	1.89–4.59
IIVEmax (CV, %)	0.04 (20.8)	62.3	0.00–0.03
EC50, ng/mL	695.0	26.0	340.2–1,049.8
IIV + IOVEC50 (%)	0.005 (7.2)	48.8	0.000–0.01
γ	1.25	6.0	1.10–1.40
IIVγ (CV, %)	0.02 (13.4)	51.4	0.00–0.04
ε (additive), IU/mL	0.04	12.2	0.03–0.05
ε (proportional)e	0.14	8.1	0.12–0.16
Rivaroxaban from the S&MAD study (Linear model)
SLOPE	0.005	6.4	0.004–0.006
IIVSLOPE (CV, %)	0.01 (10.8)	43.7	0.00–0.02
ε (additive), IU/mL	0.04	11.7	0.03–0.05
ε (proportional)e	0.29	13.0	0.21–0.36
(d) PT (INR)
GCC4401C from the SAD and S&MAD studies (Sigmoid Emax model)
EMAX, INR	1.32	20.3	0.79–1.85
IIVEmax (CV, %)	0.48 (78.0)	43.0	0.08–0.87
EC50, SAD, ng/mL	426.0	24.4	222.2–629.8
EC50, SAD/MAD, ng/mL	1350.0	27.3	628.7–2,071.3
IIVEC50 (CV, %)	0.89 (120.1)	52.3	−0.02–1.81
γ	1.23	7.5	1.05–1.41
IIVγ (CV, %)	0.11 (34.3)	74.1	−0.05–0.27
IOVγ (CV, %)	0.04 (19.9)	69.6	−0.01–0.09
ε (proportional)e	0.05	7.7	0.04–0.06
Rivaroxaban from the S&MAD study (Simple Emax model)
Emax, INR	0.71	26.5	104.9–119.1
EC50, ng/mL	434.0	37.3	116.5–751.5
IIV + IOVEC50 (CV, %)	0.06 (25.8)	53.9	0.00–0.13
ε (additive), INR	0.04	6.2	0.04–0.05
(e) Prothrombin time (seconds)
GCC4401C from the S&MAD study (Sigmoid Emax model)
Emax, sec	15.2	21.5	8.8–21.6
IIVEmax (CV, %)	0.41 (71.6)	64.7	−0.11–0.94
EC50, SAD, ng/mL	563.0	34.3	184.7–941.3
EC50, SAD/MAD, ng/mL	1450.0	30.0	597.4–2302.6
IIVEC50 (CV, %)	0.77 (107.8)	64.5	−0.20–1.75
γ	1.16	8.0	0.98–1.34
IIVγ (CV, %)	0.04 (18.9)	65.0	−0.01–0.08
IOVγ (CV, %)	0.03 (17.8)	60.1	−0.01–0.07
ε (proportional)e	0.04	6.9	0.04–0.05
Rivaroxaban from the S&MAD study (Simple Emax model)
Emax, sec	6.86	39.1	1.61–12.11
EC50, ng/mL	418.0	60.3	−75.9–911.9
IIV + IOVEC50 (CV, %)	0.07 (26.6)	71.5	0.00–0.13
ε (additive), sec	0.04	9.3	0.03–0.04
(f) Activated PT (seconds)
GCC4401C from the SAD and SAD/MAD studies (Sigmoid Emax model)
Emax, SAD, sec	16.9	13.1	12.5–21.3
Emax, SAD/MAD, sec	20.4	12.5	15.4–25.4
IIVEmax (CV, %)	0.09 (30.3)	86.1	−0.06–0.24
EC50, ng/mL	573.0	22.7	318.2–827.8
IIVEC50 (CV, %)	0.33 (62.4)	62.3	−0.07–0.73
γ	1.37	13.2	1.02–1.72
IIVγ (CV, %)	0.19 (45.9)	39.2	0.04–0.34
IOVγ (CV, %)	0.03 (17.8)	35.5	0.02–0.11
ε (proportional)e	0.05	1.0	0.05–0.05
Rivaroxaban from the S&MAD (Sigmoid Emax model)
Emax, sec	12.4	10.3	9.9–14.9
EC50, ng/mL	135.0	14.3	97.2–172.8
γ	0.94	18.1	0.61–1.28
IIV + IOVγ (CV, %)	0.27 (55.7)	38.5	0.07–0.47
ε (additive), sec	0.04	9.3	0.03–0.04
(g) AT III activity
GCC4401C from the SAD study (Linear model)
SLOPE	0.006	44.8	0.001–0.011
IIVSLOPE (CV, %)	3.73 (637.8)	38.6	0.91–6.55
ε (additive)	9.28	10.9	7.30–11.3
(h) LMWH
GCC4401C from the SAD study (Simple Emax model)
Emax	3.83	11.4	2.98–4.68
IIVSLOPE (CV, %)	3.73 (637.8)	38.6	0.91–6.55
EC50, ng/mL	759.0	15.2	533.6–984.4
IIVEC50 (CV, %)	0.29 (57.4)	33.9	0.10–0.47
ε (additive)	0.08	20.6	0.05–0.11
ε (proportional)e	0.17	14.3	0.12–0.22

AT III, antithrombin III; CI, confidence interval; CV, %, % coefficient of variation (CV), calculated by CV (%)=sqrt(exp(omega)−1))*100; EC₅₀, plasma GCC4401C concentration at half‐maximum effect; E_max, maximum achievable effect in the maximum effect model; IIV, interindividual variability; INR, international normalized ratio; IOV, interoccasional variability, variance (% coefficient of variation (CV), calculated by CV (%)=sqrt(exp(omega)−1))*100; LMWH, low‐molecular‐weight heparin; PT, prothrombin time; RSE, relative standard error (standard error divided by the parameter estimate); S&MAD, single and multiple‐ascending dose; SAD, single ascending dose trial; SAD/MAD, single and multiple ascending dose trial; γ, shape parameter in sigmoid maximum effect model.^e ε (proportional) is represented as SDs.

Figure 3.

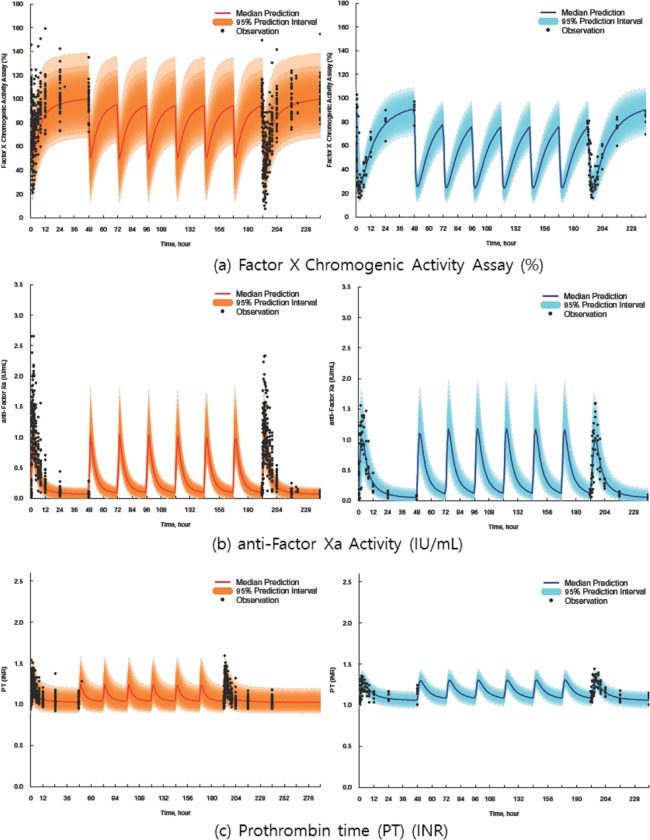
Representative model prediction vs. observation plots for pharmacodynamic models of anti‐Factor Xa activity (%), coagulation factor X (%), prothrombin time (international normalized ratio (INR)) (left column, GCC‐4401C; right column, rivaroxaban) on single and multiple oral administration of GCC‐4401C at 40 mg and rivaroxaban at 20 mg. The shaded area represents the 95% prediction interval, and the solid red line represents the median prediction. Plots are standardized ones to dose at 40 mg (prediction‐corrected visual predictive check).

Monte‐Carlo simulation for plasma concentration and PD markers over time

Using the final PK and PD models constructed in this study, Monte‐Carlo simulations for plasma concentration and PD markers over time after various dosing regimens of GCC‐4401C and rivaroxaban were performed, and the respective median and 95% prediction intervals were visualized to compare the PK and PD between the two drugs. Some representative PD plots for the simulations are displayed in Figure 4. In the PK simulation, the area under concentration time curves of GCC‐4401C and rivaroxaban were predicted to be similar at the same dosage, as evidenced by the similar total clearances (12.0 L/hr for GCC‐4401C, and 10.1 L/hr for rivaroxaban), as shown in Table 2. However, GCC‐4401C was predicted to reach maximum concentrations and maximum effect in shorter times.

Figure 4.

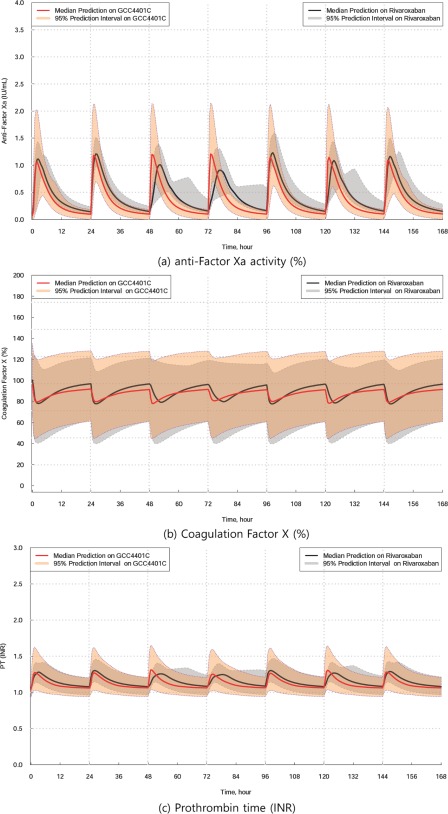
Simulated plots for anti‐Factor Xa activity (%), coagulation factor X (%), prothrombin time (international normalized ratio (INR)) over time on GCC‐4401C, 40 mg in comparison to rivaroxaban, 20 mg. The solid red line represents the median prediction for GCC‐4401C, and the solid black line represents the median prediction for rivaroxaban.

Although direct comparisons of PD markers between GCC‐4401C and rivaroxaban are not feasible because of the changing shapes of PD markers over time are quite different between the two drugs, rough comparisons based on the simulation plots suggest that 20 and 40 mg of GCC‐4401C are comparable to 10 and 20 mg of rivaroxaban in CFX assay, respectively. In other PD markers, the simulation showed that 10 mg of GCC‐4401C was comparable to 20 mg of rivaroxaban in AFX assay and 30–40 mg of rivaroxaban in FXCAA and PT, whereas 20 mg of GCC‐4401C was comparable to ∼40 mg of rivaroxaban in AFX and PT, and 80 mg of rivaroxaban in FXCAA (Supplementary Figure S4).

DISCUSSION

Using the PK and PK/PD models constructed in this study, plasma concentrations and PD markers over time were simulated for various dosing regimens of GCC‐4401C and rivaroxaban. These simulations were used to determine therapeutic dosing regimens of GCC‐4401C by comparison with approved regimens of rivaroxaban.

The population PK/PD model of rivaroxaban has been reported in previous studies, in which the two‐compartment model best described the PK of rivaroxaban, and CFX activity by inhibitory E_max model, whereas PT followed the linear model.20, 21, 22 In the current PK analysis, WT was associated with V_c of GCC‐4401C in the power function. However, the difference of V_c by WT are predicted to be minimal in the model.

The association between WT and V_c was also statistically significant in rivaroxaban PK. However, the final model was chosen as a base model without any covariate because the PK model for rivaroxaban containing WT as a covariate was not successful, with frequent rounding errors, which is likely because of less data for rivaroxaban in the current study. Similarly, the PK model for rivaroxaban from healthy subjects reported by Mueck et al.22 was a two‐compartment model without WT as a covariate, whereas an effect of WT was found in a model from a patient with atrial fibrillation. Age and CLR are other known covariates for the PK of rivaroxaban.23 Rivaroxaban is eliminated by liver metabolism (mainly via CYP3A4) and renal excretion.24 In contrast, GCC‐4401C is eliminated mainly by a nonrenal route according to typical CLNR of 11.2 L/hr and CLR of 0.78 L/hr in the current PK model (Table 2), consistent with in vitro results showing liver metabolism (unpublished data). Therefore, GCC‐4401C might be affected less by renal function compared to rivaroxaban. The renal elimination of GCC‐4401C was shown to be saturable in high plasma concentrations following the inhibitory E_max model. Although the reason of saturable elimination is not clear, there might be carrier‐mediated secretory process during renal elimination. However, the effect of nonlinear renal elimination on the systemic exposure of GCC‐4401C would be minimal because the fraction of renal elimination is small.

Inclusion of D₁ and ALAG₁ and their IOVs significantly improved the PK model for GCC‐4401C, which suggest the possibility of dissolution rate limitation during absorption together with absorption delays observed at higher doses. In this case, bioavailability of GCC‐4401C could be enhanced by taking it shortly after food consumption. In the current SAD and S&MAD studies, GCC‐4401C was administered in a fasted status, whereas rivaroxaban was administered in a fed status, as recommended.14 According to data from healthy subjects, there were no significant differences in PK parameters between fed and fasting conditions with doses of up to 10 mg rivaroxaban. With higher doses, taking rivaroxaban with food resulted in high bioavailability and predictable PK properties.25 The PD effect of GCC‐4401C might be higher than predicted in this analysis if the drug was taken after a meal.

There was no time delay between the PK and PD effects of GCC‐4401C and rivaroxaban, and GCC‐4401C was absorbed more rapidly with a more rapid decline. Accordingly, PD effects appeared and disappeared more rapidly in GCC‐4401C compared to rivaroxaban, reflecting the PK of the two compounds. This difference in PD changes over time should be interpreted in terms of both treatment effect and safety. The more rapid onset of the PD effect from GCC‐4401C could be beneficial in an emergency situation, whereas the more rapid disappearance of the PD effect might result in an insufficient treatment effect but also suggest that GCC‐4401C is safer, all of which should be tested in further trials in patients.

From previous reports, it is expected that the AFX activity assay would explain the PD of rivaroxaban relatively well due to a linear, concentration‐dependent relationship, and PT prolongation in plasma with rivaroxaban occurs in a concentration‐dependent linear fashion.16, 17 Moreover, conversion to an INR is not useful for monitoring rivaroxaban because the INR was originally developed for normalizing PT in patients receiving VKAs.26, 27, 28 Other studies with rivaroxaban that measured aPTT showed nonlinear, variable prolongation.29, 30 Besides, ecarin‐based assay was used in other previous studies to test dabigatran, a prodrug of thrombin inhibitor showing concentration‐dependent linear relationship, but insensitive to rivaroxaban,31, 32, 33 which might explain the unclear dose‐response relationship in ESTA observed in this study. Overall, current simulation results suggest that roughly 20 mg and 40 mg of GCC‐4401C are comparable to 10 mg and 20 mg of rivaroxaban, respectively, in terms of efficacy. However, if the bioavailability of GCC‐4401C is found to be higher when administered under fasted status compared to fasting status, as in the case of rivaroxaban, the efficacy on the GCC‐4401C would be higher than predicted in this study.

In summary, the first PK/PD model of GCC‐4401C, a novel, direct factor Xa inhibitor, showed dose‐dependent, predictable PK and PD characteristics. We predicted PK and PD of GCC‐4401C for several dosing regimens, in comparison to rivaroxaban by Monte‐Carlo simulation using the models constructed from the data obtained in the early stage of the clinical development. The simulation suggests that roughly 20 and 40 mg of GCC‐4401C administered under fasting status are comparable to 10 and 20 mg of rivaroxaban dosed under fed status, respectively, based on the simulated PD changes over time profiles. We hope this model will evolve with future clinical trials in patients with various clinical statuses and provide safe, effective dosing regimens. This model will help guide the further clinical development of this novel compound.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information