Revisiting antibody modeling assessment for CDR-H3 loop

Abstract

The antigen-binding site of antibodies, also known as complementarity-determining region (CDR), has hypervariable sequence properties. In particular, the third CDR loop of the heavy chain, CDR-H3, has such variability in its sequence, length, and conformation that ordinary modeling techniques cannot build a high-quality structure. At Stage 2 of the Second Antibody Modeling Assessment (AMA-II) held in 2013, the model structures of the CDR-H3 loops were submitted by the seven modelers and were critically assessed. After our participation in AMA-II, we rebuilt one of the long CDR-H3 loops with 13 residues (A52 antibody) by a more precise method, using enhanced conformational sampling with the explicit water model, as compared to our previous method employed at AMA-II. The current stable models obtained from the free energy landscape at 300 K include structures similar to the X-ray crystal structures. Those models were not built in our previous work at AMA-II. The current free energy landscape suggested that the CDR-H3 loop structures in the crystal are not stable in solution, but they are stabilized by the crystal packing effect.

Introduction

Antibodies are the most popular biological drugs, and accurate structural modeling is required for the development of better and more effective antibody drugs (Leavy, 2010). To improve antibody engineering and modeling methods, two blind contests, the first and second Antibody Modeling Assessments (AMA), were held, where the modelers were requested to build three-dimensional (3D) structural models of antibodies from amino acid sequences provided beforehand (Almagro et al., 2011, 2014). The variable region of the antibody, Fv, consisting of heavy (H) and light (L) chains, has six hypervariable loops called the complementary-determining region (CDR) H1, H2, H3, L1, L2, and L3 loops. At the second AMA, after the ordinary 3D structural modeling of 11 antibodies, the building of only their CDR-H3 loops was attempted, with the 3D atomic coordinates of the other regions given (Teplyakov et al., 2014). We participated as the JOA, a joint collaboration between Astellas Pharma and Osaka University, and made fairly good predictions by a combination of bioinformatics, expert knowledge, and molecular simulations (Shirai et al., 2014). Following our experiences mainly at Stage 1 of AMA-II, a web service, Kotai Antibody (http://kotaiab.org/, Yamashita et al., 2014), was developed to predict 3D antibody structures from the amino acid sequences of the heavy and light chains, without any molecular simulation.

For Stage 2 of the AMA-II blind contest, our predictions using molecular simulations mostly provided acceptable 3D structural models except for the target Ab10, the A52 antibody, which nonspecifically binds to DNA and is strongly associated with autoimmune disease. The CDR-H3 loop of the A52 antibody has 13 amino acid residues, representing the second longest loop among the AMA-II targets, with two Arg residues at the fourth and fifth positions with two successive Gly residues, and our bioinformatics modeling using Spanner (Lis et al., 2011) / OSCAR (Liang et al., 2011) generated one of the best models, with a root-mean-square deviation (RMSD) of 1.03 Å at Stage 2. However, our molecular simulations did not sample many different loop structures including the X-ray crystal structures, because salt bridges were formed in the simulated structures between the Arg residues and the surrounding residues in the heavy chain near the CDR-H3 loop.

At Stage 2 of AMA-II, we applied the multicanonical molecular dynamics (McMD) method to detect the stable structures, after drawing the free energy landscapes. The advantages of McMD include a high sampling efficiency by randomly walking inside a wide temperature region (e.g. 280–700 K) and the ability to obtain a canonical ensemble at a given temperature by the reweighting procedure. However, at AMA-II, no explicit water model was applied, and the distant-dependent dielectric approximation was used to reduce the total number of atoms in the system and to speed up the sampling, because of the short contest period.

In this study, we sought to rebuild the 3D structural model of CDR-H3 of the target Ab10, A52, with 13 residues, using the explicit solvent molecules with a TIP3P water model and small ions, Na⁺ and Cl⁻, to neutralize the system, and the more effective McMD method, TTP-V-McMD (TTP, trivial trajectory parallelization), starting from the results of Stage 1 of AMA-II.

The TTP-V-McMD method was developed to effectively execute an McMD simulation by the combination of TTP-McMD and virtual-system coupled (V)-McMD. The TTP-McMD method (Higo et al., 2009; Ikebe et al., 2011) can provide high-quality statistics by executing parallel simulations starting from different initial structures. The V-McMD method (Higo et al., 2013) has several virtual states that cover different energy ranges, where neighboring virtual states overlap with each other. Each trajectory is initially assigned to one virtual state, and a transition between virtual states occurs when particular conditions are satisfied.

The current molecular simulation successfully sampled varieties of the 3D structures of CDR-H3 loops as the stable structures in the free energy landscape, in which loops similar to those in the X-ray crystal structures were included. The free energy landscape suggested that the crystal structures are not stable in solution, but they are stabilized by the crystal packing effect.

Materials and methods

Simulation system of an antibody CDR-H3 loop

Our CDR-H3 loop target sequence is A(H93)R(H94)G(H95)R(H96)L(H97)R(H98)R(H99)G(H100)G(H100a)Y(H100b)F(H100c)D(H101)Y(H102) from the monoclonal antibody A52, where the characters in parentheses are the residue numbers by Chothia's scheme (Chothia and Lesk, 1987; Chothia et al., 1989) and by North's CDR definition (North et al., 2011). The crystal structure of A52 (PDBID 4m61, Stanfield and Eilat, 2014), which contains two similar Fab domains, was obtained from the Protein Data Bank (Berman et al., 2007), and the Fab domain of chains A and B was used for modeling. The initial structure of the CDR-H3 loop was taken from our previous model (Shirai et al., 2014), which had been built with the MODELLER program (Sali and Blundell, 1993), followed by energy minimization with the myPresto/cosgene program (Fukunishi et al., 2003). This structure, named joaAb10m3.pdb, is available at the AMA-II Web site (http://www.3dabmod.com). The other part of the antibody structure was exactly the same as the X-ray crystal structure. The rest of the Fab domain other than the Fv domain was deleted, in order to reduce the computational costs. The dangling bonds corresponding to the C-termini of the heavy and light chains were capped by N-methyl groups. After modeling, the system consisted of 232 residues, GluH1-SerH113 (total 120 residues) in the heavy chain and AsnL1-LysL107 (total 112 residues) in the light chain. The residue IDs are indicated by Chothia's definition, and the total residue numbers are described in parentheses. A rectangular water box with dimensions of 54 × 61 × 67 ų was placed around the antibody. Sodium and chloride ions were added to neutralize the system and to achieve a physiological concentration (100 mM). The final system consisted of 20 265 atoms (3547 antibody atoms, 5 sodium ions, 15 chloride ions, and 5566 TIP3P water molecules). The force field parameters for the antibody, ions, and water molecules were derived from the AMBER ff99SB force field (Hornak et al., 2006; Wang et al., 2000), the halide monovalent ion parameters (Joung and Cheatham, 2008), and the flexible TIP3P water model (Jorgensen et al., 1983), respectively. The 500 steps of conjugated gradient energy minimizations (i) with positional restraints on the heavy atoms of the solute using a force constant of 1.0 kcal / (mol Å²), (ii) with positional restraints on the backbone heavy atoms of the solute using a force constant of 1.0 kcal / (mol Ų), and (iii) without restraints, were executed sequentially. Next, the system was equilibrated for 500 ps by Berendsen's NPT (constant Number of particles, Pressure and Temperature) algorithm (Berendsen et al., 1984) at 300 K and 1bar, using the Particle Mesh Ewald method (Essmann et al., 1995) with a damping factor α = 0.35 Å⁻¹ for the electrostatic interactions and a time step of 0.5 fs. Here, the positions of the heavy atoms of the antibody were restrained with a force constant of 1.0 kcal / (mol Å²). After the NPT simulation, the cell dimensions were equilibrated to 51.4 × 59.6 × 63.9 Å³. The myPresto/cosgene program (Fukunishi et al., 2003) was used for the energy minimizations and the NPT simulation.

Enhanced sampling of CDR-H3 structures

We applied the improved algorithm of the McMD method, TTP-V-McMD, which was described elsewhere (Higo et al., 2013; Kamiya et al., 2002; Nakajima et al., 1997; Higo et al., 2012), to enhanced sampling of CDR-H3 loops. The psygene-G program (Mashimo et al., 2013) was used for the current simulation, which consisted of (i) a canonical MD run at high temperature to generate largely deviated structures from the initial structure, (ii) a canonical MD run at various temperatures to roughly estimate the density of states of a system, (iii) pre-runs to estimate the density of states of each virtual state, and (iv) a productive run to sample structures.

The actual procedures were as follows: (i) Eight 1.5-ns canonical MD simulations at 700 K were executed, starting from the final structure of the NPT simulation with different random seeds for the initial velocity of the atoms. (ii) Eight 0.5-ns canonical MD simulations starting from the final structure of the first run were executed at eight different temperatures (i.e. 280, 306, 338, 377, 426, 490, 576, and 700 K). (iii) Seven virtual states, v₁–v₇, which covered the temperature range from 280 to 700 K, were prepared for the pre-runs and the productive run, as shown in Table I. The transition between virtual states was judged every 20 000 MD steps. The transition occurred with a probability of 1, if the energy value (E) of the system was in an overlapping virtual state, and otherwise with a zero probability (i.e. E < −61 848 kcal/mol in v₁ and E > −45 768 kcal/mol in v₇). The pre-runs were repeated 26 times, with a total simulation time of 3.1 μs. (iv) In total, 768 ns of the productive run (3 ns × 256 trajectories) were executed. All runs were executed with a time step of 1.0 fs. Electrostatic interactions were treated by the zero dipole summation (ZD) method (Fukuda et al., 2011, 2014; Fukuda, 2013; Kamiya et al., 2013; Wang et al., 2016), with a cutoff distance of 11 Å and a damping factor α of 0.0 Å⁻¹. The cutoff distance of the van der Waals interactions was set to 11 Å. The SHAKE algorithm (Ryckaert et al., 1977) was applied to constrain the covalent bonds between heavy and hydrogen atoms. The structure trajectory was stored every 1000 MD steps (1 ps) during the productive run.

Table I.

Virtual states of the TTP-V-McMD simulation

Virtual state	Initial potential energy (kcal/mol)	Final potential energy (kcal/mol)	Initial temperature (K)	Final temperature (K)
v1	−62 920	−60 776	278	307
v2	−61 848	−59 704	292	322
v3	−60 776	−58 632	307	339
v4	−59 704	−54 344	322	411
v5	−58 632	−50 056	339	497
v6	−54 344	−45 768	411	596
v7	−50 056	−41 480	497	709

To avoid putative large structure deformation of the antibody frame regions during the simulation with the system run with high energies, the distances between atoms were restrained with reference to the energy minimized structure according to our flexible docking study by McMD (Kamiya et al., 2008), as follows. The 21 residues (ValH89-GluH106) located in the CDR-H3 loop, plus 4 residues from the N- and C-termini of the loop, were treated as fully flexible. The pairs of the backbone heavy atoms and the side-chain Cβ atom of the ith and jth residues (|i–j| > = 2) in the other residues than the above 21 residues were included in the restraint list, if the distance of the atom pair was <6 Å (7352 pairs). For the residues with distances between the mass-centers to the above 21 residues greater than 20 Å, the distances between the backbone atoms and the side-chain heavy atoms were also included in the restraint list (1389 pairs). A flat-bottom harmonic potential with a force constant of 0.1 kcal/(mol Å²) was applied to the above 8741 pairs when the distance was longer or shorter than the threshold distance, which was a distance in the minimized structure ± 1.0 Å.

Canonical MD simulations starting from the crystal structure

To assess the stability of the X-ray crystal structure, we executed canonical MD simulations at 300 K, starting from the A52 crystal structure composed of chains A and B (PDBID 4m61). The computational system was built with similar protocols to those described above for the enhanced sampling. The prepared system consisted of 20 214 atoms (3547 antibody atoms, 5 sodium ions, 15 chloride ions, and 5549 water molecules). After the NPT simulation, the cell dimensions were equilibrated to 64.6 × 52.1 × 58.8 Å³. Six 50-ns canonical MD simulations at 300 K with a time step of 1 fs were executed, using different random seeds for the initial velocity of the atoms. The treatment of the electrostatic interactions, the constraint of bonds with SHAKE, and the MD program were the same as those for the enhanced sampling. The structure trajectory was stored every 1000 MD steps (1 ps) during the productive run.

Analysis of the free energy landscape

The structures of the CDR-H3 loop plus four residues from each terminal (ValH89-GluH106) were sampled during the current McMD simulation. The principal component analysis (PCA) was performed for the 3D coordinates of 21 Cα atoms from ValH89 to GluH106 after superimposing them onto the reference structure, the energy minimized structure, where these 21 atoms were excluded in the superimposition. All of the structures were projected on the two-dimensional space, the first and second principal components, PC1 and PC2, respectively, followed by the calculation of the potential of mean force (PMF).

$$\mathrm{P}\mathrm{M}\mathrm{F}=-RT\ln P.$$ (1)

Here, R, T, and P are the Boltzmann constant, the temperature, and the probability of the structure, respectively, and we called this map the free energy landscape. The trajectories obtained from the canonical MDs at 300 K were projected on the free energy landscape for structure comparison.

Results and discussion

The potential energy distributions from the production run of TTP-V-McMD are shown in Fig. S1. The flat energy distributions of all virtual states (v₁–v₇) ensure that the density of states of the system from 280 to 700 K was estimated properly. The reweighted canonical distributions at 300, 400, 500, and 600 K are also shown in Fig. S1. The number of structures covered by the distribution at 300 K was 235 065.

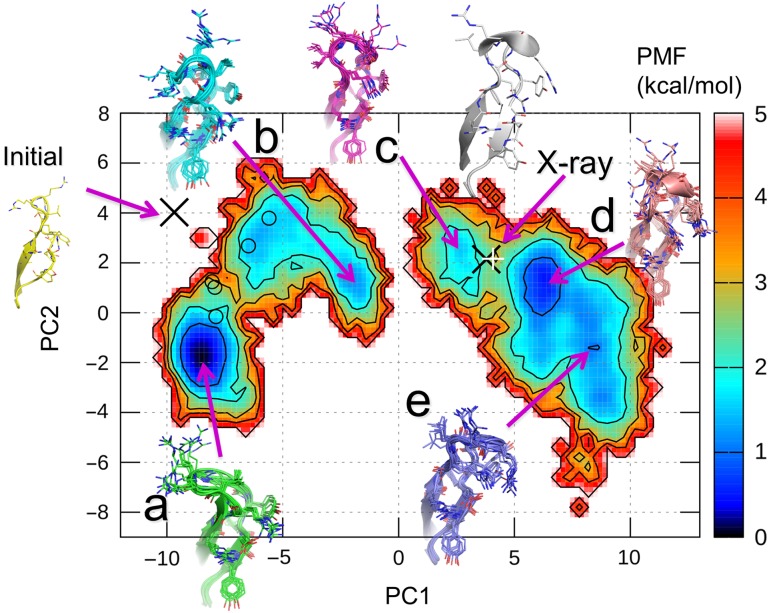
We analyzed the structures at 300 K by PCA, and obtained the contribution ratios from the first to fifth components as 76.2%, 6.0%, 5.5%, 2.4%, and 1.5%, respectively. These results demonstrated that PC1 significantly contributes to the structure ensemble at 300 K. The free energy landscape of the CDR-H3 loop at 300 K projected onto the PC1 and PC2 axes is shown in Fig. 1, and displays a ragged nature with barriers between several local minima. There are two wide and deep minima at the positions of a and d and three shallow minima at b, c, and e, and their PMF values are shown in Table II. The free energy barrier between minima b and c is higher than 5 kcal/mol, and the reason is discussed later. Representative structures in each minimum, denoted as models a–e, are shown in Fig. 1. While the top of the loop was on the left-hand side from the stem of the loop in model a, it was on the right-hand side in model e. Therefore, PC1 corresponds to the right and left directions with respect to the axis, which spans from the stem to the top of the loop. Models b, c, and d protruded from the bases toward the tips of the CDR-H3 loops. In contrast, the tips of the loops of models a and e laid on left and right sides, respectively. Therefore, the PC2 axis corresponds to the protrusion of the loops.

Fig. 1.

Free energy landscape along PC1 and PC2 of the CDR-H3 loop, obtained from the current sampling simulation at 300 K. The PMF is shown by the color in the contour bar. The five PMF minima, a–e, and the positions of the initial MD structure and the X-ray structures are shown by purple arrows with structures. The X-ray structures of chains B and D are indicated by black cross and white cruciform, respectively, are mapped on the landscape. The five model structures built in our previous AMA-II work are also shown by open circles.

Table II.

RMSDs of the CDR-H3 models versus the X-ray crystal structure

Models	PMFa (kcal/mol)	Backbone RMSDb (Å)	All atoms RMSDc (Å)
Model a	0.00	3.89	5.02
Model b	1.13	3.24	4.27
Model c	1.46	1.65	2.75
Model d	0.43	1.59	2.68
Model e	0.92	2.24	3.13
Initiald	–e	3.90	4.87
AMA-II model1f	1.59	3.69	5.16
AMA-II model2f	1.39	3.34	4.62
AMA-II model3f	2.69	3.74	4.78
AMA-II model4f	2.98	3.69	5.07
AMA-II model5f	1.54	3.42	5.03
X-ray structure in chain B	2.22	0.00	0.00
X-ray structure in chain D	3.28	0.35	1.78

^aPMF values of the models and X-ray structure on the free energy landscape in Fig. 1. The reference is the PMF of model a.

^bThe RMSD values of the backbone heavy atoms of the CDR-H3 loop in each model with reference to the X-ray crystal structure (chain B), where the Cα atoms in the residues other than the CDR-H3 loop from ArgH93 to TyrH102 were superimposed to the crystal structure (chain B).

^cThe RMSD values of the all heavy atoms of the CDR-H3 loop in each model with reference to the X-ray crystal structure (chain B), where the Cα atoms in the residues other than the CDR-H3 loop from ArgH93 to TyrH102 were superimposed to the crystal structure (chain B).

^dThe initial model as the Stage 1 result of AMA-II for the current McMD simulations.

^eThe initial structure was not sampled by the current simulation, and it is out of the free energy landscape.

^fThe Stage 2 models of AMA-II by the McMD computations.

Our previous CDR-H3 models generated by McMD at AMA-II were very different from the X-ray structure, chain B in the PDB file, 4m61. In fact, all five models are located at a cluster containing minima, a and b, and are not at the other clusters including the X-ray structure on the free energy landscape (Fig. 1). The stabilities of these structures are indicated as the PMF values in Table II. The structure modeled in the first stage of our previous work (Shirai et al., 2014), which corresponds to the initial structure of the current simulation, is in an unstable location, where PMF was much larger than 5 kcal/mol on the free energy landscape at PC1 ~−9 and PC2 ~4. Three of the five models generated by McMD at the second stage of AMA-II are in stable regions where the PMF values are <2 kcal/mol, and the others are in less stable regions having the PMF values between 2 and 3 kcal/mol.

There is another antibody crystal structure, chains C and D, in the same asymmetric unit of A52 crystal structure, whose backbone RMSD of the CDR-H3 against that in chain B is only 0.35 Å, very similar to the CDR-H3 structure in chain B (Table II). Both X-ray CDR-H3 structures, in chains B and D, are located at the unstable region with PMF equal to 2.22 and 3.28 kcal/mol, respectively, on a hill region between minima c and d (Fig. 1 and Table II).

In the current work, five models, a–e, were chosen from the free energy landscape as the predicted structures. The RMSDs of the CDR-H3 loop in models a–e with reference to the X-ray crystal structure in chain B are listed in Table II, where the Cα atoms of the residues other than the CDR-H3 loops from ArgH93 to TyrH102 were superimposed on the crystal structure. The current simulation in an explicit water model successfully sampled a wider conformational space than our previous study did at AMA-II, and we consequently predicted structures, models c and d, that are similar to the X-ray crystal structure.

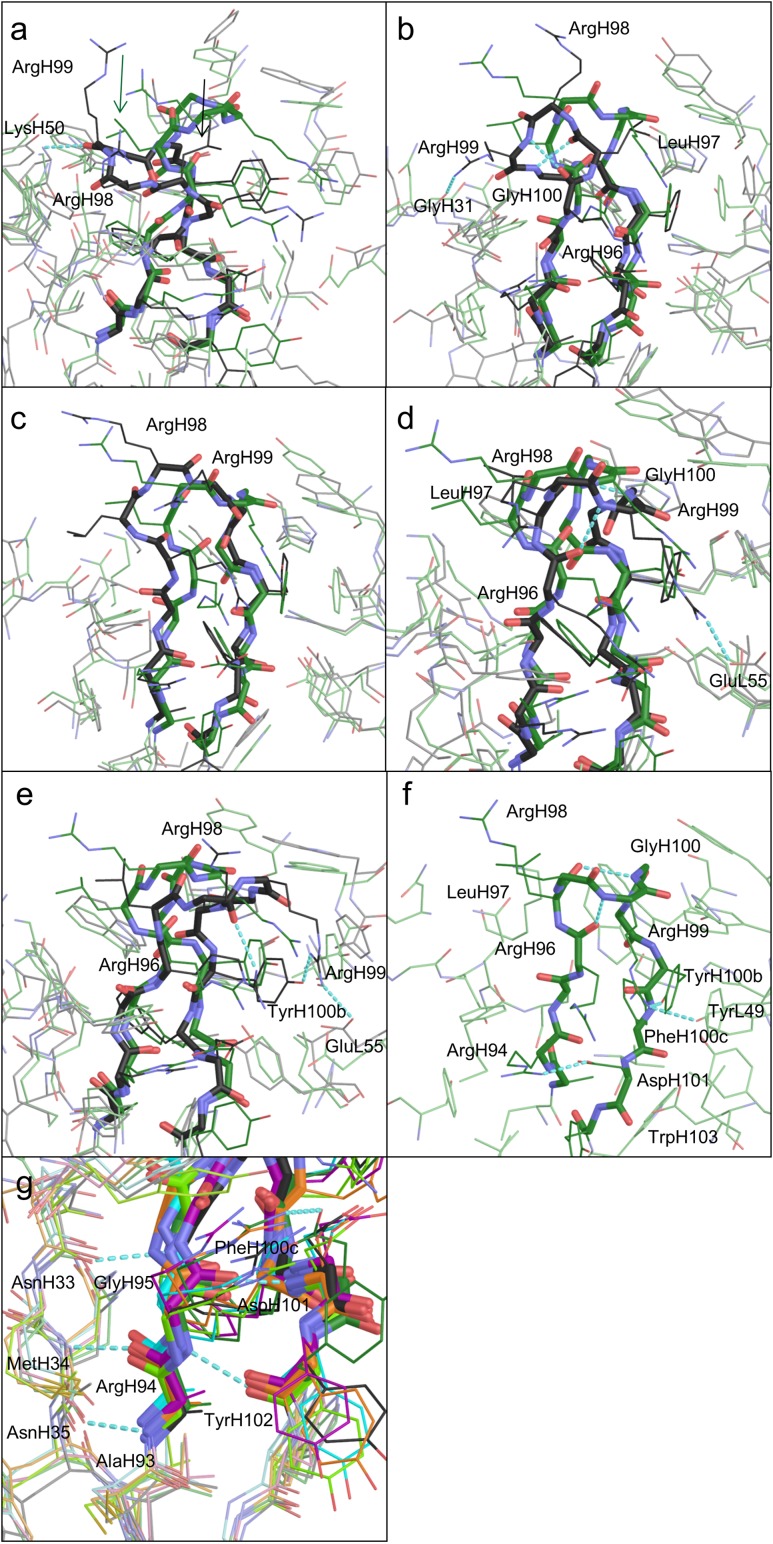
Models a–e of the CDR-H3 loop and its surroundings are shown in Fig. 2a–e. The CDR-H3 loop is divided into a base and a β-hairpin, which correspond to the stem of the loop and the other part of the loop, respectively. The structures of the bases are similar to each other, because they are stabilized by a salt bridge and hydrogen bonds. In each X-ray crystal structure, a hydrogen bond is formed between the backbone carbonyl oxygen of PheH100c and the side chain of TrpH103, and a salt bridge exists between the side chains of ArgH94 and AspH101 (Fig. 2f). The structure satisfies the kinked base in the H3-rules (Kuroda et al., 2008; Shirai et al., 1996, 1999). This salt bridge is also present in all of the models (Fig. 2g). Other similarities exist among all of the models and the X-ray structures, as follows. The strands of AlaH93-ArgH94-GlyH95 and PheH100c-AspH101-TyrH102 participate in forming a β-sheet via hydrogen bonds between their backbone atoms (Fig. 2g). The AsnH33-MetH34-AsnH35 strand also participates in the β-sheet formation, via backbone hydrogen bonds to AlaH93-ArgH94-GlyH95 (Fig. 2g), and there are no significant differences in the ϕ and ψ angles of the bases (i.e. AlaH93, ArgH94, GlyH95, TyrH100b, PheH100c, AspH101, and TyrH102, see Table III).

Fig. 2.

(a–e) Representative models of the CDR-H3 loop and the surroundings at PMF minima a–e, respectively, colored black. The X-ray crystal structure (PDBID 4m61) is shown in green, for comparison. The backbones of CDR-H3 are shown in stick models, and the side chains are in wire models. The surrounding residues are shown in light colors. (f) The X-ray structure of the CDR-H3 loop in chain B and its surroundings. (g) The base of the CDR-H3 loop and the surrounding areas of models a–e, colored black, purple, cyan, yellow-green, and orange, respectively, and the X-ray structure, colored green. Oxygen and nitrogen atoms are colored red and blue, respectively.

Table III.

ϕ (top) and ψ (bottom) angles^a of residues in the CDR-H3 loop

Model/residue	AlaH93	ArgH94	GlyH95	ArgH96	LeuH97	ArgH98	ArgH99	GlyH100	GlyH100a	TyrH100b	PheH100c	AspH101	TyrH102
Model a	−138.2	−73.5	−80.1	−78.1	−120.7	−62.3	−79.7	178.2	56.5	−75.4	−70.6	−116.9	−167.7
Model b	−156.9	−102.4	−72.7	−151.3	−58.8	50.3	54.2	−172.4	58.1	−69.5	−61.9	−86.6	−150.6
Model c	−154.4	−85.2	−142.2	−66.8	−55.4	−124.0	−95.9	110.0	−58.7	−57.8	−72.4	−101.5	−134.8
Model d	−137.1	−75.2	−140.5	−125.2	−62.6	−60.7	−109.7	98.7	−82.8	−71.6	−95.5	−106.8	−123.9
Model e	−147.2	−77.4	−82.0	−76.4	−122.7	−80.7	49.7	162.2	−137.9	−81.0	−95.1	−112.5	−127.1
X-ray in chain Bb	−148.3	−71.5	−104.3	−93.5	−46.8	−78.5	−112.3	103.1	99.9	−57.2	−88.3	−123.3	−131.4
X-ray in chain Dc	−151.0	−78.2	−95.4	−115.3	−55.4	−54.2	−98.2	103.8	94.0	−66.2	−92.0	−108.8	−140.2
Model a	126.7	140.7	169.7	−28.5	163.7	−39.0	−26.8	−100.0	−169.9	171.5	133.7	−15.9	150.9
Model b	139.4	130.4	172.3	−40.5	118.0	38.8	34.4	−116.8	−133.0	156.1	96.1	−27.7	121.0
Model c	131.7	150.8	159.8	128.2	−42.9	−31.5	50.9	117.5	−13.4	139.6	126.3	−59.2	134.6
Model d	129.2	151.0	147.7	88.8	−31.1	−18.6	16.9	157.7	1.9	166.7	135.2	−57.5	135.6
Model e	132.6	114.1	122.0	142.1	−32.5	126.0	40.0	171.3	18.0	176.3	116.4	−34.3	149.6
X-ray in chain Bb	131.0	131.2	139.0	70.2	−47.1	1.0	12.5	−9.7	12.9	154.9	135.4	−26.8	135.4
X-ray in chain Dc	132.6	134.3	156.0	87.4	−46.1	−34.8	13.6	−5.0	20.7	160.4	129.8	−17.7	136.7

^aUnits of ϕ and ψ angles are in degrees.

^bChain B X-ray crystal structure of A52.

^cChain D X-ray crystal structure of A52.

In contrast, the β-hairpin regions of the CDR-H3 loops were different among the five structures (Fig. 2a–e). The X-ray structure in chain B (Fig. 2f) shows the hydrogen bonds formed among the side chains of TyrL49 (TyrL55 as the PDB residue number), ArgH99 and TyrH100b, between the backbone atoms of ArgH96 and ArgH99, and between the backbone atoms of LeuH97 and GlyH100. Model a in Fig. 2a, which had the most stable PMF value, formed a hydrogen bond between the backbone carbonyl group of ArgH99 and the side-chain amino group of LysH50. The side chains of ArgH98 and ArgH99 were exposed to the solvent. Model b in Fig. 2b formed hydrogen bonds between the side chain of ArgH99 and the backbone of GlyH31, between the backbone atoms of ArgH96 and ArgH99, and between the backbone atoms of LeuH97 and GlyH100. The side chain of ArgH98 was exposed to the solvent. Model c, which was the least stable model, lacked a hydrogen bond near the top of the loop, and the side chains of ArgH98 and ArgH99 were exposed to the solvent (Fig. 2c). Model d in Fig. 2d, which was the closest model to the X-ray structure, formed hydrogen bonds between the backbone atoms of ArgH96 and ArgH99, and between the backbone atoms of LeuH97 and GlyH100. The side chain of ArgH98 was exposed to the solvent. A salt bridge between the side-chain atoms of ArgH99 and GluL55 (GluL61 as the PDB residue number) was also seen in this model. Finally, model e in Fig. 2e formed hydrogen bonds between the backbone atom of ArgH98 and the side-chain atom of ArgH96, and between the side-chain atoms of ArgH99 and TyrH100b. The side chain of ArgH98 was exposed to the solvent. A salt bridge between the side-chain atoms of ArgH99 and GluL55 was also seen in model e.

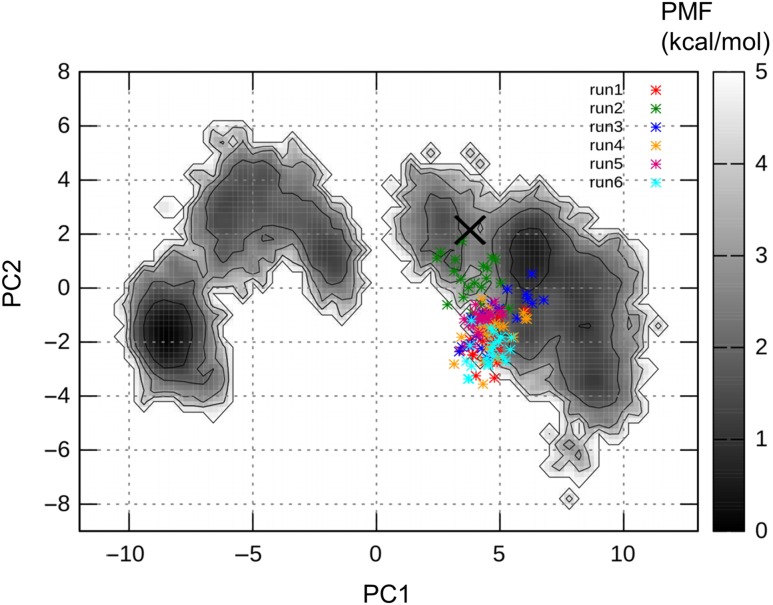
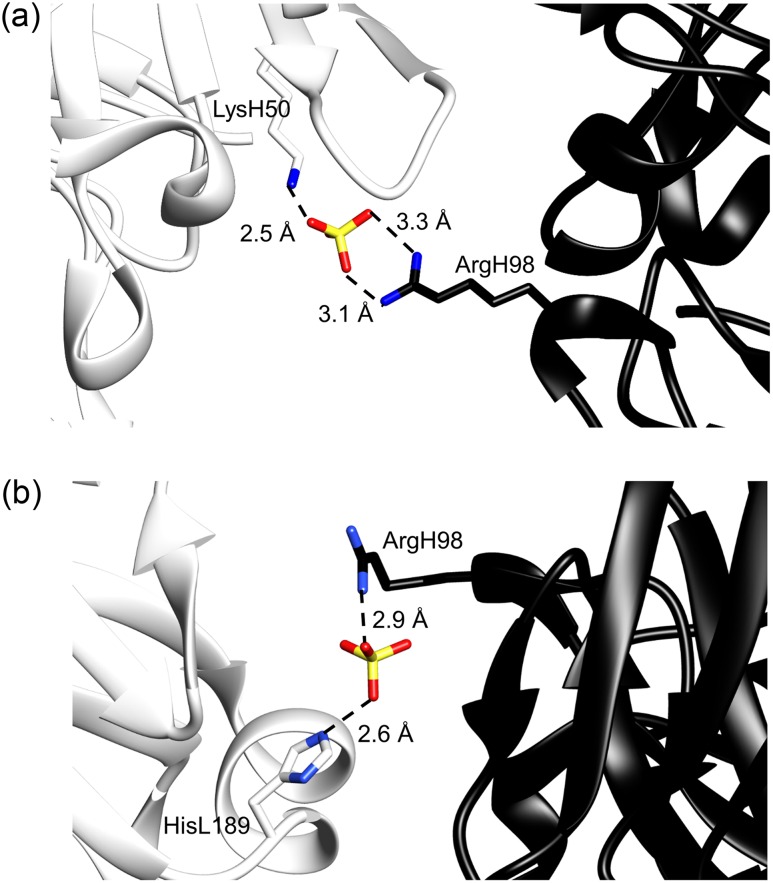
As mentioned above, the X-ray crystal structure seems to be unstable, based on the free energy landscape. Therefore, we performed further short canonical MD simulations starting from the crystal structure at 300 K with different atomic velocities in explicit water, to examine the stability of the crystal structure. The RMSDs of the CDR-H3 loop fluctuated between 0.4 and 1.8 Å after 10 ns (Fig. S2a), and the MD trajectories were projected on the free energy landscape at 300 K (Fig. 3). Most of the trajectories were located near the low PMF region away from the X-ray structure, and the loops obtained from five simulations formed bent structures (Fig. S2b). Two of the six simulations conducted their trajectories toward the minimum d. Thus, the X-ray crystal structure is, in fact, unstable. A careful examination of the X-ray crystal structure revealed 19 sulfate ions, and one forms a salt bridge between the side chain of ArgH98 in chain B and that of LysH50 in chain D in the other crystal unit, as shown in Fig. 4a (Stanfield and Eilat, 2014). In the asymmetric unit of A52 crystal structure, there is another antibody molecule, chains C and D. Interestingly, the side chain of ArgH98 in chain D forms another salt bridge with the side chain of HisL189 (HisA194 as the PDB residue number) in chain A in the other crystal unit across another sulfate ion, as shown in Fig. 4b.

Fig. 3.

Canonical MD trajectories starting from the X-ray crystal structure, projected on the free energy landscape at 300 K. Each trajectory from 40 to 50 ns was used for the projection. Six trajectories are shown in different colors in the figure. The initial crystal structure is shown as the cross. The PMF is shown by the gray color in the contour bar.

Fig. 4.

(a) X-ray crystal structure of A52, showing the salt bridge between the side chain of ArgH98 in chain B (black) and that of LysH50 in chain D in the other crystal unit (white) across a sulfate ion. (b) The other heavy chain D in the asymmetric unit of A52, which forms the salt bridge between side chain of ArgH98 (black) and that of HisL189 (HisL194 of chain A as the PDB residue number) in the other crystal unit (white) across another sulfate ion.

Namely ArgH98 in the CDR-H3 loops of the both crystal structures in chains B and D should be biased by the crystal packing effect, which is well known to significantly modify protein loop structures (Rapp and Pollack, 2005). Thus, the A52 CDR-H3 loops in the X-ray structures are probably stable in the crystal with sulfate ions, but they are not stable in solution. Our model d, which is the second most stable structure in our free energy landscape, could be the solution structure, although its backbone RMSD value deviated by 1.59 Å from the crystal structure (chain B).

When we examined whether crystal packing artifacts also exist in the other 10 antibodies (Teplyakov et al., 2014), we found many contacts, in 9 cases out of the total 11 antibodies, between the CDR-H3 loops and the surface residues in the other neighboring unit cells, as shown in Table IV. As the long CDR-H3 loops tend to protrude, contacts caused by the crystal packing effects should often be observed. In the two cases where no contacts are observed between the CDR-H3 loops and the residues in the other unit cells, the average temperature factors of the CDR-H3 loops tend to be high, especially when we consider the effects from all atoms including side-chain atoms (Table IV).

Table IV.

Crystal packing effects at the CDR-H3 loops in the X-ray crystal structures

Target (PDBID)	Lengtha	Crystal packing effectb	Resolution (Å)	Backbone average B-factor (Å2)c	All atoms average B-factor (Å2)d
Ab01 (4ma3)	10	SB between ArgH95sc and GluH1sc	2.00	25.0	28.5
Ab02 (4kuz)	13	SB between AspH100sc and ArgH103sc; HB between ArgH103sc and AspH31sc	2.70	23.4	24.3
Ab03 (4kq3)	10	SB between GluH101sc and ArgL210sc; HB between TyrH102sc and carbonyl of ArgL210bb; HB between carbonyl of GluH101bb and LysL189sc	1.92	23.7	28.1
Ab04 (4kq4)	10	SB between ArgH101sc and GluH10sc	2.45	82.9e	91.2e
Ab05 (4m6m)	10	(No contact)	2.00	25.2	33.4
Ab06 (4m6o)	16	SB between AspH108sc and ArgH30sc; HB between TyrH100sc and carbonyl of HisH228bb; HB between HisH105sc and HisH227sc	2.80	48.1	47.2
Ab07 (4mau)	10	SB between AspH100sc and LysH214sc; SB between AspH105sc and LysH214sc	1.90	24.0	25.6
Ab08 (4m7k)	13	HB between TyrH102sc and carbonyl of LysL194bb	1.90	25.9	29.3
Ab09 (4kmt)	12	(No contact)	2.10	27.7	34.6
Ab10 (4m61)	13	SB between ArgH98sc in chain B and LysH50sc in chain D across a sulfate ion (this study) SB between ArgH98sc in chain D and HisL189sc in chain A across a sulfate ion (this study)	1.62	24.7 (chain B) 15.4 (chain D)	27.6 (chain B) 19.4 (chain D)
Ab11 (4m43)	12	HB between AspH98bb and SerL122sc; Van der Waals contact between AspH98bb and SerL122sc	1.85	14.4	17.2

^aLength of the CDR-H3 represented by the number of residues.

^bSB, salt bridge and HB, hydrogen bond between the residue in the CDR-H3 loop and the residue in the other neighboring unit cell. sc indicates a side chain, and bb is a backbone. The residue numbers are those in the PDB files, except for the current study for Ab10.

^cTemperature factor of the backbone heavy atoms averaged for each CDR-H3 loop, where N- and C-terminal 2 residues at the base were not counted.

^dTemperature factor of the all heavy atoms averaged for each CDR-H3 loop, where N- and C-terminal 2 residues at the base were not counted.

^eTemperature factors of the entire chains in this PDB entry (4kq4) are all very large by an unknown reason.

As shown in Fig. 1, a large free energy barrier exists between minima b and c along PC1, which divides the structure ensemble into two clusters, consisting of models a and b, and the others. We found that the side chains of LeuH97 adopt different directions between the two big clusters, as shown in Fig. 2a, where these side chains in model a and the X-ray structure are depicted by arrows. The ψ angles of ArgH96 and LeuH97 clearly distinguished models a and b from the others (Table III). Therefore, LeuH97 should flip by the rotation of the ψ angles of ArgH96 and LeuH97 during the transition between the two clusters. Since the transition probability might be rare at 300 K, a high barrier was found in the landscape.

In the free energy landscape obtained from this work, the most stable structure, model a, largely deviated from the X-ray crystal structures, and the second most stable structure, d, was similar to the crystal structures. Here, we discuss the implications of this structure. The target antibody of this work, A52, is related to a systematic lupus erythematosus-like disease (Theofilopoulos and Dixon, 1985). Although the antigen of the A52 antibody is known to be either single-stranded or double-stranded DNA, no complex structure is available. Only a few structures of antibodies that bind to DNA are available (Stanfield and Eilat, 2014), such as that of the DNA-1 antibody (Tanner et al., 2001), which adopts multiple conformations in the apo-state (Schuermann et al., 2005). If the A52 antibody has similar properties to the DNA-1 antibody, then our free energy landscape consisting of several stable structures may capture the structural properties of the A52 antibody in the apo-state. In fact, there are sequence identities in TyrL32 (TyrL38) of the CDR-L1 loop and in HisL91 (HisL97) of the CDR-L3 loop, where the residue numbers used in the PDB file of the A52 antibody are shown in parentheses. In addition, TyrH100 and TyrH100a, which are important residues for ligand recognition by the DNA-1 antibody (Schuermann et al., 2005), correspond to TyrH100b and PheH100c in the A52 antibody. If the structural changes, which occur upon antigen binding between the X-ray structure and model a for the A52 antibody (Fig. S3a), are similar to those between the apo- and holo-antibodies for the DNA-1 antibody (Fig. S3b), then our model a is a candidate that may bind ligands tightly.

Conclusion

Re-modeling of the long CDR-H3 loop with 13 amino acid residues, as the target Ab10 at the AMA-II, was performed with more precise molecular models with the explicit solvent molecules and the more effective McMD method than those used in our previous modeling at AMA-II. The observed free energy landscape provided a variety of stable loop structures, with some similar to the crystal structure.

In addition, the crystal structures were suggested to be unstable in solution, because they are stabilized by the crystal packing effect. As the crystal structures are used for the assessment of the blind contest, these artifacts in the crystal structures are not appropriate. The purpose of the contest is not to make a struggle among the participants to predict the most similar 3D structure to the crystal structure, but to improve the modeling techniques. The crystal packing effect to the structural bias for the CDR-H3 seems to be a common phenomenon, which is revealed from our observation of the other 10 antibodies. As the long CDR-H3 loops tend to protrude, it is not surprising to often observe such crystal packing effects. Thus, for modeling these flexible CDR-H3 loops as they are in solution, not only a single candidate structure is predicted, but also many putative stable and semi-stable structures should be sampled. One may appear as an apo-structure, and another one may correspond to a holo-structure with the antigen, as proposed by the population-shift paradigm (Okazaki and Takada, 2008).

Supplementary data

Supplementary data are available at PEDS online.

Funding

This work was supported by a Grant-in-Aid for Scientific Research C (16K07331) from the Japan Society for the Promotion of Science (JSPS) to N.K.H.N. was supported by a Grant-in-Aid for Scientific Research on Innovative Areas (24118008) and a Grant-in-Aid for Challenging Exploratory Research (16K14711) from JSPS. This work was performed in part under the Cooperative Research Program of the Institute for Protein Research, Osaka University, CR-15-05 to N.K. This research was partly supported by the HPCI Research Project (hp150146) to N.K.