A Framework for Parameter Estimation and Model Selection from Experimental Data in Systems Biology Using Approximate Bayesian Computation

Abstract

As modeling becomes a more widespread practice in the life- and biomedical sciences, we require reliable tools to calibrate models against ever more complex and detailed data. Here we present an approximate Bayesian computation framework and software environment, ABC-SysBio, which enables parameter estimation and model selection in the Bayesian formalism using Sequential Monte-Carlo approaches. We outline the underlying rationale, discuss the computational and practical issues, and provide detailed guidance as to how the important tasks of parameter inference and model selection can be carried out in practice. Unlike other available packages, ABC-SysBio is highly suited for investigating in particular the challenging problem of fitting stochastic models to data. Although computationally expensive, the additional insights gained in the Bayesian formalism more than make up for this cost, especially in complex problems.

Introduction

Experimental data and mathematical models are beginning to take equal billing in systems biology. Experimental observations without a framework in which to link them offer us only limited insights into how biological systems work. Equally, mathematical analysis without concrete grounding in, and immediate relevance to, experimental observations risks being biologically irrelevant. Here we adopt a very flexible notion of what constitutes a system, and merely assume that we have quantitative (e.g. proteomics, transcriptomics or metabolomics) data concerning the change over time in the abundances or concentrations of a number of different molecular species; signal transduction and stress response pathways, and gene expression regulatory circuits naturally fall under this loose definition, as do metabolic pathways, and combinations thereof.

Models summarize our understanding of biological mechanisms in an equally convenient as well as precise form; they enable us to make predictions that test our understanding; and model those aspects of a system that are not directly accessible to experimental observation. In the analysis of gene expression dynamics, for example, proteomic and transcriptomic data are rarely measured together and, if they are, not always at the same time-points. Models thus provide the context in which data are best interpreted and the function of biological systems is understood.

Linking models and data, however, remains a formidable challenge. Even when a plausible, perhaps even ‘almost correct’, model is available, we require numerical values for all the mathematical parameters that describe the behavior of the mathematical system. And suitably parameterized models are few and far between.

Two schools of thought can be distinguished. The first, traditional approach is to collect parameter values from the literature and plug these values into the mathematical equations making up the model. The second approach places the experimental data at the heart of the analysis and seeks to infer the parameters from the available observations^1,2. A host of different approaches, or inferential procedures, have been proposed in the literature and used in practice³. Statistical inference typically tries to obtain the best estimates of the reaction rates as well as their respective uncertainties (Figure 1). Optimization-based frameworks contend with the ‘best’ value. A common method is to specify an objective function that quantifies the discrepancy between the experimental data and the model’s predictions, and then to search through parameter combinations in order to minimize this discrepancy⁴. A broad range of optimization algorithms exists, which provide a variety of different (often heuristic) methods for performing this search and thereby identifying the ‘best’ parameter set. If such an optimization approach is adopted, a key consideration is to avoid over-fitting the data (i.e. fitting the noise). Another concern is the problem of local optima, which means that there will often be many parameter combinations that provide locally optimal fits, but determining whether or not they are truly the ‘best’ parameters (or if, alternatively, we could have found better ones by performing a more thorough search) is typically very challenging. Finally, optimization approaches must always be concerned with the robustness of the parameter estimates, and the confidence that is placed in them. Bootstrapping⁵ and data subsampling approaches provide a class of (computationally intensive) methods for robustness quantification, by generating a collection of ‘new’ datasets from the initial set of observations, and then assessing the variability in the parameter estimates obtained across this collection.

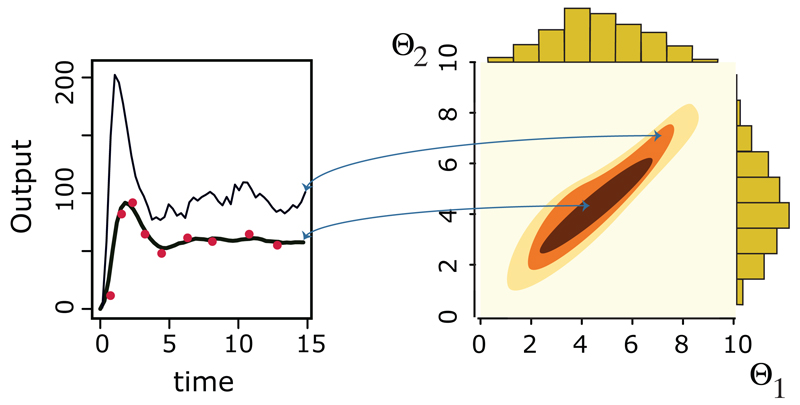
Figure 1. Data and Posteriors.

The aim of Bayesian inference is to infer parameters that have high or appreciable probability of having generated some observed data (red dots in the left panel). If a model has two parameters, θ₁ and θ₂, then our aim is to obtain the joint distribution over both parameters, indicated by the contour diagram in the right panel. Please note that in this panel, the darker the color of the contour the higher the posterior probability density. The two simulated trajectories in the left panel correspond to two different parameter combinations. The parameter combination associated with the thicker trajectory (which provides the better explanation of the observed data) is in a region of high posterior density, whereas the parameter combination of the thinner trajectory is located in a region of lower posterior density. Often, as here, the joint distribution will differ from the product of the (marginal) distributions of the individual parameters (histograms at the top and right of the contour plot) – statistical dependence between the two parameters means that their joint posterior distribution is not simply the product of the individual/marginal parameter posteriors. Secrier et al.⁶⁸ discuss a range of such examples.

Although the best parameter value is of obvious interest, so too is an assessment of how much uncertainty there is in the estimate. As an alternative to heuristic optimization approaches, Bayesian inference has gained attention in recent years as a flexible and formally coherent way in which to approach the problem of model calibration^1,6,7. Bayesian approaches provide an opportunity to specify any prior beliefs or information that we have about the unknown parameters (which may, for example, have been obtained through previous experimentation), while also: (i) automatically avoiding the problem of over-fitting; and (ii) providing assessments of confidence by assessing the uncertainty that remains in the unknown parameters. Although the problem of adequately exploring the space of parameter combinations remains, and it must be carefully considered, methods for Bayesian inference typically take great pains to address these concerns. The key object of interest when performing Bayesian parameter inference is the ‘posterior distribution’. This distribution describes the uncertainty that remains in the parameters after observing the data, and is obtained via Bayes rule in a manner that combines our prior beliefs (the beliefs we had regarding the parameters before performing the current experiments) with an assessment of the fit provided to the observed data. Formally, we usually write this relationship as⁸,

$$p(\theta |D)\propto \ell (\theta |D)p(\theta ),$$

where θ denotes the vector of parameters, D is the observed data, and ℓ the likelihood function; or, in words, as,

$$\text{posterior}\propto \text{likelihood}\times \text{prior}.$$

Here, the prior is a distribution that formally expresses the information or beliefs that we have about the parameters before we performed the current experiment, while the likelihood is a function of the parameters that describes in a formal, probabilistic manner how well each parameter explains the observed data.

The prior distribution clearly has an important role in Bayesian inference, providing an opportunity to express the beliefs we have regarding the parameters before dataset D is obtained. Exactly how we should elicit and specify priors is a highly debated issue that is largely beyond the scope of the present article, and we refer the interested reader to the literature^9–12. Since the use of ‘objective’ priors (i.e. ‘vague’ priors, such as maximum entropy and Jeffreys priors, specified according to mathematical principles, rather than according to the subjective prior belief of the investigator conducting the analysis) has received some criticism¹³, we would recommend biophysically motivated priors (i.e. priors which genuinely reflect the researcher’s knowledge of any biophysical constraints) wherever possible. In cases where this is not possible, it is advisable to explore the influence of prior choice explicitly, as done in, for instance, Toni et al.¹⁴.

The likelihood is typically defined by a parametric probability model, p(D|θ), for the data, such that ℓ(θ|D) is given by considering p(D|θ) as a function of the parameters θ (with D, the observed dataset, fixed). In contrast to maximum likelihood approaches, which treat the likelihood as an objective function and use optimization approaches to search for the single ‘best’ parameter vector that maximizes p(D|θ), Bayesian approaches are concerned with elucidating (or, at least, obtaining samples from) the posterior distribution of parameter vectors, p(θ|D). It is usually impossible to write down an expression for the posterior distribution analytically, in which case it is necessary to use computational approaches, such as Markov chain Monte Carlo (MCMC) techniques¹⁵.

It is worth reiterating that Bayesian inference attempts to assess the probability of a parameter to be the ‘correct’ parameter given the data⁸; this naturally includes an assessment of the uncertainty of the inference as all parameter values that have finite probability to have generated the data are the target of the inference procedure. This uncertainty, it has turned out, can play a pivotal role in the analysis of a system’s dynamics^16–18. And appreciation of this uncertainty yields direct insights into the degree to which the behavior predicted by the model is robust to changes to the parameters, especially when the distribution over the different reaction rates is considered jointly (Figure 1). Although they come at computational expense, the insights gained from considering this joint distribution over parameters may outweigh these costs. When analyzing data in the context of a mathematical model, we always ought to calibrate the model against the available data, i.e. to estimate parameters from the data directly. Relying on parameter values obtained independently, such as from the literature, is fraught with potential problems as biochemical reaction rates can vary between different conditions (e.g. as a function of temperature, ambient pH, or changes due to factors not explicitly modeled).

A great deal of recent research has considered situations in which it is impossible to write down an expression for the likelihood, ℓ(θ|D), but it is nevertheless possible to simulate data from our model. Such ‘likelihood free’ approaches have become known as ‘approximate Bayesian computation’ (ABC)¹⁹.

The simplest ABC approach, ABC rejection^20,21, proceeds by: (i) sampling a parameter vector, θ*, from the prior distribution; (ii) plugging θ*into our model and running a simulation in order to generate a synthetic dataset, D*; (iii) using a distance function, d, to quantify the discrepancy between D* and the observed data, D; and (iii) accepting θ* if the distance, d(D, D*), between D and D* is less than some threshold value, ε. This process may be repeated many times in order to obtain a collection of accepted parameter vectors. It is important to note that, if noise is present in the observed dataset D, then, to avoid introducing biases, it should also be present in the synthetic dataset D*, which for known noise characteristics can be straightforwardly incorporated. In some contexts (e.g. when modeling data using ordinary differential equations) simply specifying a model for the measurement noise will imply a likelihood²², but here we are concerned with complex stochastic models for which this is not the case. In the models that we consider, there are components of output uncertainty that are typically much larger than the measurement noise (e.g. in the context of biochemical reaction networks, the times at which reactions occur), and therefore it has become common practice to assume that measurement noise is negligible compared to these other sources of stochasticity^23–25.

In the limit as the threshold value ε tends to zero, the accepted collection of parameter vectors will represent a sample from the posterior distribution, p(θ| D). In practice, if ε is set to be too small, the acceptance rate (i.e. the proportion of times we have d(D, D*) < ε) will be unacceptably low. This consideration (and its computational implications) has motivated researchers to introduce a number of sequential approaches^26–28, in which a decreasing schedule of ε values is used in such a way that these approaches gradually move from sampling from the prior (when ε is very large) toward sampling from the posterior (as ε tends toward zero). In this protocol we focus on an ABC algorithm based on sequential Monte-Carlo approaches (ABC-SMC) introduced by Toni et al. ²⁷. An overview of the ABC-SMC algorithm is provided in Box 1. In cases where the dataset, D, is very high-dimensional or has a particularly complicated structure (e.g. if D is from a network), a number of authors have considered comparing summaries of the data, i.e. calculating vectors of statistics, ρ(D) and ρ(D*), for the observed and simulated datasets, and only accepting θ* if d(ρ(D), ρ(D*)) < ε. However, this approach will usually result in some loss of information (which can have negative theoretical and practical consequences), and hence considerable care must be taken to choose appropriate, informative summaries of the data^29–33. In ABC-SysBio, we only consider direct comparisons between the observed and simulated datasets, rather than using summaries of the data.

Box 1. Overview of ABC-SMC Algorithm.

ABC-SMC as employed by ABC-SysBio attempts to find an approximation to the true posterior in a sequential manner²⁷. To this end, a set of intermediate distributions — also known as populations — is constructed, where for each population, t, all accepted particles give rise to simulated data, D*, that differ from the true experimental data, D, by at most a distance, Δ(D*,D)<ε_t. This approach requires a sequence of decreasing thresholds or tolerances as shown in the figure above, with the final tolerance, ε_T, setting the desired final agreement between real and simulated data.

Successive populations are generated from the previous population (or from the prior if t=1) using a sequential importance sampling scheme, by perturbing particles using an appropriate so-called perturbation kernel, to ensure that the parameter space is explored sufficiently well. Each accepted particle has an associated weight and in ABC-SysBio we require a fixed number of particles in each population. Choice of the kernel and the sequence for ε_t can affect the speed of the algorithm.

In addition to parameter estimation, ABC approaches can also be used for model ranking and selection³⁴. In this case, we associate a model indicator, m, with each model under consideration, and seek samples from the joint posterior distribution over models and parameters, p(m, θ|D). From these samples we may derive estimates of the marginal posterior probability of a model, p(m|D), which may be used to rank the models of interest. As we discuss in the Limitations section below, the issues mentioned above regarding the use of statistics to summarize the data (which we avoid in ABC-SysBio) are particularly problematic in the context of model selection.

The key strength of ABC approaches is that they can be applied to problems with intractable likelihoods^35,36 (for example, complex stochastic models). However, ABC approaches are much more broadly applicable, since they can be used regardless of whether or not it is possible to write down a likelihood function^37,38. The only requirement is that we must be able to simulate from the models under consideration. This property makes ABC an ideal methodology for software implementation, enabling it to be applied ‘out of the box’ to a broad range of problems. ABC-SysBio is an efficient and very generally applicable software implementation for performing parameter estimation and model selection within the ABC framework.

Applications and key papers: ABC-SMC and ABC-SysBio

Likelihood-free inference in the form of simple ABC rejection was first introduced in the area of population genetics^21,39, and, due to the size of the models and parameter space, the algorithm was soon extended to adopt more powerful MCMC⁴⁰ and SMC ²⁶ samplers. Since then, there has been an explosion of papers advancing the ABC methodology and its applications (see ⁴¹ for a review). As described above, ABC methods can be used for a wide range of applications for fitting models to different types of data; here we restrict the discussion to biological applications with data ranging from gene expression and proteomic time series data, to imaging data, and protein-protein interaction data. ABC-SysBio was conceived with the aim of solving precisely these types of problem. The parameter estimation algorithm was used to fit the deterministic and stochastic mechanistic models of the phage shock protein stress response in Escherichia coli, which then served to propose novel hypotheses about the stress response system dynamics⁴². An Akt signaling pathway model was among the largest models to which the parameter inference algorithm has been applied to date³. The obtained posterior distribution was used to study in detail the sensitivity and ‘sloppiness’ of the kinetic parameters affecting Akt signaling. The parameter estimation algorithm was also used to find the parameter region for a model of Hes1 transcription dynamics, that captures the oscillatory behavior of Hes1 expression levels observed in mouse cell lines⁴³. Oscillatory behavior poses considerable challenges to parameter estimation problems²², and in this study the parameter distribution obtained by ABC served as prior information for another powerful algorithm that can efficiently infer parameters giving rise to oscillatory behavior.

Toni et al. used the model selection algorithm to distinguish between several models of the phosphorylation dynamics of the ERK MAP kinase by fitting the models to time series proteomic data¹⁴. The model selection algorithm was also used to study leukocyte migration in zebrafish embryos in response to injuries⁴⁴. In this application, model selection was used to distinguish between different models of the chemokine stimulus gradient, and, based on migration trajectories obtained from live imaging data, the model was chosen that best describes the in vivo leukocyte dynamics. This study is a prime example of an application for which ABC is particularly appropriate: here the definition of a likelihood has thus far proved elusive, whereas simulating from these models is possible. Other applications of ABC-SMC (based on ABC-SysBio) have emerged in synthetic biology ⁴⁵, where we can use this framework to identify molecular reaction networks that have high (or appreciable) probability of fulfilling a given set of design-objectives, such as different switch-like or sensor behaviors. In regenerative medicine and stem-cell biology a related approach has been used to map out the behavior of hematopoietic stem cells and their progeny in the bone marrow stem cell niche⁴⁶.

Comparison with other methods

ABC methods fill a gap in the apparatus of statistical inference. Their advantages are two-fold. First, they enable researchers to apply the whole Bayesian formalism — in approximation — to problems that defy conventional statistical inference⁴⁷. Second, in their wake we may be able to close such gaps in the applicability of conventional statistical inference either through computational advances or new developments of e.g. suitable approximations to the likelihood^23,48–51.

The distinct applications and strengths of ABC methods complicate comparison with other methods. Pure ABC packages are typically targeted either at ABC cognoscenti and require the provision of e.g. simulation routines (typically provided as R or C functions), or at population geneticists such as DIYABC ⁵². In the latter realm, some packages have achieved a level of sophistication that enables non-expert users to study hard problems in population genetics, such as population sub-division and movement between different demes^53,54. But for the practicing systems biologist, packages such as easyABC (http://easyabc.r-forge.r-project.org) lack, for example, the ability to parse mathematical models provided in the SBML exchange format or the ability to simulate efficiently (e.g. via GPU-support^55,56) different models.

In the context of likelihood-based Bayesian inference, several packages exist (typically employing MCMC algorithms) for systems modeled by ordinary differential equations (ODEs). These include primarily BioBayes⁵⁷. Stochastic dynamics, whether modeled using stochastic differential equations (SDEs) or chemical master equation formalisms, incur huge computational costs and there is a distinct lack of ‘general’-purpose software aimed at the systems biology community. Here, however, we see the main use of ABC methods at present. For ODEs it is possible, and indeed desirable, to employ likelihood-based inference, but for many stochastic models, ABC-based approaches enable researchers to address inference problems that simply cannot be tackled by conventional Bayesian approaches^50,58.

Likelihood-based MCMC or SMC approaches, and nested sampling are also emerging as inferential frameworks for stochastic dynamical systems. This development is particularly promising when dealing with cases where the likelihood of a set of stochastic (time-series) realizations of a system can be approximated in a computationally favorable way. One such way is to use, for instance, the linear noise approximation or generalizations thereof to model the time-evolution of stochastic dynamical systems⁴⁸. Such simulation routines may, of course, also be gainfully employed in ABC frameworks.

Limitations

ABC methods are designed to work where other, likelihood-based approaches cannot (perhaps, yet) be applied. Nevertheless, when used to address any challenging problem, ABC methods will also be computationally expensive. And obviously, the curse of dimensionality still applies: thus the more parameters we seek to infer, the more challenging the inference will become and models with even only dozens of parameters will defy serious analysis by ABC, or, indeed, any other Bayesian approach.

There have been developments in computational aspects of ABC^36,59,60, which promise to make inference more efficient and affordable, but these developments cannot overcome the more generic problems encountered by all inference algorithms.

One area where limitations of ABC procedures have received widespread attention is model selection^31,33,61. The limitations that have been highlighted in the literature are pertinent for cases where inferences are based on summary statistics of the data instead of the data themselves, an approach conventionally adopted in population genetics applications. In these cases model selection is notoriously dependent on arbitrary choices made in the set-up of the ABC inference, and can swing in favor of any plausible model, irrespective of which is the correct one. This tendency causes problems in any real-world application, where the correct model is obviously not known.

The type of inference problem considered in this protocol does not require the use of summary statistics of the data. In the context of the dynamical systems models considered here, ABC inference may be conducted using the whole time-course dataset, rather than summary statistics thereof. Thus ABC model selection is possible in the current setting, and is implemented in ABC-SysBio.

Protocol overview

The ABC-SysBio software is designed for parameter inference and model selection. However, it can also be used to parse and simulate sbml models (models written in the format of the Systems Biology Markup Language standard). It enables researchers to perform simulations using ODE and SDE solvers, and the Gillespie algorithm.

In the ABC-SysBio software parameter inference and model selection are performed in a sequential manner (as described in Box 1). At each iteration of the algorithm, a set of parameter vectors is constructed; these parameter vectors are called ‘particles’ and form a ‘population’. Each particle is a vector of length equal to the number of parameters to be estimated. In this protocol, we refer to the number of particles in a population as the ‘population size’. The populations are constructed so that the particles forming the population give rise to simulated data that differ from the observed data by at most a predetermined threshold. Therefore each population is associated with a threshold; these thresholds decrease in consecutive populations, starting from a typically quite high threshold at population 1 and tending toward zero. Selecting appropriate settings for the algorithm, such as the number of particles per population or the decreasing threshold schedule, involves some trial-and-error and experience. Some basic guidance is given in Box 3.

Box 3. Algorithms Set-Up and Advanced Options.

Many of the settings of the algorithm affect convergence to the true posterior and may require careful consideration in new applications of ABC-SysBio. We provide some basic guidance on the most important parameters below.

particles: The number of particles has to be large enough in order to efficiently cover the entire parameter search space and should increase with the number of parameters, or for model selection applications

epsilon: As an alternative to user-specified tolerance schedules we can also choose automated tolerances, which are based on the distributions of the recorded distances between simulated data from the previous population and the observed data. The next threshold is the <alpha> quantile of this distribution, where <alpha> is a parameter of the algorithm that needs to be defined. For example:

<autoepsilon>

<finalepsilon> 0.0 </finalepsilon>

          <alpha> 0.1 </alpha>

</autoepsilon>

restart: For a user-defined tolerance schedule, it can happen that a tolerance value is too strict, in which case the acceptance rate drops drastically. The user can stop the algorithm and restart it from the last finished population with a new tolerance schedule by setting in the input file:

<restart> True </restart> The algorithm will then apply the new tolerance schedule.

prior distribution: Currently implemented prior distributions are: constant x (constant parameter with value x), normal a b (normal distribution with location a and variance b), uniform a b (uniform distribution on the interval [a, b]) and lognormal a b (lognormal distribution with location a and variance b). If plausible parameter ranges are known, prior distributions should be defined accordingly. In this case the user can either trust these values (‘constant‘ prior) or set a small prior range around this value (for example, a normal distribution centered on a literature value).

Initial conditions: can be inferred as parameters if priors are provided, e.g.

<initial>

<ic1> uniform 0.0 100.0 </ic1>

<ic2> uniform 1.0 10.0 </ic2>

<ic3> constant 0.0 </ic3>

</initial>

infers initial conditions for species 1 and 2 (with uniform priors), but starts from 0 for species 3.

distance function: ABC-SysBio computes the sum of squares (Euclidean distance) between data and the simulated trajectories. The user has the option to use a custom distance function (see section 5.3 of the ABC-SysBio manual). Adaptations of the distance function can help to avoid convergence problems⁶³.

kernel: The implemented perturbation kernels are: uniform (component-wise uniform kernels), normal (component-wise normal kernels), multiVariateNormal (multi-variate normal kernel whose covariance is based on the previous population), multiVariateNormalKNeigh (multi-variate normal kernel whose covariance is based on the K nearest neighbours of the particle), multiVariateNormalOCM (multi-variate normal kernel whose covariance is the OCM).

dt: For SDE-models the user has to set the numerical time step ‘dt’. This time step needs to be reasonably small (for most systems dt<0.01) in order to avoid numerical errors, but smaller time steps result in longer simulation times.

In this protocol, we demonstrate how to use ABC-SysBio to infer parameters of an example system given a data-set and how to rank two candidate models. Two mRNA self-regulatory models have been created to serve as tutorial. One of them was used to generate an in silico data set, which will be used in the parameter inference and model selection scheme.

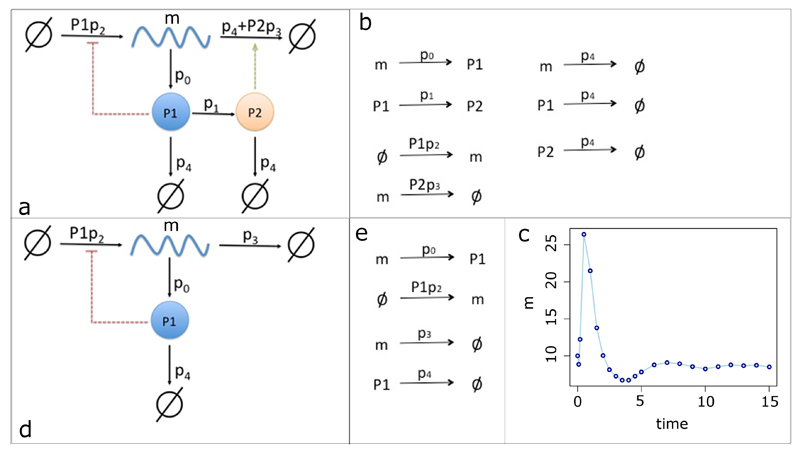
In the first example system, mRNA (m) is translated into a protein (P1) that regulates the production of its own mRNA, m. Furthermore P1 can be modified (through an assumed post-translational modification) at some rate resulting in P2, which degrades m. All three molecular species are degraded at a constant rate. This system therefore contains seven reactions. A schematic of the system, together with the seven reactions are shown in Figure 2 (a,b). The species, parameter and reactions are defined in an sbml model file, which is provided as Supplementary data 1. In the first part of the Procedure (steps 1-18) we illustrate how to infer parameters of this system (denoted by p0, p1, p2, p3 and p4 in Figure 2) using the in silico–generated data set. We explain how to use sbml models, guide through the algorithm settings and explain the output of ABC-SysBio.

Figure 2. Models and data.

The full mRNA self-regulation model is shown in (a). mRNA (m) produces protein P1, which can be transformed into protein P2. P1 is required to produce mRNA, whereas P2 degrades mRNA. P1 and P2 can also be degraded. The reactions that occur according to this model are shown in (b). Fitting of the model to the data (c), which comprise mRNA measurements over time. The second model (d) is based on the first model, but it does not contain protein P2. The relevant reactions are shown in (e).

In the second part of the Procedure (steps 19–29) we illustrate the use of the model selection tools to discriminate between two models: the model described above and a simplified model of the mRNA self-regulation represented in Figure 2 (d, e). We use a similar data set as in the first part of the procedure. However, in this second part of the protocol we assume that only the total protein measurements are available, although not for all time points.

For other models that are not part of this protocol, sbml model files can either be generated manually, by several pieces of software (Copasi, Mendel, ShorthandSBML) or in the case of published models it can be found in the BioModels database (http://www.ebi.ac.uk/biomodels-main/). An excellent tutorial on understanding and generating sbml files can be found in Wilkinson⁶².

Although this protocol contains a Timing section, the length of time required for the parameter inference and the model selection algorithm to run is highly dependent on the system hardware. The computational cost also depends on the size of the model, the complexity of the data, the dimension of the parameter space as well as on all the algorithm settings (such as the number of particles, the perturbation kernel, etc.). A full list of all algorithm settings is provided within the documentation of the ABC-SysBio package.

Materials

Equipment

ABC-SysBio is a Python package, which runs on Linux and Mac OS X systems (Windows is not currently supported but we have succesfully installed matplotlib, numpy, scipy, libsbml and abc-sysbio on Windows Vista using WinPython.). Python can be downloaded from http://www.python.org.

Necessary dependencies are: Numpy (http://sourceforge.net/projects/numpy/files/), Scipy (http://sourceforge.net/projects/scipy/files/), Matplotlib (http://sourceforge.net/projects/matplotlib/files/). Optional dependencies are Swig (http://sourceforge.net/projects/swig/files/), libSBML (http://sourceforge.net/projects/sbml/files/libsbml/) (both necessary to follow this protocol) and cuda-sim (http://sourceforge.net/projects/cuda-sim/files/).

Equipment Setup

Install Python and the relevant dependencies according to the procedure detailed in the Supplementary Methods.

Install ABC-SysBio according to the instructions in Box 2

Box 2. Installation of ABC-SysBio.

1. Download the ABC-SysBio package from http://sourceforge.net/projects/abc-sysbio/files/ and unzip it.

   In the following steps (2-3) replace <dir> with the full path to a location. This will be the location containing the lib and bin directories (usually /usr/local by default, where Python is installed).

2. Open a terminal and type

   cd abc-sysbio-2.06

   python setup.py install --prefix=<dir>

   Please note that the --prefix=<dir> option is recommended since it will guarantee that each package picks up the correct dependencies. This places the ABC-SysBio package into

   <dir>/lib/python2.6/site-packages/

   and generates the scripts

   <dir>/bin/abc-sysbio-sbml-sum

   <dir>/bin/run-abc-sysbio

3. Add the script directory to the path (this must be done in each session or added to the shell configuration files, e.g. .bashrc or .cshrc file)

   export PATH=<dir>/bin:$PATH (bash shells)

   setenv PATH <dir>/bin:$PATH (c shells)

4. Type the command

   run-abc-sysbio –h ,

   which should lead to the display of a list of options and put you in the position to run the examples.

   CRITICAL STEP: Should any problem occur, refer to the ABC-SysBio manual, which is included in the package and can be downloaded from sourceforge. In general this manual includes many more examples and details than those covered in this protocol. Especially the advanced software settings and options will be presented in the manual in more detail.

   TROUBLESHOOTING

Procedure

Preparing the folder structure TIMING 2 min

• 1.In a terminal, go to the working directory and create a project folder ‘paramInference’:

  mkdir paramInference

  cd paramInference

Downloading the first sbml file TIMING 2 min

• 2.Download the Supplementary data 1. This is a zipped folder, which contains the files ‘mRNAselfReg1.sbml’ and ‘mRNAselfReg2.sbml’. Unzip this folder. The sbml model file ‘mRNAselfReg1.sbml’ is all you need to analyze the model. Copy the file ‘mRNAselfReg1.sbml’ into the folder ‘paramInference’.

Parsing the sbml file TIMING 2 min

• 3.The ABC-SysBio package contains two main functions: abc-sysbio-sbml-sum and run-abc-sysbio. The first one reads an sbml file and provides a model summary. It also creates a template file, which will be used as an input file in all further steps. In the terminal type (as one line):

  abc-sysbio-sbml-sum --files mRNAselfReg1.sbml --input_file_name input_file1.xml

  which will print to the terminal:

  input_files: [' mRNAselfReg1.sbml']

  data: None

  filename: input_file1.xml

  sumname: model_summary.txt

  (TROUBLESHOOTING)

• 4.Type

  ls –l

  and all files that are now in the project folder will be listed:

  mRNAselfReg1.sbml

  input_file1.xml

  model_summary.txt

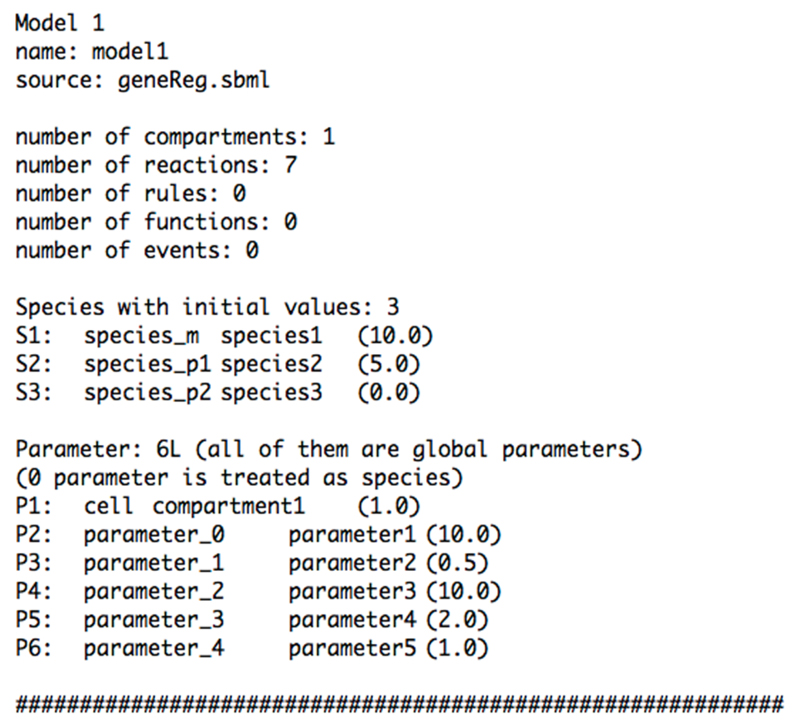
  Please note that the file model_summary.txt contains information about the provided sbml model file. The summary of this example is shown in figure 3.

Figure 3. Automatically generated model summary file.

The function abc-sysbio-sum reads the sbml model file and extracts all model specific information. The file contains the (always included) number of compartments and reactions. Some models also contain rules, functions and events. The file acts as a ‘dictionary’ for all ABC-SysBio steps. The software renames parameters and species. In the second column are the original sbml identifiers, while the new names are in the third column. The numbers in brackets denote the default values as defined in the sbml model file.

Modifying the input file TIMING 10 min

CRITICAL: The generated input file (/paramInference/input_file1.xml) is written in the xml standard, i.e. specific tags — which correspond to machine and (arguably) human readable definitions — are written as

<tag> … </tag>

It contains all information about the settings specifying the algorithm setup, the parameters, the data and the model. The automatically generated template file already has the right format, e.g. the number of parameters and species corresponds to the sbml model file. In case no sbml model file is used, the input file has to be generated separately. We recommend using one of the example input files as a template on which to base any customized files.

CRITICAL: Implementation of the following sub-section of the Procedure (steps 5–14) contains instructions on how to set up the input file. This can be avoided by using an already prepared input file provided in Supplementary data 2. To follow this option download Supplementary Data 2 and unzip this file. In the folder are the two files ‘input_file1.xml’ and ‘input_file2.xml’. Copy the file ‘input_file1.xml’ into the folder ‘paramInference’ and proceed with step 15.

• 5.Define a tolerance schedule; this is one of the important parameters that controls the rate at which the ABC-SMC algorithm converges. The default option is an automatically generated schedule. In this example we will use a fixed user-defined schedule. Therefore replace

  <autoepsilon>

  <finalepsilon> 1.0 </finalepsilon>

  <alpha> 0.9 </alpha>

  </autoepsilon>

  with

  <epsilon>

  <e1> 50 48 46 43 41 39 37 35 32 30 28 26 24 22 20 18 16 15 </e1>

  </epsilon>

• 6.Set the number of accepted particles per ABC-SMC population by typing:

  <particles> 100 </particles>

  Please note that this command defines the population size, which is set to a low value here for demonstration purpose. To obtain a good approximation of the posterior parameter distribution, the population size should be much larger (for this example around 1,000 particles will suffice), depending on how many parameters are to be estimated. As a rule of thumb: the more parameters are to be estimated, the larger the population size needs to be.

• 7.Set the numerical step size — a parameter used by the numerical solvers — to

  <dt> 0.01 </dt>

• 8.Set the type of the parameter perturbation kernel

  <kernel> uniform </kernel>

  Implementing this command means the sampled parameters are perturbed uniformly in linear space.

• 9.Provide the data by typing the following lines in the input file:

  <times> 0 0.1 0.2 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 </times>

  <variables>

  <var1> 10.000 8.861 12.241 26.408 21.474 13.776 10.038 8.127 7.264 6.716 6.725 7.244 7.830 8.772 9.076 8.941 8.539 8.246 8.543 8.780 8.666 8.736 8.505 </var1>

  </variables>

  This instruction sets the times at which observations are taken, as well as the measured values for all observed species (here only var1 is observed). The data are shown in Figure 2c.

• 10.Provide all model information in the section <models>. To achieve this objective, type the lines

  <name> mRNAselfReg1 </name>

  <source> mRNAselfReg1.sbml </source>

  which define the name of the model and the sbml model file containing the relevant model description.

• 11.The ABC-SysBio package can simulate SDE and ODE models, as well as Markov jump processes (MJP). The algorithms used are summarized in table 1. We will analyze the system as an SDE model. Type the lines:

  <type> SDE </type>

• 12.Since the data only describe the temporal behavior of the mRNA species, which is species1, set

  <fit> species1 </fit>

• 13.The initial conditions, i.e. the state of our model system at time 0 (here the amount of each species before any reaction takes place), are known, so they must be defined as ‘constant’ by typing:

  <initial>

  <ic1> constant 10.0 </ic1>

  <ic2> constant 5.0 </ic2>

  <ic3> constant 0.0 </ic3>

  </initial>

• 14.Define the parameters’ prior distributions. The first parameter describes the sbml model specific parameter ‘compartment size’, which in the majority of models is set to 1. All known model parameters must be set ‘constant’. In this case parameter6 (mRNA and protein degradation rate) is assumed to be known and set to 1. For this protocol define the prior parameter distributions of the remaining parameters as follows:

  <parameters>

  <parameter1> constant 1.0 </parameter1>

  <parameter2> uniform 0 50 </parameter2>

  <parameter3> uniform 0 10 </parameter3>

  <parameter4> uniform 0 50 </parameter4>

  <parameter5> uniform 0 10 </parameter5>

  <parameter6> constant 1.0 </parameter6>

  </parameters>

  This defines for example the prior distribution of parameter 2 as a uniform distribution between 0 and 50. Other implemented prior distributions are ‘normal’ and ‘lognormal’.

Table 1. Implemented algorithms for numerical simulation of biological systems and references.

All three algorithms are implemented in Python, C and PyCuda. The Python implementation is the default option, which is used in this protocol. The C routines are applied when adding ‘the option ‘-c++’ to the command line in step 15, while the cuda routines are used when using ‘-cu’.

type of model	Numerical algorithm	lit. reference
ODE	LSODA	64
SDE	Euler–Maruyama	65
MJP	Gillespie	66

Running ABC-SysBio for parameter inference TIMING 20 min until population 12, 3 h until population 16

• 15.Start the ABC-SysBio program by typing in the terminal:

  run-abc-sysbio -i input_file1.xml -of=results –f –sd=2

  Here the tag ‘-i ‘ defines the input file, ‘-of= ‘ defines the name of the folder that will contain all results and ‘-f ‘ results in printing a full report to the terminal. The ABC-SysBio program will now import the sbml model file and translate it into Python syntax, specific to the supplied SDE solver. This file mRNAselfReg1.py now becomes the project solver. The tag ‘-sd=2’ sets the seed of the random number generator in numpy. This tag is useful for debugging or comparison of results. It is not generally needed to run the algorithm. Since we set the population to only 100, we recommend the user to use this tag in order to better compare the results with the results presented here.

  (TROUBLESHOOTING)

• 16.Carefully check all algorithm parameters that the program will print to ensure that the information is correct. This information should correspond to the above-described instructions in the input file (for example make sure that the number of particles is set to 100). After around 1 minute (depending on the computer on which ABC-SysBio is run) the first ABC-SMC population will be finished and the summary of this population will be printed to the terminal:

  ### population 1

         sampling steps / acceptance rate : 1211 / 0.0825763831544

         model marginals : [1.0000000000000007]

  This output appears after each finished ABC-SMC population. A new folder will be created, in this case ‘results’, which will contain all other outputs of the program.

• 17.The results folder is updated every time an ABC-SMC population is finished. Every time this happens, check the files inside the results folder by typing:

  cd results

  ls –l

  The output will comprise the following files

  copy

  _data.png

  distance_Population1.txt

  rates.txt

  results_ mRNAselfReg1

  traj_Population1.txt

  The file ‘_data.png’ shows a plot of the data provided in the input file. The file ‘rates.txt’ contains in its first column the population number, followed by the tolerance value epsilon, the number of sampled parameter combinations in order to obtain a full ABC-SMC population, and the achieved acceptance rate (i.e. the fraction of simulations that gave rise to simulated data that was within the specified distance from the observed data). The last column shows the time it took to obtain this population in seconds. This information is useful when redefining the tolerance schedule in order to increase the algorithm’s performance. The files ‘distance_Population1.txt’ and ‘traj_Population1.txt’ contain the accepted simulations and their corresponding distances from the provided data. The folder ‘results_ mRNAselfReg1’ contains a folder for each finished population.

• 18.To view the files generated after the first ABC-SMC population type:

  cd results_ mRNAselfReg1/Population_1

  ls –l

  which will list the following files:

  data_Population1.txt

  data_Weights1.txt

  ScatterPlots_Population1.png

  Timeseries_Population1.png

  weightedHistograms_Population1.png

  The accepted parameter combinations will be saved in ‘data_Population1.txt’, where columns represent the parameter and initial conditions. In this example the initial conditions are known and set to be constant. However, it is possible to infer them by defining a prior distribution. The statistical weights corresponding to the parameter combinations are stored in the file ‘data_Weights1.txt’. The ‘.png’ files show simulations for 10 of the accepted particles, the marginal posterior distributions as histograms and pairwise scatterplots providing an overview of the posterior parameter distributions. The scatter plots show the most recent population plotted on top of all previous populations marked by different colors. An example of the output is shown in Supplementary Data 3. Furthermore example trajectories are plotted (Figure 4). These plots are useful for monitoring purposes and enable the user to follow the progress of the algorithm. Please note that sometimes it is advisable not to generate these diagnostic plots (hence the definition of this step as optional), for example when analyzing models with a high dimensional parameter space (models with a large number of parameters to estimate). Generating these diagnostic plots is time consuming, which slows down the algorithm, hence it is advisable in these cases to run the algorithm as in step 15 adding the command ‘—diagnostic’ at the end of the line..

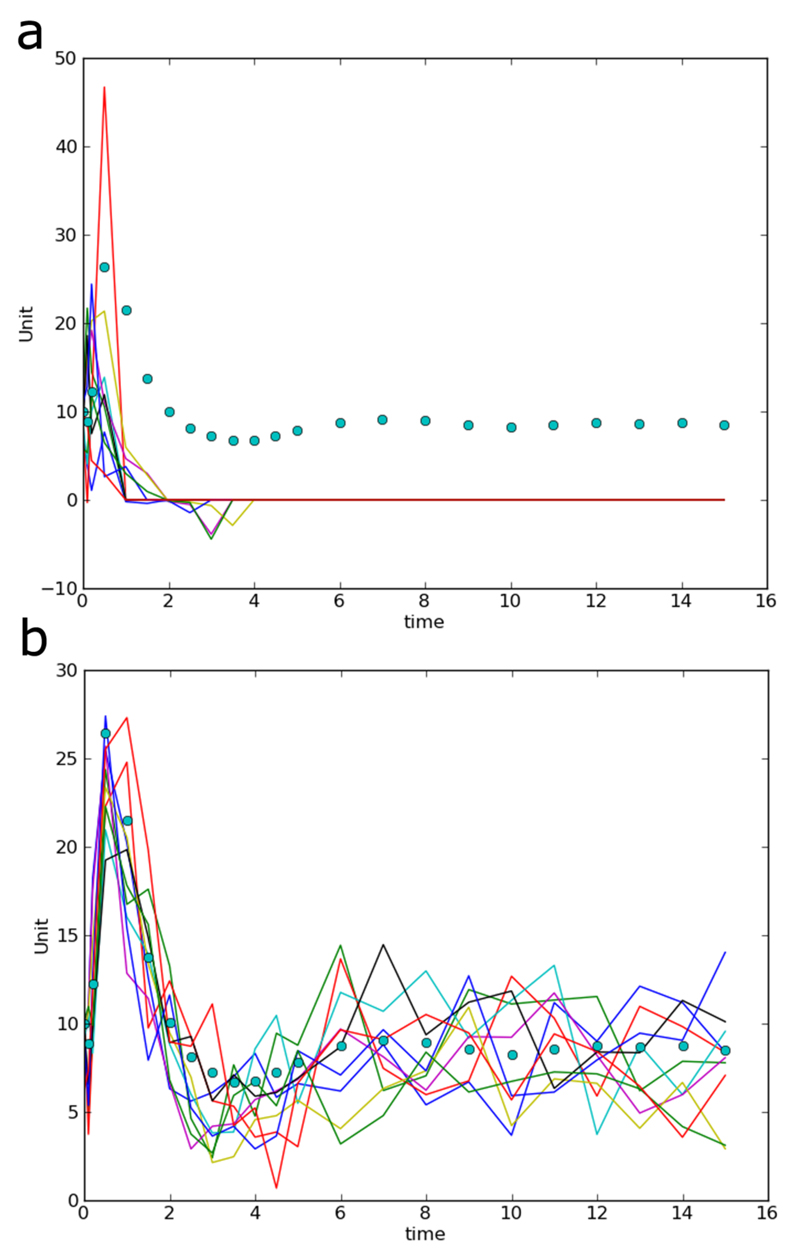
Figure 4. Example trajectories of intermediate and final ABC-SMC populations.

After each population, the software produces diagnostic plots, which enable the user to follow the progress of the algorithm implementation. These plots include 10 example trajectories plotted in comparison with the data. Shown are these trajectories for the first ABC-SMC population (a) and the last ABC-SMC population (b).

Preparation of a new project folder TIMING 2 min

• 19.As in step 1, in a terminal, go to the working directory and create a new project folder ‘modelSelection’. Type:

  mkdir modelSelection

  cd modelSelection

Downloading the sbml files for model selection TIMING 2 min

• 20.In step 2, Supplementary Data 1 was downloaded and unzipped. Copy the two sbml model files (mRNAselfReg1.sbml and mRNAselfReg2.sbml) .into the folder ‘modelSelection’..

Parsing both sbml model files TIMING 2 min

• 21.In the terminal type (as one line):

  abc-sysbio-sbml-sum --files mRNAselfReg1.sbml,mRNAselfReg2.sbml

  --input_file_name input_file2.xml

  (TROUBLESHOOTING)

• 22.Type the following to list all files:

  ls –l

  This command generates again the model_summary.txt, which contains now information about both models, and the input_file2.xml. The latter is automatically in the right format for the model selection algorithm.

  CRITICAL: Implementation of the following sub-section of the Procedure (steps 23–28) can again be avoided by using an already prepared input file provided in Supplementary data 2. To follow this option download Supplementary Data 2 and unzip this file. In the folder are the two files ‘input_file1.xml’ and ‘input_file2.xml’. Copy the file ‘input_file2.xml’ into the folder ‘modelSelection’ and proceed with step 29.

Modifying the second input file TIMING 10 min

• 23.Apply the same tolerance schedule as in step 5: replace

  <autoepsilon>

  <finalepsilon> 1.0 </finalepsilon>

  <alpha> 0.9 </alpha>

  </autoepsilon>

  by

  <epsilon>

  <e1> 380 370 360 340 300 250 150 100 90 </e1>

  </epsilon>

• 24.Set the number of accepted particles to 100 (note that this is a very low number and is only used for the purpose of this tutorial example, but should typically be much higher in real inference applications):

  <particles> 100 </particles>

• 25.Set the numeric step size, the parameter perturbation kernel and the data as in steps 7, 8 and 9 respectively. Note that the data are now described by two time series, where the first (<var1>) is set as before. Furthermore the second time series includes missing values (NA) for some time points.

  <dt> 0.01 </dt>

  <kernel> uniform </kernel>

  <times> 0 0.1 0.2 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 </times>

  <variables>

  <var1> 10.000 8.861 12.241 26.408 21.474 13.776 10.038 8.127 7.264 6.716 6.725 7.244 7.830 8.772 9.076 8.941 8.539 8.246 8.543 8.780 8.666 8.736 8.505 </var1>

  <var2> NA NA NA NA 144.147 NA 140.720 NA 103.582 NA 82.268 NA 77.614 82.699 88.346 90.024 89.033 87.776 87.291 87.431 87.706 87.839 87.826 </var2>

  </variables>

• 26.Provide the information about the two models considered. On the top of the file note the tag

  <modelnumber> 2 </modelnumber>

  In the section <model> will be now the two tags <model1> and further down in the file <model2>.

• 27.Define all parameters for <model1> as done in steps 10-14:

  <name> mRNAselfReg1</name>

  <source> mRNAselfReg1.sbml </source>

  <type> SDE </type>

  <fit> species1 species2+species3 </fit>

  <initial>

  <ic1> constant 10.0 </ic1>

  <ic2> constant 5.0 </ic2>

  <ic3> constant 0.0 </ic3>

  </initial>

  <parameters>

  <parameter1> constant 1.0 </parameter1>

  <parameter2> uniform 0 50 </parameter2>

  <parameter3> uniform 0 10 </parameter3>

  <parameter4> uniform 0 50 </parameter4>

  <parameter5> uniform 0 10 </parameter5>

  <parameter6> constant 1.0 </parameter6>

  </parameters>

  The fitting instruction <fit> now includes two expressions, one for each provided time series in <data>. The second time series describes the total amount of measured protein, which is in this first model the sum of species2 and species3.

• 28.For <model2>, set:

  <name> mRNAselfReg2 </name>

  <source> mRNAselfReg2.sbml </source>

  <type> SDE </type>

  <fit> species1 species2 </fit>

  <initial>

  <ic1> constant 10.0 </ic1>

  <ic2> constant 5.0 </ic2>

  </initial>

  <parameters>

  <parameter1> constant 1.0 </parameter1>

  <parameter2> uniform 0 10 </parameter2>

  <parameter3> uniform 0 10 </parameter3>

  <parameter4> uniform 0 30 </parameter4>

  <parameter5> uniform 0 30 </parameter5>

  </parameters>

  Note that in this second model we have only one protein species. For this reason the fitting instruction for the second time series is only ‘species2’. The algorithm automatically chooses the model selection algorithm if more than one model is provided. Parameter inference is also carried out as part of the model selection procedure. The final edited input file is provided in Supplementary data 2 (input_file2.xml).

Running ABC-SysBio for model selection TIMING 10 min until population 6, 1 h until population 9

• 29.To start the model selection algorithm, type the same command in the terminal as in step 16:

  run-abc-sysbio -i input_file2.xml -of=results –f –sd=2

  No further commands are required for model selection, because all necessary information is contained in the input file. Once the first ABC-SMC population is finished (this should be in a few seconds) the algorithm prints to the terminal:

  ### population 1

        sampling steps / acceptance rate : 1478 / 0.0676589986468

        model marginals : [0.5900000000000003, 0.4100000000000002]

  The model marginals represent the probability of the two models in light of the data, i.e. they describe which of the models describes the data best. Please note that it takes 3 to 4 hours for the whole algorithm to be run, but already after a few populations a clear tendency is visible.

  (TROUBLESHOOTING)

• 30.Compared to the parameter inference algorithm, in the results folder we now have additional files. View them by typing:

  cd results

  ls –l

  The output will be comprised of the following files:

  copy

  _data.png

  distance_Population1.txt

  ModelDistribution_1.png

  ModelDistribution.txt

  rates.txt

  results_ mRNAselfReg1

  results_ mRNAselfReg2

  traj_Population1.txt

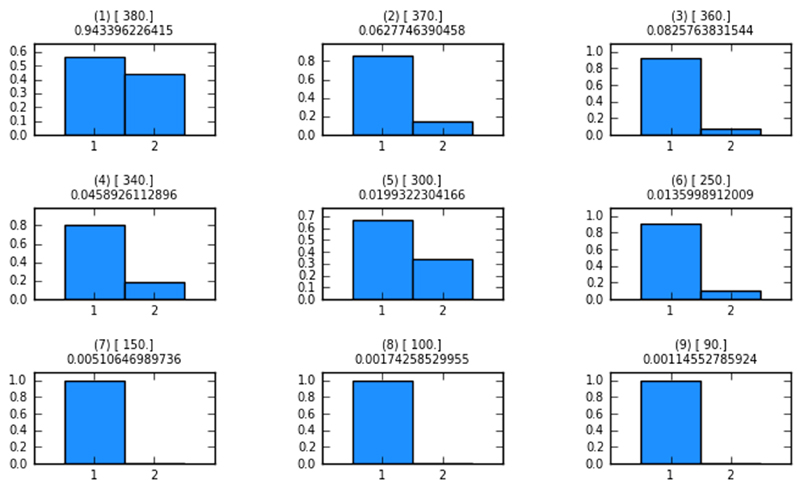
  The file ‘_ModelDistribution_1.png’ shows a bar plot representing the model probabilities. This figure is updated after each ABC-SMC population. The file ‘ModelDistribution.txt’ lists the model probabilities for each finished ABC-SMC population. A results folder for each model is created, in which the ABC-SMC populations are listed (according to the parameter inference algorithm). Figure 5 shows the model probabilities from population 1 to 16.

Figure 5. Model probabilities after each ABC-SMC population.

Each of the histograms in this figure is produced after each ABC-SMC population. Shown are the model probabilities as barplots. The numbers in () represent the population number; numbers in [] are the distance thresholds for each population (epsilon-schedule); numbers below the above-mentioned parentheticals are the acceptance rates. In population 1 both models have approximately the same probability of representing the data. After population 16 model 1 has a much higher probability of representing the data best.

Timing.

➢ Preparing the folder structure:	2 min
➢ Downloading the first sbml file:	2 min
➢ Parsing the sbml file:	2 min
➢ Modifying the input file:	10 min
➢ Running ABC-SysBio for parameter inference:      - until population 12:      - until population 16:	20 min 3 h
➢ Preparation of a new project folder:	2 min
➢ Downloading the sbml files for model selection:	2 min
➢ Modifying the second input file:	10 min
➢ Running ABC-SysBio for model selection:      - until population 6:      - until population 9:	10 min 1 h

Troubleshooting.

step	problem	possible reason	possible solution
3,21	Error: “can not parse sbml model file”	The sbml model file does not exist or contains errors.	Make sure the model name provided in the input file (or command line) is exactly the same as the model file. If the sbml model file was manually generated, make sure all tags are correct and closed and only sbml standard acceptable expressions and syntax is used.
15,29	Error: “Please do not give empty strings for model names!”	The model names contain invalid strings.	Check the names of each provided model in the input file
15,29	Error: “The number of given prior distributions for model X is not correct”	The model contains a different number of parameters than was defined in the input file.	Provide one prior distribution per parameter defined in the model. If some parameters are known, they still need to be defined (as ‘constant’). Note: when using an sbml model file an additional parameter appears, which defines the compartment size. This parameter is always defined as ‘parameter 1’. For the vast majority of systems this parameter is constant 1.0
15,29	Error: “Please provide an initial value for each species in model X.”	The number of species in the model and in the input file does not correspond to each other.	Check the input file and make sure that the initial conditions are correctly defined. For each species in the model one initial condition needs to be provided. This can either be ‘constant’ if the initial condition is known, or one of the following, if the initial condition needs to be inferred: ‘uniform’, ‘normal’, ‘lognormal’.
15,29	Error: “The prior distribution of parameter X is wrong defined.”	Invalid expression in the input file.	Check the type of distribution for parameter X in the input file. Possible types are: “uniform”, “normal”, “lognormal” and “constant”.
15,29	Error: “The integration type for model X does not exist.”	Invalid expression in the input file.	Check the integration type for model X. Allowed expressions are “ODE”, “SDE” and “Gillespie”.
15,29	Error: “The results folder already exists.”	There is already a file/folder called ‘results’ in the working directory.	Either change the working directory, change the name of the existing folder or remove the folder.
15,29	Error: ”Please provide a fit instruction for each model”	Wrong or no fitting instruction is provided.	Always provide the same number of fitting instructions as provided time series (if the number of species differs from the number of data series). Fitting instructions can be simple expressions such as ‘species1’, but also more advanced instructions such as ‘species1+10*species3’. This is particularly useful when data need to be scaled or only combinations of species are observed.

Anticipated Results

The typical output after performing Bayesian parameter inference in ABC-SysBio consists of a set of weighted particles that summarize the approximate posterior distribution. A particle is a parameter vector containing a value for each of the reaction rates to be estimated. The weight associated with a particle is proportional to the probability that this parameter vector can explain the observed data. In this section we describe how to analyze and interpret the posterior distribution obtained.

First, the marginal posterior distribution (i.e. the probability distribution of each reaction rate considered independently) can be obtained using a weighted histogram. ABC-SysBio provides these weighted histograms at each step of the sequential algorithm. If the marginal distribution is very peaked around a parameter value, we say that the reaction rate is well inferred (see for example Figure 6c leftmost plot). In most biological systems, however, only a few reaction rates can be inferred given an observed dataset and different parameter vectors can explain the observed data (almost) equally well^16,18,67. Such issues are especially obvious and important to consider when looking at the joint probability distribution over all reaction rates.

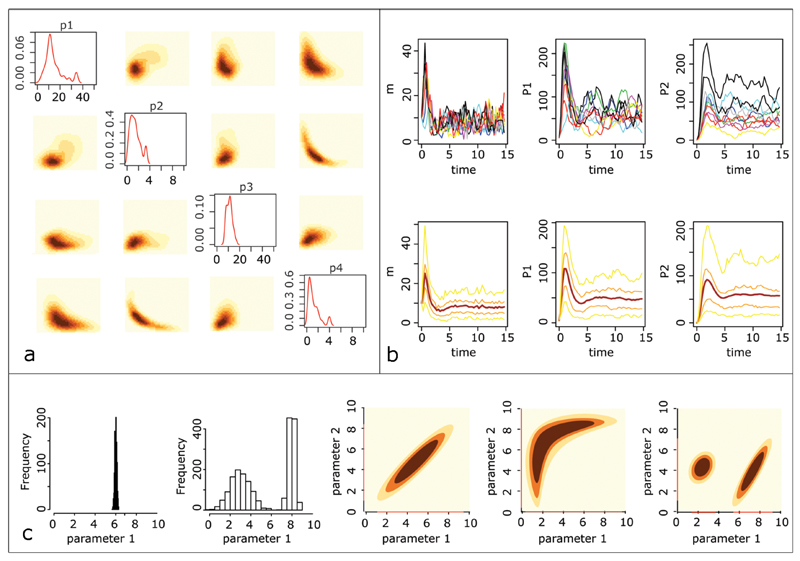
Figure 6. Analyzing the posterior distribution.

(a) The marginal posterior density for each of the four reaction rates to be estimated in the mRNA self-regulation model (diagonal) as well as the joint pairwise posterior distribution for each couple of reaction rates. The two-dimensional distributions are represented with orange-contours, where the darker the color the higher the probability. (b) Exploiting the posterior distribution to predict the evolution of the three species (from left to right: mRNA, P1 and P2) of the mRNA self-regulation model. We plot 10 simulated trajectories for 10 parameter vectors sampled from the posterior distribution (top). To analyze the distribution of the evolution of the three species, we sample 1000 parameters sets from the posterior distribution and plot the mean (dark red), the 25 and 75 percentiles (orange) and the 5 and 95 percentiles (yellow) of the simulated (bottom). (c) Examples of posterior distributions. From left to right: the marginal posterior distribution for a well-inferred parameter; a bi-modal posterior distribution; a posterior distribution over two linearly correlated parameters; a posterior distribution over two parameters that are highly dependent, but in a non-linear manner; a bi-modal posterior distribution over two parameters.

In order to study the correlation between parameters, an investigator typically plots the joint posterior distribution of pairs of reaction rates. Different examples of joint pairwise posterior distributions are shown in Figure 6 (a, c). Here we observe that the correlation can be linear or highly non-linear and that the posterior distribution can have several peaks, i.e. that the distribution is multimodal. Secrier et al. described how to analyze a posterior distribution and perform sensitivity analysis^44,68. Such an analysis of inferred posterior distributions over parameters also enables researchers to consider factors such as parameter identifiability and sloppiness^49,67.

Parameter inference is not just an aim in its own right, and the posterior distribution can also be exploited for a predictive purpose. For example, it is possible to study the evolution of some of the species that have not been measured, or to predict the behavior of the biological system under different experimental conditions (Figure 6b). This task is easily performed by sampling a set of particles from the obtained posterior distribution and simulating the model (or the variation of the model) for each of the particles⁶⁹. Each simulated trajectory corresponds to a possible behavior. If all the simulated trajectories are very similar, then this behavior is of high probability given the assumed mechanistic model, the prior distribution over the parameters and the observed data. On the other hand, if the simulated trajectories significantly vary from one particle to another then the behavior of the corresponding species cannot be accurately predicted. This analysis serves as a basis for the design of experiments that could help improve such predictions^69,70.

Analysis of marginal distributions provides an assessment of the probabilities of different candidate models — which represent different mechanistic hypotheses — in light of data. Making use of these probabilities we can, for example, rank these models. Or we can identify similarities among models that receive statistical support from the data³⁸. If, for example, all models that have appreciable posterior probability share certain types of interactions, then we might hypothesize that these interactions are more likely to be real than interactions that receive little statistical support.

A frequent occurrence in inference is the long times it takes for computers to evaluate the approximate posteriors. ABC-SysBio provides access to advanced GPU hardware which, when available, will result in a considerable acceleration of the simulation process. Alternatively, Python can be dropped in favor of C-routines, which also increases speed of simulation. In its simplest form, relying on Python as the primary language, ABC-SysBio is readily usable and highly suited for preliminary analysis of models. As always in computing, there is a potential trade-off between the time it takes to implement computational analyses and the computer run-time the analysis takes. Here ABC-SysBio provides the user with the flexibility gradually to scale up in computational sophistication as and when needed.

It is important to remember that ABC methods only provide an approximation of the posterior distribution. The ABC-SMC algorithm has been tested for examples where the true posterior distribution is known and it has been shown that the obtained posterior distribution is similar to the true one^27,43. For more realistic examples where the true posterior distribution is unknown, a sensible and precautionary approach to check the quality of the obtained posterior distribution is to study the predictive distribution by comparing the simulated data to the observed ones. Of course even if the simulated data are almost identical to the observed ones, there is no guarantee that the obtained posterior distribution is the whole ‘true’ (but unknown) one. In particular, some regions of the posterior distribution may not be covered due to too few particles. We recommend to run the software repeatedly and to compare the obtained posterior distributions.

The accuracy of the obtained approximation of the posterior distribution is highly dependent on the last value of epsilon²⁸ but also on the number of particles per population, the tolerance schedule, the distance function and the perturbation kernels. Some of the computational aspects of ABC are still active areas of research and ABC-SysBio will continue to incorporate these developments. These improvements will come from two directions: there are non-trivial speed gains to be achieved by employing modern computer architectures or streamlined programming in low-level languages — ABC-SysBio allows for this, and we would recommend users to make use of the GPU implementations, or providing C rather than Python routines — and recent developments in simulating stochastic dynamical systems more efficiently. The second type of improvement may result from research into the underlying ABC foundations. ABC is increasingly considered as a distinct inferential formalism and not merely as an approximation to conventional Bayesian inference.

In summary, however, ABC provides a pragmatic, rarely optimal but often applicable, framework in which cutting-edge scientific problems can be addressed from a Bayesian perspective. ABC-SysBio makes this framework, as well as state-of-the-art computational tools available to computational and systems biologist.