Super-resolved Parallel MRI by Spatiotemporal Encoding

Abstract

Recent studies described an alternative “ultrafast” scanning method based on spatiotemporal (SPEN) principles. SPEN demonstrates numerous potential advantages over EPI-based alternatives, at no additional expense in experimental complexity. An important aspect that SPEN still needs to achieve for providing a competitive acquisition alternative entails exploiting parallel imaging algorithms, without compromising its proven capabilities. The present work introduces a combination of multi-band frequency-swept pulses simultaneously encoding multiple, partial fields-of-view; together with a new algorithm merging a Super-Resolved SPEN image reconstruction and SENSE multiple-receiving methods. The ensuing approach enables one to reduce both the excitation and acquisition times of ultrafast SPEN acquisitions by the customary acceleration factor R, without compromises in either the ensuing spatial resolution, SAR deposition, or the capability to operate in multi-slice mode. The performance of these new single-shot imaging sequences and their ancillary algorithms were explored on phantoms and human volunteers at 3T. The gains of the parallelized approach were particularly evident when dealing with heterogeneous systems subject to major T₂/T₂* effects, as is the case upon single-scan imaging near tissue/air interfaces.

1. Introduction

One of Magnetic Resonance Imaging (MRI’s) most important aspects concerns the development of schemes delivering the best possible images in the shortest acquisition times. Fast two-dimensional (2D) imaging usually relies on either covering k-space on a line-by-line basis using short repetition times TR [1–3], or scanning the full 2D k-space in a single continuous acquisition. Echo Planar Imaging (EPI) [4] and its variants [5, 6] are foremost choices to implement this second, “ultrafast” kind of single-shot scanning. Although capable to deliver 2D images at multi-Hz rates, EPI involves tradeoffs in the image’s spatial definition and in robustness to inhomogeneity- or shift-derived artifacts. EPI is thus chosen when demanding high temporal resolution or avoiding motion-induced blurring [7,8]. During recent years a single scan alternative has been discussed, based on a spatiotemporal encoding (SPEN) of the spin interactions. In its original conception SPEN was proposed for acquiring multidimensional NMR spectra within a single scan [9, 10]. When extended to single scan imaging contexts [11–16] this modality was found akin to earlier proposals developed by Kunz and Pipe [17–19], which tie the position of the spins to distinct instants of excitation/inversion and of detection. SPEN achieves this by relying on swept radiofrequency (RF) pulses that progressively excite or invert the spins, and on a final acquisition gradient that locally unravels each location’s contribution. The resulting time domain signal (FID) is proportional to the spatial spin density profile ρ being sought. This FID(t) α ρ(r) condition avoids usual Nyquist constraints, and can endow SPEN with significantly higher robustness to field inhomogeneities vis-a-vis EPI counterparts. Additional advantages arise from the possibility of implementing SPEN in a “full refocusing” mode that compensates all T₂*-related effects throughout the acquisition [14,20], to examine restricted fields-of-view (FOVs) without suffering from folding artifacts, and to extract spectral images of multiple chemical sites simultaneously at no additional cost in experimental complexity [13,21]. Last but not least, initial bottlenecks pertaining low spatial resolution or excessive specific absorption rate (SAR) values, could be circumvented by using super-resolution (SR) reconstruction algorithms [22–24].

While these advances enable a wider range of ultrafast MRI SPEN applications, fundamental sampling limits constrain further reductions in scanning times and ensuing improvements in image quality. Parallel MRI (pMRI) may overcome these bottlenecks by departing from the serial collection of the individual data points, and switching to a mode whereby the different spatial sensitivities of phased- or multi-coil arrays [25–29] make up for unfulfilled Nyquist demands. Several pMRI strategies have been proposed to skip R points in k-space –thereby reducing scan times by the same factor R– without suffering from the penalties of k-undersampling [30–33]. The equivalences and differences between many of these approaches have been extensively discussed in the literature [34,35]; regardless of their specific form, the advantages resulting from pMRI have been unambiguously demonstrated [31].

Stimulated by this background, and by the widespread availability of parallel receiving facilities, this study explores a number of parallel imaging equivalents in the SPEN scenario. In fact uses of pMRI in a SPEN-related approach known as RASER, have been reported in a conference proceeding by Garwood et al [36]. The main feature investigated in such study concerned the pulse shaping approach needed for the implementation of parallel MRI in this kind of method; a conclusion from that report was the important advantages that could be gained, pending the resolution of a number of technical issues. The present study revisits this problem, albeit with the use of different pulse shapes and of different image reconstruction algorithms. Particular attention is paid on how to endow pMRI SPEN acquisitions with multi-slice capabilities, and on incorporating onto the multiple-coil reconstruction super-resolving algorithms. It is found that parallel SPEN imaging involving a multi-band linear chirp pulse and data reconstruction by a suitably modified SR-enhanced version of SENSE, benefits the ensuing single-scan images thanks to a substantial reduction of the excitation and acquisition times. Phantom- and human-based MRI examples of the ensuing capabilities and benefits are demonstrated; the advantages of relying in pMRI SPEN methods become particularly evident when exploring inherently heterogeneous media –for example when acquiring single-scan images next to air/tissue interfaces.

2. Theory: SENSE and SR-Enhanced SENSE Reconstruction of Parallelized SPEN Acquisitions

2.1. Parallelizing SPEN MRI by Imposing Multiple Stationary-Point (SP) Conditions

SPEN’s encoding is easiest to visualize in a single dimension, which for simplicity we will denote as y, while ignoring chemical shifts or other kinds of offsets. In SPEN a chirp 90° excitation or a post-excitation 180° swept inversion pulse is applied, sweeping at a constant rate a targeted field-of-view of length FOV, between initial $O_i=-\frac{\gamma G_{exc}FOV}{2}$ and final $O_f=-\frac{\gamma G_{exc}FOV}{2}$ offset values given by an excitation gradient G_exc. These sweeps, lasting a time T_exc, impose on the spins’ transverse magnetization a quadratic phase profile of the form (24)

$${\varphi }_{exc}\left(y\right)={\alpha }_2{y}^2+{\alpha }_{1}y+{\alpha }_0$$ (1)

where ${\alpha }_2=-\frac{{\left(\gamma G_{exc}\right)}^2{T}_{exc}}{2\Delta O},$ ${\alpha }_1=-\gamma G_{exc}{T}_{exc}\frac{O_i}{\Delta O}$ and ${\alpha }_0=-T_{exc}\frac{{O_i}^2}{2\Delta O}$ for the case of a 90° encoding; and ${\alpha }_2=-\frac{{\left(\gamma G_{exc}\right)}^2{T}_{180}}{\Delta O},$ α₁ = 0, ${\alpha }_0=-T_{180}\frac{{O_i}^2}{\Delta O}$ for a 180° pulse encoding (T₁₈₀ being the duration of the swept 180° pulse). In these expressions ΔO = O_f − O_i, α₁ is a linear term, and α₀ is an unimportant constant-phase term heretofore disregarded. SPEN’s signal S is acquired under the action of a field gradient G_acq acting over an acquisition time T_acq, and adding a linear phase ϕ_acq(y,t) = γG_acqt · y = k(t) · y to eq. (1). This leads to a time-dependent signal:

$$S\left(t\right)={\displaystyle \underset{-\frac{FOV}{2}}{\overset{+\frac{FOV}{2}}{\int }}\rho \left(y\right)}{e}^{i{\varphi }_{exc}\left(y\right)}{e}^{i\cdot k\left(t\right)y}dy$$ (2)

Assuming that, if need be, an initial purging gradient k_prg has shifted the minimum of eq (1)’s parabola to the edge of the targeted FOV, G_acq will displace the vertex of the evolution phase –i.e., the single coordinate fulfilling the stationary-point (SP) condition [24]

$$\frac{f}{fy}{\left[{\phi }_{exc}\left(y\right)+\left(k_{prg}+\gamma G_{acq}t\right)y\right]}_{y=ySP}=0$$ (3)

according to y_SP(t) = -(FOV/2) + FOV(t/T_acq). Given the destructive interference occurring at all points other than those in the neighborhood of y_SP(t), it follows that monitoring S(t) can reflect the sample’s density ρ(y) in a point-by-point manner –not by Fourier transform, but rather by direct measurement of ||S(t)||’s magnitude (24).

Parallel MRI exploits the distinct spatial sensitivities {C_j}_1≤j≤Nc available in an array of N_c receiver coils, to separate multiple signals that sparse sampling may have otherwise aliased into one another. A reduction R in sampling time, R ≤ N_c, can thus be achieved by skipping measurement of every other R points in a k-domain array, and FOV unfolding the image distortions that this will incur in thanks to the use of N_c independent coils to detect these signals [3, 31]. One of the main considerations arising upon envisioning the use of pMRI in SPEN-based acquisitions, is the fact that the latter are not based on Fourier principles. In consequence, Fourier-based unfolding arguments will not apply in the kind of “rasterization” that, according to eq. (2), SPEN makes of the spin density. Still, pMRI’s advantages could manifest themselves in SPEN-based experiments, in a number of different fashions. Simplest among these is probably the incorporation of parallel protocols with multi-slice excitations tailored to parallel discrimination by distinct coils [37]. Still, the scenario that we consider in this paper involves parallelizing the image-retrieval protocol along the SPEN dimension: as is the case with EPI counterparts, speeding up acquisitions along this low-bandwidth dimension offers added advantages in terms of a higher immunity to shifts and/or magnetic field inhomogeneities, and therefore stronger signals and fewer distortions along the corresponding plane. To achieve this pMRI will still require, as is the case with conventional imaging, to simultaneously retrieve multiple portions of the image to be generated in the real-space domain. This will in turn demand imparting, at the time of the SPEN encoding, multiple stationary-point conditions. Multi-SPs can be achieved in a number of ways, including multi-band hyperbolic secant excitation pulses [36], or the interspersing of pulses with periods of RF-free evolution [38]. The present study implemented such multi-SP conditions by synthesizing a single continuous waveform, made up by a vector sum of N_SP chirp pulses sweeping multiple adjacent FOV/N_SP fields-of-view simultaneously. Assuming that the sweep rates of these pulses as well as the gradient strength used in the acquisition are kept as in a conventional SPEN scan, this would complete the encoding of the full field-of-view in N_SP shorter times; a similar compression would affect the data acquisition process. These two features could improve the resultant image quality by reducing T₂/T₂* decays effects and limiting the effects of other decoherences during the excitation and acquisition processes –this, provided that the final image is retrieved with minimal reconstruction-related noises.

It follows that the experiments here proposed will rely on sweeping multiple frequency ranges simultaneously, and hence imposing simultaneous parabolic phase profiles on different parts of the sample. The amplitude and phase of the required RF pulse can be summed up as

$$RF\left(t\right)=B_1\left(t\right)e^{i{\phi }_1\left(t\right)}\left(1+{\displaystyle \sum _{n=1}^{N_{sp}-1}{e}^{it\left(\frac{\Delta O}{N_{sp}}\right)n}}\right)$$ (4)

where B₁(t) and φ₁(t) are the amplitude and phase of a “basis” chirp pulse, and ΔO = γG_exc FOV is as in Eq. (1). As the spectral range of the “basis” pulse is kept at $\frac{\Delta O}{N_{sp}}$ for all SP components, all sub-pulses will then impart profiles that are identical to one another yet shifted in space. In other words, each parabolic phase will fulfill an encoding

$${\varphi }_{exc}^n\left(y_n\right)={\alpha }_2^n{y_n}^2+{\alpha }_1^n{y}_n+{\alpha }_o^n$$ (5)

where $-\frac{FOV}{2}+\frac{FOV}{N_{sp}}\cdot \left(n-1\right)\le y_n\le -\frac{FOV}{2}+\frac{FOV}{N_{sp}}\cdot n,\mathit{1}\le n\le N_{SP};{\alpha }_2^n={\alpha }_2$ for all parabolas, ${\alpha }_1^n=-\gamma G_{exc}{T}_{exc}\frac{O_i^n}{\Delta O}\text{with}{O}_i^n=O_i+\frac{\Delta O}{N_{sp}}\cdot \left(n-1\right),\text{and}{\alpha }_0^n=-T_{exc}\frac{{\left(O_i^n\right)}^2}{2\Delta O}.$ During the course of the SPEN acquisition this pattern will originate a signal:

$$S\left(t\right)={\displaystyle \underset{-\frac{FOV}{2}}{\overset{+\frac{FOV}{2}}{\int }}{\displaystyle \sum _{n=1}^{N_{sp}}\rho \left(y_n\right)e^{i{\varphi }_{exc}^n\left(y_n\right)}}{e}^{i.k\left(t\right)y_n}dy}$$ (6)

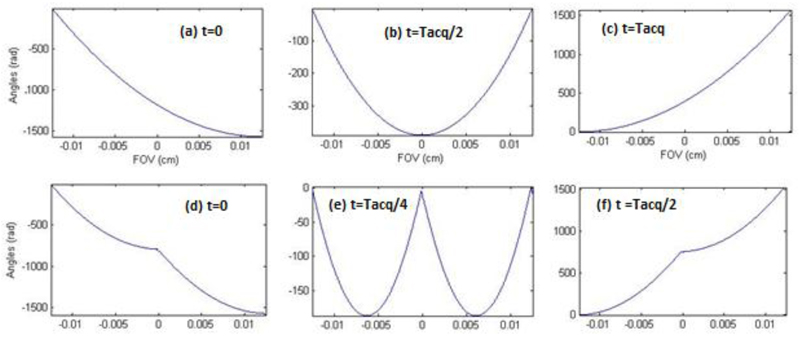
Figure 1 displays excitation phase patterns imparted by such multi-band RF pulse combination for the simplest N_SP = 2 relevant case, and illustrates the progression of the parabolas thus imparted during the SPEN acquisition.

Figure 1.

Comparison between the progression of the spins’ parabolic phase profile under a conventional (top) and a parallel (N_SP = 2, bottom) SPEN imaging experiment. (a, d) Post-excitation phase profiles. (b, e) Mid-acquisition phase profiles (c, f) End-of-acquisition phase profiles. The top panels (a-c) describe the phase imparted by a single 90° chirp pulses for N_SP=1 in a time T_acq. The bottom panels (d-f) represents the phases imparted by a combination of two-band 90° chirp pulse, achieved in a time T_acq/2. Notice that the vertices of the phase profiles cover the full FOV (assumed as 2.5 cm) during both signal acquisitions.

2.2. Reconstructing multi-SP SPEN MRI Data

The panels in Figure 1 indicate that, at any point over the acquisition time, the signal S(t) arising from the multi-SP excitation will reflect contributions from N_SP (>1) stationary points. In this respect N_SP plays a role akin to the R acceleration factor in conventional pMRI; both in terms of the number of image fold-overs, and of the factor by which the original acquisition time is sped-up. Also as for pMRI, SPEN will need to rely on a parallel-receive strategy to resolve the ensuing imaging ambiguities associated to multiple stationary points. To carry this out we exploit the fact that the signal that any given coil j will detect in this kind of multi-SP experiments can be written as:

$${\widehat{S}}_j^{\left(m\right)}\left(t\propto y_{m,n}\right)\propto {\displaystyle \sum _{n=1}^{N_{sp}}{C}_j\left(y_{m,n}\right){\widehat{\rho }}_0\left(y_{m,n}\right)e^{i{\varphi }_{exc}^n\left(y_{m,n}\right)}{e}^{i·k\left(t\right)y_{m,n}}}$$ (7)

where n = 1,2…, N_SP denotes the number of imparted parabolas, the index 1 ≤ j ≤ N_c denotes a particular receiving coil, and m = 1,2,..M reflects the discretization of the y-coordinate being imaged. A single homogeneous coil fulfilling C_j (y_m,n) = 1 does not allow one to unravel the individual folded images. By contrast this opportunity does arise in SPEN MRI, even though at the expense of the image’s spatial resolution. This is a consequence of the different ${\alpha }_1^n$ factors corresponding to each of the imprinted parabolas; the mathematics of the image reconstruction procedure in such instance, are further described in the Appendix to this work. Although this single-coil multiband approach is of potential usefulness, we focus here on a more common pMRI scenario, involving an array of coils possessing distinct C_j (y_m,n) sensitivity profiles. A strategy that can then be adopted to exploit this information involves a straightforward use of the SENSE formalism, relying on the uneven spatial sensitivity profiles of an array of detection coils to unravel the encoding imparted on specific regions by the multi-SP procedure. Indeed, as the signals S_j(t) in SPEN are a direct reflection of the spin density at different points, their magnitude values |S_j(t)| is directly equivalent to the I_j(y) images employed in a real-space SENSE reconstruction. In the spirit of SENSE’s reconstruction one can then relate the signals originating in the different coils with the spin density being sought as

$$\left|S_j\left(t\right)\right|=\left|{\displaystyle \sum _{n=1}^{N_{sp}}{C}_j}\left(y_{m,n}\right){\widehat{\rho }}_0\left(y_{m,n}\right)\right|$$ (8)

where j=1,2,…..N_c and { y_m,n }_m,n bears the same meaning as in equation (7). This again represents N_c simultaneous equations with N_SP unknowns; provided N_c ≥ N_SP, a pseudo-inverse operation ρ̂ = C⁻¹S can reconstruct from this an unaliased image.

The procedure just described involves performing a SENSE reconstruction on a set of signals arising from multiple coils, akin to the one that would arise in a “magnitude-mode” SPEN image reconstruction –apart from potential differences in the receiving phases of the various coils. It is known, however, that SPEN images obtained by magnitude signal calculations might suffer a resolution penalty when compared against Fourier-transformed (FT) images [16], unless acquired under strong excitation gradients or long encoding times associated to high SAR values. As mentioned, these deficiencies can be alleviated by SR-based algorithms [22] exploiting the oversampling occurring in this kind of experiments. SR image improvements can also be exploited in the multi-SP parallel MRI framework just introduced, once suitably incorporated into SENSE-type reconstructions. We refer the ensuing formalism as SR-SENSE. Like its conventional single-SP counterpart, SR-SENSE employs the extensive prior knowledge that the encoding and the acquisition parameters are available in a SPEN experiment. Also in this case the SR algorithm will approach the data arising from a multi-band chirp pulse leading to N_SP signals emerging simultaneously from adjacent fields-of-view, as an algebraic problem defined by an a priori known matrix A(t,y), that describes the phase modulation imparted by the action of the encoding pulses plus the dynamic evolution arising from all encoding and decoding gradients, for each position y within the sample. The signals S_j(t) collected by each coil can then be described as

$$S(t)={\displaystyle \underset{-\frac{FOV}{2}}{\overset{+\frac{FOV}{2}}{\int }}{\displaystyle \sum _{n=0}^{N_{sp}-1}A(t,y_n)C_j(y_n)\rho (y_n)}dy}$$ (9)

The point-spread-function of each encoded field-of-view fraction, A(t,y_n) will have periodic quadratic phase profiles repeating in space, as depicted in the lower plots of Figure 1. Because of the need to numerically solve for the density distributions arising from the ρ(y_n), it is convenient to describe each of these periodic distributions by a discrete index (m) rather than by a continuous variable y; eq. (9) can then be rewritten in matrix-like form as

$$\begin{array}{l}\left[\begin{array}{c}{S}_1\\ S_2\\ ⋮\\ S_{N_c}\end{array}\right](t)=\left[\begin{array}{cccc}A(t,y_{m,0})& A(t,y_{m,1})& \dots & A(t,y_{m,N_{sp}-1})\end{array}\right]\left[\begin{array}{cccc}{C}_1(y_{m,0})& C_2(y_{m,0})& \cdots \cdots & C_{N_c}(y_{m,0})\\ C_1(y_{m,1})& C_2(y_{m,1})& \cdots \cdots & C_{N_c}(y_{m,1})\\ ⋮& ⋮& \cdots \cdots & ⋮\\ C_1(y_{m,N_{sp}-1})& C_2(y_{m,N_{sp}-1})& \cdots \cdots & C_{N_c}(y_{m,N_{sp}-1})\end{array}\right]\left[\begin{array}{c}\rho (y_{m,0})\\ \rho (y_{m,1})\\ ⋮\\ \rho (y_{m,N_{sp}-1})\end{array}\right]\\ =\left[\begin{array}{cccc}A(t,y_{m,0})C_1(y_{m,0})& A(t,y_{m,1})C_1(y_{m,1})& \cdots \cdots & A(t,y_{m,N_{sp}-1})C_1(y_{m,N_{sp}-1})\\ A(t,y_{m,0})C_2(y_{m,0})& A(t,y_{m,1})C_2(y_{m,1})& \cdots \cdots & A(t,y_{m,N_{sp}-1})C_2(y_{m,N_{sp}-1}\\ ⋮& ⋮& & ⋮\\ A(t,y_{m,0})C_{N_c}(y_{m,0})& A(t,y_{m,1})C_{N_c}(y_{m,1})& \cdots \cdots & A(t,y_{m,N_{sp}-1})C_{N_c}(y_{m,N_{sp}-1}\end{array}\right]\left[\begin{array}{c}\rho (y_{m,0})\\ \rho (y_{m,1})\\ ⋮\\ \rho (y_{m,N_{sp}-1})\end{array}\right]\end{array}$$ (10)

The formulation is then akin to the classical SR formula S = Aρ [22], except for the fact that A [i.e. A(t, y_m,n)] is now weighted by the sensitivity profile C_j(y_m,n). Such an extended SR formulation can be written as S_ext = A_extρ_ext [22], with A_ext = A(t, y_m,n)C j (y_m,n). This kind of equation can be inverted and the spatial density ρ can thereby be retrieved throughout FOV, provided A_ext is well-conditioned –for instance, by using least squares criteria and iterative regularization procedures to find A_ext’s pseudoinverse matrix $A_{ext}^{+}$. In the present case, and due to the relatively high condition numbers involved, solutions based on pseudoinverse matrices were found to introduce artifacts. To get rid of these, and following [22], a Gaussian weighting of the point-spread-functions A_X around their main diagonal and a complex conjugation of the resulting $A_{ext}^{\prime }$ ($A_{ext}^{\prime }$⁺, which is the first iteration of Conjugate Gradient formalism) were used for the spatial density reconstruction. To use $A_{ext}^{\prime }$⁺, however, it is necessary to further normalize the coils’ different sensitivity contributions. This can be appreciated from the simplest two-channels example: assuming an encoding based on N_SP = 2

$$\begin{array}{c}{A_{ext}^{\prime }}^{+}{S}_{ext}={A_{ext}^{\prime }}^{+}{A}_{ext}{\rho }_{ext}\\ \iff \left[\begin{array}{cc}A\left(t,y_{m,0}\right)C_1\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_1\left(y_{m,1}\right)\\ A\left(t,y_{m,0}\right)C_2\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_2\left(y_{m,1}\right)\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{S}_1\\ S_2\end{array}\end{array}\right]\\ =\left[\begin{array}{cc}A\left(t,y_{m,0}\right)C_1\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_1\left(y_{m,1}\right)\\ A\left(t,y_{m,0}\right)C_2\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_2\left(y_{m,1}\right)\end{array}\right]\left[\begin{array}{cc}A\left(t,y_{m,0}\right)C_1\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_1\left(y_{m,1}\right)\\ A\left(t,y_{m,0}\right)C_2\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_2\left(y_{m,1}\right)\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\rho }_I\\ {\rho }_{II}\end{array}\end{array}\right]\\ =\left[\begin{array}{cc}{C_1}^{\prime }\left(y_{m,0}\right)A^{\prime }\left(t,y_{m,0}\right)& {C_2}^{\prime }\left(y_{m,0}\right)A^{\prime }\left(t,y_{m,0}\right)\\ {C_1}^{\prime }\left(y_{m,1}\right)A^{\prime }\left(t,y_{m,1}\right)& {C_2}^{\prime }\left(y_{m,1}\right)A^{\prime }\left(t,y_{m,1}\right)\end{array}\right]\left[\begin{array}{cc}A\left(t,y_{m,0}\right)C_1\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_1\left(y_{m,1}\right)\\ A\left(t,y_{m,0}\right)C_2\left(y_{m,0}\right)& A\left(t,y_{m,1}\right)C_2\left(y_{m,1}\right)\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\rho }_I\\ {\rho }_{II}\end{array}\end{array}\right]\\ =\left[\begin{array}{cc}{C}_1^2+C_2^2& {\epsilon }_2\\ {\epsilon }_1& C_1^2+C_2^2\end{array}\right]\left[\begin{array}{c}{\rho }_I\\ {\rho }_{II}\end{array}\right]\end{array}$$ (11)

where ε₁ = C₁′(y_m,1)A′(t,y_m,1)A(t,y_m,0)C₁(y_m,0)+C₂′(y_m,1)A′(t,y_m,1)A(t,y_m,0)C₂(y_m,0) and ε₂ = C₁′(y_m,0)A′(t,y_m,0)A(t,y_m,1)C₁(y_m,1)+C₂′(y_m,0)A′(t,y_m,0)A(t,y_m,1)C₂(y_m,1). The ε cross-terms appearing in eq. (11) complicate a stable calculation of the spatial densities (ρ_n)_n=I,II. Since cross-terms of the A′_X A_Y type are very small, this complication was bypassed by using

$${\rho }_{ext}=\frac{{A^{\prime }}_{ext}{S}_{ext}}{\left|diag\left({A^{\prime }}_{ext}{A}_{ext}\right)\right|}$$ (12)

to invert eq. (11) and reconstruct the spatial spin density images throughout this study.

3. Materials and Methods

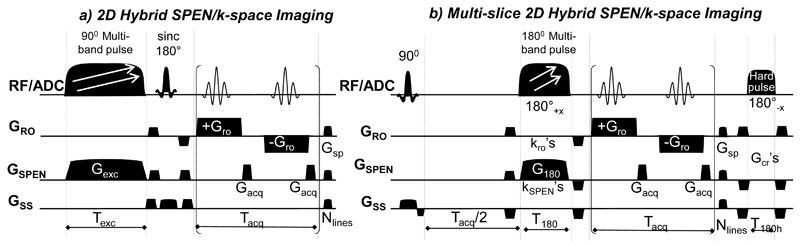
To explore the potential benefits of SPEN pMRI, the 2D “Hybrid” SPEN/k-space parallelized sequences displayed in Figure 2 were tested. In both of these sequences SPEN replaces EPI’s phase encoding, whereas the high-bandwidth axes remain encoded in the usual k-space. Also in both cases, the image acquisition process is parallelized along the SPEN-encoded dimensions. To achieve this the sequence in panel (a) employs a multiband 90° frequency-swept chirp pulse and imparts slice selectivity along the third dimension by a slice-selective sinc 180° pulse; the sequence in panel (b) adapts this hybrid experiment to rapid 3D multi-slicing by replacing the initial 90° excitation with a slice-selective pulse, implementing SPEN by an adiabatic multi-band 180° inversion of the excited spins, and adding a second, hard 180° pulse restoring the magnetizations of all the non-excited slices back to the +z axis for preventing unnecessary saturation effects. The timing of the various pulses was set as described in [20] in order to achieve full T₂* refocusing of all voxels decoded along the SPEN dimension: T_exc=T_acq for the 90° multi-band pulse, and T₁₈₀=T_acq/2 for the 180° multi-band pulse.

Figure 2.

Sequences assayed for the Hybrid SPEN/k-space pMRI experiments. (a) Single-slice version based on a 90° multi-band pulse encoding simultaneously adjacent spatial regions; slice selection is done by the sinc180° pulse (b) Multi-slice hybrid SPEN/k-space pMRI sequence using a multi-band adiabatic 180 inversion pulse to simultaneously encode adjacent spatial regions; a final 180° hard pulse serves to return all the magnetization that was not addressed by the initial 90° slice-selective pulse, back to the +z axis. The RF/ADC line displays both the pulses and the timing of the acquisitions (ADC for Analogue-to-Digital Converter); G_RO, G_SPEN and G_SS rows display respectively the gradients applied along the readout, the spatiotemporally-encoded and the slice-selective directions. The parameters of the scans are as described in previous SPEN implementations [14. 20]; their novelty lies in the replacement of the 90° and 180° swept pulses by multi-band swept analogues, and the concomitant reduction of the encoding and acquisition times by a factor equal to the number of employed bands. Main experimental parameters are: T_acq, G_acq –acquisition duration and gradient strength associated to the slow SPEN dimensions; T_ro, G_ro – acquisition duration and gradient strength associated with the orthogonal k-space readout dimension; N_slices, N_lines –number of slice-selective and of SPEN-decoded elements; T_exc, G_exc, T₁₈₀, G₁₈₀ –chirp pulse duration and associated gradient strength in (a) and in (b), respectively; k_ro and k_SPEN– pairs of prewinding gradients flanking the adiabatic 180° inversion and imparting ≈ϒG_roT_ro/2 and ≈ϒG₁₈₀T₁₈₀ encodings respectively; G_cr and G_sp –crusher and spoiler gradients applied on all axes.

In order to implement the SR-SENSE algorithm described above, a variety of choices for retrieving and combining the coil sensitivity maps were explored. For conventional SENSE reconstruction several options are available [35], such as normalizing each channel image by an additional body coil image, or normalizing each channel image by a “sum of square” image combined from the channels maps. pMRI experiments were here normalized by the “sum of square” channels image principle, for single shot SPEN, single shot EPI, and multi-shot spin-echo MRI. In the first case $C_j=\raisebox{1ex}{$S_j$}\!\left/ \!\raisebox{-1ex}{$\sqrt{{\displaystyle \sum _{j=1}^{N_c}{\left|S_j\right|}^2}}$}\right.$ while for the two others $C_j=\raisebox{1ex}{$I_j$}\!\left/ \!\raisebox{-1ex}{$\sqrt{{\displaystyle \sum _{j=1}^{N_c}{\left|I_j\right|}^2}}$}\right.$, where S_j is the signal measured in SPEN experiment and I_j is the image (after Fourier Transform) measured in the k-space-based experiments. The three options were found operational without distinct differences in reconstructed phantom images; in all phantom and human brain images that will be presented here the first choice was applied (using SPEN R=1 for sensitivity maps), while for breast images the multi-shot scan was used for sensitivity maps.

All the hybrid sequences here assayed were custom written and implemented on a 3T Siemens TIM TRIO clinical system, using a 4-channels head, a 32-channels head and a 4-channels breast coil. The multi-sweep RF and gradient waveforms were synthesized based on available Siemens software, modified for the sequences in Figure 2 purposes. Images were reconstructed in all instances using custom-written MATLAB packages, which included the possibility to process hybrid SPEN-/k-space data with/without super-resolution along the SPEN dimension, while using FFT along the k-dimension. Data manipulation before SR processing [22] included alignment of positive and negative readout echoes; zero-filling, weighting and other routine procedures along the k-domain. In addition, a variety of reconstruction pMRI scripts were written and applied within MATLAB, using as a basis and test platform the PULSAR open source [39]. Experiments were then conducted first on phantoms –the ACR MRI Accreditation Program Phantom when assaying the brain coil and two bottles with NaCl saline solutions mimicking human tissue in the breast coil setup– to test the method’s ability to provide quality single-scan spatial images. This phantom is also ideally suited for a quantitative comparison on the relative SNR merits of conventional SPEN vs its pMRI variant, as well as between SPEN and EPI. The performance of the pMRI hybrid SPEN sequences and reconstruction algorithms was also examined with a series of in vivo experiments on human volunteers (n = 5), focusing on both brain and breast scans. These two regions were chosen owing to their distinct imaging characteristics, with the former characterized by high homogeneity and a relatively static nature, and the latter encompassing tissue heterogeneities and unavoidable cardiac motions. All human imaging sessions were performed according to procedures approved by the Internal Review Board of the Wolfson Medical Center (Holon, Israel) after obtaining written consents, and focused on both brain and breast scans.

As the mutli-SP approach discussed above involves the design and use of new RF pulses, SAR estimations become relevant. In hybrid sequences of the kind illustrated in Figure 2 the estimated energy delivered by conventional chirp pulses has been reported [16]. The RF nutation for a 90° chirp is then $\gamma B_1=2\pi \times 0.27\times \sqrt{\gamma G_{exc}FOV/T_{exc}}.$ Since the 2SP chirp pulse is a sum of two individual chirp pulses, the maximal power level to reach 90° flip angle by the two field-of-view parts (or SPs) is estimated to be proportional to $\sqrt{2\cdot \gamma G_{exc}FOV/T_{exc}}$ (as was verified by running Bloch simulation). SAR values proportional to ∫|B₁|²dt therefore become higher, but given the amplitude intereferences resulting from the multi-band pulse phase modulations this integral was <1.5x higher than comparable single-band encoding pulses. This was verified experimentally prior to the in vivo scans, by running sets of power calibration tests.

4. Results and Discussion

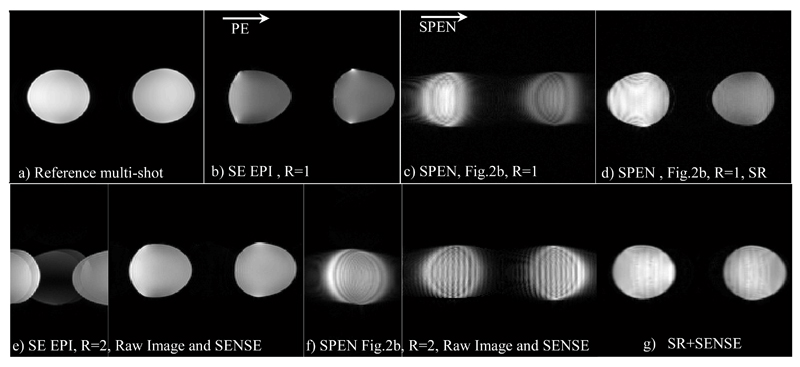
Comparisons between results afforded by scanner-supplied pMRI EPI protocols and results afforded by the hybrid SPEN/k-space parallel imaging sequence of Figure 2a, are illustrated in Figure 3. These single-slice results were implemented on an ACR MRI phantom on the 3T scanner, and in the SPEN instance they relied on a shaped pulse involving two adjacent bands that were simultaneously encoded by a dual-sweep chirp pulse. A two-fold reduction in both the encoding and the decoding times were thus achieved; also in the EPI case, undersampling with R=2 lead to a similar two-fold reduction in scan time. The data was collected in both cases using a four-receiver head-coil array; two pairs of receivers thus contributed to the multi-SP sensitivity encoding along the SPEN dimension. In this latter case, the SENSE algorithm summarized in eq. (12) was applied on data collected by these four receivers after the latter was subject to 1D FT along the k-axis; these results are presented with and without the use of the SR algorithm (i.e., in the latter case, involving a final magnitude calculation). A comparison of the EPI and hybrid SPEN pMRI results illustrates the good unfolding that the SENSE algorithm implements on both of these methods. Unfolded images are also characterized by a higher robustness to inhomogeneity due to shorter echo times, but still retain minor experimental artifacts in the form of “ghosts” in the EPI case. A coarse, limited resolution characterizes SPEN images if relying on pure-magnitude calculations (Figs. 3c and 3f). By relying on a super-resolved processing (Figs. 3d, 3g) the image improvement is clear. A comparison among the two SR-SPEN images in Figure 3 serves well to illustrate the main features associated to pMRI: by acting over adjacent regions in parallel, the full FOV can still be imaged while increasing the signal intensity of some image regions by nearly five-fold at no expense in image resolution. At the same time, a seam between the two bands involved in the chirp excitation pulse, is also evident for the N_SP =2 case. The SNR ratios of R=1 and R=2 images was compared between SPEN and EPI scans, and are summarized at Table 1. The comparison was conducted using average signals measured at three areas – one at the edge of the object, second at its center and last at another edge, and standard deviation outside the object for the noise estimation. At the first image edge, the SNR ratios for EPI and SPEN were similar, while at the “first excited” edge (the second area in Table 1) the T₂ signal losses in the N_SP = 2 SPEN image are considerably reduced, and SNR consequently enhanced (similar reduced T₂ weighting appears in the third region). Further evidence for this effect is evident in Figure 4, which presents a comparison between SPEN phantom images acquired with the usual SPEN strategy (i.e., R=1), against one acquired with an R = 4 acceleration factor. The more homogeneous signal intensities that the pMRI approach achieves by shortening the excitation/acquisition times and attenuating the T₂ losses, is evident.

Figure 3.

Phantom images collected using a head coil on an ACR MRI phantom. (a) Reference multi-shot image. (b) R=1 EPI image. (c,d) R=1 images SPEN collected with the sequence in Fig. 2a and reconstructed by magnitude-mode and super-resolved calculations, respectively. Bottom row: (e) Pre- and post-SENSE reconstructed EPI R = 2 images. (f) Same as (e) but for a hybrid SPEN acquisition (Fig. 2a) reconstructed using eq. (8) arising from the four-coil signals. Notice that the “raw” images in (e) and (f) have been flipped in the figure for display purposes. (g) SR-SENSE reconstruction of the raw data illustrated in (f). Illustrated for the EPI and SR-SENSE SPEN images, are the regions chosen for the SNR comparison given in Table 1 (yellow regions: the signals of interest; blue region: noise estimation area). Common parameters: FOV = 22x22 mm², slice thickness = 5 mm. Common parameters for the R=1 SPEN and EPI scans: acquired points 100x100, T_acq=57ms; in addition, for EPI TE = 63ms, for SPEN TE = 5-94 ms, G_exc= 0.05 G/cm, T_exc=57ms. Common parameters for the R=2 SPEN and EPI scans: number of acquired points 100x50, T_acq=28.5ms; in addition, for EPI TE=33ms and for SPEN TE=5-56ms, G_exc= 0.07 G/cm, T_exc=28.5ms. Multi-scan parameters: number of acquired points 384x384, TE=71ms, TR=1500ms.

Table 1. SNR ratio comparison – SNR_R=2/SNR_R=1 for SPEN and EPI (Figure 3).

	SPEN SNRR=2/SNRR=1	EPI SNRR=2/SNRR=1
Region of interest in the image, edge #1	0.61	0.74
Region of interest in the image, center #2	1	0.64
Region of interest in the image, edge #3	1.14	0.65

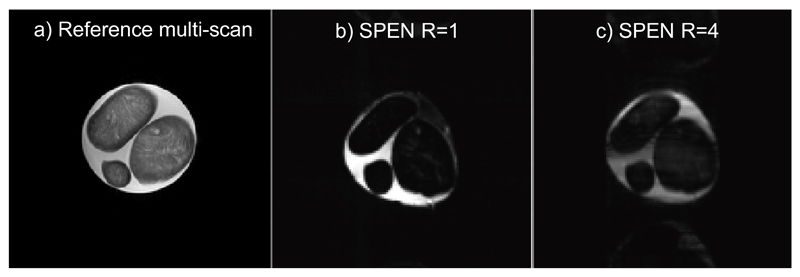
Figure 4.

Images collected on a phantom involving three cheese spheres in water, using a 32-coil head array. (a) Reference spin echo multi-shot image. (b,c) R=1 and R=4 SPEN images collected with the sequence in Fig. 2a; (c) was reconstructed using SR-SENSE reconstruction. Common parameters: FOV = 22x22 mm², slice thickness = 5 mm. R=1 SPEN parameters: acquired points 256x256, T_acq=300ms,TE = 5-385 ms, G_exc= 0.03 G/cm, T_exc=80ms. R=4 SPEN parameters: acquired points 256x64, T_acq=75ms,TE = 5-113 ms, G_exc= 0.03 G/cm, T_exc=33ms. Multi-scan parameters: number of acquired points 384x384, TE=71ms, TR=1500ms.

The experiments illustrated in Figures 3 and 4 involved a 90° chirp SPEN sequence and a four-channel head coil detector for R=2 and a 32-channel head coil detector for R=4 acceleration factors. Figure 5 illustrates results obtained utilizing the 180° -based sequence in Figure 2b, as tested on a phantom using a breast four-coil array for N_SP = 1, 2. This is an environment which can benefit even further than the brain from an accelerated scan, given its need to cope with usually high inhomogeneities in field. Figure 5 shows results reached using this sequence when executed under full-refocusing conditions. Comparisons are here made upon using single- versus dual-band inversion pulses to encode the SPEN FOV, as well as upon processing the data by “magnitude-mode” calculation or after SR-SENSE. A one-to-one comparison of these data confirms that the SR-SENSE pMRI always delivers the highest image quality. The improvement brought upon by the fully refocused SPEN acquisitions vis-à-vis their EPI counterpart in terms of the shape of the objects’ shapes –which compare much better with the multi-scan references for the former than from the latter– are also evident in these images.

Figure 5.

Phantom images collected using a multi-receiver breast coil on a phantom made by two saline solution bottles. The panels present analogous acquisitions as described in panels (a)-(g) of Figure 3, but this time SPEN images were collected with the sequence in Fig. 2b. Common parameters: FOV = 37x37 mm², slice thickness = 5 mm. Common parameters for the R=1 SPEN and EPI scans: number of acquired points 160x160, T_acq=88ms; for EPI - TE=94ms; for SPEN TE=56-144 ms, G₁₈₀= 0.02 G/cm, T₁₈₀=44ms. Common parameters for the R=2 SPEN and EPI scans: number of acquired points 160x80, T_acq=44ms; for EPI TE=48ms and for SPEN TE=32-76ms, G₁₈₀= 0.06 G/cm, T₁₈₀=22ms. Multi-scan parameters were as in Figure 3.

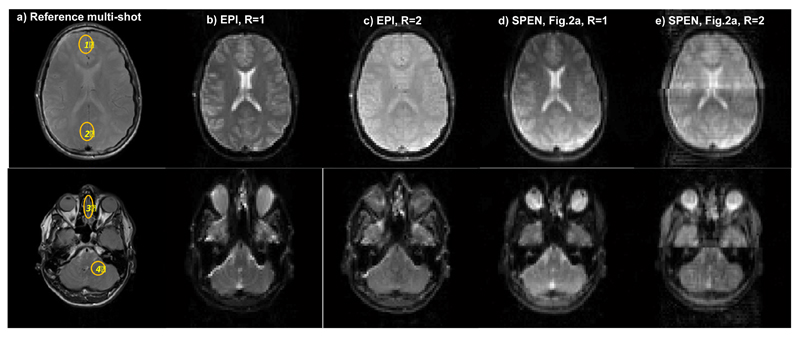
To complete these tests, the performance of the sequences discussed so far was examined on human volunteers. Figure 6 compares a number of brain scans, collected on 5 mm wide axial slices chosen at two different positions. The top row focuses on a middle cross section of the brain; this is a region liable to very good shimming, where the performance of the R = 2 spin-echo EPI sequence proves best. In particular, a signal distortion near the seam line can be observed for the SPEN R = 2 counterpart. The lower row, by contrast, focuses on a cross-section near the eyes, which is usually more prone to distortions due to B₀ inhomogeneities. In this latter region a conventional single-sweep Hybrid SPEN scan based on a chirped 90° excitation, shows already a significant image improvement compared to spin-echo EPI; its ability to refocus field inhomogeneities under the executed full-refocusing conditions, is particularly evident when comparing the characteristic shapes of the eyeballs. Parallelizing the Hybrid SPEN experiment by dual-band 90° chirps improves this image even further, ameliorating further the inhomogeneity effects while increasing the image’s SNR due to its shorter encoding and acquisition durations.

Figure 6.

Single-slice brain images of a volunteer scanned at two different locations. (a) Reference spin echo multi-scan images. (b) Spin-echo EPI images for R=1. (c) Idem for R=2. (d) Single-band hybrid SPEN, processed by SR and FT. (e) Parallelized Hybrid SPEN collected using the sequence in Fig. 2a, R = 2, and processed by SR-SENSE. Common parameters: FOV = 22x22 mm², slice thickness = 5 mm. Common R=1 SPEN and EPI scan parameters: number of acquired points 80x80, T_acq = 40ms; for EPI TE = 45ms; for SPEN TE = 5-68 ms, G_exc = 0.05 G/cm, T_exc = 40ms. Common R=2 SPEN and EPI scan parameters: number of acquired points 80x40, T_acq=20ms; for EPI TE = 30 ms and for SPEN TE = 5-42ms, G_exc = 0.1 G/cm, T_exc=20ms. Multi-scan parameters: number of acquired points 384x384, TE = 71ms, TR = 1500ms. Also shown are SNR_R=2/SNR_R=1 ratios measured for SPEN and EPI in the (1)-(4) regions displayed in (a).

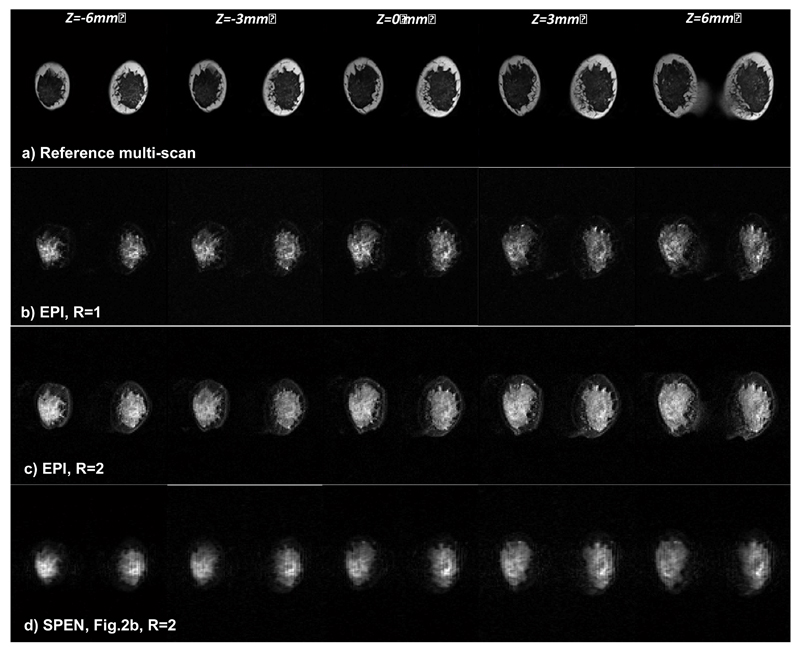
Single-scan methods could be particularly relevant for breast imaging, as in combination with diffusion weighting and diffusion tensor methods they can provide qualitative and quantitative information about tissue lesion types [40]. A multi-slice test based on the sequence in Figure 2b, lead to the breast images presented in Figure 7. These fat-suppressed human volunteer studies compare EPI and SPEN with R=2, using SENSE for the former and SR-SENSE for the latter reconstruction. Both give similar results, with much better performance and higher SNR from the connective tissues than their R = 1 counterpart. The fat signal that can be observed around the connective tissue is better suppressed in SPEN than in EPI, although the same fat suppression technique was used in both instances. Still, although a higher SNR is observed in the SPEN R=2 scan, this image still suffered from more blurring than its EPI counterpart. These effects probably reflect an incomplete reversal of the inversion procedure arising from the swept pulses; further improvements on this matter are being sought.

Figure 7.

Comparison between multi-slice breast images of a volunteer collected using multi-scan MRI (top row), EPI images with R=1 (2^nd row) and with R=2 (3^rd row), and SPEN R=2 images collected using the sequence in Fig. 2b (bottom). Common parameters: FOV = 28x28 mm², slice thickness = 3 mm. For the R=1 EPI scan: number of acquired points 120x120, T_acq=66ms, TE=72ms. Common R=2 SPEN and EPI scan parameters: number of acquired points 120x60, T_acq=33ms; for EPI TE=38ms; for SPEN TE=42-72ms, G₁₈₀=0.07 G/cm, T₁₈₀=17ms. Both the EPI and SPEN experiments used fat suppression; the multi-scan acquisition did not. Other multi-scan parameters: number of acquired points 384x384, TE=71ms, TR=1500ms.

5. Conclusions

The aim of this study was to translate pMRI’s advantages, within a SPEN-based single-scan imaging context. As described in Ref. 36, a basic ingredient to enable the parallelization of these experiments involves using multi-band swept pulses encoding multiple adjacent spatial regions simultaneously –either during excitation, or by inversion. Different methods of image reconstruction were explored, starting from conventional SENSE reconstructions of “magnitude-mode” images and evolving to SR-based SENSE strategies. Major improvements in spatial resolution were observed upon using this SR-SENSE algorithm; two additional advantages worth noting upon employing this algorithm included the removal of ripple image modulations occurring in simple SENSE, as well as a nearly seamless image reconstruction of the region interfacing the various multi-band pulses. It is interesting to note that, despite the approximations that are involved upon using A_ext‘s pseudoinverse as matrix solution of eq. (14), simulations indicate that our image reconstruction protocol in the pMRI case is still imperfect –leaving ≈15% signal distortions at the regions of inter-band interfacing. While further research to eliminate this residual via regularization procedures is in progress, it is already clear that the potential of pMRI to improve sensitivity and minimize time-dependent distortions can also be ported to this real-space ultrafast scanning mode. Further clinical implementations of these advantages are currently in progress.

Abbreviation

EPI

Echo-Planar Imaging

FOV

Field of View

FT

Fourier Transform

MRI

Magnetic Resonance Imaging

NMR

Nuclear Magnetic Resonance

PE

Phase-Encode

pMRI

Parallel MRI

RF

Radio frequency

RO

Read-Out

SAR

Specific Absorption Rate

SENSE

Sensitivity Encoding

SP

Stationary Point

SPEN

SPatio-temporal ENcoding

SR

Super-resolution

TE

Echo Time

Appendix

Image reconstruction by Fourier shift - Hybrid SPEN pMRI with a single coil

We describe here another strategy for reconstructing images encoded with multi-band pulses, that does not depend on sensitivity information –but rather on the differing terms that according to eq. (7), multiple stationary points will exhibit in the values of their linear ${\left\{{\alpha }_1^n\right\}}_{\text{n}=1\dots \text{NSP}}$ terms. The method is based on performing a Fourier-based filtration of the signals corresponding to each stationary point, based on these linear differences. For example, for the N_sp = 2 case, the signal S(t) in equation (8) can be written as:

$$S(t)={\displaystyle \underset{-\frac{FOV}{2}}{\overset{+\frac{FOV}{2}}{\int }}\left[\rho (y_{m,0})A(t,y_{m,0})+\rho (y_{m,1})A(t,y_{m,1})\right]}dy$$ A.1

The specific of a particular {ρ(y_m,n)}_n=1,2 SP can then be carried out by multiplying the signal S(t) with A(t, y_m,n)’s complex conjugate; it’s phase modulation would this be canceled while the modulations of all other SPs will remain, and this could be the basis of each SP’s signal separation. For example, multiplying the signal in A.1 by the phasor corresponding to the 1^st stationary point (n=0) leads to

$${\epsilon }^{n=0}\left(y\right)=S\left(t\right)\cdot A^{*}\left(t,y_{m,0}\right)={\displaystyle \underset{-\frac{FOV}{2}}{\overset{+\frac{FOV}{2}}{\int }}\left[\rho \left(y_{m,0}\right)+{\displaystyle \sum _{n=1}^{N_{sp}-1}\rho \left(y_{m,n}\right)A}\left(t,y_{m,n}\right)A^{*}\left(t,y_{m,0}\right)\right]dy}$$ A.2

This operation negates the quadratic phase-term, corresponding to the 1^st SP. Similarly multiplying with the phase of n^th SP negates the phase of that SP. A Fourier transform along the acquisition time/space variable (which in SPEN are equivalent) ε̂ ⁿ⁼⁰ (k_y) = FT{εⁿ⁼⁰(y)}, leads to a k-space signal composed of two kind of terms: one will be an amplitude-modulated but centered at k = 0 representing the contribution of the demodulated stationary point; the second will be a series of amplitude and phase modulated terms, corresponding to the remaining SPs and dispersed away from k = 0. Provided that the object being imaged can be described by a reasonably-behaved real function, the first term will occupy the center of k-space whereas the rest will be shifted from this low-frequency region. The central echo can thus be isolated using a filtering window in the k_- domain, whose width is determined by one over the spatial resolution desired along the SPEN domain. A final step composed by an inverse Fourier transform of the filtered k-domain data back to the y-domain,

$$\left\{\rho (y_{m,0})\right\}=F{T}^{-1}\left\{{\widehat{\epsilon }}_{filt}^{n=0}(k_y)\right\}=F{T}^{-1}\left\{{\widehat{\epsilon }}^{n=0}(k_y)\cdot {\Psi }_{DC}(\Delta y^{-1})\right\}$$ A.3

eliminates the image components arising from all the non-demodulated terms, yielding the raw data associated with a single SP out of the multi-band, multi-SPs that were excited. Each of these bands can then be separated by an analogous procedure, and they can be recombined –following if needed suitable SR reconstruction– to deliver the full image being sought. Always while relying on a single-coil acquisition.

One important aspect of the FFT based algorithm just discussed, pertains is the efficiency of the echo-separation procedure in the k_y–domain. In order to optimize this process, the different echoes should be well separated from each other. This requirement can be fulfilled by suitably adjusting the experimental parameters used. With each echo’s location calculated in advance, this separation process can be optimized. Still, a main drawback of this Fourier-based multi-SP processing –and the reason why it is not pursued in further detail– pertains its loss of information vis-à-vis the SR SPEN alternative discussed in the main text. This limitation can be readily understood via the following example: taking N_sp = 2 and M = 64, the echo-filtering process is carried out by isolating one of the echoes, locating it at the center of the k_y Fourier space, and then filtering out the rest half of the k-axis. This decreases the number of data points in the filtered echo from 64 to 32, a number of pixels that is preserved by the inverse Fourier transform. Repeating the same process of SP #2 eventually yields a 64 pixels image. This result is, however, problematic, due to the fact that the original goal of acquiring M sample points using two SPs was to produce an image that would have double that number of pixels; i.e., N_SP⋅M. Therefore, and at least as presented in this Appendix, this method cannot gain resolution while shortening the excitation/acquisition times. Its underlying concept may, however, be found effective for other needs –for instance for shortening the encoding/decoding times, and thereby reduce T₂ and strong intravoxel T₂* effects.