Robust Cell Detection and Segmentation in Histopathological Images Using Sparse Reconstruction and Stacked Denoising Autoencoders

Abstract

Computer-aided diagnosis (CAD) is a promising tool for accurate and consistent diagnosis and prognosis. Cell detection and segmentation are essential steps for CAD. These tasks are challenging due to variations in cell shapes, touching cells, and cluttered background. In this paper, we present a cell detection and segmentation algorithm using the sparse reconstruction with trivial templates and a stacked denoising autoencoder (sDAE). The sparse reconstruction handles the shape variations by representing a testing patch as a linear combination of shapes in the learned dictionary. Trivial templates are used to model the touching parts. The sDAE, trained with the original data and their structured labels, is used for cell segmentation. To the best of our knowledge, this is the first study to apply sparse reconstruction and sDAE with structured labels for cell detection and segmentation. The proposed method is extensively tested on two data sets containing more than 3000 cells obtained from brain tumor and lung cancer images. Our algorithm achieves the best performance compared with other state of the arts.

1 Introduction

Reproducible and accurate analysis of digitized histopathological specimens plays a critical role in successful diagnosis and prognosis, treatment outcome prediction, and therapy planning. Manual analysis of histopathological slides is not only laborious, but also subject to inter-observer variability. Computer-aided diagnosis (CAD) is a promising solution. In CAD, cell detection and segmentation are often prerequisite steps for critical morphological analysis [10,16].

The major challenges in cell detection and segmentation are: 1) large variations of cell shapes and inhomogeneous intensity, 2) touching cells, and 3) background clutters. In order to handle touching cells, radial voting based detection method achieves robust performance with an assumption that most of the cells have round shapes [7]. In [14], an active contour algorithm is applied for cell segmentation. Recently, shape prior model is proposed to improve the performance in the presence of weak edges [2,15].

In this paper, we propose a novel cell detection and segmentation algorithm. To handle the shape variations, inhomogeneous intensity, and cell overlapping, the sparse reconstruction using an adaptive dictionary and trivial templates is proposed to detect cells. In the segmentation stage, a stacked denoising autoencoder (sDAE) trained with structural labels is used for cell segmentation.

2 Methodology

An overview of the proposed method is shown in Figure 1. During the training for cell detection, a compact cell dictionary (Figure 1(b)) is learned by applying K-selection [6] to a cell patch repository containing single centered cells. In the testing (Figure 1(a)–(e)), a sample patch from the testing image is first used as a query to retrieve similar patches in the learned dictionary. Since the appearance variation within one particular image is small, any sample patch containing a centered cell can be used. Next, sparse reconstruction using trivial templates [13] is utilized to generate a probability map to indicate the potential locations of the cells. Finally, weight-guided mean-shift clustering is used to compute the seed detection. Different from [13], our algorithm removes the sparsity constraints for the trivial templates. Therefore, the proposed method is more robust to the variations of the cell size and background. During the segmentation stage (Figure 1(f)–(i)), the sDAE is trained using the gradient maps of the training patches and their corresponding human annotated edges (Figure 1(f)). Our proposed segmentation algorithm is designed to handle touching cells and inhomogeneous cell intensities. As shown in (Figure 1(h)), the false edges are removed, the broken edges are connected, and the weak edges are recovered.

Fig. 1.

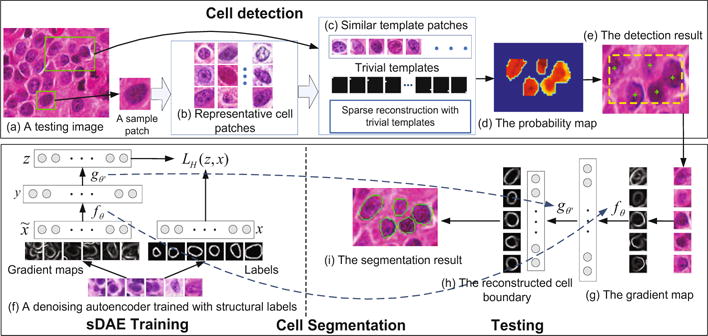
An overview of the proposed algorithm.

2.1 Detection via Sparse Reconstruction with Trivial Templates

Adaptive Dictionary Learning

During cell dictionary learning, a set of relevant cell patches are first retrieved based on their similarities compared with the sample patch. Considering the fact that pathological images commonly exhibit staining variations, the similarities are measured by normalized local steering kernel (nLSK) feature and cosine similarity. nLSK is more robustness to contrast change [9]. An image patch is represented by the densely computed nLSK features. Principal component analysis (PCA) is used for dimensionality reduction. Cosine distance: $D_{\mathit{cos}}=({\mathbf{v}}_i^T{\mathbf{v}}_j)/(\Vert {\mathbf{v}}_i\Vert \Vert {\mathbf{v}}_j\Vert )$, where v_i denotes the nLSK feature of patch i, is proven to be the optimal similarity measurement under maximum likelihood decision rule [9]. Therefore, it is used to measure the similarities. The dictionary patches are selected by a nearest neighbor search.

Probability Map Generation via Sparse Reconstruction with Trivial Templates

Given a testing image, we propose to utilize sparse reconstruction to generate the probability map by comparing the reconstructed image to the original patch via a sliding window approach. Because the testing image patch may contain part of other neighboring cells, trivial templates are utilized to model these noise parts. When the testing image patch is aligned to the center of a cell, it can be linearly represented by the cell dictionary with small reconstruction errors. The touching part can be modeled with trivial templates. Let ${\mathbf{p}}_{ij}\in {ℝ}^{\sqrt{m}\times \sqrt{m}}$ denote a testing patch located at (i, j), and B represent the learned cell dictionary, this patch can be sparsely reconstructed by: p_ij ≈ Bc+e = [B I][c e]^T, where e is the error term to model the touching part, and I_m×m is an identity matrix containing the trivial templates. The optimal sparse reconstruction can be found by:

$$\underset{\stackrel{\sim }{\mathbf{c}}}{\min }{\Vert {\mathbf{p}}_{ij}-\stackrel{\sim }{\mathbf{B}}\stackrel{\sim }{\mathbf{c}}\Vert }^2+\mathrm{\lambda }{\Vert \mathbf{d}\odot \mathbf{c}\Vert }^2+\mathrm{\gamma }{\Vert \mathbf{e}\Vert }^2,s.t.{\mathbf{1}}^T\mathbf{c}=1,$$ (1)

where $\stackrel{\sim }{\mathbf{B}}=[\mathbf{B}\mathbf{I}],\stackrel{\sim }{\mathbf{c}}={[\mathbf{c}\mathbf{e}]}^T$, and d represents the distance between the testing patch and the dictionary atoms, ⊙ denotes element-wise multiplication, and λ controls the importance of the locality constraints, and γ controls the contribution of the trivial templates. The first term incorporates trivial templates to model the touching cells, and the second term enforces that only local neighbors in the dictionary are used for the sparse reconstruction. The locality constraint enforces sparsity [12]. In order to solve the locality-constrained sparse optimization, we first perform a KNN search in the dictionary excluding the trivial templates. The selected nearest neighbor bases together with the trivial templates form a smaller local coordinate system. Next, we solve the sparse reconstruction problem with least square minimization [12].

The reconstruction error is defined as ${\epsilon }_{\mathit{\text{rec}}}=\Vert ({\mathbf{p}}_{ij}-\stackrel{\sim }{\mathbf{B}}\stackrel{\sim }{\mathbf{c}})\odot k(u,v)\Vert$, where k(u, v) is a “bell-shape” spatial kernel that penalizes the errors in the central region. A probability map is obtained by $P_{ij}=\frac{|{\epsilon }_{\mathit{\text{rec}}}-\max (E)|}{\max (E)-\min (E)}$, where P_ij denotes the probability at location (i, j), and E represents the reconstruction error map. We demonstrate the reconstruction results of touching cells with and without trivial templates in Figure 2(a)–(b). The final cell detection is obtained by running a weight-guided mean-shift clustering on the probability map.

Fig. 2.

(a) A demonstration of sparse reconstruction with/without trivial templates. From row 1 to 3: a testing patch, the sparse reconstruction without trivial templates, the sparse reconstruction with trivial templates. Row 4 and 5 are the first term and the second term in equation p_ij ≈ Bc + e, respectively. (b) A demonstration of reconstruction errors obtained from a testing patch aligned to the center of the cell and from those misaligned patches. Row 1 displays a small testing image. The green box shows a testing patch aligned to the cell. Boxes in other colors show misaligned testing patches. From row 2 to row 5: A testing image patch with occlusion from a neighboring cell, the reconstruction of the testing patch, the reconstructed patches with the occlusion part removed, and the visualization of the reconstruction errors. Note that the aligned testing patch has the smallest error. (c) From left to right: the original testing patches, the gradient magnitude maps, and the recovered cell boundaries using sDAE.

2.2 Cell Segmentation via Stacked Denoising Autoencoders

In this section, we propose to train a stacked denoising autoencoder (sDAE) [11] with structural labels to remove the fake edges while preserving the true edges. An overview of the training and testing procedure is shown in Figure 1 (f)–(i). Traditionally, denoising autoencoders (DAE) are trained with corrupted versions of the original samples, which requires the clean image as a premise. In our proposed method, we use the gradient images of the original image patches as the noisy inputs and the human annotated boundaries as the clean images. The DAE is trained to map a noisy input to a clean (recovered) image patch that can be used for segmentation.

We first focus on training a single layer of the DAE. Let $\stackrel{\sim }{\mathbf{X}}\in {ℝ}^m$ denote the noisy gradient magnitude map of the original image patch centered on a detected center of the cell (seed). The DAE learns a parametric encoder function $f_{\theta }(\stackrel{\sim }{\mathbf{x}})=s(\mathbf{W}\stackrel{\sim }{\mathbf{x}}+\mathbf{b})$, where s(·) denotes the sigmoid function to transform the input from the original feature space into the hidden layer representation y ∈ ℝ^h, where θ = {W, b} and W ∈ ℝ^{h, m}. A parametric decoder function g_θ′ (y) = s (W′y + b′), θ′ = {W′, b′} is learned to transform the hidden layer representation back to a reconstructed version Z ∈ ℝ^m of the input $\stackrel{\sim }{\mathbf{X}}$.

Since it is a reconstruction problem based on real-valued variables, a square error loss function of the reconstruction z and the manually annotated structural label x is chosen, and the sigmoid function in g_θ′ is omitted. The parameters {θ, θ′} are obtained by:

$$\underset{\mathbf{W},\mathbf{b},\mathbf{W}\prime ,\mathbf{b}\prime }{\min }{\Vert \mathbf{x}-g_{\theta \prime }\circ f_{\theta }(\stackrel{\sim }{\mathbf{x}})\Vert }^2.$$ (2)

We choose tied weights by setting W′ = W^T [11]. The fake edges are suppressed in the reconstructed patches (Figure 2(c)). The final results are obtained by applying five iterations of an active contour model to the convex hull computed from the reconstructed image.

3 Experimental Results

Data set

The proposed algorithm is extensively tested on two data sets including about 2000 lung tumor cells and 1500 brain tumor cells, respectively. For the detection part, 2000 patches of size 45 × 45 with a centralized single cell are manually cropped from both data sets. K = 1400 patches are selected by K-selection. The parameter γ in equation (1) is set to 10⁻⁴. In the segmentation part, contours of more than 4900 cells are annotated. Training sample augmentation is conducted via rotation and random translation. In total more than 14 × 10⁴ training patches are used and each of them is resized to 28 × 28. A two-layer sDAE with 1000 maps in the first layer and 1200 maps in the second layer is trained on the data set. An active contour model [4] is applied to obtain the final segmentation result. All the experiments are implemented with MATLAB on a workstation with Intel Xeon E5-1650 CPU and 128 GB memory.

Detection Performance Analysis

We evaluate the proposed detection method through both qualitative and quantitative comparison with four state of the arts, including Laplacian-of-Gaussian (LoG) [1], iterative radial voting (IRV) [7], and image-based tool for counting nuclei (ITCN) [3], and single-pass voting (SPV) [8]. The qualitative comparison of two patches is shown in Figure 3.

Fig. 3.

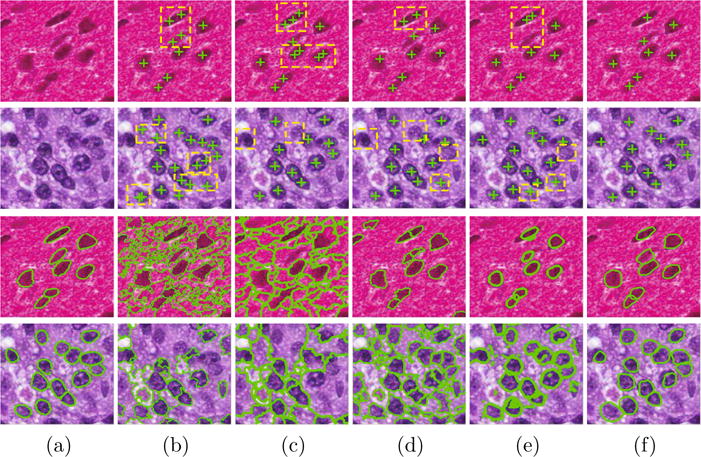
Detection and segmentation results of two testing images randomly selected from the two data sets. Row 1 and row 2 show the comparison of the detection results: (a) is the original image patches. (b)–(f) are the corresponding results obtained by LoG [1], IRV [7], ITCN [3], SPV [8], and the proposed method. Row 3 and row 4 show the comparison of the segmentation results: (a) is the ground truth. (b)–(f) are the corresponding results obtained by MS, ISO [5], GCC [1], RLS [8], and the proposed method.

To evaluate our algorithm quantitatively, we adopt a set of metrics defined in [14], including false negative rate (FN), false positive rate (FP), over-detection rate (OR), and effective rate (ER). Furthermore, precision (P), recall (R), and F₁ score are also computed. In our experiment, a true positive is defined as a detected seed that is within the circular neighborhood with 8-pixel distance to a ground truth and there is no other seeds within the 12-pixel distance neighborhood. The comparison results are shown in Table 1. It can be observed that the proposed method outperforms other methods in terms of most of the metrics on the two data sets. We also observed that in solving equation (1), increase of the number of nearest neighbors can help the detection performance. Such effect vanishes when more than 100 nearest neighbors are selected. Friedman test is performed on the F₁ scores obtained by the methods under comparison. P–values< 0.05 are observed. The proposed detection algorithm is based on MATLAB and is not yet optimized with respect to efficiency. It takes about 10 minutes to scan an image of size 1072 × 952.

Table 1.

The comparison of the detection performance.

	Brain tumor data							Lung cancer data
Methods	FN	FP	OR	ER	P	R	F1	FN	FP	OR	ER	P	R	F1
LoG [1]	0.15	0.004	0.3	0.8	0.94	0.84	0.89	0.19	0.003	0.13	0.78	0.96	0.80	0.88
IRV [7]	0.15	0.04	0.07	0.76	0.95	0.83	0.88	0.33	0.014	0.21	0.64	0.98	0.66	0.79
ITCN [3]	0.22	0.0005	0.01	0.77	0.99	0.77	0.87	0.31	0.002	0.05	0.68	0.98	0.69	0.81
SPV [8]	0.1	0.02	0.06	0.86	0.98	0.89	0.93	0.18	0.008	0.006	0.79	0.98	0.81	0.89
Ours	0.07	0.0007	0.04	0.92	0.99	0.93	0.96	0.15	0.01	0.06	0.81	0.96	0.85	0.90

Segmentation Performance Analysis

A qualitative comparison of performance between the sDAE and the other four methods, including mean-shift (MS), isoperimetric graph partitioning (ISO) [5], graph-cut and coloring (GCC) [1], and repulsive level set (RLS) [8], is shown in Figure 3. It is clear that the proposed method learns to capture the structure of the cell boundaries. Therefore, the true boundaries can be recovered in the presence of inhomogeneous intensity, and a better segmentation performance is achieved. The quantitative comparison based on the mean and variance of precision (P), recall (R), and F₁ score is shown in Table 2. In addition, Friedman test followed by Bonferroni-Dunn test is conducted on the F₁ scores. P–values are all significantly smaller than 0.05. The Bonferroni-Dunn test shows there does exist significant difference between our methods and the other state of the arts.

Table 2.

The comparison of the segmentation performance.

	Brain tumor data						Lung cancer data
Methods	P.M.	P.V.	R.M.	R.V.	F1 M.	F1. V.	P.M.	P.V.	R.M.	R.V.	F1 M.	F1. V.
MS	0.92	0.02	0.59	0.08	0.66	0.05	0.88	0.01	0.73	0.04	0.77	0.02
ISO [5]	0.71	0.04	0.81	0.03	0.71	0.03	0.75	0.03	0.82	0.025	0.75	0.02
GCC [1]	0.87	0.03	0.77	0.044	0.78	0.024	0.87	0.03	0.73	0.04	0.77	0.02
RLS [8]	0.84	0.01	0.75	0.09	0.74	0.05	0.85	0.013	0.82	0.04	0.81	0.02
Ours	0.86	0.018	0.87	0.01	0.85	0.009	0.86	0.023	0.85	0.012	0.84	0.01

We also explored the interaction between the segmentation performance and the number of training epochs. The result is shown in Figure 4(a). As one can tell that the performance increases as the number of training epochs increases, and it converges after 200 epochs. The number of training samples needed for a reasonable performance depends on the variation of the data. In our setting, it is observed that around 5000 samples are sufficient. The interaction between the performance and the model complexity is shown in Figure 4(b), where the dimension of the second layer is fixed to 200. The proposed segmentation algorithm is very efficient. It takes only 286 seconds for segmenting 2000 cells. This is because it takes only four vector-matrix multiplications using the two-layer sDAE to compute the outputs for one cell. Finally, a set of learned feature maps are shown in Figure 4(c).

Fig. 4.

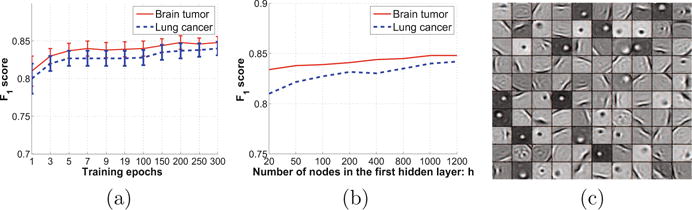
(a) F₁ score as a function of the number of training epochs. (b) F₁ score as a function of the model complexity. (c) A set of learned feature maps in the first hidden layer.

4 Conclusion

In this paper we have proposed an automatic cell detection and segmentation algorithm for pathological images. The detection step exploits sparse reconstruction with trivial templates to handle shape variations and touching cells. The segmentation step applies a sDAE trained with structural labels to remove the non-boundary edges. The proposed algorithm is a general approach that can be adapted to many pathological applications.