Robust neuronal dynamics in premotor cortex during motor planning

Abstract

Neural activity maintains representations that bridge past and future events, often over many seconds. Network models can produce persistent and ramping activity, but the positive feedback that is critical for these slow dynamics can cause sensitivity to perturbations. Here we use electrophysiology and optogenetic perturbations in mouse premotor cortex to probe robustness of persistent neural representations during motor planning. Preparatory activity is remarkably robust to large-scale unilateral silencing: detailed neural dynamics that drive specific future movements were quickly and selectively restored by the network. Selectivity did not recover after bilateral silencing of premotor cortex. Perturbations to one hemisphere are thus corrected by information from the other hemisphere. Corpus callosum bisections demonstrated that premotor cortex hemispheres can maintain preparatory activity independently. Redundancy across selectively coupled modules, as we observed in premotor cortex, is a hallmark of robust control systems. Network models incorporating these principles show robustness that is consistent with data.

Introduction

Neurons in frontal and parietal cortex show slow dynamics, including persistent and ramping activity, related to motor planning ^1-4, action timing ^{5, 6}, working memory ^7-10 and decision making ^11-13. Neurons have intrinsic time constants on the order often milliseconds ¹⁴. Slow dynamics over seconds are presumably an emergent property of neural circuits, likely involving feedback drive ¹⁵ (but see ^{16, 17}).

Network models can produce persistent and ramping activity, including integrators ^{15, 18-21} and trained recurrent networks ^22-24. The amplification that prolongs the model network response may cause fragility to perturbations of activity ²⁵. In contrast, biological systems are typically robust to internal and external perturbations ^26,27.

Controlled transient perturbations can probe the mechanisms underlying the dynamics in neural networks ^{13, 25, 28, 29}. Deviations from normal activity patterns are related to network structure. For example, attractor-like models predict recovery of the attractor state with altered dynamics, whereas chaotic systems diverge over time ²⁵. Comparison of perturbed dynamics and behavior can reveal which elements of the original dynamics are necessary.

We measured behavioral and neural responses after transiently silencing parts of mouse premotor cortex (anterior lateral motor cortex, ALM). ALM neurons in both hemispheres, which are coupled via callosal axons, exhibit persistent preparatory activity that predicts specific movement directions, seconds before the movement ^{3, 30}. We report that preparatory activity is robust to unilateral perturbations. Theoretical analyses suggest that premotor networks are organized into redundant modules.

Preparatory activity in ALM

Mice performed pole location discrimination with their whiskers ^{3, 30} (Fig. 1a). During a subsequent delay epoch (1.3 s - 1.7 s) mice planned the upcoming response. An auditory ‘go’ cue (0.1 s) signaled the beginning of the response epoch, and mice reported pole position by licking one of two ports (posterior→ lick right; anterior→ lick left).

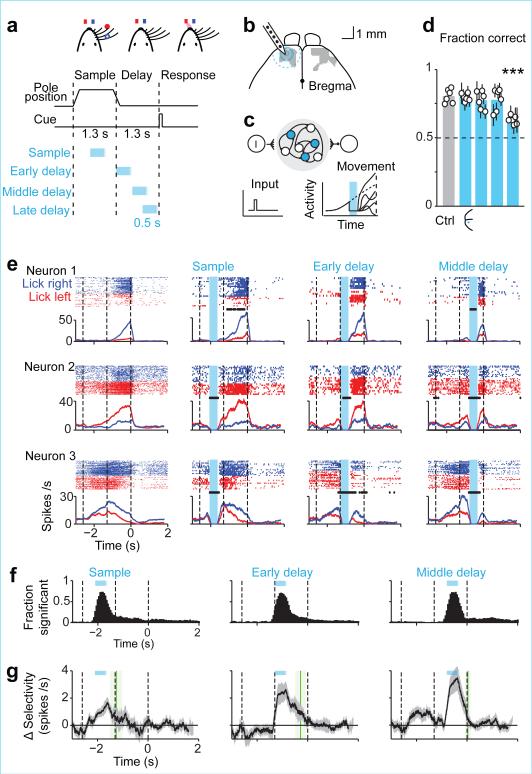
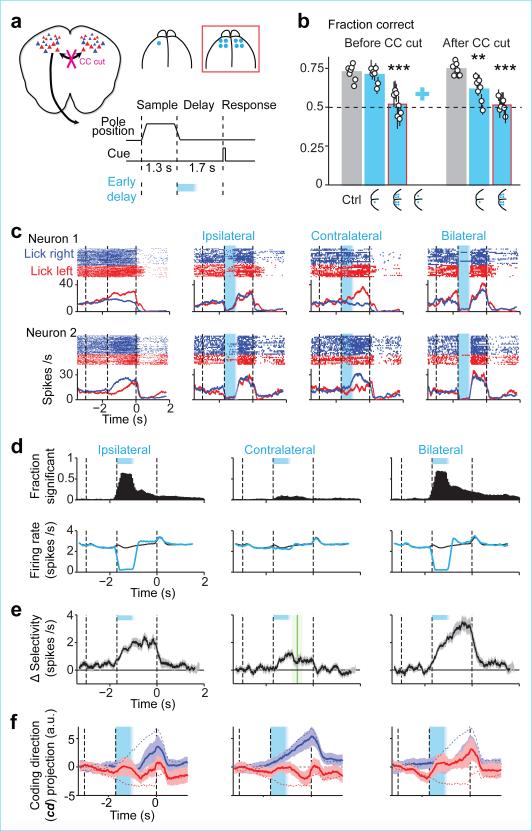
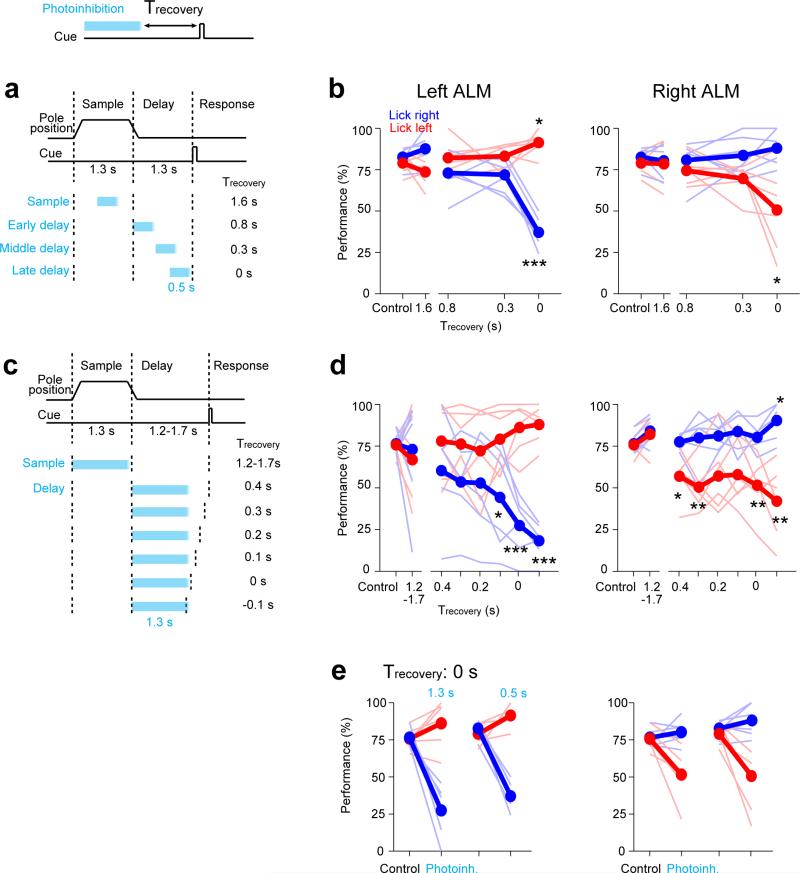
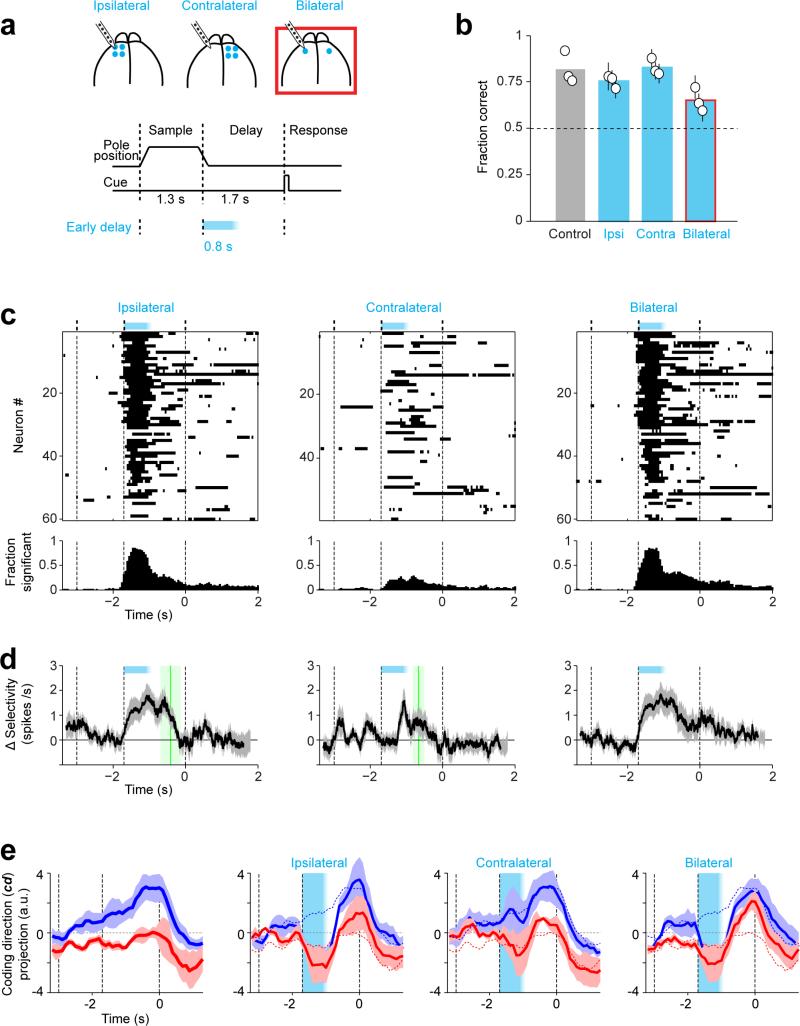
Figure 1. ALM preparatory activity is robust to photoinhibition.

a. Mice discriminate pole location during the sample epoch and respond “lick right” or “lick left” after a delay. Cyan, photoinhibition.

b. Grey, ALM; area that produced behavioral effects with photoinhibition throughout the delay epoch (Methods; Allen Reference Atlas). Cyan, contours of photoinhibition (small, 90% reduction in activity; medium, 80%; large/dashed, 50%).

c. Schematic network models and responses to transient inactivation of subsets of neurons (cyan). Dashed line, unperturbed activity trajectory; solid line, perturbed activity trajectories.

d. Behavioral performance (see timing in a). Bar, mean. Symbols, individual mice (mean ± s.e.m, bootstrap). ***p<0.001, two-tailed t-test against control.

e. Example neurons. Top, spike raster. Bottom, PSTH, averaged over 200 ms. “Lick right” (blue) and “lick left” (red) trials, grouped by instructed movement. Dashed lines, behavioral epochs. Cyan, photoinhibition. Black ticks above PSTH, significant spike rate change (p<0.01, two-tailed t-test).

f. Fraction of neurons with significant spike rate change (n=168, 168, 175). Cyan, photoinhibition.

g. ΔSelectivity from control (mean ± s.e.m. across neurons, bootstrap; selective neurons tested for >3 trials in all conditions, n=55). Green lines, recovery to 80% of control (mean ± s.e.m. bootstrap). Sample, 373±260 ms; early delay, 510±218 ms; late delay, 327±112 ms.

ALM is involved in planning directional licking ^{3, 30, 31}. We recorded single units from left ALM (n = 1012 units from 12 mice; Methods) (Fig. 1b). Most ALM pyramidal neurons distinguished trial types (634/890, p<0.05, t-test; sample epoch, 176/890; delay epoch, 337/890; response epoch, 493/890, Methods) (Extended Data Fig. 1). Selectivity was defined as the spike rate difference between “lick left” and “lick right” trials. Individual ALM neurons exhibited diverse patterns of activity during different task epochs, including persistent activity and ramping activity during the delay epoch, similar to activity seen across frontal cortex ^{1, 2, 4, 5, 8-10, 32, 33}, parietal cortex ^{6, 12}, and subcortical brain areas ³⁴.

Preparatory activity after unilateral silencing

Models of persistent and ramping activity ^{5, 18, 22-24, 35-37} do not recover after transiently silencing subsets of neurons (Fig. 1c; Extended Data Fig. 1f-i). We transiently silenced preparatory activity (Fig. 1a) (‘photoinhibition’, Extended Data Fig. 2; Methods)³. The standard photostimulus was one laser spot³, silencing 58 % of one ALM hemisphere (> 80 % reduction of activity, Methods) (Fig. 1b). Transient (duration, 0.5 s) unilateral photoinhibition of ALM up to the ‘go’ cue (late delay) caused an ipsilateral response bias (n = 5 mice, p < 0.01, two-tailed t-test; Fig. 1d), similar in magnitude to photoinhibition over the entire delay epoch (Extended Data Fig. 3) ^{3, 30}. In contrast, photoinhibition ending at least 0.3 s prior to the ‘go’ cue produced minimal behavioral effects (middle delay, early delay; p > 0.1, two-tailed t-test).

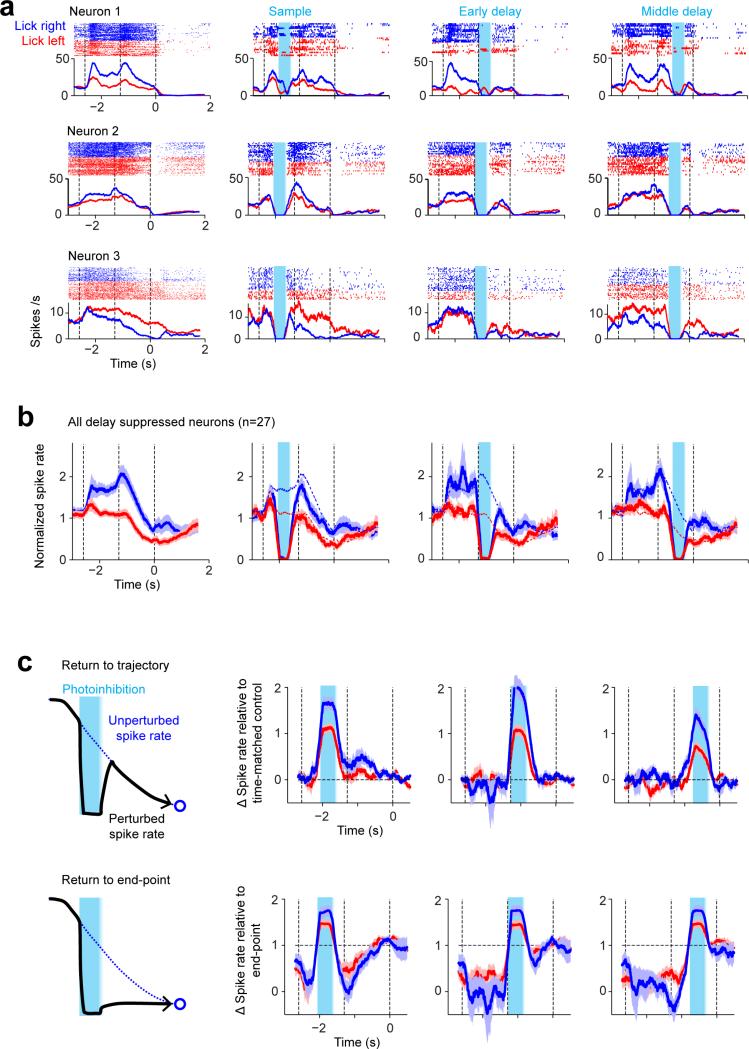
ALM activity was abolished during photoinhibition (Fig. 1e) (n = 6 mice). After photoinhibition offset preparatory activity recovered. ALM neurons that normally exhibited ramping activity during the delay epoch accelerated their ramping after photoinhibition so that activity “caught up” to reach the same level as in unperturbed trials (Fig. 1e, neuron 1 and 2). Recovery was not due to non-specific overshoots in spike rate after photoinhibition (i.e. “rebound”). First, we used photostimuli optimized to minimize rebound ³ (Extended Data Fig. 2c). Second, selectivity also recovered, so that activity reached the appropriate spike rate for each trial type. Finally, neurons that normally did not exhibit increasing ramps during the delay epoch also recovered their activity (Fig. 1e, neuron 3; Extended Data Fig. 4). Within 400 ms after photoinhibition, spike rates became indistinguishable from the unperturbed condition in 90% of the neurons; only 10% of neurons retained a sustained change in spike rate (Fig. 1f). ALM neurons recovered > 80% of their selectivity relative to the unperturbed trials within 514 ms after photoinhibition (Fig. 1g).

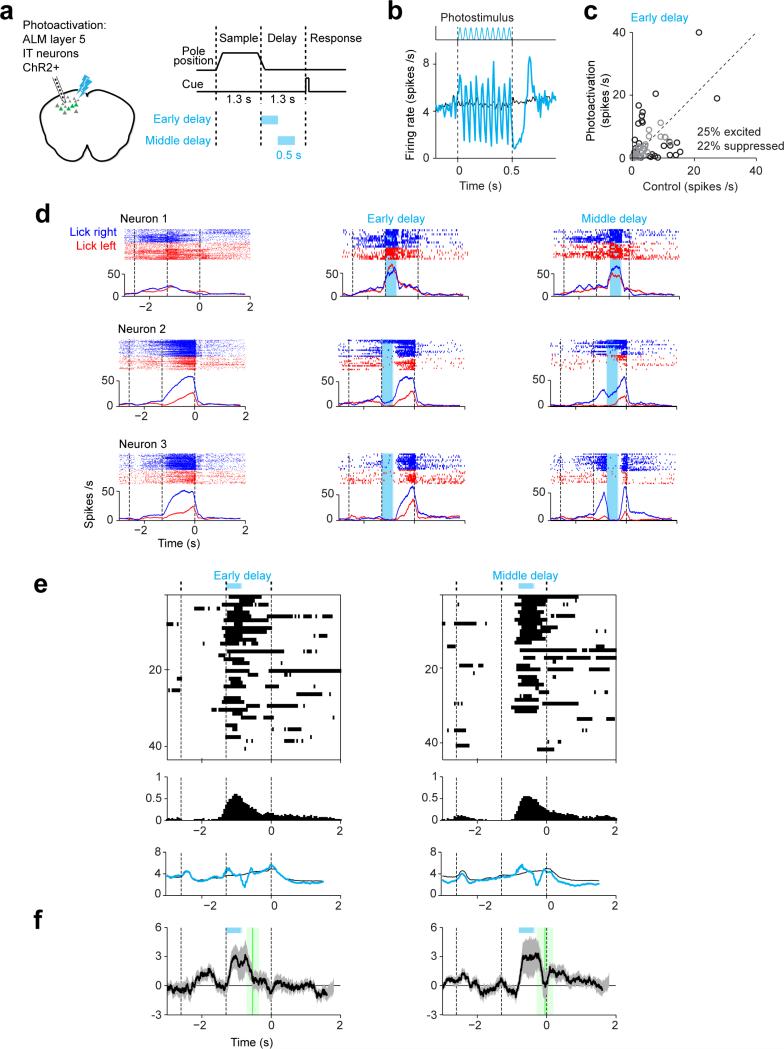
In separate experiments we transiently (500 ms) photostimulated a subset of layer 5 pyramidal neurons (Extended Data Fig. 5) ³⁰. After photostimulus offset, ALM activity and selectivity recovered with a time-course that was similar to recovery after photoinhibition. Thus, ALM premotor activity is robust to large perturbations of activity.

Preparatory activity after bilateral silencing

Perturbed ALM likely inherits preparatory activity from a connected area. ALM is bilaterally connected through the corpus callosum and preparatory activity is found in both hemispheres ³⁰. We tested for coupling between hemispheres by silencing ALM activity either unilaterally or bilaterally (n=13 mice) (Fig. 2a; Methods), using four protocols: 1) unilateral photoinhibition with one laser spot (left or right hemisphere); 2) bilateral photoinhibition using one spot on each side; 3) unilateral photoinhibition using a grid of four spots (1 mm spacing), silencing all of ALM and surrounding regions (Fig. 1b); 4) bilateral photoinhibition using four spots on each side. Photoinhibition (duration 0.8 s or 1.3 s) was deployed during either the sample or early in the delay epoch, ending at least 0.4 s before the response cue (Fig. 2a).

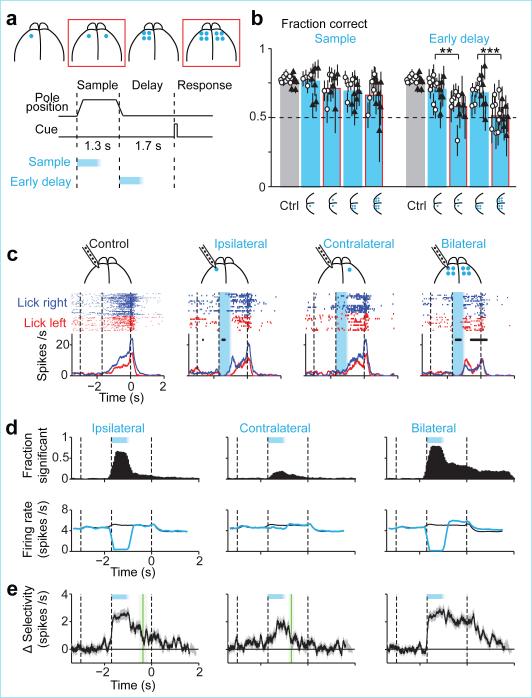
Figure 2. Bilateral photoinhibition disrupts preparatory activity.

a. Unilateral and bilateral (red) photoinhibition.

b. Behavioral performance. Bar, mean. Symbols, individual mice (mean ± s.e.m, bootstrap). Open circle, photoinhibition duration, 800 ms; solid triangle, 1300 ms. **,p<0.01, ***, p<0.001, two-tailed t-test against control.

c. Example ALM neuron. Cyan, photoinhibition.

d. Fraction of neurons with significant spike rate change (n=276, 283, 332). Bottom, average spike rate across the population (black, control; cyan, photoinhibition).

e. Average change in population selectivity from control (n=143). Same as Fig. 1g. Selectivity recovery: ipsilateral, 538±178 ms; contralateral, 192±114 ms; bilateral, no recovery.

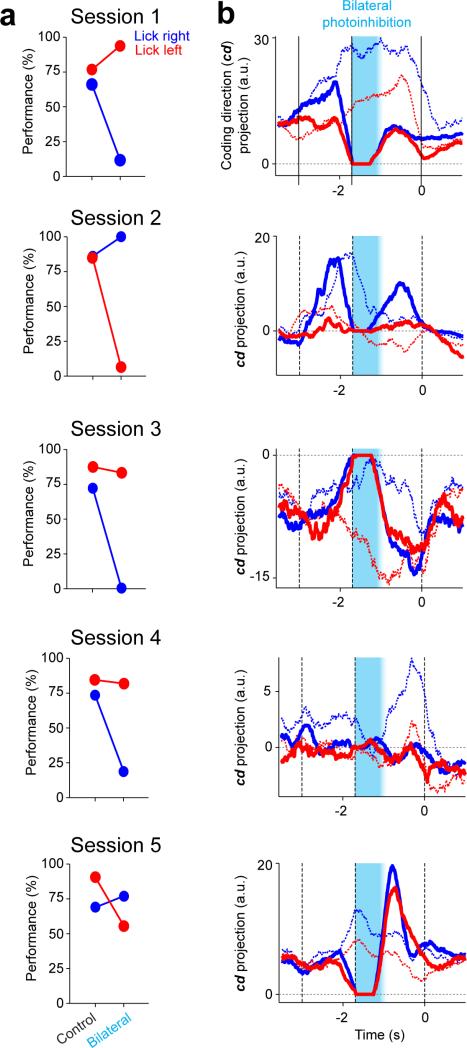
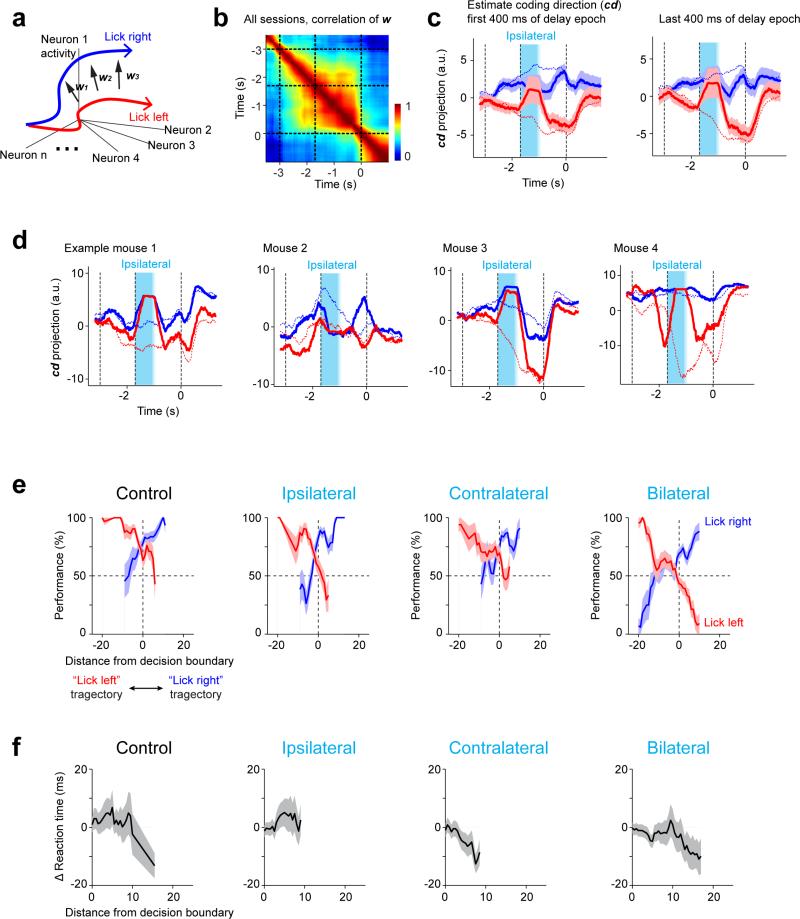
Behavioral performance was only slightly affected after unilateral photoinhibition with a single spot during the early delay epoch (Fig. 2b, 70.3% correct, p = 0.009, two-tailed t-test against control); unilateral photoinhibition with four spots had small additional effect (67.7%, p=0.003). In contrast, using only two spots across both hemispheres caused performance to degrade severely (Fig. 2b, 58.0%, p<0.001; difference from 4 spot unilateral: p<0.05, two-tailed t-test); four spots bilaterally further reduced performance to near chance level (4 laser spots: 51.4%, p<0.001). This implies that the larger effects of bilateral photoinhibition were not simply due to the strength of photoinhibition. Bilateral photoinhibition biased movements inconsistently across mice and sessions (Extended Data Fig. 6a); we use this feature later to explore the relationship between ALM population dynamics and movement.

We next recorded from left ALM during photoinhibition of left ALM (“ipsilateral”, one laser spot), right ALM (“contralateral”, one laser spot), and both hemispheres (four laser spots on each side) (n=7 mice). As before (Fig. 1), spike rate (> 90 %) (Fig. 2c, d) and selectivity (> 80%) (Fig. 2e) recovered 600 ms after ipsilateral perturbation. ALM activity was hardly affected by contralateral photoinhibition (Fig. 2c, d; Extended Data Fig. 2e).

After bilateral photoinhibition neurons recovered their spike rate on average (Fig. 2c, d), but selectivity failed to recover (Fig. 2c-e). Bilateral photoinhibition with one laser spot produced a larger persistent change in selectivity than unilateral photoinhibiton with four laser spots (Extended Data Fig. 7). Recovery of selectivity after unilateral photoinhibition was less robust with larger photoinhibition size (Extended Data Fig. 7e), similar to behavior (Fig. 2b). Robustness to perturbation results from redundancy within the bilateral ALM network.

Robustness along the coding direction

Robust systems maintain critical functions in response to perturbations, whereas non-critical features may remain uncorrected ²⁶. We analyzed population dynamics in “activity space”, where each dimension corresponds to activity of one neuron (6-20 neurons recorded simultaneously; average, 11 neurons; 16 sessions) ³⁸. Preparatory activity for different movements (“lick left” versus “lick right”) corresponded to distinct trajectories in the activity space (Fig. 3a).

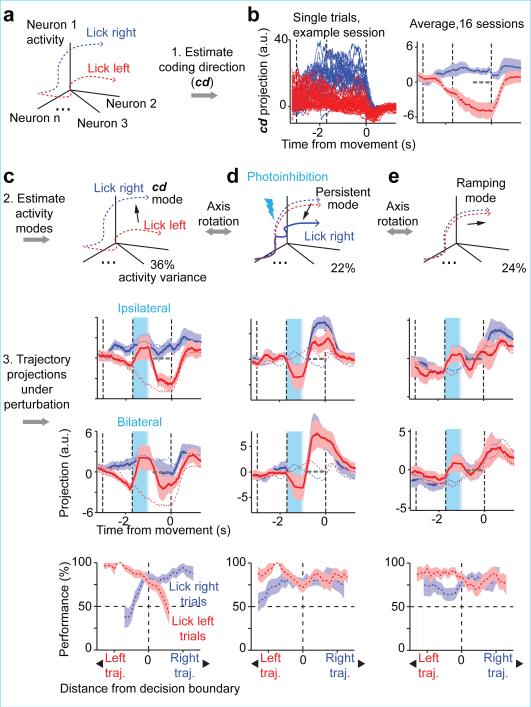
Figure 3. Preparatory activity preferentially recovers along coding dimension in activity space.

a. Schematic, movement-specific trajectories in activity space.

b. Left, activity on correct “lick right” (blue) and “lick left” (red) trials projected onto the coding direction (cd). One session, 12 neurons. Right, average trajectories from all sessions (± s.e.m. bootstrap, Methods). All unperturbed trials (correct and incorrect), grouped by instructed movement. Dotted gray line, decision boundary. Averaging window, 400 ms.

c. Top, illustration of the cd mode. Middle, activity in ipsilateral and bilateral photoinhibition trials projected onto the cd. All perturbed trials (correct and incorrect), grouped by instructed movement. Dashed blue and red lines, means for unperturbed trials (from b). Bottom, behavioral performance in “lick right” (blue) and “lick left” (red) trials as a function of trajectory distance from the decision boundary. Performance was computed by binning along the cd distance. s.e.m. was obtained by bootstrapping the trials in each bin.

d. Same as (c) for activity along persistent mode, which maximizes the difference between perturbed and unperturbed activity at the time of movement onset. This mode does not carry movement-specific information (middle; note that red and blue dashed lines are near each other) and does not predict movement direction (bottom).

e. Same as (c) for population activity along the ramping mode, which explains most of the remaining activity variance (Methods). This mode shows robust ramping but is non-selective (middle) and does not predict movement direction (bottom).

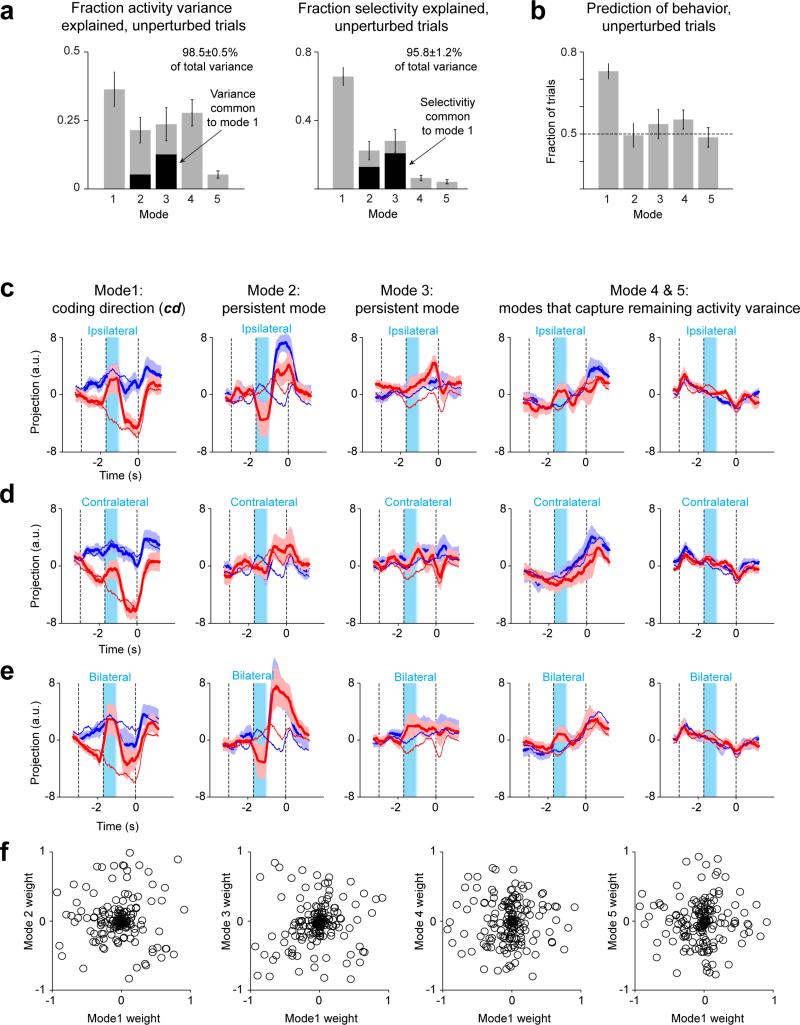
We decomposed activity into several modes. First, we estimated the ‘coding direction’ (cd) along which preparatory activity maximally discriminated upcoming directional licking (Methods, Fig. 3b). After ipsilateral photoinhibition the cd mode recovered to trajectories similar to the unperturbed trials (Fig. 3c; ROC values between trajectories at the end of delay epoch: control, 0.76 ± 0.03; ipsilateral, 0.73 ± 0.02; mean ± s.e.m. across sessions, Methods). Contralateral photoinhibition had little effect (Extended Data Fig. 8; ROC, 0.74 ± 0.03). As expected (Fig. 2), trajectories were permanently altered after bilateral photoinhibition, resulting in small separation between the trajectories for different trial types at the time of movement onset (ROC, 0.58 ± 0.03). We used a decision boundary, on the cd that separated the “lick left” versus “lick right” trials (Methods), to predict upcoming movement on a trial-by-trial basis. Deviations toward the “lick right” trajectory predicted more frequent “lick right” responses and vice versa (Fig. 3, Extended Data Fig. 8). Activity along the cd predicts trial type.

Second, we obtained a mode that maximized sustained effects of ipsilateral perturbations (‘persistent mode’, Fig. 3d). By construction, the persistent mode was altered by the perturbation, up to and beyond movement onset. However, this projection did not discriminate trial type nor predict behavior on control trials.

Third, a mode that maximally captured the remaining activity variance, showed non-selective ramping during the delay epoch, did not predict behavior, and was resistant to unilateral and bilateral perturbations (Fig. 3e; see Extended Data Fig. 8 for a full decomposition of ALM dynamics). This ‘ramping mode’ could reflect non-specific ‘urgency’ ³⁹ driven by a source external to ALM.

Preparatory activity is therefore maintained by ALM populations along specific trajectories in a sub-space of neural activity space. Circuit dynamics are actively restored along behavior-related directions in the activity space, but not along certain non-informative directions ^{33, 40}.

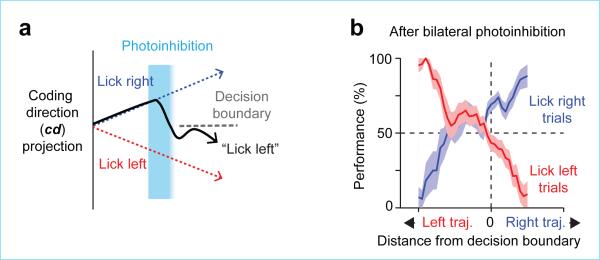
We next examined ALM population activity after bilateral perturbation and its relationship to behavior. Individual trials with a deviation toward the “lick right” trajectory along the cd predicted more frequent “lick right” responses and vice versa (Fig. 4, Extended Data Figs 6b and 9). This analysis shows that even after average selectivity is destroyed by perturbations, ALM population dynamics still dictate upcoming movements.

Figure 4. ALM predicts upcoming movements after bilateral perturbations.

a. Schematic, using preparatory activity projected onto the coding direction (cd) to predict upcoming movement.

b. Behavioral performance as a function of trajectory distance from the decision boundary. Same as Fig. 3c for bilateral photoinhibition trials. See Extended Data Fig. 9 for unilateral photoinhibition trials.

Contralateral input is required for recovery

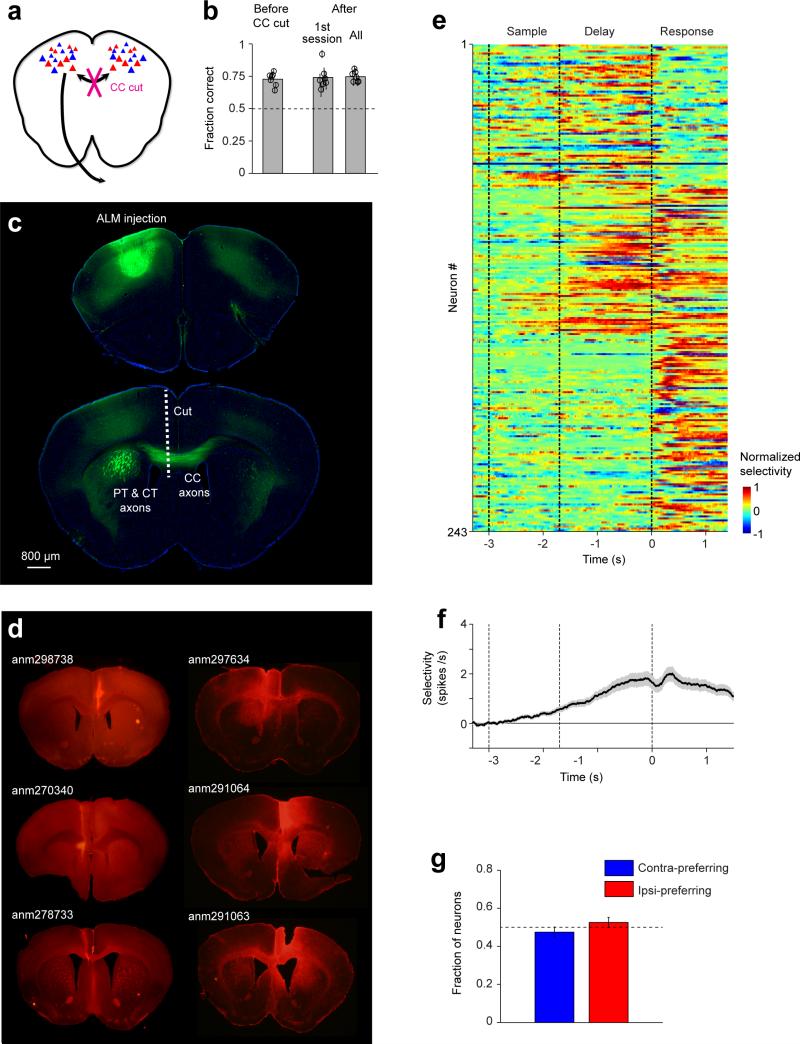
Preparatory activity is coupled across the two ALM hemispheres (Figs 2, 3). The small effect seen on activity with contralateral inhibition (Extended Data Figs 2e, 8d) implies further that ALM hemispheres function as “modules”, maintaining preparatory activity independently ²⁸. After unilateral perturbation, information from the unperturbed side helps recover function of the perturbed side. To directly test the role of contralateral ALM input as the corrective signal, we bisected the ALM corpus callosum (CC) (n=7 mice) (Fig. 5a, Methods), sparing pyramidal tract and corticothalamic axons (Extended Data Fig 10).

Figure 5. Contralateral ALM input is required for recovery of preparatory activity.

a. Left, corpus callosum (CC) bisection. Right, unilateral and bilateral photoinhibition during early delay epochs.

b. Behavioral performance. Bars, mean. Symbols, individual mice (mean ± s.e.m, bootstrap). **,p<0.01, ***, p<0.001, two-tailed t-test against control. Cyan cross, performance for bilateral photoinhibition, 1 spot, in a separate group of control mice (data from Fig. 2b).

c. Two example ALM neurons, after callosotomy.

d. Fraction of neurons with significant spike rate change (n=325, 322, 313). Bottom, average spike rate across the population.

e. Average change in population selectivity from control (n=129). Same as Fig. 2e. Selectivity recovery: ipsilateral, no recovery; contralateral, 217±228 ms; bilateral, no recovery.

f. Population activity in photoinhibition trials projected onto the coding direction (cd). Same as Fig. 3c for ipsilateral, contralateral, and bilateral photoinhibition.

Remarkably, behavioral performance was unaffected (Fig. 5b, control trials, before vs. after callosotomy, p>0.05, two-tailed t-test), with normal performance 17 hours after callosotomy (Extended Data Fig. 10b). However, behavioral performance was now highly sensitive to transient unilateral photoinhibition (Fig 2b, 1 laser spot: p=0.0019, two-tailed t-test against control). There was a significant interaction between callosotomy and unilateral photoinhibition (p=0.0035, repeated measure two-way ANOVA). Behavioral performance after unilateral photoinhibition dropped to the same level as bilateral photoinhibition in control mice (Fig 5b, blue cross).

Preparatory activity in callosotomized mice (n=7 mice) was similar to control mice (Fig. 5c; Extended Data Fig. 10), providing additional evidence that the two ALM hemispheres can maintain preparatory activity independently. After ipsilateral photoinhibition, ALM neurons recovered their average spike rate (Fig. 5c, d), but selectivity failed to recover (Fig. 5e). Selectivity in the cd direction was reduced (Fig. 5f, 16 sessions). Preparatory activity is distributed redundantly across interacting modules in the two ALM hemispheres.

Robust model networks

We compared ALM population dynamics under perturbations (Figs 1, 2) to predictions from network models (Extended Data Fig. 1). After ipsilateral photoinhibition ALM activity rapidly recovered to the unperturbed trajectory (Figs 1, 3). This is inconsistent with attractors with a pair of fixed points (one for each choice condition) ²⁹. Upon release from perturbation these models decay to the final fixed point and do not return to the trajectory (Extended Data Fig. 4c). Integrator models with a continuum of fixed points generate ramping activity by integrating their inputs ^{5, 41,28,37}; these models predict an activity offset compared to the unperturbed trajectories, inconsistent with the data (Extended Data Fig. 1f, g). We also tested randomly connected recurrent networks trained to produce ramping triggered by a transient input ^22-24 (“trained RRNs”). These models failed to recover from perturbations (Extended Data Fig. 1h, i). Overall, all “monolithic” models consisting of one network were unable to explain robustness.

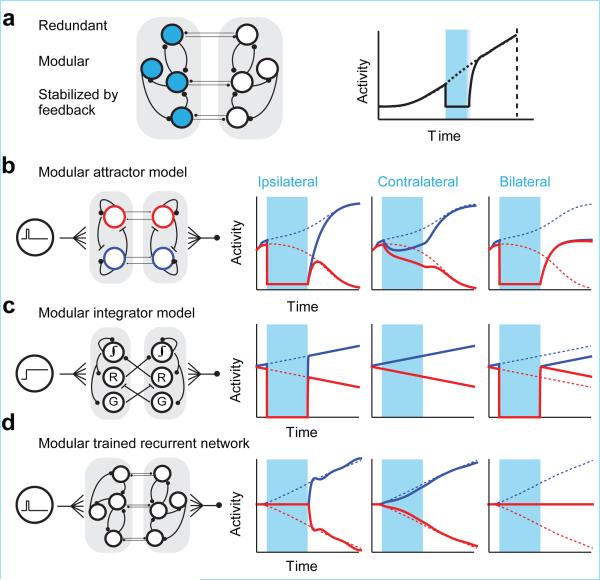
Preparatory activity is distributed across modules in both ALM hemispheres (Figs 2, 3, 5). We therefore explored models with the following organizational principles (Fig. 6a): each module can produce ramping independently; recovery from unilateral perturbation is achieved by specific inter-module connectivity (e.g. commissural axons); the intermodule connections have little net effect during normal operation. Figure 6b shows a model comprised of two identical modules (corresponding to hemispheres), each consisting of a pair of identical units that inhibit each other and excite themselves to produce ramping activity towards one of two fixed points (representing “lick right” or “lick left” movements; Methods). Selective commissural connections restored activity on the other side after unilateral transient silencing (Fig. 6b). When the two sides are silenced, the network drifts to one of the fixed points randomly. Similar schemes allowed the integrator and trained RRN to be adapted into a modular and redundant architecture that is robust to unilateral perturbations (Fig. 6c, d; Methods). Imposing modular architecture upon any monolithic model allowed it to reproduce the stability found in the data, suggesting the modular architecture itself, and not any particular detail of the models, as the key factor in robustness.

Figure 6. Modular network models of premotor dynamics.

a. Schematic, a modular network robust to transient inactivation of one module.

b. Modular attractor model. Neurons with right (blue) and left (red) preferences provide self-excitation and mutual inhibition. Connections between modules involve neurons with similar preference. See Methods for model parameters in b-d.

c. Modular integrator model ¹⁵. Connections between modules restore activity on other side (“recovery” neurons, “R”). Gating neurons (labeled “G”) cancel the inter-module coupling during normal operation.

d. Modular recurrent network trained with FORCE learning ²² to recapitulate single hemisphere perturbation.

Discussion

Our neurophysiological and behavioral analysis of preparatory activity provides three insights. First, preparatory activity is robust to large, transient perturbations of the network (Fig. 1). Second, unperturbed parts of the network remain functional during the perturbation and help the perturbed part of the network recover after the perturbation (Figs 2, 5). Third, premotor cortex preparatory activity recovers in dimensions relevant to behavior and less so in other dimensions (Fig. 3). This implies that premotor networks are organized into functionally segregated modules that interact selectively depending on their mutual state (Fig. 6).

ALM is involved in both planning and driving movements³⁰. Consistent with this view, unilateral photoinhibition of ALM late in the delay epoch abolished the contralateral motor command, resulting in ipsilateral bias (Fig. 1, Extended Data Fig. 3); furthermore, bilateral photoinhibition during the early delay epoch abolished the motor plan and scrambled future movements (Fig. 2). Previous optogenetic inactivation studies focusing on related brain areas have interpreted a lack of effect of transient inactivation as a lack of role in behavior^{13, 42}. Our results imply that redundancy across a distributed network could mask possible causal roles in optogenetics experiments.

Modular architecture and functional redundancy are key components of robust engineered systems ²⁶. Similarly, our data and previous experiments ^{3, 30} imply that the cortical networks maintaining motor plans are organized in a redundant and modular fashion. When ALM is silenced in one hemisphere, preparatory activity in the other hemisphere is weakly affected (Fig. 2, Extended Data Figs 2e, 8d). However, after the perturbation, activity in the unperturbed hemisphere is critical to restore the perturbed preparatory activity in the opposite hemisphere. Preparatory activity is thus distributed in a redundant fashion across functional modules that can both operate independently and correct each other. The cortical networks involved in working memory could be organized in a similar manner ^7-10. It is likely that modularity and redundancy operate in circuits contained in one hemisphere, perhaps even spatially interdigitated.

The responses of ALM neurons to perturbations can be decomposed into three types of dynamics: modes that are rapidly restored after unilateral perturbation; modes that remain perturbed; modes that are restored both for unilateral and bilateral perturbation and are thus likely to be driven externally. Only behavior-relevant modes recovered quickly. ALM responses to perturbations resembles robust systems, where critical state variables are particularly stiff ²⁶. Selective stability of neural dynamics supports the idea that behavior-related activity comprises only a low-dimensional subspace of neural activity space ^{33, 40}, constrained by the structure of neural circuits ⁴³. Our findings place constraints on the circuit architectures that underlie memory-related cortical activity and suggest general principles of robust system control in the brain.

Methods

Mice

This study is based on data from 33 mice (both males and females, age > P60). 10 VGAT-ChR2-EYFP mice (Jackson laboratory, JAX Stock#014548) and 9 PV-ires-cre ⁴⁴ crossed to Rosa26-LSL-ReaChR, red-shifted channel rhodopsin reporter mice (JAX 24846) ⁴⁵, were used for photoinhibition behavior experiments. A subset of these mice (5 VGAT-ChR2-EYFP mice, 7 PV × ReaChR mice) were used for simultaneous electrophysiology and behavior. 7 mice (6 VGAT-ChR2-EYFP, 1 PV × ReaChR mice were used for) were used for the callosotomy experiment. 2 Tlx_PL56-cre (MMRRC 036547) ⁴⁶ crossed to Ai32 (Rosa26-ChR2 reporter mice, JAX Stock#012569) ⁴⁷ mice were used for photoactivation experiment. 2 untrained VGAT-ChR2-EYFP mice and 2 untrained PV × ReaChR mice were used to characterize the photoinhibition in ALM. 1 Tlx_PL56-cre mouse was used for anatomical characterization of the ALM axonal projection pattern.

All procedures were in accordance with protocols approved by the Janelia Institutional Animal Care and Use Committee. Mice were housed in a 12:12 reverse light:dark cycle and tested during the dark phase. On days not tested, mice received 1 mL of water. On other days, mice were tested in experimental sessions lasting 1 to 2 hours where they received all their water (range, 0.5 to 2 mL). If mice did not maintain a stable body weight, they received supplementary water ⁴⁸. All surgical procedures were carried out aseptically under 1-2 % isofluorane anesthesia. Buprenorphine HCl (0.1 mg/kg, intraperitoneal injection; Bedford Laboratories) was used for postoperative analgesia. Ketoprofen (5 mg/kg, subcutaneous injection; Fort Dodge Animal Health) was used at the time of surgery and postoperatively to reduce inflammation. After the surgery, mice were allowed to recover for at least three days with free access to water before water restriction.

Behavior and surgery

Mice were prepared for photoinhibition and electrophysiology with a clear-skull cap and a headpost ³. The scalp and periosteum over the dorsal surface of the skull were removed. A layer of cyanoacrylate adhesive (Krazy glue, Elmer's Products Inc) was directly applied to the intact skull. A custom made headpost ⁴⁸ was placed on the skull with its anterior edge aligned with the suture lambda (approximately over cerebellum) and cemented in place with clear dental acrylic (Lang Dental Jet Repair Acrylic; Part# 1223-clear). A thin layer of clear dental acrylic was applied over the cyanoacrylate adhesive covering the entire exposed skull, followed by a thin layer of clear nail polish (Electron Microscopy Sciences, Part# 72180).

The behavioral task and training have been described ^{3, 48}. The stimulus was a metal pin (0.9 mm in diameter), presented at one of two possible positions (Fig. 1a). The two pole positions were 4.29 mm apart along the anterior-posterior axis (approximately 40 deg of whisking angle) and were constant across sessions. The posterior pole position was 5 mm from the whisker pad. A two-spout lickport (4.5 mm between spouts) was used to record answer licks and deliver water rewards.

At the beginning of each trial, the vertical pole moved into reach of the whiskers (0.2 s travel time), where it remained for 1 second, after which it was retracted (retraction time 0.2 s). The sample epoch is defined as the time between the pole movement onset to 0.1 s after the pole retraction onset (sample epoch, 1.3 s, Fig. 1a). Mice touched the object at both pole positions, typically with a different set of whiskers. The delay epoch (durations, 1.2-1.7 s) followed the sample epoch. An auditory ‘go’ cue indicated the end of the delay epoch (pure tone, 3.4 kHz, 0.1 s duration). Licking early during the trial was punished by a loud alarm sound (siren buzzer, 0.05 s duration), followed by a brief timeout (1-1.2 s). Licking the correct lickport after the ‘go’ cue led to a liquid reward (3 μL). Licking the incorrect lickport triggered a timeout (2-5 s). Trials in which mice did not lick within a 1.5 second window after the ‘go’ cue were rare and typically occurred at the end of a session.

Photoinhibition

Light from a 473 nm laser (Laser Quantum, Part# Gem 473) or a 594 nm laser (Cobolt Inc., Part# Colbolt Mambo 100) was controlled by an acousto-optical modulator (AOM; Quanta Tech) and a shutter (Vincent Associates). Photoinhibition of ALM was performed through the clear-skull cap implant by directing the laser over the skull (beam diameter: 400 μm at 4σ). The light transmission through the intact skull is 50% ³. Photoinhibition was deployed on 25% of the behavioral trials during behavioral testing. To prevent the mice from distinguishing photoinhibition trials from control trials using visual cues, a ‘masking flash’ (40 1ms pulses at 10 Hz) was delivered using 470 nm or 591 nm LEDs (Luxeon Star) near the eyes of the mice. The masking flash began as the pole started to move and continued through the end of photoinhibition. For silencing we stimulated cortical GABAergic neurons in VGAT-ChR2-EYFP mice, or parvalbumin-positive interneurons in PV-ires-cre mice crossed to reporter mice expressing ReaChR ⁴⁵. The two methods resulted in similar photoinhibition (Extended Data Fig. 2). The photoinhibition silenced 90% of spikes (Extended Data Fig. 2b) in a cortical area of 1mm radius (at half-max) through all cortical layers ³ (Extended Data Fig. 2d). To minimize rebound excitation after photoinhibition offset, we linearly ramped down the laser power (100 or 200 ms). This photostimulus was empirically determined ³ to produce robust photoinhibition with minimal rebound (Extended Data Fig 2c).

The duration of the delay epoch varied to accommodate different photoinhibition conditions. In the unilateral photoinhibition experiment (Fig. 1, Extended Data Fig. 2a), a fixed 1.3 s delay epoch was used. We used a 40 Hz photostimulus with a sinusoidal temporal profile (1.5 mW average power) and a 100 ms linear ramp. We photoinhibited for 0.5 s, including the 100 ms ramp, during different task epochs (Fig. 1a). Photostimuli ended 1.6 s (sample), 0.8 s (early delay), 0.3 s (late delay), or 0 s (before cue) before the ‘go’ cue. We also tested unilateral photoinhibition of longer durations in separate experiments (1.3 s including a 100 ms ramp, Extended Data Fig. 3). To accommodate the longer photoinhibition, we randomly varied the duration of the delay epoch from 1.2 s to 1.7 s in 0.1 s increments. This resulted in photoinhibition that terminated at different times before the ‘go’ cue.

In the bilateral photoinhibition experiment (Fig. 2), a fixed 1.7 s delay epoch was used to allow more time for neuronal activity to recovery after photoinhibition. We photoinhibited for 0.8 s, including a 200 ms ramp during offset, either at the beginning of the sample epoch or at the beginning of the delay epoch. To photoinhibit single cortical locations (Fig. 2a, 1 laser spot), we used the 40 Hz sinusoidal photostimulus (1.5mW average power). To photoinhibit multiple cortical locations (Fig. 2a, multiple laser spots), we used a constant photostimulus and a scanning galvo (GVSM002, Thorlabs), which stepped the laser beam sequentially through the photoinhibition sites at the rate of 1 step per 5ms (step time: < 4.8 ms; measured using a photodiode). Peak power was adjusted depending on the number of cortical locations to achieve 1.5 mW average power per location. The photoinhibition during scanning was similar to the standard condition (Extended Data Fig. 2).

To estimate the proportion of ALM silenced by photoinhibition, we estimated the boundaries of ALM using photoinhibition behavioral data from ³. ALM was defined as the area where photoinhibition over the entire delay epoch produced significant behavioral effects. ALM boundaries (Fig. 1b, grey area) were derived by deconvolving the area producing significant behavioral effects with the point-spread function of the photoinhibition method (Extended Data Fig. 2d) ³. At 80% activity reduction, photoinhibition with 1 laser spot covered 58% of ALM in one hemisphere (Fig. 1b).

Photoactivation

For photoactivation we stimulated layer 5 intratelencephalic neurons in Tlx_PL56-cre mice ⁴⁶ crossed to reporter mice expressing ChR2 (Ai32) ³⁰. The delay epoch was 1.3 s long. The photostimulus was a 20 Hz sinusoid (0.53 mW average power) applied during different task epochs (Extended Data Fig. 5b). Photoactivation was deployed on 40% of the behavioral trials during electrophysiology.

Electrophysiology

A small craniotomy (diameter, 1 mm) was made over left ALM (centered on 2.5 mm anterior, 1.5 mm lateral) one day prior to the recording session ³. Extracellular spikes were recorded using NeuroNexus silicon probes (Part# A4×8-5mm-100-200-177). The 32 channel voltage signals were multiplexed, digitized by a PCI6133 board at 312.5 kHz (National instrument) at 14 bit, demultiplexed (sampling at 19531.25Hz) and stored for offline analysis. Three to seven recordings were made from each craniotomy. To minimize brain movement, a drop of silicone gel (3-4680, Dow Corning, Midland, MI) was applied over the craniotomy after the electrode was in the tissue. The tissue was allowed to settle for several minutes before the recording started.

During electrophysiology, photoinhibition was deployed on 40% of the trials to obtain a larger number of trials per condition. Three photoinhibition conditions were tested during each recording session. In the unilateral photoinhibition experiment (Fig. 1, Extended Data Fig. 2a), photoinhibition during sample, early delay, and late delay epoch were tested. In the bilateral photoinhibition experiment (Fig. 2, Extended Data Fig. 2a), photoinhibition of left ALM (“ipsilateral”, 1 laser spot), right ALM (“contralateral”, 1 laser spot), and both hemispheres (4 laser spot) were tested. In separate experiments (Extended Data Figs 2a and 7), ipsilateral photoinhibition with 4 laser spots, contralateral photoinhibition with 4 laser spots, and bilateral photoinhibition with 1 laser spot were tested.

Callosotomy

The placement of the corpus callosum (CC) cut was determined based on ALM axonal projection patterns. AAV2/1.CAG.EGFP (Addgene, plasmid 28014) was injected into one hemisphere of ALM (Extended Data Fig. 10c). The injection coordinate was 2.5 mm anterior to bregma and 1.5 mm lateral to the midline. The injection was made through the thinned skull using a custom volumetric injection system. Glass pipettes (Drummond) were pulled and beveled to a sharp tip (outer diameter of 30 μm). Pipettes were back-filled with mineral oil and front-loaded with viral suspension immediately before injection. 50 nl volumes were injected 500 and 800 μm deep. Two weeks post injection, mice were perfused and their brains were sectioned (50 μm) and processed using standard fluorescent immunohistochemical techniques. Confocal images were acquired on a Zeiss microscope, a 10× objective and a Hamamatsu Orca Flash 4 camera ⁴⁶.

ALM axons extend caudally from the injection site. CC axons separate from PT and CT axons approximately 1.2 mm anterior to bregma. ALM CC axons were confined to the anterior regions of CC and were densest around 1 mm from bregma (Extended Data Fig 10c). CC axon bisection was made through an elongated craniotomy either over the left (3 mice) or right (4 mice) hemisphere. A 3.5 mm-deep cut was made using a micro knife (Fine Science Tools, Part# 10318-14) mounted on a micromanipulator (Sutter Instrument). The cut was 0.5 mm from the midline and was at a slight angle to avoid the PT and CT axons (Extended Data Fig 10d). The cut extended from 1.5 mm anterior to bregma to 1 mm posterior. Care was taken to avoid damaging the superior sagittal sinus. In the same surgery, a second craniotomy was made over left ALM for electrophysiology. Approximately 17 hours after the surgery mice were tested in behavioral experiments (Fig. 5, Extended Data Fig 10). Mice were tested in daily recording sessions for 5-7 days after the callosotomy. Mice were perfused immediately after the last recording session and the brains were processed for histology (Extended Data Fig 10d). In a subset of the mice, brain sections were stained for GFAP (mouse; Sigma G3893, 1:2,000 dilution) (Extended Data Fig. 10d).

Behavioral data analysis

Performance was computed as the fraction of correct reports, excluding “lick early” trials (Figs 1-5). Chance performance was 50 %. We also separately computed the performance for “lick right” and “lick left” trials (Figs 3, 4; Extended Data Figs 3, 6, 9). Behavioral effects of photoinhibition were quantified by comparing the performance under photoinhibition with control performance using two-tailed t-test (Figs 1, 2, 5; Extended Data Fig. 3).

Electrophysiology data analysis

The extracellular recording traces were band-pass filtered (300-6 kHz). Events that exceeded an amplitude threshold (4 standard deviations of the background) were subjected to manual spike sorting to extract single units ³. 1012 single units were recorded during behavior across 58 recording sessions (20 sessions of unilateral experiments, Fig. 1; 38 sessions of bilateral experiments, Fig. 2, Extended Data Fig. 7). Spike widths were computed as the trough-to-peak interval in the mean spike waveform. Units with spike width < 0.35 ms were defined as fast-spiking (FS) neurons (72/1012) and units with spike widths > 0.45 ms as putative pyramidal neurons (890/1012). Units with intermediate values (0.35 - 0.45 ms, 50/1012) were excluded. This classification was previously verified by optogenetic tagging of GABAergic neurons ³. We concentrated our analyses on the putative pyramidal neurons.

Neurons were tested for significant trial-type selectivity during the sample, delay, or response epochs, using the spike counts from the “lick left” and “lick right” trials (two-tailed t-test, p<0.05). Neurons that significantly differentiated trial types during any one of the trial epochs were deemed “selective” (634/890). To compute selectivity (Figs 1, 2, 5, and Extended Data Fig. 1), we first determined each neuron's preferred trial type using spike counts from a subset of the trials (10 trials), selectivity is calculated as the spike rate difference between the trial types on the remaining data. Standard errors of the mean were obtained by bootstrap across neurons.

To quantify the effect of photoinhibition on individual ALM neuron spike rates (Figs 1, 2, 5, and Extended Data Figs 5, 7), we used a two-tailed t-test on spike counts binned in 400 ms windows (control vs. photoinhibition). Spike counts from “lick right” trials and “lick left” trials were pooled. Spike rates were tested at different times during the task (in 50 ms time steps) and significance was reported for p < 0.01.

Quantification of the effects of perturbations on movement selectivity was complicated by the fact that ALM selectivity is coupled to upcoming movements. Grouping trials by the final movement (e.g. using only correct “lick right” trials) to compute selectivity would miss the trials in which photoinhibition caused the mice to switch future movements, thus underestimating the effects of photoinhibition on selectivity. We therefore used all trials (correct and incorrect) to compute selectivity when quantifying selectivity changes caused by photoinhibition (Figs 1, 2, 5, and Extended Data Figs 5, 7). Selectivity change was the selectivity difference between control and photoinhibition trials. To quantify the recovery time course of selectivity after photoinhibition, we looked for the first time bin when selectivity on photoinhibition trials reached 80 % of the control selectivity (Figs 1g, 2e, 5e, and Extended Data Figs 5, 7, green lines). Standard errors of the mean were obtained by bootstrap across neurons.

Analysis of population dynamics in the activity space

To analyze the relationship between ALM population activity and upcoming movements, we restricted analysis to the recording sessions from the bilateral photoinhibition experiments (Fig. 2) with > 5 neurons recorded simultaneously for > 5 trials per condition (16/38 sessions, Figs 3, 4, and Extended Data Figs 6, 8, 9). For a population of n neurons, we found an n × 1 vector, in the n dimensional activity space that maximally separated the response vectors in “lick right” trials and “lick left” trials, we term this vector the “coding direction“ (cd).

Average spike counts were computed in a 400 ms window in 10 ms steps. For each movement direction (“lick right” and “lick left”, correct trials only) we computed the average spike counts x̄_{lick right} and x̄_{lick left}, n × 1 response vectors that described the population response at that time. During the sample and delay epochs the direction of the difference in the mean response vectors, w_t = x̄_{lick right} – x̄_{lick left}, was stable (correlation of w_t's between late sample epoch vs. late delay epoch, 0.61 ± 0.05; Extended Data Fig. 9b). We averaged the w_t's from the sample and delay epochs to obtain cd. Because our estimate of the covariance was noisy, the cd gave better discrimination than the linear discrimant vector (cd divided by the within-group covariance).

The projection along the cd captured 65.6±5.1% of the population selectivity for “lick left” and “lick right” trials over the sample and delay epochs (root mean square, RMS, of the spike rate difference between “lick right” trials and “lick left” trials), and 36.4±6.3% of the total variance in ALM task-related activity (Extended Data Fig. 8a). Activity variance was quantified as the RMS of the baseline subtracted activity over the sample and delay epoch.

To project the ALM population activity along the cd we used independent control and perturbation trials from the trials used to compute the cd. For each trial we computed the spike counts for each neuron, x (n × 1), at each time point. The projected trajectories in Fig. 3, 5 and Extended Data Figs 6, 7, 8, and 9 were obtained as cd^T x. Both correct and incorrect trials were used to compute the projected trajectries, grouped by the instructed movements. To quantify the separation between trajectories on “lick right” and “lick left” trials, we computed ROC values using cd^T x at the end of the delay epoch for each session. To average trajectories across multiple behavioral sessions (Fig. 3, 5 and Extended Data Figs 7, 8, and 9), we first offset the trajectories for a particularly session by subtracting the mean cd^T x across all trials and time points in that session. This removed fluctuations in mean activity from session to session. The offsets were computed using the independent control trials that were used to calculate the cd. Standard errors of the mean was obtained by bootstrapping individual sessions.

To predict upcoming movements using ALM responses projected onto the cd (Fig. 3, 4 and Extended Data Fig. 8b, 9), we used the response vector x from the last time bin before the ‘go’ cue (last 400 ms of the delay epoch). For each session, we computed a decision boundary to best separate the projected responses, cd^T x, from “lick right” and “lick left” trials:

$$decisionboundary=\frac{\langle {\mathit{cd}}^T{\mathit{x}}_{lickright}\rangle ∕{\sigma }_{lickright}^2+\langle {\mathit{cd}}^T{\mathit{x}}_{lickleft}\rangle ∕{\sigma }_{lickleft}^2}{1∕{\sigma }_{lickright}^2+1∕{\sigma }_{lickleft}^2}$$

σ² is the variance of the projected responses cd^T x across multiple “lick right” or “lick left” trials. Both the cd and decision boundary were computed using independent control trials and separate control and photoinhibtion trials were used to predict performance. Data from multiple sessions were pooled in Fig. 3, 4, and Extended Data Fig. 9.

We decomposed ALM activity into three forms of dynamics (Fig. 3; Extended Data Fig. 8). The modes were computed using a subset of control trials (correct trials only) and ipsilateral perturbation trials. The projections in the figures are for independent control trials and perturbation trials. The projection along the cd (mode 1) captured the movement selectivity in activity. The ‘persistent mode’ (mode 2) was the difference in the mean response vectors between ipsilateral perturbed and unperturbed “lick right” trials at the ‘go’ cue. Mode 3 was the mean response vectors between ipsilateral perturbed and unperturbed “lick left” trials at the ‘go’ cue, further rotated using Gram-Schmidt Process to be orthogonal to Mode 2. We did not orthogonalize the ‘cd mode’ and ‘persistent mode’, so that any potential selectivity common to these modes was not removed. There was a small overlap between mode 1 and modes 2-3 (the activity variance and selectivity shared by modes 1-3 are quantified in Extended Data Figure 8a). Mode 2 & 3 describe the vast majority of the persistent changes in activity after ipsilateral perturbations.

Two additional modes (4 & 5) captured the remaining activity variance. We first found eigenvectors of the population activity matrix using singular value decomposition. The data for the SVD was an n × t matrix, consisting of the baseline-subtracted PSTHs for n neurons, with the “lick right” and “lick left” trials concatenated together (t time bins). The first two eigenvectors (n × 1) were rotated using the Gram-Schmidt Process to be orthogonal to modes 1-3, yielding modes 4 & 5. Mode 1-5 together explained 98.5±0.5% of the total variance of task-related activity and 95.8±1.2% of population selectivity over the sample and delay epochs. To predict upcoming movements using the projected responses on peristent mode and ramping mode (Fig. 3), we computed decision boundaries on the projected responses using the same procedures as for the cd mode.

Modeling and simulation

To model those features of ALM dynamics relevant for the purposes of this study, we constructed neural networks that have the ability to produce slow ramps of preparatory activity with transient or constant input. Our models included explicit integrators (Fig. 6c; Extended Data Fig. 1f, g), recurrent neural networks trained to produce ramping output (Fig. 6d; Extended Data Fig. 2h, i), and a more phenomenological attractor model (Fig. 6b). Simulating the dynamics of the models, we compared their responses to the response of ALM to transient silencing.

All networks were simulated for two seconds. Photoinhibition was simulated by holding the activity of half of the neurons in each network at zero for times 0.2 s < t < 1.0 s. Activity of the i^th neuron r_i(t) was governed by the equation:

$$\tau \frac{d{r}_i\left(t\right)}{dt}=-r_i\left(t\right)+\sum _{j=1}^N{W}_{i,j}f\left(r_j\left(t\right)\right)+I_i\left(t\right)+T_i\left(t\right)+{\xi }_i\left(t\right)$$

The cellular time constant, τ, the connectivity matrix, W, and the synaptic non-linearity, f(x), were chosen differently for each model class in the subsections below. N is the number of neurons, T_i(t)+ξ_i(t) is a tonic and non-selective input, and ξ_i(t) is Gaussian random noise. In all simulations networks received either transient (0.05 s < t < 0.1 s) or persistent (0.1 s< t < 1.9 s) sensory inputs I_i(t), unless stated otherwise. The specifics of each model are described below.

Modular attractor (Fig. 6b)

Two identical two-neuron unilateral attractor network modules were constructed so that each neuron excited itself with weight 0.5235 and inhibited the other neuron in the same module with −0.5235. Each neuron was reciprocally connected with one partner from the other module with strength 0.3. τ = 100 ms and f(x) = g (x) – g(0) where $g\left(x\right)=\frac{1.4}{1+e^{-(x-.5)∕.3}}$. Transient external input I_i (t) with amplitude 0.1 was provided to either the right preferring (blue, Fig. 6b) or left preferring (red, Fig. 6b) neurons depending on the trial type. All neurons received a non-selective tonic input T_i(t) with amplitude 0.5 and noise ξ_i(t) with variance 0.01.

Modular integrator (Fig. 6c)

This network consisted of two modules with inter-module connections tuned to produce robustness against unilateral inactivations. Each module consisted of four neurons: Right preferring integrator neuron (1); left preferring integrator neuron (2); recovery neuron (3); inhibitory neuron (4). Integration was produced by positive feedback achieved through mutual inhibition between neurons 1 and 2 with strength −1. This integrating pair is represented schematically by one circle labeled “∫” in Figure 6c. The network received constant sensory input I_i (t) with amplitude 0.04 to the right preferring neuron and −0.04 to the left preferring neuron during “lick right” trials. The signs of the inputs were flipped for “lick left” trials. In addition, each integrator neuron received non-selective tonic input T_i(t) with amplitude 40.0 to establish baseline activity at 20.0.

To establish robustness the two modules were coupled via the recovery (labeled “R”; Fig. 6C) and inhibitory (labeled “I”; Fig. 6C) neurons. These neurons receive positive feedback from the right preferring neuron and negative feedback from the left preferring neuron. The role of the recovery neuron is to restore the activity of the contralateral integrator neurons upon removal of inhibition. This restorative connection has strength 0.5. To avoid excessive feedback during normal function the recovery neuron is strongly inhibited by the inhibitory neuron with strength − 6.0. The full connectivity matrix is shown below. For one module, indices 1-4 correspond to the right preferring, left preferring, recovery and inhibitory neurons. Indices 5-8 are part of the second module. For example, element W_1,7 is the connection from the recovery neuron in module 2 (neuron 7) onto the right preferring neuron of module 1 (neuron 1).

$$W=\left(\begin{array}{cccccccc}\hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0.5& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -0.5& \hfill 0\\ \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -6\\ \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0.5& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -0.5& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -6& \hfill 1& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0\end{array}\right)$$

The time constant of this network was τ = 10 ms. Synapses in this network were linear, but firing rates were restricted to be positive. ξ_i(t)=0 in this network.

Modular tamed chaos (Fig. 6d)

FORCE training ²² was performed on a network with τ = 200 ms, f (x) = tanh(x), N = 400. Each neuron received a transient input during 0.05 s < t < 0.1 s with amplitude drawn from a Gaussian distribution with variance equal to 1. The inputs for “lick left” and “lick right” trials had the same amplitude, but opposite sign. Prior to training the connectivity matrix was sparse (connection probability p = 0.1). Non-zero connections were chosen from a Gaussian random distribution with variance $\frac{{1.5}^2}{pN}$. The gain factor 1.5 was chosen to produce chaotic activity ⁴⁹. Training was performed for 30 iterations.

The activity of the output units z was given by $z\left(t\right)={\sum }_{n=1}^N{w}_{out,n}{r}_n\left(t\right)$. The network consisted of two modules which were each trained independently to produce ramping activity at their output. The inter-modular connections were trained in the presence of transient unilateral inactivations, so that the output of the inactivated side would recover upon removal of inactivation and the output of the other side would be minimally affected by the inactivation. The network did not receive tonic input and ξ_i(t)=0.

Extended Data

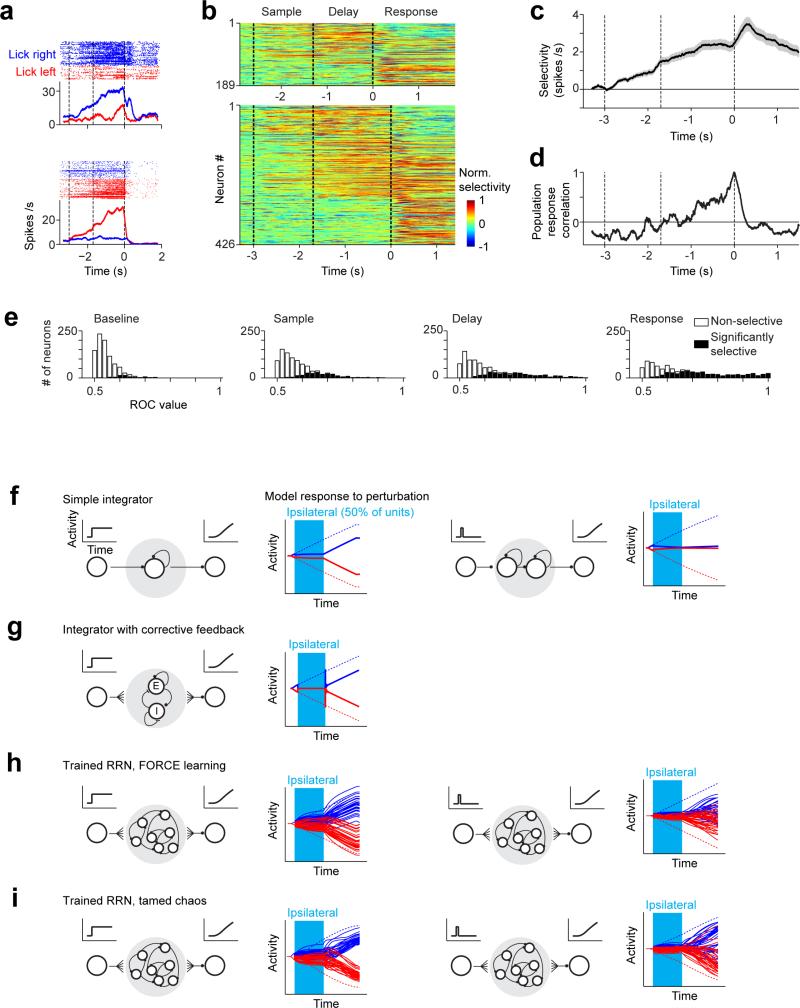
Extended Data Figure 1. Anterior lateral motor cortex (ALM) activity during motor planning and network models of premotor dynamics.

a. Two example ALM neurons with selectivity during the object location discrimination task, out of 890 putative pyramidal neurons from 12 mice (Methods). Correct “lick right” (blue) and “lick left” (red) trials only. Dashed lines demarcate behavioral epochs. Averaging window, 200 ms.

b. ALM population selectivity. Top panel, delay epoch was 1.3 s; bottom panel, delay epoch was 1.7 s. Selectivity is the difference in spike rate between the preferred and non-preferred trial type, normalized to the peak selectivity (Methods). Only putative pyramidal neurons with significant trial selectivity are shown (n=634/890). In addition, neurons tested for <15 trials for each trial type (19/634) were excluded.

c. Average population selectivity in spike rate (black line, ± s.e.m. across neurons, bootstrap).

d. Population response correlation. Pearson's correlation between the population response vectors at different times during the task and the population response vector at the onset of the ‘go’ cue (Time = 0). All selective putative pyramidal neurons were used, even if not recorded at the same time (ignoring potential correlations between neurons). To equalize the contributions of individual neurons, each neuron's response was mean-subtracted and normalized to the variance of its response across the entire trial (computed in time bins of 200 ms).

e. Distribution of selectivity across the population during different epochs. For each neuron, a ROC value between “lick right” and “lick left” trials was computed using the spike counts during the particular behavioral epoch. Solid bars, neurons with significant trial-type selectivity (p<0.05, two-tailed t-test using spike counts).

f-i, modeling description (reproduced from Methods)

All networks were simulated for 2 seconds. Photoinhibition was simulated by holding the activity of half of the neurons in each network at zero for times 0.2 s < t < 1.0 s. Activity of the i^th neuron r_i(t) was governed by the equation:

$$\tau \frac{d{r}_i\left(t\right)}{dt}=-r_i\left(t\right)+\sum _{j=1}^N{W}_{i,j}f\left(r_j\left(t\right)\right)+I_i\left(t\right)$$

where the cellular time constant τ, the connectivity matrix W and the synaptic non-linearity f(x) were chosen independently for each model. N is the number of neurons. In all simulations networks received either transient (0.05 s < t < 0.1 s) or persistent (0.1 s < t < 1.9 s) sensory inputs I_i(t) unless stated otherwise. The specifics of each model are described below.

f. Simple integrator model. The network was simulated with N = 100 neurons, τ = 100 ms, and linear synapses (i.e. f (x) = x). The connectivity matrix was constructed so that all eigenvalues except for one were equal to zero. The non-zero eigenvalue was set to 0.99, producing feedback so that the firing rate of the network decays with a time constant given by τ / (1–0.99) =10s ³⁵. In the network on the left the input was a task-selective persistent current I_i(t). In the simulation on the right the input was a task-selective transient input, and the signal from this integrator was then cascaded into a second identical network to produce ramping activity. Silencing was simulated by holding the activity of a randomly-selected population of 50 neurons at zero from times 0.2 s < t < 1.0 s.

g. Integrator with corrective feedback³⁷. Corrective feedback is incorporated into an integrator network, consisting of a pair of excitatory and inhibitory neurons, to confer robustness against perturbations. This corrective feedback was achieved by a mismatch in the time constants for excitatory and inhibitory connections, which generates negative derivative feedback. The network exhibits robustness against random perturbations that equally affect the excitatory and inhibitory neurons, but is not robust against asymmetric activation of inhibitory neurons (e.g. photoinhibition).

The function f(r) is determined by the differential equation :

$${\tau }_{\mathrm{syn},i,j}\frac{d{f}_{i,j}\left(t\right)}{dt}=-f_{i,j}\left(t\right)+r_j\left(t\right).$$

The synaptic time constant τ_syn,i,j determines how quickly the post-synaptic currents respond to changes in presynaptic activity. The synaptic time constants were: inhibitory synapses, 10 ms; excitatory to inhibitory neurons, 25 ms; excitatory to excitatory neurons, 100 ms. As in the simple integrator model, the network received a task-selective persistent input. Photoinhibition was simulated by injecting large currents into the inhibitory neuron and disallowing negative firing rates, which results in silencing of the excitatory neuron.

h. Randomly connected recurrent networks trained using FORCE learning to produce ramping dynamics (“trained RRNs”). FORCE learning is useful for training recurrent neural networks to produce custom input-output relationships that are relatively stable to noise. As stated in Methods: FORCE training was performed with τ = 200 ms, f(x) = tanh(x), N = 400. The network was given a brief pulse of external current during the interval 0.05 s < t < 0.1 s, representing transient sensory input. The initial connectivity matrix was chosen to be sparse with 90% of connections equal to zero. Non-zero connections were chosen from a Gaussian random distribution. The variance in connection strength was $\frac{{1.5}^2}{pN}$ where p=0.1 is the connection probability. 1.5 is a gain factor which is sufficiently strong to produce chaotic activity ⁴⁹. Training was performed for 30 iterations where the weights were adjusted at each time step as described in ²². Each solid line represents the activity of the network's output in response to transiently clamping the activity of a randomly-selected population of 200 (i.e. N/2) neurons to zero. The network received either persistent (left) or transient (right) sensory input. For persistent input the network behaved similar to an integrator exhibiting a recovery of selectivity, albeit at an offset level upon removal of photoinhibition.

i. RRN trained with FORCE as described above and further stabilized (tamed chaos)²³. The algorithm was designed to stabilize selected trajectories in chaotic networks via a recursive retuning of recurrent connection strengths based on a recursive least-squares rule ⁵⁰. To minimize the number of synapses that required tuning, the FORCE network was made sparse by eliminating weak connections that were smaller than an arbitrary threshold and using linear regression to slightly modify the remaining weights to maintain the dynamics. Elimination of weak synapses greatly reduced the time needed to train the network. Twenty iterations of the tamed chaos algorithm were then run with weights being adjusted every 10^th time step. Perturbations were applied as described for the FORCE trained network above. This training resulted in a modest increase in the robustness of the network.

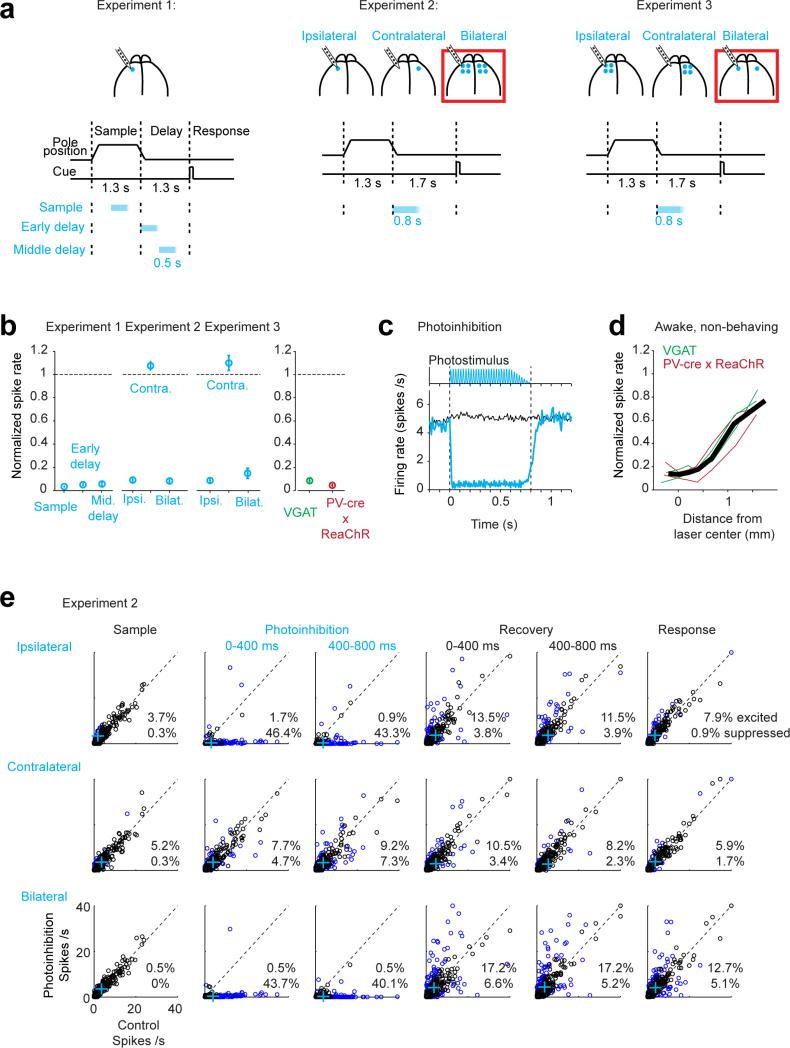
Extended Data Figure 2. Characterization of photoinhibition.

a. Silicon probe recording and photoinhibition in different experimental configurations used in this study. Experiment 1, data presented in Fig. 1, Extended Data Figs 3, 4; Experiment 2, data presented in Figs 2, 3, 4, Extended Data Figs 6, 8, 9; Experiment 3, data presented in Extended Data Fig. 7.

b. Effect of photoinhibition on putative pyramidal neurons. For each neuron, spike rate during photoinhibition was normalized to spike rate in control trials. Left, experiment 1: n=117, 110, 109 neurons from 6 mice; experiment 2: n=300, 294, 301 from 7 mice; experiment 3: n=52, 52, 102 from 3 mice. Ipsilateral and bilateral photoinhibition similarly silenced neuronal activity. Average spike rate across the population was little affected by contralateral photoinhibition. Right, comparison of photoinhibition in VGAT-ChR2-EYFP mice and PV-ires-cre mice crossed to a ReaChR reporter line (Methods) ⁴⁵. Photoinhibition was similar in the two mouse lines (>90% activity reduction). Data from ipsilateral photoihibition from experiment 2 (n=94 neurons from 3 VGAT mice; n=201 from 4 PV-cre × ReaChR mice). Error bars, s.e.m. over neurons. Neurons with mean spike rate of <1 spikes/s were excluded.

c. Top, photostimuli were shaped to minimize rebound activity after photoinhibition. Peak photostimulus intensity was gradually reduced over 200 ms during stimulus offset. Bottom, average spike rate across the population (black, control; cyan, photoinhibition). Data from experiment 2, ipsilateral photoinhibition, n=300 neurons from 7 mice.

d. Effect of photoinhibition versus distance from the laser center under the standard photostimulus (1 laser spot). Neurons were pooled across cortical depths. Recording data were obtained from ALM of 4 untrained mice under awake and non-behaving conditions. Recording procedures were described in ³. Thin lines, individual mice (n=246 neurons, 2 VGAT-ChR2-EYFP mice, 2 PV-ires-cre × ReaChR mice).

e. Average spike rates on control versus photoinhibition “lick right” trials during different epochs of the task. Data from experiment 2. Photoinhibition was for 800ms at the beginning of the delay epoch. The delay epoch was 1.7s. Columns from left to right: the last 400ms of the sample epoch, the first 400ms of the photoinhibition, the last 400ms of the photoinhibition, the first 400ms after photoinhibition, 400-800ms after photoinhibition, first 400ms of the response epoch (see a for trial structure). Top row, ipsilateral photoinhibition (1 laser spot, Methods); middle, contralateral photoinhibition (1 laser spot); bottom, bilateral photoinhibition (4 laser spots). Colored dots, neurons with significant spike rate change (p<0.01, two tailed t-test). Crosses, population means. No rebound excitation was detected after photoinhibition offset on average (d). A small proportion of neurons showed rebound excitation which was balanced by a low level of sustained inhibition in a larger proportion of neurons. Results are similar for “lick left” trials (not shown).

Extended Data Figure 3. Unilateral photoinhibition of ALM immediately before movement causes ipsilateral bias.

a. Unilateral photoinhibition of ALM during different task epochs. Sample epoch, 1.3s; delay epoch, 1.3s. Photoinhibition, 0.5 s (0.4s and 0.1s ramp, Methods).

b. Performance with 0.5s photoinhibition of left or right ALM during different trial epochs. Performance was plotted as a function of time interval between photoinhibition offset (the end of ramp offset) and the onset of ‘go’ cue (T_recovery). Performance was not significantly affected for T_recovery>0.3s. Thick lines, mean; thin lines, individual mice (n = 5). *p<0.05, **p<0.01, ***p < 0.001, two-tailed t-test.

c. Unilateral photoinhibition of ALM during different task epochs. Sample epoch, 1.3s; delay epoch, variable duration, 1.2s – 1.7s in 0.1s increments. Trials with different delay epoch durations were randomly interleaved. Photoinhibition was for 1.3s (1.2s and 0.1s ramp, Methods), resulting in different T_recovery.

d. Performance with 1.3s photoinhibition. Plot is similar to (b). Performance was not significantly affected for T_recovery > 0.3s.

e. Photoinhibition (0.5 s) immediately before the ‘go’ cue is similar to the behavioral effect caused by photoinhibition during the entire delay epoch (1.3 s). Photoinhibition data at T_recovery=0 from (b) and (d) was re-plotted.

Extended Data Figure 4. ALM neurons with decreasing spike rates during the delay epoch recovered their normal spike rates after unilateral photoinhibition.

a. Three example ALM neurons with decreasing spike rates during the delay epoch. Top, spike raster. Bottom, PSTH. All “lick right” (blue) and “lick left” (red) trials. Dashed lines, behavioral epochs. Blue shades, photoinhibition.

b. Normalized spike rate for all neurons with significant spike rate decrease at the end of the delay epoch compared to the beginning of the delay epoch (p < 0.05, two-tailed t-test; 400 ms windows; pooled across trial types). 27 neurons from 6 mice. The spike rate for each neuron was normalized to the mean spike rate. Blue, preferred trial type; red, non-preferred. Mean ± s.e.m. across neurons, bootstrap. Dotted lines, spike rates in control trials.

c. The data is consistent with a return to the normal trajectory and inconsistent with decay to the end point. Top, spike rate difference between perturbed trials and the time-matched spike rates in control trials. Bottom, spike rate difference between perturbed trials and the spike rates at the end of the delay epoch in control trials. Data from (b). Mean ± s.e.m. across neurons, bootstrap. Spike rate difference relative to time-matched control show significantly smaller root-mean-squared error (RMS) than spike rate difference relative to end point (p<0.001, paired t-test). RMS was computed during the epoch between photoinhibition offset and the ‘go’ cue.

Extended Data Figure 5. Preparatory activity is robust to photoactivation.

a. Left, silicon probe recording during unilateral photoactivation of a subset of excitatory neurons. Tlx_PL56-Cre mice (MMRRC 036547) were crossed to Ai32 (Rosa26-ChR2 reporter mice, JAX Stock#012569) to express ChR2 in layer 5 intratelencephalic (IT) neurons ⁵⁰. Right, task structure and timing of photoactivation (cyan).

b. Top, photostimulus. Bottom, average spike rate across the population (n = 69 neurons from 2 mice). Black, control; cyan, photoactivation. Rebound inhibition was observed after photoactivation.

c. Effect of photoactivation on spike rates. Data is for photoactivation during early delay epoch. Black circles, neurons with significant spike rate change (p<0.01, two tailed t-test). Photoactivation during sample epoch: 19% excited, 22% suppressed; late delay epoch: 15% excited, 17% suppressed. “Lick right” and “lick left” trials were pooled to compute spike rates.

d. Three example ALM neurons. Top, spike raster. Bottom, PSTH. All “lick right” (blue) and “lick left” (red) trials. Dashed lines, behavioral epochs. Blue shades, photoinhibition.

e. Top, significant spike rate changes relative to control are highlighted for individual neurons. Neurons (rows) are sorted based on their mean spike rate across the trial epoches. Neurons with mean spike rate below 1 spikes/s or tested for less than 3 trials are excluded. Middle, fraction of neurons with significant spike rate change (n=43, 44 from 2 mice). Bottom, average spike rate across the population.

f. Average population selectivity change from control (ΔSelectivity ± s.e.m. across neurons, bootstrap). Only selective neurons tested for >3 trials in all conditions are shown (n=26). Green lines, time points when the selectivity recovered to 80% of control selectivity (mean ± s.e.m. across neurons, bootstrap). Sample epoch: 249 ± 68 ms to recover to 80 % of control selectivity; early delay: 275 ± 168 ms; middle delay: 250 ± 218 ms.

Extended Data Figure 6. ALM dynamics predicts upcoming movements at the level of behavioral sessions.

a. Behavioral performance on control and bilateral photoinhibition trials.

b. Time course of activity trajectories projected onto the coding direction (cd). Dotted lines, average trajectories from control “lick right” (blue) and “lick left” (red) trials. Solid lines, average trajectories from bilateral photoinhibition trials. Each plot shows data from one session for one mouse. Trajectories in photoinhibition trials were similar to control trials before photoinhibition and were persistently altered by transient bilateral photoinhibition. The resultant trajectories were inconsistent from session to session: in some cases the altered trajectories were closer to the “lick right” control trajectories (blue dotted lines), and in other cases closer to the “lick left” control trajectories (red dotted lines). Averaging window, 400ms. In sessions with altered activity trajectories that were closer to the control “lick left” trajectories, movements were biased to the left, resulting in high performance in “lick left” trials and low performance in “lick right” trials (session 1, 4). The opposite behavioral bias was observed when altered activity trajectories were closer to the control “lick right” trajectories (session 2, 3, 5). The biases in movement were predicted based ALM activity trajectories. Session 1-5, n=20, 16, 18, 10, 12 neurons.

Extended Data Figure 7. Bilateral photoinhibition disrupts ALM dynamics and behavior.

a. Silicon probe recording during unilateral (4 laser spots) and bilateral (1 laser spot; red box) photoinhibition.

b. Behavioral performance. Bar, mean across all mice (n=3). Symbols, individual mice (mean ± s.e.m, bootstrap).

c. Top, significant spike rate changes for individual neurons (black). Neurons (rows) are sorted based on their mean spike rate across the trial epoches. Neurons with mean spike rate below 1 spikes/s or tested for less than 3 trials are excluded (n=60, 59, 60). Photoinhibition is indicated on the top. Bottom, fraction of neurons with significant spike rate change.

d. Average population selectivity change from control (ΔSelectivity ±s.e.m. across neurons, bootstrap). Only selective neurons tested for >3 trials in all conditions are shown (n=40). Green lines, time points when the selectivity recovered to 80% of control selectivity (mean ± s.e.m. across neurons, bootstrap). Ipsilateral: 490±280 ms to recover to 80% of control selectivity; contralateral: 235±156 ms; bilateral: no recovery at end of delay period.

e. Time course of activity trajectories on “lick right” (blue) and “lick left” (red) trials projected onto the coding direction (cd). Average trajectories from all sessions (± s.e.m. across sessions, bootstrap, Methods). From left to right panels: control trials, ipsilateral photoinhibition (4 laser spots), contralateral photoinhibition (4 laser spots), and bilateral photoinhibition (1 laser spot). Dotted line, trajectories in control trials. Only sessions with >5 simultaneously recorded neurons tested for >3 trials in each condition. We quantified the separation between trajectories at the end of delay epoch by computing ROC values for each session: control, 0.80 ± 0.08; ipsilateral, 0.64 ± 0.10; contralateral, 0.68 ± 0.15; bilateral, 0.54 ± 0.8. Mean ± s.e.m. across sessions, Methods.

Extended Data Figure 8. Decomposition of ALM dynamics after perturbation.

a. Decomposition of activity into five modes based on control trials and ipsilateral perturbations (Methods). Fraction of activity variance (left) and selectivity (right) explained by modes 1-5. The overlap in variance and selectivity between mode 1 and modes 2 & 3 are highlighted in black. Error bars, s.e.m. across sessions. Data from 16 sessions, 7 mice. Activity variance here is computed using trial-averaged activity (Methods), thus they reflect variance across time and neurons. Activity variance across trials is not reflected. The fraction of variance explained for the single-trial activity would be much lower.

b. Fraction of upcoming movements predicted based on modes 1-5. Trajectory distance from the decision boundary at the time of the ‘go’ cue is used to predict behavior. “Lick right” and “lick left” trials are pooled. Error bars, s.e.m. across sessions.

c. Projections of activity along modes 1-5 for ipsilateral perturbation trials (solid). Dashed blue and red lines correspond to the means for control trials. Errorbars, s.e.m. across sessions. For the cd mode, a different set of trials was used here to compute cd compared to Fig. 3c (Methods). This resulted in small differences in the projected trajectories.

d. Projections of activity in the same dimensions as in (c) for contralateral perturbation trials.

e. Projections of activity in the same dimensions as in (c) for bilateral perturbation trials.

f. Weights of each neuron for mode 1 versus modes 2-5. Mode 1 and modes 2-5 involve overlapping populations of neurons. Data from all sessions were pooled.

Note that the ramping modes (4 & 5) are resistant to all perturbations, including bilateral perturbations, suggesting that overall ramping may be driven by a source external to ALM.

ROC values between trajectories along the cd mode at the end of delay epoch: control, 0.76 ± 0.03; ipsilateral, 0.73 ± 0.02; contralateral, 0.74 ± 0.03; bilateral 0.58 ± 0.03. ROC values during the time period of photoinhibition: control, 0.72 ± 0.02; ipsilateral, 0.54 ± 0.03; contralateral, 0.64 ± 0.03; bilateral 0.54 ± 0.01.

Extended Data Figure 9. ALM dynamics along the coding direction predicts upcoming movements.

a. Schematic of trajectory analysis in activity space. The difference in the mean response vectors between “lick right” and “lick left” trials, w, was estimated across different time windows (400ms) during sample and delay epochs.

b. w are similar during sample and delay epoch. Correlation of w's across time. Data from 16 sessions, 7 mice. The coding direction, cd, was taken as the average of w over time.

c. The recovery of ALM dynamics along the coding direction (cd) is robust to the choice of time window for the calculation of cd. Left, cd was the average of w's from the first 400 ms of the delay epoch. Right, cd was the average of w's from the last 400 ms of the delay epoch.

d. The recovery of ALM dynamics along cd is robust across mice.

e. Behavioral performance in “lick right” and “lick left” trials as a function of trajectory distance from the decision boundary at the time of the ‘go’ cue. Positive values on the x-axis indicate closer distance to the control “lick right” trajectory. From left to right panels: control trials, ipsilateral photoinhibition trials, contralateral photoinhibition trials, and bilateral photoinhibition trials. Performance was computed by binning along the cd distance (bin size, 4 on the cd distance scale). s.e.m. was obtained by bootstrapping the trials in each bin.

f. Reaction times are faster on trials in which the trajectory is far from the decision boundary at the time of the ‘go’ cue. ΔReaction time is relative to the mean reaction time from each session. Data from 16 sessions, 7 mice. Data from “lick right” and “lick left” trials were pooled.

Extended Data Figure 10. Behavioral and ALM dynamics after Corpus Callossum (CC) hemisection.

a. Schematic. CC was bisected while sparing the pyramidal tract (PT) and corticothalamic (CT) projections.

b. Behavioral performance. Bar, mean across all mice (n=7). Symbols, individual mice (mean ± s.e.m, bootstrap). Performance was not affected by the CC bisection. 1^st session was ~ 17 hours after the CC bisection.

c. Location of the CC cut superimposed on axonal projections from ALM. AAV2/1-CAG-EGFP was injected into ALM. A vertical cut ~3.5 mm deep was made approximately 0.5 mm from the mid-line. The cut extended from bregma anterior 1.5 mm to posterior 1 mm. The cut was either made in the left hemisphere (3 mice) or the right hemisphere (4 mice). The cut spared the PT and CT axons.

d. Coronal section showing the CC bisection in 6 mice. Left column, autofluoresence; right column, GFAP immunofluorescence (Methods).

e. ALM shows normal preparatory activity after the CC bisection. ALM population selectivity. Selectivity is the difference in spike rate between the preferred and non-preferred trial type, normalized to the peak selectivity (Methods). Only putative pyramidal neurons with significant trial selectivity are shown (n=254/496). In addition, 11/254 neurons tested for <15 trials for each trial type were excluded.

f. Average population selectivity in spike rate (black line, ± s.e.m. across neurons, bootstrap).

g. Proportion of contra-preferring vs. ipsi-preferring neurons. Error bars, s.e.m. across mice, bootstrap.