Rawlsian maximin rule operates as a common cognitive anchor in distributive justice and risky decisions

Significance

Distributive justice is a highly controversial issue across many societies. Compared with the accumulation of various normative (“ought”) theories by philosophers over the centuries, our empirical (“is”) understanding of people’s distributive judgments remains insufficient. In a series of experiments, we show that the “maximin” concern (maximizing the minimum possible payoff) operates as a strong cognitive anchor in both distributive decisions for others and economic decisions for self, and that the right temporoparietal junction, associated with perspective taking, plays a key role in this linkage. Our approach illustrates how rigorous methods from behavioral, cognitive, and neural sciences can be combined to shed light on functional elements of distributive justice in our minds, and potential neural underpinnings shared by other nonsocial decisions.

Abstract

Distributive justice concerns the moral principles by which we seek to allocate resources fairly among diverse members of a society. Although the concept of fair allocation is one of the fundamental building blocks for societies, there is no clear consensus on how to achieve “socially just” allocations. Here, we examine neurocognitive commonalities of distributive judgments and risky decisions. We explore the hypothesis that people’s allocation decisions for others are closely related to economic decisions for oneself at behavioral, cognitive, and neural levels, via a concern about the minimum, worst-off position. In a series of experiments using attention-monitoring and brain-imaging techniques, we investigated this “maximin” concern (maximizing the minimum possible payoff) via responses in two seemingly disparate tasks: third-party distribution of rewards for others, and choosing gambles for self. The experiments revealed three robust results: (i) participants’ distributive choices closely matched their risk preferences—“Rawlsians,” who maximized the worst-off position in distributions for others, avoided riskier gambles for themselves, whereas “utilitarians,” who favored the largest-total distributions, preferred riskier but more profitable gambles; (ii) across such individual choice preferences, however, participants generally showed the greatest spontaneous attention to information about the worst possible outcomes in both tasks; and (iii) this robust concern about the minimum outcomes was correlated with activation of the right temporoparietal junction (RTPJ), the region associated with perspective taking. The results provide convergent evidence that social distribution for others is psychologically linked to risky decision making for self, drawing on common cognitive–neural processes with spontaneous perspective taking of the worst-off position.

The “Occupy Wall Street” protests in New York garnered worldwide attention, highlighting growing concerns about wealth inequality. A remarkable feature of the protests was that not only the financially disadvantaged but middle-class citizens, who were relatively wealthy in the current economy, also joined the movement. Traditional economic models that assume utility only for self-related outcomes (1, 2) fail to explain such a mass phenomenon.

However, there is one important psychological dimension that seems to characterize the wide civic involvement in the movement yet has been unaddressed in cognitive and social neuroscience—concern about the lowest, worst-off outcomes. Notice that, in the “Occupy” protests, people were not just concerned about the inequality (variance) of wealth distribution generally, but specifically advocated increasing the incomes of society’s most disadvantaged. John Rawls, an eminent modern social philosopher, similarly argued that the benefit to the least well-off should be maximized according to the “maximin principle” (maximizing the minimum possible payoff) (3). Indeed, several behavioral studies suggest that such concerns about minimums may operate as a strong psychological anchor not only in social distributions for others but also in economic decisions for oneself. Research using behavioral games has shown that, when making distributive choices for others, people generally prefer to improve everyone’s payoffs but are more concerned about raising the payoffs of the worse-off individuals than the better-off individuals (4–7). Similarly, in the risky-decision–making literature, parallel evidence is emerging that people often pay particular attention to their worst possible payoff as well as the expected mean when choosing among gambles (8, 9). Maximin strategies (those that maximize the minimum outcome) in risky choices are also used by some nonhuman animals during foraging (10), which likely reflects that real-world concerns about risk are often dominated by the rarest but most disastrous outcome (11). However, the neural circuitry that may underlie this common maximin concern remains unknown.

A recent and growing body of evidence suggests that social decisions for others may involve similar neural circuitry to that of economic decisions for oneself (12–18). Using functional magnetic resonance imaging (fMRI), Shenhav and Greene (13) showed that moral judgments about human life and death recruit “domain-general” valuation mechanisms to integrate probability and magnitude; as in economic decisions under risk (15–18), in moral judgments the anterior insula (AI) was sensitive to probability (i.e., variability of losing/saving lives), whereas the putamen was responsive to magnitude (i.e., number of lives lost/saved). Likewise, Hsu et al. (14) showed that, when allocating resource to others as a third party, the AI was responsive to inequality in resources among the recipients (Gini coefficient), whereas the putamen was responsive to overall efficiency of allocation (the total amount allocated). These studies suggest that moral or distributive judgments for others may be linked to economic decisions for self, through a common neural circuitry that responds to the variance/inequality and magnitude/efficiency parameters of a decision task separately.

Here, we investigate the hypothesis that distributive judgments may also be linked to risky decisions psychologically via another parameter—spontaneous concern about the minimum, worst-off position. Although ecologically the minimum parameter is often correlated with the variance/inequality parameter, they are conceptually distinguishable from each other (3, 11, 19). We conjecture that perspective taking may be a key to understanding the potential linkage between distributive and risky decisions. Perspective taking here means mentally simulating a different standpoint (20–25)—how one would feel if placed in situations that differ physically or temporally (“other/future”) from one’s immediate environment (“myself/now”). Choosing a distribution as a third party often entails taking the perspectives of those affected by the decision (3, 19). Making risky financial decisions also requires mental simulations about one’s potential future conditions (20–22). Recent neural evidence suggests that economic decisions involve taking the perspective of one’s “future self” to evaluate possible outcomes at a distant time (26).

Of course, ideologies and choice preferences vary across individuals, ranging from “Rawlsian” [maximizing the minimum (3)] to “utilitarian” [overall maximizing (19, 27)] in distributions for others (4–7, 14), and from risk avoiding to risk seeking in economic decisions for self (8–11). However, we predict that, across tasks and individual differences, the minimum, worst-case scenario will tend to be a primary locus of perspective taking and function as a spontaneous cognitive anchor. We first test this thesis behaviorally using an attention-monitoring technique (28). Then we examine potential neural underpinnings of such a maximin bias using a brain-imaging technique with a focus on the right temporoparietal junction (RTPJ)—the brain region known to play a crucial role in perspective taking to infer others’ experiences (20–25) and in shifting attention away from the here-and-now to imagine one’s own experiences in different situations (20–22, 26, 29).

Experiment 1 (Behavioral Experiment)

Task.

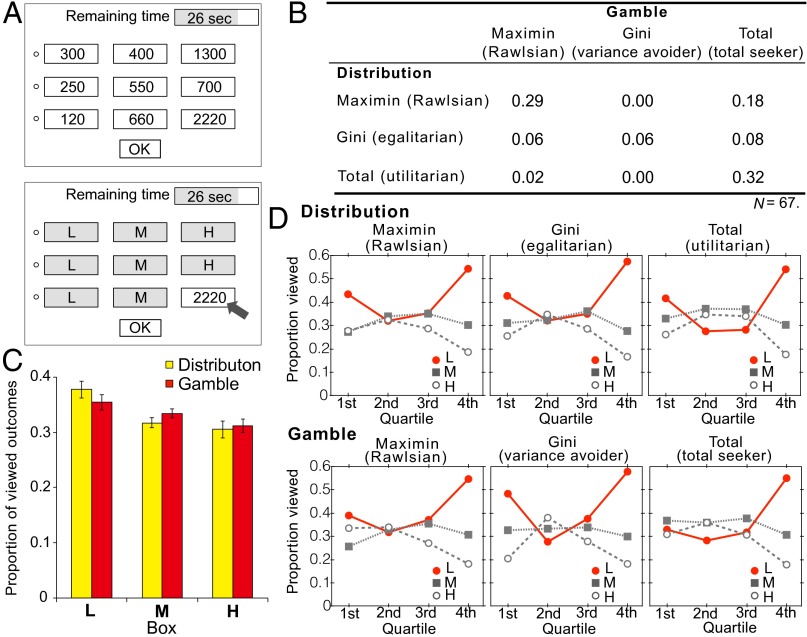
To investigate the connection between seemingly disparate decisions about distributions for others and gambles for self, we first conducted a behavioral experiment. Sixty-seven participants were provided three options in each trial (Fig. 1A, Top): one with the largest minimum (maximin), one with the smallest variance in terms of the Gini coefficient, and one with the largest total. We tracked participants’ information search behavior during decision making using the Mouselab technique (28). On the screen, numerical outcome information was hidden behind boxes labeled “L,” “M,” or “H” (Fig. 1A, Bottom). When the mouse pointer was held over a box, its numerical information was displayed, and when the pointer was moved away, the information was hidden again, so that participants could only view one box at a time. Participants had to make choices within 30 s in each trial, during which they were free to view any boxes in any order. Participants made one set of 40 third-party distribution choices, from which one was randomly designated as a real reward allocation for three unknown others participating in a different ongoing experiment (14). Participants also made another set of 40 choices as gambles for themselves, with one choice randomly designated as the lottery from which one of the three outcomes would be randomly selected as their own real reward (Materials and Methods). The numerical structure of the choice options was identical across the two tasks (Table S1), task order was counterbalanced across participants, and presentation order of the 40 choice sets within each task was randomized.

Fig. 1.

Stimulus and results from the behavioral experiment. (A) A numerical example (in yen) of the three choice options (Top) and “Mouselab” interface (Bottom) displayed to participants. Numerical outcome information, initially hidden behind boxes labeled L, M, or H (low, medium, or high), was displayed only when participants held the pointer over a box. Column order was counterbalanced across participants (LMH or HML). Row order of the three options was randomized across participants and choice sets in each task. (B) Consistency of participants’ types in the two tasks, displayed as proportion classified as each type by their most frequent choices [χ² (4) = 37.20; P < 0.0001]. Interpretive labels provided in parentheses. (C) Average proportion of L, M, or H views preceding choices. Participants viewed L boxes most frequently in both tasks [F_(2,264) = 35.15; P < 0.0001]. Error bars represent SEM. (D) Temporal changes in the average proportions of L, M, or H views when decision time used by each participant in each trial was divided into quartiles, as a function of task and participant type. The selective focus on minimums (shown in red) was largest in the final quartile of decision time in each trial [F_(2,80) = 117.31; P < 0.0001].

Table S1.

Forty choice sets used in the behavioral experiment

Choice no.	Option	π1	π2	π3	Total	Minimum	Gini
1	1	410	580	2,510	3,500	410	0.6
	2	510	770	1,720	3,000	510	0.4
	3	400	800	800	2,000	400	0.2
2	1	150	1,190	1,660	3,000	150	0.5
	2	460	480	1,060	2,000	460	0.3
	3	420	510	570	1,500	420	0.1
3	1	20	660	2,820	3,500	20	0.8
	2	400	400	2,200	3,000	400	0.6
	3	100	700	700	1,500	100	0.4
4	1	60	1,280	2,160	3,500	60	0.6
	2	600	610	1,790	3,000	600	0.4
	3	390	420	690	1,500	390	0.2
5	1	110	390	2,500	3,000	110	0.8
	2	210	380	1,410	2,000	210	0.6
	3	120	660	720	1,500	120	0.4
6	1	300	650	1,550	2,500	300	0.5
	2	450	500	1,050	2,000	450	0.3
	3	400	550	550	1,500	400	0.1
7	1	90	520	2,890	3,500	90	0.8
	2	190	420	1,390	2,000	190	0.6
	3	140	620	740	1,500	140	0.4
8	1	410	930	2,160	3,500	410	0.5
	2	580	580	1,340	2,500	580	0.3
	3	550	750	770	2,000	550	0.1
9	1	200	1,350	1,950	3,500	200	0.5
	2	530	680	1,290	2,500	530	0.3
	3	450	450	600	1,500	450	0.1
10	1	80	1,590	1,830	3,500	80	0.5
	2	650	810	1,540	3,000	650	0.3
	3	430	490	580	1,500	430	0.1
11	1	30	1,140	1,830	3,000	30	0.6
	2	360	480	1,160	2,000	360	0.4
	3	310	580	610	1,500	310	0.2
12	1	240	570	2,690	3,500	240	0.7
	2	380	740	1,880	3,000	380	0.5
	3	310	780	910	2,000	310	0.3
13	1	220	460	2,320	3,000	220	0.7
	2	280	440	1,280	2,000	280	0.5
	3	240	570	690	1,500	240	0.3
14	1	20	860	2,120	3,000	20	0.7
	2	350	550	1,600	2,500	350	0.5
	3	270	860	870	2,000	270	0.3
15	1	210	1,080	1,710	3,000	210	0.5
	2	510	730	1,260	2,500	510	0.3
	3	440	470	590	1,500	440	0.1
16	1	230	590	2,680	3,500	230	0.7
	2	380	490	1,630	2,500	380	0.5
	3	210	630	660	1,500	210	0.3
17	1	420	900	2,180	3,500	420	0.5
	2	440	520	1,040	2,000	440	0.3
	3	410	530	560	1,500	410	0.1
18	1	150	1,100	2,250	3,500	150	0.6
	2	500	510	1,490	2,500	500	0.4
	3	320	560	620	1,500	320	0.2
19	1	120	660	2,220	3,000	120	0.7
	2	300	400	1,300	2,000	300	0.5
	3	250	550	700	1,500	250	0.3
20	1	70	1,360	1,570	3,000	70	0.5
	2	560	630	1,310	2,500	560	0.3
	3	540	720	740	2,000	540	0.1
21	1	80	450	2,470	3,000	80	0.8
	2	250	500	1,750	2,500	250	0.6
	3	150	900	950	2,000	150	0.4
22	1	20	860	2,120	3,000	20	0.7
	2	410	430	1,660	2,500	410	0.5
	3	270	510	720	1,500	270	0.3
23	1	190	660	2,650	3,500	190	0.7
	2	460	580	1,960	3,000	460	0.5
	3	340	1,070	1,090	2,500	340	0.3
24	1	140	920	1,940	3,000	140	0.6
	2	390	720	1,390	2,500	390	0.4
	3	360	480	660	1,500	360	0.2
25	1	240	570	2,690	3,500	240	0.7
	2	330	340	1,330	2,000	330	0.5
	3	210	630	660	1,500	210	0.3
26	1	70	570	2,860	3,500	70	0.8
	2	280	640	2,080	3,000	280	0.6
	3	140	920	940	2,000	140	0.4
27	1	200	300	3,000	3,500	200	0.8
	2	320	350	1,830	2,500	320	0.6
	3	210	780	1,010	2,000	210	0.4
28	1	220	560	1,720	2,500	220	0.6
	2	380	440	1,180	2,000	380	0.4
	3	330	540	630	1,500	330	0.2
29	1	310	580	2,110	3,000	310	0.6
	2	480	540	1,480	2,500	480	0.4
	3	400	800	800	2,000	400	0.2
30	1	300	1,150	2,050	3,500	300	0.5
	2	690	710	1,600	3,000	690	0.3
	3	670	910	920	2,500	670	0.1
31	1	110	820	2,570	3,500	110	0.7
	2	500	500	2,000	3,000	500	0.5
	3	300	450	750	1,500	300	0.3
32	1	580	590	2,330	3,500	580	0.5
	2	610	890	1,500	3,000	610	0.3
	3	570	660	770	2,000	570	0.1
33	1	160	730	2,610	3,500	160	0.7
	2	290	420	1,790	2,500	290	0.6
	3	170	560	770	1,500	170	0.4
34	1	240	920	2,340	3,500	240	0.6
	2	420	660	1,420	2,500	420	0.4
	3	400	800	800	2,000	400	0.2
35	1	140	220	2,140	2,500	140	0.8
	2	260	280	1,460	2,000	260	0.6
	3	130	640	730	1,500	130	0.4
36	1	160	1,080	2,260	3,500	160	0.6
	2	580	640	1,780	3,000	580	0.4
	3	510	980	1,010	2,500	510	0.2
37	1	120	370	2,510	3,000	120	0.8
	2	330	340	1,830	2,500	330	0.6
	3	110	680	710	1,500	110	0.4
38	1	260	530	2,710	3,500	260	0.7
	2	330	590	1,580	2,500	330	0.5
	3	290	820	890	2,000	290	0.3
39	1	150	390	2,960	3,500	150	0.8
	2	380	440	2,180	3,000	380	0.6
	3	180	1,140	1,180	2,500	180	0.4
40	1	320	750	2,430	3,500	320	0.6
	2	400	400	1,200	2,000	400	0.4
	3	300	600	600	1,500	300	0.2

Note: The second column denotes the defining characteristic of each option [1: largest total; 2: maximin (largest minimum); or 3: lowest Gini coefficient] in each choice set. The third through fifth columns indicate amounts (in yen) received by the unknown persons A, B, and C in the distribution task, and amounts received by the participant if event A, B, or C occurred (with 1/3 probability each) in the gambling task. The sixth column indicates the total amount, the seventh column indicates the minimum amount, and the last column indicates the Gini coefficient for each option. The order of the three options in each choice set and the order of the 40 choice sets were randomized across participants and the two tasks, and did not follow the order of entries in the table.

Results.

We first analyzed participants’ behavioral choices. The maximin option was chosen more frequently in distributions [mean (M) = 16.4 of 40 choices] than in gambles (M = 14.4) [F_(1,66) = 25.79; P < 0.0001], indicating that the maximin concern is more pronounced in social distributions for others than in gambles for self.

Choice concordance.

Interestingly, however, individuals’ choice preferences were highly consistent across the two tasks. In Fig. 1B, we classified participants into three “types” according to their most frequent choices in each task. Rawlsians, who chose maximin reward allocations for others most frequently, also favored maximin gambles most for themselves, whereas utilitarians, who favored the largest-total distributions, also preferred the largest-total gambles most. The infrequent “Gini” type (making up only 6% of participants), who preferred the least variable option most in gambling for themselves, were all classified as “egalitarians,” choosing relatively equal social distributions most frequently [χ² (4) = 37.20; P < 0.0001]. To examine individual choice differences in a continuous (rather than discrete) manner, we also analyzed each participant’s preferences using an economic model [“quasi-maximin model” (6)]. Applied to our three-outcome (π₁, π₂, π₃) cases, the model posits that the utility of option x for participant i is given by the following:

$$U_i\left(x\right)={\alpha }_i\cdot \text{min}\left[{\pi }_1\mathrm{,}{\pi }_2\mathrm{,}{\pi }_3\right]\mathrm{+}\left(1\mathrm{-}{\alpha }_i\right)\cdot \left({\pi }_1\mathrm{+}{\pi }_2\mathrm{+}{\pi }_3\right),$$ [1]

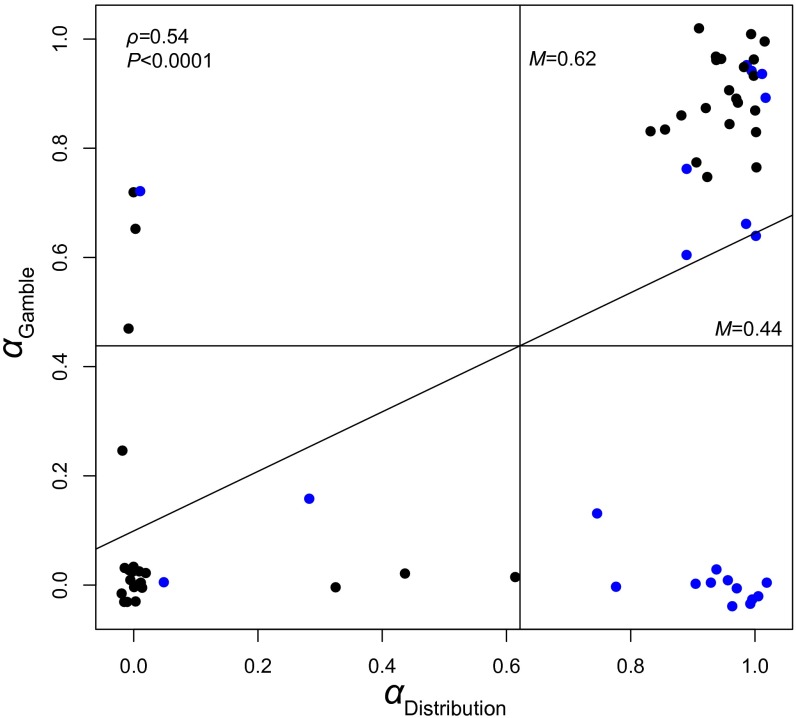
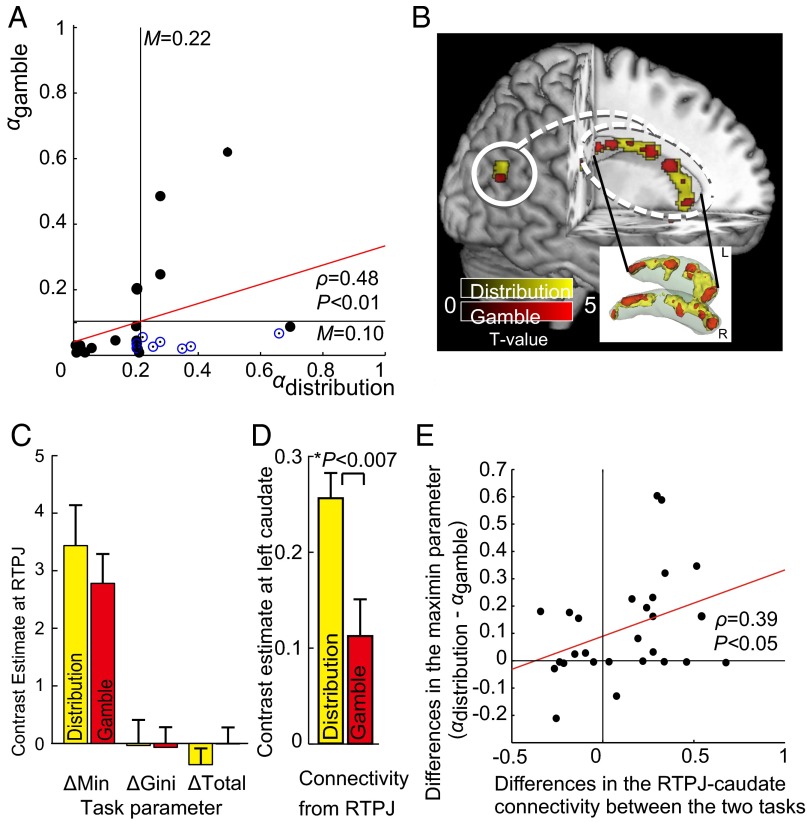
where α_i ∊ [0, 1] captures the individual weight reflecting the maximin principle. Setting α = 1 in distributions corresponds to pure Rawlsian preferences, in which the welfare of the option is measured solely by the maximin principle, whereas setting α = 0 in distributions corresponds to pure utilitarian preferences. For each participant, we estimated the maximin weight, α_i, for distributions (α_distribution) and for gambles (α_gamble) separately. As shown in Fig. S1, participants who favored the maximin distributions for others (higher α_distribution) tended to prefer the maximin gambles for themselves (higher α_gamble) (ρ = 0.54; P < 0.0001). Also, mean α was greater in distributions (M = 0.62) than in gambles (M = 0.44) [F_(1,65) = 14.39; P = 0.001], corroborating the more frequent maximin choices in distributions than in gambles (for details, see SI Materials and Methods, Economic model for maximin weight estimation).

Fig. S1.

Scatterplots of individual maximin weights for distributions (α_distribution) and gambles (α_gamble) derived from participants’ 40 choices using Charness–Rabin’s quasi-maximin model (6) (Eq. S1). α_i ∊ [0, 1] is a parameter that captures the weight reflecting the maximin principle. Individuals with α = 1 in distributions correspond to pure Rawlsians, for whom welfare is measured solely by the maximin criterion. Individuals with α = 0 in distributions correspond to pure utilitarians (for details of the quasi-maximin model, see SI Materials and Methods, Economic model for maximin weight estimation). Participants who preferred the maximin distributions for others (higher α_distribution) tended to favor the maximin gambles for themselves (higher α_gamble) (ρ = 0.54; P < 0.0001). The mean α was also significantly greater in distributions (M = 0.62) than in gambles (M = 0.44) [F_(1,65) = 14.39; P < 0.001], corroborating the more frequent maximin choices in distributions than in gambles. Points colored in blue correspond to the participants classified as Rawlsians in distributions for others but largest-total seekers in gambles for self according to their most frequent choices (Fig. 1B).

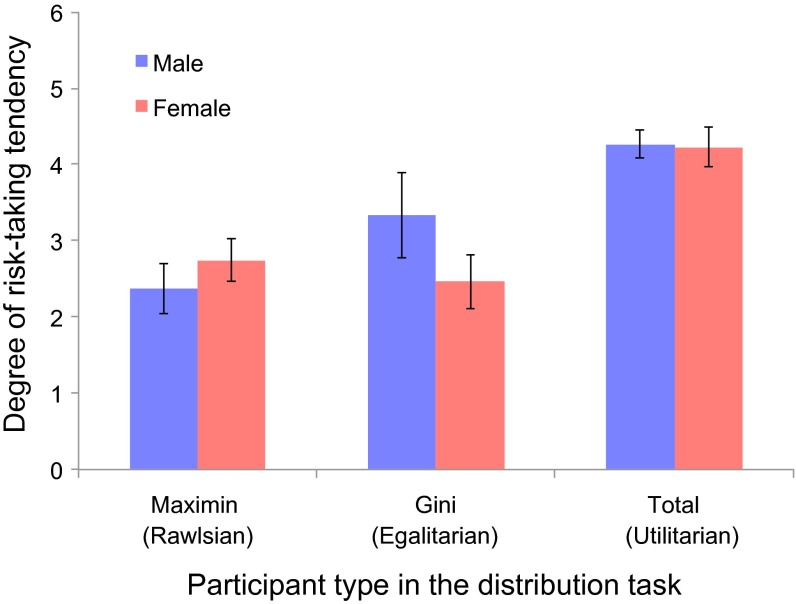
It could be argued that these behavioral consistencies were simply the result of the common stimulus features (i.e., the same display format and numeric structure) shared between the two tasks. However, responses on a separate risk attitude measure (30) in the postsession questionnaire, which had a totally different display format and numerical structure, revealed the same pattern (Fig. S2). Utilitarians, as classified according to their most frequent choices in distributions, were more risk seeking than the other two types (Rawlsians and egalitarians) [F_(2,56) = 9.80; P < 0.001], confirming the coherence between distributive and risk preferences.

Fig. S2.

Average risk-seeking tendency (as measured by the postsession risk attitude questionnaire) according to participant type (classified according to most frequent choices) in the distribution task, by sex. Utilitarians, as classified according to their most frequent choices in distributions, were more risk seeking than the other two types (Rawlsians and egalitarians) [F_(2,56) = 9.80; P < 0.001]. Error bars represent SEM. For details, see SI Materials and Methods, Analysis of the relation between participants’ distributive choices for others and risk preferences as measured by a separate risk attitude questionnaire.

Information search.

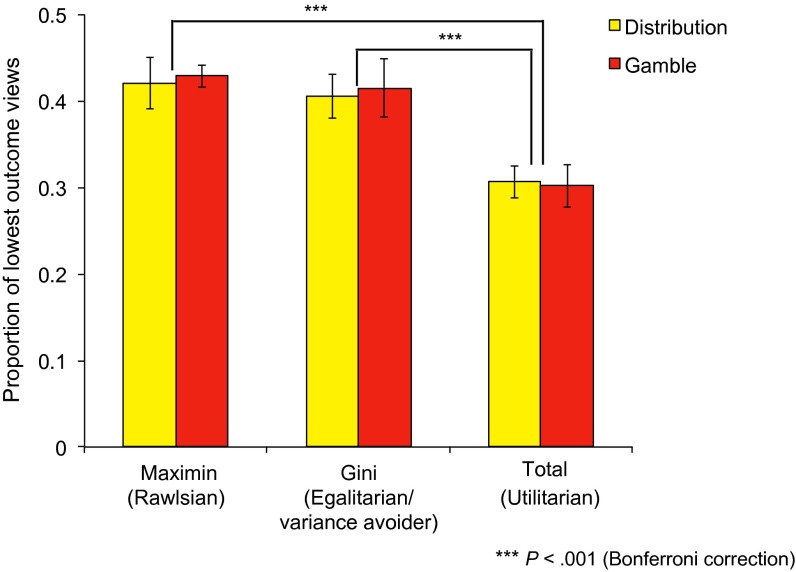
More importantly, information search behavior preceding participants’ choices was also remarkably similar between the two tasks. On average, participants viewed L (low) boxes most frequently in both tasks [F_(2,264) = 35.15; P < 0.0001] (Fig. 1C; see also Fig. S3). To examine the time course of information search behavior, we divided the decision time used by each participant in each trial into quartiles. Fig. 1D displays information search in each quartile as a function of task and participant type. The selective focus on minimums (shown in red) was largest in the final quartile of decision time in each trial, which persisted across participants [F_(2,80) = 117.31; P < 0.0001]. Confirming minimums just before the choice was dominant across tasks and participant types.

Fig. S3.

Average proportion of lowest outcome (L) views preceding choices by participant type. Utilitarians viewed the lowest outcomes less frequently than Rawlsian and Gini types [F_(2,132) = 9.82; P < 0.001]. Error bars represent SEM. For details, see SI Materials and Methods, Analysis of frequencies of lowest outcome (“L”) view by participant type.

It should be noted that the third-party reward allocation implemented in this experiment involved zero monetary risk for participants themselves. However, participants’ distributive preferences for others matched their own risk preferences, and most importantly, spontaneous focus on the worst cases characterized participants’ thinking about both distributions for others and gambles for self. Taken together, these behavioral and cognitive similarities suggest that distributive judgment may be psychologically linked to risky decision making through spontaneous maximin concern.

SI Materials and Methods

Behavioral Experiment (the Mouselab Experiment).

Experimental procedure.

Sixty-seven participants made one set of 40 choices as third-party reward allocations, with one choice randomly designated as a real cash reward for three unknown others who were participating in a different ongoing experiment (14), and another set of 40 choices as gambles for themselves, with one choice randomly designated as the lottery from which one of the three outcomes was randomly selected as their own real cash reward. The numerical structure of the choice options was identical for the two tasks (Table S1). Informed consent was obtained from each participant using a consent form approved by the Institutional Review Board of the Center for Experimental Research in Social Sciences at Hokkaido University (No. 23-4).

Experimental instructions.

“Thank you for coming to our experiment. In this experiment, you will be asked to make various decisions for yourself and for others. At the end of the experiment, you will receive in cash the amount you earn in this experiment plus a 200-yen show-up fee as compensation for your participation. We assure you that there is nothing distasteful or embarrassing in the experiment. But should you find any part of the experiment uncomfortable, you can leave the experiment any time; we will still compensate for your participation.”

“The experiment has two parts. We will explain Part 1 first. The explanation of Part 2 will be given after you finish Part 1.”

[In the following example, Part 1 is the distribution task and Part 2 is the gambling task. The order of these tasks was counterbalanced across participants in the experiment.]

“We will explain the task and the procedure using the following slides. Please click the ‘Next’ button located at the bottom of the screen to proceed to the next page.”

Part 1 (distribution Task).

“In Part 1, you will be asked to allocate monetary rewards for three people who are currently participating in another experiment in our laboratory. Here, let us call them Person A, Person B, and Person C. As shown in the example screen below, you will have three allocation options to determine monetary rewards (in yen) for the three persons.” [See Fig. 1A, Top.]

“On the actual computer screen you will see in the experiment, numeric information about rewards for the three persons is initially hidden behind boxes labeled ‘L,’ ‘M,’ or ‘H.’ These labels refer to the numeric order of the rewards for the three persons, in that Person A would receive the lowest amount, B the middle amount, and C the highest amount in the selected allocation.”

[See Fig. 1A, Bottom. The instruction here is for the LMH order. There were two column orders, LMH or HML, in the experiment, which were counterbalanced across participants.]

“To see the exact amount (in yen) behind each box, you have to move the mouse pointer over the box. The amount will be displayed as long as you keep the pointer over the box, but when you move the pointer away from the box, the amount will be hidden again.”

“You have 30 seconds to choose one option from the three reward allocations. During the 30 seconds, you are free to view any boxes in any order. When you decide on one allocation option, please click the button next to the option and then confirm your choice using the confirmation button. Then you can proceed to the next page.”

“In this experiment, you will be asked to make a total of 40 such allocation choices for the three others. At the end of the experiment, one of your 40 allocation choices will be randomly selected to determine the actual rewards to be paid to the three persons in cash (please note that your allocation choices for the three others do not affect your own reward). We guarantee that you will not see the three persons when you leave the experiment and that you will remain completely anonymous after the experiment.”

[After this screen, participants were asked to make a total of 40 allocation decisions. See Table S1 for the 40 choice sets used in the experiment.]

Part 2 (gambling task).

[Instructions for Part 2 were given after participants finished Part 1.]

“We will now proceed to Part 2. In this part, you will be asked to choose one of three lotteries for your own reward. As shown in the example screen, each lottery yields one of three monetary outcomes (in yen), Outcome A, Outcome B, or Outcome C, with equal likelihood, 1/3.”

“On the actual computer screen you will see in the experiment, numeric information about lottery outcomes is initially hidden behind boxes labeled ‘L,’ ‘M,’ or ‘H.’ These labels refer to the numeric order of the three possible outcomes, in that Outcome A would be the lowest amount, B the middle amount, and C the highest amount in the selected lottery.”

[The instruction here is for the LMH order. There were two column orders, LMH or HML, in the experiment, which were counterbalanced across participants in the experiment.]

“To see the exact amount (in yen) behind each box, you have to move the mouse pointer over the box. The amount will be displayed as long as you keep the pointer over the box, but when you move the pointer away from the box, the amount will be hidden again.”

“You have 30 seconds to choose one option from the three lotteries. During the 30 seconds, you are free to view any boxes in any order. When you decide on one lottery, please click the button next to the option and then confirm your choice using the confirmation button. Then you can proceed to the next page.”

“In this experiment, you will be asked to make a total of 40 such lottery choices for yourself. At the end of the experiment, one of your 40 lottery choices will be randomly selected. One of the three monetary outcomes in the selected lottery will then be picked with one-third probability to determine your reward. You will be paid the money in cash at the end of the experiment.”

[After this screen, participants were asked to make a total of 40 lottery choices. See Table S1 for 40 choice sets used in the experiment. After participants finished part 2, they were asked to answer a short postsession questionnaire measuring their risk attitudes (30).]

Economic model for maximin weight estimation.

We used a Charness–Rabin quasi-maximin model (6) to estimate each participant’s maximin concern when he or she made distribution and gambling decisions. Denoting monetary outcomes in an option as π₁, π₂, and π₃, the utility of option x for participant i is given by the following:

$$U_i\left(x\right)={\alpha }_i\mathrm{·}\text{min}\left[{\pi }_1,{\pi }_2,{\pi }_3\right]+\left(1-{\alpha }_i\right)\mathrm{·}\left({\pi }_1+{\pi }_2+{\pi }_3\right),$$ [S1]

where α_i ∊ [0, 1] is a parameter that captures the weight reflecting the maximin principle. Individuals with α = 1 in distributions correspond to pure Rawlsians, for whom welfare is measured solely by the maximin criterion. Individuals with α = 0 in distributions correspond to pure utilitarians.

For each participant, we obtained maximin weights for distributions (α_i,_distribution) and gambles (α_i,_gamble) by applying maximum-likelihood estimation to the participant’s binary choices in each task. In experiment 1, the maximum likelihood estimation used the following logit (softmax) model:

$$\mathrm{Pr}\left(\text{choosing}\hspace{0.17em}\text{option}\hspace{0.17em}\text{A}\right)=\frac{{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}A\right)}}{{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}A\right)}+{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}B\right)}+{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}C\right)}},$$ [S2]

where U(option A) is modeled by Eq. S1 and parameter γ reflects the participant’s sensitivity to utility differences between the options. We used the Broyden–Fletcher–Goldfarb–Shanno method for numerical estimation implemented in R (www.r-project.org).

Analysis of the relation between participants’ distributive choices for others and risk preferences as measured by a separate risk attitude questionnaire.

It could be argued that the behavioral consistencies between the two tasks (e.g., Fig. 1B and Fig. S1) were the result of their shared stimulus features (e.g., use of the same display format and numeric structure). To address this point, we also measured participants’ risk attitudes using separate items with a totally different display format and numerical structure [developed by Eckel and Grossman (30)] in a postsession questionnaire. This kind of risk attitude questionnaire is commonly used in behavioral economics and has been shown to be a good predictor of various economic decisions. Fig. S2 displays the degree of risk-seeking tendency (as measured by the questionnaire) of the three participant types with different distributive tendencies (Rawlsian, egalitarian, utilitarian). Utilitarians, as classified according to their most frequent choices in distributions, were significantly more risk seeking than the other two types [F_(2,56) = 9.80; P < 0.001], in a 3 (Type) × 2 (Sex) analysis of variance (ANOVA). No sex difference was observed [F_(1,56) = 1.30, ns].

Analysis of frequencies of lowest outcome (“L”) view by participant type.

Fig. S3 displays mean proportion of lowest outcome (L) views preceding choices by participant type. On average, “utilitarians” viewed the lowest outcomes less frequently than “Rawlsian” and “Gini” types, F_(2,132) = 9.82, P < 0.001, in a 3 (Type) × 2 (Task) ANOVA. No other effects were significant. As shown in Fig. 1D, this difference primarily reflects fewer L views by utilitarians during the second and third quartiles of decision time compared with the other two types. However, the selective focus on L during the fourth quartile, just before making decisions, is robust across all participant types.

Main fMRI Experiment.

Experimental procedure.

Thirty healthy, right-handed student volunteers participated in the study. After passing an initial screening and providing consent in accordance with a protocol approved by the Institutional Review Board of the Brain Research Center at Tamagawa University (No. C25-9), participants received explanations of the overall experimental procedure. They were told that they would work on two decision tasks, distributions and gambles, in the fMRI scanner.

For the distribution task, participants were told that they would choose one of two options in each trial (Fig. S4A) regarding how they would distribute money to three unknown others, identified anonymously as person Red, Green, and Blue, who were participating in another experiment. It was emphasized that participants would never meet the three recipients after the experiment and that they would remain completely anonymous to the recipients. Participants were told that they would make 36 such distribution decisions as a neutral third party (14), from which one choice would be designated as the reward for the others.

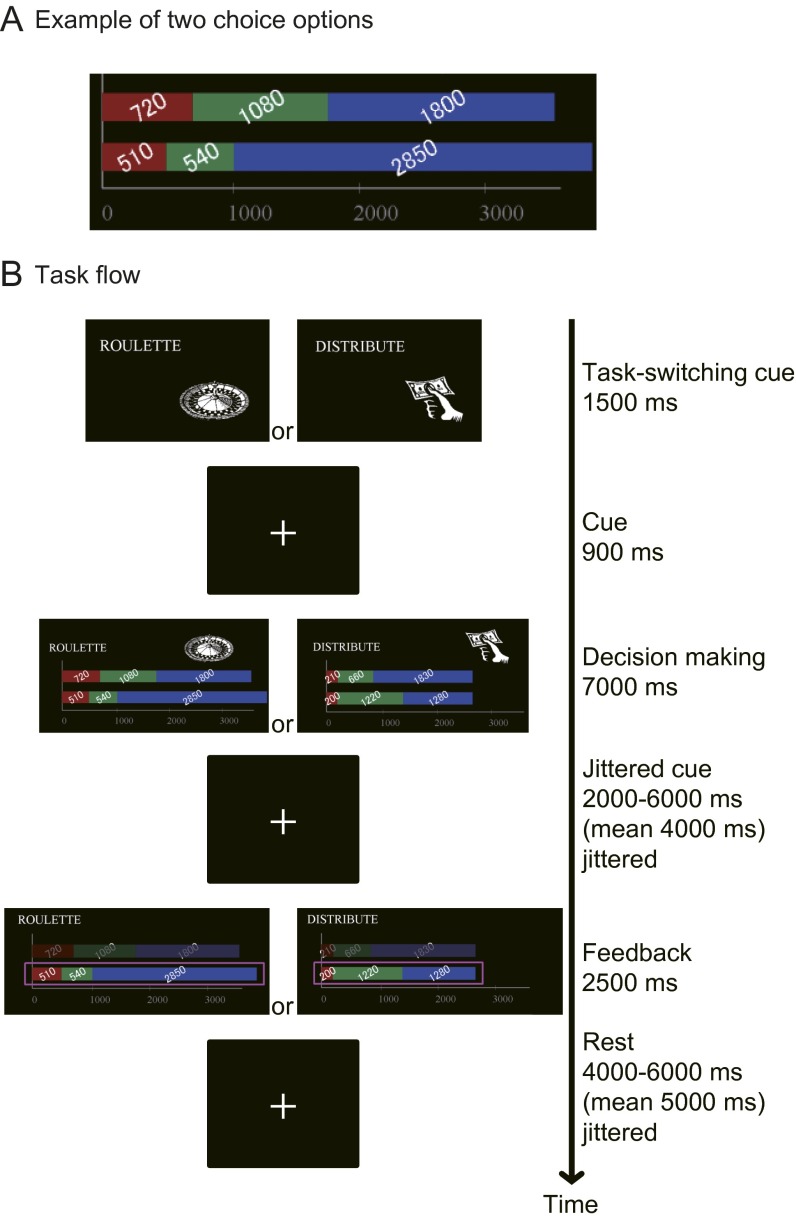
Fig. S4.

An illustration of the distribution and gambling tasks in the fMRI experiment. (A) Example display of two choice options. In option 1, Total = 3,600, Min = 720, and Gini = 0.3, and in option 2, Total = 3,900, Min = 510, Gini = 0.6, so the three parameters used in the regression analysis are ΔTotal = 300, ΔMin = 210, and ΔGini = 0.3. (B) Task flow and duration.

For the gambling task, participants were told that they would choose one of two lotteries in each trial. Each lottery could yield three monetary outcomes with an equal likelihood of 1/3 (outcomes depicted in Fig. S4A). Participants were instructed that they would make 36 such lottery choices; one choice would be randomly selected at the end of the experiment and one of the three monetary outcomes in the chosen lottery would be picked with one-third probability to determine their own cash reward. No feedback was provided to participants about monetary outcomes resulting from their distribution and lottery choices until the end of the experiment.

After receiving the instructions, participants were given a practice session using a computer display setup equivalent to that used during the fMRI scanning session. A short quiz was administered immediately thereafter to confirm that participants understood the two tasks and the overall procedure correctly, and then participants were taken to the scanning room.

Experimental instructions.

[The instructions below were read aloud to the participant in the waiting room before she/he entered the fMRI scanner. The participant was also given a written version to read while listening to the experimenter’s instructions.]

“Thank you for coming to our experiment. In this experiment, you will be asked to make various decisions for you and for others in the fMRI scanner. At the end of the experiment, you will receive in cash the amount you earn in this experiment plus a 2,500-yen show-up fee as compensation for your participation. We assure you that there is nothing distasteful or embarrassing in the experiment. But should you find any part of the experiment uncomfortable, you can leave the experiment any time; we will still compensate for your participation.”

“The experiment has two tasks. One task is allocating monetary rewards for others and the other task is choosing lotteries for yourself.”

“When the allocation task begins, the following ‘Distribute’ screen will appear first on a monitor, and you will work on this task consecutively for next several rounds.”

[See Fig. S4B, Top Right.]

“In this task, you will be asked to allocate monetary rewards for three people who are currently participating in another experiment in our laboratory. Here, let us call them Person Red, Person Green, and Person Blue. As shown in the example screen below, you will have two allocation options to determine monetary rewards (in yen) for the three persons. If you choose the top option in this example, Person Red will receive 210 yen, Person Green 660 yen, and Person Blue 1,830 yen. You have to choose one of the two allocation options within 6 seconds.”

[See Fig. S4B, Middle Right.]

“After you make a decision, the chosen option will be highlighted as in the example screen below.”

[See Fig. S4B, Bottom Right.]

“When the lottery task begins, the following ‘Roulette’ screen will appear first on a monitor, and you will work on this task consecutively for next several rounds.”

[See Fig. S4B, Top Left.]

“In this task, you will be asked to choose one of two lotteries for your own reward. As shown in the example screen, each lottery yields one of three monetary outcomes (in yen), Outcome Red, Outcome Blue, or Outcome Green, with equal likelihood, 1/3. You will have two lottery options (in yen) for the three outcomes. If you choose the top option in this example, you will receive 720 yen if Outcome Red occurs, 1,080 yen for Outcome Green, and 1,800 yen for Outcome Blue. You have to choose one of the two lottery options within 6 seconds.”

[See Fig. S4B, Middle Left.]

“After you make a decision, the chosen option will be highlighted as in the example screen below.”

[See Fig. S4B, Bottom Left.]

“During the experiment, several consecutive rounds for the allocation task will alternate with several consecutive rounds for the lottery task. When the task is switched to the other task, you will be notified either with the ‘Distribute’ screen or the ‘Roulette’ screen.”

“For the allocation task, you will be asked to make a total of 36 choices for the three others. At the end of the experiment, one of your 36 allocation choices will be randomly selected to determine the actual rewards to be paid to the three persons in cash (please note that your allocation choices for the three others do not affect your own reward). We guarantee that you will not see the three persons when you leave the experiment and that you will remain completely anonymous after the experiment.”

“For the lottery task, you will be asked to make a total of 36 choices for yourself. At the end of the experiment, one of your 36 lottery choices will be randomly selected. One of the three monetary outcomes in the selected lottery will then be picked with one-third probability to determine your reward. You will be paid the money in cash at the end of the experiment.”

[After receiving the instructions, participants were given a practice session using a computer display setup equivalent to that used during the fMRI scanning session. A short quiz was administered immediately thereafter to confirm that participants understood the two tasks and the overall procedure correctly. Then participants were taken to the scanning room.]

Scanning sessions.

After we acquired a T1 structural image, participants underwent two functional scanning sessions (see scanning parameters in SI Materials and Methods, Scanning parameters). Each session had 36 trials consisting of four nine-trial blocks (two blocks for the distribution task and two blocks for the gambling task). Across the two scanning sessions, participants made 72 decisions, 36 distribution decisions for the unknown others, and 36 gambling decisions for themselves. The task order was counterbalanced across participants.

Scanning parameters.

The fMRI data and structural data were acquired with a Siemens 3T Trio Tim whole-body scanner with a 12-channel head coil. T1-weighted images were obtained at the beginning of the scanning session with the following parameters: echo time (TE), 2 ms; repetition time (TR), 2,000 ms; flip angle, 10°; resolution, 1 × 1 × 1 mm³; bandwidth, 250 Hz/pixel. For functional imaging, whole-brain T2*-weighted echo-planar images (EPIs) were obtained using a gradient-echo sequence with the following parameters: 42 oblique slices; TE, 25 ms; TR, 2,500 ms; flip angle, 90°; field of view, 192 × 192 mm²; slice thickness, 3 mm; interslice gap, 0 mm; in-plane resolution, 3 × 3 mm²; bandwidth, 1,905 Hz/pixel. A total of 293 volumes including five dummy scans preceding each run was acquired twice (∼12 min for each run). On the basis of anatomical information obtained from the T1 image, the EPI’s field of view was tilted 30° to forehead from the anterior commissure (AC)–posterior commissure (PC) plane to encompass the whole brain and to minimize susceptibility artifacts in the orbitofrontal cortex (51).

Task structure and task flow.

The numeric structure of the choice sets was held identical between the two tasks (Table S2). Presentation order of the 36 choice sets within each task was also randomized.

Table S2.

Thirty-six choice pairs used in the fMRI experiment

Pair no.	Option	π1	π2	π3	Total	Min	Gini
1	1	290	500	1,010	1,800	290	0.4
	2	350	380	1,070	1,800	350	0.4
2	1	150	780	870	1,800	150	0.4
	2	50	800	950	1,800	50	0.5
3	1	230	620	950	1,800	230	0.4
	2	200	320	1,280	1,800	200	0.6
4	1	260	560	980	1,800	260	0.4
	2	160	220	1,420	1,800	160	0.7
5	1	350	560	890	1,800	350	0.3
	2	330	810	960	2,100	330	0.3
6	1	360	540	900	1,800	360	0.3
	2	190	880	1,030	2,100	190	0.4
7	1	330	600	870	1,800	330	0.3
	2	150	750	1,200	2,100	150	0.5
8	1	330	600	870	1,800	330	0.3
	2	210	420	1,470	2,100	210	0.6
9	1	400	640	760	1,800	400	0.2
	2	630	660	1,110	2,400	630	0.2
10	1	470	500	830	1,800	470	0.2
	2	460	760	1,180	2,400	460	0.3
11	1	440	560	800	1,800	440	0.2
	2	380	680	1,340	2,400	380	0.4
12	1	440	560	800	1,800	440	0.2
	2	380	440	1,580	2,400	380	0.5
13	1	470	680	1,550	2,700	470	0.4
	2	240	1,140	1,320	2,700	240	0.4
14	1	290	1,040	1,370	2,700	290	0.4
	2	100	1,150	1,450	2,700	100	0.5
15	1	200	1,220	1,280	2,700	200	0.4
	2	210	660	1,830	2,700	210	0.6
16	1	220	1,180	1,300	2,700	220	0.4
	2	40	730	1,930	2,700	40	0.7
17	1	600	690	1,410	2,700	600	0.3
	2	490	1,120	1,390	3,000	490	0.3
18	1	390	1,110	1,200	2,700	390	0.3
	2	280	1,240	1,480	3,000	280	0.4
19	1	480	930	1,290	2,700	480	0.3
	2	130	1,240	1,630	3,000	130	0.5
20	1	480	930	1,290	2,700	480	0.3
	2	390	420	2,190	3,000	390	0.6
21	1	610	940	1,150	2,700	610	0.2
	2	730	1,180	1,390	3,300	730	0.2
22	1	630	900	1,170	2,700	630	0.2
	2	550	1,210	1,540	3,300	550	0.3
23	1	710	740	1,250	2,700	710	0.2
	2	410	1,160	1,730	3,300	410	0.4
24	1	550	1,060	1,090	2,700	550	0.2
	2	10	1,630	1,660	3,300	10	0.5
25	1	250	1,660	1,690	3,600	250	0.4
	2	710	740	2,150	3,600	710	0.4
26	1	600	960	2,040	3,600	600	0.4
	2	580	640	2,380	3,600	580	0.5
27	1	690	780	2,130	3,600	690	0.4
	2	380	680	2,540	3,600	380	0.6
28	1	510	1,140	1,950	3,600	510	0.4
	2	300	480	2,820	3,600	300	0.7
29	1	670	1,180	1,750	3,600	670	0.3
	2	630	1,470	1,800	3,900	630	0.3
30	1	640	1,240	1,720	3,600	640	0.3
	2	270	1,800	1,830	3,900	270	0.4
31	1	790	940	1,870	3,600	790	0.3
	2	590	770	2,540	3,900	590	0.5
32	1	720	1,080	1,800	3,600	720	0.3
	2	510	540	2,850	3,900	510	0.6
33	1	910	1,060	1,630	3,600	910	0.2
	2	1,010	1,340	1,850	4,200	1,010	0.2
34	1	760	1,360	1,480	3,600	760	0.2
	2	660	1,620	1,920	4,200	660	0.3
35	1	870	1,140	1,590	3,600	870	0.2
	2	610	1,300	2,290	4,200	610	0.4
36	1	910	1,060	1,630	3,600	910	0.2
	2	660	780	2,760	4,200	660	0.5

Note: The third through fifth columns indicate amounts (in yen) received by the unknown persons Red, Green, and Blue in the distribution task, and amounts received by the participant if event Red, Green, or Blue occurred (with 1/3 probability each) in the gambling task. The sixth column indicates the total amount, the seventh column indicates the minimum amount, and the last column indicates the Gini coefficient for each option. The order of the two options in each pair and the order of the 36 pairs were randomized across participants and the two tasks, and did not follow the order of entries in the table. None of Pearson’s correlations between the key task parameters was significant (r_{ΔTotal, ΔMin} = 0.06, P = 0.74; r_{ΔTotal, ΔGini} = 0.00, P = 1.00; r_{ΔMin, ΔGini} = 0.17, P = 0.32).

The task flow and duration are shown in Fig. S4B. First, a picture of a hand offering cash (distribution task) or a picture of a roulette wheel (gambling task) was shown for 1.5 s. This event appeared only once at the beginning of each nine-trial block. After a 0.9-s fixation cross, two choice options were displayed for 7 s, during which participants had to make a decision using an MRI-compatible hand-held button box (Fiber Optic Response Devices; Current Designs). After a fixation cross was displayed for 2–6 s, a feedback screen appeared for 2.5 s, in which the chosen option was highlighted with a magenta-colored frame. Each trial ended with a rest period of 4–6 s. We used Matlab R2011a (The MathWorks) with a Cogent Graphics toolbox (Cogent 2000, version 1.32) to present stimuli and record responses with the button box device. During scanning, the visual stimuli were displayed via a liquid-crystal display (LCD) projector (Victor DLA-G150CL) onto a rear-projection screen behind the participant’s head, which could be viewed using a fixed mirror on the head receive coil.

Goodness-of-fit tests of three economic models for participants’ behavioral choices.

We examined goodness of fit of three economic models to see how each model could explain participants’ behavioral choices in distributions for others and gambles for self.

As in experiment 1, we first applied the quasi-maximin model (Eq. S1). Because the number of options in each choice set was two in experiment 2, the maximum-likelihood estimation used the following logit (softmax) model:

$$\mathrm{Pr}\left(\text{choosing}\hspace{0.17em}\text{option}\hspace{0.17em}\text{A}\right)=\frac{{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}A\right)}}{{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}A\right)}+{\text{e}}^{\mathrm{\gamma }U\left(option\hspace{0.17em}B\right)}},$$ [S3]

where U(option A) is modeled by Eq. S1 and parameter γ reflects the participant’s sensitivity to utility differences between option A and option B.

As an alternative choice model, we applied a constant relative risk aversion (CRRA) model to estimate each participant’s risk preference. This model has been used widely in economics to assess individual utility functions (42). Applied to our equally likely three-outcome cases, the CRRA model posits that the utility of option x for participant i is given by the following:

$$U_i\left(x\right)\hspace{0.17em}=\hspace{0.17em}1/3\cdot \frac{{{\pi }_1}^{\left(1-r_i\right)}}{\left(1-r_i\right)}+1/3\cdot \frac{{{\pi }_2}^{\left(1-r_i\right)}}{\left(1-r_i\right)}+1/3\cdot \frac{{{\pi }_3}^{\left(1-r_i\right)}}{\left(1-r_i\right)},$$ [S4]

where r_i is a parameter representing the curvature of participant i’s utility function. Individuals with r = 0 are risk neutral; 0 < r < 1, risk averse; and r < 0, risk seeking. For each participant, we obtained the model parameters separately for distributions (r_{i,distribution}) and gambles (r_i,gamble) by applying maximum-likelihood estimation to the participant’s binary choices in each task. The maximum-likelihood estimation used the same logit (softmax) model as in Eq. S3. We used the simulated annealing algorithm for numerical estimation implemented in R (www.r-project.org).

As a third choice model, we also applied a mean-variance model (11, 14) to estimate each participant’s concern about outcome variability. This model has been used commonly in the decision-making literature concerning financial risk (e.g., refs. 15 and 17). Applied to our equally likely three-outcome cases, the mean-variance model posits that the utility of option x for participant i is given by the following:

$$U_i\left(x\right)=1/3\cdot \left({\pi }_1+{\pi }_2+{\pi }_3\right)-{\beta }_i\cdot \text{variance}\left[{\pi }_1,{\pi }_2,{\pi }_3\right],$$ [S5]

where β_i captures the individual weight reflecting the concern about outcome variability. For each participant, we obtained the model parameters separately for distributions (β_{i,distribution}) and gambles (β_i,gamble) by applying maximum-likelihood estimation to the participant’s binary choices in each task. The maximum-likelihood estimation used the same logit (softmax) model as in Eq. S3. We used the Nelder–Mead algorithm for numerical estimation implemented in R (www.r-project.org).

In Table S4, we summarized goodness of fit of the quasi-maximin model (Eq. S1), the CRRA model (Eq. S4), and the mean-variance model (Eq. S5) to each participant’s 36 choices in terms of Akaike information criterion (AIC) (52). As seen in Table S4, the mean AIC scores for the quasi-maximin model are the smallest in both distributions for others (M = 27.858) and gambles for self (M = 30.460), suggesting that the quasi-maximin model (6) (Eq. S1) provides the best fit to the participants’ choices in both tasks among the three models.

Table S4.

Goodness of fit of the quasi-maximin model, the CRRA model, and the mean-variance model to each participant’s choices in distributions and gambles in terms of AIC

Participant	Distribution: AIC			Gamble: AIC
	Maximin model	CRRA model	Mean-variance model	Maximin model	CRRA model	Mean-variance model
1	9.664	35.932	22.110	18.279	41.542	29.578
2	31.885	29.944	23.332	31.141	29.565	40.483
3	20.672	12.860	12.828	20.676	12.213	11.188
4	27.757	36.891	35.189	23.956	40.516	36.634
5	16.263	37.539	26.263	26.688	39.463	33.013
6	21.943	40.845	27.973	28.695	22.946	26.618
7	9.664	35.932	22.110	22.792	33.695	22.535
8	29.310	40.606	41.539	41.287	45.578	44.131
9	—	—	—	42.530	39.303	32.643
10	46.196	42.861	47.189	34.939	34.301	39.153
11	20.107	15.141	38.140	20.654	17.041	37.137
12	47.439	40.485	47.167	48.772	48.672	43.889
13	31.640	41.456	33.142	23.314	31.747	45.905
14	5.897	39.967	26.701	35.426	20.264	14.827
15	46.642	48.701	47.865	34.951	33.119	41.098
16	48.935	51.442	46.276	42.815	46.308	40.784
17	20.647	17.328	15.339	20.659	16.201	13.982
18	23.586	37.067	23.004	39.510	35.876	27.449
19	22.832	31.758	21.177	22.313	39.029	26.179
20	29.901	29.742	28.587	37.872	37.079	42.783
21	21.088	26.724	15.146	20.649	17.360	15.339
22	47.110	49.373	44.411	34.615	35.799	43.661
23	33.969	40.773	47.892	47.058	41.455	47.871
24	14.639	19.633	43.451	16.492	21.314	44.403
25	16.608	40.309	28.427	17.573	39.755	30.803
26	44.924	43.993	47.592	46.525	41.847	47.542
27	29.527	30.553	40.011	24.826	24.172	28.873
28	33.325	30.162	31.667	27.865	4.660	4.113
Average	27.858	35.112	32.760	30.460	31.815	32.593

Note: For details about the models, see SI Materials and Methods, Goodness-of-fit tests of three economic models for participants’ behavioral choices. Participant 9 failed to respond to two of the 36 questions in the distribution task within the time limit. Due to the missing responses, it was impossible to estimate the parameters (and AIC) of any of the three models for this participant. Accordingly, participant 9’s data were not included in the analysis reported in Fig. 2 A and E in the main text.

Image processing and statistical analysis.

The data analysis was performed with Statistical Parametric Mapping 8 (SPM8) (www.fil.ion.ucl.ac.uk) running on Matlab R2011a. The fMRI data that we used for the analyses are available at neurovault.org/collections/CGWFWEXV. The first five images of each run were discarded to allow for T1 equilibration effects. For each participant, all volumes were spatially realigned to the first volume of the first session to correct for between-scan motion. Realigned T1-weighted images were segmented into gray, white, and cerebrospinal fluid (53), and spatially normalized to the Montreal Neurological Institute (MNI) anatomical brain template using the VBM8 toolbox (Structural Brain Mapping Group, University of Jena, Jena, Germany; dbm.neuro.uni-jena.de/vbm). The spatial transformation derived from segmentation was then applied to the realigned EPIs for normalization and resampled in 1.5 × 1.5 × 1.5-mm³ voxels using trilinear interpolation in space. All functional volumes were then spatially smoothed with a 6-mm full-width at half-maximum (FWHM) isotropic Gaussian kernel for the group analysis.

Functional data were analyzed using a random-effect model (54) implemented in a two-level procedure. For each participant, all instances of a particular event type were modeled through convolution with a canonical hemodynamic response function. At the first level, neural responses while participants made decisions (i.e., the time window from appearance of the choice option until the participants made decisions with varying durations up to 7,000 ms) in the two conditions (distributions for others and gambles for self) were modeled in a series of general linear models. We used three parametric regressors, ΔMin, ΔTotal, and ΔGini, viz., the absolute difference in minimum, total, and the Gini coefficient between the two choice options (Fig. S4A and Table S2). In addition, cue events for task switching with a duration of 1,500 ms, choice feedback events with a duration of 2,500 ms, and postdecision period (i.e., the time window from the participants’ decision making until disappearance of the choice options) were modeled as regressors of no interest. Activation due to observation of the fixation cross during intertrial intervals was used as a baseline measure.

As the quasi-maximin model (Eq. S1) provided the best fit to the behavioral-choice data in the model selection (SI Materials and Methods, Goodness-of-fit tests of three economic models for participants’ behavioral choices and Table S4), we first analyzed how RTPJ activity responded to the maximin parameter (Fig. 2B). We regressed the RTPJ activity during decision making to absolute difference in minimum (ΔMin) between the two options, viz., the parameter representing the superiority of one option to the other on the maximin criterion using the following participant-specific model:

$$\begin{array}{c}\text{BOLD}={\beta }_0\cdot X_0\\ \mathrm{+}\left({\beta }^D\mathrm{+}{\beta }_M^D\cdot \mathrm{\Delta }{\text{Min}}^D\right)\cdot X_1\\ \mathrm{+}\left({\beta }^G\mathrm{+}{\beta }_M^G\cdot \mathrm{\Delta }{\text{Min}}^G\right)\cdot X_2\\ \mathrm{+}{\beta }_{postdecision}^{D+G}\cdot X_3\\ +{\beta }_{feedback}\cdot X_4\\ +{\beta }_{cue}\cdot X_5\\ +\epsilon ,\end{array}$$ [S6]

where X denotes the modeled design and β denotes the estimated value. Superscripts D and G index the distribution task and the gambling task, respectively, and subscript M indexes Min. In addition, we modeled the feedback, task-switching cue, and residual error ε as explanatory variables.

Fig. 2.

Results from the fMRI experiment. (A) Concordance of individual maximin weights between distributions (α_distribution) and gambles (α_gamble). Points colored in blue correspond to the participants classified as Rawlsians in distributions for others but largest-total seekers in gambles for self according to their most frequent choices (Table S3). Spearman rank correlation between α_distribution and α_gamble is significant even with these “switching” participants (ρ = 0.48; P < 0.01). (B) Activity of the right temporoparietal junction (RTPJ) during decision making. RTPJ activation was positively correlated with increase in absolute difference in minimum (ΔMin) between the two options (solid circle). Activation of the RTPJ was also functionally connected to activation of the caudate (dotted oval). (C) Dissociation between ΔMin and the other parameters (ΔTotal, ΔGini) in the RTPJ at peak coordinates [44 −64 21] identified by conjunction analysis between the two tasks (T = 3.17; P_FWE = 0.025). Error bars represent SEM. (D) Stronger RTPJ–caudate connectivity in distributions for others than in gambles for self (T = 2.83; P < 0.007) at the peak caudate coordinates [−20 −27 27] identified by conjunction analysis between the two tasks. Error bars represent SEM. (E) Individual scores for elevated maximin concern in distributions over gambles, as indexed by differences in RTPJ–caudate connectivity (contrast estimate_distribution − contrast estimate_gamble) and differences in maximin weight (α_distribution − α_gamble).

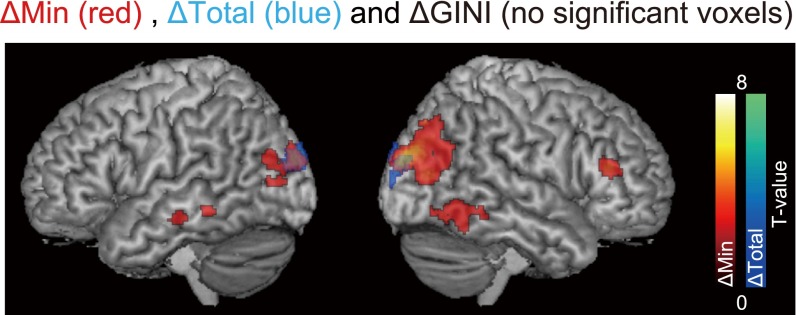
Next, to see that the RTPJ activity is dissociable from the other two task parameters (ΔTotal: the absolute difference in total; ΔGini: the absolute difference in Gini between the two choice options), we included these parameters in the regression (Fig. 2C). To allow these parametric regressors to compete for variance, we turned off the orthogonalization option in SPM8 as recommended by Mumford et al. (50), in the following analysis:

$$\begin{array}{c}\text{BOLD}={\beta }_0\cdot X_0\\ \mathrm{+}\left({\beta }^D\mathrm{+}{\beta }_M^D\cdot \mathrm{\Delta }{\text{Min}}^D+{\beta }_T^D\cdot \mathrm{\Delta }{\text{Total}}^D+{\beta }_G^D\cdot \mathrm{\Delta }{\text{Gini}}^D\right)\cdot X_1\\ \mathrm{+}\left({\beta }^G+{\beta }_M^G\cdot \mathrm{\Delta }{\text{Min}}^G+{\beta }_T^G\cdot \mathrm{\Delta }{\text{Total}}^G+{\beta }_G^G\cdot \mathrm{\Delta }{\text{Gini}}^G\right)\cdot X_2\\ \mathrm{+}{\beta }_{postdecision}^{D+G}\cdot X_3\\ \mathrm{+}{\beta }_{feedback}\cdot X_4\\ \mathrm{+}{\beta }_{cue}\cdot X_5\\ \mathrm{+}\epsilon ,\end{array}$$ [S7]

where subscripts T and G index Total and Gini, respectively, and the other notations are identical to those used in Eq. S6. As in Eq. S6, we also modeled the feedback, task-switching cue, and residual error ε as explanatory variables. Thus, parameter estimates for each regressor were calculated for each voxel, obtained by maximum-likelihood estimation. For a second-level random-effect analysis, the contrast images for each participant were entered into a repeated-measures ANOVA to compute statistical maps of the experiment (55).

Connectivity analysis.

We examined the functional connectivity between the RTPJ associated with ΔMin of presented options and the caudate, a value-related region, using psycho-physiological interaction (PPI). We first confirmed that the caudate, the region of interest (ROI) in this PPI analysis, was actually involved in tracking the utility of participants’ choices in a similar way to the previous studies (14, 38). As Hsu et al. (14) argued in their analysis, the choice utility became most salient during the feedback phase in which the participants’ choices were highlighted visually. Thus, following the same procedure as in Hsu et al. (14), the utility difference between chosen and unchosen options [i.e., U_chosen – U_unchosen (=ΔU) calculated by the quasi-maximin model (6) using α estimated for each participant] was entered as a trial-by-trial parameter for the feedback phase into the design matrix of analysis. We modeled the brain activities in the participant-specific manner as the following equation:

$$\begin{array}{c}\text{BOLD}={\beta }_0\cdot X_0\\ \mathrm{+}{\beta }^D\cdot X_1\\ +{\beta }^G\cdot X_2\\ \mathrm{+}{\beta }_{postdecision}^{D+G}\cdot X_3\\ +\left({\beta }^{FB}+{\beta }_U^{FB}\cdot \mathrm{\Delta }U\right)\cdot X_4\\ \mathrm{+}{\beta }_{cue}\cdot X_5\\ \mathrm{+}\epsilon ,\end{array}$$ [S8]

where X denotes the modeled design and β denotes the estimated value. Superscripts D and G index the distribution task and the gambling task, respectively, and FB indexes feedback. Subscript U indexes utility. The task-switching cue and residual term were also modeled. The result after small-volume correction (SVC) of the anatomically defined caudate nucleus using the “Hammersmith atlas” (56) showed that the caudate tracked the utility difference between the chosen and unchosen options (T = 5.04; P_FWE < 0.05). Even in the whole-brain result, the caudate was significantly associated with the utility difference (Table S6).

Table S6.

Summary of the whole-brain result of parametric modulation analysis (U_chosen – U_unchosen)

Regions	MNI coordinates of peak, mm			T value (peak)	No. of voxels
	x	y	z
Uchosen – Uunchosen
Cerebellum	−6	−44	−48	5.99	12,364
	39	−50	−32	4.91	133
	18	−63	−30	4.71	58
	18	−32	−35	4.39	77
Caudate	6	18	6	5.04	360
MCC	14	17	36	4.72	101
Precuneus	15	−41	41	4.71	58
LPFC	26	35	23	4.63	60
Visual area	−9	−83	21	4.57	133
Lingual gyrus	11	−60	0	4.51	215
PG	12	−3	−18	4.39	23
SPL	−18	−48	44	4.10	58
Insula	33	15	−14	4.08	38
Postcentral gyrus	−57	3	14	4.05	52
vmPFC	−12	53	8	3.99	48
	11	42	6	3.91	69
IPL	−51	−35	32	3.90	20
Front polar	−23	44	2	3.82	23
Thalamus	−6	−6	−3	3.76	20

LPFC, lateral prefrontal cortex; MCC, middle cingulate cortex; PG, parahippocampal gyrus; SPL, superior parietal lobule; vmPFC, ventromedial prefrontal cortex. P_uncorrected < 0.001.

For the PPI analysis, we used the same model as in Eq. S6 to specify the effect of decision-making period. As shown in Fig. 2, we have already confirmed that the RTPJ was sensitive to ΔMin in both tasks (e.g., Fig. 2 B and C, Fig. S5, and Table S5). Here, we first identified the voxels in the RTPJ for each participant that were significant in the omnibus F test of Eq. S6 (distributions and gambles were conditions of interest) with the threshold of P_uncorrected < 0.001. From these voxels, the most significant peak coordinates were individually identified within 10 mm from the average coordinates (x = 46, y = −63, z = 23) in the RTPJ based on related previous studies (see Materials and Methods, Experiment 2, fMRI Experiment, in the main text). We could have used the group-level average peak of distinct RTPJ activity in response to ΔMin (x = 44, y = −64, z = 21; Fig. 2C in the main text) in this analysis, but that group-level peak was inferred using SVC originated at the average coordinates above; thus, individual peaks identified using these coordinates could have been away from the original region of interest. Therefore, to avoid a “double inference,” the average coordinates (x = 46, y = −63, z = 23) based on the previous studies (35, 44–49) were again used to identify individual peaks, which were used as the seeds to extract brain activity for the PPI analysis. This analysis included the interaction term between the time course of activity in the seed region [i.e., extracted blood oxygen level-dependent (BOLD) signal] and the psychological variables (decision making vs. post-decision making in distribution and gambling tasks). The interaction terms of the distribution and gambling tasks were entered as regressors into the design matrix of the PPI model. Then model estimation was performed at the single-participant level to reveal the brain areas with significant connectivity in the whole brain to and from the seed region. As a group analysis, contrast estimates of the PPI results of distribution and gambling tasks were entered into a repeated-measures ANOVA.

Fig. S5.

Regions that were sensitive to ΔMin (red), ΔTotal (blue), and ΔGini (no significant voxels) displayed on the average activation of distribution and gamble. P_uncorrected < 0.005 and cluster size > 50.

Table S5.

Summary of the whole-brain imaging results of parametric modulation analysis (ΔMin, ΔTotal, ΔGini)

Regions	MNI coordinates of peak, mm			T value (peak)	No. of voxels
	x	y	z
Distribution ΔMin
Visual areas	14	−81	6	13.70	12,364
	−18	−87	20	5.86	918
Cerebellum	3	−59	−36	4.55	61
	21	−56	−45	4.16	270
	−21	−41	−36	3.79	80
R IFG	56	33	15	3.89	39
R angular gyrus (TPJ)	41	−63	26	3.80	33
R ITG	54	−54	−20	3.80	29
L IFG	−45	30	−15	3.80	21
R SPL	21	−75	44	3.74	25
L OFC	−26	15	−23	3.71	40
L MTG	−54	−26	−15	3.62	26
R lingual gyrus	9	−57	4	3.43	20
Gambling ΔMin
Visual areas	14	−80	4	12.16	4,406
	−26	−60	1	3.81	43
	−11	−92	12	3.80	84
	−15	−68	9	3.45	21
SFG	−20	−11	44	4.56	77
	29	24	53	4.02	193
	20	42	48	3.80	28
Cerebellum	−3	−53	−54	4.29	137
	−45	−60	−41	4.06	58
	−26	−75	−54	3.72	39
	−33	−65	−39	3.55	25
	38	−68	−50	3.52	13
R ITG	59	−47	−11	4.39	425
R lingual gyrus	11	−33	−5	4.20	235
R SPL	23	−74	45	4.15	118
L MMC	−5	−32	33	3.91	333
MTG	−66	−41	−9	3.73	40
	63	−56	3	3.42	18
	−47	−24	−3	3.44	13
R IFG	51	36	18	3.65	49
L fusiform gyrus	−36	−31	−23	3.54	14
R angular gyrus (TPJ)	44	−59	20	2.91	38
Distribution ΔTotal
Visual areas	12	−83	3	7.56	1,613
R Putamen	29	5	11	3.77	15
Gambling ΔTotal
Visual areas	12	−83	3	11.36	5,845
	−12	−78	−8	5.54	1,154
	−20	−90	23	4.77	646
	−18	−69	12	3.55	54
R precuneus	18	−57	35	3.74	20
L Insula	−42	−4	11	3.39	11
Distribution ΔGini
No significant area
Gambling ΔGini
No significant area

IFG, inferior frontal gyrus; ITG, inferior temporal gyrus; L, left; MTG, middle temporal gyrus; R, right; SFS, superior frontal sulcus. P_uncorrected < 0.001, cluster size > 10.

We sought voxels in the caudate, the brain region associated with marginal utility of choice options in social distribution (28, 38) (see also the utility analysis above), in which activity was correlated with the extracted activity of the seed in RTPJ. We used exactly the same caudate ROI as in the utility analysis [i.e., anatomically defined caudate nucleus using the Hammersmith atlas (56)] for SVC in this parametric modulation analysis, because we wanted to check the overlap of significant areas in the caudate between the utility analysis and this parametric modulation analysis. The results reported in the main text are significant at P_FWE < 0.05 (corrected for familywise error) at the voxel level after SVC.

Both left and right caudates were functionally connected with the RTPJ (Fig. 2B in the main text; we used 3D slicer, version 4.4, https://www.slicer.org, for this figure). We also performed a conjunction analysis to locate peak coordinates that coactivated with the RTPJ in both distributions and gambles. The RTPJ–caudate connectivity at the peak caudate coordinates of the conjunction (x = −20, y = −27, z = 27) was stronger in distributions than in gambles (T = 2.83; P < 0.007) (Fig. 2D in the main text), which corroborates the behavioral result (Fig. 2A) that mean maximin weight (α) was greater in distributive choices (M = 0.22) than in gambling choices (M = 0.10).

Finally, we confirmed that the significant area in the caudate responding to the utility difference overlapped (54 voxels) with the regions of caudate found in the PPI analysis. These results suggest that the brain regions of RTPJ and caudate and their functional connectivity reflect utility processing as suggested by the economic model (6).

Follow-Up fMRI Experiment.

It could be argued that the activation of the RTPJ in the main fMRI experiment simply reflected the abstract numeric comparison of minimum values of presented options per se, and was not necessarily specific to distribution or gambling contexts. To address this issue, we conducted an additional fMRI experiment using a simple calculation task, asking participants to compare two options in terms of minimum, mean, and variance without providing any specific decisional contexts. This follow-up experiment aimed to show that the activation associated with simply comparing minimums of options in the absence of specific decisional contexts was distinct from the activation observed in the main experiment.

Participants.

Twenty-one healthy right-handed students of the University of Tokyo participated in this experiment (12 males; mean age, 21.0 ± 1.9 y). All participants gave written informed consent before the experiment. This study was approved by the Institutional Review Board of the Department of Social Psychology at the University of Tokyo (SPUT-2014-08).

Experimental procedure.

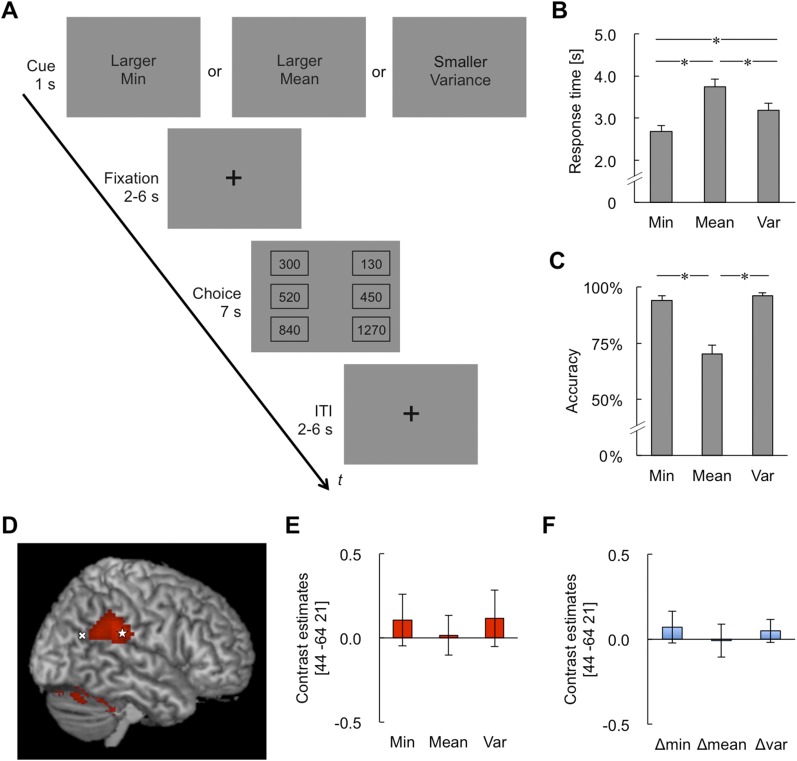
Participants performed a number comparison task (Fig. S6A). In each trial, a condition cue (“larger min,” “larger mean,” or “ smaller variance”) was presented for 1 s, followed by a stimulus onset asynchrony of 2, 4, or 6 s. Then, two options were presented on the left and right side of the fixation cross for 7 s. Each option included three numbers (i.e., a low, middle, and high number) presented vertically. The condition cue of “larger min” asked the participant to choose the option with the larger minimum (hereafter, Min condition). Likewise, participants were asked to choose the option with the larger average for the cue “larger mean” (Mean condition) and to choose the option with the smaller variance for the cue “smaller variance” (Var condition). Participants were instructed to press a button to indicate their choice as soon as possible during the presentation of options (i.e., within 7 s). The choice options were presented for this fixed duration, irrespective of when participants pressed the button. Intertrial interval was 2, 4, or 6 s with a fixation cross.

Fig. S6.

Results from the follow-up fMRI experiment. (A) Task flow of each trial. (B) Response time in the three conditions: larger minimum (Min), larger mean (Mean), and smaller variance (Var). Asterisks show significant difference (*P < 0.05). (C) Response accuracy. (D) The activation in the RTPJ observed in the contrast “Min vs. others” (red colored). Labeling of this activation indicated the supramarginal gyrus. The star symbol shows the overlaid peak of this activation. The “X” shows the overlaid peak (based on the conjunction analysis) from the main experiment. (E) The RTPJ activity in each condition. (F) Parametric modulation for ΔMin, ΔMean, and ΔVariance in the RTPJ in Min trials.

There were 12 trials for each condition, 36 trials in total. We selected 12 pairs from the 36 pairs used in the main fMRI experiment (pairs 6, 7, 8, 18, 19, 23, 24, 30, 31, 32, 35, and 36 in Table S2), based on the constraint that the difference in minimum, average, or variance between two options should be sufficiently large and never zero. The three conditions (Min, Mean, and Var) alternated every four trials, with the order counterbalanced across participants. The ordering of numbers in an option (i.e., low–middle–high or high–middle–low from the top) also alternated every six trials.

Stimuli were presented on an MRI-compatible 32-inch LCD display (NordicNeuroLab) placed at the back of the MR bore. An MRI-compatible response pad (Current Designs) was used to record responses. We used Psychtoolbox on Matlab R2014a (MathWorks) to present stimuli and record responses in this follow-up experiment.

A 3T Prisma scanner (Siemens Medical Systems) equipped for EPI was used to acquire functional magnetic resonance images. A 64-channel head-sized volume coil was used for transmission and reception of radiofrequency signals. Cushions minimized participants’ head movement. Thirty-eight slices of functional images were acquired using BOLD imaging (192 mm × 192 mm × 142.5 mm; in-plane resolution, 64 × 64; in-plane resolution, 3 mm × 3 mm; thickness, 3 mm; 25% distance factor; TR, 2.0 s; TE, 25 ms), covering the entire cerebrum. We used an oblique technique consistent with the main experiment, in which the images were tilted 30° from the AC–PC line to the forehead. We acquired 292 scans after discarding the first 3 scans to ensure magnetization equilibrium.

We used SPM8 (Wellcome Department of Cognitive Neurology, University College London, London, UK) on Matlab to process the scanned images. We performed slice-timing correction using the middle slice as a reference, scan-to-scan realignment, normalization to the EPI template of SPM8, resampling the images with the voxel size of 3 mm × 3 mm × 3 mm, and spatial smoothing (FWHM, 8-mm isotropic Gaussian kernel). A high-pass filter of 128 s was used to remove low-frequency noise. We modeled brain activity for cue presentation (Cue), the duration from option onset to button press (Comp), and the rest of option presentation after button press (PostRes). At the first-level analysis, we retained the three conditions (Min, Mean, and Var) for the second phase (Comp), whereas for the first and the third phases (Cue and PostRes), we treated the three conditions as a single condition. At the second-level analysis, we applied a voxel-level threshold of P_uncorrected < 0.001 to identify clusters of activation, and then the significant clusters were identified using a cluster-level threshold of P_FWE < 0.05.

Experimental instructions.

[The instructions below were read aloud to the participant in the waiting room before she/he entered the fMRI scanner. The participant was also given a written version to read while listening to the experimenter’s instructions.]

“Thank you for coming to our experiment. In this experiment, you will be asked to make simple numeric calculations in the fMRI scanner. At the end of the experiment, you will receive 3,000 yen in cash for your participation. We assure you that there is nothing distasteful or embarrassing in the experiment. But should you find any part of the experiment uncomfortable, you can leave the experiment any time; we will still compensate for your participation.”

“In the experiment, you will be asked to make a series of simple calculations. As shown in the example screen, you will be presented two column options, Left or Right, with three numbers respectively. You will be asked one of the following questions about these two options in the experiment:

• (a) which of the two options (Left or Right) has a larger minimum?

• (b) which of the two options (Left or Right) has a larger mean?

• (c) which of the two options (Left or Right) has a smaller variance?”

“In the experiment, one of these three questions will appear randomly just before the two column options are presented.”

[See Fig. S6A, Top.]

“Please select one of the two column options that you think is correct for the question within 7 seconds. You will be asked to answer a total of 36 questions (12 each for one of the three questions) in the experiment.”

[See Fig. S6A, Middle. The example here is for the LMH order (rowwise: from the Top to the Bottom). There were two row orders (LMH or HML) in the experiment, which were counterbalanced across participants.]

[After receiving the instructions, a short quiz was administered to confirm that participants understood the two tasks and the overall procedure correctly. Then participants were taken to the scanning room.]

Behavioral results.

The behavioral data were analyzed using two-way repeated-measures ANOVAs, which yielded a difference among conditions in response time [F_(2,40) = 28.2; P < 0.001] (Fig. S6B), and accuracy [F_(2,40) = 30.7; P < 0.001] (Fig. S6C). Participants responded faster in the Min condition than in the other two conditions, and also faster in the Var condition than in the Mean condition (P < 0.05, corrected for multiple comparisons using the Bonferroni method). Responses were more accurate in the Min and Var conditions than in the Mean condition (P < 0.05, corrected for multiple comparisons using the Bonferroni method).

fMRI results.

Our main target for this follow-up experiment was the brain activation related to the comparison of the minimum numbers of the presented options. The contrast of Min vs. the other conditions showed significant activation in regions including the anterior part of RTPJ (Fig. S6D). The other contrasts (i.e., Mean vs. the other conditions and Var vs. the other conditions) showed no significant activation. Our concern was whether the activation of the RTPJ was different between the main experiment and this follow-up experiment. The peak activation of the contrast Min vs. the other conditions (x = 63, y = −33, z = 23, in MNI coordinates, shown with a star symbol in Fig. S6D) was substantially anterior to the coordinates reported in the main text (i.e., x = 42, y = −64, z = 25 in distributions and x = 44, y = −66, z = 18 in gambles, both in MNI coordinates; the location of the peak coordinates by conjunction analysis is shown with an “X” in Fig. S6D). Identification and labeling using SPM Anatomy Toolbox showed that the activation of the RTPJ in this follow-up experiment included the superior temporal gyrus and the supramarginal gyrus but not the angular gyrus, corresponding to the canonical social TPJ (39), where the peak coordinates in the main experiment were located. These results indicate that the RTPJ activation in this follow-up experiment was totally different from that in the main experiment.

We further confirmed that the brain activity in the RTPJ related to distribution or gambling contexts reported in the main text was unrelated to the simple comparison of minimum numbers in this follow-up experiment. An ROI of the RTPJ was defined as a sphere of 8-mm radius centered at the group-level peak identified by the conjunction of distributions and gambles (x = 44, y = −64, z = 21, in MNI coordinates; see also Fig. 2C in the main text). Contrast estimates in this ROI for the three conditions were calculated using MarsBaR toolbox. In all three conditions, the activity was similarly close to zero [F_(2,40) = 0.539; P = 0.587] (Fig. S6E). In addition, we analyzed the brain activity in Min trials modulated by absolute differences of minimum, average, and variance (i.e., ΔMin, ΔMean, and ΔVariance) between the two options. Variance here was defined as the Gini coefficient for consistency with the main experiment. These parametric modulations on activity in the RTPJ were also close to zero in Min trials [F_(2,40) = 0.297; P = 0.745] (Fig. S6F). It should be noted that the task here was not performed in the context of either distributions or gambles. These results corroborate our conclusion that the activation for simply calculating and/or comparing minimums of options outside of a specific decisional context was distinct from the activation in the main experiment. Again, these findings support the results described in the main text that RTPJ activity is associated with spontaneous perspective taking according to the maximin criterion when distributive or risky decision making is required.

Experiment 2 (fMRI Experiment)

Task.

To examine our hypothesis that perspective taking (3, 19–26, 29)—the cognitive ability to adopt a different viewpoint beyond one’s immediate situation (myself/now)—is a key to the behavioral–cognitive linkage between the two distinct decisions, we conducted an fMRI experiment. Similar to the behavioral experiment, 30 participants made 36 distribution decisions for unknown others as a third party and 36 gamble choices for themselves (Table S2). Participants had two options in each trial (Materials and Methods).

Region of Interest.

Recent neural evidence suggests that the RTPJ plays a crucial role in adopting a different viewpoint and shifting attention away from one’s own immediate environment to others (20–25) and to different times and locations (20–22, 26, 29). This region has also been implicated in empathy (31), moral reasoning (32, 33), and altruistic behavior (34, 35), for which perspective taking is required. Although previous studies on gambling have not addressed the role of perspective taking directly, they have also reported value-related activity in the intraparietal cortex, located near the TPJ (36, 37). Thus, we chose the RTPJ as the region of interest. Our behavioral experiment above revealed that participants generally directed spontaneous attention to the worst possible outcomes in both distributions for others and gambles for self. If, as we hypothesized, such selective attention reflects participants’ perspective taking of the worst-case scenarios, we predict that the RTPJ will be activated to track how choice options compare in terms of the worst possible outcomes (i.e., the maximin criterion) while participants make decisions in both tasks.

Results.

We first confirmed the behavioral-level coherence in participants’ responses between distributions for others and gambles for self.

Choice concordance.

As in the behavioral experiment, participants’ types according to their most frequent choices were consistent across the two tasks (P = 0.004 by Fisher’s exact test) (Table S3). Fig. 2A shows scatterplots of the maximin weight, α_i, for distributions and for gambles, estimated by the economic model (Eq. 1). The maximin weights were correlated across the two tasks (ρ = 0.48; P = 0.007), whereas mean α was greater in distributions (M = 0.22) than in gambles (M = 0.10) [F_(1,54) = 5.63; P = 0.018].

Table S3.

Classification of participants according to their most frequent choices in each task in the fMRI experiment

Distribution	Gamble
	Maximin (Rawlsian)	Total (total seeker)
Maximin (Rawlsian)	0.30	0.30
Total (utilitarian)	0	0.40

P = 0.004 by Fisher’s exact test. n = 30. Note: Because none of the participants were classifiable as the Gini type (variance avoider) in gambling, here we classified participants into either Maximin or Total type according to their most frequent choices in 21 of 36 choice sets where the maximin and the total choices were distinguishable from each other (Table S2). Two participants who were excluded from the fMRI data analysis (Materials and Methods) were also included. The analysis excluding these two participants yielded the same statistical results.

RTPJ activity.

Having replicated the behavioral results, we then examined neural responses (SI Materials and Methods, Image processing and statistical analysis). As the quasi-maximin model (Eq. 1) provided the best fit to the behavioral-choice data in the model selection (Table S4), we first analyzed how RTPJ activity responded to the maximin parameter. We regressed RTPJ activity during decision making to absolute difference in minimum (ΔMin) between the two options, that is, a parameter representing the superiority of one option to the other on the maximin criterion (see Fig. S4A for illustration). If participants’ perspective taking focuses on the worst-off position, it is expected that RTPJ activity will track how the two options compare in terms of minimum outcomes. As expected (Fig. 2B, solid circle), RTPJ activation increased with ΔMin between the two choice options in both distributions (T = 4.47, P_FWE = 0.001 with the peak at x = 42, y = −64, z = 25) and gambles (T = 3.14, P_FWE = 0.043 with the peak at x = 44, y = −66, z = 18). To see that this RTPJ activity is dissociable from the other two task parameters (ΔTotal: the absolute difference in total; ΔGini: the absolute difference in Gini between the two choice options), we then included these parameters in the regression. As seen in Fig. 2C, the RTPJ responded to ΔMin only. Thus, as predicted, the RTPJ tracked the superiority of one choice option to the other by the maximin criterion in both tasks (see also Fig. S5 and Table S5).

Functional connectivity.

To see how such RTPJ activity may be functionally connected to other brain regions, we next conducted a psychophysiological interaction (PPI) analysis. The quasi-maximin model (Eq. 1) posits that the minimum outcome is linearly integrated into the option’s utility by the maximin weight α. Given the involvement of RTPJ in tracking minimum outcomes, the economic model predicts that RTPJ activity will be linearly related to overall valuation of the choice option. Because previous studies found that caudate activity correlated with valuation of options in resource allocations for others (14, 38) (see also Table S6), we focused on the caudate in the PPI analysis (SI Materials and Methods, Connectivity analysis). As predicted, RTPJ activity was connected to activity of both left and right caudates while participants made decisions in both tasks (Fig. 2B, dotted oval). Furthermore, the mean RTPJ–caudate connectivity was stronger in distributions for others than in gambles for self (T = 2.83; P < 0.007) (Fig. 2D), corroborating the behavioral result that the mean α was greater in distributive choices (M = 0.22) than in gambling choices (M = 0.10; Fig. 2A).

Individual differences.

So far, we have reported results from a group-level analysis, but it remains to be seen how individual choice differences may relate to the neural responses observed during decision making. Although behavioral data from the two experiments consistently showed that the maximin concern was generally more pronounced in distributions for others than in gambles for self, the degree of this elevation varied widely across participants (Fig. 2A). We thus examined neural correlates of these individual behavioral differences. For each participant, we calculated the degree of enhanced maximin concern in distributive choices over gambling choices (α_distribution − α_gamble). As the RTPJ–caudate connectivity was stronger in distributions than in gambles at the group level (Fig. 2D), we also calculated the differences in connectivity between the two tasks (contrast estimate_distribution − contrast estimate_gamble) for each participant. Fig. 2E shows scatterplots of these two individual scores. The correlation was significant (ρ = 0.39; P < 0.05).

Abstract numeric comparison.

Finally, it could be argued that the observed commonality of the RTPJ activation between the two tasks in the main fMRI experiment might simply result from the abstract numeric comparison per se, without necessarily being related to distributive or gambling contexts. Therefore, we conducted an additional fMRI experiment using a simple calculation task, in which a different set of participants (n = 21) compared two numeric options in terms of minimum, mean, or variance without any specific decisional context (for details of the procedure and results, see SI Materials and Methods, Follow-Up fMRI Experiment and Fig. S6). Brain activity during the abstract numeric tasks was situated in the superior temporal gyrus and the supramarginal gyrus. In contrast, the peak RTPJ coordinates in the main experiment were located in the angular gyrus, corresponding to the “canonical social TPJ,” which was identified by a recent comprehensive metaanalysis (39) using the Neurosynth database (neurosynth.org) with more than 10,000 fMRI studies. The results confirmed that the RTPJ activity in the main fMRI experiment is clearly distinct from the brain activity involved in this abstract numeric comparison.

Taken together, these convergent results provide strong evidence for our prediction that the RTPJ, the region associated with perspective taking (20–26, 29), tracks the superiority of one choice option to another by the maximin criterion in both distributions for others and gambles for self.

Discussion

Distributive justice is one of the most fundamental building blocks for organizing societies. However, compared with the accumulation of various normative theories by philosophers over the centuries (e.g., refs. 3, 19, 27, and 40), our empirical understanding of people’s distributive judgments remains insufficient. In a series of experiments using attention-monitoring and brain-imaging techniques, we investigated the hypothesis that distributions for others may be psychologically linked to risky decisions for self through the spontaneous perspective taking of the minimum, worst-off position.

The results supported our hypothesis. At the behavioral level, choice preferences varied widely, with Rawlsians who endorsed the maximin principle making up only 47% of participants in distributive choices for others and 37% in gambling decisions for self (Fig. 1B). Interestingly, however, individuals’ choices were highly concordant between the two seemingly distinct tasks—roughly summarizable as risk-averse Rawlsians vs. risk-seeking utilitarians—even though distribution for others as a third party involved no monetary risk for the decision-making participants. More importantly, the worst possible outcome served as a common cognitive anchor during decision making, attracting spontaneous attention across both tasks and participant types.

At the neural level, this common focus on the “floors” was reflected in the activity of the RTPJ, a brain region implicated in mental simulation of a standpoint physically or temporally distant (other/future) from one’s immediate environment [myself/now (20–26, 29)]. The exact role of the RTPJ in social cognition is currently debated, including whether switching between the immediate and distant perspectives is a specialized or domain-general process (23, 29), and how multiple functions of the RTPJ are spatially organized in the region (39, 41). The RTPJ peak coordinates we identified in both tasks (Fig. 2B) were situated in the angular gyrus, corresponding to the canonical “social TPJ” (39), which is associated with theory of mind (23), empathy (31), moral reasoning (32, 33), and altruistic behavior (34, 35). As predicted, the RTPJ activity observed during decisions tracked how options compared according to the maximin criterion in both tasks. The RTPJ was responsive only to this maximin parameter, ΔMin, among the three task parameters. Furthermore, as the quasi-maximin model implied, RTPJ activity covaried with the activity of the caudates, the brain region associated with tracking marginal utilities of options in distributions for others (14, 38). Taken together, these convergent neural results suggest that participants spontaneously engaged in “what-if” thinking according to the maximin criterion in both tasks.

Thus far, we have discussed the similarities of these two seemingly distinct decisions at the behavioral, cognitive, and neural levels. We also observed systematic differences between participants’ responses to the two tasks, including greater maximin concern in distributions for others than in gambles for self, both at the behavioral level (more frequent maximin choices in Fig. 1B and Table S3, and greater α in Fig. 2A and Fig. S1), and at the neural level (stronger RTPJ–caudate connectivity in Fig. 2D). These robust differences indicate that the maximin concern is more central in distributive-justice judgments for others than in personal risky choices.

Importantly, the degree to which the maximin concern was accentuated in social distributions also varied substantially across individuals. For example, as seen in Fig. 1B, although most participants (67%) “remained” in the same types according to their most frequent choices across the two tasks, 18% of the participants “switched” categorically from the largest-total–seeking (i.e., risk-seeking) type when deciding on gambles for self to the Rawlsian type when choosing distributions for others (see Table S3, Fig. S1, and Fig. 2A for similar patterns). These consistent patterns prompted us to explore the neural correlates of such individual differences. As shown in Fig. 2E, the enhanced maximin concern in behavioral distribution choices (α_distribution − α_gamble) correlated with enhanced RTPJ–caudate connectivity in distributions. Participants who had elevated functional RTPJ–caudate connectivity in distributions over gambles also had elevated maximin preferences in distributive choices over gambling choices. We conjecture that the aforementioned “switchers” (the risk-seeking Rawlsians who made up 18% of the participants in Fig. 1B) may be willing to take risks in their personal choices but endorse the maximin principle as a “socially just” policy in the public arena. Notice that the opposite off-diagonal combination in Fig. 1B (i.e., risk-averse utilitarians) was quite rare, making up only 2% of the participants (and 0% in Table S3). Future research focusing more directly on the neural underpinnings of these ideological differences would seem to be important and promising.

Overall, our findings suggest that concern about misfortune, for oneself or others, operates as a strong cognitive anchor in our decision making, if not determining behavioral choices unilaterally. Indeed, among the three choice models applied to analyze the behavioral data (SI Materials and Methods, Goodness-of-fit tests of three economic models for participants’ behavioral choices), the quasi-maximin model (6) (Eq. 1) provided the best fit to participants’ behavioral choices, outperforming the traditional constant relative risk aversion model (42) and the mean-variance model (11) in both distributions for others and gambles for self (Table S4). These results imply that the maximin parameter, which is often ecologically correlated with, yet conceptually distinguishable from, the variance/inequality parameter (3, 11, 19), merits a systematic investigation in cognitive and social neurosciences. Although still suggestive at this point, we believe that disentangling the behavioral and neural effects of the maximin concern from those of the variance/inequality concern will be essential in future research to shed light on the relative contributions of these task parameters in social as well as nonsocial decision making.

Of course, this robust maximin bias in people’s choices bears no normative implication about how we should allocate resources—as Hume’s famous dictum says, we cannot derive “ought” from “is” (40). Nevertheless, we conjecture that this consistent attention to the least fortunate position may serve as a reasonable starting point for designing distributive policies in modern societies (4–7, 14), seeking “common ground not where we think it ought to be, but where it actually is” [Greene (ref. 43, p. 291)]. Our approach also illustrates how cognitive, economic, and neural science methods may be systematically combined to illuminate the functional components of distributive justice in our minds and possibly the common neural underpinnings shared by other nonsocial decisions (12–18).

Materials and Methods

Experiment 1 (Behavioral Experiment).

Participants.

Sixty-seven student volunteers at Hokkaido University (Sapporo, Japan) (32 males; mean age, 18.8 ± 0.78 y) participated in the behavioral experiment. Informed consent was obtained from each participant using a consent form approved by the Institutional Review Board of the Center for Experimental Research in Social Sciences at Hokkaido University (No. 23-4).

Experimental procedure.

Each participant was seated in a private cubicle with a computer. During the experiment, participants worked individually on the two decision tasks, with task order counterbalanced (Fig. 1A).

In the distribution task, participants were asked to choose one of three options as an allocation to three unknown others (identified anonymously as persons A, B, and C) who were participating in another experiment. Participants were asked to make 40 such distribution choices, from which one choice would be randomly designated as a real cash reward for the others; person A would receive the lowest outcome; B, the middle outcome; and C, the highest outcome. It was emphasized that participants and recipients would remain completely anonymous to each other.

In the gambling task, participants were asked to choose one of three lotteries for themselves. Each lottery option had three monetary outcomes with equal likelihood of 1/3. Participants were told that they would make 40 such lottery choices, from which one choice would be randomly selected at the end of the experiment; one of the three monetary outcomes in the chosen lottery would then be randomly picked to determine their own cash reward. No feedback was provided to participants about outcomes resulting from their distribution or lottery choices until the end of the experiment. For details, see SI Materials and Methods, Experimental procedure.

After completing the two decision tasks, participants were asked to answer a short questionnaire to measure their risk attitudes (30). At the end of the experiment, participants received the randomly selected monetary outcome from their lottery choices plus a 200-yen (approximately US$2 at the time) show-up fee as compensation for their participation. They were then dismissed, after which the recipients were paid the allocated rewards from the distribution task. The data are available in Dataset S1.

Experiment 2 (fMRI Experiment).

Participants.

Thirty healthy, right-handed student volunteers at Tamagawa University (Tokyo, Japan) (15 males; mean age, 20.9 ± 1.7 y) with no relevant medical history participated in this study. Informed consent was obtained from each participant using a consent form approved by the Institutional Review Board of the Brain Research Center at Tamagawa University (No. C25-9). All participants had normal or corrected-to-normal visual acuity. We had to exclude data from one participant due to abnormal brain structure, and another due to head movement in excess of the acquired voxel size.

Experimental procedure.

The task setup was identical to that of the behavioral experiment except that we used two choice options instead of three to reduce the visual complexity of the stimuli (Fig. S4A). Participants made 36 choices of reward distributions (14) for three unknown others who were participating in another experiment, and another set of 36 choices as gambles for themselves. The numerical structure of the stimuli was identical between the two tasks (Table S2), the task order was counterbalanced across participants, and presentation order of the 36 choice sets within each task was randomized. For details, see SI Materials and Methods, Experimental procedure–SI Materials and Methods, Task structure and task flow. The behavioral data are available in Dataset S2.

Small-volume correction.

We applied small-volume correction to focus on RTPJ within a 6-mm sphere centered at the mean coordinates (x = 46, y = −63, z = 23), which were calculated from previous studies examining RTPJ activity when taking another’s perspective for altruistic helping (35, 44, 45) or shifting attention away from the here-and-now to imagine one’s own experience at a different time (46–49). The mean coordinates were situated in the canonical social TPJ identified by a recent comprehensive metaanalysis (39).

Statistical analysis.

Neural responses while participants made decisions in the two conditions (distributions for others and gambles for self) were modeled in a series of general linear models. We examined distinct neural correlates of the three parametric regressors, ΔMin, ΔTotal, and ΔGini, defined respectively as the absolute difference in minimum, total, and the Gini coefficient between the two choice options. To allow these parametric regressors to compete for variance, we turned off the orthogonalization option in SPM8 as recommended by Mumford et al. (50). For details, see SI Materials and Methods, Image processing and statistical analysis.