Large-scale recovery of an endangered amphibian despite ongoing exposure to multiple stressors

Significance

Human influences are causing the disappearance of species at a rate unprecedented in millions of years. Amphibians are being particularly affected, and extinctions of many species may be inevitable. The Sierra Nevada yellow-legged frog (Rana sierrae) was once common in the mountains of California (United States), but human impacts have driven it near extinction. Repeated surveys of thousands of water bodies in Yosemite National Park show that the decline of R. sierrae has recently reversed and that population abundance is now increasing markedly in part because of reduced influence of stressors, including disease and introduced fish. These results suggest that some amphibians may be more resilient than is assumed, and with appropriate management, declines of such species may be reversible.

Abstract

Amphibians are one of the most threatened animal groups, with 32% of species at risk for extinction. Given this imperiled status, is the disappearance of a large fraction of the Earth’s amphibians inevitable, or are some declining species more resilient than is generally assumed? We address this question in a species that is emblematic of many declining amphibians, the endangered Sierra Nevada yellow-legged frog (Rana sierrae). Based on >7,000 frog surveys conducted across Yosemite National Park over a 20-y period, we show that, after decades of decline and despite ongoing exposure to multiple stressors, including introduced fish, the recently emerged disease chytridiomycosis, and pesticides, R. sierrae abundance increased sevenfold during the study and at a rate of 11% per year. These increases occurred in hundreds of populations throughout Yosemite, providing a rare example of amphibian recovery at an ecologically relevant spatial scale. Results from a laboratory experiment indicate that these increases may be in part because of reduced frog susceptibility to chytridiomycosis. The disappearance of nonnative fish from numerous water bodies after cessation of stocking also contributed to the recovery. The large-scale increases in R. sierrae abundance that we document suggest that, when habitats are relatively intact and stressors are reduced in their importance by active management or species’ adaptive responses, declines of some amphibians may be partially reversible, at least at a regional scale. Other studies conducted over similarly large temporal and spatial scales are critically needed to provide insight and generality about the reversibility of amphibian declines at a global scale.

The Earth’s biodiversity is imperiled by pervasive and increasing human pressures, with current rates of species loss unprecedented since the last mass extinction event 65 Mya (1). Although all classes of vertebrates contain a significant fraction of threatened species, amphibians stand out as the most at risk. Of 5,743 amphibian species reviewed in the first global assessment of amphibians (2, 3), >30% were categorized as globally threatened with extinction, and several hundred may already be extinct (4). This proportion is far higher than that for birds or mammals, an alarming statistic given that most amphibian lineages persisted through the last four mass extinctions (5). Primary drivers of these ongoing declines include habitat loss, overutilization, introduced species, contaminants, and the infectious disease chytridiomycosis (5). Chytridiomycosis is caused by the amphibian chytrid fungus [Batrachochytrium dendrobatidis (Bd)], a recently emerged pathogen that is now present in amphibian populations worldwide. This disease is implicated in the decline or extinction of hundreds of amphibian species, and threatens hundreds more (4, 6). This impact of Bd has been described as “the most spectacular loss of vertebrate biodiversity due to disease in recorded history” (4).

The Sierra Nevada yellow-legged frog (Rana sierrae) (7) is emblematic of the global decline of amphibians. A century ago, R. sierrae was one of the most abundant amphibians in lakes, ponds, meadows, and streams in California’s Sierra Nevada mountains, including in Yosemite National Park (8, 9), the location of the current study. Despite most of its range being highly protected, R. sierrae has disappeared from >93% of its historical distribution (7). This decline is characterized by precipitous decreases in both occupancy and abundance across the species’ range, including within the most protected landscapes (10–12). To prevent its extinction and facilitate recovery, R. sierrae was recently listed as “endangered” under the US Endangered Species Act (13) and as per the International Union for Conservation of Nature (IUCN) Red List of Threatened Species (3). As with many declining amphibian species, it remains an unanswered question whether R. sierrae can recover given the ongoing impacts of multiple stressors.

The decline of R. sierrae in the Sierra Nevada, including in the protected habitats of Yosemite National Park, is the result of several factors. Declines began in the early 1900s (8) with the introduction of nonnative fish (predatory trout: primarily Oncorhynchus spp. and Salvelinus sp.) into naturally fishless habitats (14–16), including the majority of perennial lakes, ponds, and streams that are the main habitat for R. sierrae (17). More recently, available information suggests that Bd emerged in the Sierra Nevada in the 1970s (18, 19), and its ongoing spread has driven additional declines and extirpations of hundreds of R. sierrae populations (18, 20). In Yosemite, Bd is now essentially ubiquitous (21), and R. sierrae populations that survived initial Bd-caused die offs currently display enzootic frog–Bd dynamics (22) with ongoing impacts to populations (23). Airborne contaminants (including pesticides) originating in California’s agricultural Central Valley are transported downwind to the Sierra Nevada (24, 25) and may also have impacts on amphibians (26, 27). However, an explicit link between pesticides and R. sierrae declines is lacking.

The specific objectives of our study were to (i) describe the trajectory of R. sierrae population sizes in Yosemite National Park over the last 20 y and (ii) relate those changes in population size to changes in stressors and the response of frogs to those stressors. Our results on the long-term dynamics of this particularly well-studied species provide an important case study and may yield more general insights into the reversibility of amphibian declines in other species facing similar stressors. To achieve our objectives, we conducted thousands of R. sierrae population surveys throughout Yosemite over a 20-y period. The large spatial and temporal scales that characterize our study are important, because although several studies have shown that amphibians can recover at local scales (28–31), studies of imperiled amphibians at the more relevant landscape scale are lacking. In addition, because landscape-scale population processes are often characterized by transient dynamics, short-term studies may fail to accurately describe longer-term trends. Our long-term dataset allows strong inferences to be made about current and future R. sierrae population trajectories.

The dataset used in this study included 7,678 frog population surveys conducted at 2,154 water bodies across Yosemite National Park, a highly protected 3,027-km² landscape in California’s Sierra Nevada that constitutes ∼13% of the range of R. sierrae. Surveys were conducted from 1993 to 2012 and included all 483 R. sierrae populations known to occur in Yosemite (16). We estimated trends in R. sierrae abundance using a hierarchical spatiotemporal modeling framework and fit models using integrated nested Laplace approximation (32, 33). Given our results showing that these populations increased substantially over the study period, we also provide results from an experiment that may explain, at least in part, how frog populations could increase in the presence of ongoing stressors, specifically disease.

Results and Discussion

Trends in Frog Abundance.

Across Yosemite, the total abundance of R. sierrae increased markedly over the 20-y study period (Fig. 1). The majority of the observed increase occurred between 1996 and 2005. The estimated intrinsic rate of growth (r) for the number of adult R. sierrae across all water bodies was 0.105 [95% credible interval (95% CI) = 0.075–0.134]. This rate is equivalent to an 11.0% annual increase in population size or a more than sevenfold increase in abundance over 20 y. We found a similar rate of increase for the number of juveniles (r = 0.119; 95% CI = 0.075–0.163; 12.6% annual increase) and an even higher rate of increase for the number of tadpoles (r = 0.227; 95% CI = 0.177–0.277; 25.5% annual increase). Counts at three relatively intensively surveyed sites that now contain some of the largest R. sierrae populations in Yosemite provide examples of these increases (Fig. 2). Substantial increases in abundance at these sites often occurred over the span of only 2–5 y and were temporally asynchronous between basins.

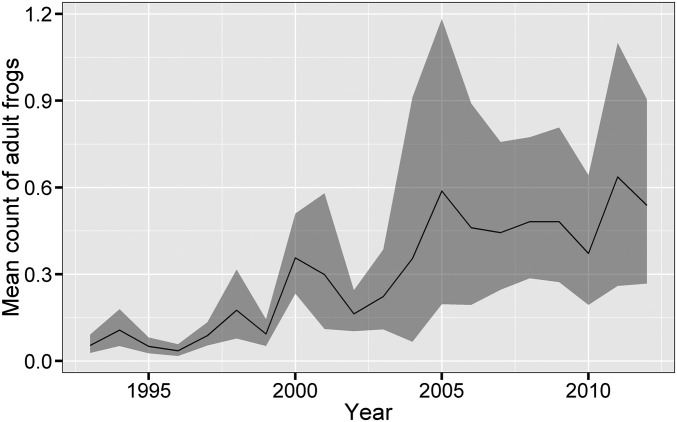
Fig. 1.

Increase in abundance of adult R. sierrae across all surveyed water bodies in Yosemite National Park from 1993 to 2012. Values in each year are the estimated numbers of frogs observed per water body during a survey (averaged across all surveys conducted per year), with a bootstrapped 95% CI. Estimates are for all 2,154 water bodies in Yosemite that were surveyed at least twice during the study period, including those that were not visited in a given year and/or where adult R. sierrae were never observed in any surveys. The relatively low predicted counts are in part because of the existence of many surveyed water bodies that are only marginally suitable and consequently, in which R. sierrae were never detected during the study. Fig. S1 shows the actual distribution of frog counts for water bodies visited in each year and the predicted counts for all water bodies.

Fig. 2.

Counts of adult R. sierrae at three relatively intensively surveyed sites (A–C) showing marked increases in abundance. These sites are fishless and currently contain some of the largest frog populations in Yosemite National Park. When multiple surveys were conducted in a single year, counts were averaged and are shown as mean ±1 SE. In A, the decrease in R. sierrae counts after 2006 may be in part because of the removal of ∼200 adults between 2006 and 2012 for use in translocations aimed at reestablishing R. sierrae populations in nearby habitats.

Positive population growth occurred broadly over most of Yosemite. For 34 of 41 grid cells arrayed across the park (Fig. 3 and details in SI Text), average estimated counts of adult R. sierrae during the last 3 y of the study (2010–2012) were higher than those during the first 3 y (1993–1995). Grid cell values also indicate large spatial variation across Yosemite in average abundance and changes in abundance during the study period (Fig. 3). Growth rates were relatively uniform and moderate across most of the northern half of the park (primarily the Tuolumne River watershed), but growth rates in the southern half of the park (Merced River watershed) showed substantial variability. In this watershed, growth rates were much faster in the eastern (headwaters) portion than in the western (downstream) portion, with five of the downstream cells exhibiting negative growth.

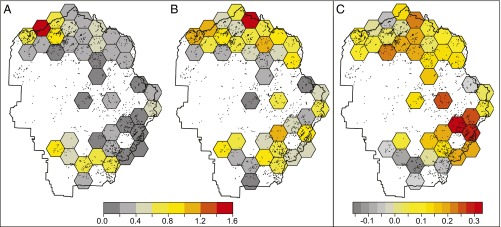
Fig. 3.

Spatial variation in population abundance and growth rate from 1993 to 2012 in counts of adult R. sierrae across Yosemite National Park. Grid cells in A and B depict the estimated counts of R. sierrae averaged across all water bodies in the cell for the first 3 y of the study (1993–1995) and the last 3 y of the study (2010–2012), respectively. Average counts are low (zero to two frogs per water body), because only a minority of water bodies in the cell provide high-quality habitat. C depicts the trend in population abundance between those two time points. Values in C are the intrinsic rates of growth (r), where values greater than zero indicate positive growth and values less than zero indicate negative growth. Frog abundance was notably higher at the end of the study compared with the beginning as reflected in the positive growth rates for most cells.

The addition of five environmental covariates to the base model (fish presence, water depth, elevation, watershed, and precipitation) (additional details are in SI Text) indicated that two covariates had important effects on population abundance: abundance was negatively related to fish presence and positively related to water depth (Tables S1 and S2; see also Table S3; additional details are in SI Text), consistent with known effects of these factors on R. sierrae occupancy and population size (16, 17, 29). More importantly, the inclusion of covariate × year interactions allowed us to examine whether trends in abundance differed with respect to each of the covariates. Results indicated different growth rates in water bodies with and without fish, but the other covariates had little influence on growth rate (Table S2).

Table S1.

Description of predictor variables in the linear mixed models used to describe trends in R. sierrae abundance

Variable name	Description
Year	Year in which survey was conducted
Day	Day of year on which survey was conducted
Water body depth	Maximum depth of water body (in meters) as estimated for deeper water bodies by sounding with a weighted line or visually for shallower water bodies (16)
Water body elevation	Elevation of the water body (meters above sea level) as estimated from 1:24,000 US Geological Survey topographic maps
Precipitation	Annual sum of monthly Merced River discharge in a given year divided by the annual sum of average monthly discharge during 1951–2000; provides a measure of the snowfall amount during the previous winter
Fish	Presence or absence of one or more species of nonnative trout as determined by gill netting for deeper water bodies or visually for shallower water bodies (16)
Watershed	Watershed in which the water body is located: Merced River or Tuolumne River
Observer	Leader of the team conducting the survey: G.M.F. or R.A.K.

Table S2.

Parameter estimates for the fixed effects in the full generalized linear mixed effects model used to describe trends in frog populations during 1993–2012

Fixed effect	Estimate	SE	Lower 95% CI*	Upper 95% CI*
Intercept	−6.562	0.534	−7.662	−5.563
Year†	0.101	0.027	0.049	0.155
Day†	0.091	0.041	0.011	0.172
Fish†	0.281	0.136	0.016	0.549
Water depth†	−3.782	0.649	−5.102	−2.553
Elevation†	0.597	0.105	0.390	0.803
Watershed†	0.560	0.291	0.002	1.146
Precipitation	0.344	0.696	−1.020	1.717
Fish × year†	0.111	0.038	0.038	0.187
Depth × year	−0.005	0.006	−0.018	0.007
Elevation × year	−0.004	0.020	−0.044	0.036
Watershed × year	−0.029	0.045	−0.118	0.059

^*The importance of predictor variables in affecting frog abundance is determined based on whether 95% CIs include zero.

^†The 95% CIs of variables with important effects do not include zero.

Table S3.

Correlation matrix for four environmental covariates included in the full model (all differ between sites but not between years)

	Depth	Elevation	Fish	Watershed
Depth	1.000	0.035	0.295	−0.065
Elevation		1.000	−0.042	0.088
Fish			1.000	0.058
Watershed				1.000

Factors Responsible for Frog Recovery.

After a century of decline, what allowed R. sierrae populations in Yosemite to begin to recover? A change in the distribution of nonnative fish is one possibility. All lakes and most streams in Yosemite were naturally fishless (16), including all 296 larger perennial water bodies (≥1 ha and ≥3-m deep) that are essential habitat for the highly aquatic R. sierrae (16, 17). Starting in the late 1800s and continuing for a century, several species of nonnative trout (Oncorhynchus spp., Salvelinus sp., and Salmo sp.) were introduced repeatedly into the majority of these habitats. This practice was greatly curtailed by the National Park Service in the late 1970s and stopped entirely in 1991. By the time that fish introductions were halted, only 43% of larger lakes remained in a fishless condition. As a result of this policy change, by 2000 and 2001, the percentage of fishless lakes had increased to 56% (34). Although fish disappeared from a relatively small proportion of lakes (because most introduced fish populations were self-sustaining) (34), this decrease in fish occupancy, nonetheless, created important habitats that, in some cases, were recolonized by R. sierrae. Of the 39 lakes that reverted to a fishless condition (“stocked-now-fishless” lakes), R. sierrae were detected at 20 (51%) during at least one survey over the study period. In contrast, at 128 lakes that contained fish throughout the study period, R. sierrae were detected at only 11 (8%; χ² test, χ² = 33.2, P < 10⁻⁸). In addition, model-estimated frog abundances in the median fish-containing lake was 28.3% (95% CI = 10.1–72.4%) of that in the median fishless lake that had never been subject to fish introductions. Frog abundances in stocked-now-fishless lakes were similar to those in never-stocked lakes (93.4%; 95% CI = 46.9–180.8%), suggestive of full recovery of R. sierrae abundance after fish disappearance. Collectively, these results indicate that the cessation of stocking likely contributed to the recovery of R. sierrae (28, 34). However, given that 20 R. sierrae populations occupying stocked-now-fishless lakes represent only a small fraction of 483 R. sierrae populations detected during our surveys, other factors likely had stronger overall influences on the observed trends in population abundance.

Unlike fish, which are relatively limited in their distribution across Yosemite, Bd infects all or nearly all R. sierrae populations (21), suggesting the potential for a strong effect of Bd on R. sierrae. In particular, a change in frog–Bd dynamics since Bd’s arrival could be an important driver of frog population increases. For example, evolutionary and immunological changes in frogs in response to Bd may have reduced their susceptibility (35, 36). We conducted a laboratory experiment to test the hypothesis that R. sierrae from populations with a long history of exposure to Bd that are persisting, despite ongoing Bd infection (such as those in Yosemite), are less susceptible than those from populations in which frogs have never been exposed to Bd. We refer to these frog types as “persistent” and “naïve,” respectively. In this experiment, we collected R. sierrae adults from each of three persistent and three naïve populations (Table S4) and exposed pairs of frogs (one from a persistent population and one from a naïve population) to one of four strains of Bd. Bd was cultured from two persistent frog populations and two populations in which frogs had recently experienced Bd-caused mass die offs (“die-off” populations). After Bd exposure, we measured Bd infection intensities (“loads”) on frogs over a 15-wk period.

Table S4.

Characteristics of the R. sierrae populations from which frogs were collected for the frog susceptibility experiment

Population identifier*	Location	Population type	Adult frog count (2009)	Bd prevalence	Average Bd load (1 SE)
1	Humboldt–Toiyabe NF	Persistent	76	0.83	45.2 (18.7)
2	Yosemite NP	Persistent	280	1.00	693.8 (173.8)
3	Yosemite NP	Persistent	46	0.44	8.0 (3.0)
4	Inyo NF	Bd naïve	993	0.00	0 (0)
5	Kings Canyon NP	Bd naïve	694	0.00	0 (0)
6	Kings Canyon NP	Bd naïve	3,531	0.00	0 (0)

NF, National Forest; NP, National Park.

^*Population identifiers are the same as those used in Fig. S3.

Frog type strongly influenced Bd load (Table 1), with the average Bd load being five times higher on naïve frogs compared with persistent frogs (Fig. 4). The magnitude of this difference was similar, regardless of the Bd strain to which frog pairs were exposed. The population from which Bd was collected affected loads on frogs (Table 1), but loads did not differ consistently between Bd cultured from persistent vs. die-off populations (see also Tables S5 and S6; details are in SI Text). During the first half of the experiment, Bd loads on frogs generally increased exponentially. We expected loads to continue to increase in subsequent weeks, but during the second half of the experiment, loads leveled off or in some cases, declined in all frog pairs (as indicated by a significant negative effect of week²) (Table 1). Regardless, loads remained higher on the Bd-naïve frog of each pair compared with the persistent frog (Fig. 4). Frogs in unexposed control tanks remained uninfected for 15 wk of the experiment. These results support the hypothesis that R. sierrae adults from persistent populations, such as those in Yosemite, are significantly less susceptible to Bd infection than those from Bd-naïve populations. In addition, since the initial collection of frogs from the three persistent and three naïve populations for use in this experiment (in 2009), Bd-caused epizootics have occurred in all three Bd-naïve populations, and all have been extirpated or nearly extirpated. In contrast, the three persistent populations have maintained stable or increasing frog numbers, and these populations continue to be characterized by enzootic host–pathogen dynamics. Collectively, these results suggest that the reduced susceptibility of R. sierrae to Bd infection may have contributed to the recovery of populations in Yosemite.

Table 1.

Parameter estimates for fixed effects in the linear mixed model used to describe the effects of frog type (persistent vs. naïve) on Bd infection intensities in the 15-wk frog susceptibility experiment

Fixed effect	Estimate	SE	df	Likelihood ratio test: χ2 (df)	P value
Intercept	1.77	0.30	28.4
Frog type (persistent)	0.87	0.15	41.9	26.1 (1)	<0.0001
Bd source				20.4 (3)	<0.001
Population 1	0.41	0.29	29.9
Population 2	−0.36	0.29	30.0
Population 7	−0.41	0.38	22.3
Population 8	0	—	—
Week	0.10	0.02	63.7	30.8 (1)	<0.0001
Week2	−7.3e-3	3.6e-3	123.0	4.0 (1)	0.046

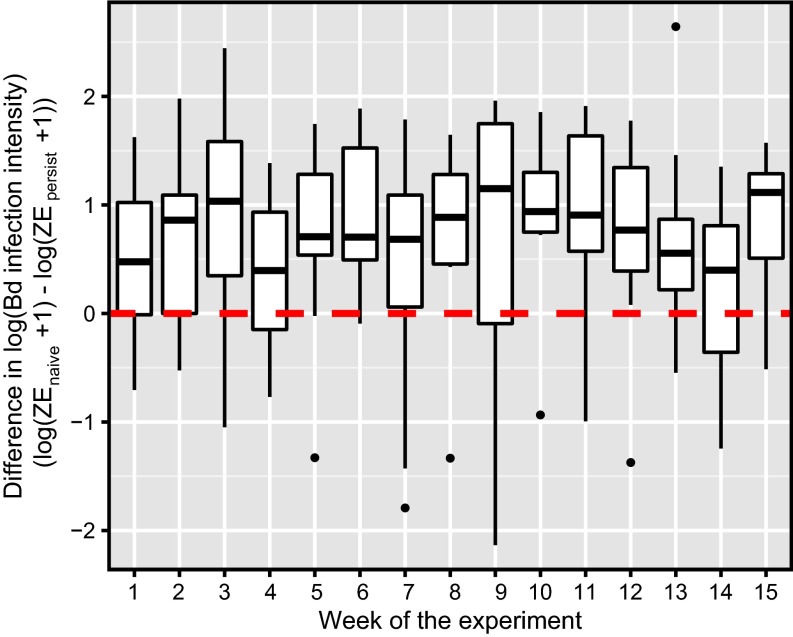
Fig. 4.

Results of the laboratory frog susceptibility experiment showing that, when exposed to Bd, frogs from Bd-naïve populations consistently had higher infection intensities than those from populations persisting with Bd. Each box plot displays the average difference in Bd infection intensity (expressed as ZEs) between the frog from a naïve population and the frog from a persistent population [log₁₀(ZE_naive +1) − log₁₀(ZE_persistent + 1)] for all tanks by week. Results from weeks 1–6 include those from all 16 replicate tanks, and results from weeks 7–15 include those from 8 tanks remaining after frogs in the other 8 tanks were killed for a separate gene expression study. Each box plot shows the mean (horizontal line), first and third quartiles (bottom and top of box: “hinge”), lowest and highest values within 1.5 × interquartile range of the lower and upper hinges (vertical lines), and any outliers (points). The horizontal dashed red line indicates a value of zero, the expected value if Bd loads were the same between paired naïve and persistent frogs.

Table S5.

Covariance parameter estimates for the repeated measures model of Bd load

Covariance parameter	Subject	Group	Estimate	SE	Z value	P value
Variance	Frogid	Bd type = die off	1.45	0.270	5.40	<0.0001
AR(1)	Frogid	Bd type = die off	0.73	0.051	14.41	<0.0001
Variance	Frogid	Bd type = persistent	0.56	0.073	7.72	<0.0001
AR(1)	Frogid	Bd type = persistent	0.34	0.085	4.03	<0.0001

Table S6.

Comparison of model fits including the alternative frog and Bd grouping variables

Fixed effects*	−2 Log likelihood	No. of parameters	AIC	BIC†
Frog type + Bd source + week + week2	774.4	10	794.4	809.0
Frog source + Bd source + week + week2	768.5	14	796.5	817.0
Frog type + Bd type + week + week2	793.4	8	809.4	821.2
Frog source + Bd type + week + week2	791.7	12	815.7	833.2

^*The frog source and Bd source variables indicate the identities of the source lakes for the frogs and Bd, whereas the frog type and Bd type variables indicate only whether the frogs and Bd came from one of the persistent populations.

^†Bayesian information criterion.

The reduced susceptibility of frogs from persistent populations could be caused by several nonmutually exclusive factors. First, the reduced susceptibility of frogs from persistent populations could be an outcome of natural selection (36) on R. sierrae that occurred after the arrival of Bd in Yosemite’s frog populations, selection to which the naïve frog populations would not have been subject. For example, if the initial invasion of Bd into Yosemite decades ago resulted in high levels of frog mortality, then the remaining populations may be descendants of individuals that possessed more effective innate or adaptive defenses against Bd (35, 37). Second, the lower susceptibility could be the result of an acquired immune response in frogs from persistent populations after their exposure to Bd in the wild, a response that itself could be subject to natural selection. If R. sierrae are, in fact, capable of mounting such a response (as is the case in other anurans) (35, 38), frogs from the persistent populations could have had at least partial immunity against Bd before the start of the experiment, and those from naïve populations would not have. A series of experiments is underway to describe adaptive immunity against Bd in R. sierrae. Third, the persistent populations from which R. sierrae were collected may have inherently lower susceptibility to Bd than those Bd-naïve populations from which R. sierrae were also collected, differences that could predate the arrival of Bd in the Sierra Nevada (36, 39).

In addition to our study, two other recent studies have also provided compelling evidence that other anuran species (both from Australia) are recovering after Bd-caused declines (30, 31). Unfortunately, neither allows insights into which (if any) of the above-described mechanisms might be associated with recovery. Elucidating the relative importance of these potential mechanisms would provide important insights into the means by which amphibians being impacted globally by Bd could eventually recover from the effects of chytridiomycosis.

Conclusions

Amphibian declines have proven difficult to reverse, especially when the causes of decline are poorly understood or challenging to ameliorate (e.g., disease, introduced species, airborne contaminants, or climate change). Those examples that do exist are generally based on only a few populations (28–31) and provide important but limited insights into the potential for large-scale recovery. As such, the prospects for global amphibian conservation and recovery in the face of the unprecedented number of declining and increasingly imperiled species appear grim (5). In contrast, the results from our study indicate that the endangered R. sierrae, after decades of decline, is now increasing in abundance in Yosemite National Park, despite the ongoing presence of multiple stressors, including disease. These increases are occurring over a large landscape and across hundreds of populations, providing a rare example of amphibian recovery at an ecologically relevant spatial scale. That said, recovery of R. sierrae in Yosemite is far from complete and at a minimum, will require the continued removal of introduced fish from key habitats and translocation of frogs to reestablish populations in areas from which they are extirpated (21). However, our research in the Sierra Nevada—and complimentary work in Australia (30, 31)—suggests that amphibian declines may be at least partially reversible at a regional scale. Similar studies conducted in other systems and over large temporal and spatial scales will provide important insight and generality about the potential for recovery of endangered amphibians at a global scale.

Materials and Methods

Frog Surveys.

Surveys targeted all lentic water bodies in Yosemite as shown on US Geological Survey 7.5′ topographic maps. Counts of R. sierrae life stages (adults, juveniles, and tadpoles) were made during diurnal visual encounter surveys of the entire water body shoreline and suitable habitat in inlet and outlet streams (16, 40) (survey details are in SI Text). During the 20-y study, a total of 8,976 frog population surveys were conducted at 3,164 water bodies. For our analyses, we excluded surveys from water bodies that were surveyed only once during the study period or conducted outside the time of peak frog activity (May 15 to September 20). We also excluded the few R. sierrae populations that were established recently via translocation (21). These restrictions resulted in 7,678 surveys conducted at 2,154 water bodies (average number of surveys per water body = 3.6) (Fig. S2).

Fig. S2.

Frequency histogram showing the number of surveys conducted per site over the 20-y study period.

Trends in Frog Abundance.

In our primary analysis, we used generalized linear mixed models to describe the effect of year on frog counts after accounting for nonindependence of counts and potentially confounding factors that could influence frog counts. We developed a single best model from a set of models that differed in their underlying distribution; inclusion of random effects to account for spatial, temporal, and location dependence in counts (details are in SI Text); inclusion of fixed effects (in addition to year) to account for factors that could influence frog counts (day of the year and observer) (Table S1); and fixed effects for temporal trend in abundance (year, our primary interest). We specified that frog counts come from one of two distributions: (i) a negative binomial distribution because of its flexibility in specifying the error distribution for counts or (ii) a zero-inflated negative binomial distribution because of its flexibility to account for excess zeros from unoccupied water bodies.

The generalized linear mixed models were fit using R (41) and the INLA package (32); the INLA package fits hierarchical models with random effects using integrated nested Laplace approximations. We used default priors when fitting models. The response variable in all models was the number of R. sierrae counted at the ith site in the tth year, C_it, rather than actual abundance, N_it (details are in SI Text). We used a state space approach to modeling the count data, assuming a direct relationship between C_it and N_it. Observation error is incorporated by assuming that the count comes from a negative binomial distribution with a mean equal to the latent abundance at the site. This approach is consistent with standard methods for modeling count data under observational uncertainty (33, 42). A drawback of this approach is that we were not able to explicitly test whether observed trends could have been generated by nonstationarity in the detection process (e.g., resulting from different observers through time). However, the same standardized protocol was used across all years, and surveys were conducted by only two teams of observers (led by G.M.F. or R.A.K.) whose survey periods broadly overlapped (1993–2012 and 2000–2012, respectively). We also included observer team (G.M.F. or R.A.K. led) as a fixed effect in models to account for potential observer effects on R. sierrae detection and resulting counts.

The base model that provided the best fit to the data was one using a zero-inflated negative binomial distribution and including the three random effects and the fixed effects year and day (but not observer). We fit separate models to counts of adults, juveniles, and tadpoles. All models produced similar results, and here, we focus primarily on the adult model. Using this “base” model, we then estimated the overall trend in frog abundance across the park during the 20-y study period. Trend was estimated as the slope of the relationship between counts and year for a model constrained using a log-link function (drawing a parallel between our statistical model and an exponential population growth model). The slope is equivalent to the intrinsic rate of increase, r. The base model was also used to map spatial variation in trends (using a conditional autoregressive random effect for the trend parameter) (43) and quantify how trend varied with respect to several environmental covariates, including water body depth, elevation, precipitation, fish, and watershed (Tables S1 and S2). Additional details on the modeling process are provided in SI Text. The dataset and R code used in the analysis are available at http://dx.doi.org/10.5061/dryad.rm382.

Frog Susceptibility Experiment.

This laboratory experiment was conducted at San Francisco State University (SFSU) and approved by Institutional Animal Care and Use Committees at SFSU; University of California, Santa Barbara; and University of California, Berkeley. To provide frogs for the experiment, adult R. sierrae were collected from each of three persistent populations (including two in Yosemite) and three Bd-naïve populations (Table S4). Frogs from the persistent populations were Bd-positive (Table S4) and therefore, cleared of infection using itraconazole (44). Naïve frogs were uninfected but treated with itraconazole concurrently to ensure that all frogs were treated similarly. To start the experiment, two frogs, one from a persistent population and the other from a naïve population, were assigned at random to 1 of 16 replicate tanks (Fig. S3). Tanks were then inoculated with one of four strains of Bd: two cultured from persistent populations (including one from Yosemite) and two from populations that had experienced recent Bd-caused die offs (18). To quantify Bd load on frogs throughout the 15-wk experiment, skin swabs were collected from all frogs (18, 45) immediately before Bd exposure and weekly thereafter and analyzed using quantitative PCR (46) (details in SI Text).

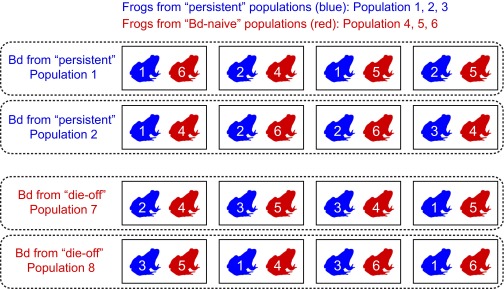
Fig. S3.

Design of the laboratory R. sierrae susceptibility experiment. Numbers associated with frogs indicate the population from which each frog was collected (listed at the top and described in Table S4). Eight control tanks that were not exposed to Bd are not shown.

We used a model selection strategy to examine the effects of frog type (collected from a persistent or naïve population), frog source (one of six populations), Bd type (collected from a persistent or die-off population), Bd source (one of four populations), and interactions of these effects on Bd load [log₁₀(zoospore equivalent [ZE] + 1)]. To select the best model, we followed the protocol by Zuur et al. (47). Additional details regarding the modeling steps are provided in SI Text. The dataset and SAS code used in the analysis are available at http://dx.doi.org/10.5061/dryad.rm382.

SI Text

Frog Survey Methods, Analysis, and Results.

Study area.

Yosemite National Park is located in the central Sierra Nevada, California, United States (37° 53.984′ N, 119° 31.762′ W). Nearly the entire park is within the range of Rana sierrae, including water bodies along an elevation gradient from the lower montane zone (∼1,650 m) to the alpine zone (3,200–3,500 m). In Yosemite, the active season for R. sierrae is from May to October. During the remainder of the year, the landscape is generally snow-covered, and during this time, R. sierrae overwinter in ice-covered perennial water bodies.

Frog counts.

Counts of R. sierrae made during diurnal visual encounter surveys of water body shorelines were used as a proxy for abundance. The degree to which counts accurately reflect abundance depends largely on animal detectability, and R. sierrae are highly detectable. Counts from visual encounter surveys conducted 6–12 d after reintroductions of 32–50 adult R. sierrae into seven lakes in Yosemite National Park indicated an average proportion counted of 0.36 (range: 0.20–0.62). This relatively high detectability results from several characteristics of R. sierrae and its habitat. First, during the day, R. sierrae adults, juveniles, and tadpoles bask in near-shore shallows, making all life stages highly visible during diurnal shoreline surveys. Second, the oligotrophic water bodies generally inhabited by R. sierrae have high water clarity with little or no aquatic vegetation. Third, tadpoles are present throughout the summer (and during all other seasons) because of the 2–3 y duration of this life stage in R. sierrae.

Trends in frog abundance.

The following provides additional details regarding all steps in the modeling process that was used to quantify trends in R. sierrae abundance from surveys conducted across Yosemite National Park during the study period. The first step was to choose the best distribution and random effect structure. We did this by comparing four models, each based on one of two distributions (negative binomial or zero-inflated negative binomial) and with or without three random effects. The three random effects were as follows.

• i)A conditional autoregressive structure (CAR) to account for spatial autocorrelation (43) in frog counts among sites. To apply this structure, we divided the study area into an array of hexagonal grid cells with centroids that were located 6,500 m apart in the east–west direction and 5,629 m apart in the north–south direction (Fig. 3).
• ii)A first-order temporal autocorrelation structure to account for temporal dependence in repeated counts at the same water body.
• iii)A random effect for variation in mean counts among all water bodies. This random effect accounted for variability in mean densities of frogs among water bodies and helped control for among-site variation when dealing with missing data (i.e., combinations of water body and year when a survey did not occur).

At this step, we also included two fixed effects in all models: day of the year on which a survey was conducted (day; as a continuous variable) (Table S1) because of its potential to confound frog counts (for example, if counts are lower in early summer compared with mid- or late summer) and survey year (year; as a continuous variable) (Table S1) to account for temporal trend, our primary interest. The deviance information criterion (DIC) was used as a measure of model fit, and we used the model with the lowest DIC value in subsequent analyses.

In the second step, we tested for evidence of differences among survey teams in mean counts and/or trend in counts across years. We compared three models: no observer effects, observer differences in mean count, and observer differences in both mean count and trend. Again, we used DIC to choose among models, and we used the model structure with the lowest DIC value in subsequent analyses. We refer to this best model as the base model.

In the third step, we used the base model to estimate an overall trend in R. sierrae abundance across the park over the 20-y study period. In addition, we fit an equivalent model to data for counts of juveniles and tadpoles to determine whether trends were consistent across all three life stages.

To explore whether environmental conditions influenced counts and/or trends across the park, our next step was to add five environmental covariates (fixed effects) to the base model (Table S1). Four of the covariates were chosen because they could be related to spatial variation in abundance of R. sierrae: water body elevation, water body depth, presence/absence of introduced fish, and watershed in which the water body was located. These variables differ between sites but not years. The fifth covariate that we considered was precipitation during the previous year, which we predicted could explain some of the year to year variation in the overall rate of population increase. This variable differed between years but within a year, was constant for all sites. Given the focus of the analysis on trends in R. sierrae abundance, we were particularly interested in whether the average rate of increase in abundance depended on each of four spatial covariates, which we evaluated by examining the interaction between year (i.e., our measure of trend) and each of four covariates (Table S2). The temporal covariate × year interactions would have a completely different meaning and would be difficult to interpret. As such, the precipitation × year and survey date × year interactions were not included in the model. In addition, no Bd-specific covariates, such as the year of Bd arrival at a site, were included, because little historical Bd data exist for Yosemite’s R. sierrae populations that could be used to describe the initial arrival and spread of Bd in this area.

Continuous covariates were standardized to have a mean = 0 and an SD = 1 to allow parameter effect sizes to be interpreted as the effect of a 1-SD change in the covariate value. The full fixed effect structure included an effect for year (i.e., trend), the five covariates, and the interaction between year and each of the spatial covariates. To examine effect sizes of all covariates, we fit the full model and made inferences about the importance of covariates based on parameter estimates and 95% CIs. Because collinearity between covariates could complicate interpretation of results, we evaluated the degree of correlation between the covariates, focusing specifically on the spatial covariates, because they were measured across the same set of sample units. Collinearity was low for all pairwise comparisons (Table S3) and would not have affected the results.

The final step was to visualize spatial variation in trends in R. sierrae abundance across the park. We accomplished this by fitting a spatially explicit model for the trend parameter, again using a CAR structure for the random effect. The random trend parameter allowed us to map variability in trends across the park while accounting for spatial autocorrelation among adjacent cells when making predictions.

Sensitivity of results.

We conducted several analyses using data subsets to assess the sensitivity of results to assumptions made in the primary analysis. The first assumption is that the number of surveys conducted per water body did not influence estimates of population trend. The number of surveys per water body ranged from 2 to 55, with an average of 3.6 (Fig. S2). To determine how robust the results are to the number of times that a site was surveyed, we reanalyzed the dataset, this time restricting the analysis to only those sites where at least five surveys were conducted and those surveys occurred over at least a 15-y period. Based on this analysis, the estimated trend (r) for the number of adult R. sierrae is 0.066 (95% CI = 0.037–0.095), equivalent to a 6.8% annual increase over the 20-y study. This estimate is somewhat lower but still quite similar to the estimated trend based on the full dataset (r = 0.105; 95% CI = 0.075–0.134; 11.0% annual increase). The estimates for juveniles and tadpoles were also somewhat lower than for the full dataset (juveniles: r = 0.079; 95% CI = 0.039–0.120; 8.1% annual increase; tadpoles: r = 0.111; 95% CI = 0.055–0.168; 11.7% annual increase). The sites included in the data subset had a higher average abundance of adult R. sierrae than those in the full dataset, likely because these larger populations were of particular interest and therefore, surveyed more frequently than small populations. As such, the somewhat lower rate of increase for the data subset may be reflective of trends in water bodies that contained larger frog populations in the early years of the study, populations that a priori might be expected to grow more slowly than those that were relatively small at the start of the 20-y study.

The second assumption that could have affected the results is that the inclusion of water bodies in which adult R. sierrae were never detected (but other life stages may have been observed) did not affect estimates of population trend. To determine the sensitivity of the results to this assumption, we excluded these sites from the data subset described above and reran the analysis. Based on this analysis, the estimated trend (r) for the number of adult R. sierrae is 0.066 (95% CI = 0.037–0.094), equivalent to a 6.8% annual increase over the 20-y study. The estimates for juveniles and tadpoles were as follows: juveniles, r = 0.079; 95% CI = 0.039–0.123; 8.1% annual increase; tadpoles: 0.116; 95% CI = 0.056–0.178; 12.3% annual increase. These estimates of trend are virtually unchanged from those obtained using a dataset that included all water bodies, regardless of whether adult R. sierrae were detected (see above), and were somewhat lower than for the full dataset.

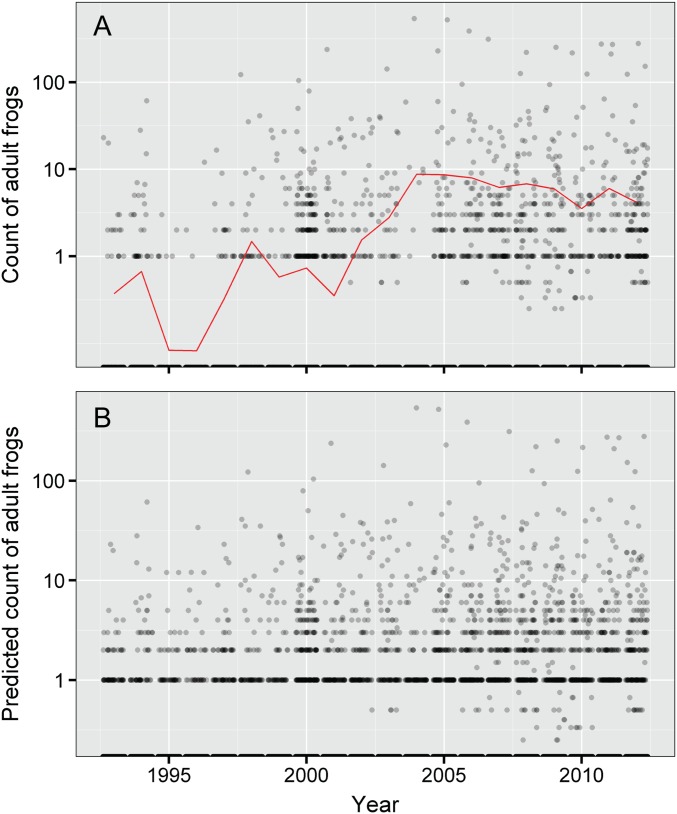
We expected frog population trends to exhibit strong temporal and spatial autocorrelation, and we accounted for these effects using temporal and spatial random effect terms. As part of our analysis, we evaluated the fit of models with and without these terms. Because of space limitations, these results are not presented in the text and are described here instead. Compared with the “full model” presented in the text, the fit of a model lacking the temporal and spatial random effect terms is much poorer (ΔDIC = 4,455). The trend estimate based on this model is 0.193 (95% CI = 0.170–0.215) (Fig. S1), much higher than the estimate from the full model of 0.10 (Fig. 1). We conclude that including the spatial and temporal effects in the model provides a much better fit to the count data and results in a more conservative estimate of trend in frog abundance.

Fig. S1.

Trends in frog abundance during the 20-y study showing results used to generate Fig. 1: (A) actual counts of adult R. sierrae for all sites sampled in each year (points) and average annual counts (red line) and (B) actual counts for sampled water bodies and predicted counts for unsampled water bodies based on the estimated distribution in the trend model. In A and B, when more than one survey was conducted per year, results were averaged by year. Y axes are shown on a log scale. Although only a subset of sites was surveyed in any 1 y (shown in A), the general distribution of points in A is similar to that in B, which is based on actual and predicted counts at all water bodies. Average values from B were used to create the trend line and 95% CI in Fig. 1.

Methods in Frog Susceptibility Experiment and Analysis.

To provide frogs for the experiment, adult R. sierrae were collected from each of three persistent populations and three Bd-naïve populations (22) (Table S4). At the time of the collections, the persistent populations had been Bd-positive for at least 10 y (and probably substantially longer) and are characterized by high Bd prevalence but low to moderate loads and relatively small populations that are stable or expanding (Table S4). The Bd-naïve populations are located ahead of the Bd “wave” that is currently spreading across Kings Canyon National Park and its vicinity (18). These six populations have been surveyed repeatedly since at least 1997, are considerably larger than the persistent populations, and through 2009, when this experiment was conducted, were Bd-negative (Table S4). Two of the persistent populations are located in Yosemite, and the third population is immediately north of the park. For three naïve populations, two are located in northern Kings Canyon National Park, and one is immediately north of the park (Table S4).

Frogs collected for the experiment from the persistent populations were Bd-positive (Table S4) and therefore, cleared of infection using itraconazole (44). Naïve frogs were uninfected but treated with itraconazole concurrently to ensure that all frogs were treated similarly. Unexpectedly, frog mortality occurred during the treatment and resulted in the loss of 58% of the frogs, a much higher mortality rate than was observed during previous or subsequent treatments of R. sierrae using the same itraconazole dose (0.01% bath applied for 5 min daily for 11 d). The cause of this mortality event is, therefore, uncertain. All surviving frogs tested negative for Bd during 2 consecutive weeks after the treatment. To start the experiment, two frogs, one from a persistent population and the other from a naïve population, were assigned at random to 1 of 16 replicate tanks (standard 10-L plastic rat containers with filtered lids that allow airflow). Two of the naïve and two of the persistent populations provided five frogs each, and the remaining naïve population and persistent population provided six frogs each (Fig. S3).

The 16 tanks were inoculated with one of four strains of Bd (selected at random). These Bd strains were cultured from two persistent frog populations (one in Yosemite) and two frog populations that had experienced recent Bd-caused die offs (18). Each tank was inoculated with a single Bd strain, and each of four strains was used to inoculate four tanks (Fig. S3). An additional eight tanks, each containing a pair of frogs, served as unexposed controls.

To quantify Bd load on frogs throughout the 15-wk experiment, skin swabs were collected from all frogs immediately before Bd exposure and weekly thereafter. Swabbing of frogs was conducted using a standardized method, with a total of 30 strokes made across the ventral portion of each animal (5 strokes each on the left and the right sides of the abdomen, left and right thighs, and left and right foot webbing) (18). After collection, swabs were air-dried, stored at −80 °C, and analyzed within 7 d of collection using a real-time quantitative PCR (qPCR) assay (46). Two weeks after the initial Bd inoculation, both frogs in 4 of 16 tanks remained uninfected. These tanks were reinoculated using the original Bd strain and the same methods as in the original inoculation. This reinoculation resulted in all frogs becoming infected. To account for the different infection timeframes between tanks, in which frogs became infected after the first vs. the second inoculation, the time course for each tank is expressed as weeks after the last inoculation.

After 6 wk, Bd infection had reached moderate levels; frogs in randomly selected 12 of 24 tanks (including 4 of 8 control tanks) were killed, and their gene expression profiles were analyzed using microarrays (these results are presented elsewhere). Frogs in the remaining tanks were followed for the full 15-wk experiment. Throughout the experiment, water in tanks (∼1.5 L carbon-filtered water) was changed weekly, and each frog was fed approximately five crickets twice weekly. At the conclusion of the experiment, all frogs were cleared of Bd infection using itraconazole (using the methods described previously) and held in captivity for use in other studies. No frog mortality occurred during this treatment period.

We used a model selection strategy recommended in ref. 47 to examine the effects of frog type (collected from a persistent or naïve population), frog source (one of six populations), Bd type (collected from a persistent or die-off population), Bd source (one of four populations), and interactions of these effects on Bd load. We also included the individual-level variables of snout-vent length (SVL; centered by subtracting the mean SVL) and sex. The response variable was Bd load as measured by log₁₀(ZE + 1); ZE was measured from qPCR, on each frog at each of the weekly time points. Results from frogs in all 16 Bd-inoculated tanks were included for weeks 1–6, tanks remaining after euthanasia of frogs from one-half of the tanks (at week 6) were included for weeks 7–15, and the analysis accounted for the change in sample size after week 6.

We first determined the best structure for the random components of the model, including all possible fixed effects, using Restricted Maximum Likelihood (REML) estimation and compared random effect models using the Akaike Information Criterion (AIC). We included correlated errors among the multiple temporal measurements on individual frogs using the REPEATED statement in PROC MIXED, with frogid as the subject and a first-order temporal autoregressive model [AR(1)]. Other temporal correlation structures were investigated, but none improved the fit. The errors differed between Bd type, and therefore, we included an error structure that allowed for different error parameters in these two groups. We investigated more complicated random effects models, including random effects of tanks, random slopes for individual frogs, random effects of frog source nested within frog type, or random effects of Bd source nested within Bd type; however, none of these improved the model fit. Satterthwaite dfs were used throughout to deal with the complex error structures. After we arrived at the best fit random effects structure, we used it in the model to compare alternative fixed effects models. Fixed effects models were fit using maximum likelihood estimation and compared using AIC. Because frog source is perfectly correlated with frog type, we could not include both of these predictor variables in the model. Likewise, we could not include both Bd source and Bd type in the model. Therefore, we compared the fit of the models that included either one or the other of the alternative frog and Bd groupings. In addition to model comparison using AIC, the significance of each fixed effect was determined by likelihood ratio tests comparing the likelihood of the full model and a model with that term of interest removed. Final parameter estimates were obtained using REML estimation (Table 1).

The best fit random effects component of the model included temporal autocorrelation in the errors for the repeated measurements of Bd load on individual frogs and different error parameters for the frogs in the Bd type groups (Table S5). For the fixed effects component of the model, the effects of week after Bd inoculation and week² (each centered by subtracting the mean) were always significant, whereas the individual-level variables of SVL and sex were not significant. Models with the alternative frog and Bd groupings were compared using AIC, and the overall best fit model included the variables frog type and Bd source (Table S6). The interactions between frog grouping (either frog source or frog type) and Bd grouping (either Bd source or Bd type) were never significant. Frog type and Bd source both had highly significant effects on Bd load, with frogs from naïve populations having significantly higher Bd loads than frogs from persistent populations (Table 1). Frogs exposed to the different Bd sources differed in their loads, but loads did not consistently differ between Bd from persistent and die-off sites. To further illustrate this point, we compared the model including frog source and Bd source with the model including frog type and Bd type. In the first of these two models, both frog source and Bd source are highly significant; however, in the second model, frog type is significant, but Bd type is not.