The nature and implications of uniformity in the hierarchical organization of nanomaterials

Abstract

In this Perspective, we present a framework that defines how to understand and control material structure across length scales with inorganic nanoparticles. Three length scales, frequently discussed separately, are unified under the topic of hierarchical organization: atoms arranged into crystalline nanoparticles, ligands arranged on nanoparticle surfaces, and nanoparticles arranged into crystalline superlattices. Through this lens, we outline one potential pathway toward perfect colloidal matter that emphasizes the concept of uniformity. Uniformity is of both practical and functional importance, necessary to increase structural sophistication and realize the promise of nanostructured materials. Thus, we define the nature of nonuniformity at each length scale as a means to guide ongoing research efforts and highlight potential problems in the field.

Life is characterized by hierarchical organization, wherein new functions and properties recursively emerge as collections of material building blocks define structures at increasingly larger length scales (1–3). To access hierarchical structures, biological systems often impose boundary conditions that restrict the chemical, physical, and structural possibilities of organization at each length scale (4). These constraints can be thought of as kinetic controls that provide a series of intermediate, metastable states to guide the system down a particular pathway (Fig. 1B) (3). This stepwise approach allows for organizational regulation and control, such that billions of species need not organize into macroscopic materials in one time-consuming step, free of error. At each organizational length scale in this process, a new level of complexity emerges that is intimately dependent on, but fundamentally different from, the previous steps. This hierarchy necessitates the definition of step-specific conceptual frameworks, the development of length-scale–specific approaches for characterization, and ultimately connections that unify each level of organization.

Fig. 1.

(A) Hierarchical organization can control structure from atoms to nanoparticles to collective ligand structures to colloidal crystals. (B) This organization builds structure through intermediate states with small activation energies, rather than in one step.

Hierarchical Organization

Inspired by the structural sophistication and impressive function of hierarchically organized systems in nature, researchers in the supramolecular chemistry and biomineralization communities have adopted these lessons as core principles (2, 5–7). Relative to biological systems, synthetic systems such as these are advantageous to study and control hierarchical organization due to the wider array of available building blocks, the deliberate control of chemical species and environmental conditions, and the ability to spatially and temporally separate each step. Whereas these synthetic advantages are also true in the context of collections of inorganic nanoparticles, these systems present unique challenges and require system-specific definitions of hierarchy.

In this Perspective, we present a framework that defines how to understand and control material structure across length scales with inorganic nanoparticles and emphasize the central challenge of uniformity (Fig. 1). Three length scales of this hierarchy are discussed (Fig. 1A): atoms arranged into crystalline nanoparticles, ligands arranged on the surface of nanoparticles, and nanoparticles arranged into crystalline superlattices. This is not intended to be a review of synthetic techniques or the forces that dominate structure formation at each length scale (7–12). Instead, we highlight and define (i) how hierarchical organization principles apply to inorganic nanomaterial systems; (ii) the nature of nonuniformity at each length scale, defined with respect to an ideal reference state; and (iii) the implications of nonuniformity on hierarchical organization and successful approaches used to control uniformity. Throughout this paper, the terms “uniform” and “nonuniform” are used in place of “monodisperse” and “polydisperse,” as the latter terms are self-contradictory or redundant and have been deprecated by the International Union of Pure and Applied Chemistry (IUPAC).

From Atoms to Crystalline Nanoparticles

To construct a gold cube with an edge length (L) of 75 nm would require ∼34 million atoms, arranged precisely into a crystalline face-centered cubic (FCC) lattice. If this hypothetical cube possessed even a 5% smaller L, this would correspond to a remarkable 14% difference in volume per nanoparticle (∼5 million atoms) and a 9% decrease in surface area (SA). The magnitude of this organization highlights the challenge of nanoparticle synthesis from atomic precursors. This Perspective focuses on challenges specific to nanoparticles with ∼10⁴ atoms, where the precisely controlled syntheses, analytical characterization techniques, and rigorous descriptions useful to smaller nanoparticles begin to break down (13) and where bulk material descriptions do not necessarily apply. Within this size regime, inconsistently applied metrics of uniformity and limitations in structural control complicate quantitative comparison of results, prevent the field from conceptual agreement and universally adopted protocols, and ultimately preclude these materials from being used as building blocks in hierarchical matter.

What Does It Mean to Be Uniform at This Length Scale?

Criterion 1: Shape.

Shape can first be defined by the collection of symmetry elements (e.g., inversion points, reflection planes, and rotational axes) present in a nanoparticle, analogous to molecular descriptions by group theory (14). Each group of symmetry elements derives from the underlying atomic crystal structure, wherein the geometric relationships between crystallographic planes are defined (Fig. 2A). The relative rate of material addition onto each family of planes influences the observed shapes. Atomic defects, such as vacancies or twinned planes, can lead to a loss of symmetry operators compared with the reference atomic lattice. Given the symmetry group, shape can be more rigorously defined by the number of faces, edges, and corners, with an emphasis on the 2D shape, crystalline structure, and chemical composition of the faces.

Fig. 2.

Common inhomogeneities in nanoparticle syntheses are shown schematically (Top) and experimentally (Bottom) for a cube with FCC crystal symmetry: (A) shape, (B) corners, and (C) size. Transmission electron microscopy images are from widely used syntheses of gold or silver cubes. (Scale bars: 50 nm.)

To illustrate the rich variety of potential shape descriptors and nonuniformities, we describe a typical anisotropic nanoparticle synthesis. For materials with FCC crystal symmetry (e.g., Ag, Au, Pd, Pt), each plane in the {100} (family of planes) is related by symmetry and oriented orthogonal to the others. Under conditions optimized to produce crystals bound by chemically identical {100} facets, one would expect cubes as products. However, symmetry-breaking events can induce structural deviations from this reference shape, where unequal growth occurs on crystallographically equivalent planes to produce nanoparticles with an aspect ratio: in this case, a rectangular prism. Alternatively, fluctuations in reaction conditions can guide nanoparticles down different growth pathways to produce a single shape, defined by more than one family of facets, or multiple different shapes bound by the same facet (12, 15–20). For lower-symmetry crystals, such as the Wurtzite form of CdSe, planes within the same family can also possess surface atoms of different compositions (15, 21, 22). These structural deviations complicate the synthesis of uniform nanoparticle building blocks and hold important consequences for hierarchical organization. In particular, different surface structures and shapes template spatially distinct arrangements of molecules on a nanoparticle surface (23, 24), and changes in symmetry alter the colloidal crystals that can form (14).

Current experimental characterization techniques lack the necessary throughput and detail to rigorously quantify the large number and variation of shape descriptors within a nanoparticle population. Approaches to quantify nanoparticle structure can be broadly classified as ensemble techniques, which can evaluate the collective properties of a sample to provide population-level estimates of average structural parameters, or local techniques, which can directly probe the structure of individual nanoparticles. Because ensemble measurements cannot be deconvoluted without significant assumptions about structure and purity, but individual measurements can be built up into population-level statistics, the latter more quantitatively describes nanoparticle uniformity for heterogeneous populations (25–27). In particular, the automated, algorithmic analysis of electron microscopy (EM) images holds tremendous potential to improve the rigor of nanomaterial characterization. This powerful tool can be used to minimize sampling bias, to improve throughput, and to quantitatively measure structure with single-nanoparticle resolution (28, 29). The largest limitation associated with this approach pertains to the informational loss in the conversion of 2D projections from EM images to 3D shapes (30, 31). For homogeneous populations, including many proteins and cellular structures, this problem can be resolved through programs that combine different angular projections into a single structure (31). However, analogous tools must still be developed for heterogeneous populations, potentially through rapid collection and automation of single-particle tomographic reconstructions (32, 33).

Criterion 2: Corners/edges.

Nanoparticle edges and corners represent deviations from ideal geometric solids (Fig. 2B). These structural defects frequently occur due to the lower coordination number of surface atoms at sharp features, where the chemical potential difference to take an atom from solution to a low-coordination position is too large, given the driving force of most nanoparticle synthesis reaction conditions. The reduced stability of these atoms further increases the likelihood of surface reorganization (i.e., where atoms can diffuse to higher-coordination environments) and oxidation (i.e., where atoms are released from nanoparticles through redox processes.). To evaluate corner rounding, it is common practice to inscribe a sphere in each corner to measure radius of curvature, and to evaluate corner truncation, one can quantify L relative to a nontruncated reference solid.

Criterion 3: Size.

To evaluate nanoparticle size, one must select the structural parameter best suited for the nanoparticle shape and application (e.g., for a surface-dependent property, SA is more informative than L) and then consider how this parameter changes across the particle (Fig. 2C). For a rectangular prism, there are 12 edges and six faces, which can be described by three unique L and three facet SAs. As the particle symmetry changes, a greater number of descriptors may be required. Size measurements for a statistically significant number of nanoparticles within a particular shape class can then be used to determine population-level uniformity statistics. In particular, the coefficient of variation (CV) is a fractional deviation determined by the division of the SD by the average size, which enables direct comparison between samples of different sizes. If CV is combined with aspect ratio, one can decouple the effect of size variation from shape variation, and if CV is combined with yield, the synthesis can be evaluated for how efficiently and uniformly it produces a particular shape.

Successful Approaches to Control Uniformity at This Scale.

Approach 1: Uniform reagents.

The history of nanomaterial synthesis can, in many ways, be told as the story of impurities. Reagent mixtures are typically purchased from distributors without full disclosure of the constituent chemicals and those mixtures can further undergo a multitude of reactions to generate new species. Without knowledge of what chemical species are present, researchers cannot understand the mechanistic underpinnings of these systems or control their uniformity (15, 19, 20, 34–36). For semiconductor metal chalcogenides, many key advances have been made with the solvent tri-N-octylphosphine oxide (TOPO). TOPO was initially hypothesized to coordinate precursor materials and nanoparticle surfaces to modulate reaction kinetics. Subsequent research instead showed that phosphonates and phosphonic acids present in or produced at high temperatures coordinate stronger than TOPO and dictate the reaction pathway (21, 34). Similarly, halide impurities in ubiquitously used surfactants for noble metal nanoparticle syntheses [e.g., cetyltrimethylammonium bromide (CTAB)] went unidentified for almost a decade of research (17, 19, 35, 36). Only after extensive efforts to identify, purify, and systematically dope in halides were researchers able to reproducibly synthesize nanostructures with controlled shape (17–19, 35, 36). In both cases, renewed attention to precursor purity enabled access to uniform nanoparticle products, which emphasizes hierarchical organization principles.

Approach 2: Temporally restricted nucleation.

To direct nanoparticle formation requires controlled nucleation (i.e., the emergence of a new phase). Nucleation begins with induced or spontaneous fluctuations (e.g., change in temperature or pressure, material addition) in supersaturated solutions. Above a critical supersaturation (σ*), the cohesive energy between precursors overcomes the surface energy penalty for creation of a new phase and results in a chemical potential driving force for nucleation. Subsequent precipitation depletes the precursor and relieves the system of this σ. Once σ returns below σ*, nucleation ceases, and growth can occur via material addition onto existing nuclei. In 1950, LaMer and Dinegar (37) proposed that a uniform colloid could be generated by temporally restricting this elevated σ, such that nuclei formed simultaneously and subsequently experienced similar growth conditions. This foundational principle of temporally restricted nucleation has been implemented particularly successfully for nanomaterials in the “hot-injection” method. Pioneered by Murray et al. (38), rapid injection of room temperature organometallic precursors into a hot coordinating solvent produced, in succession, a sudden increase in σ, a short burst of nucleation, reagent depletion, and a drop in temperature that temporally restricted nucleation and resulted in a uniform size distribution of cadmium chalcogenide nanoparticles. High-temperature solvents proved necessary in this process to decompose molecular precursors into reactive monomers, to provide sufficient energy for dynamic atom and ligand interactions, and to access high σ. Within a decade, this approach had been adapted to III–V (InAs, InP, GaP), IV–VI (PbS, PbSe, PbTe), and metal nanoparticles and used to synthesize a wide variety of complex shapes via manipulation of the subsequent growth stages (15, 39).

Approach 3: Seed-mediated synthesis.

Whereas the previous approach focused on temporally discrete nucleation, greater control can be achieved via spatiotemporally separated nucleation and growth. In particular, nanoparticles can be used as precursors, or “seeds,” to template the heterogeneous nucleation of material. The presence of a preexisting phase (i.e., the seed) lowers the σ required for nucleation and allows for finer control of growth kinetics. Consequently, low σ conditions are used to suppress homogeneous nucleation in favor of seed-mediated growth. This strategy provides an intermediate stage between atomic precursors and nanoparticle products and illustrates how a hierarchical synthesis can enable greater uniformity. Although deceptively straightforward, the presence of a seed does not ensure “seed-mediated growth,” and material may instead alloy with or oxidize seeds (20). This becomes particularly important for small seeds (<5 nm), where the low surface coordination can decrease melting temperature, decrease oxidation potential, and increase reactivity (13, 40–43). If material deposition occurs, the seed can act as a template that guides the structure of the final product. However, the low stacking fault energies of many noble metals (e.g., Au, Ag) can lead to a fluxional defect structure at small sizes, which complicates correlation between precursor and product structure (40, 43). Similar effects occur in polytypic semiconductors (i.e., materials capable of adopting two different crystalline structures), where the energy difference between polytypes can fall within the temperature fluctuations of the system (15, 16, 22). These problems can be circumvented with larger seeds whose fate can be monitored and directly correlated with product structure (28). Indeed, if literature-reported seed-mediated syntheses optimized for a particular shape are repeated with larger, more uniform seeds, yields can be improved to >95% with CV <5% for at least eight different nonspherical shapes with widely tunable sizes (28). This represents a particularly powerful advance that emphasizes the importance of seed stability and uniformity in the synthesis of homogeneous products.

Ligands Arranged on Nanoparticle Surfaces

Few nanomaterial surfaces are bare, and in solution chemical species can adsorb, coordinate, or bond to a nanomaterial surface. These “surface ligands” play important roles in nanoparticle synthesis to modulate reaction kinetics and growth pathways; in colloidal stabilization to passivate coordinatively unsaturated surface atoms, preserve structure, and prevent flocculation; and in surface chemistry to regulate the accessibility and reactivity of the nanoparticle surface (15, 44–47). Surface ligands also form the interface between a nanoparticle and its surroundings to dictate how nanoparticles interact with each other and their environment (8, 9, 48). Ligand uniformity—including variation in ligand structure, number, and arrangement on each nanoparticle in a population—represents an underexplored area of research. This is particularly true of the nanoparticle size range discussed here, where many probes designed to understand ligand structure on small nanoparticles break down, due to (i) the smaller percentage of surface atoms, (ii) the orders of magnitude difference in mass between nanoparticles and surface ligands, and (iii) the larger number of surface ligands often attached to each nanoparticle. Surface ligand uniformity becomes even more challenging to understand in systems where ligand–surface interactions are dynamic, due to surface reorganization or weak interaction strength, and in ligand exchange processes, where preexisting ligands influence the organization of subsequent ligands. Consequently, the descriptions of ligand uniformity given here are forward looking, indicative of our best understanding, but in need of further analytical development. This section focuses on the structure of surface ligands as it pertains to hierarchical organization, rather than chemical connectivity (45–47).

What Does It Mean to Be Uniform at This Length Scale?

Criterion 1: Discrete ligands.

A wide variety of ligands have been used either directly in nanoparticle synthesis or after ligand exchange, including metal complexes, small molecules, surfactants, biomolecules, and polymers (45–47). In the context of this discussion, these ligands can be broadly separated into structurally defined ligands and nonuniform ligands. Nonuniform ligands typically vary in their molecular weight (i.e., length and/or size), monomer sequence (i.e., the specific arrangement of chemical constituents), and stereoregularity (i.e., the stereochemistry of chiral centers). On a nanoparticle surface, these ligand inhomogeneities can dramatically affect the spatial arrangement, packing density, structure, and accessibility of functional groups at the solution interface. Consequently, each parameter should be analytically evaluated before use with nanoparticles to ascertain the potential effect of this distribution.

Criterion 2: Number (density).

The number of ligands attached to a nanoparticle surface is considered in two limits: a low limit, where small numbers of ligands are attached, and a high limit, where ligands are densely packed (Fig. 3A). In the low limit, a Poisson distribution can typically be used to describe the number of ligands per nanoparticle, because each ligand attachment occupies insufficient SA to impact subsequent attachments (i.e., attachment events are independent) (49). Given this distribution, an average number of ligands can be a deceptive metric that may not fully describe sample heterogeneity and should be used with caution (46, 49). In the high limit, the number of ligands can be approximated as dense packing and is dictated by a complex interplay of nanoparticle shape and SA, interligand interactions, and ligand–solvent interactions (10, 44). At this high limit, the variation in ligand number often represents a small fraction of the overall number and thus an average is a representative metric. With careful determination of the available SA, ligand number can be converted to density to compare between nanoparticles.

Fig. 3.

Nanoparticles act as templates to direct ligand arrangement. (A) Nanoparticles shown with low (Left) and high (Right) density of ligands. (B) Ligand coverage can be asymmetrically distributed based on facets or curvature (Left), spatial regions (Center), and localized patches (Right).

Criterion 3: Conformation.

The conformations of ligands free in solution are often very different from those on a nanoparticle surface. In particular, the configurational states accessible to each ligand significantly decrease when anchored, the chemical properties and 3D structure of a ligand can change based on interactions with the nanoparticle surface, and surface ligands can adopt collective conformations restricted and influenced by their neighbors (10, 44, 50, 51). The extent of these effects depends on ligand density, hydrodynamic ligand size, and particle size and shape. In the low-density limit, flexible surface ligands can adopt a coiled, random-walk configuration that maximizes configurational entropy. In the high-density limit, flexible surface ligands can adopt an extended polymer brush structure that sacrifices configurational entropy to maximize attractive van der Waals interactions, as with self-assembled monolayers, or to minimize steric or electrostatic repulsion, as with charged ligands (e.g., nucleic acids) (44, 50, 51). Corner and edge features introduce defects that disrupt densely packed structures due to the greater accessible free volume for surface ligands at these sites. Surface ligand interactions are also chemically modulated by their local environment, where variables such as solvent wetting (related to adhesive intermolecular forces between solvent and ligand), the solvent dielectric constant (related to solvent polarity and how far charge extends in solution), pH (related to protonation and charge of functional groups), and salt (related to the screening of charged moieties) can play important roles (8, 10). From a structural perspective, each surface ligand can thus be described by its hydrodynamic size, conformation, and direction. In the low-density limit, these structural parameters can vary significantly from ligand to ligand and with time, as they do for free ligands in solution, which can act as a source of inhomogeneity. In the high-density limit these parameters vary significantly less and, as a result, can often be described based on average values.

Criterion 4: Spatial distribution.

Ligands may also be nonuniformly distributed across a nanoparticle surface, and this anisotropy can lead to directionally dependent interactions between nanoparticles. This inhomogeneity can derive from spatial differences of a single ligand or the presence of multiple distinct ligands. Spatial distributions may be localized to a geometrically specified region (e.g., facet, hemisphere) or to a region of high (or low) positive (or negative) curvature (Fig. 3B). If a single ligand possesses spatial heterogeneity, this can be described by the density, symmetry, and structure of ligands within each region. For multiple, chemically distinct ligands, the number of each may also be heterogeneous within a localized region and can be best described by relative ratios to indicate a skewed distribution of ligands or complete spatial separation.

Although ligand characterization techniques have advanced to enable determination of the average number of ligands per nanoparticle, and even an average chemical environment for many ligands (45, 46), direct measurement of ligand structure or spatial distribution requires further work. This limitation arises from (i) the significant difference in mass and electron density between organic ligand shells relative to inorganic nanoparticle cores, which complicates the use of many probes that rely on these principles, and (ii) an insufficiently narrow distribution of structural properties of both the ligand (e.g., number, length) and nanoparticle (e.g., size, shape) that prevents distinction between inhomogeneities via separations techniques (26).

Successful Approaches to Control Uniformity at This Scale.

Approach 1: Structurally defined surface ligands.

Structural control begins with an ability to precisely control the composition and uniformity of discrete ligands. In particular, chemically and structurally defined biomolecules such as oligonucleotides and polypeptides can be synthesized with a deliberately controlled number and identity of constituent monomers (7, 48, 52–54). This modular structure enables researchers to program the length of DNA surface ligands with subnanometer precision based on the number of nucleobases. Control of surface ligand length and orientation is enhanced with double-stranded rather than single-stranded DNA, which increases the persistence length from 2 nm to 50 nm (55), and with increased surface density, wherein the polymer brush effect aligns and extends surface ligands (7, 44, 48, 54, 56). Tunable length allows precise control of interparticle spacing in nanoparticle crystallization experiments and sequence specificity allows one to program in chemical complementarity into surface ligands, which can be used to specifically cocrystallize nanoparticles of different sizes, shapes, and compositions (57, 58). Recent advances in the synthesis of structurally uniform polymers represent a promising direction to build upon these investigations and enable novel structural control.

Approach 2: Asymmetric functionalization.

The structural sophistication that can be achieved at each level of hierarchical organization directly relates to the amount of “assembly information” that can be encoded (14, 54, 59). At the ligand level, this information can be programmed through chemical specificity or asymmetric spatial distributions. Whereas significant advances have been made in the synthesis of so-called “patchy” or “Janus” particles composed of polymer or micrometer-sized particles, many of these approaches are difficult to adapt to smaller nanoparticles (60). Two particularly successful approaches to uniformly encode anisotropy into the ligand shell are through the geometric features of the nanoparticle core and templated ligand exchange procedures. The nanoparticle core acts as a template to guide the 3D arrangement of surface ligands, and the crystallographic facets that bound a nanoparticle can present chemically and structurally distinct coordination environments to localize surface ligands (7, 23, 24, 61). Nanoparticle curvature at the length scale of the ligands can also alter their “effective” spatial distribution (61). With positive curvature (e.g., a sphere), for example, the distance between ligands increases away from the surface, which can reduce “polymer brush” effects and result in a lower areal density of functional groups at the solution interface. These structural changes can induce localized chemical changes in the ligands, such as the acidity and chemical potential, to produce spatially distributed “patches” that control interparticle interactions (61). At the molecular level, ligand exchange in the presence of a chemical or physical barrier (e.g., a substrate, a liquid–liquid interface, a chemical protecting group) that prevents attachment to blocked regions of a nanoparticle can be used to create asymmetrically functionalized nanoparticles. In contrast, attachment to the barrier can be used to “print” surface ligands onto the contacted area. Nanoparticle size and shape can be used to modulate the SA or specific facets that are blocked in this process, and in principle, iterative ligand exchange can be used to modify different regions with chemically orthogonal surface ligands. Despite these impressive achievements, significant work remains to arbitrarily define ligand arrangement independent of nanoparticle structure, to access high yields of printed or exchanged patches of ligands, and to inhibit surface diffusion of ligands and their homogenization over time.

From Nanoparticles to Colloidal Crystals

Nanoparticle interactions originate from the interplay of the physical properties of the nanoparticles, the attached ligands, and the surrounding environment (7–11, 14, 54). The forces involved in these interactions can occur at the whole-nanoparticle level (e.g., entropic forces that drive the packing of hard spheres into a dense lattice) (8, 62) or in localized regions (e.g., the hybridization of complementary DNA molecules attached to particles) (52), and often these levels function cooperatively (63, 64). Whereas most interactions are relatively short ranged at the nanoscale and rarely influence next-nearest neighbor interactions, many-body effects and population-level interactions become important in crystalline assemblies, given the large number of particles, and thus we focus on these effects here. Organizations of nanoparticles generally fall into two categories: discrete and extended. Discrete assemblies typically consist of n = 2–10 particles arranged in a well-defined geometry. To realize uniform discrete structures requires the inherent interaction symmetry of the building blocks to be broken, and due to this challenge, the literature centers on valency clusters with a defined n, but highly variable or uncertain relative geometry (53, 65). A discussion of discrete assemblies is omitted here, but with further advances, one can imagine such clusters as nanoparticle-based “molecules,” which could be used as more structurally sophisticated material building blocks. Extended assemblies are best defined by the presence of long-range translational symmetry and described by a defined repeat unit. Because crystalline assemblies rely on the symmetry of the nanoparticle building blocks to achieve long-range order (66), small deviations in uniformity can create propagating error that can greatly frustrate crystal nucleation and crystal formation (58, 67). Thus, one must take great care to understand and engineer the interactions between particles to realize uniform assemblies.

What Does It Mean to Be Uniform at This Length Scale?

To build on the discussion of previous sections, it is helpful to compare atomic and nanoparticle building blocks. Many parameters that define the uniformity of nanoparticles built from atoms (e.g., shape, size) also apply to colloidal crystals built from nanoparticles, but with several unique considerations (Fig. 4).

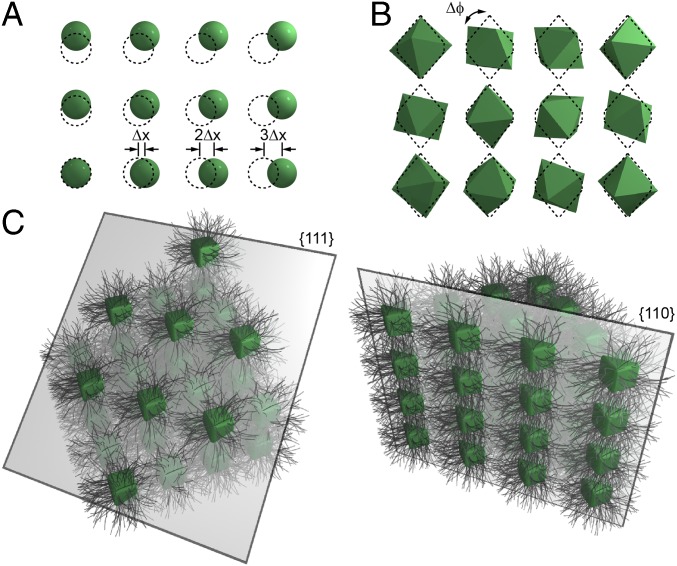
Fig. 4.

Inhomogeneities unique to colloidal crystals include variation in (A) position, (B) orientation, and (C) complex interfaces. In A and B, ideal reference lattices are indicated with dashed lines and used to demonstrate positional error propagation (by a distance Δx between lattice sites) and orientation misalignment (by an angle Δϕ). In C, two different interfaces are shown cut from the same simple cubic lattice of cubic nanoparticles.

Criterion 1: Position.

Because atomic radii and bond lengths are nearly identical for a given element, nanoparticles with >10⁴ atoms are nearly perfect crystals, perhaps with high-symmetry grain boundaries (e.g., twins). As a result, one is rarely concerned with the crystalline order of the atoms that compose a nanoparticle. In contrast, nanoparticle assemblies always possess a distribution in particle size and effective bond length, which in the case of colloidal crystals leads to a higher defect density. Even in a hypothetical system with perfectly uniform nanoparticles, colloidal crystallization would be more challenging to control due to the softer interparticle potentials that originate from deformable ligand shells and the presence of longer-ranged interactions (68).

For a collection of nanoparticles, the ideal reference state is often a crystalline arrangement with a defined symmetry and interparticle spacing. Deviations from this structure include the absence of a nanoparticle from a lattice site (i.e., a vacancy), a disruption in crystalline packing (e.g., grain boundaries, one-dimensional edge and screw dislocations) (69, 70), or positional variation. A system may also exhibit a high degree of local positional uniformity, but as a result of error propagation via nonuniform particles, may gradually lose order at a global level (Fig. 4A). These positional defects are frequently probed at the local level (i.e., specific nanoparticles within the first few layers of a crystal) through EM (71) and at the global level (i.e., many crystals simultaneously) through X-ray scattering techniques (72). Vacancies and dislocations can be difficult to identify with these techniques, due to convolution by other defects, but positional variation can be probed via the presence of strain fields within a crystal (72).

Criterion 2: Orientation.

The vast majority of nanoparticle assemblies reported use spherical building blocks that, as a result of their continuous rotational symmetry, can adopt any orientation in a crystal and remain equivalent (57, 62, 73–75). The use of anisotropic nanoparticles as building blocks breaks this symmetry and generates inequivalent particle orientations (Fig. 4B) (14, 24, 58, 61, 66). Although not a necessary precondition, it is often the case that hierarchy arises in systems with anisotropic interactions between building blocks, as the inequivalence of different fundamental directions favors structure formation along different time and length scales. In many cases, favorable particle orientations template crystals with a particular crystallographic symmetry (14, 24, 66, 76), and in these cases nonuniformity in the orientation results in positional disorder or the formation of a crystal with a different symmetry. However, positional and orientational order need not be strongly correlated. For example, ligands can be made sufficiently long and flexible to disguise the anisotropy of the underlying particle, but still induce a crystalline state, albeit with orientational disorder (58, 66). In other systems with hard interparticle interactions, sphere-like anisotropic shapes can pack into “plastic crystals” or “rotator phases” that lack strong orientational order. Direct characterization of orientation is complicated by the limited penetration and subsequent bias for surface structure of EM techniques, resulting primarily in qualitative evaluations (71). Recent advances in the scattering theory of polyhedra in lattices overcome this issue and enable ensemble measurements such as small-angle x-ray scattering to quantify an orientational order factor, given assumptions about nanoparticle structure and defect density (58, 72).

Criterion 3: Interfaces.

Because crystals are never infinite, nanoparticle assemblies always exist at some 2D boundary between phases, such as the interface between the surface of a nanoparticle assembly and the surrounding environment, or between different domains within a nanoparticle-based crystal (74, 77). As with atoms, the chemical potential of nanoparticles at an interface will be different from in solution or in the bulk. Therefore, the key parameters to define uniformity are the surface energy and interfacial area, which depend on a complex interplay of chemical, physical, and structural parameters. Whereas broken bond models can provide a first-order approximation for the surface energy of atomic systems, effective nanoparticle-based “bonds” are typically more complicated in that they may involve polyvalent ligand interactions and multiple fundamental forces operating over a range of length scales (Fig. 4C). Whereas positional and orientational order may be strongly correlated to interfacial nonuniformity, this observation need not always be true. For example, depending on processing conditions, nanoparticle superlattices with high positional order can be synthesized as polycrystalline materials or faceted supracrystals, wherein the interfacial energy of poorly defined grain boundaries is different from that of crystallographically well-defined facets (78). At present, molecular dynamics and density functional theory simulations offer our most thorough insight into the nature of interfaces, albeit with assumptions about structure and interaction potentials, and computational limitations at large sizes. Looking forward, imaging techniques that directly probe dynamic nanoparticle behavior in a liquid environment could be used to recreate the assembly process in situ to more precisely probe the energetics of interfacial interactions (79).

Successful Approaches to Control Uniformity at This Scale.

Approach 1: Uniform building blocks.

Unlike atomic or molecular crystallization, nanoparticle crystallization requires the ordering of imperfect building blocks. Consequently, improvements in nanoparticle uniformity can profoundly improve the long-range order in colloidal crystals (24, 58, 76). To illustrate the dramatic influence of nanoparticle uniformity on crystal quality, we compiled a figure from unpublished data from our group (Fig. 5). The challenge that precludes the establishment of broadly applicable rules for these relationships stems from the diversity of systems, each of which possesses different interaction potentials, and the complex interplay between the role of the inorganic nanoparticle and the surrounding ligand layer. For systems that interact via hard-sphere potentials (e.g., those with short, relatively inflexible alkyl ligands), the uniformity of the inorganic core is crucial and a CV < 5% is typically required to achieve meaningful levels of crystallization (62). When particles of two different shapes are cocrystallized, constraints on the uniformity of each component are even more extreme to favor a well-mixed state and avoid phase separation (58). Theoretical work on colloidal suspensions has shown that even the nucleation of crystals from nonuniform starting materials can be suppressed (67). Interestingly, there is some evidence that these constraints on the uniformity of the inorganic core can be alleviated with longer and semiflexible ligands such as DNA or polymers. In these cases, well-ordered systems are observed for spherical particles with CV ∼ 8–10%. Alternatively, one can make perfection from imperfection by encapsulating a nonuniform population of difficult to crystallize nanoparticles inside molecularly defined scaffolds. For example, polyhedral DNA cages capable of hybridizing a single particle on their inner surface have been used to generate long-range ordered superlattices (80).

Fig. 5.

Nanoparticle uniformity dictates the long-range order in colloidal crystals. Gold cubes of the same average size, but different CV, were crystallized under the same experimental conditions. (A, C, and E) For each sample, an SEM image of the crystal is shown with an Inset of individual nanoparticles. (B, D, and F) Fast Fourier transforms of many images (Insets) can be azimuthally averaged to quantitatively evaluate uniformity.

Approach 2: Slow crystallization.

In conventional crystallization processes, slow gradients in reaction conditions are used to allow building blocks to sample their environment and adopt thermodynamically preferred positions within a lattice (Fig. 6A). Order via slow crystallization thus requires (i) fine control of the crystallization time scale relative to the organizational processes involved and (ii) dynamic, reversible interactions to enable rearrangement, which for nanoparticles often arises from the surface ligands. For materials formed from atomic or molecular species, samples are often annealed over hours or days to form large single crystals. In these crystallization processes, however, the time scale for grain growth is considerably slower than the time scale for atomic ordering. For example, to prevent atomic diffusion altogether and form a “metallic glass,” cooling rates on the order of 10⁶ °C/s are necessary for some systems (81). In contrast, the diffusion of nanoparticles can be thousands of times slower and, as a result, crystallization must be controlled over significantly longer times. This has been observed for many nanoparticle systems where annealing over many hours or days is necessary to access ordered structures given the constraints on particle uniformity (62, 78).

Fig. 6.

Colloidal crystal uniformity can be controlled via (A) slow crystallization and (B) templated crystal growth. In A, thermodynamically preferred lattice sites with higher coordination can be accessed via slow growth. In B, a preformed template (blue) directs controlled heterogeneous nucleation.

Crystallization typically proceeds from a state with dynamic, reversible interactions to a state with fixed interactions. Interaction strength is typically modulated between these states based on slow changes in reagent concentration/pressure or the chemical or physical environment (e.g., temperature, ionic strength). For systems with temperature-dependent interactions (analogous to atomic systems), dynamic interactions occur when the available thermal energy is comparable to the interaction energy, such that only those configurations with maximum thermodynamic stability are allowed. This approach has proved particularly successful for DNA-mediated nanoparticle crystallization, where elevated temperatures are necessary to increase the rates of DNA hybridization and dehybridization to drive the system away from kinetic (disordered) states and toward thermodynamic (ordered) ones (7, 48, 54). Indeed, the thermodynamic control of DNA-mediated crystallization has enabled the predictable formation of colloidal crystals with >30 unique lattice symmetries, lattice parameters tuned over two orders of magnitude, and well-defined crystal habits, all built from a library of building blocks with different shapes, sizes, and compositions (7, 48, 54, 58, 78, 80). For systems less responsive to temperature, dynamic interactions often occur under dilute (e.g., entropically driven assembly), weakly ionic (e.g., electrostatic-mediated assembly), or favorable solvent conditions, and interaction strength can be increased in all cases via solvent evaporation. This solvent evaporation-based approach has proved particularly successful for interfacial assembly at liquid–solid or liquid–liquid interfaces and has produced a remarkable diversity of colloidal crystals with millimeter-scale order (24, 62, 73, 74).

Approach 3: Templated crystallization.

Rather than relying entirely on the thermodynamics of unconstrained crystal growth in solution or on a substrate, a patterned template, consisting of well-defined structurally or chemically distinct features, can guide the formation of ordered systems with controlled superlattice positions, shapes, sizes, and crystallographic orientations (textures) (11). Templated approaches represent a colloidal crystal example of heterogeneous nucleation principles, where a preexisting surface can significantly lower the barrier to nucleation and can define where crystallization occurs (Fig. 6B). Depending on the design, the template can enact spatial restrictions on crystal growth and, in principle, may be able to kinetically direct different symmetries on the basis of the template shape (69, 76). In particular, photolithography techniques can be used to define micrometer-scale patterns to control the microscopic dimensions of a superlattice (69), or alternatively, one can pattern individual nanoparticle binding sites on a substrate to control crystallization with higher-resolution and lower-throughput tools, such as electron-beam lithography (Fig. 6B) (82, 83). Using the principle of epitaxy, nanoparticle superlattices of one type can even be used as a template for the growth of subsequent nanoparticle crystals of a different type (75). To realize the full potential of this approach, it would be advantageous to develop high-throughput printing techniques that could define nanoscale features into microscale patterns over millimeter lengths. The ability to pattern in three dimensions, for example through 3D printing and other additive manufacturing techniques, offers an additional means to program hierarchical structure into the final crystals.

Beyond Colloidal Crystals

Although significant challenges still remain at each level of organization, which together preclude perfect colloidal crystals, this Perspective highlights the importance of approaches that consider and connect uniformity at each scale. One can imagine extending these lessons beyond the scope of this Perspective, wherein macroscopic colloidal materials could be built from microscopic colloidal crystals. Unlike previous levels, these building blocks could be manipulated by more conventional processing techniques or even used as colloidal crystal inks to print structures defined from the nanometer to meter scale. Borrowing further from nature’s hierarchical organization processes, dynamic feedback loops could be used to connect each level to its constituent and final structures to provide a built-in mechanism of structural regulation or refinement. To operate such feedback mechanisms within a single environment, analogous to a cell, would require compartmentalization, encoded by chemical specificity or physical/structural boundaries, to minimize crosstalk and maximize uniformity within each level (59, 84). With a sufficient understanding of hierarchy principles, these advances could enable a future where systems are programmed to operate independent of human intervention.