Nonlinear two-dimensional terahertz photon echo and rotational spectroscopy in the gas phase

Significance

Molecular rotations of small molecules provide a useful testbed for examining light−matter interactions with quantum mechanical systems, but the methods of modern spectroscopy have been largely unavailable in the terahertz frequency range where most of the rotational states that are thermally populated at ordinary temperatures absorb light. Applying a pair of strong terahertz pulses, we excite molecular rotations coherently, interrogate thermally populated rotational states, manipulate the rotational motions nonlinearly, and observe connections between different rotational states spectroscopically. The method is applicable to polar molecules in flames and other reactive conditions, and it enables enhanced control over molecular motion with light.

Abstract

Ultrafast 2D spectroscopy uses correlated multiple light−matter interactions for retrieving dynamic features that may otherwise be hidden under the linear spectrum; its extension to the terahertz regime of the electromagnetic spectrum, where a rich variety of material degrees of freedom reside, remains an experimental challenge. We report a demonstration of ultrafast 2D terahertz spectroscopy of gas-phase molecular rotors at room temperature. Using time-delayed terahertz pulse pairs, we observe photon echoes and other nonlinear signals resulting from molecular dipole orientation induced by multiple terahertz field−dipole interactions. The nonlinear time domain orientation signals are mapped into the frequency domain in 2D rotational spectra that reveal J-state-resolved nonlinear rotational dynamics. The approach enables direct observation of correlated rotational transitions and may reveal rotational coupling and relaxation pathways in the ground electronic and vibrational state.

Recent years have witnessed increasing interest in 2D infrared (IR) vibrational spectroscopy techniques for studying structural dynamics and correlations between coupled molecular motions in biological systems such as water, proteins, and DNA (1–3). Multidimensional optical spectroscopies were applied to probe the high-order correlations of excitons in quantum wells and organic complexes (4, 5). However, it remains an experimental challenge to extend multidimensional spectroscopies into the terahertz (THz) frequency range where a rich variety of material degrees of freedom, including gas molecular rotations, lattice vibrations in solids, magnetization dynamics in magnetically ordered materials, and many others (6), find fundamental and technological importance. Despite challenges involved, there have been examples of 2D THz and 2D THz−Raman spectroscopies in the studies of electronic nonlinearities in solids (7, 8), coupled vibrational modes in liquid molecules (9), and hydrogen bond dynamics in water (10).

Rotations of gas molecules have been the subjects of intensive recent efforts in coherent spectroscopy and coherent control, motivated by interests in rotational angular momentum and energy relaxation processes, high-order optical interactions with multilevel quantum systems, and applications of molecular alignment and orientation for various forms of orbital tomography, for example using high-harmonic generation to probe the molecular orbital structures of rotating molecules (11, 12). Strong optical fields have been used to drive high-order rotational coherences and to populate high-lying rotational levels (13), to control molecular alignment dynamics (14), and to induce rotational alignment echoes (15, 16). Strong microwave fields can drive high-order rotational responses and have been used for double-resonance and 2D rotational spectroscopies (17–22), mostly at low rotational temperatures. In recent work, we demonstrated second-order interactions between THz frequency fields and molecular rotations, measuring net molecular dipole orientation, manipulating two-quantum coherences (2QCs), and observing rotational populations and their superradiant decays (23–25). Higher-order THz field interactions have been treated theoretically, including photon echoes resulting from molecular orientation predicted by classical phase-space distribution calculations (15) and full quantum mechanical simulations (26). The recent experimental and theoretical results motivate developments in nonlinear multidimensional rotational spectroscopy in the THz frequency range that includes many of the transitions of small molecules at ordinary temperatures.

In this work, we used variably delayed single-cycle THz pulse pairs to demonstrate the full suite of third-order rotational responses—rephasing (R, i.e., photon echo), nonrephasing (NR), two-quantum (2Q), and pump−probe (PP) signals (27)—separated from each other and fully J-state-resolved through 2D THz time domain spectroscopy measurements. The results demonstrate the capability for full elucidation of rotational population and coherence dynamics with subpicosecond time resolution, applicable to polar gas molecules under conditions that could lead to extremely fast relaxation and dephasing, such as high (including supercritical) pressure and temperature, flames, and reactive mixtures. We also observe higher-order responses due to five field−dipole interactions, showing that extensive THz field control over successive populations and coherences can be executed to explore microscopic pathways involving multiple rotational J levels.

An ultrashort THz pulse induces coherent molecular rotations via resonant field−dipole interactions. The linear interaction term, $H_1=-\overrightarrow{\mu }\cdot {\overrightarrow{E}}_{\text{THz}}=-\mu E_{\text{THz}}\cos \theta$, where θ is the angle between molecular dipoles and the THz electric field polarization, couples adjacent rotational states J and $J+1$, yielding one-quantum coherences (1QCs) among the thermally populated rotational states. Each 1QC oscillates at a frequency of $f_{J,J+1}=2Bc\left(J+1\right)$, where B is the rotational constant in units of wavenumber and c is the speed of light. The superposition of 1QCs with frequencies that are integer multiples of the lowest frequency $2Bc$ gives rise to short-duration events of net molecular dipole orientation with a nonzero orientation factor $\langle \cos \theta \rangle$ that recur with the quantum rotational revival (28) period of $T_{\text{rev}}={\left(2Bc\right)}^{-1}$. This phenomenon is analogous to the laser pulse train from a mode-locked oscillator with a distribution of equally spaced cavity modes (29). Upon each revival, the net dipole orientation results in a macroscopic polarization that emits a burst of coherent THz frequency radiation. The free-induction-decay (FID) signal thus consists of a sequence of such bursts separated by $T_{\text{rev}}$. Two successive interactions between the incident THz field and the molecular dipoles can couple rotational states J and $J+2$ to yield 2QCs whose superposition shows dipole alignment revivals with the period equal to $T_{\text{rev}}/2$, and can transfer population between states J and $J+1$, both outcomes manifested as a transient birefringence of the molecular ensemble (23). It has been shown that two time-delayed field−dipole interactions can coherently control the rotational populations and coherences to significantly enhance the 2QC amplitudes and the corresponding degree of net molecular alignment $\langle {\cos }^2\theta \rangle$ (24). These examples of THz second-order interactions and spectroscopy set the stage for multidimensional spectroscopy at third and higher orders.

Results

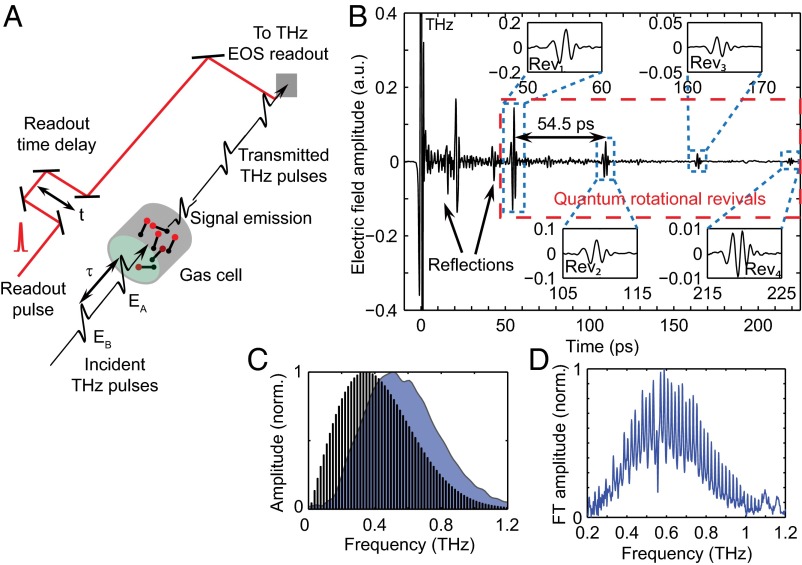
The experimental setup is shown schematically in Fig. 1A (for details, see SI Appendix, Experimental Setup). Two THz pulses denoted as A and B separated by a time delay $\tau$ were focused into a static pressure sample cell in collinear geometry. The transmitted THz fields and the subsequent emitted signals were detected through the birefringence they induce in an electrooptic (EO) crystal (30), measured using a 100-fs optical readout pulse (EO sampling) that was delayed by time t relative to pulse B. The measurements were performed on gaseous acetonitrile (CH₃CN, dipole moment $\mu =3.92\hspace{0.17em}\text{debye}$) at room temperature and 70-Torr pressure. The rotational constant is $B=0.310{\hspace{0.17em}\text{cm}}^{-1}$, corresponding to $T_{\text{rev}}=54.5\hspace{0.17em}\text{ps}$ (31). A single THz excitation pulse was used to measure the FID signal from one field−dipole interaction, which shows the expected revivals (Fig. 1B, blue dashed boxes). The rotational transitions from thermally populated J levels in CH₃CN overlap with the spectrum of our THz field as shown in Fig. 1C. Fourier transformation of the FID signal in Fig. 1B reveals the rotational transition peaks within our THz excitation bandwidth, as shown in Fig. 1D.

Fig. 1.

Pulse sequence and sample linear response. (A) Two collinearly propagating THz pulses with a delay $\tau$ are focused into the gas cell with CH₃CN. Transmitted THz pulses and induced nonlinear signals are detected by EO sampling (EOS). (B) Linear FID signal of CH₃CN induced by one THz excitation pulse interacting once with the sample. The signals in the blue dashed boxes are the quantum rotational revivals (enlarged views shown in Insets. Rev₁, Rev₂, etc., denotes revival 1, 2, etc.). Water vapor in the THz propagation path outside the gas cell and signals owing to double reflection of the THz pulse in the detection crystal and cell windows are observed, but they do not affect the nonlinear responses of interest in this work. (C) Calculated rotational populations of CH₃CN at thermal equilibrium at 300 K as a function of $J\to J+1$ transition frequency, overlapped with the spectrum of the THz pulses (blue shaded area) used in the experiments. Each bar represents a rotational transition originating from a distinct rotational J level. (D) Experimental rotational spectrum of CH₃CN, Fourier-transformed from the FID signal in the red dashed box in B. Each sharp peak represents a rotational transition from an initial J level to the final $J+1$ level. THz absorption by water vapor causes a dip at 0.56 THz in the spectrum.

We implemented a differential chopping detection method (32) to extract the nonlinear signals resulting from two THz pulses interacting with the molecular dipoles (SI Appendix, Experimental Setup). There are four distinct types of signals observed that arise from three THz field interactions with the molecular dipoles, i.e., four third-order signal types that are all distinguished in the time domain traces of $E_{NL}\left(\tau ,t\right)$: (i) R (i.e., photon echo) and (ii) NR signals, generated through one field interaction with pulse A and, after time delay $\tau$, two field interactions with pulse B; and (iii) 2Q and (iv) PP signals, arising from two instantaneous interactions with pulse A and, after time delay $\tau$, one interaction with pulse B.

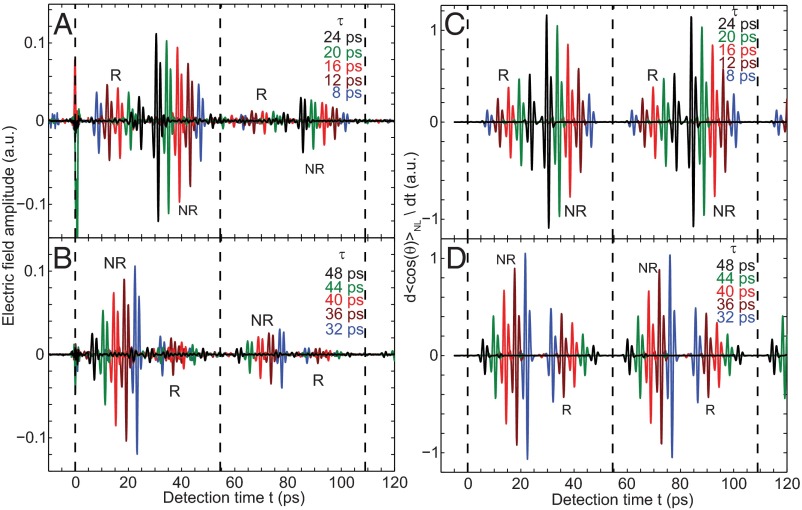
These signals are of the same origins as those in 2D IR and optical spectroscopies. The nonlinear traces $E_{NL}\left(\tau ,t\right)$ at varying delays $\tau >0$ (color coded in figure legend) are shown in Fig. 2 A and B for selected time delays $\tau$. Because all of the signals are emitted from the full collection of third-order 1QCs involving the entire set of thermally populated J levels whose transition frequencies are included in the THz pulse spectrum, they all take the same form as the first-order FID, namely, periodic bursts of THz radiation separated by revival time $T_{\text{rev}}$. However, the signals do not all appear at the same time after the two incident THz pulses. For any delay $\tau <T_{\text{rev}}$ between pulses A and B, the first R (photon echo) signal (type i) appears only after an equal time $t=\tau$ after pulse B, and, including their revivals, the echo signals appear at $t=\tau +n{T}_{\text{rev}}\left(n=\mathrm{0,1,2,3}...\right)$. The NR signals (type ii) appear as changes to the first-order FID amplitude from pulse A caused by the action of pulse B, so they appear at times $t=-\tau +n{T}_{\text{rev}}\left(n=\mathrm{1,2,3}...\right)$. The 2Q signals (type iii) appear at $t=-2\tau +n{T}_{\text{rev}}\left(n=\mathrm{1,2,3}...\right)$ as the 2QCs induced by pulse A evolve with approximately twice the frequency of 1QCs for time $\tau$, after which they are projected by pulse B back to the 1QC manifold and continue to evolve with the 1QC frequency. Thus, the completion of the third-order coherence rotational cycle occurs $2\tau$ earlier than the 1QC revivals of pulse B (i.e., $\tau$ earlier than the 1QC revivals of pulse A). The PP signals (type iv) appear coincident with pulse B, whose absorption is modified by the nonthermal population distribution created by pulse A, and, including their revivals, the signals appear at times $t=n{T}_{\text{rev}}\left(n=\mathrm{0,1,2,3}...\right)$. Due to their small amplitudes, the 2Q and PP time domain signals are shown in detail in SI Appendix, Fig. S2.

Fig. 2.

THz photon echoes and NR signals in the time domain. (A) Experimental time domain traces $E_{NL}$ at delays $\tau <T_{\text{rev}}/2$ between THz pulses A and B. THz pulse B is fixed at time 0. The rephasing (R) signals appear at $t=\tau +n{T}_{\text{rev}}$ (n = 0 and 1 shown), and the nonrephasing (NR) signals appear at $t=-\tau +n{T}_{\text{rev}}$ (n = 1 and 2 shown). For $\tau <T_{\text{rev}}/2$, each R signal appears earlier than its counterpart NR signal. The vertical dashed lines mark the position of pulse B (t = 0) and its first two revivals ($t=T_{\text{rev}}$ and $2T_{\text{rev}}$), where the PP signals appear. (B) Experimental time domain traces $E_{NL}$ at delays $\tau >T_{\text{rev}}/2$. Each R signal appears later than the counterpart NR signal. (C and D) Simulated time domain response of the derivative of the orientation factor, $d\cos {\langle \theta \rangle }_{\text{NL}}/dt$, at delays (C) $\tau <T_{\text{rev}}/2$ and (D) $\tau >T_{\text{rev}}/2$. Except for the effects of dephasing that are not accounted for, the simulations show good agreement with the experimental results.

The experimental traces were compared with semiclassical calculations of the dipole orientation responses in Fig. 2 C and D. The simulations were performed by numerically integrating the Liouville−von Neumann equation of the density matrix under decoherence- and decay-free conditions (SI Appendix, Numerical Simulation). The time derivative of the ensemble-averaged orientation factor, $d\cos {\langle \theta \rangle }_{NL}/dt$, was calculated to account for the THz field radiated from the collective polarization formed by the dipole orientation and showed good agreement with the experimental data. A noticeable difference is that the simulated photon echo signal peaks at interpulse delay time $\tau =T_{\text{rev}}/2$ whereas, in the experimental data, the maximum occurs earlier. This is attributed to the relatively fast decoherence of rotations under our experimental pressure and temperature conditions.

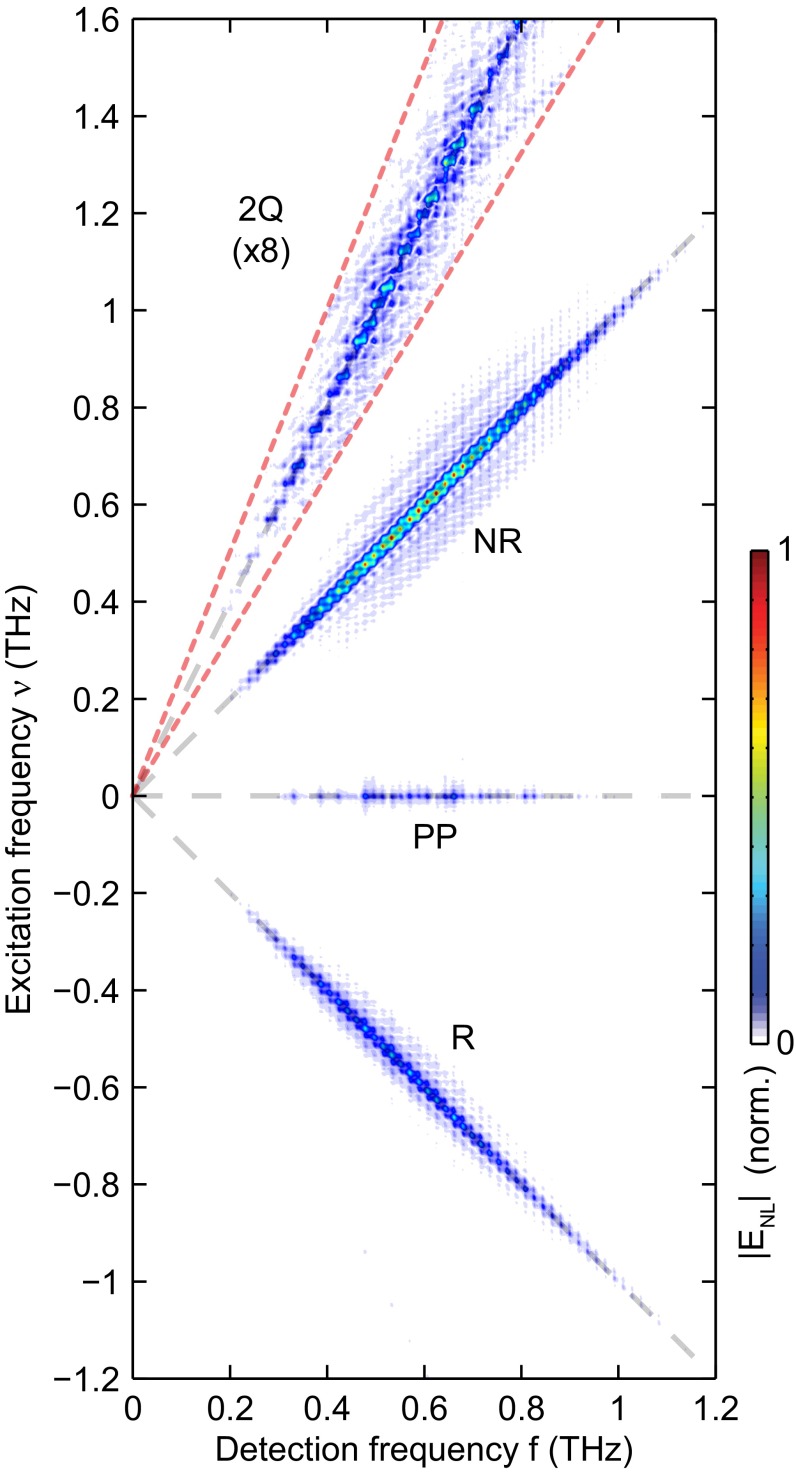
The 2D time domain nonlinear signal $E_{NL}\left(\tau ,t\right)$ was recorded as a function of $\tau$ and t (SI Appendix, Fig. S3). A numerical 2D Fourier transformation with respect to $\tau$ and t yielded the complex 2D rotational spectrum as a function of the corresponding frequency variables $\nu$ and f. The 2D magnitude spectrum is shown in Fig. 3. All of the signals are fully J-resolved in both dimensions. The full 2D spectrum can be separated into R and NR quadrants, as the R signals are distinguished from the NR signals by negative values of the excitation frequency $\nu$ due to the reversed phase accumulation of the former. The 2D spectrum clearly includes all four of the signal types discussed above. Examples of each signal type are discussed as follows. For the R and NR signals, THz pulse A interacts once with the molecular dipoles to produce first-order 1QCs described by density matrix terms $|J\rangle \langle J+1|$. After interpulse delay $\tau$, pulse B interacts twice with the dipoles, first to produce rotational populations $|J+1\rangle \langle J+1|$ and, from these, to generate third-order 1QCs $|J\rangle \langle J+1|$ (NR) or $|J+1\rangle \langle J|$ (R) from which the measured signals are radiated during time t. The third-order nonlinear signal field $E_{NL}\left(\tau ,t\right)$ shows oscillations at the 1QC frequencies along the two time variables, and, in this example, the frequencies are the same, so Fourier transformation of the signal with respect to both time variables yields J-state-resolved diagonal peaks in the 2D spectrum. For 2Q and PP signals, pulse A interacts twice with the molecular dipoles to produce either 2QCs $|J\rangle \langle J+2|$ or populations $|J+1\rangle \langle J+1|$, respectively. After interpulse delay $\tau$, pulse B interacts once with the dipoles to produce third-order 1QCs $|J\rangle \langle J+1|$ that radiate the measured signals during time t. The 2Q signal field $E_{NL}\left(\tau ,t\right)$ shows oscillations as a function of $\tau$ at the 2QC frequencies and oscillations as a function of t at the 1QC frequencies, giving rise to J-state-resolved peaks at $\nu \cong 2f$. For PP signals, there is no coherence evolution during the interpulse delay, so the signal appears in the 2D spectrum at zero frequency along $\nu$ and at J-state-resolved positions along f.

Fig. 3.

The 2D THz rotational spectrum $\left|E_{\text{NL}}\left(\nu ,f\right)\right|$ is obtained by taking the absolute value of the 2D Fourier transformation of the time domain signal $E_{NL}\left(\tau ,t\right)$. The light dashed lines are along $\nu =0,\pm f\hspace{0.17em}\text{and}\hspace{0.17em}2f$, respectively. The observed third-order spectral peaks include NR, R, PP, and 2-Q (magnified 8× inside the red dashed area) signals. The spectrum is normalized and plotted according to the color map shown.

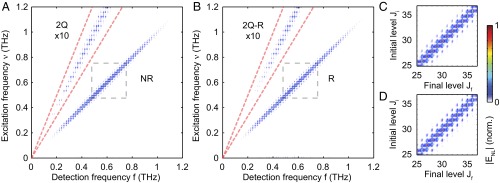
The NR and R quadrants are plotted separately in Fig. 4 A and B, with the R quadrant f frequency values made positive. J-state-resolved diagonal peaks are clearly observed along $\nu =f$ in both plots, consistent with the discussion above. In addition, for each excitation frequency $\nu =f_{J,J+1}=2Bc\left(J+1\right)$, off-diagonal peaks are observed at detection frequencies $f=f_{J-1,J}=2BcJ$ and $f=f_{J+1,J+2}=2Bc\left(J+2\right)$, indicating that the first-order $|J\rangle \langle J+1|$ coherences induced via one interaction of the molecular dipoles with THz pulse A are correlated via two interactions with THz pulse B with not only the third-order $|J\rangle \langle J+1|$ coherences discussed above but also the third-order coherences $|J-1\rangle \langle J|$ and $|J+1\rangle \langle J+2|$ involving two neighboring J levels. Similar effects have been observed at microwave frequencies (19, 21). Three distinct NR pathways that can be executed by the action of the second pulse are as follows:

$$\text{diagonal}\hspace{0.17em}\text{peak}\mathrm{:}|J\rangle \langle J|\stackrel{E_A}{\to }|J\rangle \langle J+1|\stackrel{E_B}{\to }|J+1\rangle \langle J+1|\stackrel{E_B}{\to }|J\rangle \langle J+1|;$$

$$\text{off}-\text{diagonal}\hspace{0.17em}\text{peak}\mathrm{:}|J\rangle \langle J|\stackrel{E_A}{\to }|J\rangle \langle J+1|\stackrel{E_B}{\to }|J+1\rangle \langle J+1|\stackrel{E_B}{\to }|J+1\rangle \langle J+2|;$$

$$\text{off}-\text{diagonal}\hspace{0.17em}\text{peak}:|J\rangle \langle J|\stackrel{E_A}{\to }|J\rangle \langle J+1|\stackrel{E_B}{\to }|J+1\rangle \langle J+1|\stackrel{E_B}{\to }|J-1\rangle \langle J|.$$

In the second pathway, the second field interaction of THz pulse B induces a transition up to $\langle J+2|$ rather than back down to the original $\langle J|$ level. In the third pathway, the first field interaction of THz pulse B returns population to $\langle J|$ rather than promoting population to $\langle J+1|$. These spectral peaks are located at J-resolved positions as shown in the 2D J-number map plotted as a function of initial and final rotational level $J_{\text{i}}$ and $J_{\text{f}}$ [related to frequencies variables by $\nu =2Bc\left(J_{\text{i}}+1\right)$ and $f=2Bc\left(J_{\text{f}}+1\right)$] in Fig. 4 C and D. Exemplar pathways for each signal type are elaborated in SI Appendix, Double-Sided Feynman Diagrams and Fig. S10.

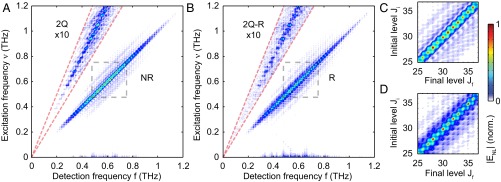
Fig. 4.

Experimental 2D THz rotational spectra. (A) NR and (B) R (excitation frequency shown as positive) quadrants of the 2D rotational spectrum of CH₃CN. Spectral amplitudes inside the red dashed area are magnified 10× to bring out the (A) 2Q and (B) 2Q-R signals. The dashed boxes cover rotational transitions from $f_{\mathrm{25,26}}$ to $f_{\mathrm{37,38}}$. (C and D) Enlarged views of the NR (C) and R (D) spectra within the dashed boxes in the NR quadrant (in A) and R quadrant (in B) as functions of initial and final J quantum numbers along the vertical and horizontal axes, respectively. Third- and fifth-order off-diagonal peaks are separated from the diagonal peaks at J-resolved positions. All of the spectra are normalized and plotted based on the color map shown.

In addition to the third-order signals, we observed spectral peaks including two-quantum rephasing (2Q-R) signals and off-diagonal NR and R signals coupling J and $J\pm 2$ levels that are due to five THz field interactions with the dipoles. Examples (SI Appendix, Fig. S10) are as follows. The 2Q-R peaks arise firstly through two field interactions by pulse A to create 2QCs $|J\rangle \langle J+2|$, which are then followed by three field interactions with pulse B, rather than one interaction as in the third-order 2Q signals. The first two interactions with pulse B create a population $|J+2\rangle \langle J+2|$, and the third induces a rephasing 1QC $|J+3\rangle \langle J+2|$ or $|J+2\rangle \langle J+1|$, which radiates during t. The 2Q-R signals were observed directly in the time domain (SI Appendix, Fig. S2), and they give rise to peaks along $\nu =2f$ in the R quadrant shown in Fig. 4B. For the fifth-order NR and R signals shown in Fig. 4 C and D, THz pulse A induces 1QCs $|J\rangle \langle J+1|$ evolving during $\tau$, and pulse B promotes them via four field−dipole interactions to fifth-order 1QCs with final rotational level $J_{\text{f}}$, two quanta away from the initial level $J_{\text{i}}$ (namely, $\left|J_{\text{i}}-J_{\text{f}}\right|=2$) at $|J+3\rangle \langle J+2|$ (R) or $|J+2\rangle \langle J+3|$ (NR). The fifth-order 1QCs then radiate signals correlated to the 1QCs induced during $\tau$. The experimental spectra are in good agreement with simulated 2D spectra shown in Fig. 5, which are generated from double Fourier transformation of the simulated 2D time domain nonlinear orientation response, $d\cos {\langle \theta \rangle }_{NL}/dt$ with respect to t and $\tau$. The simulated spectra capture all of the third- and fifth-order signals discussed above.

Fig. 5.

Simulated 2D THz rotational spectra. (A) NR and (B) R quadrants of the 2D magnitude spectra obtained from numerical Fourier transformation of the simulated 2D time domain rotational response. The excitation frequency of the R quadrant is made positive. Spectral amplitudes inside the red dashed area are magnified 10× to bring out the (A) 2Q and (B) 2Q-R signals. The dashed boxes cover rotational transitions from $f_{\mathrm{25,26}}$ to $f_{\mathrm{37,38}}$. (C and D) Enlarged views of the NR (C) and R (D) spectral peaks in the dashed boxes in the NR (in A) and R (in B) quadrants as functions of rotational quantum number J. Our simulation reproduces well the third- and fifth-order J-resolved spectral peaks observed experimentally. All of the spectra are normalized and plotted based on the color map shown.

Discussion

We have shown that the main features of the R, NR, 2Q, PP, and 2Q-R signals are in good agreement with our expectations for third- and fifth-order interactions between the incident THz pulse pair and the molecular dipoles and with our numerical simulations based on those expectations. The third- and fifth-order signals scale with the fourth and sixth powers, respectively, of the molecular dipole moment (SI Appendix, Eq. S5). For common molecules with dipole moments of 1 debye, using similar gas pressures, interaction lengths, and single-cycle THz field profiles, comparable signal levels would require peak fields of about 2.5 MV/cm, which are already available in tabletop sources (33). Significant improvements in 2D rotational spectroscopy methodology, including single-shot readout of the signal field (34) and the use of frequency-tunable multicycle THz pulses (35) to enhance field−dipole interactions and nonlinear signals involving selected rotational levels, will substantially relax the field strength requirements and may enable multidimensional THz rotational spectroscopy in the nonperturbative limit.

In the 2D THz spectra, there are weaker sets of features that are not readily explained on the same basis. The experimental R and NR spectra, in addition to the diagonal and off-diagonal peaks attributed to third- and fifth-order field−dipole interactions of the two incident pulses, include weaker, farther off-diagonal peaks that are apparent in the 2D J-number plots showing correlations between initial levels $J_{\text{i}}$ and final levels $J_{\text{f}}=J_{\text{i}}+n\left(n=\mathrm{3,4,5},\hspace{0.17em}\text{etc}.\right)$ in Fig. 4 C and D. These features are also displayed in 1D line-out plots (SI Appendix, Fig. S6). The relative strengths of the off-diagonal features do not vary substantially with gas pressure (SI Appendix, Fig. S6) or incident field strength, indicating, respectively, that they are not due to intermolecular dipole−dipole interactions or to high-order interactions with the field. We suggest that the distinct features may be explained by the collective polarization formed by the oriented dipoles during each revival and the resulting nonlinear signal emission, i.e., by superradiance. We have shown previously that this unique type of superradiance results in a series of sudden reductions of the induced rotational populations in every J level, which must occur to provide the energy carried away by each FID burst (25). Coupling among all of the states involved in superradiant emission may be highlighted in the 2D spectrum, which displays correlations among their transitions explicitly. Further work is required to determine the origins of these far off-diagonal peaks.

In conclusion, we have measured the 2D rotational spectra of molecular rotors using two time-delayed single-cycle THz pulses. We have observed all of the third-order signal contributions expected and some fifth-order signals. The approach we have demonstrated permits direct measurement of rotational dephasing and population relaxation dynamics and spectral correlations that are hidden in linear rotational spectra. By including a third THz pulse at a controlled delay with respect to the second pulse (36), the rotational population time can be varied and 2D rotational spectroscopy with three THz pulses can enable measurements of the time-dependent evolution of off-diagonal spectral peaks and spectral diffusion as in other 2D spectroscopies (37, 38). Such measurement can reveal specific rotational energy transfer and relaxation pathways (due to collisions/dipole−dipole interactions) by comparing the strengths and line shapes of the 2D spectral peaks for different population times. Independent control of the THz pulse polarizations could reveal the dynamics of relaxation among the M sublevels of the rotational J levels. The approach could provide information that is complementary to conventional microwave rotational spectroscopies (17–22, 39, 40), molecular orientation and alignment induced by optical fields (13–16), and laser centrifuge experiments (41–43).

Materials and Methods

Experimental Setup.

The laser we used was a Ti:Sapphire amplifier system (Coherent) operating at 1-kHz repetition rate with an output power of 4 W delivering pulses at 800 nm with 100-fs duration; 95% of the laser output was split equally into two optical paths with a controlled time delay between them. The two delayed optical pulses were recombined in a single lithium niobate (LN) crystal to generate two time-delayed collinearly propagating THz pulses by optical rectification using the tilted-pulse-front technique (44, 45). The delay between the two optical pulses was not reduced below 3 ps to avoid nonlinear interactions between them in the LN crystal. The generated THz pulses were collimated and focused by a pair of 90-degree off-axis parabolic mirrors, resulting in peak field strengths of 400 kV/cm in each pulse reaching the sample gas cell. The transmitted THz fields and THz emission signals from molecular orientation were collimated and refocused by another pair of parabolic mirrors. The remaining 5% of the laser output was attenuated and used to detect the electric field profile of the THz signals by EO sampling in a 2-mm ZnTe crystal at the focus of the last parabolic mirror. The setup was under constant dry air purging to eliminate THz absorption by water vapor in the atmosphere.

Differential Chopping Detection.

We used two optical choppers at frequencies of 500 Hz and 250 Hz to modulate the two variably delayed optical pulses for THz generation. In successive laser shots, the choppers allowed generation of both THz pulses A and B, A only, B only, and neither pulse. The choppers and laser were synced to a data acquisition card (National Instruments), which measured the signal from EO sampling (46). With background noise subtraction and averaging over 50 laser shots for each data point, the sensitivity of the experiment was in excess of 10⁻³. The total data acquisition time for a complete 2D spectrum was typically about 7 d. Real-time measurement of the THz signal field (34) could reduce the acquisition time by alleviating the need for scanning of the EO sampling time variable t.

Sample Details.

CH₃CN is a prolate symmetric top molecule with two identical moments of inertia along axes that are perpendicular and much larger than the moment of inertia of the dipole axis. The THz−dipole interaction induces rotation of the dipole axis but does not couple to the rotations about the dipole axis (the selection rule for the transition is $\mathrm{\Delta }K=0$) (47). Consequently, in our study, CH₃CN can be approximated as a linear molecule and described by the quantum mechanical rigid rotor model (31).

To prepare the CH₃CN gas, liquid CH₃CN was frozen in a storage vessel using liquid nitrogen. The storage vessel, a transfer line, and the gas cell were evacuated. The storage vessel containing CH₃CN was then warmed to room temperature. The vaporized CH₃CN was allowed to diffuse into the gas cell with a path length of 1.25 cm until the pressure in the cell equilibrated with that in the vessel and reached 70 Torr, the vapor pressure of CH₃CN at room temperature.