Significance
Collagen plays crucial biomechanical roles in a wide array of animal tissues, but its mechanical properties remain largely static over short timescales. However, echinoderms (sea cucumbers, starfish) are striking exceptions to this rule, having “mutable collagenous tissue” with changeable mechanical properties, enabling complex locomotion, postural maintenance, defense, and reproductive strategies. Using a high-resolution X-ray probe that measures how the building blocks—fibrils—of echinoderm connective tissue stretch, slide, or reorient in real time, we show that sea cucumbers achieve this remarkable property by changing the stiffness of the matrix between individual fibrils, rather than the properties of the fibrils themselves. Understanding the mechanisms of mutability in this unique tissue may help design novel mechanically tunable synthetic biomaterials.
Keywords: mutable collagenous tissue, synchrotron small-angle X-ray diffraction, nanoscale mechanics, fibrillar deformation, sea cucumbers
Abstract
The mutable collagenous tissue (MCT) of echinoderms (e.g., sea cucumbers and starfish) is a remarkable example of a biological material that has the unique attribute, among collagenous tissues, of being able to rapidly change its stiffness and extensibility under neural control. However, the mechanisms of MCT have not been characterized at the nanoscale. Using synchrotron small-angle X-ray diffraction to probe time-dependent changes in fibrillar structure during in situ tensile testing of sea cucumber dermis, we investigate the ultrastructural mechanics of MCT by measuring fibril strain at different chemically induced mechanical states. By measuring a variable interfibrillar stiffness (EIF), the mechanism of mutability at the nanoscale can be demonstrated directly. A model of stiffness modulation via enhanced fibrillar recruitment is developed to explain the biophysical mechanisms of MCT. Understanding the mechanisms of MCT quantitatively may have applications in development of new types of mechanically tunable biomaterials.
The mechanical properties of biological tissues are usually optimized to operate within specific physiological loading and strain ranges (1, 2). With the exception of the common phenomenon of strain stiffening that occurs during mechanical loading (3), material-level changes in the overall mechanical properties of tissues typically occur slowly, driven by growth, remodeling, or aging (4). The molecular-level mechanisms underpinning these changes often involve permanent, irreversible changes, including covalent cross-linking via disulphide bridges in tendon (5), formation of metal-ion/protein complexes (6), or replacement of water with an inorganic phase as in biomineralization (7), although viscoelastic mechanical responses may involve transient cross-linking (8). In contrast, changes in the mechanical properties of animal tissues that occur actively and reversibly within a few seconds are canonically mediated by ATP-dependent molecular motors, as in muscle (9). A notable exception is the mutable collagenous tissue (MCT) of echinoderms (e.g., starfish, sea urchins, sea cucumbers), which undergoes rapid changes in stiffness under the control of the nervous system via ATP-independent mechanisms (10–12). MCT is ubiquitous in echinoderms (12), for example, in the dermis (skin) of sea cucumbers (13, 14), in the compass depressor ligament (CDL) of sea urchins (15–17), and in the arms of feather stars (18). The presence of MCT enables functionally diverse behaviors; for example in starfish, MCT enables body wall stiffening during feeding on prey and it also enables irreversible body wall softening before arm autotomy as a defense against predation (12). Thus, MCT represents an evolutionary adaptation of collagenous tissue to change mechanical properties dynamically, whereas in other phyla collagenous tissues largely act as passive mechanical springs. The benefits of MCT also include a much lower energy expenditure (19) compared with muscle tissue and the presence of MCT is considered to have been a major factor in the evolutionary success and ecological diversity of echinoderms [reviewed in Barbaglio et al. (20)].
The initial identification of connective tissue of echinoderms as having mechanically unusual properties—illustrated by its denotation as “catch” connective tissue—was through the observed stiffening and softening response of such tissues to sea water of different ionic compositions, as well as neurotransmitters (e.g., acetylcholine) (14) and drugs (e.g., cocaine) (21). Such chemical means to induce mutability in MCT remain a convenient and reproducible method to induce mechanically altered states (15, 22, 23). Specifically, previous studies demonstrated that alteration of extracellular Ca2+ and K+ levels modulates the stiffness of living tissues in sea urchin spine ligaments (14, 24–28), holothurian dermis (13, 22, 29, 30), and starfish (30). Increased K+ concentration increases the stiffness of these particular examples of MCT, whereas decreased Ca2+ concentration lowers stiffness, compared with artificial sea water (ASW) as a reference solution. The changes induced by these chemical methods are within the same order of magnitude as physiologically relevant mechanical changes occurring in MCT in vivo: Under mechanical stimulation (pressing the tissue by hand), starfish body wall MCT stiffens by a factor of ∼3.3 (30), whereas increasing K+ concentration leads to an increase of ∼6.1 (30). Conversely, the reduction of stiffness in calcium-free artificial sea water is considerable (31), which is comparable to the reduction to zero in the extreme case of limb autotomy where the tissue disintegrates structurally (32).
The unusual mechanical properties of MCT must arise from the micro- and ultrastructure of this tissue, which shows both commonalities with, as well as some clear differences from, the more familiar vertebrate collagenous tissues such as skin, tendon, and bone. At the molecular level, the collagen of sea cucumber MCT is different from heterotrimeric vertebrate type I fibrillar collagen, consisting of homotrimers with three α1 polypeptide chains (12). These collagen molecules aggregate into discontinuous spindle-shaped collagen fibrils with a mean diameter of ∼17 nm (33). Proteoglycans are bound to the fibrillar surfaces, which along with noncollagenous proteins such as tensilin, stiparin, softenin, and fibrosurfin compose the interfibrillar matrix (34–36). Together with fibrillin-rich microfibrils (34) the fibrillar collagen network comprises the bulk of the extracellular matrix (ECM) of MCT. Dispersed in this ECM are clusters of juxtaligamental cells (JLCs) (12, 15, 19, 24, 28, 29) (as seen from transmission electron and light microscopy), which are MCT-effector cells that are under neural control (12, 15). Furthermore, it is the innervation of MCT that is a key distinction between echinoderm and vertebrate collagenous tissues (15).
Initial hypotheses about the ultrastructural mechanism enabling the mechanical mutability described above focused on ion-mediated creation of physical cross-links between fibrils and within the interfibrillar matrix in the ECM (11, 23). Divalent calcium ions were proposed to be especially effective in increasing interfibrillar matrix stiffness, and their depletion in Ca2+-free sea water solutions was believed to be a major reason for the reduced stiffness. However, this hypothesis was disproved when cell-lysed MCT showed no mechanical mutability in the presence of such solutions (35). It is therefore believed that the ionic treatments directly affect cellular secretion pathways in the JLCs, inducing release of proteins that alter interfibrillar binding, thus changing the stiffness of the tissue (12). Several such proteins, including tensilin, softenin, and novel stiffening factor (NSF), have been identified (31, 34, 35, 37, 38). It is believed that the JLCs secrete such effector proteins as a result of external stimuli (such as touch, aggressive attack or alteration in the ionic strength of the sea water around the animal), thereby changing the stiffness of the tissue. Biochemical evidence to support this hypothesis includes the structural similarity of some of these proteins to the tissue inhibitors of matrix metalloproteinases (TIMPs) found in vertebrates (39). Consistent with this notion, it has also been suggested that cysteine-rich sea urchin fibrillar domains (SURFs), found so far in the sea urchin collagen 2α and 5α N-propeptides, as well as fibrosurfin (an interfibrillar protein) (36, 40), play a role in enabling mutability. The 2α N-propeptides and fibrosurfin colocalize on collagen fibril surfaces in adult sea urchins. However, despite this considerable level of biochemical insight into MCT (12), the biophysical mechanisms by which the alteration in mechanics is mediated by the nanostructure—whether at the fibrillar or the intrafibrillar level—are still not completely understood.
Techniques used to correlate ultrastructure with mechanics have been by necessity largely static and indirect, including imaging tissue after alteration of mechanical state with techniques like transmission electron microscopy (15). These introduce unavoidable artifacts from sample preparation and do not measure the changes as they occur in real time. The use of in situ synchrotron X-ray diffraction to provide molecular- and supramolecular-level images of the ultrastructural conformation during alteration of the mechanical state of MCT is a direct way to overcome these limitations (41–44). The axial periodicity of electron density along the long axis of collagen fibrils (45), with a repeat distance of D ∼ 65–67 nm, leads to Bragg diffraction peaks in X-ray scattering in the small-wavevector domain (<5 nm−1) characteristic of small-angle X-ray diffraction (SAXD) (45). Shifts in these peaks, as would be induced by mechanical loading or ionic treatments, are therefore a measure of the nanoscale fibril strain demonstrated for vertebrate tissues (41–43, 46, 47). By combining micromechanics with in situ small-angle X-ray scattering, it has been possible to shed light on the fundamental ultrastructural mechanisms enabling viscoelasticity, toughness, and force generation in vertebrate tissues ranging from tendon (48), bone (44, 46), and aorta (49) to muscle (50), as well as more unusual examples of biological optimization such as armored fish scales (43). Using SAXD, it was found that in cross-link–deficient fibrils, increased molecular slippage led to larger fibril strains, compared with normal collagen fibrils (48); that high toughness of antler bone was due to inorganic/organic friction at the intrafibrillar level (41); and that fibrillar reorientation blunted crack propagation in skin (51), among other examples.
When combined with high-intensity synchrotron X-ray sources, time-resolved SAXD with in situ micromechanical loading could be used to quantify the fibrillar deformation mechanisms of MCT in various states of mechanical mutability, thus clarifying the biophysical mechanisms enabling this remarkable behavior. Here, we apply these techniques to the sea cucumber dermis as a model system (Fig. 1). Understanding the molecular mechanisms enabling mutability may have applications in developing dynamic biomaterials, systems capable of changing their mechanical properties, and the design of mechanically tunable implants. The adaptive mechanical properties in MCT could, for example, provide insight into the repair of connective tissue pathologies in soft tissue, such as therapy in tendon or ligament weakening resulting from surgery or immobilization (12); into the design of implants capable of generating active forces; and into the area of neural implants where variable stiffness during insertion and implantation has been proposed (52).
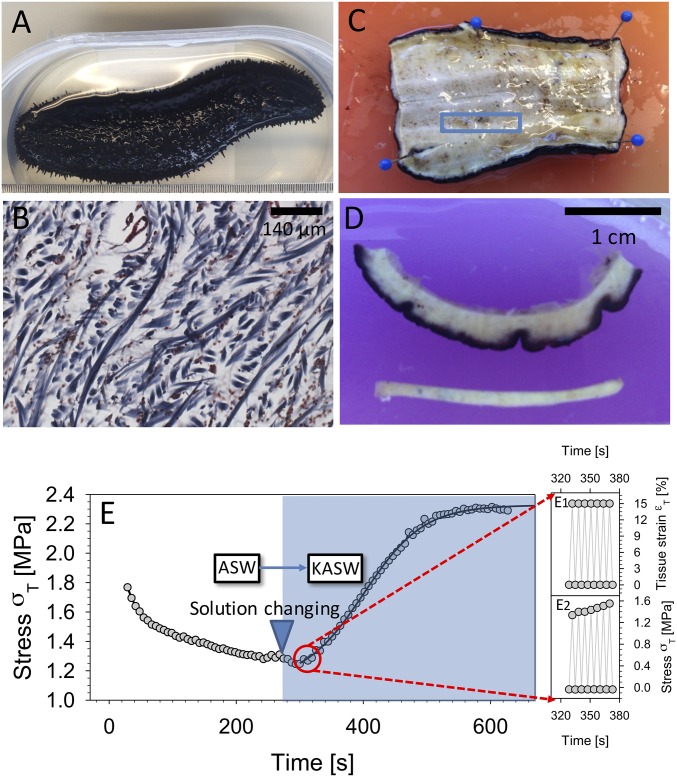
Fig. 1.
Sea cucumber body wall MCT. (A) Sea cucumber H. leucospilota. (B) Transverse section of sea cucumber body wall stained using Masson’s trichrome method. Collagen fibrils appear blue. (C) The sheet of body wall after the animal was cut in half along the longitudinal plane. The blue rectangle indicates the dimensions and location of the sectioned specimen, with the long dimension along the longitudinal axis. (D, Upper) View of sectioned sea cucumber dermis including dark outer dermis and inner layer. (D, Lower) The tensile test specimen. Before testing, the dark-pigmented outer dermis as well as the inner layer was removed, leaving only the center part of the specimen. (E) Time-dependent change in sea cucumber MCT mechanics induced via ionic treatment. The peak stress (per cycle) is plotted during strain-controlled cyclic loading of sea cucumber dermis at 0.3 Hz (to 15% tissue strain), with tissue immersed in ASW until ∼290 s, followed by a change of the immersing solution to KASW (stiffening agent). A clear rise of peak stress (per cycle) is observed, fitted with a sigmoidal curve as a guide to the eye. Insets (E, Right) show a magnified time range over a few (seven) cycles, with both maximum and minimum stress and strain indicated.
Results
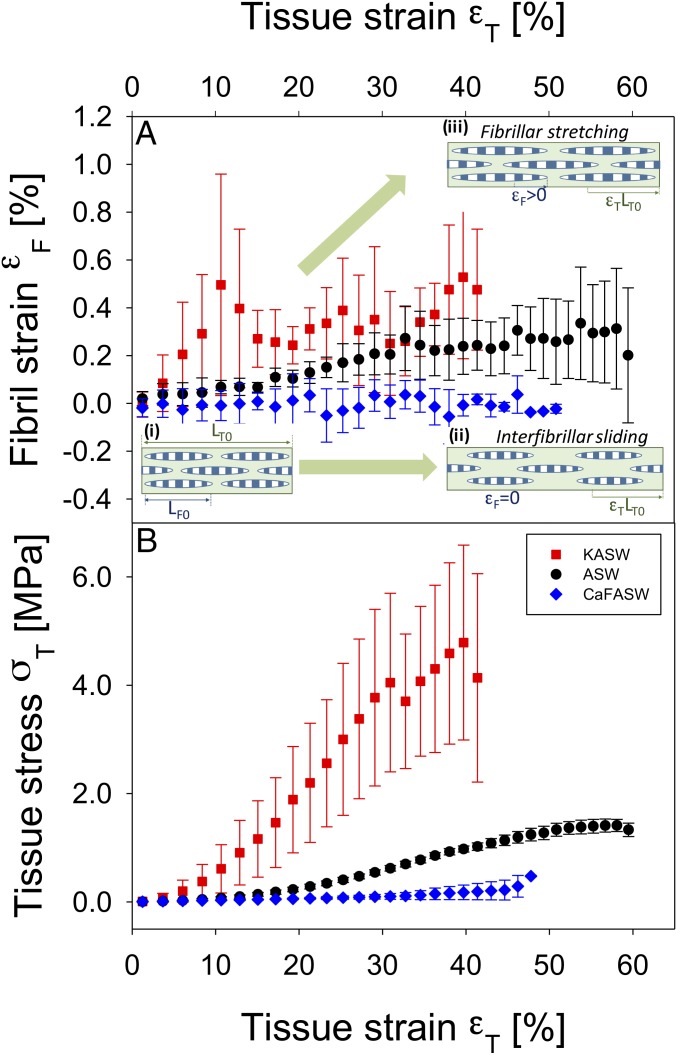
Synchrotron SAXD measurements of fibrillar strain in MCT from sea cucumber dermal tissue were carried out at beamline ID02 at the European Synchrotron Radiation Facility as shown in Fig. 2. Before testing, tissue specimens were chemically incubated in ASW and two ionically modified solutions of ASW [potassium-rich ASW (KASW) and calcium-free ASW (CaF-ASW)], which are known to induce standard state, stiffening and softening of sea cucumber dermis, respectively (22, 23) (details in Materials and Methods). The fibril strain εF is the fractional increase in fibril length (measured from the shifts in the meridional Bragg peaks in the SAXD pattern of MCT collagen fibrils), whereas tissue strain εT is the fractional increase in MCT sample length and tissue stress σT is the force divided by sample area (Materials and Methods). Considering the fibrillar-level strain εF and tissue stress developed in MCT during stretch to failure tests, it is observed (Fig. 3A) that fibrils in tissues with different chemical stimulation—CaF-ASW, ASW, and KASW—show a differing extent of elongation at the same tissue strain εT. At a given tissue strain, the amount of fibril strain is proportional to the stress taken up by the fibrils. At a tissue strain εT around 10%, fibrils in KASW tissue have a much higher extension of ∼0.5% compared with ASW (0.07%). Likewise, the fibril strain for CaF-ASW is much lower (∼0.001%), indicating mainly interfibrillar sliding. The maximum fibril strain developed in KASW is much larger than in CaF-ASW, and the fibril strain in ASW is in between that of KASW and CaF-ASW. Fig. 3B shows corresponding averaged mean strain–stress curves for body wall tissue in KASW (red), ASW (black), and CaF-ASW (blue). The averaged macroscopic stress σT with tissue strain εT at 40% for KASW-treated (4.08 MPa) specimens is significantly higher than for CaF-ASW (0.13 MPa), whereas the ASW-treated (0.77 MPa) specimens are in between these extremes. We note that the increase of fibril strain with applied tissue strain is not completely smooth in all cases, as evidenced by the error bars. This is most noticeable in the case of KASW-treated tissue, where there are clear local peaks at ∼10% and 30% strain followed by dips. The structural reasons for this behavior are considered further when the model to explain fibrillar deformation is developed in Discussion. Further, the variation of the macroscopic tensile stress (at the tissue level) for the whole specimen for all treatments (KASW, ASW, and CaF-ASW) is much greater compared with the strain developed at the fibril level (Fig. 3A), indicating that interfibrillar components of the extracellular matrix are important in mechanisms of MCT.
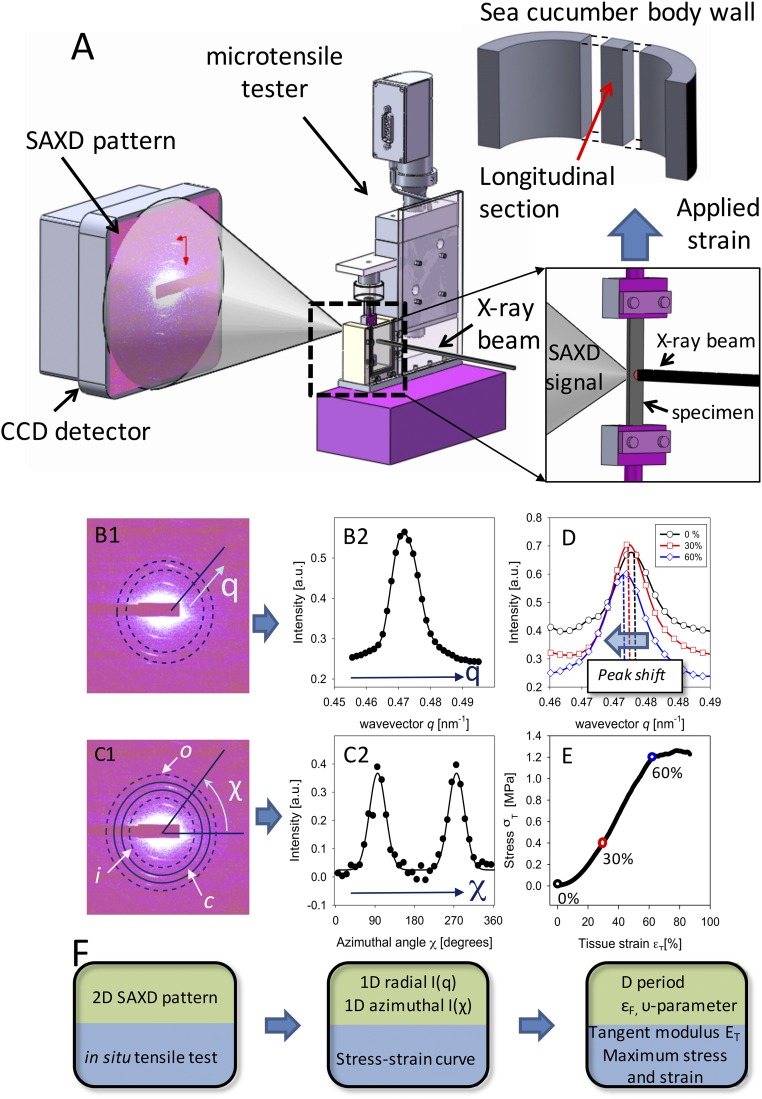
Fig. 2.
In situ nanomechanics with synchrotron SAXD. (A) Experimental configuration: Tensile tester (Center) with MCT specimen mounted along the X-ray beam path in transmission geometry with CCD detector (Left). (A, Right, Inset) Magnified view of sample in chamber and incident X-ray beam (right) with SAXD scattering shown on left. The tensile strain is applied along the vertical direction. (A, Upper Right) Schematic of body wall of sea cucumber shown in Fig. 1, with tensile test specimen sectioned with long axis parallel to the long axis of the animal. (B) Data reduction pipeline: (B, 1) A 2D SAXD pattern from collagen fibrils in sea cucumber dermis MCT with predominant fibril orientation vertical. Radial (q) direction is indicated. Dotted lines denote the ring over which the azimuthal averaging of intensity is carried out. (B, 2) The azimuthally averaged radial intensity profile I(q) for the pattern in B, 1. (C, 1) The same 2D SAXD pattern as in B, 1, with the inner, outer, and central rings (i, o, and c, respectively) shown schematically, over which radial averaging of intensity is carried out. Azimuthal (χ) direction is indicated. (C, 2) The radially averaged intensity profile I(χ). In B, 2 and C, 2 both experimental data (solid circles) and fits to model functions (solid lines) are shown. (D) Radial intensity profile I(q) for three levels of applied tissue strain εT = 0% (circles), 30% (squares), and 60% (diamonds), showing the shift of peak position to lower wavevector with increasing strain. (E) Tissue stress–tissue strain plot for sea cucumber dermis in tension, with circles (black, 0%; red, 30%; blue, 60%) indicating the points from which the I(q) plots in D are shown. (F) Flowchart corresponding to the data reduction steps in B, 1–C, 2, with parameters obtained at each step indicated.
Fig. 3.
Altered fibrillar stress and strain take-up in ionically treated MCT. (A) Fibril strain vs. applied tissue strain from ionically treated sections of MCT dermis, measured from the peak shifts of the fifth-order collagen reflections in the SAXD pattern. The rate of increase of fibril strain with tissue strain (εF/εT) is proportional to the amount of stress taken up by the collagen fibrils. Data are from control (ASW) (black circles, n = 4), stiffened (KASW) (red squares, n = 4), and softened (CaF-ASW) (blue diamonds, n = 3) MCT. All samples in each group are binned according to tissue strain with bin widths of 2.0%; error bars are SDs. Stiffened MCT exhibits a higher rate of increase of fibril strain compared with control, whereas softened MCT shows essentially no increase in fibril strain. Inset schematics: (A, i) Fibrils (striated ellipsoids; length LF0) separated by interfibrillar matrix, in unloaded MCT of length LT0; (A, ii) in softened MCT (CaF-ASW treated), while the tissue elongates (εT > 0), the fibrils do not stretch, but slide in the interfibrillar matrix (εF = 0); (A, iii) in stiffened MCT (KASW treated), there is increased stress transfer to the fibrils, leading to fibrillar stretching (εF > 0). (B) Corresponding macroscopic tensile stress/strain curves for the control, stiffened, and softened groups, binned according to tissue strain (error bars: SDs), showing clear differences in tangent modulus and maximum stress achieved.
The differences in Ca2+ or K+ concentrations in CaF-ASW, ASW, and KASW led to changes of maximum tangent modulus and maximum tissue stress (Fig. 4). Ca-FASW–treated (0.69 ± 0.59 MPa) samples had ∼80% lower maximum tangent modulus compared with ASW (3.23 ± 0.40 MPa), whereas the maximum tangent modulus for KASW-treated samples (17.27 ±6.70 MPa) was four times larger. Concurrently, the maximum stress of each state is very different, with the loads borne by CaF-ASW–treated tissue (0.30 ± 0.32 MPa) being much less (∼80%) compared with ASW tissue (1.30 ± 0.20 MPa) whereas KASW tissue (6.39 ± 0.44 MPa) had maximum stress four times higher than the control. Similarly, nanoscale parameters like fibril strain also show clear differences between treatments (Fig. 4 C and D). Compared with maximum fibril extension (Fig. 4C) developed in KASW (0.94%), fibrils in CaF-ASW (0.09%) and ASW (0.35%) had a reduced elongation, with ∼95% and 80% less strain, respectively. Fig. 4D shows the ratio of fibril strain to tissue strain (εF/εT) for the three states, which is observed to be consistent with Fig. 4C, showing that stiffened tissue sections have (εF/εT) of 0.044, larger than control specimens, whereas softened tissue sections have almost negligible fibril strain take-up (εF/εT ∼ 0). The parameter εF/εT is used to confirm the modeling results, which are illustrated in Model and Discussion.
Fig. 4.
Quantified MCT mechanics. (A and B) Averaged maximum tangent modulus (A) and maximum stress (B) for control (ASW; black; n = 4), stiffened (KASW; red; n = 4), and softened (CaF-ASW; blue; n = 3) specimens from MCT dermis. Error bars are SDs. n denotes the number of samples in each treatment group. At the tissue level, stiffened MCT always exhibits remarkably higher mechanical properties compared with the control group, and for the softened one, the binned maximum tangent modulus and the maximum stress are almost negligible. (C and D) At the fibrillar level, the fibril strain (C) and the ratio of the fibril strain to tissue strain (D, the fraction of the deformation taken up at the fibril level) for the stiffened, control, and softened MCT follow the same trend with properties at the tissue level.
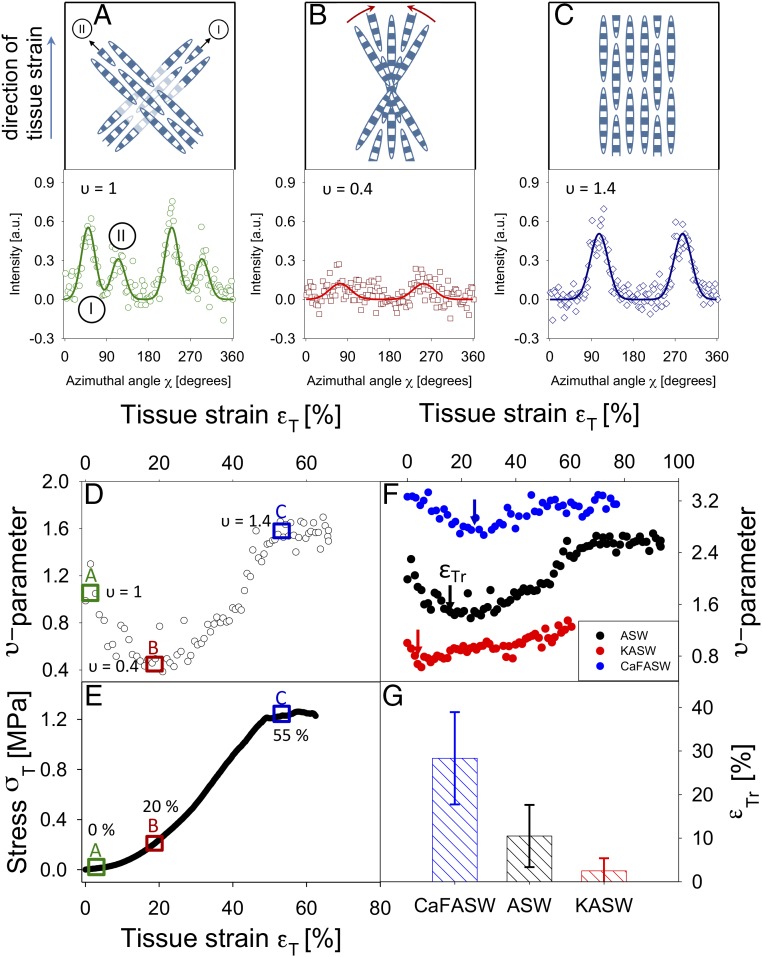
In a complementary manner, we consider the alterations in the fibril orientation distribution on application of external load. The υ parameter, derived from the angular distribution of the SAXD intensity, is a dimensionless number that is zero when fibrils are distributed at all angles with equal likelihood and positive when fibrils are aligned either along one or along a couple of principal directions (Materials and Methods). A representative plot of the υ parameter as a function of tissue strain (Fig. 5A) exhibits an initially high value of ∼1.3 [corresponding to two main fibril directions equidistant (azimuthally) from the vertical direction] that is followed by a decrease to a minimum around 20% tissue strain. The initial two directions correspond to two principal helical fiber pitches along the long axis of the animal. The initial reduction in the υ parameter corresponds to a more random fibril orientation, indicated schematically in Fig. 5 A–C, and represents the stress-induced breakdown of the two main fibril directions into a single broad distribution centered on the (vertical) direction of applied tensile load. For tissue strains larger than 20%, the υ parameter increases monotonically with increasing tissue strain, before leveling off near tissue strains of ∼40–50% close to macroscopic failure. The increase of the υ parameter represents a narrowing of the azimuthal width of the initial broad fibril distribution around the direction of applied load. The tissue strain at the transition between the reduction of the υ parameter and the subsequent increase is denoted by εTr. The analysis of mean εTr across three groups of specimens is shown in Fig. 5D. The results indicate that soft (CaF-ASW) samples always have a higher εTr, relative to the control (ASW) and stiffened (KASW) samples, which implies that the rate of reorientation (from the initial distribution with two main directions to a random and then highly oriented distribution) is slower for the softened MCT.
Fig. 5.
Strain-induced fibril alignment of MCT in stiffened, control, and softened states: (A–C, Upper) Schematic illustration of fibril distribution at increasing tissue strain levels. (A–C, Lower) Corresponding I(χ) plots for a control (ASW) sample with corresponding υ parameter. The vertical arrow to the left of the plots indicates the direction of applied tissue strain. A (0% strain) shows bimodal distribution due to two groups of fibers (I and II) inclined to the direction of tensile load at two principal fiber directions (arrows). In the I(χ) profile (A, Lower), the two sets of peaks arising from these two groups of fibers are labeled I and II, respectively. B (20% strain) shows a wider range of orientations due to fibrils progressively reorienting (indicated by the red arcing arrows) toward the tensile axis (low υ) and C (55% strain) shows highly aligned fibers along the vertical direction (higher υ). (D) Initial decrease followed by increase of the υ parameter with increased tissue strain, for control (ASW) MCT, exhibiting an initial decrease and a local minimum at tissue strain ∼20%, followed by an increase. (E) A typical stress–strain curve for ASW-treated MCT. In D and E, rectangles indicate strain locations corresponding to A–C. (F) Variation of the strain-induced changes in the υ parameter as a function of the mechanical state of MCT due to ionic treatment. Data from one representative MCT specimen in each state are shown. The tissue strain corresponding to the local minimum in υ is indicated by a vertical arrow, denoted εTr, and is lowest for the stiffened and highest for the softened specimen. (G) Averaged εTr across the three treatments [control (ASW; black; n = 4), stiffened (KASW; red; n = 4), and softened (CaF-ASW; blue; n = 3)]. Error bars are SDs.
Model and Discussion
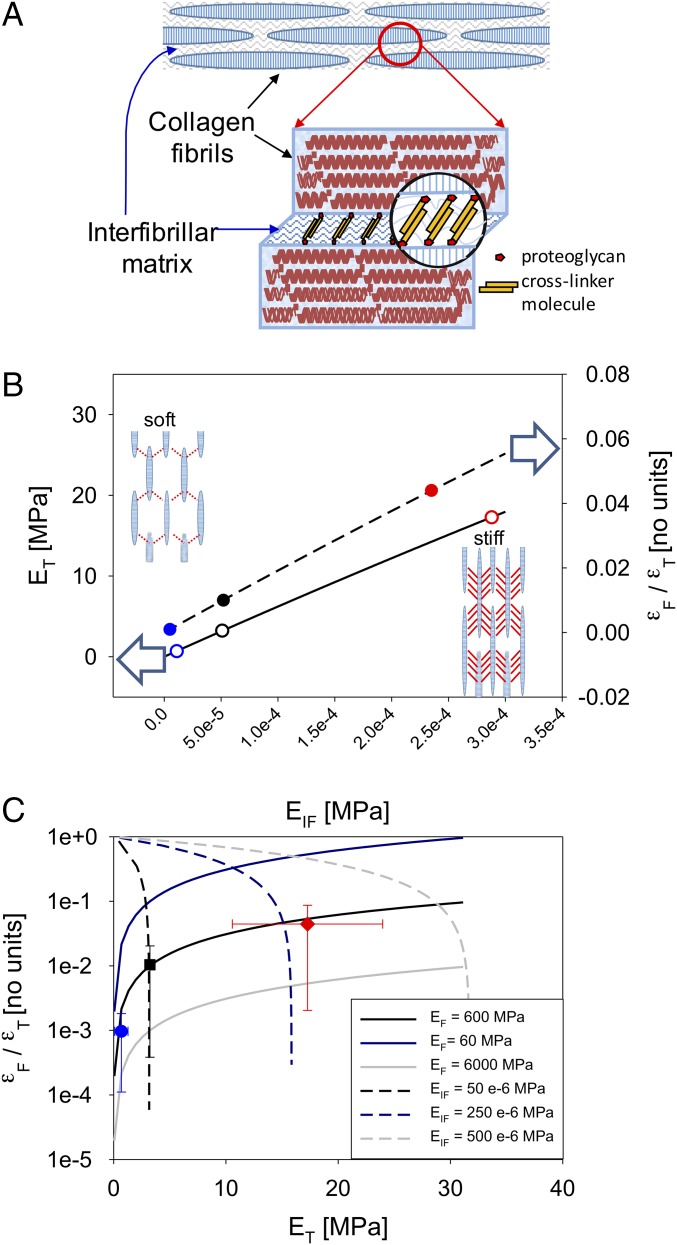
These experimental results, showing clear alterations in the deformation at the fibrillar level when MCT is stimulated into its stiff and soft states, can be used to build a simple model that sheds light on the key biophysical mechanisms enabling mutability (31, 34, 35, 37, 38). Prior research has proposed, but not directly demonstrated, that certain proteins secreted by JLCs including tensilin (35, 37), stiparin (34), and NSF (31) act to cross-link the fibrils. A complete ultrastructural mechanism for MCT mutability has not, however, been quantitatively established, and each protein appears to be involved only in a specific subset of the mechanical response, such as in stiffening a compliant specimen back to the reference state [as is the case for tensilin (35, 37)]. At the ultrastructural level, the parallel-packed fibrils and interfibrillar matrix of MCT can be represented as shown in Fig. 6A. The covalently cross-linked (α1)3 collagen fibrils are expected to have much greater stiffness [∼0.5–2 GPa (53)] than the interfibrillar matrix [which can be considered a negatively charged hydrated gel (54)], although precise values for the interfibrillar matrix modulus are unknown. Under tensile loading, the highly anisotropic fibrillar structure together with the expected stiffness mismatch between the fibrils and the interfibrillar matrix will lead to a characteristic inhomogeneous deformation field at the nanoscale. In this deformation field, tensile forces develop in the fibrils and matrix, and significant shear occurs in the interfibrillar matrix connecting fibrils (55). The shearing force lines are shown in Fig. 6B, Insets, and can be considered as representations of the cross-linking between fibrils proposed previously (12). Consequently, the fibril strain is only a fraction of the total strain (due to the remaining shearing strain in the interfibrillar matrix).
Fig. 6.
Staggered model of MCT nanomechanics. (A) Staggered model for MCT: discontinuous, spindle-shaped collagen fibrils aggregating in parallel. The attached proteoglycans serve as a binding site for interfibrillar cohesion mediated by cross-linker molecules (12). (B) Elevation of interfibrillar stiffness EIF leads to a corresponding increase in both tissue modulus ET (left-hand abscissa; solid line, staggered model prediction) and fibril-to-tissue strain ratio (εF/εT) (right-hand abscissa; dashed line, staggered model prediction). Symbols show experimental values for each tissue group with EIF calculated from the staggered model equations (solid symbols from Eq. 1; open symbols from Eq. 2). Open arrows indicate the abscissa each line belongs to. B, Inset schematics show the shear transfer, and consequent stress take-up, between fibrils in softened (Left) and stiffened (Right) states. Increased shear stress in the stiffened interfibrillar matrix is shown qualitatively by a larger number of interfibrillar shear lines. (C) Positive correlation between εF/εT and ET demonstrates that interfibrillar stiffening is the mechanism for alteration of MCT mechanics. The staggered-model relations between (εF/εT) and ET (Eq. 3) are shown via solid curves (with a positive gradient) for varying EIF and three fixed levels of EF (blue, 60 MPa; black, 600 MPa; and gray, 6,000 MPa). Likewise, dashed lines show staggered-model predictions for (εF/εT) vs. ET for varying EF and three fixed levels of EIF (black, 50 × 10−6 MPa; blue, 250 × 10−6 MPa; and gray, 500 × 10−6 MPa). Symbols show experimental (εF/εT) and ET, which show a clear positive correlation, indicating interfibrillar stiffening (blue, CaF-ASW; black, ASW; and red, KASW; error bars are SDs).
To keep the model analytically simple we consider a unidirectional fiber composite; whereas the initial unstrained MCT shows two main fibril directions around the direction of stretch (Fig. 5B), it is observed that for tissue strains larger than ∼20% the fibrils are highly aligned to the direction of applied stress and the uniaxial fibril arrangement is expected to be a good approximation for this region at least. This type of model, denoted a staggered model, has been proposed before, by us (41) and others (55, 56) for deformation of the ultrastructure of bone mineralized fibrils, tendon, enamel, and dentine (46, 57), where a similar high-stiffness element in tension (e.g., mineral platelet) is effectively in serial loading with a low-stiffness element loaded in shear (e.g., collagen fibrils). The deformation of the fibril εF, shear of the interfibrillar matrix γIF, and tissue level stress σT, among other quantities, have been calculated from load-balance equations at the nanoscale (41). These lead to expressions for the fibril to tissue strain ratio, and the tissue modulus ET, in terms of the structural and constitutive parameters
| [1] |
| [2] |
In the equations above, Φ1 denotes the fibril volume fraction, ρ1 the fibril aspect ratio, EF the fibril elastic modulus, and EIF the interfibrillar modulus, and γIF ∼ 0.40 is the ratio between shear (GIF) and tensile (EIF) modulus of the interfibrillar matrix (GIF = γIFEIF) (41); other terms have been defined earlier in the text. As our scheme enables measurement of deformation at the fibrillar level concurrently with tissue-level mechanical stress and strain, a parametric variation of fibril strain and tissue modulus may now be carried out and compared with the experimental results reported earlier in Figs. 4 and 5. These results are shown in Fig. 6B and discussed below.
Considering, for the moment, that the collagen fibrils have a constant elastic modulus EF, we first examine the effects of altering the interfibrillar modulus on the change in tissue stiffness. Such a scenario corresponds to an alteration in cohesion due to secretion of stiffening factors such as tensilin, stiparin, and NSF. As seen in Eq. 2, the increase in tissue stiffness arises due to both the increased load borne by the interfibrillar matrix (second term on the right-hand side in Eq. 2) and—much more significantly—the increased stress borne by the collagen fibril due to the larger shear stress transferred by the interfibrillar matrix (first term on the right-hand side). The stress borne by the collagen fibril is large due to the large contact surface area between the fibrils and the interfibrillar matrix due, in turn, to the large fibril aspect ratio ρ1. Concurrently with the increase in tissue stiffness, the fibril strain increases as a fraction of the tissue strain, as larger tensile forces are transferred to the elastic fibrils with increased fibril strain.
To compare the model predictions with experimental data (Fig. 6 B and C), initial estimates of some of the unknown parameters need to be made. The length and fibril diameter distributions for echinoderm collagen fibrils have been estimated previously (33, 58). Whereas the maximum and minimum values span a wide range, a constant spindle-shaped morphology was reported (33). The most frequent value (mode) in the diameter distribution was ∼100 nm (58), and the length ranged from 50 µm to 1 mm. Using the constant shape of the collagen fibrils reported previously (33) and the diameter distribution shown in ref. 58, these values can be used to estimate the maximal length to be ∼120 µm. These lead to an aspect ratio of ∼1,000. The fibril modulus for individual sea cucumber fibrils isolated from the tissue was measured to be ∼500 MPa (53). As described in Supporting Information, these values can be used, together with the experimentally determined values of εF/εT and ET, to obtain estimates of fibril volume fraction Φ1 ∼ 0.54 and the interfibrillar modulus EIF ∼ 50 × 10−6 MPa (in the ASW case). The fibril volume fraction will not vary across treatments, but the interfibrillar modulus will change. With these numerical values, the two trends described above—increase in tissue stiffness (ET) as well as in fibril strain ratio εF/εT with increasing EIF—are plotted in Fig. 6B, together with the experimentally measured values for the softened, control, and stiffened groups. Eq. 1 is used to calculate interfibrillar matrix stiffness EIF for each tissue group from measured εF/εT, which are then plotted (symbols) together with model curves (lines). In a similar manner, Eq. 2 is used to obtain EIF from measured tissue moduli ET for each group. For consistency of the model, the two calculated sets of EIF should match, and indeed it is observed that both methods give similar values for EIF across the tissue groups.
In principle, however, there are two distinct ways in which the stiffness of MCT can be modified: either by the interfibrillar matrix stiffening (considered above) or by alterations of the mechanics of the collagen fibrils, possibly by modulation of intrafibrillar cohesion. These two scenarios—fibrillar vs. interfibrillar stiffening—lead to different behaviors at the fibrillar level. In the fibrillar stiffening case, the fibrillar strain (as a fraction of tissue strain) will reduce as the tissue stiffens, whereas in the interfibrillar stiffening case, the fibrillar strain will increase as the tissue stiffens, as can be seen by combining Eqs. 1 and 2 to obtain parametric plots of εF/εT and ET as functions of EIF and EF
| [3] |
In the model, changing the aspect ratio by ±10% leads to a variation of 20% in both εF/εT and ET (Supporting Information, Sensitivity of Fibril Strain Ratio and Tissue Modulus to Model Parameters). To conclusively demonstrate interfibrillar stiffening and exclude fibrillar stiffening as the key mechanism for mechanical changes in MCT, the experimental data for εF/εT and ET are plotted in Fig. 6C together with two sets of three predictive curves from the model. The first set of three curves (solid lines) corresponds to a continuous increase in interfibrillar modulus (for several discrete values of fibrillar stiffness), whereas the second set (dashed lines) corresponds to continuously increasing fibrillar stiffness for several values of interfibrillar stiffness. It is clearly seen that the experimental data show an increase in εF/εT with ET, corresponding to the case of interfibrillar matrix stiffening. Further, it is apparent that the mean values lie along the predicted curve for a collagen fibril modulus EF = 600 MPa, which is close to the value of 500 MPa reported by Eppell et al. (53). This finding provides evidence in support of the long-held, but not directly demonstrated, hypothesis that the alteration of MCT mechanical properties arises due to changes in interactions between fibrils (through changes in the interfibrillar matrix) rather than alterations in the mechanical properties of the fibrils themselves (12).
From the variation of interfibrillar matrix stiffness certain observations can be made. In MCT, EIF is, even in the stiffest state, ∼0.25 kPa—at least six orders of magnitude lower than the stiffness of the fibril ∼0.6 GPa. In the state of least stiffness, there is a factor of ∼100 reduction in EIF relative to the already low value of 0.25 kPa, to ∼5–10 Pa, and the matrix can be considered a fluid. However, the increased stiffness of MCT in the stiffened state [necessary for its physiological maintenance of posture or locomotion (12)] is almost entirely due to the increased fibrillar recruitment to bear stress and not due to the stress carried in the interfibrillar matrix. The ratio of the stress in the interfibrillar matrix to that in the fibril can be calculated from
i.e., only ∼0.7% of the total stress is borne by the interfibrillar matrix. Under alteration of mechanical state, the relative increase in fibril stress can be calculated from the change in fibril strain ratio, via
We observe that fibril stress increases by a factor of ∼4 (Fig. 4D) in the stiff state compared with the standard state. Conversely, in the softened state, the fibril stress decreased by a factor of ∼10 relative to the standard state. We also note that we have (for simplicity) considered the interfibrillar matrix to stiffen homogeneously. In practice, there can be local heterogeneities (both temporal and spatial) in stiffness, possibly due to conformational changes in the noncollagenous proteins, local entanglements, and other phenomena. Such heterogeneities would lead to local increases (or decreases) in interfibrillar stiffness, which would increase (or decrease) stress transfer between fibrils. Such alterations in stress transfer would explain the local maxima and minima in the fibril strain measured in stiffened KASW-treated MCT observed in Fig. 3A. In this regard, the recent finding of collagen molecular shortening—due to water content changes—leading to large tensile stresses in tendon may be of relevance (59).
These findings shed light on the synergistic action at the nanoscale enabling mutability in MCT. By itself, the stress in the stiffened (or softened) interfibrillar matrix is by no means sufficient to account for the change in tissue stiffness. However, due to the large anisotropy and surface to volume ratio of the fibrils, considerable contact area exists for binding of the interfibrillar proteins and glycosaminoglycans to the fibrils. Such binding is likely to occur at the gap zones (separated by D ∼ 65–67 nm) identified previously as putative binding sites for proteoglycans in collagens (60). As a result, the total stress transferred to the collagen fibrils is effectively amplified by the anisotropy factor ρ ∼ 1,000. Small changes in the mechanical properties of the interfibrillar matrix are thus amplified to apply considerable stress to the elastic fibrils, as a consequence of which the fibrils are more effectively recruited to bear load. Prior biochemical evidence suggests the involvement of proteins like tensilin and NSF in the stiffening of the matrix (31, 35, 37). It is probable that these proteins physically cross-link to the existing glycosaminoglycans and proteoglycans, which in turn are bound to the gap zones in collagen fibrils. It is conjectured that these proteins are acting like a bridge, binding the proteoglycan/GAG sites of two adjacent fibrils together (12, 29). In this manner, increased matrix stiffening combined with effective shear load transfer to the fibrils enables MCT to undergo considerable (by a factor of ∼25; Fig. 6B) changes in tissue stiffness. The physical cross-linking process is a time-dependent one (Fig. 1E), most likely due to diffusion of proteins secreted by the JLCs in between the collagen fibrils, combined with progressive occupation of binding sites for these proteins in the interfibrillar matrix. This process of increased interfibrillar stiffening, enabling alteration of mechanical behavior, is likely to be a general property of MCT in echinoderms.
Conclusion
In summary, in this first direct measurement of the nanoscale fibrillar deformation mechanisms of MCT, we have demonstrated that the mutability of mechanical properties in this unique invertebrate collagenous tissue is achieved solely by interfibrillar matrix cross-linking and uncross-linking. Increasing interfibrillar cohesion in the mechanically active state leads to nearly a 50-fold increase in fibrillar stress, underpinning the transition of MCT from a soft to a stiff state. A greater fibrillar stress recruitment, mediated by shear transfer from the interfibrillar matrix, leads to an over 20-fold increase in tissue modulus over the timescale of several seconds. The use of in situ X-ray methods together with mechanical testing has enabled us to quantify both the material-level mechanisms and the constitutive properties of the components of MCT as they undergo these changes in real time. The ability of MCT to undergo such large changes in stiffness with minimal dimensional changes and solely by increasing fibrillar recruitment highlights the potential of such fibrillar-hydrogel composites to act as dynamic biomaterials that can change their mechanical state rapidly. Such materials could find application as new pharmacological agents, whereas the design of a new class of mechanically responsive nanocomposites (12) could enable energetically efficient biomaterials and devices that not only provide structural support but also can dynamically adjust their properties to the external environment for responding to different demands. The approach opens up several promising further avenues of investigation; e.g., alterations in the molecular-level diffraction patterns would provide combined molecular as well as fibrillar real-time structural information, and the use of novel synthetic peptides mimicking the stiffening or softening agents in MCT could be tested in situ for efficacy (61). Finally the combination of experiments with molecular modeling methods would enable us to link mechanisms at the smallest structural levels to macroscopic behavioral patterns.
Materials and Methods
Dissection of Sea Cucumber Body Wall Preparations.
Specimens of the sea cucumbers (Holothuria leucospilota) were obtained from a commercial wholesaler (Marine Life) and delivered to the synchrotron SAXD beamline (in tanks of artificial sea water) a few hours before use. To prepare sea cucumber samples for the mechanical testing in different ionic solutions, we followed a protocol similar that used in previous studies of the mechanics of sea cucumber dermis (19, 62). Specifically, after letting the sea cucumbers rest for 1 h in sea water, samples from the white central part of the body wall dermis (Fig. 1) were prepared. The attached viscera and muscle layers on the inside were pulled off with forceps, and the pigmented outer dermis was removed using razor blades, leaving only the collagenous part. Rectangular-shaped collagenous tissue pieces (10–20 mm × 1.0 mm × 1.0 mm) were cut out, using a specialized construct with twin razor blades fixed on either side of a 1-mm-thick steel section, to keep the thickness constant to 1 mm. The sectioning was done in the longitudinal direction of the body wall, used for tensile testing (Fig. 1 C and D). Whereas the total length of the sample varied between specimens, the gauge length was kept constant to 6 mm during the tensile testing (described in the next section). Samples were rinsed in ASW after sectioning. After the sections were prepared, and before mechanical testing, all samples were allowed to relax in ASW for 1 h. Following this, specimens were incubated in ASW (control), KASW (stiff; high [K+]), or CaF-ASW (soft) for 1.5 h. Compositions of these three solutions (ASW, KASW, and CaF-ASW) followed the protocol described previously by Motokawa and Tsuchi (14). As expected, this procedure resulted in relative elevation and reduction of stiffness for KASW-treated and CaF-ASW–treated dermis, consistent with other studies of chemically treated MCT (30). All studies were carried in accordance with the Animals (Scientific Procedures) Act 1986 of the United Kingdom, including revision 2013; invertebrates (except cephalopods) are not considered protected species under the Act.
In Situ Mechanical Testing with SAXD.
A compact micromechanical tester, designed by our group (41), specialized for holding biological tissues and capable of being fixed on the sample stage of a synchrotron SAXD beamline, was used. The tester contains a load cell (100 N rating), with attached amplifier (RDP Electronics Ltd.). Strain is applied by displacement of a DC motor with an encoder (M-126.DG; Physik Instrumente). A customized LabVIEW (National Instruments) interface on a control PC was used to control the applied tissue strain and strain rates. Adherence of the sample to the tensile tester grips was improved by using sandpaper of various grades between the tissue and the grip. The machine compliance of the tester was measured using a thick steel section. Compliance was found to be negligible compared with the stiffness of the sea cucumber body wall tissue under investigation. Engineering tissue strain (εT0) was calculated from the ratio of the displacement of the sample grips to the unstressed gauge length ∼6 mm. As MCT is a soft tissue capable of considerable elongation, the engineering tissue strain (εT0) was converted into true tissue strain (εT), using εT = ln(1 + εT0) (Supporting Information, Engineering Tissue Strain εT0 and True Strain εT) (63). Tissue stress σ was obtained by dividing force by sample area (1.0 mm2). Rate of increase of stress with tissue strain [tangent modulus ET (63)] was obtained from a linear regression between σ and εT with a moving window of ∼ΔεT = 0.5%.
Combined microtensile deformation experiments with time-resolved acquisition of SAXD patterns were carried out at the High Brilliance ID02 beamline at the European Synchrotron Radiation Facility (ESRF). Body wall preparations were mounted in the microtensile tester immediately after incubation in test solutions. Samples with gauge length ∼6 mm were stretched to failure at a constant velocity of 0.01 mm/s (corresponding to a strain rate of ∼0.167%/s). Samples were kept hydrated by dropwise addition of the incubation solution during the test. SAXD patterns were acquired with a FReLoN CCD detector (64) with a 0.5-s exposure time, using a highly collimated synchrotron X-ray beam [beam size 20 μm (height) × 25 (width) μm] at sample and detector positions, wavelength λ = 0. 9951 Å (X-ray energy 12.46 keV) at a sample-to-detector distance of 1,006.8 ± 1.0 mm determined with silver behenate at the sample position. Each SAXD pattern had a resolution of 2,048 × 2,048 pixels and a pixel area of 23.63 × 23.97 μm2. SAXD patterns were collected continuously up to failure of the specimen, with an interval between acquisitions of ∼1.5% strain. Each SAXD pattern is therefore acquired on a tissue location that is ∼6 mm × 0.015 = 90 μm shifted from the previous measurement. The beam diameter is much smaller (approximately one-fifth of this shift) and there is thus no overlap of the beam onto tissue locations across SAXD measurements. As a result radiation damage, due to multiple exposure of the beam to the same tissue location, is minimized. Radiation damage of protein assemblies and solutions occurs via a combination of free radicals produced by water photolysis with free radicals from the proteins, leading to protein unfolding, aggregation, or breakage (65). Our strategy of continuous sample movement to avoid repeat exposures of the same point is one of several successful approaches to minimize radiation damage (65). Other methods, including continuously replacing the sample (e.g., continuous flow in liquids) or adding radical scavengers to solutions (assuming no structural consequences) (65), are not applicable in the case of strain-stressed tissues considered here. Failure of the specimen usually occurred between 50% and 70% strain. As a result, typically about 40 patterns per sample (60%/1.5% = 40) were acquired.
Determination of Fibril Strain from SAXD.
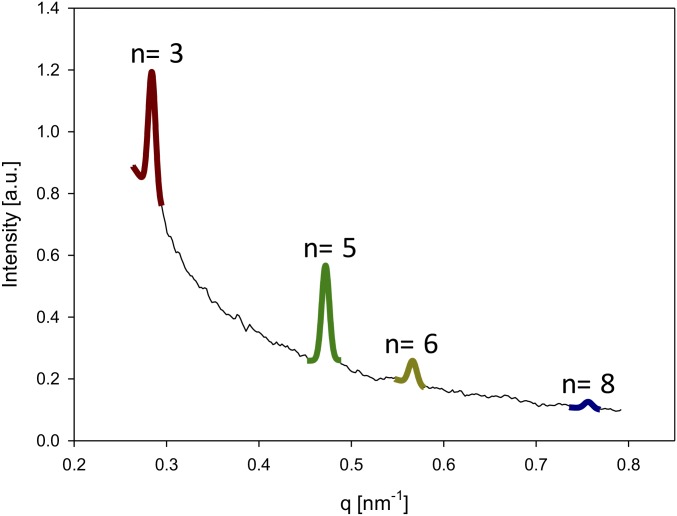
Two-dimentional SAXD patterns of sea cucumber body wall collagen were obtained (Fig. 2B) and averaged azimuthally (in the angular plane of the X-ray detector) to obtain the Bragg peaks arising from the D periodicity of SAXD fibrils. The azimuthal average of the intensity provides a 1D intensity profile I(q) (q being the wavevector), which has characteristic Bragg peaks at integer multiples of 2π/D. The software package Fit2D (66) was used, with the CAKE/INTEGRATE command, to carry out the integration. The fifth-order peak was used for fitting as it had the strongest peak intensity among the visible Bragg orders, enabling accurate peak fitting and determination of peak shifts [Supporting Information, Radial Intensities of Different Meridional Bragg Peaks in I(q) and Fig. S1]. To center the pattern around the clear fifth-order peak at ∼0.48 nm−1, inner and outer wavevector limits of 0.45 nm−1 and 0.50 nm−1, respectively, were used. Subsequently, the selected fifth-order peak was fitted by a Gaussian function with a linear background term to account for the diffuse intensity scattering
| [4] |
Fig. S1.
Radial intensity profile I(q) for sea cucumber dermis, with wavevector ranging from 0.26 nm−1 to 0.79 nm−1, showing all visible peaks (third, fifth, sixth, and eighth).
Here I05, q05, and w represent the peak amplitude, peak position, and meridional peak width, respectively (I00 and I′01 are diffuse background terms). The D period was calculated from the relation D = 5 × 2π/ q05. The percentage changes in D value at nonzero external force (relative to the unstressed state) provide the critical fibril strain parameter εF. The method described here has been used extensively by us for vertebrate collagenous tissues, specifically for bone and tendon (41, 42, 46, 67)
| [5] |
To obtain the fibril strain ratio εF/εT for each sample, a linear regression of fibril strain εF vs. tissue strain εT was carried out (Sigma Plot; Systat Software), and the slope of the linear regression provided εF/εT (41, 44, 46, 48). The values of εF/εT for each sample from the different treatment groups are given in Table S1.
Table S1.
Calculated values for εF/εT along with SE of estimate
| Ionic treatment | Sample index | Fit estimate of εF/εT [no units] | SE of εF/εT estimate [no units] |
| ASW | 1 | 0.0074 | 0.0003 |
| 2 | 0.0039 | 0.0002 | |
| 3 | 0.0042 | 0.0003 | |
| 4 | 0.0007 | 0.0003 | |
| KASW | 5 | 0.0166 | 0.0018 |
| 6 | 0.1060 | 0.0068 | |
| 7 | 0.0032 | 0.0011 | |
| 8 | 0.0166 | 0.0015 | |
| CAF | 9 | 9.36E-05 | 0.0003 |
| 10 | 0.0018 | 0.0004 | |
| 11 | 0.0010 | 0.0005 |
Determination of Fibril Orientation Measured from SAXD.
In a complementary manner to fibril strain, the angular fibril distribution was calculated from the azimuthal intensity profile I5(χ) of the fifth-order Bragg reflection of the collagen D spacing. The azimuthal profile was calculated by first integrating (using the Fit2D/CAKE command) the 2D intensity pattern radially in a narrow band of wavevectors around the peak position q05 ∼ 0.48 nm−1 of the fifth-order reflection, i.e., over the wavevector range 0.45–0.50 nm−1. The background-corrected azimuthal intensity distribution Icorrected(χ) was calculated by first averaging the azimuthal intensity profiles in two rings around the fifth-order peak position and subtracting the averaged intensity from the center (peak) ring, as described earlier for bone (68), and is shown in Fig. 2 C, 1 and Fig. S2
| [6] |
Fig. S2.
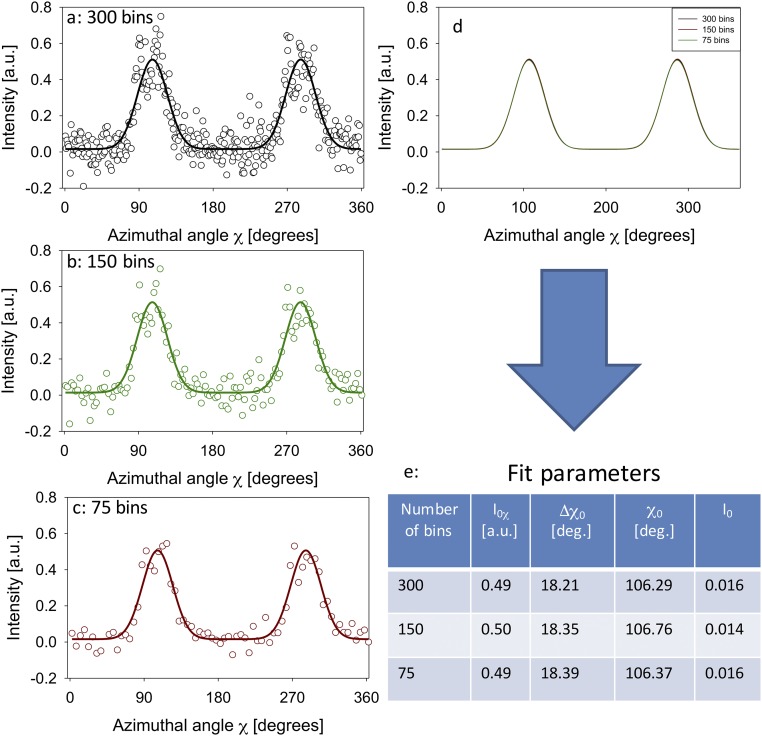
(A–C) Plots of azimuthal intensity profiles I(χ) for a single SAXD pattern with three different numbers of azimuthal bins, along with the fits to the model function of two Gaussians with a constant. (D) Superimposition of the fit functions for A–C, showing that the functions are close to identical. (E) Likewise, the fit parameters for the model function are shown in Table S1 to be very similar.
To ensure the full azimuthal width of the peaks was captured, the intensity profile was calculated over the full circle (0°–360°). Angular coordinates corresponding to high values of Icorrected(χ) denote a greater proportion of fibrils along the specified azimuthal angle. The profile Icorrected(χ) was then fitted to a function with two Gaussian peak profiles, separated by 180°
| [7] |
The parameter χ0 defines the main direction of orientation of the fibrils, whereas Δχ0 is a parameter characterizing the width of the distribution and I0χ is an amplitude term proportional to the total SAXD intensity of the fifth-order reflection. It is noted that whereas applied forces will induce shifts in q05 over the course of the test, these will turn out (shown in Results) to be sufficiently small such that the same narrow band around the initial peak position can be used over the entire test.
A collagen fibril distribution with a narrow angular width (corresponding to well-oriented fibrils) is characterized by a low value Δχ0 and twin sharp peaks in Icorrected(χ) above a low baseline intensity, whereas a distribution with a wide angular dispersion in fibril orientation is characterized by high Δχ0 and a nearly constant Icorrected(χ). We define a dimensionless parameter υ, derived from Icorrected(χ), which can be used to determine whether the fibril distribution is narrow or broad
| [8] |
It can be seen that an isotropic (wide) fibril angular distribution, corresponding to a nearly constant Icorrected(χ), will have υ ∼ 0, whereas υ will increase as the angular width reduces.
Initial Estimation of Φ1 and EIF
Eqs. 1 and 2 in the main text are reproduced below with additions
| [S1] |
| [S2] |
From Fig. 4 it is observed that εF/εT is of the order of 0.01, and hence
| [S3] |
Hence we can neglect the “1” term in Eq. 1, leading to
| [S4] |
| [S4′] |
The above amounts to approximating
| [S5] |
As estimates for fibril modulus EF = 600 MPa and experimental values for εF/εT ∼ 0.01 are known, the term in parentheses below can be estimated as
| [S6] |
where the right-hand side (RHS) is a known quantity. In an analogous manner, the approximation in Eq. S5 can be used in Eq. S2 to get
| [S7] |
The expression in parentheses in the last line is the same as that estimated in Eq. S6. Further, as the aspect ratio ρ1 >> 1, the first term on the second line is much larger than the second term, which can be neglected
| [S8] |
where Eq. S6 has been used in the last step. Because the tissue modulus (or tangent modulus) is known to be ET ∼ 3.23 MPa for ASW (Fig. 4), and EF ∼ 600 MPa, an estimate for the fibril volume fraction is obtained
| [S9] |
Using this value for Φ1 in Eq. S6, along with estimates of the fibril aspect ratio ρ1 ∼ 1,000 and the numerical prefactor γIF = 0.4, an estimate for the interfibrillar modulus EIF is obtained,
| [S10] |
leading to EIF ∼ 50 × 10−6 MPa.
From the foregoing, the required estimates for fibril volume fraction Φ1 and interfibrillar modulus EIF are obtained.
Sensitivity of Fibril Strain Ratio and Tissue Modulus to Model Parameters
Variation in Aspect Ratio ρ.
Fibril strain ratio εF/εT.
By taking a differential of the inverse of Eq. S1, we obtain
where the approximation sign is because (for all experimentally observed fibril strain ratios) εF/εT << 1 as stated in the main text, and as a result and can be neglected. Hence, we have
As a result, a 10% variation in aspect ratio will lead to a 20% variation in the fibril strain ratio. This relatively large variation with aspect ratio is expected on physical grounds, as increased aspect ratio will increase the interfacial area over which shear stress will be transferred to the fibril.
Tissue modulus ET.
Using Eq. S2, we have
(using the same approximation for the denominator as above):
Considering the first term within brackets on the RHS, because ρ1 >> 1 and the other terms are of the order of 1 (Φ1 ∼ 0.54 and γIF = 0.4), it is clear that the first term will be much larger than the second term, which can be neglected in comparison. We obtain
As a result, on a variation in aspect ratio ρ1 we have, similar to εF/εT
with the similar consequence that a 10% variation in aspect ratio will lead to a 20% variation in the fibril strain ratio.
Variation in Fibril Volume Fraction Φ1.
Fibril strain ratio εF/εT.
Similarly, we can show that
Therefore, at a fibril volume fraction of Φ1 ∼ 0.54, a 10% variation in volume fraction leads to a ∼21.7% variation in fibril strain ratio.
Tissue modulus ET.
Similarly, we can show that
which implies that a 10% variation of fibril volume fraction (initial volume fraction of Φ1 ∼ 0.54) leads to a 31.7% variation in tissue modulus. This high rate of variation highlights the increased efficiency of the fibrils in reinforcing the tissue (and increasing the modulus).
Engineering Tissue Strain εT0 and True Strain εT
The incremental strain due to a small increase in stress is defined as the ratio of the differential increase in length to the sample length. The total strain is, therefore, the sum of all these incremental strains. When the sample length does not change significantly over the course of the test, the total strain can therefore be approximated as the change in length divided by the original length, which is the engineering tissue strain εT0,
where l1 is the final length and l0 the initial length. This approximation will not hold if the sample length does change significantly over the course of the test, as occurs in many soft biological tissues. For this case, the exact definition of strain (true strain εT) is the sum of all of the incremental strains, defined by the integral
where in the last step the definition for engineering strain is used.
εF/εT for Each Individual Sample
The calculated values for εF/εT along with SE of estimate are reported in Table S1.
Radial Intensities of Different Meridional Bragg Peaks in I(q)
Considering Fig. S1, as the fifth peak has the highest peak intensity, the peak fitting is most accurate when using the fifth order rather than a much weaker peak such as the sixth order.
Further, it is also not as close to the primary beam and the region of strong diffuse background scattering compared with the lower Bragg orders like n = 2 or 3. As seen in Fig. S1, at low orders, the background intensity is strongly nonlinear as a function of wavevector q. As a result, it is more difficult to subtract the background for such lower orders, and the fit function used here (Gaussian and linear background) does not fit the data as well.
Finally, the fifth-order peak is also better for measuring peak shifts than lower Bragg orders (3) because the shift in the peak due to fibril strain is linearly proportional to the order; i.e., the fifth order will shift by –5(2π/D0)εF, compared with 3(2π/D0)εF for the third order. As the detection of larger peak shifts via peak fitting is more accurate compared with that of smaller peak shifts, this makes determination of fibril strain from peak shifts more accurate when using the fifth-order peak compared with the third order.
Fig. S2: Spread of I(χ) Data with Three Different Numbers of Bins
To show that the choice of the number of bins does not significantly affect the fitted curve, we plotted the azimuthal intensity profile for the same SAXD pattern with three different choices of bin numbers: 300, 150, and 75. Concurrently, the fitted curve for each I(χ) data set, along with the fit parameters, is shown in Fig. S2. It can be seen that the fitted curves overlap very well and that the fit parameters are nearly identical for the choice of the different bins. This result indicates that choice of different bin numbers does not alter the fit results.
Acknowledgments
We thank Jun Ma (School of Engineering and Materials Science, University of London) for help designing the software interface for the tensile tester, Vince Ford (School of Engineering and Materials Science, University of London) for technical support in manufacturing parts for the tensile tester, and T. Narayan (Beamline ID02, ESRF) for excellent support during the beamtime. The principal SAXD experiments were performed on beamline ID02 at the ESRF. J.M. is supported by the China Scholarship Council. H.S.G. and M.R.E. acknowledge support from the Engineering and Physical Sciences Research Council (EP/J501360/1), the Biotechnology and Biological Sciences Research Council (BB/M001644/1), and the Royal Society through the Equipment Grant scheme (SEMF1A6R). L.M.B., H.S.G., and M.R.E. acknowledge support from the Institute of Bioengineering at Queen Mary University of London.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1609341113/-/DCSupplemental.
References
- 1.Egan P, Sinko R, LeDuc PR, Keten S. The role of mechanics in biological and bio-inspired systems. Nat Commun. 2015;6:7418. doi: 10.1038/ncomms8418. [DOI] [PubMed] [Google Scholar]
- 2.Meyers MA, Chen PY, Lin AYM, Seki Y. Biological materials: Structure and mechanical properties. Prog Mater Sci. 2008;53(1):1–206. doi: 10.1016/j.jmbbm.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 3.Fung Y-c. Biomechanics: Mechanical Properties of Living Tissues. Springer Science & Business Media; Berlin: 2013. [Google Scholar]
- 4.Weinkamer RDJ, Brechet Y, Fratzl P. All but diamonds—Biological materials are not forever. Acta Mater. 2013;61(3):880–889. [Google Scholar]
- 5.Eyre DR. Collagen: Molecular diversity in the body’s protein scaffold. Science. 1980;207(4437):1315–1322. doi: 10.1126/science.7355290. [DOI] [PubMed] [Google Scholar]
- 6.Harrington MJ, Masic A, Holten-Andersen N, Waite JH, Fratzl P. Iron-clad fibers: A metal-based biological strategy for hard flexible coatings. Science. 2010;328(5975):216–220. doi: 10.1126/science.1181044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fratzl P, Fratzl-Zelman N, Klaushofer K. Collagen packing and mineralization. An x-ray scattering investigation of turkey leg tendon. Biophys J. 1993;64(1):260–266. doi: 10.1016/S0006-3495(93)81362-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ciarletta P, Ben Amar M. A finite dissipative theory of temporary interfibrillar bridges in the extracellular matrix of ligaments and tendons. J R Soc Interface. 2009;6(39):909–924. doi: 10.1098/rsif.2008.0487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Julicher F, Ajdari A, Prost J. Modeling molecular motors. Rev Mod Phys. 1997;69(4):1269–1281. [Google Scholar]
- 10.Motokawa T. Connective-tissue catch in echinoderms. Biol Rev Camb Philos Soc. 1984;59(2):255–270. [Google Scholar]
- 11.Wilkie IC. Variable tensility in echinoderm collagenous tissues - a review. Mar Behav Physiol. 1984;11(1):1–34. [Google Scholar]
- 12.Wilkie I. 2005. Mutable collagenous tissue: Overview and biotechnological perspective. Echinodermata, ed Matranga V (Springer-Verlag, Berlin), pp 221–250.
- 13.Motokawa T. Effects of ionic environment on viscosity of Triton-extracted catch connective tissue of a sea cucumber body wall. Comp Biochem Physiol B. 1994;109(4):613–622. [Google Scholar]
- 14.Motokawa T, Tsuchi A. Dynamic mechanical properties of body-wall dermis in various mechanical states and their implications for the behavior of sea cucumbers. Biol Bull. 2003;205(3):261–275. doi: 10.2307/1543290. [DOI] [PubMed] [Google Scholar]
- 15.Ribeiro AR, et al. New insights into mutable collagenous tissue: Correlations between the microstructure and mechanical state of a sea-urchin ligament. PLoS One. 2011;6(9):e24822. doi: 10.1371/journal.pone.0024822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Benedetto CD, et al. Production, characterization and biocompatibility of marine collagen matrices from an alternative and sustainable source: The sea urchin Paracentrotus lividus. Mar Drugs. 2014;12(9):4912–4933. doi: 10.3390/md12094912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wilkie IC, et al. Mechanical properties of the compass depressors of the sea-urchin Paracentrotus lividus (Echinodermata, Echinoidea) and the effects of enzymes, neurotransmitters and synthetic tensilin-like protein. PLoS One. 2015;10(3):e0120339. doi: 10.1371/journal.pone.0120339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Birenheide R, Motokawa T. Contractile connective tissue in crinoids. Biol Bull. 1996;191(1):1–4. doi: 10.2307/1543055. [DOI] [PubMed] [Google Scholar]
- 19.Takemae N, Nakaya F, Motokawa T. Low oxygen consumption and high body content of catch connective tissue contribute to low metabolic rate of sea cucumbers. Biol Bull. 2009;216(1):45–54. doi: 10.1086/BBLv216n1p45. [DOI] [PubMed] [Google Scholar]
- 20.Barbaglio A, et al. The mechanically adaptive connective tissue of echinoderms: Its potential for bio-innovation in applied technology and ecology. Mar Environ Res. 2012;76:108–113. doi: 10.1016/j.marenvres.2011.07.006. [DOI] [PubMed] [Google Scholar]
- 21.Jordan H. Die holothurien als hohlorganartige tiere und die tonusfunktion ihrer muskulatur [The holothurians as hollow organ-like animals and their muscle tone] Zool Jahrb Abt. 1914;34:365–436. [Google Scholar]
- 22.Motokawa T. The stiffness change of the holothurian dermis caused by chemical and electrical stimulation. Comp Biochem Physiol C. 1981;70(1):41–48. doi: 10.1016/0306-4492(81)90076-9. [DOI] [PubMed] [Google Scholar]
- 23.Motokawa T. Factors regulating the mechanical properties of holothurian dermis. J Exp Biol. 1982;99:29–41. [Google Scholar]
- 24.Wilkie IC, Carnevali MDC, Bonasoro F. The compass depressors of Paracentrotus-Lividus (Echinodermata, Echinoida) - ultrastructural and mechanical aspects of their variable tensility and contractility. Zoomorphology. 1992;112(3):143–153. [Google Scholar]
- 25.Hidaka M, Takahashi K. Fine structure and mechanical properties of the catch apparatus of the sea-urchin spine, a collagenous connective tissue with muscle-like holding capacity. J Exp Biol. 1983;103(1):1–14. [Google Scholar]
- 26.Diab M, Gilly WF. Mechanical properties and control of non-muscular catch in spine ligaments of the sea urchin, Strongelocentrotus franciscanus. J Exp Biol. 1984;111(1):155–170. [Google Scholar]
- 27.Szulgit G, Shadwick R. The effects of calcium chelation and cell perforation on the mechanical properties of sea urchin ligaments. In: David B, Guille A, Féral J-P, Roux M, editors. Echinoderms Through Time, Proceedings of the Eighth International Echinoderm Conference. CRC Press; Boca Raton, FL: 1994. pp. 887–892. [Google Scholar]
- 28.Trotter JA, Koob TJ. Collagen and proteoglycan in a sea urchin ligament with mutable mechanical properties. Cell Tissue Res. 1989;258(3):527–539. doi: 10.1007/BF00218864. [DOI] [PubMed] [Google Scholar]
- 29.Trotter JA, Lyons-Levy G, Thurmond FA, Koob TJ. Covalent composition of collagen fibrils from the dermis of the sea cucumber, Cucumaria frondosa, a tissue with mutable mechanical properties. Comp Biochem Physiol A. 1995;112(3–4):463–478. [Google Scholar]
- 30.Motokawa T. Mechanical mutability in connective tissue of starfish body wall. Biol Bull. 2011;221(3):280–289. doi: 10.1086/BBLv221n3p280. [DOI] [PubMed] [Google Scholar]
- 31.Yamada A, Tamori M, Iketani T, Oiwa K, Motokawa T. A novel stiffening factor inducing the stiffest state of holothurian catch connective tissue. J Exp Biol. 2010;213(Pt 20):3416–3422. doi: 10.1242/jeb.044149. [DOI] [PubMed] [Google Scholar]
- 32.Oji T, Okamoto T. Arm autotomy and arm branching pattern as anti-predatory adaptations in stalked and stalkless crinoids. Paleobiology. 1994;20(1):27–39. [Google Scholar]
- 33.Trotter JA, Chapman JA, Kadler KE, Holmes DF. Growth of sea cucumber collagen fibrils occurs at the tips and centers in a coordinated manner. J Mol Biol. 1998;284(5):1417–1424. doi: 10.1006/jmbi.1998.2230. [DOI] [PubMed] [Google Scholar]
- 34.Trotter JA, et al. Stiparin: A glycoprotein from sea cucumber dermis that aggregates collagen fibrils. Matrix Biol. 1996;15(2):99–110. doi: 10.1016/s0945-053x(96)90151-1. [DOI] [PubMed] [Google Scholar]
- 35.Koob TJ, Koob-Emunds MM, Trotter JA. Cell-derived stiffening and plasticizing factors in sea cucumber (Cucumaria frondosa) dermis. J Exp Biol. 1999;202(Pt 17):2291–2301. doi: 10.1242/jeb.202.17.2291. [DOI] [PubMed] [Google Scholar]
- 36.Cluzel C, Lethias C, Humbert F, Garrone R, Exposito JY. Characterization of fibrosurfin, an interfibrillar component of sea urchin catch connective tissues. J Biol Chem. 2001;276(21):18108–18114. doi: 10.1074/jbc.M009597200. [DOI] [PubMed] [Google Scholar]
- 37.Tipper JP, Lyons-Levy G, Atkinson MA, Trotter JA. Purification, characterization and cloning of tensilin, the collagen-fibril binding and tissue-stiffening factor from Cucumaria frondosa dermis. Matrix Biol. 2002;21(8):625–635. doi: 10.1016/s0945-053x(02)00090-2. [DOI] [PubMed] [Google Scholar]
- 38.Trotter JA, et al. Collagen fibril aggregation-inhibitor from sea cucumber dermis. Matrix Biol. 1999;18(6):569–578. doi: 10.1016/s0945-053x(99)00050-5. [DOI] [PubMed] [Google Scholar]
- 39.Ribeiro AR, et al. Matrix metalloproteinases in a sea urchin ligament with adaptable mechanical properties. PLoS One. 2012;7(11):e49016. doi: 10.1371/journal.pone.0049016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cluzel C, Lethias C, Garrone R, Exposito JY. Distinct maturations of N-propeptide domains in fibrillar procollagen molecules involved in the formation of heterotypic fibrils in adult sea urchin collagenous tissues. J Biol Chem. 2004;279(11):9811–9817. doi: 10.1074/jbc.M311803200. [DOI] [PubMed] [Google Scholar]
- 41.Gupta HS, et al. Intrafibrillar plasticity through mineral/collagen sliding is the dominant mechanism for the extreme toughness of antler bone. J Mech Behav Biomed Mater. 2013;28:366–382. doi: 10.1016/j.jmbbm.2013.03.020. [DOI] [PubMed] [Google Scholar]
- 42.Screen H, Seto J, Krauss S, Boesecke P, Gupta H. Extrafibrillar diffusion and intrafibrillar swelling at the nanoscale are associated with stress relaxation in the soft collagenous matrix tissue of tendons. Soft Matter. 2011;7(23):11243–11251. [Google Scholar]
- 43.Zimmermann EA, et al. Mechanical adaptability of the Bouligand-type structure in natural dermal armour. Nat Commun. 2013;4:2634. doi: 10.1038/ncomms3634. [DOI] [PubMed] [Google Scholar]
- 44.Zimmermann EA, et al. Age-related changes in the plasticity and toughness of human cortical bone at multiple length scales. Proc Natl Acad Sci USA. 2011;108(35):14416–14421. doi: 10.1073/pnas.1107966108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hulmes DJ, Jesior J-C, Miller A, Berthet-Colominas C, Wolff C. Electron microscopy shows periodic structure in collagen fibril cross sections. Proc Natl Acad Sci USA. 1981;78(6):3567–3571. doi: 10.1073/pnas.78.6.3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gupta HS, et al. Cooperative deformation of mineral and collagen in bone at the nanoscale. Proc Natl Acad Sci USA. 2006;103(47):17741–17746. doi: 10.1073/pnas.0604237103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Stock SR, Almer JD. Strains in bone and tooth via high energy X-ray scattering. Bone. 2009;44(2):S270. [Google Scholar]
- 48.Puxkandl R, et al. Viscoelastic properties of collagen: Synchrotron radiation investigations and structural model. Philos Trans R Soc Lond B Biol Sci. 2002;357(1418):191–197. doi: 10.1098/rstb.2001.1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gasser TC, et al. Spatial orientation of collagen fibers in the abdominal aortic aneurysm’s wall and its relation to wall mechanics. Acta Biomater. 2012;8(8):3091–3103. doi: 10.1016/j.actbio.2012.04.044. [DOI] [PubMed] [Google Scholar]
- 50.Linari M, et al. Force generation by skeletal muscle is controlled by mechanosensing in myosin filaments. Nature. 2015;528(7581):276–279. doi: 10.1038/nature15727. [DOI] [PubMed] [Google Scholar]
- 51.Yang W, et al. On the tear resistance of skin. Nat Commun. 2015;6:6649. doi: 10.1038/ncomms7649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Capadona JR, Shanmuganathan K, Tyler DJ, Rowan SJ, Weder C. Stimuli-responsive polymer nanocomposites inspired by the sea cucumber dermis. Science. 2008;319(5868):1370–1374. doi: 10.1126/science.1153307. [DOI] [PubMed] [Google Scholar]
- 53.Eppell SJ, Smith BN, Kahn H, Ballarini R. Nano measurements with micro-devices: Mechanical properties of hydrated collagen fibrils. J R Soc Interface. 2006;3(6):117–121. doi: 10.1098/rsif.2005.0100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Fratzl P. Collagen: Structure and Mechanics, an Introduction. Springer; Amsterdam: 2008. [Google Scholar]
- 55.Jäger I, Fratzl P. Mineralized collagen fibrils: A mechanical model with a staggered arrangement of mineral particles. Biophys J. 2000;79(4):1737–1746. doi: 10.1016/S0006-3495(00)76426-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gao H, Ji B, Jager IL, Arzt E, Fratzl P. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc Natl Acad Sci USA. 2003;100(10):5597–5600. doi: 10.1073/pnas.0631609100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fratzl P. Nature’s hierarchical materials. Prog Mat Sci. 2007;52(8):1263–1334. [Google Scholar]
- 58.Trotter JA, Thurmond FA, Koob TJ. Molecular structure and functional morphology of echinoderm collagen fibrils. Cell Tissue Res. 1994;275(3):451–458. doi: 10.1007/BF00318814. [DOI] [PubMed] [Google Scholar]
- 59.Masic A, et al. Osmotic pressure induced tensile forces in tendon collagen. Nat Commun. 2015;6:5942. doi: 10.1038/ncomms6942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Scott JE. Proteoglycan:collagen interactions and subfibrillar structure in collagen fibrils. Implications in the development and ageing of connective tissues. J Anat. 1990;169:23–35. [PMC free article] [PubMed] [Google Scholar]
- 61.Elphick MR. The protein precursors of peptides that affect the mechanics of connective tissue and/or muscle in the echinoderm Apostichopus japonicus. PLoS One. 2012;7(8):e44492. doi: 10.1371/journal.pone.0044492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tamori M, et al. Tensilin-like stiffening protein from Holothuria leucospilota does not induce the stiffest state of catch connective tissue. J Exp Biol. 2006;209(Pt 9):1594–1602. doi: 10.1242/jeb.02178. [DOI] [PubMed] [Google Scholar]
- 63.Vincent JF. Structural Biomaterials. Princeton Univ Press; Princeton, NJ: 2012. [Google Scholar]
- 64.Narayanan T, Diat O, Boesecke P. SAXS and USAXS on the high brilliance beamline at the ESRF. Nucl Instrum Methods Phys Res A. 2001;467:1005–1009. [Google Scholar]
- 65.Jeffries CM, Graewert MA, Svergun DI, Blanchet CE. Limiting radiation damage for high-brilliance biological solution scattering: Practical experience at the EMBL P12 beamline PETRAIII. J Synchrotron Radiat. 2015;22(2):273–279. doi: 10.1107/S1600577515000375. [DOI] [PubMed] [Google Scholar]
- 66.Hammersley AP. FIT2D: A multi-purpose data reduction, analysis and visualization program. J Appl Crystallogr. 2016;49:646–652. [Google Scholar]
- 67.Karunaratne A, et al. Significant deterioration in nanomechanical quality occurs through incomplete extrafibrillar mineralization in rachitic bone: Evidence from in-situ synchrotron X-ray scattering and backscattered electron imaging. J Bone Miner Res. 2012;27(4):876–890. doi: 10.1002/jbmr.1495. [DOI] [PubMed] [Google Scholar]
- 68.Karunaratne A, et al. Multiscale alterations in bone matrix quality increased fragility in steroid induced osteoporosis. Bone. 2016;84:15–24. doi: 10.1016/j.bone.2015.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]