Variation in predictive ability of common genetic variants by established strata - The example of breast cancer and age

Abstract

Background

Recent studies of breast cancer and common genetic markers have failed to identify pervasive gene-gene and gene-environment interactions. Theoretical considerations also suggest that the contribution of modest interactions to risk discrimination in the general population is likely small. However, the clinical utility of common breast cancer risk markers may still differ across strata defined by known risk factors, such as age.

Method

We examined the age-specific per-allele odds ratios of 15 common SNPs found to be associated with breast cancer in 1,142 breast cancer cases and 1,145 controls from the Nurses’ Health Study. We calculated the age-specific discriminatory ability of risk models incorporating these SNPs. We then conducted simulation studies to explore how hypothetical underlying genetic models may fit the observed results.

Results

Although all individual SNP-by-age interactions were modest, we found a negative interaction effect between age and a genetic risk score defined by the sum of risk alleles (P=0.04). We also observed a decrease in discriminatory ability, as measured by the area under the curve (AUC), of the SNPs with age (P = 0.04). Simulation studies revealed models where the AUC can differ by strata defined by a risk factor without the presence of interactions; however, our study suggests that the observed differences in AUC are explained by the age-specific effect of the SNPs.

Conclusion

The identification of risk factors that alter the effect of multiple genetic variants can help to explain the genetic architecture of multifactorial diseases and identify sub-groups of persons who may benefit from genetic screening.

Introduction

Identifying synergistic effects between genetic variants or between genetic variants and non-genetic risk factors in complex diseases, and leveraging these effects for risk prediction faces multiple challenges. First, because interaction effects are expected to be smaller than marginal effects, their identification requires larger sample size than for detection of marginal effects. Second, in an agnostic search for interaction effects, the number of tests conducted increases dramatically with the number of predictors considered, aggravating multiple-testing issues. Third, when studying the effect of complex exposures such as air pollution or non-occupational pesticide exposure, additional concerns will arise from multi-dimensionality aspects or time-dependent effects of the risk factor.¹ Interaction effects are not only difficult to assess, but they may also be of limited utility for risk prediction in the general population in many realistic scenarios. We recently showed that when the effect sizes of interactions are low and involve multiple risk factors with various magnitudes and directions, saturated risk models including main and interaction effects do not generally improve discrimination ability as compared with risk models including only the marginal effect of each risk factor.²

Despite these limitations, the identification of interaction effects might still be of interest for risk prediction when the purpose is not prediction in the general population, but rather the identification of a small group of individuals at high risk. This may happen in two situations: (1) in the presence of interaction effect of large magnitude and (2) in the presence of a measurable characteristic that similarly alters the effect of multiple risk factors. We will call such a characteristic a risk regulator. Empirical data suggest that interaction effects of large magnitude involving genetic variants are unlikely to exist unless they involve rare causal variants, rare exposures, or rare allelic combinations of common risk variants. Common genetic variants involved in low-order interactions with large effect should display large marginal effects, and most common complex traits do not harbor such genetic risk factors. The identification of interaction effects with rare variants or rare exposures will require large sample sizes (or clever, targeted study designs) and will likely be extremely challenging. On the other hand, several recent publications have demonstrated the presence of risk regulators involving, for example obesity and the consumption of sugar-sweetened beverages,³ type 2 diabetes and BMI,⁴ breast cancer and hormone receptor status⁵ and prostate cancer and age.⁶ In the latter study by Lindström et al., the authors evaluated the discriminatory ability of 25 prostate cancer SNPs in 7,509 cases and 7,652 controls in age-specific strata. The area under the receiver operating characteristic curve, equal to 0.642 in the whole sample, decreased from 0.679 for the younger persons (≤ 60 years) to 0.599 for the older persons (>75 years). Even though such improvement in AUC may have limited clinical utility, it highlights the potential of identifying specific subgroups in the population where clinically meaningful genetic risk models can be generated.

In this study, we address two subsidiary questions related to the presence of a risk regulator – first whether differences in predictive ability of genetic variants by established risk strata may be caused by differences of genetic effects and, second, if there are statistical artifacts or statistical models that may explain differences of genetic effects in strata defined by a strong risk factor. To do so we used both simulated data and an empirical dataset of 1,142 breast cancer cases and 1,145 controls from the Nurses’ Health Study that have been genotyped as part of the Cancer Genetic Markers of Susceptibility study. We show that the AUC of a genetic risk model based on 15 single nucleotide polymorphisms (SNPs) found associated with breast cancer decreases with age and that this difference is likely explained by multiple monotonic interactions of low magnitude between the SNPs and age. We then demonstrate through simulations that these interaction effects observed on the log-odd scale are likely to explain the differences in predictive ability of the SNPs. Finally we rule out the possibility that the difference in genetic effects by age is caused by ascertainment bias or that it reflects a cumulative effect of genetic risk factors on a liability scale, a model that is known to display interaction effects on the log-odd scale.

Results from age-stratified analysis of breast cancer cases and controls

Odds ratio and SNP effects

We conducted an age-stratified analysis of 1,142 cases and 1,145 age-matched controls from the Cancer Genetic Markers of Susceptibility study⁷ to evaluate the age-specific per-allele log odds ratios of 15 risk SNPs that have been found to be associated with breast cancer at the genome-wide significance level and replicated in independent studies (eAppendix1 and eTable 1). We also evaluated the age-specific discriminatory ability of these SNPs by calculating the receiver operating characteristic curve in each age strata. The sample was split into three groups based on age tertiles derived from the whole sample. Mean age in each of the three tertiles was 58.60 (standard deviation [SD]=3.11), 66.16 (1.85) and 73.66 (3.11). SNP effects were extracted from the literature in order to avoid overfitting the data. The AUC for the total sample and each of the three age tertiles (Table 1) were 0.613 (standard error [SE]=0.020) for the first tertile), 0.594 (SE=0.020) for the 2^nd tertile), and 0.579 (SE=0.020) for the 3^rd tertile) (p_trend = 0.043).

Table 1.

Area under the receiver operating characteristic curve (AUC) by age in tertiles in the Genetic Markers of Susceptibility study data

Group	Age min	Age max	Age Mean (SD)	No.	% Cases	AUC (SE)
Whole sample	44	83	66 (6.7)	2287	0.50	0.596 (0.012)
Age tertile
1	44	63	59 (3.1)	760	0.49	0.613 (0.020)
2	63	69	66 (1.8)	767	0.51	0.594 (0.020)
3	69	83	74 (3.1)	771	0.49	0.579 (0.020)

We estimated the per-allele log odds ratio of each SNP in the whole sample and in each age tertile using multivariate regression. The comparison of the observed effects in each age class and the estimated effects extracted from the literature are presented in Table 2. Six SNPs among the 15 tested were significantly associated with breast cancer at the 5% level (without correction for multiple testing) in the total sample. One or two SNPs (depending on the tertile analyzed) were nominally significant in age-specific strata. The average of the estimates in the total sample (0.127 [SD=0.055]) was equal to the average of the estimates from the literature (0.127 [0.086]). The SNP effects decreased with increasing age, with tertile-specific average estimates of 0.168 (SD=0.223), 0.130 (0.096) and 0.085 (0.143) for first, second and third age tertiles, respectively.

Table 2.

Estimates of SNP effects in the Genetic Markers of Susceptibility study data

SNP id	Published effect	Whole sample effect (p-value)	Age stratified effect (p-value)a
			Tertile 1	Tertile 2	Tertile 3
rs6504950	0.05	0.20 (0.001)	0.16 (0.159)	0.16 (0.138)	0.25 (0.020)
rs704010	0.07	0.18 (0.003)	0.19 (0.078)	0.19 (0.073)	0.16 (0.114)
rs3817198	0.07	0.10 (0.095)	0.06 (0.559)	0.21 (0.045)	0.03 (0.769)
rs13281615	0.08	0.24 (0.150)	0.61 (0.072)	0.18 (0.575)	0.12 (0.645)
rs1011970	0.09	−0.01 (0.931)	−0.45 (0.192)	0.17 (0.603)	0.06 (0.832)
rs4973768	0.10	0.18 (0.003)	0.28 (0.009)	0.07 (0.523)	0.16 (0.129)
rs865686	0.11	0.04 (0.604)	0.28 (0.051)	−0.07 (0.610)	−0.05 (0.745)
rs889312	0.12	0.15 (0.015)	0.13 (0.235)	0.14 (0.204)	0.19 (0.076)
rs614367	0.14	0.09 (0.302)	0.09 (0.564)	0.22 (0.134)	−0.03 (0.855)
rs11249433	0.15	0.03 (0.637)	0.20 (0.069)	0.00 (0.966)	−0.14 (0.207)
rs10995190	0.15	0.30 (0.000)	0.36 (0.001)	0.28 (0.009)	0.33 (0.002)
rs10941679	0.17	0.05 (0.474)	−0.03 (0.812)	0.16 (0.162)	0.00 (0.971)
rs13387042	0.18	0.17 (0.045)	0.24 (0.095)	0.05 (0.709)	0.24 (0.109)
rs2981582	0.18	0.11 (0.093)	0.18 (0.125)	0.01 (0.901)	0.09 (0.433)
rs3803662	0.25	0.09 (0.198)	0.22 (0.066)	0.17 (0.152)	−0.16 (0.162)
Average (SD)	0.127 (0.055)	0.127 (0.086)	0.168 (0.223)	0.130 (0.096)	0.085 (0.143)

^aThe sample was split in three groups based on age tertiles.

Test of interaction between age and the SNPs

We evaluated whether the age-dependent differences in SNP effects were significant by testing for interaction between the SNPs and age. We compared logistic regression models assuming a linear interaction effect between each SNP and age coded either as a continuous variable or in tertiles (0, 1 or 2). Only two SNPs showed a nominally significant interaction effect in at least one model (eTable 2). However, none of them passed the Bonferroni-corrected p-value threshold of 0.003 (i.e. the nominal significance threshold after correcting for the 15 SNP-by-age interaction tests). The average interaction effect estimates, equal to −0.038 (SD=0.074) and −0.042 (0.108) for age coded in tertiles and continuously, respectively, were in agreement with the differences observed when estimating the marginal genetic effect by tertile (Table 2). We then built a genetic risk score based on the count of risk alleles. This risk score was strongly associated with breast cancer in all models considered, and the interaction effect between the risk score and age was nominally significant for age coded continuously (P=0.04) and suggestively significant when age was coded in tertiles (P=0.09) (Table 3).

Table 3.

Test of interaction between the genetic risk score and age in the Genetic Markers of Susceptibility study data

Predictor	estimate (p-value)
Model	SNPs only	Age coded as a continuous variable		Age coded in tertile
	GRS	GRS + age.TERT	GRS × age.TERT	GRS + age.STD	GRS × age.STD
intercept	−1.63 (1.4E-14)	−1.62 (9.4E-14)	−2.05 (1.2E-09)	−1.63 (1.4E-14)	−1.63 (1.3E-14)
GRS	0.13 (3.5E-15)	0.13 (3.5E-15)	0.16 (4.7E-10)	0.13 (3.5E-15)	0.13 (3.3E-15)
age	- -	−0.01 (0.84)	0.42 (0.11)	0.00 (0.94)	0.43 (0.04)
age × GRS	- -	- -	−0.03 (0.09)	- -	−0.03 (0.04)

Abbreviation: GRS, genetic risk score, the sum of all risk alleles; age.STD correspond to the standardized continuous value for age; age.TERT correspond to the age coded in tertile (0,1,2)

Hence, while none of the SNP-by-age interaction effects was significant after accounting for multiple comparisons, the cumulative effect of the 15 SNPs, when summarized in a single variable (i.e. the genetic risk score), decreased significantly with age. Although this decrease in genetic effects might cause the observed differences in AUC by age, other explanations are also possible. First, as shown in a recent study by Kerr et al,⁸ interaction effects observed in AUCs and odds ratios are not always overlapping concepts, and AUCs derived in a strata defined by a strong risk factor may differ even when no interaction effect exists on the log-odd scale. Second, the relatively large effect of age or ascertainment may explain the differences in estimates, leading to differences in AUCs. Third, alternative models not requiring modeling of the interaction effects may fit the data as well as a log-odds model including interactions. For example, it has been showed that under a liability threshold model, the risk associated with a risk factor will decrease in strata defined by a gradient of another risk factor.⁹

Simulation studies

Because none of the three questions that arose from the analysis of the Genetic Markers of Susceptibility study samples can be answered using these data, we conducted simulation studies to address each of them. We explore first some extension of the example 3 from Kerr et al⁸ to identify under which circumstances we may expect to see differences in AUC by strata defined by a binary risk factor. We then generated thousands of samples that mimic the Genetic Markers of Susceptibility study data with or without the interaction effect in the disease risk model. Last, we explored whether a liability threshold model could explain the observed interaction effect.

Differences in AUC without interaction on the log-odd scale

The model that has been described by Kerr et al⁸ showing differences in AUC without interactions on the log-odds scale was as follows:

$$\mathit{\text{logit}}(\text{Pr}(D=1|X,Y))=\propto +{\beta }_x*X+{\beta }_{y}Y,$$ (A)

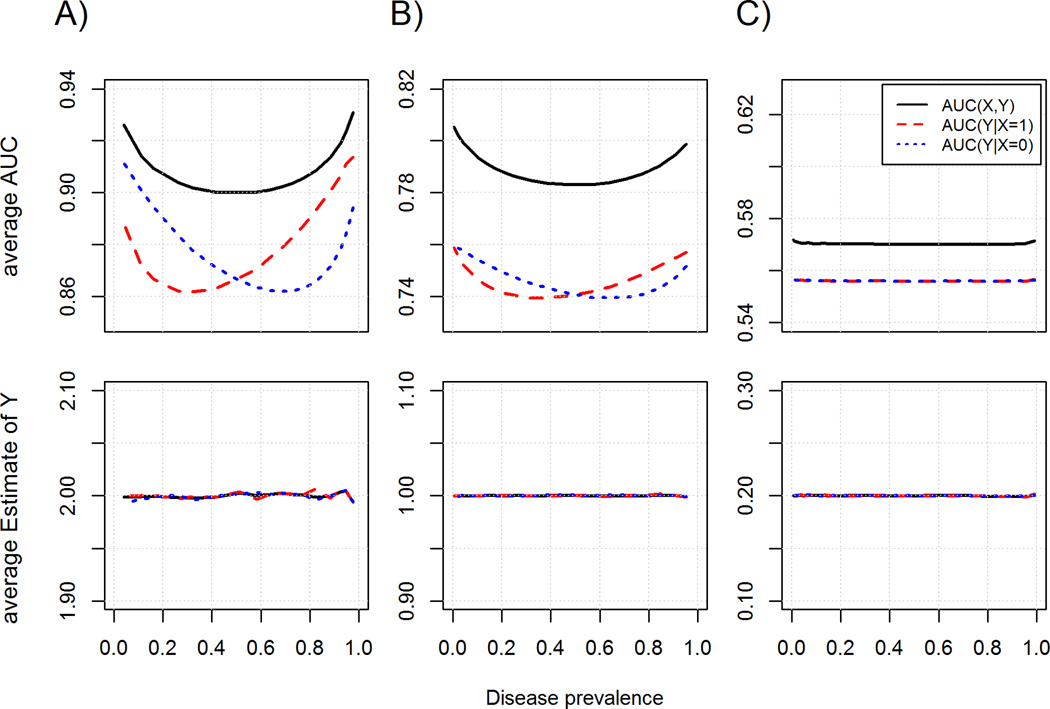
where X is a binary variable with prevalence 0.5 and effect β_x =1, and Y is a normally distributed variable with mean X and variance 1 and effect β_y =2. We vary α so that the prevalence of the disease ranges from 0.01 to 0.99 (in the original study α was set to 0 resulting in a disease prevalence of approximately 0.6). We simulated 1,000 replicates of 1,000,000 individuals under this model while changing the baseline risk of the disease to account for potential differences due to the prevalence. We derived the average AUC and the average effect of Y in strata defined by X (either X=0 or X=1) over all replicates.

Simulations confirm that AUC can change dramatically by strata defined by a risk factor (X) with large effect without the presence of interaction on the log-odd scale (Figure 1A). In fact, AUCs by X strata were always different except when prevalence was close to 0.5, while the estimates of Y by X-strata were independent of the prevalence. Notably the magnitude and direction of the difference was highly dependent of disease prevalence. Since the ratio of cases to controls changes with prevalence of the outcome, we explored whether these differences explain the differences in AUC. We estimated the AUC of Y from an X-matched case-control dataset of 2000 individuals extracted from the previous simulation and observed a similar pattern (eFigure 1A), which rules out this hypothesis. Instead, the AUC might change with prevalence because under Model (A), the distributions of Y in cases and in controls change with prevalence.

Figure 1.

AUC (upper panel) and estimates of Y (bottom panel) by disease incidence for the model logit(pr(D=1)) = bx.X + by.2Y, where bx and by are respectively equal to [1;2] (A), [0.5, 1] (B) and [0.1, 0.2] (C). The two parameters were plotted for the whole sample (black), the sub-sample of individuals with X=1 (red) and the sub-sample of individuals with X=0 (blue). Analysis was conducted in a large cohort of 300,000 individuals.

Overall, for disease prevalence levels close to those observed for breast cancer (in this study, an age-specific incidence around 0.004), the trend in AUC shown in Figure 1A was similar to that observed in the Genetic Markers of Susceptibility study data. However the effects simulated in this model were extremely large. When we used smaller effects for X and Y, (Figure 1B, 1C, eFigure 1B and eFigure 1C), we observed that the differences in AUC were decreasing dramatically, with no difference in AUC for effects similar to the magnitude of breast cancer risk factors (odds ratio between 1.1 and 2). Finally, we noted that the averages of the estimates in the case-control design were slightly larger than those observed in the full cohort (for simulated β_y of 2.0, 1.0 and 0.2, we observed average $\widehat{{\beta }_y}$ of 2.000, 1.000 and 0.200 in the full cohort, and 2.008, 1.002 and 0.202 in the case-control data). This is explained by the smaller sample size used in the case-control analysis, which is known to induce overestimation of the odds ratio in logistic regression.¹⁰

Potential effect of age and ascertainment

We show that both the AUC and the estimated effects of risk factors can change in strata defined by another risk factor. To further investigate how these parameters may change in the presence or absence of interaction effects when multiple markers are involved, we conducted a second simulation in which we compared a model including interaction effects between SNPs and age similar to those observed in the Genetic Markers of Susceptibility study data (log(OR) interaction effects were randomly sampled from a normal distribution with mean of −0.04 and variance of 0.1), and one including only the marginal effect of age and the SNPs (see eAppendix 2). We kept the one-year incidence rate of breast cancer and the marginal effect of SNPs and age the same in both models. We measured the average AUC and the mean effect of SNPs across 1,000 simulations in the whole sample and in the three sub-samples defined by age tertiles, while analyzing either a large cohort of 300,000 individuals or a nested age-matched case-control dataset of 2000 subjects extracted from the full cohort to mimic the Genetic Markers of Susceptibility study data.

As shown in Table 4, the AUC and estimates derived in the whole sample were similar across all scenarios and similar to those expected based on empirical data,¹¹ validating the simulation model. Conversely, large differences were observed between the two simulated models in the age-stratified samples. The average SNP effect and the AUC across the case-control replicates for the interaction model (estimates equal to 0.173, 0.133 and 0.091, and AUC equal to 0.611, 0.594 and 0.561, for each age tertile, respectively) were close to those observed in Table 1 and Table 2. There was no similar trend in the no-interaction model (estimates equal to 0.133, 0.130 and 0.130 and AUC equal to 0.592, 0.592 and 0.592, for the three age tertiles, respectively), so that the observed differences in SNP effects are unlikely to be explained by the relatively large effect of age. Whether or not interaction was simulated, there was no qualitative difference in the analysis of the age-matched case-control data as compared with the full cohort; point estimates were concordant under the two-study design, while the variance of these estimates were, as expected, larger for the case-control data.

Table 4.

Estimated genetic effect and AUC from 1,000 simulations for various models and study designs

Model simulated	Cohort, no interaction		Cohort, interaction		case-control, no interaction		case-control, interaction
Model testeda	Est (SD)	AUC (SD)	Est (SD)	AUC (SD)	Est (SD)	AUC (SD)	Est (SD)	AUC (SD)
G	0.127 (0.012)	0.591 (0.009)	0.121 (0.012)	0.588 (0.009)	0.129 (0.020)	0.592 (0.013)	0.124 (0.020)	0.589 (0.013)
G+A	0.127 (0.012)	0.609 (0.008)	0.121 (0.012)	0.604 (0.009)	NA	NA	NA	NA
G+A+I	NA	NA	0.164 (0.020)	0.601 (0.009)	NA	NA	0.171 (0.034)	0.576 (0.012)
Tert1	0.127 (0.025)	0.591 (0.017)	0.165 (0.024)	0.610 (0.016)	0.133 (0.043)	0.592 (0.027)	0.173 (0.039)	0.611 (0.025)
Tert2	0.126 (0.023)	0.591 (0.015)	0.125 (0.020)	0.592 (0.015)	0.130 (0.034)	0.592 (0.023)	0.133 (0.036)	0.594 (0.023)
Tert3	0.127 (0.020)	0.591 (0.013)	0.089 (0.014)	0.561 (0.014)	0.131 (0.029)	0.592 (0.019)	0.091 (0.014)	0.561 (0.020)

Abbreviation: Est, average of estimated genetic effect of the 15 SNPs.

^aFor all models, estimates are derived in a first sample using a fix set of parameters, AUC are then derived in a second sample generated using the same set of parameters but using the estimates obtained from the first sample. In model G, only the SNP effects are estimated; in model G+ A, effect of the SNPs and age are estimated jointly; in model G +A +I, SNP, age and SNP by age interaction are estimated; in model Tertn, SNP effects are estimated within each age tertile.

Interestingly the simulations also show that the risk model including all simulated SNP-by-age interactions did not perform better than the simpler model including only the marginal effect of each SNP and age (AUC in the full cohort was equal to 0.601 and 0.604 for the interaction risk model and the marginal risk model, respectively). This is partially explained by the very small magnitude of interaction effects and the very large sample size that would be required to obtain precise estimates of all effects. In additional simulations where interaction effects had larger magnitude (logOR_interaction in [0.05,0.2]), the AUC of the interaction model increased, becoming higher than the AUC of the model without an interaction term for an average interaction odds ratio above 1.1 (or below 0.91 for inverse effects), which is in agreement with a previous study we conducted.² Hence while low interaction effects are unlikely to improve risk prediction in the general population, when they are controlled by a single risk regulator (i.e. when interactions with the risk regulator are mostly synergistic or mostly antagonistic) they can be leveraged to identify sub-groups of individuals in which the genetic risk model has better performance.

A liability-threshold model

Other statistical models may fit the data without requiring a non-linear interaction term between the SNPs and age. Among them, the liability threshold model is of particular interest. It has been shown that under such a model, SNPs may display different effects in strata defined by another risk factor.⁹ Briefly, in a liability-threshold model, disease status is a function of a hidden quantitative trait (the liability); all persons having a liability above 0 are disease cases and they are controls otherwise. For breast cancer, the liability L can be defined as follows:

$$L=m+{\gamma }_{\text{Age}}\mathit{\text{Age}}+{\mathrm{\Sigma }}_N{\gamma }_{\mathrm{G}i}{G}_i+\epsilon$$ (B)

where Age is the normalized age and has an effect on the liability scale defined by γ_Age; the G_i are the normalized genotypes of the risk SNPs and the γ_Gi are their respective effect on the liability scale; N, the number of SNPs is here equal to 15; and ε is normally distributed with mean zero and variance one. The baseline parameter m is chosen so that Pr(L>0|Age=Age₀) is equal to the population incidence at the reference age Age₀.

Under such a model, the magnitude of the SNP per-allele odds ratios among persons who are older is expected to be smaller than among younger persons (see eAppendix 3 for derivation of odds ratio in the liability threshold model). For example, Figure 2 shows the expected odds ratio for a single SNP as a function of the prevalence of a binary outcome modeled under a liability threshold for various minor allele frequencies and SNP effects on the liability scale (see eAppdenix3 for the odds ratio derivation). Using this plot, we can show that a SNP with a minor allele frequencies of 0.4 displaying an OR of 1.13 (~logOR=0.13) for an incidence of 0.0042 (the incidence for the median age in the Genetic Markers of Susceptibility study data), will have an effect of 0.03 on the liability scale. Using these parameters (minor allele frequencies=0.4, γ_Gi=0.03), the logOR for this SNP are expected to be equal to 0.130, 0.126 and 0.124 for incidence equal to 0.0028, 0.0040 and 0.0045, respectively, which correspond to the average incidence rate expected in each of the three age tertile.

Figure 2.

Expected odds ratio for a SNP with minor allele frequency of 0.1(A) and 0.4(B), as a function of the prevalence of a disease that has been simulated under a liability threshold model. The proportion of variance explained by the SNP under the liability threshold model (gamma.G) varies from 0.005 to 0.08.

Hence, for a single SNP the variation of effects on the log-odds scale is likely to be much smaller than that observed if the underlying model is a liability-threshold model including a single SNP and age. We confirm this result by generating data analogous to the Genetic Markers of Susceptibility study under a liability threshold model. Among 1,000 replicates, the average estimates of SNP effects, measured through standard logistic regression with a logit link function, were equal to 0.14 (SD=0.03), 0.13 (0.03) and 0.12 (0.03) for each of the three age tertiles. The interaction effect between age and the genetic risk score built from the SNPs was −0.0014 (SD= 0.012). The interaction observed in the Genetic Markers of Susceptibility study data was significantly different (logOR_interaction=−0.034, P_difference=0.003). Hence, while this simulation does not rule out the possibility that the underlying model is a liability-threshold model, it shows that interactions should also exist on the liability scale to fit the data.

Discussion

We identified an interaction effect on breast cancer between age and a genetic risk score, coded as the sum of 15 risk alleles that have been found to be associated with breast cancer. Through simulations, we showed that this interaction effect is likely to explain the observed decrease in discrimination ability of these SNPs by age, with an AUC decreasing from 0.613 to 0.579 for the youngest and oldest tertile of women, respectively. While we confirm that interactions as measured by the AUC and by standard logistic regression are not always overlapping concepts, our simulations suggest that for low to moderate marginal effects, such as those observed in breast cancer, differences in AUC across strata of a risk regulator are likely to correspond to differences in genetic odds ratios across strata. We also ruled out the possibility that the observed differences in AUC and SNP effects were due to either the large effect of age, the case-control ascertainment or because of additive effects of SNPs and age on a liability scale. While the slightly larger prediction ability of SNPs in younger women may not have immediate major clinical utility for genetic screening, this result shows that the identification of risk regulators that modify the effect of multiple SNPs in the same direction can potentially be leveraged for risk prediction purposes, allowing for the identification of sub-set of individuals that would benefit the most from genetic testing.

We tested for differences in the average effect of SNPs by age strata, thus assuming the interaction effects to be homogenous across all of the 15 SNPs considered. This is almost equivalent to summing all interaction terms and giving them equal weights. When the homogeneity assumption does hold, this approach has maximum power, as it fits a single parameter that captures all of the interaction effects. Allowing for heterogeneity of interaction effects across SNPs can be done by adding degrees of freedom. The penalty for these additional degrees of freedom is a decreased power in the presence of homogeneous effects. In general, the magnitude and direction of the interaction effects for the true underlying model might at least slightly differ from SNP to SNP, and it would be of interest to evaluate more precisely SNP-specific interaction effects with age. However, reliably identifying an interaction effect with an odds ratio of 1.03 at genome-wide significance level with 80% power for a risk allele with a MAF of 0.3 requires more than 200,000 subjects. When analyzing only a subset of SNPs (e.g. 15 as in the present study), one will still need more than 80,000 subjects to achieve the same power at the significance level of 0.003 (the p-value threshold after correction for multiple comparison). The Table 2 and eTable 2 indicate that for some of the SNPs, the interaction effect might be larger, accounting for most of the decrease in the effect of the genetic risk score with age, such that sample size required to detect the interaction might be smaller (although we acknowledge that these differences might also be due to random noise). Finally, while the present data do not allow further evaluation of the underlying model, extended analysis using more categories for age (eFigure 2) indicated that the underlying model may not be linear.

Several biological models may explain the differences in SNP effects. If the genetic pathways that lead to disease are changing with age, the effect of the SNPs involved in these pathways is also likely to change with age. Age might also affect the proportion of breast cancer subtypes, and hence change the effect of SNPs that have differential effects across subtypes.¹² Some caution drawing biological inferences from the presence or absence of interaction between SNPs and age on the log odds scale is warranted, however.^13–16 These effects may be consequences of the properties of the logistic link; under a different link the SNP and age effects may be additive. The liability-threshold model, for example, assumes only additive SNP effects but displays heterogeneous effects of SNPs on other scales. While we ruled out the possibility that a liability-threshold model explains the observed interaction effects, other alternatives with similar characteristics might be explored further. Regardless of the underlying biological model, the results of this study emphasize two important characteristics of interaction effects in multifactorial traits. First, it shows that testing for interaction effect using environmental or genetic background (here measured as the sum of risk alleles) instead of each risk factor independently can improve detection of interaction effects in the presence of a “genetic risk regulator” such as age. Second, while all recent studies showed that genetic risk models for breast cancer that are based on identified GWAs SNPs have very limited discrimination ability,^17–19 our results suggest that the identification of interaction patterns where a single factor modifies the effect of multiple SNPs might allow for the identification of sub-groups of the population that will benefit the most from genetic testing.