Abstract
Axonal loss in the spinal cord is one of the main contributing factors to irreversible clinical disability in multiple sclerosis (MS). In vivo axonal loss can be assessed indirectly by estimating a reduction in the cervical cross-sectional area (CSA) of the spinal cord over time, which is indicative of spinal cord atrophy, and such a measure may be obtained by means of image segmentation using magnetic resonance imaging (MRI). In this work, we propose a new fully automated spinal cord segmentation technique that incorporates two different multi-atlas segmentation propagation and fusion techniques: The Optimized PatchMatch Label fusion (OPAL) algorithm for localising and approximately segmenting the spinal cord, and the Similarity and Truth Estimation for Propagated Segmentations (STEPS) algorithm for segmenting white and grey matter simultaneously. In a retrospective analysis of MRI data, the proposed method facilitated CSA measurements with accuracy equivalent to the inter-rater variability, with a Dice score (DSC) of 0.967 at C2/C3 level. The segmentation performance for grey matter at C2/C3 level was close to inter-rater variability, reaching an accuracy (DSC) of 0.826 for healthy subjects and 0.835 people with clinically isolated syndrome MS.
Histopathological studies have provided evidence of spinal cord grey matter (GM) and white matter (WM) changes in a large spectrum of neurological conditions1. In particular, the loss of axons in the spinal cord is thought to represent one of the main contributing factors to clinical disability. In vivo, axonal loss can be assessed indirectly by estimating the reduction in cervical cord cross-sectional area (CSA) over time (i.e., spinal cord atrophy) from magnetic resonance imaging (MRI) through the use of image segmentation methods; the reduction in CSA over time has been shown to correlate with clinical scores of physical disability2,3,4. It must be noted that the measure of cord CSA alone cannot differentiate between the individual rates of GM and WM atrophy, which may have different clinical relevance, and should be best studied independently5. However, in pathologies such as multiple sclerosis (MS) where the presence of focal and diffuse lesions may obscure the boundary between tissue-types6, tissue-specific segmentation can be challenging, and may potentially lead to biased morphometric estimates. Spinal cord GM area was the strongest correlate of disability in MS using multivariate models that include brain GM and WM volumes, fluid-attenuated inversion recovery lesion load, T1 lesion load, spinal cord CSA, number of spinal cord T2 lesions, age, sex, and disease duration3,4.
Over the last two decades, a number of semi-automated segmentation methods have been proposed for the estimation of spinal cord CSA2,7,8,9,10,11,12,13,14,15, and more recently, methods that jointly segment both CSA and GM16,17,18,19,20. Recent studies by El Mendili et al.14,21, which are based on the threshold-based method (TbM) previously described by Losseff et al.2, has shown high reproducibility and accuracy in measuring cord CSA using a semi-automated double threshold-based method (DTbM) that requires minimal manual intervention. As compared to the reference method, DTbM had a Dice Similarity Coefficient (DSC) value of 0.98 for cord CSA at C2 vertebral level in a group of 82 healthy subjects and 30 patients with various neurological conditions such as amyotrophic lateral sclerosis, spinal muscular atrophy and spinal cord injury. While semi-automated methods have improved considerably over the years, reducing intra- and inter-rater variability could have direct implications for future clinical trials of neuroprotection or longitudinal observational studies.
Multi-atlas automated segmentation methods have been used successfully in different parts of the brain. A fully automated spinal cord segmentation method, based on an iterative Non-Local Simultaneous Truth And Performance Level Estimation (iNLS) multi-atlas framework, has also been presented recently16. The method demonstrated high segmentation accuracy for the non-pathological spinal cord with a median DSC of 0.81 for CSA segmentation and 0.72 for GM segmentation. More specifically, the iNLS multi-atlas framework uses 3 degrees-of-freedom rigid body transform per template propagation step in order to achieve the reported accuracy.
Recently, a different multi-atlas segmentation propagation and fusion technique called STEPS (Similarity and Truth Estimation for Propagated Segmentations)22 has demonstrated a statistically significant increase in segmentation accuracy in several key brain structures such as the hippocampus compared with other methods. The algorithm operates in two steps as follows. In the first step, there is the segmentation propagation, where each element of the template library is registered to the target image using an affine registration (12 degrees-of-freedom), followed by a non-rigid registration; in the second step, the best deformed templates are selected based on the locally normalised cross correlation, and are fused into a consensus segmentation. The combination of a local similarity metric for image fusion and the use of non-rigid registration for template propagation makes STEPS a good candidate algorithm for CSA and GM segmentation. However, the affine/non-rigid registration steps require a good initialisation to achieve high accuracy.
Another patch-based multi-altas segmentation and fusion technique is PatchMatch23,24,25. While the original PatchMatch algorithm was designed to look for similarities between two 2D images26, multiple extensions to include 3D MR images have been proposed since. Of relevance here is the optimized PatchMatch Label fusion (OPAL), which was first used to produce accurate and fast segmentations of the hippocampus23,25. This work has been recently extended to multi-modal data (4D) for the purpose of MS lesion detection24. PatchMatch methods are normally good at localising and roughly segmenting objects in images due to the computational efficiency of the OPAL random search algorithm, albeit with reduced accuracy.
In this work, we propose a new fully automated spinal cord segmentation technique that incorporates two different multi-atlas segmentation propagation and fusion algorithms: OPAL and STEPS. The OPAL random search is used to localise and roughly segment the spinal cord, and the STEPS algorithm is then used to perform slice-wise tissue segmentation. The proposed method is evaluated retrospectively using a dataset that includes healthy volunteers and people with MS.
Methods
Segmentation methods
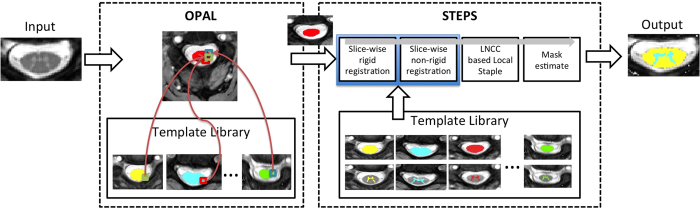
The proposed method combines two existing label fusion segmentation techniques: OPAL for detecting the spinal cord and STEPS for accurately segmenting the GM and whole spinal cord. Bearing in mind that the typical slice thickness of spinal cord images is approximately 3–5 mm27, the proposed method performs all registrations and segmentations in a 2D slice-wise manner before merging them into a 3D volume. A schematic representation of the proposed pipeline is shown in Fig. 1. Additional details pertaining to each step individually are discussed in subsequent sections.
Figure 1. Schematic representation of the proposed pipeline.
The spinal cord images were cropped only for visualisation purposes.
Step 1: Localisation using OPAL
While the original PatchMatch algorithm was designed to match 2D patches within the same image26, the method has been recently extended to 3D23,25 and 4D data24, with the search range extended to an external reference library. Due to the excellent performance in terms of computational time and good segmentation accuracy in some applications, OPAL is used here in its original form to simply localise the spinal cord. This cord localisation step is achieved by providing an external database of spinal cord images and associated manually segmented cords to the OPAL algorithm, all of which are then propagated to the new unseen image. This step has an average computational time of less than 1 sec. While OPAL was found to perform well both for cord and GM segmentations in healthy volunteers, the segmentation performance degraded rapidly in the presence of pathology (e.g. MS lesions), not allowing to use the default application over MS subjects. OPAL is publicly available inside NiftySeg software package (niftyseg.sf.net).
Step 2: Segmentation using STEPS
The main characteristic of STEPS is that it introduces a spatially variant image similarity term in a STAPLE framework22, enabling the characterisation of both image similarity and human rater performance in a unified manner. The STEPS segmentation process is divided into two stages: segmentation propagation and fusion. Starting from a template library with associated manual segmentations, all the templates (excluding the image under analysis) are first registered to the target image using initially a rigid-only registration and then a non-rigid registration. All registration was done using the NiftyReg software package (niftyreg.sf.net). The normalised cross correlation (NCC) was then estimated between each deformed template and the target image, quantifying the similarity between the two images. The most similar deformed templates according to the NCC were finally fused into a consensus segmentation according to the locally normalised cross correlation (LNCC) between the registered template images and the target image. A consensus probabilistic CSA and GM segmentation is obtained using the STEPS algorithm as implemented in NiftySeg (niftyseg.sf.net). The probabilistic nature of the consensus segmentation implicitly encodes partial volume effect, improving tissue boundary localisation and delineation. Finally, to produce binary segmentations, the probabilistic consensus masks were thresholded at 0.5.
Note that, in order to increase the performance of the fusion step, the centre of mass of the OPAL cord segmentation was used to initialise the rigid registration step between templates and target image. The OPAL cord segmentation was also used to mask non-cord regions from the non-linear registration step, further improving the performance of the template registration step.
Algorithm Parameters
The pipeline works in a slice-wise manner (2D). All experiments used the following parameters. OPAL was used with the original parameters23,25. The 2D patch size was 5 × 5 voxels and the number of inner iterations was 5. Finally, the numbers of threads and the number of best-matches were both set to 10.
The OPAL mask was then dilated eight times to ensure that there was sufficient boundary information to perform both affine and non-rigid registrations28,29.
For STEPS, the parameters used were as suggested by Cardoso et al.22. The number of best templates was X = 15, standard deviation of the Gaussian smoothing kernel for LNCC estimation σ = 1.5 and the Markov Random Field (MRF) spatial consistency set to 0.55.
The linear registration of the templates for the STEPS label fusion has been done using a symmetric 6 degree-of-freedom affine registration using a block matching approach30,31. The non-rigid alignment has been done using the fast free-form registration algorithm32 with the LNCC (σ = 1) as a similarity measure. The pyramidal approach was set to use 6 levels, and the grid spacing at the lowest level of the pyramid set to 5 voxels.
The input image was resampled to the template library resolution using a linear interpolation, and the obtained binary masks were resampled back to the original resolution using nearest-neighbour interpolation in order to maintain their categorical nature.
Data
We analysed data acquired in 102 subjects participating in a study of spinal cord MR imaging in MS33. There were: 25 healthy controls, 19 people with clinically isolated syndrome (CIS), 20 with primary progressive multiple sclerosis (PPMS), 17 with secondary progressive multiple sclerosis (SPMS), and 21 with relapsing remitting multiple sclerosis (RRMS). We recruited people with different types of MS because they are expected to have a different degree of pathological changes in the spinal cord. MS lesions involving at least two spinal cord WM columns and extending to the GM are more frequent in SPMS than in the early phase of MS33. Written informed consent was obtained from all participants and this work was approved by the local research ethics committee.
Using a 3T Philips Achieva MRI system with dual-transmit technology (Philips Healthcare, Best, Netherlands) and the manufacturer’s product 16-channel neurovascular (NV) coil, the cervical cord was imaged in the axial-oblique plane (i.e. slices perpendicular to the cord) with the center of the imaging volume positioned at the level of C2-3 intervertebral disc. The MRI acquisition parameters were: Fat-suppressed 3D slab-selective fast field echo (3D-FFE) with TR = 23 ms; TE = 5 ms, flip angle α = 7 degrees, FOV = 240 × 180 mm, voxel size = 0.5 × 0.5 × 5 mm3, NEX = 8, 10 contiguous axial slices, scanning time = 13:34 min.
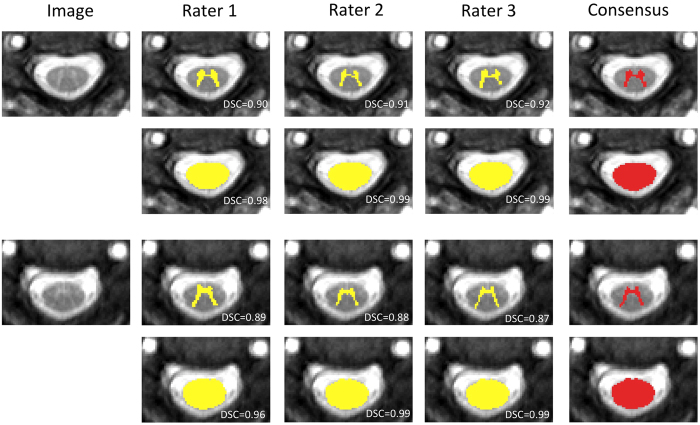
Three expert raters working independently and with the raw images, first outlined GM manually and semi-automatically outlined the cord CSA using the ‘cord finder’10 option available with JIM v.6 (Xinapse systems, www.xinapse.com/). Based on the previously published methodology by Losseff et al.2, a 15 mm section of the high-resolution 3D-FFE volumetric scan (i.e. 3 slices) was extracted, with the middle slice passing through the C2-3 intervertebral disc. ‘Cord finder’ option runs an active surface model that it needs the manual place of a seed. Raters manually positioned a seed in the centre of the cord in each of the three slices. For each subject, the associated consensus segmentation of the three raters (at least two raters agree) for the cord CSA and GM were estimated using majority voting, see Fig. 2.
Figure 2. Example of GM and CSA consensus masks obtained from the three raters masks intersection.
Consensus mask for a healthy control (rows 1 and 2) and a RRMS patient (rows 3 and 4). DSC respects the consensus mask is overlayed in each segmentation.
The C2-3 cervical cord level was used to estimate the performance of the proposed algorithm as the inter-rater variability was found to be lower in cord areas surrounded by CSF. Nonetheless, the application to other spinal cord segments, such as thoracic or lumbar areas would only require an area specific template database. Losseff et al.2 indicates that, within the cord, this location (C2-3 level) yields the most reproducible cross-sectional area values and it is the most convenient region to measure atrophy in the spinal cord.
To avoid bias due to lack of consensus between manual segmentations, segmentations with a 3D DSC lower than 0.7 between two of the three expert raters, or images of poor quality (due to noise, motion, etc.) were excluded from this study. A total of 7 subjects (4 PPMS, 2 SPMS and 1 RRMS) were excluded, which resulted in a final group of 95 subjects (25 controls, 19 CIS, 16 PPMS, 15 SPMS and 20 RRMS). Table 1 shows the demographic information of the selected data.
Table 1. Demographic data for each group.
| Control (N = 25) | CIS (N = 19) | PPMS (N = 16) | SPMS (N = 15) | RRMS (N = 20) | |
|---|---|---|---|---|---|
| Gender | 7F:18M | 7F:12M | 9F:7M | 5F:10M | 8F:12M |
| AgeMean (std) | 40.4(10.1) | 36.0(4.6) | 52.5(11.0) | 55.2(7.4) | 41.8(9.1) |
| Disease durationMean (std) | — | 0.4(0.3) | 11.5(8.7) | 22.1(14.1) | 7.8(6.1) |
| EDSS scoreMedian (range) | — | 1(0–3.5) | 6(2–7) | 6.5(4.5–7.5) | 2.5(0–6.5) |
First row: gender - female(F):male(M); second row: mean age in years; third row: mean disease duration in years; and last row: median EDSS score. Std: standard deviation.
Template library
The template library used in this work consisted of 3D imaging volumes from the 95 subjects described in the Data section. For each subject there were three 2D slices, with the centre slice through the C2-3 level. In order to maximise the size of the library, all the scans were left-right flipped, resulting in a final template library of 570 2D images in total. For each image in the template library, the associated consensus segmentation of the three raters for the cord CSA and GM was used as template (see Fig. 2).
Leave-one-out cross-validation
The proposed fully automated method, which estimates the CSA and segments the GM at the same time, was compared to the consensus segmentation of 3 raters. We also compared the performance of the proposed method to the iNLS multi-atlas framework - a fully automated GM/WM spinal cord segmentation method16. iNLS has been used with the parameters presented in Asman et al.16. A leave-one-out strategy was used for both iNLS and the proposed method, i.e. the image being segmented as well as its left-right flipped version15, were removed from the template library during segmentation. Both iNLS and the proposed method used the same library as described in the Data section.
All binary segmentations obtained using the proposed method were compared to the manual segmentations, the consensus segmentation and the iNLS results. To assess the performance, we used the 3D DSC, the mean surface distance (MD) and the Hausdorff distance (HD) between the masks15,34. Statistical differences in performance were estimated using a two tail unequal variance paired t-test as the error distribution was approximately Gaussian in most experiments. Furthermore, all patients’ data (CIS, PPMS, SPMS and RRMS) were split into two independent groups, one with visible lesions at C2/C3 level and one without, in order to assess the impact of the presence of lesions on the segmentation performance.
Test-retest assessment
For assessing the reliability of the presented method we performed a test-retest experiment. Test-retest data were composed of 5 different healthy controls that repeated the same MR imaging protocol 3 times on separate occasions, with a minimum of a week and a maximum of two weeks between measurements. We segmented the images using the same library as described in Data Section and one rater analysed all the data.
Results
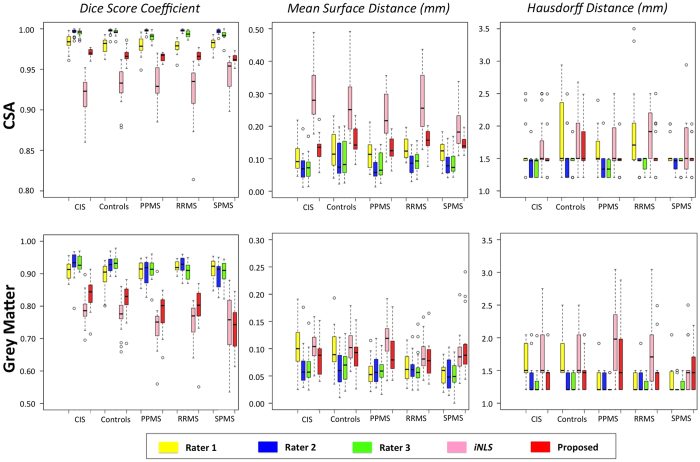
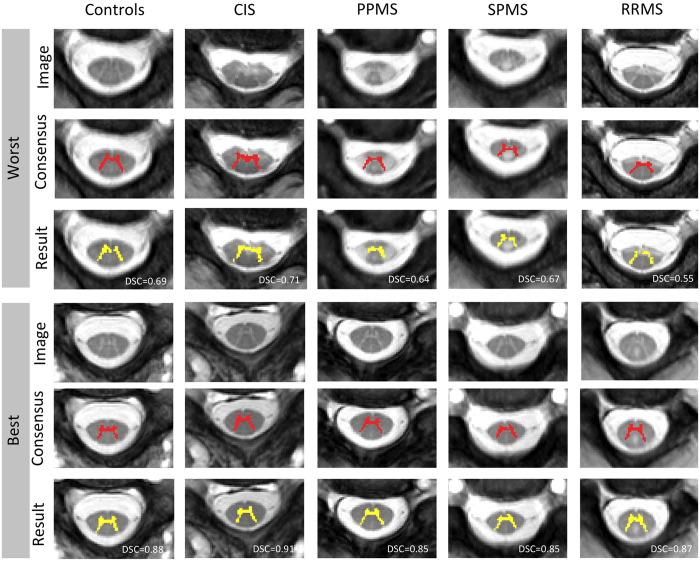
Tables 2, 3 and Fig. 3, show the evaluation results for the CSA and GM segmentation at C2/C3 level respectively, with the mean (std) and p-value for the DSC, MSD and HD estimated with respect to the consensus masks. In Tables 2 and 3, significant differences (p < 0.05) have been marked with “*”. For the qualitative results, the best and the worst DSC results are shown for each patient group for GM segmentation (see Fig. 4).
Table 2. Evaluation results for the CSA segmentation, with the mean (std) Dice score coefficient (DSC), mean surface distance (MSD), Hausdorff distance (HD) (all with respect to the consensus).
| Rater 1 | Rater 2 | Rater 3 | iNLS | Proposed | ||
|---|---|---|---|---|---|---|
| Controls (N = 25) | DSC | 0.980 (0.009)* | 0.997 (0.004)* | 0.996 (0.003)* | 0.931 (0.021)* | 0.968 (0.008) |
| MSD | 0.130 (0.056)* | 0.096 (0.056)* | 0.101 (0.052)* | 0.265 (0.094)* | 0.153 (0.042) | |
| HD | 1.785 (0.544) | 1.494 (0.302)* | 1.448 (0.150)* | 1.809 (0.429) | 1.649 (0.349) | |
| CIS (N = 19) | DSC | 0.983 (0.010)* | 0.996 (0.004)* | 0.995 (0.004)* | 0.917 (0.025)* | 0.971 (0.005) |
| MSD | 0.107 (0.051)* | 0.071 (0.043)* | 0.072 (0.036)* | 0.295 (0.088)* | 0.132 (0.037) | |
| HD | 1.598 (0.334) | 1.401 (0.182) | 1.393 (0.131)* | 1.673 (0.408) | 1.533 (0.282) | |
| PPMS (N = 16) | DSC | 0.979 (0.008)* | 0.997 (0.002)* | 0.990 (0.005)* | 0.932 (0.024)* | 0.965 (0.005) |
| MSD | 0.114 (0.046) | 0.066 (0.034)* | 0.080 (0.040)* | 0.230 (0.078)* | 0.133 (0.037) | |
| HD | 1.600 (0.344) | 1.383 (0.226) | 1.345 (0.143)* | 1.698 (0.405)* | 1.468 (0.188) | |
| SPMS (N = 15) | DSC | 0.981 (0.008)* | 0.996 (0.003)* | 0.992 (0.006)* | 0.943 (0.022)* | 0.963 (0.005) |
| MSD | 0.121 (0.036)* | 0.086 (0.037)* | 0.089 (0.039)* | 0.202 (0.074)* | 0.148 (0.026) | |
| HD | 1.585 (0.213) | 1.413 (0.129)* | 1.428 (0.115) | 1.677 (0.476) | 1.540 (0.236) | |
| RRMS (N = 20) | DSC | 0.978 (0.008)* | 0.998 (0.002)* | 0.993 (0.004)* | 0.921 (0.036)* | 0.967 (0.006) |
| MSD | 0.130 (0.034)* | 0.083 (0.033)* | 0.093 (0.030)* | 0.269 (0.093)* | 0.154 (0.037) | |
| HD | 1.936 (0.610)* | 1.429 (0.115)* | 1.420 (0.127)* | 1.981 (0.773) | 1.588 (0.305) | |
| All (N = 95) | DSC | 0.980 (0.009)* | 0.997 (0.003)* | 0.994 (0.005)* | 0.928 (0.027)* | 0.967 (0.006) |
| MSD | 0.121 (0.047)* | 0.082 (0.044)* | 0.088 (0.041)* | 0.256 (0.091)* | 0.145 (0.037) | |
| HD | 1.717 (0.466)* | 1.430 (0.211)* | 1.411 (0.137)* | 1.778 (0.523)* | 1.565 (0.288) |
The script * represents significant differences (paired t-test with p < 0.05) between a rater/iNLS versus the proposed method.
Table 3. Evaluation results for the GM segmentation, with the mean (std) Dice score coefficient (DSC), mean surface distance (MSD), Hausdorff distance (HD) (all with respect to the consensus).
| Rater 1 | Rater 2 | Rater 3 | iNLS | Proposed | ||
|---|---|---|---|---|---|---|
| Controls (N = 25) | DSC | 0.894 (0.039)* | 0.927 (0.022)* | 0.931 (0.020)* | 0.776 (0.049)* | 0.826 (0.046) |
| MSD | 0.100 (0.035) | 0.063 (0.031)* | 0.067 (0.028)* | 0.106 (0.030)* | 0.089 (0.030) | |
| HD | 1.637 (0.274)* | 1.285 (0.128)* | 1.315 (0.135)* | 1.723 (0.420)* | 1.444 (0.204) | |
| CIS (N = 19) | DSC | 0.908 (0.026)* | 0.930 (0.040)* | 0.933 (0.021)* | 0.789 (0.046)* | 0.835 (0.047) |
| MSD | 0.104 (0.044) | 0.065 (0.035)* | 0.064 (0.029)* | 0.104 (0.029)* | 0.083 (0.033) | |
| HD | 1.654 (0.285)* | 1.360 (0.251) | 1.307 (0.208) | 1.766 (0.475)* | 1.393 (0.207) | |
| PPMS (N = 16) | DSC | 0.907 (0.030)* | 0.905 (0.038)* | 0.911 (0.033)* | 0.735 (0.073)* | 0.780 (0.056) |
| MSD | 0.057 (0.027)* | 0.061 (0.027)* | 0.061 (0.023)* | 0.118 (0.043)* | 0.091 (0.039) | |
| HD | 1.320 (0.200) | 1.294 (0.134)* | 1.239 (0.088)* | 1.920 (0.536)* | 1.611 (0.517) | |
| SPMS (N = 15) | DSC | 0.914 (0.032)* | 0.894 (0.041)* | 0.903 (0.035)* | 0.745 (0.100) | 0.735 (0.069) |
| MSD | 0.054 (0.019)* | 0.055 (0.030)* | 0.052 (0.024)* | 0.091 (0.039) | 0.107 (0.056) | |
| HD | 1.339 (0.234) | 0.930 (0.117) | 1.198 (0.353)* | 1.517 (0.388) | 1.444 (0.503) | |
| RRMS (N = 20) | DSC | 0.923 (0.017)* | 0.925 (0.027)* | 0.906 (0.026)* | 0.754 (0.049)* | 0.793 (0.069) |
| MSD | 0.065 (0.024) | 0.063 (0.022)* | 0.063 (0.029)* | 0.088 (0.032) | 0.078 (0.031) | |
| HD | 1.327 (0.136) | 1.322 (0.186) | 1.213 (0.309)* | 1.821 (0.578) | 1.441 (0.340) | |
| All (N = 95) | DSC | 0.908 (0.031)* | 0.918 (0.035)* | 0.919 (0.029)* | 0.762 (0.065)* | 0.799 (0.066) |
| MSD | 0.079 (0.038) | 0.062 (0.029)* | 0.062 (0.027)* | 0.101 (0.035)* | 0.089 (0.038) | |
| HD | 1.475 (0.280) | 1.306 (0.171)* | 1.261 (0.233)* | 1.753 (0.489)* | 1.461 (0.357) |
The script * represents significant differences (paired t-test with p < 0.05) between a rater/iNLS versus the proposed method.
Figure 3. Quantitative analysis per patient group on GM and CSA segmentation of the spinal cord.
Figure 4. GM segmentation results showing the worst (1–3) and the best (4–6) result for each patient group.
Rows 1 and 4 show one slice of the input image, rows 2 and 5 correspond to the consensus segmentation, and rows 3 and 6 are the obtained segmentation by the proposed method with DSC overlay.
We have found that the proposed method provides more accurate results for the CSA segmentation at C2/C3 level when compared to iNLS (DSC and MSD - p < 0.05) for all groups. When comparing the proposed method (see Table 3) with the iNLS, superior results were found for healthy controls, however, lower performance, but not statistically significant, is obtained for GM DSC on SPMS group. There are significant differences for GM segmentation (DSC - p > 0.05) between the methods for CIS, PPMS and RRMS subjects. Overall, the proposed method outperforms the state-of-the-art method iNLS (p < 0.05) for CSA and GM segmentation at C2/C3 level (see last row in Tables 2 and 3), and for GM segmentation the obtained MSD and HD by Rater 1 are not significantly different from proposed method.
Table 4 shows the results from splitting the patients’ data into two groups depending on the presence of visible lesions at the C2/C3 level. There were significant differences for CSA and GM segmentation between the absence and presence of lesions. Finally, Table 5 presents the reliability assessment results for CSA and GM regions mean and std.
Table 4. Results from splitting the patients’ data into two groups depending on the presence of visible lesions at the C2/C3 level, with the mean (std) Dice score coefficient (DSC), mean surface distance (MSD), Hausdorff distance (HD) (all with respect to the consensus).
| With visible lesions (N = 45) | Without visible lesions (N = 25) | ||
|---|---|---|---|
| CSA | DSC | 0.965 (0.143)* | 0.970 (0.005)* |
| MSD | 0.143 (0.036) | 0.139 (0.035) | |
| HD | 1.534 (0.291) | 1.538 (0.196) | |
| GM | DSC | 0.762 (0.067)* | 0.838 (0.039)* |
| MSD | 0.096 (0.045)* | 0.076 (0.025)* | |
| HD | 1.525 (0.472) | 1.364 (0.176) |
The script * represents significant differences (paired t-test with p < 0.05) between groups.
Table 5. Test-retest measurements obtained from C2-3 spinal cord level.
| Volume (mm3) | Area (mm2) | COV (%) | DSC | ||
|---|---|---|---|---|---|
| CSA | Manual | 1323.6 (92.6) | 88.2 (6.2) | 0.8 (0.5) | 0.965 (0.005) |
| Proposed | 1321.4 (89.9) | 88.1 (6.0) | 1.2 (0.9) | ||
| GM | Manual | 209.8 (20.8) | 14.0 (1.4) | 7.2 (1.9) | 0.791 (0.041) |
| Proposed | 186.6 (21.2) | 12.4 (1.4) | 7.4 (4.9) |
Mean (std) for volume, area, coefficient of variation (COV) and Dice score coefficient (DSC).
Experiments were performed on a server (12 CPUs 2.8 Ghz and 64 Gb RAM). The average computational time was 30 minutes per target image using only 2 CPU threads.
Spinal Cord GM Challenge 2016
The proposed method was used to segment 40 healthy spinal cord images from 4 independent centres and 2 different vendors as part of a spinal cord segmentation challenge that was organized as a satellite of ISMRM 2016 (cmictig.cs.ucl.ac.uk/niftyweb/program.php?p=CHALLENGE). The challenge was comprised of 6 teams with widely varying approaches ranging from multi-atlas propagation20 and deep learning35, to active contours19 and variational Bayes probabilistic segmentation17. The proposed method (named as JCSCS in the challenge) obtained the highest rank in 5 out of 10 evaluation metrics, with a mean(std) DSC, MSD, HD of 0.79(0.04), 0.39(0.44), 2.65(3.34) respectively. A future publication presenting an extended and more detailed analysis of the results is currently under preparation.
Discussion
We propose the combined use of OPAL and STEPS for the segmentation of the whole spinal cord CSA and GM. Although we have found the output of OPAL was highly dependent on the amount of noise and the presence of lesions (producing highly spurious segmentations in some situations), our results nonetheless demonstrate that OPAL can provide a sufficiently accurate initial segmentation of the spinal cord in order to facilitate a constrained STEPS label fusion process.
Asman et al.16,36 highlight some caveats of using non-rigid registration for spinal cord imaging. In the proposed method, the OPAL segmentation was used to initialise and constrain, providing a region mask to the slice-wise non-rigid registration performed by STEPS, thus ameliorating most of these concerns. The computational time needed to perform these slice wise non-rigid registrations was also deemed adequate, taking approximately one second per slice and template. Moreover, the use of non-rigid registration reduces the need for a refinement step as proposed in Asman et al.36.
The fact that the proposed method gets lower, but not statistically different, performance for GM DSC on SPMS group (see Table 3) maybe due to the low number of subjects and the presence of large lesions. The use of non-rigid registration in the proposed method might be detrimental in subjects with very large lesions, as the non-rigid step introduces too much flexibility and uncertainty when deforming the candidate labels (see columns SPMS and RRMS at Fig. 4). Overall, similar differences were found for the MSD and HD scores. Table 4 shows the effect of the presence or absence of lesions, these differences are specially large and significant for GM (DSC and MSD p < 0.05).
Results in Tables 2 and 3 show that the proposed method is able to segment the CSA with a very high accuracy, and only slightly different to the three rater consensuses. Method gets a DSC of 0.968 that is not a clinically significant difference. The low variability between raters for CSA segmentation is thanks to the semi-automated nature of the ‘cord finder’ method from JIM. We would like to note that the results presented have been obtained in a three slice subset of the full volume. As spinal cord imaging usually has dozens or hundreds slices per volume, consistency across slices can be exploited in the future to reduce the amount of errors produced by the proposed algorithm. Moreover, the reduced number of slices and voxels per mask, in conjunction with the evaluation metrics, highlight the quality of the obtained results. Covering a larger spinal cord area would hide any small miss-segmented area due to repetitive spinal cord nature.
On a group specific basis, the CSA segmentation performed very well in all the groups and the presence of lesions has a low impact (see Table 4). Test-retest assessment also confirms these results (see Table 5). It is also important to note that the proposed method has a lower CSA segmentation HD than Rater 1 for all groups, suggesting that the errors introduced by human raters with different levels of expertise or training can be larger than the errors introduced by the proposed method, further justifying the need for advanced automated segmentation techniques for multi-centre studies and trials.
Regarding the GM segmentation, the proposed method provided acceptable results for the groups without lesions (healthy controls and CIS), achieving better MSD and HD than Rater 1. While Rater 1 tended to over-segment the GM when comparing to the consensus mask, the presented method had a tendency to only slightly under-segment the GM when compared to the consensus mask, resulting in lower MSD and HD. On a group specific basis, the GM segmentation performed better in healthy controls and CIS patients than in the other three MS groups, which is likely to be related to the limited number of lesions identified in the CIS cohort33. GM test-retest assessment results are also promising (see Table 5).
From Figs 3 and 4, one can observe that the worst results correspond to outliers in terms of Dice score. In these situations, the presence of hyperintensities favour the use of anatomical a priori assumptions by the human raters. In future we will include anatomical priors and uncertainty estimates in the segmentation process so that the segmentation algorithm reverts back to the prior model in very uncertain situations.
The state-of-the-art results obtained as part of the ISMRM 2016 satellite spinal cord challenge further demonstrate that the proposed method is robust to differences in scanner manufacturer and acquisition parameters when compared to 4 independent rater segmentations.
In summary, this paper introduces a fully-automated GM and whole spinal cord segmentation technique based on a collaborative effort between two multi-label fusion techniques. OPAL quickly finds the cord and then STEPS segments GM and CSA. Both healthy and different types of MS subjects were used for performance assessment, and the results have been compared to the consensus of three expert manual segmentations. The accuracy of the proposed method was found to be close, comparable and in some situations better, than a single rater. GM segmentation results obtained in PPMS, SPMS and RRMS subjects showed promising results but further work is necessary to remove the influence of MS lesions.
The proposed method has only been applied to the cervical area (C2-3 level) of the spinal cord because it is the most convenient region to measure atrophy in the spinal cord in MS. Specifically, the obtained results for the CSA segmentation suggests that it may be used in a large multi-centre neuroprotective trials in progressive MS. Moreover, application to other spinal cord segments, such as thoracic or lumbar areas, or other sequences would only require an area/sequence specific template database.
Additional Information
How to cite this article: Prados, F. et al. Fully automated grey and white matter spinal cord segmentation. Sci. Rep. 6, 36151; doi: 10.1038/srep36151 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Acknowledgments
FP is funded by the National Institute for Health Research University College London Hospitals Biomedical Research Centre (NIHR BRC UCLH/UCL High Impact Initiative-BW.mn.BRC10269). SO receives funding from the EPSRC (EP/H046410/1, EP/J020990/1, EP/K005278), the MRC (MR/J01107X/1), the NIHR Biomedical Research Unit (Dementia) at UCL and the NIHR BRC UCLH/UCL-BW.mn.BRC10269. ML received funding from the Swiss National Science Foundation (fellowship P2EZP3_148749, P300PB_161087), joint research funding from UCL and the Neuroscience Center Zürich, and the UK Multiple Sclerosis Society. This work was also supported by the Medical Research Council, the UK Multiple Sclerosis Society (grant 892/08), the Brain Research Trust and by Capital Project number R&D03/10/RAG0449 from NIHR BRC UCLH/UCL. The authors are grateful to Bennett Landman and Benjamin N. Conrad for the help provided to successfully install and use iNLS. We gratefully acknowledge the support of NVIDIA Corporation with the donation of the GPU card used for this research.
Footnotes
FP, MJC, MY, LH, ET, HK, ML, CWK and SO declare no competing financial interests. DM has received honoraria through payments to his employer, UCL Institute of Neurology, for Advisory Committee and/or Consultancy advice in multiple sclerosis studies from Biogen Idec, GlaxoSmithKline, Novartis, Merck, Chugai, Mitsubishi Pharma Europe and Bayer Schering Pharma. He has also received compensation through payments to my employer for performing central MRI analysis of multiple sclerosis trials from GlaxoSmithKline, Biogen Idec, Novartis and Merck. OC is a consultant for Novartis, Biogen-Idec, Genzyme and General Electric, and all the payments are made to the UCL Institute of Neurology. She is an associate editor of Neurology.
Author Contributions F.P., M.J.C., M.C.Y., C.A.M.G.W.-K. and S.O. conceived the experiments. F.P. and M.J.C. conducted the experiments and wrote the paper. M.C.Y., L.R.H. and E.T. performed manual segmentations. H.K., M.C.Y., D.H.M. and O.C. conducted the patient recruitment and assessment. F.P., M.J.C., M.C.Y. and M.D.L. analysed the results. O.C., C.A.M.G.W.-K. and S.O. provided expert guidance. All authors reviewed the manuscript.
References
- Amukotuwa S. A. & Cook M. J. (eds) Spinal disease: neoplastic, degenerative, and infective spinal cord diseases and spinal cord compression (Clinical Gate, 2015). [Google Scholar]
- Losseff N. a. et al. Spinal cord atrophy and disability in multiple sclerosis. A new reproducible and sensitive MRI method with potential to monitor disease progression. Brain 119, 701–708 (1996). [DOI] [PubMed] [Google Scholar]
- Schlaeger R. et al. Spinal cord gray matter atrophy correlates with multiple sclerosis disability. Annals of Neurology 76, 568–580 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlaeger R. et al. Association between thoracic spinal cord gray matter atrophy and disability in multiple sclerosis. JAMA Neurology 72, 897–904 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yiannakas M. C. et al. Feasibility of grey matter and white matter segmentation of the upper cervical cord in vivo: A pilot study with application to magnetisation transfer measurements. NeuroImage 63, 1054–1059 (2012). [DOI] [PubMed] [Google Scholar]
- Kearney H., Miszkiel K., Yiannakas M., Ciccarelli O. & Miller D. A pilot mri study of white and grey matter involvement by multiple sclerosis spinal cord lesions. Multiple Sclerosis and Related Disorders 2, 103–108 (2013). [DOI] [PubMed] [Google Scholar]
- Hickman S., Hadjiprocopis A., Coulon O., Miller D. & Barker G. Cervical spinal cord MTR histogram analysis in multiple sclerosis using a 3D acquisition and a B-spline active surface segmentation technique. Magnetic Resonance Imaging 22, 891–895 (2004). [DOI] [PubMed] [Google Scholar]
- Tench C. R., Morgan P. S. & Constantinescu C. S. Measurement of cervical spinal cord cross-sectional area by mri using edge detection and partial volume correction. Journal of Magnetic Resonance Imaging 21, 197–203 (2005). [DOI] [PubMed] [Google Scholar]
- Zivadinov R. et al. Comparison of three different methods for measurement of cervical cord atrophy in multiple sclerosis. AJNR. American journal of neuroradiology 29, 319–325 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horsfield M. a. et al. Rapid semi-automatic segmentation of the spinal cord from magnetic resonance images: Application in multiple sclerosis. NeuroImage 50, 446–455 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh C., Hamarneh G., Toom M. & Tam R. C. Spinal cord segmentation for volume estimation in healthy and multiple sclerosis subjects using crawlers and minimal paths. Proceedings - 2011 1st IEEE International Conference on Healthcare Informatics, Imaging and Systems Biology, HISB 2011 25–31 (2011).
- Bergo F., Franca M., Chevis C. & Cendes F. Spineseg: A segmentation and measurement tool for evaluation of spinal cord atrophy. In Information Systems and Technologies (CISTI), 7th Iberian Conference on, 1–4 (2012).
- Chen M. et al. Automatic magnetic resonance spinal cord segmentation with topology constraints for variable fields of view. NeuroImage 83, 1051–1062 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Mendili M.-M. et al. Validation of a semiautomated spinal cord segmentation method. Journal of Magnetic Resonance Imaging 41, 454–459 (2015). [DOI] [PubMed] [Google Scholar]
- De Leener B., Taso M., Cohen-Adad J. & Callot V. Segmentation of the human spinal cord. Magnetic Resonance Materials in Physics, Biology and Medicine 29, 125–153 (2016). [DOI] [PubMed] [Google Scholar]
- Asman A. J., Bryan F. W., Smith S. a., Reich D. S. & Landman B. a. Groupwise multi-atlas segmentation of the spinal cord’s internal structure. Medical Image Analysis 18, 460–471 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaiotta C., Freund P., Curt A., Cardoso M. J. & Ashburner J. A probabilistic framework to learn average shaped tissue templates and its application to spinal cord image segmentation. In Proceedings of the 24th Annual Meeting of ISMRM, Singapore, 1449 (ISMRM, 2016).
- Prados F. et al. Fully automated grey and white matter segmentation of the cervical cord in vivo. In Proceedings of the 24th Annual Meeting of ISMRM, Singapore, 1133 (ISMRM, 2016).
- Datta E. et al. Gray matter segmentation of the spinal cord with active contours in mr images. NeuroImage – (2016). In press. [DOI] [PubMed] [Google Scholar]
- Dupont S. M. et al. Fully-integrated framework for the segmentation and registration of the spinal cord white and gray matter. NeuroImage – (2016). In press. [DOI] [PubMed] [Google Scholar]
- El Mendili M.-M. et al. Cervical spinal cord atrophy profile in adult smn1-linked sma. Plos-ONE 11, e0152439 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardoso M. J. et al. STEPS: Similarity and Truth Estimation for Propagated Segmentations and its application to hippocampal segmentation and brain parcelation. Medical Image Analysis 17, 671–684 (2013). [DOI] [PubMed] [Google Scholar]
- Ta V., Giraud R., Collins D. & Coupé P. Optimized PatchMatch for near real time and accurate label fusion. MICCAI, Part III. LNCS 8675, 105–112 (2014). [DOI] [PubMed] [Google Scholar]
- Prados F. et al. Multi-Contrast PatchMatch Algorithm for Multiple Sclerosis Lesion Detection. In ISBI - Longitudinal MS Lesion Segmentation Challenge, 1–2 (2015). [Google Scholar]
- Giraud R. et al. An optimized patchmatch for multi-scale and multi-feature label fusion. NeuroImage 124, Part A, 770–782 (2016). [DOI] [PubMed] [Google Scholar]
- Barnes C., Shechtman E., Golman D. B. & Finkelstein A. The generalized patchmatch correspondence algorithm. ECCV, Part III. LNCS 6313, 29–43 (2010). [Google Scholar]
- Wheeler-Kingshott C. a. & Cohen-Adad J. (eds) Quantitative MRI of the Spinal Cord (Academic Press, San Diego, 2014). [Google Scholar]
- Clarkson M. J. et al. Comparison of phantom and registration scaling corrections using the ADNI cohort. NeuroImage 47, 1506–1513 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung K. K., Ridgway G. R., Ourselin S. & Fox N. C. Consistent multi-time-point brain atrophy estimation from the boundary shift integral. NeuroImage 59, 3995–4005 (2012). [DOI] [PubMed] [Google Scholar]
- Ourselin S., Roche A., Subsol G., Pennec X. & Ayache N. Reconstructing a 3D structure from serial histological sections. Image and vision computing 19, 25–31 (2001). [Google Scholar]
- Modat M. et al. Global image registration using a symmetric block-matching approach. Journal of Medical Imaging 1, 024003 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modat M. et al. Fast free-form deformation using graphics processing units. Computer methods and programs in biomedicine 98, 278–284 (2010). [DOI] [PubMed] [Google Scholar]
- Kearney H. et al. Grey matter involvement by focal cervical spinal cord lesions is associated with progressive multiple sclerosis. Multiple Sclerosis 1–11 (2015). [DOI] [PubMed] [Google Scholar]
- De Leener B., Kadoury S. & Cohen-Adad J. Robust, accurate and fast automatic segmentation of the spinal cord. NeuroImage 98, 528–536 (2014). [DOI] [PubMed] [Google Scholar]
- Brosch T. et al. Deep 3d convolutional encoder networks with shortcuts for multiscale feature integration applied to multiple sclerosis lesion segmentation. IEEE Transactions on Medical Imaging 35, 1229–1239 (2016). [DOI] [PubMed] [Google Scholar]
- Asman A. J., Smith S. a., Reich D. S. & Landman B. a. Robust GM/WM segmentation of the spinal cord with iterative non-local statistical fusion. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 8149 LNCS, 759–767 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]