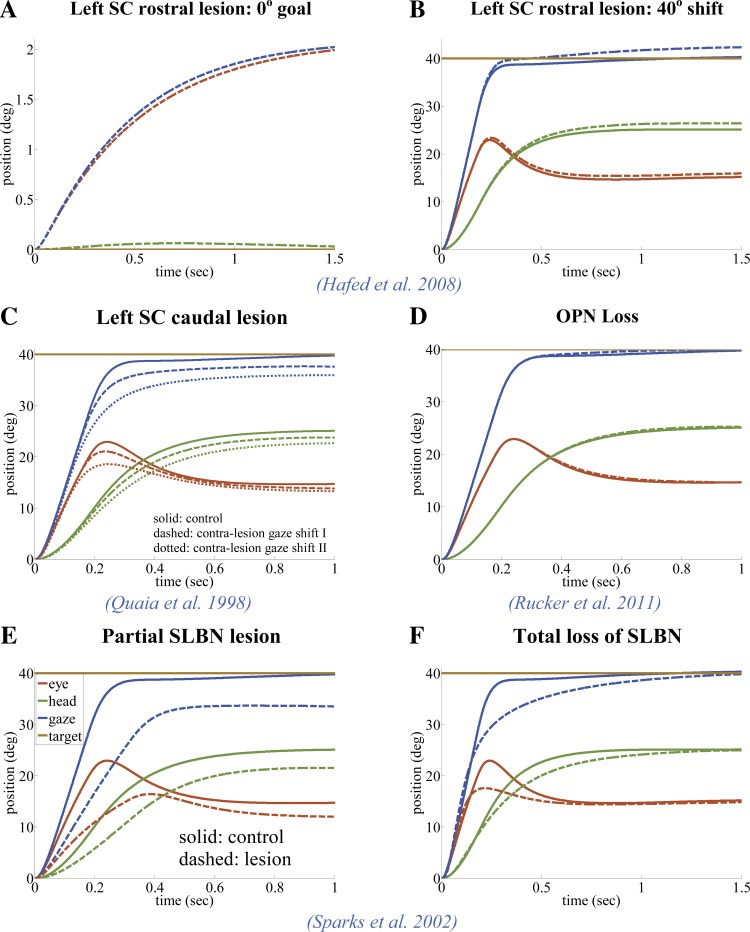
We propose a network-based approach with emphasis on topology to model the gaze orientation system based on sensory-motor fusion and that has implications in other systems (e.g., reaching, posture, and locomotion) of the central nervous system. The same structure with the same parameter set can replicate numerous experimental observations at different levels and contexts with an unprecedented scope, including behavioral and neural responses, lesion and perturbation studies, etc., all without any need for complex trajectory planning or gaze decomposition.
Keywords: gaze shifts, common error feedback, eye-head coordination, vestibular compensation, saccade and fixation, network modeling
Abstract
During gaze shifts, the eyes and head collaborate to rapidly capture a target (saccade) and fixate it. Accordingly, models of gaze shift control should embed both saccadic and fixation modes and a mechanism for switching between them. We demonstrate a model in which the eye and head platforms are driven by a shared gaze error signal. To limit the number of free parameters, we implement a model reduction approach in which steady-state cerebellar effects at each of their projection sites are lumped with the parameter of that site. The model topology is consistent with anatomy and neurophysiology, and can replicate eye-head responses observed in multiple experimental contexts: 1) observed gaze characteristics across species and subjects can emerge from this structure with minor parametric changes; 2) gaze can move to a goal while in the fixation mode; 3) ocular compensation for head perturbations during saccades could rely on vestibular-only cells in the vestibular nuclei with postulated projections to burst neurons; 4) two nonlinearities suffice, i.e., the experimentally-determined mapping of tectoreticular cells onto brain stem targets and the increased recruitment of the head for larger target eccentricities; 5) the effects of initial conditions on eye/head trajectories are due to neural circuit dynamics, not planning; and 6) “compensatory” ocular slow phases exist even after semicircular canal plugging, because of interconnections linking eye-head circuits. Our model structure also simulates classical vestibulo-ocular reflex and pursuit nystagmus, and provides novel neural circuit and behavioral predictions, notably that both eye-head coordination and segmental limb coordination are possible without trajectory planning.
NEW & NOTEWORTHY
We propose a network-based approach with emphasis on topology to model the gaze orientation system based on sensory-motor fusion and that has implications in other systems (e.g., reaching, posture, and locomotion) of the central nervous system. The same structure with the same parameter set can replicate numerous experimental observations at different levels and contexts with an unprecedented scope, including behavioral and neural responses, lesion and perturbation studies, etc., all without any need for complex trajectory planning or gaze decomposition.
the gaze orientation system of the central nervous system (CNS) governs the acquisition and tracking of targets in the visual world. In this work we examine coordination of eyes and head to generate a fast orienting movement of the visual axis (gaze) to a flashed target, followed by fixation or slow corrections. The coordination of these moving platforms is a complex system involving multiple levels of the CNS, including the cortex, cerebellum, brain stem, spinal cord, and muscle feedback. All these levels rely heavily on complex mutual interconnections, and this makes it very difficult to deduce the role of different levels in generating compensatory responses after lesions, functional deficits, or platform perturbations. Models can offer a different viewpoint and suggest new protocols or testing paradigms, but a model requires at least some simplifications that are theoretically and anatomically consistent. Otherwise, a “model” is so complex that it interferes with clear interpretations of functional strategies. We rely on reduction methods: our first network simplification is to embed the effect of cerebellar pathways within the parameter set for brain stem networks, and the role of cortical systems is relegated to selection of a target and its direction. This is acceptable under the assumption that the original network is in a stable “status quo,” not requiring learning. As described in methods, these simplifications highlight that the complex brain stem can support many experimental findings without trajectory planning, but first we summarize basic gaze shift characteristics in human, monkey, and cat; three species in which gaze shift control has been widely studied.
The gaze shift system has two main characteristics: the fast and slow phases of gaze orientation. During the fast or saccadic phase, a rapid gaze shift toward a target is supported by the maximum possible collaboration of all platforms, generally the eyes, head, and trunk all moving in the same direction. Once the target is acquired, the system switches to the slow phase (“gaze fixation” mode) wherein the eyes move in a direction opposite to the head, the compensatory direction, to maintain the visual axis on target and a stable image on the foveae. The classic view holds that the fast phase ends when gaze reaches the target, at which point the slow phase begins. However, this pattern is often violated because the eye can turn around in the orbit, before the end of the gaze saccade (Munoz et al. 1991a; Phillips et al. 1995; Tomlinson and Bahra 1986). As a result, corrective drifts in gaze are often seen postsaccade and are especially prevalent in large gaze shifts (>40°–50°).
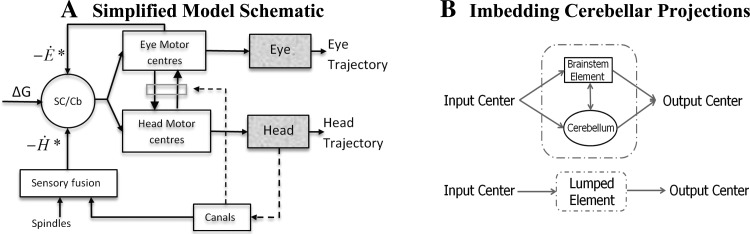
The characteristics of gaze and associated eye-head trajectories have been explained by optimal planning of eye/head contributions (Kardamakis and Moschovakis 2009) or by fitting behavior (Freedman 2008). We offer a simpler hypothesis stating that all known characteristics of head-free gaze shifts emerge with a fixed parameter set, from the brain stem interconnections between eye and head circuits, their sensors and muscles, and the current context (initial conditions, training). In other words, a priori computations and platform assignments are not necessary. This hypothesis is schematically summarized in Fig. 1A. As in our initial model (Galiana and Guitton 1992), two important properties are 1) early fusion of sensory and motor reafference and 2) sharing of these signals between platforms at multiple levels. This results figuratively in the eye and head “pulling” on each other. Our hypothesis is consistent with the anatomical complexity of circuits coordinating eye and head movements (Fig. 2A). Model reduction is applied to this complex system (e.g., Fig. 1B and 2B) to focus on brain stem topology.
Fig. 1.
A gaze controller fusing sensory and reafference signals. A: proposed schematic interconnecting eye and head centers, in response to a flashed target distance (ΔG). B: embedding cerebellar pathways in this reduced gaze controller, i.e., effects of parallel or feedback processes can be reflected in parameter choices for the simplified pathways. See Fig. 2 for more details on bidirectional interactions between cerebellum and brain stem at all levels of gaze control. See glossary for definitions.
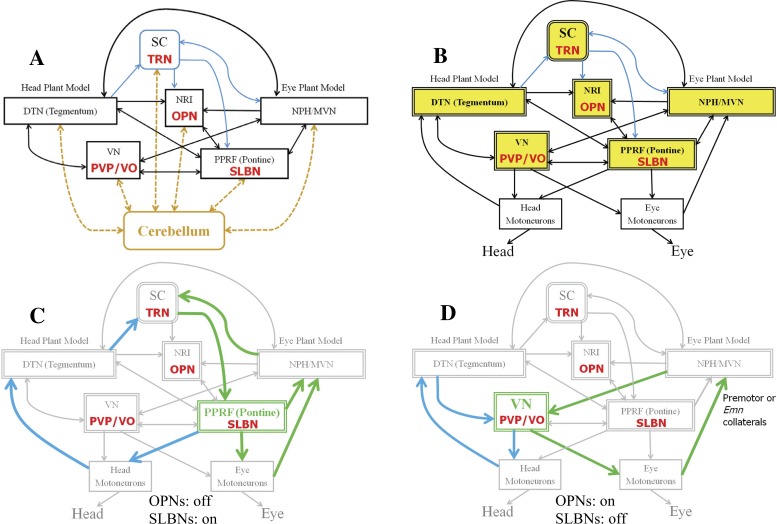
Fig. 2.
Multiple loops for gaze control interconnect eye and head platforms. The stimuli are the vestibular system (through VN) and visual targets (through SC). A: connections with SC are highlighted in blue, and modeled cell types are denoted in red. Dashed cerebellar pathways to/from fastigial nucleus interconnect with all shown sites in the brain stem, especially during saccades. this is consistent with data referred to by Noda et al. (1990) and Optican (2005) but now represented in a different, extended, network topology. B: the cerebellar projections are absorbed into the brain stem structure using appropriate parameters (see text). Each lumped element in B–D (double-lined blocks) embeds both the named site and its local cerebellar projections. C and D: a few loop examples for head (blue) and eye (green) with shared elements, with OPNs off and SLBNs on during the saccadic phase (C) and with OPNs on and SLBNs off during the fixation phase (D). The SC gaze loop in C is also active in D using NPH and DTN (not shown for clarity). See glossary for definitions.
The gaze orientation system has been modeled in numerous studies (Daemi and Crawford 2014; Daye et al. 2014; Dean 1995; Freedman 2001; Galiana et al. 2001; Galiana and Guitton 1992; Guitton et al. 1990; Kardamakis et al. 2010; Laurutis and Robinson 1986; Lefèvre et al. 1992; Miles and Lisberger 1981; Phillips et al. 1995; Prsa and Galiana 2007; Quaia et al. 1999; Robinson 1981a; Tomlinson and Bahra 1986; Zee et al. 1976). A brief comparison of the general characteristics of several models can be found in Table 1 (see a more comprehensive comparison in Table 3). Nevertheless, there is still no consensus on the main principles of gaze control or even on fundamental aspects of a structure that would explain the diversity of experimental eye-head coordination patterns. In addition, prior models focus on the replication of saccadic trajectories and relegate the fixation of a target to “integrators” that hold the current gaze direction. Put another way, a model should provide both vestibular and saccade control such that saccades (orientation) and target fixation are embedded as modes in a single controller. Our hypothesis is that these modes interact because they share pathways; hence, platform responses during a saccade can influence the subsequent slow phase trajectories (and vice versa). Finally, controversy is still strong on the integrity of vestibularly derived compensation during saccades: the classic vestibulo-ocular reflex (VOR) pathway is thought to be restricted to fixation or slow phase intervals when key cells in the vestibular nuclei (VN) are active. Yet, head perturbations in humans (Boulanger et al. 2012), during saccades, can also be associated with compensated gaze shifts of robust accuracy and trajectory (for monkeys, see Cullen et al. 2004; Tomlinson and Bahra 1986).
Table 1.
Selected models for gaze orientation and their general characteristics
| Scope (Replicated Experiments) |
General Features |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Saccade (fast phase) | Fixation (slow phase) | Switching (OPN) | Eye only or eye/head movements | Central responses | Lesions | Initial conditions | Perturbations during gaze shift | Independent head goals | Independent plant controller or shared feedback controller | Black box or Physiological model | Includes ideal integrators or plant models | 1D, 2D, or 3D gaze orientation | Model includes cerebellum |
| Zee et al. (1976) | Y | N | N | E | N | VL | N | N | N | B | II | 1D | N | |
| Miles and Lisberger (1981) | N | Y | N | EH | N | VL | N | N | Y | P&B | 1D | N | ||
| Laurutis and Robinson (1986) | Y | Y | Y | EH | N | None | N | Y | Y | I | P&B | II | 1D | N |
| Lefèvre et al. (1992) | Y | Y | Y | EH | N | VL | N | N | Y | I | P&B | II | 1D | N |
| Galiana and Guitton (1992) | Y | Y | Y | EH | Y | L | Y | N | N | SF | P | PM | 1D | N |
| Dean (1995) | Y | N | N | E | N | VL | N | N | N | B | II | 1D | Y | |
| Phillips et al. (1995) | Y | Y | Y | EH | N | VL | N | N | N | I | P | II | 1D | N |
| Goossens and Van Opstal (1997) | Y | Y | N | EH | N | VL | Y | N | Y | SF | P&B | II | 2D | N |
| Quaia et al. (1999) | Y | Y | N | E | N | L | N | N | N | P | 2D | Y | ||
| Freedman (2001) | Y | Y | N | EH | N | None | N | N | Y | I | B | II | 1D | N |
| Prsa and Galiana (2007) | Y | Y | Y | EH | Y | M | Y | N | N | SF | P | PM | 1D | N |
| Kardamakis et al. (2010) | Y | Y | Y | EH | Y | VL | Y | N | Y | I | P | II | 1D | N |
| Daye et al. (2013) | Y | Y | N | EH | N | VL | Y | N | Y | SF | P&B | II | 2D | Y |
| Daemi and Crawford (2014) | Y | Y | N | EH | N | None | Y | N | Y | I | B | 3D | N | |
OPN, omnipause neurons; Y, yes; N, no; E, eye movement; EH, eye/head movement; VL, very limited lesions; L, limited lesions; M, multiple lesions; I, independent plant controller; SF, shared feedback; B, black box model; P, physiological model; II, ideal integrators; PM, plant models; 1D, 2D, and 3D indicate 1-, 2-, and 3-dimensional.
Table 3.
Comparison of the new SMF model with three earlier approaches
| Shared Gaze Feedback |
Independent Controllers |
||||
|---|---|---|---|---|---|
| Comparison Criterion | SMF | Daye et al. (2013) | Freedman (2008) | Kardamakis et al. (2010) | |
| Behavior | |||||
| 1 | Accuracy (ΔG < OMR) | Y | Y | Y | Y |
| 2 | Accuracy (ΔG > OMR) | Y/E | Y/D | Y/D | |
| 3 | Eye/gaze velocity profiles with single or double peaks | Y/E | Single/D | Y/D | Y/D |
| 4 | Functional fixation without perfect integrators | Y/E | N | N | N |
| 5 | Maximum eye deviation not necessarily aligned with switching (OPN on); early turnaround | Y/E | Y/E | N | N |
| 6 | NL scaling of final eye/head contributions with initial gaze error or target eccentricity | Y/D | N | Y/D | Y/D |
| 7 | Main sequences (size, duration, velocity) | Y/E | Y/D | Y/D | Y/D |
| 8 | Corrective gaze drifts during “fixation” (slow phase) | Y/D | N | N | N |
| 9 | Soft eye position/gaze velocity saturation | Y/D | Y/D | N | N |
| 10 | Nystagmus in passive VOR and visual pursuit | Y/E | N | N | N |
| Cells | |||||
| 11 | OPN switching levels | Y | N | N | Y |
| 12 | Saturation on SLBNs and decay during saccade | Y/E | Y/E | N | N |
| 13 | Modulation of SLBN and VO activity by external head perturbations | Y/D | SLBN/D | N | N |
| 14 | Modulation of PVP in saccade and fixation intervals | Y/D | N | N | N |
| 15 | Eye and head motoneural activity | Y | Y | Y | Y |
| Robust gaze accuracy/trajectory | |||||
| 16 | Robust gaze accuracy with diverse parameter sets and variable eye/head trajectories | Y/E | Y/E | N | N |
| 17 | Robust gaze trajectory with diverse parameter sets and variable eye/head trajectories | Y/E | N | N | N |
| 18 | Unaffected gaze accuracy by head perturbations during saccades | Y/D | Y/E | N | N |
| 19 | Unaffected gaze trajectory by sustained “nonreversing” head perturbations during saccades | Y/E | N | N | N |
| 20 | Robust gaze trajectory for diverse initial conditions (H0, E0, (H0), …) | Y/E | N | E0/D | E0/D |
| 21 | Robust gaze accuracy with independent gaze and head goals | Y/E | Y/E | N | N |
| 22 | Robust gaze trajectory with independent gaze and head goals during the saccadic phase | Y/E | N | N | N |
| Lesions | |||||
| 23 | Gaze shifts without OPNs (no slow mode); identical to control | Y/E | |||
| 24 | Gaze shifts without SLBNs; very slow “saccades” | Y/E | N | N | N |
| 25 | Saccades stop without SC rostral zone | Y/E | N | N | |
| 26 | Gaze shifts overshoot with acute vestibular lesions | Y/E | N | N | N |
For comparisons: Y, yes; N, No; E, emerging property; and D, designated property; field is blank if the criterion was not reported or D (by design) if intentionally selected a priori; see methods for details. The models of Freedman (2008) and Kardamakis et al. (2010) use independent controllers for eye and head after decomposition. ΔG, gaze shift size; OMR, oculomotor range; OPN, omnipause neurons in NRI; SLBN, short-lead burst neuron; VO, vestibular-only cells in VN that respond only to passive head movements; PVP, position-vestibular-pause cells in VN that carry vestibular and eye position signals (Fuchs et al. 2005; Roy and Cullen 2004); E0 and H0, initial eye and head position; ˙H0, initial head velocity.
It will be shown that the organization of neural networks controlling eye-head coordination merges many sensory signals during gaze shifts and so can itself coordinate eye and head contributions in an autonomous or reflex fashion. Thus we name our modeling approach sensory-motor fusion (SMF). In this scheme, trajectory planning is unnecessary once the circuits are tuned by learning. Finally, we will demonstrate that a shared gaze controller can still accommodate separate head goals in space, by adding a simple “head offset” (see Fig. 3) to head motor signals, without changing gaze shift accuracy or trajectory. Prior models do provide gaze shift accuracy with independent head goals, but at the cost of a modified gaze trajectory, since the head contribution changes during a saccade without vestibular compensation (Freedman 2008). The driving source for this head offset command could be from the superior colliculus (SC; Cowie and Robinson 1994; Walton et al. 2007) or other centers (Walton et al. 2008).
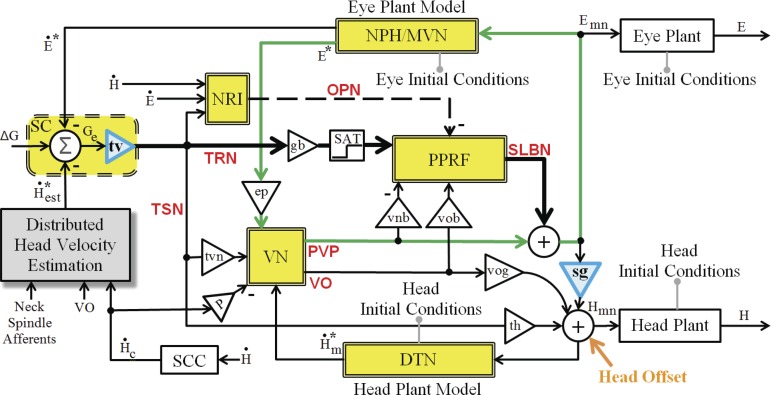
Fig. 3.
Schematic of the SMF model implemented in MATLAB/Simulink, incorporating all anatomical loops in Fig. 2 (e.g., the classical VOR in green). Each double-lined yellow block represents both the named site and its local cerebellar projections. Two blue triangles are nonlinear gain fields discussed in methods. The “head offset” (bottom right) represents an additional input to the head system used only when spatial gaze and head goals are presented concurrently; this offset is 0 in default gaze shifts. Separate head goals do not change parameters in the rest of the circuit (see parameters in Table 2). See glossary for definitions.
We next summarize current controversies in eye-head coordination, followed by the model development and simulation results that match experimental reports at both behavioral and key cellular levels.
Current Views of Gaze Control: Requirements for a Valid Model
There are several points of debate regarding the coordination of eyes and head that are briefly summarized below, and the directions selected in our SMF model are indicated. Justification for the implementation of these choices, based on anatomy and physiology, is provided in methods.
Shared or dedicated motor signals for eye and head platforms (eye and head)?
The eye (i.e., conjugate eye) and head interact through sensory and premotor coupling so that for the same gaze shift, eye or gaze can move with or against the head without loss of gaze accuracy. For example, before the end of a gaze shift, the eye often reaches its maximum deviation in the orbit and rotates in a direction opposite to the gaze and head movements (Guitton and Volle 1987; Laurutis and Robinson 1986; Phillips et al. 1995; Tomlinson and Bahra 1986). Moreover, with specific sets of platform initial orientations, the eye can move in a direction opposite to the gaze and head movements during the entire gaze shift (Boulanger et al. 2012). Such observations have led to suggestions (and models) that the eye and the head must have separate goals and dedicated motor drives during each gaze shift (Goossens and Van Opstal 1997; Phillips et al. 1995); in this view, a common drive is expected to result in similarly directed responses from the eye and head platforms. We argue instead that different eye and head trajectories can indeed arise from a shared drive, because of different platform dynamics, initial conditions, and instructions to subjects. For example, if instructed to move fast, a subject could raise the level of premotor loops by increasing sensitivity to premotor commands (Galiana and Guitton 1992).
Gaze feedback control or platform-based error feedback?
The use of negative feedback in a system can increase stability, increase sensitivity to the input of the system, reduce sensitivity to parameter variability, and reduce the impact of internal or external noise (Kuo and Golnaraghi 2003). In addition, a feedback system does not require prior trajectory planning or gaze decomposition. In fact, the fast and slow phases of gaze responses have impressive robustness to external perturbations (Boulanger et al. 2012; Guitton and Volle 1987; Sylvestre and Cullen 2006; Tomlinson and Bahra 1986). Accordingly, we previously proposed that the gaze control system is structured as a feedback loop, closed on a gaze error signal (Galiana and Guitton 1992; Guitton et al. 1990; Prsa and Galiana 2007). There is strong recent support for gaze feedback control in head-free conditions, since both gaze shift accuracy and trajectory are preserved during long-duration head perturbations that even outlast the gaze shift (Boulanger et al. 2012). Also, gaze accuracy (but not trajectory) is maintained despite passive opposing head perturbations during head fixed-on-body gaze saccades (Daye et al. 2015; Sylvestre and Cullen 2006). Moreover, the study of Choi and Guitton (2009) in monkey supports the shared gaze feedback scheme: when the head is fully braked during a gaze shift, the activity on the SC map responds at ∼10-ms latency to brake onset and quickly reorganizes itself to be centered on the remaining gaze position error, not the error of an individual platform.
Despite the elegance of gaze feedback control, some investigators prefer the concept of independent eye and head control (Freedman 2001; Kardamakis and Moschovakis 2009; Phillips et al. 1995). For example, Kardamakis et al. (2010) have argued that a gaze feedback controller is unlikely to be a realistic structure in the CNS, since the specific gaze feedback model they tested in their experiments did not replicate experimentally observed aspects of gaze shifts: namely, “double peaks” on eye and gaze velocity in monkey during large gaze shifts and/or blinks (Cullen and Guitton 1997; Freedman 2001; Gandhi 2012). Independent controller models have been proposed to replicate this double-peak phenomenon (Freedman 2001; Kardamakis et al. 2010), using a priori decomposition of goals for each platform or optimal design of trajectory profiles. We will show that single- or double-peaked velocity profiles can arise in the brain stem network, by simply varying a few projection weights to and from VN; this effect is most visible for larger gaze shifts. This phenomenon can be seen in the work of Gandhi (2012), where it is suggested that the appearance of double-peak velocity profiles in monkey was the result of blinks during gaze shifts. Although some correlation exists between blinks and double peaks, causality has not been proved (i.e., blinks causing double peaks or both events being the result of another cause). For example, in the same paper it was shown that in head-free conditions, the probability of double peaks in gaze velocity is much higher for larger gaze shifts and/or larger head velocities. Also, with or without blinks, in some subjects double peaks appear only when the head is free (see Gandhi 2012). Moreover, Evinger et al. (1994) suggested a reciprocal relationship between blinking and saccadic gaze velocity, because of the shared command for saccadic gaze shifts and the eyelid muscle. The exact mechanisms for gaze shift and blink interactions are outside the scope of this article. However, whether double peaks are a design characteristic for optimal control of gaze shifts (Kardamakis and Moschovakis 2009) or are a side effect of blinking, we will show that they are feasible within the brain stem network.
Accounting for initial conditions: simple internal circuit dynamics or adaptive computation?
For gaze shifts of the same amplitude and direction, the eye and head trajectories change their spatiotemporal profiles depending on the initial conditions (position, velocity, and acceleration) of the participating platforms, even if their sum (gaze) starts and ends at identical locations (Freedman 2008). As a result, a realistic model for gaze orientation should also accommodate variable initial conditions. In the independent controller schemes, the handling of initial conditions requires a new computation for trajectory planning of each gaze shift and for each set of initial conditions, i.e., gaze error decomposition to replicate the experimental results (Freedman 2001). In contrast, a feedback controller based on gaze error provides a convenient solution: feedback ensures the acquisition of the target, whereas initial conditions simply introduce decaying components that change platform trajectories but not the final goal. We suggest that the effect of initial conditions is an emerging property of circuit dynamics in the brain stem.
Gaze shift variability among species: common circuit or species specific?
For a given gaze shift vector, the amplitude and velocity of the eye and head platforms can vary among species. For example, cats and squirrel monkeys have an oculomotor range limited to ∼20° from central position (Cullen et al. 1991), compared with ∼50° in macaque monkeys (Munoz and Wurtz 1995; Russo and Bruce 1996) and humans (Fuller 1992; Guitton and Volle 1987). Furthermore, two subjects in a given species may do the same task with identical initial conditions and gaze shift amplitude but with different eye and head contributions. Similarly, a given subject can produce the same gaze shift vector differently in two trials due to fatigue, task instructions on speed or accuracy, etc. (Guitton and Volle 1987; Stahl 1999). In a feedback controller approach, the structure ensures gaze accuracy despite parametric changes and noise in the system that might affect dynamics (time constants). Thus variations in component trajectories can be replicated simply by adding parametric variability related to context. Shared gaze error feedback can easily embed subject/species variability during eye-head coordination.
Nonlinear sensitivity to shared gaze error or decomposition of eye and head goals?
Many nonlinearities exist in neural firings and platform responses during gaze shifts.
behavior.
The relative contributions of the eye and head change systematically with the size of an intended gaze shift. This holds whether the contributions are measured at the end of the gaze saccade or at the end of the fixation period, when all plants are stable (stop moving). For smaller gaze shifts (<20°), most of the task (after the fixation interval) is done by the eye, whereas for large gaze shifts (>50–60°), most is done by the head (Daye et al. 2014; Freedman 2008). In a multiplant “linear” system, the ratio of steady-state plant contributions should be constant across all output amplitudes, but this is not the case in gaze control. Kardamakis and Moschovakis (2009) demonstrated that a nonlinear pattern of contributions is consistent with optimally derived subgoals for eyes and head that minimize energy and saccade duration; they proposed that the gaze error is neurally decomposed for independent eye and head controllers based on minimal energy (see also Freedman 2001, 2008). With the use of decomposition, the nonlinear (NL) behavior related to amplitude is relegated to the computation of subgoals, whereas the platform trajectories remain linearly related to their subgoal with fixed time constants. However, another sign of nonlinearity is that trajectory time constants also depend on the amplitude of a gaze shift. In a linear system, normalizing platform trajectories by the size of the gaze shift should produce overlapping curves for each platform (Robinson 1964). Instead, experimental trajectories do not overlap after normalization, indicating a highly NL behavior, including variable time constants with the gaze shift size. Again, models using decomposition can replicate this by scaling the loop gains of independent eye and head subcontrollers responding to assigned goals. Yet, a gaze error shared by all platforms in our controller can replicate such gaze shifts and avoid the need for trajectory planning, so long as the distribution of gaze error to platforms is itself NL; there is evidence for such NL weighting of premotor signals.
neural activities supporting nl gaze dynamics.
We focus here on two classes of burst neurons (Horn 2006; Scudder et al. 1996a, 1996b): tectoreticular neurons (TRN; a type of long-lead burst neuron, or LLBN) and short-lead burst neurons (SLBN) (see Implementation and Supporting Anatomy and Physiology). TRNs and SLBNs fire strongly during saccades and gaze shifts, dominating the saccadic drive; TRNs also fire weakly during slow phases (Missal et al. 1996; Scudder et al. 1996a). Rostral-to-caudal sites in the SC encode small-to-large saccades, respectively. More importantly, there is a NL distribution of gaze error from TRNs in the SC visuomotor map to SLBNs in the reticular formation driving eye saccades (Grantyn et al. 2002; Izawa et al. 1999; Moschovakis 1996; Paré et al. 1994; Roucoux et al. 1980). TRN collaterals also project to head motor centers in cat (Grantyn et al. 1987; Izawa et al. 1999) and in monkey (Scudder et al. 1996b). The direct tectospinal neural (TSN) projections to head motor centers are much weaker in monkeys compared with cats (Nudo and Masterton 1989). Thus it has been suggested that in monkeys, the dominant pathway to head centers is the indirect tectal projection through reticulospinal neurons (Scudder et al. 1996b). Moreover, stimulation of the monkey SC has been shown to result in neck muscle responses (Corneil et al. 2002a, 2002b), even when the eye is not moving. As will be shown, a NL gain field from SC to SLBNs, driving both eye and head motor centers, can support the NL gaze shift properties mentioned above without decomposition. Additionally, SLBNs are also NL, with a soft saturation level on larger activities (Scudder et al. 2002), together with a silent period during slow phases. Experimental results show that beyond a certain gaze shift amplitude, the contributing eye deviation saturates or even reverses direction before saccade end (Boulanger et al. 2012; Guitton 1992; Guitton and Volle 1987).
Compensation for head perturbations at all times or only during slow phases?
The VOR, in its classical interpretation, is an ocular “slow-phase” response that compensates for head movements when gaze is close to a target of interest. The gain of the VOR during gaze shifts has been tested repeatedly with brief impulsive head perturbations; the results were interpreted as inactivation of the VOR during saccades with gradual reactivation near end of saccade (Lefèvre et al. 1992; Roy and Cullen 1998). This approach is used in several models to allow eye reversal in the head near the end of large gaze shifts, which they consider as the VOR (Daye et al. 2014; Goossens and Van Opstal 1997; Lefèvre et al. 1992). This concept is consistent with the fact that position-vestibular-pause (PVP) neurons in the VN are usually (but not always) inhibited during saccades; they can exhibit slow recovery of activity near the end of gaze shifts and are the main carrier of vestibular information to ocular motoneurons during slow phases (Roy and Cullen 1998). We show below that the eye turnarounds can occur even without an active VOR [with omnipause neurons (OPNs) off]. In addition, recent evidence suggests the existence of at least some compensation for head perturbation even during early saccadic intervals in gaze shifts (Boulanger et al. 2012; Choi and Guitton 2009; Sylvestre and Cullen 2006). While this does not fall under the classical view of VOR function, it is indeed a VOR since its impact on the eye trajectory can be fully compensatory (preserve gaze trajectory) when perturbations are applied to the head movement: such corrections appear on SLBN activity within the 6- to 7-ms delays seen in classical VOR responses (Sylvestre and Cullen 2006). Thus a challenge in modeling gaze orientation is to embed short-latency compensations during gaze shifts (i.e., saccades and fast phases). Whereas PVP cells are essentially inactive during fast phases, there are other cells in the VN that remain active during all head movements and during saccades: for example, vestibular-only (VO) cells in the VN modulate during passive head rotations, but not if the same head movement is actively performed (Cullen et al. 2011; Cullen and Roy 2004; McCrea et al. 1999; Roy and Cullen 2004). In the words of Cullen and colleagues, VO cells “prefer” the unexpected components of head movements and are active during both slow and fast phases. Fuchs et al. (2005) have also suggested the possible presence of “other vestibulo-oculomotor pathways” that are not gated off like PVPs during gaze shifts. They consider partial PVPs unlikely to be the sole source of vestibular compensation during the saccadic phase. We propose that the VO neurons support this alternative vestibulo-ocular pathway that is active even during the saccadic phase. Hence, VO cells are included in the SMF model as a likely substrate for compensation of head perturbations at all times.
METHODS
SMF stands for sensory-motor fusion in the circuits coordinating eye and head trajectories: i.e., visual, vestibular, and proprioceptive signals are intermingled with reafferent motor signals at many levels. The SMF model presented in this article is a shared-drive nonlinear feedback controller that has evolved from our prior model for gaze orientation (Prsa and Galiana 2007). As shown in Fig. 1A, the gaze motor error projects to both eye and head motor centers, with “interconnections” between these centers (Galiana and Guitton 1992; Guitton et al. 1990). Note that such interconnections are crucial to the results presented below, and the projections supporting these interconnections will be introduced later.
Brain Stem Focus by Model Reduction
The cerebellum (Cb) is known to be essential for normal motor performance. In the case of eye movements, the caudal fastigial nuclei (cFN) have been suggested to provide additional directional drive to the eyes, keep track of ongoing gaze shift toward the target, and interact with the SC to force saccade termination (reviews in Dean 1995; Optican 2005; Quaia et al. 1999). However, it is not practical to include such a massive network (Fig. 2A) in an already complex brain stem and expect to gain new insight. This would result in unreliable predictions, since the experimental data are too sparse to properly define a distributed parameter set in this complex topology. Yet, this large connectivity must be considered during network reduction. An example of this is shown in Fig. 1B: two pathways acting in parallel but interconnected can be merged into one combined process (at the parameter level) in the desired simpler structure.
The large number of reciprocal connections between Cb and brain stem sites creates loops that support each other and provide high redundancy (Fig. 2A). By absorbing the Cb connections into the brain stem sites, the circuit is simplified (Fig. 2B) while known loops interconnecting eye and head systems are preserved (Fig. 2, C and D). The SMF model in Fig. 3 illustrates the “reduced” form of the larger network in MATLAB/Simulink: it is used in all simulated protocols to explore brain stem mechanisms. The focus is on the main components for eye-head coordination in the superior colliculi (SC), paramedian pontine reticular formation (PPRF), vestibular nuclei (VN), nucleus prepositus hypoglossi (NPH), and dorsal tegmental nuclei (DTN). Recall that the parameters in this reduced model embed Cb effects, because the simulations reproduce the behavioral and cell responses when Cb contributions are intact. Any lesions in loops included explicitly or implicitly in a model require a rational change in parameters, based on known anatomy or neurophysiology. Each case is described in results. Despite model reduction, many observations are replicated; e.g., the timing of OPN activities and near-normal gaze shifts and fixation despite lesions at key sites. We next outline the interpretation of data for the deduced SMF model structure.
Implementation and Supporting Anatomy and Physiology
SC efferent signals.
The use of a gaze error signal and the effect of head perturbations (e.g., Choi and Guitton 2009) can be explored in our reduced model. The SC receives the “desired” gaze shift amplitude (ΔG) at the map location of its activity peak; it also provides a dynamically updated gaze error signal (Choi and Guitton 2009) according to spatially filtered estimates of eye and head signals (Abrahams and Rose 1975; McCrea and Horn 2006; Nagy and Corneil 2010). In the model, collicular map signals are first smoothed with a time constant of ∼10 ms to represent spatial filtering effects and observed delays (Goossens and Van Opstal 2006; Munoz and Wurtz 1995; Paré and Guitton 1994) with response tolerance to map delays (Choi and Guitton 2009; see SC afferents: efference copies of expected platform contributions). Since we are dealing with gaze shifts in one dimension (horizontal, 1-D), the typical two-dimensional (2-D) summation over the map (Badler and Keller 2002; Katnani et al. 2012; Sparks 1988; Van Gisbergen et al. 1987) then reduces to a population average along the rostrocaudal axis of the map:
| (1) |
where an is the map activity on the n-th cell (on the rostrocaudal line in this case) and wn is the downstream SC projection weight associated with that cell. During the gaze shift, at each moment, the an values are updated through feedback from plants, whereas wn values are constant. We can define
| (2) |
as the center of SC activity at each moment in time, which corresponds to the ongoing (remaining) gaze error Ge. Using this definition, we can simplify the SC population projection as
| (3) |
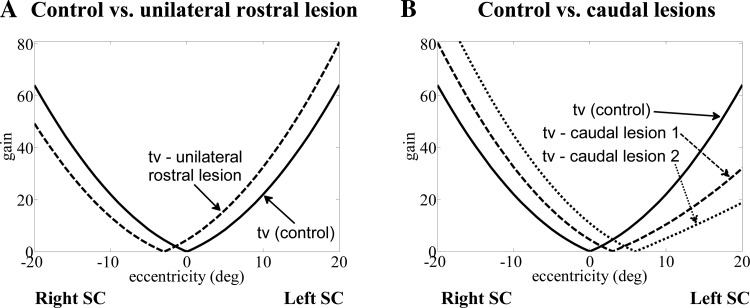
where tv is a NL projection function that changes depending on the location of the SC center of activity Ge. In other words, tv(Ge) represents the net downstream SC projection from the combined wn, when the center of SC activity is at map location n, correlated with the remaining error Ge.
Hence, in the reduced model, the NL gain field tv(Ge) embodies the reported NL distribution of projections from SC to TRN (Büttner-Ennever et al. 1999; Grantyn et al. 2002; Hafed et al. 2008); it is tuned to have increasing amplitude from small to large eccentricities (in the SC rostrocaudal direction). Thus the activity of TRNs is given by
| (4) |
The tv projection field merges SC activation levels with efferent projection strengths to TRNs; thus it is possible to change gaze shift velocities (by scaling the tv function) without changing their target (ΔG = initial Ge). The TRNs drive both the eye and head systems in response to a flashed target. TRN cells also project to the OPNs in the nucleus raphe interpositus (NRI) (Büttner-Ennever et al. 1999; Chimoto et al. 1996; Horn 2006; Keller 1979; Paré and Guitton 1994, 1998) and to LLBNs/SLBNs in the brain stem (Altman and Carpenter 1961; Horn 2006; Kawamura et al. 1974; May 2006; Raybourn and Keller 1977). In addition, TRNs send collaterals to the NPH in its boundary with VN (May 2006; McCrea and Horn 2006) and to neck motoneurons (Mn) (Corneil et al. 2002a, 2002b; Munoz and Guitton 1985; Murray and Coulter 1982; Olivier et al. 1994). We interpret the former NPH targets as interneurons to VN and so use a direct weighted connection (tvn) from TRN to VN. This does not alter simulation results, since the alternative side projection via NPH impinges on the same NPH-VN loop system.
SC afferents: efference copies of expected platform contributions (NPH/MVN and DTN).
As early as the 1950s, the use of efference copies or internal plant models was proposed to provide neural activity related to self-generated movement (Sperry 1950; Von Holst and Mittelstaedt 1950). For the gaze orientation system, the NPH, which serves as a main source of afferents to the SC, has been reported to receive afferents from CNS centers that project to the extraocular motor nuclei and the cervical spinal cord (McCrea and Horn 2006). In the SMF model, we embed the dynamics of the real plants into their internal models and drive these “ideal” internal models with motoneuron (Mn) reafference. Mixed velocity and position signals related to eye movements are found throughout the neural circuits. In particular, some neurons in the NPH that interconnect with those in the medial VN have discharges proportional to eye position/velocity in the orbit, thereby encoding an efference copy of eye state (Büttner and Büttner-Ennever 2006; Delgado-Garcia et al. 1989; Lopez-Barneo et al. 1982). Thus NPH projections to SC reported by McCrea and Horn (2006) are used to provide feedback of ongoing eye velocity to the SC map. In addition, cell activities in a subpopulation of neurons in the DTN have been shown to track changes in head velocity in the rat (Sharp et al. 2001), vestibular afferents project to SC (Maeda et al. 1978), and some cells in NPH also modulate with head movements (Baker and Berthoz 1975; Blanks et al. 1977; Stechison et al. 1985). Moreover, there is also evidence of head proprioceptive afferents to the SC (Nagy and Corneil 2010). Hence, instead of a discrete site (as NPH for eye) for the source of head platform information, we propose a distributed site (distributed head velocity estimation) weighing signals from many sources to provide an optimal estimate of head velocity to the SC (see Head velocity estimation). Combining these two sources (for eye and head signals) results in dynamic updating of gaze error on the SC map from its initial value (ΔG in Fig. 3). Note that in the present study, we do not address the controversy concerning moving hills on the SC map and whether activity should reach the rostral zone to stop a saccade. There is no explicit spatiotemporal map for the SC here (this is explained in more detail in discussion, Moving SC hill vs. decaying SC hill).
Vestibular nuclei.
A group of neurons in the VN called PVP neurons are key components driving the slow phase of the VOR but have weak or no activity during contralateral saccades (Fuchs et al. 2005; Highstein and Holstein 2006): they combine canal signals (SCC) with eye efference copies (E*) from NPH/MVN and are excitatory to contralateral abducens Mn. They are (fully or partially) silenced during ipsilateral saccades by inhibitory SLBNs on the same side (Fuchs et al. 2005; Hikosaka et al. 1980). For the sake of simplicity, the PVP neurons in the SMF model represent the net effect of all PVPs (partial or full pause PVPs with different position and velocity sensitivities) without explicitly segregating them. Another group of VN neurons are VO neurons that distinguish the passive component (which they encode) from the active component of head movements (Cullen et al. 2011; Roy and Cullen 2004). VO cells project to neck Mn (Boyle et al. 1996; McCrea et al. 1999). We predict, on the basis of simulations, that VO cells also project to SLBNs. They are a likely substrate for fast vestibular compensation of head perturbations during saccades by causing short-delay changes in SLBN activity (Sylvestre and Cullen 2006). The need for this type of projection is discussed later, but it is motivated by the observations of Boulanger et al. (2012) that gaze shift trajectories (not just accuracy) can remain intact when the head is perturbed during saccades.
Paramedian pontine reticular formation.
The PPRF contains the burst neurons (SLBNs) needed for saccade generation (Figs. 2 and 3). SLBNs are driven (Fig. 3) by the NL gaze error signal from TRNs (see references cited in SC efferent signals above), interneurons in the VN (e.g., burster-driving neurons, BDNs) carrying vestibular signals (Hikosaka et al. 1980; Ohki et al. 1988), and VO cells extracting the passive component of head velocity (hypothesized projection). The SLBN pool excites the ipsilateral abducens nucleus. Mirror connections from inhibitory SLBNs project to the opposite abducens. Note that Fig. 3 only illustrates the net effect of inhibitory and excitatory connections, because this schema shows the collapsed overall effect of the left and right sides of the brain. Saccade-related bursts of activity are also found in the electromyography (EMG) of neck muscles rotating the head during eye saccades (Andre-Deshays et al. 1988; Corneil et al. 2002a, 2002b), and some SLBNs have collaterals to drive both the eye and head (Grantyn et al. 1987; Izawa et al. 1999). Thus SLBN cells in the model project directly to the eye and indirectly to the head via gain field sg, thereby coordinating a fast gaze shift to the target.
Omnipause neurons of the nucleus raphe interpositus.
In control-systems theory, the gaze orientation system is a so-called “hybrid” system; i.e., it switches between two phases (fast, slow) with different dynamics, and the OPNs serve as the switching mechanism between the two. The OPNs are inhibitory neurons that fire tonically during fixation or slow gaze movements to suppress SLBN activity; they pause during gaze shifts (Horn 2006; Paré and Guitton 1998), thereby releasing the SLBNs. OPNs in the model monitor gaze error and eye/head states to switch saccades on (OPNs off) or off (OPNs on) (see review, Prsa and Galiana 2007). As argued below, OPN activity is the most reliable signal for defining fast phase (saccade) intervals, and it is used to switch modes in the model. It is worth noting that the suppression and activation intervals of the OPNs are generally aligned with those of the PVPs. However, the major difference between the PVP and OPN arises not from their discharge timing, but rather from their discharge modulation with respect to the ongoing gaze shift and fixation: the PVP discharge is highly modulated by the current head velocity and eye position (Fuchs et al. 2005), whereas the OPN response has little modulation and generally jumps between two fixed on/off states (Evinger et al. 1982).
External head plant and eye plant dynamics.
Both plants are second-order systems: two equal time constants of 300 ms for the head (critically damped), and time constants of 200 and 30 ms for the eye (Prsa and Galiana 2007; Robinson 1981b) (see equations in appendix).
Semicircular canals.
The vestibular sensors are represented with high-pass filters of head velocity, with a time constant of ∼15 s (including velocity storage; Raphan et al. 1979; Robinson 1981a). The SCC are assumed to be linear (no saturations). If we were to include canal NL sensitivities, this would simply require slight changes in the shapes of the NL gain fields (sg, tv) to preserve the trajectory characteristics described in results (as was done for vergence context in the binocular VOR by Ranjbaran Hesarmaskan and Galiana 2013).
NL plant contributions: field gain.
The drive to the head includes a projection from SLBN neurons and from VN cells through a gain field, sg (Fig. 3). We use a NL gain to replicate larger head contributions for more eccentric target locations, throughout gaze shifts (saccade and fixation intervals), as reported by Freedman (2008). When using neurons, this could be implemented by a large population of units, recruited by target eccentricity.
Head velocity estimation.
An accurate head velocity estimate conveyed to the SC is likely derived from weighted combinations of canal signals (SCC), internal head model predictions VO cells, and/or neck spindle afferents even during perturbations; i.e., this estimate need not be limited by canal dynamics (Abrahams and Rose 1975; Maeda et al. 1978; Nagy and Corneil 2010). The combination is expected to be idiosyncratic, varying with subjects and species. A possible site for the fusion of vestibular and neck afferent inputs projecting to the SC is the NPH (McCrea and Horn 2006; Stechison et al. 1985), although more recent reports suggest insignificant head movement-related outputs from the NPH, at least in rhesus monkeys (Dale and Cullen 2013). From the modeling standpoint, this head velocity feedback to the SC is presumed accurate and is simply set to the concurrent behavioral head velocity, regardless of the likely distributed location for its estimation.
Most of the major elements mentioned above are either original to this modeling work (e.g., integration of the NL SC efferent signals, VO neurons, and their projections, NL plant contributions, and head velocity estimation block) or significantly upgraded from the Prsa-Galiana model (Prsa and Galiana 2007). The most significant novelties are the two NL gain fields (tv and sg), the addition of VO cells, and predicted connections from VO to SLBN cells: these allow a variety of behavioral and neural responses simultaneously in a single structure. The results also provide insight into the nonlinear aspects of gaze coordination and how that can impact data analysis.
Model Structure and Parameter Sets
The MATLAB/Simulink implementation of the SMF model (Fig. 3) represents the net effect of a bilateral network with bilateral projections onto Mn. Accordingly, cell sensitivities to motion direction are applied with sign changes. For example, excitatory SLBN bursts during saccades will be positive for rightward gaze shifts (ipsilateral SLBN) and negative for leftward gaze shifts (contralateral SLBN). Excitatory or inhibitory projections are used for the modeled cell types, according to their net effect on the movement direction (right, positive; left, negative). All projections in the schematic are considered excitatory unless denoted with a minus sign, for cells that are inhibitory to their target. The classical VOR pathway is highlighted in green in Fig. 3 for comparison with Fig. 2D. The model contains both localized anatomical blocks (e.g., PPRF and VN) and distributed structures (e.g., distributed head velocity estimation block), as described above.
A glossary of anatomical sites, neural cell types and model parameters is provided in the Introduction. Equations linking responses at different sites in the model and transfer functions for eye and head plants are provided in appendix: model components and equations, with a brief analysis of expected steady states during fixation for platform contributions. The circuit creates internal estimates of platform movements and is consistent with the arguments presented above. Initial conditions are embedded in the eye and head plants and their associated “models,” as they would be in the biological case.
Simulation conditions.
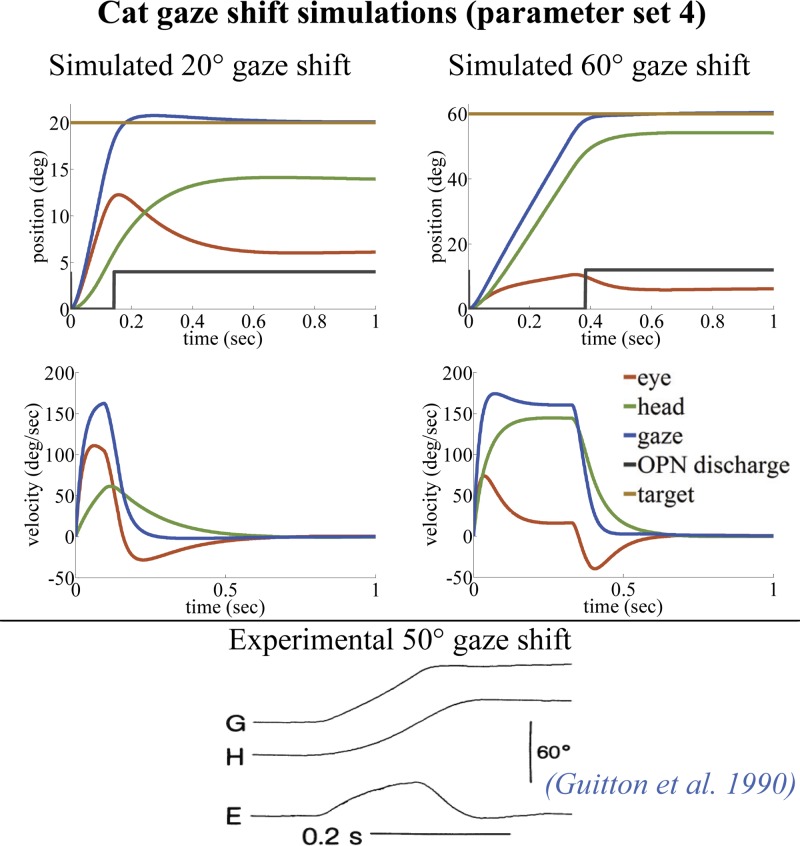
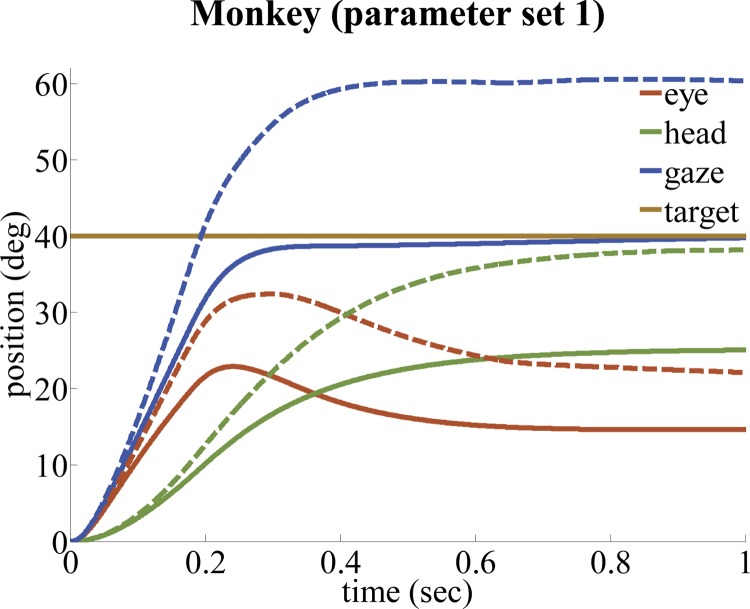
The parameter sets for simulations were chosen on the basis of the desired general behavioral characteristics seen in primate or cat (Table 2). Minor changes in parameters are sufficient for the following cases: parameter set 1 provides slower single-peak velocity profiles during gaze shifts, typically seen in humans or untrained monkeys, in the presence of head restraints and/or random perturbations (Boulanger et al. 2012; Goossens and Van Opstal 1997; Guitton and Volle 1987); parameter set 2 is included to replicate faster, double-peak eye velocities in large gaze shifts seen in humans and monkeys without restraints (no helmet or head/bite bar; Freedman 2001; Freedman and Sparks 1997; Roy and Cullen 1998); parameter set 3 allows for very fast primate gaze shifts without double peaks (Gandhi 2012); and parameter set 4 is provided as a guide for another species that relies more on its head for gaze shifting; it is tuned for cat gaze shifts by emphasizing its larger head contribution over the eye, given the cat's limited oculomotor range (OMR) (Guitton et al. 1984, 1990).
Table 2.
Parameter sets used across protocols and species
| Primate |
Cat | |||
|---|---|---|---|---|
| Default parameter set 1 Single peak, low speeds | Parameter set 2 Double peak, mid speeds | Parameter set 3 Single peak, high speeds | Parameter set 4 Single peak, smaller eye range | |
| *tv(x) | sign(x)(0.1|x|2 + 1.2|x|) | sign(x)(0.6|x|2 + 0.5|x|) | sign(x)(0.01|x|2 + 6|x|) | sign(x)(0.01|x|2 + 4|x|) |
| *SAT | 40 | 40 | 100 | 35 |
| *P | Fast phase: 2 | Fast phase: 2.3 | Fast phase: 2.7 | Fast phase: 2 |
| Slow phase: 0.28 | Slow phase: 0.25 | Slow phase: 0.27 | Slow phase: 0.22 | |
| *vnb | 0.02 | 0.05 | 0.02 | 0.02 |
| Kept constant in all cases: | ||||
| sg(x) | 2.2(3.31 × 10−7|x|3 + 2.65 × 10−4|x|2 + 8.4 × 10−3|x|) | −3.17 × 10−5|x|3 + 2.9 × 10−3|x|2 + 7.1 × 10−3|x| | ||
| tvn | 0.4 | |||
| gb | 1 | |||
| th | 0.05 | |||
| SCTc | 10 ms | |||
| vog | Type I: 0.1 inhibitory; Type II: 0.6 excitatory | |||
| vob | 0.35 | |||
| ep | Fast phase: 11; Slow phase: 1.31 | |||
| eg | Fast phase: 0.09; Slow phase: 0.759 | |||
The first four parameters (marked with an asterisk) vary mildly to generate different characteristics between the given parameter sets. Parameter set 1 provides slower single-peak velocity profiles during gaze shifts, typically seen in humans or untrained monkey, in the presence of head restraints and/or random perturbations (Boulanger et al. 2012; Goossens and Van Opstal 1997; Guitton and Volle 1987). In this case, large targets cause a soft saturation plateau for eye position (typical monkey or human trajectories). Parameter set 2 results in double peaks in velocity for larger target eccentricities in both gaze and eye trajectories (Freedman 2001; Freedman and Sparks 1997; Roy and Cullen 1998). Parameter set 3 replicates single-peak gaze velocities with high speeds reported by Gandhi (2012). Parameter set 4 provides an example of species-specific trends: it is similar to the default except that the forward gain tv is enhanced for faster gaze shifts and the head gain field sg is increased to emphasize the head and limit eye deviations (as in the cat; Guitton et al. 1984, 1990). Refer to the model in Fig. 3, to the glossary in the Introduction for definitions and to the appendix for the role of parameters in controller signals.
There are only 13 parameters/functions to reproduce the experimental data from contexts, with minor changes for each species. For example, only 4 of the original 13 parameters/functions change in Table 2 depending on the species or the lesion under study. These include the form of NL gain curves for sg and tv. Simulations in the MATLAB environment used the “ode4 (Runge-Kutta)” algorithm at a 1-kHz sampling rate. This is more than required for the expected response bandwidth (30 Hz) but is desirable to view the timing of switching with good resolution (1 ms). Each gaze shift emulates the response to a flashed target (in the dark) with or without the presence of external head perturbations. In the interest of simplicity and “proof of principle,” single-step gaze shifts in the horizontal plane are the focus of this study. The latest implemented MATLAB Simulink version of the SMF model, along with a graphical user interface (GUI) to conveniently run it, can be downloaded from https://www.dropbox.com/sh/970rhcxk57mvnnr/AAA_wjRZdwFqWTkvxMWbm1sma?dl=0.
formal definition of fast-phase/saccade intervals.
Typically, the interval from saccade start until the moment of maximum eye eccentricity is used to estimate saccade duration from behavioral data (Freedman 2008; Freedman and Sparks 1997; Kardamakis et al. 2010). Instead, we argue that a saccade interval during gaze shifts should be based on the silent interval of OPN activity, since that is associated with changes in circuit dynamics and “topology.” OPNs remain silent when a gaze shift is not yet on target, even if the eye reaches its saturation plateau or counterrotates in the orbit while gaze continues its approach to the target in a rapid fashion (Freedman 2001; Goossens and Van Opstal 1997; Guitton and Volle 1987; Laurutis and Robinson 1986; Paré and Guitton 1998; Phillips et al. 1995; Tomlinson and Bahra 1986). Peak eye deviation is an unreliable estimate of saccade end time. Because of the common drive of the platforms in our structure, our definition of saccade interval applies to all platforms (eye and head), namely, the OPN silent period. We expect changes in head trajectory dynamics during saccadic and fixation intervals of gaze, just as for the eye (Guitton et al. 1990).
Analysis of simulated trajectory characteristics.
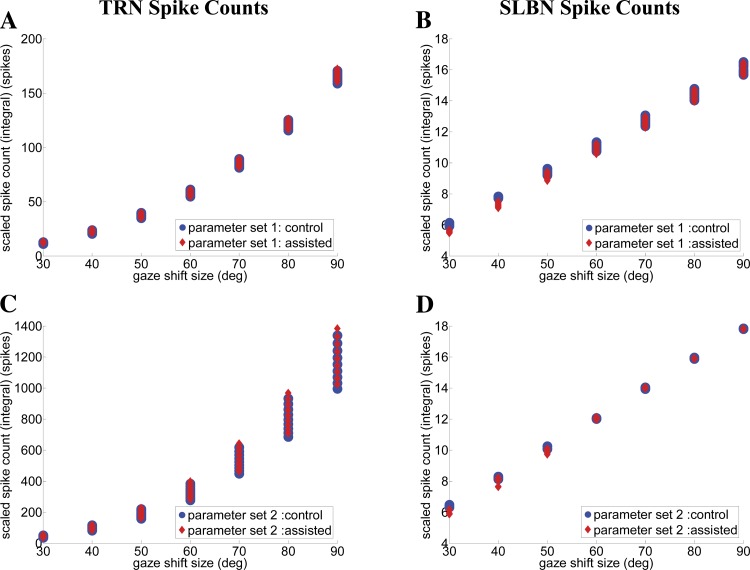
Several characteristics of gaze shift trajectories from our SMF model are next compared with published data. Given variability in the literature on published metrics, the measurement of characteristics during simulated gaze shifts uses the following definitions: Saccade or gaze shift interval is the duration of the silent period in OPNs. Peak eye deviation is the maximal eye eccentricity in its orbit during the saccade, often used for gaze shifts starting from central position or the null eye position in the orbit. Eye and head contribution to saccade is the eye and head eccentricity at the moment OPNs are reactivated. The eye contribution is often slightly smaller than peak eye deviation because of the eye rollback before the end of the saccade. Eye and head final amplitude is the measured eye and head eccentricity in steady-state, when all platforms have stabilized (at zero velocity) and gaze is on target during fixation. When the head is unrestrained, final amplitudes are rarely the same as saccadic contributions above. Average head velocity is measured from the initiation of the gaze shift until the end of the gaze shift simulation time. By that time, the head was nearly stable for all simulations. Average eye/gaze velocity is measured during the saccade interval. Simulated spike counts are the time integral of the firing rate in simulations, which is equivalent to counting spikes in experimental spike trains (Goossens and Van Opstal 2006).
RESULTS
We focused on reproducing diverse experimental observations with a single realization of connectivity, consistent with anatomy and neurophysiology, and with a single parameter set. Minor parametric changes (central sensitivities) are only used for special cases such as lesions or species-related effects (see Table 2). Again, we relied on the OPN pause as the indicator of saccade intervals, and the OPN reactivation time was deemed the endpoint of a saccade for all platforms. However, unlike some previous models, simulations were run well beyond the end of a saccade, when OPNs were reactivated, to allow expression of steady states (stable responses) for eye and head platforms during fixation. The results highlight that changing eye-head contributions with target eccentricity are possible without planning, provided the motor drives contain a NL gaze allocation to platforms.
Variable Gaze Characteristics from a Single Architecture
Using the provided parameter sets, several experimental observations were replicated without changing the system connectivity (anatomical structure).
Eye-head contributions and early interactions during saccades.
Figure 4 shows examples of 20° and 60° gaze shifts characterized by single-peak gaze velocities (Fig. 4A, parameter set 1) or double-peak gaze velocities (Fig. 4B, parameter set 2). [Figure 5 shows simulation examples of cat gaze shifts with the SMF model (parameter set 4).] In both cases, the responses replicate observed increases in both durations and peak speeds, with gaze shift size (see also metrics in Fig. 13) and attenuation of eye contributions during the saccade if the head speed is high (Fig. 4B, 60° shift). Thus, even if the eye is far from its saturation level, interactions between eye and head controls can produce a “soft” limit on the allowed excursions (soft saturations are also discussed in Daye et al. 2014). These results are compatible with observations in cat and monkey (Tomlinson and Bahra 1986; Guitton et al. 1984).
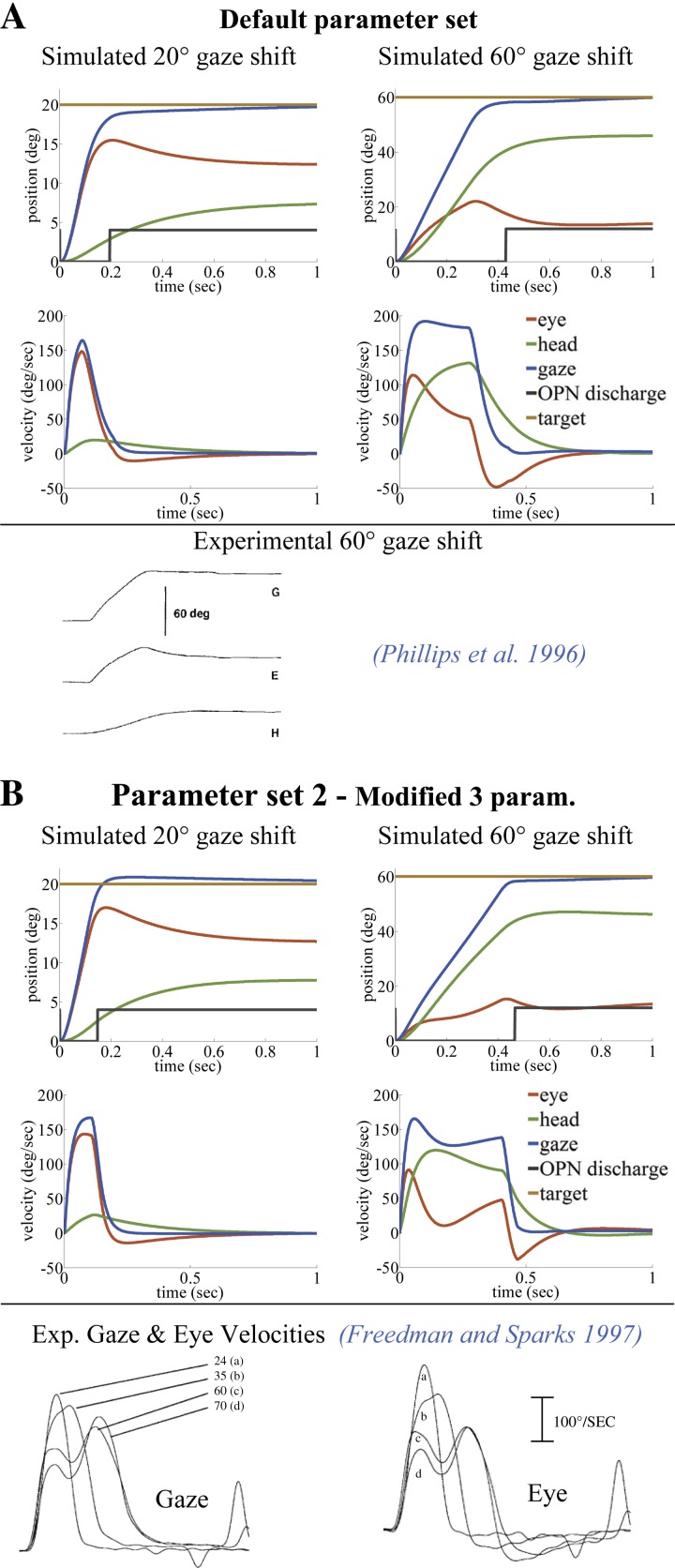
Fig. 4.
Comparison of typical gaze trajectories in primate, simulated with single-peak (A) or double-peak (B) eye/gaze velocities (left, 20°; right, 60°). Only 3 of the 13 default parameters in A are modified in B for the double-peak effect (see Table 2). As reported, double peaks appear only for larger gaze shifts. The black switch line in position traces shows the OPN pause period, which can end before or after the peak eye deviation. Simulations in A and B replicate reported observations by Phillips et al. (1996) and Freedman and Sparks (1997), respectively.
Fig. 5.
Cat gaze shifts simulated by the SMF model with parameter set 4 (left, 20°; right, 60°). Only 3 of the 13 default parameters in parameter set 1 are modified to produce parameter set 4 for cat (see Table 2). Because of the limited oculomotor range in cats (Cullen et al. 1991), they rely more on the head plant for making gaze shifts. The SMF model, using parameter set 4, replicates this phenomenon that is present in experimental observations (Guitton et al. 1990).
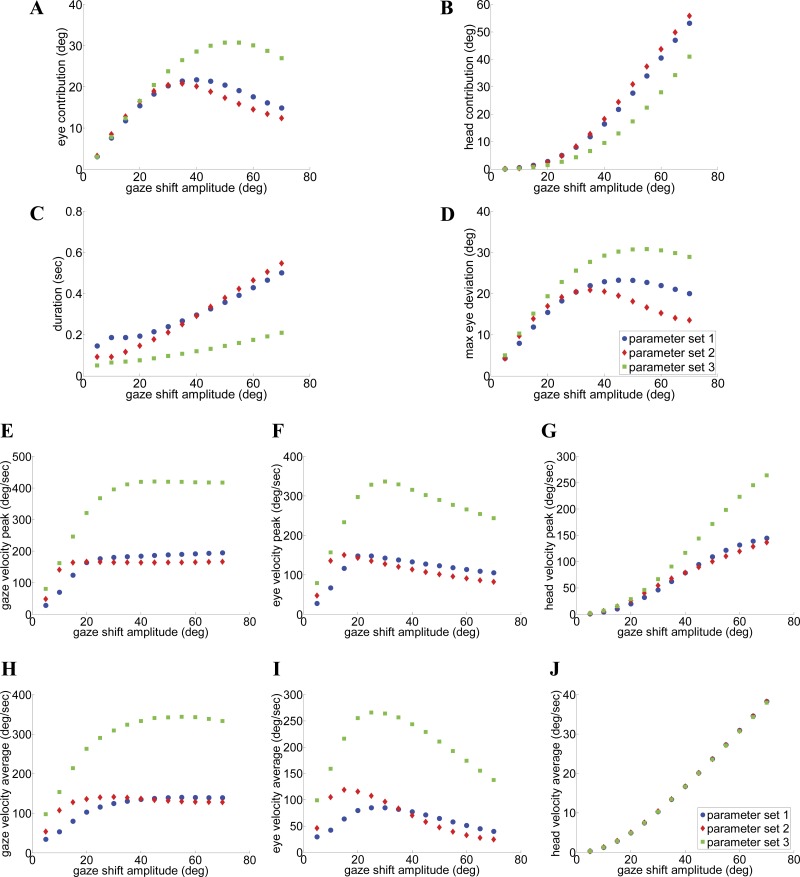
Fig. 13.
A–J: characteristics and main sequences of SMF trajectories. Sample data shown in green replicate the observations of Gandhi (2012) with parameter set 3 (fast gaze shifts with single velocity peaks). In contrast, parameter sets 1 and 2 correspond to slower gaze shifts in primate with single-peak (set 1) or double-peak (set 2) velocity profiles. Nevertheless, there are common trends and characteristics; thus the circuit topology can support variations across species or subjects.
Single-peak vs. double-peak velocity profiles.
The presence of single or double peaks in velocity during a saccade depends solely on model topology: the neural coupling strength between head velocity sensed by the canals (via VN) and saccadic SLBNs can cause double peaks. For example, the first two parameter sets used in Fig. 4, A and B, differ only in 1) the forward SC gain field (tv) projecting gaze error, 2) the gain of canal-to-VN projections (P), and 3) the gain of VN projections to SLBN (vnb) during fast phases (see Fig. 3). These three parameters are elevated in parameter set 2 (Table 2), associated with double peaks in velocity. In the SMF model, increasing the projection strength from SC sites (tv) is equivalent to increasing activities on the SC map or the set point of TRN, as seen in cat during faster saccades to identical targets (Paré et al. 1994). Because of the higher speeds, parameter set 2 reduces the duration of the smaller 20° gaze, as expected. In addition, 1) the trajectory shapes during 20° gaze shifts remain qualitatively similar for either parameter set, whereas 2) double peaks in eye and gaze velocity traces now appear in 60° gaze saccades (Fig. 4B). Both characteristics are compatible with results reported in trained monkeys (Cullen and Guitton 1997; Freedman and Sparks 1997; Freedman 2001; Gandhi 2012; Roy and Cullen 1998). Single-peak velocities appear with parameter set 1, regardless of the size of a gaze shift, as reported for human data (Boulanger et al. 2012; Goossens and Van Opstal 1997; Guitton and Volle 1987).
Double peaks in velocity have been replicated by design in previous models by decomposing and optimizing eye and head goals a priori for minimal time and energy, or by postulating direct vestibular inhibition of ocular drives (Freedman 2001; Kardamakis et al. 2010; Kardamakis and Moschovakis 2009). In the present model, interactions between eye and head drives are also used, but they are bidirectional and autonomous: vestibular inhibition of bursters with head speed interacts with enhancement of the eye drive if the head slows down (e.g., perturbations). Parameter set 2 raises the sensitivity of the head to gaze error (larger tv), whereas larger vestibular inhibition from VN (P) increases the damping of eye velocity by concurrent head velocity (via SLBNs; Fig. 3). The result is the appearance of double peaks in eye and gaze velocity for the larger gaze shifts. This can cause faster gaze shifts of shorter duration, but not always: it depends on the balance between the two pathways through SLBNs. Similarly, PVP responses in the model are inhibited by the SCC signal with sensitivity P (see appendix). P (weight of SCC to VN) is larger during saccades than slow phases in all parameter sets used to replicate changes in bilateral projections during switching in this lumped model (see Galiana 1991 for more details). The result is sudden inhibition, even silencing, of ipsilateral PVP cells during saccades (see also Fig. 6G).
Fig. 6.
Model responses at central and behavioral levels, with and without brief (50 ms) opposing head torques (default parameter set). The responses from the SMF model are concurrent for each of the perturbed or control situations. Modified trajectories (A) and neural activities (C, E–H) due to perturbations are consistent with the literature; note longer gaze shift duration but with preserved accuracy for the perturbed case (A, B, F). The brief perturbation causes a dip in SLBN activity (C) matching the observations (D) of Sylvestre and Cullen (2006) associated with a dip in ipsilateral type I VO (excitatory) cell activity (H) and/or burst on contralateral type II VO (inhibitory). The increase in PVP activity (G) after the perturbation is a prediction of the model. See glossary for definitions.
Increasing duration of gaze shifts with their amplitude.
The reported trend in the literature is an increase in saccade duration as gaze shift size increases (Freedman and Sparks 1997; Gandhi 2012; Goossens and Van Opstal 1997). This is examined in the SMF responses by using the OPN silent period as the measure of gaze shift duration. In Fig. 4, the 20° saccade with parameter set 2 has the shortest duration, whereas single-peak 60° shifts (parameter set 1) end earlier than in the double-peak example (parameter set 2; compatible with Gandhi 2012). The pattern within a given parameter set is still consistent: durations increase smoothly with gaze shift size (Fig. 13C compares 3 parameter sets).
NL distribution of final platform contributions during fixation.
In the model, the variable partitioning of final eye and head contributions at stable fixation (when head motion has ceased) is achieved by design: a NL projection gain, sg, sets the relative weight of neck vs. eye motor drives by scaling it with target eccentricity from the body midline (see appendix, Eq. A13 and Table 2). In Fig. 4, the final contributions of eye and head are ∼60% and 40%, respectively, for a 20° shift, but this reverses to eye and head final contributions of ∼25% and 75%, respectively, for a 60° shift. Final platform contributions to a given gaze shift (Fig. 4) are identical for parameter sets 1 and 2 despite their diverse speed profiles, because their sg fields are identical (see Table 2). Hence, platform contributions can be tuned independently from platform speeds (dominated by the SC gain field, tv). On the other hand, end-of-saccade platform contributions depend on a mix of sg with tv (vestibular and SLBN interactions) and so will vary with parameter sets (or experimental lesions). An emerging property is that head contributions increase with gaze shift size during both saccadic and fixation intervals of gaze orientation, consistent with experimental data (Freedman 2008; Phillips et al. 1995).
Robust Gaze Shifts Despite Platform or Context Perturbations
Because VOR responses during slow phases are well known, the focus in this work, instead, is on head perturbations during gaze saccades (when OPNs are off). Perturbing the head during a gaze saccade results in changes in eye and head trajectories, which can be partially or fully compensated to preserve the gaze trajectory and/or its accuracy. We examine perturbations of two types: long duration and short duration. Short-duration perturbations are impulsive torque pulses applied to the head for a very brief duration, such as 20 ms in monkeys (Sylvestre and Cullen 2006). Long-duration torques assist or oppose the head during a gaze shift for an interval comparable to the gaze shift duration in the control trials; e.g., 500 ms for a 70° gaze shift in humans (Boulanger et al. 2012). An important hypothetical model element is the VO cell type that monitors the passive component of head movements (Cullen and Roy 2004). These neurons have been integrated into the SMF model to account for reported gaze compensation during saccades. During a gaze shift in the model, passive perturbations applied to the head modulate VO neurons, which then, we hypothesize, innervate bursters (SLBN) via gain vob and head Mn via gain vog in parallel. This assumed mechanism provides the drive for rapid compensatory responses during external head perturbations as reported by Boulanger et al. (2012).
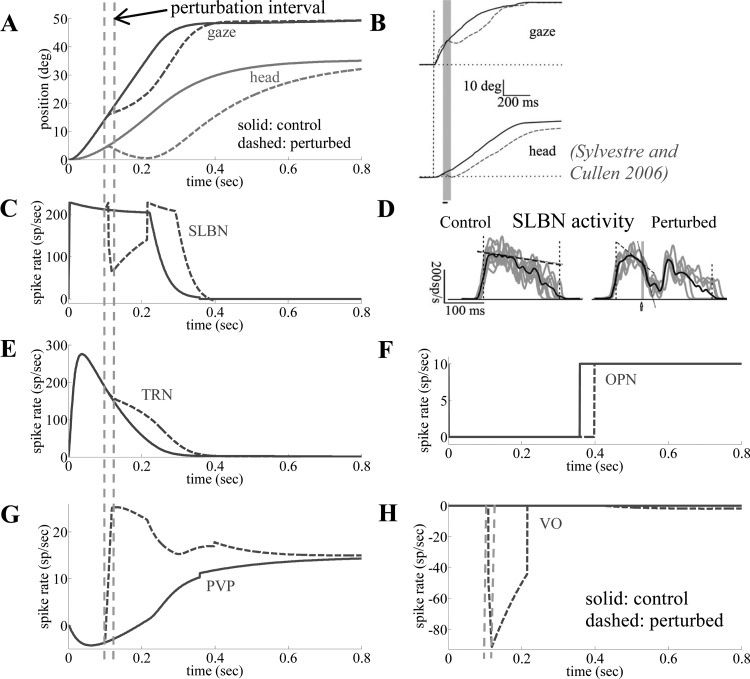
Control vs. brief head torques: behavior and predicted neural activities.
Figure 6 shows simulated platform trajectories (A) and neural activities (C, E–H) from the SMF model for 50° gaze shifts with parameter set 1. This produces single-peak velocities for the control gaze shift, consistent with experimental data in monkeys from Sylvestre and Cullen (2006), who also imposed brief head trajectory perturbations (Fig. 6, B and D). Two cases are compared: control responses (solid lines) and perturbed trajectories (dashed lines), where the head is heavily braked with a torque motor for 20 ms that temporarily reverses the head direction. Scaled neural activities are provided for simulated TRNs projecting to brain stem SLBNs (Scudder et al. 1996a), OPNs (Sylvestre and Cullen 2006), and PVP and VO cells (Roy and Cullen 1998, 2001). The effects of the perturbation on simulated cell activities and platform trajectories are all consistent with the literature: an extended saccadic interval, with strong short-latency inhibition of SLBN activity lasting longer than the opposing torque, and a reflection of the passive head pulse on the VO activity profile (Fig. 6H). In addition, the model predicts enhanced postperturbation activity on TRNs to guide gaze back on target. SC map activity has been recorded (Choi and Guitton 2009), but recall that the TRN in our model is a population average from the whole SC map and therefore cannot represent spatial elements of such site recordings. Instead, Fig. 6E provides an estimate of the net pooled response of TRNs in the brain stem. Finally, a reactivation of PVP cells (Fig. 6G), silent before the perturbation, is expected. The PVP response during an impulsive perturbation trial is a prediction of our model, because we did not find experimental reports on PVPs for that case. This example demonstrates the advantage of a circuit-based model: the capacity to emulate both behavior and neural discharges simultaneously. A brief, strong head perturbation in the model replicates reported changes in the trajectory of a gaze shift and preservation of its final accuracy, with associated neural discharges.
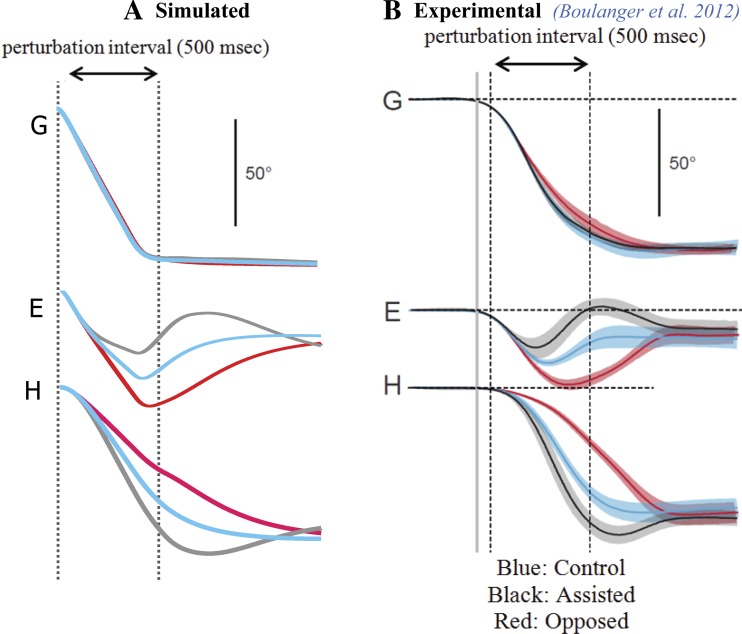
Control vs. sustained head perturbations during saccades.
Boulanger et al. (2012) reported that prolonged (≥500 ms) head perturbations in humans, either assisting or opposing the head motion, produce heavily modified head and eye trajectories despite preserved gaze trajectories. It is noteworthy that such perturbations were equivalent in duration to that of the gaze saccade but never slowed the head enough to reverse its direction (as opposed to impulses in monkeys, as described above). Despite trajectory variability for each plant, the gaze trajectories remained nearly identical to the control cases and reached the target (Fig. 7B). Experimental curves can be compared with the model simulations with parameter set 1 used for all head perturbation conditions (Fig. 7A). The SMF simulations closely replicate the data: 1) assisting torques in the direction of head movement cause early attenuation of the eye contribution; 2) opposing torques enhance the eye contribution and delay reversal toward the end of the gaze saccade for an increased eye contribution (at the beginning of fixation); 3) the saccadic gaze trajectories remain close to the control case, despite very large modifications in eye and head platform trajectories; and 4) the final amplitudes of eye and head platforms during the fixation phase are not significantly different in control and perturbed gaze shifts. Thus gaze shift accuracy, duration, and trajectory are well preserved in all cases, due, we argue, to the compensatory role of the model VO cells. The large deviations in eye and head contributions compensate each other during both the saccade and fixation intervals. Again, the robustness of eye/head final amplitudes is a reflection of the fixed sg NL gain field that was used in all these simulations.
Fig. 7.
Vestibular compensation during gaze shifts: sustained perturbations that last throughout the gaze shifts (default parameter set). Simulations (A) match reported human responses obtained using a head clutch (B). The default parameter set produces the slower spontaneous gaze shifts seen in human subjects restrained by a bite bar (B; Boulanger et al. 2012). Note the robust gaze trajectories despite widely varying eye and head movements. In this case, contrary to data in Fig. 6, head direction is not reversed by the brake, and both duration and accuracy of gaze trajectories are better preserved.
Pertinent to this, note that depending on the type of the opposing head perturbation (impulsive short duration or long duration), the SMF model is able to replicate two seemingly paradoxical phenomena: preserved gaze trajectory for the case of the long-duration perturbation (Fig. 7) and modified gaze trajectory for the case of the impulsive opposing perturbation (Fig. 6), as seen in experimental observations. The reason for this is explained in the discussion.
Effects of context perturbations: different initial eye and head orientations.
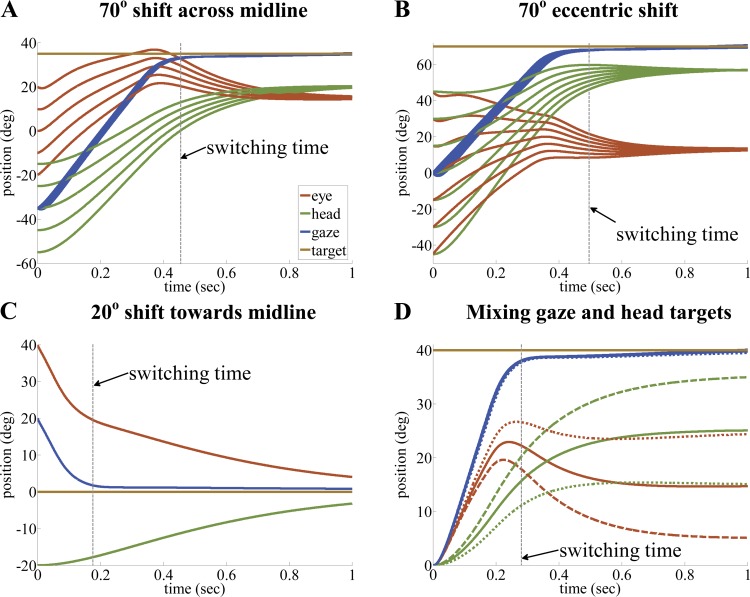
We next examined the sensitivity of the controller's response to changes in eye-in-head and head-on-body initial positions. First, large 70° gaze shifts (again with parameter set 1) were simulated symmetrically across the midline (Fig. 8A, from −35° to +35°) or eccentrically (Fig. 8B, from 0° to +70°). In each case, different combinations of initial eye and head directions maintained a fixed initial gaze orientation (starting point of blue curves) and a fixed initial gaze error of 70°. The responses evolved automatically without further intervention or any precomputation. As expected from gaze feedback, all gaze shifts reached the goal despite widely different eye and head trajectories. However, the gaze trajectory was much more robust than its recruited platforms. Robust gaze shifts were seen even when the eye was near-stationary or counterrotating opposite to the head during the gaze shift (Fig. 8B, top 2 eye traces). This occurs when the eye or head starts near or even beyond its final amplitude; yet the gaze always approaches the target at saccadic speeds, as seen experimentally (Boulanger et al. 2012; Freedman and Sparks 1997).
Fig. 8.
Robust gaze shifts despite variable directions and goals for platforms (default parameter set in all cases). A and B: 70° gaze shifts with variable initial platform orientations below the gaze goal; this can result in early reversals of the eye so that it may move opposite to the head well before fixation (consistent with report by Boulanger et al. 2012). Gaze shifts are quite robust, particularly for cross-midline shifts. In C, the gaze goal is between the initial orientations of the eye and head, requiring a 20° gaze shift; now the eye and gaze both move opposite to the head throughout saccade and fixation intervals, delimited by the switching line (matches Fig. 10 in Goossens and Van Opstal 1997). D: independent head targets, determined using the head offset input in Fig. 3, are presented concurrently with the 40° target. The modified head trajectories for head goals of 35° (dashed lines) or 15° (dotted lines) barely affect the 40° gaze shift so long as the eye remains in its working range during the eye/head interactions. The default head trajectory (solid line) settles between the two cases at 25° when head offset is null. Model parameters are fixed (except for non-zero head goals in D).
Next, when the target at the null position was between the initial eye and head orientation (Fig. 8C), then the eye and head moved opposite to each other throughout the gaze saccade and fixation, without slowing the gaze shift, as reported by Goossens and Van Opstal (1997). There is a simple explanation for such counterrotation of head vs. eye/gaze directions (Fig. 8C): for a desired final goal for gaze, there are specific final resting positions for eye and head that are determined by the system parameters (i.e., sg gain) and target location. For the case of the gaze shift shown in Fig. 8, the final position of gaze, eye, and head are all at 0. Now, since the eye/gaze and head start from locations on different sides of their final position, they have to counterrotate to reach their resting position. This happens whenever the initial platform positions are on opposite sides of their individual final positions.
In summary, a shared gaze error feedback controller can produce gaze shifts with eye and head trajectories moving in unusual directions during gaze saccades while gaze moves in a stereotypical trajectory to the target. The network interactions cause a reduction in gaze error with a surprising result: slow-phase-like eye-in-head responses can occur in the saccadic part of a gaze shift. These simulations were made with parameter set 1, but even if some parameters in the system were to change, for example, due to internal variability, this controller would preserve the general shape of trajectories and achieve its goal without a priori computations. Finally, despite variable initial conditions, the 70° examples all have near-identical gaze saccade durations (OPN dashed switching lines in Fig. 8, A and B). This is consistent with Freedman and Sparks (1997), who reported that gaze saccade duration was not affected by platform initial conditions, given identical start-stop gaze locations. However, the simulations do indicate that same-size gaze shifts will have slightly longer durations if made eccentrically (from midline) rather than across the midline (∼15-ms difference in the cases shown in Fig. 8, A and B). Note that analyses in the literature often define the end of a gaze saccade as the moment when the eye reaches its peak deviation in the orbit or when saccade velocity crosses a minimal threshold. We argue that both approaches, especially the former, can produce biased saccade durations, given the range in peak eye positions in Fig. 8, even with a known fixed OPN switching time.
It should be added that by platform initial conditions, we do not refer to initial positions only. Although not demonstrated here, the SMF easily handles initial plant velocities and accelerations in the same fashion it handles their initial positions: by embedding all initial conditions in the eye and head plants and their associated “models.” The same method cannot be applied to the independent controller models, because in those, each set of initial conditions is treated as a new input profile, requiring a dedicated decomposition or trajectory planning paradigm.
Coordinating Two Platforms with Two Spatial Goals
Eye and head trajectories can be quite diverse and still provide robust gaze shift trajectories. The question now is whether adding a specific head goal is feasible without modifying the gaze trajectory, or at least its final accuracy. The curves in Fig. 8D show 40° gaze shifts for three sets of conditions: 1) control condition with no imposed head goal (solid lines), where positions stabilize at default endpoints (25° for head due to network properties, not to an imposed head goal), or 2) gaze shifts to the same target (dashed and dotted lines), in which an additional head drive is imposed at time 0, moving the head to +10° or −10° compared with the default final head position. In the model (Fig. 3), using the same default parameter set (including the same sg nonlinearity), a “head offset” is now introduced at the level of head Mn, which normally defaults to zero.
A surprising feature, which was not imposed, is the demonstrated insensitivity of the temporal profile of the gaze shift to the additional head drive: there are only minor changes in the saccadic gaze profile and no loss of accuracy in the fixation phase. The gaze controller automatically compensates for an altered final head contribution with an altered eye contribution. An optional head offset can be imposed at any time during gaze shifts and does not require any changes in the model parameters. In this example, the two tasks were imposed simultaneously at the beginning of the saccade; hence, the eye and head trajectories are both modified from control throughout the response (saccade and fixation intervals) while still preserving the global gaze trajectory and its duration (switching time). This demonstrates that, during a gaze task, a single controller can coordinate two platforms with distinct dynamics and, in addition, easily integrate a separate task for the head. The robustness of gaze trajectories during dual tasks could deteriorate depending on the choice of parameter sets or with lesions, which may provide new diagnostic clues, as considered below. It is noteworthy that the concept of independent head goals was also present in the studies of Daye et al. (2014) and Laurutis and Robinson (1986). However, in those studies, an independent head goal was necessary for each head-free gaze shift. In our case, that is optional: i.e., active head-free gaze shifts can happen without specifying an independent head goal (or head offset) input; the head will settle on a position determined by the network parameters alone.
Gaze Shifts with Neural or Sensory Deficits
Because the SMF model has explicit neural substrates, it can be probed for the effects of specific sensory or central deficits. Such tests can serve not only to validate its structure and properties by comparison with experiments but also to shed light on some still mysterious properties of the system. For example, it is still unclear how saccades stop despite experimental lesions that have been used to test the role of key sites controlling saccade timing (start/stop) or saccade dynamics/accuracy. Classically, gaze shifts are believed to stop with the activation of OPNs. However, as considered below, this is not a necessary condition for stopping a gaze shift. One has to consider the relative importance of cell types at three levels: brain stem OPNs-SLBNs, the role of SC with rostral “fixation” sites vs. caudal sites, and SLBN sensitivity. For example, to stop a saccade (fixate), we might expect at least one of the following: 1) OPN activation via low activity on the caudal SC and/or increased activity in the rostral pole of the same SC (Optican 1994); 2) OPN activation due to insufficient inhibition from SLBN ipsilateral to saccade direction: e.g., when projections from rostral SC (excitatory) overwhelm motor reafferents (inhibitory) regardless of current saccade speed; this can occur with lesions of the SC caudal zone (Hafed et al. 2008) or low gaze velocity with SLBN lesions (Prsa and Galiana 2007); or 3) OPN activation directly through other projections to the NRI and/or indirectly by inhibiting SLBNs that in turn inhibit OPNs (e.g., through Cb projections; Noda et al. 1990).
Our model suggests that interpretation of past reports is difficult, given the interconnections between key cell pools within and between the three levels of control in Fig. 3. Indeed, gaze shifts “stop” even when OPNs are deactivated (e.g., cannot turn on; Rucker et al. 2011) or when the SC's rostral zone is deactivated (Hafed et al. 2008). We argue that this is because the saccade phase of the gaze orientation system is itself stable, and hence can reach a steady state on its own without OPNs. In this case the system could remain in the fast-phase mode, even though gaze is stable and appears to be fixating (see below).
We simulated gaze shifts using model conditions that mimic deficits caused by muscimol or lidocaine injections in several experimentally tested sites (i.e., rostral vs. caudal SC, SLBN pool in PPRF, OPN pool), as well as the impact of bilateral SCC plugging in the monkey. Our simulation results are consistent with reported lesion experiments and further validate the SMF model topology. We found that gaze shifts can stop despite lesions in numerous zones affecting saccade timing. Pure switching anomalies need not affect accuracies, but lesions within neural loops (such as PVPs, SLBNs, etc.) are expected to change gains and cause asymmetries in saccade trajectories.
Focal lesions on the SC map.
The spatiotemporal mapping of SC activities involves a summation of cell activities with different projection weights (see Implementation and Supporting Anatomy and Physiology). Thus a “hole” anywhere on the map does not mean that a gaze error is no longer represented, but rather that the center of SC activation (Eq. 2) and the NL projection field (Eq. 3) will be distorted, leading to biases in gaze position or attenuation of gaze velocities. Figure 9 describes tentative changes in the tv projection fields for SC lesions.
Fig. 9.
Modifications to SC nonlinear gain field, tv, with acute lesions in the left SC map (only tv changes in the default parameter set). The control case uses a symmetric NL mapping (solid curve) as the combined effect of both colliculi with overlapping rostral zones; a range of ±20° gaze shifts is provided for rightward or leftward saccades (positive, via left SC; negative, via right SC to contralateral brain stem). A: a rostral lesion on the left colliculus shifts the minimum of the tv curve (dashed curve) toward the healthy side by ∼2° (the size of the rostral area; May 2006). B: a unilateral lesion on the left caudal colliculus in addition to displacement of the balance point (similar to A) reduces the slope of that arm of the tv curve. The severity of the displacement of the balance point and the slope change due to a caudal lesion depend on the site and severity of the lesion (compare the exemplary lesions illustrated with the dashed and dotted tv curves in B with their impact on position trajectories in Fig. 10E).
For unilateral rostral SC lesions (reported by Hafed et al. 2008), we used a shift in the tv gain field by ∼2° toward the healthy SC to represent the lesion-imposed projection imbalance of activities from the overlapping rostral zones of both SC (Fig. 9A). Fixation of a central target or a contralesional target of 40° was then simulated. The results match reports: for central targets, a contralesional drift and a small steady-state bias on the healthy side (Fig. 10A) and hypermetria of contralesional saccades with a bias similar to the null bias (Fig. 10B). Note that a rostral lesion only affects the location of the zero-error null point but leaves saccade dynamics mainly unchanged. Importantly, despite the fact that the rostral zone is defective, we find that simulated gaze saccades still stop, using the balance between OPN and SLBN activity in the brain stem and the location of the tv minimum.
Fig. 10.
Gaze shifts in the SMF model can stop despite focal lesions in key sites (default parameter set, except as specified). Solid lines are control, and dashed or dotted lines are lesion cases; experimental sources are cited in panels. A and B: the SC gain field tv is shifted laterally by ∼2° toward the healthy side: this results in a shift of the null position (target at 0; A) and slightly hypermetric contralateral saccades with the same bias (B). C: unilateral focal lesions in the caudal SC reduce the SC gain field in that region compared with the control case, as well as shifting the tv curve null position, due to their impact on the location of minimal projection strength. The result is slower hypometric gaze shifts in the contralesional direction (consistent with Quaia et al. 1998). Two exemplary lesion cases are illustrated in this figure: case II (dotted lines) represents a more severe caudal lesion compared with case I (dashed lines). The distinction between A and C is that in A the lesion is inside the rostral zone, which corresponds to the retinal areas represented strongly by both colliculi, whereas in C the lesioned area corresponds to a visual field represented by one colliculus (see Fig. 5 for the changes in bilateral projection fields from SC). D: loss of OPNs in the circuit forces the response to remain in saccadic mode; hence, the response is the same as the control during the saccade interval, with a small increase in drift speed during the fixation interval due to the unmasked faster dynamics. E: ipsilateral SLBN gain (B) is reduced by 50% throughout, causing slower and hypometric gaze shifts to the ipsilateral side, replicating lidocaine injections in the PPRF. F: total loss of SLBN (acute) results in very slow, but accurate, gaze shifts with the dynamics of the slow mode.
In the case of caudal SC lesions (Aizawa and Wurtz 1998; Quaia et al. 1998), the simulated tv gain field is now attenuated in the caudal area of the affected SC (Fig. 9B), and the tv curve minimum is shifted in the caudal direction of the affected SC. Thus the end of a saccade is interrupted earlier because the minimum is closer to the initial caudal activity. The simulations replicate slow contralesional hypometric gaze shifts whose speed and amplitude deficits are correlated with the severity of a caudal lesion (Quaia et al. 1998) (2 deficits with control shown in Fig. 10C). Feedback through the SC is often interpreted as requiring activation of the rostral site(s) to stop saccades, but here instead, the SC field minimum actually controls the null set point that releases OPN with reduced SLBN inhibition. Caudal sites control saccade size, whereas the slope of the tv projection field controls the speed of the gaze shift. Both aspects are assumed tuned a priori by the cFN in the control case.
OPN lesions.
The OPNs are known to be essential to perform network alterations that allow a return to slow-phase dynamics after a gaze shift, and this is also true for our SMF model. However, does that necessarily imply that saccades cannot stop if the OPNs are lesioned or inhibited? Rucker et al. (2011) showed that in the case of OPN lesions, gaze shifts are normometric and the only difference from control was the appearance of oscillations right after gaze was on target (the beginning of the fixation phase in normal gaze shifts). The SMF model also predicts normometric gaze shifts after OPN lesions, with only small differences after the gaze reaches the target (Fig. 10D). But how does the gaze stop without switching? The important concept is that switching phases is not a necessary condition for stopping saccades. When we deactivate the OPNs in our model, we are trapped in the saccadic mode. However, if the steady-state gain of the saccadic response is unity, i.e., the fast phase stabilizes on the desired gaze displacement (as with any filter) and ends on target, then saccades still “stop” (stabilize) even in the saccadic phase: a virtual fixation behavior. For an analysis of the model and how it is tuned to produce unity gains for both phases, refer to appendix, Steady-State Analysis of the Model. The presence of reported oscillations simply depends on whether the saccadic mode has high gains in the rostral SC neighborhood (complex poles). In part because of the minimal differences between active gaze shifts before and after OPN lesions, some have concluded that OPNs “play essentially no role” in gaze shifts (Quaia et al. 1999). However, active gaze shifts do not seem to be the right protocol to evaluate the role of OPNs in gaze shifts, because the fast phase, by itself, can facilitate a quasi-normal gaze shift without any switching. We propose that perturbed gaze orientation trials, which necessitate switching, should be utilized to evaluate the role of OPNs in gaze orientation.
Partial or total loss of saccadic bursters (SLBNs).
Finally, the effects of a deficit in the saccade circuitry are considered, namely, saccade burst neurons in PPRF (Fig. 10, E and F). In gaze control, OPNs are silenced by inhibitory SLBNs, to switch into fast-saccade dynamics. Without such SLBNs, the OPNs remain active regardless of the context. Hence, to simulate this lesion, SLBNs were either reduced in sensitivity by 50% (Fig. 10E; mimicking lidocaine injections by Sparks et al. 2002) or completely removed from the circuit (Fig. 10F); all other parameters were kept at default levels. The resulting gaze responses, when the target is in the ipsilesional direction (dashed lines), can be compared with the control 40° gaze shift (solid lines). For partial loss, the gaze shift is slower than control with hypometric gaze shifts, and the head contribution is also below normal, as reported by Sparks et al. (2002). Total loss of SLBN has a much more drastic effect. Note that in this case there still remains an active control of gaze error through SC loops, but now gaze shift dynamics are very slow, as expected from the slow-phase mode (OPNs remain on). The gaze trajectory reaches the target much later than the control (duration ∼1 s instead of ∼350 ms for control), consistent with observations (Sparks et al. 2002). The slow-phase system (fixation/pursuit) in the model matches the saccade gain of 1 with respect to retinal error, and so this sluggish gaze shift is still accurate. However, if the slow-phase system did not have a gain of 1, then this “slow saccade” would be biased from the target. Similar effects could be observed for gaze orientations accompanied by microstimulation of the OPNs (to keep the system in slow phase; Gandhi and Sparks 2007). However, special care must be taken while analyzing OPN microstimulation results, because those could cause antidromic SC activation and hence influence the ongoing gaze motor error drive (Gandhi and Keller 1997).
It is noteworthy that effects similar to the ones following the partial deactivation of SLBNs (i.e., change of gaze shift dynamics and gaze shift dysmetria) could very well be expected following the deactivation or lesioning of centers projecting to the SLBNs (e.g., providing additional directional drive). A prime example is the cerebellar cFN (Noda et al. 1990; Quaia et al. 1999). This is addressed in more detail in discussion, Impact on Interpretation/Analysis of Experimental Data.
Bilateral loss of SCC modulation.
We considered the model responses for 40° gaze shifts in the monkey, before and after bilateral SCC plugging; the amplitude of the gaze shift was selected to match existing data, and only the SCC afferent signals were impaired. As previously, parameter set 1 was used both pre- and postplug (Fig. 11 and Table 2). The control cases in Fig. 11 (solid lines) resemble typical gaze shifts seen previously (Fig. 4). To emulate plugging, the following parameters were altered from control in the acute condition: 1) the canal dynamics were modified to match the altered dynamics found by Sadeghi et al. (2009) after plugging in the monkey. i.e., gain of 0.3 and canal time constant of 0.03 s (refer to appendix); 2) feedback accuracy of head velocity to the SC, postlesion, was decremented by 50% (gain 0.5) to reflect the deficient estimation of true head speed (e.g., assumed to rely only on remaining neck spindles, reafference, and proprioception information). Aside from these changes, all parameters and circuitry were left intact from control. Figure 11 (dashed line) provides postplug acute gaze shifts. The faulty gaze error estimate in SC causes gaze overshoot as reported by Dichgans et al. (1973). Simulations successfully replicate results after such experimental lesions in monkeys (Newlands et al. 1999): the postplug position traces resemble normal platform trajectories to a larger target, so gaze shifts are hypermetric; the peak eye deviation in the plugged monkey is larger than that of the control for the intended 40° target.
Fig. 11.
Animals with acute bilateral vestibular loss can still produce trajectories with “virtual VOR” segments during gaze fixation. Solid lines are control, and dashed lines represent acute stage of vestibular loss using the monkey default parameters (set 1 in Table 2), except that in the lesion case the healthy semicircular canals are replaced with plugged canals (see appendix for dynamic changes) and a 50% reduction of the head velocity estimate is imposed for feedback to SC (reduced from 1 to 0.5). Eye-head coordination patterns appear normal in plugged monkey, including a VOR-like reversal of eye velocity during fixation, but gaze itself is hypermetric, as reported by Newlands et al. (1999).
Despite hypermetric gaze shifts, eye-in-head trajectories still have a “normal” aspect: i.e., they contain a saccade component followed by “apparent compensatory” eye roll back as the head continues to a final position (dashed lines in Fig. 11). All points are consistent with experimental observations. The main result is that canal plugging does not remove the capacity of the eye to counterrotate in the orbit when gaze stabilizes. Put another way, we predict VOR-like intervals even without canals. Note that this acute behavior is not the result of adaptation, but rather of simple unmasking of existing eye/head interactions.
In the normal animal, vestibular projections to SLBNs attenuate the latter's response to gaze error, whereas VO cells (appendix, Eq. A6) have little or no modulation since the difference between SCC inputs and intended head velocity is near zero during active gaze shifts (Cullen et al. 2011; Roy and Cullen 2004). After canal plugging, the mechanism for compensatory eye movements near and after gaze fixation is not necessarily the classical VOR. Because the eye-head trajectories are still interacting through their shared feedback loops in the brain stem, the loss of canal signals will cause an emergence of VO activity (appendix, Eq. A6), now modulated only by an internal estimate of head velocity . A prediction of our model is that the VO cells, along with the proprioceptive afferents to the SC, form a signal that can cause eye reversals according to estimated head velocity, derived from motor reafference and neck proprioceptors.
Comparing Model Metrics and Main Sequences with Reported Data
The SMF model was used to generate an ensemble of gaze shifts ranging from 5° to 90°, with each of the parameter sets 1, 2, and 3 (Table 2). This was repeated with nine different sets of initial conditions, in either the control or perturbed scenarios. The initial conditions for eye (E0) and head (H0) were chosen from the range [−40, +40] in steps of 10° such that E0 + H0 would be equal to 0 with the eye and head in different eccentric positions: all gaze shifts started from G0 = 0 (midline). Perturbed cases were identical to Boulanger et al. (2012), as in Fig. 7. The first interesting result relates to spike counts on TRNs and SLBNs during gaze saccades (Fig. 12). Goossens and Van Opstal (2006) reported that the number of spikes on TRNs in the monkey was the most robust indicator of the size of an intended gaze shift. Cullen et al. (1993) also showed the same relationship between the SLBN number of spikes and gaze shift size. The simulated spike counts in Fig. 12 are consistent with these reports. They were produced by integrating the simulated neural activities during the saccade interval for all the cases mentioned above. Both parameter sets 1 and 2 produced significant correlations of TRN and SLBN spike counts with the gaze shift size (Fig. 12). The increased speed of double-peak saccades increases the scale and scatter on TRN counts (Fig. 12C), but they still resemble the curved shape of the plot for single-peak saccade velocities (Fig. 12A). For both parameters sets, SLBN counts remain robust and at the same scale (Fig. 12, B and D). Note the much lower level of scatter for SLBN counts despite superposition of cases with/without head perturbations and nine variable initial conditions. In summary, the presence of head perturbations has little effect on the relationships between TRN/SLBN spike counts and the size of gaze shifts for single-peak gaze velocities. The linear trend that is particularly strong in SLBNs regardless of parameter sets is consistent with the results of Cullen et al. (1993).
Fig. 12.
Burst neuron spike counts for gaze shifts with and without long-duration assisting head perturbations. A and C: TRN. B and D: SLBN. A and C describe counts with parameter set 1 (default) providing single-peak gaze velocities; B and D use parameter set 2 for double-peak gaze velocities. Results are consistent with reports on TRN cells (Goossens and Van Opstal 2006) and SLBN cells (Cullen et al. 1993), particularly the stronger linear relation of SLBN spike counts with gaze shift size compared with TRN results. The shapes of these curves are not affected by the presence of assisting perturbations (red dots) of the type used in Fig. 7, a model prediction.
With regard to main sequences, multiple aligned (initial conditions = 0) gaze shifts to targets ranging from 5° to 70° with 5° increments were simulated using parameter sets 1, 2, and 3. The intent was to verify whether the predicted metrics and main sequences would match controls reported in the literature, despite the fact that model parameters were not selected a priori to fit reported metrics. The ensemble of simulations also validates the model against experimentally acquired data. In this analysis we did not include perturbed gaze shifts, since main sequences in the presence of perturbations have not been reported yet. The plots in Fig. 13 provide eye and head contributions to gaze saccade (A and B) at the moment of saccade end (OPN switching), saccade duration (OPN off) and maximum eye deviation (C and D), and peak and average velocity metrics for eye and gaze during saccade intervals and for head during the whole simulation interval (1 s; E–J). All of these are compatible with published data (Freedman and Sparks 1997; Gandhi 2012; Goossens and Van Opstal 1997) with the use of three parameter sets for primates (Table 2; e.g., compare the main sequence plots of parameter set 3 in Fig. 13, E–J, with the experimental results of Gandhi 2012). This is an important validation of the properties of this SMF model: the choice of parameters was only based on desired dynamics (time constants and average duration of saccades). As a result, all the metrics in Fig. 13 are emerging properties of the proposed structure and support the choice of parameters and connectivity. Because Boulanger et al. (2012) showed invariant gaze trajectories despite long-duration perturbations, the model predicts robust main sequences for the gaze variables even during head perturbations, despite increased scatter in individual eye and head metrics.
DISCUSSION
We propose a mechanism for eye-head coordination that relies on fusing relevant sensory information with motor reafference in an anatomically compatible circuit, i.e., sensory-motor fusion (SMF). As a result, many experimental observations at both behavioral and neural levels can be reproduced, allowing for species differences or specific subject performance in one circuit realization. Highlights are summarized in Table 3, and the impact of this view on data interpretation and on predicted anatomical connections is discussed. The model attempts to replicate multiple experimental observations, in particular, gaze shift perturbations and central lesions, and adds testable predictions for neurophysiologists (see below). Limitations are also addressed.
The main hypothesis is that eye and head systems can share the same neural systems to coordinate their movements and yet preserve their distinct trajectories during gaze shifts. This sharing extends to both fast (saccadic) and slow (fixation) modalities, with OPN activity controlling the mode selection. There is anatomical and neurophysiological evidence to support this postulate (see Introduction and methods). In Table 1 we list many of the available models for gaze orientation in the literature along with their general features, and in Table 3 we summarize the key features of the SMF and compare them with three representative models from that list that have a scope similar to the SMF. Table 3 lists properties of the gaze control system that have been identified experimentally and indicates whether available models can or cannot provide these features. For example, our model is the only one to embed robust gaze trajectories with head perturbations during saccades (Table 3, item 19) and to preserve execution of a gaze shift despite lesions in major neural sites (Table 3, items 23–27). In addition, the SMF model provides tentative discharge characteristics for brain stem burst neurons (TRN, SLBN) and several VN cell types during gaze shifts (PVP, VO): the latter are key for the preservation of gaze trajectory and accuracy when the head is perturbed. The major points raised in Table 3 are addressed separately below, showing that our SMF model provides a substrate to explain previously reported data and to plan tests on predictions.
Variability of Eye/Head Contributions in a Shared Neural Circuit
Robust trajectories without planning.
The most important result is the feasibility of replicating widely different coordination patterns for eyes and head in different species, within a single model structure. Mild changes in parametric weights in the SMF circuit can produce responses seen in the cat, human, or monkey or within subjects before and after training. We conclude that platform coordination can result from pure low-level sensory-motor interactions in a shared circuit, hence the name “sensory-motor fusion” (SMF). Cortical involvement could focus on target selection and projection to a sensory-motor map like the frontal eye field/SC. Task execution itself could remain isolated in the brain stem and spinal cord unless error levels detected in the cerebellum or cortex necessitate parametric “tuning;” adaptation is not considered in this work.
In the control case, simulations of the SMF model showed highly variable trajectories for eye and head without affecting either gaze trajectories or gaze accuracy. These were demonstrated using head perturbations (Figs. 6 and 7), variable platform starting points, and enforced head goals (Fig. 8). Moreover, Figs. 10 and 11 provide gaze trajectories compatible with the literature, during acute lesions to SLBNs, SC rostral and caudal zones, and acute loss of SCCs by plugging. Some lesions cause hypermetric saccades (e.g., loss of canals) or hypometria (e.g., partial SLBN loss), whereas others have no effect on gaze shift size (e.g., total loss of SLB, or loss of OPN) but alter trajectory dynamics (albeit very little change in the case of OPN loss). Clearly, the relative directions of eye and head trajectories are poor indicators of the saccadic intervals versus slow fixation. Therefore, seemingly uncorrelated eye/head trajectories or movement directions do not warrant the previous rejection of the common drive hypothesis (Goossens and Van Opstal 1997; Phillips et al. 1995). Taken together, the results validate the structure of the SMF system and support the concept of a shared error drive in gaze control, recently confirmed experimentally (Daye et al. 2015).
Gaze Drift During Fixation (Slow Phase)
Another feature of the SMF model is allowing gaze movement during the slow phase (Missal et al. 1996) with a fixed target. Most models (including independent controllers) assume a perfect VOR during fixation. They produce fast gaze shifts and then relegate slow phases (fixation) to perfect integrators that hold the final gaze position, together with an active VOR (drive eye opposite to any head movement). Consequently, they cannot replicate experimentally observed drift if the gaze saccade slightly undershoots or overshoots (Phillips et al. 1995; Tomlinson and Bahra 1986). The SMF model allows for such drifts (e.g., Figs. 4 and 8). PVP neurons in the VN are the substrate for this effect: they receive gaze error projections via TRNs-NPH with the gain tvn. If the system is in slow phase but not exactly on target, this projection excites the PVPs, which continue to drive motoneurons and gaze toward the target with the sluggish dynamics of the slow phase. During saccades, PVPs are inhibited by a large vestibular input, which overwhelms the gaze error pathway. In contrast, at the end of a saccade, this projection becomes weak as TRNs approach low activity. At this point, the PVPs respond mainly to eye orientation and head perturbations, for the classic VOR requirements. The modulation of PVPs with gaze error is also the mechanism in the model to produce slow gaze displacements in the absence of SLBNs (Fig. 10G). An important point to add is that in the SMF model, “there are no perfect integrators”: in the SMF model, the time integration of signals (e.g., eye or head signals) is done either by non-ideal integrators (i.e., the SC whose response is a low-passed version of the ongoing gaze error and not its exact value; see Implementation and Supporting Anatomy and Physiology and Table 2) or by the feedback loops (e.g., the NPH/DTN/VN feedback loop that enforces gaze holding) and not by perfect integrators.
Impact on Interpretation/Analysis of Experimental Data
Evaluating sites that start/stop saccades and control metrics.
We next address whether focal lesions in a complex network allow deduction of the role of a site in a complex gaze orientation system. Figures 10 and 11 replicate different kinds of lesions in brain stem sites and SCC. A common result in all these cases is that none prevents gaze shift from “stopping.” With regard to their size, gaze shifts are hypermetric (Fig. 10, A and B, and Fig. 11), normometric (Fig. 10, D and F), or hypometric (Fig. 10, C and E). Nevertheless, they all stop. Another example are cFN lesions: The effects of unilateral lesions of the cFN on gaze orientation have been reported by Goffart and Pélisson (1998) and Quinet and Goffart (2007). Unilateral cFN lesions result in changes in the dynamics of the gaze shift trajectory and, very importantly, in permanent saccade size dysmetria with directional asymmetries. This is why some have considered the Cb to be responsible for determining the saccade size through choking of the collicular drive once gaze is on target (Quaia et al. 1999). However, there could be another explanation: the cFN has been reported to have projections to numerous oculomotor brain stem centers, including the bursters in the PPRF (Noda et al. 1990). In Fig. 10E we show how the decrease in the SLBN sensitivity results in hypometric ipsiversive gaze shifts. Similarly, an increase in the SLBN sensitivity results in hypermetric ipsiversive gaze shifts. As a result, an explanation for the impact of cFN lesions on gaze shift size could be that cFN lesions influence SLBN sensitivity, which, depending on the direction of movement compared with the lesion site, result in hypo- or hypermetric gaze shifts similar to what we demonstrate in Fig. 10E (for the hypometric case). In addition, these deficits are expected to be permanent, since adaptation itself is compromised as a result of Cb lesions. There could be other explanations for gaze shift dysmetria following unilateral cFN lesions aside from the one just mentioned above: the cFN projects to numerous oculomotor sites, and its lesion could change other gaze system parameters, resulting in changes in dynamics and accuracy as reported. This is indeed a crucial point, because in this viewpoint the Cb is not necessarily controlling gaze shift size, but rather it is the whole gaze network that performs that task. Because in our current model we have not included an explicit Cb, we will leave proper modeling of the impacts of Cb lesions on gaze orientation for future work. Two conclusions follow: 1) The gaze orientation system is highly robust when it comes to stopping saccades. There is no single element (such as the OPN center) that can be designated as solely responsible for stopping a saccade and fixate. 2) Lesions in the SC, cFN, BNs, and canals result in changes in the gaze shift size. Does this mean that the SC, cFN, BNs, or canals are involved in controlling the gaze shift size? The answer seems to be yes and no! In the SMF model, stopping saccades and determining their size or dynamics is a distributed property of the “network” and, again, cannot be attributed to isolated elements of the network.
We suggest that the effects of such localized lesions should be analyzed as an ensemble to clarify the compatible topologies for components in the network, rather than using them in isolation to reject model hypotheses. Such observations will restrict the possible neural organization in a gaze control model.
Moreover, the evaluation of platform onset times based on velocity thresholds can result in inaccurate interpretations of comparative delays in platform contributions simply because the plants have very different dynamics. A better method to evaluate potential shared drives is to compare the associated motoneuron pool activity onsets or EMGs, because those are more closely tied to intended plant motion regardless of their dynamics (Corneil et al. 2001).
Independent tuning of platform contributions and gaze velocity profiles.
Figures 4 and 6–8 were all generated in the control case with the same NL gain field, sg (see Table 2): it weighs a collateral of the eye motoneuronal signal for transmission to head motoneurons (see schematic in Fig. 3). Figure 4, A and B, shows very different single-peak or double-peak velocity profiles, yet the final eye/head contributions during fixation are converging on identical levels. With both parameter sets, the final eye and head contributions for each size saccade are asymptotically approaching the same levels (compare Fig. 4, A and B, for each gaze shift amplitude). The gain field sg forces the final head contribution to be [sg × (final eye contribution)], and it automatically changes with the size of the gaze shift. In other words, the ratio of final head/eye contributions, at least in this model, provides a noninvasive window into the nonlinearity distributing motor signals to the eye and head. Hence, this could be used to estimate the eye/head preference, regardless of other parameters that mainly affect saccade timing and trajectory dynamics.
Despite similar final contributions, the trajectories in Fig. 4 are very different, with the conditions in Fig. 4B usually, but not always, producing faster gaze shifts and earlier saccade termination (note switching lines). In other words, parameter set 2 allows duplication of behavioral characteristics with double-peak gaze and eye velocities but does not support the argument that double peaks in experimental data necessarily optimize energy consumption or minimize saccade duration (Kardamakis and Moschovakis 2009). Producing double peaks in this case depends on a trade-off between increased global sensitivity to gaze error (gain field tv), which can reduce time constants for gaze shifts and reduce saccade duration, versus increased vestibular inhibition of SLBNs (parameter P), which damps the eye velocity at high head speeds. With parameter set 2, double-peak gaze velocities only achieve smaller saccade durations for cases with gaze shifts below 40° (see Fig. 13C). The 60° gaze shift is actually slower than the single-peak example (Fig. 4), and its gaze trajectory has become almost straight during the fast phase. Interestingly, near-straight gaze trajectories can be seen in the large gaze shifts reported by Boulanger et al. (2012). In this highly interconnected circuit, several parameter sets can achieve similar goals with different cost functions; this should be advantageous given potential differences in subjects' head size, platform limits, sensory states, motivation, etc. Various trajectory shapes can be tolerated for platforms without compromising robust final platform contributions or gaze accuracy.
Defining the fast-phase/saccade interval.
Fast-phase durations are typically reported in experimental work 1) as the interval between saccade initiation and maximum eye deviation (Freedman 2008; Freedman and Sparks 1997; Kardamakis et al. 2010); 2) with a behavioral velocity threshold on gaze velocity (or acceleration) (Goossens and Van Opstal 1997); or 3) from the silent interval on OPN activity (Paré and Guitton 1994). The latter authors have shown, and we hereby corroborate, that marking the moment of maximum eye deviation as the switching time is a very unreliable choice that could occur before, on, or possibly even after the end of the fast phase (or saccade), as defined by the OPN gate (Figs. 4 and 8). Use of a velocity threshold on the gaze profile to extract fast-phase intervals seems more reliable but should be applied to normalized trajectories to minimize context effects. We reiterate that the best and most reliable method for determining the fast-phase interval is by monitoring OPN activity, but this is clearly not feasible in human studies or in noninvasive animal studies. In a noninvasive behavioral approach, an iterative classification-identification method can optimize classification of slow/fast-phase intervals for the best fits and estimate mode intervals more efficiently (Ghoreyshi and Galiana 2010, 2011; Ranjbaran et al. 2015). The seemingly paradoxical findings of Fuchs et al. (2005) and Roy and Cullen (1998, 2002) provide an example of the impact of different interpretations of the saccadic interval on the evaluation of neural firings. Fuchs et al. reported that the majority of their identified PVP neurons were full-pause PVPs (complete pause during the gaze shift) and not partial pause PVPs (partial pause during the gaze shift), whereas Roy and Cullen appeared to report the opposite. Closer inspection reveals that Fuchs et al. marked the end of the gaze shift as the moment of maximum eye deviation (item 1 above), whereas Roy and Cullen applied a threshold on gaze velocity to extract this moment (item 2 above), which we consider more accurate. If the same method is applied to both studies for determining the saccadic interval, the results are consistent (i.e., PVPs are mostly partial pause with the latter definition for the saccadic interval).
Defining fast-phase/saccade intervals in a shared structure.
The term “saccade” has been widely used to refer to rapid eye movements in the head-fixed condition. If, as claimed here, the eye and head share a common drive, then if the eye is in saccadic mode, the head must also be in this mode. However, we expect the impact of phase changes on the head trajectory to be much less dramatic compared with their impact on the eye trajectory simply because of the more sluggish low-pass nature of the head plant compared with the eye plant. For example, one can find better correlation between the eye velocity profiles and OPN firing profiles in Fig. 4 compared with the head velocity profiles and the OPN firing profiles, even though we know that all of those simulated responses come from a common drive model. Phillips et al. (1999) suggested that due to the insignificant correlation of OPN firing with head movement during a head-free gaze shift, it is unlikely that the OPNs control the head movements and are instead limited to controlling eye burst generators. However, their recorded experimental gaze shifts and OPN profiles are quite similar to our simulated gaze shifts using the common drive SMF model, which challenges their conclusion [e.g., compare Fig. 3A of Phillips et al. (1999) with our Fig. 4A]. This article suggests the generalization of the definition of a saccade to include “saccadic head movements” during OPN pause intervals, which is consistent with the observation of bursts on neck EMG during eye saccades (Berthoz et al. 1982; Corneil et al. 2002a, 2002b; Lestienne et al. 1984; Vidal et al. 1982). In other words, the changing dynamics of slow and fast responses should appear on both eye and head trajectories: the head response dynamics are not constant (like the eye), and analysis of head trajectories should take this into account. In our view, gaze control is a multimode system for both eye and head (and any other platform supporting gaze), with OPNs acting as the global state controller.
Moving SC hill vs. decaying SC hill.
A topic of controversy concerning the role of the SC and strategies in gaze orientation is whether the activity on the SC during a gaze shift resembles 1) a moving hill, with the location of the center of activity pointing to the ongoing gaze error (suggested in cats by Guitton et al. 2003; Matsuo et al. 2004; Munoz et al. 1991b), or 2) a decaying hill, with the height (i.e., net activity) of the hill representing the ongoing gaze error (suggested in monkeys by Van Opstal and Kappen 1993; Waitzman et al. 1991). A major argument for rejecting the moving hill hypothesis is that in monkeys, the hill of activity, moving rostrally toward the fixation zone during a gaze shift, lags the ongoing gaze error and hence is considered unlikely to cause saccade termination at the appropriate time (Soetedjo et al. 2002). Although the SMF model does not make any strict assumption as to the SC strategy for providing and updating its feedback (i.e., does not take sides with regard to moving vs. decaying hill hypotheses), it provides interesting insight for this debate: all of the simulations described in this article were done using a filtered (∼delayed) version of the ongoing gaze error as the output of the colliculus block (see Implementation and Supporting Anatomy an Physiology, Table 2, and appendix, Eq. A2). The time constant for the collicular low-pass filter is SCTc = 10 ms in the simulations. However, this time constant can even be multiplied by a factor of 4 without distorting the gaze shift (this can be tested on the model simulator provided). This has a crucial implication: the SMF model is quite robust to the update delay of the collicular drive. This suggests that “delays between the center of activity on the SC and the actual ongoing gaze error do not necessarily reject the moving hill hypothesis.” Further investigations on this topic are left to SC-focused work in the future.
Measures of a Good Model for Gaze Orientation
Are main sequences enough to validate a model?
Numerous models for gaze orientation have been proposed, each having its own advantages and drawbacks (Tables 1 and 3 list a few). Some focus on active gaze shifts and ignore external head perturbations during saccadic components (Freedman 2001; Kardamakis et al. 2010); others focus mainly on behavior without comparing internal signals to reported neural responses (Daye et al. 2014; Freedman 2001; Goossens and Van Opstal 1997; Kardamakis et al. 2010), and some treat the gaze shift technically as one saccadic phase, assuming integrators will hold the endpoints (Daye et al. 2014; Freedman 2001).
Daye et al. (2014) suggested that the ability of a model to replicate main sequences is a good measure to guarantee its compatibility with behavior. We propose that simulating behavior should include responses to external perturbations as a very important aspect of the behavior. This component is absent in current main sequence reports. Also, the main sequence results coming from one model structure could be quite variable depending on the parameters used in the components (Fig. 13 is an example with some changes in specific metrics for 3 parameter sets using the same structure). Moreover, main sequence analyses typically consider aligned gaze shifts starting from the midline, and hence their scope is very limited with respect to initial conditions. The data in Fig. 8 confirm that such simple modifications can have significant effects on behavior. In addition, the high level of scatter typically observed in main sequence results (see references cited above) prevents us from accurate model parameter estimation. A strategy typically used to mimic main sequence results is to replicate an average fit (e.g., Daye et al. 2014), which severely limits the observed response variability. Moreover, main sequence figures are often generated by defining the switching time as the moment of maximum eye deviation, which is known not to be necessarily consistent with the OPN firing profile (Freedman 2001; Goossens and Van Opstal 1997; Guitton and Volle 1987; Laurutis and Robinson 1986; Paré and Guitton 1998; Phillips et al. 1995; Tomlinson and Bahra 1986). This could be partly responsible for the huge amount of observed scatter in main sequence plots. In all of our main sequence plots we have used the definition of saccadic/fixation intervals based on OPN activity. This could account for slight mismatches between our main sequence results and the ones reported in the literature (although the overall shapes are pretty similar). Altogether, based on the mentioned limitations, main sequences can be inefficient in discovering the underlying structure of the gaze orientation system. In this article, we have emphasized central responses and lesions as an intrinsic aspect of model validation. Main sequence analysis cannot, in isolation, validate a proposed model structure. Put another way, many models can produce the same behavior with diverging assumptions (a realization problem with infinite solutions), whereas validation of those assumptions requires more than just replicating behavior: behavioral models can be forced a priori to accurately match current main sequences, but they cannot make any testable predictions on neural interactions or lesions. Models based on neural topology, once refined and validated, can produce useful predictions to aid in mapping behavioral symptoms into lesion sites. The exercise in this article is a step in that direction.
Predictions on Neural Connectivity and Discharges
VO cell anatomy and projections.
In the SMF model, we have hypothesized projections from VO cells to the SLBNs (inhibitory type II to ipsilateral SLBN and/or excitatory type I to ipsilateral SLBN). Aside from the behavioral implications for generating VOR-like responses during fast phases with long-duration perturbations (discussed above; Fig. 7), these postulated projections could explain some central observations: SLBNs are reported to react almost instantaneously (<7 ms) to external head perturbations during fast phases (Sylvestre and Cullen 2006), despite heavy suppression of PVP activity. Hence, some cell type with vestibular sensitivity, other than PVPs or BDNs, must project the passive component of head movement to SLBNs, as predicted by Fuchs et al. (2005). VO neurons seem to be the perfect fit for this role (Cullen et al. 2011; Cullen and Roy 2004; McCrea et al. 1999; Roy and Cullen 2004). VO projections to eye Mn have not been found in previous studies, but their fibers were traced near the PPRF (Boyle et al. 1996). Validating a VO projection to SLBNs would require tracing studies or spike-triggered averaging during saccades when SLBNs are active; otherwise, detection would be impossible with hyperpolarized bursters. Another interesting question is deducing the projection directions (ipsi- or contralateral) of the type I and II VO cells to resolve an apparent paradox: long-duration perturbations result in compensatory responses from the eye and head to preserve gaze trajectories, whereas short-duration perturbations that reverse head motion result in seemingly anti-compensatory responses (compare Figs. 6A and 7). To explain this, we should consider the bilateral nature of the gaze orientation system and the difference between the two experiments: opposing long-duration perturbations of Fig. 7 (Boulanger et al. 2012) did not result in head reversals like the short-duration perturbations of Fig. 6 (Sylvestre and Cullen 2006). Any head reversal could lead to the inactivation of ipsiversive (to the direction of the gaze shift) type I VO neurons and activation of contraversive type II cells. In the SMF model, the projection type of ipsiversive type I VO neurons is chosen to be excitatory to replicate the long-duration experiments, whereas contraversive type II VO neurons have inhibitory projections, to resolve the apparent conflict in experimental results. The simulations are consistent with published results, but the assumed projections have not been confirmed and remain hypothetical. Note that without VO cells during perturbations, this model can still produce gaze shifts that land on target using the gaze-error loop, but at the cost of an altered gaze shift trajectory. The characteristics of VO or similar cells are essential to provide compensation with short delays and to preserve both gaze shift accuracy and its trajectory. Such cells must react only to the passive (unexpected) component of head motion.
The VO pathway for perturbation compensation is indeed a substrate for a kind of VOR. However, it is not the VOR in its classical sense where the PVP is the second level of the three-neuron arc. A complication arises in analyzing the VOR gain at different moments during gaze orientation and fixation: the interplay of the two PVP/VO mechanisms makes it difficult to define their individual contributions to vestibular compensation (e.g., VOR gain). The SMF model predicts a variety of vestibular compensation profiles based on the possible combination of gains for these two pathways. This is probably why, as mentioned by Fuchs et al. (2005), “…For these large gaze shifts, the depth and time course of VOR suppression varies widely from subject to subject.”
NL gain fields projecting to head Mn.
Much of the flexibility in eye/head trajectories relies on two NL gain fields in the circuit. The first is part of the projection from SC to the brain stem (tv) and is consistent with existing data (Grantyn et al. 2002) regarding increasing projection numbers and sensitivities when moving from rostral to caudal areas of the SC. The second NL field tunes the sensitivity of head motoneurons to collaterals of eye motoneuronal drives (sg). The implementation relies on a premotor pool projecting to head Mn that would exhibit either a typical recruitment effect (more active neurons for larger target eccentricities) or a shift in active neural pool (different neurons selected for different goal eccentricities relative to trunk midline). Both are equivalently embedded in the NL curves described in the methods and appendix. If this mechanism for adaptive changes in eye-head contributions is to be validated, it will require that neural activity in such a pool be correlated simultaneously with both head metrics (position/velocity) and target eccentricity relative to the trunk, a necessary condition to replicate the NL behavior of eye/head final amplitudes and still allow for added head goals.
Coordinate system of an independent head goal.
Despite coordinated responses of eye and head during a gaze shift, it remains possible to also drive the head to an independent spatial goal (re body). This requires that the eye remain within its OMR to reach the gaze target (T), and therefore that the additional head goal (H) satisfy |T − H| ≤ OMR. In the model, an independent head goal (separate from gaze goal) only requires adding another input to head Mn in the current circuit (Fig. 3). This could be carried directly to head Mn by TSN (already in Fig. 3; Rezvani and Corneil 2008) or by separate pools from the SC responding to head goals (Walton et al. 2007). The coordinate system for independent head goals needs to be explored experimentally. In this model, we relied on a head offset that is correlated with the distance between the desired specific head goal and the default head goal; in other words, it is not in head motor coordinates, but rather related to the retinal distance between gaze and head targets. Clearly, other options are possible and should be explored on the basis of recent observations in the SC during head-free tasks with separate goals for gaze and head (Corneil et al. 2002a; Stuphorn 2007; Walton et al. 2007). Anatomically, the SMF model postulates a separate input from the SC to the NRG area known to project to head Mn, to allow distinct head and gaze goals. The present study confirms that head goals need not perturb a gaze task, but the mechanism used in biology remains unknown.
Weaknesses and Limitations: Future Work
Inclusion of an explicit Cb in the gaze model.
Cerebellar networks have been submerged in the current SMF model, with the use of appropriate parameters for brain stem processes. This allowed us to illustrate the available diversity of responses from the brain stem networks themselves. However, Cb interconnections are essential to handle learning protocols, or recovery from lesions in SC, brain stem, and sensory areas, that do not include Cb lesions (Cullen 2012; Lisberger 1996; Miles and Lisberger 1981; Optican and Robinson 1980; Yang and Lisberger 2014a, 2014b). As a result, the assumption behind our Cb integration into the brain stem elements was that the SMF model represents the tuned gaze system at its adjusted state (no learning required). Thus the current SMF model cannot account for learning, plasticity, and compensation in the gaze system. Whereas the Cb model reduction by integration into the brain stem counterparts is the common practice among most gaze models (see Table 1), Optican and colleagues propose a Cb-centric model for gaze orientation in their works (Daye et al. 2014; Quaia et al. 1999; Lefèvre et al. 1998). It necessitates the inclusion of an “explicit” Cb as the key element in gaze orientation. Their logical basis for this scheme is that lesions in many brain stem centers (e.g., SC and OPNs) do not result in permanent deficits in saccade generation (velocity and accuracy; Aizawa and Wurtz 1998; Quaia et al. 1998), whereas Cb lesions do (Optican and Robinson 1980). Hence they consider the SC “less important” and the Cb “more relevant” with regard to saccade generation (Quaia et al. 1999). However, there are a few points to consider. When the Cb is lesioned, two deficits occur: 1) several loops in the circuit are interrupted, since it is connected to many brain stem sites; and 2) there is a loss of the capacity to learn or correct deficits (as opposed to SC-focal lesions). The first effect (1) in any circuit will cause simultaneous changes in dynamics (time constants) and accuracy (gain), as reported with inaccurate saccades (Optican and Robinson 1980). However, and this is noteworthy, saccades are still executed! The second effect (2) means that there is no mechanism left to correct the deficit. Therefore, our interpretation is opposite to either SC-centric or Cb-centric views. We believe that a brain stem circuit (BN and OPN) is essential for the generation of rapid eye movements, whereas the main effect of Cb loss is decalibration of the brain stem circuit and loss of the capacity to recalibrate. Correlating the presence or absence of an element with a specific function is not reliable in a complex system. Lesion studies may be useful in providing us with some insight or intuition on possible roles for subprocesses, but they are insufficient to serve as the sole ground for adapting or rejecting different hypotheses. In addition, although the model studies of Lefèvre et al. (1998), Quaia et al. (1999), and Daye et al. (2014) did include a reduced explicit cerebellar network for head-free saccades, they did not address how to apply it in a Cb-lesion or learning context: in these models, if the Cb is lesioned, the choking mechanism will inevitably be compromised, which would in turn result in an inability to stop gaze shifts. In the words of Quaia et al. (1999), “. . . the duration of the [SC] drive is such that it always would produce hypermetric movements” and that the cerebellum “. . . ends the saccade by choking off the collicular drive.” However, as mentioned earlier, Cb lesions have been shown to result in gaze shift size dysmetria (including hypometria; Büttner and Büttner-Ennever 2006), with no effect on their ability to stop. As a result, the presence of an explicit Cb in these models does not seem to guarantee better predictions of lesion effects.
To conclude, like many before us (see Table 1), we have decided not to include an explicit Cb in the current version of the SMF model and have instead integrated it into the parameters of brain stem counterparts. The main reasons for this are as follows: 1) Our focus is on modeling the “calibrated state” of the gaze system that does not require tuning, compensation, or calibration. Within this defined scope, model reduction (i.e., the implicit representation of the Cb in the model) does not equate loss of function (see Fig. 2 for a visual summary of our model reduction). 2) There are insufficient simultaneous recordings of different brain stem and Cb regions. As a result, we do not have sufficient quantitative insight into the exact interplay of the Cb oculomotor regions and the different brain stem centers. However, we have much more data from the brain stem recordings that embed the total effect of the brain stem and Cb projections. As a result, lumping the Cb and brain stem seems to better reflect the state of the art of our knowledge with regard to gaze orientation. The inclusion of an explicit Cb calls for numerous speculations about the actual projection weights, since there are insufficient data for robust evaluation of these weights. 3) Lesion studies can be quite inconclusive when it comes to understanding the roles of individual elements in a complex system (e.g., removing the car battery results in the total failure of the car as a complex system, but does this mean that the battery is the most important constituent of the car? How can one quantitatively evaluate the relative “importance” and “interplay” of different system elements through lesion studies?). As a result, the observations of the effects of Cb lesions (Optican and Robinson 1980) are not sufficient to justify a Cb-centric viewpoint or to necessitate the inclusion of an “explicit” Cb, for that matter.
In the future, given the availability of more recordings from the Cb oculomotor and the brain stem centers, an explicit Cb could be added to allow for additional functions and predictions, especially when it comes to plasticity and learning in the gaze system. The classical paper by Miles and Lisberger (1981) is a prime example of how Cb pathway can change during learning, appearing dominant in the short term but retreating to normal levels once long-term compensation is achieved.
Bilateral circuits for binocular eye/head coordination in horizontal plane.
The circuit is limited to a “conjugate eye” coordinated with the head in the horizontal plane. Modeled VN cells are PVP/BDN and VO types, excluding well-known eye-head velocity (EHV) cells that serve an important role in the nonlinear aspects of disconjugate binocular reflexes (Chen-Huang and McCrea 1999; Meng and Angelaki 2006). EHVs are currently included in our bilateral models of the binocular VOR (Ranjbaran Hesarmaskan and Galiana 2013). The SMF model should be expanded to a bilateral form, including two SC maps, PVP/VO and EHV cells (in bilateral VN) to study binocular adaptive or context-dependent responses. For example, there is little work on vergence responses during horizontal head-free gaze shifts, yet transient vergence responses have been reported in the monkey, even when executing head-fixed saccades to targets requiring only version (Sylvestre et al. 2002).
Applications to reflexes with nystagmus.
The SMF model can replicate horizontal nystagmus during head-free pursuit, VOR during whole body passive rotation in the dark, and combined active pursuit/VOR; the key is the OPN mechanism to switch modes and the fusion of vestibular/visual signals in circuits shared by eye and head. Simulations and validation of such responses are beyond the scope of this article and will be addressed elsewhere. The point is that a model of gaze control should produce realistic behavioral and central responses even if only subcomponents of its circuit are available. For example, if the head is fixed to the body, this opens the feedback loop, providing an efference copy of head velocity (from DTN) and so activates VO cells (for the case of passive rotations). A moving target in the light with a free head instead activates all potential loops including via vision (retinae), two colliculi, and weak VO activity in the absence of perturbations. It is clear that the characteristics of any nystagmus will depend heavily on the experimental conditions.
Extending to higher dimensions.
Our focus in the current SMF model is on horizontal gaze orientations where a sum/average effect is sufficient to represent the SC (1-D). A natural extension would be to combine horizontal and vertical aspects of eye-head coordination by interconnecting two SMF-style models, each dedicated to one motor direction, with 2-D maps from bilateral colliculi. With the current approach (Fig. 3), the addition of a vertical component interconnected with the horizontal circuit could replicate the curved gaze trajectories in 2-D reported by Tweed et al. (1995) and Goossens and Van Opstal (1997) during head-free gaze shifts. Preliminary results for 2-D pursuit have been published previously and demonstrate the feasibility of this approach (Lee and Galiana 2005).
Explicit implementation of a head velocity estimate.
At this time, an accurate head velocity estimate is presumed to exist and is fed back to the SC, together with eye velocity, to update gaze error. Reconstruction of such a head estimate should be implemented explicitly, based on the known dynamics of potential contributors (spindles, tendon organs, premotor SLBN, or reafference). This would allow evaluation of the importance of each contribution and hence predict the effect of losses for rehabilitation. Lidocaine injections in neck proprioceptive afferents may allow evaluation of some elements without damage to central circuits.
Other motor systems.
This model of eye-head coordination raises new possibilities in motor control. The concepts proposed have been transferred to arm control, for example, in a preliminary study by Stefanovic and Galiana (2014, 2016) on simple reaching. The results show the feasibility of a spinal approach such that two limb segments are coordinated without trajectory planning, as in gaze control, and share an endpoint error (finger/wrist to target) using similar NL gain fields. Understanding a possibly general strategy for platform or segment coordination could lead to more user-friendly prosthetics with lower computational demands (no planning).
GRANTS
This research was supported by the Canadian Institutes of Health Research and National Sciences and Engineering Research Council of Canada. I. Haji-Abolhassani was supported by a Fonds de recherche du Québec - Nature et technologies scholarship and a bursary from the Systems Biology Training Program at McGill University.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
I.H.-A. and H.L.G. conception and design of research; I.H.-A. and H.L.G. performed experiments; I.H.-A., D.G., and H.L.G. analyzed data; I.H.-A., D.G., and H.L.G. interpreted results of experiments; I.H.-A. and H.L.G. prepared figures; I.H.-A. and H.L.G. drafted manuscript; I.H.-A., D.G., and H.L.G. edited and revised manuscript; I.H.-A., D.G., and H.L.G. approved final version of manuscript.
Glossary Cell Types, Brain Stem Sites, and Signals
- DTN
Dorsal tegmental nucleus
- E
Eye position (deg)
Eye velocity (deg/s)
- E*
Efference copy of eye position from NPH/MVN
Internal estimate of eye velocity available from “model” with reafference to NPH
- eg
Projection gain of PVP to motoneurons
- Emn
Eye motoneurons; scaled firing activity
- ep
Projection gain from the eye efference copy (E*) to VN
- gb
Projection gain from TRN to SLBN
- ΔG
Initial gaze error; required gaze shift size imposed = TL − (E0 + H0); i.e., initial retinal error
- Ge
Dynamic gaze error from SC driving eye/head coordination, low-pass filtered using 10-ms time constant to smooth sudden steps as seen in tectal responses
- H
Head position (deg)
Head velocity (deg/s)
Sensory estimate of head velocity from the semicircular canals
Internal estimate of active component of head velocity from DTN using reafference
Accurate estimate of head velocity to update gaze error using sensory fusion
- Hmn
Head motoneurons; scaled firing activity
- LLBN
Long-lead burst neurons; scaled firing activity
- Mn
Motoneuron
- MVN
Medial vestibular nucleus
- NPH
Nucleus prepositus hypoglossi
- NRG
Nucleus reticularis gigantocellularis
- NRI
Nuclear raphe interpositus
- OPN
Omnipause neurons, switching controller circuit between slow and fast parameter sets
- P
Projection gain from primary vestibular signals to VN
- PPRF
Paramedian pontine reticular formation
- PVP
Position-vestibular-pause neurons projecting to motoneurons; scaled firing activity
- SAT
Saturation limit for SLBN sensitivity to TRN projections
- SC
Superior colliculus
- SCC
Semicircular canals; scaled firing activity
- sg
Nonlinear gain from Emn to Hmn that controls relative plant contributions; the nonlinearity is a function of target location relative to the trunk (TL)
- SLBN
Short-lead burst neurons in pontine reticular formation, active during saccades or VOR fast phases and projecting to ocular motoneurons and pre-spinal areas; scaled firing activity
- th
Projection gain from TRN to Hmn
- TL
Target location relative to the trunk: ΔG + (E0 + H0)
- TRN
Tectoreticular neurons; scaled firing activity
- tv
Nonlinear gain field from Ge on the SC map to TRNs
- tvn
Projection gain from TRN to VN
- VN
Vestibular nucleus
- vnb
Projection gain from PVP cells to SLBN
- VO
Vestibular-only neurons in the VN that respond only to the passive component of head velocity (perturbations or forced body/head motion); scaled firing activity
- vob
Projection gain from VO to SLBN
- vog
Projection gain from VO to Hmn
Appendix: Model Components And Equations
Refer to the glossary in the Introduction for definitions of anatomical sites, neural cell types, and model parameters used in the following equations.
Equations Defining Central Cell Responses (in Fig. 3)
| (A1) |
represents ongoing gaze error (not shown in Fig. 3).
| (A2) |
is filtered gaze error, which is the low-passed version of Geu.
| (A3) |
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
| (A9) |
where TL is target location relative to the trunk midline.
Transfer Functions for Canals and Eye/Head Platforms
For SCC,
where the time constant Tc = 15 s and gain = 1 (including velocity storage). For a plugged canal,
where Tc = 30 ms with gain of 0.3.
For head plant,
where the double time constant = 300 ms and gain = 1. For eye plant,
where time constants = 200 and 30 ms and gain = 1.
The head speed model
matches real head plant velocity. The head velocity estimation assumes all sensory sources:
The eye plant model
matches real eye plant velocity.
Steady-State Analysis of the Model
Gaze orientation to a flashed target uses remembered target in space as the input (step = initial error pulse integrated by the SC); eye and head trajectories are the responses (outputs) to this stimulus. We can calculate the transfer functions for the plant responses in the Laplace domain, assuming linearity of the model (i.e., constant static parametric gains for tv and sg) in the equations above. This is a valid assumption in steady state, despite the embedded NL gain fields, for two reasons: 1) sg is fixed throughout a given gaze shift by the target location relative to the trunk (TL), and 2) in steady state, tv nonlinearity has decreased to its lower limit for small gaze errors. The steady-state gains for the platforms can then be estimated for both saccadic and slow-phase (fixation) responses, which reflect platform contributions expected at the end of saccades or slow phases. These gains define the final amplitude of each platform divided by gaze position relative to the trunk at the end of each phase:
A steady-state gain in the fast phase is the observed eye and head amplitude if the controller remained trapped in the fast mode, normalized by the target location retrunk. This is never seen unless OPNs are forcibly kept silent by chemicals or other means. On the other hand, the slow-phase steady states can be seen at the end of fixation periods and so are measurable. Given
we have
| (A10) |
To ensure that the system acquires the target correctly in both modes, we should have
| (A11) |
As a result, we have the necessary conditions
| (A12) |
which simplify the steady-state gains to
| (A13) |
Hence, the ratio of steady-state contributions of the head/eye is simply sg in this model, for a given target location. As a result, a NL sg gain, modulated by target retrunk in a given task, can account for the different eye and head final amplitudes so long as the assumed conditions in Eq. A12 are satisfied. If not, a fixed ratio will still appear but will now depend on sg and other parameters.
REFERENCES
- Abrahams V, Rose P. Projections of extraocular, neck muscle, and retinal afferents to superior colliculus in the cat: their connections to cells of origin of tectospinal tract. J Neurophysiol 38: 10–18, 1975. [DOI] [PubMed] [Google Scholar]
- Aizawa H, Wurtz RH. Reversible inactivation of monkey superior colliculus. I. Curvature of saccadic trajectory. J Neurophysiol 79: 2082–2096, 1998. [DOI] [PubMed] [Google Scholar]
- Altman J, Carpenter MB. Fiber projections of the superior colliculus in the cat. J Comp Neurol 116: 157–177, 1961. [DOI] [PubMed] [Google Scholar]
- Andre-Deshays C, Berthoz A, Revel M. Eye-head coupling in humans. Exp Brain Res 69: 399–406, 1988. [DOI] [PubMed] [Google Scholar]
- Badler JB, Keller EL. Decoding of a motor command vector from distributed activity in superior colliculus. Biol Cybern 86: 179–189, 2002. [DOI] [PubMed] [Google Scholar]
- Baker R, Berthoz A. Is the prepositus hypoglossi nucleus the source of another vestibulo-ocular pathway? Brain Res 86: 121–127, 1975. [DOI] [PubMed] [Google Scholar]
- Berthoz A, Vidal P, Corvisier J. Brain stem neurons mediating horizontal eye position signals to dorsal neck muscles of the alert cat. In: Physiological and Pathological Aspects of Eye Movements, edited by Roucoux A, Crommelinck M. The Hague: Dr. Junk, 1982, p. 385–398. [Google Scholar]
- Blanks R, Volkind R, Precht W, Baker R. Responses of cat prepositus hypoglossi neurons to horizontal angular acceleration. Neuroscience 2: 391–403, 1977. [DOI] [PubMed] [Google Scholar]
- Boulanger M, Galiana HL, Guitton D. Human eye-head gaze shifts preserve their accuracy and spatiotemporal trajectory profiles despite long-duration torque perturbations that assist or oppose head motion. J Neurophysiol 108: 39–56, 2012. [DOI] [PubMed] [Google Scholar]
- Boyle R, Belton T, McCrea RA. Responses of identified vestibulospinal neurons to voluntary eye and head movements in the squirrel monkey. Ann NY Acad Sci 781: 244–263, 1996. [DOI] [PubMed] [Google Scholar]
- Büttner-Ennever JA, Horn AK, Henn V, Cohen B. Projections from the superior colliculus motor map to omnipause neurons in monkey. J Comp Neurol 413: 55–67, 1999. [DOI] [PubMed] [Google Scholar]
- Büttner U, Büttner-Ennever J. Present concepts of oculomotor organization. Prog Brain Res 151: 1–42, 2006. [DOI] [PubMed] [Google Scholar]
- Chen-Huang C, McCrea RA. Effects of viewing distance on the responses of horizontal canal-related secondary vestibular neurons during angular head rotation. J Neurophysiol 81: 2517–2537, 1999. [DOI] [PubMed] [Google Scholar]
- Chimoto S, Iwamoto Y, Shimazu H, Yoshida K. Functional connectivity of the superior colliculus with saccade-related brain stem neurons in the cat. Prog Brain Res 112: 157–165, 1996. [DOI] [PubMed] [Google Scholar]
- Choi WY, Guitton D. Firing patterns in superior colliculus of head-unrestrained monkey during normal and perturbed gaze saccades reveal short-latency feedback and a sluggish rostral shift in activity. J Neurosci 29: 7166–7180, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corneil BD, Olivier E, Munoz DP. Neck muscle responses to stimulation of monkey superior colliculus. I. Topography and manipulation of stimulation parameters. J Neurophysiol 88: 1980–1999, 2002a. [DOI] [PubMed] [Google Scholar]
- Corneil BD, Olivier E, Munoz DP. Neck muscle responses to stimulation of monkey superior colliculus. II. Gaze shift initiation and volitional head movements. J Neurophysiol 88: 2000–2018, 2002b. [DOI] [PubMed] [Google Scholar]
- Corneil BD, Olivier E, Richmond FJ, Loeb GE, Munoz DP. Neck muscles in the rhesus monkey. II. Electromyographic patterns of activation underlying postures and movements. J Neurophysiol 86: 1729–1749, 2001. [DOI] [PubMed] [Google Scholar]
- Cowie RJ, Robinson DL. Subcortical contributions to head movements in macaques. I. Contrasting effects of electrical stimulation of a medial pontomedullary region and the superior colliculus. J Neurophysiol 72: 2648–2664, 1994. [DOI] [PubMed] [Google Scholar]
- Cullen K, Belton T, McCrea R. A non-visual mechanism for voluntary cancellation of the vestibulo-ocular reflex. Exp Brain Res 83: 237–252, 1991. [DOI] [PubMed] [Google Scholar]
- Cullen KE. The vestibular system: multimodal integration and encoding of self-motion for motor control. Trends Neurosci 35: 185–196, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cullen KE, Brooks JX, Jamali M, Carriot J, Massot C. Internal models of self-motion: computations that suppress vestibular reafference in early vestibular processing. Exp Brain Res 210: 377–388, 2011. [DOI] [PubMed] [Google Scholar]
- Cullen KE, Guitton D. Analysis of primate IBN spike trains using system identification techniques. II. Relationship to gaze, eye, and head movement dynamics during head-free gaze shifts. J Neurophysiol 78: 3283–3306, 1997. [DOI] [PubMed] [Google Scholar]
- Cullen KE, Guitton D, Rey CG, Jiang W. Gaze-related activity of putative inhibitory burst neurons in the head-free cat. J Neurophysiol 70: 2678–2683, 1993. [DOI] [PubMed] [Google Scholar]
- Cullen KE, Huterer M, Braidwood DA, Sylvestre PA. Time course of vestibuloocular reflex suppression during gaze shifts. J Neurophysiol 92: 3408–3422, 2004. [DOI] [PubMed] [Google Scholar]
- Cullen KE, Roy JE. Signal processing in the vestibular system during active versus passive head movements. J Neurophysiol 91: 1919, 2004. [DOI] [PubMed] [Google Scholar]
- Daemi M, Crawford D. Theoretical understanding of three-dimensional, head-free gaze-shift. BMC Neurosci 15: P184, 2014. [Google Scholar]
- Dale A, Cullen KE. The nucleus prepositus predominantly outputs eye movement-related information during passive and active self-motion. J Neurophysiol 109: 1900–1911, 2013. [DOI] [PubMed] [Google Scholar]
- Daye PM, Optican LM, Blohm G, Lefèvre P. Hierarchical control of two-dimensional gaze saccades. J Comput Neurosci 36: 355–382, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daye PM, Roberts DC, Zee DS, Optican LM. Vestibulo-ocular reflex suppression during head-fixed saccades reveals gaze feedback control. J Neurosci 35: 1192–1198, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean P. Modelling the role of the cerebellar fastigial nuclei in producing accurate saccades: the importance of burst timing. Neuroscience 68: 1059–1077, 1995. [DOI] [PubMed] [Google Scholar]
- Delgado-Garcia J, Vidal P, Gomez C, Berthoz A. A neurophysiological study of prepositus hypoglossi neurons projecting to oculomotor and preoculomotor nuclei in the alert cat. Neuroscience 29: 291–307, 1989. [DOI] [PubMed] [Google Scholar]
- Dichgans J, Bizzi E, Morasso P, Tagliasco V. Mechanisms underlying recovery of eye-head coordination following bilateral labyrinthectomy in monkeys. Exp Brain Res 18: 548–562, 1973. [DOI] [PubMed] [Google Scholar]
- Evinger C, Kaneko C, Fuchs AF. Activity of omnipause neurons in alert cats during saccadic eye movements and visual stimuli. J Neurophysiol 47: 827–844, 1982. [DOI] [PubMed] [Google Scholar]
- Evinger C, Manning KA, Pellegrini JJ, Basso MA, Powers AS, Sibony PA. Not looking while leaping: the linkage of blinking and saccadic gaze shifts. Exp Brain Res 100: 337–344, 1994. [DOI] [PubMed] [Google Scholar]
- Freedman EG. Coordination of the eyes and head during visual orienting. Exp Brain Res 190: 369–387, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman EG. Interactions between eye and head control signals can account for movement kinematics. Biol Cybern 84: 453–462, 2001. [DOI] [PubMed] [Google Scholar]
- Freedman EG, Sparks DL. Eye-head coordination during head-unrestrained gaze shifts in rhesus monkeys. J Neurophysiol 77: 2328–2348, 1997. [DOI] [PubMed] [Google Scholar]
- Fuchs AF, Ling L, Phillips JO. Behavior of the position vestibular pause (PVP) interneurons of the vestibuloocular reflex during head-free gaze shifts in the monkey. J Neurophysiol 94: 4481–4490, 2005. [DOI] [PubMed] [Google Scholar]
- Fuller JH. Head movement propensity. Exp Brain Res 92: 152–164, 1992. [DOI] [PubMed] [Google Scholar]
- Galiana H, Guitton D. Central organization and modeling of eye-head coordination during orienting gaze shifts. Ann NY Acad Sci 656: 452–471, 1992. [DOI] [PubMed] [Google Scholar]
- Galiana H, Smith H, Katsarkas A. Modelling non-linearities in the vestibulo-ocular reflex (VOR) after unilateral or bilateral loss of peripheral vestibular function. Exp Brain Res 137: 369–386, 2001. [DOI] [PubMed] [Google Scholar]
- Galiana HL. A nystagmus strategy to linearize the vestibulo-ocular reflex. IEEE Trans Biomed Eng 38: 532–543, 1991. [DOI] [PubMed] [Google Scholar]
- Gandhi NJ. Interactions between gaze-evoked blinks and gaze shifts in monkeys. Exp Brain Res 216: 321–339, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandhi NJ, Keller EL. Spatial distribution and discharge characteristics of superior colliculus neurons antidromically activated from the omnipause region in monkey. J Neurophysiol 78: 2221–2225, 1997. [DOI] [PubMed] [Google Scholar]
- Gandhi NJ, Sparks DL. Dissociation of eye and head components of gaze shifts by stimulation of the omnipause neuron region. J Neurophysiol 98: 360–373, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghoreyshi A, Galiana H. Automatic classification and robust identification of vestibulo-ocular reflex responses: from theory to practice. J Comput Neurosci 31: 347–368, 2011. [DOI] [PubMed] [Google Scholar]
- Ghoreyshi A, Galiana HL. Simultaneous identification of oculomotor subsystems using a hybrid system approach: introducing hybrid extended least squares. IEEE Trans Biomed Eng 57: 1089–1098, 2010. [DOI] [PubMed] [Google Scholar]
- Goffart L, Pélisson D. Orienting gaze shifts during muscimol inactivation of caudal fastigial nucleus in the cat. I. Gaze dysmetria. J Neurophysiol 79: 1942–1958, 1998. [DOI] [PubMed] [Google Scholar]
- Goossens H, Van Opstal AJ. Dynamic ensemble coding of saccades in the monkey superior colliculus. J Neurophysiol 95: 2326–2341, 2006. [DOI] [PubMed] [Google Scholar]
- Goossens H, Van Opstal AJ. Human eye-head coordination in two dimensions under different sensorimotor conditions. Exp Brain Res 114: 542–560, 1997. [DOI] [PubMed] [Google Scholar]
- Grantyn A, Brandi AM, Dubayle D, Graf W, Ugolini G, Hadjidimitrakis K, Moschovakis A. Density gradients of trans-synaptically labeled collicular neurons after injections of rabies virus in the lateral rectus muscle of the rhesus monkey. J Comp Neurol 451: 346–361, 2002. [DOI] [PubMed] [Google Scholar]
- Grantyn A, Ong-Meang Jacques V, Berthoz A. Reticulo-spinal neurons participating in the control of synergic eye and head movements during orienting in the cat. Exp Brain Res 66: 355–377, 1987. [DOI] [PubMed] [Google Scholar]
- Guitton D. Control of eye-head coordination during orienting gaze shifts. Trends Neurosci 15: 174–179, 1992. [DOI] [PubMed] [Google Scholar]
- Guitton D, Bergeron A, Choi WY, Matsuo S. On the feedback control of orienting gaze shifts made with eye and head movements. Prog Brain Res 142: 55–68, 2003. [DOI] [PubMed] [Google Scholar]
- Guitton D, Douglas R, Volle M. Eye-head coordination in cats. J Neurophysiol 52: 1030–1050, 1984. [DOI] [PubMed] [Google Scholar]
- Guitton D, Munoz DP, Galiana HL. Gaze control in the cat: studies and modeling of the coupling between orienting eye and head movements in different behavioral tasks. J Neurophysiol 64: 509, 1990. [DOI] [PubMed] [Google Scholar]
- Guitton D, Volle M. Gaze control in humans: eye-head coordination during orienting movements to targets within and beyond the oculomotor range. J Neurophysiol 58: 427–459, 1987. [DOI] [PubMed] [Google Scholar]
- Hafed ZM, Goffart L, Krauzlis RJ. Superior colliculus inactivation causes stable offsets in eye position during tracking. J Neurosci 28: 8124–8137, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Highstein SM, Holstein GR. The anatomy of the vestibular nuclei. Prog Brain Res 151: 157–203, 2006. [DOI] [PubMed] [Google Scholar]
- Hikosaka O, Igusa Y, Imai H. Inhibitory connections of nystagmus-related reticular burst neurons with neurons in the abducens, prepositus hypoglossi and vestibular nuclei in the cat. Exp Brain Res 39: 301–311, 1980. [DOI] [PubMed] [Google Scholar]
- Horn AK. The reticular formation. Prog Brain Res 151: 127–155, 2006. [DOI] [PubMed] [Google Scholar]
- Izawa Y, Sugiuchi Y, Shinoda Y. Neural organization from the superior colliculus to motoneurons in the horizontal oculomotor system of the cat. J Neurophysiol 81: 2597–2611, 1999. [DOI] [PubMed] [Google Scholar]
- Kardamakis A, Grantyn A, Moschovakis A. Neural network simulations of the primate oculomotor system. V. Eye-head gaze shifts. Biol Cybern 102: 209–225, 2010. [DOI] [PubMed] [Google Scholar]
- Kardamakis AA, Moschovakis AK. Optimal control of gaze shifts. J Neurosci 29: 7723–7730, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katnani HA, Van Opstal AJ, Gandhi NJ. A test of spatial temporal decoding mechanisms in the superior colliculus. J Neurophysiol 107: 2442–2452, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawamura K, Brodal A, Hoddevik G. The projection of the superior colliculus onto the reticular formation of the brain stem an experimental anatomical study in the cat. Exp Brain Res 19: 1–19, 1974. [DOI] [PubMed] [Google Scholar]
- Keller E. Colliculoreticular organization in the oculomotor system. Prog Brain Res 50: 725–734, 1979. [DOI] [PubMed] [Google Scholar]
- Kuo BC, Golnaraghi MF. Automatic Control Systems. New York: John Wiley & Sons, 2003. [Google Scholar]
- Laurutis V, Robinson D. The vestibulo-ocular reflex during human saccadic eye movements. J Physiol 373: 209–233, 1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee WJ, Galiana HL. An internally switched model of ocular tracking with prediction. IEEE Trans Neural Syst Rehabil Eng 13: 186–193, 2005. [DOI] [PubMed] [Google Scholar]
- Lefèvre P, Bottemanne I, Roucoux A. Experimental study and modeling of vestibulo-ocular reflex modulation during large shifts of gaze in humans. Exp Brain Res 91: 496–508, 1992. [DOI] [PubMed] [Google Scholar]
- Lefèvre P, Quaia C, Optican LM. Distributed model of control of saccades by superior colliculus and cerebellum. Neural Netw 11: 1175–1190, 1998. [DOI] [PubMed] [Google Scholar]
- Lestienne F, Vidal P, Berthoz A. Gaze changing behaviour in head restrained monkey. Exp Brain Res 53: 349–356, 1984. [DOI] [PubMed] [Google Scholar]
- Lisberger SG. Motor learning and memory in the vestibulo-ocular reflex: the dark side. Ann NY Acad Sci 781: 525–531, 1996. [DOI] [PubMed] [Google Scholar]
- Lopez-Barneo J, Darlot C, Berthoz A, Baker R. Neuronal activity in prepositus nucleus correlated with eye movement in the alert cat. J Neurophysiol 47: 329, 1982. [DOI] [PubMed] [Google Scholar]
- Maeda M, Shibazaki T, Yoshida K. Labyrinthine and visual inputs to the superior colliculus neurons. Prog Brain Res 50: 735–743, 1978. [DOI] [PubMed] [Google Scholar]
- Matsuo S, Bergeron A, Guitton D. Evidence for gaze feedback to the cat superior colliculus: discharges reflect gaze trajectory perturbations. J Neurosci 24: 2760–2773, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May P. The mammalian superior colliculus: laminar structure and connections. Prog Brain Res 151: 321–378, 2006. [DOI] [PubMed] [Google Scholar]
- McCrea R, Horn A. Nucleus prepositus. Prog Brain Res 151: 205–230, 2006. [DOI] [PubMed] [Google Scholar]
- McCrea RA, Gdowski GT, Boyle R, Belton T. Firing behavior of vestibular neurons during active and passive head movements: vestibulo-spinal and other non-eye-movement related neurons. J Neurophysiol 82: 416–428, 1999. [DOI] [PubMed] [Google Scholar]
- Meng H, Angelaki DE. Neural correlates of the dependence of compensatory eye movements during translation on target distance and eccentricity. J Neurophysiol 95: 2530–2540, 2006. [DOI] [PubMed] [Google Scholar]
- Miles F, Lisberger S. Plasticity in the vestibulo-ocular reflex: a new hypothesis. Annu Rev Neurosci 4: 273–299, 1981. [DOI] [PubMed] [Google Scholar]
- Missal M, Lefèvre P, Delinte A, Crommelinck M, Roucoux A. Smooth eye movements evoked by electrical stimulation of the cat's superior colliculus. Exp Brain Res 107: 382–390, 1996. [DOI] [PubMed] [Google Scholar]
- Moschovakis AK. The superior colliculus and eye movement control. Curr Opin Neurobiol 6: 811–816, 1996. [DOI] [PubMed] [Google Scholar]
- Munoz D, Guitton D. Tectospinal neurons in the cat have discharges coding gaze position error. Brain Res 341: 184–188, 1985. [DOI] [PubMed] [Google Scholar]
- Munoz DP, Guitton D, Pelisson D. Control of orienting gaze shifts by the tectoreticulospinal system in the head-free cat. III. Spatiotemporal characteristics of phasic motor discharges. J Neurophysiol 66: 1642–1666, 1991a. [DOI] [PubMed] [Google Scholar]
- Munoz DP, Pelisson D, Guitton D. Movement of neural activity on the superior colliculus motor map during gaze shifts. Science 251: 1358–1360, 1991b. [DOI] [PubMed] [Google Scholar]
- Munoz DP, Wurtz RH. Saccade-related activity in monkey superior colliculus. I. Characteristics of burst and buildup cells. J Neurophysiol 73: 2313–2333, 1995. [DOI] [PubMed] [Google Scholar]
- Murray EA, Coulter J. Organization of tectospinal neurons in the cat and rat superior colliculus. Brain Res 243: 201–214, 1982. [DOI] [PubMed] [Google Scholar]
- Nagy B, Corneil BD. Representation of horizontal head-on-body position in the primate superior colliculus. J Neurophysiol 103: 858–874, 2010. [DOI] [PubMed] [Google Scholar]
- Newlands SD, Ling L, Phillips JO, Siebold C, Duckert L, Fuchs AF. Short-and long-term consequences of canal plugging on gaze shifts in the rhesus monkey. I. Effects on gaze stabilization. J Neurophysiol 81: 2119–2130, 1999. [DOI] [PubMed] [Google Scholar]
- Noda H, Sugita S, Ikeda Y. Afferent and efferent connections of the oculomotor region of the fastigial nucleus in the macaque monkey. J Comp Neurol 302: 330–348, 1990. [DOI] [PubMed] [Google Scholar]
- Nudo R, Masterton R. Descending pathways to the spinal cord: II. Quantitative study of the tectospinal tract in 23 mammals. J Comp Neurol 286: 96–119, 1989. [DOI] [PubMed] [Google Scholar]
- Ohki Y, Shimazu H, Suzuki I. Excitatory input to burst neurons from the labyrinth and its mediating pathway in the cat: location and functional characteristics of burster-driving neurons. Exp Brain Res 72: 457–472, 1988. [DOI] [PubMed] [Google Scholar]
- Olivier E, Kitama T, Grantyn A. Anatomical evidence for ipsilateral collicular projections to the spinal cord in the cat. Exp Brain Res 100: 160–164, 1994. [DOI] [PubMed] [Google Scholar]
- Optican L. Control of saccade trajectory by the superior colliculus. In: Contemporary Ocular Motor and Vestibular Research: A Tribute to David A Robinson, edited by Fuchs AF, Brandt T. Büttner U, and Zee D. New York: Thieme Medical, 1994, p. 98–105. [Google Scholar]
- Optican LM. Sensorimotor transformation for visually guided saccades. Ann NY Acad Sci 1039: 132–148, 2005. [DOI] [PubMed] [Google Scholar]
- Optican LM, Robinson DA. Cerebellar-dependent adaptive control of primate saccadic system. J Neurophysiol 44: 1058–1076, 1980. [DOI] [PubMed] [Google Scholar]
- Paré M, Crommelinck M, Guitton D. Gaze shifts evoked by stimulation of the superior colliculus in the head-free cat conform to the motor map but also depend on stimulus strength and fixation activity. Exp Brain Res 101: 123–139, 1994. [DOI] [PubMed] [Google Scholar]
- Paré M, Guitton D. Brain stem omnipause neurons and the control of combined eye-head gaze saccades in the alert cat. J Neurophysiol 79: 3060, 1998. [DOI] [PubMed] [Google Scholar]
- Paré M, Guitton D. The fixation area of the cat superior colliculus: effects of electrical stimulation and direct connection with brainstem omnipause neurons. Exp Brain Res 101: 109–122, 1994. [DOI] [PubMed] [Google Scholar]
- Phillips J, Ling L, Fuchs A, Siebold C, Plorde J. Rapid horizontal gaze movement in the monkey. J Neurophysiol 73: 1632–1652, 1995. [DOI] [PubMed] [Google Scholar]
- Phillips J, Ling L, Siebold C, Fuchs A. Behavior of primate vestibulo-ocular reflex neurons and vestibular neurons during head-free gaze shifts. Ann NY Acad Sci 781: 276–291, 1996. [DOI] [PubMed] [Google Scholar]
- Phillips JO, Ling L, Fuchs AF. Action of the brain stem saccade generator during horizontal gaze shifts. I. Discharge patterns of omnidirectional pause neurons. J Neurophysiol 81: 1284–1295, 1999. [DOI] [PubMed] [Google Scholar]
- Prsa M, Galiana H. Visual-vestibular interaction hypothesis for the control of orienting gaze shifts by brain stem omnipause neurons. J Neurophysiol 97: 1149, 2007. [DOI] [PubMed] [Google Scholar]
- Quaia C, Aizawa H, Optican LM, Wurtz RH. Reversible inactivation of monkey superior colliculus. II. Maps of saccadic deficits. J Neurophysiol 79: 2097–2110, 1998. [DOI] [PubMed] [Google Scholar]
- Quaia C, Lefèvre P, Optican LM. Model of the control of saccades by superior colliculus and cerebellum. J Neurophysiol 82: 999–1018, 1999. [DOI] [PubMed] [Google Scholar]
- Quinet J, Goffart L. Head-unrestrained gaze shifts after muscimol injection in the caudal fastigial nucleus of the monkey. J Neurophysiol 98: 3269–3283, 2007. [DOI] [PubMed] [Google Scholar]
- Ranjbaran M, Galiana HL. The horizontal angular vestibulo-ocular reflex: a nonlinear mechanism for context-dependent responses. IEEE Trans Biomed Eng 60: 3216–3225, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranjbaran M, Smith H, Galiana H. Automatic classification of the vestibulo-ocular reflex nystagmus: integration of data clustering and system identification. IEEE Trans Biomed Eng 63: 850–858, 2016. [DOI] [PubMed] [Google Scholar]
- Raphan T, Matsuo V, Cohen B. Velocity storage in the vestibulo-ocular reflex arc (VOR). Exp Brain Res 35: 229–248, 1979. [DOI] [PubMed] [Google Scholar]
- Raybourn MS, Keller EL. Colliculoreticular organization in primate oculomotor system. J Neurophysiol 40: 861–878, 1977. [DOI] [PubMed] [Google Scholar]
- Rezvani S, Corneil BD. Recruitment of a head-turning synergy by low-frequency activity in the primate superior colliculus. J Neurophysiol 100: 397–411, 2008. [DOI] [PubMed] [Google Scholar]
- Robinson D. The mechanics of human saccadic eye movement. J Physiol 174: 245–264, 1964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson D. The use of control systems analysis in the neurophysiology of eye movements. Annu Rev Neurosci 4: 463–503, 1981a. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Models of the mechanics of eye movements. In: Models of Oculomotor Behavior and Control, edited by Zuber BL. Boca Raton, FL: CRC, 1981b, p. 21–41. [Google Scholar]
- Roucoux A, Guitton D, Crommelinck M. Stimulation of the superior colliculus in the alert cat. Exp Brain Res 39: 75–85, 1980. [DOI] [PubMed] [Google Scholar]
- Roy JE, Cullen KE. Dissociating self-generated from passively applied head motion: neural mechanisms in the vestibular nuclei. J Neurosci 24: 2102–2111, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy JE, Cullen KE. A neural correlate for vestibulo-ocular reflex suppression during voluntary eye-head gaze shifts. Nat Neurosci 1: 404–410, 1998. [DOI] [PubMed] [Google Scholar]
- Roy JE, Cullen KE. Selective processing of vestibular reafference during self-generated head motion. J Neurosci 21: 2131–2142, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy JE, Cullen KE. Vestibuloocular reflex signal modulation during voluntary and passive head movements. J Neurophysiol 87: 2337–2357, 2002. [DOI] [PubMed] [Google Scholar]
- Rucker JC, Ying SH, Moore W, Optican LM, Büttner-Ennever J, Keller EL, Shapiro BE, Leigh RJ. Do brainstem omnipause neurons terminate saccades? Ann NY Acad Sci 1233: 48–57, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russo GS, Bruce CJ. Neurons in the supplementary eye field of rhesus monkeys code visual targets and saccadic eye movements in an oculocentric coordinate system. J Neurophysiol 76: 825–848, 1996. [DOI] [PubMed] [Google Scholar]
- Sadeghi SG, Goldberg JM, Minor LB, Cullen KE. Effects of canal plugging on the vestibuloocular reflex and vestibular nerve discharge during passive and active head rotations. J Neurophysiol 102: 2693–2703, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scudder CA, Kaneko CR, Fuchs AF. The brainstem burst generator for saccadic eye movements. Exp Brain Res 142: 439–462, 2002. [DOI] [PubMed] [Google Scholar]
- Scudder CA, Moschovakis AK, Karabelas AB, Highstein SM. Anatomy and physiology of saccadic long-lead burst neurons recorded in the alert squirrel monkey. I. Descending projections from the mesencephalon. J Neurophysiol 76: 332–352, 1996a. [DOI] [PubMed] [Google Scholar]
- Scudder CA, Moschovakis AK, Karabelas AB, Highstein SM. Anatomy and physiology of saccadic long-lead burst neurons recorded in the alert squirrel monkey. II. Pontine neurons. J Neurophysiol 76: 353–370, 1996b. [DOI] [PubMed] [Google Scholar]
- Sharp PE, Tinkelman A, Cho J. Angular velocity and head direction signals recorded from the dorsal tegmental nucleus of gudden in the rat: implications for path integration in the head direction cell circuit. Behav Neurosci 115: 571, 2001. [PubMed] [Google Scholar]
- Soetedjo R, Kaneko CR, Fuchs AF. Evidence against a moving hill in the superior colliculus during saccadic eye movements in the monkey. J Neurophysiol 87: 2778–2789, 2002. [DOI] [PubMed] [Google Scholar]
- Sparks D. Population coding of saccadic eye movements by neurons in the superior colliculus. Nature 332: 24, 1988. [DOI] [PubMed] [Google Scholar]
- Sparks DL, Barton EJ, Gandhi NJ, Nelson J. Studies of the role of the paramedian pontine reticular formation in the control of head-restrained and head-unrestrained gaze shifts. Ann NY Acad Sci 956: 85–98, 2002. [DOI] [PubMed] [Google Scholar]
- Sperry RW. Neural basis of the spontaneous optokinetic response produced by visual inversion. J Comp Physiol Psychol 43: 482, 1950. [DOI] [PubMed] [Google Scholar]
- Stahl JS. Amplitude of human head movements associated with horizontal saccades. Exp Brain Res 126: 41–54, 1999. [DOI] [PubMed] [Google Scholar]
- Stechison M, Saint-Cyr J, Spence S. Projections from the nuclei prepositus hypoglossi and intercalatus to the superior colliculus in the cat: an anatomical study using WGA-HRP. Exp Brain Res 59: 139–150, 1985. [DOI] [PubMed] [Google Scholar]
- Stefanovic F, Galiana HL. Efferent feedback in an adaptive spinal-like controller: reaching with perturbations. IEEE Trans Neural Syst Rehabil Eng 24: 140–150, 2016. [DOI] [PubMed] [Google Scholar]
- Stefanovic F, Galiana HL. A simplified spinal-like controller facilitates muscle synergies and robust reaching motions. IEEE Trans Neural Syst Rehabil Eng 22: 77–87, 2014. [DOI] [PubMed] [Google Scholar]
- Stuphorn V. New functions for an old structure: superior colliculus and head-only movements. Focus on “The role of primate superior colliculus in the control of head movements”. J Neurophysiol 98: 1847–1848, 2007. [DOI] [PubMed] [Google Scholar]
- Sylvestre PA, Cullen KE. Premotor correlates of integrated feedback control for eye-head gaze shifts. J Neurosci 26: 4922–4929, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sylvestre PA, Galiana HL, Cullen KE. Conjugate and vergence oscillations during saccades and gaze shifts: implications for integrated control of binocular movement. J Neurophysiol 87: 257–272, 2002. [DOI] [PubMed] [Google Scholar]
- Tomlinson R, Bahra P. Combined eye-head gaze shifts in the primate. II. Interactions between saccades and the vestibuloocular reflex. J Neurophysiol 56: 1558–1570, 1986. [DOI] [PubMed] [Google Scholar]
- Tweed D, Glenn B, Vilis T. Eye-head coordination during large gaze shifts. J Neurophysiol 73: 766–779, 1995. [DOI] [PubMed] [Google Scholar]
- Van Gisbergen J, Van Opstal A, Tax A. Collicular ensemble coding of saccades based on vector summation. Neuroscience 21: 541–555, 1987. [DOI] [PubMed] [Google Scholar]
- Van Opstal A, Kappen H. A two-dimensional ensemble coding model for spatial-temporal transformation of saccades in monkey superior colliculus. Network 4: 19–38, 1993. [Google Scholar]
- Vidal P, Roucoux A, Berthoz A. Horizontal eye position-related activity in neck muscles of the alert cat. Exp Brain Res 46: 448–453, 1982. [DOI] [PubMed] [Google Scholar]
- Von Holst E, Mittelstaedt H. Das Reafferenzprinzip. Wechselwirkungen zwischen Zentralnervensystem und Peripherie. Naturwissenschaften 37: 464–476, 1950. [English translation: The reafference principle: interaction between the central nervous system and the periphery. In: The Organization of Action, edited by Gallistel CR. New York: Wiley, 1980, p. 176–209.] [Google Scholar]
- Waitzman DM, Ma TP, Optican LM, Wurtz RH. Superior colliculus neurons mediate the dynamic characteristics of saccades. J Neurophysiol 66: 1716–1737, 1991. [DOI] [PubMed] [Google Scholar]
- Walton MM, Bechara B, Gandhi NJ. Effect of reversible inactivation of superior colliculus on head movements. J Neurophysiol 99: 2479–2495, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walton MM, Bechara B, Gandhi NJ. Role of the primate superior colliculus in the control of head movements. J Neurophysiol 98: 2022–2037, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Lisberger SG. Purkinje-cell plasticity and cerebellar motor learning are graded by complex-spike duration. Nature 510: 529–532, 2014a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Lisberger SG. Role of plasticity at different sites across the time course of cerebellar motor learning. J Neurosci 34: 7077–7090, 2014b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zee DS, Optican LM, Cook JD, Robinson DA, Engel WK. Slow saccades in spinocerebellar degeneration. Arch Neurol 33: 243–251, 1976. [DOI] [PubMed] [Google Scholar]