Optimizing Solute-Solute Interactions in the GLYCAM06 and CHARMM36 Carbohydrate Force Fields Using Osmotic Pressure Measurements

Abstract

GLYCAM06 and CHARMM36 are successful force fields for modeling carbohydrates. To correct recently identified deficiencies with both force fields, we adjusted inter-solute nonbonded parameters to reproduce the experimental osmotic coefficient of glucose at 1M. The modified parameters improve behavior of glucose and sucrose up to 4M, and improve modeling of a dextran 55-mer. While the modified parameters may not be applicable to all carbohydrates they highlight the use of osmotic simulations to optimize force fields.

Graphical Abstract

The indispensable nature of carbohydrates to much of biology^1–2 has made them an increasingly important focus of computational studies that make use of molecular dynamics (MD) simulations. Two very popular empirical force fields used for modeling carbohydrate systems are GLYCAM06³ and CHARMM36.^4–6 The former has been devised to be directly compatible with the AMBER force field,^7–8 while the latter is compatible with the rest of the CHARMM force field.^9–11 Since both force field families include parameters for proteins, nucleic acids, and lipids, GLYCAM06 and CHARMM36 are well placed to describe many important aspects of glycobiology.

In an exhaustive survey of carbohydrate force fields,¹² the Woods group has highlighted some of the challenges associated with developing accurate and transferrable parameters for sugars. For example, the partial charge distributions of different stereoisomers of the same monosaccharide can differ significantly, and the conformational preferences exerted by carbon substituents must account for the anomeric effect, whereby heteroatomic substituents at the sugar C1 carbon (the anomeric carbon) prefer the more sterically hindered axial position over the less hindered equatorial position.¹² Despite these complexities, a number of modern sugar force fields have been shown to accurately capture important features of the conformational behavior of simple carbohydrates such as the rotameric populations of the O6-C6-C5-O5 torsion (ω-angle) in gluco- and galactosides.¹³ This suggests that current carbohydrate force fields can perform rather well in terms of reproducing intramolecular conformational preferences.

On the other hand, recent simulation studies have suggested that other aspects of carbohydrate behavior might not be so well reproduced. For example, a number of groups have reported that in simulations of cellulose performed with the GLYCAM06 force field, a nonphysical over-twisting of the fibers can occur;^14–19 importantly, the Woods group has shown that this effect can be alleviated by globally reducing the strengths of Lennard-Jones interactions involving solute atoms.²⁰ More recently, the Grafmüller group has reported issues with both the CHARMM36 and GLYCAM06 force fields.²¹ Simulations using CHARMM36 together with TIP3P water model²² were shown to significantly underestimate the hydration free energies of three simple carbohydrates: the experimental hydration free energy of α-D-glucose, for example, is −104 kJ/mol whereas CHARMM36 predicts −67 kJ/mol. Despite this, simulations of simple sugars using this force field produced behavior that appeared to be in quite good agreement with experiment, consistent with what had been shown previously by the MacKerell group.^4–6 Similar simulations using GLYCAM06 with TIP3P, on the other hand, produced hydration free energies in closer agreement with experiment, but exhibited a non-physical aggregation of β-D-glucose solutions even at comparatively low solute concentrations (0.5 mol kg⁻¹).²¹

The above studies underline the challenges that come with the development of empirical force fields. In particular, as has been emphasized by the Smith group,^23–24 it is crucial that a proper balance between solute-solute, solute-solvent, and solvent-solvent interactions be established. This can be especially difficult to achieve, however, when there is a scarcity of experimental data that can be directly compared to measurements from MD.¹² One way to establish a quantitative link between the thermodynamics of simulated and experimental intermolecular interactions is to perform simulations that measure the osmotic pressure of solutes in concentrated solutions. Murad et al.^25–28 and Luo and Roux²⁹ have described a practical simulation method for doing this in which virtual walls are experienced by solute molecules that are not seen by solvent molecules. Such a set-up mimics a semi-permeable membrane, with the forces exerted by the solute molecules on the virtual walls providing the osmotic pressure of the solution.²⁹

Importantly, the osmotic coefficient (i.e., the ratio of the measured osmotic pressure to that expected from a corresponding ideal solution) can be interpreted quite straightforwardly: an osmotic coefficient above 1 implies net repulsive interactions of the solutes (which can arise from short-range steric interactions and/or more long-range electrostatic interactions), while an osmotic coefficient below 1 indicates net attractive solute-solute interactions. A simulated osmotic coefficient that is too low relative to experiment, therefore, is indicative of excessively favorable solute-solute interactions. Both the Roux and the Aksimentiev groups have already shown that comparisons with osmotic pressure measurements can be used to parameterize intermolecular (or interionic) potential functions: the Roux group significantly improved the behavior of highly concentrated salt solutions (i.e. NaCl and KCl)²⁹ while the Aksimentiev group reparameterized cation—phosphate, cation—acetate,³⁰ amine—carboxylate, and amine—phosphate³¹ interactions to much more closely match experimental osmotic pressure data. Here, we have followed a similar strategy in order to first test, and then refine, the nonbonded parameters of the GLYCAM06 and CHARMM36 force fields.

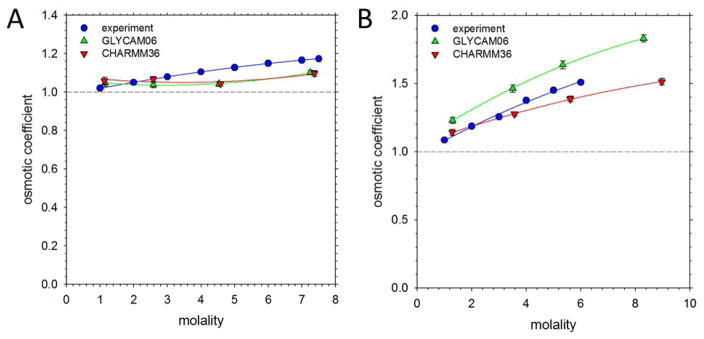
We first performed simulations of glucose and sucrose solutions over a range of concentrations and measured the average osmotic pressure of each system (see Figure 1A for a view of a typical system). Our results for glucose – which was simulated at a ratio of 1:2 α-D-glucose to β-D-glucose in order to match experiment³² – are shown in Figure 2A, while those for sucrose are shown in Figure 2B; tests showing that the results are essentially independent of anomer population and of simulation box size are shown in Figures S1 and S2 respectively. With both sugars, the experimental osmotic coefficient (blue circles) is above 1 at all concentrations, rising as the solute concentration increases; this reflects the high solubilities of both sugars observed experimentally. With the GLYCAM06 force field (green upward triangles), the osmotic coefficients for both sugars are much lower than 1, with the values being so low as to indicate aggregation; this behavior, which is consistent with the recent report of glucose aggregation from the Grafmüller group,²¹ was confirmed by a visual examination of the simulations (see, e.g. Figure 1B). With the CHARMM36 force field (red downward triangles), the osmotic coefficients for both sugars are considerably closer to the experimental values and aggregation is at least not obvious visually; nevertheless, the values are clearly still considerably lower than experiment. Overall, therefore, the simulations suggest that both force fields require modifications to match osmotic coefficients from experiment.

Figure 1. Setup for osmotic pressure simulations and aggregation of glucose molecules in GLYCAM06.

A. Shown is a typical setup for osmotic pressure simulations where solutes are constrained within two virtual walls (dotted grey surface) that are implemented in the simulations in the form of flat-bottomed restraints. B. Typical snapshot of a simulation of glucose at 1 M performed with the original GLYCAM06 parameters showing non-physical aggregation.

Figure 2. Comparison of osmotic coefficients obtained from simulations using original force fields with experiment.

A. Osmotic coefficient of glucose plotted versus glucose concentration expressed in molality. Experimental data are taken from ref. 35; simulated data are from this work using the original GLYCAM06 and CHARMM36 force fields. Dashed horizontal line indicates ideal behavior. Error bars shown are computed from the standard deviation of five estimates of the osmotic coefficient, each obtained from 20 ns of simulation data (see Computational Methods); they are generally smaller than the symbol sizes. B. Same as A but showing results for sucrose.

While there are several modification strategies that might be adopted, we have chosen here to adjust the strengths of nonbonded interactions between sugar molecules (i.e. solute-solute interactions) while leaving unaltered the strengths of sugar-water interactions and the strengths of intramolecular nonbonded interactions. We do this as follows. Nonbonded interactions in both force fields are expressed by the conventional Lennard-Jones (LJ) potential:

$${\mathrm{V}}_{\text{LJ}}=4\mathrm{\epsilon }\left[{\left(\frac{\mathrm{\sigma }}{\mathrm{r}}\right)}^{12}-{\left(\frac{\mathrm{\sigma }}{\mathrm{r}}\right)}^6\right]$$ (1)

where V_LJ is the interaction energy, ε is the well-depth of the interaction, σ is the distance at which the interaction changes from being positive to negative, and r is the distance between the atoms. In the standard implementation, the σ and ε values for two interacting atoms are calculated using the Lorentz-Berthelot combination rules;^33–34 however, as exploited by both the Roux²⁹ and Aksimentiev^30–31 groups, these values can usually be overridden for specified interactions in MD programs (see Computational Methods in Supporting Information for implementation details in GROMACS). In our approach, therefore, we chose to override and adjust the ε values for inter-solute interactions while leaving their σ values unchanged (see below). Our hope was that by changing only ε it would be easier to maintain the geometries of sugar-sugar interactions, and that by changing only the inter-solute terms we would be able to preserve the force fields’ original descriptions of the conformational preferences of the sugars, which have been carefully parameterized to reproduce experiment by both the Woods³ and MacKerell groups.^4–6

All parameterization work was performed with 1 M glucose (i.e. ~1.1 m), for which the experimental osmotic coefficient is 1.02.³⁵ In an initial attempt at reparameterizing the GLYCAM06 force field, we decreased ε the values for all inter-solute C-C (ε_CC), C-O (ε_CO), and O-O (ε_OO) interactions in increments of 0.1 kJ/mol until the resulting value dropped to 0.05 kJ/mol (too small of an ε value can lead to an unrealistic suppression of steric interactions). As shown in Figure S3A, decreasing the ε values in this way had the effect of increasing the osmotic coefficients substantially. However, while the osmotic coefficients came quite close to matching experiment, we found that further changes to the ε values actually worsened the agreement (Figure S3A). In particular, examination of the simulation trajectories suggested that lowering the ε_OO values too much caused excessive hydrogen bonding between OH groups and led to the formation of honeycomb-like aggregates (Figure S3B). In passing we note that a similar inability to reach the experimental value was observed when we tried the alternative approach of adjusting σ for O-O interactions instead of ε (Figure S3C; see Computational Methods for details).

Based on these findings, we decided to pursue an incremental approach whereby ε_CC values were changed first, with ε_CO values being changed next, and with ε_OO values being left unaltered. For GLYCAM06, only one value of ε_CC is used for all types of C-C interactions; for CHARMM36, there are three different values of ε_CC that are used for C-C interactions. All of these ε_CC values were decreased in magnitude in intervals of 0.1 kJ/mol, again unless the resulting value dropped below 0.05 kJ/mol. Figure 3A plots the osmotic coefficients that result from using these adjusted ε_CC values. For GLYCAM06 (green symbols), decreasing ε_CC results in a monotonic increase in the osmotic coefficient from 0.13 to 0.85. For CHARMM36 (red symbols) – for which we plot the mean of the three ε_CC values – the ε_CC values in the original force field are significantly smaller than those in GLYCAM06, so there is less room for adjustment. Despite this, similar behavior is observed: decreasing the ε_CC values results in an increase in the osmotic coefficient from 0.78 to 0.96. With both force fields, however, it is not possible to match the experimental osmotic coefficient by altering only ε_CC. Keeping ε_CC at the lowest value tested, therefore, we further decreased the ε values for C-O interactions (ε_CO) and repeated the osmotic coefficient measurements (Figure 3B). With both force fields, we again find that the osmotic coefficient increases monotonically with decreasing ε_CO. Importantly, the computed values cross the experimental value (dashed line) when only a modest decrease is made to ε_CO; the final set of ε_CO values used in all subsequent simulations was obtained by interpolating from a quadratic fit to both sets of data shown in Figure 3B. The optimized ε values for all interactions are listed in Table S1.

Figure 3. Effect of adjustments to ε values for nonbonded interactions on computed osmotic coefficients.

A. Simulated osmotic coefficient of 1 M glucose plotted as a function of the ε_CC value; for both data series, the right-most data point indicates the osmotic coefficient obtained with the original force field. Dashed horizontal line indicates the experimental osmotic coefficient for glucose at 1 M (i.e. 1.1 m).³⁵ Error bars (see legend to Figure 2) are shown but are generally smaller than the symbol sizes. B. Same as A but showing results as a function of the ε_CO value; for all data points shown in this panel, the ε_CC values were held fixed at the minimum value shown in A.

While the above shows that is possible to adjust intermolecular nonbonded parameters in order to reproduce the osmotic coefficient of glucose at 1 M, it is important to determine whether these optimized parameters also improve the description of glucose at other concentrations, and whether they also can be applied to other sugars to improve their behavior. To this end, we repeated the simulations of glucose and sucrose that were shown in Figure 2 using the newly optimized parameters; the results are shown in Figure 4A for glucose and Figure 4B for sucrose. For glucose, it is apparent that the new parameters dramatically improve the level of quantitative agreement with the experimental data throughout the concentration range 1 to 7 m (compare Figure 4A with Figure 2A); note, however, that despite this much better result, the shape of the curve could still be improved. For sucrose, it is important to stress that the results shown in Figure 4B represent entirely predictive tests of the new parameters: the ε_CC and ε_CO parameters that were optimized for glucose were not re-optimized for sucrose. Despite this, the measured osmotic coefficients obtained with both of the modified force fields again represent a dramatic improvement over the original force fields (compare Figure 4B with Figure 2B). This suggests that the weakening of sugar-sugar interactions reflected in the optimized ε_CC and ε_CO parameters is likely to improve the description of other sugar systems.

Figure 4. Comparison of osmotic coefficients obtained from simulations using modified parameters with experiment.

A. Osmotic coefficient of glucose plotted versus glucose concentration expressed in molality. Experimental data are taken from ref. 35; simulated data are from this work using the modified parameters described in the text. Dashed horizontal line indicates ideal behavior. Error bars (see legend to Figure 2) are shown but are generally smaller than the symbol sizes. B. Same as A but showing results for sucrose.

Before determining whether the optimized parameters would also work in the context of modeling polysaccharides (see below), we looked to see whether the effort to reproduce the osmotic coefficient had adverse effects on other system properties. First, we determined the densities, dielectric constants and shear viscosities of concentrated glucose solutions using the original and modified parameters and compared them with each other as well as with experiment.³² For all three solution properties, which we express relative to the corresponding pure water values, we found no significant difference between the results obtained using the original and modified parameter sets for either the GLYCAM06 and CHARMM36 force fields (Figure S4): with both force fields, the density ratios are in good agreement with experiment, although a little high, while the dielectric and viscosity ratios are lower than experiment. While it is somewhat disappointing to find that adjusting the parameters to improve agreement with osmotic coefficients did not improve the description of other system properties, the modifications at least did not worsen the agreement with experiment.

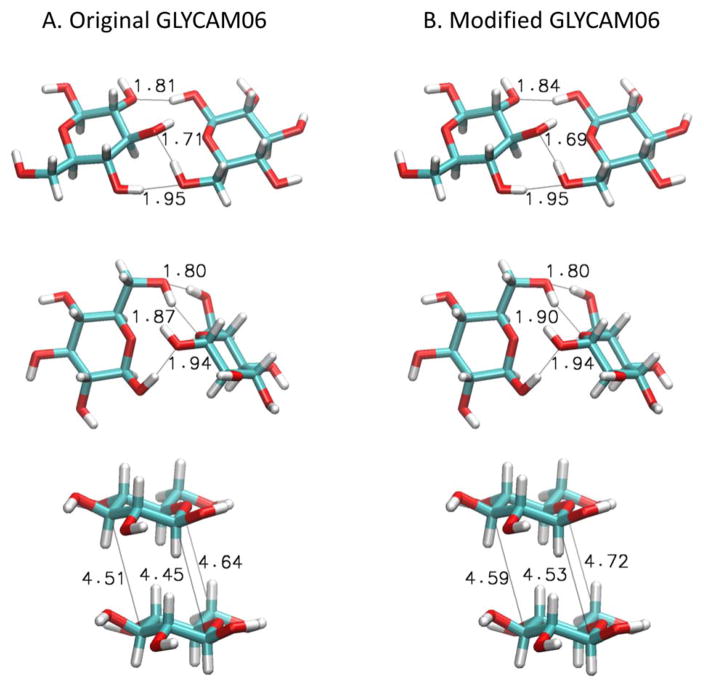
We next examined the interaction energies of two glucose molecules in vacuum in order to determine to what extent modification of the parameters affected the energies and geometries of sugar-sugar complexes; this is especially important to address for GLYCAM06 given that our modifications to the ε_CC and ε_CO parameters for this force field are considerable (see above). The interaction geometries that we chose to explore were: (a) two glucose molecules with their ether oxygens aligned in the same direction (‘adjacent’), (b) two glucose molecules with their ether oxygens facing each other (‘facing’), and (c) two glucose molecules with their rings stacked within a few Ångstroms of each other (‘stacked’) (Figure 5). We did not examine sugar-water complexes as our approach, by construction, does not modify their interactions at all. We minimized each of the modeled complexes with both the original and modified GLYCAM06 force fields and compared their total energies and interaction energies (see Computational Methods). Figure 5 compares the minimized structures, from which it is apparent that our reparameterization preserves the interaction geometries of hydrogen-bonded and stacked complexes, with the largest difference being an increase in the distance between stacked glucose molecules of 0.08 Å. Figure S5 compares the energies of the complexes: Figure S5A compares the total energies of the three structures, while Figure S5B compares their interaction energies (i.e. the difference between the total energy of the complex and the energies of the two separated sugar molecules). In both panels of the Figure, we find that the values computed with the modified parameters (red bars) are more positive than those computed with the original parameters (blue bars); this is consistent with the decreased ε_CC and ε_CO values that we introduced. More importantly, however, the relative energies of the three different interaction geometries are preserved: these data suggest, therefore, that we have succeeded in changing the strength of the nonbonded interactions between molecules while preserving the geometries and the relative energies of these different modes of interaction.

Figure 5. Interaction energies of two glucose molecules in three different geometries.

A. From top to bottom: two glucose molecules placed in the following arrangements: ‘adjacent’, ‘facing’, and ‘stacked’. Selected atom-atom distances are shown after 1000 steps of steepest descent minimization of these structures with the original GLYCAM06 parameters. B. Same as A but showing results obtained with the modified GLYCAM06 parameters.

We next explored whether our modified parameters can also correctly describe the behavior of oligo- and poly-saccharides in aqueous solution. For GLYCAM06, we first verified that the use of the modified parameters did not lead to significant changes in the ϕ, ψ, ω dihedral angle distributions of the glucose disaccharide α-D-glucopyranosyl-(1,6)-α-D-glucopyranose in aqueous solution (Figure S6; see Computational Methods). Next, as a more important test, we simulated a 55-mer dextran molecule (Figure S7) for 500 ns and computed its radius of gyration (R_g). As described in Computational Methods, we identified two independent experimental datasets reporting R_g as a function of molecular weight for dextrans (Figure S8), we fit both to power-law functions, and in both cases found a predicted R_g of about 3.5 nm for a dextran of this size (molecular weight of 8965.7 g/mol). The cumulative mean values of R_g obtained from MD simulations of the same type of dextran are plotted versus simulation time for all four force fields (two original and two modified) in Figure 6. For GLYCAM06 (Figure 6A), the original parameters (upward triangles) lead to a collapse of the polymer within 5 ns that drastically underestimates the expected experimental R_g. When the modified GLYCAM06 parameters are used instead (downward triangles), no such collapse occurs and the mean R_g value is very close to the expected value. For CHARMM36 (Figure 6B), the effects are less dramatic but qualitatively similar: the original parameters again lead to an R_g value that is clearly lower than expected experimentally, but there is no abrupt collapse like that seen with the original GLYCAM06 parameters. Again, however, use of the modified parameters leads to an increased R_g value that, while still slightly lower than the expected value, is nevertheless in much closer agreement. Overall, therefore, the data shown in Figure 6 indicate that parameters optimized to reproduce the behavior of monosaccharide solutions also improve the description of the polysaccharide dextran.

Figure 6. Radius of gyration (R_g) of a dextran 55-mer as a function of force field parameters.

A. Cumulative average of the simulated R_g value plotted versus simulation time for the original and modified GLYCAM06 parameters. Dashed horizontal line indicates the expected experimental value (see text). Data points are shown at intervals of 10 ns. B. Same as A but showing results for the original and modified CHARMM36 parameters.

Finally, at the request of a reviewer, we carried out simulations of a second polysaccharide, cellulose Iβ, using a protocol very similar to that used by the Woods group,²⁰ in order to determine whether our parameter modifications affect the microfibril twisting behavior observed in previous cellulose simulations (see Computational Methods & Figure S9).^14–19 Figure S10 plots the running average of the twist angles (θ_twist) of the cellulose microfibril (normalized to one cellobiose unit) versus simulation time. Data for GLYCAM06 are plotted in Figure S10A where it can be seen that the original GLYCAM06 parameters (upward triangles) resulted in an overall average θ_twist of ~0.8° per cellobiose unit, while our modified parameters (downward triangles) resulted in a considerably lower average θ_twist of ~0.2°. While the absolute value that we obtain with the original parameters differs somewhat from that reported by the Woods group²⁰ (~1.2° per cellobiose unit), the finding that weakening the inter-sugar Lennard Jones interactions decreases the twist value significantly is qualitatively identical to that reported previously.²⁰ The corresponding data for CHARMM36 are plotted in Figure S10B. In this case we observed an increase in the average θ_twist from ~0.8° with the original CHARMM36 parameters (upward triangles) to ~1.2° with the modified parameters (downward triangles); our result with the original CHARMM36 parameters corresponds well with the average θ_twist of 0.7–0.8° per cellobiose unit reported by the Himmel and Brady groups for similar systems.¹⁴ The observation that our parameter modifications have divergent effects on the twisting behavior of the cellulose microfibril – decreasing twisting in the case of GLYCAM06 and increasing it in the case of CHARMM36 – indicates that while parameters devised for simple monosaccharides may work well for single-chain polymers such as dextran (see above), they may have more equivocal effects on the behavior of multi-chain assemblies such as the cellulose microfibril. At this stage, therefore, we cannot claim that our proposed modifications will be appropriate for all types of carbohydrate systems.

To summarize, we have presented simple but effective parameter modifications for both the GLYCAM06 and CHARMM36 carbohydrate force fields that are focused on correcting excessively attractive nonbonded interactions between sugar molecules. Although the parameters have been optimized only to reproduce the experimental osmotic coefficient of glucose at a concentration of 1 M we have shown that they: (a) also work well for considerably more concentrated solutions, (b) appear to be readily transferrable to the more complicated disaccharide sucrose, (c) improve the modeling of the glucose-based polymer dextran, but (d) have equivocal effects on the twisting behavior of cellulose microfibrils. It is of course possible to imagine other reparameterization schemes that might lead to similar or better results. But the approach adopted here – which specifically targets only the Lennard-Jones interactions that act between different sugar molecules – has the advantage that it allows force field parameters that have been previously optimized to reproduce other desirable features, such as conformational preferences or hydration free energies, to be retained completely unaltered. As such, it potentially offers a very rapid way to expand the applicability of proven force fields such as GLYCAM06 and CHARMM36 to situations different from those for which they were originally designed. Regardless of this issue, the results reported here further reinforce the ideas presented previously by the Roux,²⁹ Aksimentiev,^30–31 and Smith^23–24 groups that osmotic pressure measurements provide an important route to validating and optimizing biomolecular force fields.