Multiscale modeling and simulation of microtubule–motor-protein assemblies

Abstract

Microtubules and motor proteins self-organize into biologically important assemblies including the mitotic spindle and the centrosomal microtubule array. Outside of cells, microtubule-motor mixtures can form novel active liquid-crystalline materials driven out of equilibrium by adenosine triphosphate–consuming motor proteins. Microscopic motor activity causes polarity-dependent interactions between motor proteins and microtubules, but how these interactions yield larger-scale dynamical behavior such as complex flows and defect dynamics is not well understood. We develop a multiscale theory for microtubule-motor systems in which Brownian dynamics simulations of polar microtubules driven by motors are used to study microscopic organization and stresses created by motor-mediated microtubule interactions. We identify polarity-sorting and crosslink tether relaxation as two polar-specific sources of active destabilizing stress. We then develop a continuum Doi-Onsager model that captures polarity sorting and the hydrodynamic flows generated by these polar-specific active stresses. In simulations of active nematic flows on immersed surfaces, the active stresses drive turbulent flow dynamics and continuous generation and annihilation of disclination defects. The dynamics follow from two instabilities, and accounting for the immersed nature of the experiment yields unambiguous characteristic length and time scales. When turning off the hydrodynamics in the Doi-Onsager model, we capture formation of polar lanes as observed in the Brownian dynamics simulation.

I. INTRODUCTION

Active matter, the novel class of nonequilibrium materials made up of self-driven constituents, presents scientific challenges to our understanding of material properties and has the potential to provide new technologies such as autonomously moving and self-healing materials. Examples of active matter include flocks of birds [1], swarms of swimming bacteria [2] or self-propelled colloidal particles [3], and the cellular cytoskeleton and cytoskeletal extracts [4–7]. Despite their differences in composition and length scale, these diverse systems show common features absent in equilibrium systems, including collective motion, nonequilibrium ordering transitions, and anomalous fluctuations and mechanical properties [8,9]. Understanding and predicting the properties of active matter require new theoretical approaches and models applicable to far-from-equilibrium, internally driven systems.

Mixtures of cytoskeletal filaments and motors are an important class of active matter that can be reconstituted outside the cell to form novel materials. Filaments driven into self-organized patterns such as vortices and asters are reminiscent of structures observed in cells [4–6,10–16]. In earlier experiments, filaments were driven into static self-organized patterns such as vortices and asters, reminiscent of structures observed in vivo. In recent experiments, active networks were formed of microtubules (MTs) and synthetic multimeric kinesin-1 motor complexes, with the aid of a depletant [7,17,18]. In the presence of ATP, motor complexes can bind pairs of MTs and walk along MTs toward their plus ends. When suspended in bulk, depletion interactions drove the formation of extended, highly ordered MT bundles characterized by bundle extension and fracture and correlated with spontaneous large-scale fluid flows [7,18]. When MT bundles were adsorbed onto an oil-water interface, they formed a dense, nematically ordered surface state and exhibited an active nematic phase characterized by the spontaneous generation and annihilation of disclination defect pairs [7].

Theoretical studies [19–30] have investigated aspects of these active-matter systems at different scales, from the dynamics and mechanical properties of filament bundles to macroscopic behavior and stability of active suspensions. Inspired by the experiments of Sanchez et al. [7], both Giomi et al. [31,32] and Thampi et al. [33–36] have studied liquid crystal hydrodynamic models with fluid flow driven by an apolar active stress [37,38]. In these rather general models the precise origins of the active stress driving the system are unidentified. Giomi et al. developed a theory for the speed at which defects move apart in active nematics, assuming the presence of a defect pair as an initial condition. Thampi et al. found an activity-independent velocity-velocity correlation length, as found in the bulk flow measurements of Sanchez et al., and studied defect dynamics in 2D simulations. These models reproduce qualitative features of the experiments. However, MT–motor-protein interactions are intrinsically polar, and how these polarity-dependent microscopic interactions manifest themselves at meso- or macroscopic scales is still unknown. Thus one theoretical challenge is how to resolve microscopic interactions between constituents in order to predict macroscopic material properties. While particle-based simulations can represent microscopic interactions in detail, computational cost typically limits cross-scale studies. Continuum models are more tractable for describing dynamics at large scales but can be difficult to connect to the microscopic dynamics quantitatively.

Here we construct a multiscale model that identifies the sources of destabilizing active stresses and study their consequences in a large-scale model [39]. We first perform detailed, hybrid Brownian dynamics–kinetic Monte Carlo (BD-kMC) simulations which incorporate excluded-volume interactions among model MTs, thermal fluctuations, explicit motors with binding-unbinding kinetics that satisfy detailed balance, and a force-velocity relation. Active extensile stress is generated from polarity sorting of antialigned MTs and from crosslink relaxation of polar-aligned MTs. It also provides coefficients for polar-specific active stresses for a kinetic theory that incorporates polarity sorting and long-range hydrodynamic interactions, using a similar approach as that used to describe bacterial suspensions [40–45], where hydrodynamic instabilities lead to large-scale collective motions including jets and vortices [37,40,41,46–49]. We use this model to study actively streaming nematic states on an immersed surface, as in the Sanchez et al. experiments [7]. Numerical experiments demonstrate dynamics strikingly similar to the experiments, with large-scale turbulent-like fluid flows and the persistent production and annihilation of defects. We correlate the defect dynamics with specific flow structures and with active stresses. We identify the hydrodynamic instability of nearly one-dimensional (1D) coherent “cracks” as being the source of the persistent dynamics. When turning off the induced background surface flow in the kinetic model, we capture the formation of polar lanes observed in the BD-kMC simulations.

II. THE MICROSCOPIC MODEL

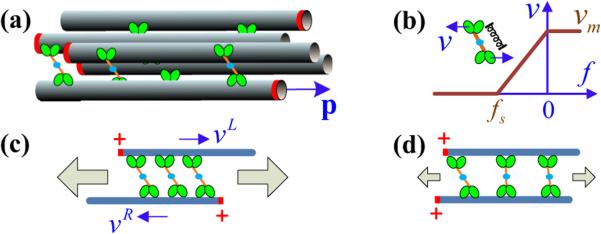
Figure 1 outlines the basic physical picture that underlies both our BD-kMC simulations and the continuum kinetic model. Consider an immersed suspension of polar MTs, each with a plus-end-oriented director p, and all of the same length l and diameter b [Fig. 1(a)]. Adjacent MTs are coupled by plus-end-directed crosslinking motors consisting of one motor head on each MT connected by a tether that responds as a spring to stretching [Fig. 1(b)]. The motor on each crosslink end point moves with a linear force-velocity relation [50]: v = v_m max[0, min(1,1 + f/f_s)], where f is the magnitude of the crosslinking force, v_m is the maximum translocation velocity, and f_s is the stall force. For a nematically aligned suspension there are two basic types of MT pair interaction. For polar antialigned MTs [Fig. 1(c)] the motors on each end of an active crosslink move in opposite directions, stretching the tether. This creates forces on each MT that, acting against fluid drag, slide the MTs relative to each other towards their minus ends. This process is termed polarity sorting [19]. Conversely, for polar-aligned MTs the motors on each end of the crosslink move in the same direction, there is little or no net sliding, and the tether pulling on the leading motor causes stretched tethers to relax [Fig. 1(d)].

FIG. 1.

(Color online) (a) Schematic of a cluster of polar-aligned and antialigned MTs, with plus ends marked by red rings. Motors walk on neighboring MTs, and (b) exert springlike forces with a piecewise linear force-velocity relation. (c) An antialigned MT pair. (d) A polar-aligned MT pair. Gray arrows characterize the magnitude of the extensile stress.

III. BROWNIAN DYNAMICS–KINETIC MONTE CARLO MODEL AND SIMULATIONS

We first perform 2D BD-kMC simulations of MTs driven by explicit motors with binding-unbinding kinetics. The main purpose is to quantify local MT pair interactions, with long-ranged hydrodynamics neglected due to its high computational cost. Our model is related to previous simulations of filaments with crosslinking motors [51–53], but new in our work are algorithmic improvements for handling crosslinks and neglect of filament elasticity that allow us to more accurately treat the statistical mechanics of crosslinking motors, simulate larger systems, and measure the stress tensor.

The particle-based BD-kMC simulations use a simple, tractable model of active biomolecular assemblies that capture key physical features, including excluded volume interactions between filaments, attractive and sliding forces exerted by motors, and the thermodynamics and kinetics of crosslinking motor binding and unbinding. Filaments (MTs) are represented as perfectly rigid rods (discorectangles in 2D) of length l and diameter b that undergo Brownian dynamics. Forces and torques on the filaments occur due to motor-mediated forces, particle-particle repulsion, friction, and thermal forces. To simulate the Brownian motion of filaments, we adopt the computational scheme of Tao et al. [54], which has been used successfully in simulations of concentrated solutions of high-aspect-ratio particles. In this scheme, the filament centers-of-mass equations of motion are

$${\mathbf{x}}_i(t+\delta t)={\mathbf{x}}_i\left(t\right)+{\Gamma }_i^{-1}\left(t\right)\cdot {\mathbf{F}}_i\left(t\right)\delta t+\delta {\mathbf{x}}_i\left(t\right)$$ (1)

for all filaments i, where the random displacement δx_i(t) is Gaussian distributed and anisotropic, with variance

$$\langle \delta {\mathbf{x}}_i\left(t\right)\delta {\mathbf{x}}_i\left(t\right)\rangle =2k_{B}T{\Gamma }_i^{-1}\left(t\right)\delta t.$$ (2)

In the above, k_B is Boltzmann's constant and T is the absolute temperature. Here ${\Gamma }_i^{-1}\left(t\right)$ is the inverse friction tensor

$${\Gamma }_i^{-1}\left(t\right)={\gamma }_{\parallel }^{-1}{\mathbf{p}}_i\left(t\right){\mathbf{p}}_i\left(t\right)+{\gamma }_{\perp }^{-1}[\mathbf{I}-{\mathbf{p}}_i\left(t\right){\mathbf{p}}_i\left(t\right)],$$ (3)

where γ_∥ and γ_⊥ are the parallel and perpendicular drag coefficients of the rod, and F_i(t) is the systematic (deterministic) force on particle i. The equations of motion for particle reorientation are

$${\mathbf{p}}_i(t+\delta t)={\mathbf{p}}_i\left(t\right)+\frac{1}{{\gamma }_r}{\mathbf{T}}_i\left(t\right)\times {\mathbf{p}}_i\left(t\right)\delta t+\delta {\mathbf{p}}_i\left(t\right),$$ (4)

where γ_r is the rotational drag coefficient, T_i(t) is the systematic torque on particle i, and the random reorientation δp_i(t) is Gaussian distributed, with variance

$$\langle \delta {\mathbf{p}}_i\left(t\right)\delta {\mathbf{p}}_i\left(t\right)\rangle =2k_{B}T\frac{1}{{\gamma }_r}[\mathbf{I}-{\mathbf{p}}_i\left(t\right){\mathbf{p}}_i\left(t\right)]\delta t.$$ (5)

The Weeks-Chandler-Andersen (WCA) potential between rods is

$$u_{\mathrm{WCA}}\left(r_{\min }\right)=\{\begin{array}{cc}4ϵ[{\left(\frac{b}{r_{\min }}\right)}^{12}-{\left(\frac{b}{r_{\min }}\right)}^6]+ϵ,\hfill & r_{\min }<2^{1∕6}b\hfill \\ 0,\hfill & r_{\min }⩾2^{1∕6}b\hfill \end{array}\phantom{\}},$$ (6)

where ϵ = k_BT, r_min is the minimum distance between the two finite line segments that define the filament axes, and ϵ sets the energy scale of the potential. Note that r_min is an implicit function of the center-of-mass positions and orientations of the two interacting MTs. For this value of ϵ, the typical distance of closest approach between rods is comparable to b, and the thermodynamic properties closely resemble those of hard rods with aspect ratio l/b, a model that is well characterized both in 2D [55] and 3D [56,57].

Because the Brownian dynamics scheme involves random particle displacements and rotations, close contacts between rods that produce large forces and torques occasionally occur, leading to instabilities in the dynamics. Such instabilities are avoided by softening the WCA potential at short distances to keep the resulting forces and torques within reasonable bounds [54]. At the same time, we adjust the integration time step to ensure that pairs of interacting particles probe the softened region of the potential infrequently, so excluded volume effects are properly accounted for.

The frictional forces are orientation dependent: Translational diffusion is characterized by two diffusion constants, D_⊥ and D_∥, which describe diffusion perpendicular and parallel to the rod axis, respectively, and D_r is the rotational diffusion coefficient. For spherocylinders where a = l/b + 1, the diffusion coefficients are [58]

$$D_{\parallel }=\frac{k_{B}T}{2\pi \eta (l+1)}(\ln a-0.207+0.980∕a-0.133a^2),$$ (7)

$$D_{\perp }=\frac{k_{B}T}{4\pi \eta (l+1)}(\ln a+0.839+0.185∕a+0.233∕a^2),$$ (8)

and

$$D_r=\frac{3k_{B}T}{\pi \eta {(l+1)}^3}(\ln a-0.662+0.917∕a-0.050∕a^2).$$ (9)

Here η is the fluid viscosity. Note that D_∥ is approximately a factor of 2 larger than D_⊥.

To model motor-mediated interactions and activity, we implement a semi-grand-canonical ensemble in which a reservoir of motors is maintained in diffusive contact at a fixed chemical potential μ_m with filaments to (from) which they can bind (unbind). The motors are assumed to be noninteracting both in solution and in the bound state, so the motor reservoir can be treated as an ideal solution, and there is no steric interference among bound motors. Bound motors have a free energy u_m(r_m), where r_m is the extension of the motor tether, which depends implicitly on the relative positions and orientations of the two filaments to which the motor is attached and on the positions of the points of attachment of the motor on the filament axes. We treat motor attachment (detachment) as a one-step process in which motors bind to (unbind from) two filaments simultaneously, and we assume a binding rate of

$$k_{\mathrm{on}}\left(r\right)=k_0{e}^{-\beta u_m\left(r\right)}.$$ (10)

and an unbinding rate of

$$k_{\mathrm{off}}\left(r\right)=k_0,$$ (11)

where β = (k_BT)⁻¹ is the inverse temperature in energy units. This choice of binding and unbinding rates ensures that the correct equilibrium distribution is recovered for static (nontranslocating) crosslinks, is a convenient choice from a computational standpoint, and has been used previously [59]. Given a distribution of motors bound to filaments, we compute the forces and torques exerted on MTs by differentiating u_m(r_m) with respect to the filament positions and orientations. As discussed in Sec. II, the end points of bound motors translocate toward the plus ends of the MTs to which they are attached with a force-dependent velocity. Motors unbind immediately upon reaching the plus end of either of the two filaments to which they are attached.

Because the motor unbinding rate is k₀, independent of motor tether extension, the probability that a given motor unbinds in a time interval δt is p = k₀δt, and the average number of motors that unbind in δt is 〈N_d〉 = k₀δtN_m, where N_m is the current number of bound motors. The number N_d of motors that unbind in a time interval δt follows a binomial distribution,

$$\mathcal{P}\left(N_d\right)=\left(\begin{array}{c}\hfill N_m\hfill \\ \hfill N_d\hfill \end{array}\right)p^{N_d}{(1-p)}^{N_m-N_d}.$$ (12)

In one time step we remove N_d randomly selected motors, where N_d is determined by sampling from the binomial distribution.

The kinetic MC procedure for motor binding is involved, because the rate of motor binding depends on motor tether extension, which in turn depends on the relative positions and orientations of the two MTs to which the motor is attached and on the positions of the points of attachment of the motor along the filament axes. To compute the relative probability and rate of motor binding to specific binding sites on a given pair of filaments we consider the statistical mechanics of the filament-motor system in the equilibrium limit of nontranslocating crosslinks. The semi-grand-canonical partition function of the filament-motor system is

$$\Xi (N,V,T,{\mu }_m)=\sum _{N_m=0}^{\infty }{z}_{\mathrm{c}}^{N_m}Z(N,V,T,N_m),$$ (13)

where z_m = e^βμm is the fugacity of the motor reservoir and N_m is the number of bound motors. Here Z(N,V,T,N_m) is the canonical partition function of a system of N filaments and N_m bound motors,

$$Z(N,V,T,N_m)=\frac{1}{N!}\int d{\mathbf{x}}^{N}d{\mathbf{p}}^N{e}^{-\beta U({\mathbf{x}}^N,{\mathbf{p}}^N)}\left[\frac{1}{N_m!}{\left(q_1\right)}^{N_m}\right],$$ (14)

where (x^N,p^N) = (x₁,x₂, . . . ,x_N,p₁,p₂, . . . ,p_N) labels the particle positions and orientations; U(x^N,p^N) is the filament potential energy, including interparticle interactions and external potentials; and q₁ is the single-motor partition function and interactions between bound motors have been neglected. The single-motor partition function depends on the filament positions x^N and orientations p^N, i.e., q₁ = q₁(x^N,p^N). Substituting Eq. (14) into the grand partition function and carrying out the summation over N_m leads to

$$\Xi (N,V,T,{\mu }_m)=\frac{1}{N!}\int d{\mathbf{x}}^{N}d{\mathbf{p}}^N{e}^{-\beta [U({\mathbf{x}}^N,{\mathbf{p}}^N)+U_m({\mathbf{x}}^N,{\mathbf{p}}^N)]},$$ (15)

where

$$U_m({\mathbf{x}}^N,{\mathbf{p}}^N)=-\frac{z_m}{\beta }{q}_1({\mathbf{x}}^N,{\mathbf{p}}^N).$$ (16)

In the limit in which the rate of motor binding and unbinding is large compared with the filament diffusion rate (adiabatic limit), U_m plays the role of an effective motor-mediated filament interaction potential that depends on the chemical potential of the reservoir. Static-crosslink-mediated interactions are generally attractive and short ranged and bear a strong resemblance to depletion-type potentials [56].

The single-motor partition function q₁ can be written as a sum of pairwise partition functions,

$$q_1({\mathbf{x}}^N,{\mathbf{p}}^N)=\sum _{i<j}^N{q}_{ij}({\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j),$$ (17)

where the sum ranges over all distinct pairs of filaments, and the pairwise partition function q_ij is

$$q_{ij}({\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j)={\rho }^2{\int }_{-l∕2}^{l∕2}d{s}_i{\int }_{-l∕2}^{l∕2}d{s}_j{e}^{-\beta u_m\left[r_m(s_i,s_j;{\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j)\right]}.$$ (18)

Here the integration variables s_i and s_j parametrize the positions of motor end points on filaments i and j, respectively; r_m is length of a motor between points specified by s_i and s_j; and ρ is the linear density of binding sites on a single filament. Then we can write the effective motor potential as the sum of pairwise effective interactions,

$$U_m({\mathbf{x}}^N,{\mathbf{p}}^N)=\sum _{i<j}^N{U}_{ij}({\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j),$$ (19)

where

$$U_{ij}({\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j)=-\frac{z_m}{\beta }{q}_{ij}({\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j)$$ (20)

is the effective motor-mediated pair potential in the adiabatic limit. Insertion of motors with the correct relative statistical weight in a kinetic MC procedure requires evaluation of the pairwise partition function q_ij [Eq. (18)] for all pairs of filaments. If the motor energy u_m increases rapidly (e.g., quadratically) with increasing motor extension, then the partition function q_ij (and the corresponding adiabatic effective potential U_ij) falls off rapidly with increasing minimum distance between filament axes and is non-negligible only for pairs of filaments in close proximity. Thus, the pairwise partition function is analogous to a short-range interaction potential, and the usual techniques for efficient handling of short-range interactions (e.g., neighbor lists) can be applied. To efficiently evaluate the double integral in Eq. (18), note that for motors modeled as zero-equilibrium-length harmonic springs, the integrand can be expressed as a sum of bivariate normal distributions. Then q_ij reduces to a sum of cumulative bivariate normal distributions, which can be rapidly evaluated using standard numerical procedures [60].

To proceed further, we consider the statistical mechanics of the motor subsystem for fixed filament positions and orientations. The grand partition function for the motor subsystem is given by

$${\Xi }_m(N,T,{\mu }_m)=\sum _{N_m=0}^{\infty }\frac{z_{\mathrm{m}}^{N_m}}{N_m!}{\left(q_1\right)}^{N_{\mathrm{m}}},$$ (21)

and the equilibrium number of bound motors for a given filament configuration is

$$\langle N_m\rangle ={\beta }^{-1}\frac{\partial }{\partial {\mu }_m}\ln {\Xi }_m=\sum _{i<j}^N\langle N_{ij}\rangle ,$$ (22)

where 〈N_ij〉 is the average number of motors between filaments i and j,

$$\langle N_{ij}({\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j)\rangle =z_m{\rho }^2{\int }_{-l∕2}^{l∕2}d{s}_i{\int }_{-l∕2}^{l∕2}d{s}_j{e}^{-\beta u_m\left[r_m(s_i,s_j;{\mathbf{x}}_i,{\mathbf{p}}_i,{\mathbf{x}}_j,{\mathbf{p}}_j)\right]}.$$ (23)

Note that 〈N_ij〉 = z_mq_ij, so the problem of computing 〈N_ij〉 is equivalent to that of computing q_ij. Introducing the explicit form of quadratic potential for harmonic motors $u_m\left(r_m\right)=-u_0+\frac{1}{2}K{r}_m^2$ leads to

$$\langle N_{ij}\rangle =z_m{\rho }^2{e}^{\beta u_0}{\int }_{-l∕2}^{l∕2}d{s}_i{\int }_{-l∕2}^{l∕2}d{s}_j{e}^{-\alpha r_m^2(s_i,s_j)},$$ (24)

where α = βK/2, and where the implicit dependence of r_m on filament coordinates has been suppressed.

The average number of motors that bind to filaments in a time interval δt is

$$\langle N_a\rangle =k_0\delta t\langle N_m\rangle =k_0\delta t\sum _{i<j}^N\langle N_{ij}\rangle .$$ (25)

As above, the number N_a of motors that bind in the interval δt follows a Poisson distribution,

$$\mathcal{P}\left(N_a\right)=\frac{{\langle N_a\rangle }^{N_a}{e}^{-N_a}}{N_a!}.$$ (26)

In the kinetic MC cycle, the number of bound motors N_a is drawn from this distribution, and N_a motors are inserted by first selecting pairs of filaments with relative probability ${\mathcal{P}}_{ij}=\langle N_{ij}\rangle ∕\langle N_m\rangle$ and then sampling from the appropriate bivariate normal distribution to choose motor end points that lie on the selected pair of filaments.

The overall hybrid BD-kMC procedure thus consists of the following steps:

• (1)Compute forces and torques on MTs and evolve MT positions and orientations δt forward in time according to the Brownian dynamics equations of motion [Eqs. (1) and (4)].
• (2)Displace each motor end point by vδt along the MT to which it is attached with translocation velocity v given by the force-velocity relation.
• (3)Determine the number N_d of motors that unbind in the time interval δt by drawing from a binomial distribution [Eq. (12)] and remove this number of motors at random.
• (4)Compute average number of bound motors 〈N_ij〉 for all pairs of MTs [Eq. (23)] and determine the number N_a of motors that bind in the time interval δt by drawing from a Poisson distribution [Eq. (26)]. Randomly select N_a pairs of MTs with relative probability $\langle N_{ij}\rangle ∕{\sum }_{i<j}^N\langle N_{ij}\rangle$, and insert a motor between each selected pair of MTs by sampling from a bivariate normal distribution.

The properties of the model depend on seven dimensionless parameters (Tables I and II): (i) the MT aspect ratio r = l/b, (ii) the MT packing fraction ϕ, (iii) the range of =motor mediated interaction R_m = [k_BT/(Kb²)]^1/2, (iv) the motor concentration c = z_mρ²b²e^u₀/(k_BT), (v) the motor run length $\ell =v∕\left(k_{0}l\right)$, (vi) the motor stall force f = f_sb/(k_BT), and (vii) the Peclet number (the ratio of translocation and diffusion rates) Pe = vηb/(k_BT). With current methods, it becomes more computationally expensive to simulate systems with MTs of high aspect ratio (e.g., r > 10). The computation time scales approximately as r³. If r doubles, then the linear dimension of the the box in the longitudinal direction must be doubled to study the same number of rods. We use square boxes to avoid any loss of information upon nematic director reorientation. Therefore the number of rods scales as r². Longer rods also have slower dynamics, because the translational and rotational mobilities go as 1/r to leading order. Therefore the time scale to reach steady state scales approximately linearly in r. We present here results of simulations with r = 10 for which we performed simulations of relatively large systems for long times over a wide range of parameters. A more limited investigation of longer rods reveal qualitatively similar behavior.

TABLE I.

Parameter values of the BD-kMC simulation.

Quantity	Parameter	Value	Notes
kBT	Thermal energy	4.11 ×10−21 J	Room temperature
l	MT length	250 nm	Chosen
b	MT diameter	25 nm	Ref. [61]
ϵ	Energy scale of the WCA potential	kBT	Refs. [55–57]
η	Fluid viscosity	1.0 Pa s	Cytoplasmic viscosity, Ref. [62]
ρ	Linear density of motor binding sites along MT	—	Appears only in dimensionless concentration
μ m	Motor chemical potential	—	Appears only in dimensionless concentration
u 0	Motor binding free energy	—	Appears only in dimensionless concentration
vw	Motor speed (zero force)	Reference 4.5 μm/s, range 0.14–18 μm/s	Of order 1 μm/s, Ref. [50]
k 0	Unbinding rate of motors	28.1 s−1	Processivity of 160 nm, Ref. [63]
fs	Stall force	1 pN	Ref. [50]
K	Motor spring constant	0.013 pN/nm	Decreased from Ref. [64] to give appropriate range of motor-mediated interaction for zero-equilibrium-length springs

TABLE II.

Dimensionless groups of the BD-kMC simulation.

Quantity	Parameter	Value	Notes
ϕ	MT packing fraction	0.54	Chosen to give nematic state at equilibrium in the absence of motors
r = l/b	MT aspect ratio	10
c = ρ 2 b 2 e β(μm+u0)	Motor concentration	1	Chosen to give average of 2 motors per nearby MT pair
$R_m=\sqrt{k_{B}T∕\left(K{b}^2\right)}$	Range of motor interaction	$1∕\sqrt{2}$	Chosen to be of order 1 for a short-range interaction
$\ell =v_w∕\left(k_{0}l\right)$	Motor run length	Reference 0.64, range 0.2–12.8	Motor-induced active stresses are largest when $\ell$ is of order 1.
f = fsb/(kBT)	Motor stall force	6
Pe = vwηb/(kBT)	Peclet number	Reference 0.68, range 0.02–2.7

A. Measurement

The dynamics and stresses experienced by individual MTs depend strongly on their local environment, in particular on the relative polarity of neighboring MTs. To identify sub-populations of MTs with distinct local environments, we define a local polar orientational order parameter

$$m_i=\frac{{\sum }_{j\ne i}^N{\mathbf{p}}_i\cdot {\mathbf{p}}_j{q}_{ij}}{{\sum }_{j\ne i}^N{q}_{ij}},$$ (27)

where q_ij is the motor pair partition function defined above. Since q_ij falls off rapidly with increasing pair separation, only near neighbors of particle i are included in the sums in Eq. (27). The polar order parameter m_i ranges from −1 (MT i surrounded by neighbors of opposite polarity) to 1 (MT i surrounded by neighbors of the same polarity).

The osmotic stress tensor of a periodic system of N interacting MTs at temperature T in a d-dimensional volume V is given by

$$\Sigma =\frac{N{k}_{B}T}{V}\mathbf{I}+\frac{1}{V}\langle \mathbf{W}\rangle ,$$ (28)

where the first and second terms on the right-hand side represent the ideal gas and interaction contributions, respectively, I is the unit tensor, and W is the virial tensor,

$$\mathbf{W}=\sum _{i<j}^N{\mathbf{r}}_{ij}{\mathbf{F}}_{ij},$$ (29)

where the sum ranges over all interacting pairs of MTs. The angular brackets in Eq. (28) denote an average over time. Here we have assumed that the temperature of the system is isotropic and well defined, so

$$\langle \sum _{i=1}^N\frac{{\mathbf{P}}_i{\mathbf{P}}_i}{m_{\mathrm{MT}}}\rangle =\frac{N{k}_{B}T}{V}\mathbf{I},$$ (30)

where P_i is the momentum of MT i and m_MT is the MT mass (here assumed the same for all MTs). Filaments have momentum based on their instantaneous movements on short time scales. This motion is in thermal equilibrium with the background fluid, connecting molecular motion to Brownian motion. While this relation is clearly true in the equilibrium case, it is less obvious that this it holds for active MT–motor systems. However, a purely mechanical definition of osmotic pressure leads to the same expression even for nonequilibrium particle suspensions in the low-Reynolds-number hydrodynamic regime [65], and we will assume that Eq. (28) holds in the following discussion.

The isotropic pressure is defined as

$$\langle \Pi \rangle =\frac{1}{d}\sum _{j=1}^d\langle {\Sigma }_{jj}\rangle ,$$ (31)

The average extensile stress is

$${\Sigma }_b=\frac{1}{d-1}\sum _{j=1}^{d-1}\langle {\Sigma }_{dd}\rangle -\langle {\Sigma }_{jj}\rangle ,$$ (32)

where the d direction corresponds to the average nematic director orientation. We further resolve the stress tensor into contributions from subpopulations of MTs, for example, according to the local polar order parameter m_i introduced above. This can be done by writing the total virial as the sum of contributions from individual MTs,

$$\mathbf{W}=\sum _{i=1}^N{\mathbf{W}}_i,$$ (33)

where

$${\mathbf{W}}_i=\frac{1}{2}\sum _{j\ne i}^N{\mathbf{r}}_{ij}{\mathbf{F}}_{ij}.$$ (34)

To calculate the pair extensile stresslet as a function of the local polar order m_i, we calculate the virial per spherocylinder. At a given time point, each interaction gives an associated virial contribution for the pair. The single-MT virial contribution is taken to be half of the pair's contribution. Contributions from forces for all interacting partners are summed to give the virial contribution for each MT. Similarly, the local polar order parameter m_i is calculated for each MT. Then the virial anisotropy contribution per MT in the nematic reference frame is determined based on its local polar order. After repeating for all time points, the histogram is normalized, leading to the calculation of the extensile pair stresslet per MT as a function of m_i.

To calculate the extensile pair stresslet in bulk simulations, we consider interacting MTs only. At each time point, the total number of interactions is calculated by summing the number of pairs for which there is a nonzero force. The total parallel and antiparallel virials in the director reference frame are calculated. Any interactions between pairs with p_i · p_j > 0 contribute to the polar-aligned virial, and the remainder contribute to the antialigned virial. This measurements is time averaged and the extensile pair stresslet calculated by dividing the average virial anisotropy by the average number of interactions.

B. Extensile stress and its origins

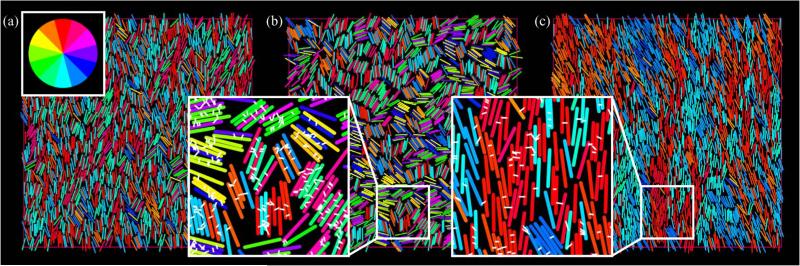
Figure 2 illustrates the long-time behavior of MT suspensions in the BD-kMC simulation model (also see video S1 [66]). Figure 2(a) shows a simulation of MTs interacting only through thermal fluctuations and steric interactions (without motors). The system develops a 2D nematic state consistent with previous work [55]. Figure 2(b) shows the result of adding immobile crosslinkers with full binding-unbinding kinetics. The system shows MT bundling due to short-range crosslink-induced attraction. Figure 2(c) shows the behavior with motors. The system now shows active MT flows driven by polarity sorting, leading to the formation of polar lanes (domains of MTs with similar polarity). These polar lanes are highly dynamic and show large fluctuations. The mean-squared displacement of MT position as a function of time shows diffusive behavior at long times in the equilibrium cases [Figs. 2(a) and 2(b)] and for active MTs when measured perpendicular to the average alignment direction. For motion parallel to the average alignment direction, the active MT mean-squared displacement is superdiffusive and nearly ballistic at long times [Fig. 3(a)].

FIG. 2.

(Color online) Snapshots of the BD-kMC particle simulations. Insets are zoomed views with motors explicitly shown in white. (a) System with no motors, illustrating the 2D nematic state. (b) An equilibrium system with static crosslinkers exhibits MT bundling due to short-range crosslink-induced attraction. (c) An active system with motors exhibits active flows and formation of polar lanes.

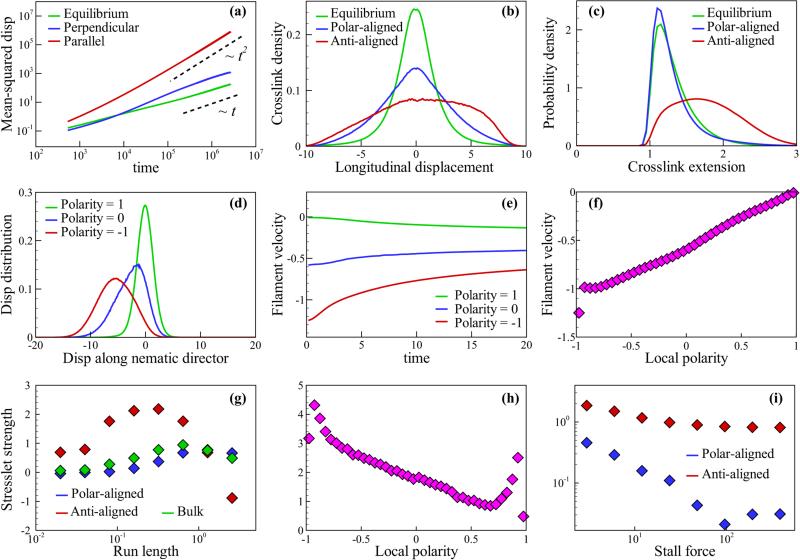
FIG. 3.

(Color online) Measurements of BD-kMC simulations. (a) Mean-squared deviation of MTs as a function of time. (b) Mean velocity of filaments along nematic director as a function of time t for different initial polar environments m_i. (c) Histogram of motor extension r_m, broken into contributions from polar-aligned and antialigned pairs in the active case. (d) Histogram of motor occupancy as a function of the particle filament longitudinal displacement s_ij, broken into contributions from polar-aligned and antialigned pairs in the active case. (e) Variation of average instantaneous velocity of filaments along the nematic director in time for different initial polar environments m_i. (f) Histogram of filament velocities at time separation t = 4.98 for various initial polar environments m_i. (g) Variation of extensile pair stresslet S with motor run length $\ell$, showing results from the entire bulk simulation and contributions of polar-aligned and polar-antialigned pairs. (h) Variation of extensile pair stresslet with local polar environment m_i. (i) Variation of extensile pair stresslet with motor stall force from simulations of isolated, perfectly parallel filament pairs.

We characterized the dynamical properties of bound motors for polar-aligned and antialigned MT pairs. For two MTs labeled i and j with orientations p_i and p_j and center-of-mass diplacement r_ij, we define the pair's longitudinal displacement by $s_{ij}=\frac{1}{2}{\mathbf{r}}_{ij}\cdot [{\mathbf{p}}_i+\mathrm{sgn}({\mathbf{p}}_i\cdot {\mathbf{p}}_j){\mathbf{p}}_j]$. For antialigned MT pairs (p_i · p_j < 0) undergoing motor-driven relative sliding, s_ij is negative when the MT pair is contracting (minus ends closer than plus ends) and becomes positive when the MT pair is extending (plus ends closer than minus ends; see Fig. 1). When crosslinks are immobile or for motors on polar-aligned MTs (p_i · p_j ≥ 0), the distribution of motors as a function of s_ij is symmetric [Fig. 3(a)]. However, for motors on antialigned MTs, the distribution of motors skews toward positive values of s_ij: More motors are bound during the extensile motion of the pair. This asymmetry occurs because of the translocation of the motors toward the MT plus ends. This biases MT pairs toward extension, yielding an extensile stress that drives active flows (see below).

The distribution of motor extension alters significantly when crosslinks translocate [Fig. 3(c)]. The minimum value of r_m is approximately 1 due to excluded-volume interactions between MTs. For polar-aligned pairs, the distribution is shifted toward smaller extensions than in the equilibrium case due to nonequilibrium tether relaxation, with important implications for the generation of extensile stress, as discussed below. For antialigned pairs, the distribution is shifted toward positive extension due to oppositely directed motor motion; this combination of motor extension and motion applies active forces that drive polarity sorting.

We measured the displacement distributions and average velocities of MTs along the nematic director and found that both are strongly correlated with an MT's initial local polar environment. Defining the nematic director n̂, we calculated MT displacement distributions in time along the projection of the local filament orientation vector onto the nematic vector: y(t) = sgn[n̂ · p_i(t₀)]n̂ · [r_i(t + t₀) – r_i(t)]. In order to examine dynamical behavior on time scales comparable to the diffusion time scale, we grouped the MT displacements at a lag time of t = 4.98 (chosen to clearly illustrate the different distributions) and their initial polar environment m_i(t₀) ≈ (−1,0,1). For MTs in an initially polar environment [m_i(t₀) ≈ 1], the displacement distribution is approximately Gaussian with mean near zero, consistent with diffusive-like dynamics [Fig. 3(d)]. For MTs in an initially antipolar environment [m_i(t₀) ≈ −1], we again find an approximately Gaussian displacement distribution, but the mean is shifted toward the MT's minus end [Fig. 3(d)]. This profile is consistent with drift plus diffusion dynamics. For more mixed initial environments [m_i(t₀) ≈ 0], we find that the dynamics are more complicated and are not likely described by a simple drift and diffusion model [Fig. 3(d)]. MTs in initially mixed or antipolar environments exhibit significant displacements toward their minus ends due to antipolar sliding.

To further examine the polarity-dependent MT movements, we measured the instantaneous MT velocity component along the nematic director, dy/dt at t = 0. Velocities of MTs are not constant because MTs experience relatively rapid changes in the polarity of their neighbors. MTs in initially antipolar environments tend to slow down rapidly, indicating that they move into more mixed environments, while MTs in polar or mixed environments tend to maintain their velocities for longer times. Filaments in polar environments have velocities near zero [Fig. 3(e)]. The instantaneous velocity depends approximately linearly on the local polar environment, as expected when filament movements are determined mainly by polarity sorting [Fig. 3(f)].

We measured the time-averaged bulk stress tensor Σ_b for our active particle system and found that, over a wide range of parameters, Σ_b is anisotropic with larger components in the average MT alignment direction than in the perpendicular direction. That is, since the MT alignment direction is essentially ŷ, the stress difference ${\Sigma }_b^{yy}-{\Sigma }_b^{xx}$ is positive, which corresponds to an extensile stress. Static crosslinkers or no motors [Figs. 2(a) and 2(b)] yield an isotropic Σ_b. The stress difference can be expressed as the sum of pair interactions between nearby MTs, with each ij pair contributing a stresslet S_ij (with units of force×length), prior to division by the bulk volume. We have characterized how the stresslet varies with system parameters and configurations. The average pair stresslet S increases with the motor speed v_m up to a maximum where the typical motor run length is the MT length [Fig. 3(g)]. Increasing v_m further leads to decreasing S because the motors rapidly move to the ends of the MTs and unbind. To understand the origins of extensile stress, we studied how S varies with the local polar environment m_i (27). The stresslet is largest when m_i is near −1, suggesting that polarity sorting is the dominant source of pairwise extensile stress [Fig. 3(h)]. As m_i increases, S drops with approximate linearity, at least away from the two isolated peaks that close examination show originate through strong steric interactions of nearly parallel MTs. Nearly, but not exactly, parallel MTs experience aligning torques due to motor-mediated attraction; the resulting steric collisions tend to promote pair extension that increases the extensile stress for nearly aligned pairs (relative to perfectly aligned pairs).

The extensile stress from antialigned pair interactions arises from asymmetries during polarity sorting: If an MT pair begins sliding when the two minus ends touch (s_ij −10) and slides under a force proportional to pair overlap until the two plus ends meet (s_ij = 10), then the contractile motion would perfectly balance the extensile motion and the total extensile stress would be zero [20,26,59,67]. In our simulations we observe two effects that break this symmetry. First, MTs are unlikely to begin interacting exactly when their minus ends are touching, decreasing the range of negative s_ij over which sliding occurs. Second, more motors are bound on average during extensional motion [so s_ij > 0; see Fig. 3(b)].

We also find the surprising and counterintuitive result that S remains positive even when m_i is near 1, that is, for polar-aligned pairs of MTs. This effect occurs due to an interplay between motor motion and excluded-volume interactions. We propose that the effect can be understood by considering equilibrium and nonequilibrium motor relaxation. For immobile motors, the system is at equilibrium and the stress tensor is isotropic; attractive interactions due to motors are balanced by excluded volume interactions and thermal fluctuations, and the system is at mechanical equilibrium. When motors are active, stress anisotropy becomes possible due to the nonequilibrium nature of the motor force-velocity relation. The tether of a longitudinally stretched motor pulls back on the leading motor, slowing it, and pulls forward on the trailing motor. Hence, the motor relaxes its longitudinal extension. This effect is observable in Fig. 3(c) as a slight but significant shift in the distribution of motor extension toward smaller values relative to the equilibrium case. As a result, the motor-induced contractile stress along the MT alignment direction is decreased, while there is no change in the transverse stress induced by motors. This leads to a net anisotropic extensile stress in the alignment direction. In this scenario, we would predict that if the motors had a force-independent velocity, the polar-aligned extensile stress would vanish because the longitudinal motor extension would be unable to relax. We tested this prediction by studying how S varies as stall force increases for simulations of perfectly aligned (unable to rotate) isolated filament pairs. We find that the extensile stress changes little with stall force for antialigned MT pairs. However, for polar-aligned MT pairs the extensile stress drops as stall force increases and goes to zero for infinite stall force [which corresponds to force-independent velocity, Fig. 3(i)]. When effects of filament rotation are also included, the results are more subtle; we find that the interplay of filament rotation and motor activity can induce extensile stress for polar-aligned pairs in bulk simulations even for infinite stall force.

While the extensile stress due to polar-aligned MT pairs is typically a factor of 2–5 smaller than for antialigned pairs, when measured per pair [Fig. 3(h)], polarity sorting and the tendency to form polar lanes [Fig. 2(c)] lead to larger numbers of polar-aligned MT pairs than of antialigned. In our BD-kMC simulations, which lack the effect of hydrodynamics, the overall contributions of polar-aligned and antialigned pairs to the extensile stress are comparable.

IV. CONTINUUM KINETIC THEORY

The BD-kMC simulations show how polar-specific MT-pair interactions give rise to extensile active stresses. To study the effect of hydrodynamic interactions and to make analytical predictions we have developed a Doi-Onsager theory [68] similar to those used to describe the dynamics of motile rod suspensions [40,41,45]. The theory's fluxes and active stresses arise from polar-aligned and antialigned MT pair interactions produced by active motors. These stresses induce chaotic flows driven by the formation of disclination defects.

A. Dynamics of polarity sorting

To coarse grain the BD-kMC simulation results and make connections with the kinetic model, we first derive a continuum-mechanics model to describe the MT dynamics. Here we assume the motor run length to be approximately the MT length, meaning that, once bound, the motors will stay on the MTs until reaching the plus ends. As shown in Fig. 4, we consider a nematically ordered local cluster of MTs undergoing polarity sorting, with n MTs pointing rightwards and m MTs pointing leftwards. Let all the MTs in this cluster be coupled by active motors which create springlike forces between the MTs and whose bound ends move at a characteristic (constant) speed v_w toward MT plus ends. For an antipolar MT pair this induces a relative sliding, each towards its negative end. The cluster is assumed small enough so all MTs experience the same local flow field. Using Stokesian slender body theory [69] we can find the velocities of the left-and rightward-pointing MTs. For each MT, the center locates at x^c, with the director p. We assume that in the cluster there are m MTs pointing leftwards (p = –x̂, with superscript L) and n MTs pointing rightwards (p = x̂, with superscript R). Each antialigned pair (say the jth and the kth MT) shares Q (Q > 1) motors

$$\begin{array}{c}\hfill {\mathbf{x}}_j^L={\mathbf{x}}_j^{L,c}+s_q^L{\mathbf{p}}_j=\left(x_j^{L,c}-s_q^L\right)\widehat{x},\hfill \\ \hfill {\mathbf{x}}_k^R={\mathbf{x}}_k^{R,c}+s_q^R{\mathbf{p}}_k=\left(x_k^{R,c}+s_q^R\right)\widehat{x},\hfill \end{array}$$ (35)

where j = 1, . . . , m,k = 1, . . . , n and q = 1, . . . , Q. As shown on the right in Fig. 4, one motor locates at $s_q^L\left(t\right)=s_{j,q}^{L,0}+v_{w}t$ and the other locates at $s_q^R\left(t\right)=s_{k,q}^{R,0}+v_{w}t$, with initial positions $s_{j,q}^{L,0}$ and $s_{k,q}^{R,0}$. The characteristic motor speed v_w is constant for the antialigned pair. Hence the distance between the two motors in the tangential direction can be calculated as

$${\Delta }_{jk}^q\widehat{x}={\mathbf{x}}_j^L-{\mathbf{x}}_k^R=\left(x_j^{L,c}-x_k^{R,c}\right)\widehat{x}-\left(s_{j,q}^{L,0}+s_{k,q}^{R,0}\right)\widehat{x}-\left(2v_{w}t\right)\widehat{x}=\left({\Delta }_{jk}^c-{\Delta }_{jk}^{q,0}-2v_{w}t\right)\widehat{x},$$ (36)

where ${\Delta }_{jk}^c=-{\Delta }_{kj}^c=x_j^{L,c}-x_k^{R,c}$, ${\Delta }_{jk}^{q,0}={\Delta }_{kj}^{q,0}=s_{j,q}^{L,0}+s_{k,q}^{R,0}$. When the motor is walking, it behaves like a linear spring with rigidity κ by exerting equal and opposite forces,

$${\mathbf{f}}_{jk}^q=-{\mathbf{f}}_{kj}^q=-\kappa {\Delta }_{jk}^q\widehat{x}.$$ (37)

As a result, the two MTs slide past one another undergoing polarity sorting. Following slender-body theory [69], the MT speed is given by ${\stackrel{.}{x}}^c=\left(\frac{\mathbf{I}+\mathbf{pp}}{\tilde{\eta }l}\right)\cdot {\sum }_{k=1}^n{\sum }_{q=1}^Q\mathbf{f}$, leading to

$${\stackrel{.}{\Delta }}_{jk}^c={\stackrel{.}{x}}_j^{L,c}-{\stackrel{.}{x}}_k^{R,c}=-\frac{2\kappa }{\tilde{\eta }l}\sum _{k^{\prime }=1}^n\sum _{q=1}^Q\left({\Delta }_{j{k}^{\prime }}^c-{\Delta }_{j{k}^{\prime }}^{q,0}-2v_{w}t\right)-\frac{2\kappa }{\tilde{\eta }l}\sum _{j^{\prime }=1}^m\sum _{q=1}^Q\left({\Delta }_{j^{\prime }k}^c-{\Delta }_{j^{\prime }k}^{q,0}-2v_{w}t\right),$$ (38)

where $\tilde{\eta }=4\pi \eta ∕\ln \left(2r\right)$, and η is the fluid viscosity. We seek the time-dependent solutions of the form ${\Delta }_{jk}^c-{\Delta }_{jk}^{q,0}=A+Bt$. The coefficients A and B can be solved as

$$A={\Delta }_{jk}^q=-\frac{\tilde{\eta }l{v}_w}{Q\kappa (m+n)},B=2v_w,$$ (39)

leading to

$${\stackrel{.}{x}}_j^{L,c}=\frac{n}{(m+n)}2v_w,{\stackrel{.}{x}}_k^{R,c}=-\frac{m}{(m+n)}2v_w,$$ (40)

which suggests $v^L=\frac{2n}{n+m}{v}_w$, $v^R=-\frac{2m}{n+m}{v}_w$. This expression shows that the speed of each population depends on how many opposing MTs there are to pull against, with their drag as the anchor and their relative velocity fixed at v^L – v^R = 2v_w by the motor protein speed. This latter observation is in agreement with observations of antialigned sliding of MTs in the mitotic spindle [70].

FIG. 4.

(Color online) Schematic for a cluster of MTs undergoing polarity sorting. The plus ends are marked by red rings. Right: an antialigned pair of the jth and the kth MTs.

Next, we consider a general situation when the MTs are not perfectly aligned but with an intersection angle, i.e., ${\mathbf{p}}_j\cdot {\mathbf{p}}_k=\pm 1+O\left({\theta }_{jk}^2\right)$, where θ_jk is a small angle between the jth and the kth MTs. As discussed later, at high concentration, the steric interactions align the neighboring MTs, which makes the small-angle assumption a reasonable approximation. Similarly to the perfectly aligned case, the positions of the two motors can now be written as:

$${\mathbf{x}}_j={\mathbf{x}}_j^c+s_j^q{\mathbf{p}}_j,{\mathbf{x}}_k={\mathbf{x}}_k^c+s_k^q{\mathbf{p}}_k,$$ (41)

where j,k = 1, . . . , N,q = 1, . . . , Q, and s = s^q,0 + v_wt. So the relative distance becomes

$$\begin{array}{cc}\hfill {\Delta }_{jk}^q& ={\mathbf{x}}_j^c-{\mathbf{x}}_k^c+s_j^{q,0}{\mathbf{p}}_j-s_k^{q,0}{\mathbf{p}}_k+v_{w}t({\mathbf{p}}_j-{\mathbf{p}}_k)\hfill \\ \hfill & ={\Delta }_{jk}^c+{\Delta }_{jk}^{q,0}+v_{w}t({\mathbf{p}}_j-{\mathbf{p}}_k),\hfill \end{array}$$ (42)

where ${\Delta }_{jk}^c={\mathbf{x}}_j^c-{\mathbf{x}}_k^c$, ${\Delta }_{jk}^{q,0}=s_j^{q,0}{\mathbf{p}}_j-s_k^{q,0}{\mathbf{p}}_k$. The motors exert tangential force ${\mathbf{f}}_{jk}^q=-\kappa {\Delta }_{jk}$. Following the same procedure, we seek solutions of the form ${\Delta }_{jk}^q=(A+Bt)({\mathbf{p}}_j-{\mathbf{p}}_k)$, yielding

$$A=\frac{\tilde{\eta }l{v}_w}{2QN\kappa },B=-v_w.$$ (43)

Then the relative moving speed of the two MTs becomes

$${\stackrel{.}{\Delta }}_{jk}^c={\stackrel{.}{x}}_j^c-{\stackrel{.}{x}}_k^c=-v_w({\mathbf{p}}_j-{\mathbf{p}}_k).$$ (44)

When p_k = –p_j, Eqs. (43) and (44) exactly recover the solutions in (40) for the perfectly aligned case. To further coarse grain the above results to facilitate a continuum modeling as discussed below, we take an average in p of Eq. (44) which directly yields a translational particle flux ẋ = q – p.

B. Flux velocity, active stress, and kinetic model

The system is described by a distribution function Ψ(x,p,t) of MT center-of-mass positions x and polar orientation vectors p (|p| = 1), evolved through a Smoluchowski equation,

$$\frac{\partial \Psi }{\partial t}+{\nabla }_x\cdot \left(\stackrel{.}{x}\Psi \right)+{\nabla }_p\cdot \left(\stackrel{.}{p}\Psi \right)=0,$$ (45)

which reflects conservation of particle number. Here ẋ and ṗ are MT conformational fluxes. Important macroscopic quantities for describing a polar nematic system are the local concentration $\Phi ={\int }_p\Psi$, the local polarity vector $\mathbf{q}={\int }_p\Psi \mathbf{p}∕\Phi$, the second-moment tensor $\mathbf{D}={\int }_p\Psi \mathbf{pp}$ which arises generically in capturing active stresses produced by active suspensions [37], the (trace-free) order parameter tensor Q = D/Φ – I/d, with d = 2 or 3 the spatial dimension, and the fourth moment $\mathbf{S}={\int }_p\Psi \mathbf{pppp}$.

Slender-body theory yields the forces each rod exerts on the fluid, and hence the volume-averaged stress [71] by polarity sorting, can be calculated. If the cluster occupies a volume V_c, then the induced extra stress tensor from antialigned sorting is ${\Sigma }_{aa}=\frac{\tilde{\eta }{v}_w{l}^2}{V_c}\frac{{\alpha }_{aa}}{2}\frac{2mn}{m+n}\mathbf{pp}$. Here $\tilde{\eta }$ is proportional to fluid viscosity η, and α_aa = s/l with s the signed distance between the centers of mass of the p and –p oriented subclusters. If the cluster is extending, then s < 0, as would be the case if motor protein binding and unbinding kinetics biased motor densities towards the plus end of the MTs. This is seen in the BD-kMC simulations [Fig. 2(e)] and is associated with local extensile flows similar to those of motile Pusher particles which collectively can drive macroscopic flow instabilities [40,41,72]. The antialigned (aa) pair stresslet strength can be derived as $S=\frac{\tilde{\eta }{v}_w{l}^2{\alpha }_{\mathrm{aa}}}{m+n}$. When taking v_w as v_m, we extract the value of α_aa ≈ −2 from the BD-kMC simulations.

While active motor motion between polar-aligned MTs yields little MT mobility, the BD-kMC simulations show that it does yield an extensile stress. However, unlike polarity sorting we lack a simple first-principles model of how polar interactions yield extensile stress, though the number of polar pair interactions within a cluster scales as m² + n². Given that the anti- and polar-aligned stresses are of the same order [Fig. 2(h)] we assume the form ${\Sigma }_{\mathrm{pa}}=\frac{\tilde{\eta }{v}_w{l}^2}{V_c}\frac{{\alpha }_{\mathrm{pa}}}{2}\frac{m^2+n^2}{m+n}\mathbf{pp}$. Comparison with the BD-kMC simulations suggests that α_pa ≈ −0.5.

We have generalized this simple example to a continuum model that captures polarity sorting of MTs and the dependence of the stress upon the local polarity of the MT field. The fluxes for Eq. (45) are given in dimensionless form by

$$\stackrel{.}{x}=(\mathbf{q}-\mathbf{p})+\mathbf{U}-D_t{\nabla }_x\ln \Psi ,$$ (46)

$$\stackrel{.}{p}=(\mathbf{I}-\mathbf{pp})({\nabla }_x\mathbf{U}+2{\zeta }_0\mathbf{D})\mathbf{p}-D_r{\nabla }_p\ln \Psi .$$ (47)

To nondimensionalize the above equations, we assume that there are M MTs in the entire computational domain of volume V_c. At high concentration, it is useful to introduce an effective volume fraction ν = nbl², where n = M/V_c is the mean number density [45,68]. Further, we=choose the characteristic length scale l_c = b/ν, the velocity scale v_c = v_w, as well as the stress scale ηv_w/l_c. In Eq. (46), U is the background fluid flow, and the last term yields translational diffusion with constant D_t. For nematically ordered suspensions, the term q – p exactly reproduces the cluster velocities induced by polarity sorting given above (note that for a perfectly polar system, no polarity sorting occurs and the flux q – p makes no contribution). In Eq. (47), the MTs are rotated by the background flow gradient ∇_xU according to Jeffery's equation [73] while the second term arises from the Maier-Saupe potential with coefficient ζ₀ which models torques and stresses arising from steric interactions at high concentration [45,74]. The last term yields rotational diffusion of the rod with constant D_r. We do not account for MT rotation through interactions with the local field, as is appropriate when the MT field is nematically ordered. All constants have been made nondimensional using characteristic velocity v_w and a characteristic length l_c appropriate for dense suspensions [45,68].

Our system is closed by specifying how U and ∇_xU are recovered from Ψ, which involves specifying the extra stress created in the fluid by activity and other sources. We assume the active stress arises separately from antialigned and polar-aligned MT interactions and construct it from D and Φqq (i.e., the simplest symmetric tensors quadratic in p). In dimensionless form, the active stress tensor takes the form

$${\Sigma }^a=\frac{{\alpha }_{\mathrm{aa}}}{2}(\mathbf{D}-\Phi \mathbf{qq})+\frac{{\alpha }_{\mathrm{pa}}}{2}(\mathbf{D}+\Phi \mathbf{qq}).$$ (48)

The first term (second term) captures active stress production via polarity sorting (motor relaxation) and exactly reproduces the form of Σ_aa (Σ_pa) for nematically ordered suspensions. The total extra stress tensor is given by Σ^e = Σ^a + Σ′, where Σ′ models extra stresses arising from flow-induced constraint forces on MTs and steric interactions [45]:

$${\Sigma }^{\prime }=\nu \beta \mathbf{S}:{\nabla }_x\mathbf{U}-2\nu {\zeta }_0\beta (\mathbf{D}\cdot \mathbf{D}-\mathbf{S}:\mathbf{D}),$$ (49)

where $\beta =\frac{\pi r}{6\ln \left(2r\right)}$.

For bulk flow modeling one typically closes the system by balancing viscous and extra stresses and solving the forced Stokes equation −∇_xp = Δ_xu = −∇_x · Σ^e and ∇_x · u = 0 with velocity u and pressure p. This generates the background velocity and its gradient needed to evolve Eq. (45) [40]. However, this approach does not describe the streaming nematic experiments of Sanchez et al. [7], where the active material is confined to an interface between oil and water, so surface motions are coupled to external fluid motions. To capture that coupling, we consider a flat layer of interacting MTs bound in the xy plane at z = 0 and immersed between two half-spaces filled with Newtonian viscous fluid (for simplicity, of the same viscosity). The activity in the MT layer generates a stress jump across the z = 0 plane and so generates a global 3D flow which is continuous at z = 0. In order to close the system, we solve the surface velocity U in terms of the extra stress Σ^e. To accomplish this, we first solve the (3D) velocity field u = (u, v, w) of fluid flow using the Stokes equations

$$\nabla \cdot \mathbf{u}=0,-{\nabla }^2\mathbf{u}+\nabla p=0,$$ (50)

where ∇ is a regular 3D spatial gradient operator. Under Fourier transform in (x,y), the above equations can be written as:

$$-i\mathbf{k}\widehat{p}+({\partial }_{zz}-k^2)\widehat{v}=0,-{\widehat{p}}_z+({\partial }_{zz}-k^2)\widehat{w}=0,i\mathbf{k}\cdot \widehat{v}+{\widehat{w}}_z=0,$$ (51)

where k is a 2D wave vector and v = (u,v) is a 2D velocity field. When solving these equations in=the upper (+) and lower (−) halves of the domain, we match at the MT layer through the continuous (2D) surface velocity U, ie., v⁺ = v⁻ = U and w⁺ = w⁻ = 0. After some algebra, we obtain

$$\begin{array}{cc}\hfill {\widehat{p}}_{\pm }& =-2i\mathbf{k}\cdot \widehat{U}{e}^{\mp kz},{\widehat{v}}_{\pm }=(\mathbf{I}\mp kz\widehat{k}\widehat{k})\widehat{U}{e}^{\mp kz},\hfill \\ \hfill {\widehat{w}}_{\pm }& =-i\mathbf{k}\cdot \widehat{U}z{e}^{\mp kz},\hfill \end{array}$$ (52)

where k = |k| and k̂ = k/k is a 2D unit wave vector. We further assume that the capillarity of the surface bounding the MT layer acts against the concentration of MTs. We denote the liquid viscous stress as σ = –pI + ∇u and match the two solutions through a traction jump on the layer σ⁺ · n – σ⁻. n = ∇_x · Σ. Here ∇_x is a 2D operator on the surface, and Σ = Σ^e + Σ^p, arising from both the extra stress Σ^e due to MTs and the stress Σ^p due to a transverse pressure gradient within the MT layer which results in the background flow being incompressible in the plane (i.e., ∇_x · U = 0). Then it is easy to eliminate Σ^p and solve the surface flow U in terms of Σ^e as:

$${\widehat{U}}_k=\frac{i}{2}(\mathbf{I}-\widehat{k}\widehat{k})\left({\widehat{\Sigma }}_k^e\widehat{k}\right).$$ (53)

It is useful to compare this expression to that for the 2D Stokes equation forced by a bulk stress: $\widehat{u}=\frac{i}{k}(\mathbf{I}-\widehat{k}\widehat{k})\left({\widehat{\Sigma }}^e\widehat{k}\right)$. The missing factor of k in Eq. (53) profoundly changes the nature of system stability for the surface and 2D bulk systems. Equation (53) not only closes the system but facilitates a pseudospectral method to solve the Smoluchowski equation (45) and the fluid flow in a coupled manner.

C. Flow, polarity, and defects

Assuming 2D periodic boundary conditions, we have simulated our active polar nematic model over long times, using Eqs. (45)–(49) as well as the velocity-stress kernel (53). For the simulations shown here, we choose α_aa,pa from −0.1 ~ −4.0 and fix β = 1.74 (i.e., aspect ratio 10), ν = 0.5, ζ₀ = 1.0, D_t = 0.5, and D_r = 0.1 (estimated from the BD-kMC parameters). The computation is performed on a 2D periodic domain of a square box with dimension L = 80. The governing equations are solved spectrally in a coupled manner, using the fast Fourier transform algorithm by expanding the variables in Fourier series and truncating the series after 200–400 modes in each spatial direction [40,45,75].

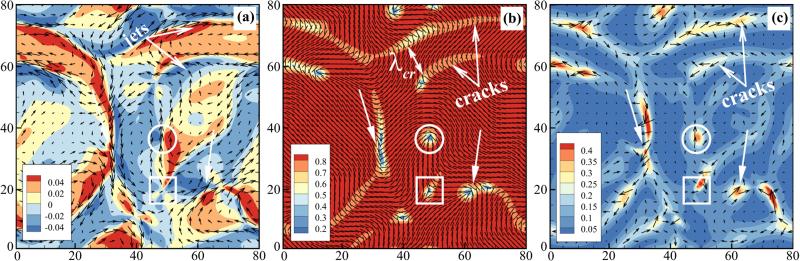
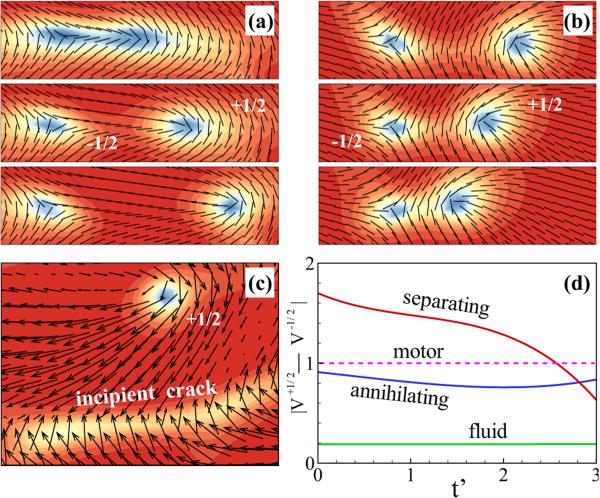
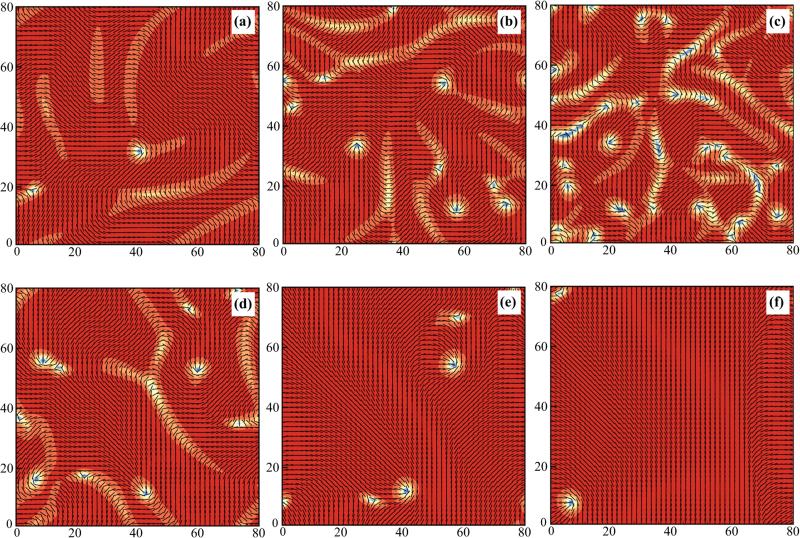
Simulating in regions of flow instability we find persistently unsteady flows correlated with continual genesis, propagation, and annihilation of ±1/2 defect pairs. When we examine simulation results at late times, from initial data near uniform isotropy, we find dynamics that are complex and appear turbulent, qualitatively similar to those reported by Sanchez et al. [7] (Fig. 5). The surface velocity and vorticity show formation of jets and swirls (Fig. 5(a), also see video S2 [66]). The local MT orientation is highly correlated with the flow structures, and the surface is littered with ±1/2 defects which propagate freely about the system (Fig. 5(b), also see video S3 [66]). These defects exist in regions of small nematic order (dark blue) and are born as opposing pairs in elongated “incipient crack” regions. These are associated with surface jets, locally decreasing nematic order, and increasing curvature of director field lines. Characteristically, the +1/2 defects propagate away along their central axis and have a+much higher velocity than those of −1/2 order. The relatively higher surface velocity in the neighborhood of a +1/2 defect appears as a well-localized jet, in the direction of defect motion, between two oppositely signed vortices.

FIG. 5.

(Color online) Snapshots of streaming MT nematics on a liquid-liquid interface. The active stress magnitudes are chosen as α_aa = −2.0 and α_pa = −0.6. (a) The background fluid velocity vector field superposed upon the color map of the associated vorticity. (b) The nematic director field n superposed on the color map of the scalar order parameter (twice the positive eigenvalue of the tensor Q). Disclination defects of order ±1/2 appear in localized regions of low order. Two defects are marked by an open circle (+1/2) and a square (−1/2). The arrow at right marks a pair of annihilating defects, while the arrow at left identifies an “incipient crack” from which a defect pair is about to emerge. Here λ_cr is a calculated characteristic length between the cracks. (c) The vector field of the active force, superimposed on its magnitude.

The active force vector field f^a = ∇_x · Σ^a is correlated with regions of rapidly changing nematic order (Fig. 5(c), also see video S4 [66]). Large active force is present along an interconnected network of ridges correlated with the stringy regions of diminished nematic order and particularly with incipient cracks. Along such cracks, the active force points in the direction from which newly nucleated +1/2 defects will emerge and propagate. Isolated high-force peaks correlate and move with +1/2 defects, with the force pointing in the direction of their motion. Negative order defects are associated with regions of relatively low force magnitude, likely due to the local symmetry of the nematic director field.

We observe both nucleation and annihilation of defect pairs (Fig. 6). The birth and separation of a defect pair begins from an incipient crack wherein the initially smooth director field [e.g., lower arrow in Fig. 5(b)] morphs into singular forms in regions of low nematic order [Fig. 6(a)]. Typically, the positively signed defect moves away faster and roughly along its symmetry axis. Following annihilation of an oppositely charged defect pair [Fig. 6(b)], the nematic order increases as the director field reknits itself into a smooth form [e.g., upper arrow in Fig. 5(b)]. We examined how the polarity field q changes near a defect and incipient crack [Fig. 6(c)]. As the +1/2 defect propagates, it leaves behind a region of increased polarity. The polarity field rapidly rotates across the incipient crack (by approximately π/2) and sometimes forms a shocklike structure that precedes the birth of a new defect pair. We measured the relative speed of the defect pairs [Fig. 6(d)]. The speeds are similar to each other and on the order of the motor protein speed in our model (normalized to unity). This is consistent with experimental observations (cf. Fig. 3 of Sanchez et al. [7]). The average fluid velocity around the defect pair is much lower than the defect speeds. Hence, as is the case for defects in more standard liquid crystalline materials, the defects here are not material structures carried along by the background surface flow.

FIG. 6.

(Color online) Time sequential snapshots of the nematic director field n for nucleation (a) and annihilation (b) of defect pairs, where α_aa = −2.0 and α_pa = −0.6 are fixed. The (dimensionless) time spacing between frames is 5. (c) Polarity field associated with a motile +1/2 defect and an incipient crack on the bottom. (d) Relative speed of the two oppositely charged defects, as well as the mean flow speed near this defect pair, as a function of dimensionless time t′. In (a), (b), and (c), the color shows the scalar order parameter, plotted with the same scale as Fig. 5(b).

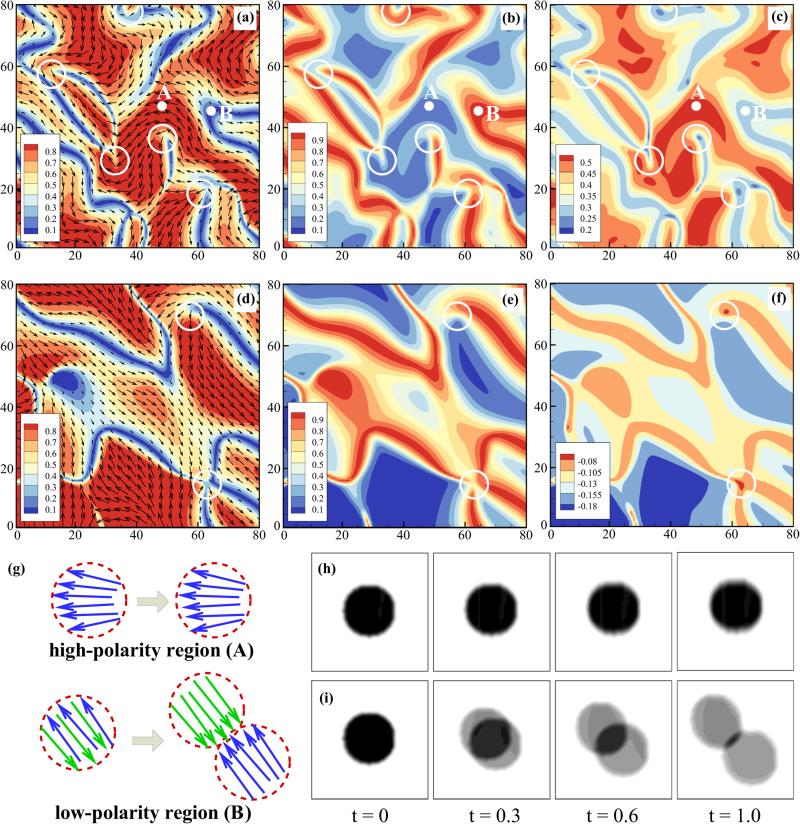
Because our model is based on polar-specific fluxes and active stresses, the polarity field q [76], polarity-dependent active stresses Σ_aa and Σ_pa, and the local MT dynamics are coupled (Fig. 7). The polarity field develops considerable spatial variation with regions of high and low polar order (Fig. 7(a), also see video S5 [66]). The two active stresses vary in strength depending on the local polarity—the polar-aligned (antialigned) stress is large in regions of high (low) polar order [Figs. 7(b) and 7(c)]. The antialigned stress yields the largest forces, by about a factor of 3 (close to the ratio α_aa/α_pa). The polarity field varies rapidly around +1/2 defects, leading to gradients in the active stresses and large active force (open circles in Fig. 7). For comparison, we did another numerical test where we assume the active stress generated during motor tether relaxation is contractile [i.e., α_pa > 0, Figs. 7(d)–7(f)]. The ratio between the antialigned and polar-aligned stress is still close to the ratio |α_aa|/|α_pa|. However, since the sign of the polar-aligned stress changes, the two stresses exist in approximately the same regions.

FIG. 7.

(Color online) Dynamics of the polarity field, the polarity-dependent active stresses, and the predicted dynamics of a photobleaching experiment. [(a)–(c)] Results from the simulation shown in Fig. 5. (a) The polarity vector field q superimposed upon its magnitude |q| (the local polar order). Circular areas labeled A and B mark regions of high and low polarity, respectively. [(b) and (c)] Polarity-dependent|active stress magnitudes, showing principal eigenvalues of the active stresses due to polarity sorting [Σ_aa (b)] and motor relaxation (Σ_pa, c). In (a)–(c), the stress magnitudes are chosen as α_aa = −2.0 and α_pa = −0.6. For comparison, (d)–(f) shows the polarity field and the polarity-dependent active stress fields when choosing α_aa = −2.0 and α_pa = 0.2. In (a)–(f), positions of +1/2-order defects are marked by open circles. (g) Schematic of predicted dynamics for a bleached spot of high nematic order in a region of high polar order (area A) and in a region of low polar order (area B). Arrows represent MTs with arrowheads denoting plus ends. In panels (h) and (i) these predictions are borne out by simulations of photobleached spots in areas A and B, respectively.

To illustrate the dramatic variation of local MT fluxes with the local polarity field, we simulated the results of a photo-bleaching experiment in which a circular region is exposed to high-intensity laser light to bleach the fluorescing molecules on the corresponding MTs [77] [Figs. 7(g)–7(i)]. In a small high-polarity region [marked A in Fig. 7(a)], little or no polarity sorting occurs. Therefore the photobleached spot remains approximately circular [Figs. 7(g) (top) and 7(h)] and would deform due to the fluid flow over longer times. In a low-polarity region of high nematic order [marked B in Fig. 7(b)], strong polarity sorting of antialigned MTs causes a photobleached spot to separate into two lobes [Figs. 7(g) (lower) and 7(i)]. Each lobe mixes with unbleached surrounding MTs due to their active relative flux, showing decreased bleaching. Through the lens of our theory, this type of experiment probes the local polarity field, and hence the origins of active stress.

D. Coherent structures and hydrodynamic instabilities

In our simulations, defect pairs are generated along elongated cracks that develop in regions of high polar order. To understand this instability, we consider nematically aligned MTs using reduced equations where particle diffusion is neglected (i.e., D_r = D_t = 0) in (47). We then adopt bipolar solutions of the form Ψ(x,p,t) = A(x,t)δ[p – q₁(x,t)] + B(x,t)δ[p – q₂(x,t)], where the concentrations A and B and orientations q_1,2 are governed by:

$$\{\begin{array}{c}\frac{\partial A}{\partial t}+{\nabla }_x\cdot \left(A\mathbf{U}\right)-{\nabla }_x\cdot \left[\frac{AB}{A+B}({\mathbf{q}}_1-{\mathbf{q}}_2)\right]=0,\hfill \\ \frac{\partial B}{\partial t}+{\nabla }_x\cdot \left(B\mathbf{U}\right)+{\nabla }_x\cdot \left[\frac{AB}{A+B}({\mathbf{q}}_1-{\mathbf{q}}_2)\right]=0,\hfill \\ \frac{\partial {\mathbf{q}}_1}{\partial t}+\mathbf{U}\cdot {\nabla }_x{\mathbf{q}}_1-\frac{B}{A+B}({\mathbf{q}}_1-{\mathbf{q}}_2)\cdot {\nabla }_x{\mathbf{q}}_1=(\mathbf{I}-{\mathbf{q}}_1{\mathbf{q}}_1)\cdot {\nabla }_x\mathbf{U}\cdot {\mathbf{q}}_1+2{\zeta }_{0}B({\mathbf{q}}_1\cdot {\mathbf{q}}_2)(\mathbf{I}-{\mathbf{q}}_1{\mathbf{q}}_1)\cdot {\mathbf{q}}_2,\hfill \\ \frac{\partial {\mathbf{q}}_2}{\partial t}+\mathbf{U}\cdot {\nabla }_x{\mathbf{q}}_2-\frac{B}{A+B}({\mathbf{q}}_1-{\mathbf{q}}_2)\cdot {\nabla }_x{\mathbf{q}}_2=(\mathbf{I}-{\mathbf{q}}_2{\mathbf{q}}_2)\cdot {\nabla }_x\mathbf{U}\cdot {\mathbf{q}}_2+2{\zeta }_{0}A({\mathbf{q}}_1\cdot {\mathbf{q}}_2)(\mathbf{I}-{\mathbf{q}}_2{\mathbf{q}}_2)\cdot {\mathbf{q}}_1.\hfill \end{array}\phantom{\}}$$ (54)

We consider the solutions for two groups of MTs undergoing polarity sorting along $\widehat{x}:A=\frac{1}{2}+\epsilon A^{\prime }$, $B=\frac{1}{2}+\epsilon B^{\prime }$, ${\mathbf{q}}_1=\mathbf{x}+\epsilon {{\mathbf{q}}^{\prime }}_1$, ${\mathbf{q}}_2=-\mathbf{x}+\epsilon {{\mathbf{q}}^{\prime }}_2$, $\mathbf{U}=\epsilon {\mathbf{u}}^{\prime }$, when q_1,2 · x̂ = 0 which ensures that the length of q_1,2 remains 1 to order ε² for |ε| << 1. At order ε, we obtain a set of linearized reduced equations:

$$\{\begin{array}{c}\frac{\partial (A^{\prime }+B^{\prime })}{\partial t}+{\nabla }_x\cdot {\mathbf{u}}^{\prime }=0,\hfill \\ \frac{\partial (A^{\prime }-B^{\prime })}{\partial t}-\frac{1}{2}{\nabla }_x\cdot ({{\mathbf{q}}^{\prime }}_1-{{\mathbf{q}}^{\prime }}_2)-\widehat{x}\cdot {\nabla }_x(A^{\prime }+B^{\prime })=0,\hfill \\ \frac{\partial ({{\mathbf{q}}^{\prime }}_1+{{\mathbf{q}}^{\prime }}_2)}{\partial t}-\widehat{x}\cdot {\nabla }_x({{\mathbf{q}}^{\prime }}_1-{{\mathbf{q}}^{\prime }}_2)=-2{\zeta }_0({{\mathbf{q}}^{\prime }}_1+{{\mathbf{q}}^{\prime }}_2),\hfill \\ \frac{\partial ({{\mathbf{q}}^{\prime }}_1-{{\mathbf{q}}^{\prime }}_2)}{\partial t}-\widehat{x}\cdot {\nabla }_x({{\mathbf{q}}^{\prime }}_1+{{\mathbf{q}}^{\prime }}_2)=2(1-\widehat{\mathbf{x}}\widehat{\mathbf{x}})\cdot {\nabla }_x{\mathbf{u}}^{\prime }\cdot \widehat{x},\hfill \end{array}\phantom{\}}$$ (55)

and the linearized active stress ${\Sigma }^e=({\alpha }_1+{\alpha }_2)\widehat{x}\widehat{x}+\epsilon \left(\frac{{\alpha }_1+{\alpha }_2}{2}\right)[({{\mathbf{q}}^{\prime }}_1-{{\mathbf{q}}^{\prime }}_2)\widehat{x}+\widehat{x}({{\mathbf{q}}^{\prime }}_1-{{\mathbf{q}}^{\prime }}_2)]+\epsilon \nu \beta \left(\widehat{x}\widehat{x}\widehat{x}\widehat{x}\right):{\nabla }_x{\mathbf{u}}^{\prime }$ in velocity-stress kernel in Eq. (53). Next, we consider plane-wave solutions ${\Psi }^{\prime }(\mathbf{x},\mathbf{p},t)=\tilde{\Psi }(\mathbf{k},\mathbf{p})\exp (i\mathbf{k}\cdot \mathbf{x}+\sigma t)$ and ${\mathbf{u}}^{\prime }(\mathbf{x},t)=\tilde{u}\left(\mathbf{k}\right)\exp (i\mathbf{k}\cdot \mathbf{x}+\sigma t)$ and assume that k̂ lies in the plane defined by $(\widehat{x},{\mathbf{q}}_1^{\prime }-{\mathbf{q}}_2^{\prime })$. This dispersion relation can be solved analytically with two branches of solutions:

$${\sigma }_{1,2}=\frac{f\left(\theta \right)}{2}-{\zeta }_0\pm \sqrt{{\left[{\zeta }_0+\frac{f\left(\theta \right)}{2}\right]}^2-\frac{k^2\cos {\left(\theta \right)}^2}{4}},$$ (56)

where

$$f\left(\theta \right)=-\frac{({\alpha }_1+{\alpha }_2)k\cos {\left(\theta \right)}^2\cos \left(2\theta \right)}{2+\nu \beta k\cos {\left(\theta \right)}^2\cos \left(2\theta \right)}.$$ (57)

As k → 0, the growth rate approaches two solutions: σ₁ = f(θ) and σ₂ = −2ζ₀, which clearly illustrates a competition between a destabilizing effect due to the active stress and a stabilizing effect due to MT alignment through steric interactions. At large k, the growth rate has an asymptotic limit Re(σ) → f(θ)/2 – ζ₀. In addition, we find that the fluid constraining stress tends to stabilize the system by effectively decreasing the magnitude of the active stress in f(θ).

Next, we perform linear stability analysis for full nonlinear equations. At the nematically ordered base state, we seek a spatially uniform solution in 2D by balancing the angular diffusion and the alignment torque as a result of steric interactions in the rotational flux [45], i.e.,

$${\nabla }_p\ln {\Psi }_0=\xi (\mathbf{I}-\mathbf{pp}){\mathbf{D}}_0\mathbf{p},$$ (58)

where ξ = 2ζ₀/D_r. This equation admits a symmetric solution as shown in Fig. 8(a):

$${\Psi }_0=\frac{\exp \left[\delta \left(\xi \right)\cos \left(2\varphi \right)\right]}{\int d{\varphi }^{\prime }\exp \left[\delta \left(\xi \right)\cos \left(2{\varphi }^{\prime }\right)\right]},$$ (59)

where δ satisfies

$$\delta =\frac{\xi }{4}\frac{\int d{\varphi }^{\prime }\cos \left(2{\varphi }^{\prime }\right)\exp \left[\delta \cos \left(2{\varphi }^{\prime }\right)\right]}{\int d{\varphi }^{\prime }\exp \left[\delta \cos \left(2{\varphi }^{\prime }\right)\right]}.$$ (60)

We then perform a shift in coordinates and rewrite the equation as

$$g\left(\delta \right)=\delta -\frac{\xi }{4}I\left(\delta \right)=0.$$ (61)

We numerically calculate δ as a function of ξ. For small ξ there is only one solution, δ = 0 associated with ${\Psi }_0=\frac{1}{2\pi }$. This bifurcates into two solutions when g′(0) = 0. Therefore, we have

$$g^{\prime }\left(0\right)=1-\frac{\xi }{4}\frac{d}{d\delta }{\phantom{\mid }\frac{{\int }_0^{2\pi }\sin \left(\omega \right)\exp \left[\delta \sin \left(\omega \right)\right]d\omega }{{\int }_0^{2\pi }\exp \left[\delta \sin \left(\omega \right)\right]d\omega }\mid }_{\delta =0}=1-\frac{\xi }{8},$$ (62)

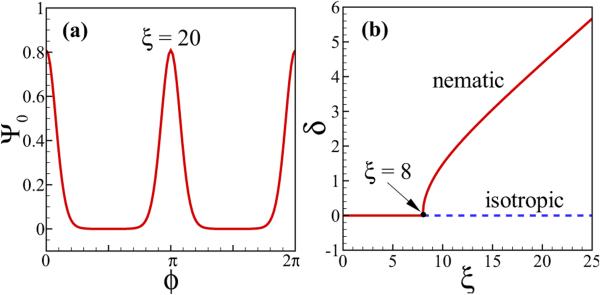
which gives that there is a second solution only for ξ > 8 [see Fig. 8(b)], suggesting that in two dimensions, the Maier-Saupe potential yields an isotropic to nematic phase transition, with increasing ζ₀, when ζ₀ = 4D_r. For all the simulations shown in the paper, we fix ζ₀ = 1.0 and D_r = 0.1, which corresponds to ξ = 20 and δ = 4.38.

FIG. 8.

(Color online) (a) Steady-state solution Ψ₀ as a function of the orientation angle ϕ when choosing δ = 4.38 and ξ = 20. (b) δ as a function of ξ. The bifurcation occurs at ξ = 8.

We perturb the nematically ordered base-state solution such that Ψ = Ψ₀(p) + εΨ′(x,p,t),U(x) = εu′(x), leading to a linearized Smoluchowski equation for Ψ′:

$${{\Psi }^{\prime }}_t+{\Psi }_0{\nabla }_x\cdot {\mathbf{q}}^{\prime }-\mathbf{p}\cdot {\nabla }_x{\Psi }^{\prime }+{\nabla }_p\cdot [{\Psi }_0(\mathbf{I}-\mathbf{pp})({\nabla }_x{\mathbf{u}}^{\prime }+2{\zeta }_0{\mathbf{D}}^{\prime })\mathbf{p}+2{\zeta }_0(\mathbf{I}-\mathbf{pp}){\mathbf{D}}_0\mathbf{p}{\Psi }^{\prime }]=D_t{\Delta }_x{\Psi }^{\prime }+D_r{\Delta }_p{\Psi }^{\prime }.$$ (63)

By using the plane-wave solutions ${\Psi }^{\prime }(\mathbf{x},\mathbf{p},t)=\tilde{\Psi }(\mathbf{k},\mathbf{p})\exp (i\mathbf{k}\cdot \mathbf{x}+\sigma t)$ and ${\mathbf{u}}^{\prime }(\mathbf{x},t)=\tilde{u}\left(\mathbf{k}\right)\exp (i\mathbf{k}\cdot \mathbf{x}+\sigma t)$, this can be rewritten as:

$$\sigma \tilde{\Psi }+{\Psi }_0(i\mathbf{k}\cdot \tilde{q})-i(\mathbf{p}\cdot \mathbf{k})\tilde{\Psi }+{\nabla }_p\cdot [{\Psi }_0(\mathbf{I}-\mathbf{pp})(i\tilde{u}\mathbf{k}+2{\zeta }_0\tilde{D})\mathbf{p}+2{\zeta }_0(\mathbf{I}-\mathbf{pp}){\mathbf{D}}_0\mathbf{p}\tilde{\Psi }]=-D_t{k}^2\tilde{\Psi }+D_r{\Delta }_p\tilde{\Psi }.$$ (64)

The perturbed velocity field satisfies

$$\tilde{u}=\frac{i}{2}(\mathbf{I}-\widehat{k}\widehat{k}){\tilde{\Sigma }}^e\widehat{k},$$ (65)

with the linearized extra stress

$${\tilde{\Sigma }}^e=({\alpha }_{\mathrm{aa}}+{\alpha }_{\mathrm{pa}})\tilde{D}+\nu \beta {\mathbf{S}}_0:\left(i\tilde{u}\mathbf{k}\right)-2\nu {\zeta }_0\beta \times ({\mathbf{D}}_0\cdot \tilde{D}+\tilde{D}\cdot {\mathbf{D}}_0-{\mathbf{S}}_0:\tilde{D}-\tilde{S}:{\mathbf{D}}_0).$$ (66)

In the above equations, $\mathbf{p}=[\cos \left(\varphi \right),\sin \left(\varphi \right)]$, ${\mathbf{D}}_0={\int }_p\mathbf{pp}{\Psi }_0$, ${\mathbf{S}}_0={\int }_p\mathbf{pppp}{\Psi }_0$, $\tilde{q}={\int }_p\mathbf{p}\tilde{\Psi }$, $\tilde{D}={\int }_p\mathbf{pp}\tilde{\Psi }$ and $\tilde{S}={\int }_p\mathbf{pppp}\tilde{\Psi }$. By changing the direction of the wave vector k̂, we discretize Ψ′ and use pseudospectral collection in the ϕ direction with 256 modes and numerically solve the eigenvalue problem for Eqs. (64)–(66) to obtain the growth rate [40].

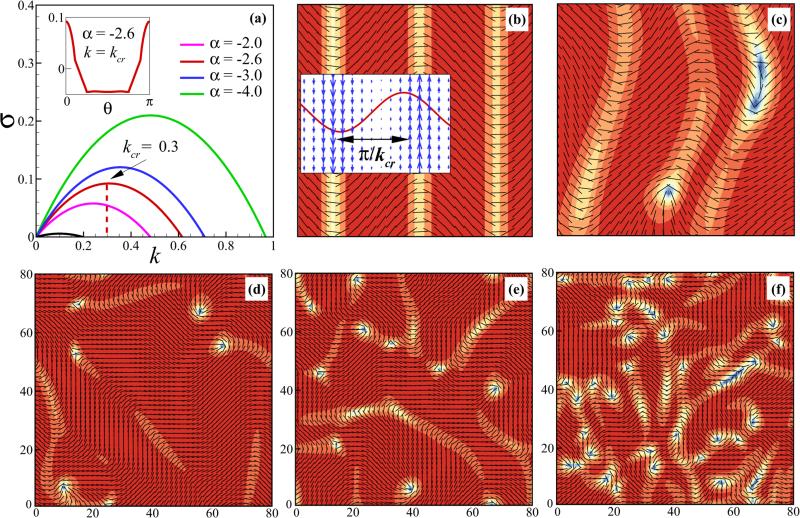
We find that the plane-wave vector of maximal growth is aligned with the nematic director (θ = 0 in Fig. 9(a) inset; also see Refs. [40,41,45]) with a wave number of maximal growth, k_cr, along this direction [Fig. 9(a)]. We find k_cr grows approximately linearly with α = α_aa + α_pa. In the 2D bulk model, the maximal growth occurs at k = 0, and so does not produce a characteristic length scale. However, in this immersed layer system, long-wave growth is cut off [see discussion following Eq. (53)] and yields a finite length scale of maximal growth. Similar effects have been reported by Leoni and Liverpool [78] in their study of swimmers confined to immersed thin films, while Thampi et al. [36] showed that adding substrate friction changes length-scale selection in 2D active nematic models.

FIG. 9.

(Color online) Linear stability analysis (a) and nonlinear simulation [(b) and (c)] for strongly antialigned MTs. (a) The real part of the growth rate as a function of wave number k for several α (α = α_aa + α_pa). Here k_cr corresponds to the maximum growth rate. Inset: Real part of the growth rate as a function of wave-angle θ when fixing k = k_cr. The black line represents the growth rate of the laning instability (without hydrodynamics). (b) Crack formation. Inset: The fluid velocity vector field (blue) and the eigenmode (red line) associated with k_cr for the linear system. (c) Genesis of defects at late times. In panels (d), (e), and (f), the active-stress magnitudes are chosen as α_aa = −0.4, 2.0, and −4.0, respectively, while α_pa = −0.6 is fixed. The snapshots accordingly show the distribution of disclination defects streaming in the domain with changing length scale. In panels (b)–(f), the nematic director field n is plotted with the contour map of the scalar order parameter. The color scale is the same as Fig. 5(b).

The result of this instability is captured in nonlinear simulations by perturbing an MT suspension that is aligned along x̂, causing a series of cracks to form along ŷ [Fig. 9(b)]. These cracks are associated with up and down moving fluid jets and bending of nematic field lines. The spatial variations of the velocity field are in excellent agreement with the velocity eigenmode associated with k_cr for the linearized system [Fig. 9(b) (inset)]: The distance between these cracks matches the half-wavelength, i.e., λ_cr = π / k_cr ≈ 10, which is in fact representative of the characteristic length between cracks seen in the full dynamics of motile defects [Fig. 5(b)]. At late times, these cracks lose stability when interacting with each other and are eventually terminated to form defect pairs reminiscent of pattern formation observed in other studies of active nematics [79,80] [Fig. 5(c)].

1. Contributions of polar-specific active stresses

Motivated by the linear stability analysis, we are able to tune the system length scale by changing the magnitude of the two active stresses. Generally, increasing either α_aa or α_pa increases the number of defect pairs, which shortens the characteristic length scale in the dynamics [Figs. 9(d)–9(f)]. However, these two stresses arise from different polar arrangements of MTs. To understand the contributions of the two active stresses, we fixed the total stress α = α_aa + α_pa while varying the individual α_aa and α_pa [Figs. 10(a)–10(c)]. The case with only polar-aligned active stress (α_aa = 0) produces more defects than does the case with only antialigned active stress (α_pa = 0). Curiously, this seems due to the defects themselves, as the passage of a +1/2-order defect leaves behind it regions of higher polar order, and thus large bulk regions for polar-aligned interactions. On the other hand, it appears that either active stress (aa or pa) taken individually will produce qualitatively similar flows and defect dynamics. Hence, the qualitative nature of the large-scale dynamics does not by itself isolate the precise origins of a destabilizing stress.

FIG. 10.

(Color online) Snapshots of motile defects when choosing different stress magnitudes. For plots in (a)–(c), α₁ + α₂ −2.0 is fixed: (a) α₁ = −2.0 and α₂ = 0; (b) α₁ = −1.0 and α₂ = −1.0; (c) α₁ = 0 and α₂ = −2.0. Panels (d)–(f) show time sequential snapshots (t = 0,100,300) of a case initially starting from the state with streaming defects but the fluid velocity field in turned off (U = 0). The system slowly relaxes to a globally nematic-aligned state. In (a)–(f), the color scale is the same as Fig. 5(b).

The linear stability analysis indicates that the instability is coupled to the long-range hydrodynamic interactions. Consistent with this, if we begin in a state with streaming defects and then turn off the fluid flow by setting U = 0, defect creation stops while defect annihilation continues, and the system relaxes to an aligned nematic [Figs. 10(d)–10(f)].

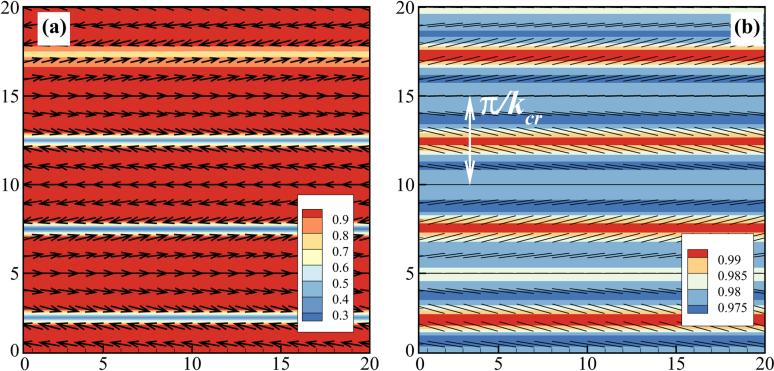
2. Formation of polar lanes

One apparent difference between the BD-kMC model and continuum kinetic theory is the formation of polar lanes observed in the BD-kMC model. To examine this discrepancy, we turned off hydrodynamics in our continuum theory by forcing U = 0. Then we find emergence of polar lanes (Fig. 11) for simulations initialized in the nematically aligned state [Eq. (59)] along the x direction. The polarity field still aligns in x̂ but forms oscillating switching bands in ŷ, with relatively small corresponding oscillations in the nematic director. Therefore, removing hydrodynamic interactions leads to dynamics that strikingly differ from the crack formation due to hydrodynamic instability discussed above. We performed numerical linear stability analysis [as in Eq. (64)] for the laning instability. This leads to a characteristic length scale π / k_cr that agrees well with the lane size in nonlinear simulations [Fig. 11(b)].

FIG. 11.

(Color online) Snapshots of polar lanes: (a) The polarity vector field q superimposed upon its magnitude, and (b) the nematic director field n superposed on the color map of the scalar order parameter.

These results suggest that the observation of polar lanes in the BD-kMC model is related to the lack of long-range hydrodynamic interactions in this model. We found that the laning instability has a slow time scale compared to the hydrodynamic instabilities [Fig. 9(a)]; therefore, in the continuum kinetic theory with long-range hydrodynamic interactions we observed the onset of hydrodynamic instabilities rather than the laning instability. This laning instability is inherently polar, because it is driven by the separation of the polarity field. Therefore, it arises from different physics than similar patterns observed in apolar models [79].

V. CONCLUSION

We have developed a multiscale polar theory to describe a suspension of MTs driven by the activity of plus-end-directed motor protein complexes (Fig. 1). First, we performed detailed BD-kMC simulations that revealed polarity sorting and polar-specific active stresses. This model differs from previous simulation models of motor-filament systems [51–53] in the treatment of motor binding and unbinding: Previous work used simple binding rules that do not obey the principle of detailed balance. Our more accurate treatment of crosslink statistical mechanics is important to determine how alterations from equilibrium motor distributions occur due to nonequilibrium activity and the resulting active stresses generated.

For MT densities that form an equilibrium 2D nematic in the absence of motors, adding motor activity leads to MT flows driven by polarity sorting and the formation of polar lanes (Figs. 2 and 3). The mean-squared displacement of MT position becomes superdiffusive and nearly ballistic at long times along the nematic director. For polar-aligned pairs, the distribution of motor tether extension shifts toward smaller extensions than in the equilibrium case due to nonequilibrium tether relaxation; for antialigned pairs, the distribution shifts toward positive extension due to oppositely directed motor motion that drives polarity sorting. MT displacement distributions and instantaneous speeds along the nematic director are strongly dependent on the local polar environment, consistent with the continuum model: The instantaneous velocity depends approximately linearly on the local polar environment, as expected when filament movements are determined mainly by polarity sorting.

Over a wide range of parameters in the BD-kMC model, anisotropic extensile stress is generated. The stress produced per MT is largest for filaments in antipolar environments, suggesting that polarity sorting is the dominant source of pairwise extensile stress. As previously noted, if an MT pair begins sliding when the two minus ends touch and slides under a force proportional to pair overlap until the two plus ends meet, then the contractile motion would perfectly balance the extensile motion and the total extensile stress would be zero [20,26,59,67]. Symmetry appears to be broken in our BD-kMC simulations first, because MTs are unlikely to begin interacting exactly when their minus ends are touching, and, second, because more motors are bound on average during extensional motion (Fig. 3). Extensile stress is also generated for polar-aligned pairs of MTs due to nonequilibrium motor tether relaxation: The tether of a longitudinally stretched motor on parallel filaments pulls back on the leading motor, slowing it, and pulls forward on the trailing motor. Because the motor relaxes to become more perpendicular to the filament pair, the motor-induced contractile stress along the director is decreased, leading to a net anisotropic extensile stress in the alignment direction. This is to our knowledge a novel mechanism of extensile stress production [39]. While the per-pair extensile stress due to polar-aligned MT pairs is typically smaller than for antialigned pairs, polarity sorting and lane formation produce larger numbers of polar-aligned MT pairs than of antialigned. In our BD-kMC simulations, which lack the effect of hydrodynamics, the overall contributions of polar-aligned and antialigned pairs to the extensile stress are comparable.

An interesting aspect of our BD-kMC study is that active stresses are extensile, which differs considerably from the contractility observed in actin-myosin gels [12]. Actin filament buckling appears to be a key microscopic mechanism driving contractility in actin-myosin systems [59,67,81–83]. The greater rigidity of MTs in our model, the nematic ordering, and the fluidity of MT motion may all contribute to extensile stress generation in our system.

We incorporated the polar-specific active stresses into a kinetic theory of Doi-Onsager type (Fig. 4) and studied the effect of hydrodynamic interactions. In the continuum model, we can derive the origin and dependencies of extensile stresses driven by polarity sorting. However, our understanding is less clear of the stress from polar-aligned interactions, and a reduced continuum model of them would be useful. We find a streaming-nematic state similar to that observed in recent experiments by Sanchez et al.[7]. Defect pairs are born along incipient cracks of low nematic order, and these cracks correlate with fluid jets (Fig. 5). The movement of +1/2 defects can be tracked by associated vortex pairs and strongly correlates with the active force (Figs. 6 and 7). We also identify a hydrodynamic instability of nearly aligned MTs that causes formation of incipient cracks (see also Giomi et al. [79]) and hence serves as a source of complex dynamics (Figs. 8 and 9).

Our results are qualitatively similar to previous work studying liquid crystal hydrodynamic driven by an apolar active stress [31–36]. These works have improved our understanding of the speed of defect motion, velocity correlations, and defect dynamics in active nematics but cannot address the microscopic origins of active stresses. Our work seeks to connect these phenomena to MT–motor-protein interactions that are intrinsically polar. Therefore, we link microscopic polar interactions to macroscopic phenomena. In future work it would be interesting to further coarse grain our kinetic model, say, through a moment closure approximation, and to generalize current apolar active liquid crystal models to include polarity sorting and polarity-dependent stresses.

Interestingly, in modeling the experiments of Sanchez et al. [7], we find that by accounting for the outer fluid drag on the immersed layer dynamics, we are able to determine a clear characteristic length scale. This does not occur in active nematic models based on bulk dynamics [31,33,45], although length selection has been reported for swimmers confined to immersed thin films [78], and substrate friction changes length-scale selection in 2D active nematic models [36].

We find that either polar-specific active stress—associated with polarity sorting or motor tether relaxation—taken individually produces qualitatively similar flow and defect dynamics. Therefore such dynamics alone do not isolate the origins of a destabilizing stress. Generally, increasing either α_aa (from antialigned interactions) or α_pa (from polar-aligned interactions) increases the number of defect pairs, which shortens the characteristic length scale in the dynamics (Fig. 9). However, these two stresses arise from different polar arrangements of MTs. Fixing α = α_aa + α_pa, the case with the case α_aa = 0 (only polar-aligned active stress) produces more defects than does the case with α_pa = 0 (only antialigned active stress). Curiously, this seems due to the defects themselves, as the passage of a +1/2 defect leaves behind it regions of higher polar order, and thence large bulk regions for polar-aligned interactions (Fig. 10). Perhaps the systematic experimental study of the dynamics of photobleached regions would reveal which of these two stresses, antialigned or polar-aligned, is actually dominant or whether the unstable dynamics arises from some other source.

One apparent difference of the kinetic theory with the BD-kMC model is the polar laning evinced by the latter. To explore this we turned off hydrodynamics in the kinetic model, since it is absent in the BD-kMC model and also found polar laning there (Fig. 11). Further, as revealed by linear stability analysis of the kinetic model, there is an instability to polar laning that occurs on a much longer time scale (consistent with the time for lanes to emerge in the BD-kMC model) than the hydrodynamic instabilities studied here. Additionally, without long-range hydrodynamic interactions, the kinetic theory does not show the persistent production of defects. It would be illuminating to compare the kinetic theory with BD-kMC simulations that incorporate hydrodynamic interactions. This might be done using fast-summation methods applied earlier to the study of motile suspensions [84].