Abstract
Susceptibility tensor imaging (STI) is a recently developed MRI technique that allows quantitative determination of orientation-independent magnetic susceptibility parameters from the dependence of gradient echo signal phase on the orientation of biological tissues with respect to the main magnetic field. By modeling the magnetic susceptibility of each voxel as a symmetric rank-2 tensor, individual magnetic susceptibility tensor elements as well as the mean magnetic susceptibility (MMS) and magnetic susceptibility anisotropy (MSA) can be determined for brain tissues that would still show orientation dependence after conventional scalar-based quantitative susceptibility mapping (QSM) to remove such dependence. Similar to diffusion tensor imaging (DTI), STI allows mapping of brain white matter fiber orientations and reconstruction of 3D white matter pathways using the principal eigenvectors of the susceptibility tensor. In contrast to diffusion anisotropy, the main determinant factor of susceptibility anisotropy in brain white matter is myelin. Another unique feature of susceptibility anisotropy of white matter is its sensitivity to gadolinium-based contrast agents. Mechanistically, MRI-observed susceptibility anisotropy is mainly attributed to the highly ordered lipid molecules in myelin sheath. STI provides a consistent interpretation of the dependence of phase and susceptibility on orientation at multiple scales. This article reviews the key experimental findings and physical theories that led to the development of STI, its practical implementations, and its applications for brain research.
Keywords: brain imaging, white matter, gradient echo MRI, phase contrast, quantitative susceptibility mapping, susceptibility tensor imaging, fiber tracking
Introduction
Magnetic susceptibility (χ) is defined as the degree of magnetization of a material in response to an applied magnetic field. The spatial variation of magnetic susceptibility of biological tissue inside an MRI scanner can lead to local magnetic field differences and thus resonance frequency variations over the tissue. Such field or frequency variations can be detected and mapped with high spatial resolution using gradient echo (GRE) signal phase imaging, especially at high field (1). However, the effect of locally varying magnetic susceptibility is non-local and can perturb the magnetic fields in distant voxels. As a result, susceptibility induced MR phase effects are non-local and depend on the object orientation with respect to the main magnetic field (2,3). Thus, the local MR phase cannot provide a direct quantitative measure regarding the molecular and cellular properties of tissue in the voxel. To overcome this limitation, quantitative susceptibility mapping (QSM) was developed to solve the ill-posed phase-to-susceptibility inverse problem and derive the voxel-based magnetic susceptibility (4-14). In recent years, QSM has been applied to investigate oxygenation levels in venous blood (15,16), cerebral hemorrhage and microbleeds (17,18), iron and myelin content changes in different neurodegenerative diseases, e.g. Alzheimer’s disease (19), Huntington disease (20,21), Parkinson’s disease (22-26) and multiple sclerosis (27-31).
One basic assumption of QSM is that the macroscopic susceptibility in an imaging voxel is isotropic. This assumption holds in gray matter or larger blood vessels where the source of susceptibility contrast mainly comes from non-heme iron or deoxyhemoglobin (11,32), respectively, and where any spatial orientation effect of smaller anisotropic structures (e.g. erythrocytes within blood or capillaries within tissue) is averaged at the macroscopic voxel level. However, in contrast to this apparent isotropic susceptibility of gray matter and blood, several studies have shown that the susceptibility of white matter depends on the orientation of fiber microstructure with respect to the main magnetic field (33-36), which persists at the macroscopic level. Such orientation dependence suggests that magnetic susceptibility of white matter is in fact anisotropic. On the one hand, the presence of susceptibility anisotropy significantly complicates the interpretation of susceptibility contrast obtained using single-orientation QSM methods. On the other hand, this provides a unique opportunity to study white matter fiber integrity and to delineate fiber orientations using GRE signal phase (37-42).
Over the past few years, the basic principles of susceptibility tensor imaging (STI) have been developed to better understand this magnetic susceptibility anisotropy and to study white matter microstructures. This paper reviews the currently available evidence underlying such susceptibility anisotropy in brain white matter, its molecular and cellular underpinnings, biophysical models of the susceptibility tensor, and different tensor reconstruction methods. In addition a comparison between STI and diffusion tensor imaging (DTI) is given, and potential applications of STI in brain research are discussed.
Evidence of susceptibility anisotropy in brain white matter
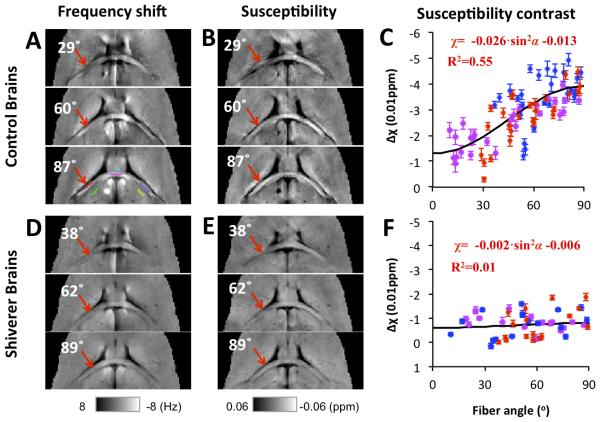
Even though magnetic susceptibility anisotropy has long been studied in liquid crystals and liquid solutions (43,44) and has been observed in biological tissue components such as proteins and lipid bilayers (45,46), it has only been very recent that the effects of susceptibility anisotropy on the scale of an MR imaging voxel in brain tissue, especially in white matter, have drawn attention (33-35). Some of the reasons for this delay may include the limited phase contrast observed at lower magnetic field strengths and the need for development of phase processing and voxel-wise dipole inversion for QSM. Several pilot studies have shown that the MR phase or resonance frequency (phase scaled by echo time) dependence on the orientation of white matter fibers with respect to the main magnetic field cannot be explained solely by its isotropic volume susceptibility (33-35). He and Yablonskiy introduced the concept of the generalized Lorentzian boundary and attributed the orientation dependence of MR phase in white matter to the elongated axonal and cylindrically shaped cellular structures and compartments in white matter fibers (33). Lee et al confirmed the dependence of MR phase or frequency on the white matter microstructure orientation using postmortem tissue samples and proposed an experimental design that allowed separation of microstructural effects from possible confounding macrostructural effects (34). In addition, they observed nonlocal phase variations outside the tissue sample caused only by changing the microstructural orientations of some tissue segments. As suggested by Lee et al, such phenomena are explained more appropriately by anisotropic susceptibility rather than the generalized Lorentzian approach (34). At about the same time, Liu also observed anisotropic frequency and susceptibility in mouse brains ex vivo and further proposed to use a symmetric second-order tensor to model this effect (35), which evolved into the STI methods to be described in later sections. Many later studies using single-orientation QSM methods have also reported consistently that magnetic susceptibility in brain white matter, both ex vivo in mouse brain or in vivo in human brain, is anisotropic and depends on the orientation of the tissue relative to the magnetic field (10,13,39,40). Figure 1 shows examples of the phase and susceptibility maps of a mouse brain ex vivo positioned at different orientations in an MR scanner. Different susceptibility contrast between white matter fibers and adjacent gray matter can be clearly seen (red arrows), with fibers more parallel to the main magnetic field (Figures 1 B and C) showing a more paramagnetic susceptibility.
Figure 1. Orientation dependence of susceptibility in brains of normal and dysmyelinating shiverer mice.
A and D: frequency maps from 3 selected brain orientations. A representative selection of ROIs is shown in the lower panel of A, with ROIs in white matter labeled red, magenta, and blue, and ROIs in adjacent gray matter green, cyan, and yellow. B and E: magnetic susceptibility maps calculated from the frequency shifts shown in A and D using QSM. C and F: susceptibility of white matter referenced to adjacent gray matter. All data points are shown as mean ± standard error over the voxels in each selected ROI. Susceptibility anisotropy is observed in those control mice but not in shiverer mice. The angles shown on the images are the angles between the direction of the white matter segment at the red ROI and the main field as determined by DTI, i.e., 0º means that the selected fiber segment is parallel to the main magnetic field. The ROI color in panel A corresponds to the data point color in panels C and F. Reprinted, with permission, from Figure 2, reference (39).
Biophysical underpinnings of susceptibility anisotropy
The molecular and cellular source of the diamagnetic susceptibility in white matter can be attributed to myelin (1,47). The importance of myelin in generating the frequency and susceptibility contrast of white matter was convincingly illustrated in an MRI study of dysmyelinating shiverer mice (48). In such mice, a deletion of the gene encoding myelin basic protein leads to significantly reduced myelin content in white matter. As a result, the phase and susceptibility contrasts between gray and white matter were reduced by more than 90% in shiverer mice compared to control mice (Figure 1). In comparison, DTI fractional anisotropy (FA) and other diffusivity contrasts were altered only slightly due to the less affected axonal structures in these mutant mice. This dependence of phase and susceptibility contrast on myelin orientation has also been observed in studies of cuprizone-induced demyelination in mouse brains (49), shiverer mice of different ages (50), and mouse brain development (51). Together, these studies convincingly show that myelin is the predominant source of the phase and susceptibility contrast between gray and white matter.
In view of the above, it was logical to conclude that the susceptibility anisotropy of brain white matter should also be related to myelin, in particular to molecular myelin components with anisotropic susceptibility. Myelin has a multi-layered membrane structure composed of lipid and proteins, with myelin water filling the spaces between the lipid bi-layers. The magnetic susceptibility of a molecule is the three-dimensional tensor addition of the contributions of the individual molecular bonds. It is known that many lipids and proteins are asymmetric molecules and therefore have an anisotropic magnetic susceptibility. For example, the anisotropic magnetic susceptibilities of model lipid bilayers and crystals of egg lecithin were reported a long time ago (52-54). Second, the rotation of the myelin lipids (~70% dry weight of myelin) and membrane proteins (~30% dry weight) is restricted to the surface of the bilayer, so that their anisotropic magnetic susceptibility can possibly be observed at the macroscopic scale due to the highly organized microstructures of white matter fibers (55). In contrast, water molecules in myelin can rotate freely and, even though some partial average orientation may be induced upon them through binding, these are not expected to contribute significantly to the bulk susceptibility anisotropy. Relevant to physiological conditions, the susceptibility anisotropy of hydrated membrane lipids from isolated human lipoproteins has been estimated to be 0.223 ppm using NMR spectroscopy at 37° C (56). This value is approximately an order of magnitude larger than the observed macroscopic susceptibility anisotropy in postmortem samples of white matter fibers (0.01~0.03 ppm) (34,48). These facts led to the hypothesis that the macroscopic magnetic susceptibility anisotropy in white matter originates from well aligned myelin lipids, while the quantitative relationship between the two is determined by the volume fraction of lipids and the patterns of their spatial alignment (39).
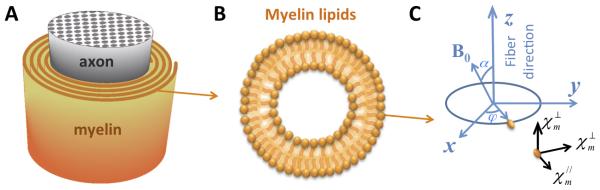
To derive the relationship between bulk susceptibility anisotropy in white matter and the anisotropy of lipid molecules, the spiraling myelin sheath (Figure 2A) has been modeled to consist of concentric cylindrical shells with lipid molecules radially aligned within these shells (Figure 2B) (39). Based on this model, the magnetization of each voxel can be calculated through the integration of molecular magnetization of all the radially aligned myelin molecules:
| [1] |
Figure 2. The axon and molecular coordinate systems.
(A) Schematic representation of the spiraling myelin sheath around an axon. (B) Schematic representation of the radial alignment of myelin lipid molecules. (C) The axon coordinate system (x, y and z) and the molecular susceptibility tensor of a myelin lipid molecule in its molecular coordinate system.
Here, mm is the molecular magnetization vector of a lipid molecule with molecular susceptibility tensor in its diagonal molecular coordinate system (Figure 2C); and are the magnetic susceptibilities parallel and perpendicular to the lipid carbon chains, Rz is the rotation matrix around the z-axis with a rotation angle of φ relative to the fiber axon coordinate, which links the molecular and the axonal frames of reference; the applied main magnetic field is H = [H0sinα,0,H0cosα]T, with α being the angle between the white matter fiber and the applied magnetic field, flipid is the volume fraction of myelin lipids. The bulk magnetic susceptibility can then be calculated as the voxel macroscopic magnetization vector M along the applied field direction divided by the corresponding field strength:
| [2] |
where is the unit vector of the applied field and H0 the field strength; χ0 is the baseline susceptibility that corrects for susceptibility variations due to the selection of an internal tissue reference. A detailed derivation is provided in reference (39). This sine square relationship is derived assuming that the long axis of the myelin lipid is perfectly aligned with the radial direction of the cylindrical shell. The same sine square relationship, with different coefficients, can also be derived for proteins and other molecules that may not be perfectly aligned with the radial direction of the cylindrical shell, given the additional assumption that the molecule of interest can freely rotate along the radial direction of the cylindrical shell. Unlike myelin lipids, the peptide chains in proteins are much less aligned, and the volume fraction of proteins in myelin is significantly lower than that of lipids, so myelin proteins are expected to contribute significantly less to the overall magnetic susceptibility anisotropy of brain white matter.
Equation 2 has two direct implications. First, given the lipid molecular susceptibility anisotropy (56), brain white matter is expected to be most paramagnetic along the fiber direction, i.e. when α is zero and the fiber is parallel to the main field. This is important for the assignment of the main direction of the tensor for STI-based fiber tracking (37). Second, the macroscopic susceptibility of white matter relates to the fiber angle in a sine-squared relationship, and the maximum variation of macroscopic susceptibility, which is equivalent to the magnetic susceptibility anisotropy (MSA) defined in a later section using the second order tensor model, can be calculated as . Given a myelin lipid fraction of 16% and the molecular susceptibility anisotropy above, Δχ in normal brain white matter is predicted to be about 0.02 ppm. Experimentally, the sine square relationship has been verified in ex vivo mouse brain (Figure 1B and C), with Δχ estimated at 0.026 ppm. In contrast, such a sine squared relationship is absent in the shiverer mice (Figures 1E and F), supporting the hypothesis that myelin is the major source for the macroscopic susceptibility anisotropy in white matter. Susceptibility anisotropy values of about 0.02 ppm were also obtained in the human brain (39,40). These measured susceptibility anisotropy values are consistent with those predicted from Eq. 2 indicating that the susceptibility anisotropies of myelin lipid molecules are likely the dominant source of the MRI-observed macroscopic magnetic susceptibility anisotropy. Furthermore, Eq. 2 also suggests that the macroscopic susceptibility of an imaging voxel can actually be modeled as a second-order tensor. The relationship between such a macroscopic susceptibility tensor and experimentally measurable MRI phase and the corresponding STI techniques are described below.
The second-order susceptibility tensor model
For tissues with isotropic magnetic susceptibility, the off-resonance field b(r) in the imaging space of r can be related to the macroscopic flux density B0and scalar magnetic susceptibility distribution χ(r) as follows:
| [3] |
This equation can be calculated as a convolution of the magnetic susceptibility distribution with the magnetic field induced by a unit magnetic dipole. The evaluation of this equation is computationally intensive in image space (6). Alternatively, this convolution can be efficiently evaluated in the frequency domain (2,3,57):
| [4] |
where ϕ(r) is the MR phase measurement; γ is the gyromagnetic ratio of water proton, TE is the echo time; μ0 is the vacuum permeability; H0 is the magnitude of the applied magnetic field; is the unit vector of the applied field (commonly defined as the z direction in the laboratory frame of reference), whose elements are Hi and i = x,y,z; k is the spatial frequency vector, with elements ki; FT represents the Fourier Transform, FT−1 represents the inverse Fourier Transform and the term 1/3 corresponds to a correction using the sphere of Lorentz. This is the well-known susceptibility to phase relationship commonly seen in the QSM literature.
For tissues with an anisotropic magnetic susceptibility, however, Eqs. 3 and 4 are no longer sufficient to describe the relationship between phase and susceptibility. In order to account for anisotropic susceptibility, Liu expanded Eq. 4 by replacing the scalar susceptibility with a rank-2 real symmetric magnetic susceptibility tensor, and derived the corresponding relationship between the field shift and susceptibility tensor χ in the Fourier domain (35):
| [5] |
, where the susceptibility χ now represents a real and symmetric 3×3 second order tensor, with elements) χij(i, j = 1,2,3), i.e. This model uses the same Lorentzian sphere correction as in Eq. 4, which may need to be modified in the presence of oriented susceptibility inclusions of cylindrical symmetry (58). A detailed derivation can be found in references (35) and (40). Equation 5 provides the forward calculation from the susceptibility tensor to a field or frequency shift and thus to MR phase, and provides the theoretical basis for susceptibility tensor reconstruction from MR phase measurements.
Image acquisition
STI involves quantifying the susceptibility tensors for each voxel from GRE phase measurements acquired at 6 or more different orientations of the brain with respect to the main magnetic field, as there are 6 unknown components in the symmetric susceptibility tensor as in Eq. 5. Since it is usually not feasible to rotate the magnet of modern MRI scanners, the image acquisition is typically achieved by physically rotating the brain inside the MRI scanner multiple times and collecting the GRE phase data at each brain position.
Typical GRE sequences used for QSM can be used directly for STI. For ex vivo experiments using fixed brain specimens, the rotation of the tissue sample inside the magnet is only constrained by the coil size, so the image acquisition is fairly straightforward. For example, a typical protocol for ex vivo mouse brain STI at 9.4T is as follows: a 3D spoiled-gradient-recalled sequence, matrix size = 256 × 128 × 128, field-of-view = 22 × 11 × 11 mm3, flip angle = 40°, TE = 20 ms, TR = 200 ms, and multiple different head orientations roughly covering the spherical surface uniformly. For human brain in vivo, due to the physical constraints on head rotation and the uncomfortable positions with tilted head, STI acquisitions with large orientation coverage are usually much harder to achieve. In practice, effective head rotation can be performed around either the anterior-posterior (AP) axis, i.e. tilting the head to the left or right shoulder, or around the left-right (LR) axis, i.e. tilting the head to the chest or back, or a combination of these two types of rotation. Note that rotation around the foot-head (FH) axis alone does not create an effective angle change between the head and the magnetic field. As will be discussed in later sections, large head rotation angles are important to obtain a good STI inverse condition and thus good image quality. Therefore, for STI acquisition a larger quadrature head coil is often preferred over the modern tight-fitting multi-channel head coils. The scan time using the quadrature head coil is typically longer since parallel imaging cannot be used. A typical protocol for human brain STI on 3T is as follows: a standard 3D gradient echo sequence, TE = 40 ms, TR = 60 ms, flip angle = 20°, FOV = 256 × 256 × 256 mm3, matrix size = 128 × 128 × 128. Several scans are needed to allow a sufficiently large range of brain orientations with respect to the main magnetic field. In addition to the established single-echo acquisition protocol described above, multi-echo GRE sequences can also be used.
Reconstruction of susceptibility tensors
Similar to QSM using multiple orientations, i.e. calculation of susceptibility through multiple orientation sampling (COSMOS) (59), after image acquisition, STI also requires image coregistration and proper phase preprocessing, which includes, 3D phase unwrapping and background phase removal. This two-stage phase preprocessing is of particular importance for the quality of STI reconstruction, which can be seen from the non-local relationship between phase and susceptibility tensor described in Eq. 5. For instance, local phase unwrapping errors will translate into non-local artifacts in the susceptibility tensor map, while incomplete removal of low frequency background phase will bias the resulting tensor values.
For 3D phase unwrapping, either traditional path-based phase unwrapping, e.g. as described in reference (60) and the PRELUDE in FSL (FMRIB, Oxford University, UK) etc., or the Laplacian-based phase unwrapping (10,61) can be used. For brain tissues, path-based and Laplacian-based phase unwrapping yield the same gray and white matter contrast after background phase removal (62). Differences are usually limited to regions around veins where the phase varies rapidly as a result of the strong paramagnetic susceptibility of the venous blood. While it is often assumed that path-based phase unwrapping is more accurate for unwrapping the phase around the veins, local errors by this method can propagate to adjacent tissues and introduce significant artifacts. In contrast, the Laplacian based method is insensitive to phase unwrapping errors around the veins due to the utilization of sine and cosine functions. As such, the Laplacian unwrapped phase usually allows STI reconstruction with less artifacts.
The unwrapped phase is typically dominated by slowly-varying contributions originating from sources outside the regions of interest (ROIs), e.g. the receiver coil, tissue air interfaces, and etc. Such low-frequency phase contributions are conventionally contained in the term “background phase”. For background phase removal, traditional homodyne filtering or polynomial filtering is insufficient, since these approaches cannot differentiate low frequency tissue phase fluctuations from background phase. Several background phase removal methods initially developed for QSM phase preprocessing can be directly applied for STI. These methods are based on two closely related properties of the background phase: i) background phase is harmonic, so that the Laplacian of the background phase is zero and ii) background phase originates predominantly from magnetic susceptibility distributions outside the brain. The sophisticated harmonic artifact reduction for phase data (SHARP) (11), SHARP edges (63), variable-radius SHARP (V-SHARP) (12), harmonic (background) phase removal using the Laplacian operator (HARPERELLA) (62), the improved HARPERELLA (iHARPERELLA) (64), the Laplacian boundary value (LBV) (65) , and the iterative spherical mean value (iSMV) (66) approaches are all based on the first property. The projection onto dipole fields (PDF) method is based on the second property (67). All of these methods allow removal of background phase while keeping low frequency tissue phase differences. Since the two properties are fundamentally equivalent or at least closely related, the performance of these methods is similar for the majority of brain tissue. The main difference is on their ability to remove background phase around the edges of the brain. All of these methods are applicable for background phase removal for STI. We have successfully applied both V-SHARP and iHARPERELLA for STI phase pre-processing.
After phase preprocessing, with the coregistered phase from multiple head orientations, susceptibility tensors can be reconstructed using Eq. 5. There are two possible STI approaches, i.e. k-space based and image-space based. The first approach calculates the susceptibility tensor in frequency domain and the Fourier transform of the normalized field shift or relative magnetic field change is expressed as a weighted sum of the six distinguishable susceptibility tensor components in k-space (37):
| [6] |
where
| [7] |
In a shorter form, we can rewrite Eq. 6 as:
| [8] |
in which A is the coefficient matrix with elements aij and χ a vectorized tensor matrix of χij. Susceptibility tensor maps can then be estimated in the frequency domain by solving in least-square sense the linear equations composed of multiple versions of Eq. 8 at different head orientations, i.e. with different field change measurements. Such inverse calculation is usually done more conveniently in the subject frame of reference (35,40). In this frame of reference, the is a different vector at each head orientation, giving different coefficients aij in Eq. 7, thus allowing the inverse calculation of the linear system described in Eq. 8 using all the acquired data. This k-space approach allows voxel-wise calculation of χ(k). The maps of susceptibility tensors can then be derived using an inverse Fourier transform.
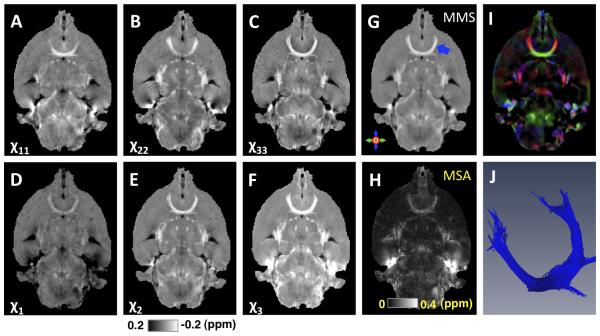
This k-space-based STI method is simple to implement, and has been successfully used to reconstruct the susceptibility tensor of the mouse brain ex vivo (Figures 3A-C showing the diagonal tensor components). Notice that for the purpose of highlighting diamagnetic white matter, the intensity scale in these images is the reverse of that of QSM in which more strongly paramagnetic tissues are shown with a higher intensity. As a real symmetric second-order tensor, the obtained susceptibility tensor can be decomposed into its eigenvalues (χ1, χ2, χ3) and the corresponding eigenvectors, i.e. in its diagonal frame of reference (Figures 3D-F showing the three susceptibility eigenvalues). Here we use the first eigenvalue χ1 to represent the most paramagnetic susceptibility eigenvalue and to denote the corresponding eigenvector the principal eigenvector (PEV) of the susceptibility tensor. Several orientation independent tensor measures can also be derived with those eigenvalues, for example the mean magnetic susceptibility (MMS) or magnetic susceptibility anisotropy (MSA) as (38, 42)
| [9] |
,
| [10] |
Figure 3. STI of a mouse brain ex vivo.
A-C: Maps of the diagonal terms of the susceptibility tensors in the subject frame. D-F: Maps of the eigenvalues of the susceptibility tensors, i.e. the susceptibilities in the local diagonal frame. G: Mean magnetic susceptibility (MMS, i.e.χ). H: magnetic susceptibility anisotropy (MSA, i.e. χχ). I: Color map of the principal eigenvector (PEV) corresponding to the most paramagnetic eigenvalue of the susceptibility tensor weighted by susceptibility index as in (37). J: Anterior commissure (corresponding to the blue arrow in G) reconstructed using STI. In panels A-G, higher intensity indicates more diamagnetic susceptibility (opposite from QSM). The mouse brain was perfused with a mixture of 0.9% saline and ProHance (10:1, v:v) (Bracco Diagnostics, Princeton, NJ), then followed by a mixture of 10% buffered formalin and ProHance (10:1, v:v). This figure was reproduced with permission from reference (37).
Similar to QSM (14), the quantification of each tensor component χij is relative due to the undefined k-space center in Eq. 5 and the limited spatial extent of the phase measurements, which are restricted to inside the brain, i.e. no phase measurement in the surrounding air region. Therefore, a reference value needs to be selected either implicitly or explicitly for the quantification of each tensor component. One possible reference selection is implicitly contained in the step of background phase removal, which essentially sets the susceptibility reference to the mean susceptibility value of the whole brain. The resulting susceptibility tensor can then be used directly for subsequent analysis. Alternatively, an explicit reference can be selected after the STI calculation. A common reference value, e.g. the mean susceptibility of a known isotropic region, may be selected for all the eigenvaluesχ1, χ2, χ3 in the diagonal frame with the directions of the eigenvectors unchanged. This is equivalent to using a scalar reference instead of a full reference tensor. Note that under both circumstances, the MSA does not require a reference since it is a calculated difference between the eigenvalues as in Eq. 10.
Empirically, tractography of white matter fiber pathways using the susceptibility tensor was indeed found to be best performed using the PEV corresponding to the most paramagnetic susceptibility eigenvalue, i.e. χ1 (Figure 3D, note that darker color means positive or more paramagnetic), which is consistent with the molecular mechanism of the susceptibility anisotropy as described above. An example PEV colormap as in ref (37) is shown in Figure 3I. Figure 3 G and H show the MMS and MSA, respectively. Shown in Figure 3J is an example map of fiber bundles of the anterior commissure of the mouse brain obtained by tractography using susceptibility-based PEVs.
The k-space-based STI method can also incorporate constraints in the frequency domain to stabilize and improve the STI reconstruction, e.g. to constrain the high frequency k-space regions, mostly corresponding to the structural boundaries, to be similar among those diagonal tensor components, and to constrain the high frequency k-space regions to be similar among those off-diagonal tensor components separately (39). The rationale is that the main susceptibility contrast is determined by low spatial frequency component, while any imperfect image registration is characterized by high frequency errors. Such constrained STI has been successfully applied to image the susceptibility tensor of the human brain (Figure 4). One limitation of the k-space based STI method is that it cannot include any spatial constraints derived in image space (40-42).
Figure 4. STI of the human brain.
A-C: Maps of the diagonal terms of the susceptibility tensors in the subject frame. D-F: Maps of the eigenvalues of the susceptibility tensors, i.e. the susceptibilities in the local diagonal frame. G: MMS color coded using the PEV corresponding to the most paramagnetic eigenvalue of the susceptibility tensor. H: DTI fractional anisotropy (FA) map color coded using the largest diffusion eigenvector. This figure was reproduced with permission from reference (39). In panels A-F, higher intensity indicates more diamagnetic susceptibility (opposite from QSM).
As compared to the k-space based STI method, image-space-based STI calculates the susceptibility tensor map χ (r) in image space directly by solving an optimization problem as
| [11] |
where with i =1…N indicating the i th head orientation; Ai represents the mapping relationship from susceptibility tensor χ(r) to field shift as described in Eq. 5. Compared to the k-space-based STI method, the image-space-based STI method is more complicated to implement and computationally more intensive. However, the advantage of this method is that constraints based on image space features can be easily incorporated into the STI inverse problem as regularization terms to improve the reconstruction quality. For example, for brain tissue with isotropic magnetic susceptibility or negligible susceptibility anisotropy at the voxel level, the susceptibility tensor becomes diagonal, i.e. within tissues such as CSF and gray matter, and χ12 = χ13 = χ23 = 0 and χ11 = χ22 = χ33. In addition, anatomical a priori information such as the tissue morphology that can be extracted from other available images, e.g. QSM images, can be used to constrain certain linear combinations of the six tensor components. One example of these is the first tensor invariant, i.e. the tensor trace, as used in the mean magnetic susceptibility regularized susceptibility tensor imaging (MMSR-STI) (42). Use of these regularizations in the STI inverse problem has been demonstrated to improve the image quality and reconstruction accuracy of STI. As compared to STI without any regularization (Figure 5A-C), MMSR-STI incorporating a priori spatial constrains (Figure 5 D-F) gives less variations in both MMS and MSA maps and gives a susceptibility PEV estimation that better resembles the DTI PEV map (Figure 5I).
Figure 5. Comparisons of STI, MMSR-STI and DTI in human brain.
A-C: MMS, MSA and PEV obtained by STI in a healthy control subject using GRE phase data collected at 10 head orientations at 3T. D-F: corresponding MMS, MSA and PEV obtained by MMSR-STI method that uses image space constraints to regularize the STI inverse. G-I, mean diffusivity (MD), FA and PEV obtained by DTI. All the PEV maps were masked by a white matter mask generated by thresholding the DTI FA map (FA>0.25). In panels A and D higher intensity indicates more diamagnetic susceptibility (opposite from QSM). This figure was reproduced with permission from reference (42).
In addition, using image space priors such as the fiber orientation information that can be obtained by DTI and assuming cylindrical symmetry of the susceptibility tensor in white matter fibers, we can further simplify the STI problem and reduce the number of required head orientations (40,41,68). Such cylindrical symmetrical susceptibility tensor mapping has been demonstrated to give more accurate quantification of susceptibility anisotropy than STI without regularization and can give a good estimation of MSA with MR phase data collected at minimum of 3 head orientations (40,41). Example MMS and MSA maps obtained by assuming cylindrical symmetry in white matter fibers in human brain at 7T are shown in Figure 6, with mostly positive MSA values around 0.01-0.02 ppm observed in major white matter fiber bundles. These values are consistent with previous findings that the magnetic susceptibility anisotropy of white matter mainly originates from the radially oriented myelin lipids.
Figure 6. Susceptibility tensor mapping of human brain assuming cylindrical symmetry.
A-D: different views of the MMS obtained in a healthy control subject using phase data at 4 head orientations at 7T. E-H: corresponding MSA map. I-L: DTI color maps, i.e. DTI FA map color coded using DTI PEV. This figure was reproduced with permission from reference (40).
Susceptibility tensors versus diffusion tensors
Since the development of DTI for tracking the white matter pathways more than two decades ago (69,70), STI is the second method that enables noninvasive mapping of white matter tracks with reasonable accuracy. While both DTI and STI rely on highly anisotropic white matter microstructures, the biophysical underpinnings underlying diffusion anisotropy and susceptibility anisotropy in white matter fibers are fundamentally different. Diffusion anisotropy originates from the hindered diffusion of water molecules due to structural barriers (predominantly axonal membrane and filaments and some myelin contributions), while the susceptibility anisotropy is related to ordered myelin lipids with an anisotropic molecular susceptibility. Given the different biophysical underpinnings, imaging results using DTI and STI have been compared in detail to gain more insight into their accordance and differences in normal and abnormal brains (38,71).
The eigenvalue maps of the susceptibility tensor and the diffusion tensor both provide excellent gray and white matter contrast. When using the susceptibility PEV (corresponding to the most paramagnetic eigenvalue) and diffusion PEV (corresponding to the largest diffusion eigenvalue) for fiber tractography, STI can provide a smooth reconstruction of major white matter fiber bundles in the mouse brain, with a similar number of fibers and slightly shorter fiber length (average/maximum) as compared to DTI using DTI Studio (Figure 7). However, STI in its current form provides less coherent fiber tracking results than that of DTI. This difference is partly due to current technical challenges of STI, which will be discussed in the last section of this review.
Figure 7. Comparison of STI and DTI fiber tracts in selected pathways.
(A) The anterior commissure; (B) the hippocampal commissure; (C) the posterior corpus callosum. In general, similar fiber tracts are reconstructed with both techniques while DTI tracts appear to be smoother at the edges of the fiber bundles. This figure was reprinted, with permission, from reference (37).
In terms of the difference between STI and DTI, first, as discussed earlier, the values of the diagonal susceptibility tensor components χ1, χ2, χ3 and the parameter MMS are relative and depend on the selection of a proper tissue reference. They can be either positive (more paramagnetic) or negative (more diamagnetic) with respect to the selected reference. In comparison, diffusion tensor components D1, D2, D3 and the mean diffusivity (MD) are absolute measures of a physical constant and always positive.
More fundamental differences can be found between susceptibility and diffusion anisotropies. According to Eq. 2, MSA is predominantly determined by the fraction of myelination of brain white matter, while the diffusion FA is predominantly due to axonal restrictions and only affected partially by myelination (72). This is evident from the shiverer mouse studies (39,48). The significantly reduced myelin lipids in shiverer mouse were associated with nearly complete loss of MSA (39), while the FA was only reduced moderately (48). Similar lack of correlation between MSA and DTI FA has also been reported in human brain (40). Additional evidence comes from studies of white matter development in mouse brain (51), in which the MSA of the fornix system was assessed on postmortem brains from animals sacrificed at post natal days 2, 7, 14, 22 and 56. It was observed in this study that the MSA did not change significantly from zero until 14 days after birth, and then increased progressively to days 22 and 56. In contrast, the DTI-based FA of this fiber started with a medium value of approximately 0.5 and plateaued at day 22 with a value of 0.62 (51). These results confirm that MSA and DTI FA have a dramatically different sensitivity to brain myelination, which is not unexpected in view of the domination of FA by the axonal membrane barrier.
In addition to its sensitivity to myelin, the MSA has also been shown to have a unique sensitivity to gadolinium, while GdDTPA has not shown significant effect on the determination of diffusion MRI parameters (73). Depending on the concentration of gadolinium-based contrast agent, the MSA of brain white matter can be altered several fold compared to that without gadolinium perfusion (38,74).
In summary, MSA provides valuable contrast for quantification of brain myelination with a unique sensitivity modulation by gadolinium.
Applications of STI in brain research
The potential of STI as a high-resolution fiber tracking technique has already been demonstrated in preclinical brain research, e.g. for MR based histology, using ex vivo specimens or mouse models (37,51,75). Tracks of major white matter fiber bundles in mouse brain obtained by STI have revealed anatomical structures comparable to DTI. In addition, due to its unique sensitivity to oriented lipid molecules, STI could provide a completely new tool to assess the white matter integrity especially myelin formation during development (51) and myelin break down in different neural diseases such as fetal alcohol spectrum disorder (FASD) (75) or multiple sclerosis (30). For example, a recent study has shown that the susceptibility contrast and susceptibility anisotropy of brain white matter can be significantly reduced by prenatal alcohol exposure while such changes could not be detected by DTI (75).
Challenges and future directions
Although STI has been available for a few years, there are still many challenges to overcome before it can be routinely applied with a quality comparable to DTI. The greatest challenge is the requirement of rotating the brain inside the magnet. While this is not a significant concern for ex vivo animal or human specimens, it is the major challenge for in vivo human brain STI due to the long scan time, and the inconveniences and restrictions associated with brain rotation. Practically, only a limited range of head rotations can be achieved due to the spatial constrains inside the MR head coil and due to the patients being uncomfortable for head positions other than supine (76). The latter has led to motion issues and a consequent poor STI inverse condition. The angular range of rotation has been shown to have a larger influence on STI reconstruction than the number of head orientations (42). One way to deal with this problem is to speed up the scan. Currently, several fast GRE acquisition methods are available for STI acquisition, e.g. multi-echo multi-shot spiral sequence (77), the Wave-CAIPI sequence (76,78), etc. Another more promising approach is to develop STI methods that do not require brain rotation. A spectrum analysis on the multi-pole magnetic response or p-space MRI has been proposed to achieve the susceptibility-based white matter fiber orientation determination without rotating the brain (79). By applying a gradient field before the normal GRE sequence or by shifting the k-space reconstruction window, the p-space method can detect a difference in sub-voxel field variations for white matter fibers at different angles relative to the main field. However, the practical utility of this approach for human brain imaging in vivo is still a subject of debate (80).
The second challenge comes from the inaccuracy of phase pre-processing. Similar to QSM, STI relies on accurate preprocessing of MR phase data. Any background phase removal error will propagate into the STI calculations leading to errors in the estimated susceptibility tensor orientations (38). It is expected that more accurate background removal combined with additional image-space constraints may further improve the accuracy of STI.
Finally, there are still several important sources or effects that the current theoretical framework of STI does not take into account. For example, recent studies have shown that, in addition to its contribution to the macroscopic susceptibility anisotropy as described in Eqs. 1 and 2, the molecular susceptibility anisotropy of myelin lipids also plays an important role in the nonlinear phase evolution in white matter (81,82). Such a phenomenon originates from the different properties of the distinct micro-compartments of white matter causing the water protons in axonal, myelin and extracellular space to have different relaxation rates and susceptibility induced frequency shifts. As a result, the GRE signal magnitude shows a multi-exponential decay, and the GRE phase evolves nonlinearly with echo time in white matter. Such magnitude and phase evolutions have been successfully modeled using a hollow cylinder model, which can be explained well in terms of the anisotropic susceptibility of myelin lipids (81). Fitting this hollow cylinder model to experimental GRE signal collected in human brain at 7T yields a susceptibility anisotropy estimate of 0.012 ppm. The convolved evolution of GRE signal from multiple compartments with different transverse relaxation rates, i.e. as a multi-exponential function of TE, has also been investigated in monkey brain and human brain, which gave a susceptibility anisotropy of 0.028 ppm in human brain (82). Though these susceptibility estimates are in general consistent with the predictions using Eq. 2 and support the notion that the susceptibility anisotropy of myelin lipids is the major source of the orientation dependent macroscopic susceptibility, STI would give a biased estimation of the underlying macroscopic susceptibility tensor (83) without considering such microstructure effect. In addition, the current STI method uses the Lorentzian sphere correction, which might not be sufficient to describe the underlying microstructure anisotropy induced by the elongated white matter axons, and a more generalized Lorentzian correction may need to be incorporated (33,58,84). With careful consideration of these effects in STI modeling, it is anticipated that better fitting of experimental data and better estimation of white matter structures should be possible in the future.
Currently, the quality of STI is still not as good as that of DTI. However, STI offers powerful advantages in terms of higher spatial resolution, reduced gradient strength requirements and lower SAR compared to diffusion weighted MRI. Therefore, there is sufficient scientific and practical motivation to solve the aforementioned technical challenges. In addition, the strong sensitivity to myelin and its unique modulation by gadolinium-based contrast agents also makes STI a useful complementary tool to probe microstructural changes in various white matter diseases. Last but not least, further development and validation of the biophysical models linking susceptibility tensors at multiple anatomical scales should allow us to gain a deeper understanding of various orientation dependent gradient echo contrasts, ultimately leading to a more accurate interpretation of the findings observed using phase and susceptibility MRI in various research and clinical settings.
Summary
The magnetic susceptibility of white matter is anisotropic, which originates predominantly from the myelin lipids with anisotropic susceptibility at molecular level. As a result, the most paramagnetic susceptibility is along the white matter fiber direction, and the magnetic susceptibility of white matter is dependent on the fraction of myelin lipids and the sine square of fiber angle with respect to the main magnetic field. This anisotropic susceptibility can be described using a symmetric rank-2 susceptibility tensor. The development of STI techniques allows the investigation of white matter integrity especially its myelination status and enables reconstruction of white matter fiber pathways exclusively using GRE signal phase. The STI formalism, currently still being developed further, is expected to provide a theoretical basis for the application and interpretation of both single and multi-orientation QSM studies of white matter disease.
Acknowledgement
This work was supported in part by the National Institutes of Health (NIH) through grants R01 MH096979 and R01NS079653 to CL and P41 EB015909 to PvZ, a Research Grant from the William & Ella Owens Medical Research Foundation to WL, and an American Heart Association (AHA) Scientist Development Grant (15SDG26020003) to WL.
References
- 1.Duyn JH, van Gelderen P, Li TQ, de Zwart JA, Koretsky AP, Fukunaga M. High-field MRI of brain cortical substructure based on signal phase. Proc Natl Acad Sci U S A. 2007;104(28):11796–11801. doi: 10.1073/pnas.0610821104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Salomir R, De Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magnetic Resonance Part B-Magnetic Resonance Engineering. 2003;19B(1):26–34. [Google Scholar]
- 3.Marques JP, Bowtell R. Application of a fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts in Magnetic Resonance Part B-Magnetic Resonance Engineering. 2005;25B(1):65–78. [Google Scholar]
- 4.Shmueli K, de Zwart JA, van Gelderen P, Li TQ, Dodd SJ, Duyn JH. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn Reson Med. 2009;62(6):1510–1522. doi: 10.1002/mrm.22135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magnetic Resonance in Medicine. 2009;61(1):196–204. doi: 10.1002/mrm.21828. [DOI] [PubMed] [Google Scholar]
- 6.de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu JL, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using Bayesian regularization: validation and application to brain imaging. Mag Reson Med. 2010;63(1):194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- 7.Kressler B, de Rochefort L, Liu T, Spincemaille P, Jiang Q, Wang Y. Nonlinear regularization for per voxel estimation of magnetic susceptibility distributions from MRI field maps. Medical Imaging, IEEE Transactions on. 2010;29(2):273–281. doi: 10.1109/TMI.2009.2023787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wharton S, Schafer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Reson Med. 2010;63(5):1292–1304. doi: 10.1002/mrm.22334. [DOI] [PubMed] [Google Scholar]
- 9.Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: Comparison with COSMOS in human brain imaging. Magnetic Resonance in Medicine. 2011;66(3):777–783. doi: 10.1002/mrm.22816. [DOI] [PubMed] [Google Scholar]
- 10.Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage. 2011;55(4):1645–1656. doi: 10.1016/j.neuroimage.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: An approach to in vivo brain iron metabolism? Neuroimage. 2011;54(4):2789–2807. doi: 10.1016/j.neuroimage.2010.10.070. [DOI] [PubMed] [Google Scholar]
- 12.Wu B, Li W, Guidon A, Liu C. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med. 2012;67(1):137–147. doi: 10.1002/mrm.23000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schweser F, Sommer K, Deistung A, Reichenbach JR. Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain. NeuroImage. 2012;62(3):2083–2100. doi: 10.1016/j.neuroimage.2012.05.067. [DOI] [PubMed] [Google Scholar]
- 14.Wang Y, Liu T. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn Reson Med. 2014;73(1):82–101. doi: 10.1002/mrm.25358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fan AP, Bilgic B, Gagnon L, Witzel T, Bhat H, Rosen BR, Adalsteinsson E. Quantitative oxygenation venography from MRI phase. Magnetic Resonance in Medicine. 2014;72(1):149–159. doi: 10.1002/mrm.24918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fan AP, Evans KC, Stout JN, Rosen BR, Adalsteinsson E. Regional quantification of cerebral venous oxygenation from MRI susceptibility during hypercapnia. NeuroImage 2015;104:146-155. doi: 10.1016/j.neuroimage.2014.09.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu T, Surapaneni K, Lou M, Cheng L, Spincemaille P, Wang Y. Cerebral microbleeds: burden assessment by using quantitative susceptibility mapping. Radiology. 2012;262(1):269–278. doi: 10.1148/radiol.11110251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu T, Wisnieff C, Lou M, Chen W, Spincemaille P, Wang Y. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magn Reson Med. 2013;69(2):467–476. doi: 10.1002/mrm.24272. [DOI] [PubMed] [Google Scholar]
- 19.Acosta-Cabronero J, Williams GB, Cardenas-Blanco A, Arnold RJ, Lupson V, Nestor PJ. In vivo quantitative susceptibility mapping (QSM) in Alzheimer's disease. PloS one. 2013;8(11):e81093. doi: 10.1371/journal.pone.0081093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.van Bergen JM, Hua J, Unschuld PG, Lim IA, Jones CK, Margolis RL, Ross CA, van Zijl PC, Li X. Quantitative Susceptibility Mapping Suggests Altered Brain Iron in Premanifest Huntington Disease. AJNR Am J Neuroradiol. 2015 doi: 10.3174/ajnr.A4617. doi: 10.3174/ajnr.A4617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dominguez DJ, Ng AC, Poudel G, Stout JC, Churchyard A, Chua P, Egan GF, Georgiou-Karistianis N. Iron accumulation in the basal ganglia in Huntington's disease: cross-sectional data from the IMAGE-HD study. J Neurol Neurosurg Psychiatry. 2015 doi: 10.1136/jnnp-2014-310183. doi: 10.1136/jnnp-2014-310183. [DOI] [PubMed] [Google Scholar]
- 22.Lotfipour AK, Wharton S, Schwarz ST, Gontu V, Schafer A, Peters AM, Bowtell RW, Auer DP, Gowland PA, Bajaj NP. High resolution magnetic susceptibility mapping of the substantia nigra in Parkinson's disease. J Magn Reson Imaging. 2012;35(1):48–55. doi: 10.1002/jmri.22752. [DOI] [PubMed] [Google Scholar]
- 23.Du G, Liu T, Lewis MM, Kong L, Wang Y, Connor J, Mailman RB, Huang X. Quantitative susceptibility mapping of the midbrain in Parkinson's disease. Movement Disorders. 2015 doi: 10.1002/mds.26417. doi: 10.1002/mds.26417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.He N, Ling H, Ding B, Huang J, Zhang Y, Zhang Z, Liu C, Chen K, Yan F. Region-specific disturbed iron distribution in early idiopathic Parkinson's disease measured by quantitative susceptibility mapping. Human Brain Mapping. 2015;36(11):4407–20. doi: 10.1002/hbm.22928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Murakami Y, Kakeda S, Watanabe K, Ueda I, Ogasawara A, Moriya J, Ide S, Futatsuya K, Sato T, Okada K, Uozumi T, Tsuji S, Liu T, Wang Y, Korogi Y. Usefulness of Quantitative Susceptibility Mapping for the Diagnosis of Parkinson Disease. American Journal of Neuroradiology. 2015;36(6):1102–1108. doi: 10.3174/ajnr.A4260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ide S, Kakeda S, Ueda I, Watanabe K, Murakami Y, Moriya J, Ogasawara A, Futatsuya K, Sato T, Ohnari N. Internal structures of the globus pallidus in patients with Parkinson’s disease: evaluation with quantitative susceptibility mapping (QSM) European Radiology. 2015;25(3):710–718. doi: 10.1007/s00330-014-3472-7. [DOI] [PubMed] [Google Scholar]
- 27.Langkammer C, Liu T, Khalil M, Enzinger C, Jehna M, Fuchs S, Fazekas F, Wang Y, Ropele S. Quantitative susceptibility mapping in multiple sclerosis. Radiology. 2013;267(2):551–559. doi: 10.1148/radiol.12120707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chen W, Gauthier SA, Gupta A, Comunale J, Liu T, Wang S, Pei M, Pitt D, Wang Y. Quantitative susceptibility mapping of multiple sclerosis lesions at various ages. Radiology. 2014;271(1):183–192. doi: 10.1148/radiol.13130353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li X, Harrison DM, Liu H, Jones CK, Oh J, Calabresi PA, van Zijl PC. Magnetic susceptibility contrast variations in multiple sclerosis lesions. J Magn Reson Imaging. 2016;43(2):463–73. doi: 10.1002/jmri.24976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wisnieff C, Ramanan S, Olesik J, Gauthier S, Wang Y, Pitt D. Quantitative susceptibility mapping (QSM) of white matter multiple sclerosis lesions: Interpreting positive susceptibility and the presence of iron. Magn Reson Med. 2015;74(2):564–570. doi: 10.1002/mrm.25420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eskreis-Winkler S, Deh K, Gupta A, Liu T, Wisnieff C, Jin M, Gauthier SA, Wang Y, Spincemaille P. Multiple sclerosis lesion geometry in quantitative susceptibility mapping (QSM) and phase imaging. J Magn Reson Imaging. 2015;42(1):224–229. doi: 10.1002/jmri.24745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Langkammer C, Schweser F, Krebs N, Deistung A, Goessler W, Scheurer E, Sommer K, Reishofer G, Yen K, Fazekas F, Ropele S, Reichenbach JR. Quantitative susceptibility mapping (QSM) as a means to measure brain iron? A post mortem validation study. NeuroImage. 2012;62(3):1593–1599. doi: 10.1016/j.neuroimage.2012.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.He X, Yablonskiy DA. Biophysical mechanisms of phase contrast in gradient echo MRI. Proc Natl Acad Sci U S A. 2009;106(32):13558–13563. doi: 10.1073/pnas.0904899106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lee J, Shmueli K, Fukunaga M, van Gelderen P, Merkle H, Silva AC, Duyn JH. Sensitivity of MRI resonance frequency to the orientation of brain tissue microstructure. Proc Natl Acad Sci U S A. 2010;107(11):5130–5135. doi: 10.1073/pnas.0910222107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liu C. Susceptibility tensor imaging. Magn Reson Med. 2010;63(6):1471–1477. doi: 10.1002/mrm.22482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Denk C, Hernandez Torres E, MacKay A, Rauscher A. The influence of white matter fibre orientation on MR signal phase and decay. NMR in biomedicine. 2011;24(3):246–252. doi: 10.1002/nbm.1581. [DOI] [PubMed] [Google Scholar]
- 37.Liu C, Li W, Wu B, Jiang Y, Johnson GA. 3D fiber tractography with susceptibility tensor imaging. NeuroImage. 2012;59(2):1290–1298. doi: 10.1016/j.neuroimage.2011.07.096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li W, Liu C. Comparison of Magnetic Susceptibility Tensor and Diffusion Tensor of the Brain. Journal of Neuroscience and Neuroengineering. 2013;2(5):431–440. doi: 10.1166/jnsne.2013.1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Li W, Wu B, Avram AV, Liu C. Magnetic susceptibility anisotropy of human brain in vivo and its molecular underpinnings. Neuroimage. 2012;59(3):2088–2097. doi: 10.1016/j.neuroimage.2011.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Li X, Vikram DS, Lim IAL, Jones CK, Farrell JAD, van Zijl PCM. Mapping magnetic susceptibility anisotropies of white matter in vivo in the human brain at 7T. NeuroImage. 2012;62(1):314–330. doi: 10.1016/j.neuroimage.2012.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wisnieff C, Liu T, Spincemaille P, Wang S, Zhou D, Wang Y. Magnetic susceptibility anisotropy: Cylindrical symmetry from macroscopically ordered anisotropic molecules and accuracy of MRI measurements using few orientations. NeuroImage. 2013;70:363–376. doi: 10.1016/j.neuroimage.2012.12.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Li X, van Zijl PC. Mean magnetic susceptibility regularized susceptibility tensor imaging (MMSR-STI) for estimating orientations of white matter fibers in human brain. Magn Reson Med. 2014;72(3):610–619. doi: 10.1002/mrm.25322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Emsley JW, Lindon JC. NMR spectroscopy using liquid crystal solvents. Pergamon Press; 1975. [Google Scholar]
- 44.Van Zijl PCM, Ruessink BH, Bulthuis J, MacLean C. NMR of partially aligned liquids: magnetic susceptibility anisotropies and dielectric properties. Acc Chem Res. 1984;17:172–180. [Google Scholar]
- 45.Worcester DL. Structural origins of diamagnetic anisotropy in proteins. Proc Natl Acad Sci U S A. 1978;75(11):5475–5477. doi: 10.1073/pnas.75.11.5475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Boroske E, Helfrich W. Magnetic anisotropy of egg lecithin membranes. Biophys J. 1978;24(3):863–868. doi: 10.1016/S0006-3495(78)85425-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu C, Li W, Tong KA, Yeom KW, Kuzminski S. Susceptibility-weighted imaging and quantitative susceptibility mapping in the brain. J Magn Reson Imaging. 2015;42(1):23–41. doi: 10.1002/jmri.24768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liu C, Li W, Johnson GA, Wu B. High-field (9. T) MRI of brain dysmyelination by quantitative mapping of magnetic susceptibility. Neuroimage. 2011;56(3):930–938. doi: 10.1016/j.neuroimage.2011.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lee J, Shmueli K, Kang B-T, Yao B, Fukunaga M, van Gelderen P, Palumbo S, Bosetti F, Silva AC, Duyn JH. The contribution of myelin to magnetic susceptibility-weighted contrasts in high-field MRI of the brain. NeuroImage. 2012;59(4):3967–3975. doi: 10.1016/j.neuroimage.2011.10.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lodygensky GA, Marques JP, Maddage R, Perroud E, Sizonenko SV, Hüppi PS. Gruetter R. In vivo assessment of myelination by phase imaging at high magnetic field. NeuroImage. 2012;59(3):1979–1987. doi: 10.1016/j.neuroimage.2011.09.057. [DOI] [PubMed] [Google Scholar]
- 51.Argyridis I, Li W, Johnson GA, Liu C. Quantitative magnetic susceptibility of the developing mouse brain reveals microstructural changes in the white matter. NeuroImage. 2014;88(0):134–142. doi: 10.1016/j.neuroimage.2013.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Scholz F, Boroske E, Helfrich W. Magnetic-anisotropy of lecithin membranes - a new anisotropy susceptometer. Biophysical Journal. 1984;45(3):589–592. doi: 10.1016/S0006-3495(84)84196-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kawamura Y, Sakurai I, Ikegami A, Iwayanagi S. Magneto-orientation of phospholipids. Mol Cryst Liq Cryst. 1981;67(1-4):733–743. [Google Scholar]
- 54.Sakurai I, Kawamura Y, Ikegami A, Iwayanagi S. Magneto-orientation of lecithin crystals. P Natl Acad Sci-Biol. 1980;77(12):7232–7236. doi: 10.1073/pnas.77.12.7232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Pu MM, Fang XM, Redfield AG, Gershenson A, Roberts MF. Correlation of vesicle binding and phospholipid dynamics with phospholipase C activity insights into phosphatidylcholine activation and surface dilution inhibition. J Biol Chem. 2009;284(24):16099–16107. doi: 10.1074/jbc.M809600200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lounila J, Alakorpela M, Jokisaari J, Savolainen MJ, Kesaniemi YA. Effects of orientational order and particle-size on the NMR line positions of lipoproteins. Phys Rev Lett. 1994;72(25):4049–4052. doi: 10.1103/PhysRevLett.72.4049. [DOI] [PubMed] [Google Scholar]
- 57.Koch KM, Papademetris X, Rothman DL, de Graaf RA. Rapid calculations of susceptibility-induced magnetostatic field perturbations for in vivo magnetic resonance. Phys Med Biol. 2006;51(24):6381–6402. doi: 10.1088/0031-9155/51/24/007. [DOI] [PubMed] [Google Scholar]
- 58.Yablonskiy DA, Sukstanskii AL. Generalized Lorentzian Tensor Approach (GLTA) as a biophysical background for quantitative susceptibility mapping. Magn Reson Med. 2015;73(2):757–764. doi: 10.1002/mrm.25538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med. 2009;61(1):196–204. doi: 10.1002/mrm.21828. [DOI] [PubMed] [Google Scholar]
- 60.Abdul-Rahman H, Gdeisat M, Burton D, Lalor M. Fast three-dimensional phase-unwrapping algorithm based on sorting by reliability following a non-continuous path. 2005. International Society for Optics and Photonics. :32–40. [Google Scholar]
- 61.Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt Lett. 2003;28(14):1194–1196. doi: 10.1364/ol.28.001194. [DOI] [PubMed] [Google Scholar]
- 62.Li W, Avram AV, Wu B, Xiao X, Liu C. Integrated Laplacian-based phase unwrapping and background phase removal for quantitative susceptibility mapping. NMR in Biomedicine. 2014;27(2):219–227. doi: 10.1002/nbm.3056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Topfer R, Schweser F, Deistung A, Reichenbach JR, Wilman AH. SHARP edges: Recovering cortical phase contrast through harmonic extension. Magnetic Resonance in Medicine. 2015;73(2):851–856. doi: 10.1002/mrm.25148. [DOI] [PubMed] [Google Scholar]
- 64.Li W, Wu B, Liu C. iHARPERELLA: an improved method for integrated 3D phase unwrapping and background phase removal. Proc Int Magn Reson Med. 2015;23:3313. [Google Scholar]
- 65.Zhou D, Liu T, Spincemaille P, Wang Y. Background field removal by solving the Laplacian boundary value problem. NMR in Biomedicine. 2014;27(3):312–319. doi: 10.1002/nbm.3064. [DOI] [PubMed] [Google Scholar]
- 66.Wen Y, Zhou D, Liu T, Spincemaille P, Wang Y. An iterative spherical mean value method for background field removal in MRI. Magnetic Resonance in Medicine. 2014;72(4):1065–1071. doi: 10.1002/mrm.24998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris AJ, Wang Y. A novel background field removal method for MRI using projection onto dipole fields (PDF) NMR Biomed. 2011;24(9):1129–1136. doi: 10.1002/nbm.1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Wharton S, Bowtell R. A Simplified Approach for Anisotropic Susceptibility Map Calculation. Proceedings of International Society for Magnetic Resonance in Medicine. 2011;19:4515. [Google Scholar]
- 69.Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophysical journal. 1994;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Mori S, Crain BJ, Chacko VP, van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Annals of Neurology. 1999;45(2):265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 71.Liu C, Murphy N, Li W. Probing white-matter microstructure with higher-order diffusion tensors and susceptibility tensor MRI. Frontiers in Integrative Neuroscience. 2013:7. doi: 10.3389/fnint.2013.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. 2002;15(7-8):435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- 73.Yamada K, Kubota H, Kizu O, Nakamura H, Ito H, Yuen S, Tanaka O, Kubota T, Makino M, Van Cauteren M, Nishimura T. Effect of intravenous gadolinium-DTPA on diffusion-weighted images: evaluation of normal brain and infarcts. Stroke. 2002;33(7):1799–1802. doi: 10.1161/01.str.0000020355.29423.61. [DOI] [PubMed] [Google Scholar]
- 74.Dibb R, Li W, Cofer G, Liu C. Microstructural origins of gadolinium-enhanced susceptibility contrast and anisotropy. Magn Reson Med. 2014;72(6):1702–1711. doi: 10.1002/mrm.25082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Cao W, Li W, Han H, O'Leary-Moore SK, Sulik KK, Allan Johnson G, Liu C. Prenatal alcohol exposure reduces magnetic susceptibility contrast and anisotropy in the white matter of mouse brains. Neuroimage. 2014;102(2):748–755. doi: 10.1016/j.neuroimage.2014.08.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Bilgic B, Xie L, Dibb R, Langkammer C, Mutluay A, Ye H, Polimeni JR, Augustinack J, Liu C, Wald LL, Setsompop K. Rapid multi-orientation quantitative susceptibility mapping. Neuroimage. 2016;125:1131–41. doi: 10.1016/j.neuroimage.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wu B, Li W, Avram AV, Gho S-M, Liu C. Fast and tissue-optimized mapping of magnetic susceptibility and T2* with multi-echo and multi-shot spirals. Neuroimage. 2012;59(1):297–305. doi: 10.1016/j.neuroimage.2011.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magnetic Resonance in Medicine. 2015;73(6):2152–2162. doi: 10.1002/mrm.25347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Liu C, Li W. Imaging neural architecture of the brain based on its multipole magnetic response. NeuroImage. 2013;67:193–202. doi: 10.1016/j.neuroimage.2012.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Straub S, Ladd ME, Wetscherek A, Laun FB. On contrast mechanisms in p-space imaging. Magn Reson Med. 2015 doi: 10.1002/mrm.25812. doi: 10.1002/mrm.25812. [DOI] [PubMed] [Google Scholar]
- 81.Wharton S, Bowtell R. Fiber orientation-dependent white matter contrast in gradient echo MRI. Proc Natl Acad Sci U S A. 2012;109(45):18559–18564. doi: 10.1073/pnas.1211075109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Sati P, van Gelderen P, Silva AC, Reich DS, Merkle H, de Zwart JA, Duyn JH. Micro-compartment specific T2* relaxation in the brain. Neuroimage. 2013;77(0):268–278. doi: 10.1016/j.neuroimage.2013.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Wharton S, Bowtell R. Effects of white matter microstructure on phase and susceptibility maps. Magn Reson Med. 2015;73(3):1258–1269. doi: 10.1002/mrm.25189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Sukstanskii AL, Yablonskiy DA. On the role of neuronal magnetic susceptibility and structure symmetry on gradient echo MR signal formation. Magn Reson Med. 2014;71(1):345–353. doi: 10.1002/mrm.24629. [DOI] [PMC free article] [PubMed] [Google Scholar]