Abstract
Objective
To develop a diffusion tensor imaging (DTI) protocol for assessing the sural nerve in healthy subjects.
Methods
Sural nerves in 25 controls were imaged using DTI at 3 T with 6, 15, and 32 gradient directions. Fractional anisotropy (FA) and apparent diffusion coefficient (ADC) were computed from nerve regions of interest co-registered with T2-weighted images.
Results
Coronal images with 0.5(RL)×2.0(FH)×0.5(AP) mm3 resolution successfully localized the sural nerve. FA maps showed less variability with 32 directions (0.559±0.071) compared to 15(0.590±0.080) and 6(0.659±0.109).
Conclusions
Our DTI protocol was effective in imaging sural nerves in controls to establish normative FA/ADC, with potential to be used non-invasively in diseased nerves of patients.
Keywords: Diffusion tensor imaging, Sural nerve, Fractional anisotropy, Image registration
1. Introduction
Diffusion tensor imaging (DTI) is a magnetic resonance (MR) technique that can be used for gaining quantitative information about tissue water diffusion. Random movement of water molecules is primarily influenced by anisotropic tissue structure of myelinated axons in white matter and peripheral nerve [1–3]. The direction-dependent water diffusion from DTI measurements can be used to compute apparent diffusion coefficient (ADC) and fractional anisotropy (FA). The former is a scalar value that quantifies molecular diffusivity and the latter is a measure of directionality of diffusion in a voxel. DTI typically shows signal attenuation in the direction of a magnetic field gradient applied in different orientations in space. The directionality and the magnitude measures of water diffusion in vivo [4,5] by FA and ADC, respectively, have been extensively used to study neural tracts and white matter fiber structures in the brain [2].
The interest in DTI for the evaluation of peripheral nerves is rapidly growing [6–11]. With their myelinated structure, peripheral nerves provide suitable structural bases to be assessed by DTI with FA measurements since diffusion is higher along axons than their perpendicular directions resulting in anisotropic diffusion. Previous studies have demonstrated the feasibility of DTI for imaging peripheral nerve structures such as the median nerves at the wrist; cervical nerve roots; the peroneal and tibial nerves at the knee, calf, and ankle; and the sciatic nerve [6,8–10,12–15]. Among these, normative values were reported only in a few studies and limited to the median nerve [8,12,15,16]. The importance of the baseline measurements of normative values was demonstrated in carpal tunnel syndrome [8] as a clinical reference for patients with disease affected nerves [8]. The sural nerve poses a unique challenge due to its much smaller size (1.5–2 mm cross-sectional diameter) compared to that of the median or tibial nerves (5 mm or larger).
Previously reported data show large inter-subject variability of ADC and FA data [12] of peripheral nerves and there is a need for more accurate baseline reference data from normal healthy subjects using an optimized robust measurement protocol. In general, the accuracy of the diffusion tensor estimation depends on the diffusion gradient encoding scheme and many studies have addressed the topic of DTI sequence optimization [17–19]. Quantification of water diffusion anisotropy in tissues, in principle, can be achieved by applying at least six non-collinear, diffusion-sensitive gradients during the magnetic resonance imaging (MRI) acquisition. When spatially even distributions of gradients have been optimized, the optimal number of diffusion gradient directions, Nd, for reliable estimates of the diffusion tensor within an acceptable acquisition time is still being investigated [20]. Studies have shown that more Nd produces better directional sensitivity and provides more accurate estimations of diffusion anisotropy. The optimal value of Nd is reported to lie in the range 20–30 [17,18,21] for brain studies. To date, no studies have addressed the effect of Nd on DTI analysis of the sural nerve. Given the advantage of DTI techniques in peripheral nerve studies, determining the optimal Nd for the measurement of FA and ADC may have a significant impact on the clinical use of DTI as a non-invasive means of nerve assessment.
Diffusion measurements show increased reliability when they are correlated to patients’ anatomical images [22] for the localization of nerve structures (Fig. 1). Studies of the brain have shown that DTI measurements depend on the precise placement of regions of interest (ROIs) in which FA and ADC are calculated [23–27]. Voxel-wise analysis of DTI relies on the consistent matching of anatomical regions across subjects. Utilizing co-registration techniques [28,29] along with algorithms for processing DTI data allows the three-dimensional (3D) visualization of correlation of tissue orientation with the anatomical MRI [6,8–10,15,30].
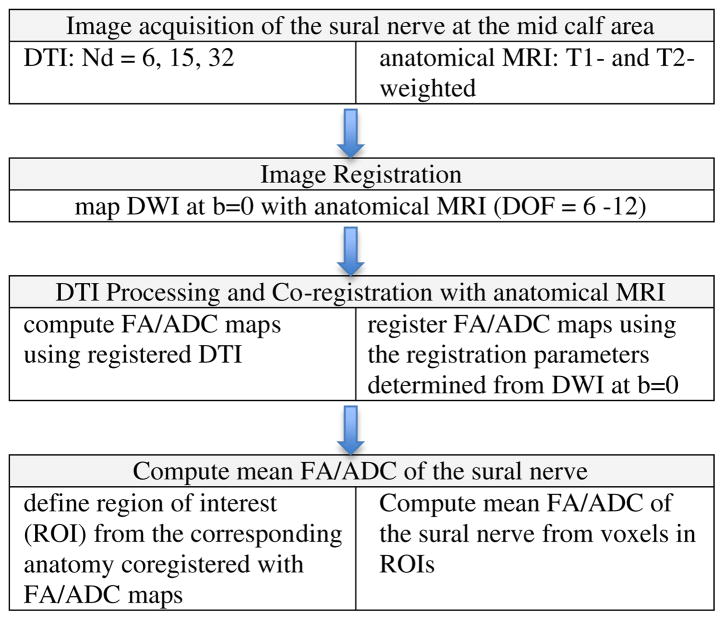
Fig. 1.
Sequential diagram of acquisition and processing of DTI data of the sural nerve.
We proposed to perform DTI on the sural nerves of healthy volunteers to determine variability of quantitative diffusion indices that can be potentially useful in the clinical assessment of the nerve integrity or abnormalities in the progression of nerve injuries. Serial sural nerve biopsies, historically used to quantitate myelinated fiber density [30] with diabetic peripheral neuropathy (DPN) [22,31–33], have been deemed too invasive [22,31,34]. While current clinical trials using intraepidermal nerve fiber density from serial skin biopsies in the leg and thigh are clearly less invasive, there is no anatomical assessment of myelinated nerve fibers [35–38]. The availability of a reliable, non-invasive imaging tool would have a huge impact on the assessment of normal and disease affected nerve fibers in patients for monitoring disease progression and response to treatment. This can potentially eliminate the need for repeat invasive biopsies and serve as a tool for making management decisions about treatment. Nevertheless, there are no quantitative studies on the DTI of the sural nerve.
The aims of our study are to establish an optimal DTI protocol for evaluating sural nerves and normative FA and ADC values in healthy subjects. We present in this work (a) the dependence of FA and ADC on Nd in the sural nerve, (b) multimodality image registration of DTI with anatomical MRI to localize the sural nerve, and (c) the variability of quantitative measurements of diffusion indices in normal subjects.
2. Materials and methods
2.1. Subjects
Twenty-five healthy volunteer subjects were recruited from the University of Michigan Clinical Studies Website (UMClinicalStudies.org) to participate in a calf area scanning of the sural nerve using DTI. The study was approved by the Institutional Review Board at the University of Michigan Medical School and written informed consent was obtained from all subjects prior to participation. All subjects underwent screening evaluations to confirm their eligibility including normal neurological examination, normal glucose tolerance, normal blood pressure, normal lipid profile, body mass index<30, free of any other causes of neuropathy, before the MRI session.
2.2. MRI/DTI data acquisition
MRI was performed with a 3-T Philips system (Achieva/Ingenia, Philips Medical Systems, Best, The Netherlands) using an eight-channel knee coil. After the scanner upgrade from Achieva to Ingenia, the protocol was converted to maintain the equivalent imaging parameters. Each subject lays in the supine position with the dominant lower extremity stabilized with soft cushions inside the coil. The dominant lower extremity from the mid-calf to right above the ankle was scanned.
2.2.1. Anatomical MRI
To identify the individual sural nerve for each subject [1], an axial high-resolution T2-weighted MRI was acquired to follow its course by scanning the length of the lower calf segment on the dominant side. The imaging parameters for a turbo spin echo (TSE) sequence were TR/TE=5000/72, FOV=140×140 mm2, image matrix=256×256, slice thickness=2 mm, and acquisition time=5:50. The sural nerve was identified on the axial images by one of two board-certified radiologists. Then a coronal orientation adjusted to follow the alignment of the nerve was defined from three serial axial images for the subsequent coronal T2-weighted MRI and diffusion images [2]. For coronal T2-weighted MRI, the orientation of the oblique coronal plane was determined by the radiologist plotting three points for each subject along the course of the nerve in the axial image. This was meant to select longest possible portion of the nerve in longitudinal direction. The images were acquired using the TSE sequence in an orientation where the three points from axial images were aligned. The imaging parameters for the coronal T2-weighted MRI were TR/TE=8150/100 ms, FOV=160×160 mm2, image matrix=256×256, slice thickness=0.5 mm, and acquisition time=4:37 [3]. T1-weighted MRI was acquired using 3D TSE volume imaging sequence for a high-resolution anatomical reference with parameters TR/TE=819/15 ms, matrix=144×144 mm2 FOV, and slice thickness=3 mm.
2.2.2. Diffusion tensor imaging
Data were acquired in the same coronal oblique plane as defined for the anatomical coronal oblique T2-weighted MRI. Diffusion images were acquired using a single-shot spin echo, echo planar imaging (EPI) sequence with the SENSE factor of two and imaging parameters, TR/TE=9187/62 ms (Achieva) and 8600/78 ms (Ingenia); image matrix=64×234 (Achieva) and 76×158 (Ingenia); FOV=150 (FH)×142(RL) mm2; slice thickness=0.5 mm; b-value=950 s/mm2. Diffusion-weighted images using 6, 15, and 32 direction encodings from low calf structures were acquired with the optimal resolution of approximately 0.5(RL)×2.0(FH)×0.5(AP) mm3 for each subject. There were no systematic differences between the data sets acquired before and after the scanner upgrade in data analysis.
2.3. DTI data processing and analysis
Flow chart in Fig. 1 shows the sequence of data acquisition and processing of DTI of the sural nerve from normal volunteers. Quantitative data analysis was performed by calculation of FA and ADC.
2.3.1. FA and ADC map computation
For the computation of FA values, images were processed using Philips View Forum 3D work stations. FA and ADC were computed using Philips fiber tracking tool, which reconstructs fibers from user-defined ROIs and using thresholded volumetric FA and ADC maps. The maps were generated from FA and ADC values of each voxel computed from registered DTI data sets of 6, 15, and 32 gradient directions. The computed FA and ADC maps were registered by the method described below to the anatomical MRI and the voxels corresponding to the sural nerve were identified. The sural nerve ROI was thresholded at the FA value of 0.3, which represents a low anisotropy index associated with the surrounding muscle [6,12]. Then FA of the sural nerve in each subject was determined by averaging FA values of all voxels in the ROI.
2.3.2. Image registration
The acquired anatomical T1- and T2-weighted MRI and DTI data and the computed FA and ADC maps were transferred to and processed using an independent software developed in the Digital Image Processing Laboratory in the Department of Radiology at the University of Michigan Medical School. To determine accurate localization of the nerve, we applied an image registration tool to map diffusion images acquired in the coronal orientation onto the anatomical T1- and T2-weighted MRI volume data in the axial orientation. Image registration was performed using Mutual Information for Automated Multimodality Image Fusion (MIAMI-Fuse) (copyrighted, University of Michigan) software [28,29]. Image registration provides the identification and visualization of the nerve to validate the computed FA maps in anatomical reference images. For this study, image registration was performed using 3D affine (i.e., global) transformations with varying degrees of freedom, up to 12, depending on each data set. Diffusion tensor images were registered with T1- and T2-weighted MRI data for the anatomical localization of the voxels with higher diffusion signal intensities pertaining to the sural nerve. The EPI image acquired without diffusion weighting (b=0) was used for determining registration parameters for mapping diffusion data to anatomical volumes and the same transformation was used to map the FA values computed from DTI data acquired with 32, 15, and 6 gradient directions.
3. Results
We report data on 25 healthy subjects (8 men, 17 women; mean age, 33±12 years; mean height, 169±10 cm; and mean body mass index, 23±3 kg/m2). Detailed clinical characteristics of these subjects are shown in Table 1.
Table 1.
Clinical characteristics of the normal subjects enrolled
| Variable | Healthy controls (n=25) |
|---|---|
| Age, years | 33±12 |
| Weight, kg | 69±12 |
| Height, cm | 169±10 |
| Body mass index, kg/m2 | 23±3 |
| HbA1c, % | 5±0.2 |
| Fasting blood glucose, mg/dl | 85±10 |
| Total cholesterol, mg/dl | 184±27 |
| Triglycerides, mg/dl | 83±42 |
| Systolic BP, mmHg | 112±6 |
| Diastolic BP, mmHg | 64±10 |
Data are mean±standard deviation; HbA1c, hemoglobin A1c; BP, blood pressure.
3.1. Diffusion-weighted images and registration with anatomical MRI
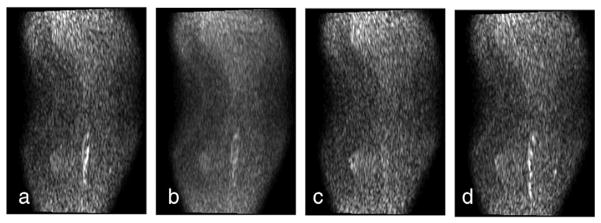
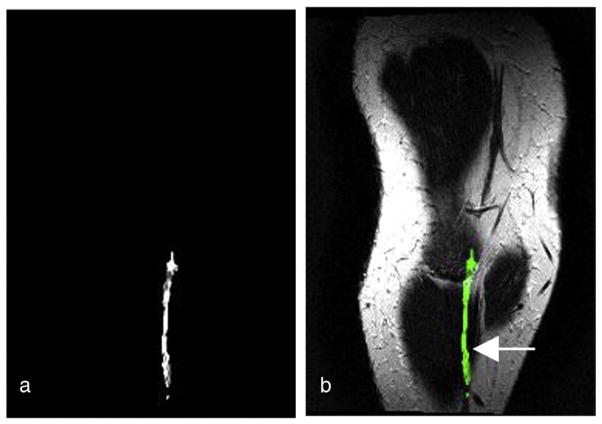
Displayed in Fig. 2a–d are a series of selected diffusion-weighted images from the low calf level acquired in 15 gradient directions using a single-shot EPI sequence in the coronal oblique orientation with a slice image resolution of 0.5×2 mm2 and slice thickness of 0.5 mm. Images show the direction-dependent sensitivity of the diffusion-weighted MR signal in a multi-directional gradient acquisition. The FA map computed from the 15 gradient DTI measurement (as displayed in Fig. 2) is presented in Fig. 3. The enhanced intensity in Fig. 3a depicts increased anisotropy in the FA map, which likely represent the myelination in the sural cutaneous nerve. The volumetric FA map was registered with the T2-weighted MRI volume from the same subject to locate the anatomical reference corresponding to the FA values using the image registration method described in the abovementioned section. The corresponding selected slice from the co-registered FA map superimposed with the T2-weighted MRI in Fig. 3b demonstrates the location of the increased anisotropy (green) in the sural cutaneous nerve (arrow) as anatomically identified by the radiologists.
Fig. 2.
DTI in the coronal plane of the mid to low calf area using 15 gradient directions. The gradient directions are (a) [1.0000 1.0000 0.0000], (b) [0.9999 −0.1561 0.9879], (c) [0.3580 −0.9800 −0.9547], and (d) [0.9999 −0.3989 −0.9171]. The anisotropic water diffusion signal in the sural nerve fiber is observed.
Fig. 3.
(a) An FA map from 15 gradient direction DTI. (b) The FA map (green) co-registered with the anatomical T2-weighted MRI of the same subject in the oblique coronal view. The figures demonstrate the localization of the anisotropic diffusion along the anatomically defined sural nerve (arrow) in MRI.
3.2. Multi-directional DTI and diffusion measurements
Following the initial localization of the sural nerve in 6- and 15-directional DTI, we have fully expanded the imaging protocol and analyses to include 32-directional DTI as a tool for a baseline FA measurement method for healthy normal subjects. By acquiring diffusion images in an adjusted coronal orientation (as described in Materials and methods) with the slice thickness of 0.5 mm, the sural nerve could be more easily localized and distinguished from the saphenous vein that runs in close proximity with the nerve.
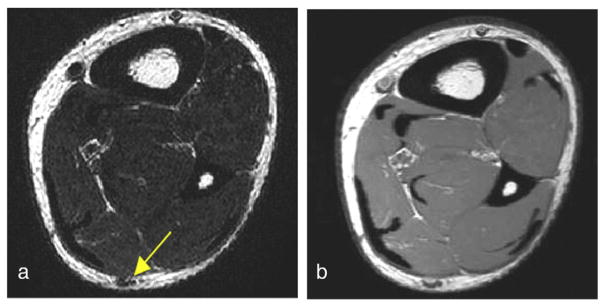
For each subject, an axial T2-weighted MRI scan was used to identify the sural nerve. Displayed in Fig. 4a and b are selected axial slice images from T2- and T1-weighted MRIs of a volunteer, respectively, that show the size and location of the nerve relative to the mid-calf anatomy. The images in Fig. 4 demonstrate the difference in contrast between the two imaging modalities. The sural nerve and the vein in close proximity were difficult to separate in T1-weighted images (Fig. 4b). While signal-to-noise ratio (SNR) seems higher in the T1-weighted MRI, the particular T2-weighted contrast was more effective for the localization of the sural nerve in this study.
Fig. 4.
Selected axial slice images from (a) T2-weighted and (b) T1-weighted MRIs of a volunteer that show the size and location of the nerve relative to the mid-calf anatomy. The images demonstrate the difference in contrast between the two imaging modalities. The sural nerve and the vein in close proximity are difficult to separate on the T1-weighted image. The T2-weighted contrast was more effective for the localization of the sural nerve.
3.3. Localization of the sural nerve
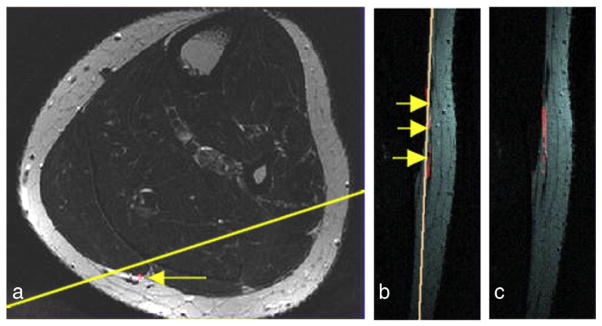
Images in Fig. 5 demonstrate the localization of the sural nerve in axial and oblique coronal slice orientations and illustrate the anatomical shape of the sural nerve in an individual subject. The location of the sural nerve in an axial image is displayed in Fig. 5a, and the definition of the coronal slice orientation that best fits the shape of the subject’s nerve is indicated by the yellow line. The registered FA map (red hue) superimposed on the anatomical reference in two sagittal consecutive slice views are shown in Fig. 5b and c. Three arrows in Fig. 5c represent three different axial slice locations used by the radiologist to follow the nerve.
Fig. 5.
The FA signal computed from the 32-direction DTI data was registered with the anatomical MRI as shown in the red hue. The sural nerve visualized in a different slice orientation illustrates the anatomical variation in individual subjects: (a) an T2-weighted MRI from the mid-calf area of a healthy subject in the in-plane voxel resolution 0.5×0.5 mm2 with the location of the sural nerve indicated by an arrow and the definition of the coronal slice orientation by the yellow line that best fits the subject’s nerve orientation; (b and c) the FA map (red hue) is superimposed on the anatomical reference as shown in two sagittal consecutive slice views; (b) the three arrows point to the sural nerve running parallel next to a vein in the FH direction.
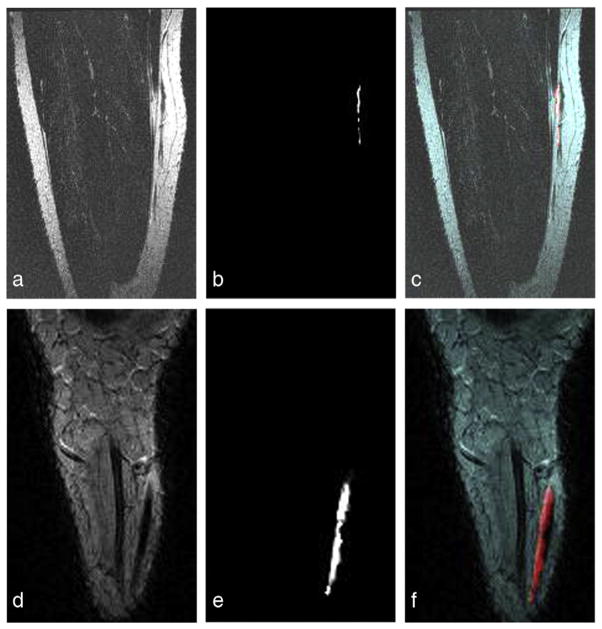
Different slice orientations of the sural nerve and FA maps computed from 32-directional DTIs from two individual subjects are illustrated in top and bottom of Fig. 6. The co-registered anatomical T2-weighted MRI in coronal orientation and FA map are shown in Fig. 6a and d and in Fig. 6b and e, retrospectively. Each FA map was registered to the T2-weighted anatomical MRI from the same subject with the registration parameters determined using the EPI images acquired with b=0. The superimposed images in Fig. 6c and f show that the high intensity FA map (red hue) follows the anatomically confirmed sural nerve structure in coronal orientations. Two different cases illustrate individual variations in the shape and orientation of the sural nerve. These figures demonstrate the localization of the diffusion indices corresponding to the sural nerves on the anatomical MRI references.
Fig. 6.
Oblique coronal T2-weighted MRIs and the co-registered FA maps computed from 32-direction DTI data from two difference subjects: Top images (a–c) are from the same subject as shown in this figure, in which the acquired coronal slice is in the orientation as defined using three different slice locations of the axial images as indicated in (a). The figure depicts (a and d) anatomical T2-weighted MRIs, (b and e) registered FA maps, and (c and f) the superposition of each FA map (red hue) to each subject’s anatomical coronal T2-weighted MRI showing that the FA map follows the anatomically confirmed sural nerve structure.
3.4. Quantitative DTI data analysis
Following the development of the DTI scanning protocols for the localization of the sural nerve, we have collected DTI data from 22 healthy volunteer subjects (mean age, 35±12 years; 9 males/16 females). Pertinent clinical characteristics of the healthy volunteer subjects are shown in Table 1. Three out of 25 subjects were excluded due to the difficulty in localization of the nerve caused by low SNR attributing to either motion or extremely small size and individual variations in the shape and location of the sural nerve.
Table 2 lists diffusion values obtained from 22 normal subjects who have been scanned using 6, 15, and 32 gradient directions. Only the mean measurement above a conclusive FA threshold (FA=0.3) was included in averaging as indicated by the number (n) of cases in Table 2. The number of cases in which the FA value fell below the threshold decreased with higher gradient resolutions. Using 32 gradient directions, we were able to obtain FA measurements from all 22 subjects, whereas from 20 subjects using 15 directions and 8 subjects [8] using 6 directions were obtained.
Table 2.
FA and mean ADC from DTI acquired from normal subjects using 32, 15, and 6 gradient directions
| 32 directions (n=22)
|
15 directions (n=20)
|
6 directions (n=8)
|
||||
|---|---|---|---|---|---|---|
| FA | ADC | FA | ADC | FA | ADC | |
| Mean | 0.559 | 0.638 | 0.590 | 0.698 | 0.659 | 0.867 |
| Standard deviation | 0.071 | 0.206 | 0.080 | 0.223 | 0.109 | 0.325 |
| Range | 0.436–0.645 | 0.455–0.781 | 0.450–0.748 | 0.425–0.802 | 0.509–0.784 | 0.465–0.919 |
ADC (10−3 mm2/s).
The values are averages in ROIs from FA maps that were confirmed to correspond to the anatomically selected sural nerves by co-registration with the anatomical T2-weighted images in individual subjects. The DTI values follow a noticeable trend with the gradient resolution that the higher the gradient density, the lower the mean FA value and the standard deviation. With 32 directions, the lowest FA and the narrowest range 0.559±0.071 (mean±STD) were observed compared to 0.590±0.080 and 0.659±0.109 of the 15 and 6 directions, respectively, as shown in Table 2 for the analyses of n=8. The similar trend is observed with n of 20 and 22.
4. Discussion
Following the widespread utilization of DTI in the brain white matter tracts, assessment of peripheral nerves by using the DTI technique in the lower extremity may offer new technical advances in non-invasive means of clinical diagnostic tool. We describe in this study a new approach in developing a DTI protocol targeted specifically for the reliable and non-invasive evaluation of the sural nerve.
Our data demonstrate that DTI at 3 T can be effectively used to localize the sural nerve at mid to lower calf and measure its diffusion indices such as FA and ADC. The particular nerve and the anatomical location were chosen since a progressive loss of myelin in the sural nerve is a hallmark finding in patients diagnosed with DPN. This study was focused on establishing the DTI protocol with the optimal number of gradients for measuring the normative FA and ADC values and for assessing the reproducibility of these values in a consistent anatomical location in healthy control volunteers. The ultimate future goal is to evaluate whether this technique can be utilized to reliably evaluate peripheral nerve damage associated with myelinated nerve fibers in patients with DPN, which would demonstrate lower FA and higher ADC similar to that seen in the tibial nerve in chronic inflammatory demyelinating polyradiculopathy or the median nerve in carpal tunnel syndrome [38,39].
One of the critical factors in imaging the sural nerve at lower calf level with DTI is the spatial resolution in association with its small size (<1 mm in diameter) and the partial volume effect from its proximity to the saphenous vein and muscles. Although anatomical images are commonly acquired in the axial image orientation for the identification of the small sural nerve by radiologists, the axial DTI may be prone to the prominent partial volume effect. Since axial DTI is commonly limited in in-plane resolution (>2×2 mm2) and slice thickness (2–3 mm) to maintain appropriate SNR for detecting diffusion signal, the localization of the fine sural nerve structure may be problematic. Using oblique coronal orientation in MRI and DTI scans with 0.5×2.0 mm2 in-plane resolution and 0.5 mm slice thickness, we were able to develop an effective imaging protocol at the 3.0-T field strength. The protocol provides a high in-plane resolution in the RL and AP directions for handling the small diameter while allowing lower resolution of 2 mm in the FH direction along the length of the nerve. Instead of the conventional axial orientation, our new DTI protocol in coronal orientation provided an appropriate image resolution for the anatomical localization and diffusion measurements of the nerve.
Most DTI analysis is performed using the vendor provided image registration tool, which offers reasonable accuracy for anatomical data sets with optimal SNR and image resolution. Nonetheless, localization error in DTI for small nerves due to the low-resolution, suboptimal SNR or the partial volume effect has not been previously addressed. In the analysis of DTI, computation error due to slightly misregistered voxels in the tiny nerve structure may have a significant impact in accuracy of diffusion measurements and attribute to the large variability across subjects. By employing an image registration tool that can handle multi-modality mapping, variation in diffusion parameters due to the localization error may be mitigated.
In this study, we register all subjects’ FA data onto an anatomical MRI before applying voxel-wise cross-subject statistics. Our image registration tool uses a diffusion image with b=0 to determine the registration parameters to align individual FA maps and compute the average of values in voxels in the ROI determined by the nerve anatomy. We employed a mutual information-based image registration tool that performs multi-modality (i.e., images of differing contrast) image mapping to sub-voxel accuracy. Our volumetric image registration method is reliable in providing an accurate means of measuring the diffusion values associated with the sural nerve anatomy and differentiate the nerve from other anatomical features. The location of the sural nerve, its course, and its divisions on FA maps computed from diffusion images correlated with the anatomical location on T1- and T2-weighted MR images. All nerve ROIs were validated by the co-registration of FA maps with anatomical MRIs that were used by the board-certified radiologists to identify the nerve. FA values of the sural nerves were determined by averaging voxels in the ROI that were thresholded at 0.3 below which represents a low anisotropy index associated with the surrounding muscle [10].
Imaging of the peripheral nerves with DTI often poses difficulties for differentiating the nerves from surrounding structures such as ligaments and muscles. Because muscle fibers are shorter than nerve fibers and have a relatively low anisotropy index, this difficulty can be overcome with use of fiber length and degree of anisotropy. For several ROIs positioned in the nerve or in areas near the nerve, different FA threshold values and tract lengths were tested in tractography to distinguish nerve from muscle fibers and ligaments previously. It was indicated that the FA value of the voxel fell below 0.3 in foot and below 0.4 in wrist when tracking had reached tissue outside the nerve. Hence, in our study, we set the anisotropy threshold at 0.3 [6,12].
Optimizing diffusion-sensitizing gradients is important in DTI sequences [1,3,4]. Accuracy in diffusion tensor estimation may depend on the number of gradient encoding directions. Studies have shown a dependence of probabilistic tractography and stronger connectivity with increasing number of diffusion gradient directions (Nd) [31,32]. The optimal Nd required for reliable estimates of diffusion indices within an acceptable acquisition time is an important issue. In comparison, the FA values for the sural nerves in our study were found to be within the range found by other previous studies that reported distal nerve FA measurements of ~0.53 or lower [39,40]. Considerably higher FA values (>0.70) reported by Hiltunen et al. [6] for the distal tibial nerves were actually the maximum values in their ROI, which seems comparable to the maximum values in our FA ranges obtained from the 6-directional DTIs. Considering that those reported values were obtained with measurements from less number of gradient directions (Nd=6,15), the higher limit in our FA values at 6 and 15 directions (Table 2) were 0.768 (0.659+0.109) and 0.689 (0.615+0.074), respectively, making the measurements of the sural nerve using less Nd in closer agreement, though in lower limit, with the previously reported values of the tibial nerve.
One limiting factor in our protocol described is a relatively long data acquisition time, which spans to 20 min for acquiring 32-directional DTI. As in some of the cases reported here, FA measurements could not be assessed in a few subjects due to the difficulty in localization of the nerve or low SNR attributing to either motion or gradient stability adding to the problem of extremely small size and individual variations in the shape of the sural nerve. Also, when the nerve is smaller than 1 mm in cross-sectional diameter, the FA values may not be accurate due to volume averaging effects. Another limitation is the potential difficulty in differentiating the nerve from the adjacent blood vessels; in patients where the nerve is in close proximity to the blood vessel on the anatomical images, the separation may not always be possible.
The strength of our study is that we were able to reliably localize the sural nerve using DTI in a significant number of healthy volunteers both men and women. We anticipate that this protocol can be used to evaluate disease-associated changes in the sural nerve in patients with DPN with the overall goal to establish quantitative diffusion indices such as FA and ADC as non-invasive markers of axonal and myelin integrity in the sural and peroneal nerves. Considering that the prevalence of diabetes has reached epidemic proportions and that DPN is the most common diabetes complication, developing a sensitive and reproducible, non-invasive diagnostic tool to monitor disease progression and the response to various therapeutic interventions may have a critical role in preventing multiple comorbidities associated with DPN.
In summary, we have successfully demonstrated that DTI at 3 T can be effectively used to localize the sural nerve at the mid to lower calf level and to measure FA and ADC values in normal healthy volunteers. Measurement of normative values in this study can be potentially used for monitoring disease progression in patients with DPN and with other forms of peripheral neuropathies.
Future studies that include the motion and distortion artifact correction between diffusion images acquired at each direction, effect of b-value, and the choice of the gradient directions could contribute to further improvement of measurement accuracy.
Acknowledgments
This study was supported by Juvenile Diabetes Research Foundation award #1-2008-1025. The authors thank Thomas L. Chenevert, Ph.D. for his contribution in developing the DTI protocol and Susan Lowe for her assistance in data acquisition. The authors also acknowledge the work of Ms. Kathleen Ryan for her assistance in subject recruitment and coordination.
Footnotes
Conflict of Interest: None.
References
- 1.Mori S, Barker PB. Diffusion magnetic resonance imaging: its principle and applications. Anat Rec. 1999;257:102–9. doi: 10.1002/(SICI)1097-0185(19990615)257:3<102::AID-AR7>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 2.Mori S, Van Zijl PC. Fiber tracking: principles and strategies—a technical review. NMR Biomed. 2002;15:468–80. doi: 10.1002/nbm.781. [DOI] [PubMed] [Google Scholar]
- 3.Nucifora PG, Verma R, Lee SK, et al. Diffusion-tensor MR imaging and tractography: exploring brain microstructure and connectivity. Radiology. 2007;245:367–84. doi: 10.1148/radiol.2452060445. [DOI] [PubMed] [Google Scholar]
- 4.Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–19. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- 5.Grant GA, Goodkin R, Maravilla KR, et al. MR neurography: diagnostic utility in the surgical treatment of peripheral nerve disorders. Neuroimaging Clin N Am. 2004;14:115–33. doi: 10.1016/j.nic.2004.02.003. [DOI] [PubMed] [Google Scholar]
- 6.Hiltunen J, Suortti T, Arvela S, et al. Diffusion tensor imaging and tractography of distal peripheral nerves at 3 T. Clin Neurophysiol. 2005;116:2315–23. doi: 10.1016/j.clinph.2005.05.014. [DOI] [PubMed] [Google Scholar]
- 7.Khalil C, Budzik JF, Kermarrec E, et al. Tractography of peripheral nerves and skeletal muscles. Eur J Radiol. 2010;76:391–7. doi: 10.1016/j.ejrad.2010.03.012. [DOI] [PubMed] [Google Scholar]
- 8.Khalil C, Hancart C, Le Thuc V, et al. Diffusion tensor imaging and tractography of the median nerve in carpal tunnel syndrome: preliminary results. Eur Radiol. 2008;18:2283–91. doi: 10.1007/s00330-008-0971-4. [DOI] [PubMed] [Google Scholar]
- 9.Meek MF, Stenekes MW, Hoogduin HM, et al. In vivo three-dimensional reconstruction of human median nerves by diffusion tensor imaging. Exp Neurol. 2006;198:479–82. doi: 10.1016/j.expneurol.2005.12.014. [DOI] [PubMed] [Google Scholar]
- 10.Skorpil M, Karlsson M, Nordell A. Peripheral nerve diffusion tensor imaging. Magn Reson Imaging. 2004;22:743–5. doi: 10.1016/j.mri.2004.01.073. [DOI] [PubMed] [Google Scholar]
- 11.Cauley KA, Filippi CG. Diffusion-tensor imaging of small nerve bundles: cranial nerves, peripheral nerves, distal spinal cord, and lumbar nerve roots—clinical applications. AJR Am J Roentgenol. 2013;201:W326–35. doi: 10.2214/AJR.12.9230. [DOI] [PubMed] [Google Scholar]
- 12.Kabakci N, Gurses B, Firat Z, et al. Diffusion tensor imaging and tractography of median nerve: normative diffusion values. AJR Am J Roentgenol. 2007;189:923–7. doi: 10.2214/AJR.07.2423. [DOI] [PubMed] [Google Scholar]
- 13.Skorpil M, Engstrom M, Nordell A. Diffusion-direction-dependent imaging: a novel MRI approach for peripheral nerve imaging. Magn Reson Imaging. 2007;25:406–11. doi: 10.1016/j.mri.2006.09.017. [DOI] [PubMed] [Google Scholar]
- 14.Tsuchiya K, Fujikawa A, Tateishi H, et al. Visualization of cervical nerve roots and their distal nerve fibers by diffusion-weighted scanning using parallel imaging. Acta Radiol. 2006;47:599–602. doi: 10.1080/02841850600699638. [DOI] [PubMed] [Google Scholar]
- 15.Yao L, Gai N. Median nerve cross-sectional area and MRI diffusion characteristics: normative values at the carpal tunnel. Skeletal Radiol. 2009;38:355–61. doi: 10.1007/s00256-008-0626-1. [DOI] [PubMed] [Google Scholar]
- 16.Andreisek G, White LM, Kassner A, et al. Evaluation of diffusion tensor imaging and fiber tractography of the median nerve: preliminary results on intrasubject variability and precision of measurements. AJR Am J Roentgenol. 2010;194:W65–72. doi: 10.2214/AJR.09.2517. [DOI] [PubMed] [Google Scholar]
- 17.Jones DK. The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: a Monte Carlo study. Magn Reson Med. 2004;51:807–15. doi: 10.1002/mrm.20033. [DOI] [PubMed] [Google Scholar]
- 18.Papadakis NG, Murrills CD, Hall LD, et al. Minimal gradient encoding for robust estimation of diffusion anisotropy. Magn Reson Imaging. 2000;18:671–9. doi: 10.1016/s0730-725x(00)00151-x. [DOI] [PubMed] [Google Scholar]
- 19.Peng H, Arfanakis K. Diffusion tensor encoding schemes optimized for white matter fibers with selected orientations. Magn Reson Imaging. 2007;25:147–53. doi: 10.1016/j.mri.2006.10.013. [DOI] [PubMed] [Google Scholar]
- 20.Hope T, Westlye LT, Bjornerud A. The effect of gradient sampling schemes on diffusion metrics derived from probabilistic analysis and tract-based spatial statistics. Magn Reson Imaging. 2012;30:402–12. doi: 10.1016/j.mri.2011.11.003. [DOI] [PubMed] [Google Scholar]
- 21.Ni H, Kavcic V, Zhu T, et al. Effects of number of diffusion gradient directions on derived diffusion tensor imaging indices in human brain. AJNR Am J Neuroradiol. 2006;27:1776–81. [PMC free article] [PubMed] [Google Scholar]
- 22.Boulton AJ. Diabetic neuropathy: classification, measurement and treatment. Curr Opin Endocrinol Diabetes Obes. 2007;14:141–5. doi: 10.1097/MED.0b013e328014979e. [DOI] [PubMed] [Google Scholar]
- 23.Bonekamp D, Nagae LM, Degaonkar M, et al. Diffusion tensor imaging in children and adolescents: reproducibility, hemispheric, and age-related differences. NeuroImage. 2007;34:733–42. doi: 10.1016/j.neuroimage.2006.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Farrell JA, Landman BA, Jones CK, et al. Effects of signal-to-noise ratio on the accuracy and reproducibility of diffusion tensor imaging-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1. 5 T. J Magn Reson Imaging. 2007;26:756–67. doi: 10.1002/jmri.21053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Landman BA, Farrell JA, Jones CK, et al. Effects of diffusion weighting schemes on the reproducibility of DTI-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1. 5T. NeuroImage. 2007;36:1123–38. doi: 10.1016/j.neuroimage.2007.02.056. [DOI] [PubMed] [Google Scholar]
- 26.Muller MJ, Mazanek M, Weibrich C, et al. Distribution characteristics, reproducibility, and precision of region of interest-based hippocampal diffusion tensor imaging measures. AJNR Am J Neuroradiol. 2006;27:440–6. [PMC free article] [PubMed] [Google Scholar]
- 27.Wakana S, Caprihan A, Panzenboeck MM, et al. Reproducibility of quantitative tractography methods applied to cerebral white matter. NeuroImage. 2007;36:630–44. doi: 10.1016/j.neuroimage.2007.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kim B, Boes JL, Frey KA, et al. Mutual information for automated unwarping of rat brain autoradiographs. NeuroImage. 1997;5:31–40. doi: 10.1006/nimg.1996.0251. [DOI] [PubMed] [Google Scholar]
- 29.Meyer CR, Boes JL, Kim B, et al. Demonstration of accuracy and clinical versatility of mutual information for automatic multimodality image fusion using affine and thin plate spline warped geometric deformations. Med Image Anal. 1997;3:195–206. doi: 10.1016/s1361-8415(97)85010-4. [DOI] [PubMed] [Google Scholar]
- 30.Mojaddidi M, Quattrini C, Tavakoli M, et al. Recent developments in the assessment of efficacy in clinical trials of diabetic neuropathy. Curr Diab Rep. 2005;5:417–22. doi: 10.1007/s11892-005-0048-6. [DOI] [PubMed] [Google Scholar]
- 31.Boulton AJ, Vinik AI, Arezzo JC, et al. Diabetic neuropathies: a statement by the American Diabetes Association. Diabetes Care. 2005;28:956–62. doi: 10.2337/diacare.28.4.956. [DOI] [PubMed] [Google Scholar]
- 32.Vileikyte L, Peyrot M, Bundy C, et al. The development and validation of a neuropathy-and foot ulcer-specific quality of life instrument. Diabetes Care. 2003;26:2549–55. doi: 10.2337/diacare.26.9.2549. [DOI] [PubMed] [Google Scholar]
- 33.Vileikyte L, Rubin RR, Leventhal H. Psychological aspects of diabetic neuropathic foot complications: an overview. Diabetes Metab Res Rev. 2004;20(Suppl 1):S13–8. doi: 10.1002/dmrr.437. [DOI] [PubMed] [Google Scholar]
- 34.Perry JR, Bril V. Complications of sural nerve biopsy in diabetic versus non-diabetic patients. Can J Neurol Sci. 1994;21:34–7. doi: 10.1017/s0317167100048733. [DOI] [PubMed] [Google Scholar]
- 35.Boulton AJ, Valensi P, Tesfaye S. The Diabetic Neuropathies: Reports from the Diabetic Neuropathy Expert Panel Meeting on Neuropathy, Toronto, October 2009: Introduction. Diabetes Metab Res Rev. 2011;27:617–9. doi: 10.1002/dmrr.1228. [DOI] [PubMed] [Google Scholar]
- 36.Dyck PJ, Albers JW, Andersen H, et al. Diabetic polyneuropathies: update on research definition, diagnostic criteria and estimation of severity. Diabetes Metab Res Rev. 2011;27:620–8. doi: 10.1002/dmrr.1226. [DOI] [PubMed] [Google Scholar]
- 37.Malik R, Veves A, Tesfaye S, et al. Small fiber neuropathy: role in the diagnosis of diabetic sensorimotor polyneuropathy. Diabetes Metab Res Rev. 2011;27:678–84. doi: 10.1002/dmrr.1222. [DOI] [PubMed] [Google Scholar]
- 38.Tesfaye S, Vileikyte L, Rayman G, et al. Painful Diabetic Peripheral Neuropathy: Consensus Recommendations on Diagnosis, Assessment and Management. Diabetes Metab Res Rev. 2011;27:629–38. doi: 10.1002/dmrr.1225. [DOI] [PubMed] [Google Scholar]
- 39.Stein D, Neufeld A, Pasternak O, et al. Diffusion tensor imaging of the median nerve in healthy and carpal tunnel syndrome subjects. J Magn Reson Imaging. 2009;29:657–62. doi: 10.1002/jmri.21553. [DOI] [PubMed] [Google Scholar]
- 40.Kakuda T, Fukuda H, Tanitame K, et al. Diffusion tensor imaging of peripheral nerve in patients with chronic inflammatory demyelinating polyradiculoneuropathy: a feasibility study. Neuroradiology. 2011;53:955–60. doi: 10.1007/s00234-010-0833-z. [DOI] [PubMed] [Google Scholar]