Analytic TOF PET reconstruction algorithm within DIRECT data partitioning framework

Abstract

Iterative reconstruction algorithms are routinely used for clinical practice; however, analytic algorithms are relevant candidates for quantitative research studies due to their linear behavior. While iterative algorithms also benefit from the inclusion of accurate data and noise models the widespread use of TOF scanners with less sensitivity to noise and data imperfections make analytic algorithms even more promising. In our previous work we have developed a novel iterative reconstruction approach (Direct Image Reconstruction for TOF) providing convenient TOF data partitioning framework and leading to very efficient reconstructions. In this work we have expanded DIRECT to include an analytic TOF algorithm with confidence weighting incorporating models of both TOF and spatial resolution kernels. Feasibility studies using simulated and measured data demonstrate that analytic-DIRECT with appropriate resolution and regularization filters is able to provide matched bias vs. variance performance to iterative TOF reconstruction with a matched resolution model.

1. Introduction

The TOF capabilities of current state-of-the-art PET scanners have brought clear benefits for the diagnostic image quality of PET studies by facilitating both improved visual and quantitative quality. TOF reconstructions have been shown to provide improved contrast-vs.-noise and bias-vs.-variance tradeoffs, faster convergence, improved lesion detectability and less sensitivity to data-correction and data-model imperfections (Karp et al., 2008; Surti and Karp, 2009; Kadrmas et al., 2009; Lois et al., 2010; Conti, 2011a, b; El Fakhri et al., 2011; Surti et al., 2011; Kadrmas et al., 2012; Daube-Witherspoon et al., 2014). Furthermore, additional (and redundant) information in the TOF data enables formulation of new reconstruction algorithms and data processing procedures (e.g., alternative analytic reconstruction algorithms, simultaneous emission-attenuation reconstruction algorithms, TOF rebinning approaches (Tomitani, 1981; Defrise et al., 2005; Watson, 2008; Cho et al., 2009; Defrise et al., 2012; Defrise et al., 2013; Li et al., 2015b; Li et al., 2016)) and also provides novel ways of handling the data and implementing reconstruction procedures. Taking advantage of this, we developed in our previous work a new TOF data-partitioning scheme - DIRECT (Direct Image Reconstruction for TOF) (Matej et al., 2009) - and implemented and evaluated TOF iterative reconstruction approaches within it. The iterative-DIRECT approach was demonstrated to provide comparable reconstruction quality to a TOF list-mode approach (for the same algorithms and resolution models) but with substantially shorter reconstruction times (Matej et al., 2009; Daube-Witherspoon et al., 2012). In this paper we have extended the DIRECT approach to include an analytic TOF algorithm.

Although statistical (iterative) reconstruction approaches are now used routinely in clinical practice, analytic algorithms have their place due to their linearity and predictable behavior. The disadvantages of classical (non-TOF) analytic techniques are increased noise levels and the lack of resolution modelling as compared to statistical algorithms. For studies involving limited count scans (as may be encountered with new tracers and multi-frame dynamic studies) and for very small structures, both of these issues can pose challenges for the precision (due to noise) and accuracy (due to partial volume effects) of non-TOF analytic reconstructions. To address these issues we have developed a TOF analytic algorithm within the DIRECT framework with carefully designed reconstruction and resolution filters.

Analytic TOF algorithms were originally proposed by Tomitani, Snyder, and others (Tomitani, 1981; Snyder et al., 1981; Philippe et al., 1982; Mallon and Grangeat, 1992) in the early days of TOF PET. As the use of TOF PET receded in the late 1980s and as iterative approaches became routine clinical tools due to their improved contrast-vs.-noise trade-offs and better visual quality, analytic (non-TOF) algorithms have lately been used only for specialized quantitative studies and as a gold standard for comparative studies evaluating the biases of reconstruction approaches (Blinder et al., 2012; Reilhac et al., 2008; van Velden et al., 2008; Badawi et al., 1999; van Velden et al., 2009; Verhaeghe et al., 2010; Walker et al., 2011; Walker et al., 2012); analytic reconstructions are also used for intrinsic spatial resolution characterization of PET scanners (NEMA Standards Publication NU 2-2001NEMA Standards Publication NU 2-2001). With the renewed interest in TOF PET, analytic TOF methods have been revisited, and several algorithms have been studied (Cho et al., 2008; Conti et al., 2005; Kao, 2008; Watson, 2007), with improved noise characteristics reported (Watson, 2007, 2008). These results suggest that TOF analytic algorithms can become more competitive with iterative algorithms as the TOF resolution improves (Westerwoudt et al., 2014). We have gone beyond those investigations to develop and evaluate an analytic (confidence-weighted) TOF algorithm that includes spatial resolution filters. This new algorithm is implemented in a unified manner within the DIRECT framework, which allows a straightforward and fair comparison with the iterative-DIRECT approach.

In Section 2 we give an overview of the basic principles and features of the DIRECT partitioning scheme and reconstruction. In Section 3 we describe the analytic-DIRECT algorithm and its implementation. Sections 4 and 5 contain methods and results of analytic-DIRECT evaluations and comparisons to iterative-DIRECT, using simulated and physical phantoms as well as patient data, followed by discussion and conclusions.

2. DIRECT framework

2.1. DIRECT data partitioning

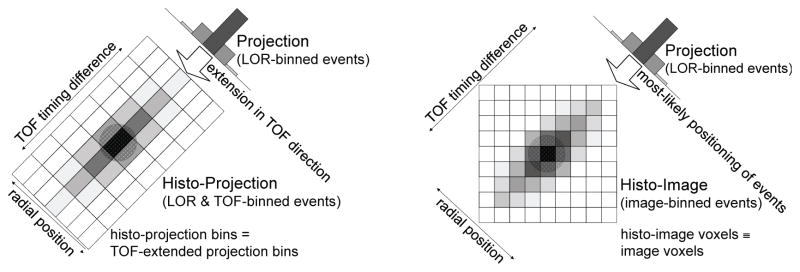
The DIRECT approach is based on image-like partitioning of the data, which involves two steps: the acquired events are (1) sorted into a limited set of “views” according to the TOF angular sampling requirements (Politte et al., 1986; Vandenberghe et al., 2006) and (2) histogrammed into a set of “histo-images” (one histo-image per view). For TOF resolutions currently achieved in practice the number of views needed is substantially reduced (typically by an order of magnitude), as compared to non-TOF data (Matej et al., 2009; Daube-Witherspoon et al., 2012). Traditionally, binned TOF events are histogrammed into “histo-projections” (projections extended in the TOF direction, as illustrated in figure 1-left). In the DIRECT approach, the acquired events are deposited directly into the “most-likely” voxels of the histo-images (figure 1-right). Histo-images are defined by the geometry and desired sampling (voxel size) of the reconstructed image. Both acquired events and correction factors are placed into the voxels of their respective histo-images (see examples in figures 2 and 3), which have a one-to-one correspondence with the reconstructed image voxels.

Figure 1.

Comparison of TOF data partitioning (for 2D case) for one angle binned into histo-projections (left) or into histo-images with the DIRECT approach (right). Histo-projections can be described as an extension of non-TOF projections (radial bins) along the TOF direction (time bins); the sampling intervals relate to the projection geometry and TOF resolution, while histo-image sampling is given by the voxel geometry of the reconstructed image. (This figure was reproduced from (Nuyts and Matej, 2015) (Figure 13.13) with permission by the IAEA.)

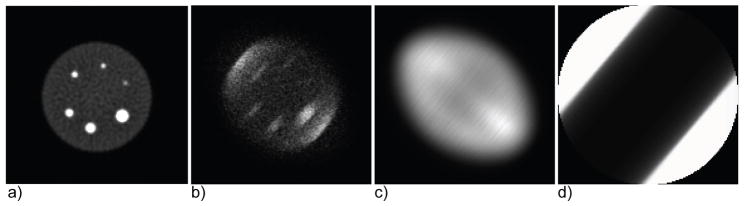
Figure 2.

Example of histo-image data structures in DIRECT for a simulated 35-cm cylindrical phantom with hot spheres – both the reconstructed image and data (histo-images) have the same image dimensions and voxels of the same size with one-to-one correspondence between images and histo-images: (a) reconstructed image, (b) prompts (trues+scatter for tilt 0 and transverse angle 50°), (c) estimated scatters, and (d) sensitivity and attenuation factors. Corresponding slices of 3D image/histo-images are shown, each scaled to its maximum and cropped out of the circular FOV. Note that the attenuation factors are approximately constant along the view direction (along the LORs) while they change dramatically in the perpendicular direction (decreasing down to about 0.035 for the central LORs).

Figure 3.

Measured data and multiplicative corrections in the histo-image format for a 35-cm cylindrical phantom showing the effect of gaps between detector modules (central slices for 2 transverse views out of 40 are shown, each scaled to its maximum, and cropped out of FOV): (a) prompts, (b) detector sensitivity factors (reflecting gaps and LOR sensitivity), (c) attenuation factors, and (d) corrected prompts. The data are from the University of Pennsylvania research (La-PET) TOF-PET system (Daube-Witherspoon et al., 2010), which has 24 detector modules with gaps between modules, each approximately 8 mm wide. Because of the grouping of angles, gaps do not show up as solid dark bands of zero value at regular intervals but as regions of variable, decreased intensity. In this example, the prompts histo-images were simplistically corrected for the gaps by dividing them by the corresponding histo-images with the sensitivity and attenuation factors, thereby providing accurate mean values but also increased noise in the gap regions.

Various deposition strategies are possible (e.g., an event is assigned with different weights to neighboring voxels), and the effect of the deposition operation can be efficiently modeled in the forward- and back-projectors during reconstruction. A deposition operation based on nearest-neighbor interpolation is similar to the one in the “most-likely-position” reconstruction technique (Snyder et al.). Deposition using more accurate interpolation kernels better preserves information about the positions of individual events and in this work we have employed a tri-linear interpolation kernel. Unlike conventional histo-projections, the histo-image format allows for efficient computation (and memory utilization) during reconstruction without repeated ray-tracing or interpolations during iterative reconstruction because the same structure is used for both data and images as well as for the corrections for physical effects. The angular sampling approximations are the same for histo-images and histo-projections, but because there are no further interpolation steps between image and data spaces, the histo-image format leads to faster reconstruction speeds without affecting resolution during forward and back-projections.

2.2. Forward- and back-projection operations in DIRECT

Forward-projection (for iterative reconstruction) is implemented within the histo-image format via a simple 3D convolution-like operation applied to the current estimate of the image using a specific kernel for each view. Each kernel has an ellipsoidal shape elongated along the view direction, as given by TOF resolution, detector (line of response, LOR) point-spread function, and other resolution effects. Back-projection is simply the transpose of forward-projection. For spatially invariant detector resolution kernels, very fast forward/back-projection operations can be implemented within DIRECT using Fourier-based approaches (Matej et al., 2009). For spatially variant and asymmetric kernels, a parallel implementation of the forward- and back-projection operations has been implemented on a graphical processing unit (GPU) (Ha et al., 2013). Recently we have also implemented and tested modelling of asymmetric point spread function deformation effects (for a dual-panel PET application) using image-based resolution models implemented within the DIRECT reconstruction (Matej et al., 2015).

2.3. Data corrections in DIRECT

Estimates of the additive contamination data (scatter and randoms) and multiplicative factors (attenuation, crystal sensitivity, and detector geometric sensitivity including gap effects) can be efficiently computed in histo-image space (see examples in figure 2 for simulated gapless data and in figure 3 for measured data with gaps between detector modules). The correction data in histo-image format are then straightforwardly applied to the deposited prompts voxel by voxel by subtracting additive terms and dividing by multiplicative factors for pre-correction in the analytic algorithm or are applied to the forward-projected estimated histo-images in iterative reconstruction.

2.3.1. Attenuation, normalization, and geometric sensitivity factors

Attenuation, normalization, and geometric sensitivity factors in histo-image format (including gap effects between detector modules) are efficiently generated by Fourier-based back-projection using the 3D projection slice theorem of their uniformly spaced LOR values into individual histo-images (Matej et al., 2009). For each histo-image view a range of sufficiently up-sampled (angularly and radially) LORs are back-projected, such as to accurately capture gap and attenuation structures. An alternative approach would be to back-project the individual attenuation and sensitivity factors into the correction histo-images along all actual scanner LORs (similar to the deposition of the prompts, but spreading them along the whole LOR instead of placing them into a single maximum-likely position). Although this second approach is more straightforward, it is computationally more expensive than the Fourier-based approach. Unlike the activity whose locations along the LORs are limited by the TOF resolution, the attenuation, normalization, and geometric sensitivity factors are spread along the whole LORs used for each view-grouped histo-image. Because of the view grouping these structures are not exactly constant along the view direction for each histo-image view, but they do change very slowly along that direction, depending on the number of views used – see examples in figures 2 and 3. Grouping more angles into fewer views leads to more variation along the view direction.

2.3.2. Detector geometry factors – corrections for gaps between the detector modules

In uncorrected LOR-based projections, there are abrupt undefined regions between the detector modules with no counts (Tuna et al., 2014). However, in histo-image format, due to the view-grouping the values in gap-affected regions change gradually and are non-zero (see figure 3-b). In iterative maximum-likelihood reconstructions that model the sensitivity within the forward-projection, the less reliable data in the gaps are updated with lower weights, so the image noise does not increase. On the other hand, for analytic approaches that use pre-corrected data, the noise in gaps can increase, as illustrated in figure 3-d. We implemented and show results for a simple correction for the detector gaps, where the shape of the histo-image gap sensitivity function is accurately pre-determined for given scanner and histo-image geometries. Direct correction through simple division by the gap sensitivity function provides gap-less histo-images with accurate values in the gaps for noiseless data. However, for limited count data, the noise is amplified in the gap regions. A more advanced procedure would be to: (1) apply the simple gap correction from above, (2) smooth the gap-corrected histo-images using 3-D low-pass filters adjusted/optimized for the count level in the acquired data, and (3) add their weighted values to the original histo-images (before gap-correction), where the weights are equal to one minus the gap-sensitivity function values, thus adding the smoothed estimates of the missing counts to the gap regions. This approach would provide uniform noise across the gap regions, but at a possible cost of having less accurate data structures within the gaps due to the contribution of the smoothed data.

2.3.3. Detector geometry factors – corrections for axial sensitivity and missing data in oblique (co-polar) views

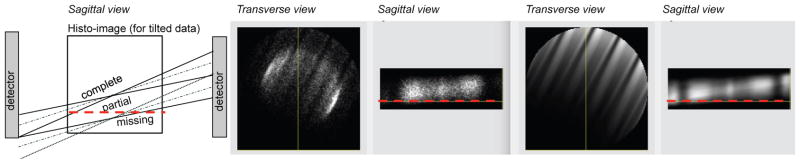
Because of the limited axial extent and limited axial acceptance angle of scanners in conjunction with axial view-grouping, the number of counts in the histo-images decrease from the center of the scanner to the axial ends. If the data are view-grouped into a single axial tilt, there are no missing axial regions in the histo-images and the axial decease of the sensitivity can be modelled and corrected by the techniques described above. However, depending on the axial acceptance angle and TOF resolution, events might need to be sorted into several oblique angles to provide sufficient angular sampling (typically into three tilts for a realistic PET scanner if a full axial acceptance angle range is used (Matej et al., 2009; Daube-Witherspoon et al., 2012)). In that case, histo-images for the oblique tilts will have undefined (missing) data regions due to the limited axial extent of the scanner.

Missing data can be estimated, similar to the 3D reprojection (3D-RP) and 3D Fourier reprojection (3D-FRP) techniques (Kinahan and Rogers, 1989; Matej and Lewitt, 2001), by forward-projecting in DIRECT 3D images initially reconstructed from non-tilted data or by inverse rebinning techniques (Cho et al., 2007; Li et al., 2016). In histo-image format, the axial data gradually decrease to missing regions (see figure 4), and similar techniques as described for the data with gaps (Section 2.3.2) can be employed to gradually fill in and combine tilted deposited data containing missing axial regions with the forward-projected data. In this work, the axial acceptance angle was restricted so one tilt provided sufficient angular sampling.

Figure 4.

(Left) Schematic illustrating the gradual decrease of values in the axial direction into “missing” axial data regions. (Middle and right) Measured data for a 35-cm cylindrical phantom in the histo-image format (transverse and sagittal slices) - example of the axially oblique data: (middle) prompts and (right) sensitivity factors.

2.3.4. Scatter

Scatter estimates are obtained by depositing scatter values from all individual LORs of the given system, using the scatter (subsampled) LOR look-up-tables from the TOF-modified single scatter simulation (TOF-SSS) method (Werner et al., 2006). This approach provides consistency with the deposited prompts, including gap and detector geometric sensitivity structures, but it has lower efficiency since all LORs have to be visited during the scatter deposition. A more efficient option to be explored in the future is to modify TOF-SSS to generate the scatter estimate directly in histo-image format. An additional advantage of this approach would be that the scatter tail fitting procedure can be applied more effectively (and with less sensitivity to noise) to a larger histo-image background region compared to the tail fitting that is done in the projection domain in standard TOF-SSS.

2.3.5. Randoms

Randoms estimates are obtained by depositing acquired events from the delayed coincidence window (delays). For variance reduction, the deposited events are smoothed using the following procedure. Delays histo-images (containing gap and sensitivity structures, similar to prompts) are first smoothed with a 3D low-pass filter and corrected for the smoothed gap structures by division with the smoothed sensitivity image, after which the original gap and sensitivity structures (shown in figure 3-b) are reintroduced to the final randoms estimate to provide consistent structures and levels with the random events present in the deposited prompts. In the smoothing procedures, the total counts are preserved.

2.4. Reconstruction within DIRECT approach

Any iterative (e.g., maximum-likelihood expectation-maximization algorithm – ML-EM (Shepp and Vardi, 1982), ordered-subset ML-EM – OSEM (Hudson and Larkin, 1994), row-action maximum-likelihood algorithm – RAMLA (De Pierro, 1989; Browne and De Pierro, 1996), maximum a posteriori algorithm – MAP (Qi et al., 1998; Leahy and Qi, 2000)) or analytic TOF algorithm can be efficiently implemented within the DIRECT framework with all reconstruction and correction operations easily applied within the image-space partitions (see flowchart in figure 5) (Matej et al., 2009). In our previous work we have implemented both RAMLA and OSEM within DIRECT and compared their performance to standard list-mode reconstructions for simulated and measured data (Daube-Witherspoon et al., 2012). Our studies confirmed that DIRECT corrections and reconstructions could handle the emission, attenuation, and sensitivity (detector and detector gaps related) structures accurately. The same (or similar) basic tools and correction data and approaches can also be utilized for analytic reconstruction, as discussed in the next section.

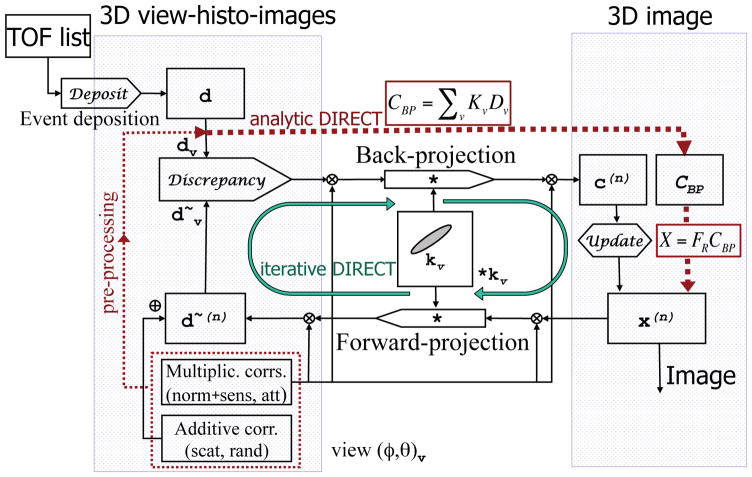
Figure 5.

Flowchart summarizing DIRECT corrections, reconstruction paths and data structures. Both iterative (green solid line loop) and analytic algorithms (red dotted line) use the same data/correction structures (histo-images) and basic reconstruction tools (DIRECT forward/back-projectors). Each 3D view-grouped histo-image contains all events from a given “view” (ϕ, θ)_v (comprising a range of azimuthal and co-polar angles). All data and corrections are in the same histo-image format. Forward- and back-projections are 3D convolution-like operations involving the proper 3D TOF resolution kernel k_v (taking into account TOF, detector, and image resolution functions) for each view v. Discrepancy and Update operators are specifically defined by each particular algorithm; for example, $d_v/d_v^{~(n)}$ and x^{(n + 1)} = c^(x) x^(x), respectively, for ML-EM algorithm, where d_v are measured data, $d_v^{~(n)}$ are forward-projected data estimates (including corrections) from image x⁽ⁿ⁾ at iteration n, and c⁽ⁿ⁾ is the correction image at iteration n derived from the back-projection of the discrepancy operator. Back-projection (C_BP) and reconstruction filter (F_RC_BP) operations for analytic-DIRECT are shown in spectral forms (see details in 3.1).

2.5. Main characteristics and benefits of DIRECT approach

The DIRECT approach using histo-image data partitioning has a number of positive characteristics and advantages:

• The histo-image coordinate system parameterization provides compact derivations without the need for coordinate transformations (e.g., during forward- and back-projection operations) and straightforward implementations of both iterative and analytic reconstruction algorithms, as well as novel reconstruction approaches (such as attenuation estimations from TOF PET data using histo-image-based consistency equations (Defrise et al., 2015; Li et al., 2015a, b)).

• Histo-images offer a natural data format, which is driven by the reconstructed image geometry, with events directly stored into the desired resolution units - voxels of the desired size - thus not compromising resolution due to projection binning.

• No (repeated) ray-tracing or interpolation steps between the data/projection and image spaces are needed within the forward/back-projectors in iterative reconstructions, which would affect their speed and resolution models, see 2.1. Although one can take interpolation effects into account through the resolution model, it would complicate the forward- and back-projection tools for histo-projection methods, while it is very simple, fast, and straightforward in the DIRECT approach.

• The data and corrections (measured events, scatter and randoms estimates, and attenuation and normalization factors) and image have the same geometry and structures, providing intuitive representations of data, correction, and image in the same space and very efficient reconstruction (forward/back-projection) operations.

• The very fast speed of DIRECT approach makes it practical to use more iterations within reconstruction and data correction procedures, thus leading to more accurate data correction and modelling procedures (e.g., allowing iterative reconstructions with detector resolution modelling or iterative scatter estimation procedures to run to convergence) without compromising practical clinical performance.

3. Analytic-DIRECT Reconstruction

3.1. Analytic TOF confidence-weighted algorithm

In the spectral domain, the TOF data D_v(ω⃗) for a particular azimuthal and co-polar view (ϕ, θ)_v can be described as the image X(ω⃗) blurred with the TOF resolution kernel K_v(ω⃗):

$$D_v(\overrightarrow{\omega })=K_v(\overrightarrow{\omega })X(\overrightarrow{\omega }).$$ (1)

For perfect noiseless data and a reasonable TOF resolution, the image estimate X̂(ω⃗) could be directly obtained from this equation for any given view. However for practical noisy data, reconstruction of the image estimate X̂(ω⃗) should take into account selectively weighted data information from all available views, as given by the analytic reconstruction formula:

$$\widehat{X}(\overrightarrow{\omega })=\int H_v(\overrightarrow{\omega })D_v(\overrightarrow{\omega })\mathrm{d}v,$$ (2)

where

$$H_v(\overrightarrow{\omega })=\frac{W_v(\overrightarrow{\omega })R(\overrightarrow{\omega })}{\int W_v(\overrightarrow{\omega })K_v(\overrightarrow{\omega })\mathrm{d}v}$$ (3)

is a reconstruction filter for view v (with azimuthal and co-polar angle (ϕ, θ)_v). Integrations are performed over views with dv being the integration variable in (2 and 3), W_v(ω⃗) is a weighting function/filter that controls how the corresponding spectral components from individual views are summed together, R(ω⃗) is an optional regularization filter, and the denominator is given by the inverse reconstruction operator (analogous to the Ramp filter in filtered back-projection). For the weighting function, a confidence-weighting filter based on the TOF resolution function (i.e., W_v(ω⃗) = K_v(ω⃗)) has been advocated to provide good (close to optimal) noise suppression properties (Watson, 2008).

For a discrete number of views and for the confidence-weighting filters, we can write the reconstruction as:

$$\widehat{X}(\overrightarrow{\omega })=F_R(\overrightarrow{\omega })C_{BP}(\overrightarrow{\omega })$$ (4)

where

$$C_{BP}(\overrightarrow{\omega })={\sum }_v{K}_v(\overrightarrow{\omega })D_v(\overrightarrow{\omega })$$ (5)

is the discrete confidence-weighted back-projection, and

$$F_R(\overrightarrow{\omega })=\frac{R(\overrightarrow{\omega })}{{\sum }_v{K}_v^2(\overrightarrow{\omega })}$$ (6)

is the reconstruction and regularization filter. In our work we have expanded the usual TOF-based kernels (K_v and W_v) in the confidence-weighted algorithm by also including a detector (LOR) resolution function (spatially invariant approximation of the detector PSF), giving an ellipsoid-shaped kernel with the long axis given by the TOF resolution and short axes given by the LOR radial and axial resolutions; this LOR kernel provides spatially invariant resolution recovery in the analytic-DIRECT algorithm.

3.2. Reconstruction steps within analytic-DIRECT

A flowchart of both iterative and analytic reconstructions within the DIRECT approach is shown schematically in figure 5. This section describes the analytic-DIRECT implementation.

1. Event deposition: List-mode events are first view-grouped and deposited into the most-likely positions in a set of histo-images d as in iterative-DIRECT.

2. Data corrections: As required for analytic reconstruction, data are pre-corrected by the detector efficiency and attenuation factors during the deposition; the deposited histo-images are then corrected for the rest of the data imperfection effects including geometric sensitivity, detector gap structures, axial missing regions in oblique data, and scatter and random events.

3. Confidence-weighted back-projection: The corrected data (d_v) are back-projected using confidence-weighted back-projection (C_BP). Fourier-based principles and the histo-image format allow very efficient implementation of the back-projection operation (similar to iterative-DIRECT). Since the histo-images have the same grid as the reconstructed image, no interpolation and spectral density weighting are required during the back-projection. The interpolation and weighting for spectral raster densities in traditional Fourier-based reconstructions are crucial operations affecting their efficiency and quality; avoiding these operations within the DIRECT approach represents a major advantage.

4. Reconstruction filtering: The image X is formed by filtering the back-projected image with the reconstruction filter F_R(ω⃗) (including regularization R(ω⃗)) in the Fourier domain. Generation of the reconstruction filter is correspondingly simple and very efficient. The denominator term of the filter formula is merely a DIRECT back-projection operation over all views v of the squared values of the data kernels (i.e., $K_v^2(\overrightarrow{\omega })$). The final image is obtained as the inverse Fourier transform of X.

4. Methods

To test and show feasibility of the proposed analytic-DIRECT approach, we have implemented and tested its basic version and compared its performance using quantitative measures with the iterative approach within the unified DIRECT framework. Our tests were done both for idealized simulated data with perfect knowledge of truth, and using measured PET phantom and patient with all data imperfections/contaminations of a typical clinical PET scanner, but for a restricted axial acceptance angle.

4.1. Simulated data

Whole body TOF data were simulated using Monte Carlo EGS4 software (Adam et al., 1999) for a scanner with a 25-cm axial field of view (FOV), continuous distribution of crystals (4.3×4.3×30 mm³) on a cylindrical detector surface (84.3-cm ring diameter with 58 rings, 57.6-cm transverse reconstruction FOV) with no gaps, 5.8-mm detector (LOR) resolution, and 300-ps TOF resolution. This simulated scanner is based on the University of Pennsylvania research (La-PET) TOF-PET system (Daube-Witherspoon et al. 2010). The simulated phantom was a 27-cm diameter cylinder with hot spherical lesions in two different slices with respect to the scanner center. The central slice contained three sets each of 10, 13, 17, and 22-mm diameter spheres at a radius of 6.25 cm (shown in figure 8). An off-center slice one-quarter of the axial FOV from the center contained eight 10-mm diameter spheres uniformly distributed at a radius of 6.25-cm. The activity uptake ratio for the hot spheres was 4:1 with respect to the background. Simulated data included attenuation effects of the uniform water cylinder but not scatter or random events.

Figure 8.

Central slices of DIRECT reconstructions of 16M-count simulated phantom: Top: iterative RAMLA (a) without RM (near convergence), (b) with RM stopped before convergence – at similar bias and variability (and MSE) levels to non-RM case, and (c) with RM near convergence; Bottom: analytic (d) without RM, (e) with RM and filtering to control noise at similar bias, variability, and MSE to the non-RM case, and (f) with RM and without post-filtering. Each pair of images (top-bottom) has similar bias/variance trade-offs indicated in figure 7 (top-left) by area I for images (a, b, d, e) and by area II for images (c, f).

We generated list-mode data with 64M counts for an axial acceptance angle limited to ±4 degrees. All counts were distributed into ensembles three different ways: 4 data sets with 16M counts each, 16 sets with 4M counts, and 64 sets with 1M counts. This gave us 12 (3×4), 48 (3×16), and 192 (3×64) sphere realizations (for 16M, 4M, and 1M cases) for each sphere size in the central slice and 32 (8×4), 128 (8×16), and 512 (8×64) realizations (for 16M, 4M, and 1M cases) of 10-mm spheres in the off-center slice. List-mode events for each set were view-grouped into 40 azimuthal angles and 1 co-polar angle (tilt) and deposited into histo-images (144×144×62 with 4-mm³ voxels).

4.2. Measured physical phantom data

The NEMA image quality phantom with six (10, 13, 17, 22, 28, 37 mm) spheres with 9.7:1 sphere:background activity ratio and a cold “lung” insert was scanned on the Philips Gemini TF Big Bore PET/CT scanner with 575-ps TOF resolution. Ten 3-min scans were performed, giving us 10 realizations, each with about 12M prompts, 1.2M delays, and a 27% scatter fraction. Randoms were estimated from delays and smoothed after deposition into histo-images. Scatter was estimated in the histo-image format by depositing scatter estimates obtained from SSS-TOF. The simple gap-correction technique (as illustrated in figure 3) was employed in this study. The axial acceptance angle was limited to ±7 degrees (limiting the counts deposited into the histo-images to about 9M prompts per realization). Consistent with the simulation study, events were grouped into 1 tilt and 40 azimuthal views and deposited into histo-images with 4-mm³ voxels.

4.3. Patient data

DIRECT reconstructions were also tested and compared using a whole-body patient study acquired on our clinical Philips Gemini TF PET/CT scanner. The subject had a BMI of 26, and 90-s scans per bed position were performed one hour post-injection of 15-mCi (555 MBq) of [F-18]-fluorodeoxyglucose. List-mode data from separately acquired 10-mm spheres scanned in air were merged with the patient’s data to create emulated lesions with a standardized uptake value (SUV) of 10. Six spheres were inserted into the liver and lung for a total of 12 emulated lesions (El Fakhri et al., 2011; Surti et al., 2011; Daube-Witherspoon et al., 2014). Separate reconstructions were performed for each frame, and the reconstructed images were then combined together post-reconstruction. Each acquired frame data contained on average 48M prompts, 26M delays, and a 37% scatter fraction. The axial acceptance angle of the used data was limited to ±7 degrees, limiting the number of the used prompts to about 29M per frame with approximately 8M true counts per frame. The list-mode data (prompts and delays) were deposited into histo-images, and correction data were generated using the same histo-image geometry and parameters as for the measured phantom.

4.4. Reconstructions

Analytic-DIRECT and iterative DIRECT-RAMLA (Matej et al., 2009) reconstructions were compared using the same histo-image data and resolution models. As noted above, for analytic-DIRECT the histo-images were pre-corrected for physical effects. For iterative-DIRECT the corrections were applied directly within the iterative reconstruction, as indicated in the flowchart in figure 5. Both algorithms were run without and with detector resolution models (RM). For the cases with no RM we did not use any resolution models for the simulated data; for the measured data, a 4-mm FWHM Gaussian LOR kernel was used to model just the crystal size. For the cases with RM we used a 6-mm FWHM Gaussian kernel to model detector blurring effects. To vary bias-vs.-variance tradeoffs, the analytic-DIRECT reconstruction was regularized using smooth apodizing filters (R(ω⃗)) of variable width (cut-off frequency). Note that in a linear analytic algorithm this is equivalent to performing post-filtering with the same filter (as done in our studies using measured data). RAMLA reconstructions were regularized either by varying the number of iterations (for simulated data) or by post-filtering the converged reconstruction (50 RAMLA iterations) using the same apodizing filters as for the analytic-DIRECT (for measured data).

4.5. Measures

We evaluated the quantitative performance of the reconstruction using the normalized bias (bias_s) and variability (std_s) of the sphere relative uptake value (m_s = v_s/b_s), where v_s is the mean sphere uptake value within ROIs (simulated data) or VOIs (measured data) of the same size (diameter s) as the physical diameter of the sphere and b_s is the local background value of the given sphere. For each count level and sphere size, the bias and variability measures were calculated over all sphere realizations (N_s) (within phantom and across data realizations). The bias was calculated as:

$${\text{bias}}_s=\frac{1}{N_s}\sum _{i=1}^{N_s}\frac{m_{s,i}-a_s}{a_s},$$ (7)

where a_s is the known sphere:background ratio of the simulated or inserted sphere. The variability was calculated as the standard deviation (std) of the normalized biases of the individual spheres:

$${\text{std}}_s=\sqrt{\frac{1}{N_s-1}\sum _{i=1}^{N_s}\frac{{(m_{s,i}-\overline{m_s})}^2}{a_s^2}},$$ (8)

We also report for each sphere size the Mean Squared Error (MSE), which provides an objective metric balancing the bias and variability measures:

$${\text{MSE}}_s={\text{bias}}_s^2+{\text{std}}_s^2.$$ (9)

5. Results

5.1. Simulated data

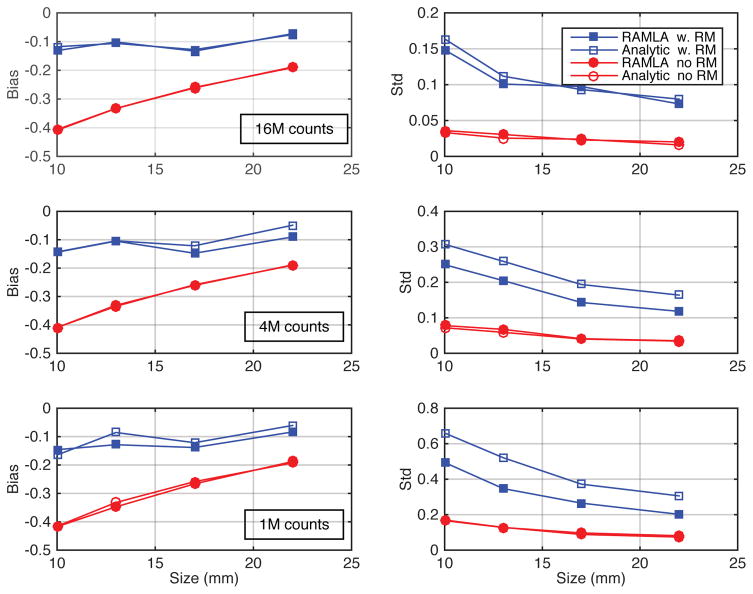
Figure 6 shows the plots of the biases and standard deviations of mean uptake values as functions of spheres size for the iterative- (RAMLA) and analytic-DIRECT reconstructions with and without resolution models and for various count levels (1M, 4M and 16M counts). There was no regularization (post-filtering) employed for these results to minimize biases, and RAMLA was run close to convergence. Both reconstructions show very similar biases for all sphere sizes and count levels for matched resolution models (i.e., with and without RM). The standard deviations are similar in both reconstructions for typical clinical count levels, as shown in the plots for the 16M true events at the top. However for the lower count levels (4M and 1M cases), the standard deviations are higher in the un-regularized analytic-DIRECT with resolution modelling compared with iterative-DIRECT. For practical applications some level of regularization might be needed (depending on the noise levels and task) to optimize the noise versus bias trade-offs.

Figure 6.

Bias and standard deviation of relative uptake values as a function of sphere diameter for the 10, 13, 17 and 22-mm spheres (in the central slice of the simulated phantom) for analytic-DIRECT and iterative-DIRECT reconstructions, both with and without resolution models (RM), at 3 different count levels (top: 16M, middle: 4M, and bottom: 1M counts). Results are shown for the converged iterative-DIRECT (RAMLA) reconstructions and for analytic-DIRECT without regularization/filtering. The bias is the fractional discrepancy between the reconstructed and true relative uptake values. Analytic and iterative reconstructions without RM show closely overlapping bias and standard deviation curves, while with RM the curves differ slightly due to the differences in noise handling in statistical and analytic algorithms, which are amplified by RM.

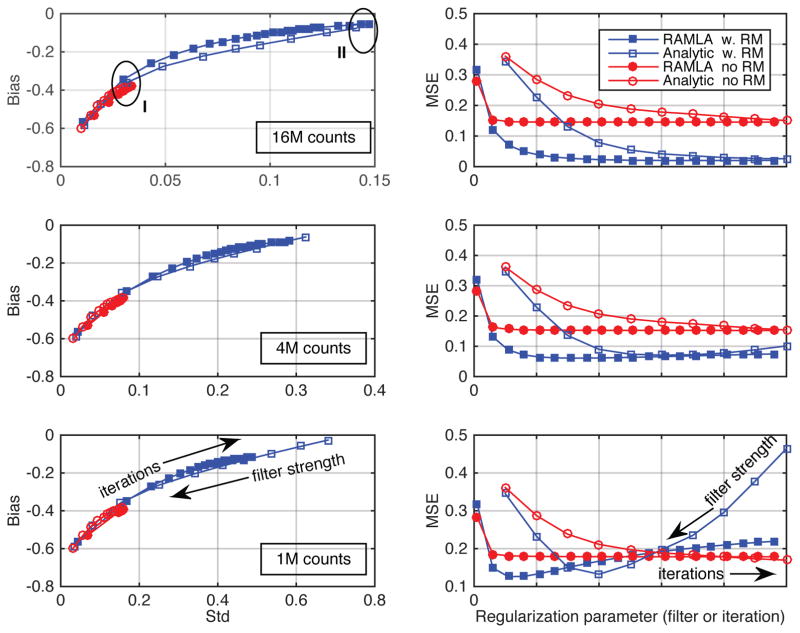
We investigated how regularization affects the comparisons of the analytic- and iterative-DIRECT algorithms by using cosine filters with varying widths for analytic-DIRECT reconstructions and by varying the number of iterations for iterative-DIRECT. Figure 7 illustrates bias-vs.-std trade-offs (left) and MSE behaviours (right) for analytic and iterative reconstructions over a range of regularization parameters for the axially off-center 10-mm spheres at the 3 count levels. It can be clearly seen (consistent with the literature (Daube-Witherspoon et al., 2011; Rapisarda et al., 2010; Rahmim et al., 2013)) that while the reconstructions with RM are able to achieve a very low/no bias, they also show higher standard deviation values at convergence and without regularization; furthermore, iterative reconstructions require substantially more iterations to converge as compared to reconstructions without RM. When optimizing the MSEs the optimum regularization parameters will trade some of the achieved accuracy (minimum bias) for the improvement in precision (decreased standard deviation), especially for low count data. These trade-offs are more sensitive to the regularization parameter values as the counts in the data decrease (as seen in the MSE plots for low counts), and careful attention has to be paid to their optimization for specific applications with low count data. Nevertheless, our results show that although the curve shapes and the locations of the minimum values of the MSEs change for different count levels, analytic- and iterative-DIRECT TOF reconstructions provide similar bias-vs.-variability tradeoffs and similar minimum MSE values, both with and without resolution modelling, for all noise levels studied.

Figure 7.

Comparisons of the (left) bias and standard deviation of mean uptake values and (right) their MSEs for 10-mm spheres located axially ¼ off-center in the simulated phantom for analytic- and iterative-DIRECT, both with and without resolution models (RM). SUV bias-vs.-std results and MSE values are shown for variable levels of regularization using spectral apodizing (Cosine) filters of various strengths (with the cut-off parameter increasing from (left) 0.4 times the Nyquist frequency to (right) no filtering) for analytic-DIRECT and various iteration numbers (5–100, from left to right) for iterative-DIRECT for 16M, 4M, and 1M counts (top to bottom). Areas I and II in the top-left plot correspond to images illustrated in figure 8.

Figure 8 shows examples of pairs of images reconstructed by iterative (RAMLA) (top row) and analytic (bottom row) DIRECT reconstructions using matched resolution models and bias-vs.-std tradeoffs for the 16M counts case. Images in the left and right columns show reconstructions without regularization thus providing the lowest possible biases for the reconstructions without (left) and with (right) resolution modelling (indicated by the areas I and II, respectively, on the individual bias-vs.-variability trade-off curves in figure 7-top-left for each of the four reconstructions). Images in the middle column show examples of reconstructions with RM that were regularized by stopping early in RAMLA and by filtering in analytic-DIRECT to provide similar bias to the no-RM reconstruction. These reconstructions are represented by the points on the RAMLA and iterative RM curves (region I in figure 7-top-left), which are closest to the end points of the respective no-RM curves. Although the matched iterative and analytic reconstructions have slightly different visual appearance (such as the differences in the noise structures and correlations), they show comparable quantitative performance. Here we have not tried to find optimum regularization parameters but rather chosen parameters to illustrate that the analytic-DIRECT algorithm is able to provide similar trade-offs to iterative-DIRECT for data with good TOF resolution. Our results demonstrate the ability of analytic-DIRECT to properly include resolution kernels within the reconstruction and to achieve comparable bias-vs.-variability trade-offs to iterative-DIRECT TOF reconstruction for the same resolution models, as well as similar visual quality at matched bias-variance levels.

5.2. Measured data

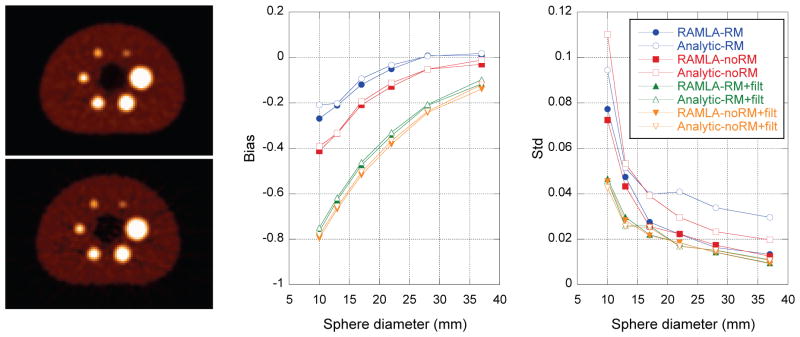
For the studies using measured data the analytic- and iterative-DIRECT reconstructions with matched resolution models were compared using the same regularization approaches. Iterative RAMLA reconstructions were run for 50 iterations to reach convergence, and both (converged) iterative- and (non-regularized) analytic-DIRECT reconstructions were then post-filtered using the same apodizing filters to guarantee matched levels of regularization.

Results for the physical NEMA phantom using analytic- and iterative-DIRECT reconstructions with matched resolution models and regularization levels are illustrated in figure 9. Figure 9-left shows (top) iterative- and (bottom) analytic-DIRECT reconstructions with no RM (modelling only the crystal width), regularized using the same post-filter (Hann window with a cutoff at 0.8 times the Nyquist frequency). Corresponding reconstructions with RM exhibited similar visual comparison between iterative- and analytic-DIRECT. Figure 9-middle and right shows measures of sphere bias and standard deviation as functions of the sphere size for the two reconstructions with and without RM and with and without post-filtering. As with the simulation study, both methods provide similar quantitative measures (with slightly different noise texture and visual appearance) for matched reconstruction model/regularization, except for somewhat increased variability (std) in the analytic reconstructions without post-filtering. The bias results for the smaller spheres are clearly affected by the voxelization/partial volume effects for all reconstructions, since the VOIs were of the same sizes as the physical sphere diameters. Although post-filtering increases those biases further, we believe that using apodizing post-filters is more predictable compared to simple regularization by stopping iterations early or using more advanced non-linear regularization techniques and might be easier to correct for quantitative purposes. As with the simulated data, the purpose of these studies was not to find the optimum regularization parameters, but rather to compare analytic- and iterative-DIRECT reconstructions for a range of resolution and regularization parameters.

Figure 9.

Results for measured NEMA phantom. (Left) Examples are shown of (top) RAMLA- and (bottom) analytic-DIRECT reconstructions without RM. RAMLA reconstruction was run to convergence, and both reconstructions were regularized by the same post-filter (Hann window with a cutoff at 0.8 of Nyquist frequency). (Middle and right) Plots of the bias and variability (standard deviation over 10 replicates) as functions of sphere size for iterative- and analytic-DIRECT reconstructions with matched resolution models and regularization post-filters. The bias is the fractional discrepancy between the reconstructed and true relative uptake values.

Figure 10 and Table 1 illustrate images and quantitative results for initial tests of DIRECT reconstructions of a patient FDG scan with inserted lung and liver lesions. Again, both iterative and analytic reconstructions used matched resolution models and post-filtering. Analytic-DIRECT shows very similar quantitative performance to iterative-DIRECT in terms of the average uptake bias and standard deviation of the uptake values over sphere locations in each organ, although the image noise related measure of image roughness (pixel-wise standard deviation (Tong et al., 2010)) is about 25% worse in the analytic reconstruction. This is consistent with visual observation; both reconstructions have similar visual appearance and sharpness/amount of the details; however under a closer inspection the analytic reconstruction exhibits different noise texture and low contrast streak artefacts propagating through and out of the object (a characteristic feature of filtered back-projection reconstructions with limited counts). These reconstructions were obtained using a limited axial acceptance angle and a simple gap compensation technique with noise amplification in the gaps that propagates through the image. Nevertheless, the analytic-DIRECT TOF reconstruction has demonstrated its ability to provide competitive quantitative quality to that of iterative-DIRECT, even with these limitations.

Figure 10.

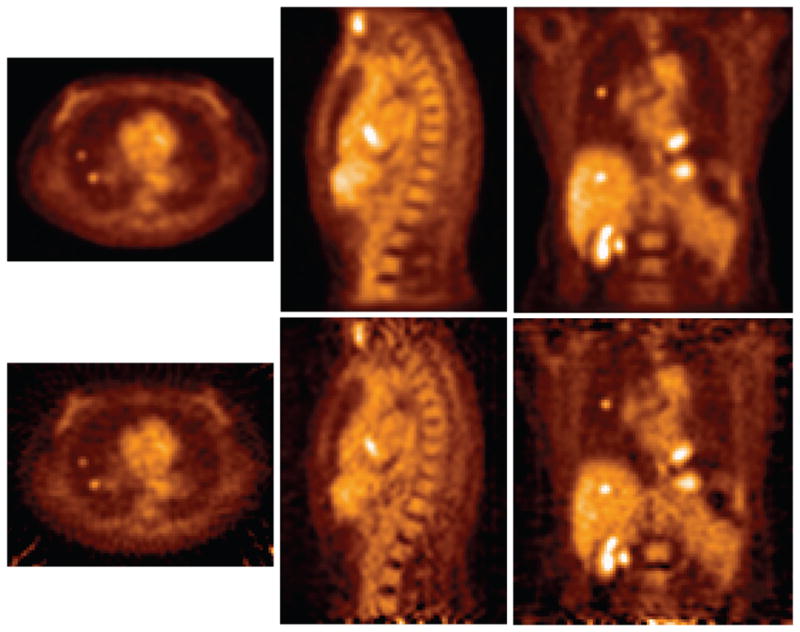
Examples (transverse, sagittal, and coronal slices) of (top) iterative- and (bottom) analytic-DIRECT reconstructions without RM of patient data with inserted lesions in lungs and liver. Both reconstructions were regularized via the same post-filter (Hann window with cut-off 0.8 times the Nyquist frequency).

Table 1.

Quantitative measures for patient data with emulated lesions (for reconstructions in figure 10).

	Lung spheres		Liver spheres		Image roughness (in liver)
	Bias	Std	Bias	Std
RAMLA-DIRECT	−0.756	0.034	−0.597	0.046	6.2%
Analytic-DIRECT	−0.742	0.037	−0.585	0.039	7.8%

6. Discussion

With the advent of TOF-PET scanners with good timing resolution the disadvantages of analytic algorithms over iterative approaches are ameliorated, with analytic TOF approaches becoming potential candidates for quantitative PET studies. In addition, TOF reconstruction constrains the noise and streak artifacts that lead to degraded image quality in non-TOF analytic reconstruction. The DIRECT implementation of the analytic algorithm allows better noise and resolution treatment through a confidence-weighting algorithm that includes both TOF and LOR resolution models and, at the same time, a very efficient implementation through histo-image data partitioning. Our tests confirmed that the quantitative performance of analytic-DIRECT is comparable to that of iterative-DIRECT for realistic TOF resolutions (375–600 ps) with competitive image quality for clinically reasonable count densities. Furthermore analytic-DIRECT implementation provides very fast, nearly a real-time, reconstruction; even on a modest laptop computer (2012 MacBook Pro) reconstruction took only about 10s per bed position for a typical clinical study. This is time comparable to 1 iteration of iterative-DIRECT, which is already about an order of magnitude faster compared to the standard list-mode reconstruction (Daube-Witherspoon et al., 2012).

For low count simulated data, the non-regularized analytic reconstructions with resolution modelling showed somewhat higher variability of uptake values (affecting the precision of the quantitative results) compared to iterative-DIRECT with the same RM (figure 6-right). However, after introducing regularization to optimize the bias-vs.-std trade-offs and to provide minimum MSE of reconstructions (figure 7), both analytic and iterative reconstructions provided similar minimum MSEs for matched RM even for the low count cases. For measured phantom and patient data, modest regularization similarly provided matched bias and variability performance in iterative and analytic reconstructions (figure 9 and Table 1).

Although the results of analytic and iterative reconstructions were comparable for fixed sphere locations and backgrounds in the simulated and real data studies, for iterative reconstructions it might be difficult to guarantee their uniform convergence and performance in practical quantitative studies across highly variable activity levels and object/organ backgrounds; consequently a large number of iterations may be needed to uniformly converge. This is where the linear analytic TOF reconstruction approaches with count-, activity-, and object-independent performance might prove to be advantageous. The purpose of this work was to compare analytic- to iterative-DIRECT for a range of conditions and resolution/regularization models/parameters not to find optimal parameters for particular application(s). It is quite possible that the two approaches will require different optimum parameters for particular applications and imaging tasks. A study of these effects as well as optimization and evaluation of analytic and iterative reconstructions within the unified DIRECT framework for particular clinical applications and tasks will be the subject of future studies.

In the studies presented in this work, we have conservatively limited the axial acceptance angle to a single tilt for simulated and measured data thus axially limiting the number of used counts for both analytic and iterative reconstructions. For clinical and research applications it will be important to utilize all acquired counts from the full axial acceptance angle. This will require partitioning the axial data into several tilts, even for practical PET systems with good timing resolution (Daube-Witherspoon et al., 2012). As illustrated in figure 4 the histo-images for non-zero tilts contain missing regions. While iterative-DIRECT can naturally handle oblique data with missing regions, the analytic algorithm requires estimation of the missing regions before it can use the oblique data, and it will be important to implement the proposed re-projection/correction approaches for the missing axial data in analytic-DIRECT (see Section 2.3.3). This will be especially important for low count studies to better utilize all of the available counts and to improve the precision (variability measures).

In the feasibility studies using measured phantom (figure 9) and patient (figure 10) data, which contained gaps between detector modules, we employed simple gap compensation techniques for analytic-DIRECT by multiplying the deposited prompt histo-images by the sensitivity correction factors. This provided accurate estimates of mean uptake values, but boosted up noise levels in the data regions with decreased counts due to the gaps and caused high noise regions/bands in the histo-images. These noisy regions propagated into the reconstructed images in the form of slightly increased image noise. For future studies using measured data, it will be important to implement and investigate more advanced gap compensation techniques, to further limit the noise and streaks propagating from the low count gap regions into the image reconstructed with analytic-DIRECT, where the streaks and noise are already somewhat constrained by the TOF information compared with a non-TOF analytic reconstruction. These methods will include optimized filters and sensitivity weighted combination of smoothed data from gaps with original unsmoothed data from non-gap regions (as discussed in Section 2.3.2).

7. Conclusions

We have developed an analytic TOF reconstruction algorithm within the DIRECT framework, thus expanding the DIRECT approach to include both linear and iterative reconstruction tools within a unified and computationally very efficient reconstruction and data-partitioning framework. Previous analytic algorithms have not included detector resolution models; within analytic-DIRECT we have expanded the confidence-weighted TOF algorithm to include detector resolution models. Our tests using both simulated and measured data confirmed the ability of analytic-DIRECT to properly include resolution kernels and compensate for the detector gaps and non-uniformities to achieve comparable bias-vs.-variability trade-offs to iterative-DIRECT reconstruction, while providing nearly a real time reconstruction speeds. Having a set of efficient iterative and analytic TOF reconstruction tools within a unified framework will be important for quantitative and task-based clinical and research imaging studies. The analytic-DIRECT reconstruction can also be an important performance evaluation tool for quality control and intrinsic spatial resolution evaluations of TOF PET systems. Our future work will involve evaluation of linear and iterative reconstruction approaches and their robustness and consistency across a range of object and scanner dependent conditions, such as across patient populations, scanners, and scanning protocols, as well as development of improved corrections for detector gaps and axial missing data.