SUMMARY
The log-rank test is widely used to compare two survival distributions in a randomized clinical trial, while partial likelihood (Cox, 1975) is the method of choice for making inference about the hazard ratio under the Cox (1972) proportional hazards model. The Wald 95% confidence interval of the hazard ratio may include the null value of 1 when the p-value of the log-rank test is less than 0.05. Peto et al. (1977) provided an estimator for the hazard ratio based on the log-rank statistic; the corresponding 95% confidence interval excludes the null value of 1 if and only if the p-value of the log-rank test is less than 0.05. However, Peto’s estimator is not consistent, and the corresponding confidence interval does not have correct coverage probability. In this paper, we construct the confidence interval by inverting the score test under the (possibly stratified) Cox model, and we modify the variance estimator such that the resulting score test for the null hypothesis of no treatment difference is identical to the log-rank test in the possible presence of ties. Like Peto’s method, the proposed confidence interval excludes the null value if and only if the log-rank test is significant. Unlike Peto’s method, however, this interval has correct coverage probability. An added benefit of the proposed confidence interval is that it tends to be more accurate and narrower than the Wald confidence interval. We demonstrate the advantages of the proposed method through extensive simulation studies and a colon cancer study.
Keywords: Censoring, Cox model, Log-rank test, Partial likelihood, Peto’s method, Proportional hazards, Score test
1. Introduction
For analysis of potentially censored survival time or other event time data in a randomized clinical trial, investigators typically use the log-rank test, which is a nonparametric method for testing the equality of two survival distributions. To reflect the magnitude of the treatment difference, investigators often supplement the log-rank test with estimation of the hazard ratio under the Cox model. In general, one can use the confidence interval to perform hypothesis testing in that exclusion of the null parameter value from the (1 − α) confidence interval implies rejection of the null hypothesis at the α nominal significance level. However, the Wald confidence interval for the hazard ratio, which is based on the maximum partial likelihood estimator (MPLE) and the corresponding Fisher information matrix, may not reject the null hypothesis of no treatment difference when the log-rank test does. Although the log-rank test and the Wald confidence interval are based on different statistics and thus need not yield the same conclusion, conflicting results can be disconcerting to investigators and regulatory agencies. In particular, if the log-rank p-value is less than 0.05 but the Wald 95% confidence interval includes the hazard ratio of 1, should one conclude that the trial is positive or negative?
Peto et al. (1977) provided a closed-form estimator of the hazard ratio and the corresponding variance estimator by using the log-rank statistic and its variance estimator. Although the original intent was to avoid iterative calculations, this method has the nice property that the (1 − α) confidence interval excludes the null value of 1 if and only if the log-rank test is significant at the α level. However, Peto’s estimator is not a consistent estimator of the hazard ratio, and the corresponding confidence interval does not have correct coverage probability. Furthermore, the use of Peto’s method deviates from the convention of adopting the partial likelihood methodology for estimation of the hazard ratio.
To resolve the aforementioned difficulties, we construct the confidence interval by inverting the partial-likelihood score test under the Cox model. That is, the (1 − α) confidence interval for the hazard ratio consists of the parameter values that are not rejected by the score tests at the α level. Although the score statistic for testing the null hypothesis of no treatment difference is the same as the log-rank statistic, the variance estimators for the two statistics are different when there are ties (i.e., multiple patients with the same observed survival times). Thus, we propose a simple modification to the partial-likelihood information matrix such that the resulting score test for the null hypothesis of no treatment difference is numerically identical to the log-rank test, with or without ties. The proposed method enjoys the nice feature of Peto’s method that the confidence interval excludes the null value of 1 if and only if the log-rank test is significant. Unlike Peto’s method, however, the proposed confidence interval has correct coverage probability (at least for large sample sizes) and is in line with the partial likelihood methodology. Another benefit of the proposed confidence interval is that it tends to be more accurate and narrower than the Wald confidence interval. We demonstrate these advantages through extensive simulation studies and provide a detailed illustration with data from a colon cancer clinical trial.
2. Methods
We consider a randomized clinical trial with two treatment arms and allow the possibility of stratified randomization. Suppose that there are K strata with nk patients in the kth stratum. (Unstratified randomization is a special case with K = 1.) For k = 1, …, K and i = 1, …, nk, let Tki denote the survival time for the ith patient of the kth stratum, and let Xki denote the corresponding indicator of the new treatment versus control. We specify the stratified Cox model
| (1) |
where β is the log hazard ratio, and λk0(·) (k = 1, …, K) are arbitrary baseline hazard functions (Kalbfleisch and Prentice, 2002, p. 118).
Let Cki denote the censoring time for Tki such that the observation consists of T̃ki ≡ min(Tki, Cki) and Δki ≡ I(Tki ≤ Cki), where I(·) is the indicator function. We obtain an efficient estimator of β by maximizing the partial likelihood function
The corresponding score function is
| (2) |
and the corresponding information matrix is
| (3) |
where .
Denote the maximizer of L(β) by β̂, which is obtained by the Newton-Raphson algorithm. For large samples, the score statistic U(β) is approximately normal with mean 0 and variance ℐ(β), and the MPLE β̂ is approximately normal with mean β and variance ℐ−1(β̂) (Andersen and Gill, 1982). Thus, the Wald confidence interval for β with coverage probability of (1 − α) is
| (4) |
where z1−α/2 is the (1 − α/2)100th percentile of the standard normal distribution. The confidence interval for the hazard ratio eβ is obtained by exponentiating the lower and upper limits.
To test the null hypothesis H0 : β = 0, we use the score test statistic U2(0)/ℐ(0), which is referred to the distribution. This test statistic is the same as the log-rank test statistic when there are no ties. In the presence of ties, U(0) is still the numerator of the log-rank test, but ℐ(0) is no longer the denominator of the log-rank test. To resolve this discrepancy, we propose to modify ℐ(β) in (3) as follows:
| (5) |
where , and . Then U2(0)/ℐ̃(0) is numerically identical to the log-rank test statistic whether there are ties or not (Kalbfleisch and Prentice, 2002, pp. 107–108).
Remark 1
In ℐ̃(β), Rki is the number of patients in the kth stratum who are under observation at time T̃ki, and Dki is the number of patients in the kth stratum who are observed to die at time T̃ki. Clearly, ℐ̃(0) is smaller than ℐ(0) when there are ties.
With the modified variance estimator, the score test statistic for testing the hypothesis β = β0 is U2(β0)/ℐ̃(β0), which is (asymptotically) -distributed if the hypothesis holds. Thus, the following confidence interval has (1 − α) coverage probability:
| (6) |
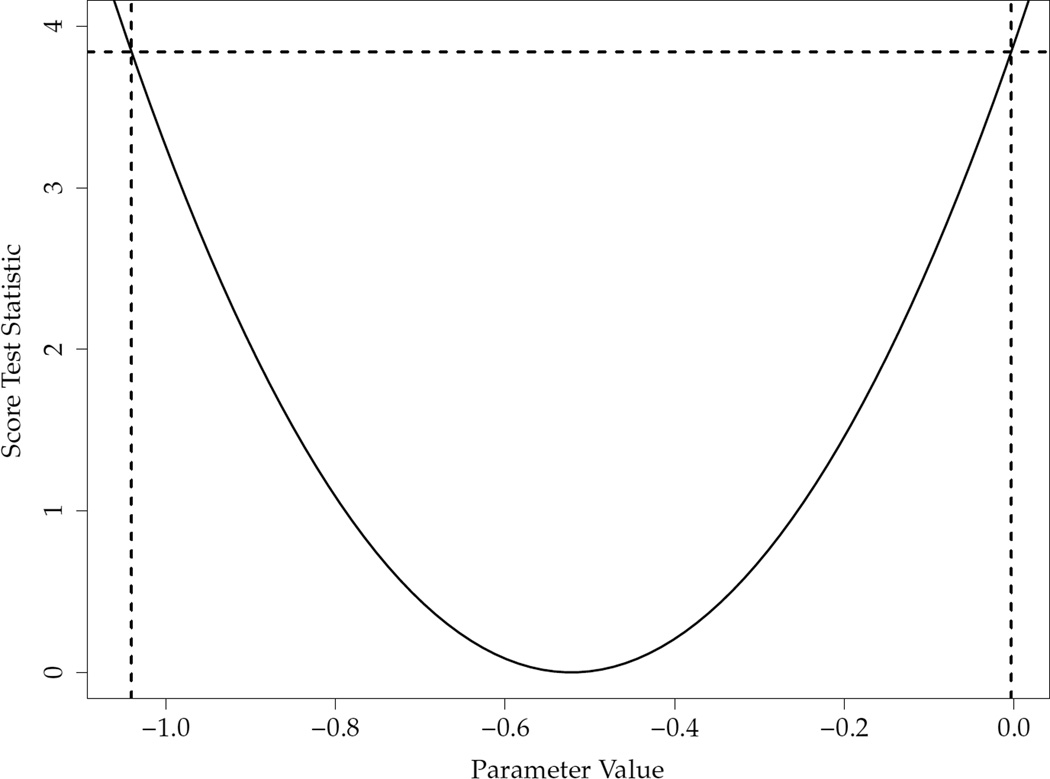
where is the (1 − α)100th percentile of the distribution. As shown in Figure 1, the U-shaped function U2(β)/ℐ̃(β) intersects the horizontal line at two values of β, the smaller of which is the lower limit of the interval and the larger of which the upper limit. The lower and upper limits, denoted by L1−α and U1−α, respectively, can be determined by the bisection method. The confidence interval for the hazard ratio is obtained by exponentiating the two limits. Since 0 is contained in (6) if and only if , this confidence interval excludes the log hazard ratio of 0 (or hazard ratio of 1) if and only if , i.e., the log-rank test is significant at the α level.
Figure 1.
Plot of the score test statistic U2(β)/ℐ̃(β) against the Parameter Value a β for particular data set. The values of β at which the function U2(β)/ℐ̃(β) intersects the horizontal line of are the limits of the 95% confidence interval.
The Wald confidence interval given in (4) excludes the value 0 if and only if . Because β̂2ℐ(β̂) is generally different from U2(0)/ℐ̃(0), it is possible for the Wald confidence interval to include the null value of 0 when the log-rank test is significant. This discrepancy may occur even if ℐ(β̂) is replaced by ℐ̃(β̂).
With 0 as the initial value for β, the first step in the Newton-Raphson algorithm for calculating the MPLE is
which is Peto’s estimator for β (Peto et al., 1977; Yusuf et al., 1985). The variance estimator for β̃ is 1/ℐ̃(0). The corresponding (1 − α) confidence interval is
Because β̃2ℐ̃(0) = U2(0)/ℐ̃(0), this confidence interval excludes the null value of 0 if and only if the log-rank test is significant at the α level. However, we show in the Appendix that β̃ is not a consistent estimator of β (unless the true value is 0), such that this confidence interval generally does not have correct coverage probability.
Remark 2
The Wald confidence interval is symmetric at β̂, whereas Peto’s confidence interval is symmetric at β̃. The score confidence interval is not symmetric at either estimator. If the log-rank p-value is exactly 0.05 and U(0) < 0, then the upper limits of the 95% confidence intervals for the score and Peto’s methods are both 0, but the lower limits are unlikely to be the same. In general, both the lower and upper limits are different among the three methods.
3. Simulation Studies
We conducted extensive simulation studies to compare the methods described in the previous section. We considered unstratified randomization with an equal allocation of patients to the two treatments. We generated survival times from model (1) with K = 1, n = 100, 200 or 500, λ(t) = 1 (i.e., standard exponential distribution), and β ranging from 0 to 1. In addition, we generated censoring times from the Uniform(0, τ) distribution, where τ was chosen to yield 50% or 80% censored observations. To create ties, we partitioned the time axis into equal intervals and replaced all of the survival times within the same interval by the midpoint of the interval. For each scenario, we used 100,000 replicates to calculate the summary statistics, such as bias and power. We present the results for the setting of no ties in Figures S1–S4 in the Supplementary Materials.
Figure S1 shows the results on the MPLE and Peto’s estimator for β. The MPLE is biased when n is small and censoring is heavy, but the bias diminishes rapidly as n increases. Peto’s estimator tends to be positively biased under 50% censoring and negatively biased under 80% censoring. The bias tends to get larger as the value of β increases and does not change appreciably with n.
Figure S2 displays the coverage probabilities of the Wald, score, and Peto’s methods. The Wald confidence interval tends to be conservative, especially for small n and heavy censoring. The score confidence interval has accurate coverage probability. Peto’s method does not have correct coverage probability unless β is close to 0, and its coverage probability tends to worsen as the value of β increases.
Figure S3 compares the width of the score and Wald confidence intervals, while Figure S4 compares the power of the log-rank and Wald tests. The score confidence interval tends to be narrower than the Wald confidence interval. In addition, the log-rank test is always more powerful than the Wald test. The differences diminish as n increases.
We present the results for the setting of 20% ties in Figures S5–S8 of the Supplementary Materials. The basic conclusions remain the same.
4. Colon Cancer Study
In a clinical trial of adjuvant therapy for patients with resected colon cancer, 315, 310, and 304 patients with Stage C disease were randomly assigned to observation, levamisole alone, and levamisole combined with fluorouracil, respectively (Moertel et al., 1990). Enrollment of patients began in March 1984 and was completed in October 1987. Overall survival was the primary endpoint of interest. At the second planned interim analysis in September 1989, the results met the protocol criteria for early termination and early reporting. Over the study period, 114, 109, and 78 patients died in the observation, levamisole alone, and levamisole+fluorouracil groups, respectively.
As an example, we compared the observation and combination therapy groups. The MPLE of the log hazard ratio is −0.398 with a standard error estimate of 0.147, and the corresponding Wald p-value is 0.0068. By contrast, the log-rank p-value is 0.0064. We then selected the first n patients that entered the trial, varying n from 5 to 619. For all 615 choices of n, the log-rank p-values are smaller than the Wald p-values. There are four values of n at which the Wald p-value is greater than 0.05 whereas the log-rank p-value is less than 0.05. Specifically, for n =62, 69, 89, and 154, the Wald p-values are 0.051, 0.055, 0.051, and 0.051, respectively, whereas the log-rank p-values are 0.045, 0.049, 0.047, and 0.048, respectively.
We focused on the first 154 patients. There are 1 and 4 (two-way) ties in the observation and combination therapy groups, respectively. The Peto estimate of the log hazard ratio is −0.515 with a standard error estimate of 0.261, such that the 95% confidence interval is (−1.027, −0.0034), which excludes the null value 0. The MPLE is −0.522 with a standard error estimate of 0.267, and the Wald 95% confidence interval is (−1.046, 0.0024), which covers the null value and thus contradicts with the log-rank p-value. The score-based 95% confidence interval is (−1.040, −0.0034), which excludes the null value and thus agrees with the log-rank test. Figure 1, which was originally presented in Section 2, pertains to the construction of this confidence interval.
For further illustration, we analyzed the data by stratifying on the number of lymph nodes. The log-rank and Wald p-values are 0.019 and 0.021, respectively; these significant results support the finding of the unstratified log-rank test. The MPLE is −0.640 with a standard error estimate of 0.277, and Peto’s estimate is −0.628 with a standard error estimate of 0.267, such that the Wald and Peto’s 95% confidence intervals are (−1.182, −0.097) and (−1.151, −0.104), respectively. The score-based 95% confidence interval is (−1.176, −0.103). All three confidence intervals exclude the null value and are thus in agreement with the score-based confidence interval in the unstratifed analysis.
5. Discussion
We have provided a simple solution to the disconcerting dilemma of conflicting results between the log-rank test and the Wald confidence interval for the hazard ratio. The (modified) score test statistic under the (possibly stratified) Cox model provides a unified framework for making inference about the hazard ratio and is in line with the current practice of using the log-rank test for hypothesis testing and the partial-likelihood methodology for parameter estimation. First, the minimizer of the score test statistic is the MPLE. Second, the score test for the null hypothesis of no treatment difference is the same as the log-rank test. Finally, the proposed confidence interval excludes the null value if and only if the log-rank test is significant. We have posted the relevant software on our website: http://dlin.web.unc.edu/software/
We have handled ties by the commonly used Breslow (1974) method, which is the default in SAS. The corresponding score statistic U(β) evaluated at β = 0 is exactly the log-rank statistic. The use of the information matrix ℐ(β) to estimate the variance of U(β) was justified by the counting-process martingale theory (Andersen and Gill, 1982). By contrast, the variance of the log-rank statistic was derived from the hypergeometric arguments (Mantel, 1966). By convention, we use ℐ−1(β̂) to estimate the variance of β̂ and ℐ̃(0) to estimate the variance of the log-rank statistic. We use ℐ̃(β) in the score test statistic, such that it will reduce to the log-rank test statistic under β = 0. Cox (1972) handled ties by applying a likelihood argument to a discrete logistic model. The resulting score function and information matrix evaluated at β = 0 are exactly the log-rank statistic and its variance estimator, respectively (Cox and Oakes, 1984, p. 104). However, the discrete-model likelihood does not yield a consistent estimator of β in model (1) if ties arise from the grouping of continuous survival times (Kalbfleisch and Prentice, 2002, p. 107).
Peto’s method was originally proposed to simplify computation. For small data sets, one can calculate the log-rank statistic by hand and then obtain the point estimate of the hazard ratio by Peto’s closed-form formula. With modern computing power, however, it takes very little time to calculate the MPLE by the Newton-Raphson algorithm, which usually converges in a few iterations. For large data sets, one has to resort to computer to perform the log-rank test anyway. Indeed, no one calculates the log-rank statistic by hand nowadays, even for small data sets.
Pike (1972) also provided a closed-form estimator for the hazard ratio based on the log-rank statistic. Simulation studies showed that Pike’s estimator tends to be less biased than Peto’s estimator (Berry et al., 1991). However, Pike’s estimator is not consistent either, and the corresponding confidence interval may not yield the same conclusion as the log-rank test. In general, it is not a good statistical practice to use inconsistent estimators. Indeed, closed-form estimators, such as Peto’s and Pike’s, have become obsolete and are not mentioned in major survival analysis texts, such as Cox and Oakes (1984), Fleming and Harrington (1991), Kalbfleisch and Prentice (2002), and Collett (2003).
Andersen et al. (1993, §V.3.1) provided an estimator for the hazard ratio θ based on the Nelson-Aalen estimators for the two cumulative hazard functions. They suggested the following test statistic for the hypothesis θ = θ0,
where θ̂ is the hazard ratio estimator, and σ̂2(θ0) is the variance estimator. The corresponding (1 − α) confidence interval is
This confidence interval is consistent with the log-rank p-value because (θ̂ − 1)2/σ̂2(1) turns out to be the same as the log-rank test statistic. However, θ̂ is not fully efficient, such that the above confidence interval tends to be wider than that of the MPLE, at least in large samples. As in the case of Peto’s estimator, the use of θ̂ deviates from the common practice of using the partial-likelihood methodology for estimation.
We have focused on superiority trials. For non-inferiority trials, we reject the null hypothesis of inferiority H0 : β ≥ δ and conclude non-inferiority with the margin of δ and type I error of α if the upper limit of the proposed (two-sided) confidence interval with the (1 − 2α) coverage probability, i.e., U1−2α, is less than δ. Likewise, we claim equivalence with the margins of ±δ and type I error of α if U1−2α < δ and L1−2α > −δ. Thus, the pro-posed confidence interval provides a unified framework for superiority, non-inferiority, and equivalence trials.
The dilemma discussed in this paper arises only when one wishes to use the log-rank statistic for testing the null hypothesis of no treatment difference. One can avoid this dilemma by using the Wald method to test hypotheses and construct confidence intervals. However, the Wald test tends to be less powerful than the log-rank test, as shown in the simulation studies and the colon cancer example, and the Wald confidence interval is wider and less accurate than the score confidence interval. For large sample sizes, the score and Wald methods yield very similar results. If there are sparse strata or continuous prognostic variables (to be adjusted for), then it is easier to use Wald statistics than score statistics.
We can also construct the confidence interval for β by inverting the partial-likelihood ratio test. Write l(β) = log L(β). The partial-likelihood ratio statistic for testing H0 : β = β0 is 2[l(β̂) − l(β0)], and the corresponding (1 − α) confidence interval is
This confidence interval may not be in agreement with the log-rank p-value since 2[l(β̂) − l(β0)] is generally different from U2(0)/ℐ̃(0). For randomized clinical trials, the log-rank test is much more popular than the likelihood ratio test, although the two tests yield similar results in large samples.
For simplicity of description, we have focused on two treatment arms. Both the log-rank test and the proposed confidence interval can be extended to multiple, say (J + 1), treatment arms. Specifically, let Xki be a J-vector of treatment indicators. We replace βXki in model (1) by βTXki, where β now pertains to a J-vector of log hazard ratios. The score function still takes the form of (2), but with . The modified information matrix in (5) becomes
The confidence region for β is given by , where is the (1 − α)100th percentile of the distribution.
Supplementary Material
Acknowledgments
This research was supported in part by the National Institutes of Health grant R01 GM047845. The authors thank Paul Bunn and Lu Mao for their programming assistance. They also thank the Editor, an Associate Editor, and a referee for helpful comments.
APPENDIX
Inconsistency of Peto’s Estimator
By the Taylor series expansion,
where β* lies between 0 and β̂. By the definition β̂, we have U(β̂) = 0. Thus,
Dividing both sides of the above equation by ℐ̃(0) and using the definition of β̃, we obtain
| (A.1) |
Because β̂ converges in probability to β as n → ∞ (Andersen and Gill, 1982), equation (A.1) implies that β̃ converges in probability to β{Σ(β*)/Σ(0)} as n → ∞, where Σ(β) is the limit of ℐ(β)/n, and β* lies between 0 and β. (Here, n denotes the total number of patients in the study.) Therefore, β̃ is consistent for β if and only if β = 0.
Footnotes
Supplementary figures, referenced in Section 3, are available with this paper at the Biometrics website on Wiley Online Libary. The data and computer code are also available.
REFERENCES
- Andersen PK, Borgan Ø, Gill RD, Keiding N. Statistical Models Based on Counting Processes. New York: Springer; 1993. [Google Scholar]
- Andersen PK, Gill RD. Cox’s regression model for counting processes: a large sample study. The Annals of Statistics. 1982;10:1100–1200. [Google Scholar]
- Berry G, Kitchin RM, Mock PA. A comparison of two simple hazard ratio estimators based on the logrank test. Statistics in Medicine. 1991;10:749–755. doi: 10.1002/sim.4780100510. [DOI] [PubMed] [Google Scholar]
- Breslow N. Covariance analysis of censored survival data. Biometrics. 1974;30:89–99. [PubMed] [Google Scholar]
- Collett D. Modelling Survival Data in Medical Research. 2nd. London: Chapman and Hall; 2003. [Google Scholar]
- Cox DR. Regression models and life tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- Cox DR. Partial likelihood. Biometrika. 1975;62:269–276. [Google Scholar]
- Cox DR, Oakes D. Analysis of Survival Data. London: Chapman and Hall; 1984. [Google Scholar]
- Fleming TR, Harrington DP. Counting Processes and Survival Analysis. New York: John Wiley; 1991. [Google Scholar]
- Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. 2nd. Hoboken: John Wiley and Sons; 2002. [Google Scholar]
- Mantel N. Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemotherapy Reports. 1966;50:163–170. [PubMed] [Google Scholar]
- Moertel CG, Fleming TR, McDonald JS, et al. Levamisole and fluorouracil for adjuvant therapy of resected colon carcinoma. New England Journal of Medicine. 1990;322:352–358. doi: 10.1056/NEJM199002083220602. [DOI] [PubMed] [Google Scholar]
- Peto R, Pike MC, Armitage P, Breslow NE, Cox DR, Howard SV, Mantel N, McPherson K, Peto J, Smith PG. Design and analysis of randomized clinical trials requiring prolonged observation of each patient. II. analysis and examples. British Journal of Cancer. 1977;35:1–39. doi: 10.1038/bjc.1977.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pike MC. Contribution to the discussion of the paper by R. Peto and J. Peto, “Asymptotically efficient rank invariance test procedures”. Journal of the Royal Statistical Society, Series A. 1972;135:1–203. [Google Scholar]
- Yusuf S, Peto R, Lewis J, Collins R, Sleight P. Beta blockade during and after myocardial infarction: An overview of the randomized trials. Progress in Cardiovascular Diseases. 1985;27:335–371. doi: 10.1016/s0033-0620(85)80003-7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.