Head-Neck Osteoplasty has Minor Effect on the Strength of an Ovine Cam-FAI Model: In Vitro and Finite Element Analyses

Abstract

Background

Osteochondroplasty of the head-neck region is performed on patients with cam femoroacetabular impingement (FAI) without fully understanding its repercussion on the integrity of the femur. Cam-type FAI can be surgically and reproducibly induced in the ovine femur, which makes it suitable for studying corrective surgery in a consistent way. Finite element models built on quantitative CT (QCT) are computer tools that can be used to predict femoral strength and evaluate the mechanical effect of surgical correction.

Questions/purposes

We asked: (1) What is the effect of a resection of the superolateral aspect of the ovine femoral head-neck junction on failure load? (2) How does the failure load after osteochondroplasty compare with reported forces from activities of daily living in sheep? (3) How do failure loads and failure locations from the computer simulations compare with the experiments?

Methods

Osteochondroplasties (3, 6, 9 mm) were performed on one side of 18 ovine femoral pairs with the contralateral intact side as a control. The 36 femurs were scanned via QCT from which specimen-specific computer models were built. Destructive compression tests then were conducted experimentally using a servohydraulic testing system and numerically via the computer models. Safety factors were calculated as the ratio of the maximal force measured in vivo by telemeterized hip implants during the sheep’s walking and running activities to the failure load. The simulated failure loads and failure locations from the computer models were compared with the experimental results.

Results

Failure loads were reduced by 5% (95% CI, 2%–8%) for the 3-mm group (p = 0.0089), 10% (95% CI, 6%–14%) for the 6-mm group (p = 0.0015), and 19% (95% CI, 13%–26%) for the 9-mm group (p = 0.0097) compared with the controls. Yet, the weakest specimen still supported more than 2.4 times the peak load during running. Strong correspondence was found between the simulated and experimental failure loads (R² = 0.83; p < 0.001) and failure locations.

Conclusions

The resistance of ovine femurs to fracture decreased with deeper resections. However, under in vitro testing conditions, the effect on femoral strength remains small even after 9 mm correction, suggesting that femoral head-neck osteochondroplasty could be done safely on the ovine femur. QCT-based finite element models were able to predict weakening of the femur resulting from the osteochondroplasty.

Clinical Relevance

The ovine femur provides a seemingly safe platform for scientific evaluation of FAI. It also appears that computer models based on preoperative CT scans may have the potential to provide patient-specific guidelines for preventing overcorrection of cam FAI.

Introduction

The sheep is an established experimental animal model for cam-type femoroacetabular impingement (FAI) [25]. FAI can be surgically induced in sheep by a closed-wedge intertrochanteric osteotomy. This purely extraarticular procedure creates a cam-type of FAI between the naturally aspheric femoral head in sheep and the posterior acetabulum in flexion (Fig. 1). As a result, typical focal intraarticular prearthritic chondrolabral lesions similar to those seen in human beings can be reproducibly generated in a few months [25]. The severity of these chondrolabral lesions is reportedly time-dependent [25] and can be monitored by biochemical MRI protocols [26].

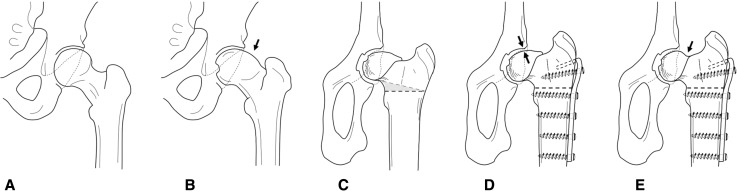
Fig. 1A–E.

The human femur normally features (A) a round head, but young and active individuals may suffer from cam-type femoroacetabular impingement (FAI) attributable to an (B) osseous bump (arrow) forming at the head-neck junction. (C) A similar situation can be surgically induced in sheep by a closed-wedge intertrochanteric osteotomy, (D) creating contact between the naturally aspherical femoral head of the sheep and the posterior acetabulum (arrows). (E) Resection of the head-neck region (arrow) can be done on the ovine FAI model as during the surgical intervention.

The ovine model offers a scientific platform for biomechanical, histologic, and radiographic investigations of cam-type FAI. As the pathomechanism is surgically induced in the model, the FAI has a clear beginning, in contrast to patients who have an underlying structural deformity and cartilage lesions long before any symptoms appear. In addition, degenerative alterations of the hip can be reproduced in just a few months, whereas they normally occur over decades in human beings. The model therefore can answer clinically relevant questions such as: “When is it too late for corrective surgery?” or “Is prophylactic surgery indicated?”

However, to perform a safe osteochondroplasty of the femoral head-neck junction in this animal model (Fig. 1), biomechanical assessment of the stability of the ovine femoral head-neck junction after offset creation is required. The forces needed to create an iatrogenic femoral neck fracture have to be referenced to known maximal forces of activities of daily living in sheep hips [1]. This is important because sheep are not able to perform partial weightbearing postoperatively. In addition, the offset creation needs to be done in the most lateral portion of the femoral head where the biomechanical stresses are maximal under axial load [5]. Ideally, the resulting femoral strength after osteochondroplasty could be predicted preoperatively using computer simulations based on finite element (FE) methods. These computer models are generated from quantitative CT (QCT) after conversion of the Hounsfield units to bone mineral density (BMD) values [2, 4, 7, 8, 10, 16] and provide an accurate measure of bone strength [31], a criterion that can discriminate patients at risk for hip fracture [6]. However, unlike numerous FE models predicting human femoral strength [2, 4, 7, 8, 10, 16], the one study dealing with FAI correction [20] relied on a single femur with simplified linear elastic material properties (ie, no microcracks) and no direct experimental validation. The simulated resections did not necessarily reflect the result of a surgical osteochondroplasty [20]. In other words, there is currently no evidence that QCT-based computer models would be sensitive enough to measure the mechanical effect of the FAI correction.

The purpose of our study was to evaluate the risk of iatrogenic femoral neck fracture after osteochondroplasty in an ovine FAI model. In addition, we wanted to validate the efficacy of an FE model based on QCT data to predict a femoral neck fracture for this model. Specifically, we asked: (1) What is the effect of a resection of the superolateral aspect of the ovine femoral head-neck junction on failure load? (2) How does the failure load after osteochondroplasty compare with reported forces from activities of daily living in sheep? (3) How do simulated failure loads and failure locations from the simulations compare with the experiments?

Materials and Methods

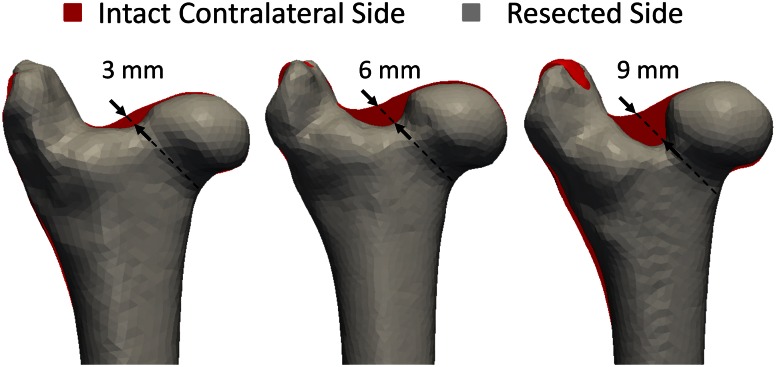
We conducted an experimental, controlled, biomechanical, in vitro study comparing the influence of resection depth of the femoral head-neck osteochondroplasty on the failure load of sheep femurs. These values then were compared with the forces evaluated from computer (FE) models that simulated the biomechanical tests. Thirty-six fresh frozen femurs (18 femoral pairs) were harvested from 18 female Swiss alpine sheep (2.5 ± 0.5 years old, 62 ± 6 kg) with approval of the veterinary board (Kantonales Veterinäramt Zürich, Switzerland, application 02/2014). The femurs were thawed at room temperature a day before any manipulations. They were stripped of soft tissues and their neck diameter was measured using a caliper (mean, 25 ± 1.5 mm; range, 22.5–28 mm). A femur from each pair was then randomly chosen for osteochondroplasty of the superolateral aspheric femoral head-neck junction. According to clinical practice, the osteochondroplasty was initiated using a curved chisel and finalized with a high-speed burr. All osteochondroplasties were performed by the same orthopaedic surgeon (MT) with extensive experience in open treatment of FAI in humans. The contralateral side remained intact to serve as a control. Three resection depths were chosen in absolute dimensions: 3, 6 and 9 mm. Those corresponded to 12% (± 0.97%), 24% (± 0.93%), and 36% (± 2.62%) of the initial neck diameters (Fig. 2). The distal part of each femur was then embedded in an 8-cm-thick layer of bone cement (polymethylmethacrylate) using a custom sample holder as a mold.

Fig. 2.

A femur from each of the 18 femoral pairs is trimmed at the head-neck junction while its contralateral side remains intact. Three groups are created based on the resection depth (3 mm, 6 mm and 9 mm) (arrows). The grey shapes correspond to the segments from the CT images of resected femurs. They were mirrored and superimposed to the segments of their contralateral sides in red. The femurs of one pair are not strictly identical, which explains why more than just the resection appears red.

All femoral pairs underwent a QCT scan (Somatom^® Definition Flash; Siemens Healthineers, Munich, Germany) (intensity: 150 mA; voltage: 140 KeV; voxel size: 0.5 × 0.5 × 0.7 mm³) with a custom-made bone density calibration phantom (QRM-BDC Phantom; QRM GmbH, Moehrendorf, Germany). Each scan was converted to BMD from the Hounsfield units (HU) through linear regressions established from our phantom’s inserts (0, 100, 200, 400, 600, 800 mg HA/cm³). While phantoms often feature a smaller number of low-density inserts (only up to 200 mg/cc) [2, 8], ours was custom-made to minimize the error in the linear HU/BMD relationship. To deal with multiple regions of interest (ROIs), ImageJ’s ROI manager [23] (National Institutes of Health, Bethesda, MD, USA) was used. The musculoskeletal axis through the femoral head and the midpoint of the distal femoral condyles was defined for each femur using the three-dimensional viewer of ImageJ [22]. The QCT images were then tilted to align musculoskeletal and Z-axes.

The femurs were mounted on a servohydraulic device (MTS Bionix^®; MTS Systems, Eden Prairie, MN, USA) for compression testing. The femurs were tilted according to their musculoskeletal axis through the femoral head and the midpoint of the distal femoral condyles. This corresponds to the main force vector seen in sheep hips [1]. During preparation, the femurs were wrapped in 0.9% saline-soaked gauze to keep them moist. Bone cement caps were fitted on the femoral heads to ensure even load distribution and uniaxial displacements were conducted until failure at a rate of 5 mm/minute. Lateral motions of the head were guaranteed by two linear bearings and a load cell underneath the sample holder recorded axial force. The fracture pattern was captured on video and photographs. Experimental failure load was defined as the maximum force on the load-deflection curve before failure. The relative reduction in the failure load of the resected femur was computed as a percentage of the intact contralateral side. The experimental failure loads were then compared with reported forces induced by treadmill exercises of sheep [1]. Those forces had been monitored through telemeterized implants and the maximal values were provided as a percentage of the sheep’s body weight (BW) [1]. Regular walking (194% BW) and starting to run, generating the highest force (370% BW), were considered for a 70-kg animal. Safety factors were determined as the ratio of the failure load of the specimen over the highest force induced by an activity. A safety factor less than 1 would therefore suggest that the animal might be at risk for fracture.

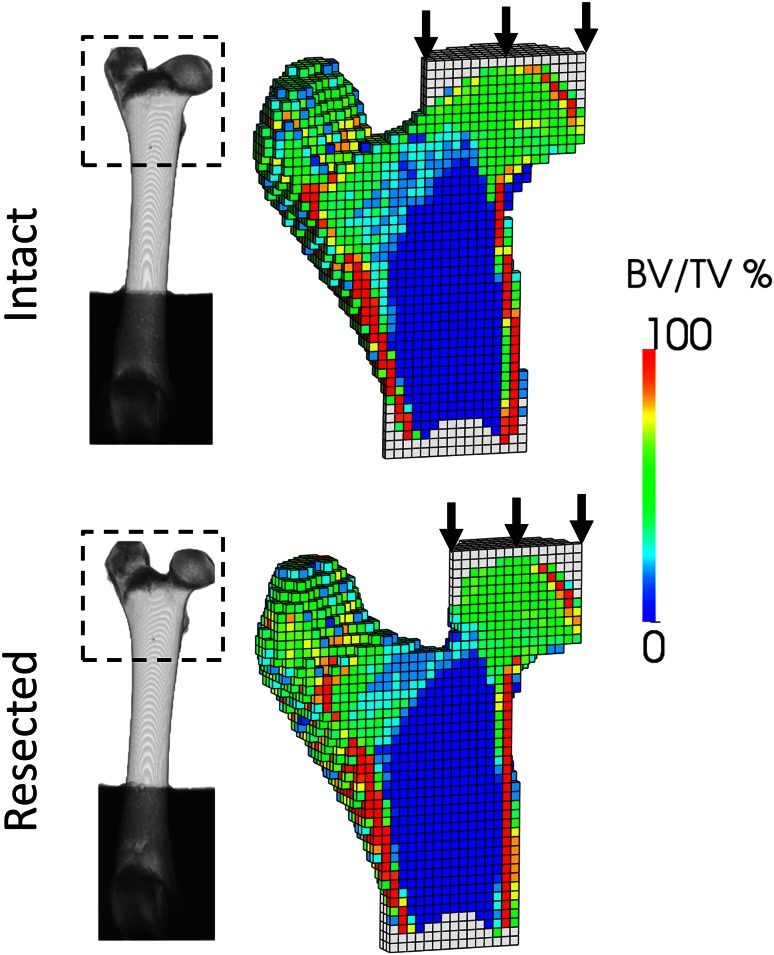
Computer models were generated for the 36 femurs from the QCT data (Fig. 3). The femurs were cropped up to 30% of the proximal part and coarsened to 1.5-mm edge length to resemble a clinical CT. Bone voxels were converted to bone volume fraction (bone volume over total volume [BV/TV]) [4]. Bone cement was added on the femoral head and under the shaft, and the voxels were converted to linear hexahedral finite elements. Unless stated otherwise, all image processing, meshing, and material properties assignation steps were automatically performed using medtool (Dr. Pahr Ingenieurs e.U, Pfaffstätten, Austria; www.dr-pahr.at). Cement was assigned isotropic elastic properties (E = 3000 MPa, ν = 0.3). Bone was modeled using a material law used in previous studies [12, 29] and featuring a damage variable mimicking the stiffness reduction owing to microcracks [24]. In the absence of reliable information regarding bone anisotropy, it was considered isotropic [4]. The elastic and strength parameters of the law were scaled to ovine tissue using indentation moduli of wet and dry sheep and human trabecular bone $(\text{scale}=\frac{E_{dry}^{ovine}}{E_{dry}^{human}}\ast \frac{E_{wet}^{human}}{E_{dry}^{human}}=\frac{27.5GPa}{14.48GPa}\ast \frac{10.99GPa}{14.48GPa})$ [3, 30]. To compensate for the lack of explicit cortex modeling, a tissue function stiffened the elements with BV/TV exceeding 50% [4]. The computer simulations were conducted using Abaqus (Abaqus 6.132, Simulia; Dassault Systemes, Velizy-Villacoublay, France) on six central processing units (CPUs) of a standard personal computer (3 GHz, 24 GB RAM). The inferior cement layer was fully constrained. Uniaxial displacement was imposed along the Z-axis to the superior cement layer that was allowed lateral motions as in the experiments. The simulations provided simulated failure load and damage distribution of each specimen. The simulations lasted between 10 and 20 minutes for FE models counting approximately 15,000 elements.

Fig. 3.

Computer (finite element) models are generated for the proximal region of the intact and resected specimens from the QCT data. To simulate experimental conditions, axial displacements are applied to the femoral head through a layer of bone cement. Aside from the resected regions, the distribution of bone volume per total volume (BV/TV) of the paired femurs is similar.

Statistical Analysis

Before the study, we performed a power analysis for the primary research question regarding strength of the femoral neck after offset creation. Two-sided level of significance of 5%, beta error of 20%, estimated load to failure of 2.4 kN after offset creation, 4.0 kN for the intact contralateral side, and an estimated SD of 1.0 kN were chosen resulting in a minimal sample size of five hips per group. Input data for the power analysis were derived from a similar cadaver experiment in humans [13] given comparable contact pressure distribution, magnitude, and mean surface stresses [15]. Each group was therefore composed of six samples to minimize alpha and beta errors.

After confirming a normal distribution with a Kolmogorov-Smirnov test, a paired two-tailed Student’s t-test was used to compare the mean failure load between study groups. The relative reduction in failure load was also computed for each resection group as the mean difference between the values of the group’s specimens and their respective intact controls (corresponding to 100% strength). A similar procedure was conducted on the computer predictions to determine whether computer models also detect the change of femoral failure load after resection. To check the consistency of the simulations, linear regression was established between in vitro and simulated failure loads, and the computed damage area was compared with the experimental fracture pattern.

Results

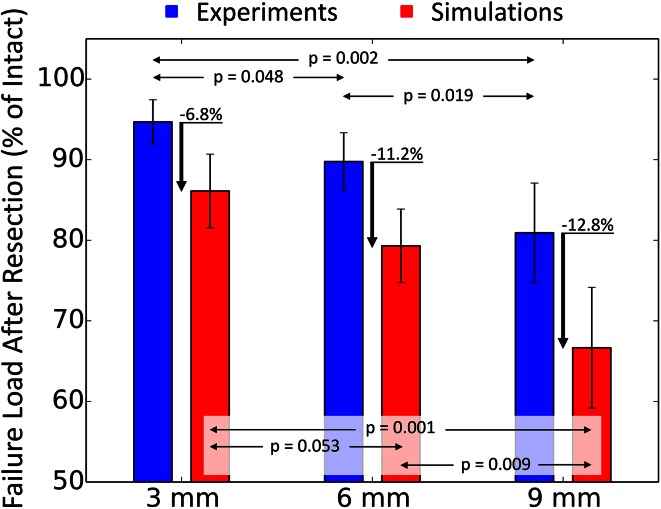
The absolute in vitro failure loads (mean + SD) were 10.4 ± 1.0 kN (95% CI, 9.4–11.4 kN) for the intact control group, 9.9 kN ± 1.0 kN (95% CI, 8.9–10.9 kN) for the 3-mm group, 8.3 kN ± 1.0 kN (95% CI, 7.3–9.3 kN) for the 6-mm group, and 7.9 kN ± 1.4 kN (95% CI, 6.5–9.3 kN) for the 9-mm group (Table 1). Accordingly, the failure loads were reduced to 95% ± 2.9% (95% CI, 92%–98%) for the 3-mm group (p = 0.0089), 90% ± 3.9% (95% CI, 86%–93%) for the 6-mm group (p = 0.00148), and 81% ± 6.7% (95% CI, 74%–87%) for the 9-mm group (p = 0.0097) compared with their respective control (Table 1).

Table 1.

Absolute and relative failure loads for the different resection depths*

Resection depth	In vitro failure load		Simulated failure load		In vitro vs simulation
	Absolute (kN)	Relative (%)	Absolute (kN)	Relative (%)	Mean difference (kN)	p value
Intact (control)	10.4 ± 1.0 (9.4–11.4)	100	9.4 ± 2.4 (6.7–11.8)	100	0.4 ± 1.6 (−0.3 to 1.2)	0.278
3 mm	9.9 ± 1.0 (8.9–10.9)	95 ± 2.9 (92–98)	9.0 ± 1.4 (7.7–10.3)	85 ± 10 (74.7–95.2)	0.9 ± 1.5 (0.5–1.3)	0.004
6 mm	8.3 ± 1.0 (7.3–9.3)	90 ± 3.9 (86–93)	6.8 ± 1.8 (5.0–8.5)	79 ± 5 (74.5–84.1)	1.5 ± 0.8 (0.6–2.5)	0.013
9 mm	7.9 ± 1.4 (6.5–9.3)	81 ± 6.7 (74–87)	5.6 ± 1.7 (4.0–7.3)	67 ± 8 (58.8–74.5)	2.3 ± 0.7 (1.3–3.3)	0.028
p value 3 mm vs control	0.007	0.009	0.023	0.010	NA	NA
p value 6 mm vs control	0.002	0.002	0.003	<0.001	NA	NA
p value 9 mm vs control	<0.001	0.010	<0.001	<0.001	NA	NA

* Values reported as mean ± SD (95% CI); NA = not applicable.

The experimental failure load of each femur was substantially greater than the forces reported for activities of daily living in sheep, independently of the resection depth. The weakest specimen had a 9-mm resection, but still could support up to 6.27 kN, which is more than 4.5 times the upmost force involved while walking (F_walking = 1.36 kN, $S{F}_{walking}^{Exp}=4.6$) and approximately 2.4 times the maximal load produced during running (F_running = 2.59 kN, $S{F}_{running}^{Exp}=2.4$).

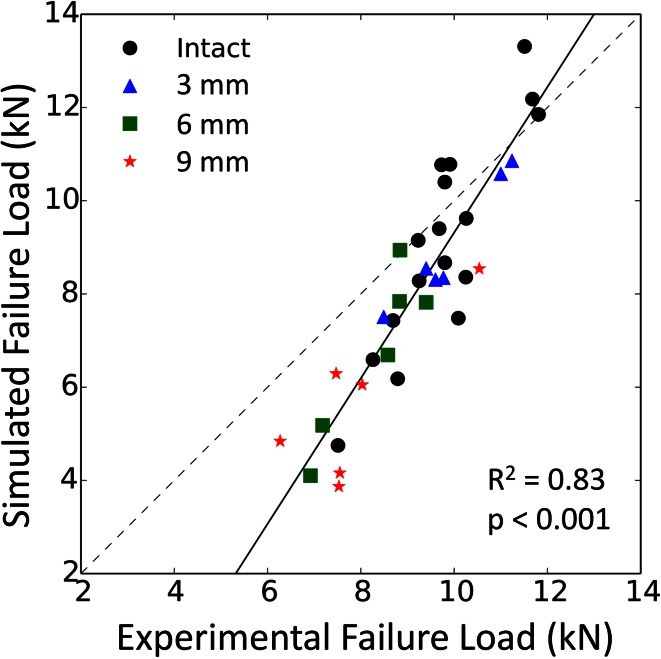
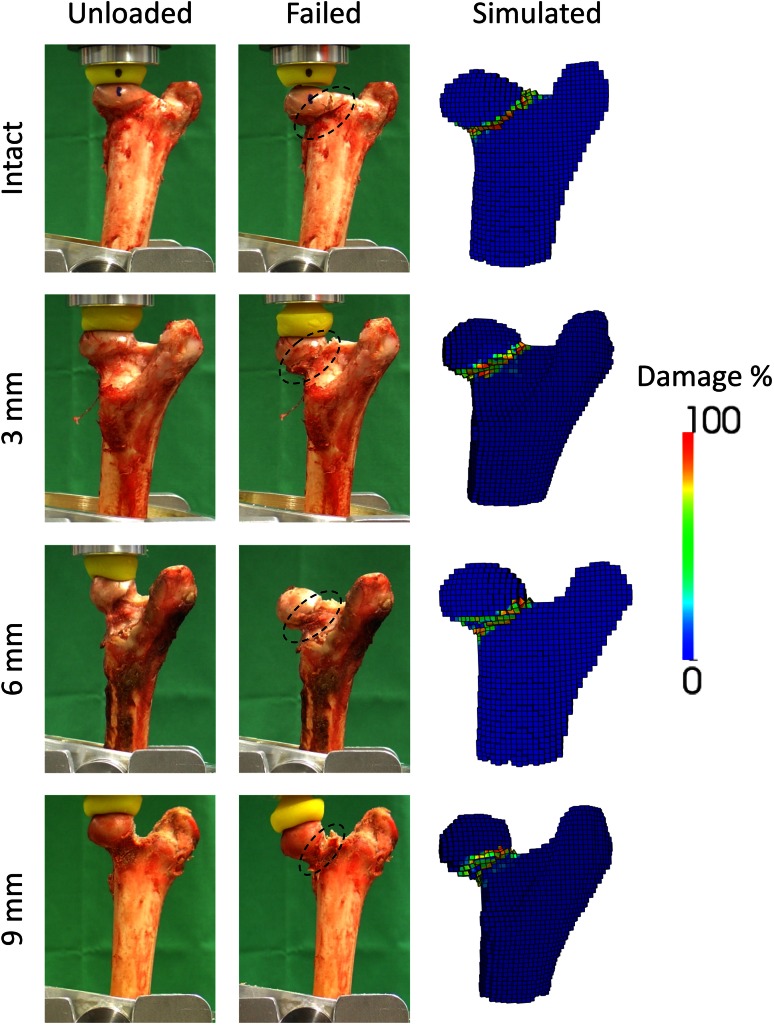
Similar trends were observed with the computer models, although simulated failure loads were consistently lower than the in vitro results (Fig. 4). Nevertheless, a strong correlation was established between the simulated and experimental failure loads (Fig. 5) (R² = 0.83; p < 0.001). Also analogous to the in vitro situation, our weakest computer model could support up to 4.84 kN. This is below our lowest experimental measure, but sufficient to support the sheep’s daily activities $(S{F}_{walking}^{FE}=3.6,S{F}_{running}^{FE}=1.9)$. Finally, the computed failure location matched the actual fracture pattern, with all of them occurring at the femoral neck independent of the defect’s size (Fig. 6).

Fig. 4.

The failure loads of the resected femurs are given as a mean percentage of the failure loads of their intact contralateral side. Error bars provide the SD. The failure load is significantly reduced by increasingly larger defects. The discrepancy between the in vitro tests and the computer models increases with the size of the resection.

Fig. 5.

Despite lower values, the failure loads yielded by the computer models correlate highly and significantly with the experimental data.

Fig. 6.

Independently of the resection depth (Intact, 3 mm, 6 mm, and 9 mm), the damaged region in the computer models (“Simulated”) corresponded to the fracture pattern observed in vitro (“Failed”) occurring at the neck (“dashed lines”). For comparison, the specimens before loading (“Unloaded”) are also displayed.

Discussion

The sheep is widely accepted as a model for humans in orthopaedic research because of its comparable BW and long bones’ dimensions [14], loading orientation [1], contact pressure, and stress distribution [15]. Ovine femurs naturally feature an aspheric femoral head-neck junction resembling a human cam deformity such that typical chondrolabral lesions can be induced experimentally in living animals by a closed-wedge extraarticular femoral osteotomy [25]. To perform a safe osteochondroplasty in this animal model, we evaluated experimentally if and how resection of the aspheric lateral portion will compromise the structural integrity of the ovine femur. We found that under in vitro testing conditions, the effect on femoral strength remained low even after resections up to 9 mm, suggesting that osteochondroplasty could be performed without risk of immediate iatrogenic femoral neck fracture. Under axial compression testing, the forces to create such a fracture exceeded at least 2.4 times the known maximal force during activities of daily living in the ovine hip. In addition, we found that QCT-based FE models can predict the failure loads and presumed location of the fracture.

Some of our methodologic choices deserve justification. First, the ovine hip is highly reproducible, especially compared with human hips. By selecting animals from the same breed, gender, and weights and by sacrificing them at the same age, we ensured the highest similarity between our samples. Little variability was found in neck diameter and absolute resection depths were therefore chosen for practical reasons. A relative depth measurement is impossible during surgery: the animals do not tolerate full dislocation and one has access only to the anterior head-neck junction of the hip. However, relative depths were still provided to enable application of the findings to male sheep from other breeds. Second, it is clear that two femurs of one pair are not identical. However, the contralateral side remains our best control and QCT data were used to check visually for any discrepancies. Finally, our loading scenario and its quasistatic nature are controllable and reproducible rather than physiologic. This choice of loading is legitimate as quasistatic and passive fatigue properties of bone scale well in terms of strains [17, 18]. It addresses the safety concerns during the first days after surgery when remodeling could be activated, but not yet in progress. The bone resorption that may accelerate the accumulation of fatigue occurs at the location of high strains [21], just as the quasistatic damage. A quasistatic analysis therefore is highly relevant in the case of cyclic loading and in the presence of strain-driven remodeling.

Our computer models also should be discussed. The cortical region was not explicitly modeled and trabecular anisotropy not accounted for despite being a main determinant of trabecular stiffness [11]. A better representation of trabecular orientation and cortex would improve our simulations [10], but extra image processing is needed to retrieve this information from clinical CT scans [9, 28]. Finally, our material law was designed for human bone and may not fully describe the mechanical behavior of ovine bone. Given the lack of information relative to the material properties of wet ovine bone, the elastic, yield, and strength parameters of human bone [19] were simply scaled.

Reshaping of the ovine femurs did not dramatically alter their load-bearing ability. Even after a 36% neck resection, more than 80% of their initial strength was preserved. Although there was no sheep study for comparison, our results are consistent with reported human data. Mardones et al. [13], who evaluated the influence of the resection depth on human femurs, reported that 85% of the strength remains after resecting 30% of the neck. They simply notched the head-neck junction of their specimens, whereas we reestablished the sphericity of our femoral heads as done in clinical routine, removing proportionally more bone in the process. The safety factors of our specimens remained above 1 $(S{F}_{walking}^{Exp}=4.6\text{and}S{F}_{running}^{Exp}=2.4\text{for our weakest specimen})$; that is, they likely would have been able to withstand the animal’s weight during its daily activities despite the aggressiveness of the osteochondroplasty. Taddei et al. [27] recently determined that the strain-based safety factor of intact human femurs during gait ranges from 1.196 to 15.558.

The computer simulations concurred with the experiments. Our predictions of in vitro failure loads (R² = 0.83) were comparable to what models of intact human femurs in stance configuration achieve (R² = 0.82–0.95) [2, 4, 7, 8, 10, 16]. QCT-based computer models were also able to catch the weakening of ovine femurs observed in vitro, even if the resection size had a larger influence on the FE predictions than it did experimentally. Although this disparity could be attributable to modeling simplifications, the computer models proved consistently more sensitive to the resurfacing than the experiments, providing the worst-case scenario for a correction surgery. Furthermore, even though our models could compute diverse failure locations [4], the simulated damage regions consistently occurred at the neck independently of the resection depth and in agreement with the fractures observed experimentally. These findings are clinically relevant. Osteochondroplasty of the head-neck region is currently performed with limited knowledge of its effect on the integrity of the femur; we propose for the first time a solution able to predict this effect beforehand from preoperative CT data.

Although their strength decreases with deeper resections, our in vitro biomechanical tests and computer simulations support that ovine femurs should not be at immediate risk of fracture for surgeries up to 36% neck diameter, which is analogous to human femurs [13]. Using ovine material, our study also yielded the first evidence of QCT-based FE models predicting worsening of femurs after head-neck osteoplasty. If this predictive value is confirmed for human bones, models based on preoperative CT could provide patient-specific guidelines for surgical corrections of cam-type impingement to prevent postoperative fractures.