A depth-sensing technique on 3D-printed compensator for total body irradiation patient measurement and treatment planning

Abstract

Purpose:

The purpose of total body irradiation (TBI) techniques is to deliver a uniform radiation dose to the entire volume of a patient’s body. Due to variations in the thickness of the patient, it is difficult to produce such a uniform dose distribution throughout the body. In many techniques, a compensator is used to adjust the dose delivered to various sections of the patient. The current study aims to develop and validate an innovative method of using depth-sensing cameras and 3D printing techniques for TBI treatment planning and compensator fabrication.

Methods:

A tablet with an integrated depth-sensing camera and motion tracking sensors was used to scan a RANDO™ phantom positioned in a TBI treatment booth to detect and store the 3D surface in a point cloud format. The accuracy of the detected surface was evaluated by comparing extracted body thickness measurements with corresponding measurements from computed tomography (CT) scan images. The thickness, source to surface distance, and off-axis distance of the phantom at different body section were measured for TBI treatment planning. A detailed compensator design was calculated to achieve a uniform dose distribution throughout the phantom. The compensator was fabricated using a 3D printer, silicone molding, and a mixture of wax and tungsten powder. In vivo dosimetry measurements were performed using optically stimulated luminescent detectors.

Results:

The scan of the phantom took approximately 30 s. The mean error for thickness measurements at each section of phantom relative to CT was 0.48 ± 0.27 cm. The average fabrication error for the 3D-printed compensator was 0.16 ± 0.15 mm. In vivo measurements for an end-to-end test showed that overall dose differences were within 5%.

Conclusions:

A technique for planning and fabricating a compensator for TBI treatment using a depth camera equipped tablet and a 3D printer was demonstrated to be sufficiently accurate to be considered for further investigation.

1. INTRODUCTION

Stem cell transplantation is a treatment that eliminates and replaces a patient’s own stem cells in order to treat hemato-oncological blood diseases.^1–4 In the case of hematopoietic stem cell transplantation, total body irradiation (TBI), is a common preparative regimen with the goal of destroying malignant cells or suppressing the recipient’s immune system thereby preventing immunologic rejection of transplanted bone marrow⁵ or blood stem cells.^6,7 In comparison with chemotherapy, TBI is simple to administer, economical, and can easily penetrate regularly throughout the body regardless of blood flow rate.^8–10

TBI aims to deliver a homogeneous dose to the entire body.^4,11–14 While a variety of TBI techniques exist, most deliver radiation from a medical linear accelerator (LINAC) with an extended source to surface distance (SSD) setup. Typical setups use large treatment fields with beams directed anterior-to-posterior and posterior-to-anterior (AP/PA technique) with the patient in a standing position, or with the beams directed toward the right and left lateral surfaces of the patient (bilateral TBI) with the patient sitting or laying supine on a couch.¹⁸ Compensators are commonly used to modulate the TBI treatment beam and enable a more uniform dose along the patient’s body.^15,16

Recently there have been a number of studies demonstrating new techniques for TBI: Chui and colleagues developed a gravity-oriented compensator to deliver uniform dose with an arc field with a patient lying on the floor.¹⁷ It delivers a highly uniform dose profile in a flat phantom but showed limitations in measuring the thickness of the patient. Gallina and colleagues presented a water compensator wherein the water level in each cell is controlled in real time to modify the dose distribution.¹⁸ It was less time-consuming and more comfortable for the patient but the system is too complicated for widespread adoption. Additional techniques utilizing dynamic couch motions and multileaf collimator (MLC) modulation are also currently under investigation.^19,20

The manual design and creation of lead compensators have conventionally been used to compensate for varying separation through the body.^21,22 To create a compensator, the patient’s position and dimensions are measured at several segments throughout the body. The thickness of each segment of the compensator is determined based on the SSD and thickness for the corresponding body segment. Strips of thin lead are then added to the compensator at each segment to modulate the radiation beam, making the dose to these several segments more uniform. The processes of measuring the patient and fabricating the compensator are typically manual in nature and require significant time to complete. Measurements of the patient are also subject to the inaccuracies inherent to the manual measurement process. In order to create a more streamlined patient workflow we propose a technique wherein a 3D camera is used to obtain the measurements necessary to design a compensator after which a 3D printer is used to fabricate the compensator. In this study, we present a proof-of-concept validation study for this technique.

2. MATERIALS AND METHODS

As a proof-of-concept experiment, the full workflow for preparing and verifying a TBI compensator was performed using an anthropomorphic phantom.

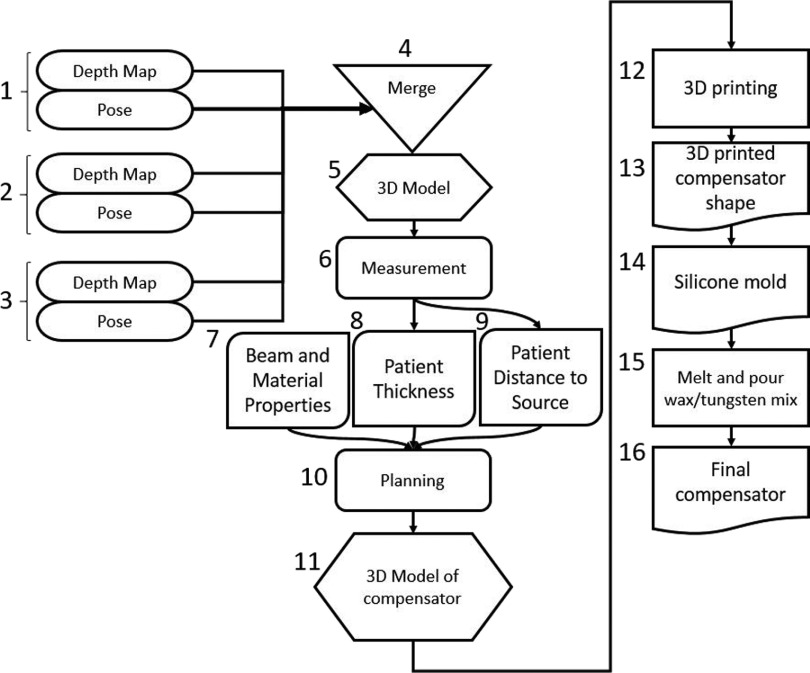
The process involved obtaining a 3D model of the phantom using a 3D camera, calculation of the necessary compensator thickness for each body segment in order to produce a uniform dose, and fabrication of the compensator. The delivered dose was measured at several segments of the phantom to verify the accuracy of the process. The dosimetric evaluation of the compensator was consistent with the guidelines from TG29 of the Radiation Therapy Committee of American Association of Physicists in Medicine (AAPM).⁵ The complete method for fabricating the 3D-printed compensator is given as a flowchart in Fig. 1. The treatment setup used in the study utilized AP/PA beams with the gantry rotated such that the beam was delivered parallel to the floor with the collimator rotated to 45°. The phantom was placed in a booth, with an acrylic spoiler on the beam facing surface.

FIG. 1.

A flowchart of the method for measuring a patient with a 3D camera and fabricating a TBI compensator with a 3D printer. A scan of a patient is performed with a depth camera during which several depth images are acquired [(1)–(3)]. These images are merged, using information from the camera pose saved at the same time each frame was acquired, (4) to make a 3d model of the patient (5). This model is then measured (6) to determine patient thicknesses (8) and source to surface distance (9). These data are combined with beam data and the experimentally determined material properties of the proposed compensator (7) to plan the necessary compensator thickness for each body level (10). The planned compensator thicknesses are then combined into a 3D compensator model (11). 3D printing (12) is then used to create the compensator shape (13). This shape is used to create a silicone mold (14), into which a wax/tungsten mixture (15) is poured to make the finalized compensator (16) for TBI treatment.

2.A. 3D model generation

To make a complete 3D model, an anthropomorphic phantom (RANDO™, Phantom Laboratory, Salem, NY, USA) was scanned using a tablet equipped with a depth-sensing camera (Project Tango Developer Kit, Google, Inc., Mountain View, CA, USA). The tablet contains an inertial measurement unit (IMU), wide angle motion tracking camera, and a projected light depth-sensing camera. Information from the IMU and wide angle camera enables the tablet to determine its pose, or position in 3D space, relative to its starting location at all times. The depth-sensing camera enables the tablet to capture a point cloud (PC), or a set of 3D points, that represents objects within its field of view.^23–25

The phantom was placed in the treatment position within the room and scanned with the tablet. The scan was complete by capturing frames from the depth camera while rotating tablet approximately 300° about the superior–inferior axis of the phantom with the entire phantom remaining within the field of view at all times. Each frame, as well as the pose of tablet at the time each frame was acquired (as determined by the IMU and motion tracking camera), was stored to the internal memory of tablet. This information was then exported to another computer where the frames were merged together to create a surface model of the phantom.^26,27 Since the points in each frame were reported in a coordinate space attached to the tablet, each frame was rotated and translated according to the pose of the tablet at the time it was captured. This enabled the points from multiple frames to be combined together to produce a single model of the phantom. Due to inaccuracies in the pose estimation of the tablet, some manual alignment of frames was necessary to produce an acceptable model of the phantom. In order to determine the geometric accuracy of the 3D scan, a computed tomography (CT) scan of the phantom was also obtained. Corresponding measurements of the phantom were made using the 3D model and the CT scan and compared.

2.B. Treatment planning and compensator design

Once the phantom had been scanned, the separation, source to surface distance, and off-axis distance for several critical body segments were measured using the 3D model. The body was divided into 8 segments from forehead to hip with reference points selected to be consistent with current clinical practice. These data were used to calculate the desired MU to be delivered to each body section at the prescription dose,

$${\displaystyle \text{MU}=\frac{D_{\text{pre}}}{k\cdot \text{TMR}\cdot S_c\cdot S_p\cdot {\left(\frac{f}{f^{\prime }}\right)}^2\cdot \text{OAR}\cdot \text{TF}},}$$ (1)

where MU is the monitor units, D_pre is the prescription dose, k is the calibration D/MU at the reference condition, and TMR is the tissue-maximum ratio at depth d for the patient-equivalent field size (r_e) at the point of prescription. S_c is the collimator scatter factor for the field size projected at isocenter (r_c), S_p is the phantom scatter factor for the patient-equivalent field size (r_e), f is the source-to-calibration point distance, f′ is the source-to-patient axis distance at the prescription point, OAR_d is the off-axis ratio at depth d, and TF is the transmission factor for the block tray, beam spoiler, or any other absorber placed between the machine diaphragm and the patient.²⁷

In order to determine the effective attenuation coefficient (μ_eff) of the proposed compensator material, several 5 × 5 cm² of the compensator material were prepared with thickness ranging from 0.5 to 4 mm. The material was made by mixing a polypropylene wax (Deurex AG, Germany) and tungsten powder (Buffalo Tungsten, Inc., Depew, NY, USA) in a 1:94 mass ratio.²⁸ The transmission of the material was measured by placing the squares at the center of an acrylic sheet in the accessory tray of a LINAC while a farmer chamber was placed at 10 depths in a 30 × 30 × 30 cm³ plastic water phantom placed at the TBI treatment booth with SSD of 580 cm. An exposure of 4000 MU was delivered at 15 MV at 600 MU/min. Each measurement was repeated three times. Using these measurements, the effective attenuation coefficient $\left({\mu }_{\text{eff}}\right)$ was calculated using the following equation:

$${\displaystyle {\mu }_{\text{eff}}=-\frac{ln\left(\frac{D_{\text{tc}}}{D_0}\right)}{\text{tc}},}$$ (2)

where D_tc and D₀ are doses at the point of compensation with and without the compensator, respectively.²⁷

After the MU s required at different body section and μ_eff of the material was determined, the thickness of the compensator necessary to deliver the determined number of MU s at different body sections was determined,

$${\displaystyle \text{thickness}=-ln\left({\text{MU}}_{sec}/{\text{MU}}_{\text{cen}}\right)/{\mu }_{\text{eff}},}$$ (3)

where MU_sec and MU_cen are the μ_eff at each body section and central axis, respectively, calculated using Formula (1).^27,29 A compensator incorporating these thicknesses was then designed with computer aided design software (SolidWorks, Dassault Systems, Waltham, MA).³⁰ Since the compensator was to be placed in the accessory tray on the head of the LINAC, the height of each section was determined by multiplying the height of each section of the phantom by the ratio of the distance from the source to the tray and the distance from the source to the patient. The width of the compensator was selected to minimize material use, while ensuring the compensator extended well beyond the limits of the phantom.

2.C. Compensator fabrication

The compensator was fabricated by first printing a mold using a fused deposition modeling 3D printer (Makerbot Z18, Makerbot Industries LLC, Brooklyn, NY). Polydimethylsiloxane (PDMS) prepolymer (SYLGARD 184, Dow Corning, Midland, MI, USA)³¹ was placed in the mold and allowed to cure. Once the PDMS had cured, the 3D-printed mold was removed. A mixture of wax and tungsten powder was heated, such that the wax became fluid, and mixed to ensure a consistent distribution of powder throughout the material. A high viscosity wax and thorough mixing were employed to ensure a uniform distribution of the powder throughout the compensator. The heated material was poured into the mold and quickly cooled to room temperature to avoid settling before being removed from the mold. The resulting compensator was then measured with a set of digital calipers (resolution of 0.05 mm).³¹

2.D. Compensator evaluation

The data presented in this section were obtained with a Varian iX LINAC (Varian Medical Systems, Palo Alto, CA). Beams were delivered at 15 MV using an AP/PA technique at an extended SSD of 580 cm. The anthropomorphic phantom was set up in the treatment area of the LINAC room in the same way it had been when the phantom was scanned. The compensator was placed on the LINAC by taping it to a piece of acrylic attached to the accessory tray on the head of the LINAC. The compensator was aligned to its desired location by aligning its shadow in the light field with the phantom. In order to minimize potential alignment error, the vertical extents of the compensator were matched to the phantom. A prescribed dose of 120 cGy was delivered at 15 MV. Optically stimulated luminescence radiation detectors (OSLD) (Landauer, Inc., Glenwood, IL, USA) were placed on the phantom’s anterior surface at the following locations: forehead, chin, neck, suprasternal notch (SSN), xiphoid, umbilicus (center), hip, and thigh. The calculated radiation dose was delivered using 15 MV from a Varian iX LINAC. After irradiation, each OSLD was read three times on a microStar reader (Landauer) that had been calibrated using clinical treatment beam at the reference condition to determine a conversion factor from light output from the OSL material to dose.^32–35 The midline dose was calculated by converting the measured surface dose to D_max dose, and then using inverse square correction and TMR to determine the midline dose. The formula used was

$${\displaystyle \text{Midline}\text{dose}={\left(\frac{\text{SSD}}{\text{SAD}}\right)}^2\cdot \text{TMR}\cdot F_{\text{sur}\_\mathrm{corr}}\cdot \text{NanoDot}\text{reading}.}$$ (4)

3. RESULTS

3.A. Accuracy of the tablet generated 3D model

Several frames acquired with the depth-sensing camera during a 30-s scan were aligned in software to produce a 3D model of the phantom. Images of the phantom, a 3D model generated from the CT scan, and the tablet generated PC model are shown in Fig. 2. The thickness measurements of several body sections taken from the PC model and CT were tabulated in Table I. The mean difference (absolute value) was 0.48 ± 0.27 cm with the maximum absolute difference occurring at the level of the hips/pelvis.

FIG. 2.

(a) A photograph in the treatment setup. (b) CT based (c) and tablet generated PC models of RANDO™ phantom.

TABLE I.

Comparison of thickness measurements of the phantom taken from the CT or PC based models.

Measurement point	Thickness of point cloud data (cm)	Thickness of CT image (cm)	Error (cm)
Forehead	20.20	19.34	−0.86
Chin	15.30	14.90	−0.40
Neck	13.00	13.49	0.49
SSN	15.70	15.29	−0.41
Xiphoid	21.40	21.24	−0.16
Umbilicus (center)	20.50	20.25	−0.25
Hip/pelvis	22.40	21.50	−0.90
Thigh	16.10	16.43	0.33
Average magnitude of error (std. dev.)			0.48 (0.27)

3.B. Compensator fabrication

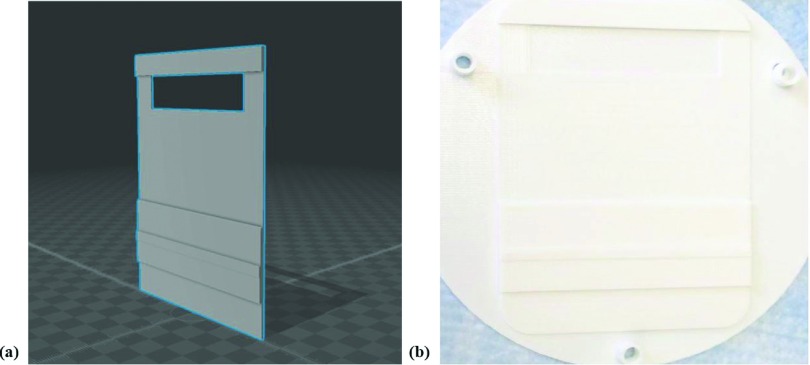
A 3D model of the designed compensator is shown in Fig. 3. The model was created by a computer aided design application and was placed on LINAC by taping it to a piece of clear acrylic that was cut to fit in the accessory tray on the head of the LINAC.

FIG. 3.

(a) The 3D model of a compensator, created by a computer aided design application, and (b) the 3D-printed shape of the compensator used to create a silicone mold for shaping the wax/tungsten powder mixture.

The effective attenuation coefficient of the compensator material was determined to be 0.041 mm⁻¹. The determined section by section MU and compensator thickness is shown in Table II. After fabrication, the final compensator was measured with a set of digital calipers (see Table II). Average fabrication error was 0.16 ± 0.15 mm with the maximum error, occurring at the chin, reaching 0.38 mm.

TABLE II.

The valence evaluation between ideal lead thickness and actual compensator thickness.

Measurement point	Calculated transmission (%)	Planned compensator thickness (PT) (mm)	Actual compensator thickness (AT) (mm)	IT-AT (mm)
Forehead	0.96	0.9	0.9	0
Chin	0.92	2.0	1.62	0.38
Neck	0.91	2.4	2.09	0.31
SSN	0.93	1.7	1.54	0.16
Xiphoid	0.99	0.1	0	0.10
Umbilicus (center)	1	0	0a	0
Hip/pelvis	1	0	0a	0
Thigh	0.93	1.9	1.92	−0.02
Average magnitude IT-AT (std. dev.)				0.16 (0.15)

Note: IT = Ideal Compensator Thickness; PT = Planned Compensator Thickness; AT = Actual Compensator Thickness.

^aIdentical values of ideal lead thickness and actual compensator thickness.

3.C. Compensator evaluation

The mean absorbed dose at critical points on the phantom measured with the compensator in place is shown in Table III. The mean dose at midline was 120.5 cGy and showed differences up to 4.6%. The in vivo measurement result in the end-to-end test of the body surface showed that the overall dose difference was within 2.96 cGy. The average value of midline dose standard deviation was 3.30 cGy.

TABLE III.

The value of the corrected nanoDot reading, midline dose, and the difference compare to the prescription dose.

Measurement point	Corrected nanoDot reading	Midline dose (cGy)	Standard deviation of midline dose (cGy)	%Diff. 120
Forehead	132.98	114.5	5.96	−4.6
Chin	133.29	121.2	0.76	1.0
Neck	134.96	125.9	5.45	4.9
SSN	135.48	122.7	2.23	2.3
Xiphoid	138.19	117.2	3.24	2.3
Umbilicus (center)	141.43	121.3	0.86	1.1
Hip/pelvis	139.03	116.5	4.01	−3.0
Thigh	137.98	124.4	3.92	3.7

Note: %Diff. 120: difference compare to the prescription dose.

The standard deviation of midline dose discrepancies from the prescription does of 120 cGy (%Diff. 120) was 3.23% and the average magnitude of deviation was 2.86%. As seen in Table III, the head, xiphoid, and hip had given a slight underdose and the rest of the areas received a slight overdose. The maximum difference occurred at the neck, but all values were within 5% acceptance criteria.

4. DISCUSSION

TBI has been used for over decades, in decreasing cancer cells and response of immune system, since it was first introduced by Chaoul and Lange in 1923. AP/PA TBI offers a more homogenous dose distribution than bilateral TBI but requires partial transmission block, such as lung block. Khan and colleagues have suggested that measured and expected doses should agree to within ±5% and dose uniformity on the patient should be within ±10% of the prescribed dose.^9,36 In order to achieve such uniformity, it is necessary to measure and adjust for differences in body thickness for different sections of the body. Current techniques are manual, time-consuming, and subject to human error. The technique demonstrated in this paper seeks to overcome these issues by providing a fast patient data capture (∼30 s) followed by an off-line analysis for the compensator design. The designed compensator was then fabricated using a 3D printer in a process that utilizes a reusable, lead free, compensator material, and that removes the majority of manual processing. The fabrication method is also capable of providing fine-grained variations in thickness not possible with lead strips.

During the 3D scan of the phantom, it is necessary to image all of the surfaces that may be required for measurements. In practice, it is best to ensure that all intervening surfaces are imaged as this aids with frame-to-frame alignment and overall model quality. As noted above, small errors in the pose of the tablet accumulated over time, necessitating manual alignment between frames. The observed errors in pose were generally the greatest with respect to rotations and the maximum errors observed were approximately 10°. While manual alignment is not an ideal method, the results in Table I indicate that the errors introduced by pose inaccuracies and the manual alignment were small. It should also be noted that pose tracking 3D model generation from depth camera frames is an active area of research and we expect future depth cameras to exhibit improved performance for both aspects of operation.^37,38

Fabrication errors in the compensator would also be expected to improve with additional advancements in molding technique. The 3D-printed compensator shapes were evaluated to be within 0.1 mm of the desired thickness, indicating that errors were introduced in the molding process.

The results of the in vivo evaluation of the compensator indicate that the largest deviation from prescribed dose occurred at the forehead and neck (Table III). While these sections showed the largest deviation in thickness measurement when the 3D scan was compared to CT data (Table I), the error is less than 1 cm. Since the necessary compensator thickness at these levels was determined to be 0 cm, there was no difference between the ideal and actual compensator for these sections (Table II). It may be possible that the difference is due to dose measurement uncertainty, as the variation amongst the three OSLDs placed at each of these levels was high (Table III). While the dose at areas of each segment away from the reference point was not investigated, the variation in body thickness, SSD, and off-axis ratio within each segment is assumed to be small.

While not demonstrated in this study, the data acquisition, processing, and fabrication methods demonstrated lend themselves to inclusion in a fully automated workflow. In particular, the technique is much simpler to implement and requires less specialized equipment than the methods presented by Chui and Gallina.^17,18 The effects of the compensator design based on point cloud data were apparent in the current TBI treatment planning methodology. The 3D-printed result provides the possibility to create a compensator for each patient in a time-efficient, repeatable manner. This technique allows the compensator thickness profile and the dose distribution to be calculated more easily and potentially more accurately. In future studies, we plan to extend our methods to create continuous thickness varying 2D compensator to deliver more accurate dose to TBI patients.

5. CONCLUSION

A technique for planning and fabricating a compensator for TBI treatment using a depth camera equipped tablet and a 3D printer was demonstrated to be sufficiently accurate to be considered for further investigation. 3D scanning using the tablet was shown to be accurate to within 1 cm when compared with CT data of an anthropomorphic phantom and dose uniformity with the fabricated compensator was within 5%. 3D scanning and printing techniques hold the potential to improve the efficiency and accuracy of the compensator design and fabrication for TBI treatments.

CONFLICT OF INTEREST DISCLOSURE

The authors have no COI to report.