An empirical extrapolation scheme for efficient treatment of induced dipoles

Abstract

Many cutting edge force fields include polarization, to enhance their accuracy and range of applicability. In this work, we develop efficient strategies for the induced dipole polarization method. By fitting various orders of perturbation theory (PT) dipoles to a diverse training set, we arrive at a family of fully analytic methods — whose nth order is referred to OPTn — that span the full spectrum of polarization methods from the fast zeroth-order approach that neglects mutual dipole coupling, approaching the fully variational approach at high order. Our training set contains many difficult cases where the PT series diverges, and we demonstrate that our OPTn methods still deliver excellent results in these cases. Our tests show that the OPTn methods exhibit rapid convergence towards the exact answer with each increasing PT order. The fourth order OPT4 method, whose costs are commensurate with three iterations of the leading conjugate gradient method, is a particularly promising candidate to be used as a drop-in replacement for existing solvers without further parameterization.

I. INTRODUCTION

Modern classical simulation methods use increasingly elaborate physics, such as multipole moments^1–11 and polarization,^12–20 to describe molecular interactions. The extra flexibility of these next-generation models affords accurate descriptions of interactions over a range of chemical environments, but introduces a computational penalty; it is important to devise algorithms that minimize this penalty in order to effectively sample configurational space. Polarization allows modeling of electron cloud distortions in response to the local electric field and is commonly effected by Drude oscillators^{12–18,21,22} or induced dipoles.^3,23–40

A Drude oscillator is simply a pair of particles with equal and opposite charges, connected by a harmonic spring. One of the particles is tethered to the atom whose polarizability is to be simulated, while the other moves in response to the field; thus providing the desired redistribution of the charge density. Because the Drude particles experience the field due to both the nuclei and the other Drude particles, minimization of the energy with respect to the Drude particle positions is formally an iterative self-consistent field (SCF) procedure. The simple charge-on-a-spring nature of Drude oscillators means that their treatment closely mirrors the classical treatment of nuclei, which makes the adaptation of existing codebases to include Drude polarization quite a straightforward, popular approach.

Induced dipoles are very closely related to Drude oscillators; instead of forming a “finite difference” dipole at each polarizable center using point charges, an analytic dipole is created. The ensuing need to evaluate dipole-dipole interactions leads to more complicated mathematical expressions than are required for the Drude model, which makes implementation into existing codes difficult. However, with fewer pairwise interactions to evaluate than for the Drude model, and with multipole evaluation algorithms being actively developed, the induced dipole strategy is widely used. The induced dipoles are defined as a response to the field resulting from the fixed charge distributions as well as the induced dipoles on other centers, so obtaining them is formally a self-consistent procedure, as for the Drude oscillators.

To avoid the computationally expensive process of self-consistently evaluating polarization, extended Lagrangian (EL) techniques have been developed for Drude oscillators,^14,15,21 induced dipoles,^3,41 and fluctuating charges.⁴² The EL approach propagates the electronic and nuclear degrees of freedom simultaneously and is therefore a classical analog to the Car-Parinello ab initio dynamics method. The choice of mass of the Drude particle can be important in the EL scheme; too light a mass will necessitate short timesteps, while too heavy a mass will cause difficulty in maintaining separation of nuclear and electronic degrees of freedom. Introducing dual thermostats for the nuclear and electronic degrees of freedom helps to maintain adiabatic separation and permits the use of timesteps commensurate with conventional dynamics simulations.¹⁴ Moreover, a potentially promising hybrid (EL/SCF) method has recently been developed that permits loose SCF convergence to be used, starting from a propagated EL guess; the resulting method offers very good energy conservation with conventional MD timesteps.⁴³

While the EL and hybrid EL methods offer much promise for efficient, scalable simulations when run under suitable conditions, we will focus on the problem of obtaining induced dipoles using methodology that is compatible with conventional integration techniques. Many numerical solvers exist for self-consistently obtaining induced dipoles but, for reasons that will be outlined in Section II, care must be exercised when using them as instabilities may result from overly permissive convergence criteria. To address this instability, while maintaining efficiency, we recently developed a strategy¹⁹ to obtain an analytic representation of induced dipoles; the analytic nature of this polarization method makes it a close relative of conventional, fixed point charge methods even though it encompasses the many-body character of induced dipoles. Based on perturbation theory (PT), our approach is equivalent to the variational, self-consistent approach at infinite order, when in the convergent regime. By analyzing the properties of the PT series, we developed an extrapolation procedure to approximate the infinite-order solution using only low order solutions. In this work, we identify deficiencies in the previous extrapolation procedure and consider a more pragmatic fitting approach to combine the lowest orders of the PT series, resulting in a series of accurate, efficient, and analytic expressions for induced dipoles.

II. THEORY

The polarization energy for a system of N induced dipoles μ can be obtained from a 3N × 3N coupling tensor T and the electric field due to permanent multipole moments, E, at the polarizable centers

$${\displaystyle U=\frac{1}{2}{\mathit{\mu }}^T\mathbf{T}\mathit{\mu }-{\mathbf{E}}^T\mathit{\mu }.}$$ (1)

The tensor T comprises two components,

$${\displaystyle \mathbf{T}={\mathit{\alpha }}^{-1}-\mathcal{T},}$$ (2)

whose diagonal blocks are the 3 × 3 inverse atomic polarizabilities, and the off-diagonal terms 𝒯 are the 3 × 3 coupling terms that describe the damped⁴⁴ interactions between induced dipoles on different centers, whose exact formulation is not important for the present discussion. For brevity, we will focus on the case where α is isotropic; the extension to anisotropic tensors is straightforward and has been discussed in Ref. 34 as have the details of the coupling terms 𝒯.

Stationarity of Eq. (1) defines the variational condition for the induced dipoles

$${\displaystyle \mathcal{R}\equiv {\left(\frac{\partial U}{\partial \mathit{\mu }}\right)}^T=\mathbf{T}\mathit{\mu }-\mathbf{E}=\mathbf{0}}$$ (3)

and the polarization energy gradient, with respect to nuclear positions r, is

$${\displaystyle \frac{\mathrm{d}U}{\mathrm{d}\mathbf{r}}=\frac{\partial U}{\partial \mathbf{r}}+\frac{\partial U}{\partial \mathit{\mu }}\frac{\partial \mathit{\mu }}{\partial \mathbf{r}}.}$$ (4)

The final term in Eq. (4) which is due to dipole response, contains derivatives of the induced dipoles $\frac{\partial \mathit{\mu }}{\partial \mathbf{r}}$. As noted in Sec. III, the μ derivatives are problematic to evaluate because μ itself is obtained as a numerical solution to Eq. (3). Because the residual ℛ appears as a factor of the dipole response terms, they are usually neglected. The extent to which the residual ℛ can be assumed to be zero depends on how tightly the numerical solution for μ is obtained; if loose convergence criteria are employed, the dipole response terms could be too large to safely neglect, leading to unstable trajectories.

The PT approach can be derived by introducing an ordering parameter, λ, into the T coupling tensor

$${\displaystyle \mathbf{T}={\mathit{\alpha }}^{-1}-\lambda \mathcal{T}}$$ (5)

and expressing the resulting dipoles using a power series in λ,

$${\displaystyle {\mathit{\mu }}_n={\mathit{\mu }}_{\left(0\right)}+\lambda {\mathit{\mu }}_{\left(1\right)}+{\lambda }^2{\mathit{\mu }}_{\left(2\right)}+\cdots +{\lambda }^n{\mathit{\mu }}_{\left(n\right)}.}$$ (6)

The nth order dipole comprises n + 1 components, which are labeled with their order in parentheses. Substituting the expanded quantities, Eqs. (5) and (6), into Eq. (3) and collecting by powers of λ yields analytic expressions for the induced dipoles at each order

${\displaystyle {\mathit{\mu }}_{\left(0\right)}=\mathit{\alpha }\mathbf{E},}$${\displaystyle {\mathit{\mu }}_{\left(1\right)}=\mathit{\alpha }\mathcal{T}\mathit{\alpha }\mathbf{E},}$${\displaystyle {\mathit{\mu }}_{\left(2\right)}=\mathit{\alpha }\mathcal{T}\mathit{\alpha }\mathcal{T}\mathit{\alpha }\mathbf{E},}$${\displaystyle \phantom{{}_2}⋮\phantom{\mathit{\alpha }\mathcal{T}\mathit{\alpha }}⋮}$${\displaystyle {\mathit{\mu }}_{\left(n\right)}=\mathit{\alpha }{\left(\mathcal{T}\mathit{\alpha }\right)}^n\mathbf{E}.}$ (7)

The nth order energy is simply

$${\displaystyle U_{\mathrm{n}}=-\frac{1}{2}{\mathbf{E}}^T{\mathit{\mu }}_n.}$$ (8)

The spectrum of PT methods represents a family of methods that each offer a different level of compromise between accuracy and efficiency. One crucial difference between a loosely converged variational solution and a PT approach is that the former requires additional linear equations to be solved to properly obtain the nuclear energy gradient, while the latter is analytically differentiable.

In our original development of PT,¹⁹ we focused on the odd terms of the U_n series, which we denoted U_PTn. Because each dipole component in the U_PTn series converges exponentially, a three-point exponential fit U_PT∞ = U_PTn − bexp(−cn) is an effective way to reach the infinite order limit, under the assumption that all components converge at the same rate. To obtain the three unknowns, U_PT∞, b, and c, would require {U_PT0, U_PT1, U_PT2} or, equivalently, {U₁, U₃, U₅}. Our extrapolated PT (ExPT) method reduced these requirements by additionally assuming that the exponent c is fixed for all systems, reducing the fit to just two points

$${\displaystyle {\mathit{\mu }}_{\mathrm{ExPT}}=c_0{\mathit{\mu }}_1+c_1{\mathit{\mu }}_3,}$$ (9)

which has a single empirical parameter due to the constraint c₀ + c₁ = 1.

Inspection of Eq. (7) reveals that generation of μ₃ also yields μ₀, μ₁, and μ₂ of which only μ₁ is utilized in the ExPT approach. In this work, we adopt a more empirical approach to determine the coefficients of the PT dipoles, which remedies the wasted information in ExPT by using a more general ansatz

$${\displaystyle {\mathit{\mu }}_{\text{OPTn}}=M_0{\mathit{\mu }}_0+M_1{\mathit{\mu }}_1+M_2{\mathit{\mu }}_2+\cdots +M_n{\mathit{\mu }}_n,}$$ (10)

where the coefficients {M₀, M₁, …, M_n} are to be determined by a fitting procedure. The resulting nth-order optimized PT method is denoted OPTn. With this notation, ExPT is a special case of OPT3, with coefficients {0, c₀, 0, c₁}. To parameterize the functional form, we will consider a diverse collection of 50 systems, described in Section III and the supplementary material.

For each system, we minimize the objective function

$${\displaystyle S=\sum _{\alpha }^{3N}{\left({\mu }_{\alpha }-{\mu }_{\text{OPTn},\alpha }\right)}^6}$$ (11)

using standard minimization techniques,⁴⁵ where the summation runs over all 3N dipole components for each system. The residual is normally raised to the second power in conventional least squares fitting, but we use a power of 6 here to favor reduction of outliers, thus creating a more uniform distribution of errors; we deem this uniformity of errors more important than obtaining a lower RMS error.

Analogous to Eq. (8), the OPTn energy is

$${\displaystyle U_{\text{OPTn}}=-\frac{1}{2}{\mathbf{E}}^T{\mathit{\mu }}_{\text{OPTn}}=-\frac{1}{2}{\mathbf{E}}^T\left(M_0{\mathit{\mu }}_0+M_1{\mathit{\mu }}_1+\cdots +M_n{\mathit{\mu }}_n\right)=-\frac{1}{2}{\mathbf{E}}^T\left(m_0{\mathit{\mu }}_{\left(0\right)}+m_1{\mathit{\mu }}_{\left(1\right)}+\cdots +m_n{\mathit{\mu }}_{\left(n\right)}\right),}$$ (12)

where, for convenience, we have expressed the induced dipoles in terms of their components using the relationship

$${\displaystyle m_i=\sum _{j=i}^n{M}_j.}$$ (13)

Because the components of μ_OPTn have an analytic form, computing polarization energy derivatives are very straightforward

$${\displaystyle \frac{\partial U_{\text{OPTn}}}{\partial \mathbf{r}}=-{\mathit{\mu }}_{\text{OPTn}}^T\frac{\partial \mathbf{E}}{\partial \mathbf{r}}+\frac{1}{2}\sum _l^n{m}_l\sum _{m=0}^{n-1}{\mathit{\mu }}_{\left(m\right)}\frac{\partial \mathcal{T}}{\partial \mathbf{r}}{\mathit{\mu }}_{(l-m-1)}.}$$ (14)

The leading term of Eq. (14) is present in both the variational and “direct” (where 𝒯 is neglected) polarization algorithms. The additional n(n + 1) terms arising from dipole response can be efficiently evaluated by caching the field and field gradient due to {μ₍₀₎, μ₍₁₎, …, μ_(n−1)} during the formation of the induced dipoles, Eq. (7).

The terms required to implement the energies and forces for OPT are similar to those needed in the variational algorithm, and we have implemented the OPT method in development versions of CHARMM,^46,47 TINKER,⁴⁸ and OpenMM.⁴⁹ All computations described hereafter were performed using the TINKER⁴⁸ simulation package.

Constructing a dataset that spans the complete chemical and configurational space is not possible, so our choice was motivated by the following considerations. Inspection of the AMOEBA parameters reveals that there is little variety in the polarization parameters for many main group atoms, with the exception of some highly polarizable species such as sulfur and chloride ions. By including some archetypal protein, RNA, and DNA systems, we have many representatives of the “typical” polarizabilities and we must be sure to include systems with sulfur and chlorine atoms to also consider the outliers. We also include some liquids with a range of dipole moments to probe homogeneous systems and solvated ions to represent the more problematic inhomogeneous liquid systems.

The resulting set of 50 training systems is detailed in the supplementary material and, for the following discussion, are loosely categorized into three groups: homogeneous liquids, solvated ions, and biological systems. The homogeneous liquids are 13 small, organic molecules including benzene, acetonitrile, dimethyl sulfoxide, ammonia, and methanol. These systems were chosen to represent a range of polarities. Because doubly charged cations are known to be tough to describe, our seven solvated ion systems comprise a 34.14 Å cubic box containing 1331 water molecules, as well as the same water box containing 1, 2, 3, 4, 5, and 6 MgCl₂ molecules. The biological systems include a range of proteins, RNA and DNA systems, harvested from the protein databank (PDB). The liquid and ion systems were equilibrated at 300 K, while the biological systems were subjected to a crude energy minimization, followed by 100 steps of dynamics to eliminate any bad contacts.

III. RESULTS

We parameterized the OPTn (n = 0–4) family of methods for each of the 50 test molecules using Equation (11) with tightly converged variational dipoles as the reference. To test the sensitivity of the optimization solutions to the initial guess coefficients, a number of starting conditions were tried. First, we used the guess coefficients {0, 0, …, 0, 1}, which correspond to the nth order perturbation theory method U_n. Second, we tried the uniform guess $\{\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n}\}$, which weights all PT components equally. Finally, after observing the oscillatory convergence of the PT series, discussed below, we tried the guess $\{0,0,\dots ,0,\frac{1}{2},\frac{1}{2}\}$ which is the mean of the two highest orders of PT, $\frac{U_n\hspace{0.17em}+\hspace{0.17em}{U}_{n-1}}{2}$. Although all of these guesses have coefficients that sum to one, consistent with the ExPT treatment, Eq. (9), no restrictions were placed on the sum of the coefficients during the optimization. For all systems in the training set and all orders of OPTn optimization, the final parameters were identical for all starting guesses.

The resulting parameters are shown alongside the resulting RMS induced dipole errors in Table I. We included OPT0 in our parameterization because this uses the same “direct” polarization algorithm as the iAMOEBA method. Direct polarization is obtained by completely neglecting coupling between induced dipoles, averting the need for any expensive matrix-vector products. In iAMOEBA, the entire set of bonded and noncovalent parameters were re-optimized to compensate for the lack of mutual dipole coupling; our PT0 parameterization simply introduces a polarization scale factor, which is equivalent to uniformly scaling all polarizabilities.

TABLE I.

Results of the OPTn fitting procedures.^a

Method	M0	M1	M2	M3	M4	$\sum _j\hspace{0.17em}{M}_j$	Dipole error (D)b
OPT0	1.044 (0.142)					1.044	0.084 (0.036)
OPT1	0.412 (0.103)	0.784 (0.096)				1.197	0.029 (0.012)
OPT2	−0.115 (0.081)	0.568 (0.079)	0.608 (0.126)			1.062	0.012 (0.006)
OPT3	−0.154 (0.036)	0.017 (0.120)	0.657 (0.050)	0.475 (0.125)		0.995	0.006 (0.003)
OPT4	−0.041 (0.032)	−0.176 (0.026)	0.169 (0.154)	0.663 (0.027)	0.374 (0.124)	0.987	0.004 (0.003)

^aThe M_j coefficients shown are those defined in Eq. (10). Standard deviations across the data set are shown in parentheses.

^bThe mean RMS error in the OPTn induced dipoles across the training set of 50 molecules with respect to the tightly-converged, variational reference values.

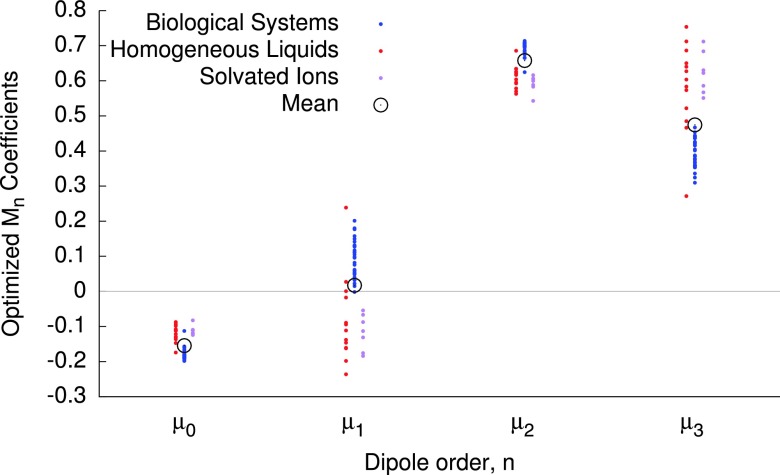
Dipole response force errors notwithstanding, a target RMS change in the dipoles of 0.01 D has been considered a sufficient stopping criterion for iterative dipole solvers in previous works.^29,50 Although modern protocols commonly specify much tighter convergence of at least 10⁻⁵ D, we will consider 0.01 D as a desirable threshold error for our methods to deliver, keeping in mind that the forces are always evaluated exactly in these approximations, unlike the loosely converged variational solutions. Inspection of Table I reveals that the mean error in the OPT2 dipoles is 0.012 D across the data set, while for OPT3 this drops to 0.006 D; we will therefore focus much of our discussion on the OPT3 method. To visualize the spread in ideal third order coefficients (i.e., those that are optimal for each system) for each system in the training set, whose mean defines the consensus OPT3 coefficients, those ideal coefficients are plotted in Figure 1, alongside the OPT3 coefficients. The homogeneous liquids and ionic liquids adopt similar coefficients, while the biological systems generally adopt more positive M₁ and more negative M₃ coefficients than the ions and liquids. Among the ionic liquids, the single outlier possessing a large M₁ and corresponding low M₃ is benzene, which, like the biological systems, has a relatively low dielectric. For the even terms in the series, the coefficients for all systems are more closely clustered.

FIG. 1.

Ideal third-order coefficients for each system in the training set, classified into three broad categories, described in the text. The mean of the set of 50 values for each coefficients constitute the OPT3 coefficients, which are depicted as hollow, black circles.

The OPT3 coefficients closely resemble an average of the two highest orders of perturbation theory, which is akin to the quantum mechanical Møller-Plesset MP2.5 method⁵¹ that is an average of the MP2 and MP3 methods, consistent with the oscillatory convergence patterns. On the other hand, the ExPT coefficients have a rather different structure, while the μ₂ coefficient in the OPT3 method is the largest for any of the four μ_n components, that same coefficient is zero in the ExPT approach as a direct consequence of the assumption that all dipole components converge exponentially, with the same exponent. Those same assumptions lead to the constraint that the ExPT coefficients must sum to one; although no such constraint was applied in the OPT3 fit, the coefficients sum to 0.995.

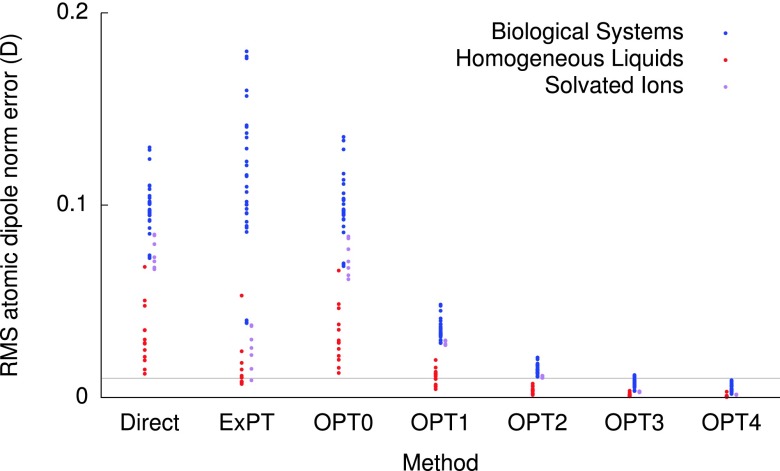
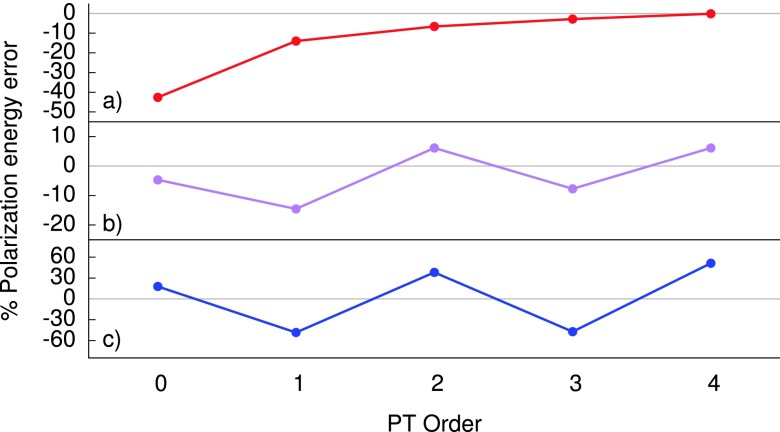
Figure 2 shows the RMS atomic induced dipole errors for each system in the training set, for a range of induced dipole algorithms. The ExPT method offers a significant reduction in the errors for the liquids and ionic systems upon which it was initially tested, but performs very poorly for the biological systems, for which even the direct algorithm offers better performance. The poor performance of ExPT for highly inhomogeneous systems can be explained by the plots in Figure 3, which depict the convergence behavior of the PT series for some representative cases for each of the three system types in our training set. The odd terms in the series are convergent for the MgCl₂ and acetic acid cases but divergent for the protein test. Our preliminary development of ExPT included a test that was divergent but exhibited convergence in the lower orders of PT before diverging; for cases such as the dry protein crystals examined herein, the lower odd orders of PT are often divergent, causing ExPT to fail. The PT0 method offers little improvement over the direct algorithm, while PT1 introduces massive improvements, especially for proteins, with all systems possessing an RMS induced dipole error below 0.05 D. The OPT4 method offers only a marginal improvement over OPT3, reducing the mean RMS induced dipole error by just 0.002 D.

FIG. 2.

The RMS atomic induced dipole errors for each system in the training set, broken down by system type, for a range of induced dipole algorithms. The horizontal gray line depicts an error of 0.01 D.

FIG. 3.

Observed behavior of polarization energy errors for the perturbation series as a function of series order for (a) a monotonically convergent case (acetic acid) (b) oscillatory convergence (6 MgCl₂ in 1331 waters), and (c) a divergent case (albumin binding protein, 1PRB).

Despite the very disparate convergence patterns observed in our training set, optimized perturbation theory performs very well across the board. Remembering that the OPT3 energy is mostly an average of U₂ and U₃, with a slight emphasis on the former, it is evident from Figure 3 that such a strategy should work. In the monotonically convergent case, both values fall close to the exact result and are pushed closer by the small amount of U₀ that is subtracted. When the series is oscillatory, whether convergent or not, the averaging of contiguous PT methods yields a result with close to zero error by virtue of the odd and even terms bounding the exact result. A detailed breakdown of the induced dipole errors, OPT3 force errors, and convergence analysis of the PT series, for each system in the training set is provided in the supplementary material.

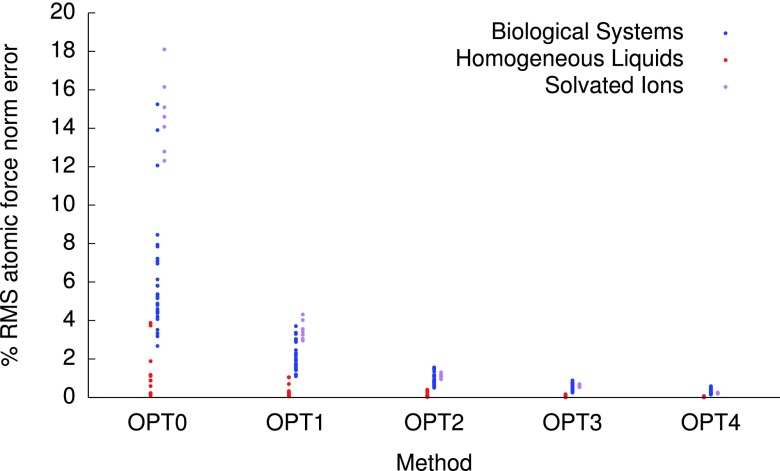
Figure 4 shows the mean error in the norm of the force on each atom, plotted for each of the OPTn methods, for all systems in the training set. The homogeneous liquids clearly represent a far less challenging system than the other cohorts; the OPT0 method produces errors in the atomic force norms within 4% of the exact value, and this drops down to 0.4% for OPT2. The solvated ions have force errors as large as 18%, which reduces below 2% for OPT2 and just 0.7% for OPT3; a similar trend is observed for the protein systems, with OPT3 delivering errors within 0.9%.

FIG. 4.

Mean absolute errors in the norm of the atomic forces, for each system in the training set for the OPTn methods developed in this work.

To gauge the quality of condensed phase properties, Table II shows some computed properties of water for OPTn (n = 0-4), ExPT and the variational reference method computed from a 1 ns NPT simulation of 729 AMOEBA03 water molecules.²⁹ The density appears to be well modeled for all methods, with the sequence OPT1 to OPT4 offering systematically decreasing errors from −0.5% for OPT1, falling to just −0.2% for OPT3 and culminating in agreement between OPT4 and the reference; OPT0 is fortuitously close for this property. The self-diffusion is harder to model correctly, with a very large deviation observed for OPT0, and even OPT3 overestimates the water self-diffusion by 10%. As is the case for the density, complete agreement is obtained between OPT4 and the reference calculation. The error in the mean potential energy is −0.19 kcal mol⁻¹ per molecule for OPT3, dropping to just 0.01 kcal mol⁻¹ per molecule for OPT4, with similar fluctuations observed for both. The formulation of ExPT considered only energies, so its deviation of just 0.08 kcal mol⁻¹ per molecule is unsurprising. This shows that accurate energies can be captured by third order methods. However, the fact that ExPT provides the poorest description of the density for all methods tested here shows that properties beyond the energy should be considered in the model development. Our use of the dipoles as a target for parameterization in OPTn has yielded a series of methods that offer systematically improving performance for describing water.

TABLE II.

Properties for AMOEBA water, computed from 1 ns NPT simulations, using a range of polarization algorithms.^a

Method	ρb	Dc	Vd
ExPT	0.992 (0.005)	1.63 (0.07)	−9.100 (0.072)
OPT0	0.999 (0.005)	4.52 (0.15)	−7.984 (0.063)
OPT1	0.995 (0.007)	1.41 (0.05)	−9.510 (0.073)
OPT2	0.997 (0.007)	1.49 (0.08)	−9.313 (0.070)
OPT3	0.998 (0.006)	2.04 (0.06)	−8.831 (0.072)
OPT4	1.000 (0.006)	1.85 (0.06)	−9.015 (0.073)
SCF	1.000 (0.006)	1.85 (0.06)	−9.025 (0.068)

^aThe SCF entry corresponds to tightly converged, variational reference values.

^bThe density (g cm⁻³) with standard deviation in parentheses.

^cThe self-diffusion constant (10⁵ cm² s⁻¹) with standard deviation in parentheses.

^dThe mean potential energy per molecule (kcal mol⁻¹) with standard deviation in parentheses.

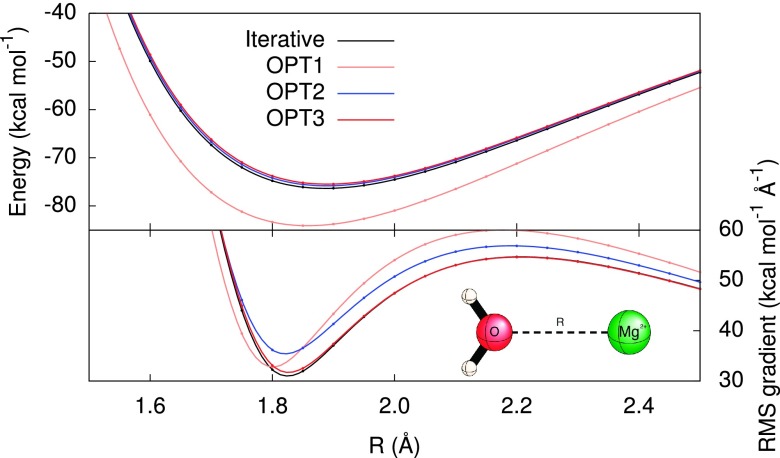
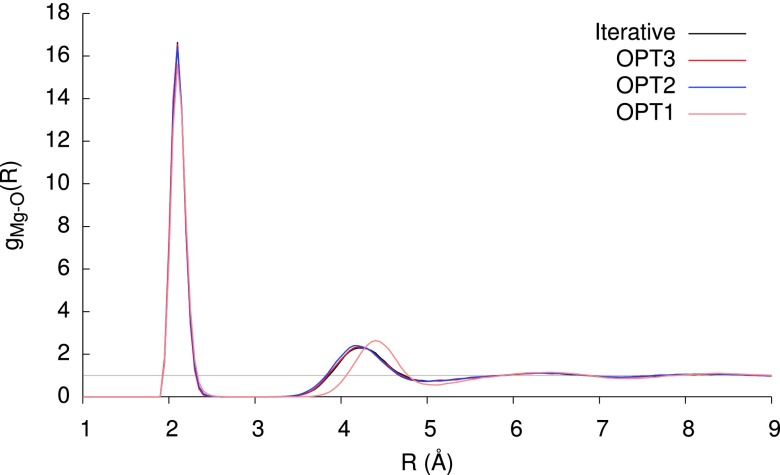
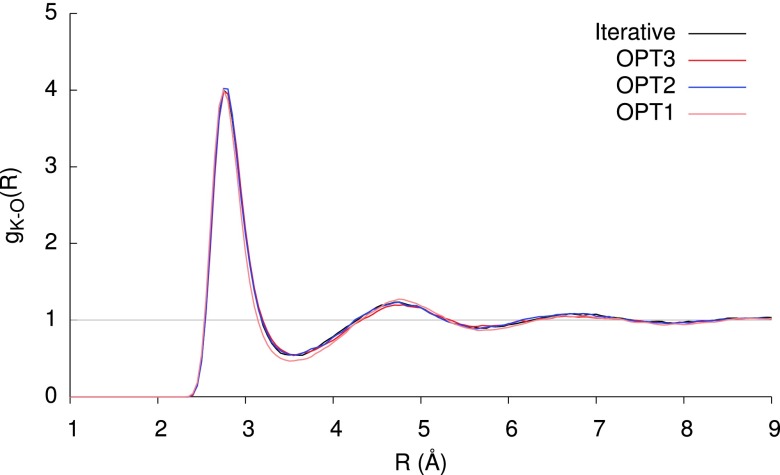
One potential pitfall of a perturbative scheme is the singularity at zero bond length, which could lead to far more extreme divergence of the series than we observe in our training set, in the presence of anomalously short contacts. The use of Thole damping — effectively blurring the point induced dipole — mitigates this, as is evident from Figure 5, which compares the OPTn (n = 1-3) methods to the iterative method in describing the potential energy curve, and derivative thereof, for H₂O⋯Mg²⁺ dissociation along the C_2v axis. At large separations, the polarization effect is small, and at short distances the Thole damping greatly diminishes the magnitude; in these extremes, the agreement for OPT2 and OPT3 with the variational reference curve is excellent. Around the equilibrium region, the OPT2 and OPT3 methods yield a slight under-binding of ca. 1 kcal mol⁻¹, but both greatly outperform the simpler OPT1 method, which greatly overestimates the polarization stabilization across the entire potential curve. The plot of the RMS force on the system reveals that, although the OPT2 energies very closely track the reference values, the forces are quite systematically overestimated along the dissociation coordinate, with a minimum that occurs at a slightly shorter bond length. To investigate the effects of these errors, we simulated a periodic system comprising a single MgCl₂ molecule in 1331 waters for 500 ps, in an NVT ensemble at 300 K; the resulting radial distribution functions are shown in Figure 6. The OPT2 and OPT3 distribution functions are almost indistinguishable from the variational reference. Although OPT1 correctly predicts a sharp peak at 2.1 Å, corresponding to the first solvation shell, the second solvation shell is erroneously placed at 4.4 Å instead of 4.2 Å. As a test of performance for monovalent ion solvation, Figure 7 shows the analogous radial distribution function for KCl. As for MgCl₂, all three OPT methods tested provide a very accurate description of the first solvation shell. The weakly-structured second and third solvation shells are described very well by OPT2 and OPT3, with OPT1 offering a very slightly over structured description in the vicinity of the second shell.

FIG. 5.

Constrained potential energy scans for the H₂O⋯Mg²⁺ dimer, using the variational, OPT1, OPT2, and OPT3 methods. The top plot depicts the potential energy while the bottom shows the RMS atomic force.

FIG. 6.

Radial distribution function for the Mg²⁺–O pair, derived from 500 ps simulation of MgCl₂ in 1331 water molecules at 300 K.

FIG. 7.

Radial distribution function for the K⁺–O pair, derived from 500 ps simulation of KCl in 1331 water molecules at 300 K.

To further probe the effect of simulation conditions on the parameterization, we studied ubiquitin with the 58 water molecules found in the PDB file, the same system with no water molecules and the same system with a total of 3071 water molecules to fill the unit cell; the resulting ideal third order coefficients are { − 0.18, 0.06, 0.70, 0.42}, { − 0.18, 0.10, 0.70, 0.39}, and { − 0.19, 0.08, 0.70, 0.40}, respectively. The same molecule with no waters and no periodic images has ideal third order coefficients of { − 0.18, 0.05, 0.70, 0.42}. Such insensitivity to periodicity and solvation effects supports the idea that a universal set of coefficients may be employed for all molecular systems.

Our preliminary implementation provides functionality for users to determine ideal expansion coefficients for any system of interest. This offers a remedy for any difficult cases that may be encountered, for which the consensus OPTn coefficients may not yield satisfactory agreement with reference values. However, any coefficient tailored this way must be explicitly reported in the interests of reproducibility.

Recent efforts to improve the efficiency of induced dipole treatments have yielded some promising methods, including conjugate gradient (CG) SCF solvers³⁴ and SCF using a propagated EL guess.⁴³ Although the number of iterations needed to converge the conventional SCF equations to a given tolerance depends on the algorithm used, the nature of the system under study and the desired convergence level, we will briefly compare the computational cost of these methods to OPTn. Reference 43 reports that the leading CG solver with a predictor guess³⁴ achieves convergence of the dipoles to 10⁻⁶ D in 5 SCF cycles, which generates a drift of 4.63 × 10⁻⁶ kcal mol⁻¹ ps⁻¹ for a water box. Because CG requires a matrix-vector product (MVP) in the setup and another in each iteration, this corresponds to 6 MVPs, which provides a good measure of the overall polarization cost. By introducing a thermostat for the auxiliary degrees of freedom used to obtain the dipole guess in the hybrid EL/SCF approach, similar energy conservation can be achieved by converging the SCF equations to just 10⁻² D, which requires 4 iterations of CG (5 MVPs);⁴³ good energy conservation (∼3 × 10⁻⁵ kcal mol⁻¹ ps⁻¹) is also realized when a criterion of 10⁻¹ D is used, at a cost of 3 iterations (4 MVPs).

The ExPT method conserves energy¹⁹ due to the forces being calculated analytically, but the water properties computed herein show some significant deviations with respect to SCF reference values. The OPT3 method, like ExPT, has analytic forces and costs 3 MVPs but provides much better properties for water. Moreover the OPT3 method produces accurate dipoles over a diverse range of compounds, where ExPT fails; this is because the former uses a less constrained parameterization scheme and makes no a priori assumptions about the convergence behavior of the PT series. Adaptation of an ExPT code to use OPT3 coefficients is trivial due to the similarity of their formulation. Similarly, generalizing the implementation for arbitrary-order OPTn is also straightforward.

IV. CONCLUSIONS

Building on our previous work, we have developed a new series of perturbation theory techniques for induced dipoles; the current work proposes new extrapolation techniques to accurately approximate the exact solution with only a few low order terms. By considering a diverse set of molecules and simply optimizing the coefficients for each term in the PT series up to nth order, we have developed the OPTn family of methods. The resulting methods form a hierarchy of approaches that span the spectrum from the “direct” algorithm, where mutual coupling is completely neglected, approaching the exact solution. One key feature of the OPTn methods is that they are fully analytic at all levels of approximation. While forces from the more approximate, lower order OPTn methods are less accurate than their higher order analogs, these forces are just as precise as the energies — leading to energy conservation. In contrast, attempting to accelerate iterative solvers by loosening convergence criteria for the variational induced dipole method yields a family of methods that are accurate but lack precision; this reduced precision can manifest itself in catastrophically erroneous forces, so caution must be exercised when attempting to tune such approaches for dynamics.

The OPT3 method offers excellent computational efficiency, requiring just three of the rate-limiting matrix-vector products and is able to deliver dipoles with an RMS error of just 0.006 D across a diverse set of 50 molecules. More extensive testing is being performed to understand how these small errors manifest themselves in various chemical properties. The data presented herein suggest that OPT3 is the minimal possible OPTn method that may be considered for use as a drop-in replacement for iterative algorithms, without any reparameterization of the force field. The more approximate OPT2 method may not be accurate enough to be considered as a drop-in replacement for CG solvers, and its use may require reparameterization of the underlying force field. We note that an algorithm equivalent to OPT1 is already used as the polarization algorithm for the POSSIM force field,⁵² with the parameters defined accordingly. The OPT4 method requires one more matrix-vector product than OPT3, but appears to be very robust with respect to accurately describing a range of compounds with a universal set of coefficients. We do not recommend pursuing higher order methods (n > 4), as they would not be competitive with currently used SCF methods.^34,43,53

SUPPLEMENTARY MATERIAL

See supplementary material for details of the training set, and a listing of the ideal coefficients, induced dipole errors, PT series convergence patterns, and OPT3 atomic force error distributions for each member of this set.