Offspring Socioeconomic Status and Parent Mortality Within a Historical Population

Abstract

Considering a network approach to health determinants, we test the hypothesis that benefits of high socioeconomic status (SES) may be transmitted up the generational ladder from offspring to parents. Studies that examine own SES and own health outcomes, or SES of parents and outcomes of young or adolescent children, are common. Those that investigate SES of offspring and their association with parental health are rare. Employing data from a historical population of individuals extracted from a comprehensive population database that links demographic and vital records across generations, this study tests the hypothesis that higher offspring SES associates with lower parental mortality after controlling for parental SES. The sample includes 29,972 individuals born between 1864 and 1883 whose offspring were born between 1886 and 1920. SES is operationalized using Nam-Powers occupational status scores divided into quartiles and a category for farmers. Models assess mortality risk after age 40. Included is a test for whether effects are proportional across parents who died younger and older. Estimated life expectancies across categories of offspring SES conditioned on parental SES are calculated to illustrate specifically how differences in SES relate to differences in years lived. Results indicate a longevity penalty for those whose offspring have low SES and a longevity dividend for those with high-SES offspring. The influence of offspring attributes on well-being of parents points to fluid and myriad linkages between generations.

Introduction

A robust and nearly axiomatic association has been found linking socioeconomic status (SES) and adult mortality spanning decades, nations, and regions, based on a range of measures, investigative approaches, and data sets (e.g., Antonovsky 1967; Balarajan and McDowall 1988; Fukuda et al. 2004; Hurd et al. 1999; Kitagawa and Hauser 1973; Mackenbach et al. 1997; Marmot et al. 1984; Marshall et al. 1993; Olausson 1991; Pappas et al. 1993; Sundquist and Johansson 1997; Townsend and Davidson 1982; Valkonen 2003; Zhu and Xie 2007). Variation in human longevity by SES provides impetus for examining the association in ways that seek an understanding of underlying mechanisms (Braveman et al. 2010; Link et al. 2008; Queen et al. 1994). In this regard, a number of perspectives have been brought to bear (e.g., Adler and Rehkopf 2008; House et al. 2005; Kristenson et al. 2004; Lantz et al. 2001). Proposed pathways differentiate health across psychological and social factors that are more proximate to health outcomes, such as access to services (Macintyre 1989), stress (Pearlin 1989), behaviors (Lantz et al. 1998; Sudhano and Baker 2006), environmental conditions (MacDonald et al. 2009), and social support (House et al. 1990; Krause 1997).

Fundamental cause theory (Link and Phelan 1995; Link et al. 2008) connects these pathways by suggesting that higher SES permits access to more and better-quality resources and psychological and social assets that allow individuals to avoid risks and adopt effective coping strategies that subsequently lengthen life. The fundamental nature of SES lies in the fact that higher SES enhances access to these superior resources regardless of historical time or place. The specific SES measures used may differ across time and place, but the fact that higher SES enhances access to salutary resources is fundamental, leading those with higher SES to enjoy longer lives.

If, as fundamental cause avers, access to resources is part of the explanation for an association between SES and mortality, it is reasonable to ask about the origins of these resources. Most of the literature on SES and mortality considers own SES, implying that resources exist strictly at the level of the individual. For instance, individuals with high income have monetary resources that allow them to purchase health care that might be unavailable to those with low income. High levels of education provide individuals with knowledge, locus of control, and ability to negotiate a health care system.

The current study begins by assuming, in concordance with a network approach to health determinants, that SES resources can be exchanged across individuals within a social milieu, particularly along generational lines. Research has indicated that the benefits of SES for health can be transmitted down the generational ladder, as it were, from parents to offspring (Bradley and Corwyn 2002; Smith et al. 2009). Few studies have examined SES associations in the other direction—up the generational ladder, from offspring to parent. Yet, non-SES characteristics of offspring have frequently been shown to associate with health of parents. For instance, social support provided by offspring has long been found to be beneficial for parental health (Berkman and Syme 1979; Cornell 1992), and migration of offspring is connected to health outcomes of parents (Krause 1997; Kuhn et al. 2011).

If an offspring’s resources can be leveraged in ways that are distinct from one’s own for the purpose of maintaining good health, then one would expect associations to exist between offspring SES and parental mortality. Studies that have examined offspring SES and parental mortality have generally confirmed such an association, although these investigations are rare and do not offer consensus. Zimmer et al. (2007) showed that for Taiwan, where older parents tend to rely heavily on their adult children for support, education of offspring is associated with mortality. However, that study suggested that the association exists mainly among parents with a serious disease, and that offspring may be helpful only after health problems appear. After a parent develops health problems, an offspring can assist, for instance, by helping to purchase heath care, negotiating the health care system, or providing support in other ways. Other studies have indicated associations in places where there is less frequent reliance on children for support. Friedman and Mare (2014) used Health and Retirement Survey data in the United States to demonstrate that the education of sons and daughters have independent influences on mortality of older parents. The authors explained this as being partly a function of the way in which the younger generation impacts upon health behaviors of the older. Torssander (2013) reported that for Sweden, offspring affect parental mortality through a wide range of resources that can be proffered by adult progeny with high levels of education.

The current study extends this analysis. To measure SES, we use Nam-Powers SES scores (Nam and Terrie 1982) and simultaneously consider scores of parents and their adult offspring. Nam-Powers SES scores are based on reported occupation. Previous studies that have investigated offspring SES and parental health have tended to consider offspring education as the SES indicator (Friedman and Mare 2014; Torssander 2013; Zimmer et al. 2007). The importance of occupation as a determinant of health has, however, been established elsewhere. A notable example is a set of analyses using data from the British Whitehall Studies (Adler et al. 2008; Marmot et al. 1991). Nam-Powers SES scores have the advantage of being derived in such a way that takes into account the association between an occupation and standard levels of education and income that are associated with that occupation (Nam and Boyd 2004). These scores are, therefore, broad indicators of SES and represent the concept more generally than discrete measures of education, income, or occupation.

Employing a large Utah-based multigenerational data resource, our analysis considers a historical population whose birthdates occurred more than 100 years ago and that has completely died out. The strategy of using a historic sample has several advantages. Subjects lived in the late nineteenth century through the end of the twentieth century, a period characterized by rapid development of health care systems, increasing life expectancies, and improving living conditions. Considering a fully deceased population means that our sample has all experienced the event we are examining (death). When all subjects are deceased, it increases statistical power of survival analysis (Hsieh and Lavori 2000). Obtaining objective information on usual occupation for both parents and offspring requires the use of vital or other administrative records (i.e., not a retrospective report), a requirement met with the use of death certificates. Accordingly, cohort studies of intergenerational SES in which all individuals are deceased provide advantages with respect to the minimization of recall bias for SES.

In summary, this study tests a basic but rarely examined hypothesis: high SES of offspring associates with a reduction in parental mortality after parental SES is controlled for.

Methods

Data Source

Data are drawn from the Utah Population Database (UPDB), a resource that links extensive and varied sources of high-quality population-based records. The UPDB has been used for numerous demographic analyses, and these have resulted in many well-cited scientific publications over the last several decades. Examples of scholarship demonstrating typical use of the data over the years include Anderton et al. (1987), Cawthon et al. (2003), Hanson et al. (2015), Mineau and Trussell (1982), and Mineau et al. (1979). The early development of UPDB was based on family group sheets provided by the Genealogical Society of Utah. These sheets contain basic three-generation information about family members, including dates of birth and death as well as place of residence. Because individuals are linked into genealogies that are connected to vital (death) records, the UPDB provides extensive multigenerational pedigrees that allow study of SES characteristics spanning generations.

In 1904, the Utah Department of Health assumed responsibility for creating death certificates for all individuals who died in Utah. Extensive information about the collection of death records can be found on the Utah state website (Utah Department of Health n.d.). In 1904, 3,266 decedent certificates were registered in Utah. As expected, these numbers have risen, and by 2014, the UPDB was receiving and integrating approximately 16,000 death certificates annually into its database. All deaths registered are recorded into UPDB. Since the earliest recording, deaths certificates in Utah have included a logging of the usual lifetime occupation of the decedent. In the current study, we use this information to connect the occupations of parent and offspring to parental mortality.

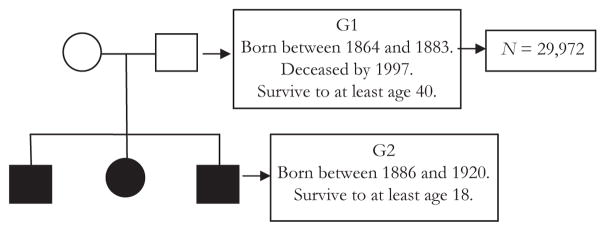
Figure 1 is a schematic illustrating the two-generational data structure used in this study. The parent generation, G1, is a cohort born between 1864 and 1883 who survived to at least age 40. There are 29,972 such individuals in the database who meet selection criteria. We impose the survival restriction to age 40 for several reasons. First, individuals included in the study would have mostly completed fertility. Second, occupation on death certificates would largely reflect long-term work history. Third, mortality after 40 mostly captures intrinsic mortality related to aging, and therefore causes of death would be sensitive to resource availability. The younger generation, G2, consists of the offspring of G1 born between 1886 and 1920. Here, the birth year restriction guarantees that these offspring were at least age 18 in 1904 and therefore would have an occupation recorded on a death certificate. The upper year restriction means that almost everyone in G2 was deceased by 2012, which is the latest year of recorded data.

Fig. 1.

Two-generation data structure

Although the sample size is large, restrictions are in place as a result of substantive needs of the research as well as practical constraints of data availability. Substantively, individuals are required to live to a minimum age so that valid measures of occupation can be obtained. Parental birth years are chosen for specific reasons. Because death certification began in Utah in 1904, deaths had to have occurred in a period such that occupations derived from death certificate data would be available for both parents and offspring, and births of offspring occurred early enough that almost all would have died by 2012, the last year for which data are available. In a strict sense, then, the results of this study will be generalizable to the historical population of parents born between 1864 and 1883 who had offspring at least age 18 by the time of death.

For those born and deceased during this period, we included every observation with available data. Data are not available in some instances, including when parents did not die in Utah and cases in which all offspring died outside Utah. In other instances, some but not full information about offspring is available. For our analysis, if information about one offspring was available, the parental record is represented in the data. Although some unavailability of data is unavoidable, earlier formal assessments of sample bias in the UPDB have suggested that the types of limitations are not likely to alter parameter estimates (Gagnon et al. 2009).

Utah Context

The Utah population is in some ways historically distinct. Many in Utah are descendants of Mormon resettlement migration. However, analysis of the historic population of Utah has indicated that the population is generally representative of other historic populations in the United States with similar Northern European pedigrees (Bean et al. 1990; Jorde 2001; Zick and Smith 2006). Further, studies of the demographic transition in Utah indicate that patterns were relatively similar to those of the rest of the country, although fertility rates were somewhat higher in Utah, and mortality rates were somewhat lower (Lindah-Jacobson et al. 2013; Moorad et al. 2011).

Because it is pertinent to the generalizability of the current analysis, a supplementary analysis was completed using historical U.S. Census Bureau data. This analysis compared distributions for occupational categories in Utah with the rest of the country for the early part of the twentieth century. The distributions are remarkably similar. The Utah population had a somewhat higher proportion involved in mineral extraction occupations, while the rest of the country was a bit more represented by manufacturing jobs. However, virtually no differences were found across other categories, such as clerical-type jobs and agricultural positions. On the surface, then, it does not seem that inequalities were more or less acute in Utah in comparison with most of the United States at that time. Ultimately, it is difficult to assure that the results in the current study are precisely comparable because of the historical circumstances that brought many Utahan residents to the state. Yet, there is no evidence to suggest that Utah would be somehow extraordinary. Many earlier studies using UPDB data (some of which we cited earlier), which were found to be generalizable to the U.S. population on many levels, add some level of reassurance as well.

Measures

Information about dates of death of G1 and occupation of G1 and G2 is obtained from death certificates. The occupations listed on the death certificates are coded into Nam-Powers SES scores (Nam and Powers 1983). Charles Nam and Mary Powers devised these scores so that they reflected not only occupational status but also the income and educational requirements associated with that occupation, thereby creating a broad indictor that encompasses a range of markers thought to be associated with the concept of SES (Nam and Boyd 2004). Nam-Powers socioeconomic (NP-SES) scores range from 1 to 99, with a higher score reflecting an occupation that links with higher education and income typically connected to the reported occupation. These scores have been used in numerous studies of SES and health (e.g., Meyer et al. 2004; Steenland et al. 2003). For G1, NP-SES scores are obtained for both spouses, and the resulting score is the highest nonmissing value for the couple. Nam-Powers scores are missing for cases where there is no recorded occupation (e.g., homemaker, student, retired). Given sex differences in occupational structures, the measure for G1 is most often based on husband’s occupation.

For G2, NP-SES scores are also the highest nonmissing scores between offspring and the offspring’s spouse. Our analysis assumes that given multiple offspring, and therefore multiple measures of SES for G2, resources that flow from offspring to parent are well represented by the offspring with the greatest quantity of resources and hence the highest SES. We tested this assumption with sensitivity analyses using alternative methods for measuring G2 SES: for instance, the average NP-SES score across all offspring with available information. We found no substantive differences in results when using alternative SES measures. However, the magnitude of the effect varied slightly, with the largest effect observed when maximum SES of children was used.

For both G1 and G2, NP-SES is divided into groups. Given the birth years of the group under study, a large percentage is listed as “farmers.” Accordingly, a separate category is created for farmers. After removing farmers from the NP-SES distribution, the remaining scores are grouped into quartiles by sex and generation (G1 and G2). The quartiles are similar across sexes; small differences across generations arise because occupational structures changed over time. The terms occupational quartile and SES are used interchangeably.

UPDB data were also used to construct additional key demographic variables. These characteristics have been shown to influence mortality and may be associated with SES of parents and offspring (Smith et al. 2009). For G1, they include birth order (firstborn versus other), sibship size, birth year, birth place (rural-born, urban-born, or not born in Utah, birthplace missing), number of sons, number of daughters, affiliation (active member, inactive member, nonmember) within the Church of Jesus Christ Latter-day Saints (LDS or Mormons, a proxy for religiosity and health behaviors) (Mineau et al. 2004), age first child was born, and age last child was born. Sibship size is divided into categories of no siblings or number of siblings is unknown, 1–4, 5–7, and 8 or more. Sibling information is not available when full information on family structure is missing. Cases where no sibling information is available are grouped with the no sibling category because we cannot distinguish between these two groups. For these cohorts, families with no children are very small (approximately 1 %).

Table 1 provides means and standard deviations for variables used in this analysis. Means for categorical variables are equivalent to proportions; multiplying these values by 100 would provide the percentage in various categories.

Table 1.

Means and standard deviations for study variables by sex

	Females		Males
	Means	SD	Means	SD
N	15,033		14,939
Parent SES (G1)
Lowest quartile	.132	.34	.135	.34
Second quartile	.102	.30	.107	.31
Third quartile	.155	.36	.170	.37
Highest quartile	.159	.37	.170	.38
Farmer	.452	.50	.421	.49
Offspring SES (G2)
Lowest quartile	.192	.39	.205	.40
Second quartile	.234	.42	.235	.42
Third quartile	.287	.45	.278	.45
Highest quartile	.235	.42	.229	.42
Farmer	.052	.22	.054	.23
Covariates (G1)
Firstborn	.304	.46	.330	.47
Rural-born	.298	.46	.321	.47
Urban-born	.540	.50	.545	.50
Non-Utah-born	.162	.37	.135	.34
Number of sons	3.18	2.10	2.83	2.09
Number of daughters	3.08	2.11	2.72	2.10
Active LDS	.668	.47	.556	.50
Inactive LDS	.137	.34	.166	.37
Non-LDS	.195	.40	.278	.45
Age at first birth	23.50	4.56	26.98	5.00
Age at last birth	36.90	5.58	38.83	6.32
Number of siblings
None/unknown	.152	.36	.190	.39
1–4	.157	.36	.158	.36
5–7	.230	.42	.215	.41
8+	.460	.50	.437	.50

Analysis

Parametric survival models were used for these analyses. Alternative distributions were tested, including lognormal, log logistic, Gamma, and Weibull models. The Weibull accelerated failure time (AFT) hazard model produced the best fit. A discrete-time Weibull model, as opposed to continuous time, is used given its capacity to incorporate a piecewise function, which we employ to model nonproportionality effects of SES across time. Discrete-time estimates reported here were compared with the continuous-time AFT model, and both produced similar estimates. Equation (1) illustrates an exponential discrete-time model, which assumes that the hazard function is constant over time:

$$log\mathrm{\lambda }\left(t,\mathbf{x}\right)=\mathrm{\alpha }\left(t\right)+{\mathbf{\beta }}^{\prime }\mathbf{x},$$ (1)

where α(t) is an unspecified function of time, β is the vector of covariates, and x are exogenous covariates. To obtain the discrete-time Weibull distribution, we specify that

$$\mathrm{\alpha }\left(t\right)={\mathrm{\alpha }}_0+{\mathrm{\alpha }}_{1}logt,$$ (2)

where α₁ is the shape parameter (Allison 1982; Kalbfleisch and Prentice 2011). Substituting Eq. (2) into Eq. (1) yields the hazard function for the discrete-time Weibull model:

$$log\mathrm{\lambda }\left(t,\mathbf{x}\right)={\mathrm{\alpha }}_0+{\mathrm{\alpha }}_{1}logt+{\mathbf{\beta }}^{\prime }\mathbf{x}.$$ (3)

G1 mortality is being observed during a period of demographic transition and rapid improvements in population health. To account for birth cohort differences in mortality, we allow each birth year to have a separate baseline hazard (i.e., a fixed effect).

The analytical strategy is to test a series of models that differ in terms of their complexity. We begin with a model that regresses the mortality hazard rate on the G1 occupational quartile controlling for all covariates. In the next model we introduce the G2 occupational quartiles. This is followed by tests for interactions between G1 and G2 occupations (described but not shown).

The test for nonproportionality determines whether associations differ for parents who died at younger versus older ages. The test addresses potential reverse causality in cases where early death of the parent may influence SES of offspring. Accordingly, we consider variation in the effect of SES on mortality separately at ages 40–59 versus 60 and older. We use a piecewise Weibull model (shown in Eq. (4)) that allows the shape parameter to vary pre-/post-age 60 (α₁ and α₂ in Eq. (4)). Using age 60 improves model fit (based on Akaike information criterion (AIC) comparisons). The model is illustrated as follows:

$$log\mathrm{\lambda }\left(t,\mathbf{x}\right)={\mathrm{\alpha }}_0+{\mathrm{\alpha }}_{1}logt\left(40-60\right)+{\mathrm{\alpha }}_{2}logt\left(60+\right)+{\mathbf{\beta }}^{\prime }\mathbf{x},$$ (4)

where α₁ is the shape parameter prior to age 60, and α₂ is the shape parameter at age 60 onward. We compared the results from this model with results from Cox nonproportional hazard models. We detected no substantive differences in results.

We use estimates from the nonproportional models in further calculations. First, we use them to determine estimated probabilities that an individual who reaches a given age will die before reaching the next age, which translate to q_x values in classic life tables. We plot the q_x values by highest and lowest G2 quartiles conditional on G1 occupations held constant at highest and lowest quartiles. We then use the q_x values as input into life table functions to generate sex-specific life tables for each combination of parent and offspring occupation. The life tables allow examination of life expectancy by G2 occupational quartiles conditioned on G1 occupational quartiles. We examine life expectancy across highest and lowest G2 quartiles conditioned on G1 being in the highest and lowest quartile. Given that median lifetime is 70, for illustrative purposes, we plot life expectancies at this age.

Results

Descriptive Results

Table 2 provides the distribution of occupational status of the offspring generation (G2) by occupational status of the parents (G1) based on Nam-Powers scores that are divided into generation-specific quartiles plus farmer. For this historical population, intergenerational mobility was noteworthy. For instance, for G1 females in the lowest quartile of occupation, one-quarter (24.9 %) of their G2 offspring was also categorized in the lowest quartile. A very small proportion was categorized as farmer (2.9 %), and almost three of four were upwardly mobile. Results are fairly similar for G1 males. This generational mobility needs to be interpreted cautiously. First, quartiles are constructed independently for G1 and G2 and are relative to the generation. Therefore, the same occupation does not necessarily fit into the same quartile for G1 and G2. Second, G2 occupation is based on highest scored occupation among all siblings and spouses. Consequently, the results do not represent all aspects of G2 intergenerational mobility but rather provide an indication of the degree to which those in the G1 population with low status had at least one offspring that achieved higher relative status. In addition to upward mobility, we detect the presence of downward mobility. G1 females and males in the highest quartile had a large proportion of offspring in a lower quartile. Also, when G1 is categorized as a farmer, offspring are infrequently farmers. This does not mean that few offspring were farmers but rather that the one offspring with the maximum Nam-Powers score in the sibship was likely to have had a nonfarming occupation.

Table 2.

Distribution of offspring (G2) SES by parent (G1) SES, based on Nam-Powers scores grouped into quartiles plus farmer, by sex

Offspring SES (G2)	Parent SES (G1)
	Lowest Quartile	Second Quartile	Third Quartile	Highest Quartile	Farmer	Total
Females
N	1,986	1,540	2,327	2,392	6,788	15,033
Lowest quartile	24.9	20.7	19.0	15.3	18.6	19.2
Second quartile	27.8	25.6	25.9	18.4	22.5	23.4
Third quartile	25.8	28.2	27.1	30.9	29.4	28.7
Highest quartile	18.6	23.2	26.0	33.9	20.6	23.5
Farmer	2.9	2.3	2.1	1.5	8.9	5.2
Total	100.0	100.0	100.0	100.0	100.0	100.0
Males
N	2,019	1,596	2,493	2,546	6,285	14,939
Lowest quartile	27.2	22.1	20.6	16.5	19.5	20.5
Second quartile	26.8	26.8	25.2	19.0	22.7	23.5
Third quartile	24.8	26.6	27.4	30.1	28.4	27.8
Highest quartile	18.0	22.4	24.7	33.0	19.8	22.9
Farmer	3.3	2.2	2.2	1.5	9.6	5.3
Total	100.0	100.0	100.0	100.0	100.0	100.0

Table 3 shows the average age at which individuals died by parental (G1) SES and offspring (G2) SES. Conditional on survival to age 40, females in the parent generation (G1) lived an average of 74.36 years, compared with 71.43 years for males. Considerable variation, however, is observed across occupational status. Looking at G1 occupation, average age at death was lowest for females in the lowest quartile (73.78 years) and highest for those in the highest (76.14 years), with increasing averages by occupational quartiles. For males, a relatively similar association exists, with lowest average age at death occurring for those in the lowest quartile (69.00) and a higher average age at death for those in the highest quartile (72.16). Looking at average age at death by offspring (G2), SES also shows a clear gradient for males and females. Average age at death when moving from lowest to highest G2 SES quartile increases from 72.79 to 75.62 for females, and from 70.13 to 72.78 for males. Female G1 farmers had an average age at death similar to those in the lowest quartiles, while male G1 farmers had relatively high life expectancy compared with other SES categories. Although this suggests that males benefit more from farming as an occupation, the difference attenuates after controls are added in multivariate models (as shown in Table 4).

Table 3.

Average age at death of parent (G1) by parent (G1) and by offspring (G2) SES and sex of parent (standard deviations are in parentheses)

	Females	SD	Males	SD
Total	74.36		71.43
Parent SES (G1)
Lowest quartile	73.78	(13.19)	69.00	(12.63)
Second quartile	73.87	(13.35)	70.95	(12.59)
Third quartile	74.46	(13.13)	69.66	(12.98)
Highest quartile	76.14	(13.12)	72.16	(12.55)
Farmer	73.97	(13.04)	72.73	(12.53)
p valuea	.00		.00
Offspring SES (G2)
Lowest quartile	72.79	(13.62)	70.13	(12.95)
Second quartile	74.24	(12.96)	70.68	(12.78)
Third quartile	74.74	(12.96)	71.79	(12.63)
Highest quartile	75.62	(12.93)	72.78	(12.46)
Farmer	72.81	(13.39)	71.97	(12.25)
p valuea	.00		.00

^aBased on F test.

Table 4.

Discrete-time Weibull model stratified regression parameter estimates predicting mortality^a

	Females				Males
	Model 1	SE	Model 2	SE	Model 1	SE	Model 2	SE
Parent SES (G1)
Lowest quartile (ref.)	—		—		—		—
Second quartile	−0.001	(0.035)	0.003	(0.035)	−0.100**	(0.035)	−0.098**	(0.035)
Third quartile	−0.052†	(0.032)	−0.046	(0.032)	−0.056†	(0.031)	−0.048	(0.031)
Highest quartile	−0.113**	(0.032)	−0.104**	(0.032)	−0.205**	(0.031)	−0.190**	(0.031)
Farmer	−0.009	(0.027)	−0.008	(0.027)	−0.236**	(0.028)	−0.237**	(0.028)
Offspring SES (G2)
Lowest quartile (ref.)	—		—		—		—
Second quartile			−0.057	(0.026)			−0.014	(0.025)
Third quartile			−0.060*	(0.026)			−0.050*	(0.026)
Highest quartile			−0.082**	(0.027)			−0.093**	(0.027)
Farmer			−0.027	(0.042)			0.001	(0.042)
Firstborn	0.044*	(0.022)	0.045*	(0.022)	0.021	(0.023)	0.020	(0.023)
Rural-born	0.081**	(0.020)	0.076**	(0.020)	0.067**	(0.020)	0.063**	(0.020)
Non-Utah-born	0.664**	(0.025)	0.657**	(0.025)	1.257**	(0.028)	1.254**	(0.028)
Number of Sons	0.024**	(0.006)	0.025**	(0.006)	0.015**	(0.005)	0.018**	(0.005)
Number of Daughters	0.019**	(0.005)	0.020**	(0.005)	0.013**	(0.005)	0.015**	(0.005)
Active LDS	−0.160**	(0.024)	−0.152**	(0.024)	−0.232**	(0.023)	−0.222**	(0.023)
Inactive LDS	0.120**	(0.031)	0.122**	(0.031)	0.043	(0.028)	0.045	(0.028)
Age at Last Birth	−0.007**	(0.002)	−0.007**	(0.002)	−0.008**	(0.002)	−0.008**	(0.002)
Age at First Birth	0.002	(0.003)	0.003	(0.003)	−0.004	(0.002)	−0.003	(0.002)
Number of Siblings
0	−0.093**	(0.033)	−0.095**	(0.033)	−0.133**	(0.034)	−0.135**	(0.034)
1–4	−0.052†	(0.028)	−0.052†	(0.028)	−0.011	(0.029)	−0.010	(0.029)
5–7	—		—		—		—
8+	−0.015	(0.022)	−0.015	(0.022)	0.007	(0.022)	0.007	(0.022)
Constant	−9.415		−9.396		−8.636		−8.620
Shape	1.950		1.951		1.895		1.896
−2 Log-Likelihood	120,000.7		119,990.7		116,580.5		116,564.5

^aCoefficients for year of birth are not shown.

^†p < .10;

^*p < .05;

^**p < .01

Regression Results

Table 4 presents the results of sex-specific, discrete-time Weibull regressions. Because the model predicts the probability of mortality, a negative coefficient is associated with a lower mortality probability—and subsequently, a higher life expectancy—at any age. Model 1 includes G1 SES categories plus covariates. Model 2 adds the SES categories of G2. The lowest quartile is omitted, and the other quartiles (plus farmer) are compared with this reference category.

Model 1 indicates that SES quartile is significantly associated with survival. Females in the third and fourth SES quartiles had significantly lower probabilities of dying in comparison with those in the lowest. For males, all higher-SES quartiles had lower probabilities than the lowest. The effect of being a farmer was protective for men but not for women.

The addition of G2 SES categories (Model 2) improves the model fit for both sexes (females Δ −2LL = 10.0, 4 df; males Δ −2LL = 16.0, 4 df). The coefficients for G1 SES do not change substantially, which indicates that both parent and offspring SES independently affected mortality risk for this historical population. Higher G2 status is associated with improved G1 survival. Being in the lowest quartile for both G1 and G2 is associated with the highest probability of dying, while being in the highest quartile is associated with the lowest probability.

Statistical interactions between G1 and G2 SES were tested, but these did not improve model fit (results not shown). We conclude that mortality is a function of G1 and G2 SES as main effects only.

Other covariates are associated with survival. Being the firstborn is a risk for females. Those born in rural Utah and outside Utah have higher risk in comparison with those born in urban Utah. Increasing numbers of sons and daughters is associated with a greater probability of dying. In relation to non-LDS individuals, being an active member of the church is protective, while being inactive increases risk. An increasing age at last birth is protective. Those without siblings, or those without sibling information available, have lower probabilities of dying than others. These results generally concur with earlier research that has examined early-life social and demographic characteristics and adult mortality using these data (Smith et al. 2002, 2009).

Nonproportional Models

Table 5 shows net estimates for parent and offspring SES using piecewise, discrete-time Weibull models that allow effects to vary by age. Results indicate nonproportionality by parental age, particularly among females, but SES remains an important determinant regardless of whether parents were younger or older at time of death. For both age groups, the effect of parental and offspring SES is stronger when moving up occupational quartiles. For males and females in either age group, offspring in the highest quartile significantly relates to lower risks of dying.

Table 5.

SES parameters for discrete-time Weibull stratified regression results predicting mortality incorporating a piecewise function to model nonproportionality by age of parent death^a

	Females				Males
	40–59	SE	60+	SE	40–59	SE	60+	SE
Parent SES (G1)
Lowest quartile (ref.)
Second quartile	0.048	(0.087)	−0.010	(0.039)	−0.112	(0.074)	−0.098**	(0.074)
Third quartile	−0.077	(0.080)	−0.058†	(0.035)	0.013	(0.064)	−0.074*	(0.036)
Highest quartile	−0.138†	(0.083)	−0.129*	(0.035)	−0.283**	(0.069)	−0.199**	(0.036)
Farmer	−0.048	(0.067)	−0.001	(0.030)	−0.347**	(0.058)	−0.263**	(0.032)
Offspring SES (G2)
Lowest quartile (ref.)
Second quartile	−0.255**	(0.061)	−0.029	(0.028)	−0.006	(0.054)	−0.013	(0.029)
Third quartile	−0.255**	(0.062)	−0.037	(0.029)	−0.076	(0.056)	−0.048†	(0.029)
Highest quartile	−0.317**	(0.066)	−0.062*	(0.030)	−0.205**	(0.061)	−0.080**	(0.030)
Farmer	−0.072**	(0.098)	−0.016	(0.047)	−0.049	(0.094)	0.021	(0.047)
−2 Log-Likelihood	116,339.2				113,897.8

^aModels adjust for other covariates in Table 4 (including firstborn, place of residence, number of sons and daughters, LDS status, age at last and first birth, and number of siblings) and include constant and piecewise shape parameters.

^†p < .10;

^*p < .05;

^**p < .01

Offspring effects are attenuated by parental age. One possible reasons for this is that, as suggested, young parental death may limit the opportunities for offspring to move up SES categories. Therefore, a stronger association between offspring SES and mortality among those who died younger may be a function of the effect of young parental death on offspring SES rather than the reverse. It is possible that the causal connection weakens at older ages because of the insidious effects of mortality selection and the unavoidable reality that individuals surviving to older ages are increasingly similar. This feature of the survival experience of a cohort makes it difficult to detect significant relative risks of almost any risk factor. Nonetheless, the finding that parent and offspring SES associate with parental mortality is consistent across models.

Predicted Probabilities and Life Expectancy

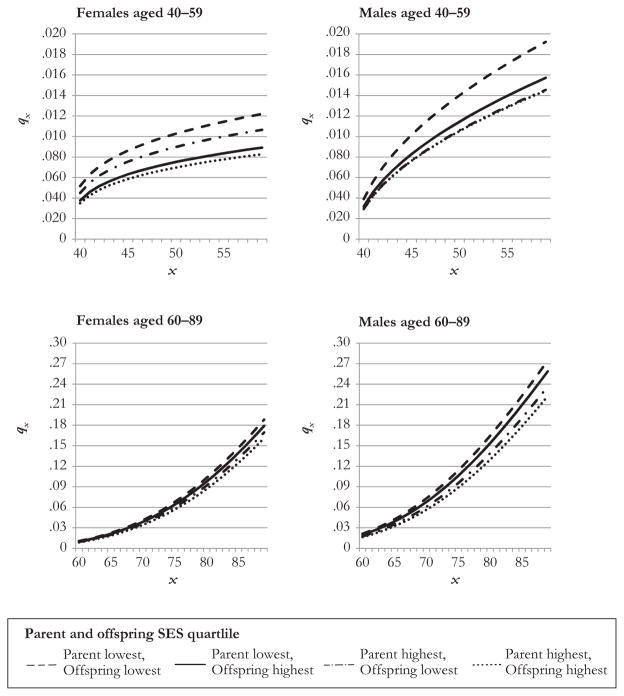
Figure 2 shows the predicted probability of dying at given ages (q_x) for highest and lowest G2 quartiles conditional on G1 SES being highest or lowest, holding other covariates constant at their mean values. Because the model assumes nonproportional mortality before age 60 versus age 60 and older, we present separate graphs for the probability of dying for those aged 40–59 and for those aged 60–89. A general pattern is observed across all ages and sexes: probabilities of dying are highest when both the parent and offspring have the lowest SES, and they are lowest when both the parent and offspring have the highest SES. When SES levels are mixed, highest and lowest mortality probabilities tend to fall in between the extremes. Consistent with Table 5, the effects of offspring SES are larger for those at younger ages.

Fig. 2.

Probability of dying (q) at given ages (x) by lowest and highest offspring (G2) SES quartile, conditioned on lowest and highest parental SES (G1), by sex of parent, for age groups 40–59 and 60–90. Calculated from the discrete-time Weibull regression results in Table 5, holding covariates constant at mean values

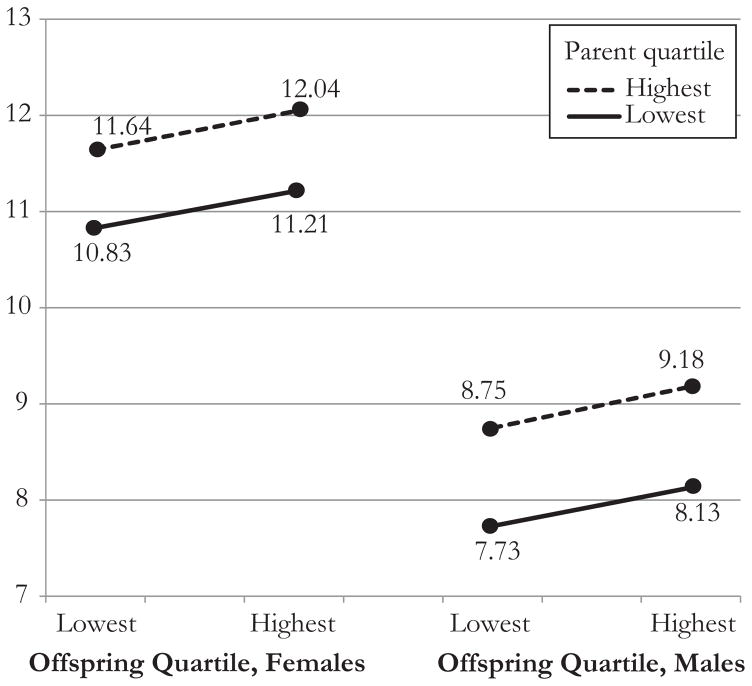
Figure 3 illustrates how these mortality probabilities translate into specific life expectancies. We plot life expectancy at age 70, the median age of survival for the population. The gap between the lines is an indication of an association between SES of G1 and life expectancy. Slopes of the plotted lines depict an association with offspring SES. Increasing SES improves G1 survival for both males and females. For instance, if G2 SES is in the lowest quartile, life expectancy at age 70 is 10.83 for females with the lowest SES versus 11.64 for females with the highest SES—a gain of 0.81 years. For males, the comparable change is 7.73 to 8.75, or an improvement of 1.02 years. The gain in life expectancy across G2 SES is less dramatic but noteworthy. For example, conditional on parental SES being in the highest quartile, life expectancy at age 70 for females is 11.64 when offspring SES is lowest and 12.04 when it is highest, representing a net increase of 0.40 years. Because the total increase in life expectancy for females moving from low-low to high-high SES is 1.21, offspring SES accounts for approximately one-third of the total increase. For males, the increase is from 8.75 to 9.18 years—a net of 0.43 years, or approximately 30 % of the total gain in male life expectancy.

Fig. 3.

Life expectancy estimates at age 70 by offspring (G2) SES quartiles conditioned on parental SES (G1) being in the lowest and highest quartile, by sex of parent. Calculated using the q_x results shown in Fig. 2

Sensitivity Analyses

We conducted supplementary analyses to test the robustness of our results. Two tests are worth reporting. First, parents were required to live to age 40 to be included in the sample, but offspring were required to live only to age 18. At age 40, parents would have more or less completed fertility and would have established a usual occupation noted on a death certificate. Offspring who died in early adulthood may provide a premature or an incomplete measure of his/her SES. We tested whether requiring offspring to live to age 40 resulted in different findings. It did not. Family sizes for this population were large, and if one offspring died young, it was still likely that another lived to at least age 40. Therefore, the NP-SES scores were often based on the offspring that lived to age 40 and not on the ones who died young. In the end, raising the survival requirement only slightly reduced the sample size (because most individuals have more than two children), had a negligible impact on the measures of the Nam-Powers quartiles, and resulted in no substantive difference in the findings.

Second, rather than dividing Nam-Powers SES scores into categories, we tested models that maintained the interval-level score and included these as continuous variables in Weibull regression models. By including both parent and offspring SES in a single model, we could establish whether each had an independent association with mortality and whether the difference in scores across generations (offspring minus parent) was significant. We estimated these models with two variants: (1) with and without farmers to test whether the heaping of scores for farmers made a difference, and (2) with and without quadratic SES terms to test whether there was a nonlinear effect of SES scores. We found that both parent and offspring SES were statistically significant in all models that we tested, paralleling the results provided earlier, and with no evidence of nonlinear effects of SES (for G1 or G2) on mortality risk.

Conclusion

Few studies have examined the association between adult mortality and SES of adult offspring. The limited literature that exists has generally addressed links between offspring education and parental mortality (Friedman and Mare 2014; Torssander 2013; Zimmer et al. 2007). These analyses have suggested that the education of offspring relates to adult mortality risk. Following this line of thinking, the current study examined survival of a historical population of 29,972 individuals across their own and their offspring’s SES, with SES based on their own and their offspring’s occupation. We found a robust association between offspring SES and parental survival after adjusting for parents’ own SES, a result consistent with the study hypothesis. Interactions between parental and offspring SES were not statistically significant, indicating that each generation’s status had an independent influence. Because effect sizes can differ as a parent ages—due to varying impacts of SES on mortality by age, mortality selection, or the possibility that the subsequent SES mobility opportunities for offspring are limited when parents die at younger ages—we considered nonproportional effects of SES. These did not change the conclusion that offspring and parent SES independently affect parental mortality, although the effect was attenuated after the parent reached age 60.

We pointed to the concept of fundamental cause (Link and Phelan 1995; Link et al. 2008) as a way to explain the association between SES and health. The fundamental cause framework suggests that higher SES allows individuals access to more and better-quality social, psychological, or material resources, and these resources are used to avoid health risks and adopt effective coping strategies, especially as new and often poorly understood health threats arise. The current analysis adds a network approach to this idea by showing that associations of SES and mortality can span generations. Therefore, SES resources that can be used to influence health can be based on a broader social (familial) network rather than strictly at the individual level, and parents with low SES can benefit from resources provided by their high-SES offspring. For example, adult offspring with available income can help a parent access and purchase quality health care. Better-educated children can assist their parent by negotiating the health care system to the parent’s advantage. Beneficial health-related behaviors of higher SES offspring could be adopted by parents at the behest of offspring. Thus, the upward mobility of offspring is important for the survival of the parents. Given a lack of interaction effects across parental and offspring SES in the current analysis, we conclude that both low- and high-SES parents benefit equally from having high-SES offspring.

Other potential mechanisms underlying our findings should be considered. One is shared genes among family members. Temby and Smith (2013) found that those with the highest SES are most likely to enjoy low adult mortality risks when they have a genetic predisposition to excess longevity. The implication of this for the current study is that there are manifold ways in which offspring SES and parental mortality could be associated due to shared genes. For example, a stronger familial predisposition to greater longevity in parents could associate with improved physical and cognitive development in offspring, which in turn leads these offspring to achieve higher SES.

This analysis considered Nam-Powers scores as indicators of SES, which are based on occupation. Although we lacked data to assess specific mechanisms, it is likely that occupation encompasses a mix of both the monetary and knowledge resources reflected in income and education. Indeed, Nam-Powers SES scores are derived in such a way that they encompass the education and income levels that are typical of an occupation (Nam and Boyd 2004). The use of occupation in this study is also an excellent match for the study period. Given the era from which these data come, education may have been less discriminating because there was less variation then than for populations today; income is difficult to measure directly and reliably in historic settings; and occupation (and its association with income in the ways that Nam-Powers incorporates it) is the SES indicator most readily available in historical data.

We analyzed farmers as a distinct group both because they constituted a large portion of the sample (more than 40 % of parental occupation is farming) and because it is difficult to place farmers into an SES quartile in the same way as other occupations. Overall, male farmers lived longer than male nonfarmers. Females classified as farmers, mostly because their husbands were farmers, were not advantaged. Farming involves considerable physical labor, which may be beneficial to longevity. Females classified as farmers may have been less likely to be engaged in the more taxing physical labor involved in farming. Instead, the tasks of being a housewife of a farmer may have been stressful without being physically advantageous. Health care for females living on a farm might not have been as favorable as females living in urban areas. Although we observed these differences, and we controlled for fertility, it is possible that farming wives have higher parity than other women, and the interplay between parity and being a farming wife may not be fully captured in our models. Little is known about male-female health differences of farmers in the late nineteenth and early twentieth century, and the evidence here suggests that this would be a topic worthy of further exploration.

In addition, SES would have varied substantially across farmers both in G1 and G2. Some may have been more prosperous landowners, while others may have had smaller holdings. There could, therefore, be unobserved variation within the farming category. This variation is difficult to tease out given the UPDB data. However, we conducted sensitivity testing by removing G1 and G2 farmers in separate runs and examining whether other effects, particularly those of other SES categories, remained consistent. The results for SES quartiles and other covariates were nearly identical regardless of whether farmers were included in the model, adding a measure of confidence that farmer variability did not influence the findings.

Our results speak empirically to the importance of occupational and SES mobility in shaping health outcomes and theoretically to the merit of considering a network approach when examining impacts of SES on health and when reflecting upon fundamental cause theory. Research on early-life conditions has suggested that some of the impact of SES on health is established at young ages. The fact that the SES of a broader family network influences mortality points to diverse factors affecting adult mortality throughout life. Therefore, interventions can occur to alter the fate and the disadvantage of those with low SES. Expanding educational opportunities for offspring, for instance, enhances social mobility and will, as this study indicates, pay longevity dividends later in life to parents. If offspring have the means to climb the SES hierarchy, they can function to improve the life chances of their low-status parents. One of many unanswered questions is how offspring SES affects not only length of parents’ lives but also the quality and morbidities that may accompany a longer life. In addition, for contemporary populations in the developed world with lower levels of fertility and higher rates of marital dissolution, it remains to be seen how the SES of one or two children may alter the mortality risks of their parents, and whether these benefits will accrue equally to parents whose marriage may no longer be intact.