Low-Frequency Bias Tone Suppression of Auditory-Nerve Responses to Low-Level Clicks and Tones

Abstract

We used low-frequency “bias” tones (BT’s) to explore whether click and tone responses are affected in the same way by cochlear active processes. In nonlinear systems the responses to clicks are not always simply related to the responses to tones. Cochlear amplifier gain depends on the incremental slope of the outer-hair-cell (OHC) stereocilia mechano-electric transductance (MET) function. BTs transiently change the operating-point of OHC MET channels and can suppress cochlear-amplifier gain by pushing OHC METs into low-slope saturation regions. BT effects on single auditory-nerve (AN) fibers have been studied on tone responses but not on click responses. We recorded from AN fibers in anesthetized cats and compared tone and click responses using 50 Hz BTs at 70-120 dB SPL to manipulate OHC stereocilia position. BTs can also excite and thereby obscure the BT suppression. We measured AN-fiber response synchrony to BTs alone so that we could exclude suppression measurements when the BT synchrony might obscure the suppression. BT suppression of low-level tone and click responses followed the traditional pattern of twice-a-BT-cycle suppression with more suppression at one phase than the other. The major suppression phases of most fibers were tightly grouped with little difference between click and tone suppressions, which is consistent with low-level click and tone responses being amplified in the same way. The data are also consistent with the operating point of the OHC MET function varying smoothly from symmetric in the base to offset in the apex, and, in contrast, with the IHC MET function being offset throughout the cochlea. As previously reported, bias-tones presented alone excited AN fibers at one or more phases, a phenomena termed “peak splitting” with most BT excitation phases ~¼ cycle before or after the major suppression phase. We explain peak splitting as being due to distortion in multiple fluid drives to inner-hair-cell stereocilia.

1. Introduction

The current conception of cochlear mechanics attributes the high sensitivity and frequency selectivity of the cochlea to amplification of cochlear mechanical responses by outer hair cells (OHCs). Movement of the basilar membrane (BM) results in deflections of OHC stereocilia and mechano-electric transduction (MET) in these stereocilia gives rise to current flow that changes OHC voltage and drives OHC somatic motility. If the resulting OHC motion is in the right phase relative to BM motion, it injects energy on a cycle-by-cycle basis into the traveling wave and amplifies the cochlear mechanical response. This process is termed “cochlear amplification.” OHC-stereocilia MET functions have saturating nonlinearities. Large stereocilia deflections into low-slope regions of the OHC MET functions reduces cochlear amplification. As sound level is increased, the oscillatory deflections of OHC stereocilia spend more time in low-slope regions, which reduces overall cochlear-amplifier gain. This reduction in gain as sound level is increased produces the compressive amplitude vs. sound-level functions of BM motion.

One line of evidence for the above scenario comes from the effect of very-low-frequency “bias” tones on cochlear responses. If the bias-tone level is high enough, the response to it can transiently push OHC stereocilia into low-slope “saturation” regions of the OHC MET function. If a low-frequency bias tone is presented simultaneously with a probe tone that is of higher frequency and receives cochlear amplification, then during the part of the bias-tone cycle when the OHC stereocilia are in a low-slope MET region, OHC deflections from the probe tone produce smaller changes in probe-frequency OHC current than the OHC current changes without the bias tone. The net effect is that the bias tone decreases cochlear amplification of the probe-tone response whenever the bias tone moves OHC stereocilia into low-slope regions at the high-deflection edges of the OHC MET function. If the OHC MET function is asymmetric, one low-slope MET edge is reached at a lower sound level than the other, which results in one gain reduction per bias-tone cycle. At higher bias-tone levels, the stereocilia deflections reach the low-slope regions on both ends of the MET function and there are two gain reductions per cycle. Many experiments have produced evidence consistent with this scenario (Sachs and Hubbard, 1981; Sellick et al, 1982; Javel et al., 1983; Patuzzi et al, 1984a,b; Rhode and Cooper, 1993; Cooper 1996; Cai and Geisler 1996a, 1996b; Rhode 2007).

The cochlea is a nonlinear system and the effect of the bias tone is one manifestation of this nonlinearity. There have been many tests of bias-tone effects on tone responses (referenced above), but there are no data on bias tone effects on auditory-nerve (AN) fiber responses to clicks. In a nonlinear system, click responses cannot always be predicted from tone responses. Although a variety of measurements show a concordance between cochlear tone and click responses (e.g. Recio et al. 1998; Kalluri and Shera, 2007) not all such measurements concur. In AN-fiber responses to clicks, Lin and Guinan (2004) found that the decaying oscillations in click skirts (the longest latency part of the click response) were sometimes not at the tone characteristic frequency (CF) even when tone and click oscillatory amplitudes were similar. This suggests that there may be differences between cochlear mechanical operation for click and tone responses. In another line of experiments, Sininger and Cone-Wesson (2004) reported that otoacoustic emissions (OAEs) evoked by tones (distortion product OAEs (DPOAEs)) were larger than OAEs from clicks (CEOAEs) in the left ear, but the opposite was true in the right ear. Although this result has been questioned (Keefe et al. 2008), it is consistent with there being differences in the cochlear mechanisms for click and tone responses.

Our primary goal was to determine whether the cochlear-amplifier processes that enhance low-level responses are affected by bias tones in similar ways for tone and click responses. This was done by measuring bias-tone effects on AN single-fiber tone and click responses. Previous reports of bias-tone effects on AN single-fiber tone responses relied on visual inspection of AN response histograms to determine the presence of bias-tone synchrony and the phase of maximal suppression. A secondary goal of our work was to develop and use objective, quantitative methods for determining the presence of suppression and the phase of maximal suppression.

2. Materials and Methods

2.1 Methods Overview and Rationale

Bias-Tone (BT) effects were measured by presenting the BT simultaneously with either clicks or tones, and determining AN single-fiber click and tone responses at different times during the BT period. The BT itself may excite AN responses when it is high enough in sound level, and these BT excitatory responses may obscure BT suppression of click or tone responses. Thus, an initial task was to determine the sound level at which the BT itself excites responses, and then to exclude such BT levels from further consideration. The rationale for this is that the bias-tone effects of interest are the BT effects on OHCs that change the cochlear amplification of click and tone responses. Deflections of OHCs stereocilia are directly coupled to displacements at the top of the organ of Corti because OHC stereocilia are imbedded in the tectorial membrane (TM). In contrast, inner-hair-cell (IHC) stereocilia are freestanding. For low-frequency stimulation (such as BTs), IHCs are sensitive to the velocity of the fluid flow in the sub-tectorial space (Sellick and Russell, 1980; Freeman and Weiss, 1990; Guinan 2012). As a result, for low-frequency BTs (which produce low-velocity responses), the mechanical drive to IHCs is greatly reduced compared to the mechanical drive to OHCs. Thus, there can be BT levels at which the BT significantly deflects OHC stereocilia while at the same time the BT produces minimal deflections of IHC stereocilia. A major task of our methods is to distinguish when this is true vs. when the BT significantly affects the IHC receptor potential and thus affects the AN firing pattern.

2.2 Animal Preparation

We report here on recordings made from 92 single AN fibers from 14 anesthetized cats using methods approved by the Massachusetts Eye and Ear Infirmary animal care committee. The surgical approach and methods for animal anesthesia, monitoring animal health during experiments and recording from AN fibers were similar to those described previously (Stankovic and Guinan, 1999; Lin and Guinan, 2000; Guinan et al, 2005). Briefly, animals were anesthetized with Nembutal in urethane. Booster doses were given as indicated by toe-pinch reflex, heart rate and breathing rate. The rectal temperature was maintained at ~38° C and fluid balance was maintained by dripping lactated ringers into a leg vein. On both sides, the ear-canals were truncated for insertion of acoustic assemblies and the bulla cavities were exposed to reveal the round windows. A silver electrode near each round window was used to measure cochlear compound action potentials (CAPs). An automated tone-pip audiogram was run from 2 to 32 kHz at octave intervals using a CAP criterion of 10 μV pp. Tone pip audiograms were run approximately every hour, and also after obtaining a useful, high-quality data series in order to ensure that the cochlea was in good health. For units with CFs > 2 kHz, all tone-pip thresholds (evaluated at unit CF by interpolation of the audiogram data versus frequency) were within 20 dB of the tone-pip-threshold curve made from good animals. For units with CFs < 2 kHz, all but 4 units had thresholds at 2 kHz and above that were within 20 dB of the good-threshold curve and the remaining 4 units were within 27 dB at 2 kHz and within 20 dB above 2 kHz. A posterior craniotomy was followed by aspiration and retraction of cerebellar tissue to expose the AN. Single AN fibers were recorded from using electrolyte-filled pipette electrodes (10-20 MΩ impedance) inserted into the visually-identified AN.

Upon isolating an AN fiber, a threshold tuning curve (TC) was obtained, the characteristic frequency (CF) was determined, and the spontaneous rate (SR) was measured from a 20 s recording with no stimulus. Next AN responses to the BT were obtained using the “BT-alone” paradigm. From these responses we determined BT levels at which the BT alone produced a response that indicated this BT level might obscure suppression. BT effects vary from fiber to fiber, so the BT-alone paradigm was run on every fiber. After this, the BT was paired with clicks or tones at CF using the “BT-on-clicks” or BT-on-tone” paradigms. Click and tone thresholds are required for these paradigms, so before running them, we obtained click and tone thresholds. Due to limited contact time for most AN fibers, not all of the paradigms were run on every fiber.

2.3 Acoustics

Experiments were done in a triple-walled chamber. Sound stimuli were delivered with an acoustic assembly consisting of two earphones and a microphone with a probe tube, as in Lin and Guinan (2000). To minimize ringing, clicks and high-frequency tones were produced by a reverse-driven condenser earphone. 50 Hz BTs were produced by a DT48 earphone. The zero phase reference of the bias period was the cosine phase of the 50 Hz earphone drive voltage. The output of each earphone was calibrated from the microphone output using prior calibrations of the microphone and probe tube.

2.4 BT-Alone and BT-on-Tone Paradigms

For both the BT-alone and the BT-on-tone paradigms, the BT was a 50 Hz tone burst (240 ms plateau with 10 ms rise/fall times, repetition period of 500 ms) presented in a randomized level series from 70 to 110 or sometimes 120 dB SPL. For the BT-on-tone paradigm, the BT level series also contained a fixed tone burst (225 ms plateau with 5 ms rise/fall times) at the AN-fiber CF that started 20 ms after the start of each BT burst (Fig. 1A, top) and was 10 to 20 dB above the fiber’s threshold determined from its tuning curve.

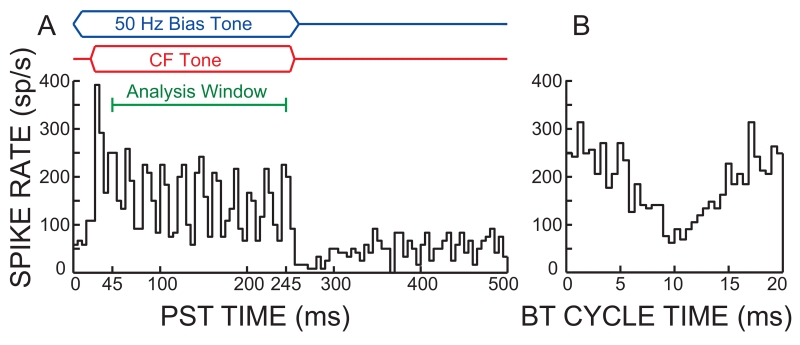
Fig. 1.

Deriving cycle histograms from tone-response post-stimulus-time (PST) histograms. A top: The timing of the bias tone (BT), the characteristic frequency (CF) tone, and the spike analysis window (45-245 ms). A bottom: PST histogram of the response to a 90 dB SPL, 50 Hz BT and a 33 dB SPL, 1.88 kHz, CF tone. B: BT-cycle histogram from the spike data within the analysis window at left. The phase reference was the cosine phase of the BT earphone drive signal. The histogram bin width was set to approximately the CF tone period so as to reject synchrony to the CF tone.

The data analysis of both paradigms used only spikes within a 200 ms window (10 BT periods) starting 10 ms after the beginning of the CF tone plateau (Fig. 1A, top). The spike times within this window were arranged into “cycle histograms” that show the number of spikes relative to the BT period (e.g. Fig. 1B). For the BT-on-tone data, the bin duration in the cycle histogram was set to the multiple of 10-μs (the time resolution of the spike-time recordings) that was closest to the period of the CF-tone stimulus. Making the cycle histogram bins nearly equal to the period of the CF tone effectively filtered out almost all of the synchronization of the fiber to the CF tone. Consequently, although the CF-tone was generally not an exact multiple of the bias-tone frequency, the bias-tone cycle histograms were little different than they would have been with an exact-integer relationship between the BT and CF tones as was used by Sachs and Hubbard (1981), Cai and Geisler (1996a) and others.

From the BT-on-tone cycle histograms we determined spike synchronization at the first and second harmonics. Synchronization was quantified by the synchronization index, “SI,” which varies from 0 (no synchronization) to 1 (all spikes perfectly synchronized). We also determined the BT phase with the largest suppression, termed the “major suppression” phase. If the cycle histogram had a 1^st harmonic but not a 2^nd-harmonic that exceeded the threshold criterion, then the major suppression phase was taken directly from the 1^st harmonic. Otherwise (i.e., when the 2^nd harmonic exceeded the threshold criterion), the major suppression phase was determined by a method termed the “half-period synchrony analysis”. For this, the BT-cycle histogram was divided into two 2^nd harmonic cycle histograms with the division in the BT-period cycle histogram at the two minimum-suppression phases of the 2^nd harmonic. For each of the two resulting half-period histograms (which were one cycle of the 2^nd harmonic), we calculated the synchrony index at the 2^nd-harmonic frequency. The suppression phase of the half-period histogram with the higher synchrony index was used as the major suppression phase of the original BT cycle histogram. We also tried a second method in which the major suppression phase was chosen by the time showing the maximum suppression in a cycle histogram that was formed by combining the 1^st and 2^nd harmonics of the original cycle histogram. This method yielded almost identical results as the half-period synchrony analysis except in a few cases that had suppression patterns with two almost equal suppression phases (which were from high-CF fibers).

2.5 BT-on-Clicks Paradigm

To determine a fiber’s threshold for clicks, an initial set of data was obtained from a randomized level series (typically 30-115 dB peak-equivalent SPL) of interleaved rarefaction and condensation clicks presented at 50/s. From these data we chose a rarefaction-click level 10-20 dB above the click threshold to be the click level in the BT-on-clicks paradigm.

The BT-on-clicks paradigm was chosen to place clicks at many different BT phases on each stimulus repetition. If clicks would have been presented at one BT phase throughout a run, and if some phases had more suppression than others, then the resulting differences in adaptation might skew the results. In the BT-on-clicks paradigm, 100 μs electrical pulses that produced rarefaction clicks were presented at a repetition interval of 18 ms starting at time=0 and lasting throughout the stimulus. The clicks were combined with a randomized level series of 50 Hz BTs presented as 1900 ms bursts (mid-rise to mid-fall) with 80 ms raised cosine rise-fall times, and a repetition period of 2160 ms. At each BT level, this produced a 180-ms repetition period with steady-state BTs in which the time slip of the 18 ms click repetition interval against the 20 ms BT period resulted in click bursts at 10 phases of the BT period (e.g. Fig 2A). The last click in this stimulus was after the BT ended and provided a click response without the bias tone.

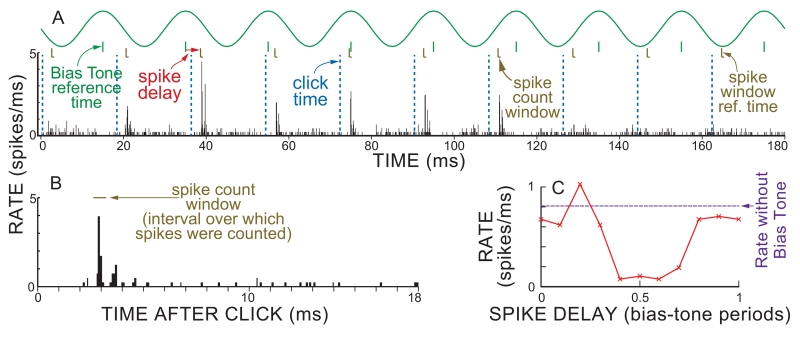
Fig. 2.

Deriving cycle histograms from BT-on-click responses. A top: BT electric drive to earphone and timing marks. A bottom: PST histogram of the response to 100 dB SPL 50 Hz BT and 60 dB SPL clicks repeated every 18 ms so that the clicks arrive at different phases of the BT. B: Expanded PST histogram from 60 dB SPL clicks without the BT showing the time window during which spikes were counted. C: BT-cycle histogram from the data within the spike-count windows in panel A. Note that going from left to right in panel A, clicks occur earlier relative to the BT reference time and therefore appear earlier in panel C, e.g. the delay labeled “spike delay” (from the BT reference time to the spike-window reference time) becomes less when moving toward the right in the panel A.

Analysis of the click-response data started by obtaining a 180-ms-long histogram which covered the 18 ms duration response to each of the clicks at the 10 distinct phases of the BT period (Fig. 2A). This histogram was then separated into the click responses at the 10 BT phases (each similar to Fig. 2B). For each BT phase, the response was obtained by counting all of the spikes within a window that contained the first large response peak and ignored adjacent peaks (Fig. 2B). The window was chosen from the histogram of a run without the BT, and this window was used for all ten BT phases. The resulting 10 spike rates then formed a 10-point cycle histogram over the BT period (Fig. 2C) which was analyzed in the same way as the more-closely-binned tone data. For cycle histograms from clicks, the phase of the spikes in a spike-count window were taken to be the BT phase at the beginning of the spike window (at 2.7 ms for the window in Fig. 2B). This choice is discussed later.

2.6 Analysis to Identify the BT-suppression Threshold and to Exclude BT-alone Excitation

In AN-fiber responses to tones, the threshold of significant synchrony is generally lower than the threshold for an increase in firing rate (Sellick et al, 1982; Javel et al., 1983; Patuzzi et al, 1984a; Cai and Geisler, 1996b; Johnson, 1980). Thus, our criteria for BT suppression and excitation were based on spike synchronization to the BT phase and not on changes in firing rate. All of the data were gathered over a series of BT levels. When the sound level of a BT presented alone is increased sufficiently, the BT modulates the fiber’s spontaneous activity and a BT-cycle histogram of the AN responses shows synchronization. With a BT added to a fixed level of click or tone stimulation, synchronization is produced when the BT reaches a sufficiently high level that it suppresses cochlear amplification of the click or tone responses at certain BT phases. The SI measured from a cycle histogram is termed “SIm” (m for measured), measured from a BT alone response is termed “SImA” (A for alone) and when measured from BT-on-tones or BT-on-clicks responses and suppression is being assessed, it is termed “SImS” (S for suppression).

In analyzing the data the task is (1) to decide when the SImA from a BT level is high enough that the response to a BT at this level might interfere with the suppression judgment so this BT level (and higher levels) should be excluded from suppression consideration, and (2) for un-excluded BT levels, to decide when SImS is high enough to indicate that suppression has taken place. The task is complicated by the fact that the AN-fiber response is probabilistic. For an underlying modulation of the IHC receptor potential that would produce a given SI if the histogram had an infinite number of spikes (termed SIun), the actual SIm is typically different from SIun. The probabilistic nature of the response is more evident when there is a smaller number of spikes, N, in the cycle histogram. As shown in the simulation results of Figure 3A,C, for large N, the average SIm approximately equals SIun, but as N decreases the average SIm becomes larger than SIun. A way to think about the increased average SIm for low N is that the randomness leaves gaps in the histogram that make it look more synchronized than the underlying process. In the extreme of a histogram with one spike, the synchronization is 1 regardless of SIun. A second thing to note from Figure 3A,C is that as N becomes smaller, the spread of SIm increases. To identify a high percentage (e.g. 90%) of the cases that are possibly being synchronized at a given SIun level (0.3 in Fig. 3A,C), the SI identification criterion needs to be <SIun. For example, for a BT sound level that evokes a BT-alone response with a SIun of 0.3 in a histogram with only 24 spikes, the criteria for identification of this SIun 90% of the time would be SIm’s of 0.17 or more (red line crossing 90% in Fig. 3C). Overall, the smaller the N, the less well an individual cycle histogram specifies what SIun it came from. Particularly for BT-alone cases, this is an important limitation because the fiber’s spontaneous activity provides the spikes that are modulated by the BT, so BT-alone cycle histograms often have few spikes. Highly-reliable identification of a high SIun underlying a low SIm in a histogram with a low spike count is important because, if this same BT sound level is paired with a CF tone that produces hundreds of spikes in its cycle histogram (as in most BT-on-tone cases), it would produce a SImS with a value greater than or equal to SIun about half of the time (Fig. 3C), i.e. it may interfere with seeing BT suppression. Thus, a key factor for understanding what a BT stimulation does is the SIun from that BT level, which can only be imperfectly determined by the SImA it produces.

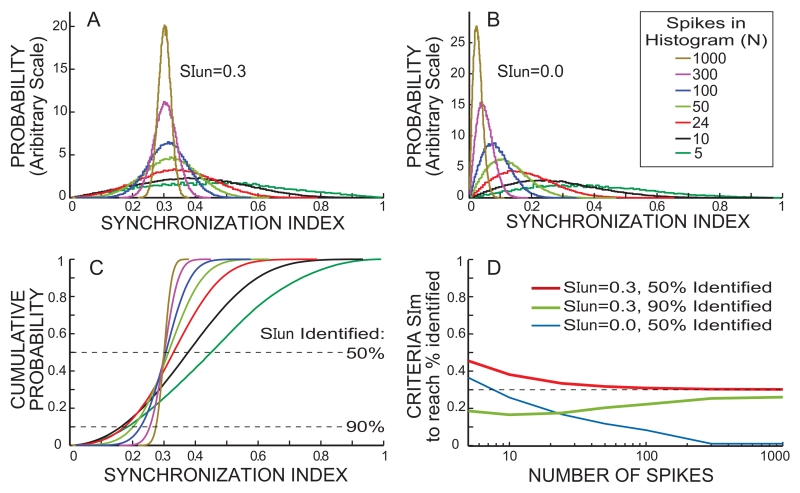
Fig. 3.

Results from simulating spike-response cycle histograms. A & B: Synchronization-Index (SI) probability for cycle histograms with “N” spikes generated with an underlying synchronization index (SIun) of 0.3 (A) or 0.0 (B) (color key in B also applies to A-C). C: SI cumulative distributions from the probabilities in A. D: Lines showing the measured SI (SIm) values needed to achieve the SIun identification rates in the key, as functions of the number of spikes in the cycle histogram.

Cycle histograms of spike data with an underlying modulation of SIun were generated by simulations consisting of series of Bernoulli trials in which either 0 or 1 spike was added to a 10-μs duration bin in histograms that spanned the 20 ms bias-tone period. The probability that a spike was added was sinusoidally modulated across the entire time span of the bins so as to achieve SIun if there were an infinite number of trials. In a single cycle-set, each bin received one independent trial. The baseline (unmodulated) probability of the Bernoulli trials was chosen so that on each cycle-set the total number of spikes in the cycle histogram increased by ~1 spike, on average. Full cycle-sets were repeated until the total number of spikes in all bins reached “N”, the desired total number of spikes. The SI of the resulting cycle histogram was calculated as in Stankovic and Guinan (2000). For each N, this process was done 100,000 times which yielded the distribution of SI’s that result from a processes with a given SIun (e.g. panels A and B).

Another factor is that a SIm above zero can also be produced by the random generation of spikes without there being any synchronous modulation (Fig. 3B). A large SIm can arise by chance from random spikes and we don’t want this to be taken as indicating there was a significant SIun. Detecting SIm values produced with a SIun>0 vs. from SIm values produced with SIun=0 might seem like a simple detection of a signal in noise but it is not because there are two signals to detect (BT-alone excitation and BT suppression) and one excludes the other. However, as in many signal-in-noise detection problems, the optimum criteria depend on the consequences of false positives vs. false negatives. For deciding that a BT-on-tone or BT-on-clicks cycle histogram has adequate synchrony to be considered as indicating that there was BT suppression, a goal of 50% identification at the SIun target criterion value (termed “SItarget”, later set to SI=0.3) was used because missing some histograms that should have passed would not change the pattern of the results. In addition, setting a criterion higher than 50% identification would include many histograms from processes with SIun’s lower than the target. Most BT-on-tone and many BT-on-clicks cycle histograms have 100 spikes or more (because the tone and click levels were 10-20 dB above threshold) and as N increases above 100, the distribution of SImS becomes sharply focused enough around SIun (Fig. 3). Thus, a 50% criteria adequately separates SImS values that originate from higher vs. lower SIun values. In contrast, for detecting the SIun from a BT alone response, the consequences depend on what the BT alone response is being used for. If the SImA is used to determine BT levels to exclude when measuring BT suppression, a missed identification of a BT level that produces a high SIun may have a bad consequence, i.e. it has the potential to contaminate the measurement of SImS. Such contamination might make the phase be that of a dip in BT excitation instead of at the phase of BT suppression. To avoid this we chose to set the criteria such that missed identifications would be at most 10% of the cases when SImA was used to determine if the BT level could be used in a suppression test. On the other hand, if the SImA is being used to determine the threshold or phase of BT excitation for comparison with the threshold or phase of BT suppression, then a criterion similar to that for BT suppression is appropriate, namely 50%.

Application of the ideas outlined above requires choosing the basic target level for SIun, (SItarget) whereby the condition, SIun > SItarget is considered as indicating significant synchrony. We chose SItarget = 0.3 because this was the criterion used by Stankovic and Guinan (2000) and because random spikes seldom produce SIm values ≥0.3 (Fig. 3C). The detection criteria values to apply to SImA or SImS to achieve the desired acceptance rates for cycle histograms with N spikes were determined from simulations (see Fig. 3).

A final additional criterion came from the desire to constrain the uncertainty of the points in the phase plots so that only accurate points would be shown. For any SI to be used, we required that the 95% confidence limits of the phase estimate be within ±16° or ±32° for 1^st or 2^nd harmonics, respectively (in the BT cycle histogram, 32° for the 2^nd harmonic is the same time interval as 16° for the 1^st harmonic). The 95% confidence limits of the phase were calculated as in Stankovic and Guinan (2000). In evaluating excitation or suppression for inclusion in the plots, a SIm was not considered to have reached the threshold unless the phase uncertainty criterion was also satisfied. This insured that only accurately determined phases were plotted. In contrast, when the BT-alone SIm was used for determining whether a given sound level should be considered for BT suppression, then the phase criterion was not applied. In this case we were not concerned with the accuracy of the phase (because it wasn’t plotted) and we wanted to keep miss-identification of SIun’s >=0.3 to be less than 10%. This use of the SI and phase-uncertainty criteria is termed the “original acceptance criteria”. As will be seen in Results, excluding BT sound levels at and above the low SImA values that would miss-identify SIun’s of 0.3 more than 10% of the time (values that were often <<0.3) had the unintended consequence of removing most suppressions from consideration. We found that this undesirable feature of the original acceptance criteria was largely removed by applying the phase criterion in all cases, i.e. even when using the BT-alone SIm to exclude sound levels from consideration for suppression. An alternative to applying the phase-uncertainty criterion would have been to apply a synchrony-uncertainty criterion. We did this and it produces a result that is similar to using the phase-uncertainty criterion. This is not surprising because the two uncertainties are highly correlated. Since the origin of the problem was too few spikes in the histograms, we also tried excluding histograms with fewer than a minimum number of spikes. This allowed more suppressions to be used, but not as many as using either phase-uncertainty or synchronization-uncertainty criteria, presumably because histograms with the same number of spikes can exhibit varying degrees of these uncertainties and the uncertainty is more important than the number of spikes.

When determining whether there was suppression, at each BT level we calculated the SI of both the 1^st and 2^nd harmonics of the cycle histogram and applied the criteria to whichever harmonic had the largest SI. For BT-alone excitation, we applied the criteria to the 1^st harmonic. As will be shown later, for the BT-alone response at threshold, the SI of the 2^nd harmonic was never much greater than the SI of the 1^st harmonic.

Rationales for the acceptance percentages were stated above but there was no mechanistic rationale for choosing the phase uncertainty criterion. We tried different values of the phase uncertainty criterion and chose a maximum phase uncertainty of ±16° to achieve plots with as many points as possible while preserving the pattern seen with very strict criteria. Values that were less strict resulted in more points on the plots but a greater percentage of the points were outside of the main clusters. Similar looking plots were obtained for a range of criterion values around those actually used. For comparison, Stankovic and Guinan (2000) used phase uncertainty ≤30°, SI uncertainty ≤0.1, and two adjacent points in a level series had to pass for any point to be accepted.

3. Results

3.1 Example Data

Example BT-alone cycle histograms are shown in Figures 4A and 5A. At high levels, there are peaks in the cycle histograms showing rates far above the fibers’ SRs, but at lower levels the peaks are offset by reductions in the response at other BT phases so that the rate changed very little (Figs. 4C and 5C). Thus, in these cases, as in most cases, the SI threshold was reached at sound levels substantially below the average-rate threshold.

Fig. 4.

Example BT-alone and BT-on-tone data. Period histograms from: (A) a BT-alone sound level series, and (B) a 32 dB SPL CF tone along with BT tones at 70-110 dB SPL. In B, the triangle shows the level and phase of criterion suppression. C-E: BT sound-level series of: (C) average firing rate, (D) Synchronization Index (SI), and (E) the phase of the major suppression. The dashed line in D shows the target SI. Error bars in E show 95% confidence intervals. Data from cat 31, unit 70, CF 2.69 kHz, spontaneous rate (SR) 32.5 sp/s.

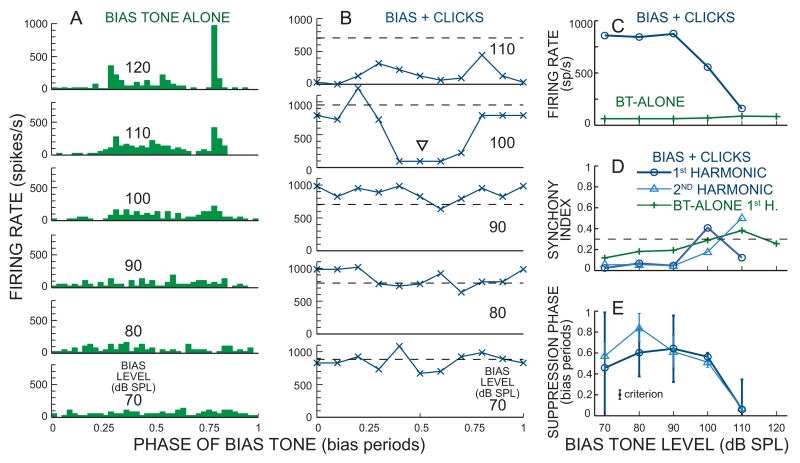
Fig. 5.

Example BT-alone and BT-on-clicks data. A: Period histograms from a BT-alone sound level series. B: Average firing rate in the spike-count window (see Fig. 2) vs. BT phase in response to 60 dB SPL clicks and BT tones at 70-110 dB SPL. The dashed line is the click response without the BT from the corresponding BT-level run (see Methods). In B, the triangle shows the level and phase of criterion suppression. C-E: BT sound-level series of: (C) Average firing rate in the spike-count windows for BT-on-clicks, and throughout the response for BT-alone, (D) Synchronization Index (SI), and (E) Phase of the major suppression. The dashed line in D shows the target SI. Error bars in E show 95% confidence intervals. Data from cat 28, unit 9, CF 0.52 kHz, SR=85 sp/s.

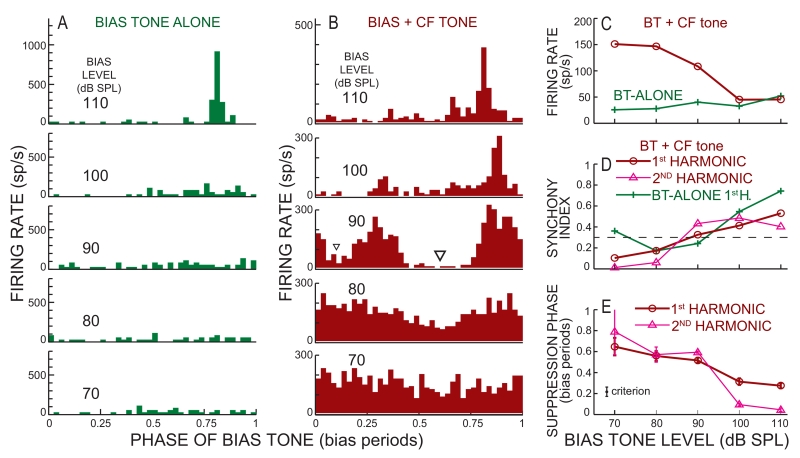
Typical results from the BT-on-tone and BT-on-clicks paradigms are shown in Figure 4B and 5B. In the fiber of Figure 4, the lowest BT level that showed criterion BT suppression was 90 dB SPL, as judged by both the 1^st and 2^nd harmonics of the BT cycle histogram reaching criterion synchrony (Fig. 4D) and the phase error reaching criterion (Fig. 4E). Since the second harmonic also passed the threshold criteria, suppression can be seen at two phases of the cycle histogram (triangles in Fig. 4B). At the BT synchrony threshold level, the BT-on-tone response also shows rate suppression (Fig. 4C). In the fiber of Figure 5, the lowest BT level that showed criterion suppression was 100 dB SPL (triangle in Fig. 5B), as judged by the 1^st harmonic of the BT cycle histogram reaching criterion SI (Fig. 5D) and the phase error reaching criterion (Fig. 5E). At this BT level, the BT-on-tone response also shows rate suppression (Fig. 5C), but the 2^nd harmonic SI was <0.3 and there was no obvious suppression at a second phase of the BT cycle histogram. Large 2^nd harmonic components and suppression at two phases were found at 110 dB SPL (Fig. 5B, D).

For the fiber in Figure 5, the BT-alone SI increased gradually and exceeded 0.3 at 110 dB SPL (Fig. 5D). However, at 100 dB SPL it exceeded the criterion for an over-10% probability of miss-identifying a response produced by a SIun of 0.3 (see Methods) which would rule out using this BT sound level and the suppression found in this fiber. For the fiber in Figure 4, the BT-alone SI was a non-monotonic function of level and it exceeded SI=0.3 at 70 dB SPL. The lower SIs of this fiber at 80 and 90 dB SPL suggest that the high SI at 70 dB SPL was largely by chance. With the original-acceptance-criteria derived in the Methods, this BT SI rules out being able to use any suppression found at levels of 70 dB or over. Thus, with the original acceptance criteria neither of the suppressions in Figures 4 and 5 would be usable. However, examination of the patterns of BT excitation and suppression in Figures 4 and 5 indicates that in these two fibers, the phase of suppression cannot be accounted for by a dip in the response caused by BT-alone excitation. In fact, the phase of BT suppression is closer to the phase of the BT-alone increase in rate than to the phase of the BT-alone decrease in rate (Figs. 4 and 5). Thus, in these fibers the BT-alone excitation has not obscured the BT suppression at the BT-suppression threshold. Results like these were a common occurrence and made us reconsider the application of the theory-driven “original acceptance criteria”. To avoid such BT-alone excitation patterns preventing us from using measurable BT suppressions from these fibers, we also used a “modified-acceptance-criteria” (See methods) which put an additional criteria on the BT-alone excitation: its phase error had to be less than the phase-error criterion.

3.2 Excitation and Suppression phases vs. AN-fiber CF

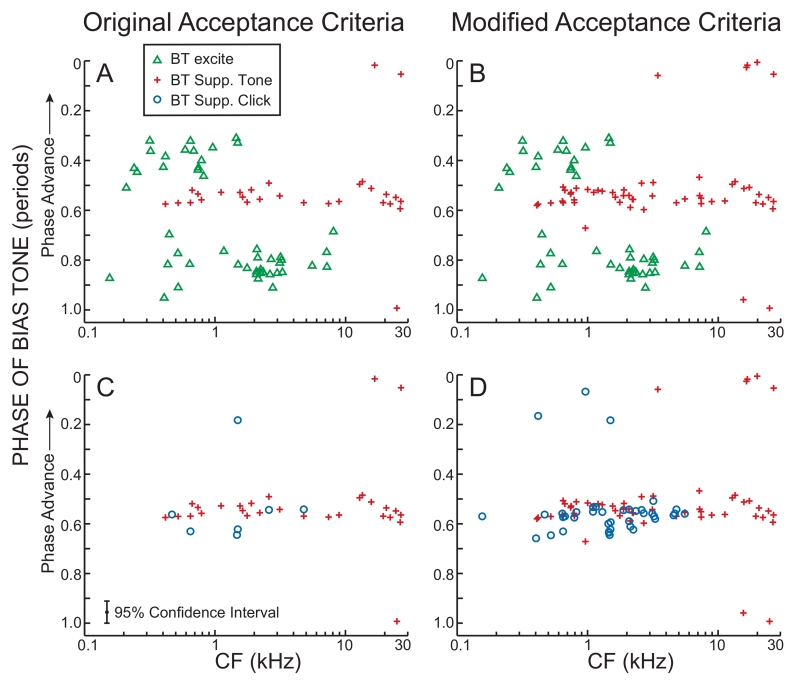
BT-tone excitation and suppression phases for both the original and the modified acceptance criteria are shown in Figure 6 We focus first on the phases at which BTs suppressed low-level CF tone responses (pluses in Figure 6). For CFs <15 kHz, almost all of these phases were tightly clustered about a value that varied little with fiber CF. For CFs above 15 kHz, there was a second cluster of suppression phases ~½ period from the main suppression phase. Similar BT-suppression patterns were found for both the original and the modified acceptance criteria (Fig. 6A vs. 6B). In general, the pattern of BT suppressions vs. CF changed very little for different choices in the various cycle-histogram acceptance and rejection criteria.

Fig. 6.

Bias tone (BT) phases at the threshold of BT excitation (triangles) and the major suppression phases for tones (pluses) and clicks (circles) at suppression threshold vs. fiber characteristic frequency (CF). The phase uncertainty, as shown by the 95% confidence interval bar in C, applies to all panels. In panels A and C, possible tone and click suppressions were excluded when they were at or above the sound level at which the BT-excite synchronization index (SI) exceeded its criterion value, without consideration of the BT-excite phase uncertainty (Original Acceptance Criteria). In panels B and D, suppression data were excluded only when they were at or above a sound level at which the BT-excite SI exceeded its criterion value and the BT-excite phase uncertainty was less than its criterion (Modified Acceptance Criteria – see text).

The phases at which BTs, by themselves, excited AN fibers are shown by triangles in Figure 6. Since the phase-uncertainty criterion was included in the original acceptance criteria for plotted phase data points, there is no difference in these points between the original and the modified acceptance criteria. The excitation phases were in two clusters, ~¼ period earlier or later than the maximum suppression phase. In each cluster, the spread of the excitatory phases was distinctly greater than the spread of the suppression phases. As CF increased, the excitation phase cluster that was most prominent transitioned at ~2 kHz from phases ~¼ period earlier than the suppression phase to phases ~¼ period later than the suppression phase. These features of the excitatory phases were robust to different choices in the various criteria except that if the phase uncertainty criterion was made less strict so that more BT-alone excitations were accepted, the spread of the clusters increased and a few points overlapped the edges of the suppression phases.

The major suppression phases for low-level click responses are shown and compared with those of tone responses in Figure 6C, D. With the original acceptance criteria there are only 7 points while with the modified acceptance criteria there are 38 points. The modified acceptance criteria makes a much bigger difference for clicks than for tones, in part because the click suppression thresholds were higher than the tone suppression thresholds. Nonetheless, the pattern of the BT suppression of click responses is similar for both the original and the modified criteria. The major suppression phases of low-level click responses were almost all clustered in a narrow phase range, but they were not as strongly clustered as the suppression of tones. There were also a few fibers in which the major suppression phase of the click response was ~½ period from the main cluster. For CFs above 6 kHz there were no BT-on-click points because the BT level was never high enough to reach the criterion for suppression. The major suppression phases of click responses overlapped with those of tone responses, but, on average, click suppression phases were slightly later. The click suppression phase directly depends on the choice of the BT phase used to represent the phases of the click response spikes in the spike-count window (see Fig. 2). For the data in Fig. 6D, the response time was taken as the start of the “spike window” (labeled “spike window ref. time” in Fig. 2A). If the click response time was taken as the center of the window, the click points would appear slightly later (down in Fig. 6C, D) and would overlap the tone points less (see Discussion). Finally, the overall pattern of click-response suppression phase changed little for different choices of the criteria.

3.3 Excitation and Suppression Thresholds

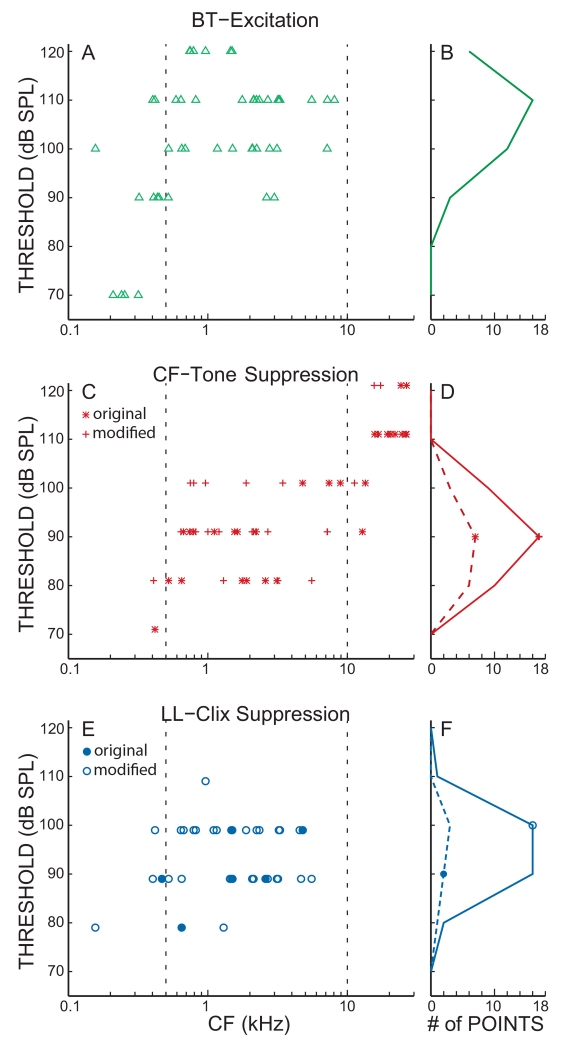
The BT threshold levels for criterion excitation and criterion suppression of tone and click responses are shown in Figure 7. For both excitation and suppression, the thresholds generally increased as CF increased, although the patterns are somewhat different across the different threshold categories. These patterns were similar for the original and the modified criteria. Both tone and click suppression thresholds appeared to grow slowly with CF in the mid-CF range (0.5< CFs <15 kHz). For CFs above 15 kHz the CF-tone thresholds increased sharply as CF increased (Fig. 7C). As noted earlier, there were no thresholds for suppression of click responses for CFs >6 kHz. In the mid-CF range, suppression of click responses typically required slightly higher (5-10 dB) BT levels than suppression of tone responses (Fig. 7F vs 7D). BT-alone did not usually excite until even higher sound levels (Fig. 7B). These high BT-alone thresholds are what allowed suppression measurements at the generally lower suppression thresholds.

Fig. 7.

A: Thresholds for BT suppression of CF-tone and low-level (LL) click responses, as well as BT-alone excitation thresholds, versus fiber CF. Thresholds are shown both for the original and modified acceptance criteria as indicated by the key at the lower right. B: Plots of the number of thresholds at each sound level for fibers with CFs 0.5-10 kHz (i.e. points within the dashed lines in A). A symbol on each line indicates which points were counted (see the key). Over the frequency range where all three categories had thresholds, tone-response suppression thresholds were lowest, click-response suppression thresholds were next and BT alone excitation thresholds were highest.

3.4 Mechano-Electric Transduction Asymmetries

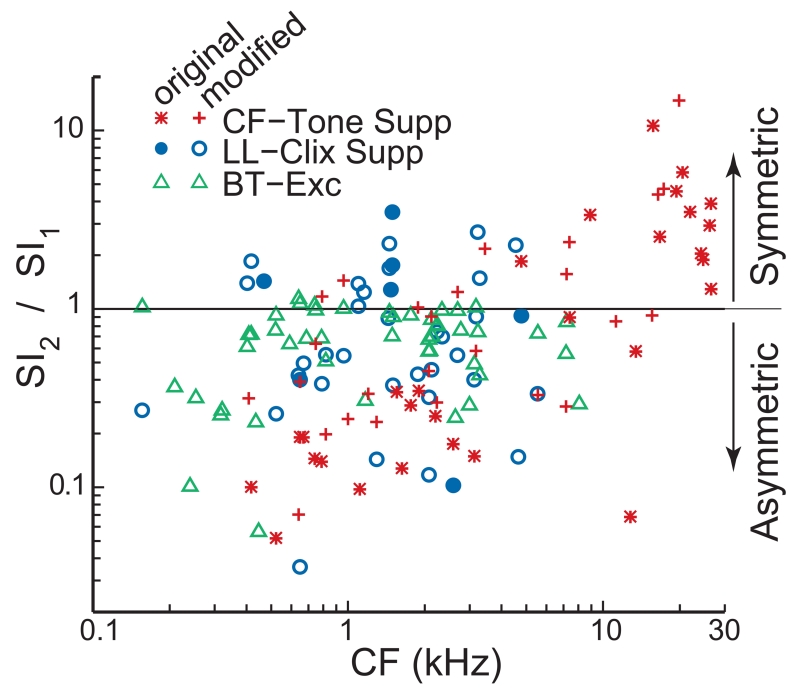
Presuming that BT suppression arises from OHC MET saturation (Cai and Geisler, 1996c), we expect that the position of the resting operating point relative to the center of the OHC MET curve determines the relationship of the 1^st and 2^nd harmonic components in BT-suppression cycle histograms. If the at-rest operating point is in the center of the OHC MET function, then at suppression threshold the BT will suppress cochlear amplification at both MET edges and the resulting two suppressions per BT cycle will yield a large 2^nd-harmonic SI (SI₂). In contrast, if the at-rest operating point is near one edge of the OHC MET function, then at suppression threshold there will be one suppression phase per BT cycle and a large 1^st-harmonic SI (SI₁). A metric that reveals this MET asymmetry is the ratio of SI₂ to SI₁, measured at suppression threshold (Fig. 8). SI₂/SI₁ ratios from the BT-on-tone suppressions increased with CF from well below unity for low CFs to well above unity for CFs 20 kHz and higher. The BT-on-clicks data appear to show a similar trend, but these data are very scattered and the comparison is incomplete because there were no BT-on-clicks suppressions for CFs above 6 kHz. Figure 8 also shows SI₂/SI₁ ratios from the BT-alone excitations. For BT-alone excitation there was no clear trend across frequency and SI₂ was never much greater than SI₁.

Fig. 8.

The ratio of the synchronization index (SI) of the 2^nd harmonic (SI₂) to the SI of the 1^st harmonic (SI₁) at threshold vs. fiber CF. The top-left key gives the symbols for BT suppression of CF-tone responses, BT suppression of low-level click responses, and BT-alone excitation. Lower-ratio values indicate more asymmetrical locations of the operating point on the mechano-electric transduction (MET) function. Note that suppression ratios show OHC MET symmetry while excitation ratios show IHC MET symmetry.

If the at-rest operating point of the OHC MET function is near the center of the function (SI₂/SI₁ ratio >1 in Fig. 8) then small deviations of the resting operating point or measurement noise could reverse the major phase of suppression. For CFs >15 kHz, all of the BT-on-tone suppressions had SI₂/SI₁ ratios that were >0.9 (Fig. 8) and six of the 14 had major suppression phases that deviated ½ period from the most common major suppression phase (Fig. 6B). Within this CF>15 kHz group there didn’t appear to be any correlation of suppression phase deviation and SI₂/SI₁ ratio (not shown). Thus, MET symmetry can lead to suppression phase reversals, but once a certain amount of symmetry is reached, more symmetry doesn’t lead to more phase reversals. At lower CFs, only one BT-on-tone suppression deviated from the mode by1/2 period (Fig. 6B) and its SI₂/SI₁ ratio was 2.2 (Fig. 8). For BT-on-clicks suppressions, there were 3 points that deviated from the mode by1/2 period (Fig. 6D) and their SI₂/SI₁ ratios were 1.9, 0.55 and 3.5 (Fig. 8). Thus, in the great majority of cases, suppressions that were ½ period from the mode had high SI₂/SI₁ ratios consistent with their originating from symmetric OHC MET functions. However, having a symmetric MET function does not mean that the suppression will be ½ period from the mode.

4. Discussion

Our main result is that the major suppression phase is very similar for tone and click responses. Before we consider this in more detail, we first discuss methodological issues that influence the interpretation of both our results and previous work.

4.1 Excluding Bias-Tone Excitation

The first data-analysis task was to prevent bias-tone excitation from contaminating suppression phase measurements by determining the minimum bias tone level at which BT excitation would obscure the measurement of suppression phase. On each AN fiber we measured the BT-alone synchronization and assessed the BT level at which the BT-alone SI was high enough that it might miss-identify a BT underlying SI (SIun) with a probability over 10%. With the original criteria, BT levels at and exceeding this criteria were excluded from inclusion in the data pool for measuring suppression. Using this theory-driven criteria two observations stand out: (1) the BT-alone SI criterion was exceeded at such low sound levels that it excluded most BT suppressions, especially BT-on-clicks suppressions. (2) The histograms showed that in many fibers the phase of a putative suppression did not correspond to the phase of the minimum in the BT-alone period histogram, which means that the putative suppression could not be attributed to BT synchronization at the IHC level and suggests that the putative suppression was a true suppression. If the BT effects on OHCs and IHCs were independent, then the BT-alone synchronization would have been superimposed on the BT suppression cycle histograms. For BT-alone excitation that was 90° from the BT suppression (as is expected from IHC stereocilia velocity sensitivity), this means that the suppression SI values would seldom be less than the SI of the BT alone response (it could be less because SI is a random function and a BT-alone SI can occasionally be large even though its underlying SI is low). However, BT-on-tone and BT-on-clicks responses often had SIs that were less than the BT-alone SI at the same sound level. For instance, for the fiber of Figure 5 at 70-90 dB SPL, the suppression SI 1^st harmonic values were consistently less than 1/3 of the BT-alone 1^st harmonic SI values (Fig. 5D). Such data contradict the assumptions used in in the Methods-section analysis that developed the original criteria.

What accounts for this discrepancy? Our analysis treated the BT effects on OHCs and IHCs as independent, but they are not independent. The drive to the IHCs is influenced by what the OHCs do, and, more important here, the response of the IHCs to the BT tone is influenced by the presence of the additional CF-tone or click. In the BT-alone data at low sound levels there was little increase in the firing rate so the BT must have produced only small modulations of the IHC stereocilia position that stayed within a relatively linear and high-gain part of the IHC MET function. On the other hand, the CF-tone and click stimuli were 10-20 dB above their threshold for increasing the firing rate. These sounds must have produced much larger IHC stereocilia deflections such that the IHC MET function produced a net rectification, an overall IHC depolarization and an increased firing rate. During the inhibitory phase of large IHC stereocilia deflections, the slope of the IHC MET function is substantially reduced from its at-rest value with the result that the slope of the IHC MET function, averaged over a stimulus cycle, is reduced. With a reduced IHC MET function slope, the BT would produce a reduced modulation of the IHC response. In short, the CF tone or click response pushes the IHC MET function into saturation regions which depresses the IHC MET response to the bias tone (A similar saturation of MET currents in OHCs is the mechanism that produces “suppression” of BM cochlear amplification. IHC MET saturation does not change BM cochlear amplification and to distinguish the effect of IHC MET saturation we term it “depression”). This IHC response depression accounts for data like those in Figure 5D where at low sound levels the BT-on-tone SI is consistently below (less than 1/3 for 70-90 dB SPL BTs) the BT-alone SI. The possibility that there was also suppression of the BT response at the OHC level by the CF tone or click is unlikely because for the 50 Hz bias tones in the CF regions we measured there is no BT-frequency cochlear amplification. Overall, CF-tone and click depression of the BT response at the IHC level accounts for our observations and explains the discrepancy between our analysis in the Method’s section and the measured data.

Even though our results show that it is an oversimplification to consider BT-alone SIs and suppression SIs as independent, we believe our theoretic analysis of this simplified case is valuable because it provides insights into the issues involved. The analysis provided the perspective that enabled us to determine that the clicks and tones produced significant depressions of the BT response at the IHC level. In addition, having a quantitative analysis method allowed us to fully explain how the data were analyzed, which is better than the visual inspection of the histograms used in other papers to decide when excitation or suppression occurred. Visual criteria may be adequate for determining whether there is significant spike synchronization to the bias tone when viewing a tone-response cycle histogram with many spikes spread through many histogram bins, but a visual criteria is less satisfactory when there are few spikes, and/or only 10 bins in the cycle histograms as in BT-on-clicks cycle histograms. The difficulty in comparing the very different looking tone and click cycle histograms was an original motivation for our seeking to use objective criteria to decide whether BT cycle histograms showed synchrony, and to have a rational basis for choosing BT-alone SI values for identifying and excluding BT-alone excitation. Our rule-based method enabled us to apply the criteria in the same way to the 10-points-per-cycle plots obtained from click responses and the many-bin cycle histograms from tone responses.

4.2 Click and Tone Responses are Suppressed at the same Bias-Tone Phase

The major suppression phases of low-level tone and click responses overlapped in the CF region where we had data on both (CFs <6 kHz) (Fig. 6C, D). Although there were a few outliers that had major suppression phases ~½ BT cycle different from the main cluster, the major suppression phases formed a smooth line without significant discontinuities for CFs < 15 kHz. For CFs over ~15 kHz, the major suppression phases were divided between the main cluster and a cluster ~0.5 period away. For BT-on-tones, the pattern of the major suppression phase vs. CF that we found (Fig. 6) is very similar to that reported for tones in cats by Cai and Geisler (1996b) in that they also found that the suppression phase varied little with frequency and was approximately ¼ period away from the excitation phases. For CFs >7 kHz, Cai and Geisler (1996b) had no data for 50 Hz suppressors but their data from 100 Hz suppressors showed some fibers with suppression phases ½ period away from the main suppression group which is similar to our data for 50 Hz suppressors. There are no previous data on the suppression of click responses that our data can be compared to. The overlap of the click suppression data with the tone suppression data is consistent with low-level click and tone responses both being due to motion amplified by the same mechanism (at least for CFs <6 kHz), i.e. by the traditional cochlear amplifier that is driven by the deflection of OHC stereocilia and amplifies low-level sound responses of any kind.

On average, the major suppression phase occurred slightly later for suppression of clicks than for suppression of CF tones (Fig. 6C, D). As the BT phase value for BT-on-clicks suppression, we used the phase at the beginning of the time window at which spikes were measured in the click PST histograms. If we presume that at the level of cochlear mechanics the suppression phase is identical for tone and click responses, the results of Figure 6C, D suggest that the BT has the biggest effect on suppressing the click response somewhat earlier in the click response than the beginning of this window and that this effect lasts throughout the rest of the response. Rhode and Cooper (1993) noted that in the cat basal turn the major suppression phase of BM motion responses was not exactly at the maximum BM displacement toward scala tympani, but was delayed by approximately 100 μs. They hypothesized that this delay occurs because in the high-Q oscillations of BM responses at CF, changes in gain are smoothed (or integrated) over a period of time (also see Cai and Geisler, 1996c). Thus, another factor that influences the BT major suppression phase is the different build up characteristic of cochlear amplification in tone and click responses. Overall, a variety of factors may be involved in producing the small time difference between the suppressions of click and tone responses.

The BT phase that produced maximum suppression was slightly more delayed for fibers with lower CFs. A similar change in the major suppression phase with fiber CF was found by Cai and Geisler (1996b). This change with CF is consistent with the peak of the BM displacement response occurring at slightly later times as the BT traveling wave moved apically. The CFs in Figure 6 are all an octave or more basal of the BT-frequency place so the 50 Hz traveling-wave velocity is very fast in this region of the cochlea and the difference in suppression delays across CFs is very small.

Most investigations of bias-tone suppression concluded that the phase of the major suppression of cochlear responses corresponds to the maximum of BM displacement toward scala tympani (Patuzzi et al., 1984b,Cooper 1996; Geisler, and Nuttall, 1997; Rhode, 2007¹). However, in the study most comparable to ours, Cai and Geisler (1996a), in cats, concluded that the major suppression phase of AN responses corresponds to the maximum BM displacement toward scala vestibuli. To draw this conclusion, Cai and Geisler deduced the phase of BM movement from measurements of the phase of the cochlear microphonic (CM) as monitored by their electrode near the round window. In contrast, direct measurements of BM movement in cats showed the opposite, namely, that in most cases the major suppression phase of BM motion responses corresponded to maximum BM displacement toward scala tympani (Rhode and Cooper, 1993). In an attempt to resolve this issue we examined the BT-alone responses recorded with our near-RW electrode but were unable to find a satisfactory sinusoidal-looking response at any of our BT levels. When there were responses with good signal-to-noise ratios at the lowest BT level (70 dB SPL), these responses were not sinusoidal and showed deflections that were reminiscent of AN CAP responses, so we did not believe that any of these recordings represented pure CM recordings. Because of this, we have not used our near-RW recordings to deduce the phase of BM motion. A variety of studies of the effect of low-frequency (≤50 Hz) bias tones on BM, IHC-receptor-potential, and/or AN responses to low-level tones at CF in guinea pigs and chinchillas have concluded that for most CFs the major suppression phase corresponds to the maximum BM displacement toward scala tympani (Sellick et al, 1982; Patuzzi and Sellick, 1984n; Patuzzi et al. 1984a,b; Cooper 1996; Geisler and Nuttall, 1997; Temchin et al, 1997; Rhode, 2007)². In our view, the most economical hypothesis for why Cai and Geisler’s (1996a) conclusion differs from the others, is that Cai and Geisler’s near-RW responses were contaminated by neural responses. Thus, our working hypothesis is that the major suppression phase of AN responses corresponds to the maximum BM displacement toward scala tympani, and that the main cluster of suppression phases shown in Figure 6 provide a measure of the phase at which BM motion shows the maximum BM displacement toward scala tympani, or close to it. The conclusion that the major suppression phase is for maximum BM motion toward scala tympani fits well with the theory developed to explain suppression (e.g. see Cai and Geisler, 1996c). This conclusion, with data in Figure 6, suggests that in CF regions below 15 kHz, the at-rest MET operating point in most OHCs is offset toward the scala-tympani edge of the MET function. In general, all of our observations are consistent with the hypothesis that suppression is caused by the saturation of OHC receptor currents produced by the BT transiently deflecting the OHC stereocilia into low-slope regions of their MET functions (Geisler et al. 1990; Cai and Geisler, 1996c).

For both BT-on-tones and BT-on-clicks, a few fibers were inhibited at a phase that was approximately ½ BT period different from the main suppression cluster. It has been previously reported that a small minority of AN fibers showed the largest suppressions at a phase that was ½ BT period different from the main suppression cluster (Cai and Geisler, 1996b). It seems unlikely that these aberrant responses would be due to a local difference in the direction of gross transverse cochlear movement. Instead, it is likely that these reversed suppression phases are due to cochlear regions in which the at-rest OHC MET operating point is nearly symmetric and was locally offset toward the scala-vestibuli edge of the MET function and/or was reversed by measurement noise. As presented in Results, almost all of the fibers with suppressions ½ period from the mode had high SI₂/SI₁ ratios consistent with their having symmetric MET functions, which means that only a small deviation of the operating point or noise in the measurement would be enough to cause a reversed phase of suppression. Measurements of BM motion in the extreme base of cats and guinea pigs showed that low-frequency tones can suppress BM motion at CF when the BM undergoes displacement toward either scala (Rhode and Cooper, 1993). This and the trend in Figure 8 are consistent with the cochlear hook-region operating point being near the center of the OHC stereocilia MET function and that the operating point systematically changing from centered (symmetric) in the base to offset (asymmetric) in the apex.

In the Introduction we speculated that click skirts may be suppressed differently than the bulk of the click response, but unfortunately, we were unable to obtain enough data on low-level click skirts to determine whether there were differences in the BT suppression phase in the click skirt compared to in the larger initial part of the click response. Also, we did not get a sufficient number of spikes in the histograms to accurately determine the oscillatory-response frequencies in the click skirts so that we could determine which AN fibers showed click-skirt oscillatory frequencies that were not at CF (only a small minority of fibers do – Lin and Guinan 2004), so that we could determine if these fibers showed any difference in BT suppression phase from the majority of fibers. Finally, the fact that we found no evidence for differences in the physiological mechanisms that suppress click versus tone responses provides no support for the report that OAEs from tones versus clicks are systematically different (Sininger and Cone-Wesson 2004, but see Keefe et al. 2008).

4.3 Bias-Tone Suppression Thresholds

Bias-tone thresholds generally increased as fiber CF increased (Fig. 7). Presumably, this is due to BM stiffness increasing from apex to base so that the BT produces less BM motion at higher CFs, and therefore suppresses (and excites) less as CF increases.

For CFs up to ~6 kHz, the suppression thresholds for BT-on-clicks were generally 5-10 dB higher than for BT-on-tones (Fig. 7). As the sound level of a CF-tone is increased, the threshold BT level for suppressing the CF-tone response increases slowly at first and then much faster (Patuzzi et al, 1984a; Cai and Geisler, 1996a; Rhode, 2007). We made only rough attempts to set the tone and click stimuli at the same level relative to their thresholds, so systematic differences might have occurred. In addition, clicks have broad spectra with off-CF energy that is in AN-fiber suppressive regions. Since clicks produce both excitation and suppression in a single AN fiber, for the BT to produce additional suppression the BT may need to be at a higher level for clicks than the BT level required for the suppression of tone responses.

There were no BT-on-clicks suppression thresholds obtained for CFs above 6 kHz. Above ~10 kHz the BT-on-tones suppression thresholds rose sharply and some reached the maximum-allowed bias-tone level of 120 dB SPL. For CFs above 10 kHz, if the suppression thresholds for BT-on-clicks continued to be ~10 dB higher than for BT-on-tones, then the projected values for BT-on-clicks suppression thresholds would have reached or exceeded 120 dB SPL. Thus, the lack of BT-on-clicks suppression data for CFs above 10 kHz may be due, in part, to the limitation in the maximum BT level that was used. In several fibers with CFs above 10 kHz on which relevant data were obtained, the shape of the BT-on-clicks cycle histograms and their SIs suggest suppression that was building up at a similar phase as the major suppression phase of BT-on-tones cycle histograms, but at the maximum BT level the BT level failed to reach the suppression threshold criteria. A final relevant factor is that the clicks were generated by 100 μsec electrical pulses that have a bandwidth of ~10 kHz, beyond which the spectrum has roll-off, ripples and zeros. Overall, our data do not indicate that at CFs above 6 kHz, the OHC MET transduction works differently in generating low-level tone and click responses.

4.4 OHC and IHC Mechano-Electric Transduction Asymmetry

The asymmetry of the OHC MET transducer function affects the ratio of the 2^nd harmonic to the 1^st harmonic in cycle histograms of BT-on-tones and BT-on-clicks suppression. At suppression threshold, we found that the ratio of SI₂ to SI₁ increased as CF increased above 20 kHz (Fig. 8). This is consistent with a variety of other evidence that indicates that in the cochlear base the at-rest operating point of OHC MET channels is near the MET center (i.e. the MET function is symmetric about the operating point) but in the cochlear apex the at-rest operating point is offset toward one edge of the OHC MET (e.g. Dallos et al., 1982; Dallos 1985; Russell and Kössl, 1991; Russell et al. 1986). Although the OHC recording data might give the impression that there is one relatively-uniform OHC MET symmetry value in the apex and another in the base, the data of Figure 8 (particularly the BT-on-tone data) suggest that the OHC MET channel symmetry continuously varies along the whole length of the cochlea.

For BT-alone excitation thresholds the picture is different. In the BT-alone data, the ratio of the 2^nd to the 1^st harmonic at threshold was almost always less than one and was never much greater than one (Fig. 8). Since the BT response received no cochlear amplification in the CF regions we sampled, the BT-alone response is not expected to be influenced by OHC MET asymmetry. Instead, the BT-alone data is shaped by the IHC MET asymmetry. The finding that at threshold the 1^st harmonic of the BT excite data is typically larger than the 2^nd harmonic (Fig. 8) is consistent with there being an off-center operating point of the IHC MET function throughout the cochlea.

4.5 Bias-Tone Excitation Phase and Peak Splitting

The bias tone alone produced synchronized increases in the AN firing rate that, at threshold, fell predominantly into two clusters with each cluster about ¼ cycle from the phase that produced suppression (Fig. 6A, B). Similar results have been found in cats, guinea pigs and chinchillas (Cai and Geisler, 1996b; Sellick et al, 1982; Temchin et al, 1997). IHC stereocilia are freestanding (their tops are not attached to the TM) and the mechanical drive to the IHC stereocilia is by fluid flow radially past the IHC stereocilia, not by direct mechanical shear as in the OHCs (Sellick and Russell, 1980; Freeman and Weiss, 1990; Guinan, 2012). At low frequencies (e.g. 50 Hz), IHC stereocilia deflection is approximately proportional to the velocity of the fluid flow, and this velocity is ~¼ cycle in advance of the structural displacements that cause the fluid flow (The IHC stereocilia hydrodynamic filter is more complicated than a simple low pass, see Freeman and Weiss, 1990). As described in detail elsewhere (Guinan, 2012), the fluid drive to IHC stereocilia is not due only to shearing between the reticular lamina (RL) and the TM. It is also due to several other cochlear micromechanical motions that cause radial fluid flows within the RL-TM gap and thereby deflect IHC stereocilia (e.g. tilting of the RL – Nowotny and Gummer, 2006; 2011). For movement of the BM toward scala vestibuli, some of these drives produce fluid flow that deflects IHC stereocilia in the excitatory direction, and some drives produce fluid flow in the inhibitory direction. These drives superimpose in their actions on IHC stereocilia with relative strengths that depend on CF, tone frequency, tone level, and many other factors. Since these out-of-phase drives act simultaneously, cancellations, or partial cancellations, of the drives cause the magnitude and direction of the net drive to IHC stereocilia to depend on the local mix of the drives. In addition, the IHC stereocilia velocity sensitivity causes a ~¼ cycle phase advance relative to structural displacements. Thus the mixing of multiple out-of-phase drives to IHCs and the approximate velocity sensitivity of IHC stereocilia explain why the bias tone excites AN fibers at phases that fall into two clusters that are ~½ BT period apart and flank the suppression phases.

There is distortion in the processes that create the IHC fluid drives (see Guinan, 2012), and this distortion causes the drives to have non-sinusoidal shapes. Two perfectly out of phase sinusoidal drives at the same frequency can cancel perfectly, but if one of these drives is not sinusoidal (e.g. it is highly peaked at one phase) then when the two drives are nearly equal in amplitude and opposite in phase, there will be only partial cancellation leaving the harmonics from the non-sinusoidal component intact. Such a drive combination could then produce an excitation pattern with two or even more peaks like the patterns seen in Figure 5A at 100-120 dB SPL, a pattern termed “peak splitting”. Peak splitting can be thought of as a by-product of their being multiple, non-sinusoidal drives to the IHCs. From this point of view, the finding in chinchillas, gerbils and cats of two or even three peaks in AN-fiber, low-frequency cycle histograms (Ruggero and Rich, 1983; Ronken, 1986, Cai and Geisler, 1996a) is a natural consequence of their being multiple non-sinusoidal drives to IHCs. The finding that these peaks are sometimes not 180° apart indicates that different drives have different nonlinearities that produce peaks at different phases.

We found that BT-alone stimulation resulted in excitation at one phase for most fibers with CFs above 2 kHz, but for fibers with CFs less than 2 kHz, the excitation phase occurred at either of two phases ~½ period apart with the most common excitatory phase being the opposite of the excitatory phase at high CFs. These bias-tone excitation results are similar those of Cai and Geisler (1996a). Further, the phase of a low-frequency tone that excites AN fibers was reported to reverse at CFs in the middle of the cochlea in guinea pigs, gerbils and chinchillas (Oshima and Strelioff, 1983; Ruggero and Rich, 1983; 1987; Temchin et al. 2012). Since a low-frequency BT suppresses responses to CF tones at approximately the same phase for all CFs, gross cochlear motion must not be reversing at mid-cochlear CFs. Instead it appears that the mix of IHC drives changes in the middle of the cochlea, which means that some aspects of cochlear micromechanics that affect the fluid flow past IHC stereocilia must change in mid-cochlea. It appears that IHC drives that are in opposite directions dominate at the basal versus apical ends of the cochlea. In the terminology of Guinan (2012), an “UP-inhibit” drive (which excites when the BM moves down toward scala tympani) is hypothesized to dominate in the apex while the “Shear” drive and/or the “OHC-Motility” drive (which causes RL tilting) dominate in the base. The concept that there are multiple drives to IHCs with some in opposite directions (Guinan, 2012) provides a way to conceptualize how it is possible for nearby AN fibers to respond at opposite phases. However, attempting to identify exactly what drives are involved is premature. Much more needs to be learned about the anatomy and physiology of the sub-tectorial space before we can fully understand the complex drives to IHCs.

In the two phase clusters produced by BT excitation, the excitatory phase distributions were not tightly grouped when compared to the tight phase distribution of suppression. The tightly-grouped bias-tone suppression is produced by movement of the cochlear partition toward scala tympani causing deflection of OHC stereocilia, and the tight distribution indicates that this deflection happens at the same phase at corresponding points along the length of the cochlea across different cats. In contrast, the wide distribution of BT excitation phases within each of the two main clusters indicates that the fluid drive to IHC stereocilia is much less consistent in its phase than the drive to OHCs. Further, the net IHC drive can have reversed phases at nearby places in a given cochlea or across cochleae. When there is cancellation of out-of-phase drives (as may normally be the case), a small change in one drive can produce a large change in the net fluid drive to the IHC stereocilia. Because of cancellations, or partial cancellations, of the IHC drives, local factors within the organ of Corti can control the magnitude and direction of the drive to IHC stereocilia. Variability in the mix of IHC drives is what leads to the scatter in the BT-alone excitation phases.

5. Conclusions

Despite the cochlea being non-linear, low-frequency bias tones produce similar patterns of suppression on AN responses to low-level clicks and CF-tones. This result supports the hypothesis that AN responses to both clicks and CF-tones share common mechanisms of cochlear amplification. Our data also provide evidence that the at-rest operating point of IHC METs is offset throughout the cochlea and that the OHC at-rest operating point slowly varies from offset in the apex to symmetric in the base. The data are also consistent with the dominant fluid drive to IHC stereocilia changing sign in mid-cochlea. Finally, peak splitting and heterogeneity in the excitatory phases from low frequency bias tones are attributable to a heterogeneous mix of multiple distorted fluid drives to IHC stereocilia.

Highlights.

• Do low-frequency “bias” tones (BTs) suppress tone and click responses similarly?

• BT-induced synchronization index (SI) was measured in cat auditory-nerve fibers.

• After excluding BT excitation, click and tone BT-suppression phases were similar.

• BT effects suggest systematic variation in hair cell transduction along the cochlea

• Distortion in IHC drives may account for auditory-nerve-fiber peak splitting.