Abstract
Numerous intrinsic currents are known to collectively shape neuronal membrane potential dynamics, or neuronal signatures. Although how sets of currents shape specific signatures such as spiking characteristics or oscillations has been studied individually, it is less clear how a neuron’s suite of currents jointly shape its entire set of signatures. Biophysical conductance based models of neurons represent a viable tool to address this important question. We hypothesized that currents are grouped into distinct modules that shape specific neuronal characteristics or signatures, such as resting potential, sub-threshold oscillations, and spiking waveforms, for several classes of neurons. For such a grouping to occur, the currents within one module should have minimal functional interference with currents belonging to other modules. This condition is satisfied if the gating functions of currents in the same module are grouped together on the voltage axis; in contrast, such functions are segregated along the voltage axis for currents belonging to different modules. We tested this hypothesis using four published example case models and found it to be valid for these classes of neurons. This insight into the neurobiological organization of currents also suggests an intuitive, systematic, and robust methodology to develop biophysical single cell models with multiple biological characteristics applicable for both hand- and automated- tuning approaches. We illustrate the methodology using two example case rodent pyramidal neurons, from the lateral amygdala and the hippocampus. The methodology also helped reveal that a single core compartment model could capture multiple neuronal properties. Such biophysical single compartment models have potential to improve the fidelity of large network models.
Keywords: biophysical model, current modules, neuronal signatures
INTRODUCTION
Interplay among intrinsic currents in a neuron can give rise to a rich repertoire of membrane potential dynamics or neuronal signatures, such as unique spiking patterns, and low- and high-threshold oscillations. Computational models have been used to study the role of intrinsic currents in shaping these membrane potential dynamics, starting with the original Hodgkin-Huxley formulation (Hodgkin and Huxley, 1952). Remarkable progress has been made in understanding the key computations performed by single neurons in the context of their role in networks (Herz et al., 2006, Brunel et al., 2014), using connectionist (Dayan and Abbott, 2005), integrate-and-fire (Vogels and Abbott, 2005, Brette, 2006, Rudolph-Lilith et al., 2012), Izhikevich (Izhikevich, 2007, Izhikevich and Edelman, 2008, Hummos et al., 2014) and biophysical (Dayan and Abbott, 2005) model formulations. Although mechanistic underpinnings of how some of the intrinsic currents help shape individual signatures of a single neuron have been reported (e.g., Bennett et al., 2000, Wilson, 2005, Barraza et al., 2009, Sciamanna and Wilson, 2011), functional insights into how they might jointly shape all the signatures simultaneously are not fully understood. Biophysical models represent a class of models that explicitly incorporate channel and synaptic neurophysiology and so are well suited to investigate the important question we address here: how might intrinsic currents interact to shape not just one, but all the diverse neuronal signatures simultaneously? A second related question we address is whether insights from intrinsic currents shaping membrane dynamics can be used for developing improved biophysical single compartment models for network applications.
Rapid advances in electrophysiological measurement techniques have resulted in rich and reliable data being generated characterizing neurophysiology of current channels, synapses, dendritic functions and plasticity (Stuart and Spruston, 2015). In parallel, such data are being incorporated into increasingly realistic biophysical conductance-based models of neurons. This has resulted in the development of single cell models of varying complexities ranging from 1 to 5 compartments to investigate network-level issues (Davison et al., 2000, Dyhrfjeld-Johnsen et al., 2007, Schneider et al., 2012, Kim et al., 2013a, Neymotin et al., 2015), to over 1000 compartments with numerous current channels to investigate details of single cell dynamics (De Schutter and Bower, 1994, Stuart and Spruston, 1998, Roth and Hausser, 2001). Single cell biophysical models are increasingly being sought by researchers modeling large networks containing possibly more than a million neurons (Schneider et al., 2012). The present paper focuses on a particular biophysical formulation of a single cell for use in network applications. Researchers have proposed different approaches to develop simplified biophysical models (Stratford et al., 1989, Rall, 1990, Traub et al., 1991, Bush and Sejnowski, 1993, Pinsky and Rinzel, 1994, Destexhe, 2001, Traub et al., 2004, Hendrickson et al., 2011). These have been formalized and several hand-tuning to automated search algorithms have been proposed (Prinz et al., 2003, Rubin and Cleland, 2006, Hemond et al., 2008, Pospischil et al., 2008). Automated searches have also been used successfully in conjunction with large databases of model neurons to select parameter sets that replicate a range of neuronal properties (Prinz et al., 2003, Gunay et al., 2008), by typically varying the maximal conductance densities, and have helped enhance the model development process considerably. These researchers have also found that some of the properties are controlled by specific currents. For instance, Gunay et al. (2008) found that the hyperpolarization activated cation current H controlled sag at hyperpolarized levels, while the persistent sodium Nap, and M-type potassium current KM were primarily responsible for spontaneous firing (other than the H current, these two currents have half-activation voltages more negative than the rest; V1/2s were much to the right for the other currents which primarily controlled spiking features). In the present study, we ask whether the other currents in the neuron also have similar functional roles, i.e., what functional insights can we gain about the simultaneous interactions of all currents in a neuron. Alternatively, how might the currents in a neuron be organized to affect multiple neuronal signatures in a robust manner. These signatures include passive properties (input resistance, time constant, resting potential), subthreshold oscillations, spiking patterns with varying degrees of adaptation, and high-threshold oscillations. Furthermore, can such insights related to intrinsic currents then be translated into a procedure to enhance the development of biophysical single compartment neuron models for network applications, for certain classes of neurons? The present paper addresses these questions.
The output of a given neuron type is largely determined by the makeup and characteristics of the voltage-gated ion channels inserted into the membrane at a given time. In a previous modeling study, we found that the underlying oscillation of a class of slow-wave bursting cell had three phases: generation, maintenance, and termination and that different modules of currents preserve the characteristics of each phase, and the currents in the modules might be ‘co-regulated’ to preserve function (Ball et al., 2010, Franklin et al., 2010). Generation is the phase during which the underlying oscillation is initiated by either a synaptic pulse or occurs endogenously. The peak and duration of the oscillation are controlled during the maintenance phase. Termination (or repolarization) is the phase during which the underlying oscillation ends and the membrane potential is brought back to its resting value. A key prediction from the study was that distinct modules of ionic currents are responsible for the different phases of generation, maintenance (of peak value and duration), and termination of the underlying oscillation and that their covariation also preserves the cellular characteristics. The finding that distinct currents were responsible for the different phases for the slow underlying oscillation was fortuitous, and we did not investigate whether the concept of modules held for all features of the membrane potential dynamics, including spiking. Also, it was not clear what specific properties of individual currents enabled them to participate in separate modules. All this led us to explore in the present study whether all neuronal membrane potential signatures might be implemented using distinct modules of currents, and if so via what specific kinetic properties of the individual currents.
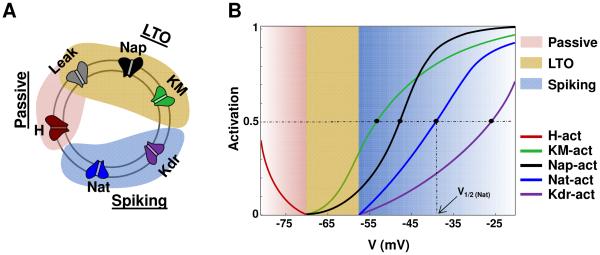
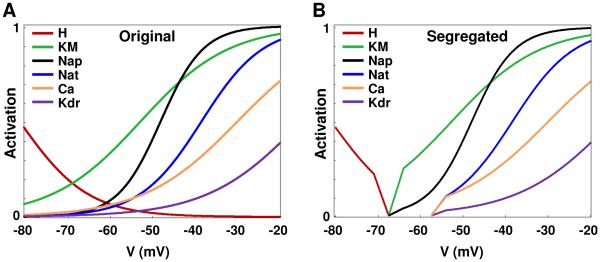
Here we hypothesize that, in single neurons, there are distinct modules of currents which are segregated by gating functions into different voltage ranges, with each current module shaping different cellular functions such as resting potential, low threshold oscillations (LTOs), and spiking. This is depicted schematically in Fig. 1. Specifically, the currents that determine LTOs, for instance, would have activation functions that start on the voltage axis at more depolarized levels (to the right on the voltage axis) compared to the module that implements passive properties. Each module would thus have distinct zones of operation on the voltage axis, and the current module on the right will have activation functions that do not extend into the zone of the module on the left. In the conceptual cartoon schematic shown in Fig. 1, for instance, the zones are: < −70 mV for the passive module, −70 to −57.5 mV for the LTO module, and above −57.5 mV for the spiking module.
Figure 1.
Current segregation hypothesis. (A) cartoon layout showing current sets involved in the three distinct modules that implement the neuronal characteristics for an illustrative neuron with the following modules: passive properties, low-threshold oscillations, and spiking. (B) Activation curves for gating functions of the currents belonging to the various modules.
We tested this segregation hypothesis using four biophysical models reported in the literature and found support for the hypothesis in all four cases. For this testing, as elaborated in methods, we first identified the different current modules and their zones of operation, and then edited the activation functions to limit the tails and consequently avoid overlap among adjacent modules. In the following, this elimination of overlap is termed segregation. The finding that currents can be segregated into distinct modules is then shown to lead to an intuitive and systematic methodology for the development of biophysical single cell models of neurons that permits simultaneous matching of biological characteristics such as passive properties (e.g., input resistance, resting membrane potential, and time constant), responses to current injections, and oscillatory potentials at both low- and high- thresholds. This is accomplished by segregating the intrinsic currents into logical units that implement each characteristic separately. The resulting models have a high degree of robustness in the sense that changes made to the maximal conductance densities of currents belonging to one module have little or no impact on properties controlled by the other modules. This insight related to segregation of currents also helped reveal that a single core compartment could capture multiple neuronal properties and this higher fidelity might be an attractive feature for applications involving large networks. The model development process, applicable to hand- and in some cases to automated- tuning procedures, is illustrated using two rodent pyramidal cell types, one from the hippocampal CA3b region (Hemond et al., 2008) and the other from the lateral amygdala (LA; which exhibits both low- and high- threshold oscillations (Pape et al., 1998)). Finally, we illustrate how single cell models with a single core compartment can be integrated into networks and compare the predictive and run-time performance for one of the example cases using a 100-cell network where the cells were connected via dual-component excitatory (e.g., glutamatergic AMPA/NMDA) and inhibitory (e.g., GABA) synapses and transmission delays.
METHODS
Biological data used to constrain a biophysical neuronal model include morphology, known current channel types and their maximal conductance densities, passive properties of the cell (e.g., input resistance, time constant, resting potential), and responses to current injections. It is also important to preserve synaptic integration characteristics, an area that is not well understood presently (Stuart et al., 2008). These properties are determined from the literature for the particular neuron prior to developing the model equations using the formulation described next.
The equation for the single compartment followed the Hodgkin-Huxley formulation (Byrne and Roberts, 2009) in eqn. 1,
| (1) |
where V is the membrane potential (mV), and are the intrinsic and synaptic currents, Iinj is the electrode current applied to the soma, Cm is the membrane capacitance, and gL is the conductance of leak channel. The intrinsic current was modeled as , where gcur is its maximal conductance, m its activation variable (with exponent p), h its inactivation variable (with exponent q), and Ecur its reversal potential (a similar equation is used for the synaptic current but without m and h). The kinetic equation for each of the gating functions x (m or h) takes the form
| (2) |
where x∞ is the steady state gating voltage- and/or Ca2+- dependent gating variable and τx is the voltage- and/or Ca2+- dependent time constant. We describe next the procedure used to test the segregation hypothesis, using four published models from the literature, including a listing of relevant biological data for each case. This is followed by descriptions of the biological data for the two single cell example cases used to illustrate the proposed modeling methodology.
Biological data for four published single cell example cases
We validated the hypothesis using four published example case models from the literature: example case 1: hippocampal CA3b pyramidal neurons (Hemond et al., 2008); example case 2: cortical/thalamic neurons (Pospischil et al., 2008); example case 3: rodent mitral cells of the olfactory bulb (Rubin and Cleland, 2006); and example case 4: rodent lateral amygdala pyramidal neurons (Alturki et al., 2015). The biological data related to these single cell models include passive properties (input resistance, resting potential, time constant), oscillatory potentials if any, and current injection responses including spiking/adaptation properties; details related to the data including numbers can be found in Appendix A1. These data are used to identify the current modules operational in the models, and highlight the fact that segregation may be common among single cell neuron models in general.
Furthermore, the proposed methodology to develop biophysical single cells models using insights related to current modules is illustrated using two of the four cited example cases, 1 and 4. Additional data are provided for these two cases to support the modeling procedure and to facilitate replication of reported results by other researchers.
Validation of hypothesis using neuronal models from literature
To test the hypothesis related to segregation of currents in single neurons, we analyzed the activation/inactivation kinetics of individual currents in four published neuronal models and asked whether distinct current modules implemented characteristics such as resting potential, low threshold oscillations, spiking/adaptation/bursting, and high threshold oscillations in these model cells. Specifically, we investigated the gating kinetics of currents along the voltage axis and categorized them into logical modules that might implement specific characteristics, as depicted in cartoon form in Fig.1A for a hypothetical neuron; the corresponding gating functions are shown in Fig.1B. In Fig. 1A, for instance, leak and the hyperpolarization activated cation current H are responsible for passive properties; leak, persistent sodium Nap, and M-type potassium current KM control low-threshold oscillations; and transient sodium Nat and delayed rectifier Kdr currents control spiking. As cited, the cartoon schematic shown in Fig. 1B shows three modules of currents, segregated into the following zones: < −70 mV for the passive module, −70 to −57.5 mV for the LTO module, and above −57.5 mV for spiking. Note that the activation functions for each module start on the voltage axis only after the zone of action of the module to its left.
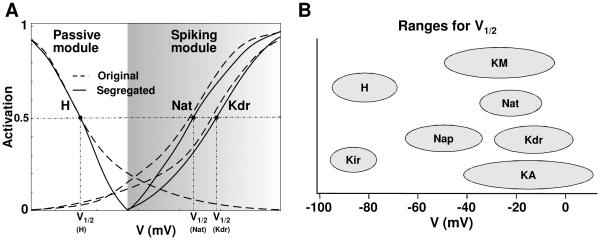
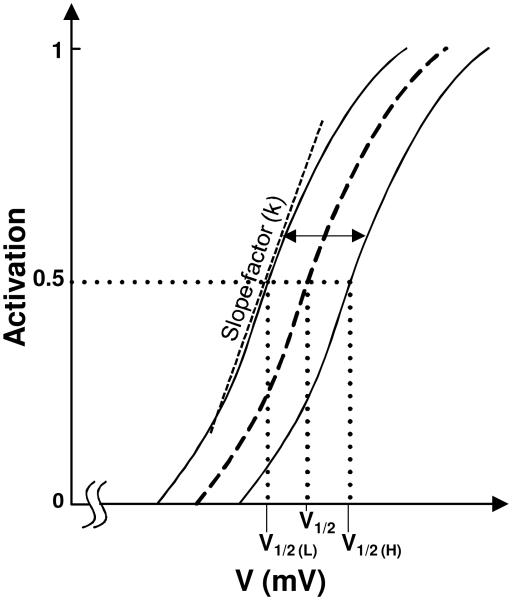
This procedure to segregate the currents into modules is illustrated in cartoon form in Fig. 2A that shows two modules in a hypothetical neuron: passive properties module and a spiking module. As a first step, the right extent of the zone of activation of the passive module is selected to be between the resting potential and the spike threshold (e.g., 3 mV above the resting potential was found adequate for some of the example cases as discussed later). In the next step, the currents are segregated. As can be seen, original activation curves have significant overlap, and this was eliminated with the proposed segregation. We highlight the fact that the activation functions used in the segregated model have sharper cut-off at the ends to minimize overlap, but preserve the other features of the original functions. It is known that activation function parameters such as half-activation voltage V1/2, are known to vary, as illustrated in Fig. 2B (adapted from Izhikevich, 2007; variations have been reported in slope factor k and time constant also, not shown here). The activation function for a model current can thus be ‘shifted’ along the voltage axis if it facilitates grouping into modules, provided they are within reported bounds as in Fig. 2B.
Figure 2.
Illustration of the segregation idea. (A) Implementing the segregation on a cartoon model that has two current modules: passive and spiking, and includes three ionic currents: H, Nat, and Kdr. The corresponding activation functions (dotted lines) are reshaped using the segregation approach (solid lines) to eliminate overlap between modules. (B) Ranges of half-activation voltages for several ionic currents (adapted from Fig. 2.21 of Izhikevich, 2007).
In the four published model neurons considered, we implemented ‘segregation’ along the voltage axis for the activation functions by limiting them to be within non-overlapping voltage ranges as illustrated in Fig. 2A (without changing their half-activation voltage V1/2 or slope factor k), and then checking whether this caused any change in the particular characteristic of the cell. In our analyses, we also found that the gating functions related to inactivation dynamics did not play any role in the interactions, possibly due to their slower kinetics. In some of the cases below, the segregation described above necessitated a retuning of the maximal conductances (only) to restore original characteristics. Descriptions of the biological details related to the four published example case single cell models are provided in Appendix A1.
Incorporating single cell models into a network
For the present study, the soma and axon are combined into one compartment, and we consider this core compartment as performing the function of integration for the neuron. Dendrites exhibit a rich repertoire of behaviors, and have been shown to have active channels (Magee and Johnston, 2005, Sun et al., 2011), and the role of dendritic channels in information processing is continuing to be unraveled (Stuart et al., 2008). Our focus on a single compartment model necessarily precludes incorporation of several such features, and we consider only two dendritic processing functions that shape the EPSP from the synapse to the soma, namely time delay and gain, and suggest how to scale synaptic gains to approximate the dendrite in a one-compartment model case. Other filtering characteristics such as changes in rise and decay times between the synapse and soma can also be incorporated if reliable information is available.
For the illustrative 100-cell model with single compartment cells, we used dual-component excitatory AMPA/NMDA synapses, and inhibitory GABAA synapses as in our prior models (Kim et al., 2013a, Kim et al., 2015). All reported models were developed using the NEURON modeling package (Carnevale and Hines, 2006). The codes will be made available upon publication via the ModelDB public database (http://senselab.med.yale.edu/ModelDB/).
RESULTS
We first discuss results from testing the hypothesis related to functional segregation of current modules in single neurons, using four models from the literature. We then show how the hypothesis leads to a systematic procedure for modeling single-compartmental neurons that consist of soma combined with axon, using two example case pyramidal cells. Such a systematic procedure facilitates hand-tuning and automated search approaches for developing models of single neurons. Finally, we illustrate how the single cell models developed using such an approach can be incorporated into networks, using a 100-cell example case network. Each of these results is discussed in separate sections below.
Different neuronal characteristics are implemented by distinct current modules
Building on the inadvertent finding in our previous study (Franklin et al., 2010), here we hypothesized that all currents in a neuron are organized into functional modules that are segregated into voltage ranges with different modules implementing cellular functions such as resting potential, low threshold oscillations, and spiking/adaptation/bursting. Segregation implies that the set of currents responsible for a particular cellular characteristic (e.g., passive properties) would have activation functions that have minimal overlap along the voltage axis with the set responsible for a different property (e.g., spiking).
Validation using published example cases
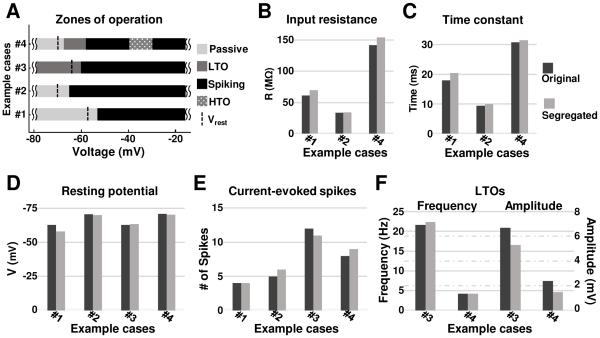
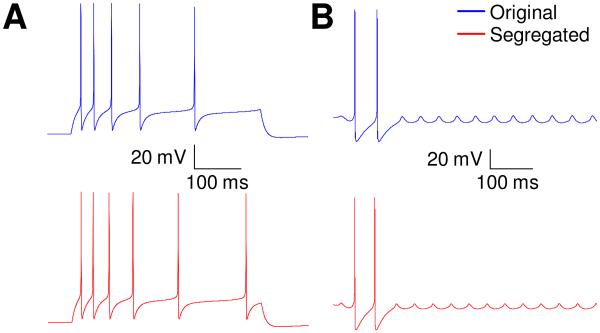
The first published example case tested deals with three types (burst-firing, adapting, and weakly-adapting) of hippocampal model cells (Hemond et al., 2008). A ‘passive properties module’, and a ‘spiking/adaptation/bursting module’ were identified with clear separation between them (case #1 in Fig. 3A). We remind the reader that all that was changed in this test was to limit the appropriate gating functions to within segregated voltage ranges for each module, without changing the functions themselves. As detailed in methods, this involved retuning the maximal conductances for a few currents in some cases, and that was the only parameter that was changed, if at all, for a current. The original and segregated models matched well as seen in figures 3 and 4. For passive properties, Vrest matched to within 7% for all cell types, while Rin and τm were within 15% and 13% respectively for the burst-firing cell, and within 26% and 33%, respectively for the adapting and weakly-adapting neurons (see Fig. 3, B-D). Considering the spiking/bursting/ adaptation module, the numbers of spikes elicited in the proposed versions were identical to that reported for burst-firing and weakly-adapting cells, and was lower by 25% for adapting cells (see Fig. 3E). It is noted that only maximal conductances were considered in this retuning; inclusion of half-activation voltages as another free parameter would result in reduced differences, but since our aim here is to illustrate the procedure, it was not considered. The membrane potential waveforms for the original and segregated cases matched very well as shown in figure 4.
Figure 3.
Comparison of neurocomputational properties between original and segregated cases for the four published single cell models, as applicable: #1: CA3b burst-firing neuron (Hemond et al., 2008), #2: Cortical/thalamic regular spiking neuron (Pospischil et al., 2008), #3: Olfactory bulb mitral cell (Rubin and Cleland, 2006), #4: Type-B LA pyramidal neuron (Alturki et al., 2015). (A) Zones of operation for each case. Comparisons of input resistance and time constant values (B & C), resting potential and current-evoked number of spikes (D & E), and low-threshold oscillations (LTOs) (F). For (B) to (F), dark gray bars - original models; and light gray bars - segregated models.
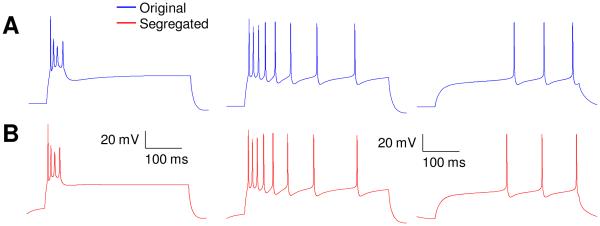
Figure 4.
Responses to 400 ms duration current injections for both original and segregated models of the three distinct hippocampal CA3 cell types in example case 1 (Hemond et al. 2008). Upper trace is for the original model and lower one for the same model after segregation and minor re-tuning of some ionic conductances. Left: burst-firing neuron, 1.53 nA. Middle: adapting neuron, 1.37 nA. Right: weakly-adapting neuron, 0.583 nA.
The second example case considers single cell models of the main classes of mammalian cortical and thalamic neurons (Pospischil et al., 2008). For this case, there were two sets of current modules for each cell type, the ‘passive properties module’ and the ‘spiking/adaptation/bursting module’. When we segregated the gating functions of these modules as described and compared the passive properties between the published model types and our modifications, the average deviation for all cell types (RS, FS, IB, and LTS) in Vrest, Rin, and τm was minimal, being 1%, 3%, and 6%, respectively (see Fig. 3, B-D). For the spiking /adaptation/bursting module, the numbers of current injection-induced spikes matched exactly with those in the original models for FS, IB and LTS neuron models, and was off by 20% for the RS model (see Fig. 3E). It is noted that the segregated models of both RS and FS cells replicated the frequency-current (F/I) relation of the corresponding original cell models presented in Pospischil et al. 2008 (data not shown). Interestingly, no changes in maximal conductance densities from the published models were required for any of the currents, in this case. The membrane potential waveforms for the original and segregated cases in panel A of figure A3 also indicate very good match.
Figure A3.
Responses to current injection for both original and segregated models for example cases 2 and 3. Upper trace is for the original model and lower one for the same model after segregation and minor re-tuning of some ionic conductances. (A) RS cell of Pospischil et al. 2008, 750 pA for 400 ms. (B) Mitral cell of Rubin and Cleland 2006, 200 pA for 1200 ms.
The third example case tested involved a model of rodent mitral cell (Rubin and Cleland, 2006) which had endogenous sub-threshold oscillations. Hence this case has a ‘low-threshold oscillations module’ and a ‘spiking/bursting module’. The frequency of subthreshold oscillations in the proposed single cell model was within 4% of reported values (Fig. 3F). Depolarization via constant current injection resulted in the number of spikes and inter-burst interval in the segregated case (with minor retuning – see appendix A1) being within 8% of the published data, and very good match between the membrane potential waveforms (Fig. A3, panel B).
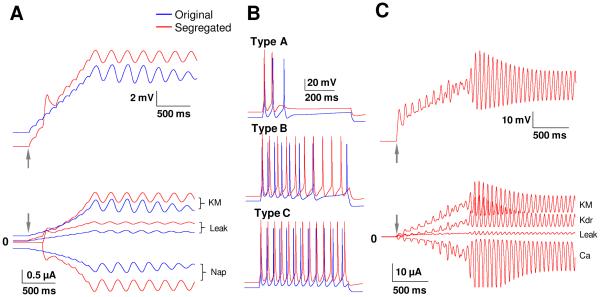
The fourth example case considered single cell models of rodent lateral amygdala pyramidal cells (Alturki et al., 2015) and data for passive properties, low-threshold oscillations (Fig. 5A), spiking/adaptation (Fig. 5B), and high-threshold oscillations (Fig. 5C). Implementation of the segregation method (by limiting gating functions to restricted zones on the voltage axis) in this model had little effect on Vrest, Rin and τm and resulted deviations from values of the original model by only 1%, 8%, and 3%; respectively (see Fig. 3, B-D). Current evoked spike numbers differed by a maximum of 14% compared to the original model (see Fig. 3E). The frequency of the high-threshold oscillation (~ 18 Hz) was not affected after implementing the segregation idea, even prior to additional tuning. However, the segregation method abolished the LTOs, possibly because of the sensitivity of the currents underlying this oscillation. Persistent sodium current which is the source of excitatory drive of the oscillation is a very small current in such neurons, with a magnitude typically 0.25% of the maximum transient sodium current (Alzheimer et al., 1993, Vera et al., 2015). This makes the Nap current highly sensitive to any change in the other currents, i.e., if an activation function of a current from another module, such as Kdr, overlaps significantly with this LTO module, Nap becomes ineffective. Retuning some of the maximal conductances restored the LTOs in the segregated model, including with a frequency within 1% of that in the original model (see Fig. 3F). Pape and Driesang (1998) found that Ca2+ was the depolarizing mechanism in HTOs, but were unable to determine which potassium currents underlie the hyperpolarizing mechanism. Our model predicts that KM and Kdr provide the hyperpolarizing mechanism, and this prediction could be tested in experiments.
Figure 5.
Comparisons of oscillatory potentials and spiking characteristics between the original (blue) and segregated (red) versions of the 1-comp LA model neuron. Arrows in the figures indicate start of current injection. (A) Membrane potential responses to a slow depolarizing current. The model starts oscillating at 4Hz around −59 mV (upper trace), due to an interplay between Nap and KM currents (lower trace) that were found to be responsible for LTOs; (B) Membrane potential responses of the three pyramidal cell types (A-C) to current injections of 400 pA for 600 ms. To prevent overlap, the segregated model is offset by 10 mV; (C) The sodium channels (Nap and Nat) were blocked and the membrane potential raised to −40 mV, as in biology, to reveal HTOs (upper trace). The primary currents involved in HTOs are found to be Ca, KM, and Kdr (lower trace). Despite considerable tuning, we could not show HTOs in the original model, explaining the lack of blue traces in panel C.
The segregation technique was also found to be applicable, with some adjustments, to the Ca2+-activated potassium currents for all the example cases. For instance, in example case 4 (LA neuron), the half-activation voltage for the Ca2+ current is −30 mV, and so the segregation technique used a value of −57.5 mV as the cut-off to edit this current, which belongs to the spiking/adaptation module. Below −57.5 mV, the calcium current was very small, and so its contribution to the calcium-pool that controls the calcium-activated potassium currents was consequently small. So, the calcium-activated potassium current to be activated at the same boundary as for the module containing the Ca2+ current. In some cases, the cut-off may need to be moved to more hyper-polarized voltages. Accordingly, we set the activation curve for KC and K_AHP to zero at the boundary itself (−52.5 mV) for example case 1, while for example case #4, we set the activation curve for KsAHP to zero below −65 mV. So, such an adjustment to the segregation method for the calcium-activated potassium currents worked for all the models we investigated that had this current (example cases 1, 3 and 4). A similar approach also worked for the Ca2+−activated Ca2+ current used in example case 2, i.e., the activation curve for I_CaL was set to zero below −60 mV.
As part of our analysis, we found that the gating function related to inactivation did not need to be considered in the segregation process, i.e., it did not affect the results, and we investigated the causes. The module controlling passive properties in all four example cases did not have any inactivation functions. This is because this module consisted primarily of leak and H currents. It is noted that leak is assumed to include all non-voltage gated channels including Na, K and chloride types. Interestingly, the module controlling low-threshold oscillations either had large inactivation time constants making them of an almost persistent type (e.g., mitral cell case in Rubin and Cleland, 2006) or did not have inactivation (e.g., LA neuron in Alturki et al., 2015). Considering the spiking/bursting module, the Na current has both activation and inactivation, while the Kdr current typically does not. Changes to the half-activation voltage for the activation function of the Na current change the spike initiation threshold while changes to the inactivation function have little effect. It is noted that the Hemond et al. (2008) study shifted both activation and inactivation of a group of currents, such as Na, KM, and Kdr, by +24 mV to match biological firing patterns. This suggests that, in the segregation approach we propose, the inactivation function should be moved the same amount as the activation one for currents that have inactivation, and so does not need to be considered separately. Finally, we noticed that among the currents responsible for HTOs in the LA neuron case, only Ca2+ has an inactivation function but that has a large time constant of 420 ms, making it persistent in the time scale of the HTOs; it needs to be explored whether this fact holds in general trend for currents implementing HTOs in other cells. The observations above suggest that the segregation process could focus on activation functions, and shift the inactivation functions by the same amount as the activation functions as in Hemond et al. (2008).
In summary, the results discussed above for the four published model neuron cases (Figs. 4, 5 and appendix Fig. A3) provide validation for our hypothesis related to segregation of the current modules based on functional characteristics (Fig. 1). The hypothesis suggests that, for instance, currents implementing the functional characteristic of spiking have activation functions that start on the voltage axis to the right (more depolarized) of the activation functions for currents that implement LTOs, and so on. Each module thus has a distinct zone of operation on the voltage axis (Fig. 3A), and the current module on the right will have gating functions that do not extend into the zone of the module on the left. For instance, the zones of operation of the current modules in the LA neuron case were as follows: the passive properties zone of operation ranged from the hyperpolarized side up to −67.5 mV (2.5 mV above rest). The LTO zone ranged between −67.5 to −57.5 mV, with bounds being about 2.5 mV above rest and 2.5 mV below spiking threshold. The spiking/adaptation zone began at −57.5 mV, about 2.5 mV below spiking threshold and through all depolarized levels. Finally, the HTO zone that involves interaction of already activated currents (KM, Kdr, Ca, and sAHP) ranged between −40 and −30 mV. As mentioned earlier, another finding was that the zone of operation for the gating functions related to inactivation did not affect the functional characteristics. Next, we investigated whether such a segregation does indeed simplify the tuning process.
Segregation facilitates the tuning process
A question that arises is whether this segregation, i.e., limiting the gating functions of the different current ‘modules’ to within specific voltage ranges in the manner cited above, does indeed simplify the tuning process. To investigate this, we considered the same four cases discussed above, in two different ways.
(i) In the first approach, we noted that the half-activation voltages for all the current modules were well segregated for all the four example cases. This suggests that the process used to optimize the four models had naturally segregated the current modules by half-activation voltages. This is an important observation in itself that appears to not have been highlighted in previous reports. The second item investigated was whether the overlap in the ‘tails’ of the gating functions across the modules causes any significant interaction among the properties they control. As cited in the previous section, some of the maximal conductance densities had to be re-tuned after the segregation to restore original values of characteristics. We asked whether the match with the original properties would still be close if the conductances had not been re-tuned after segregation. In three of the four cases, prior to retuning some of the conductances, the differences were indeed significant. For instance for the case of mitral cells (Rubin and Cleland, 2006), the subthreshold oscillations could not be sustained beyond a few cycles prior to re-tuning, and the spiking behavior was abolished completely. Similarly, for the CA3b burst-firing neuron (Hemond et al. 2008), the bursting was converted to tonic spiking, and the values for Rin and τm differed by 25% and 30%. For the LA pyramidal cells case (Alturki et al. 2015), the values for Rin and τm differed by 23% and 16%; and current injection responses increased by around 40-100% for all three cell types. Importantly, low threshold oscillations were completely abolished with the change, and the highly-adaptive type A cell was converted to an endogenous spiker. These studies revealed that the properties of a particular module are affected significantly by overlap of activation functions of currents from other modules. From our own experience in tuning the LA model neurons, this overlap makes the tuning process very difficult; removal of the overlap, on the other hand, simplified the development of LA models considerably, and we believe the same would hold for the other example cases. It is important to note that matching all properties (passive, LTO, spiking/adaptation, and HTO) simultaneously in the LA neuron was possible only in the segregated case. Interestingly, the differences between original and segregated models for the Pospischil et al. (2008) example case were minimal without re-tuning, indicating that the advanced automated search process they used seemed to have found a solution that minimized overlap among the modules, the key idea we propose in the present paper. It is noteworthy that the authors were unaware of this additional dimension of optimality in their solution.
(ii) In a second approach to check whether segregation does indeed facilitate the tuning process, we changed the parameter values for currents in one of the modules in the same published models and investigated the effect on the properties controlled by other modules. Our hypothesis is that tuning would be made easier because making changes to one module would have a negligible impact on the others. We investigated this for four model cases below.
CA3b models (Example case 1)
Increasing the maximal conductance density of KM even 10-fold in the segregated model resulted in no change (0%) in Vrest and Rin. However, for the original (non-segregated) model, a change to KM by 2.7-fold was sufficient to drop Vrest by 1.5 mV and decrease Rin by 7 MΩ (> 12% change), compared to the baseline case. Similarly, changing the conductance of KA even 10-fold made no change in Vrest and Rin in the segregated model (0% change), but a 2.5-fold change in KA in the original model dropped Vrest by 2.4 mV and decreased Rin by 10.6 MΩ (18% change).
Cortical/thalamic (Example case 2) and Mitral cell models (Example case 3)
The current modules, as noted, were well segregated in the Pospischil et al. (2008) case, and so changes made to conductance densities of any current in one module had negligible effect on the others. For instance, the intrinsically bursting (IB) cell had a resting potential around −85 mV and had two modules: passive properties module governed by leak and the spiking/adaptation/ bursting module controlled by Na, Kdr, KM, and L-type Ca currents. As shown in table 3, the half-activation voltages of Na, Kdr, KM, and L-type Ca at −29, −28.8, −35 and −33 mV, respectively, are considerably above the resting potential of −85 mV, achieving robust segregation between the modules. In particular, the tails of the activation functions for currents shaping the spiking/bursting module were less than 0.01 at −82 mV (3 mV above rest). A 2.5-fold increase in either KM, Na, Ca or Kdr conductance had no effect on Vrest and Rin (changes were <1%) indicating that the currents are well segregated.
Table 3.
Activation function parameters for the cortical/thalamic and mitral model neurons.
|
Activation
kinetics |
Cortical/thalamic neurons
(Pospischil et al. 2008) |
Mitral cell (Rubin and Cleland, 2006) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Na | KM | Kdr | CaL | CaT | H | Nap | KA | Nat | Kdr* | Ca | |
| V1/2 (mV) | −29 | −35 | −28.8 | −33 | −57 | −84.1 | −48.7 | −42 | −29 | −12.9* | 3.2 |
| Slope factor (k) | 7.4 | 10 | 11 | 4.6 | 6.2 | −10.2 | 4.4 | 13 | 7.4 | 10.1* | 7.1 |
The activation kinetics of Kdr followed experimental data that started activation at −40 mV. Parameters were extracted from the model using the MATLAB curve fitting tool.
In the mitral cell model (Rubin and Cleland 2006), the authors used a two-step semi-automated process that starts first by varying the conductance values of the four currents responsible for the subthreshold oscillations (Nap, H, KA, and Kca) over a parameter space that produced ~ 60,000 possible combinations. Each parameter set was then simulated in NEURON and data of all the ~ 60,000 trials were then analyzed using MATLAB to obtain a best-fit solution in terms of voltage-dependent frequency of subthreshold oscillations in comparison with reported experimental data. A second step then involved tuning the remaining higher-threshold active currents (Nat, Kdr, and Ca) using a similar parametrization technique to that of the first step, to match spiking/bursting properties. The above two-step fitting method the authors used has similarities to our segregation idea, but was not fully developed. For instance, the authors reported that they shifted the activation curve of Nap left by 7-10 mV (i.e., made it more negative; towards the left of the range for half-activation voltages for Nap shown in Fig. 2B adapted from Izhikevich 2007) to that of the spiking sodium current Nat. This allowed Nap to activate at the lower-threshold STOs levels (~−64 mV), with an activation gating value being at 0.05 compared to 0.003 for Nat. This shifting is one of the key points we suggest in the proposed segregation idea. Additionally, the authors implemented an experimental curve for the activation function for the delayed rectifier potassium currents (both fast and slow), and these were activated positive to −40 mV, i.e., much above the STO levels, making the ‘tails’ zero at STO levels. This implies that the authors used the higher range of half-activation voltage for Kdr (see Fig. 2B) to possibly minimize interference with the currents implementing STOs. Indeed, this segregation made STOs robust to variations in high-threshold activation currents, such as Nat, Kdr, and Ca which in turn controlled the spiking/bursting properties. Nap and KA which were main contributors to the STOs had half-activation voltages at −48.7 and −42 mV, respectively, with activation gating values at STOs levels of 0.05 and 0.18, respectively. On the other hand, the half-activation voltages of Nat, Kdr, and Ca which were involved in the bursting activities were segregated being at a relatively higher-threshold, −29, −12.9, and 3.2 mV, respectively, with activation gating values at STOs levels of much smaller values than those of Nap and KA, at 0.003, 0, and 0.0001, respectively. This segregation in half-activation voltages among currents responsible for tuning the two different modules, in addition to limiting the extended tails of activation functions, created a mitral cell model that is well segregated and robust.
LA neuron models (Example case 4)
A similar comparison using the LA type B model cell revealed that even a 10-fold increase in the maximal conductance density of KM in the segregated model resulted in no change (0%) in Vrest and Rin, but a much smaller 2.5-fold change in the original (non-segregated) case dropped Vrest by 2.5 mV and decreased Rin by 26 MΩ (> 15% change). In another comparison we varied the conductance value of Nap involved in the LTO module. A 0.8-fold increase in Nap conductance in the non-segregated model was enough to increase Vrest and Rin by 3.5 mV and 35 MΩ (22%) respectively, compared to no change at all in Vrest and Rin with even a 10-fold change in Nap conductance in the segregated model. Also, a 10-fold decrease in Nat conductance or a 10-fold increase in Ca conductance had no effect on LTOs in the segregated model, but even a 0.5-fold decrease in Nat conductance or a 0.3-fold increase in Ca conductance was enough to abolish the LTOs in the original model. Another important observation was that tuning only the spiking/adaptation module in the segregated case easily generated the A, B and C cell types, without affecting their passive properties or LTO characteristics. However, unintended interactions among the current modules made a similar tuning with the original models much more demanding and not feasible without compromising on the properties of the other modules. Also, as shown in a later section, we were not able to tune the original model to exhibit HTOs, but tuning the segregated model to exhibit HTOs was easy and efficient. This supports the idea of segregation of currents along the voltage axis into non-interacting modules for neurons with multiple signatures.
With this insight about distinct current modules shaping different characteristics, we propose an intuitive methodology in the next section to model biophysical single neurons using two published example cases. Finally, we illustrate how the single cell models can be integrated into networks using an example case.
Potential caveats of the proposed segregation hypothesis
The proposed segregation scheme for single compartmental models has been demonstrated for certain classes of neurons described above; their applicability to other classes requires further research. For instance, the original squid model reported by Hodgkin and Huxley (1952) has three currents, transient sodium Nat, delayed rectifier Kdr, and leak, implementing two functions, resting and spiking. Considering the activation curves, Kdr is found to contribute several millivolts to the resting potential and so segregating both currents from rest caused Vrest to be significantly depolarized. A potential explanation for this might be the fact that cells with limited sets of currents (e.g., squid) may not have functional segregation among the currents. Also, if the focus is on spiking patterns rather than spiking waveforms, segregation schemes may work for such cases also and requires further study.
The class of globus pallidus neurons studied by Gunay et al. (2008) has currents with gating functions organized into modules that exhibit overlap. In their carefully developed models, H is shown to control the sag at hyperpolarized levels, and the current pair Nap and KM are noted as being primarily responsible for spontaneous firing. The same current pair of Nap and KM was responsible for low-threshold oscillations in the LA example case discussed earlier. However, different from the LA example case, the gating functions for Nap and KM were found to extend significantly left into the rest module, suggesting a non-modular arrangement. Interestingly, a closer investigation of the dynamics revealed that Nap and KM in the Gunay et al. model had time courses that were significantly different from the currents active at rest, enabling them to be the primary currents involved in spontaneous firing. This in turn suggests that functional segregation among modules could also be accomplished via different time courses among the module currents, even though their gating functions may overlap, and this interplay between time constants and gating functions has not been investigated here, but is an important topic of future study. The other currents in their model, Naf, Kdr, KA, Ca, and Ca-activated AHP K controlled (in addition to KM) spiking and adaptation, and had half-activation parameters that were significantly larger than those of the rest and spontaneous firing (Nap and KM) modules.
The spiking and HTO modules had interactions in the LA neuron case and this can be explained by the fact that HTOs, as cited earlier, are revealed in LA neurons only with block of Nat with TTX (Pape et al., 1998). So, interestingly, the interaction between the modules in this case is a characteristic of the biological neuron, and does not violate the key finding of a neurobiological organization of currents into modules. Neuromodulation is known to change the current kinetics and impact circuit function (Marder et al., 2015). Although not considered in our study, neuromodulation effects can be included without compromising on the segregation idea if the kinetics they impact are known. Although the segregation approach was applicable to the calcium-activated potassium and calcium currents in all the example cases, applicability to other types of such calcium-activated currents should be investigated. Finally, the reported findings are limited to single compartmental models which precludes incorporation of the functions known to be implemented by dendrites. Nevertheless, the present study is a significant first step towards understanding the underlying principles of how various neuronal signatures may be implemented by the suite of currents in a neuron in a robust manner. Also, the methodology for developing neuronal models using the segregation approach will be useful in applications involving large networks where spiking patterns, rather than the waveforms or detailed biophysics, are more important.
Application of finding - Single compartment model can capture salient neuronal dynamics
The finding that currents may be neurobiologically organized into distinct modules in a neuron suggest a methodology to capture its salient dynamics in a single core (soma+axon) compartment, as summarized in Box 1. This efficient and robust procedure is applicable to hand-tuned, and to some extent, to automated- search approaches, for developing single model neurons. We illustrate the proposed methodology below with two specific example cases; details related to these can be found in Appendices A1 and A2.
Box 1. Overview of segregation procedure for modeling biophysical single neurons.
Neuronal signatures: Select the neuronal signatures to be modeled, e.g., passive properties, current injection responses, and oscillatory potentials, if any, such as low- and high-threshold oscillations.
Intrinsic currents: Determine the currents reported for the neuron. Find the ranges of maximal conductance densities for each current.
Zones of operation for each neuronal signature: The gating kinetics may be available as experimental or mathematical curves. Using a plot of the activation functions of the currents as a function of voltage, estimate the zones of operation for each neuronal signature. For instance, the passive module is below −75 mV, etc. (see description of ‘zones of operation’ in results). This will reveal the currents participating in each module (Fig. 1B).
Activation functions and ranges for parameters V1/2 and k (see illustration in appendix Fig. A2): Using biological data for ranges for the half-activation voltages of activation functions (e.g., Fig. 2B adapted from Izhikevich, 2007), find the ranges that minimize overlap between the modules (Figs. 1 and 2). The activation functions for currents within the module start at the beginning of the zone for that module. Activation functions of the Boltzmann type will require reshaping the ‘tails’ to avoid overlap, as shown in Fig. A1 (also see appendix A2). Experimental activation curves typically have such sharp cut off already and so these or similar mathematical curves can be used directly. The parameters V1/2 and k for each current are then restricted to these ranges, defining their parameter spaces.
With the information above, a hand- or, in some cases, an automated- tuning approach can search over the parameter space of activation kinetics (V1/2 and k) and maximal conductance densities, or can fix the activation kinetics (as in most automated schemes) and search only over the space of maximal conductance densities. As a more efficient alternative of this approach, one could tune the segregated modules sequentially, starting with the one furthermost to the left on the voltage axis, and then progress (right) to more depolarized levels. For instance, in the case of the LA neuron, such an alternative approach would follow the sequence: passive module, LTO module, spiking/adaptation module, and HTO module.
Modeling Single Cells: Hippocampal CA3b pyramidal neurons of example case 1
The first example case to illustrate the proposed scheme uses a published 135-compartment CA3b single pyramidal cell model from the hippocampus (Hemond et al., 2008). We investigated whether a 1-compartment version could reproduce all the characteristics reported for the multi-compartmental version. The equivalent single compartmental model preserved the total surface area of the detailed model, and had both diameter and length of 96.87 μm. The maximal conductance densities for each current were obtained by averaging across all compartments. We then tuned around these values (max deviation from original values were ~30%) to obtain the match with biological data. Since the parameter values are on a per unit area basis, any value of neuronal area would work in general for all properties except input resistance.
Passive properties
Currents active at rest were leak and the two hyperpolarization activated currents: H and KD; all other currents were segregated to be active only above rest. So, the tuning process (see Box 1 and Appendix) to match biological data for Vrest, Rin, and τm involved conductances for H, KD and leak, the reversal potential for leak, and the membrane capacitance. The parameters for the gating functions were unchanged. The resulting values for Vrest, Rin, and τm for the burst-firing, adapting, and weakly-adapting proposed models matched biological values (Hemond et al., 2008) closely: Vrest: −57 mV, −59 mV, and −64 mV, matching to within 3% for all types; Rin: 58 MΩ, 74 MΩ, and 56 MΩ, matching to within 2, 1 and 18%; and τm: 21 ms, 34 ms, and 31.5 ms, matching to within 5, 0 and 30%.
Spiking properties
The spiking module in this model consisted of Nat, Kdr, KA, L-type Ca, and KM, in addition to KD which was active in the previous module. The activation functions of these currents were non-zero just above Vrest, beginning at −52.5 mV, producing a good match with biological data (Hemond et al., 2008). The number of current-evoked spikes matched data reported in the paper: 1.53 nA for 400 ms elicited a burst of 4 spikes in both for the burst-firing case,1.37 nA elicited 8 spikes in both for the adapting case, and 0.58 nA caused 3 spikes in both for the weakly-adapting case. The spiking behaviors of both proposed and original models of the three different cell types presented in Hemond et al. 2008 are shown in Fig. 4. The maximal conductance densities for the currents after tuning are shown in table 1.
Table 1.
Maximal conductance densities of currents in the CA3b neuron models of Hemond et al. (2008), with adjustments for the segregated case, if any, shown after “/”
| Conductance (mS/cm2) | Na | Kdr | KM | H | Cal | KD | KA | Kahp | KC | Leak | τ Ca |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Burst-firing neuron | 22 | 5/6 | 17/19 | .01/.02 | 0.01 | - | 20 | 0.1 | 0.05 | 0.0394 | 100 |
| Adapting neuron | 22 | 10 | 17/18 | 0.01 | 0.01 | - | 20 | - | - | 0.0394 | 100 |
| Weakly-adapting neuron | 22 | 10 | - | 0.01 | 0.01 | 1.1/0.55 | 20 | - | - | 0.0394 | 100 |
Modeling Single Cells: Lateral amygdala principal cells of example case 4
In the second example case to illustrate the methodology, we consider the LA pyramidal cell. Following the procedure listed in the previous section, we begin with a one-compartmental model to represent soma and axon. The diameter and length of the compartment were selected as 24.75 μm and 25 μ m, respectively.
Passive properties
A plot of the gating functions revealed four currents to be active at rest (Kim et al., 2013a): Nap, KM, H, and leak. Since LA neurons exhibit LTOs caused by Nap and KM, we set these currents to zero when tuning passive properties, i.e., only H and leak currents were active. Leak reversal potential was set to −72 mV. H and leak conductance values were tuned and yielded passive properties that matched biological data very well: Vrest was −70.4 mV (empirically measured mean of −69.5 mV (Washburn and Moises, 1992)), input resistance (Rin) was ~ 154 MΩ (measured 150 MΩ (Faber et al., 2001)), and τm was ~ 31.5 ms (measured 29 ms (Faber et al., 2001)).
Low-threshold oscillations
We activated Nap and KM currents immediately above rest, at −67.5 mV, and segregated the H current to be active only below −67.5 mV, i.e., it was not active in the voltage range of LTOs. The half activation voltage (V1/2) and slope factor (k) for Nap and KM were adjusted to ensure that the LTOs occurred around ~ −59 mV. The time constant curve parameters were then adjusted so that the depolarizing current was faster (by a factor of 7) compared to the hyperpolarizing one in this voltage range. We then iteratively tuned the maximal conductance for KM so that it dominated leak. Upon membrane depolarization (via current injection) to −59 mV, the single cell model replicated biological data: LTOs occurred at a frequency of 4 Hz and had an amplitude of 1.5 mV, compared to biological ranges of 0.5-9 Hz and 2-6 mV (Pape and Driesang, 1998). Furthermore, blocking either Nap or KM abolished the oscillations as noted in experiments (Pape and Driesang, 1998).
Spiking/adaptation properties
Nat, Kdr, and Ca currents were activated just above LTOs levels, starting at −57.5 mV, but below spiking threshold of −56 mV (Washburn and Moises, 1992). The calcium-activated sAHP current should be active while tuning the spiking properties since it controls spike frequency adaptation in LA neurons; hence it was activated at −65 mV.
High-threshold oscillations
Both Nap and Nat were blocked to abolish LTOs and spiking. In LA principal cells, HTOs occur around ~ −40 mV, with depolarization by a group of calcium currents and hyperpolarization by a combination of delayed rectifier, calcium dependent potassium and other voltage dependent potassium currents (Pape and Driesang, 1998). The model used a fast calcium current with a very slow inactivation as a depolarizing current and both KM and Kdr currents for hyperpolarization. As in the case of LTOs, Kdr and KM were slower than the depolarizing Ca current around HTO levels. Maximal conductance values of KM and Kdr were tuned such that leak was not dominant, else it precluded oscillations. A strong KM current was found to prevent membrane depolarization to HTO levels when sodium channels are blocked. Also, since KM affects LTOs and Ca and Kdr affect spiking, tuning this module involved iteration with properties of LTO and spiking/adaptation modules since the HTO module did not have unique currents of its own. After such a tuning, the model had HTOs at 16.7 Hz, with an amplitude of 17 mV. As cited earlier, despite considerable tuning, we were unable to incorporate HTOs in the original model, highlighting the importance of segregation.
Remarkably, a 1-compartmental model with the parameters listed in tables 2 and A2 was able to match the biological passive properties and current injection responses of LA principal cells, including the three spike frequency adaptation types (A-C), LTOs and HTOs (Fig. 5). To our knowledge, this is the first report where all these properties are captured in a biophysical single cell model.
Table 2.
Maximal conductance densities used in model LA neurons (Alturki et al., 2015)
|
Conductance
(mS/cm2) |
Na | Kdr | KM | H | Ca | Nap | KA | sAHP | Leak | τ Ca |
|---|---|---|---|---|---|---|---|---|---|---|
| Type-A | 27 | 1.5 | 0.6 | 0.015 | 0.55 | 0.142 | 2 | 0.3 | 0.055 | 1000 |
| Type-B | 0.15 | |||||||||
| Type-C | 0.115 |
Integrating segregation ideas into automated schemes
Two important characteristics of automated parameter search techniques are its objectivity in the exploration of the parameter space, and its relative ease of use once developed. The findings we report related to segregation of currents into modules using functional insights has the potential to make such automated searches more efficient and robust for the classes of neurons cited above. The methodology we propose involves segregating the half-activation voltages (V1/2) and slope factors (k) of the gating functions, and eliminating overlap by removing the ‘tails’ appropriately (see text). Both V1/2 and k are typically not known precisely, and are known to vary with factors such as neuromodulation, (e.g., Harris-Warrick et al., 1995, Heys and Hasselmo, 2012). If the ranges of variation of such parameters are known (e.g., Fig. 2B), these ranges, together with the ranges for the maximal conductances can be provided to the automation schemes. Thus, the only change to the automation scheme is limiting the gating parameters to be within certain voltage ranges (zones) using insights related to the neuronal signatures. It is noted that most of the automation schemes seem to search only over the maximal conductance space, after fixing the parameters involved in the current kinetics. In either case, with or without searching over the activation kinetics, one has to ensure that the overlap of activation functions is minimized (see appendix for details, including figures).
Performance of single cell models in a neuronal network
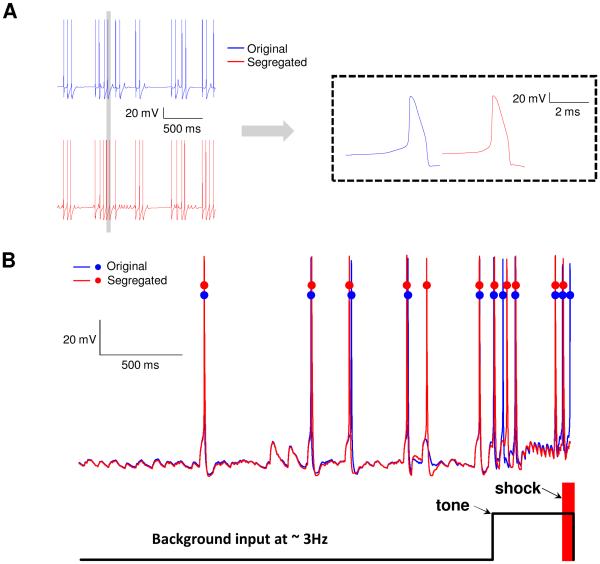
We illustrate the application of single cell models developed using the proposed segregation technique in a network application. A 100-cell network model of the rodent lateral amygdala is adapted from a recently reported model from our group (Kim et al., 2013a, Kim et al., 2015, Feng et al., 2016) where dendritic processing was largely limited to shaping the PSP from the synapse to the soma. Specifically, the performance of the one-compartmental model developed using the proposed approach is compared with that of a 3-compartmental model in Kim et al. (2013a). Briefly, in the Kim et al. study, the authors (i) developed three types of pyramidal 3-compartmental single cells with high (type A), intermediate (B), or low (C) spike frequency adaptation, to reproduce the biologically reported continuum of spike frequency adaptation due to the differential expression of a Ca2+-dependent K+ current. The three types of pyramidal and one inhibitory interneuron single cell models also reproduced biological in vitro properties, including passive (input resistance, resting potential and time constant) and current injection (three values) responses; and (ii) integrated the single cell models into a network model, subjected the model to a Pavlovian fear conditioning protocol, and showed how the network could reproduce the reported conditioning-induced formation of ‘plastic’ cells with enhanced tone responses (Repa et al., 2001). The auditory fear-conditioning protocol (see Fig. 1 above) included three phases (habituation, conditioning and extinction), comprised of 8, 16 and 20 trials, respectively. Each trial featured a 0.5-s tone CS followed by a 3.5s gap. Only during conditioning, a shock (100 Hz) was administered 100 ms prior to the end of the tone, so that they co-terminated. The entire protocol lasted 276 seconds. Details can be found in Kim et al. (2013a).
We used a 100-cell version of the network and first tuned the network model with 3-compartmental cells from Kim et al. (2013a) and recorded all its outputs including spiking times of all 100 cells throughout the fear conditioning protocol. We then investigated how well the 1-compartment version could reproduce all features of the outputs. To test this, we replaced the 3-compartment single cell model in the 100-cell network with its one-compartment equivalent. The excitatory and inhibitory synaptic gains in the 3-compartment case were scaled using ratios dependent on the appropriate areas. The ratio of the total area of the 3-compartmental neuron to the somatic area of the 1-compartmental case was 4.7, and so the GABAergic synapses were scaled down by this number. For the glutamatergic synapses, the area along the path from the soma to the dendrite having the synapse was used, instead of the total area, and this number was divided by the somatic area to get the ratio of 1.24 which was used to scale excitatory synapses. These ratios provide reasonable starting points for tuning. In our case, we had to tune only the glutamatergic synapses, with the ratio for GABAergic synapses being unchanged. No other changes were made to the model, i.e., no adjustments to any other parameters such as learning rates or thresholds were made. To compare the network output with 3- and 1-compartment cell models, we recorded the spiking responses of all 100-cells throughout the 276 second protocol, and computed their tone responses (i.e., spikes within first 300-ms of tone onset) for the three types of pyramidal cells (Kim et al., 2013a).
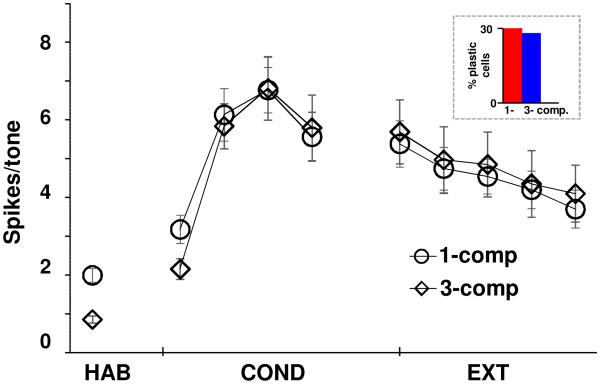
In addition to very good comparisons between 3- and 1-compartment LA models at the single cell level, their predictive capabilities when incorporated into the 100-cell network model also compared well, using the following measures: (i) the conditioning induced numbers of plastic cells were 30% and 28%, respectively, of the total; (ii) the profiles of conditioning for the pyramidal cell types were similar to that in biology and in Kim et al. (2013a). Moreover, types B and C conditioned in much larger proportions than type A as in Kim et al. (2013a); and (iii) the average tone responses of the 1- comp case during conditioning and extinction phases compared very well with the 3-comp case (Fig. 6). The maximum difference was 14% during the first block of conditioning, and 6% during the last block of extinction, which is well within the biological variability of ~20% in Repa et al. (2001). Note that with more than 2000 free network parameters, such models cannot be tuned to achieve preferred outputs, and so differences within biological limits are acceptable. Importantly, we believe that the higher tone responses for 1-compartment case during habituation and early conditioning can be attributed to its higher fidelity due to the inclusion of low- and high-threshold oscillations, since the 3-compartment model was not designed to include oscillations. This comparison demonstrates that the proposed approach to develop single compartment models and the scaling approach used for synapses successfully captures the salient intrinsic and synaptic integration properties for this application.
Figure 6.
Comparison of tone response of 1- and 3-compartment single cell models in a 100-cell LA network model. Average tone response of plastic cells in the two network models were almost identical. Excitatory and inhibitory synaptic weights in the 1-compartment model case were rescaled according to the procedure described in “methods”.
DISCUSSION AND CONCLUSIONS
Neurons typically have numerous current channels and exhibit a diversity of neuronal signatures ranging from low threshold oscillations to complex spiking waveforms, and to high threshold oscillations (Izhikevich, 2007, Byrne and Roberts, 2009). Although several reports have delineated how a few currents regulate one specific signature/property, it is not clear how the entire set of currents interact to implement the suite of signatures for a neuron. We report novel insights related to the role of distinct current modules in shaping the dynamics of the various membrane potential features of model neurons. This insight into the neurobiological grouping of intrinsic currents in a neuron is in turn shown to lead naturally to a systematic, efficient and robust methodology to develop biophysical single cell models for certain classes of neurons, with potential for automated tuning in certain cases.
Neuronal signatures are controlled by distinct modules of currents
Our hypothesis that distinct current modules might implement different neuronal signatures, with minimal interactions across modules, was found to hold for four published biophysical single cell model classes that differ in type and functional characteristics. This finding also suggests that some of the hand- and automated- schemes for tuning biophysical models have probably been converging onto solutions that segregated currents along voltage ranges, at least for these classes of neurons. Support for this also come from the fact that only the maximal conductances (and not current kinetics V1/2 and k also) needed to be tuned for all of the example cases reported. Interestingly, one of the example cases utilized a sophisticated automated approach for determining the ‘optimal’ current parameters to fit biological data (Pospischil et al., 2008). Our analysis revealed that this optimal model had the current modules segregated so well that the errors in functional characteristics were uniformly small when we confined the gating functions to be within non-overlapping voltage ranges, i.e., the segregation we highlight here seems to have been automatically accomplished by their search algorithm. Alternatively, this may be an inherent part of the biophysics of the neuron. The segregation approach becomes critical for neurons with multiple neuronal signatures such as the LA neuron example case, with passive properties, LTOs, HTOs, spiking and adaptation. This is highlighted in Fig. 5C by the missing plot for the ‘original’ case, since were not able to hand-tune the original LA neuron to exhibit HTOs, i.e., only after segregation could we model HTOs in these neurons. As cited in results, another important attribute of the segregation approach is its robustness, i.e., changes made to the parameters of currents in one module minimally impacted the characteristics controlled by currents of other modules, for all the example cases. The neurobiological insight related to segregation also provides predictive power: if a current has unknown kinetics, but is known to belong to a certain module, then its kinetics (V1/2 and k) should confine its activation curve to within the voltage zone of that module (Fig. 1, 2); on the other hand, if it is known to belong to a different module, the kinetics should be sufficiently segregated.
If currents can be grouped into distinct modules, can we further quantify how ‘close’ the activation functions of the currents within one module were on the voltage axis, and how ‘far’ they were from other modules. Such a quantification was possible considering an average of the half-activation values, V1/2, of the currents within a module (see table 3 and appendix for values for all example cases). For the passive modules, V1/2 for the H currents ranged between −84 and −73 mV, all below Vrest. In the example cases with LTOs (#3 and #4; Tables A1 and A2), the differences between V1/2 values for the two LTO currents in both cases were less than 7 mV. In contrast, the distance of the LTO module (taking average of V1/2 values for currents in that module) from a similar grouping for the passive module was 35 mV, and, in turn, the distance from the LTO module to the spiking module was 24 mV. Therefore, the differences between V1/2 values for currents within the LTO module in both cases were considerably smaller compared to differences across the modules. As expected, the currents in the spiking module had the largest separation in V1/2 between the depolarizing and hyperpolarizing currents with an average of 17 mV across all four examples. HTOs were seen only in one example case (#4) and since this module did not have its unique currents, no quantification was considered. So, a further prediction from these models is that currents within a module should have V1/2 values close to each other. Future studies should consider such quantification issues in more detail.
Effective biophysical models for network simulations – the big picture
Simplified computational models of neurons (Bush and Sejnowski, 1993, Pinsky and Rinzel, 1994, Destexhe, 2001, Tobin et al., 2006), including as point processes, are popular in theoretical neuroscience research (Herz et al., 2006, Brunel et al., 2014) and have provided valuable insights into numerous analytical issues including stability and oscillations. Advances in recording techniques over the past decades have led to the development of viable biophysical models that include channel and synaptic neurophysiology, and more realistic morphologies, with some including dendritic processing (Stuart et al., 2008), and neuromodulation (Marder et al., 2015). Such models have to also accommodate large naturally occurring variations in maximal conductances in putative identical cells (Schulz et al., 2006), and possible variations in the activation kinetics of currents (Fig. 2B; Izhikevich 2007). Our emerging understanding of additional functions such as intrinsic and synaptic compensation (Marder, 2011, Turrigiano, 2011), and the role of cellular and synaptic parameters in the growing area of network oscillations (Skinner, 2012, Krook-Magnuson et al., 2015) will be aided by biophysical models that incorporate neurophysiology to represent such phenomena adequately.
In addition to the presence of more than 10 parameters in the Hodgkin-Huxley formulation for each current, it is also known that channel and synaptic conductances (e.g., Marder, 2011), as well as half-activation voltages and time constants vary (e.g. Fig. 2B) over ranges, due possibly to several factors including state dependent neuromodulation (e.g., Marder et al. 2015). Possibly for these reasons, systematic methods for the development of biophysical single cell models do not seem to be reported in the literature, with present methods ranging from hand tuning to several types of automated search algorithms (Bhalla and Bower, 1993, Prinz et al., 2003, Druckmann et al., 2007, Hemond et al., 2008, Pospischil et al., 2008, Marder and Taylor, 2011, Bahl et al., 2012, Forren et al., 2012).
Using the finding related to the distinct current modules cited in the previous section and its predictive power, we suggest a systematic methodology to develop biophysical single cell models using the Hodgkin-Huxley formulation. In this scheme, the activation functions for currents in each module on the right are segregated such that they do not extend into the voltage zone of the module on the left (see Figs. 1 and 2). For the four example cases we considered, such a segregation approach was found to result in similar time courses for membrane potential dynamics (Figs. 4, 5 and A3). The segregation process provides bounds for the activation kinetics for the currents and these bounds can then be utilized effectively in hand- or automated- tuning approaches. The search could occur simultaneously over the activation kinetics and maximal conductance densities of all currents, or only over the maximal conductance densities if the activation kinetics are pre-determined and held fixed. The methodology was illustrated using two model neurons from the literature.
The proposed methodology and related findings for developing single compartment models for specific classes of neurons are attractive for large network applications. The significance of these findings for classes of neurons can be summarized as follows: (1) automated parameter search techniques for neuronal models could potentially incorporate consideration of functional characteristics for certain classes of neurons. The method we propose (Box 1 and appendix A2) is based on recognizing the role of current modules in shaping neuronal signatures; it makes the tuning process easier and converges on a solution rapidly since it precludes unintended interactions between different currents. We highlight that it is the tails of the gating functions in the Boltzmann equation (Byrne and Roberts, 2009) that cause unintended interactions among currents of different modules, and so we suggest using gating functions with sharper cut-off to implement segregation, including specific splines or hand-tuned curves with sharp cut-off (e.g., experimental curve for Kdr with sharp cut-off in Rubin and Cleland 2006). Although at the cost of matching spike patterns only rather than the spike waveform itself, usage of the method results in models that are robust in the sense that the currents within one module minimally impact the properties controlled by other modules, making the matching of multiple properties considerably easier and efficient; (2) usage of the modules idea led to the finding that a single core compartment representing the soma and axon had the capability to capture multiple neuronal properties; (3) improved understanding of the effects of synaptic and intrinsic neurophysiology on phenomena such as oscillations is becoming very important in rapidly growing application areas such as non-invasive brain stimulation (Krook-Magnuson et al., 2015). Biophysical single cell models with increasing fidelity at finer neurophysiological levels, including incorporation of LTOs and HTOs, will be sought for such applications. As cited in results, the relevance of the proposed methodology come to the fore for cases where multiple neuronal signatures have to be modeled simultaneously, as in the LA neuron example case. Adding the segregation idea to automated searches could enhance their efficiency in some cases, particularly if the scheme is limited to only a few neuronal properties; (4) the idea of segregating currents led to the finding that KM and Kdr may provide the hyperpolarizing mechanism for high-threshold oscillations reported in experiments for the LA neuron case (Pape et al., 1998), a prediction that could be tested in biology. The approach will facilitate discovery of similar functional characteristics for other cells; and (5) large variations in baseline parameters for identical neuron types has led researchers to advocate development of families of biophysical models for neurons, rather than a nominal model (Marder and Taylor, 2011). For instance, intrinsic compensation mechanisms are thought to co-regulate specific sets of conductances to preserve output (Schulz et al., 2007, Temporal et al., 2014). Using the proposed scheme, a family of models with specified variations in one or more dynamic characteristics can be generated easily and efficiently by adjustments to parameters of currents restricted to the specific modules responsible for those properties.
Figure A2.
Range of half-activation voltage. A cartoon illustration of determining the range for V1/2 to be considered in the parameter search such that overlap between modules is minimized. The “dashed” curve is bounded by two “solid” curves and is free to move within these boundaries during the search process.
HIGHLIGHTS.
Currents may be grouped into distinct modules that shape various membrane potential dynamics of neurons
Such groupings may be accomplished by segregating the activation functions of currents to minimize overlap across modules
The hypothesis was found to be valid for four classes of single neuron models in the literature
A single compartment model was found to be sufficient to capture multiple neuronal properties for two classes of neurons
Suggest a method to develop single compartment models with multiple signatures for classes of neurons, for use in networks
ACKNOWLEDGMENTS
This research was supported in part by NIMH grant MH087755 to SSN.
APPENDIX.
A1. Biological data related to the four published example case models.
While details about the biological data for the four example cases (1-4) can be found in appropriate references, the pertinent information required to follow the development reported in the present paper are provided in this section. More elaboration is provided for two of the example cases (1 and 4) since these two are used to illustrate the development of a single cell model using our proposed segregation scheme.
Example case 1. Pyramidal neurons in the hippocampal area CA3b (Hemond et al., 2008)
Characteristics of hippocampal neurons have also been reported extensively in the literature (see (Cutsuridis V et al., 2010) for a review). The principal cells in the CA3b region exhibit three distinct types of firing patterns: adapting (regular firing), weakly adapting, and burst firing. Accordingly, Hemond et al. created single compartmental models for these three distinct neurons using over 20 million combinations of conductance densities ranging from 0, 0.25, 0.5, 1, 2, to 4 times the values in a baseline model. The 135-compartment single cell models (soma, axon, 52 dendrites and 81 apical dendrites) had the following morphology: soma area of 548 μm2, total area of 30,090 μm2, and axon length of 100 μm. The following currents were modeled: Na, Kdr, KA, three types of Ca2+ (N, L and T), two types of Ca-dependent K (KC and KAHP), and H in both soma and dendrites; in addition, soma had KM and KD. The axon had three currents: Na, Kdr, and KA (Hemond et al., 2008). The resting potential Vrest was − 60.5 ± 5.4 mV, and spiking threshold was 20 mV above rest. Membrane time constant τ and input resistance Rin were 61.4 ± 4 ms, and 126 ± 8 MΩ respectively. Spiking behaviors were as in Fig. 4A. Mean latency for the late firing neuron type was 340 ms. Passive properties used: τ =35 ms, Rm=25 kΩ.cm2, Ra=150 Ω.cm, Cm=1.41 μF/cm2. Maximal conductance densities are provided in table 1.
Analyzing the Hemond et al. (2008) model from ModelDB (https://senselab.med.yale.edu/ ModelDB/), we found that ionic currents could be segregated into two distinct modules. The passive properties (i.e., resting potential Vrest, input resistance Rin, and membrane time constant τm) module involved H, slowly-inactivating potassium KD and leak and so all the other currents were segregated to be above −52.5 mV (rest was −57 mV) using the procedure described earlier. The spiking/adaptation/bursting module involved Nat, Kdr, KA, L-type Ca, KCa, KAHP, and KM, which were activated only above −52.5 mV. Also, H current is limited to be within −52.5 mV, i.e., set to zero above this voltage. So, this neuron had two zones, one below −52.5 mV for the passive module, and one above it for the spiking module. The maximal conductance values of the currents Kdr, KM, H, KD, and KA had to be adjusted in the process, with the average change being 34% from published values. The maximal current densities of the original and segregated models are listed in table 1. Table A1 lists the expressions for the gating functions.
Example case 2. Models of cortical and thalamic neurons (Pospischil et al., 2008)
Pospischil and group reported models of cortical and thalamic neurons with passive properties (resting potential, input resistance), bursting, spiking, as well as spike frequency adaptation. The four cell types were tuned differently by the authors. Regular spiking (RS) and fast spiking (FS) neurons models used an automated search to explore the parameter space that included maximum conductance densities, voltage shift of activation and inactivation functions, and a time constant scaling factor. Hand-tuning was used for the other two cells (intrinsically bursting, IB and low-threshold spiking, LTS) due to difficulties in evaluating the error functions needed for the automatic-fitting search. Our segregation analysis suggested that these neuron models exhibit only two modules: passive as well as spiking/adaptation/bursting. All active currents were found to minimally contribute at rest. The activation functions for all voltage-gated currents (Na, Kdr, KM, L-type and T-type Ca) were segregated to be only above −65 mV (rest at −70 mV), and below this value only leak was present. The five active currents listed shaped the spiking/adaptation/bursting module. So, this neuron also had two zones, one below −65 mV for the passive module and one above it for the spiking module. Interestingly, no changes had to be made to the values of the maximal current densities for any current for any of the four model types.
Example case 3. Rodent mitral cells of the olfactory bulb (Rubin and Cleland, 2006)
These cells exhibited endogenous subthreshold oscillations as well as intrinsic bursting properties. We segregated the currents in this published 4-compartmental model into two sets implementing two distinct modules: resting/subthreshold oscillation and spiking/bursting. The model did not report passive properties, such as input resistance, and hence those were not considered. The subthreshold oscillations module included the following set of currents: Nap, KA, KCa, and H. All other currents were segregated by setting their activations to zero below −60 mV (reported rest level is −64 mV). The spiking/bursting module was controlled by Nat, KA, KCa, Ca, and Kdr currents as highlighted in the paper. The activation function for H was segregated to be below −55 mV (involved some iteration) making it inactive in the operation range of this spiking/bursting module, however currents trace (results not shown) still show that the H current is involved in the spike initiation process before its activation function is terminated at −55 mV. So, the two zones in this case were one below −60 mV and the other above it.
No changes were made to gating kinetics, such as half-activation voltage and slope factor to implement the segregation hypothesis on the original models cited above. Tuning only the maximal conductance density of H (increased by 25%), among the many, was sufficient to restore properties.
Example case 4. Pyramidal neurons of the lateral amygdala (Alturki et al., 2015)
Amygdala has been the focus of intensive studies related to Pavlovian fear conditioning in rodents (see (Tovote et al., 2015) for a recent review). This has resulted in a rich biological literature characterizing neurons in the lateral amygdala, including passive properties (e.g., Washburn and Moises, 1992, Faber et al., 2001); voltage responses to intracellular current injection (e.g., Faber et al., 2001) and low- and high- threshold oscillations (Pape and Driesang, 1998). Utilizing these biological data, biophysical models related to LA neurons have also been reported for different applications including from our group (e.g., Power et al., 2011, Kim et al., 2013b) which we draw upon for the LA models reported below.
A diversity of spike frequency adaptation is seen in principal LA neurons (Faber and Sah, 2003), with three types of regular spiking principal cells, with high (type-A), intermediate (type-B), or low (type-C) spike frequency adaptation, due to the differential expression of a Ca2+-dependent K+ current. Current injection responses of the types A, B, and C cells were as follows: 0.4 nA for 400 ms elicited 3, 11, and 14 spikes; respectively, and decreasing it to 0.3 nA resulted in 1, 5, and 7 spikes, respectively. Biological recordings report that LA neurons also exhibit slow-rhytmic deflections (LTOs) at depolarized levels positive to resting potential (positive to −60 mV (Pape et al., 1998)) that are below and near spiking threshold level. These LTOs were found to play a major role in synchronization and timing of synaptic inputs (Pape et al., 1998), and were found to be caused by an interplay between the fast amplifying persistent sodium and the slow resonating M-type potassium currents (Pape and Driesang, 1998). The frequency of this oscillation ranged from 0.5 to 9 Hz and amplitude was 2-6 mV (Pape and Driesang, 1998). Blockade of sodium currents in experiments using TTX to abolish LTOs and spiking revealed another type of oscillation at depolarized levels beyond −40 mV. This high-threshold oscillation (HTO) had a frequency from 1 to 7.5 Hz and an amplitude from 5 to 10 mV (Pape et al., 1998).
The current channels used in the LA pyramidal cell models were adapted from a 69-compartment model (Power et al., 2011) that used several biological sources for data including from hippocampal pyramidal cells (Gasparini et al., 2004, Pape and Pare, 2010). Based on these biological reports, we included the following current channels in our LA single cell models: leak (IL), voltage-gated persistent muscarinic potassium (IKM), high-voltage activated Ca2+ (ICa), persistent sodium (INap), spike-generating sodium (INat), potassium delayed rectifier (IKdr), a hyperpolarization-activated nonspecific cation (IH) currents and a slow apamin-insensitive, voltage-independent afterhyperpolarization current (IsAHP) (Power et al., 2011). The ranges for the parameters are as follows: capacitance 1.0-4.0 μF/cm2, membrane resistance 20-100 KΩ-cm2; axial resistivity Ra 150-200 Ω-cm; resting membrane potential, Vrest from −66 to −75 mV; input resistance (Rin) of 150±10 MΩ and τm of 30±1 ms; sources provided in Kim et al. (2013a)
Our LA model exhibited four distinct signatures: passive properties, low-threshold oscillations, spiking/adaptation properties, and high-threshold oscillations. We limited the currents active at rest (~ −70 mV) to just H and leak, and these were capable of matching all passive properties, when the activation curves of all other currents were segregated to be active only above −67.5 mV. Low-threshold oscillation (LTO) module (at ~ −59 mV) required the activation of both Nap and KM right above rest, and we did that at −67.5 mV. The activation function for H is limited to be active only below −67.5 mV, so that only Nap, KM, and leak are active at LTO levels. The spiking/adaptation module had Nat, sAHP, Ca, and Kdr channels, and all of these were activated starting −57.5 mV, except for sAHP which was activated at −65 mV. Note that unlike the other voltage-dependent currents in the LA case, sAHP is both voltage- and Ca-dependent current and the segregation can still be implemented on such type of currents. The last module implemented the high-threshold oscillations (HTOs) that are revealed in biology when sodium channels (Nap and Nat) are blocked and the membrane is depolarized to −40 mV (Pape and Driesang, 1998). Currents involved in this oscillation include Ca, KM and Kdr. So, there were four zones of operation for neuronal currents in this case: < −67.5 mV for the passive module, −67.5 to −57.5 mV for the LTO module, above −57.5 mV for the spiking module, and – 40 to −30 mV for the HTO module. This segregation process is shown in Fig. A1. Again, only minor changes to the maximal conductance densities of a few currents had to be made to segregate the modules, with the maximum change being <25%.
A2. Procedure for segregating currents and pre-processing modules for tuning schemes
The procedure below is suited to hand- and, in some cases, to automated- tuning processes involving a search over pre-determined ranges for V1/2 and maximal conductance densities of the currents. We remind the reader that the pre-determined ranges for V1/2 are selected such that the segregation of current modules is always maintained. The sequential tuning process, progressing with modules from left to right on the voltage axis, was found to be efficient and robust.
(i) Biological ranges for neuronal parameters, and pre-processing
Collect biological data for the neuron including ranges for morphological features such as dimensions of soma, axon and the major proximal dendrites; ranges for membrane capacitance and axial resistance; and ranges for the gating function parameters (e.g. V1/2, k, and time constant) and maximal conductance densities of all known currents. Decide on the neuronal signatures to be modeled and their biological ranges.
Zones of operation
Using the activation functions of currents in the soma and axon, and information in biology, determine the zones of operation along the voltage axis for each module (e.g., Fig. 1, 2; also see methods). For instance, the zone of operation of the passive module on the voltage axis is thus defined as being from negative potentials to any value between Vrest and the boundary of the next zone to the right (3 mV above Vrest in Fig. 1B). This process has to be performed off-line. The reader is reminded that the process of segregation is implemented by ensuring that the current module on the right has activation functions that do not extend into the zone of the module on the left (except for some currents involved in multiple modules).
Reshaping the activation functions
If the standard Boltzmann curve is used for an activation function, it should be re-shaped to prevent the ‘tail’ from extending to infinity. This can be implemented by limiting the curve to stay within the zone of operation (determined in the previous step) by setting the tail of the activation function abruptly to zero at the edge of the zone. After the design parameters are finalized by the tuning process (see below), the sharp drop to zero can be smoothed if needed by using a straight line from the edge of the zone to the function over a span of ~ 2-3 mV, or with a pre-determined slope, e.g., of 2. Such a procedure was used for the LA neuron example case in Fig. A1, i.e., the tuning was performed using sharp cut-off, and the edges were smoothened after the set of parameters were finalized. A similar shaping can be used for experimental curves in case they have extended tails. No such re-shaping is required in the direction where the activation function approaches 1. For convenience, although both half-activation parameter V1/2 and slope factor k can be adjusted within biological limits (see Fig. 2B), the development below mentions changes in only V1/2. The steps below assum that the activation functions have been re-shaped in this manner.
Figure A1.
Illustration of the segregation approach to model development using the LA neuron example case. Original activation functions of ionic currents in the published models (A), and after implementing the segregation idea (B). Activation functions of leak and sAHP currents are not purely voltage-gated, and so not shown.
We investigated whether editing the activation functions, as shown in Fig. A1 (for the LA neuron) with discontinuity in slope (not function), would introduce instability in membrane potential responses. Interestingly, we found no trace of instabilities even with realistic Poisson inputs up to 20 Hz, including when step-function discontinuous fits were used (Fig. A4-A). Moreover, realistic inputs mimicking those that a neuron would receive in the 100-cell LA network did not reveal any instabilities either (Fig. A4-B). Two reasons for this may be that such fits are typically made at the ‘tails’ of these activation functions where the magnitudes are small, and that the activation functions are integrated in the code and never differentiated.
Figure A4.
Investigating whether edits to gating functions cause any instabilities in responses. (A): Membrane potential responses to Poisson stimuli at 5 Hz for example case 3 (mitral cell). The inset to the right compares a single action potential trace from the original and segregated cases on an expanded time scale. (B) Responses of the original and segregated models to realistic stimuli for example case 4 (LA cell). A conditioning trial with tone (~ 12 Hz; step in panel) and shock (40 Hz; in red, 500 ms at end of tone), is shown; details in Kim et al. (2013a).
(ii) Passive module
Match biological values for rest potential Vrest, input resistance Rin, and membrane time constant τ. Adjustable parameters: membrane capacitance Cm, membrane resistance Rm, leak reversal potential Eleak, and half-activation parameter V1/2 for the relevant voltage-gated currents in this module, in addition to maximal conductance densities of all currents active in this module.
Determine the currents active at Vrest, typically leak and hyperpolarization activated currents, e.g., H current. From a functional perspective, these currents determine the passive properties to be matched. All other high-threshold currents should contribute minimally to Vrest, and so restrict the activation functions of these currents to start on the voltage axis above Vrest. As cited, the zone of operation of the passive module on the voltage axis is thus defined as being from negative potentials to any value between Vrest and the boundary of the next zone to the right (3 mV above Vrest in Fig. 1B). The V1/2 values in activation functions of all voltage-gated currents in the passive module should be selected, consistent with biological ranges (Fig. 2B), to ensure segregation of the modules as described above. This then determines the range for the activation parameter V1/2 to be used by the hand- or automated- parameter search algorithm.
Observations
Selection of the reversal potential of the leak current is somewhat arbitrary in the literature, due possibly to the fact that currents are typically not segregated clearly into distinct modules. Depending on the currents active at rest, select a leak reversal potential such that the desired resting potential can be achieved. Input resistance Rin and time constant τ are tuned by injecting a negative current (e.g., −100 pA) and measuring the change in membrane potential ΔV.
(iii) Low threshold oscillations module
If applicable, match biological values for frequency and amplitude of the low-threshold oscillations (LTOs). Adjustable parameters: activation parameters: V1/2 and maximal conductance densities for the voltage-gated currents active in this module. LTOs, if present, occur at voltage levels below spiking threshold and are typically initiated and maintained by an interplay between two non- or very slowly-inactivating currents: a fast depolarizing current and another relatively slower hyperpolarizing one. The non-inactivating hyperpolarizing current should dominate leak for oscillations. Not being voltage-gated, leak linearly follows membrane potential fluctuations, and so does not play a major role in oscillations. All other voltage-gated currents that were zero at rest should still be zero here.
The activation curves for all the currents not involved in the LTO module (e.g., H) are set to zero above the boundary for the passive module. Begin the activation curves for the two LTO currents at the boundary so that the currents active at LTO potentials are limited to leak and the two LTO currents. Limit the half-activation voltage V1/2 of the activation curves of the LTO currents so that their interactions occur at potential levels below spike threshold. Thus the zone of operation of the LTO module is the narrow voltage range for the module (e.g., see Fig. A1).
Observations
The depolarizing current has to be faster than the hyperpolarizing current within the LTO voltage range, and so the time constant of the amplifying current (Nap in the LA neuron case) should be smaller than that for the resonant current (KM in the LA case). Once the membrane potential comes down, the fast depolarizing current should activate and depolarize the membrane again, continuing the oscillation.
(iv) Spiking/adaptation/bursting module
Match current-evoked biological responses including frequency-current and adaptation characteristics. Adjustable parameters: activation parameter V1/2 and maximal conductance density of all voltage-gated currents in the module.
Typical currents involved in spiking are transient sodium and delayed rectifier potassium. If the neuron exhibits bursting or spike frequency adaptation, determine and model the appropriate currents involved. Thus the zone of operation of the spiking module ranges from a value below spike threshold (3 mV was adequate for our example cases) and extending to the more depolarized voltage levels. It is noted that calcium-activated currents such as sAHP may need to be activated earlier, and so are handled differently as cited earlier.
Observations
The strength of adaptation can be controlled by adjusting the conductance value of the hyperpolarizing current that is responsible for terminating the spike train, such as the sAHP current in the LA neuron case. Also, increasing burst activity can be accomplished by increasing the conductance of depolarizing currents such as the high-threshold calcium current as in the case of the repetitive intrinsically bursting neuron in Pospischil et al. (2008).
(v) High-threshold oscillations module
Match biological values for frequency and amplitude of the HTOs, at reported membrane potential. Adjustable parameters: activation parameter V1/2 and maximal conductance densities for the voltage-gated currents active in the module. High-threshold oscillations occur at voltages more depolarized to spike threshold. For this reason, revealing HTOs in experiments requires that Na be blocked to abolish both LTOs and spiking, and the membrane then be depolarized to HTO levels, e.g., −40 mV (Pape and Driesang, 1998, Pape et al., 1998). From biological reports, determine the currents implicated in HTOs. The zone of operation of the HTO module on the voltage axis is thus defined according to the data reported in biology such that it starts immediately below the voltage at which such oscillation is triggered and ends at the voltage level where the oscillation is diminished. It is found in the LA neuron case that the zone of operation for the HTO module starts at −40 V and ends at −30 mV.
Observations
Similar to the case in LTOs, adjust the time constant curves such that the depolarizing currents are faster than the hyperpolarizing ones at HTO voltage levels. Also, ensure that the hyperpolarizing currents in HTOs dominate leak, else it precludes oscillations. Additionally, the hyperpolarization current should not be so strong as to prevent the membrane potential from getting to the HTO voltage range with Na blocked.
Note that if some currents participate in more than one module (e.g., KM , which is involved in both LTOs and HTOs for the LA neuron example case), iteration will be required between the tuning of these modules. It is also noted that the characteristics above are not comprehensive, and meant to be only a representative list. For instance, another module could be the set of currents that control up-down states in certain cortical neurons. All such modules need to be considered prior to initiating the modeling process.
Table A1.
Gating function parameters of ion channels in Hemond et al. (2008) model
|
Current
Type |
Gating
Variable |
α | β | x∞ | τx(ms) |
|---|---|---|---|---|---|
| INa | p=3 | ||||
| q=1 | |||||
| IKdr | p=1 | exp[−0.113(V − 37)] | exp[−0.0791(V − 37)] | ||
| IH | q=1 | exp[0.0833(V + 75)] | exp[0.0333(V + 75)] | ||
| IKM | p=1 | ||||
| IKA | p=1 | ||||
| q=1 | exp[0.113(V + 32)] | — | 0.26 * (V + 26) | ||
| ICaL | p=2 | 0.29 * exp [−V/10.86] | |||
| IKD | p=1 | exp[0.113(V + 33)] | exp[0.0791(V + 33)] | ||
| IKC | p=1 | ||||
| IKahp | p=1 | 1e8 * ([Ca]i)4 | — |
Table A2.
Gating function parameters of ion channels in LA neuron models of Alturki et al. (2015)
|
Current
Type |
Gating
Variable |
α | β | x∞ | τx(ms) |
|---|---|---|---|---|---|
| INa | p=3 | ||||
| q=1 | |||||
| IKdr | p=1 | exp[−0.1144(V + 15)] | exp[−0.0801(V + 15)] | ||
| IH | q=1 | exp[0.0832(V + 75)] | exp[0.0333(V + 75)] | ||
| IKM | p=2 | ||||
| ICa | p=2 | — | — | ||
| q=1 | — | — | 420 | ||
| INap | p=1 | — | — | 2.5 + 14 * exp[−|V + 40|/10] | |
| IsAHP | p=1 | 48 |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Alturki A, Nair A, Guntu V, Nair SS. Single neuron models for network simulations. Indian Control Conference; Chennai, India. 2015. [Google Scholar]
- Alzheimer C, Schwindt PC, Crill WE. Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex. J Neurosci. 1993;13:660–673. doi: 10.1523/JNEUROSCI.13-02-00660.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahl A, Stemmler MB, Herz AVM, Roth A. Automated optimization of a reduced layer 5 pyramidal cell model based on experimental data. J Neurosci Methods. 2012;210:22–34. doi: 10.1016/j.jneumeth.2012.04.006. [DOI] [PubMed] [Google Scholar]
- Ball JM, Franklin CC, Tobin A-E, Schulz DJ, Nair SS. Coregulation of ion channel conductances preserves output in a computational model of a crustacean cardiac motor neuron. J Neurosci. 2010;30:8637–8649. doi: 10.1523/JNEUROSCI.6435-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barraza D, Kita H, Wilson CJ. Slow spike frequency adaptation in neurons of the rat subthalamic nucleus. J Neurophysiol. 2009;102:3689–3697. doi: 10.1152/jn.00759.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett BD, Callaway JC, Wilson CJ. Intrinsic membrane properties underlying spontaneous tonic firing in neostriatal cholinergic interneurons. J Neurosci. 2000;20:8493–8503. doi: 10.1523/JNEUROSCI.20-22-08493.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhalla US, Bower JM. Exploring parameter space in detailed single neuron models: simulations of the mitral and granule cells of the olfactory bulb. J Neurophysiol. 1993;69:1948–1965. doi: 10.1152/jn.1993.69.6.1948. [DOI] [PubMed] [Google Scholar]
- Brette R. Exact simulation of integrate-and-fire models with synaptic conductances. Neural Comput. 2006;18:2004–2027. doi: 10.1162/neco.2006.18.8.2004. [DOI] [PubMed] [Google Scholar]
- Brunel N, Hakim V, Richardson MJE. Single neuron dynamics and computation. Curr Opin Neurobiol. 2014;25:149–155. doi: 10.1016/j.conb.2014.01.005. [DOI] [PubMed] [Google Scholar]
- Bush PC, Sejnowski TJ. Reduced compartmental models of neocortical pyramidal cells. J Neurosci Methods. 1993;46:159–166. doi: 10.1016/0165-0270(93)90151-g. [DOI] [PubMed] [Google Scholar]
- Byrne JH, Roberts JL. From Molecules to Networks, Second Edition: An Introduction to Cellular and Molecular Neuroscience. Academic Press; 2009. [Google Scholar]
- Carnevale N, Hines M. The NEURON Book. Cambridge University Press; UK: 2006. [Google Scholar]
- Cutsuridis V, et al. Hippocampal microcircuits : a computational modeler's resource book. Springer; New York: 2010. [Google Scholar]
- Davison AP, Feng J, Brown D. A reduced compartmental model of the mitral cell for use in network models of the olfactory bulb. Brain Res Bull. 2000;51:393–399. doi: 10.1016/s0361-9230(99)00256-7. [DOI] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. MIT Press; Cambridge, MA: 2005. [Google Scholar]
- De Schutter E, Bower JM. An active membrane model of the cerebellar Purkinje cell. I. Simulation of current clamps in slice. J Neurophysiol. 1994;71:375–400. doi: 10.1152/jn.1994.71.1.375. [DOI] [PubMed] [Google Scholar]
- Destexhe A. Simplified models of neocortical pyramidal cells preserving somatodendritic voltage attenuation. Neurocomputing. 2001;38-40:167–173. [Google Scholar]
- Druckmann S, Banitt Y, Gidon A, Schürmann F, Markram H, Segev I. A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Frontiers in neuroscience. 2007;1:7–18. doi: 10.3389/neuro.01.1.1.001.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyhrfjeld-Johnsen J, Santhakumar V, Morgan RJ, Huerta R, Tsimring L, Soltesz I. Topological determinants of epileptogenesis in large-scale structural and functional models of the dentate gyrus derived from experimental data. J Neurophysiol. 2007;97:1566–1587. doi: 10.1152/jn.00950.2006. [DOI] [PubMed] [Google Scholar]
- Faber ES, Callister RJ, Sah P. Morphological and electrophysiological properties of principal neurons in the rat lateral amygdala in vitro. J Neurophysiol. 2001;85:714–723. doi: 10.1152/jn.2001.85.2.714. [DOI] [PubMed] [Google Scholar]
- Faber ES, Sah P. Ca2+-activated K+ (BK) channel inactivation contributes to spike broadening during repetitive firing in the rat lateral amygdala. J Physiol. 2003;552:483–497. doi: 10.1113/jphysiol.2003.050120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng F, Samarth P, Pare D, Nair SS. Mechanisms underlying the formation of the amygdalar fear memory trace: A computational perspective. Neuroscience. 2016;322:370–376. doi: 10.1016/j.neuroscience.2016.02.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forren E, Johnson-Gray M, Patel P, Smolinski TG. NeRvolver: a computational intelligence-based system for automated construction, tuning, and analysis of neuronal models. BMC Neurosci. 2012;13:P36. [Google Scholar]
- Franklin CC, Ball JM, Schulz DJ, Nair SS. Generation and preservation of the slow underlying membrane potential oscillation in model bursting neurons. J Neurophysiol. 2010;104:1589–1602. doi: 10.1152/jn.00444.2010. [DOI] [PubMed] [Google Scholar]
- Gasparini S, Migliore M, Magee JC. On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J Neurosci. 2004;24:11046–11056. doi: 10.1523/JNEUROSCI.2520-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunay C, Edgerton JR, Jaeger D. Channel density distributions explain spiking variability in the globus pallidus: a combined physiology and computer simulation database approach. J Neurosci. 2008;28:7476–7491. doi: 10.1523/JNEUROSCI.4198-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Barazangi N, Guckenheimer J, Gueron S. Dopamine modulation of transient potassium current evokes phase shifts in a central pattern generator network. J Neurosci. 1995;15:342–358. doi: 10.1523/JNEUROSCI.15-01-00342.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemond P, Epstein D, Boley A, Migliore M, Ascoli GA, Jaffe DB. Distinct classes of pyramidal cells exhibit mutually exclusive firing patterns in hippocampal area CA3b. Hippocampus. 2008;18:411–424. doi: 10.1002/hipo.20404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrickson EB, Edgerton JR, Jaeger D. The capabilities and limitations of conductance-based compartmental neuron models with reduced branched or unbranched morphologies and active dendrites. J Comput Neurosci. 2011;30:301–321. doi: 10.1007/s10827-010-0258-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herz AV, Gollisch T, Machens CK, Jaeger D. Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science. 2006;314:80–85. doi: 10.1126/science.1127240. [DOI] [PubMed] [Google Scholar]
- Heys JG, Hasselmo ME. Neuromodulation of Ih in layer II medial entorhinal cortex stellate cells: A voltage-clamp study. J Neurosci. 2012;32:9066–9072. doi: 10.1523/JNEUROSCI.0868-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hummos A, Franklin CC, Nair SS. Intrinsic mechanisms stabilize encoding and retrieval circuits differentially in a hippocampal network model. Hippocampus; 2014. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Computational neuroscience. MIT Press; Cambridge, Mass.: 2007. Dynamical systems in neuroscience the geometry of excitability and bursting. [Google Scholar]
- Izhikevich EM, Edelman GM. Large-scale model of mammalian thalamocortical systems. Proceedings of the National Academy of Sciences. 2008;105:3593–3598. doi: 10.1073/pnas.0712231105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D, Pare D, Nair SS. Mechanisms contributing to the induction and storage of Pavlovian fear memories in the lateral amygdala. Learn Mem. 2013a;20:421–430. doi: 10.1101/lm.030262.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D, Pare D, Nair SS. Assignment of model amygdala neurons to the fear memory trace depends on competitive synaptic interactions. J Neurosci. 2013b;33:14354–14358. doi: 10.1523/JNEUROSCI.2430-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D, Samarth P, Feng F, Pare D, Nair S. Synaptic competition in the lateral amygdala and the stimulus specificity of conditioned fear: a biophysical modeling study. Brain Structure and Function. 2015:1–20. doi: 10.1007/s00429-015-1037-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krook-Magnuson E, Gelinas JN, Soltesz I, Buzsaki G. Neuroelectronics and biooptics: Closed-loop technologies in neurological disorders. JAMA Neurol. 2015;72:823–829. doi: 10.1001/jamaneurol.2015.0608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee JC, Johnston D. Plasticity of dendritic function. Curr Opin Neurobiol. 2005;15:334–342. doi: 10.1016/j.conb.2005.05.013. [DOI] [PubMed] [Google Scholar]
- Marder E. Variability, compensation, and modulation in neurons and circuits. Proc Natl Acad Sci U S A. 2011;108(Suppl 3):15542–15548. doi: 10.1073/pnas.1010674108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, O'Leary T, Shruti S. Neuromodulation of circuits with variable parameters: single neurons and small circuits reveal principles of state-dependent and robust neuromodulation. Annu Rev Neurosci. 2015;37:329–346. doi: 10.1146/annurev-neuro-071013-013958. [DOI] [PubMed] [Google Scholar]
- Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci. 2011;14:133–138. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin SA, McDougal RA, Sherif MA, Fall CP, Hines ML, Lytton WW. Neuronal calcium wave propagation varies with changes in endoplasmic reticulum parameters: a computer model. Neural Comput. 2015;27:898–924. doi: 10.1162/NECO_a_00712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pape HC, Driesang RB. Ionic mechanisms of intrinsic oscillations in neurons of the basolateral amygdaloid complex. J Neurophysiol. 1998;79:217–226. doi: 10.1152/jn.1998.79.1.217. [DOI] [PubMed] [Google Scholar]
- Pape HC, Pare D. Plastic synaptic networks of the amygdala for the acquisition, expression, and extinction of conditioned fear. Physiol Rev. 2010;90:419–463. doi: 10.1152/physrev.00037.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pape HC, Pare D, Driesang RB. Two types of intrinsic oscillations in neurons of the lateral and basolateral nuclei of the amygdala. J Neurophysiol. 1998;79:205–216. doi: 10.1152/jn.1998.79.1.205. [DOI] [PubMed] [Google Scholar]
- Pinsky PF, Rinzel J. Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. J Comput Neurosci. 1994;1:39–60. doi: 10.1007/BF00962717. [DOI] [PubMed] [Google Scholar]
- Pospischil M, Toledo-Rodriguez M, Monier C, Piwkowska Z, Bal T, Frégnac Y, Markram H, Destexhe A. Minimal Hodgkin-Huxley type models for different classes of cortical and thalamic neurons. Biol Cybern. 2008;99:427–441. doi: 10.1007/s00422-008-0263-8. [DOI] [PubMed] [Google Scholar]
- Power JM, Bocklisch C, Curby P, Sah P. Location and function of the slow afterhyperpolarization channels in the basolateral amygdala. J Neurosci. 2011;31:526–537. doi: 10.1523/JNEUROSCI.1045-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Billimoria CP, Marder E. Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J Neurophysiol. 2003;90:3998–4015. doi: 10.1152/jn.00641.2003. [DOI] [PubMed] [Google Scholar]
- Rall W. Perspectives on neuron modeling. In: Binder MD, Mendell LM, editors. The Segmental motor system. Oxford University Press; New York: 1990. p. 397. xv. [Google Scholar]
- Repa JC, Muller J, Apergis J, Desrochers TM, Zhou Y, LeDoux JE. Two different lateral amygdala cell populations contribute to the initiation and storage of memory. Nat Neurosci. 2001;4:724–731. doi: 10.1038/89512. [DOI] [PubMed] [Google Scholar]
- Roth A, Hausser M. Compartmental models of rat cerebellar Purkinje cells based on simultaneous somatic and dendritic patch-clamp recordings. J Physiol. 2001;535:445–472. doi: 10.1111/j.1469-7793.2001.00445.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB, Cleland TA. Dynamical mechanisms of odor processing in olfactory bulb mitral cells. J Neurophysiol. 2006;96:555–568. doi: 10.1152/jn.00264.2006. [DOI] [PubMed] [Google Scholar]
- Rudolph-Lilith M, Dubois M, Destexhe A. Analytical integrate-and-fire neuron models with conductance-based dynamics and realistic postsynaptic potential time course for event-driven simulation strategies. Neural Comput. 2012;24:1426–1461. doi: 10.1162/NECO_a_00278. [DOI] [PubMed] [Google Scholar]
- Schneider CJ, Bezaire M, Soltesz I. Toward a full-scale computational model of the rat dentate gyrus. Front Neural Circuits. 2012;6:83. doi: 10.3389/fncir.2012.00083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard J-M, Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat Neurosci. 2006;9:356–362. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard J-M, Marder EE. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proceedings of the National Academy of Sciences. 2007;104:13187–13191. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sciamanna G, Wilson CJ. The ionic mechanism of gamma resonance in rat striatal fast-spiking neurons. J Neurophysiol. 2011;106:2936–2949. doi: 10.1152/jn.00280.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner FK. Cellular-based modeling of oscillatory dynamics in brain networks. Curr Opin Neurobiol. 2012;22:660–669. doi: 10.1016/j.conb.2012.02.001. [DOI] [PubMed] [Google Scholar]
- Stratford K, Mason A, Larkman AU, Major G, Jack J. They modeling of pyramidal neurones in the visual cortex. In: Richard D. e. a., editor. The computing neuron. Addisson-Wesley Longman Publishing Co, Inc; 1989. pp. 296–321. [Google Scholar]
- Stuart G, Spruston N. Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J Neurosci. 1998;18:3501–3510. doi: 10.1523/JNEUROSCI.18-10-03501.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart G, Spruston N, Hausser M. Dendrites. Oxford University Press; Oxford ; New York: 2008. [Google Scholar]
- Stuart GJ, Spruston N. Dendritic integration: 60 years of progress. Nat Neurosci. 2015;18:1713–1721. doi: 10.1038/nn.4157. [DOI] [PubMed] [Google Scholar]
- Sun W, Maffie JK, Lin L, Petralia RS, Rudy B, Hoffman DA. DPP6 establishes the A-type K(+) current gradient critical for the regulation of dendritic excitability in CA1 hippocampal neurons. Neuron. 2011;71:1102–1115. doi: 10.1016/j.neuron.2011.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temporal S, Lett Kawasi M, Schulz David J. Activity-dependent feedback regulates correlated ion channel mRNA levels in single identified motor neurons. Curr Biol. 2014;24:1899–1904. doi: 10.1016/j.cub.2014.06.067. [DOI] [PubMed] [Google Scholar]
- Tobin AE, Van Hooser SD, Calabrese RL. Creation and reduction of a morphologically detailed model of a leech heart interneuron. J Neurophysiol. 2006;96:2107–2120. doi: 10.1152/jn.00026.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tovote P, Fadok JP, Luthi A. Neuronal circuits for fear and anxiety. Nat Rev Neurosci. 2015;16:317–331. doi: 10.1038/nrn3945. [DOI] [PubMed] [Google Scholar]
- Traub RD, Bibbig A, LeBeau FE, Buhl EH, Whittington MA. Cellular mechanisms of neuronal population oscillations in the hippocampus in vitro. Annu Rev Neurosci. 2004;27:247–278. doi: 10.1146/annurev.neuro.27.070203.144303. [DOI] [PubMed] [Google Scholar]
- Traub RD, Wong RK, Miles R, Michelson H. A model of a CA3 hippocampal pyramidal neuron incorporating voltage-clamp data on intrinsic conductances. J Neurophysiol. 1991;66:635–650. doi: 10.1152/jn.1991.66.2.635. [DOI] [PubMed] [Google Scholar]
- Turrigiano G. Too many cooks? Intrinsic and synaptic homeostatic mechanisms in cortical circuit refinement. Annu Rev Neurosci. 2011;34:89–103. doi: 10.1146/annurev-neuro-060909-153238. [DOI] [PubMed] [Google Scholar]
- Vera JA, Jalcayaga J, Bacigalupo J, Sanhueza M. Contribution of persistent Na+ current and muscarine-sensitive K+ current to perithreshold theta resonance in CA1 pyramidal neurons; Socieity for Neuroscience Annual Meeting; Chicago, IL. 2015. 480.408. [Google Scholar]
- Vogels TP, Abbott LF. Signal propagation and logic gating in networks of integrate-and-fire neurons. J Neurosci. 2005;25:10786–10795. doi: 10.1523/JNEUROSCI.3508-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washburn MS, Moises HC. Electrophysiological and morphological properties of rat basolateral amygdaloid neurons in vitro. J Neurosci. 1992;12:4066–4079. doi: 10.1523/JNEUROSCI.12-10-04066.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ. The mechanism of intrinsic amplification of hyperpolarizations and spontaneous bursting in striatal cholinergic interneurons. Neuron. 2005;45:575–585. doi: 10.1016/j.neuron.2004.12.053. [DOI] [PubMed] [Google Scholar]