Rippling ultrafast dynamics of suspended 2D monolayers, graphene

Significance

Rippling is an intrinsic feature of 2D materials, responsible for their structural stability, transport properties, and electron–hole charge redistribution. Modulating these ripples in a controlled manner not only provides a better understanding of their structural properties, but also has potential impact for applications. Here, we examine graphene monolayer as a prototypical 2D material. An ultrafast attenuation of the ripples intrinsically present in the graphene plane is followed by a significant enhancement of the rippling effect on a longer time scale, as driven by the successive excitation of in-plane and out-of-plane phonon modes. The methodology described is of a general nature and is suitable for the investigation of other 2D materials, where we expect to observe similar rippling effects.

Abstract

Here, using ultrafast electron crystallography (UEC), we report the observation of rippling dynamics in suspended monolayer graphene, the prototypical and most-studied 2D material. The high scattering cross-section for electron/matter interaction, the atomic-scale spatial resolution, and the ultrafast temporal resolution of UEC represent the key elements that make this technique a unique tool for the dynamic investigation of 2D materials, and nanostructures in general. We find that, at early time after the ultrafast optical excitation, graphene undergoes a lattice expansion on a time scale of 5 ps, which is due to the excitation of short-wavelength in-plane acoustic phonon modes that stretch the graphene plane. On a longer time scale, a slower thermal contraction with a time constant of 50 ps is observed and associated with the excitation of out-of-plane phonon modes, which drive the lattice toward thermal equilibrium with the well-known negative thermal expansion coefficient of graphene. From our results and first-principles lattice dynamics and out-of-equilibrium relaxation calculations, we quantitatively elucidate the deformation dynamics of the graphene unit cell.

For a long time it was believed that 2D materials could not exist in nature due to a crumpling effect induced by long-wavelength thermal fluctuations (1–3). Recently, however, graphene was isolated from graphite by Novoselov et al. using the simple Scotch tape idea (4), and since then more and more 2D materials have been produced from bulk layered crystals (5, 6). In a strict definition, so far no isolated 2D layers have been found to be perfectly flat due to the presence of ripples, a microscopic roughening of the 2D plane, as observed in almost all cases (7, 8), apart from those in perfect contact with a substrate (9). Accordingly, rippling can be considered as an intrinsic feature of 2D materials, and is widely accepted to be at the origin of their structural stability (7, 10, 11).

Graphene, as the first 2D material, has attracted enormous interest due to extraordinary properties originating from the quasi-relativistic character of its electronic band dispersion (12). Most impressively, graphene's excellent transport properties, such as ultrahigh carrier mobility and electrical conductivity, have found a wide range of applications in new generations of nanoelectronic devices (13, 14). Considering that ripples can strongly affect the transport properties of graphene by inducing effective magnetic fields (15–17) and changing local potentials (18, 19), one of the remaining open questions is whether it is possible to modulate the rippling such that active control of the transport properties can be achieved. To address this issue, the main challenge lies in the ability to modulate ripples in a controlled manner at the mesoscopic and microscopic length scales. Bao et al. (20) have introduced a strain-engineering method to create periodic ripples on suspended graphene. Their work undoubtedly provides an improved understanding of suspended 2D layers and graphene devices. However, the lateral size of the generated ripples is one order of magnitude larger than the value generally reported for intrinsic rippling (∼10 nm), which may have a different impact on the transport. Theoretically, Smolyanitsky and Tewary (21) have proposed a dynamic way to tune the ripples by using the excitation of terahertz waves. They predicted that it is possible to significantly flatten graphene exploiting the interplay between intrinsic thermally induced and externally excited ripples.

In this work, we use femtosecond laser pulses to excite the electronic states of a suspended graphene layer and modulate the rippling structure via the excitations and the anharmonic interactions of different phonon modes. To investigate the real-time response of the atomic structure of the suspended graphene to the ultrafast optical excitation, we used ultrafast electron crystallography (UEC), which represents a unique tool for investigating energy transport processes and structural dynamics of nanomaterials (22–24). Compared with other ultrafast optical and X-ray time-resolved techniques, UEC offers not only a higher spatial resolution, down to the atomic scale, but also a high sensitivity to small material volumes, such as monoatomic layers, due to a higher electron/matter scattering cross-section.

Following a femtosecond optical excitation, the temporal behavior of graphene’s diffraction pattern is monitored as a function of the delay time between laser pump and electron probe. An energy evolution process from photocarrier excitation to thermal lattice equilibration is well resolved and understood in the framework of electron–phonon and phonon–phonon couplings. Here we support the experimental observation with first-principles simulations of the phonon dynamics via Boltzmann-transport equations. The excitation of in-plane and out-of-plane phonon modes via anharmonic interactions generates very specific structural dynamics. In particular, a transient nonthermal expansion mediated by in-plane phonons takes place on the 5-ps time scale, inducing an ultrafast attenuation of the ripples present in the graphene layer through the layer’s expansion. This attenuation is followed by a slower thermal equilibrium contraction, caused by out-of-plane phonons with a time constant of 50 ps, which induces a long-term recovery or even enhancement of the rippling structure. Because ripples are ubiquitous in 2D materials, we expect these results to be of general validity and of potential applications in ultrafast photoelectronics.

Intrinsic Rippling at Steady State

From a theoretical point of view, Landau and Lifshitz (1), Peierls (2), and Mermin (3) showed that in the harmonic approximation, long-wavelength thermal fluctuations are able to destroy the long-range order of a perfect 2D lattice, resulting in melting at finite temperature. Beyond the harmonic approximation, however, the interaction between bending and stretching phonon modes could in principle suppress long-wavelength fluctuations and thus stabilize the 2D lattice through an out-of-plane deformation with strong height modulations (11). In an elegant transmission electron microscopy (TEM) experiment, Meyer et al. (7) revealed that a suspended graphene sheet is not perfectly flat but exhibits pronounced out-of-plane corrugations (ripples) with a lateral size of ∼10 nm and height up to 1 nm. The ripples, whose formation results from the freezing of thermal out-of-plane phonon modes (generally referred to as ZA modes), would lead to a gain in elastic energy and thus a minimization of the total free energy (10).

This 3D warping is able not only to stabilize the 2D lattice, but also to influence the electronic structure and transport properties of graphene. In particular, the bending of the graphene sheet will induce two main effects (19): (i) a π–σ rehybridization between nearest neighbors, which shifts the π-orbital energy, resulting in a local potential variation; and (ii) a change in the nearest-neighbor hopping integral, which introduces an effective vector potential. As a result, due to the bending, the electrons are subject to a potential depending on the local curvature of the graphene lattice (12) and, therefore, Dirac fermions will be effectively scattered by the ripples, providing an additional contribution to the electrical resistivity. In fact, carrier mobilities higher than 200,000 cm²/Vs have been calculated in the case of a perfect 2D lattice, whereas one order of magnitude smaller values are experimentally reported for monolayer graphene at low temperatures (25). Moreover, a recent work has shown that periodic nanoscale ripples in graphene can induce a significant bond stretching able to open up the band gap by values as large as 0.13 eV (26). Therefore, the ability to control in space and time the lattice distortion in graphene, which allows modulation of the ripples, represents a powerful methodology for tuning graphene's electronic and transport properties.

Rippling Dynamics Under Optical Excitation

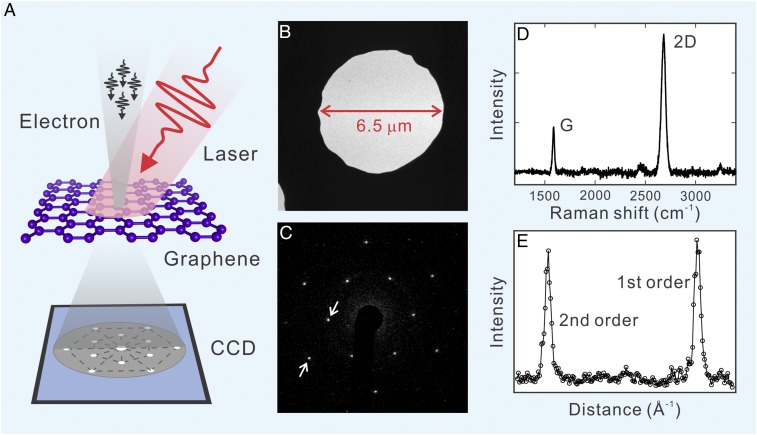
Femtosecond laser pulses are able to perturb the anharmonic coupling between bending and stretching modes, thus modulation of the rippling structure might be expected. To monitor such changes at the atomic scale, we adopt UEC. The UEC experiments are schematically shown in Fig. 1A and detailed in Materials and Methods. Briefly, a monolayer graphene, grown by chemical vapor deposition (CVD) and characterized by Raman spectroscopy, electron microscopy, and diffraction, is transferred via a poly(methyl methacrylate) (PMMA) layer onto a TEM copper grid. The diffraction pattern in Fig. 1 C and E and the Raman spectrum in Fig. 1D exhibit the typical fingerprint of a single layer of sp² carbon atoms (27). Here, particular care has been taken to remove the PMMA layer, and a very low amount of residue is present on the graphene, as shown by the TEM image in Fig. 1B. For comparison, a commercially available monolayer graphene TEM grid (from Ted Pella, Inc.), which shows an increased amount of PMMA residue, has also been investigated. The dynamics are initiated by a 120-fs laser pulse (800 nm, 2 kHz) and probed by a 20-keV electron pulse as a function of the delay time between optical pump and electron probe pulses. The evolution of the diffraction pattern is quantitatively evaluated by measuring the temporal change of the diffraction intensity and peak position of Bragg reflections.

Fig. 1.

Concepts of UEC probing of dynamics and sample characterization. (A) UEC experimental arrangement for the photon-pump/electron-probe measurements of suspended monolayer graphene. (B) TEM image of monolayer graphene suspended on a 2000 mesh circular aperture TEM grid. (C) Static electron diffraction pattern acquired within the UEC setup using an electron energy of 20 keV. (D) Background-free Raman spectrum at 514 nm for a monolayer of graphene. (E) Plot of the diffraction intensity profile extracted along the line indicated by the arrows in the diffraction pattern shown in C.

Shown in Fig. 2A are the observed transients of the diffraction intensity of the second-order Bragg reflections at two different excitation fluences. Similar results are obtained for the first-order spots, although with a smaller intensity change. Because the six Bragg reflections associated with the same diffraction order show the same behavior, the transients displayed in Fig. 2A have been obtained by averaging over these six spots to improve the signal-to-noise ratio. Within the time window of interest, the transients can be well described by a single-exponential decay.

Fig. 2.

Temporal behavior of the diffraction intensity and fluence dependence. (A) Measured transient behavior of the second-order Bragg reflections for two different excitation fluences. The solid lines are single-exponential fit of the experimental data. (B) Experimental (circles) and calculated (solid lines) intensity change as a function of the excitation fluence (bottom axis), or equivalently, as a function the laser-induced temperature rise in graphene (top axis). (C) Temperature dependence (bottom axis) and fluence dependence (top axis) of the decay time of the diffraction intensity. The solid line is a fitting curve using Eq. 1. The blue and red circles indicate the homemade and commercial graphene TEM grids, respectively. Very similar dynamics for the intensity change are observed in both cases (see text for details).

As shown in Fig. 2B, the magnitude of the intensity change as a function of excitation fluence (i.e., the laser-induced temperature rise) is quantitatively described by the in-plane Debye–Waller (DW) factor [with in-plane Debye temperature ${\theta }_{in}=$ 2,100 K (28) or 2,300 K (29)], indicating that most of the absorbed energy has eventually been converted into the thermal heating of the lattice. Here, the temperature rise is estimated based on the absorbed laser energy with the absorption of 2.3% per layer (30) and the heat capacity given in ref. 31. Note that in the case of an electron beam at normal incidence, as adopted here, the scattering vector lies in the graphene plane and thus only in-plane atomic displacements contribute to the DW factor. The decay of the diffraction intensity is, therefore, mainly associated with the excitation of in-plane phonon modes, which would induce a stretching of the graphene plane (32). The characteristic time constant, obtained from a single-exponential fit of the experimental data, varies from 7 to 18 ps with decreasing fluence (Fig. 2C). These values are similar to the decay time of optical phonons (OPs) into thermal acoustic phonons (via nonthermal acoustic phonons), reported for graphite (33–35). The fluence dependence of the time constant is mainly due to an increased phonon–phonon scattering under higher excitation condition. To achieve a simple description of the decay process, we adopt the single relaxation time approximation (36, 37) and define an average relaxation time of the phonon modes τ as

$$\tau \propto 1/\left(1+\alpha \cdot T\right),$$ [1]

where T is the lattice temperature at equilibrium, $\alpha \approx \left(2k_B/\hslash \omega \right)$, k_B is the Boltzmann constant, and $\hslash \omega$ is the phonon energy. This equation has been derived from the expression for the phonon relaxation due to the anharmonic scattering processes (see equation B2 of ref. 37 for more details), when the following simplifications apply: (i) only decays from one high-energy phonon to two low-energy ones are considered, whereas phonon reabsorption is neglected because of the lower occurrence probability; and (ii) the Bose–Einstein distribution for the phonon density has been expanded to a first order considering that $\hslash \omega \ll k_{B}T$ for the acoustic phonons. As shown in Fig. 2C, Eq. 1 provides a satisfactory fitting of the time constant as a function of the effective lattice temperature, from which a phonon energy $\hslash \omega$ = 100 meV is obtained. This value is of the same order of magnitude as the typical energies associated with in-plane acoustic phonons and the in-plane Debye temperature in graphene.

It is worth mentioning that further increase of the excitation fluence will damage the graphene sample. The highest equilibrium temperature reached is 2,400 K, which is close to the stability limit of suspended CVD graphene (38), thus further verifying the validity of the estimated temperature.

As mentioned above, the intensity change in the transmission geometry adopted can mainly probe in-plane atomic vibrations. Nevertheless, out-of-plane deformation effectively modifies the projected atomic position (or unit cell) in the basal plane. It is thus possible to study out-of-plane fluctuations by monitoring the position change of Bragg reflections. To eliminate the effect of the transient electric field (TEF) (39) on the peak position, we extract the Brillouin zone area A, as schematically shown in Fig. 3A (Inset) instead of the absolute peak position. This method is indeed effective because the TEF shifts each Bragg reflection of the same amount along the same direction in the detector plane. The transient behavior of A can then be converted into the strain dynamics of the unit cell via $\epsilon \left(t\right)\simeq -0.5\cdot \left(A\left(t\right)/A_0-1\right)$, as shown in Fig. 3A, where A₀ is the zone area before optical excitation and ε is the in-plane strain. Differently from the case of the diffraction intensity, the strain dynamics show a more unique behavior, composed of an initial ultrafast expansion and a following slower contraction.

Fig. 3.

Deformation dynamics of the graphene unit cell. (A) Measured temporal evolution of the in-plane strain as derived by monitoring the change of the Brillouin zone area (first three Brillouin zones as shown in the inset). The solid line is a multiexponential fit of the experimental data. Note the positive change of the strain before its negative value behavior. (B) The magnitude of the transient lattice expansion (as indicated in A) is shown as a function of the excitation fluence. The blue and red circles indicate the homemade and commercial graphene TEM grids, respectively. Very similar dynamics for the lattice expansion are observed in both cases.

The thermal contraction of graphene has been widely studied at equilibrium and is attributed to the large negative thermal expansion coefficient due to thermal fluctuation of out-of-plane (ZA) modes (20, 40). The relatively long-time contraction (time constant of 50 ± 10 ps) observed here can thus be associated with the gradual population of ZA modes. Because the out-of-plane thermal fluctuations are believed to be at the origin of the intrinsic rippling observed in graphene (11), the increased population of ZA modes is responsible for an enhanced corrugation of the graphene plane, as also attested by an increased contraction observed under higher excitation fluence. Here, the temperature range in which the thermal contraction persists is consistent with the theoretical prediction of ref. 41.

Besides the slow contraction, we also observed an ultrafast (5 ps) lattice expansion. This observation demonstrates the transient atomic sensitivity of UEC, in contrast to previous investigations of the lattice deformation of suspended graphene, which have been performed only under static or quasi-static conditions (20, 40). Because the time scale of the lattice expansion is similar to the value observed for the intensity change, which involves in-plane phonon modes, and consistent with the lifetimes of OPs (∼4–5 ps) as calculated by first-principles simulations (42, 43), we attribute the expansion to the excitation of in-plane nonthermal longitudinal and transverse acoustic phonons (LA and TA) anharmonically decayed from OPs. In fact, the nonthermal excitation of LA and TA modes would be able to induce a stretching of the lattice plane, thus reducing the height of the ripples intrinsically present in graphene.

We can thus describe the observed dynamics as a fast decay from OPs to in-plane acoustic phonons, followed by a slower excitation of ZA modes. The origin of these two characteristic relaxation times can be traced back to: (i) the scattering selection rule (44), and (ii) the conservation laws of energy and momentum. The reflection symmetry z→−z of graphene limits the possible scattering processes such that only events containing an even number of out-of-plane phonons are allowed, excluding several possible channels. In addition, considering that the energy of ZA phonons is much smaller than the energy of in-plane OPs, the constraint on energy and crystal momentum conservation further suppresses the decay from OPs to ZA phonons. These intuitive arguments are corroborated by a detailed theoretical analysis of scattering rates by Singh et al. (45).

It is worth noting that Gao and Huang (32) have theoretically predicted that anharmonic interactions among in-plane phonon modes could cause a linear and positive thermal expansion, as we have observed here (Fig. 3B). Nevertheless, a conceptual difference still exists between the present data and their theoretical results. In fact, in the present case the attenuation of the ripples at the early time after the ultrafast excitation is due to the excitation of only in-plane LA and TA modes, which cause the stretching of graphene, while the lattice is still far from equilibrium. Out-of-plane ZA modes take a much longer time to be populated, finally leading the system to the thermal equilibrium. The cross-over from positive to negative expansion is thus mainly due to a consequential excitation of first in-plane and then out-of-plane modes. In contrast, the theoretical simulations from Gao and Huang (32) are performed at thermal equilibrium and would predict a transition from negative to positive expansion with an increased lattice temperature as caused by the competing effects induced by in-plane and out-of-plane modes.

Graphene Dynamics Simulations

In this section we model from first-principles the lattice dynamics of monolayer graphene following the optical excitation. An ideal, yet computationally unfeasible, approach involves the description of the full excitation chain: photons exciting electrons, which decay into phonons that eventually thermalize. Because the electron relaxation occurs on a time scale much shorter than that of the lattice dynamics (46), we simplify the problem by neglecting this electron dynamical effect, and begin directly exciting a nonequilibrium phonon population and study its relaxation to equilibrium. We thus suppose that the laser instantaneously introduces additional internal energy in the layer with respect to the initial conditions, which means that the temperature of graphene is instantaneously brought from 300 K to a higher value T.

The initial condition in the simulations of nonthermal phonon populations is imposed by first considering that electron–phonon couplings are much stronger for in-plane OPs. Therefore, we suppose that the electronic relaxations have excited only these phonons, while in-plane and out-of-plane (both acoustic and optical) modes, which interact weakly with electrons, are left populated according to the Bose–Einstein distribution at room temperature. To excite the in-plane OPs, we assume that they follow a Bose–Einstein distribution at an excited temperature $T^{\ast }$, chosen such that the total energy of the initial configuration matches the internal energy E of the system after the excitation: $E={{\displaystyle \sum }}_{\mu }\hslash {\omega }_{\mu }\left({\overline{n}}_{\mu }+1/2\right)$, where ${\overline{n}}_{\mu }$ is the Bose–Einstein distribution function at temperature T.

We let the nonthermal phonon populations evolve in time according to the linear Boltzmann transport equation (BTE):

$$\frac{\partial (n_{\mu }\left(t\right)-{\overline{n}}_{\mu })}{\partial t}=\frac{1}{V}{\displaystyle \sum }_{\mu \prime }{\Omega }_{\mu \mu \prime }(n_{\mu \prime }\left(t\right)-{\overline{n}}_{\mu \prime }),$$ [2]

where $n_{\mu }\left(t\right)$ is the phonon population at time t of the phonon mode μ [a shorthand notation for $\mu =(\mathit{q},s)$, to label both phonon wavevectors q and phonon branches s], V is a normalization volume, and ${\Omega }_{\mu \mu \prime }$ is the scattering matrix derived from first-principles. The term ${\Omega }_{\mu \mu \prime }$ contains the rates for all possible transitions $\mu \to \mu \prime$ and is built with three-phonon scattering rates and isotopic scattering (to lowest order in perturbation theory) at natural abundances. Harmonic phonon properties and phonon–phonon scattering rates are computed from density-functional perturbation theory (47) as implemented in Quantum ESPRESSO (48) (see Materials and Methods for further details). We stress that the solution to the BTE is found by diagonalizing the complete scattering matrix, i.e., beyond the single-mode relaxation time approximation. Therefore, we obtain the time evolution of the phonon population $n_{\mu }\left(t\right)$ for each phonon mode, from which we can compute the transient change of lattice properties (see Materials and Methods for details).

The time evolution of the DW factor is reported in Fig. 4A for various temperatures, showing a good agreement with the experimental data of Fig. 2A, and thus confirming that the modulation of the laser fluence is directly tuning the thermal energy of the layer. Despite the complexity of the microscopic time evolution of phonons, the DW factor relaxes to the equilibrium value approximately as a single exponential with an effective relaxation time ${\tau }_{sim}$. The temperature dependence of ${\tau }_{sim}$ shown in Fig. 4B agrees well with the experimental trend in Fig. 2C, and qualitatively captures the values within a factor of ∼1.5. Therefore, notwithstanding the approximations adopted in the present modeling, we retain the main features of the experimental lattice dynamics and provide an adequate description of the system in the out-of-equilibrium conditions. We attribute the remaining discrepancy mainly to the choice of initial conditions of the phonon populations, which is the only free parameter of the simulation. The inclusion of the electron dynamics and their decay, which nevertheless formidably increases the modeling complexity and goes out of the scope of this article, could provide a parameter-free description of the very first femtoseconds after the laser pulse and eliminate the arbitrariness in the initial phonon populations.

Fig. 4.

Theoretical simulations of the ultrafast lattice dynamics. (A) Time evolution of the simulated DW factor of the second-order Bragg reflections for two different excitation fluences. (B) Calculated effective decay time of the DW factor as a function of the lattice temperature. The solid line is a fit using Eq. 1 (see text for details). (C) Calculated time evolution of the lattice pressure as obtained from Eq. 3 (see text). The horizontal dashed line defines the lattice pressure of the system at thermal equilibrium at 300 K before the laser excitation.

The lattice dynamics simulations also provide an insight into the ultrafast evolution of strain. In particular, the excitation of the phonon gas is able to induce a change of the lattice pressure, causing the crystal to expand or contract. Within the quasi-harmonic approximation (49) (which we extend here to the time-dependent case) the lattice pressure can be obtained as

$$P\left(t\right)=\frac{1}{V}{\displaystyle \sum }_{\mu }\hslash {\omega }_{\mu }{\gamma }_{\mu }\left(n_{\mu }\left(t\right)+\frac{1}{2}\right),$$ [3]

where ${\gamma }_{\mu }=-\left(1/2{\omega }_{\mu }\right)\left(\partial {\omega }_{\mu }/\partial \epsilon \right)$ is the Grüneisen parameter. Therefore, the time-dependent phonon population allows immediate access to the lattice pressure, which we plot in Fig. 4C as a function of time for various temperatures. At short times, pressure has larger positive values, indicating the expansion of the graphene crystal. The pressure then decreases, well below the room temperature value, leading to the layer contraction. Although we are neglecting the electron dynamics, the model is able to capture the qualitative features of the ultrafast expansion/contraction as experimentally observed by the strain dynamics in Fig. 3A. This behavior can easily be interpreted in terms of Eq. 3 and of ${\gamma }_{\mu }$. In fact, in-plane phonons, populated at the shortest times, are characterized by positive ${\gamma }_{\mu }$ (41) and thus drive the fast expansion of the graphene unit cell. Out-of-plane ZA modes have negative values of ${\gamma }_{\mu }$, much larger in absolute value than ${\gamma }_{\mu }$ associated with in-plane modes, and determine the contraction of the layer once they are excited at longer times. To see why the contraction dominates at equilibrium (>20 ps), notice that phonons are occupied according to the Bose–Einstein occupation, which at high temperatures reduces to $n_{\mu }\approx kT/\hslash {\omega }_{\mu }$. Hence, by referring to Eq. 3, the equilibrium pressure is essentially a sum over Grüneisen parameters, which is dominated by the large contribution to contraction of the ZA mode.

Summary and Conclusions

The dynamic response of suspended graphene to ultrafast laser pulses, as experimentally observed and theoretically simulated here, is schematically pictured in Fig. 5A. At early times (∼5 ps) after the ultrafast excitation, the ripples are stretched out by anharmonic excitation of in-plane phonons, which should reduce their height. On a longer time scale (50 ps), the excitation of ZA phonon modes increases the out-of-plane thermal fluctuation, resulting in an increase of the ripple height. The modulation of the rippling by ultrashort laser pulses not only improves our understanding of structural stability of graphene, but also provides possibilities for new generations of ultrafast photoelectronics. As described before, because ripples are “imperfections” on an otherwise perfect 2D lattice, they have a significant impact on the properties of graphene, including electronic transport, magnetoresistance, and chemical activity. By controlling the rippling structure on an ultrafast time scale, it would thus be possible to significantly modify the physical properties within a very short time window. As an example, we estimated the modulation of the electric resistivity of graphene resulting from the nonthermal in-plane stretch at different initial temperatures based on the theory given in ref. 50, as shown in Fig. 5B. At the maximum expansion experimentally reached, the resistivity due to thermal out-of-plane phonons is reduced more than one order of magnitude compared with the value without tension. This reduction is obtained in only few picoseconds, and thus graphene could be used as an ultrafast switch, as conceptually shown in Fig. 5C. When an ultrashort laser pulse illuminates the suspended graphene, the electric resistivity decreases at least by one order of magnitude in 5 ps, generating an ultrashort electrical current.

Fig. 5.

Calculated strain and resistivity, together with a schematic for the importance of time scales of rippling. (A) Schematic representation of the ultrafast attenuation (5 ps) of the intrinsic ripples due to the excitation of nonthermal in-plane acoustic phonons (LA and TA), followed by a recovery, or even enhancement, of the rippling structure in 50 ps, as caused by the increased population of out-of-plane phonon modes (ZA). (B) The effect of the in-plane strain on the electrical resistivity of graphene at different initial temperatures, as derived from the theory given in ref. 50, is depicted for strain values experimentally measured here. The blue line represents the contribution from in-plane phonons, whereas the gray lines represent the contribution from ZA phonons at three different strains. (C) Conceptual drawing of an ultrafast optical switch based on graphene.

In conclusion, we have visualized the spatiotemporal behavior of suspended monolayer graphene under femtosecond optical excitation using UEC and first-principles simulations of the real-time lattice dynamics. Because of the high electron/matter scattering cross-section, the atomic-scale spatial resolution, and the ultrafast temporal resolution of UEC, we were able to resolve the energy evolution process in graphene from the optical excitation to the lattice thermal equilibrium and reveal the deformation dynamics of graphene unit cell. An ultrafast expansion occurs in 5 ps, which is responsible for an initial reduction of the ripples intrinsically present in graphene, followed by a long-term contraction in 50 ps, which leads to a recovery or even enhancement of the original rippling. This is driven by a sequential excitation and interaction of in-plane and out-of-plane acoustic phonon modes. The results reported here demonstrate the ability to modulate rippling in graphene by using ultrashort laser pulses and, because ripples are ubiquitous in 2D materials, they are expected to be of general validity with potential applications in ultrafast photoelectronics.

Materials and Methods

Sample Preparation.

The monolayer graphene sample used here is grown by CVD. After spin-coating a PMMA layer on one face of the graphene plane, the sample was then placed on the surface of a soluble polymer (so-called “Trivial Transfer Graphene,” purchased from ACS Material LLC). After polymer was dissolved in deionized water, the graphene with PMMA was collected with a circular aperture 2000 mesh TEM grid (hole diameter of 6.5 μm, Ted Pella, Inc.). The grids were then dried by annealing at 50 °C for 10 min, followed by a further bake at 100 °C for 10 min, to enhance the adhesion of graphene with the copper grid and flatten out the wrinkles. The grid was then dipped into acetone for 15 min to dissolve the PMMA layer and rinsed several times using ethanol to improve the cleanness of the graphene layer. Finally, the grid with graphene was annealed in a furnace with Ar (∼500 standard cubic centimeters per minute, sccm) and H₂ (∼500 sccm) at 400 °C for 3 h to minimize the PMMA residue. We also investigated a commercially available monolayer graphene suspended on the 2000 mesh grid (Ted Pella, Inc.), which shows a nonnegligible amount of PMMA impurities resulting in a strong background scattering in the diffraction pattern. The layer number of both samples was identified by the ratio between the intensities I_first and I_second of the first-order and second-order diffraction spots, respectively. For the case of a monolayer I_first/I_second is around 1, whereas for a bilayer I_first/I_second is around 0.5 (see ref. 27).

UEC Experiments.

The UEC experiments have been performed in the transmission geometry. Briefly, a laser-pump/electron-probe scheme is adopted to detect the photoinduced change as a function of the delay time between the pump and probe pulses. The pump pulse (800 nm, 120 fs), generated from a Ti:sapphire amplifier at the repetition rate of 2 kHz, is used to initiate the dynamics with an incident angle of 45° with respect to the sample surface. The electron probe beam (subpicosecond), emitted by a LaB₆ photocathode under the illumination of a 266-nm UV laser pulse and then accelerated to 20 keV, is used to produce diffraction patterns off the sample at a certain delay time. Because of the limited lateral size of monolayer graphene flakes, the electron beam is tightly focused on the sample position with a spot size of 31 × 13 μm². To minimize space-charge effects, each electron probe pulse contains only ∼300 photoelectrons and the upper limit of the electron pulse duration is estimated to increase to 2.1 ps in the present experiment. The spatial overlap between pump and probe beams is ensured with a precision of ∼20 μm by maximizing the transmission of both beams through a 150-μm aperture at the sample plane. The diffraction patterns are recorded on a microchannel plate/phosphor screen/CCD assembly working in the gate mode.

First-Principles Calculations.

We used Quantum ESPRESSO (48) for density-functional theory and density-functional perturbation theory calculations, using the local-density approximation, norm-conserving pseudopotentials from the PSLibrary (qe-forge.org/gf/project/pslibrary/), a plane-wave cutoff of 90 Ry, and a Methfessel–Paxton smearing of 0.02 Ry. The slab geometry used to simulate graphene has a relaxed lattice parameter of a = 4.607 Bohr and a cell height c = 3a. We integrate the Brillouin zone with a Gamma-centered Monkhorst–Pack mesh of 24 × 24 × 1 points and compute second- and third-order force constants on meshes of 16 × 16 × 1 and 4 × 4 × 1 points, respectively.

Lattice Dynamics Simulations.

The scattering matrix is built to include 3-phonon and harmonic isotopic scattering (37, 51) at natural carbon abundances (98.93% C¹², 1.07% C¹⁴), and is constructed using the same computational parameters of refs. 36, 52 (a Gaussian smearing of 10 cm⁻¹ and a mesh of 128 × 128 × 1 points for integrating the Brillouin zone). The scattering matrix is diagonalized exactly using the routine PDSYEV of the ScaLAPACK library (53).

The DW factor is computed according to

$$DW\left(t\right)=e^{-2W\left(t\right)},$$

with

$$W\left(t\right)=\hspace{0.17em}\frac{\hslash }{2N}{\displaystyle \sum }_{\mu }{\left[{\displaystyle \sum }_{sb}\frac{\mathit{G}\cdot {\mathit{z}}_{\mu }^{sb}}{M_b}\right]}^2\frac{1}{{\omega }_{\mu }}\left(n_{\mu }\left(t\right)+\frac{1}{2}\right),$$

where G is the momentum transfer vector, b is the index over the basis of atoms in the primitive unit cell of the crystal, M_b is the mass of the atom b, and $\mathit{z}$ is the phonon polarization vector. The equation is a direct extension of the standard equation for the DW factor used for an out-of-equilibrium, time-dependent case.