Hurricane Sandy’s flood frequency increasing from year 1800 to 2100

Significance

This study demonstrates quantitatively that the frequency of Hurricane Sandy-like extreme flood events has increased significantly over the past two centuries and is very likely to increase more sharply over the 21st century, due to the compound effects of sea level rise and storm climatology change.

Abstract

Coastal flood hazard varies in response to changes in storm surge climatology and the sea level. Here we combine probabilistic projections of the sea level and storm surge climatology to estimate the temporal evolution of flood hazard. We find that New York City’s flood hazard has increased significantly over the past two centuries and is very likely to increase more sharply over the 21st century. Due to the effect of sea level rise, the return period of Hurricane Sandy’s flood height decreased by a factor of ∼3× from year 1800 to 2000 and is estimated to decrease by a further ∼4.4× from 2000 to 2100 under a moderate-emissions pathway. When potential storm climatology change over the 21st century is also accounted for, Sandy’s return period is estimated to decrease by ∼3× to 17× from 2000 to 2100.

In October of 2012, Hurricane Sandy flooded the US East Coast with extreme storm surges. At the Battery tide gauge in New York City (NYC), the storm surge reached 2.8 m; the storm tide, which includes also the astronomical tide, reached a record height of 3.44 m (the North American Vertical Datum of 1988). Estimating the frequency of Sandy-like flood events, including how it changes over time, provides critical information for coastal risk mitigation and climate adaptation. Previous studies have investigated the frequency of Hurricane Sandy under the historical climate (1–4). In this study, we focus on how the frequency of extreme floods induced by Sandy-like events varies in response to changes in the sea level (5) and storm activity (6, 7) due to climate change. In particular, we investigate (i) the influence of historical sea level rise in shaping the current flood hazard in NYC and (ii) the impact of projected future climate change and sea level rise on Sandy-like flood events.

To compare flood events across time periods, we define the flood height as the peak water level during a storm relative to a baseline mean sea level (e.g., the mean sea level in 2000). Here we focus on the sea level components that vary with the climate and do not account for the effect of astronomical tide. Thus, we calculate the flood height as the sum of the peak storm surge and relative sea level (RSL; relative to the baseline). Then, for a given climate state, the return period (reciprocal of frequency) of floods of different heights can be estimated by combining (i) the storm frequency (assuming that the storms arrive as a Poisson process) and (ii) the cumulative distribution function (CDF) of the flood height, which can be obtained by combining the CDF of the storm surge and the probability distribution function (PDF) of RSL (Methods). In such a framework, we integrate the estimated RSL PDF with modeled storm frequency and storm surge CDF (which, together, describe storm surge climatology) to estimate NYC’s flood return periods from year 1800 to 2100.

We consider storm surges induced by hurricanes/tropical cyclones. (Extratropical cyclones can also induce coastal flooding in NYC (8), although the flood magnitude is often smaller.) We estimate the current and future hurricane surge climatology for NYC following ref. 9, using large numbers of synthetic surge events that are generated with a statistical deterministic hurricane model (10) and a high-resolution hydrodynamic model (11). Specifically, in ref. 9, the NYC surge climatology was estimated for the observed climate of 1981–2000 based on the National Centers for Environmental Prediction (NCEP) reanalysis, as well as for the global climate model (GCM) modeled climate of 1981–2000 and projected climate of 2081–2100 (under the A1B emission scenario of Intergovernmental Panel on Climate Change Special Report on Emissions Scenarios) based on four GCMs [CNRM-CM3 (Centre National de Recherches Météorologiques, Météo-France), ECHAM5 (Max Planck Institute), GFDL-CM2.0 (NOAA Geophysical Fluid Dynamics Laboratory), and MIROC3.2 (Center for Climate System Research/National Institute for Environmental Studies/Frontier Research Center for Global Change, Japan)]. The analysis of ref. 9 accounted for the variation of storm track and intensity and their changes with the climate conditions, but it applied a statistical mean storm size. Here, based on recent research on storm size (12, 13), we incorporate the statistical size variation into the analysis (Methods). However, how storm size changes with the climate is still not accounted for, given the limited physical understanding of what controls the storm size (12) and initial numerical evidence that storm size may change little on average over the 21st century climate (14). By comparing the NCEP estimates and GCM estimates for the same period of 1981–2000, ref. 9 bias-corrected the projected storm frequency for 2081–2100, assuming the model bias does not change over the projection period. Here we apply the same assumption and bias-correct the projected storm surge CDF for 2081–2100 through quantile−quantile mapping (15) (Methods). Then, we assume that the NCEP-estimated surge climatology of 1981–2000 represents that of 2000 and the (unbiased) GCM-projected surge climatology of 2081–2100 represents that of 2100, and we estimate the surge climatology for every decade between 2000 and 2100 through linear interpolation. We do not consider potential changes of storm climatology from 1800 to 2000; i.e., in the analysis, the surge climatology between 1800 and 2000 is represented by the NCEP estimates for year 2000.

We set year 2000 to be the baseline (RSL = 0 m). For the future RSL, we use the probabilistic, localized projections of RSL at the Battery generated as part of ref. 16’s global set of RSL projections. The projections are based on combined PDFs for (i) thermal expansion and ocean dynamic changes derived from the Coupled Model Intercomparison Project Phase 5 (17); (ii) glacier mass balance changes derived from the projections of ref. 18; (iii) ice sheet mass balance based upon a fusion of the expert assessment of ref. 19 and structured expert elicitation of ref. 20; (iv) land water storage estimated as a function of global population; (v) nonclimatic, approximately linear, long-term sea level change due to glacial isostatic adjustment (GIA), subsidence, and other processes, estimated from tide gauge data; and (vi) the static equilibrium fingerprints of sea level change caused by glacier and ice sheet mass fluxes (21). Here we use 10,000 Monte Carlo (MC) samples of the projected RSL time series to estimate the PDF of RSL for the Battery for every decade from 2000 to 2100, under the emissions scenario Representative Concentration Pathway (RCP) 4.5 (roughly comparable to the A1B scenario used for the surge climatology projection; see ref. 22). We note that the thermal expansion, ocean dynamic, and glacier contributions to these RSL projections are based upon a large number of GCMs (given equal weights); given the inherent correlation between storm climatology change and sea level rise (23), future research may develop RSL projections for individual GCMs to be combined with the storm surge projection for the corresponding GCMs.

We apply an estimate of past RSL from 1800 to 2000 for NYC based on a spatiotemporal empirical hierarchical statistical model (24) that incorporates data from (i) the Battery tide gauge (1856 to present with 18 missing or incomplete years); (ii) other, shorter tide gauges in the Northeast US Atlantic coast; (iii) a high-resolution, three-century proxy RSL reconstruction from Barnegat Bay, NJ (25); and (iv) lower-resolution proxy RSL reconstructions from elsewhere in New Jersey (24, 26, 27) (Methods).

Results

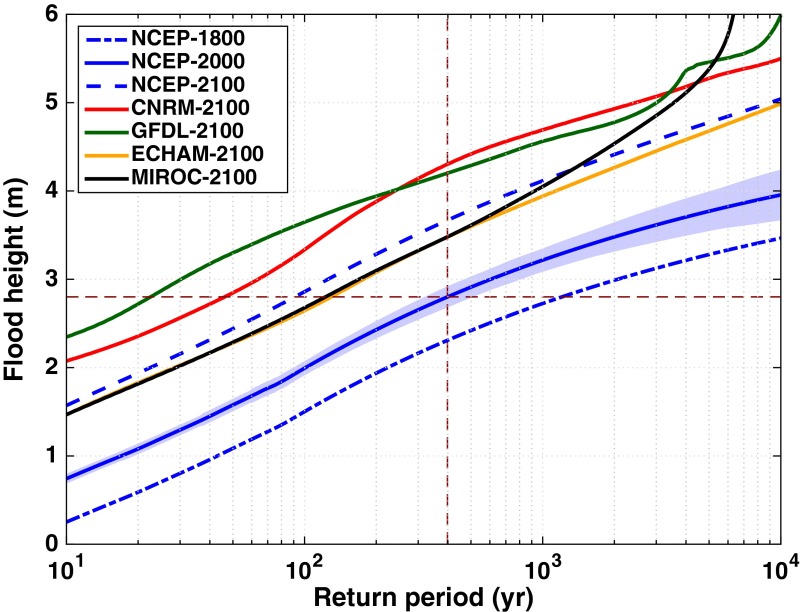
We integrate the estimated storm surge climatology and RSL to estimate the return periods for various flood heights (0 m to 6 m) for NYC for every decade from 1800 to 2100. Fig. 1 shows the estimated flood return period curves for the years 1800, 2000, and 2100. The return period of a storm surge (also flood height) of 2.8 m, similar to Hurricane Sandy, is 398 y in 2000 (RSL = 0 m). This estimate is lower than the 516-y estimate found in ref. 9, indicating that neglecting the storm size variation can significantly underestimate the surge hazard. As demonstrated by the substantial shift of the flood return period curve, the flood hazard for NYC has increased significantly from 1800 to 2000 and will increase even more sharply to 2100. Considering only the effect of RSL rise, the return period of Sandy’s flood height (2.8 m) is estimated to be ∼1,200 y in 1800 and ∼90 y in 2100. Storm surge climatology change can also significantly affect the flood return periods over the 21st century; when it is accounted for, the estimated return period of Sandy’s flood height in 2100 becomes ∼23 y to 130 y, depending on the applied climate models. The flood height with Sandy’s return period (398 y) is estimated to be about 2.3 m in 1800 and 3.7 m in 2100, considering only the effect of RSL rise. When the change of storm climatology is also accounted for, this flood magnitude becomes about 3.5 m to 4.3 m in 2100.

Fig. 1.

Return periods of flood heights (relative to the mean sea level of the baseline year 2000) in NYC, estimated for years 1800, 2000, and 2100. The solid blue curve shows the return period of flood heights (also storm surges as RSL = 0 m) for year 2000, estimated based on NCEP reanalysis. Other solid curves show the return period of flood heights for 2100, based on the projected RSL distributions and surge climatology projected by the various climate models(CNRM-CM3, GFDL-CM2.0, ECHAM5, and MIROC3.2). The dashed blue curve shows the return period of flood heights for 2100 based on the projected RSL of 2100 and the NCEP surge climatology (of 2000, neglecting the change of surge climatology from the baseline). The dash-dotted blue curve shows the return period of flood heights for 1800 based on the estimated RSL of 1800 and the NCEP surge climatology (of 2000, neglecting the change of surge climatology). The blue shading shows the 90% confidence interval of the 2000 NCEP curve (the statistical confidence interval for the other curves is similar). The red dashed lines highlight Sandy’s flood height of 2.8 m (horizontal) and Sandy’s estimated return period in 2000 of 398 y (vertical).

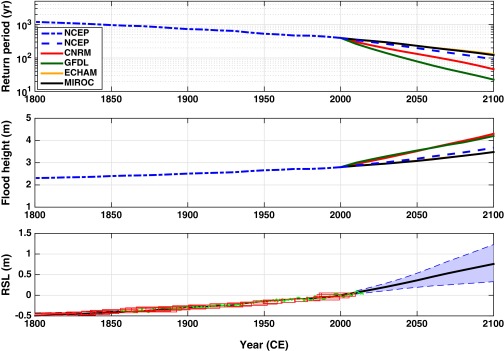
To better demonstrate the temporal evolution of the frequency and magnitude of Sandy’s flood in NYC, we display time series of the estimated return period for Sandy’s flood height (2.8 m) and flood height with Sandy’s estimated return period (398 y) from 1800 to 2100, along with the estimated/projected RSL (Fig. 2). Between 1800 and 2000, RSL in NYC rose by 50 ± 8 cm. During this same interval, global mean sea level rose by about 13 cm to 18 cm [14 cm in the 20th century and −1 cm to +4 cm in the 19th century, depending upon modeling assumptions (24)]. About half of the RSL rise in NYC was due to GIA [about 1.3 mm/y to 1.5 mm/y, or 26 cm to 30 cm total (24, 25)]. The remainder of the difference between NYC and global sea level likely reflects ocean dynamics. Under RCP 4.5, RSL rise in NYC over the course of the 21st century will likely (67% probability) be between 0.5 m and 1.0 m and will very likely (90% probability) be between 0.4 m and 1.2 m, with a “worst case” (1-in-1,000 probability) rise of 2.6 m (16). The projected RSL rise in NYC is higher than the projected global mean sea level rise (likely 0.5 m to 0.8 m under RCP 4.5) because of the combined effects of (i) GIA, (ii) potential changes in ocean dynamics (likely −5 cm to +23 cm over the 21st century under RCP 4.5), and (iii) increased sensitivity of RSL rise in NYC to mass loss from Antarctica (by about a factor of 20% for the West Antarctic Ice Sheet and 4% for the East Antarctic Ice Sheet). However, NYC experiences a less-than-global rise due to mass loss from Greenland (by about 60%) and glaciers (by about 40%) (16). Because of the accelerating rise in RSL, NYC’s flood hazard will increase more significantly over the 21st century than over the past two centuries. This effect of RSL rise may, again, be further intensified by the change of surge climatology, although relatively large uncertainty exists in the storm climatology projections by the GCMs [largely due to their very different projections of the storm frequency (9)].

Fig. 2.

Estimated temporal evolution of Sandy’s return period and flood height and of RSL from year 1800 to 2100 (relative to the sea level of the baseline year 2000). (Top) Return period of Sandy’s flood height of 2.8 m. (Middle) Flood height with Sandy’s estimated return period of 398 y (in 2000). As in Fig. 1, solid curves show the estimates accounting for the change in both RSL and surge climatology, and dashed and dash-dotted blue curves show the estimates accounting for only the change in RSL. (Bottom) Estimated past and projected future RSL (black solid curve, mean; shading, 5% to 95% quantile range). Annual mean sea level observed at the Battery tide gauge is shown by the green curve, and the proxy reconstruction from Barnegat Bay is represented by the red rectangles, showing 2σ vertical and geochronological uncertainties.

Discussion

The results of this analysis demonstrate how dramatically the frequency and magnitude of NYC’s extreme floods may increase over time, due to the compound effects of sea level rise and storm climatology change. The absolute value of the return period of extreme surges like Sandy (i.e., about 400 y), however, may be overestimated, because the physically based hurricane modeling (necessary for analyzing the impact of climate change) does not account for the effect of extratropical transition. With Hurricane Sandy as a pronounced example, a significant portion of tropical cyclones moving into high latitudes of the US Atlantic coast undergo extratropical transition (28); improved understanding of extratropical transition and its impact on surge hazard warrants future research.

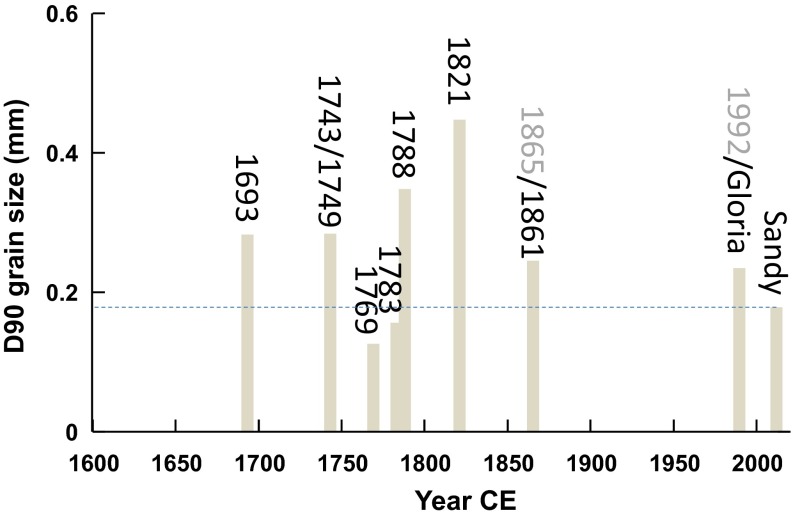
At least two well-documented hurricane strikes in NYC in the late 18th and early 19th centuries (1788 and 1821) (29, 30) likely resulted in storm surges similar to or greater than that of Hurricane Sandy. Moreover, based on a sediment record of coastal inundation events in the region (2), a series of coarse-grained flood-induced event beds were deposited over the last 350 y (Fig. 3). Absolute maximum water levels cannot be directly estimated from these storm deposits, but at least six of these event beds are coarser than the event bed associated with Hurricane Sandy, which suggests that these events had more energetic currents and/or waves capable of transporting coarser material. The combination of historical archives and geological proxies (see also ref. 30) points toward higher probabilities of extreme coastal flooding in NYC compared with estimates derived from physical modeling as in this study and from instrumental water level records (3).

Fig. 3.

Maximum grain size of event beds from Seguine Pond, Staten Island. D90 is the grain size (in millimeters) where 90% of the grains are finer. Likely storms responsible for each event bed are noted. Labels in black are historically documented hurricanes, and labels in gray are extratropical storms. (In some cases, definitive attribution is difficult because multiple events occur close together in time and, given age model uncertainties, more than one storm is a plausible candidate.) Six of the event deposits from the late 17th to 20th centuries are coarser than the deposit associated with Hurricane Sandy (dashed line). Data were obtained from the proxy record of ref. 2.

Estimating the return period of extreme flood events is challenging, and the process of risk analysis requires continuous updates wherein improved modeling and new data inform frequency estimates. Also, large uncertainties exist in GCM projections on both future storm activity and RSL rise, as shown in this study; future research should examine the GCMs on their capability to accurately project the key atmospheric and ocean variables that control hurricane activity and sea level dynamics. Ultimately, proxy storm records that span centuries to millennia, over various climate states, may provide critical information for evaluating model projections of both the frequency of extreme floods (31, 32) and how they change with the climate (33).

Methods

We apply the nine storm datasets generated by ref. 9 for NYC. The nine datasets were generated for the 1981–2000 climate estimated by NCEP reanalysis and the 1981–2000 and 2081–2100 climates estimated by each of the four GCMs. Each dataset includes 5,000 storms that pass within 200 km of the Battery with maximum wind speed greater than 21 m/s, with estimated annual frequency. These storms were generated with a statistical deterministic approach (10), which models the storm track and intensity deterministically given the storm environmental conditions, which in turn were simulated or sampled based on statistics. The model also estimates the storm radius of maximum wind deterministically, given an externally supplied storm outer radius (storm size). In ref. 9, the observed basin mean storm size was applied to all storms. In this study, we account for the variation of the storm size. For each storm, we sample the storm size from a statistical log-normal distribution (12) for the Atlantic basin and assume it is constant over the lifecycle of the storm [as it is observed not to change much over the storm lifetime (13)]. Then, we apply a recently developed theoretical wind model (13) that connects inner ascending and outer descending regions of the storm to estimate the radius of maximum wind from the storm outer size and intensity. With the updated storm characteristics, we use the same method as described in ref. 9 to estimate the storm surface wind and pressure to drive the storm surge simulation using a high-resolution hydrodynamic model (11).

The hydrodynamic modeling has been validated by previous studies (8, 9) and is relatively accurate (error < 10%) in simulating historical NYC surge events, including Hurricanes Irene and Sandy. It does not resolve relatively small factors such as wave setup, riverine flow, and stratification (34), as these conditions are either not defined for synthetic storms or too computationally demanding to incorporate for this case involving 45,000 simulations. Also, the current coastline and bathymetry are applied for the end-of-the-century simulations, and we focus on the first-order impact of climate change and sea level rise; future study may also investigate the effect of the long-term changes of the shoreline and estuaries (35).

Based on the simulated storm surge peaks at the Battery, we perform statistical analysis on each dataset. To obtain the storm surge CDF, we apply the peaks-over-threshold method to model the tail of the distribution with a generalized Pareto distribution, using the maximum likelihood method, and we model the rest of the distribution with nonparametric density estimation, as described in ref. 9. The statistical confidence intervals of the estimated return levels (estimated using the Delta Method as in ref. 9) are similar across the datasets and are relatively small, as very large numbers of numerical samples are applied.

Climate model projections can be biased, and thus they should be bias-corrected before applications. In particular, the GCM projected surge climatology should be unbiased before being combined with RSL distributions to estimate flood hazards. We bias-correct the storm frequency and storm surge CDF separately. We consider the storm frequency and storm surge CDF estimates based on the NCEP reanalysis to be accurate for the 1981–2000 climate. We unbias the GCM-projected storm frequency by multiplying it with a correction factor, which is simply the ratio of the NCEP-estimated frequency and GCM-estimated frequency for the 1981–2000 climate. We unbias the storm surge CDF through quantile−quantile mapping (15): The GCM-estimated surge CDF for the 1981–2000 climate is first matched with the NCEP-estimated surge CDF, generating a correction function depending on the quantile, which is then used to unbias the GCM-projected surge CDF for the 2081–2100 climate quantile by quantile.

The unbiased storm surge climatology is then interpolated over time and combined with RSL estimates to investigate the evolution of the flood hazard. The RSL estimates are 19-y running averages (16), and thus, here, we neglect the interannual variation of the sea level. Many previous studies (9, 36) have considered deterministic RSL estimates (e.g., 1 m or the 90th percentile). Here we incorporate the uncertainty in RSL estimates. We neglect the relatively small nonlinear interaction between the surge and RSL at the Battery (9, 36) and estimate the flood height (H^f) as the sum of surge (H) and RSL (S). The CDF of the flood height is then obtained simply through a convolution operation over the CDF of the surge and the PDF of RSL

$$P\left\{H^f\le h\right\}=P\left\{H+S\le h\right\}=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}P\left\{H\le h-s\right\}{f}_S\left(s\right)ds.$$ [1]

Then, assuming that, under a given climate, the storms arrive as a stationary Poisson process with the rate as the annual storm frequency λ, we estimate the (mean) return period of (storms with) floods exceeding level h as

$${\overline{T}}_{H^f}\left(h\right)=\frac{1}{\lambda \left(1-P\left\{H^f\le h\right\}\right)}.$$ [2]

We perform this analysis for every 10-y time point between 1800 and 2100 to obtain the time-varying flood height return periods.

The PDF of RSL for each decade over 2000–2100 is obtained simply through kernel density estimation using the 10,000 MC samples generated by ref. 16. To reconstruct past RSL over 1800–2000, we apply a spatiotemporal empirical hierarchical model developed by ref. 24. In this model, the sea level field is viewed as the sum of a time-varying, spatially uniform term g(t), a spatially varying, temporally linear term l(x)(t-t₀), and a temporally and spatially varying term m(x,t)

$$f\left(\mathbf{x},t\right)=g\left(t\right)+l\left(\mathbf{x}\right)\left(t-t_0\right)+m\left(\mathbf{x},t\right).$$ [3]

Individual observations y_i are modeled as noisy observations of f(x,t)

$$y_i=f\left({\mathbf{x}}_{\mathbf{i}},t_i\right)+w\left({\mathbf{x}}_i,t_i\right)+y_0\left({\mathbf{x}}_i\right)+\hspace{0.17em}{\epsilon }_i^y,$$ [4]

$$t_i={\widehat{t}}_i+{\epsilon }_i^t,$$ [5]

where x_i is the spatial location of observation i, t_i is its age, $w\left({\mathbf{x}}_i,t_i\right)$ is a white noise process that captures sea level variability at a subdecadal level (which we treat here as noise), ${\widehat{t}}_i$ is the mean observed age, ${\epsilon }_i^t$ and ${\epsilon }_i^y$ are errors in the age and sea level observations, and $y_0\left({\mathbf{x}}_i\right)$ is a site-specific datum offset. The terms g, l, m, w, and y₀ have mean zero Gaussian process priors with Matérn covariance functions. The covariance functions are characterized by hyperparameters reflecting prior expectations about the amplitude, spatial scale, and temporal scales of variability, which we set using a maximum likelihood method. To apply the model to the New York and New Jersey region, we use the high-resolution (1σ errors of approximately ±3 cm) Barnegat Bay, NJ, proxy record of ref. 25; the Common Era NJ proxy database of ref. 24, which has a lower resolution (approximately ±10 cm or more) but provides more extensive spatial coverage; and tide gauge data from the Battery, from Sandy Hook, Atlantic City, and Cape May, NJ, from Philadelphia, PA, from Lewes, DE, from Willets Point, Long Island, and from Bridgeport, CT. Results shown in the paper are for the site of the Battery tide gauge, and the PDF of RSL at each time point is Gaussian.

The effect of astronomical tide can be significant for flood risk, and it should be investigated in future research. This effect may be incorporated through applying joint probability analysis on the surge and tidal distributions (9) and accounting for the effects of surge-tide nonlinearity (9) and surge duration (4). If the tidal effect is included, Sandy’s return period based on its storm tide level (3.44 m) will be significantly longer than the return period estimated here based on its storm surge level (2.8 m), because Sandy’s surge peak at the Battery happened very unusually on the abnormal high tide. However, the tidal effect will not change with the climate, and thus the trend of flood frequency change will be similar.