Evidence from mixed hydrate nucleation for a funnel model of crystallization

Significance

Molecular crystallization, and its promotion and inhibition, is important across a broad range of fields. Previous work has asserted, although not substantiated, that crystallization and protein folding are somehow similar processes. Here, through detailed analysis of gas hydrate nucleation, we demonstrate that hydrate nucleation involves funnel-shaped potential energy landscapes, and put forth a funnel model of crystallization. This funnel model of crystallization provides a lens for exploring and understanding crystallization and potentially other ordering processes. We show that the phenomenological similarities between crystallization and protein folding result from underlying similarities between essential features of these microscopic ordering processes. This work thus provides a key connection between these two important but disparate research domains, thereby enabling knowledge advancement in both.

Abstract

The molecular-level details of crystallization remain unclear for many systems. Previous work has speculated on the phenomenological similarities between molecular crystallization and protein folding. Here we demonstrate that molecular crystallization can involve funnel-shaped potential energy landscapes through a detailed analysis of mixed gas hydrate nucleation, a prototypical multicomponent crystallization process. Through this, we contribute both: (i) a powerful conceptual framework for exploring and rationalizing molecular crystallization, and (ii) an explanation of phenomenological similarities between protein folding and crystallization. Such funnel-shaped potential energy landscapes may be typical of broad classes of molecular ordering processes, and can provide a new perspective for both studying and understanding these processes.

Molecular crystallization and its inhibition are important to a broad range of fields. For example, some organisms [such as Antarctic fish (1) and winter rye (2)] have developed a rich chemistry of antifreeze proteins to control internal freezing, and there is significant interest in exploiting antifreeze proteins for food applications (e.g., see ref. 3). Gas hydrate formation in oil and gas pipelines is a major industrial concern (4). For pharmaceuticals, there is much interest in understanding and controlling crystal polymorphism (e.g., see ref. 5). A better understanding of molecular crystallization, and factors influencing these processes, has potential to aid further advancements in such fields. As highlighted by a recent review on crystallization (6), traditional theoretical models of crystallization (e.g., classical nucleation theory) have proven to be problematic for a variety of systems and there remain technical challenges to studying crystallization both experimentally and computationally, so a clear understanding of crystal nucleation has yet to emerge.

Molecular crystallization is one of the major classes of molecular ordering processes. Other molecular ordering processes include micelle formation, the formation of coordination polymers, and protein folding. Previous work has asserted, although not substantiated, that crystallization and protein folding are somehow similar processes. For example, protein folding has been speculatively described as a first-order phase transition similar to liquid–solid transitions (7). It has also been proposed that both the water–ice transition and protein folding are difficult to study in silico because both are complex searches for relatively few ordered structures among numerous disordered alternative structures (8). The aim of this study is twofold: (i) to provide a conceptual description of molecular crystallization (simply referred to as crystallization henceforth), and (ii) to provide an explanation of the apparent similarities between crystallization and protein folding. On the basis of extensive simulations of the nucleation of a gas hydrate (i.e., a molecular solid) and detailed analysis of these simulations, it is herein demonstrated that hydrate nucleation involves funnel-shaped potential energy landscapes akin to those associated with protein folding, and it is proposed that funnel-shaped potential energy landscapes may be characteristic of other crystallization processes (e.g., ice nucleation). Funnel-shaped potential energy landscapes afford a conceptual framework for understanding crystallization.

Protein folding has been very successfully characterized in terms of funnel-shaped energy landscapes (i.e., the funnel model of protein folding) (9–11). For a protein, there are many high-energy conformations corresponding to unfolded structures, and relatively few low-energy conformations corresponding to native-like structures. The transition between these two regimes (i.e., protein folding) involves ordering in stages (e.g., creation of internal hydrogen bonds and the development of hydrophobic cores) so that there is a narrowing in the number of accessible conformations with decreasing system energy (10). Therefore, protein folding tends to involve funnel-shaped potential energy landscapes and ordering in stages. Free-energy barriers to protein folding can arise when decreases in energy associated with a protein moving deeper in the funnel are not sufficient to compensate for the entropic losses experienced by the system (9). Such a free-energy barrier can be visualized as the rapid narrowing in the width of the funnel such that the regions contiguous to the hole leading further down the funnel are essentially flat. An individual copy of a protein must spend time traversing this relatively energetically flat region of configuration space until it finds one of the comparatively few configurations through which it can proceed further down the funnel (10), i.e., the protein’s search is akin to a random walker. An individual copy of a protein will stochastically overcome such barriers. There are multiple pathways (i.e., routes) to the bottom of the funnel (9–11), such that different denatured copies of a protein can pass through different sets of microstates (i.e., specific arrangements) as they reconfigure to the protein’s native structure (10). The sides of the funnel can be rugged with local energy minima that can kinetically trap individual copies of the protein in nonnative structures (9, 10). Work with heteropolymers (i.e., model systems for protein folding) has revealed that kinetic traps can delay folding to native structures such that pathways involving kinetic traps have different kinetics compared with throughway pathways that proceed directly to native structures (12), as is illustrated by the moat funnel landscape in ref. 10. Thus, the role of multiple pathways and kinetic traps is important for understanding the kinetics of protein folding. In summary, three key characteristics of the funnel model of protein folding are (i) funnel-shaped potential energy landscapes and ordering in stages; (ii) barriers and stochasticity; and (iii) multiple pathways and kinetic traps.

To explore the possible connections between protein folding and crystallization, gas hydrate nucleation was studied. Gas hydrates are crystalline structures where water molecules form host lattices of polyhedral hydrogen bond cages that are occupied by small gas molecules (e.g., methane). Understanding hydrate formation is a pressing industrial issue. For example, hydrates often form plugs in oil and gas pipelines, and are a major concern at both onshore and offshore facilities (4). Chemical inhibitors are one of the key strategies for preventing hydrate formation; however, chemical inhibition can be costly (e.g., see ref. 13). A better molecular understanding of hydrate formation could, for example, support the development of improved inhibitors (4).

Despite significant interest, the molecular mechanism of hydrate nucleation is not fully understood (14). The molecular-level details of hydrate nucleation are beyond the spatiotemporal resolution limits of current experimental techniques. However, hydrate nucleation can now be reproducibly studied in silico with direct, unbiased simulations using atomistic water models (e.g., as in refs. 15–18). Comparable simulations of crystallization in other molecular systems are difficult (see ref. 6). For example, the direct calculation of ice nucleation rates for atomistic water models remained an open challenge until 2015 (19). Therefore, in contrast to other crystallization processes, gas hydrate nucleation is an industrially relevant crystallization process that is amenable to detailed investigation through simulation.

To probe hydrate nucleation, 10 independent 200-ns isobaric, isothermal simulations were performed at 50 MPa and 250 K for a system of 3,375 molecules that was 90% H₂O, 5% CH₄, and 5% H₂S. In all of the simulations, the initial configuration of the system was a CH₄/H₂S nanobubble in liquid water. Based on the models and conditions used in this study, the simulated system was metastable with respect to both the CH₄ and H₂S hydrate phases, but not with respect to hexagonal ice (see Supporting Information for a discussion of the system's metastability). Both CH₄ and H₂S favor the formation of the same hydrate phase (i.e., the sI hydrate structure) (20, 21). Additional methodological details concerning system preparation and the simulations are provided in Supporting Information.

During hydrate nucleation, a system’s potential energy decreases with approximately concurrent increases in both: (i) the number of water cages in the system, and (ii) system order according to molecular-level, water-based order parameters [e.g., the F₄ order parameter (22)]. This can be seen by comparing the time evolution of these properties for one of this study’s trajectories (e.g., see run 2 in Fig. 1 A–C) with structural snapshots from that trajectory (Fig. 1D). More detailed descriptions of the water cages of interest and average F₄ values are provided in Fig. 1 legend. Six of this study’s 10 simulations had nucleated and were in a growth regime by the time they had reached 200 ns (Fig. 1), and analysis of these 6 simulations will be the focus of the rest of this paper. Upon extension to 260 ns, three of the remaining trajectories had nucleated. These additional trajectories were used as a separate analysis test set and provide confirmation that the results for hydrate nucleation in this paper reasonably capture ensemble behavior (see Supporting Information, Fig. S1).

Fig. 1.

Time evolution of (A) potential energy, (B) average F₄ value, and (C) number of 5¹²6ⁿ – 4¹5¹⁰6^m cages in the 10 independent trajectories for the CH₄/H₂S nanobubble–liquid water system. The color scheme in A is also used for B and C. System-averaged F₄ values have been previously used to monitor hydrate nucleation in simulations (e.g., as in refs. 15, 16, 18, 23)_. F₄ is an order parameter that depends on the torsion angles between adjacent H₂O molecules and relates to the planarity of hydrogen bond rings (22). The mathematical details of the F₄ order parameter can be found in ref. 22. The average F₄ values for liquid water, the sI hydrate phase, and ice are −0.04, 0.7, and −0.4, respectively (24). The simulations contained insufficient CH₄ and H₂S to completely convert to a hydrate phase, and consequently could not attain F₄ values of 0.7. A 4^b5^c6^d cage has its water molecules arranged so that they form b quadrilateral, c pentagonal, and d hexagonal hydrogen bond rings. The 5¹²6ⁿ – 4¹5¹⁰6^m cages (where n = 0, 2, 3, 4 and m = 2, 3, 4) are associated with hydrate formation according to previous visual (25) and algorithmic (26) analysis. A modified version of the FSICA program (26) was used to detect cages and determine cage occupancies within the simulations. The potential energy, F₄, and cage population curves in this figure and the remainder of the paper are based on 1-ns averages as detailed in Supporting Information. (D) Snapshots of the nucleation process in run 2. The oxygen atoms of the water molecules comprising the largest cluster of 5¹²6ⁿ – 4¹5¹⁰6^m cages are connected by red tubes. CH₄ and H₂S within this cluster are blue and green spheres, respectively. The oxygen atoms of the water molecules that are not part of the cluster are small purplish-blue points.

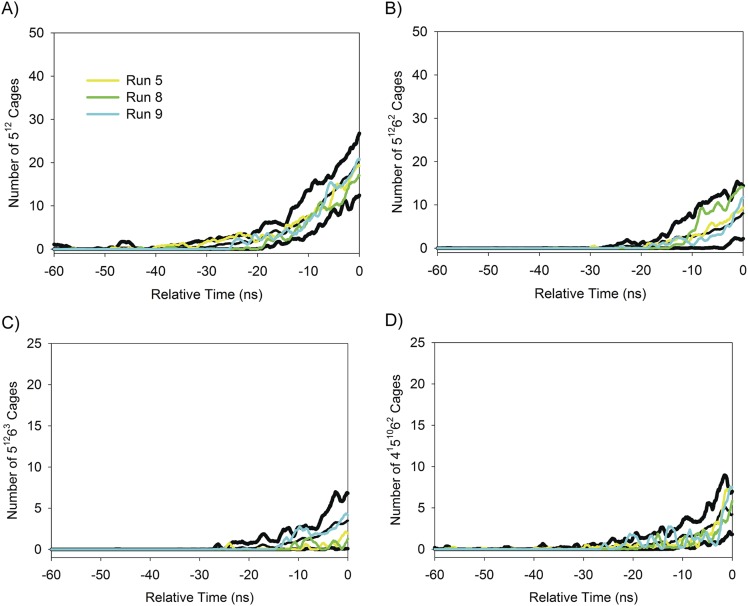
Fig. S1.

Time evolution of the number of (A) 5¹², (B) 5¹²6², (C) 5¹²6³, and (D) 4¹5¹⁰6² cages in the additional nucleating trajectories (i.e., runs 5, 8, and 9 from the original set of 10 simulations). For each cage type, the black curves in the panel represent the max-mean-min distribution for that cage type based on the original six nucleating trajectories (i.e., runs 1–4, 6, and 10). The color scheme in A is also used in B–D.

During nucleation, the changes in potential energy, number of 5¹²6ⁿ – 4¹5¹⁰6^m cages, and average F₄ value are not completely simultaneous. This can be seen based on the normalized curves in Fig. 2A where changes in potential energy precede changes in the average F₄ value, which in turn precede changes in the number of cages. This behavior is expected because lower-order structure (e.g., as captured by the F₄ order parameter) must be present if higher-order structures (e.g., cages) are to form. This staged description of hydrate nucleation is consistent with previous work (27, 28). For example, see figure 14C in ref. 27, although the authors did not interpret their results as such. More importantly, several of the plotted order parameters in ref. 27 are different from those used in this study, which highlights that the staged nature of hydrate nucleation is not dependent on the particular order parameters used to track hydrate nucleation. This evidence confirms that hydrate nucleation exhibits ordering in stages as system potential energy decreases. This is a key part of characteristic (i) of protein folding funnels as described above.

Fig. 2.

Comparing nucleating trajectories. (A) Superimposed normalized potential energy, average F₄, and 5¹²6ⁿ – 4¹5¹⁰6^m cage curves for one nucleating trajectory (run 1 in Fig. 1). The potential energy curve has been inverted to facilitate comparisons. (B) Temporally aligned average F₄ curves for the nucleating trajectories exhibiting excellent overlap during nucleation, i.e., the t_relative < zero-ns regime. Relative times provide a temporal frame of reference for comparing the nucleating trajectories. (C) The number of each of the 5¹²6ⁿ – 4¹5¹⁰6^m cages during nucleation as averaged across the six nucleating trajectories. (D) Occupancy of 5¹²6ⁿ – 4¹5¹⁰6^m cages during nucleation as averaged across the nucleating trajectories. (E) The max-mean-min distributions for the number of 5¹² and 5¹²6² cages during hydrate nucleation. The max-mean-min distribution for a given cage type is a set of three curves indicating the evolution of the maximum, mean, and minimum number of that particular cage type across the set of aligned nucleating trajectories. (F) The decreasing relative standard deviations in the numbers of 5¹² and 5¹²6² cages among the aligned trajectories as nucleation and growth proceed. The average curves and max-mean-min distributions in C–E are based on the analysis of over 49,000 configurations from 6 nucleating trajectories.

To help further elucidate the general mechanistic features of hydrate nucleation and its similarities to protein folding, it is advantageous to compare nucleation behavior within the set of nucleating trajectories in Fig. 1. Such comparisons require a mechanism for temporally aligning nucleating trajectories given that the process of interest does not occur at the same time within each trajectory, a common challenge with stochastic processes. The F₄ curves are an appropriate basis for temporally aligning the nucleating trajectories. First, the F₄ curves are apparently more sensitive to the early structural changes during nucleation than cage populations (Fig. 2A). Second, the F₄ curves are less sensitive to nonhydrate system fluctuations than the potential energy curves (e.g., the potential energy curves depend on the evolution of the CH₄/H₂S nanobubble in addition to the structuring of the aqueous phase). Therefore, the F₄ curves were leveraged to temporally align the trajectories using the following procedure.

A four-parameter sigmoidal fitting was applied to each trajectory’s F₄ curve in Fig. 1B. These sigmoidal fits had R² values greater than 0.99. For each trajectory, the time corresponding to the inflection point of the F₄ curve’s sigmoidal fit was subtracted from the trajectory’s simulation times yielding relative times. Zero ns in this alternative temporal frame of reference has a universal meaning, namely the point in time of fastest ordering in the nucleating trajectories with respect to the F₄ order parameter. The temporally aligned F₄ curves for the nucleating trajectories have excellent overlap, particularly for t_relative < 0 ns, as can be seen in Fig. 2B. Given the definition of t_relative = 0 ns, nucleation occurs when t_relative < 0 ns, so the focus of the remaining analysis is on the nucleating trajectories in the t_relative < 0 ns regime.

According to Fig. 2C, hydrate nucleation in the CH₄/H₂S nanobubble system is typically associated with first the appearance of 5¹² cages, then 5¹²6² cages, and then both 5¹²6³ and 4¹5¹⁰6² cages approximately simultaneously. During the early stages of hydrate formation, the average populations of these cages are in the same order as their appearance, namely 5¹² > 5¹²6² > 5¹²6³ ≅ 4¹5¹⁰6². For the simulated system, the thermodynamically favored hydrate crystal structure, sI, consists of only 5¹² and 5¹²6² cages. The appearance of a variety of cages stems from the lower entropic penalty associated with transitioning from the liquid to a slightly disordered lattice rather than directly to the fully ordered thermodynamically favored structure.

Entropy can also play a critical role in the appearance of specific cage types. For example, 5¹² cages are highly symmetric, and each consists of 20 H₂O molecules, the same as the average hydration number of aqueous methane (29). Other 5¹²6ⁿ – 4¹5¹⁰6^m cages have more water molecules, lower symmetry, or both. Therefore, 5¹² cages are structurally more consistent with the aqueous phase and have higher degeneracy, so there would be a smaller entropic penalty associated with their formation. However, space-filling structures cannot be created from 5¹² cages alone, so the formation of a hydrate structure requires the appearance of additional cages. Meanwhile, 5¹²6² cages have higher symmetry than 4¹5¹⁰6² cages and contain fewer water molecules than 5¹²6³ cages, so the earlier formation of 5¹²6² cages is expected to be entropically favorable. The remaining 5¹²6ⁿ – 4¹5¹⁰6^m cages are either larger or have lower symmetry than 4¹5¹⁰6² and 5¹²6³ cages, and hence appear later. Large cages (e.g., 5¹²6⁴ cages) are not expected to have large populations because these cages have volumes that exceed the sizes of CH₄ and H₂S. In turn, their formation entails the creation of excess and larger void volumes. Void volumes, i.e., cavities, are unfavorable in aqueous environments (e.g., see ref. 30). This latter point is emphasized by the rarity of empty cages as can be seen in Fig. 2D. Therefore, the staged appearance of cage types and cage occupancy stems from the tendency of water molecules to rearrange to form the hydrate phase so that entropic penalties are minimized, i.e., hydrate nucleation proceeds so that a system’s phase-space manifold connecting the solution and hydrate macrostates encompasses the maximum possible number of microstates. Previous work has described this manifold as the “reactive tube” along the hydrate nucleation pathway (31). The potential energy landscape for nucleation would then be a projection of the microstates encompassed by this manifold as a function of the system’s potential energy.

The existence of multiple microstates at each stage along the solution–hydrate transition implies that there can be stochastic differences in the exact number of each cage type for any specific trajectory as nucleation proceeds. This variation is highlighted by the max-mean-min distributions for the 5¹² and 5¹²6² cages in Fig. 2E. However, among the nucleating trajectories, the relative standard deviations in the populations of 5¹² and 5¹²6² cages decrease as the trajectories progress along the solution–hydrate transition (Fig. 2F). This apparent structural convergence implies that the manifold of accessible microstates, i.e., the potential energy landscape, narrows as the hydrate macrostate is approached. However, cages do not fully capture the solution–hydrate transition because there exist early stages along this transition where the system is ordering at the molecular level and cages have yet to appear (see the F₄ and cage curves in Fig. 2A).

Convergence among the trajectories is also observed in the properties of the individual water molecules, which can probe all stages along the solution–hydrate transition. S_g is a water-based order parameter sensitive to local tetrahedral structure (32), as is described in Fig. 3 legend. The S_g probability distributions before and after hydrate nucleation are provided in Fig. 3A. The narrowing and shifting of the S_g probability distribution reveals that there is decreased variation in the local arrangements of water molecules following nucleation and that the water molecules form more tetrahedral arrangements. This transition begins at approximately t_relative = −25 ns, and there is a marked change in apparent behavior at approximately t_relative = −10 ns (Fig. 3B). The former coincides with the approximate appearance of 5¹²6ⁿ – 4¹5¹⁰6^m cages whereas the latter occurs as the maximum formation rate of these cages is approached (compare Figs. 3B and 2D). Therefore, S_g probability distributions are sensitive to the formation of the hydrate phase while also probing the behavior of the solution phase. The probability distribution for the translational mean-squared displacement (MSD) values of the water molecules also sharpens and shifts to lower values during the nucleation process as can be seen in Fig. 3C, and as is expected for a solution–hydrate transition. However, this sharpening occurs more gradually than for the S_g distribution as can be seen by comparing Fig. 3D with Fig. 3B. Previous work has indicated that gas hydrate nucleation proceeds with the formation of solvent-separated guest molecules and water molecule rearrangement to yield cages (33). Therefore, the early reductions in the MSD values of the water molecules, without commensurate changes to the tetrahedral ordering of the aqueous phase, may be indicative of early stage ordering of guest molecules in the aqueous phase.

Fig. 3.

Evolution of molecular property distributions during nucleation. (A) The probability distribution for the S_g values of water molecules at t_relative = −50 ns and t_relative = 0 ns. The distributions have been calculated using the 10-ps average configurations from all of the nucleating trajectories for the stated relative times. The S_g order parameter reflects the degree to which the four nearest neighbors of a water molecule exhibit tetrahedrality with S_g values closer to 0 indicating increased tetrahedrality (30). The mathematical details of the S_g order parameter can be found in ref. 30. The average S_g values for ice and liquid water are 0.0117 and 0.100, respectively (30). (B) The temporal evolution of the relative probability distribution of S_g values. For a given point in time, S_g values with probabilities approaching that of the most probable S_g value for that point in time (e.g., ∼0.03 for t_relative = −50 ns based on A) are black whereas S_g values of decreasing relative probability are increasingly green. The S_g probability distribution was sampled every 0.5 ns in the interval of t_relative = −50 to 0 ns. Like A, B is based on the analysis of 10-ps average configurations from all of the nucleating trajectories for the stated relative times. (C) The probability distribution of the translational MSD values of water molecules at t_relative = −50 ns and t_relative = 0 ns. The line types are the same as in A. (D) The temporal evolution of the relative probability distribution of MSD values. The relative probabilities are color encoded the same way as for B. The MSD values used to construct C and D correspond to the variances in the water molecule positions for the 10-ps average configurations used to construct A and B, respectively. (E) The systemic decrease in potential energy during hydrate formation. The color scheme is the same as in Fig. 2B.

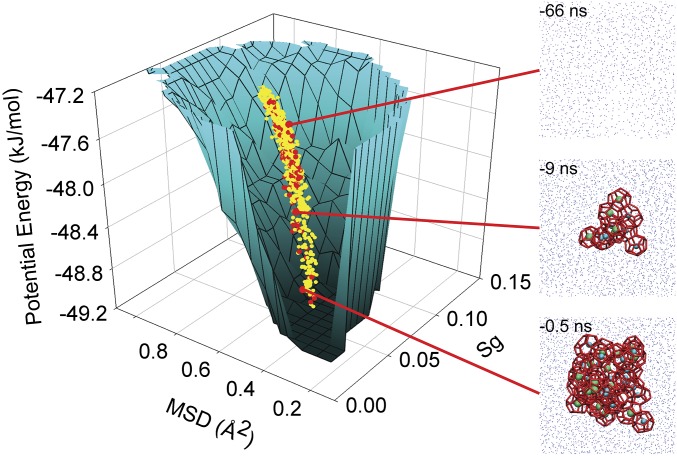
During hydrate nucleation, the number of microstates sampled by the system as a whole can be expected to depend on the number of molecular microstates readily accessible to the water molecules. Molecular property distributions are indicative of the accessible molecular microstates. As the molecular property distributions are narrowing, the potential energy of the system is decreasing as can be seen by comparing Fig. 3E with Fig. 3 A–D. Fig. 4 then captures this funneling of molecular properties with lower system potential energies. This funneling is observed for other molecular properties beyond those in Fig. 4 provided that these properties are reasonably chosen (see Fig. S2 for another funnel based on two other properties of the water molecules). As a system descends deeper into the funnel, hydrate structures begin to appear as is highlighted in Fig. 4 by the molecular configuration insets on the right-hand side. By extension of the funnel in Fig. 4, the system will have more accessible microstates during the solution–hydrate transition the closer the system is to the high-energy fluid macrostate and relatively fewer as it approaches the hydrate macrostate. However, as system descriptors, molecular property distributions lack the specificity of individual system microstates, so the system’s potential energy landscape will necessarily be more complex than the molecular properties funnel shown in Fig. 4. Therefore, hydrate nucleation is ordering in stages involving funnel-shaped potential energy landscapes, and fully satisfies characteristic (i) of the funnel model of protein folding as described above.

Fig. 4.

Funneling of molecular properties during hydrate nucleation. For each nucleating trajectory, average configurations were calculated using a 10-ps averaging window at every 0.5-ns point within the time interval of t_relative = −72.5 ns to t_relative = 0 ns. These average configurations were histogramed according to their corresponding system potential energies. Then, for the set of configurations within a given potential energy range, the water molecules of those configurations were histogramed according to their S_g and MSD values (see Fig. 3 for a description of S_g and MSD values). This yielded a 3D histogram based on the analysis of more than 2.5 million water molecules from 876 configurations. For each potential energy interval, the illustrated surface bounds the set of (S_g, MSD) values that are readily accessible to the water molecules, i.e., have a relative probability ≥5% compared with the most probable (S_g, MSD) values for that potential energy interval. The surface is color encoded so that low and high system potential energies are black and cyan, respectively. The central dots indicate how the trajectories move through the (S_g, MSD, system potential energy)-space based on the average MSD and S_g values for the configurations comprising the trajectories. The red and yellow points correspond to run 2 and all of the other nucleating trajectories, respectively. The molecular configurations on the right represent the system in run 2 when it has reached the enlarged and attached red points. These configurations have the same visual encoding as those in Fig. 1D, and the time stamps on the configurations are relative times.

Fig. S2.

Alternative view of the funneling of molecular properties during hydrate nucleation. The surface was constructed using the same approach as Fig. 4, but using different water molecule properties (the rotational RMSD and S_k order parameter). The S_k order parameter (an alternative to the S_g order parameter) measures the tetrahedrality of neighboring water molecules with an S_k value of 0 corresponding to perfectly tetrahedral local arrangements (32). The surface bounds the set of readily accessible (rotational RMSD, S_k) values for the water molecules, i.e., those values that have a relative probability of ≥5% compared with the most probable (rotational RMSD, S_k) values for a given potential energy interval. The surface has been partially clipped at the front to show the interior of the funnel.

The stochastic nature of hydrate nucleation can be explained within a funnel model by assuming that its funnel-shaped potential energy landscape, similar to proteins, has a relatively flat upper portion corresponding to the solution macrostate and a comparatively narrow lower region leading to the hydrate macrostate. Like proteins, individual trajectories will stochastically diffuse across the flat upper region of the funnel until they encounter structures through which they can descend deeper into the funnel. Related to this, estimates of hydrate critical nuclei based on simulations indicate that a hydrate system’s nucleus can have a variety of structures at the apparent hydrate nucleation transition state (28), which is similar to how protein-folding transition states are characterized as ensembles of protein conformations (9). Therefore, the funnel-shaped potential energy landscapes associated with hydrate nucleation apparently exhibit barriers and stochasticity, characteristic (ii) of the funnel model of protein folding as described above.

Hydrate nucleation also exhibits multiple pathways and kinetic traps, characteristic (iii) of the funnel model of protein folding as described above. The hydrate nuclei in this study sample somewhat different structures as nucleation progresses (e.g., see Fig. 2E). Given that amorphous hydrate nuclei can be annealed to more crystalline structures (16, 34, 35), it can be inferred that the potential energy landscape for a hydrate-forming system is rugged with kinetic traps, i.e., local minima, corresponding to amorphous structures, and that these kinetic traps impeded the nucleating trajectories in this study from achieving the sI crystal structure. In the gas hydrate literature, it has been proposed that there are multiple pathways to the crystalline hydrate state which may or may not involve amorphous intermediates (18). Whether or not individual trajectories form amorphous structures would depend on how these trajectories enter and descend the funnel with some pathways leading more directly to the crystalline hydrate phase than others. Therefore, hydrate nucleation involves funnel-shaped potential energy landscapes with many topological similarities to those of protein folding, which explains the phenomenological similarities between protein folding and crystallization.

For the protein community, the funnel model of protein folding provided a new view on the phenomenon and a conceptual framework for understanding protein folding kinetics (10). Crystallization funnels can similarly now form a conceptual framework for interpreting crystallization and nucleation phenomenology, which should aid future work. To highlight this framework, funnel-shaped potential energy landscapes will now be used to: (i) compare hydrate and ice nucleation (i.e., two ordering processes involving hydrogen-bond networks of water), and (ii) interpret the results of previous studies on ice nucleation. Small clusters of water molecules have been demonstrated to have rugged, funnel-shaped potential energy landscapes (e.g., see figure 5 in ref. 36); therefore, it is reasonable to conjecture that: (i) ice nucleation involves a funnel-shaped potential energy landscape, and (ii) this landscape is rugged, even though this funnel has yet to be extracted.

Ice nucleation is apparently far more difficult to study in silico than hydrate nucleation. This may seem unexpected given that hydrate nucleation represents a multicomponent crystallization process. Ice nuclei are almost solely comprised of double-diamond and hexagonal water cages as illustrated in figures 5 and 6 of ref. 19, whereas hydrate nuclei contain many more different types of water cages (25, 26, 35). From the perspective of combinatorics, there are many more possible hydrogen-bond structures for hydrate nuclei than there are for ice nuclei. Therefore, the regions of an ice-forming system’s potential energy landscape that correspond to nucleation and crystal growth are narrower than those of a hydrate-forming system (assuming that there is a sufficient concentration of guest species in the latter to induce hydrate nucleation). In contrast, the metastable liquid regions of the ice-forming system’s potential energy landscape are wider than those of the hydrate-forming system. The presence of hydrophobic solutes (e.g., CH₄) in the metastable liquid aqueous phase of the hydrate-forming system results in a more structured liquid aqueous phase compared to pure liquid water. This can be seen in Fig. 3B where, before hydrate nucleation, the most probable S_g values for the water molecules in this study’s hydrate-forming system are already significantly lower than the S_g value of 0.100 for liquid water (32).

Therefore, an ice nucleation simulation would appear to involve a greater search problem than a comparable hydrate nucleation simulation. The ice nucleation trajectory is less confined as it meanders through the fluid portion of its potential energy landscape, and is simultaneously searching for a smaller target. Ice nucleation in pure water systems is thus a significantly rarer event than hydrate nucleation in multicomponent guest–water systems of appropriate local composition. The ice search is further hindered by the comparatively slower dynamics in ice nucleation simulations arising from the lower temperatures used to probe ice nucleation in silico. Taken together, these factors render ice nucleation more difficult to study in silico.

The behavior of supercooled water is still not fully understood, particularly in “no man’s land” (i.e., water at temperatures between its homogeneous nucleation temperature and its glass transition temperature). For example, there exists a temperature (T) in no man’s land below which liquid water is not metastable (37). Funnel-shaped potential energy landscapes can provide a conceptual framework for explaining observed phenomenology in the vicinity of T.

Given that the liquid water macrostate of a pure water system is associated with more, higher-energy microstates than the ice macrostate, the liquid water macrostate will experience a greater reduction in its number of accessible microstates as the system is quenched toward T. Therefore, the excess entropy of liquid water compared to ice decreases as T is approached (37), and the system cannot access as much of the upper regions of the funnel. The system is thus more likely to encounter microstates leading to the lower regions of the funnel as temperature is decreased, so the formation rate of ice increases as temperature is decreased toward T (as was observed in ref. 37). As the system is quenched below T, the accessible portion of the upper region of the funnel is sufficiently small that the system samples, with comparable likelihood, both liquid-like microstates and microstates that lead to the lower regions of the funnel. Therefore, liquid water is no longer metastable with respect to ice, and crystallization can occur more rapidly than the relaxation of liquid water (37). The system’s exploration of the funnel is now corresponding to spinodal-like behavior. However, the funnel is rugged with local minima. This is why vitrified low-density amorphous ice forms upon rapid quenching of aqueous systems (37). Below T, the overall ice formation rate is dependent on the rate at which the system can escape the funnel’s local minima, and so lowering the system’s temperature beyond T reduces the formation rate of ice (as was observed in ref. 37). Therefore, the formation rate of ice reaches a maximum at T, and this can be explained in terms of how water systems explore their funnel-shaped potential energy landscapes.

Through extensive simulations and detailed analysis of hydrate nucleation, this study has revealed that the potential energy landscapes of hydrate-forming systems are funnel shaped. Hydrate nucleation is still not fully understood (14), so the conceptual framework of funnel-shaped potential energy landscapes offers an important tool in advancing the community’s understanding of hydrate nucleation, a process relevant to several areas in science and technology. Through a comparison of hydrate nucleation and protein folding, it was demonstrated that the phenomenological similarities of these processes are indicative of similarities in the features of their underlying potential energy landscapes. To demonstrate the conceptual power of funnel-shaped potential energy landscapes, the features of these landscapes were used to rationalize: (i) differences between hydrate and ice nucleation, and (ii) behavior of low-temperature water. Whereas ice nucleation was conjectured to involve a funnel-shaped potential energy landscape, future work is needed to demonstrate and probe this funnel. Funnel-shaped potential energy landscapes may be applicable to many other crystallization processes, and perhaps other molecular ordering phenomena (e.g., the formation of metal-organic frameworks or micelles). Future work should explore the topologies of the potential energy landscapes associated with these processes. These topologies are expected to be diverse [as is thought to be the case for proteins (10)], and to reflect the rich phenomenology of crystallization and ordering processes. With the common conceptual framework of funnel-shaped potential energy landscapes, there are greater opportunities for both the protein and physical chemistry communities to reappropriate and share concepts and techniques, which should promote their mutual advancement. For example, crystallization processes may have equivalents to the secondary, tertiary, and quaternary structures of proteins. There are still many open challenges in crystallization and protein folding research, and the connections made in this article will empower researchers with a fresh perspective as they embark in this research.

Methodological Details of the Simulations

Model Details.

H₂O was represented with the TIP4P/2005 model (38). CH₄ was simulated using a united atom model with Lennard-Jones parameters of ε = 1.22927 kJ/mol and σ = 3.700 Å as has been previously used in hydrate simulations (39). H₂S was represented using the four-site H₂S model developed by Forester et al. (40) with the H–S bond distance set to 1.34 Å. All of the models are rigid, so appropriate rigid-body dynamics were used for the simulations (specifically, the quaternion-based leapfrog algorithm designated RVV1 in ref. 41).

Computational Details.

Electrostatics interactions were calculated using smooth particle mesh Ewald (42) with a tolerance of 10⁻⁵. Eighth-order splines were used for interpolation, and the real-space cutoff was set to 8.0 Å. A 10.0-Å cutoff was used for Lennard-Jones interactions, and geometric combining rules were used for the Lennard-Jones cross-terms. Temperature was regulated using a four-member Nosé–Hoover chain thermostat (43, 44) with 1-ps coupling constants. Pressure was regulated using an isotropic Berendsen barostat (45) with β = 4.5 × 10⁻⁵ bar⁻¹ and a relaxation time of 100 fs.

System Preparation.

The CH₄, H₂S, and H₂O molecules were arranged on a cubic lattice in a cubic simulation cell such that: (i) the CH₄ and H₂S formed an approximately spherical nanobubble surrounded by pure water, and (ii) the bubble had a CH₄ core and a H₂S shell. The system was then equilibrated at 300 K and 50 MPa for 100 ns to ensure equilibration of the nanobubble and aqueous phases. The system was then quenched sequentially to 290, 280, and 270 K. For these temperature quenches, the system was simulated for 10, 10, and 20 ns, respectively. At the start of the 270 K quench, the velocities of the molecules were randomized to produce 10 independent trajectories. At the end of the 270 K simulations, the 10 independent trajectories were quenched to 250 K for production run simulations. This quench scheme was used to minimize the convolution of the nucleation behavior at 250 K with other possible nonequilibrium system behavior.

The production run simulations at 250 K were metastable with respect to both the H₂S and CH₄ hydrates, but not ice. For the H₂O and H₂S models used in this study, the pure H₂S hydrate has a dissociation temperature of 290.9 ± 5.2 K at 10 MPa (46). Based on the work of Conde and Vega (47), the CH₄ hydrate/H₂O_(l)/CH_4(g) three-phase coexistence temperature is ∼277 K at 50 MPa when using the TIP4P/2005 water model and a united atom CH₄ model in conjunction with Lorentz–Berthelot rules to calculate the Lennard-Jones parameters for the H₂O–CH₄ interaction. Based on the most up-to-date phase diagram for the TIP4P/2005 water model (48), the melting temperature of ice at 50 MPa is just below 250 K.

Analysis Details

Data Processing for Figures.

The average F₄ value and cage analyses were performed for each simulation using configurations that had been saved every 10 ps. All F₄ and cage curves in the paper are 1-ns rolling averages. The potential energy curves are based on sequential, nonoverlapping 1-ns block averages. System configurations were visualized using VMD (49).

Distribution Sampling.

The analysis presented in the paper focused on 6 nucleating trajectories from an initial set of 10 independent trajectories. To verify the representative nature of the distributions presented in the paper, particularly the cage distributions, the remaining four trajectories were extended to 260 ns, by which time three of them had undergone nucleation. For these additional nucleating trajectories, their cage population curves during nucleation (i.e., t_relative < 0 ns) are essentially bounded by the max-mean-min cage distributions determined from the original set of six nucleating trajectories as can be seen in Fig. S1. This indicates that a relatively small number of trajectories are needed to achieve qualitative convergence in the cage distributions during nucleation. The molecular distributions in Figs. 3 and 4 of the paper are based on large numbers of individual particle values, and are thus relatively well converged. Therefore, the hydrate nucleation results presented in the paper are expected to be reasonably representative of ensemble behavior.

Funneling of Molecular Properties.

Another representation of the funneling of molecular properties during hydrate nucleation was created using the rotational root-mean-squared-displacement (rotational RMSD) and S_k (32) values of the water molecules (instead of their MSD and S_g values) while leveraging an otherwise the same histogramming procedure as the one described in Fig. 4 legend. This funnel is provided in Fig. S2, and overall shows a funnel shape similar to Fig. 4.