Inferring interaction partners from protein sequences

Significance

Specific protein−protein interactions play crucial roles in the stability of multiprotein complexes and in signal transduction. Thus, mapping these interactions is key to a systems-level understanding of cells. Systematic experimental identification of protein interaction partners is still challenging. However, a large and rapidly growing amount of sequence data is now available. Is it possible to identify which proteins interact just from their sequences? We propose an approach based on sequence covariation, building on methods used with success to predict the three-dimensional structures of proteins from sequences alone. Our method identifies specific interaction partners with high accuracy among the members of several ubiquitous prokaryotic protein families, and provides a way to predict protein−protein interactions directly from sequence data.

Abstract

Specific protein−protein interactions are crucial in the cell, both to ensure the formation and stability of multiprotein complexes and to enable signal transduction in various pathways. Functional interactions between proteins result in coevolution between the interaction partners, causing their sequences to be correlated. Here we exploit these correlations to accurately identify, from sequence data alone, which proteins are specific interaction partners. Our general approach, which employs a pairwise maximum entropy model to infer couplings between residues, has been successfully used to predict the 3D structures of proteins from sequences. Thus inspired, we introduce an iterative algorithm to predict specific interaction partners from two protein families whose members are known to interact. We first assess the algorithm’s performance on histidine kinases and response regulators from bacterial two-component signaling systems. We obtain a striking 0.93 true positive fraction on our complete dataset without any a priori knowledge of interaction partners, and we uncover the origin of this success. We then apply the algorithm to proteins from ATP-binding cassette (ABC) transporter complexes, and obtain accurate predictions in these systems as well. Finally, we present two metrics that accurately distinguish interacting protein families from noninteracting ones, using only sequence data.

Many key cellular processes are carried out by interacting proteins. For instance, specific protein−protein interactions ensure proper signal transduction in various pathways. Hence, mapping specific protein−protein interactions is central to a systems-level understanding of cells, and has broad applications to areas such as drug targeting. High-throughput experiments have recently elucidated a substantial fraction of protein−protein interactions in a few model organisms (1), but such experiments remain challenging. Meanwhile, there has been an explosion of available sequence data. Can we exploit this abundant new sequence data to identify specific protein−protein interaction partners?

Specific interactions between proteins imply evolutionary constraints on the interacting partners. For instance, mutation of a contact residue in one partner generally impairs binding, but may be compensated by a complementary mutation in the other partner. This coevolution of interaction partners results in correlations between their amino acid sequences. Similar correlations exist within single proteins, for example, between amino acids that are in contact in the folded protein. However, the simple fact of a correlation between residues in a multiple sequence alignment is only weakly predictive of a 3D contact (2–4), as correlation can also stem from indirect effects. Fortunately, global statistical models allow direct and indirect interactions to be disentangled (5–7). In particular, the maximum entropy principle (8) specifies the least-structured global statistical model consistent with the one- and two-point statistics of an alignment (5). This approach has recently been used with success to determine 3D protein structures from sequences (9–11), to predict mutational effects (12–14), and to find residue contacts between known interaction partners (7, 15–19). Pairwise maximum entropy models have also been used productively in various other fields (20–26).

Here we present a pairwise maximum entropy approach that uses sequence data to predict interaction partners among the paralogous genes belonging to two interacting protein families. We use histidine kinases (HKs) and response regulators (RRs) from prokaryotic two-component signaling systems (Fig. 1A) as our main benchmark. Two-component systems constitute a major class of pathways that enable bacteria to sense and respond to environment signals. Typically, a transmembrane HK senses a signal, autophosphorylates, and transfers its phosphate group to its cognate RR, which induces a cellular response (28). Most HKs are encoded in operons together with their cognate RR, so interaction partners are known, which enables us to assess performance. There are often dozens of paralogs of HKs and RRs in each genome, making prediction of interaction partners from sequences alone highly nontrivial.

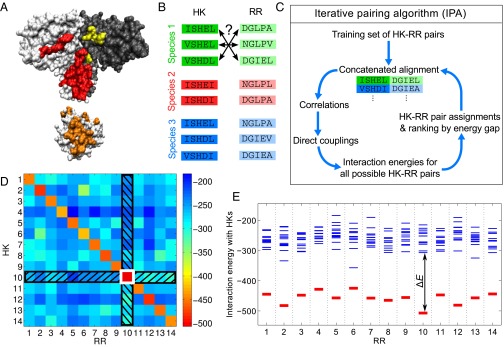
Fig. 1.

Iterative pairing algorithm (IPA). (A) Surface representations of an HK dimer (top) and an RR (bottom), from a cocrystal structure (27); the HK−RR contacts in each molecule are highlighted in color. (B) To correctly pair HKs and RRs in each species from their sequences alone, we start from multiple sequence alignments of HKs and RRs, including 64 amino acids from the HK and 112 from the RR. (C) Schematic of the main steps of the IPA. (D and E) Example of HK−RR pair assignment and ranking by energy gap for one species. (D) Color map of the matrix of HK−RR interaction energies in E. coli K-12 MG1655 from the final iteration of the IPA performed on our standard dataset, with a training set of $N_{\text{start}}=100$ HK−RR pairs, and an increment step of $N_{\text{increment}}=200$ pairs. As in every IPA iteration and every species, the pair with the lowest interaction energy is selected first (here, HK 10 and RR 10, boxed in white), and this HK and RR are removed from further consideration (black hatches). Then, the next pair with the lowest energy is chosen, and the process is repeated until all HKs and RRs are paired. (E) Energy spectrum from D, showing the interaction energies with all of the HKs for each RR, with the correct HK−RR pairs shown in red. The energy gap $\mathrm{\Delta }E$ is shown for RR 10. A confidence score based on the energy gap is used to rank all assigned HK−RR pairs, and this ranking is exploited to build the CA for the subsequent IPA iteration. See Materials and Methods for details.

To address this challenge, we developed an iterative pairing algorithm (IPA) (Fig. 1) that pairs proteins based on their effective interaction energies as predicted by a pairwise maximum entropy model. At each iteration, the highest-scoring predicted HK−RR pairs are incorporated into the concatenated sequence alignment from which the model is built. This yields a major increase of predictive accuracy through progressive training of the model. First, we consider the case where the IPA starts with a training set of known HK−RR partners. We obtain good performance even with few training pairs. Then, we show that the IPA can make accurate predictions starting without any known pairings, as would be needed to predict novel protein−protein interactions. We trace the origin of this success to the preferential recruitment of new correct pairs by those already in the concatenated alignment (CA). We also demonstrate how multiple random initializations can be leveraged to improve performance. We show that our algorithm works more generally by successfully applying it to ATP-binding cassette (ABC) transporter proteins. Finally, we develop two IPA-based methods that distinguish interacting protein families from noninteracting ones, using only sequence data.

Results

IPA.

We have developed an iterative method to predict interaction partners among the paralogs of two protein families in each species, using just their sequences (Fig. 1 A and B). In each iteration (Fig. 1C and Materials and Methods), we compute correlations between residues from a CA of paired sequences. The initial CA is either built from a training set of correct protein pairs or made from random pairs, assuming no prior knowledge of interacting pairs. We then infer couplings for all residue pairs using a pairwise maximum entropy model built from the CA using a mean-field approximation (9, 29). We calculate the interaction energy for every possible protein pair within each species by summing the interprotein couplings assigned by the model. Such “energies” capture evolutionary correlations, and correlate to physical energies for lattice proteins (30). Using these interaction energies, we predict protein pairs [assuming one-to-one specific HK−RR interactions (28), Fig. 1D]. We attribute a confidence score to each predicted protein pair, using the energy gap between this pair and the next best alternative (Fig. 1E). The CA is then updated by including the highest-scoring protein pairs, and the next iteration can begin. At each iteration, all pairs in the CA are reselected based on confidence scores (except initial training pairs, if any), allowing for error correction.

Unless otherwise specified in what follows, our results were obtained on a standard dataset comprising 5,064 HK−RR pairs for which the correct pairings are known from gene adjacency. Each species has, on average, $\langle m_p\rangle =11.0$ pairs, and at least two pairs (Materials and Methods).

Starting from Known Pairings.

We begin by predicting interaction partners starting from a training set of known pairs. To implement this, we pick a random set of $N_{\text{start}}$ known HK−RR pairs from our standard dataset, and the first IPA iteration uses this CA to train the model. We blind the pairings of the remaining test set, and predict them. At each subsequent iteration $n>1$, the CA used to retrain the model contains the initial training pairs plus the $\left(n-1\right)N_{\text{increment}}$ highest-scoring predicted pairs from the previous iteration (Materials and Methods).

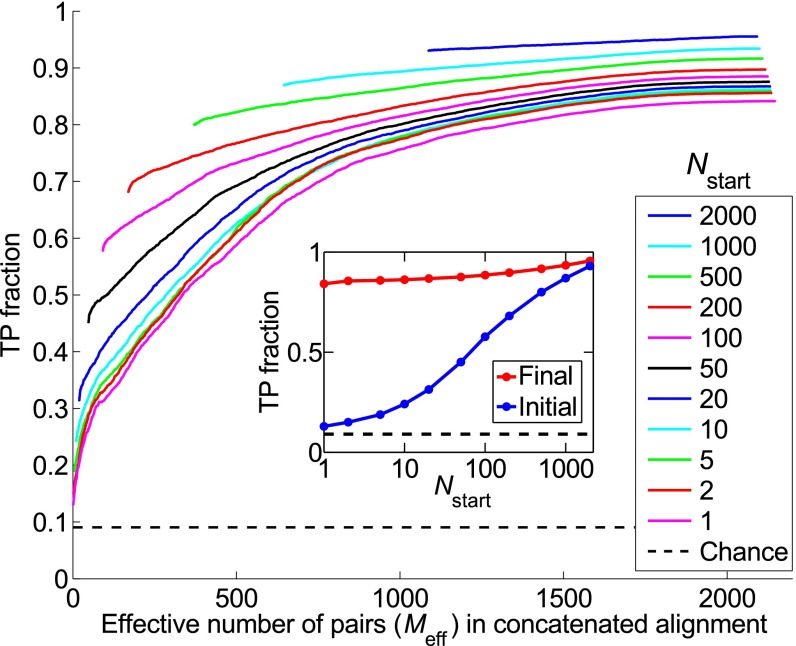
At the first iteration, the fraction of accurately predicted HK−RR pairs [true positive (TP) fraction] depends strongly on $N_{\text{start}}$, and is close to the random expectation (0.09) for small training sets, ranging from 0.13 at $N_{\text{start}}=1$ to 0.93 for $N_{\text{start}}=\mathrm{2,000}$ (Fig. 2, Inset, blue curve). The TP fraction increases with subsequent iterations (Fig. 2). Strikingly, the final TP fraction depends only weakly on $N_{\text{start}}$. For $N_{\text{start}}=1$, the IPA achieves a final TP fraction of 0.84, a huge increase from the initial value of 0.13 (Fig. 2, Inset, red curve). This demonstrates the power of iterating: Incorporating high-scoring predicted pairs progressively increases the predictive accuracy of the model.

Fig. 2.

Fraction of predicted pairs that are true positives (TP fraction), for different training set sizes $N_{\text{start}}$. The progression of the TP fraction during iterations of the IPA is shown. The TP fraction is plotted versus the effective number of HK-RR pairs ($M_{\text{eff}}$; see SI Appendix, Eq. S1) in the CA, which includes $N_{\text{increment}}=6$ additional pairs at each iteration. The IPA is performed on the standard dataset, and all results are averaged over 50 replicates that differ by the random choice of training pairs. The dashed line shows the average TP fraction obtained for random HK−RR pairings. (Inset) Initial and final TP fractions (at first and last iteration) versus $N_{\text{start}}$.

Starting Without Known Pairings.

Given the success of the IPA with very small training sets, we next ask whether predictions can be made without any prior knowledge of interacting pairs. To test this, we randomly pair each HK with an RR from the same species and use these 5,064 random pairs to train the initial model. At each subsequent iteration $n>1$, the CA is built just from the $\left(n-1\right)N_{\text{increment}}$ highest-scoring pairs from the previous iteration (SI Appendix).

Fig. 3 shows the progression of the TP fraction for different values of $N_{\text{increment}}$; it increases in all cases, and the iterative method performs best for small increment steps (Fig. 3, Inset). The low-$N_{\text{increment}}$ limit of the final TP fraction is 0.84, identical to that obtained with a single training pair (Fig. 2). This striking TP fraction of 0.84 is attained without any prior knowledge of HK−RR interactions: The IPA bootstraps its way toward high predictivity. The low-$N_{\text{increment}}$ limit is almost reached for $N_{\text{increment}}=6$; thus we generically use $N_{\text{increment}}=6$ to reduce computational time while retaining near-optimal performance. The final TP fraction is robust with respect to different initializations: For $N_{\text{increment}}=6$, its standard deviation (over 500 replicates) is 0.04. For the complete dataset (23,424 HK–RR pairs), the IPA yields a TP fraction of 0.93 with no training data (see Dependence on Features of the Dataset).

Fig. 3.

Starting from random pairings, i.e., without known pairings. Shown is the TP fraction during iterations of the IPA versus the effective number of HK−RR pairs ($M_{\text{eff}}$) in the CA, which includes $N_{\text{increment}}$ additional pairs at each iteration. Different curves correspond to different $N_{\text{increment}}$. The IPA is performed on the standard dataset, and all results are averaged over 50 replicates that differ in their initial random pairings. Note that the first point of each curve corresponds to the second iteration. The dashed line shows the average TP fraction obtained for random HK−RR pairings. (Inset) Final TP fraction versus $N_{\text{increment}}$.

Training Process.

The ability to accurately predict interaction partners without training data is surprising; to understand it, we examine the evolution of the model over iterations of the IPA. In a well-trained model, the residue pairs with the largest couplings have been shown to correspond to contacts in the protein complex (7, 16, 31). Up to iteration $\sim 100-150$ (with $N_{\text{increment}}=6$), models starting from random pairings do no better than chance at identifying contacts. Subsequently, they improve rapidly and soon predict contacts nearly as well as models constructed from correct pairs (Fig. 4 and SI Appendix, Fig. S1A).

Fig. 4.

Training of the couplings during the IPA. Residue pairs comprising an HK site and an RR site were scored by the Frobenius norm (i.e., the square root of the summed squares) of the couplings involving all possible residue types at these two sites. The best-scored residue pairs were compared with the 27 HK−RR contacts found experimentally in ref. 27. Solid curves show the fraction of residue pairs that are real contacts (among the k best-scored pairs for four different values of k) versus the iteration number in the IPA. Dashed curves represent the ideal case, where, at each iteration, $N_{\text{increment}}$ randomly selected correct HK−RR pairs are added to the CA. The overall fraction of residue pairs that are real HK−RR contacts, yielding the chance expectation, is only $3.8\times {10}^{-3}$. The IPA is performed on the standard dataset with $N_{\text{increment}}=6$, and all data are averaged over 500 replicates that differ in their initial random pairings.

At early stages, the model, constructed from few almost random HK−RR pairs, poorly predicts real contacts and correct HK−RR pairs. However, couplings associated with residue pairs that occur in the CA increase, raising the scores of HK−RR pairs with high sequence similarity to those already in the CA, and making them more likely to be added to the CA. We thus examine sequence similarity between the HK−RR pairs in the CA in consecutive iterations. Specifically, we consider two HK−RR pairs to be “neighbors” if the sequence identities between the two HKs and between the two RRs are both >70%. We find that sequence similarity is crucial in the early recruitment of new HK−RR pairs to the CA (SI Appendix, Fig. S1B).

Understanding the initial increase of the TP fraction requires a further observation. In our standard dataset, among all possible within-species HK−RR pairs, the average number of neighbor pairs per correct HK−RR pair is 9.66, of which 99% are correct. In contrast, the average number of neighbor pairs per incorrect HK−RR pair is 5.25, of which less than 1% are correct. Thus, correct pairs are more similar to each other than they are to incorrect pairs, or than incorrect pairs are to each other. We call this fact the “Anna Karenina effect,” in reference to the first sentence of Tolstoy’s novel (32): “All happy families are alike; each unhappy family is unhappy in its own way.” Biologically, this effect makes sense: Each HK−RR pair is an evolutionary unit, so a correct pair is likely to have orthologs of both the HK and the RR in multiple other species, whereas an incorrect pair is less likely to have orthologs of both the HK and the (noncognate) RR in other species. Hence, in early iterations, the number of neighbors recruited per correct pair is higher than per wrong pair (SI Appendix, Fig. S1B), increasing the TP fraction in the CA. To summarize, sequence similarity is crucial at early stages, and the Anna Karenina effect helps to increase the TP fraction in the CA, thus promoting training of the model. This finding suggests that the IPA might be further enhanced by initially scoring HK−RR pairs based on similarity (33).

Application of the IPA to ABC Transporters.

To demonstrate the utility of the IPA beyond HK−RRs, we applied it to several protein families involved in ABC transporter complexes. Bacterial genomes typically contain multiple paralogs of these transporters, involved in the translocation of different substances (34). We built alignments of homologs of the Escherichia coli interacting protein pairs MALG−MALK, FBPB−FBPC, and GSIC−GSID (see SI Appendix). These protein pairs are respectively involved in maltose, iron, and glutathione transport systems. The IPA starting from random pairings yields respective final TP fractions 0.90, 0.89, and 0.98 for these pairs in the low-$N_{\text{increment}}$ limit (Fig. 5, black curves). These accurate predictions demonstrate the broad applicability of the IPA beyond HK−RRs.

Fig. 5.

Results for ABC transporter pairs and impact of the number of pairs per species. Shown is the final TP fraction versus $N_{\text{increment}}$ for three different pairs of protein families involved in ABC transport complexes (black curves), and for three HK−RR datasets with different distributions of the number of pairs per species yielding different means $\langle m_p\rangle$ (colored curves). All datasets include ∼5,000 protein pairs, and the IPA is started from random pairings, apart from the red dashed curve, where it is started from incorrect random pairings. All results are averaged over 50 replicates that differ in their initial pairings. Arrows with the same line style as each curve indicate the average TP fractions obtained for random pairings in each dataset. (Inset) Distribution of the number of pairs per species in the three different HK−RR datasets (red, standard dataset; green and blue, datasets comprising the species with, respectively, lowest or highest numbers of pairs in the full HK−RR dataset).

Dependence on Features of the Dataset.

To apply the IPA approach more widely, it is important to understand what dataset characteristics enable its success. The number of paralogous pairs per species is likely important, because pairing is more difficult when there are more incorrect possibilities. Indeed, higher TP fractions are obtained in datasets with fewer average pairs per species both across different ABC transporter protein pairs and across HK−RR datasets with different numbers of pairs per species (Fig. 5). Moreover, the presence of species with a small number of pairs is crucial (SI Appendix, Fig. S2), although, in their absence, the TP fraction can be rescued by a sufficiently large training set (SI Appendix, Fig. S3). Perhaps surprisingly, for small $N_{\text{increment}}$, the final TP fraction does not depend on how many pairs in the initial CA are correct (Fig. 5, red curves, and SI Appendix, Fig. S4). Hence, the importance of species with few pairs does not stem from a more favorable initialization. Rather, protein pairs from species with few pairs tend to obtain higher confidence scores because they have fewer competitors, making them more likely to enter the CA at early stages (SI Appendix, Fig. S5). This bias in favor of species with few pairs combines with the Anna Karenina effect to favor correct pairs early in the learning process.

Because sequence similarity is crucial at early iterations, it should strongly impact performance. Indeed, a lower final TP fraction (0.58 vs. 0.84) is obtained in an HK−RR dataset where no two correct pairs are >70% identical, but it can be rescued by a sufficiently large training set (SI Appendix, Fig. S6).

Another important parameter is dataset size. For HK−RRs, the final TP fraction increases steeply above ∼1,000 sequences, and saturates above ∼10,000 (SI Appendix, Fig. S7). For the complete dataset (23,424 HK−RR pairs; Materials and Methods), we obtain a striking final TP fraction of 0.93. Larger datasets imply closer neighbors, which is favorable to the success of the IPA, particularly in the absence of training data.

Optimization.

To improve the predictive ability of the IPA, we exploit multiple different random initializations of the CA. For each possible within-species HK−RR pair, we calculate the fraction $f_r$ of replicates of the IPA in which this pair is predicted. High $f_r$ values are excellent predictors of correct pairs, outperforming average TP fractions from individual replicates (SI Appendix, Fig. S8). The quality of $f_r$ as a classifier is demonstrated by the area under the receiver operating characteristic: It is 0.991, very close to 1 (ideal). The very high TP fraction of the pairs with highest $f_r$ can be exploited by taking some as training pairs and running the IPA again. This “rebootstrapping” process can be iterated, yielding further performance increases, particularly for small datasets (SI Appendix, Fig. S9).

Determining Whether Two Protein Families Interact.

The IPA correctly predicts most interacting protein pairs no matter which initial random pairing is used. This suggests that the distribution of replication fractions $f_r$ (over all possible within-species pairs) should distinguish pairs of protein families that interact from those that do not. To test this idea, we consider three pairs of families with similar $\langle m_p\rangle$: the subset of HK−RRs homologous to BASS−BASR, the homologs of the interacting ABC transporter proteins MALG−MALK, and a pair with no known interaction, homologs of BASR−MALK. For both interacting protein families, the distribution of replication fractions $f_r$ strongly favors values close to 0, mostly corresponding to wrong pairs, and close to 1, mostly corresponding to correct pairs (Fig. 6 A and B). No such bimodality is observed for BASR−MALK (Fig. 6C). We constructed null models for each dataset by randomly scrambling the amino acids at each site (column) of the alignment, thus retaining conservation while removing correlations. For BASR−MALK, the observed $f_r$ distribution is very similar to the null-model distribution, whereas, for both interacting pairs, the results and the null strongly differ (Fig. 6). The standard HK−RR dataset can be similarly contrasted with an HK−RR dataset lacking correct pairs (SI Appendix, Fig. S10). Comparing the observed $f_r$ distribution to the null thus distinguishes interacting from noninteracting protein families using sequence data alone. For these family pairs, the difference in $f_r$ distributions is visible down to dataset sizes M ≈ 500. Another signature of interacting families is the strength of the top predicted contacts (SI Appendix, Fig. S11).

Fig. 6.

An IPA-derived signature of protein−protein interactions. For three pairs of protein families, we compute the fraction $f_r$ of IPA replicates in which each possible within-species protein pair is predicted as a pair. (A and B) Protein families with known interactions: (A) BASS−BASR homologs and (B) MALG−MALK homologs. (C) Protein families with no known interaction (BASR–MALK homologs). Red curves show the distribution of $f_r$ obtained for each alignment. Blue curves show the same distribution obtained by running the IPA on alignments where each column is scrambled (null model). Alignments include ∼5,000 pairs, with $\langle m_p\rangle \approx 5$, and each distribution is estimated from 500 IPA replicates that differ in their initial random pairings, using $N_{\text{increment}}=50$.

Discussion

We have presented a method to infer interaction partners among two protein families with multiple paralogs, using only sequence data. Our approach is based on pairwise maximum entropy models, which have proved successful at predicting residue contacts between known interaction partners (7, 15–19). To our knowledge, the important problem of predicting interaction partners among paralogs from sequences has only been addressed by Burger and van Nimwegen (6), who used a Bayesian network method. Pairwise maximum entropy-based approaches were later shown to outperform this method for orphan HK−RR partner predictions, starting from a substantial training set of partners known from gene adjacency (15). Importantly, our method enables partner prediction without any initial known pairs, whereas even the seminal study (6) included a training set via species that contain only a single pair. This lack of a training set is important to predict novel protein−protein interactions, because, in this context, no prior knowledge of interacting pairs would be available.

We first benchmarked our IPA on HK−RR pairs. The top-scoring predicted HK−RR pairs are progressively incorporated into the CA used to build the maximum entropy model. This enables progressive training of the model, providing major increases in predictive accuracy. Strikingly, the IPA is very successful even in the absence of any prior knowledge of HK−RR interactions, yielding a 0.93 TP fraction on our complete dataset. The success of the IPA with no training data relies on initial recruitment of pairs by sequence similarity. Correct pairs are more similar to one another than incorrect pairs, favoring recruitment of correct pairs, a process we called the Anna Karenina effect.

IPA performance is best for large datasets (with strong sequence similarity), and when species with few pairs are included. The first condition is easily met for HK−RRs (a 0.84 TP fraction was obtained with 5,064 pairs, out of 23,424, and our rebootstrapping approach yields a 0.64 TP fraction even for a dataset of only 502 pairs; SI Appendix, Fig. S9B) and is realized for a large and growing number of other protein families. Indeed, in the protein family database PfamA-30 (35), 62% of the 15,701 entries classified as “domains” or “families” comprise more than 500 distinct Uniprot sequences. The mean number of paralogs per species in PfamA-30 domains or families is 3.9, so the HK−RR system actually constitutes an unusually difficult case in this respect (28). The success we obtained for ABC transporter proteins, which form permanent complexes, whereas HK−RRs interact transiently, further points to the broad applicability of the IPA. So far, we have only applied the IPA to one-to-one interactions, but the method should be fruitful beyond this domain.

Our approach could be combined with those of refs. 7, 13, and 15–19 to improve protein complex structure prediction; it solves the major issue (17–19) of finding the correct interaction partners among paralogs, which is a prerequisite for accurate contact prediction. In particular, better paralog partner predictions will help extend accurate contact prediction to currently inaccessible cases such as eukaryotic proteins, for which genome organization cannot be used to find partners.

Finally, we have introduced two distinct IPA-based signatures that distinguish between interacting and noninteracting protein families. These results pave the way toward predicting novel protein−protein interactions between protein families from sequence data alone.

Materials and Methods

Extended materials and methods are presented in SI Appendix.

HK−RR Dataset.

Our dataset was built from the P2CS database (36, 37), which includes two-component system proteins from all fully sequenced prokaryotic genomes. All data can thus be accessed online. We considered the protein domains through which HKs and RRs interact, namely the Pfam HisKA domain present in most HKs (64 amino acids) and the Pfam Response_reg domain present in all RRs (112 amino acids). We focused on proteins with known partners, i.e., those encoded in the genome in pairs containing an HK and an adjacent RR. Discarding species with only one pair, for which pairing is unambiguous, we obtained a complete dataset of 23,424 HK−RR pairs from 2,102 species. A smaller “standard dataset” of 5,064 pairs from 459 species was extracted by picking species randomly.

IPA.

Here, we summarize each of the steps of an iteration of the IPA (Fig. 1C).

Correlations.

Each iteration begins with the calculation of empirical correlations from the CA of paired HK−RR sequences. The empirical one- and two-site frequencies, $f_i\left(\alpha \right)$ and $f_{ij}\left(\alpha ,\beta \right)$, of occurrence of amino acid states α (or β) at each site i (or j) are computed for the CA, using a reweighting of similar sequences, and a pseudocount correction (SI Appendix, Eqs. S1–S4) (7, 9, 15, 29). The correlations are then computed as

$$C_{ij}\left(\alpha ,\beta \right)=f_{ij}\left(\alpha ,\beta \right)-f_i\left(\alpha \right)f_j\left(\beta \right).$$ [1]

Couplings.

Next, we construct a pairwise maximum entropy model of the CA (SI Appendix, Eq. S6). It involves one-body fields $h_i$ at each site i and (direct) couplings $e_{ij}$ between all sites i and j, which are determined by imposing consistency of the pairwise maximum entropy model with the empirical one- and two-point frequencies of the CA (SI Appendix, Eqs. S7 and S8). We use the mean-field approximation (9, 29): Couplings are obtained by inverting the matrix of correlations,

$$e_{ij}\left(\alpha ,\beta \right)=C_{ij}^{-1}\left(\alpha ,\beta \right).$$ [2]

We then transform to the zero-sum gauge (7, 31).

Interaction energies for all possible HK−RR pairs.

The interaction energy E of each possible HK−RR pair within each species is calculated as a sum of couplings,

$$E\left({\alpha }_1\mathit{,}\dots \mathit{,}{\alpha }_{L_{\text{HK}}}\mathit{,}{\alpha }_{L_{\text{HK}}+1}\mathit{,}\dots \mathit{,}{\alpha }_L\right)={\displaystyle \sum _{i=1}^{L_{\text{HK}}}{\displaystyle \sum _{j=L_{\text{HK}}+1}^L{e}_{ij}\left({\alpha }_i,{\alpha }_j\right)}}\mathit{,}$$ [3]

where $L_{\text{HK}}$ denotes the length of the HK sequence, and L denotes that of the concatenated HK−RR sequence.

HK−RR pair assignments and ranking by gap.

In each species, the pair with the lowest interaction energy is selected first, and the HK and RR involved are removed from further consideration, assuming one-to-one HK−RR matches (Fig. 1D). Then, the pair with the next lowest energy is chosen, until all HKs and RRs are paired. Each pair is scored at assignment by a confidence score $\mathrm{\Delta }E/\left(n+1\right)$, where $\mathrm{\Delta }E$ is the energy gap (Fig. 1E), and n is the number of lower-energy matches discarded in assignments made previously, within that species and at that iteration (SI Appendix, Fig. S12). All of the assigned HK−RR pairs are then ranked in order of decreasing confidence score.

Incrementation of the CA.

At each iteration $n>1$, the $\left(n-1\right)N_{\text{increment}}$ assigned pairs that had the highest confidence scores at iteration $n-1$ are included in the CA. In the presence of an initial training set, the $N_{\text{start}}$ training pairs are also included in the CA. Without a training set, the initial CA is built by randomly pairing each HK of the dataset with an RR from the same species, and, for $n>1$, the CA only contains the above-mentioned $\left(n-1\right)N_{\text{increment}}$ assigned pairs. Once the new CA is constructed, the next iteration can start.

Note.

While submitting this manuscript, we learned that T. Gueudre, C. Baldassi, M. Zamparo, M. Weigt, and A. Pagnani are preparing a related paper on predicting interacting paralog pairs.