In vivo delineation of subdivisions of the human amygdaloid complex in a high‐resolution group template

Abstract

The nuclei of the human amygdala remain difficult to distinguish in individual subject structural magnetic resonance images. However, interpretation of the amygdala's role in whole brain networks requires accurate localization of functional activity to a particular nucleus or subgroup of nuclei. To address this, high spatial resolution, three‐dimensional templates, using joint high accuracy diffeomorphic registration of T1‐ and T2‐weighted structural images from 168 typical adults between 22 and 35 years old released by the Human Connectome Project were constructed. Several internuclear boundaries are clearly visible in these templates, which would otherwise be impossible to delineate in individual subject data. A probabilistic atlas of major nuclei and nuclear groups was constructed in this template space and mapped back to individual spaces by inversion of the individual diffeomorphisms. Group level analyses revealed a slight (∼2%) bias toward larger total amygdala and nuclear volumes in the right hemisphere. No substantial sex or age differences were found in amygdala volumes normalized to total intracranial volume, or subdivision volumes normalized to amygdala volume. The current delineation provides a finer parcellation of the amygdala with more accurate external boundary definition than current histology‐based atlases when used in conjunction with high accuracy registration methods, such as diffeomorphic warping. These templates and delineation are intended to be an open and evolving resource for future functional and structural imaging studies of the human amygdala. Hum Brain Mapp 37:3979–3998, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

The amygdaloid complex is a collection of nuclei and associated transition regions in the medial temporal lobe, immediately rostral of the hippocampal formation [Amaral et al., 1992]. It plays a key role in emotion and motivation [Aggleton, 2000; Whalen, 2009], and is roughly homologous across all amniotes [Moreno and Gonźalez, 2007]. Although there is increasing interest in the role of the amygdala in uniquely human psychological processes, social behaviors and mental health [Adolphs, 2010; Savitz et al., 2010], progress has been slowed by the challenges of assigning task‐related functional MRI (fMRI) activation to amygdala nuclei. The amygdala is functionally heterogeneous [McDonald, 1998], but is often treated as a single region in many high‐profile fMRI studies [Li et al., 2011; Nikolova et al., 2014]. As the spatiotemporal resolution of fMRI improves, the assignment of activity to amygdala subregions becomes increasingly important in the context of whole‐brain networks.

In primates, the amygdaloid complex is conventionally divided into thirteen nuclei [Amaral et al., 1992], many of which can only be delineated ex vivo histologically using a combination of Nissl, myelin, and acetylcholinesterase stained sections [Garćıa‐Amado and Prensa, 2012]. The identification of internuclear boundaries in individual human high‐resolution structural MRI data is notoriously difficult, motivating various strategies including spectral clustering of the diffusion tensor data [Solano‐Castiella et al., 2010], bivariate clustering of structural image intensity [Solano‐Castiella et al., 2009], manual heuristic segmentation based on the Mai [Mai et al., 2008] brain atlas [Entis et al., 2012; Pŕevost et al., 2011], parcellation based on cortical signal correlations [Bickart et al., 2012], diffusion tractography‐based parcellations [Bach et al., 2011; Saygin et al., 2011], and mapping of histologically defined subregions to an MRI template (the Juelich histological atlas) [Amunts et al., 2005; Eickhoff et al., 2005, 2006]. None of these approaches have generated more than four subdivisions of the amygdala, with the majority isolating basolateral, superficial, and centromedial groups.

In this work, we create unbiased templates, using a joint cost function over both T₁‐weighted (T1w) and T₂‐weighted (T2w) imaging data [Avants et al., 2007, 2008b]. Unbiased templates, equivalent to minimum deformation templates [Kochunov et al., 2001] or group mid‐spaces [Reuter et al., 2012; Smith et al., 2002], are generally constructed by iterative registration of a set of images to a template that in turn is updated after each iteration. Examples of unbiased structural MRI reference brain templates include the MNI ICBM templates [Mazziotta et al., 2001] widely used in fMRI analysis packages such as SPM and FSL, and the Human Connectome Project (HCP) release templates [Van Essen et al., 2013]. These templates are unbiased in the sense that no individual's brain influences the shape or intensity of the template more than any other. The advantage of using a joint cost function in this work is that it calculates a weighted sum of the cost functions for each image contrast, resulting in an individual‐to‐template mapping that balances information from both T1w and T2w image contrasts.

Our primary atlas reference is the 34‐year‐old adult reference atlas released by the Allen Brain Institute as part of its wider human brain transcriptome [Amunts et al., 2005] project [Hawrylycz et al., 2012]. This atlas was chosen for its use of a standard, whole brain ontology, which includes all major amygdala nuclei and subnuclear divisions and its open availability online (http://www.brain-map.org). Our secondary reference is the Mai, Paxinos, and Voss Atlas (3rd Edition) [Mai et al., 2008], which in turn cites two earlier parcellations of the amygdala [Brockhaus, 1939; Sanides, 1957] and uses a very similar nomenclature to the Allen Brain Atlas. Several equally valid naming schemes exist for the nuclei and subdivisions of the amygdaloid complex, for example, by [Amaral et al., 1992] (see Table 1). However the division boundaries are relatively consistent amongst nomenclatures since they are all based on microstructural, histological and immunohistochemical classifications.

Table 1.

Summary of common nomenclatures used in the literature and reference atlases

Amygdala subdivision nomenclatures
Group	Nucleus	Amaral	Mai	Allen	This Atlas
Deep or basolateral nuclear group	Lateral	L	L	AMY‐BLN‐La	La
	Basolateral	B	BL	AMY‐BLN‐BL	BLDI, (BLVP)
	Accessory Basal	AB	BM	AMY‐BLN‐BM	BM
	Paralaminar	PL	BLPL	AMY‐BLN‐PL	(BLVP)
Superficial or corticomedial group	Medial	M	Me	AMY‐CMN‐Me	(CMN)
	Cortical	CO	ACo/PCo	AMY‐CMN‐Co	(CMN)
	Nucleus of the Lateral Olfactory Tract	NLOT	–	Cx‐ACx‐NLOT	(CMN)
	Periamygdaloid Cortex	PAC	PAA/PHA	ATA‐ACTA	(ATA)
Remaining nuclei	Anterior Amygdaloid Area	AAA	AAA	AMY‐AAA	AAA
	Central	CE	Ce	AMY‐CEN	CEN
	Amygdalohippocampal Area	AHA	AHi	AMY‐CMN‐AHA	(CMN)
	Intercalated Nuclei	I	–	AMY‐INA	(AMY)
Transition areas	Amygdalostriatal Transition Area	ASA	Astr	ATA‐ASTA	ASTA

Subdivisions of the basolateral and corticomedial group nuclei can be difficult to identify, even in histological stained sections. The amygdala divisions used in this atlas are determined primarily by which boundaries can be explicitly traced or implicitly defined from other landmarks in the T1w and T2w MRI templates. Merged divisions in this atlas are indicated by their parent group in parentheses. Nuclei not defined in a source but present in [Amaral et al., 1992] are indicated with a dash.

To summarize, this work has four primary aims: (1) to delineate more amygdala subregions than has been possible previously in group averaged in vivo human brain images, (2) to bridge the gap between histological parcellation of the amygdala and state‐of‐the‐art non‐invasive neuroimaging, (3) assess the impact of sex, hemisphere and age on amygdala total and subdivision volumes in a healthy adult population, and (4) release the resulting templates and probabilistic delineations as a research community resource.

METHODS

Source Data

All structural imaging data were obtained from the Human Connectome Project (HCP) Q1–Q6 500 subject release, August 2014 [Van Essen et al., 2013], which includes 526 MRI datasets from individual adult human subjects, including 700 µm isotropic T1w and T2w whole brain images. The only inclusion criterion applied was that the T1w and T2w structural images were constructed by simple averaging of two single‐average images following six‐parameter rigid body alignment [Glasser et al., 2013], which reduced the available sample to 208 subjects. Age and sex unbiasing was performed by balancing the number of male and female subjects at each integer age between 22 and 35 years old (inclusive), resulting in a final sample of 168 individuals (84 males and 84 females, mean ± sd age in both groups = 28.9 ± 3.6 years). All structural images provided by the HCP500 data release were gradient non‐linearity and RF bias corrected, rigid‐body AC‐PC aligned, and readout distortion corrected with accurate co‐registration of the individual T2w to T1w imaging spaces [Glasser et al., 2013]. Sinc‐ and spline‐based interpolation was used throughout by the HCP preprocessing pipeline to minimize cumulative smoothing from repeated resampling. However, some residual blurring and spatial noise correlation are inevitable in the final individual T1w and T2w images used to construct the templates below.

Group template construction

An unbiased template was constructed using diffeomorphic registration with a joint cost function over both T1w and T2w high‐resolution three‐dimensional (3D) images from all 168 retained subjects. All registrations were performed using the bivariate symmetric normalization (SyN) algorithm implemented by the Advanced Normalization Toolbox (ANTs) [Avants et al., 2007]. Initial unbiased seed templates were constructed for T1w and T2w volumes by simple averaging across all subjects since all volumes were already rigid‐body AC‐PC aligned (i.e., without linear scaling) by the minimal HCP structural preprocessing pipeline.

The initial unbiased bivariate template was refined iteratively by the concatenation of affine and diffeomorphic registrations of individual T1w and T2w structural images to their respective templates generated by the previous iteration. A single diffeomorphic mapping was optimized for each individual brain using a joint cross‐correlation similarity metric with equal weighting to the T1w and T2w images [Avants et al., 2008b]. Only a single diffeomorphism is required since the individual T1w and T2w images were accurately co‐registered during HCP preprocessing [Glasser et al., 2013]. The velocity field of the diffeomorphic transform was regularized using a local Gaussian‐weighted kernel with σ = 3.0 voxels to avoid overfitting the warp field to image noise [Avants et al., 2008a]. It should be noted that the ANTs template construction pipeline includes normalization to the whole volume mean intensity and a Laplacian edge enhancement filter by default. The purpose of the edge enhancement is to compensate for blurring induced by intensity averaging alone, and serves the same purpose as the blurring inversion proposed by Avants et al. for the symmetric group normalization (SyGN) algorithm in [Avants et al., 2010]. Both approaches result in edge enhanced templates that emphasize both the shape and appearance of anatomical structures. The template refinement was terminated after four iterations, resulting in AC–PC aligned T1w and T2w unbiased templates with 700 µm isotropic spatial resolution. These templates are subsequently referred to as the CIT168 templates.

Probabilistic Atlas Construction

Amygdala subdivisions are difficult to delineate in individual structural images from the HCP dataset. In contrast, the internal divisions of the amygdala become sufficiently well‐defined to allow manual labeling in unbiased bivariate templates generated from approximately 80 or more registered individual structural images (see Supporting Information). The final iteration of the joint template construction results in 168 T1w and T2w image pairs warped from individual spaces to the template space, which are then averaged to generate the final T1w and T2w templates. Consequently, we constructed validation templates from 84 T1w and T2w warped image pairs, selected randomly from the full set of 168 image pairs in template space. The unselected 84 image pairs were used to construct complementary T1w and T2w templates, which were also used for labeling validation. This process was repeated with new random samples to generate eight (four pairs of complementary) T1w and T2w templates for manual labeling by two experienced observers, was considered to be a reasonable balance between total labeling time (typically 4–8 hours per template per observer) and the need for intra‐observer validation.

Both observers (JMT and WMP) labeled the left amygdala in each of the eight validation templates using a pre‐agreed upon, ordered approach, with the Allen Brain Atlas as primary reference. The joint unbiased T1w and T2w templates were viewed simultaneously in ITK‐SNAP (version 3.2.0) [Yushkevich et al., 2006] using a yoked 3D cursor allowing tissue volumes to be defined by referencing both contrasts. For most of the amygdala nuclei and surrounding structures, the T2w template provided the highest tissue contrast, though in some structures, such as the anterior commissure and optic tract, the T1w image was the primary image contrast. Labeling was performed in the left amygdala only, starting with delineation of the entire amygdala [Amaral et al., 1992]. The most readily defined nuclei with explicit boundaries, the lateral (La), dorsal and intermediate basolateral (BLDI) and central (CEN) divisions were then completed, constrained within the previously defined whole‐amygdala label. Parcellation continued with the estimation of implicit boundaries for remaining nuclear subdivisions using the approaches reported in the Results section below. Any voxels assigned to the entire amygdala but not to any specific subregion were collected in the Amygdala (Other) label. Since each of the eight validation templates were constructed in the master CIT168 template space (see above), the probabilistic labels for each division were constructed by simple averaging over all manually labeled volumes.

Left amygdala labels for each observer and validation template were mapped to the right amygdala using the following approach. Each T1w and T2w validation template was reflected about the mid‐sagittal plane and warped to its unreflected version using a joint cost function affine and diffeomorphic transform. The combination of a reflection and affine then diffeomorphic transform (reflection warp) results in an anatomically constrained, high accuracy mapping of points in the left amygdala to their homotopic counterparts in the right amygdala. The reflection warp is then applied to the observer labels with nearest neighbor interpolation to generate a bilateral amygdala labeling. Each bilateral subregion label was then averaged over all 16 label volumes (eight validation templates with two observers). This resulted in a bilateral probabilistic amygdala atlas with minimal left–right observer bias (any unique observer variations in the left amygdala would be duplicated in the right amygdala). Labeling only one hemisphere is not without precedence in the subcortical atlas literature (Yushkevich et al., 2015; Van Leemput et al., 2009]. The accuracy of reflection warping is addressed in the Supporting Information and total amygdala volume bias is estimated by comparison to independent results from the HCP (see “Comparison with Existing Atlases” below).

Intra‐ and inter‐observer labeling reliability between equivalent labels was assessed using two similarity measures: (1) the Dice coefficient, D, (also known as the S¨orensen index) defined as a ratio of the intersection volume of two labels to the mean volume of the two labels, in the range [0,1] [Dice, 1945]. (2) the Hausdorff distance, H. To calculate H between two labeled regions, we first determined for each voxel in the first image the minimum Euclidean distance to any voxel of the same label in the second image, and then determined the maximum of all these distances. The Hausdorff distance has identical units to the voxel dimensions, and is a measure of proximity between two regions which takes account of shape and orientation. It finds frequent application in machine vision to locate a template object within a scene [Huttenlocher et al., 1993].

It should be noted that the Dice coefficient is sensitive to the average volume of the two regions being compared. As the average volume decreases, small errors in overlap begin to dominate, until in the extreme of a single voxel label, a single voxel overlap error results in a Dice coefficient of zero. We, therefore, do not expect Dice coefficients for small volume labels to approach those typically encountered for large volume labels, such as brain masks, which routinely exceed 0.95 [Eskildsen et al., 2012]. The Hausdorff distance is sensitive to small outlier regions present in one label only, so that even a single voxel at a distance from the main label region can skew the final metric if it is not present in the compared label volume. Taken together, the two metrics provide complementary information about label shape, positioning and overlap similarities within and between observers and between atlases.

Individual Variation in Amygdala Nuclear Volumes

Total amygdala and subdivision volumes in individual brains were estimated by inverting the spatial transform, mapping individual brains to the unbiased template space generated during the final iteration of template construction. The forward mapping from individual space to template space was expressed as the concatenation of optimized affine and symmetric image normalization (SyN) diffeomorphic transforms [Avants et al., 2008a]. The inverse mapping was similarly constructed from the individual inverse affine and the inverse diffeomorphic transform generated by the SyN algorithm. The inverse transform was then used to map label probability maps from the CIT168 template space to individual spaces, where total label volume was estimated by integration of the label probability over the whole volume.

Statistical Analysis

The impact of sex (male versus female), age, and hemisphere (left versus right) on individual subdivision and total amygdala volume were explored using Markov chain Monte Carlo generalized linear mixed models (MCMC GLMM) implemented by the MCMCglmm package (version 2.21) in R (version 3.13) [Hadfield, 2010]. Sex, age, and hemisphere were modeled as fixed effects on volume with a single random effect of individual subject. Model selection for the fixed effects was performed using the total amygdala volume data only, starting with a full three‐way interaction model. The deviance information criterion (DIC), a generalization for hierarchical models of the Aikaike and Bayesian information criteria, was used for all model comparisons [Spiegelhalter et al., 2002]. All full two‐way and three‐way interaction models were found to have a higher DIC than the simple main effect model, supporting the use of the simple main effect model for all subsequent analyses. All amygdala subdivision volumes and the total amygdala volume were modeled independently in separate GLMMs. MCMC parameters were as follows: 13,000 maximum iterations, 3,000 burn‐in iterations, thinning every 10 iterations (resulting in effective sample sizes of approximately 1,000, and Gaussian trait distributions.

Comparison with Existing Atlases

As an external validation, we compared the CIT168 amygdala atlas with two well‐established probabilistic atlases, namely the Harvard–Oxford atlas released with FSL [Desikan et al., 2006; Frazier et al., 2005] and the Juelich atlas released as an SPM toolbox [Eickhoff et al., 2005]. Comparisons between the amygdala labels of these atlases were performed in MNI152 space at 1 mm isotropic spatial resolution to match the native resolution of the Juelich and Harvard–Oxford atlases. A combination of univariate SyN diffeomorphism and affine transform was optimized to map the CIT168 T1w template to the MNI152 (FSL) or Colin27 (SPM) T1w templates with 1 mm isotropic spatial resampling by sinc interpolation. The Harvard‐Oxford atlas provides a single, bilateral probabilistic label for the amygdala constructed by registration of manually labeled individual in vivo structural images. The Juelich atlas was constructed by elastic registration of delineations performed in histological sections to an MRI template, and provides three main subdivisions to the amygdala, specifically laterobasal, centromedial, and superficial groups. We chose to merge the medial nucleus with the cortical nuclear group and label the central nucleus separately (see “Results” below). Consequently, a comparison was performed between the combination of corticomedial and superficial groups in the Juelich atlas and the combined CMN, CEN, AAA, and ATA labels in the CIT168 atlas (see Table 1 for abbreviations). The basolateral complex label, generated by merging La, BL, and BM, could be compared directly between the two atlases.

All Dice coefficients and Hausdorff distances were calculated for binarized labels of the probabilistic map where P ≥ 0.5. An additional comparison was performed with the Juelich atlas labels binarized at P ≥ 0.25, since the amygdalostriatal label (ASTR) did not survive binarization at P ≥ 0.5.

Finally, an independent validation of the total amygdaloid complex volume was performed by comparing results from a P ≥ 0.5 thresholding and binarization of the CIT168 atlas and the Freesurfer amygdala labels generated by the HCP structural analysis pipeline. Dice coefficients and Hausdorff distances were computed at the individual level. An MCMC GLMM analysis was performed on the total amygdala volume for the fixed effects of site (CIT vs. HCP), hemisphere (Right vs. Left) and their interaction, and the random effect of subject. MCMC parameters were identical to those used above for analysis of sex, age, and hemisphere effects.

RESULTS

Subdivisions of the amygdala complex are difficult to delineate accurately at the individual subject level in the HCP T1w and T2w data (Fig. 1a). Following unbiased multivariate diffeomorphic registration, boundaries between the largest nuclei, specifically, the lateral, basal, and basomedial nuclei emerged and were more prominent in the T2w template (Figs. 1c and 2).

Figure 1.

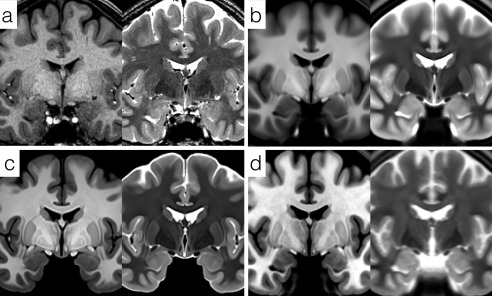
Comparison of high resolution, bivariate whole‐brain templates. (a) Single subject T1w and T2w images from the adult Human Connectome Project HCP500 release. (b) Average HCP500 release templates created using FNIRT non‐linear registration. (c) Unbiased bivariate templates generated by diffeomorphic registration of 168 subjects' data from the HCP500 release. (d) High‐resolution (500 µm, isotropic) templates from the MNI ICBM152 2009b atlas.

We can compare the unbiased multivariate diffeomorphic templates to two other published templates, namely the FNIRT registered templates provided by the HCP based on a superset of the data used here, and the MNI ICBM 2009b high resolution templates (Fig. 1b,d). The HCP templates are qualitatively similar to those generated for this study, but use the entire subject sample (n = 500), including both male and female subjects in a wider age range and the unbiased template generation was based on the FNIRT algorithm which has been demonstrated to provide lower local registration accuracy than the SyN algorithm implemented by ANTs [Avants et al., 2008b; Klein et al., 2009]. Consequently, subdivisions of the amygdala and other midbrain structures in the HCP average templates are less pronounced, though the residual noise texturing in deeper brain areas is less than that seen in our templates due to the larger number of brains averaged. The MNI ICBM152 2009b templates are sampled at 500 µm isotropically and were constructed by non‐linear iterative registration of images from 152 healthy adults [Fonov et al., 2011]. The T1w ICBM template is very comparable in quality to the T1w template constructed here, with amygdala subdivisions such as the lateral nucleus identifiable. However, the T2w template is noticeably more blurred due to the use of two‐dimensional (2D) multislice images with a slice thickness of 2 mm rather than 3D volumetric T2w source data [Fonov et al., 2011] (Fig. 1d).

Amygdala Subdivisions

The amygdala complex is traditionally subdivided into thirteen nuclei in three major groups, namely the deep, superficial, and remaining nuclei [Whalen, 2009] (Table 1). The deep group or basolateral complex (BLA) is comprised of the lateral, basolateral, and basomedial nuclei. The superficial group includes the medial nucleus, cortical nuclei, the nucleus of the olfactory tract, and periamygdaloid cortex, sometimes referred to as the cortical transition area. The remaining nuclei include the anterior amygdaloid area, central nucleus, amygdalohippocampal transition area, and intercalated nuclei. With the exception of the central nucleus, the remaining nuclei have at least one boundary that must be implicitly rather than explicitly defined in the current templates (Fig. 3). For a more detailed and complete review of the cytoarchitecture and functional circuits of the primate amygdaloid complex, see for example [McDonald, 1998; Whalen, 2009].

Figure 3.

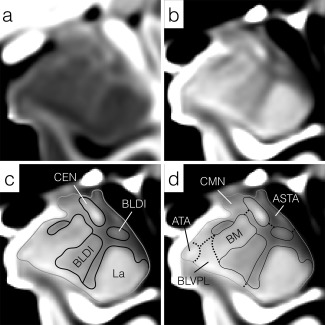
Enlargements of mid rostrocaudal sections through the left amygdala in (a) the T1w and (b) T2w templates. The general approach to subregion delineation is outlined in (c) and (d). Initially, the entire amygdala is delineated (solid gray line) followed by divisions with explicit boundaries (solid black lines), including the lateral nucleus (La), central nucleus (CEN) and dorsal/intermediate divisions of the basolateral nucleus (BLDI). Finally, implicit boundaries such as the ventromedial margin of the basomedial (BM) nucleus, are estimated from a combination of explicit superficial and internal boundary landmarks (d, dotted lines). Regions of the amygdala unassigned to a specific subdivision or nucleus remained to be collected into the whole‐amygdala (AMY (Other)) label. All images have been resampled to 200 µm isotropically and the intensity contrast increased relative to Figure 2 to highlight explicit boundaries within the amygdala. For abbreviations, see Figure 2 and Table I.

Completely and Partially Resolved Nuclei

Lateral nucleus (La)

The lateral nucleus is the primary recipient of neocortical input to the amygdaloid complex and can be divided into four subdivisions histologically, none of which can be differentiated currently by in vivo MRI, or in the templates used here. The lateral nucleus is readily identified in both T1w and T2w templates and is clearly bounded by more heavily myelinated tissue medially and dorsally within the amygdala, by the temporal horn of the lateral ventricle ventrally and caudally and by temporal lobe white matter laterally (Figs. 2 and 3).

Figure 2.

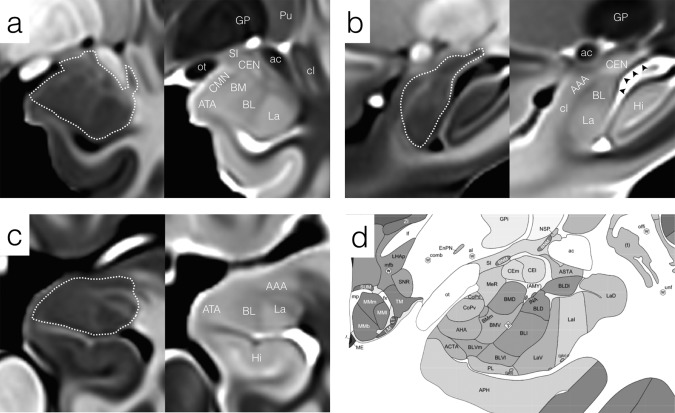
General appearance of the left amygdala and neighboring structures in the CIT168 templates in (a) coronal, (b) sagittal, and (c) axial sections. The approximate margin of the amygdala is indicated by a dotted white contour. (a) Mid rostrocaudal coronal section through the amygdala in T1w (left) and T2w (right) templates. The boundary between La and BL is apparent in both contrasts. (b) Mid medial‐lateral sagittal section locating the amygdala with respect to the anterior commissure and hippocampus. The heavily myelinated stria terminalis is indicated by black arrowheads in the T2w template. (c) Mid dorsal–ventral axial section showing the myelinated fiber bands penetrating and bounding the lateral nucleus (hyperintense in the T1w template). (d) Mid rostrocaudal coronal section through the amygdaloid complex from the Allen Brain Institute 34‐year‐old human reference atlas. Abbreviations: Amygdala subdivisions, Table I; Hi, hippocampus; GP, globus pallidus; Pu, putamen; SI, substantia innominata; cl, claustrum; ac, anterior commissure; ot, optic tract.

Basolateral nucleus (BL)

The basolateral nucleus lies medial to the lateral nucleus from which it receives strong projections. In turn, the basolateral nucleus not only projects strongly to the central and medial nuclei, but also to many cortical regions, closing the sensory information loop between neocortex and amygdala [Whalen, 2009]. The basolateral nucleus is more readily identified in the T2w template and is bounded laterally by the lateral nucleus and medially by the basomedial nucleus and cortical transition area. Histologically, the basolateral nucleus can be further divided into three sub‐nuclei: the magnocellular or dorsal (BLD), intermediate (BLI), and parvocellular or ventral (BLV) divisions (Fig. 2d). The dorsal and intermediate divisions stain far more strongly for acetylcholinesterase than does the ventral division [Garćıa‐Amado and Prensa, 2012]. A similar contrast also appears in the T2w template and is more likely to be driven by differences in microstructural organization, including cell sizes between BLD, BLI, and BLV, than by myelination level [Garćıa‐Amado and Prensa, 2012]. Consequently, the dorsal and intermediate divisions are merged into a single BLDI division. No visible boundary between BLV and the paralaminar nucleus (see below) can be inferred in either the T1w or T2w template, so these two divisions are merged into a single BLVPL label.

Basomedial Nucleus (BM)

The third and final nucleus of the deep group, the basomedial (or accessory basal) nucleus receives strong projections from the lateral nucleus and in turn projects strongly to the neighboring central nucleus with moderate projections to a subset of the superficial nuclei. In the templates, BM is slightly hyperintense relative to surrounding tissue in the T2w template with a hypointense core (Figs. 2 and 3). The ventral boundary of BM with BLV is poorly defined in both T1w and T2w contrasts. The dorsal medial extent of BM coincides with a presumably more heavily myelinated structure (possibly associated with the stria terminalis) which appears as hypointense in the T2w template and is used as a dorsomedial boundary in [Garćıa‐Amado and Prensa, 2012] (Fig. 3). The rostral and caudal boundaries of BM are also poorly defined in both contrasts and were inferred from comparison with the histological atlases.

Cortical and Medial Nuclei (CMN)

The cortical and medial nuclei of the superficial group lie along the dorsomedial surface of the amygdala. The cortical nucleus receives projections from the BLA, central nucleus, and medial nucleus with the anterior division of the cortical nucleus (CoA) receiving strong direct projections from the olfactory bulb [Whalen, 2009]. Internal boundaries between CoA, posterior cortical nucleus (CoP), the amygdalohippocampal area (AHA), nucleus of the lateral olfactory tract (NLOT), and the medial nucleus (Me) cannot be identified in either the T1w or T2w template, so for this atlas all these divisions are merged into a single CoMe group (Fig. 3). The CoMe group is bounded medially by BM, ventrally by the amygdalocortical and amygdalohippocampal transition areas (ATA), and dorsally by the medial nucleus (Me). Only the dorsomedial border of this nucleus, bounded by cerebrospinal fluid (CSF), is well defined in the imaging templates (Figs. 2 and 3).

Central Nucleus (CEN)

The central nucleus is a primary recipient of intrinsic connections within the primate amygdala and one of the major output nuclei. It lies dorsally and caudally within the complex and is hyperintense with relatively well‐defined borders in all directions in the T2w template (Figs. 2 and 3). The full rostral–caudal extent of this nucleus is best appreciated in sagittal sections (Fig. 2b), where the caudal tail extends over the anterior horn of the lateral ventricle beyond the head of the hippocampal complex.

Anterior Amygdala Area (AAA)

The anterior amygdala area occupies a rostral and dorsal position within the amygdala complex and is separated in part from the basolateral complex by a thin band of myelinated fibers visible in T1w and T2w templates, particularly in sagittal and axial sections. The AAA is contiguous with the periamygdaloid claustrum and this boundary is invisible and therefore implicit in MR images. The AAA is hypointense in the T1w template and is better delineated in this contrast than in the T2w template (Fig. 2b,d).

Amygdala Transition Areas (ATA)

Three amygdala transition areas are identified in the Allen Brain Atlas: the amygdalocortical, amygdalohippcampal, and amygdalostriatal. The amygdalocortical and amygdalohippocampal areas are contiguous and together form a band separating the entorhinal cortex from the corticalmedial group (CMN) of the amygdala. The amygdalostriatal transition area is anatomically distinct and treated separately below. The absence of a visible boundary between the first two transition areas forces their merger in this atlas into a single ATA. The periamygdaloid cortex described by [Pitkänen and Amaral, 1998] is similarly indistinguishable and is merged into ATA. This combined transition area is delineated here in coronal sections using inferred boundaries supported by neighboring anatomic features, specifically the semiannular sulcus and the medial angle of the white matter separating the ventral amygdala boundary from the dorsal surface of the entorhinal cortex. The amygdalostriatal Transition (ASTA) lies medial and ventral to the temporal branch of the anterior commissure and is most easily delineated in coronal T1w sections as a slightly hypointense band between the central nucleus and the anterior commissure, ventral to the substantia innominata and contiguous with the ventral putamen with which it has an implicit boundary (Fig. 3).

Unresolved Nuclei

Paralaminar nucleus (PL)

The paralaminar nucleus (PL) is readily distinguished in Nissl stained histological sections but is merged with the BLV to form the BLVPL label in this delineation for reasons outlined above. It should be noted that the contrasting band (hypointense in T1w, hyperintense in T2w) seen in coronal sections running the full length of the ventral boundary of the amygdala (Fig. 3a,b) is unlikely to correspond to the PL. Inspection of sagittal sections (Fig. 2b) suggests that this is most probably a partial volume effect from the thin layer of CSF separating the hippocampal head from the ventrocaudal surface of the BLA.

Intercalated Nuclei (I)

The intercalated nuclei are small cell masses found at the boundaries between the basal, basomedial, and lateral nuclei and ventral to the central nucleus [Whalen, 2009]. Although functionally important in mediating interactions between lateral and central nuclei, they are unresolvable by MRI and are omitted from this atlas, without assignment to other nuclei.

Neighboring Structures

The amygdala is surrounded by a variety of heterogeneous tissue structures, which, although not part of the amygdaloid complex, help define its superficial boundaries. The head of the hippocampal complex lies immediately caudal to the amygdaloid complex, separated by a thin extension of the temporal horn of the lateral ventricle that remains unresolved in the current templates. Subfields of the hippocampus are not identified in this atlas, since there have been extensive efforts to develop robust automated segmentation methods for this area [Adler et al., 2014; Pipitone et al., 2014; Yushkevich et al., 2015]. The amygdaloid complex is partly bounded medially and ventrally by the temporal horn of the lateral ventricle, which is very well defined in the T2w template. The caudal extensions of the central and medial nuclei are separated from the lateral ventricle by the stria terminalis, a major output pathway of the amygdala running caudally from its origins in the basomedial and central nuclei to its terminations in the thalamus, bed nuclei of the stria terminalis (BNST), hypothalamus and septum. The stria terminalis is very well defined in both T1w and T2w templates due to its high level of myelination, which is best appreciated in sagittal sections (Fig. 2b).

The ventral, diffuse, limitans, and periamygdala divisions of the claustrum [Mai et al., 2008] provide important landmarks for the segmentation of the amygdala complex and are marginally better defined in the T1w template than in the T2w template (Fig. 2a,b). As mentioned previously, the periamygdaloid and ventral claustrum are contiguous or adjacent to the rostral amygdala and provide useful landmarks for constraining the amygdala boundary. The ventral tail or peduncle of the putamen runs medially to the anterior commissure and can be located in the imaging templates by extension of the main body of the putamen in coronal and sagittal sections. Subdivisions of the ventral putamen, including the peduncle of the lentiform nucleus cannot be identified in the CIT168 templates. The substantia innominata, including the basal nucleus of Meynert, provides a convenient dorsal boundary to the mid‐rostrocaudal amygdaloid complex. It appears hypointense in the T1w template and extends mediolaterally between the optic tract and anterior commissure.

Finally, several large or distinct white matter structures lie in close proximity to the amygdaloid complex. The optic tract and anterior commissure are two of the most prominent white matter tracts neighboring the amygdala complex dorsally. The optic tract ascends dorsolaterally from the chiasm and follows the medial boundary of the medial nucleus until its termination in the lateral geniculate nucleus. The temporal branch of the anterior commissure descends laterally to the main amygdaloid complex in close proximity to the amygdalostriatal area.

Individual and between group volume differences

The template space probabilistic atlas formed by averaging all 16 manually labeled validation templates (Fig. 4) was mapped to individual spaces by inverse diffeomorphic warping, where amygdala and subdivision volumes could be estimated for group analysis. Example individual variations can be visualized in a maximum likelihood representation [Amunts et al., 2005] of the transformed probabilistic atlas (Fig. 5). Mean total amygdala and subdivision volumes by age and sex are summarized in Table 2 and Figures 6 and 7, both in absolute units (mm³) and following normalization of the amygdala volume to intracranial volume (ICV) and the subdivision volumes to the amygdala volume. We find that adult amygdala volumes in this study range from approximately 1,000 to 2,000 mm³ (1.0–2.0 mL) with coefficients of variance (CoVs) for amygdala and subdivision volumes ranging between 8% and 14%. The MCMC GLMM analysis (Table 3) revealed a slight but consistent asymmetry in the absolute and ICV‐normalized volumes of the entire amygdaloid complex (Fig. 6a,c), with the right amygdala being about 2% larger than the left. Weak, but statistically significant left–right asymmetries were observed in absolute La volume and normalized volumes of the BL and BM divisions (Fig. 7a,c). No effect of age was observed (Figs. 6b,d and 7b,d), which is unsurprising considering that all subjects were adults aged between 22 and 35 years old, at the tail end of development and with little age‐related atrophy. Male subjects had larger amygdala and subdivision volumes in general, but this effect disappeared following normalization to total amygdala or intracranial volume (Table 3).

Figure 4.

Probabilistic maps for the entire amygdala complex and all 10 subdivisions (nine nuclear and one non‐nuclear) generated from a total of 16 manual segmentations by two experienced observers. The non‐nuclear AMY (Other) label represents amygdala tissue within the boundary but unassigned to any particular nucleus or transition area. All labeling was performed in the CIT168 mid‐space using templates created by random, counter‐balanced subsampling of 84 from the 168 individual images.

Figure 5.

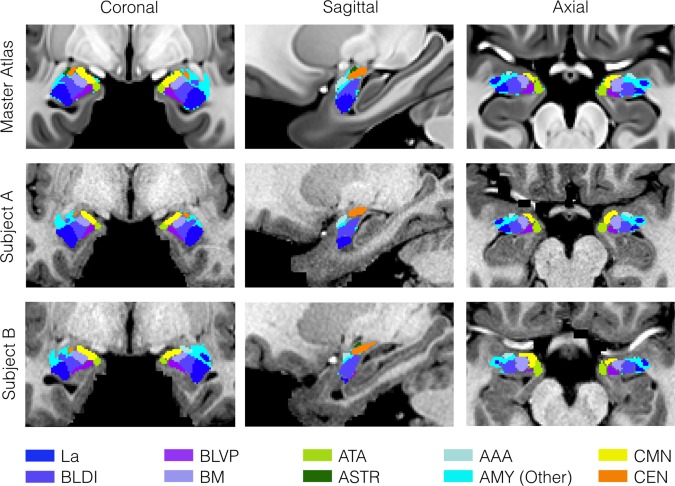
Comparison of atlas labels in the CIT168 template space and two individual subjects. Maximum likelihood labels for the amygdala sub‐divisions was generated by simple competition between the probabilistic labels with a P ≥ 0.5 threshold. Labels were mapped from the template to individual spaces by inversion of the individual diffeomorphic warp transforms used during unbiased template construction.

Table 2.

Total amygdala and subdivision volumes by sex and age group

Amygdala and subdivision volumes (mm3)
		Amygdala		La		BLDI		BLVP		BM		CMN		CEN		AAA
Sex	Hemisphere	Mean (mm3)	CoV (%)	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV
Female	Left	1351.1	8.8	301.2	10.6	174.9	10.7	103.9	12.1	98.5	12.6	138.7	12.9	44.8	9.8	50.8	13.0
	Right	1396.9	8.6	312.9	11.0	175.7	11.0	105.3	12.0	100.3	11.9	142.9	13.2	45.7	10.3	52.4	12.2
Male	Left	1542.5	8.4	334.1	11.7	198.1	9.5	118.0	11.3	114.0	12.7	160.6	13.3	52.8	12.0	59.3	13.5
	Right	1570.8	8.8	346.3	12.5	195.1	10.7	117.9	10.0	114.4	13.8	161.3	14.1	53.0	11.0	59.3	13.3

Normalized amygdala and subdivision volumes
		Amygdala		La		BLDI		BLVP		BM		CMN		CEN		AAA
Sex	Hemisphere	Mean x1000	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV	Mean	CoV
Female	Left	1.04	6.91	0.23	10.03	0.13	10.01	0.08	10.30	0.08	11.09	0.11	11.07	0.03	8.25	0.04	11.97
	Right	1.07	6.68	0.24	10.37	0.13	10.53	0.08	10.06	0.08	10.10	0.11	10.63	0.04	10.17	0.04	11.41
Male	Left	1.04	7.42	0.23	12.05	0.13	9.92	0.08	10.49	0.08	11.65	0.11	11.86	0.04	10.31	0.04	11.97
	Right	1.06	7.65	0.23	12.81	0.13	10.49	0.08	8.40	0.08	11.90	0.11	12.85	0.04	9.33	0.04	10.64

The upper table shows mean and coefficient of variation (mean/sd × 100%) of the absolute volume in mm³ for each subdivision and the entire amygdala (sum of subdivision volumes). The lower table shows the same data normalized at the individual level. The total amygdala volume is normalized to the intracranial volume and multiplied by 1000 for clarity. The subdivision volumes are normalized to the total amygdala volume.

Figure 6.

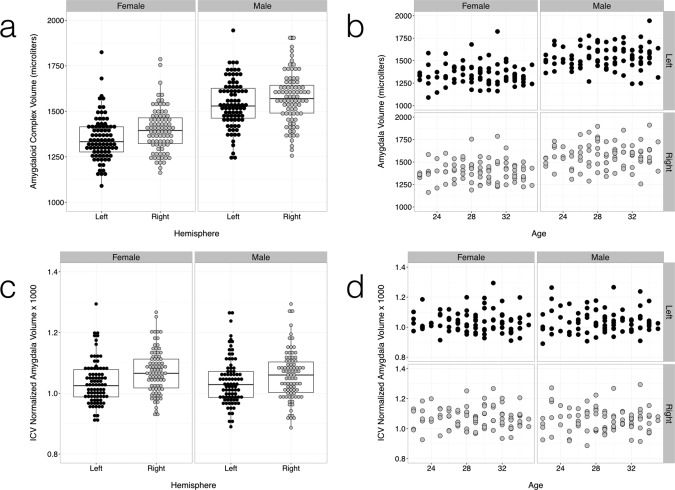
Group distributions of absolute (a,b) and ICV normalized (c,d) amygdala volumes over all individuals. Individual amygdala volumes were calculated by inverse diffeomorphic mapping of the probabilistic labels to individual subject spaces. Amygdalae were on average larger in volume in males than in females (a,c), with a slight (∼2%) overall bias towards a larger right amygdala. Normalization to ICV eliminated the sex difference in volume. No effect of age on amygdala volume was observed in the age group studied (adults, 22–35 years old) (b,d). Results for the left and right amygdalae are in dark gray and light gray respectively. Linear models are overlaid with 95% confidence intervals in the volume versus age graphs. See Tables II and III for statistical summaries.

Figure 7.

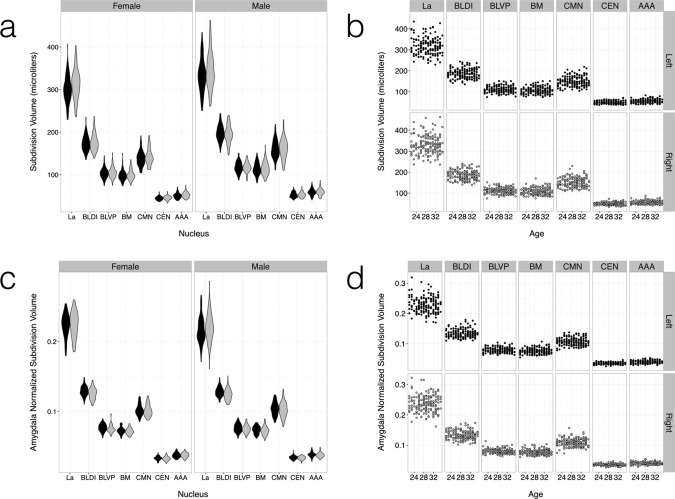
Group distributions of absolute and normalized volumes for the seven largest amygdala subdivisions over all individuals (a,c). The subdivision volumes follow the same trends observed in the total amygdala volume (Fig. 7), with group sex differences vanishing after normalization (c,d) and no age effect (b,d). Results for the left and right amygdalae are in dark gray and light gray, respectively. Linear models are overlaid with 95% confidence intervals in the volume versus age graphs. See Tables II and III for statistical summaries.

Table 3.

Results of Markov chain Monte Carlo generalized linear mixture modeling (MCMC GLMM) of both absolute and normalized amygdala subdivision models

Amygdala and subdivision volumes (microliters)
	Amygdala		La		BLDI		BLVP		BM		CMN		CEN		AAA
(Intercept)	1,148	1,458***	270	354***	149	196***	90	119***	76	107***	105	153***	38	50***	40	56***
Sex (Male)	151	219***	22	44***	16	27***	10	17***	11	18***	15	26***	6	9***	6	10***
Age	−4	6	−2	1	−1	1	−1	0	−0	1	−0	1	−0	0	−0	0
Hemisphere (Right)	27	46***	8	15***	−3	1	−1	2	−0	3	0	4*	−0	1	−0	2

Amygdala and subdivision normalized volumes
	Amygdala (×1,000)		La (×100)		BLDI (×100)		BLVP (×100)		BM (×100)		CMN (×100)		CEN (×100)		AAA (×100)
(Intercept)	0.967	1.143 ***	21.1	25.3***	12.3	14.0***	7.4	8.5***	6.5	7.6***	8.8	10.8***	3.1	3.7***	3.2	4.0***
Sex (Male)	−0.026	0.017	−1.0	0.0*	−0.3	0.1	−0.2	0.1	0.0	0.2	−0.1	0.4	0.0	0.2**	0.0	0.1
Age	−0.004	0.002	−0.1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.1	0.0	0.0	0.0	0.0
Hemisphere (Right)	0.019	0.033 ***	0.0	0.4*	−0.5	−0.3***	−0.2	−0.1**	−0.2	0.0**	−0.2	0.0	−0.1	0.0*	−0.1	0.0

95% confidence intervals are reported with significance indicated by asterisks (*: P < 0.01, **: P < 0.001, ***: P ≈ 0.0). Significant inter‐individual differences (intercepts) in both absolute and normalized volumes are observed. Right amygdala volumes are slightly larger in general, but this trend is not observed consistently in absolute or normalized subdivision volumes. Normalization to the intracranial volume (for the amygdala) or total amygdala volume (for the subdivisions) eliminates almost all sex differences.

Intra‐ and Interobserver Reproducibility

The probabilistic maps for each amygdala subdivision and the entire amygdaloid complex (Fig. 4) encode both intra‐ and inter‐observer differences, and structural variability between the randomized validation templates. Intra‐ and inter‐observer Dice and Hausdorff similarity measures for the entire amygdala and subdivision volumes are summarized in Table 4 and reveal a high level of intraobserver reproducibility for the whole amygdaloid complex and the largest subdivisions, La, BLDI with Dice coefficients exceeding 0.8. All other subdivisions exhibit Dice coefficients greater than 0.6, with the exception of the residual whole‐amygdala tissue label [AMY (Other)]. Interestingly, the inter‐observer similarities are consistently higher than the intra‐observer similarities for all labels, suggesting that there were non‐trivial differences between the validation templates, which could be reliably captured by independent observers. The sensitivities of the Dice coefficient and Hausdorff distance to small label volumes and outlier voxels, respectively, are discussed below.

Table 4.

Internal and external validations of entire amygdaloid complex and individual nuclei or nuclear group labels

Intra‐ and inter‐observer similarity
	Amygdala		La		BLDI		BM		CEN		CMN		BLVP		ATA		ASTA		AAA		AMY (Other)
	D	H (mm)	D	H	D	H	D	H	D	H	D	H	D	H	D	H	D	H	D	H	D	H
Intra‐observer Observer 1	0.90	2.24	0.87	1.19	0.83	1.51	0.78	1.51	0.74	1.46	0.72	1.79	0.72	3.03	0.63	2.09	0.62	1.74	0.65	2.03	0.45	2.82
Observer 2	0.93	2.23	0.86	1.28	0.79	1.55	0.73	1.94	0.71	1.94	0.70	2.24	0.64	1.73	0.63	2.34	0.59	2.68	0.63	1.96	0.51	2.82
Combined	0.91	2.24	0.87	1.24	0.81	1.53	0.76	1.72	0.73	1.70	0.71	2.01	0.68	2.38	0.63	2.22	0.60	2.21	0.64	1.99	0.48	2.82
Inter‐observer	0.91	2.52	0.88	1.33	0.82	1.55	0.80	1.11	0.77	2.19	0.77	1.88	0.73	2.74	0.76	1.31	0.74	1.26	0.78	1.37	0.50	3.31

Inter‐atlas similarity
Threshold		Amygdala		Basolateral Complex		Corticomedial and Superficial Groups		Amygdalostriatal Transition Area
		D	H (mm)	D	H (mm)	D	H (mm)	D	H (mm)
Harvard–Oxford	50%	0.75	3.00	–	–	–	–	–	–
Juelich	50%	0.65	5.39	0.56	7.14	0.35	10.25	0.00*	Undefined*
	25%	0.65	3.46	0.52	5.10	0.46	2.45	0.22	2.83

Label similarities were calculated using the Dice coefficient (D) and Hausdorff distance (H). Intra‐ and inter‐observer Dice coefficients exceed 0.9 for the entire amygdaloid complex and remain high in the basolateral complex with corresponding Hausdorff distances on the order of 1.0–2.5 mm in these regions. Dice coefficients decrease with nuclear volume and are lowest for the AMY (Other) label. Similarly, Hausdorff distances increase generally with subdivision volume, up to approximately 3.3 mm for the AMY (Other) label. Intra‐atlas comparisons between the CIT168, Harvard–Oxford, and Juelich probabilistic atlases were calculated for amygdala‐related labels using a 50% probability threshold throughout. *The Amygdalostriatal transition area label does not survive a 50% threshold, so an additional comparison was performed using a 25% threshold.

Comparison to Other Atlases

Inter‐atlas similarity comparisons between entire amygdaloid complex and subdivision labels in the CIT168 Amygdala, Harvard–Oxford, and Juelich atlases are summarized in Table 4 and Figure 8. Similarity between the CIT168 and Harvard–Oxford whole amygdala labels (D = 0.75, H = 3.0 mm) was comparable to that seen for intra‐ and inter‐observer similarities for many of the smaller subdivisions of the CIT168 atlas (D = 0.6–0.8, H = 1.0–2.5 mm). Similarity to the Juelich subdivisions was substantially lower, with whole amygdala Dice coefficients between 0.6 and 0.7. Only moderate similarity was observed for the basolateral complex and poor similarity for the corticomedial/superficial and ASTA labels (D < 0.5, H = 2.5–10.0 mm). Reasons for these poorer similarity metrics are discussed below.

Figure 8.

Comparison of amygdaloid complex probabilistic labels for (a) the CIT168, (b) Harvard–Oxford, and (c) Juelich cytoarchitectonic atlases. Voxel tissue probabilities are indicated in orange‐yellow for P ≥ 0.5 (a–c) and in extended lower for the Juelich atlas in blue for 0.25 ≤ P < 0.5 (c). Comparison of amygdala subdivision probabilities between the CIT168 atlas (d,f,h) and the Juelich atlas (e,g,i). The subregions are as follows: (d,e) Basolateral group (La + BL + BM), (f,g) Centromedial + Superficial Group (CMN + CEN + ATA + AAA) and (h,i) Amygdalostriatal area (ASTA). Voxel tissue probabilities are indicated in orange‐yellow for P ≥ 0.5 (a–c) and are extended lower for the Juelich atlas in blue for 0.25 ≤ P < 0.5. No voxels survived a P ≥ 0.5 threshold for the Juelich ASTA label.

As a final external validation the total left and right amygdaloid complex volume obtained from Freesurfer segmentation in the HCP pipeline and that obtained from integration of the equivalent probability map in the CIT168 atlas are compared in Figure 9. A MCMC GLMM of total amygdala volume for random effects of subject and fixed effects of site, hemisphere and their interaction resulted in the following posterior mean estimates: Intercept = 1,417 µL, Site (HCP) = 193 µL, Hemisphere (Right) = 34 µL, and Site (HCP) by Hemisphere (Right) = 54 µL. MCMC approximations of posterior densities are summarized in Figure 9.

Figure 9.

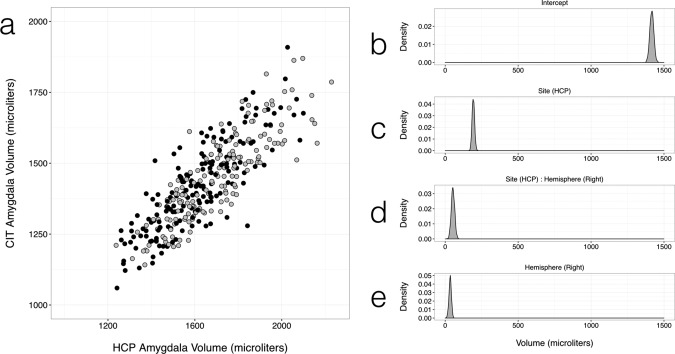
Comparison of CIT168 total amygdala volumes with those estimated by the HCP in the same individuals. (a) Scatter plot of total amygdala volume in the left (black) and right (gray) hemispheres estimated by Freesurfer in the HCP structural analysis pipeline and that estimated from the P ≥ 0.5 thresholded volume from the CIT168 probabilistic atlas. Posterior density estimates by an MCMC GLMM using the data of (a), for (b) Intercept, (c) Site (HCP), (d) the interaction of Hemisphere (Right) and Site (HCP), and (e) Hemisphere (Right).

DISCUSSION

The aim of this study was to address the ongoing need for a finer grained in vivo parcellation of the human amygdaloid complex, than is currently available using heuristic or automated methods. For this purpose, we used an accurate, symmetric diffeomorphic registration approach to create unbiased multivariate templates based on the high‐resolution in vivo structural MRI data provided by the Human Connectome Project. The specific diffeomorphic registration approach used (SyN) is one of the most consistently accurate of such algorithms for inter‐subject registration [Klein et al., 2009] and the implementation by ANTs remains one of the few to support unbiased, multivariate (i.e. simultaneous T1w and T2w) template construction. Using this approach, we were able to extend on previous efforts of in vivo parcellations of the amygdala, as it was possible to distinguish 9 amygdala nuclei. Furthermore, our results contribute to the ongoing investigation for assessing individual variations and hemispheric asymmetries in total amygdala and subdivision volumes in healthy adults. The use of accurate, symmetric diffeomorphic registration allows for more extreme deformations, extending potential application of the atlas to pediatric, geriatric, and pathological brains.

Although a variety of nomenclatures exist for the divisions of the amygdala complex, we have attempted to harmonize these in a way that is consistent with identifiable tissue divisions observed in the T1w and T2w image templates (see Table 1). Because the amygdala delineation developed here is based on in vivo MRI, particular care was taken to address this method's well‐known constraints during atlas construction. The most notable constraint on in vivo imaging in humans is the necessary trade‐off between total imaging time, signal‐to‐noise ratio (SNR), contrast‐to‐noise ratio (CNR) and spatial resolution seen in individual subject data (Fig. 1a). The lower SNR of deep brain regions results in a lower CNR between subdivisions of the amygdala, and is exacerbated by increased structured noise from acquisition acceleration (in this case GRAPPA) [Griswold et al., 2002]. Consequently, there is a danger that artificial local boundaries arising from structured noise will influence the diffeomorphic mapping, rather than true tissue boundaries. To address this, we use both T1w and T2w individual images and a joint cost function, which reduces the chance that identically structured noise is present in both imaging contrasts, which in turn minimizes the impact of noise structuring on the final joint templates.

Multivariate diffeomorphic template construction has the additional advantage that the resulting inverse warp fields can be applied to the anatomical delineations on the template level, to infer volumes and boundaries of amygdala nuclei at the individual level. While some subnuclei boundaries are clearly represented in individual in‐vivo T1w or T2w images, this inference is necessary, as we found that not all boundaries of subnuclei and signal gradients are apparent to a human observer in the individual in‐vivo T1w and T2w images. This inference is possible as we do observe well defined internuclear boundaries and signal gradients at the template level, and the presence of boundaries and gradients in the template averages indicate that this information is present in the noisy individual images as well. Simulation of template construction in numerical phantoms confirms that the bivariate diffeomorphic approach is reliable at the contrast‐to‐noise ratios within individual amygdalae for HCP data (see Supporting Information). Finally, inconsistent registration of a given internuclear boundary over all individuals will reduce the apparent sharpness of the boundary in the template. This in turn reduces the ability of observers to identify this boundary reproducibly and will be encoded as a low boundary gradient in the probabilistic atlas.

A previous study [Brabec et al., 2010] observed some discrepancy in the post mortem literature regarding total amygdala volume and interhemispheric asymmetry, most of which arises from differences in definition of amygdala boundaries and in the use of corrections for tissue shrinkage. The large variance in amygdala volume estimates from in vivo MRI has been noted before in an earlier meta‐analysis by [Brierley et al., 2002]. This study concluded that anatomic definition was the largest methodological factor influencing amygdala volume estimates. For example, previous volume estimates often suffered from the difficulty of differentiating the ventral claustrum from amygdala at 1 mm isotropic T1w images. In contrast, this differentiation is possible at the resolution and contrast of our CIT168 templates. Volumetric analysis of the amygdala complex revealed a high level of inter‐hemispheric symmetry with no sex or age‐related differences following normalization to intracranial volume (ICV). The right amygdala volume was observed to be approximately 2% larger in our sample (Table 3).

Intra‐ and inter‐observer labeling was found to be highly reliable for the entire amygdala and most distinct subdivisions (La and BLDI), and reliable for all the remaining subdivisions except for the residual amygdala tissue label (D < 0.5, H > 2.5 mm). This result is perhaps unsurprising, but the construction of a probabilistic rather than deterministic atlas helps encode observer uncertainty in a natural and well‐established way. Comparison of the P ≥ 0.5 amygdaloid complex label between the macroscopically defined CIT168 and Harvard–Oxford atlases is encouraging, with a relatively high similarity coefficient (0.76), suggesting that the external amygdaloid complex boundary is generally comparable between the two atlases. Comparison of the HCP Freesurfer amygdala volumes with those estimated from the CIT168 atlas in the same 168 subjects (Fig. 9) reveals a modest effect of site (193 µL) most likely due to site‐dependent differences in delineation instructions. Only a small interaction between site and hemisphere (54 µL larger right amygdala for HCP) is observed, suggesting that only minimal interhemispheric bias is introduced by the reflection warp used to map labels from the left to right amygdala. This is consistent with the observed accuracy of the reflection warp in mapping homotopic structures between the left and right amygdala (see Supporting Information). The right amygdala is 34 µL or 2% larger on average by this method, consistent with previous results above.

The Juelich probabilistic atlas is derived from extremely accurate delineations in histological sections and is the only widely distributed probabilistic atlas to include subdivisions of the amygdala.

Much of the boundary uncertainty seen in Figure 8c,e,g and i may arise from the regularization of the elastic deformations used to construct the probabilistic maps, which in turn reflects the tremendous technical challenge of registering histological sections to volumetric MR data [Amunts et al., 2005; Eickhoff et al., 2005]. The similarities between the CIT168 and Juelich amygdala divisions are moderate to poor, but we do not conclude that the CIT168 atlas is unreliable at defining amygdala subdivision boundaries, only that direct comparison between two atlases with such broadly different boundary uncertainties cannot be well represented by metrics such as the Dice coefficient or Hausdorff distance.

Finally, any atlas or template delineation should be an evolving resource, amenable to changes and corrections as approaches to the nomenclature and assignment of tissue divisions improve. This is particularly appropriate when the templates and labels are in a digital form and version control and curation are readily performed using database management tools. The current templates are of sufficient quality to allow similar parcellations of major mid‐brain structures, including the thalamus and basal ganglia, containing many tens of identifiable divisions. Consequently opening the atlas to further editing by independent groups provides a potential mechanism for probabilistic atlas construction across multiple observers over all subcortical structures.

CONCLUSIONS

The amygdaloid complex plays a key role in social and emotional human behavior, but the details of this role and its relation to the rest of the brain remain an open question. As the spatiotemporal resolution of functional neuroimaging methods improves there is an increasing and unmet demand for an in vivo reference template that allows accurate localization of functional activity to subregions and even nuclei of the amygdala. To address this, we have developed a candidate template parcellation based on high‐resolution MRI data from 168 neurotypical adult brains offering probabilistic delineations for ten subdivisions (nine nuclear and one non‐nuclear) of the human amygdaloid complex. The group average templates and associated delineation can be registered accurately to high‐quality individual structural and functional images acquired in vivo, allowing assignment of functional activity to subregions of the amygdala with a specificity not previously attainable using existing atlases.

Supporting information

Supporting Information