Substrate and Cofactor Dynamics on Guanosine Monophosphate Reductase Probed by High Resolution Field Cycling ³¹P NMR Relaxometry

Abstract

Guanosine-5′-monophosphate reductase (GMPR) catalyzes the reduction of GMP to IMP and ammonia with concomitant oxidation of NADPH. Here we investigated the structure and dynamics of enzyme-bound substrates and cofactors by measuring ³¹P relaxation rates over a large magnetic field range using high resolution field cycling NMR relaxometry. Surprisingly, these experiments reveal differences in the low field relaxation profiles for the monophosphate of GMP compared with IMP in their respective NADP⁺ complexes. These complexes undergo partial reactions that mimic different steps in the overall catalytic cycle. The relaxation profiles indicate that the substrate monophosphates have distinct interactions in E·IMP·NADP⁺ and E·GMP·NADP⁺ complexes. These findings were not anticipated by x-ray crystal structures, which show identical interactions for the monophosphates of GMP and IMP in several inert complexes. In addition, the motion of the cofactor is enhanced in the E·GMP·NADP⁺ complex. Last, the motions of the substrate and cofactor are coordinately regulated; the cofactor has faster local motions than GMP in the deamination complex but is more constrained than IMP in that complex, leading to hydride transfer. These results show that field cycling can be used to investigate the dynamics of protein-bound ligands and provide new insights into how portions of the substrate remote from the site of chemical transformation promote catalysis.

Introduction

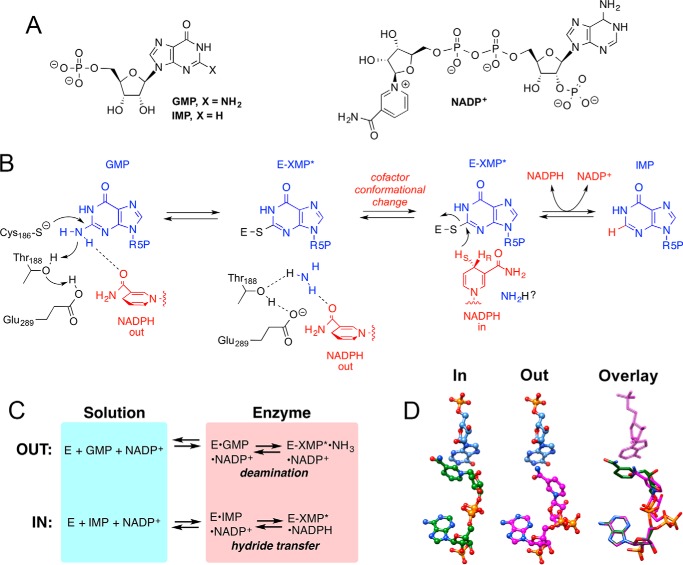
Enzymes modulate the dynamics of bound substrates and cofactors. Although this modulation is a critical feature of catalysis, few studies have addressed the dynamics of bound ligands experimentally. Guanosine-5′-monophosphate reductase (GMPR)³ presents an excellent opportunity to investigate the dynamics of substrate and cofactor conformations in an enzyme active site. GMPR catalyzes the reductive deamination of GMP to IMP and NH₃ with concomitant oxidation of NADPH (Fig. 1). This enzyme plays an important role in the interconversion of guanine and adenine nucleotides and can also provide a route for GMP biosynthesis in ammonia-rich environments. The enzyme is a homotetramer of 37-kDa subunits. The GMPR monomer has a (β/α)₈ structure, also known as a TIM barrel, which is the most common enzyme fold, and contains the standard phosphate binding loop that is found throughout the TIM barrel superfamily (1, 2). The reaction consists of two different chemical transformations, deamination and hydride transfer (3). In the deamination step, Cys¹⁸⁶ attacks C2 of GMP to create a covalent thioimidate intermediate (E-XMP*; Fig. 1, A and B). The ammonia leaving group is activated by proton relay through the Thr¹⁸⁸-Glu²⁸⁹ dyad. Approximately 15–20% of the enzyme accumulates as E-XMP* during the steady state. The second step involves hydride transfer from NADPH to E-XMP*, producing IMP. GMPR also catalyzes two partial reactions: 1) GMP reacts to form ∼20% E-XMP*·NH₃ in the presence of NADP⁺, and 2) in the absence of ammonia, IMP and NADP⁺ react to form ∼20% E-XMP*·NADPH (Fig. 1C) (3).

FIGURE 1.

The GMPR reaction. A, structures of substrates and cofactor. B, the proposed mechanism. C, partial reactions catalyzed by GMPR. D, the superimposed IN and OUT IMP and cofactor conformations as found in the x-ray crystal structure of E·IMP·NADPH (PDB entry 2C6Q). In the overlay, IMP from the OUT conformation is displayed as green lines, visible through the transparent magenta sticks of IMP from the IN conformation. This figure was rendered with UCSF Chimera (27).

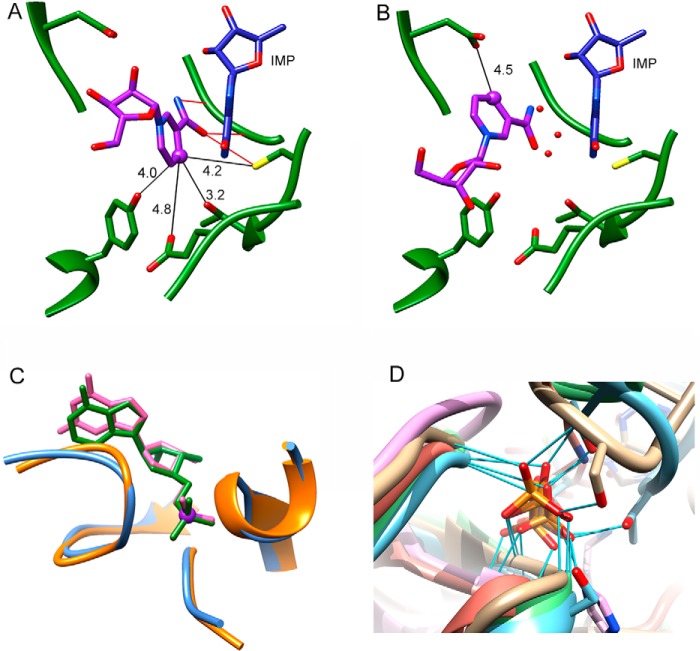
How does GMPR catalyze two different chemical transformations at the same active site? X-ray crystal structures of the GMPR complex with IMP and NADPH revealed the presence of two different cofactor conformations (Fig. 1D) (3). In the “IN” conformation, the nicotinamide ring of the cofactor is stacked parallel against the purine base of IMP, in an alignment suitable for hydride transfer. In the “OUT” conformation, the nicotinamide is far away from the purine ring, as would be required for the deamination step. In addition, in the IN conformation, the nicotinamide predominantly interacts with atoms from protein and IMP (Figs. 1D and 2A), whereas in the OUT conformation, the nicotinamide moves away from IMP and interacts with several water molecules (Fig. 2B). The cofactor diphosphates also change position, whereas the adenosine portion of the cofactor, including the monophosphate, remains in the same position. Likewise, the position of IMP, including the monophosphate, is unchanged in the two complexes (Fig. 1D). The position of IMP observed in the NADPH complex is very similar to that of GMP in the binary E·GMP complex (Fig. 2C) (4). The substrate monophosphates bind in the standard phosphate binding site found in many (β/α)₈ proteins. These observations suggest that the interactions of the substrate monophosphate remain constant throughout the catalytic cycle.

FIGURE 2.

Interactions of substrate and cofactors with GMPR. A, interaction of nicotinamide riboside (purple) in the IN conformation (PDB code 2C6Q; subunit B). Residues within 5 Å of nicotinamide are shown (the diphosphates and 2′-phosphoadenosine are omitted for clarity). The distances are depicted by black lines and have Å units. Nicotinamide hydrogen bonds are presented by red lines. IMP is depicted in blue, and GMPR is shown in green. B, interactions of the nicotinamide riboside portion of NADP⁺ (purple) in the OUT conformation (PDB code 2C6Q; subunit A). The red spheres represent additional water molecules that were found in the OUT conformation within 3.5 Å of inosine. C, substrate phosphate group binding in GMPR. Structure and interaction of phosphate group in E·GMP (backbone in orange and GMP in magenta; PDB code 2A7R) and E·IMP·NADPH (backbone in steel blue and IMP in green; PDB code 2C6Q) crystal structures. D, superposition of the standard phosphate binding site in (β/α)₈ barrel proteins. Representatives of five different (β/α)₈ superfamilies are shown (2): GMPR (2C6Q, chain A) (tan); thiamine phosphate synthase (2TPS, chain A) (blue); quinolinate phosphoribosyltransferase (1QPR, chain A) (pink); triose-phosphate isomerase (1TPH, chain 1) (green); and ribulose-bisphosphate carboxylase/oxygenase (1RBL, chain A) (orange). The hydrogen bonds between the phosphate group and the protein residues are depicted by light blue lines. This figure was rendered with UCSF Chimera (27).

Although there is some experimental support for the catalytic relevance of the IN and OUT conformations (3), it is important to recognize that the E·IMP·NADPH complex is inert and may not actually mimic catalytically competent complexes. More importantly, the static views provided by the x-ray crystal structure do not provide any information about the dynamics of bound substrates and cofactors.

We used an underappreciated NMR technique, subtesla high resolution field cycling NMR relaxometry (5–9), to study the dynamics of GMP, IMP, and NADP^{+ 31}P nuclei when bound to GMPR. Field cycling relaxometry, particularly of ¹H, is a mature field (10–12). Major components of the sample (often solvent) dominate the relaxation profile because all chemical shifts overlap as the field decreases. The extension of field cycling to a “high resolution” mode provides a way of separating the relaxation rates for multiple species in solution. The experiment consists of polarizing spins of molecules at high field, shuttling the sample to low field for relaxation, and then returning the sample back to the high field to measure the resultant magnetization of each nucleus of interest (5, 6). This provides a way to measure spin-lattice relaxation rates over a wide magnetic field range (from 11.7 down to 0.003 T) for multiple molecules binding to the same protein or macromolecular complex regardless of its size. Variations of this technique have monitored ³¹P resonances for soluble ligands binding to membrane-localized proteins (13) and identified specific phospholipid binding sites on proteins transiently bound to membranes (14–16).

For a small molecule in solution, chemical shift anisotropy (CSA) dominates the ³¹P spin-lattice relaxation rate, R₁, in high magnetic fields; by comparison, the dipolar contribution to relaxation is very small. However, if the small molecule spends part of its time bound in a larger complex, such as an enzyme, then the observed R₁ is a weighted average of the very small R₁ of the free population and the much larger R₁ of the bound population. This effect depends on magnetic field strength, the ratio of ligand to protein, and the proximity of the ³¹P to proton dipoles in either the small molecule or the enzyme.

Our field cycling results demonstrate a difference in the dynamics of bound substrates and cofactors in GMPR, as measured by correlation time. This finding is in contrast to crystal structures of the complexes, which suggest comparable interactions of substrates with the protein. Relaxation profiles show the importance of the substrate phosphate group in the catalytic reaction and how ligand dynamics change in each step of the reaction. These observations are not consistent with the conventional view that such distal phosphate groups simply tether their substrates to the active site. Instead, the phosphate group must actively participate in the catalytic cycle.

Results

IMP and GMP Are in Fast Exchange with GMPR

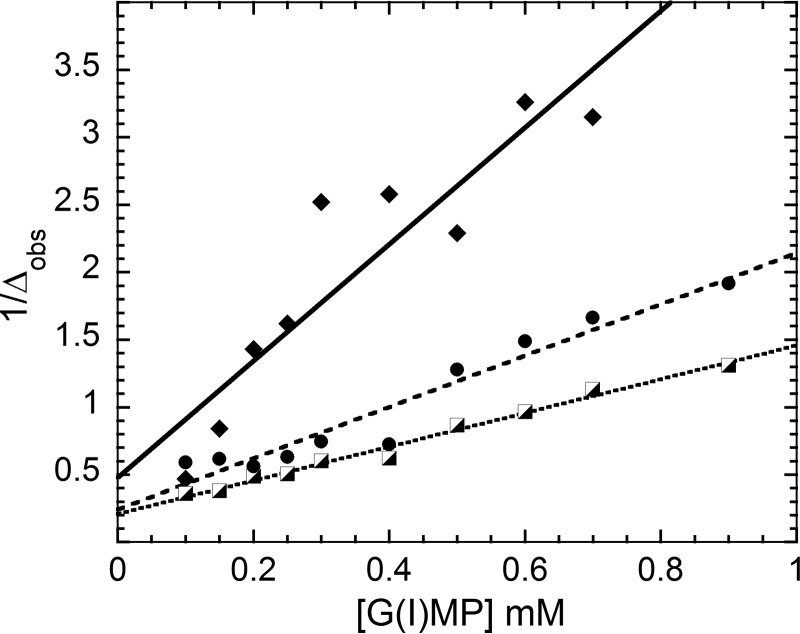
To compare the relaxation properties of two different ligand complexes, the ligands must both be in fast exchange, and the exchange must occur on the same time scale. To confirm that IMP and GMP have similar exchange properties in their respective NADP⁺ complexes, we monitored the NMR line widths of the H2 and H8 protons upon the addition of GMPR (hypoxanthine (8.5 and 8.1 ppm) and guanine (8.1 ppm), respectively; Fig. 3). The chemical shifts of these protons are well resolved. The concentration of IMP or GMP was varied between 0.1 and 1.2 mm at fixed enzyme and NADP⁺ concentrations (0.05 and 0.06 mm, respectively). The average dissociation constants are 165 ± 36 and 110 ± 60 μm for IMP and GMP, respectively. These results indicate that IMP and GMP bind to the protein in the fast exchange regime, and GMPR should be saturated with each substrate ligand under the conditions of the field cycling experiments. Thus, any difference in extracted field cycling parameters must derive from different time-averaged proximities of the substrate monophosphates to protons inside the active site. Likewise, NADP⁺ binds to the protein in the fast exchange regime. NMR line width analysis of well resolved cofactor protons (nicotinamide (9.2 ppm) and adenosine (8.3 ppm)) gave average dissociation constants of 120 ± 50 and 40 ± 10 μm for E·IMP·NADP⁺ and E·GMP·NADP⁺ complexes, respectively.

FIGURE 3.

Changes in the line width of GMP and IMP protons in the presence of GMPR and NADP⁺. The plot shows the reciprocal of the change in ligand line width with an increase of [L]₀ (total ligand concentration) at constant protein and NADP⁺ concentrations: GMP H8 (8.1 ppm; filled diamonds); IMP, H2 (8.5 ppm; half-filled squares) and H8 (8.1 ppm; filled circles). Here line width is defined as a full width of the ¹H resonance at half-height as measured at 800 MHz.

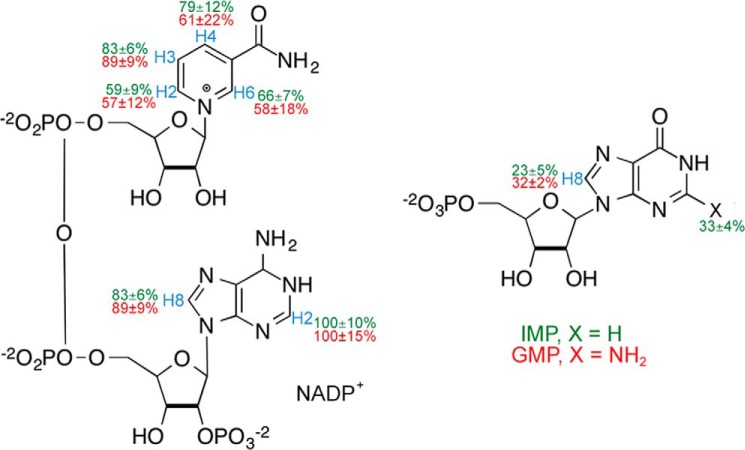
We also performed saturation transfer difference ¹H NMR (STD-NMR) experiments at 800 MHz to characterize the substrate and cofactor binding epitopes (17). In this method, the selective saturation of some protein signals is efficiently spread throughout the protein by spin diffusion (intramolecular NOEs). Magnetization also transfers to ligand protons in contact with the protein surface (intermolecular NOEs). If the free and bound ligand states are in fast exchange, saturation can be observed in the free ligand signal. Furthermore, the transfer of magnetization will be more efficient with a much stronger corresponding STD signal for those hydrogen atoms of the ligand establishing close contacts to the protein surface. The STD signals of H2 and H8 of the adenosine moiety of NADP⁺ are similar in both complexes, suggesting that the interactions of this portion of the cofactor with protein are the same. This finding is also consistent with the x-ray crystal structure of the E·IMP·NADPH complex, which shows that the adenosine portion of the cofactor has identical interactions in both the IN and OUT conformations (3). The STD signals of the nicotinamide protons are also similar, although there is much greater error associated with the GMP complex, perhaps reflecting a more dynamic cofactor in the E·GMP·NADP⁺ (see below). The crystal structure suggests that three protein residues are within 4 Å of H4 in the IN cofactor conformation, whereas only one protein residue is near H4 in the OUT conformation (Figs. 2 (A and B) and 4). Although the errors in measuring the STD signal are significant, all protons from the nicotinamide except H4 show the same average effect in the two ternary complexes. Thus, H4 may have an increased STD signal in the E·IMP·NADP⁺ complex because the cofactor is spending more time in the IN conformation in E·IMP·NADP⁺ than in E·GMP·NADP⁺. In contrast to the cofactor, the STD results show slightly different, but statistically real, protein-to-ligand magnetization transfer for the H8 of IMP and GMP in both complexes (Fig. 4) with a higher value, 32 ± 2% for GMP compared with 23 ± 3% for IMP. The magnitude of the STD for this substrate proton is also considerably smaller than that for the cofactor protons. The crystal structures show the same protein-ligand interactions for the purine bases of IMP and GMP (Fig. 2C). However, the STD results suggest that there may be a difference in substrate interactions with the protein.

FIGURE 4.

Epitope mapping of G(I)MP and NADP⁺. STD-NMR results for 2 mm IMP/GMP and NADP⁺ in the presence of 40 μm GMPR. Protons are labeled in blue. The relative degree of saturation of the individual hydrogens is mapped onto the structure and normalized to the largest STD intensity of hydrogen H2 for adenosine for E·IMP·NADP⁺ (X = H, green) and E·GMP·NADP⁺ (X = NH₂, red). For more explanation, see “Experimental Procedures.”

In summary, these NMR experiments show that 1) ligands are in fast exchange between protein bound and free states, and 2) on fast time scales, the cofactor engages in similar interactions with the protein, whereas there is a small difference for the substrate with a higher magnetization transfer for GMP. However, these experiments do not really address dynamics and environments of the bound ligand species on a slower time scale that might shed light on catalysis.

The Low Field Values of R₁ of Substrate ³¹P Nuclei Increase When Bound to GMPR

³¹P field cycling experiments were used to determine the relaxation rates of ³¹P nuclei in the E·IMP·NADP⁺ and E·GMP·NADP⁺ complexes and compare the conformational dynamics of substrates and cofactors during the GMPR reaction. As noted above, E·IMP·NADP⁺ undergoes a partial reaction to E-XMP*·NADPH, which involves the structural and functional features of the IN cofactor conformation. Likewise, E·GMP·NADP⁺ undergoes the partial deamination reaction, which is believed to require the OUT conformation. Typical one-dimensional ³¹P spectra for different relaxation delays at 0.2 T are shown in Fig. 5, in this case for the cofactor diphosphate resonances in the E·GMP·NADP⁺ complex.

FIGURE 5.

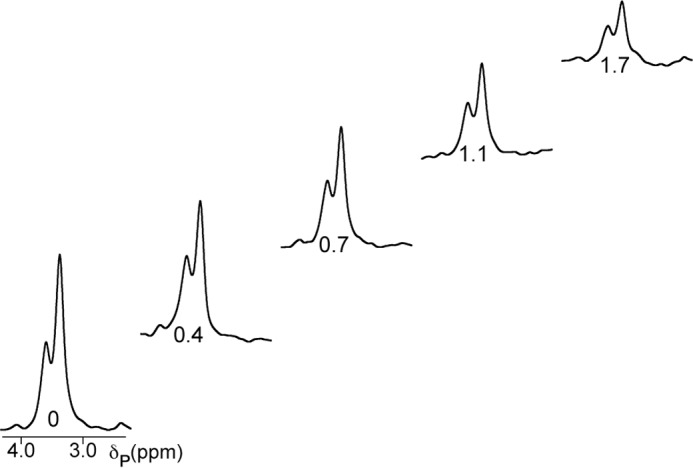
³¹P spectra from the R₁ experiment at 0.2 T for the NADP⁺ diphosphate resonances. The sample contains 0.4 mm GMPR, 1.6 mm GMP, and NADP⁺ in 75 mm Tris-HCl, pH 7.8. The relaxation delay time in seconds spent at 0.2 T is shown below each spectrum.

In the absence of enzyme, the ³¹P resonances in all of the phosphorylated small molecules exhibit a small constant value of R₁ at low fields (<1 T) that rises at higher fields (>4 T) due to CSA relaxation. The inset in Fig. 6 shows this increase in R₁ at high fields for the IMP ³¹P. The value of τ for this relaxation mechanism is <1 ns. This behavior is typical for ³¹P in small molecules in solution.

FIGURE 6.

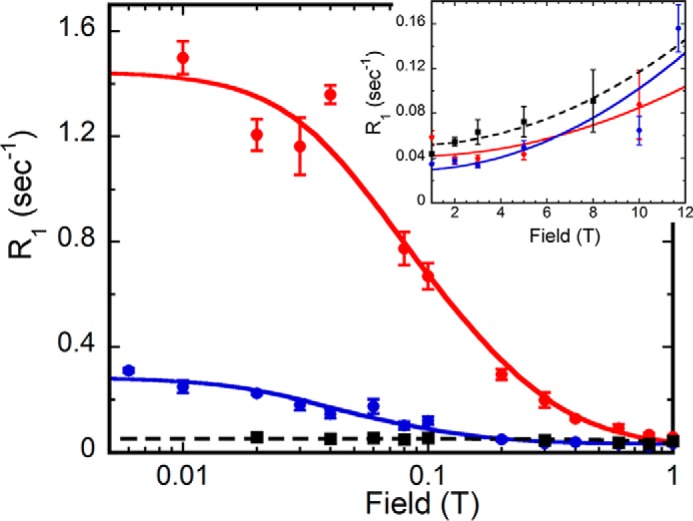
Field dependence of substrate monophosphates R₁ in the presence and the absence of GMPR. Samples (E·IMP·NADP⁺ in red, E·GMP·NADP⁺ in blue, IMP/NADP⁺ in black) are in 75 mm Tris-HCl, pH 7.8, 100 mm KCl, 1 mm DTT, and 0.5 mm EDTA with 24% D₂O. The lines represent the best fit of Equation 6 to these data. The inset shows the high field part of the same data expanded for clarity. Error bars, S.E.

When GMPR was added to the IMP/NADP⁺ sample, the values of R₁ increased significantly at low field (Fig. 6 and Table 1). Such increases are expected if free substrate is in fast exchange with enzyme-bound substrate. In terms of the spectral densities used to describe the relaxation behavior (see “Experimental Procedures”), this occurs when ω² τ² ≪ 1. The increase in R₁ at low fields occurs because the ligand is more effectively relaxed (with correlation time τ) by nearby protons when it is bound to the tetrameric enzyme. These ³¹P-¹H dipolar interactions can be intermolecular (via proton residues on the enzyme) as well as intramolecular (the P-O-C-H interactions). In the presence of enzyme, the effective value of the correlation time τ for the bound IMP dipolar interaction shown in Fig. 6 was 45 ± 2 ns. At least three different field cycling experiments were performed with each ternary complex, wherein individual R₁ data were acquired at a minimum of 15 different fields. In the case of IMP in the E·IMP·NADP⁺ complex, the average over all of the experiments was 55 ± 12 ns (Table 1).

TABLE 1.

Relaxation parameters for ³¹P for E·NADP⁺ complexes of IMP and GMP extracted from field cycling experiments

31P	Complex	τa	R0a	τ /R0 (× 108)a
		ns	s−1
IMP	IMP·NADP+	55 ± 12	1.9 ± 0.9	3.3 ± 1.1b
GMP	GMP·NADP+	72 ± 13	0.30 ± 0.02	24 ± 5b
NADP+ monophosphate	IMP·NADP+	103 ± 23	2.9 ± 1.2	3.8 ± 0.9
	GMP·NADP+	47 ± 11	0.6 ± 0.1	8.6 ± 2.3
NADP+ diphosphates	IMP·NADP+	88 ± 13	1.4 ± 0.3	6.6 ± 1.2
		82 ± 17	1.6 ± 0.3	5.1 ± 0.9
	GMP·NADP+	44 ± 5	0.5 ± 0.2	9.2 ± 2.4
		45 ± 8	0.5 ± 0.1	9.3 ± 2.5

^a Each τ, R₀, and τ/R₀ entry is the average of values determined in at least three independent experiments; the error is the S.D.

^b One field cycling experiment; the error is S.E.

GMP in the E·GMP·NADP⁺ complex also showed an increase in R₁ at low fields (Fig. 6). The value of τ for protein-bound GMP was 64 ± 10 ns in the experiment shown. The average τ from several experiments was 72 ± 13 ns, similar to that of IMP (Table 1).

Substrate Proximity to Effective Relaxer Protons Varies in Cofactor Complexes with GMPR

STD-NMR experiments showed similar binding epitopes for both substrates bound to GMPR, at least in reference to the purine rings. Superposition of the structures of the E·IMP·NADPH and E·GMP complexes shows that the substrate phosphate groups are perfectly aligned, as are the surrounding protein residues (Fig. 2C). Crystal structures of E·IMP·NADPH and E·GMP show that the substrate phosphate groups bind to the standard phosphate binding site in the (β/α)₈ barrel protein superfamily (Fig. 2D) (1, 2). These observations suggest that substrate phosphate groups also bind at the same site in E·IMP·NADP⁺ and E·GMP·NADP⁺ complexes.

Surprisingly, although the values of τ are similar, field cycling shows that the values of R₀ (the relaxation rate extrapolated to zero field) for the ³¹P nuclei of IMP and GMP are strikingly different in the two NADP⁺ complexes (Fig. 6 and Table 1). R₀ is related to the averaged distance of the ³¹P to the protons that relax it. The value of R₀ for the ³¹P of GMP is lower than that of IMP by more than a factor of 6 (Table 1), suggesting a significant difference in the binding dynamics of the two substrates.

The sixth root of the ratio τ/R₀ is proportional to the distance between the ³¹P nuclei and relaxer protons. The value of τ/R₀ is almost 8-fold higher for GMP than IMP. The calculated r_eff, the on-enzyme distance between the ³¹P and nearby relaxer protons, is correspondingly higher for the ³¹P of GMP. The extrapolated ³¹P–¹H distances for the substrate phosphate are 4.1 ± 0.2 Å for E·GMP·NADP⁺ and 2.9 ± 0.2 Å for E·IMP·NADP⁺. Because both GMP and IMP bind in the fast exchange regime in their respective NADP⁺ complexes, these results suggest that the ³¹P of GMP is not proximal to the protons that contribute to dipolar relaxation of IMP in the ternary complex.

The Substrate Monophosphates Have Similar Dynamics in the Binary Complexes

To explain the loss of the dipolar relaxation, we compared the relaxation rates of ³¹P nuclei in the binary E·IMP and E·GMP complexes (Fig. 7). In the absence of cofactor, IMP and GMP have similar values of τ: 43 ± 6 ns for IMP and 43 ± 4 ns for GMP. Values of R₀ are also similar for both E·IMP and E·GMP complexes (2.3 and 2.1 s⁻¹, respectively), as are the values of τ/R₀ (1.9 and 2.0 × 10⁻⁸ s², respectively). Note that the observation of an increase in R₀ at low field indicates that IMP and GMP bind to the protein in the fast exchange regime. These observations suggest that the substrate ³¹P nuclei are in the same environment in both E·IMP and E·GMP binary complexes.

FIGURE 7.

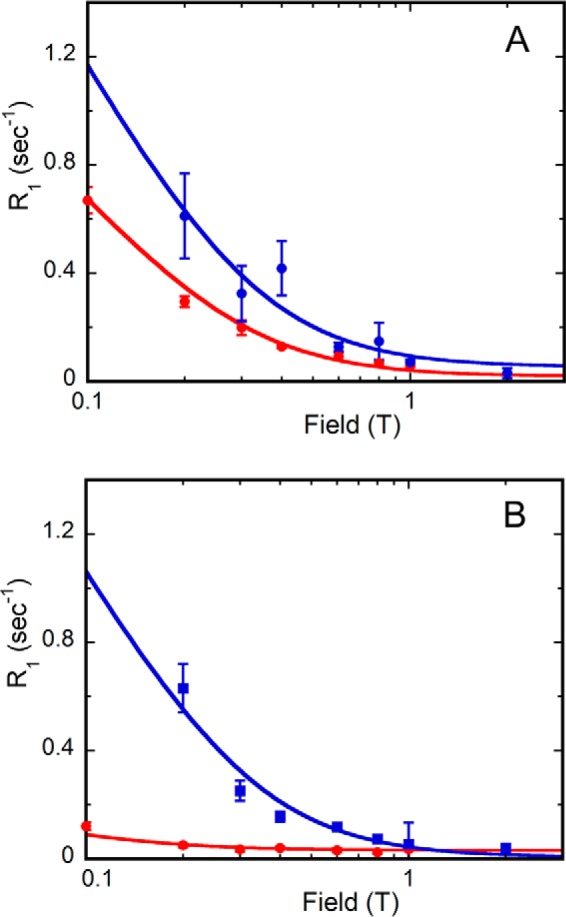
Magnetic field dependence of substrate phosphate ³¹P R₁ in the presence and absence of NADP⁺. Substrate is binding to GMPR alone (blue) or with NADP⁺ added (red). A, E·IMP; B, E·GMP. Error bars, S.E.

Although the relaxation of the ³¹P of IMP is similar in both the binary and ternary complexes (Fig. 7A), the value of R₀ for GMP was significantly smaller when NADP⁺ was present (2.1 s⁻¹ for E·GMP and 0.30 ± 0.02 s⁻¹ for E·GMP·NADP⁺; Fig. 7B). These differences must derive from different proximities of the substrate monophosphates to relaxer protons (either intramolecular or intermolecular) in the presence of cofactor. Thus, the field cycling experiments indicate that the deamination reaction involves a conformation of GMP and/or a phosphate binding site distinct from those observed in the x-ray crystal structures.

Cofactor in E·GMP·NADP⁺ Has More than One Bound Conformation

The x-ray crystal structures suggested that the relaxation of the cofactor diphosphates would be different in the IMP and GMP complexes. Although relaxation of the diphosphates is expected to have a homonuclear ³¹P-O–³¹P dipolar contribution, we reasoned that this contribution would be the same in all complexes because only two bonds separate the ³¹P nuclei. The value of τ for the adenosine monophosphate ³¹P nucleus was comparable with those of the diphosphates within a given complex, suggesting that the correlation time reflected behavior of the whole cofactor molecule. However, the values of τ_eff for the cofactor ³¹P nuclei were longer for E·IMP·NADP⁺ than for E·GMP·NADP⁺ (82–103 versus 44–47 ns, respectively; Table 1).

The values of R₀ change in proportion to the τ values, so that the values of τ/R₀ for the three ³¹P nuclei are similar for the cofactor in both complexes (3.8–6.6 × 10⁻⁸ and 8.6–9.3 × 10⁻⁸ s² for the IMP and GMP complexes, respectively; Table 1), with no significant change in the extrapolated ³¹P–¹H distances:E·IMP·NADP⁺, 2.8 ± 0.2 Å for monophosphate and 3.0 ± 0.1 Å for diphosphates; E·GMP·NADP⁺, 3.1 ± 0.1 Å for monophosphate and 3.2 ± 0.1 Å for diphosphates. These observations suggest that the cofactor ³¹P occupies the same site in both complexes but that a dynamic process associated with cofactor binding is different.

Several processes contribute to the value of τ, including overall rotation of the complex and conformational exchange of the protein and/or small molecule. Rotational relaxation will be dominated by the tumbling of the protein, which should be the same for all bound ligands unless the oligomerization state of the protein is different in the two complexes. Therefore, we measured the diffusional properties of the complexes with dynamic light scattering using exactly the same concentration of enzymes and ligands as for field cycling experiments. The diffusion coefficients (μm²/s) and hydrodynamic radii (nm) of E·IMP·NADP⁺ and E·GMP·NADP⁺ are the same within error: 53.2 ± 0.1 μm²/s and 4.6 ± 0.1 nm for E·IMP·NADP⁺ and 52.1 ± 1.5 μm²/s and 4.7 ± 0.1 nm for E·GMP·NADP⁺. These results indicate that the two complexes have the same oligomeric state. The measured hydrodynamic radii are similar to the radius of gyration calculated from the crystal structure of the GMPR tetramer in complex with IMP and NADPH (R_g = 4.2 nm, calculated with HydroPro (18) using PDB code 2C6Q (3)). Hence, the different values of τ must derive from changes in cofactor conformational dynamics within the complexes.

The value of τ estimated from the molecular weight using Stokes law for spherical proteins is ∼70 ns (5), which is similar to that observed for the cofactor in the E·IMP·NADP⁺ complex (Table 1). Thus, we propose that the cofactor possesses a more rigid conformation in E·IMP·NADP⁺ such that τ is dominated by protein tumbling (τ = 80–100 ns). There are several possible explanations for the smaller values of τ for cofactor in E·GMP·NADP⁺: 1) the protein environment of NADP⁺ has enhanced flexibility but not altered relaxer proton distance (because τ/R₀ is similar for both ternary complexes); 2) there are two populations of the E·GMP·NADP⁺ complex, one with τ and R₀ comparable with the IMP ternary complex and the other with a shorter τ such that both field dependence profiles overlap; and 3) the NADP⁺ in the E·GMP·NADP⁺ complex has significant internal motion.

Fig. 8A shows how these three models affect the analysis of the field dependence for one E·GMP·NADP⁺ experiment. In the case of the first model, the NADP^{+ 31}P nuclei in the complex are characterized by a single τ = 37 ± 6 ns and R₀ = 0.43 ± 0.02 s −¹, shown by the thin black line.

FIGURE 8.

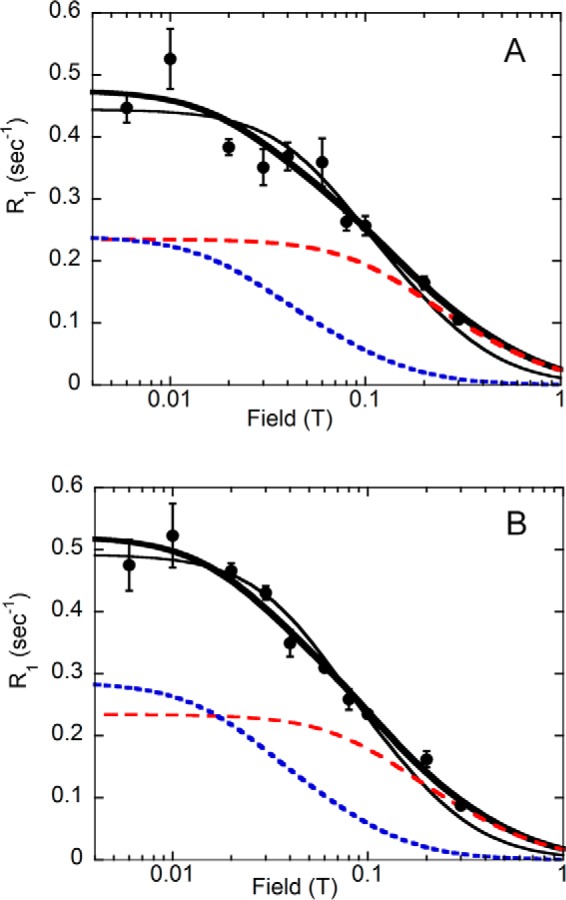
Magnetic field dependence of R₁ for NADP⁺³¹P in the E·GMP·NADP⁺ complex. NADP⁺ diphosphates are shown in A, and the NADP⁺ monophosphate is shown in B. The thin line represents a fit to Equation 6 with a single correlation time (37 and 45 ns for the diphosphate and monophosphate, respectively) and R₀ of 0.5 and 0.6 s⁻¹ for the di- and monophosphates, respectively. The thick line represents the best fit with Equation 1 and Equation 2, which describe two distinct dipolar contributions to the observed cofactor ³¹P R₁: 1) a lower field component (blue dashed line) characterized by a long correlation time and R₀ consistent with overall rotation of the protein complex with values taken from the E·IMP·NADP⁺ complex (Table 1) and 2) a second contribution (red dashed line) with a shorter correlation time (16 ns) and reduced R₀ values (0.28 and 0.26 s⁻¹ for the di- and monophosphates) that dominates the relaxation around 0.1 T. The parameter F, the fractional contribution of the slower τ, was found to be 0.16 and 0.10 for the diphosphate and monophosphate, respectively. Error bars, S.E.

For the other two explanations, the observed R₁ at each magnetic field will be a combination of two different τ, R₀ contributions (Equations 1 and 2).

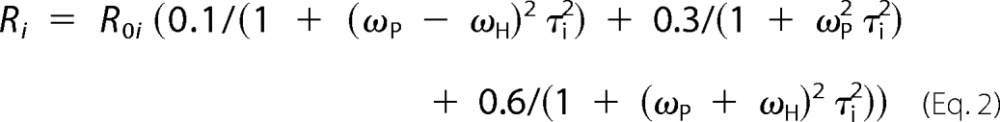For case 2 (i.e. two distinct populations of protein), F is the fraction of protein where the NADP⁺ motion has a correlation time consistent with overall rotation of the protein complex (90 ns) and R₀ comparable with the E·IMP·NADP⁺ complex (1.5 s⁻¹). Parameters for the fraction of protein (1 − F) with a shorter correlation time can be extracted by fitting the observed data to the sum of two Equations 2, with one representing protein tumbling and the other a faster motion. For these analyses, only fields less than 0.4 T were used to avoid any complication from CSA relaxation. One obtains F = 0.16, so that only 16% of the total complex has values of τ and R₀ comparable with the cofactor in the E·IMP·NADP⁺ complex, whereas the other 84% of the ternary complex is characterized by τ = 16 ± 9 ns and R₀ = 0.28 ± 0.07 s⁻¹. The two dashed lines (Fig. 8) show the contribution of each of these species to the observed R₁.

Equation 1 also describes explanation 3, where relaxation is due to the internal motions of the bound cofactor as well as the overall rotation of the enzyme complex (19). The extracted numbers are the same, but here F is usually represented by S², an order parameter squared. Here, the S² is defined as the fraction of R₁ contributed by overall rotational motion of the complex, and then (1 − S²) indicates the portion of R₁ due to the internal motion of the bound diphosphates. Because (1 − S²) is close to 1, this means that the NADP⁺ diphosphates have considerable internal motion in the GMP ternary complex, characterized by τ = 16 ± 9 ns. This motion provides the major pathway for relaxing the ³¹P at fields between 0.01 and 1 T (red line in Fig. 8A).

The same analysis (Equation 1) for cofactor monophosphate parallels the diphosphate results (Fig. 8B). For case 1, the monophosphate in the complex yields a single τ = 45 ± 4 ns and R₀ = 0.49 ± 0.02 s⁻¹. For case 2, we used 100 ns and 2.9 s⁻¹ for τ and R₀, respectively, because these values characterized substrate in the E·IMP·NADP⁺ complex. Only 10% of the total complex has values of τ and R₀ comparable with the cofactor in the E·IMP·NADP⁺ complex, whereas the other 90% of the ternary complex is characterized by τ = 19 ± 7 ns and R₀ = 0.26 ± 0.05 s⁻¹. For explanation 3, the internal motion of the cofactor monophosphate provides a major pathway for relaxing the ³¹P, especially at fields around 0.1 T. We suggest that this internal motion is the major relaxation pathway for the NADP⁺ in the GMP ternary complex.

Relative Dynamics of Substrate and Cofactor Change during the GMPR Catalytic Cycle

If overall protein tumbling dominates dipolar relaxation of the bound small molecules, the values of τ are expected to be similar for all of the phosphates within a given complex. However, this is not the case. The value of τ for the ³¹P nucleus of GMP is longer than those for the cofactor ³¹Ps within the E·GMP·NADP⁺ (72 ± 13 versus 44–47 ns; Table 1 and Fig. 9, A and B). In contrast, the value of τ for the ³¹P of IMP is shorter than those for the cofactor ³¹P nuclei within the E·IMP·NADP⁺ complex (55 versus 82–103 ns). These observations suggest that the relative dynamics of the substrate and cofactor change during the catalytic cycle. The cofactor is more dynamic (i.e. has faster local motions) than GMP during deamination, whereas the phosphate of IMP is less constrained than the cofactor in the complex, leading to hydride transfer (Fig. 10).

FIGURE 9.

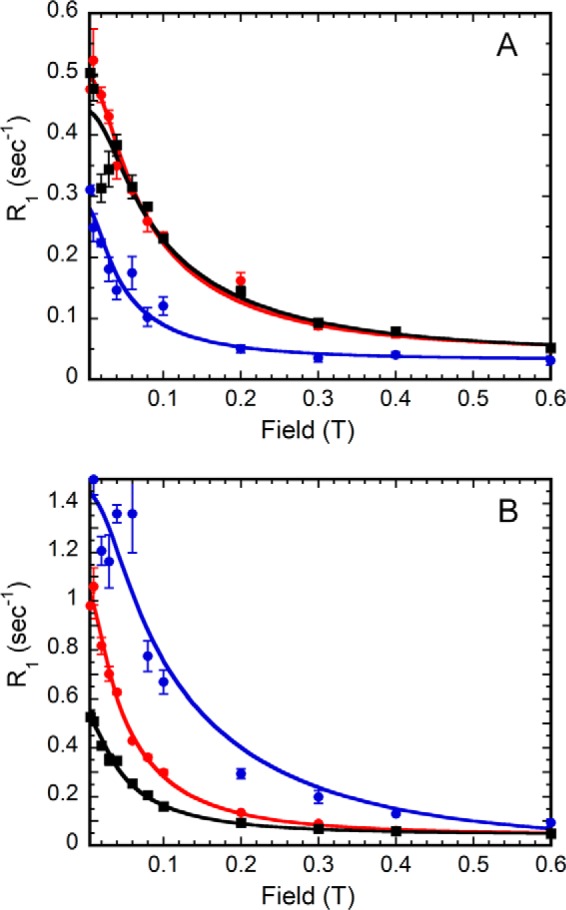
Comparison of field dependence profiles of ³¹P in substrate and cofactor in each E·NADP⁺ ternary complex. For the E·GMP·NADP⁺ (A) and E·IMP·NADP⁺ (B) profiles, substrate monophosphate is blue, NADP⁺ monophosphate is red, and NADP⁺ diphosphates are black. Error bars, S.E.

FIGURE 10.

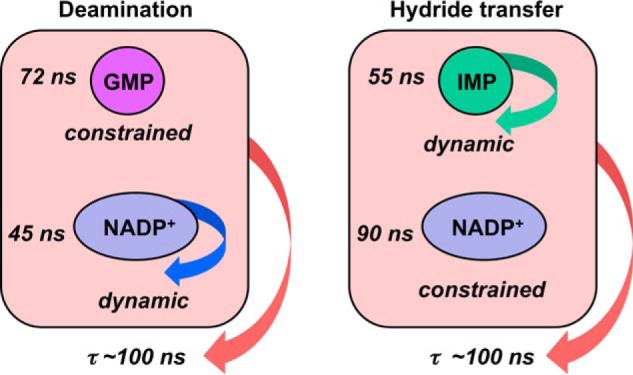
Dynamic properties of ternary complexes. Field cycling experiments suggest that the substrate monophosphate is more dynamic than the cofactor in the E·GMP·NADP⁺ complex but less dynamic in the E·IMP·NADP⁺ complex.

Discussion

Catalysis is an inherently dynamic process, dependent on the motions of both substrate and enzyme. Although x-ray crystallography allows important insights into the mechanisms of enzyme catalysis, these structures are only static views of usually inert complexes and can therefore be misleading. Molecular mechanics/molecular dynamics simulations can provide information about reaction dynamics, but the size of the enzyme often requires the dynamic regions to be constrained to a portion of the protein in the immediate vicinity of the chemical transformation, so that the contribution of more distal regions is not considered. Our work shows that high resolution field cycling provides a means to monitor the dynamics of catalytically competent complexes, providing new and unanticipated insights into catalysis.

In the case of GMPR, all of the available crystal structures suggested that the monophosphates of IMP and GMP have identical interactions (Fig. 2C). Moreover, these interactions are found in many other (β/α)₈ enzymes (Fig. 2D). These observations suggest that the monophosphates serve as anchors that tether the reactive portion of the substrate to the active site, a role consistent with a uniform binding interaction as proposed by Burbaum et al. (20) or the Jencks Circe effect (21). Our field cycling experiments reveal that, in the catalytically active E·GMP·NADP⁺ complex, the monophosphate of GMP is farther from relaxer protons than is that of IMP in its catalytically active NADP⁺ complex. This could occur by the ternary complex stabilizing the GMP conformation so that the ³¹P-O–C–¹H is maximally extended (reducing intramolecular dipolar relaxation), by reducing the effect of nearby protein relaxer protons (intermolecular dipolar relaxation), or by a combination of both. Our observation indicates that the interactions of the substrate monophosphate change during the catalytic cycle. Thus, the substrate monophosphate is intimately coupled with the chemical transformations. The importance of the phosphate moiety was not suspected before the field cycling experiments and probably would not have been considered in molecular mechanics/molecular dynamics simulations of the reaction.

This work demonstrates the utility of field cycling NMR to study the dynamics of phosphorus-containing substrates inside an enzyme active site and clearly shows the importance of substrate dynamics in the catalytic cycle. We propose that the different relaxation behavior of the E·GMP·NADP⁺ and E·IMP·NADP⁺ complexes reflects the dynamic properties of different steps in the catalytic cycle of GMPR. In the deamination step, the bound monophosphate of GMP is less effectively relaxed than IMP. This could occur intramolecularly by stabilization of an extended GMP conformation that does not occur with bound IMP. However, the lower R₀ for bound GMP may also result from a change in proton density around the monophosphate contributed by the protein. The increased R₀ for GMP in the binary complex, with a correlation time similar to what is observed in the ternary complex, is consistent with significant protein contribution to ³¹P dipolar relaxation. The τ for the GMP in E·GMP·NADP⁺ is also longer than that for the cofactor. The internal motion of the cofactor is likely to be coordinated with the OUT conformation of the cofactor.

In contrast, in the hydride transfer step, the monophosphate of substrate IMP is more effectively relaxed by protons than GMP, and cofactor is more rigid because the τ for the three ³¹P nuclei are all longer and comparable with overall tumbling of the complex. Whether changes in the effectiveness of substrate dipolar relaxation occur intra- or intermolecularly, the net result is that the two substrates are bound differently in the ternary complex, and this is correlated with the conformational behavior of the cofactor.

Last, completion of the catalytic cycle requires the transition between these two dynamic states. As shown in Fig. 1B, the deamination reaction occurs in the OUT conformation, producing E-XMP* and ammonia. The ammonia must move to allow the nicotinamide to access the IN conformation required for hydride transfer. The ammonia is missing from E·IMP·NADP⁺ complex, perhaps accounting for the less dynamic conformational state of the cofactor in this complex. We suggest that the movement of NH₃ gates the transition between the two dynamic states, and future work will investigate this hypothesis.

Experimental Procedures

Materials

NADP⁺ was obtained from Roche Diagnostics. IMP was purchased from MP Biomedicals. GMP was purchased from Sigma. D₂O (99.9%), deuterated Tris-d₁₁ (98%), was obtained from Cambridge Isotopes.

Overexpression and Purification of Escherichia coli GMPR

Expression and purification of recombinant E. coli GMPR was carried out as described previously (3) with modifications to increase production of purified enzyme. The crude cell lysate from a 6-liter culture was loaded onto nickel-nitrilotriacetic acid-agarose resin (Molecular Cloning Laboratories Inc.) and incubated overnight. The resin was washed with 5, 30, and 60 mm imidazole buffer 1 (100 mm potassium phosphate, pH 7.8, 500 mm KCl, 1 mm β-mercaptoethanol, 10% glycerol). GMPR was eluted at 250 mm imidazole buffer 1. The fractions with high GMPR activity were collected and dialyzed against buffer 2 (75 mm Tris-HCl, pH 7.8, 100 mm KCl, 1 mm DTT, 0.5 mm EDTA, 5% glycerol). The protein purity was verified by SDS-gel electrophoresis. The protein concentration was determined by A₂₈₀ using the extinction coefficient calculated with ProtParam (22). Protein was concentrated using Amicon Ultra centrifugal 10K filters for NMR samples.

K_d Measurements

One-dimensional NMR spectra were recorded on a Bruker Avance spectrometer operating at 800.13 MHz (¹H) and equipped with TXI cryoprobe and pulsed field gradients. All experiments were performed at 25 °C. NMR data were processed and analyzed using TOPSPIN (Bruker Biospin Inc.). For the analysis of the line shape of the ¹H resonance of substrates in the presence of GMPR, a linearization method for chemical exchange of ligand was used (23). When the ligand is present in excess to the protein concentration, [L] = [L]₀, [L]₀ ≫ [P]₀, the ligand line width can be expressed in the following relationship,

where [P]₀ represents protein concentration, [L]₀ is total ligand concentration, and Δ_obs and Δ_max are the observed and maximum change in ligand line width, respectively. K_d is obtained from the slope and the y intercept of a plot of 1/Δ_obs versus [L]₀.

STD-NMR Experiments

All STD experiments were acquired on the 800-MHz spectrometer using 40 μm GMPR and 2 mm substrates in 75 mm deuterated Tris-HCl, pH 7.8, 100 mm KCl, 0.5 mm DTT. All experiments were performed at 20 °C with 1600 scans and selective saturation of protein resonances at −0.7 ppm using a train of 50-ms Gaussian-shaped radio frequency pulses at −0.7 and −30 ppm for the on-resonance and off-resonance spectra, respectively (1-ms delay between pulses) for total saturation times ranging from 0.6 to 7 s. The off-resonance frequency was set at a value that is far from any ligand or protein signal. This signal was used as a reference signal intensity, I_off. The on-resonance frequency was for selective irradiation of aliphatic protein signals, and its intensity was set as I_on. NMR data were processed and analyzed using TOPSPIN (Bruker Biospin Inc.). The measured intensities I_off and I_on were used to calculate the fractional STD signal using the following equations,

and

where [L]_T and [E]_T are the total ligand and protein concentrations, respectively. The epitope mapping was obtained by calculating the slope of the STD_AF build-up curve at a saturation time of 0 s (24). Saturation data were fitted to an exponential equation, STD_AF = STD_AF(max)(1 − exp(−k_satt)), where STD is the STD signal intensity of a given proton at saturation time t, STD_AF(max) is the maximal STD intensity at long saturation times, and k_sat represents the observed saturation rate constant. Multiplication of STD_AF(max) and k_sat yields the slope of the curve at t = 0 s.

Dynamic Light Scattering

The dynamic light scattering (DLS) experiments were performed using an ALV goniometer. Absolute Rayleigh ratios of aqueous solutions were determined by using pure toluene as a standard (25). The radii r_H of GMPR complexes were obtained from DLS measurements in 75 mm Tris-HCl, pH 7.8, 100 mm KCl, 1 mm DTT, 0.5 mm EDTA using 0.4 mm GMPR and 1.6 mm G(I)MP and NADP⁺ (26). All samples were filtered through 0.2-μm GSWP filters before being analyzed.

High Resolution ³¹P Field Cycling NMR Measurements

Each sample was prepared by mixing enzyme with ligands stock solutions, either IMP/NADP⁺ or GMP/NADP⁺, to obtain 400 μm GMPR and 1.6 mm ligands in the 75 mm Tris-HCl, pH 7.8, with 100 mm KCl, 1 mm DTT, and 0.5 mm EDTA. Buffer contained 24% D₂O. The ³¹P field cycling spin-lattice relaxation rate (R₁) measurements were taken at 25 °C on a Varian INOVA 500 spectrometer using a standard 10-mm Varian probe in a device that was built to move the sample from the conventional sample probe location (at 11.7 T) to a higher position within or above the magnet, where the magnetic field can be as low as 0.04 T (5). To program lower fields, down to 0.006 T, a permanent magnet was mounted at the top of the superconducting magnet dewar. Relaxation experiments at a given field strength were typically 3–6 h long (depending on field strength), each with 6–7 programmed delay times. Data were analyzed with an exponential function to extract the spin-lattice relaxation rate R₁ = 1/T₁.

³¹P Field Cycling NMR Data Analysis

Spectra were plotted, and intensities were measured by Vnmr 6.1c software. Dependence of R₁ on magnetic field allows the extraction of the effective correlation time (τ) for the ligand bound to GMPR and the dipolar relaxation rate extrapolated for zero field (R₀), as described by Equation 6,

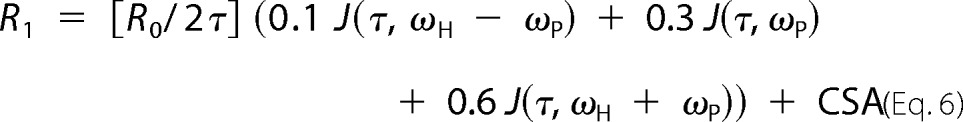where CSA = C_Lω_P²J(ω_P) + C_Hω_P²H². Here J(τ,ω) is the spectral density function and equal to 2τ/(1 + ω_P²τ²); C_L and C_H are low frequency and high frequency contributions of the CSA interaction to relaxation; and ω_H and ω_P are the proton and ³¹P gyromagnetic ratios multiplied by magnetic field, H (in teslas). The contribution C_Lω_P²J(ω_P) was introduced to account for relaxation occurring in the region from 0.5 to 4 T that could otherwise not be accounted for by dipolar and the CSA detected at high fields (3). As such it is an empirical “correction.” In this work, we ignore CSA except to improve fits of the data. The averaged distance from the nearest protons to the ³¹P is proportional to the sixth root of τ/R₀,

where h is Planck's constant, μ₀ is the permeability of free space, and γ_P and γ_H are the gyromagnetic ratios for ³¹P and ¹H. We define r_eff as the on-enzyme distance between the ³¹P and nearby protons that are responsible for the dipolar relaxation. It is not normalized to a specific number of protons because that is not known.

Author Contributions

M. M. R., A. R., and M. F. R. designed the experiments. M. M. R. conducted the experiments. M. M. R. and M. F. R. analyzed the data. L. H. conceived the idea for the project. M. M. R., M. F. R., and L. H. wrote the paper.