Genus Ranges of 4-Regular Rigid Vertex Graphs

Abstract

A rigid vertex of a graph is one that has a prescribed cyclic order of its incident edges. We study orientable genus ranges of 4-regular rigid vertex graphs. The (orientable) genus range is a set of genera values over all orientable surfaces into which a graph is embedded cellularly, and the embeddings of rigid vertex graphs are required to preserve the prescribed cyclic order of incident edges at every vertex. The genus ranges of 4-regular rigid vertex graphs are sets of consecutive integers, and we address two questions: which intervals of integers appear as genus ranges of such graphs, and what types of graphs realize a given genus range. For graphs with 2n vertices (n > 1), we prove that all intervals [a, b] for all a < b ≤ n, and singletons [h, h] for some h ≤ n, are realized as genus ranges. For graphs with 2n − 1 vertices (n ≥ 1), we prove that all intervals [a, b] for all a < b ≤ n except [0, n], and [h, h] for some h ≤ n, are realized as genus ranges. We also provide constructions of graphs that realize these ranges.

1 Introduction

A rigid vertex in a graph is a vertex with a prescribed cyclic order (called a rotation system) of its incident edges. We consider embeddings of 4-regular rigid vertex graphs in orientable surfaces. The notion of 4-regular rigid vertex graphs have been studied extensively in knot theory in various contexts. For example, they can be seen as virtual link projections [16]. When a 4-regular rigid vertex graph corresponds to a virtual knot projection (i.e., the image of a single circle), it is called transversely connected. In this case, it is described by a double occurrence word (in which each letter appears twice), known as an (unsigned) Gauss code. Transversely connected 4-regular rigid vertex graphs in space are also called singular knots (e.g., [4]). An embedding of a 4-regular rigid vertex graph in a surface is required to preserve the given cyclic order of edges at every vertex. The minimum genus of virtual knots have been studied [5, 13], and the genus range of diagrams corresponding to a given Gauss code is of interest in knot theory. For example, necessary and sufficient conditions for the planarity of graphs represented by Gauss codes are given in [7, 8], which in turn plays a key role in making knot tables.

Graphs with 4-valent rigid vertices and end points, called assembly graphs, have been also used to model DNA rearrangements, in which each 4-valent vertex represents a recombination site [3, 2]. Spatial embeddings of these graphs could be seen as a physical representations of the molecules at the moment of rearrangement, and it is of interest to study certain combinatorial properties and embeddings of a given graph that reflect questions from such biological processes. Genera of these graphs may measure their spatial complexity.

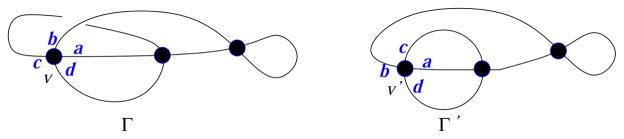
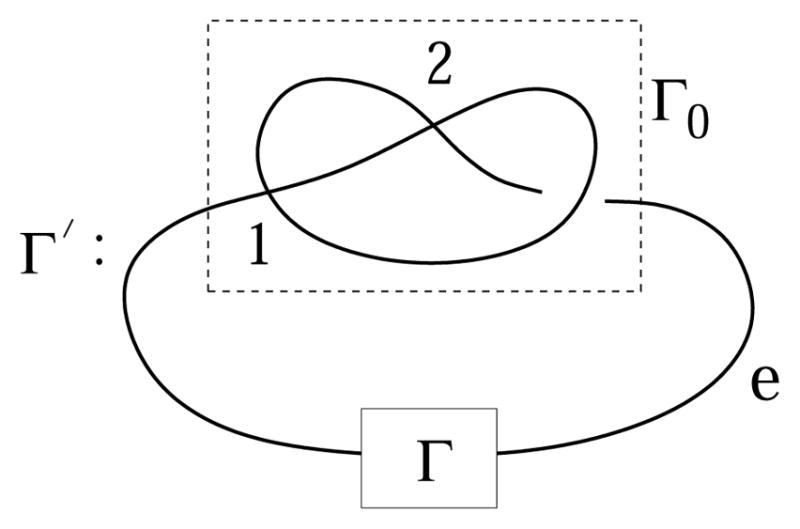
The genus of a graph (also known as minimum genus) is a well-known notion in topological graph theory, and has been studied for a variety of ordinary (non-rigid vertex) graphs (e.g., [17, 14]). It represents the minimum genus of a surface in which the graph can be embedded. The orientable genus range of a given graph is the set of all possible genera of orientable surfaces in which the graph can be embedded cellularly (where the complement consists of open disks). There is a one-to-one correspondence between cellular embeddings of graphs in oriented surfaces and rotation systems, that specify cyclic orders (rotation schemes) of edges at each vertex [17]. In this paper we study the genus ranges of transversely connected 4-regular rigid vertex graphs. A cellular embedding of a 4-regular rigid vertex graph in an orientable closed surface corresponds to specifying a set of two rotation schemes at each vertex, one being the reverse of the other, while the genus ranges for ordinary graphs consider all possible rotation schemes at every vertex. Since any embedding of rigid vertex graphs must preserve the fixed ordering of incident edges to each vertex, their genus ranges are more restricted, compared to those of ordinary (non-rigid vertex) graphs. For example, the graphs Γ and Γ′ depicted in Figure 1 are isomorphic as graphs, but not isomorphic as rigid vertex graphs. At the vertex v in Γ, the cyclic order of edges (a, b, c, d) in counter-clockwise is changed to an inequivalent cyclic order (a, c, b, d) at the corresponding vertex v′ in Γ′. The genus range of Γ and Γ′, as ordinary graphs, is {0, 1, 2} and as rigid vertex graphs, are {1} and {0, 1}, respectively. Hence, results on the genus for ordinary graphs may not be directly applicable to rigid-vertex graphs. Thus in this paper we study the genus ranges of 4-regular rigid vertex graphs. Other variations of restricted graph embeddings in surfaces have been studied in the literature. In [18], for example, embeddings of graphs in orientable surfaces with respect to a certain set of walks was defined. In our context, a walk corresponds to the boundary curve of a face of the complement.

Figure 1.

Difference of genera between regular graphs and rigid vertex graphs

We set forth the following two problems.

Problem 1

1. For a positive integer n, what sets of integers do or do not appear as genus ranges of 4-regular rigid vertex graphs with n vertices?

2. Identify the class of 4-regular rigid vertex graphs with a given genus range.

With this paper we provide some answers to these questions. In particular, we observe that a genus range of a 4-regular rigid vertex graph is always a set of consecutive integers (Lemma 4). This result is known [12] for general graphs up to graph equivalence, but it is a new observation for rigid vertex graphs. Further, we show (Theorem 32) that every set {m, m + 1, …, m′} for 0 ≤ m < m′ ≤ n appears as a genus range of some transversely connected 4-regular rigid vertex graph with 2n vertices. The same family, without the set {0, 1, …, n}, appears as a genus range of some transversely connected 4-regular rigid vertex graph with 2n − 1 vertices. We also observe that none of such graphs with 2n − 1 vertices has genus range {0, …, n} (Lemma 16) nor genus range {n} (Lemma 18). We characterize those graphs with genus range {0} (Proposition 20). For a given number n, even or odd, we leave it open to determine the numbers h such that the set {h} appears as a genus range of a transversely connected 4-regular rigid vertex graph of n vertices.

The paper is organized as follows. In the rest of this section we define transversely connected 4-regular rigid vertex graphs, the genus range of these graphs and introduce several useful constructions. In Section 2 we discuss and prove general observations about properties of genus ranges of these graphs motivated by the computational studies in Table 1. In Section 3 we prove the existence of certain genus ranges in their most general form, and in Section 4, we investigate which intervals of integers appear as genus ranges. We conclude with remarks on distributions of genus ranges.

Table 1.

Computer calculations of possible genus ranges of graphs with n vertices.

	𝒢ℛn :
n = 2	{0}, {1}.
n = 3	{0}, {1}, {0, 1}, {1, 2}.
n = 4	{0}, {1}, {0, 1}, {1, 2}, {0, 1, 2}.
n = 5	{0}, {1}, {2}, {0, 1}, {1, 2}, {2, 3}, {0, 1, 2}, {1, 2, 3}.
n = 6	{0}, {1}, {2}, {3}, {0, 1}, {1, 2}, {2, 3}, {0, 1, 2}, {1, 2, 3}, {0, 1, 2, 3}.
n = 7	{0}, {1}, {2}, {3}, {0, 1}, {1, 2}, {2, 3}, {3, 4}, {0, 1, 2}, {1, 2, 3}, {2, 3, 4}, {0, 1, 2, 3}, {1, 2, 3, 4}.

1.1 Terminology

In this section we define the concepts we use in the paper, and introduce constructions that will be used in later sections to find various genus ranges.

1.1.1 Four-regular rigid vertex graphs and double occurrence words

A rigid vertex is a vertex for which a cyclic order (or its reverse) of its incident edges is specified. For a rigid vertex that has 4 incident edges, if its incident edges appear in order (e₁, e₂, e₃, e₄), then the corresponding rotation schemes specified at this vertex are cyclic permutations of (e₁, e₂, e₃, e₄) and cyclic permutations of its reverse (e₄, e₃, e₂, e₁). For the ordered edges (e₁, e₂, e₃, e₄), we say that e₂ and e₄ are neighbors of e₁ and e₃ with respect to v. The neighboring edges are consecutive with respect to all rotation schemes assigned to the vertex. We observe that valency 4 is the smallest valency that makes difference in cyclic ordering of edges and we concentrate here on 4-valent vertices only. Two 4-regular rigid vertex graphs are isomorphic if they are isomorphic as graphs and the graph isomorphism preserves the cyclic order of the edges incident to a vertex.

A trail (a closed walk with no edge repetition) in a graph is called a transverse path, or simply a transversal, if consecutive edges of the path are never neighbors with respect to their common incident vertex. For 4-regular rigid vertex graphs, a transversal is considered as the image of a circle in the graph that goes through every vertex “straight ahead”, and takes non-consecutive edges with respect to the rotation schemes of each vertex. A 4-regular rigid vertex graph that has an Eulerian (visiting all edges) transversal is called a transversely connected 4-regular rigid vertex graph. For a transversely connected 4-regular rigid vertex graph, if a transversal is oriented, the graph is called oriented. We note that in a transversely connected 4-regular rigid vertex graph, if a vertex v is an endpoint of a loop e, then e must be a neighbor of itself.

Convention

In the rest of the paper, unless otherwise stated, all graphs are transversely connected 4-regular rigid vertex graphs.

A double-occurrence word w over an alphabet set is a word which contains each symbol of the alphabet set exactly 0 or 2 times. (Double-occurrence words are also called (unsigned) Gauss codes in knot theory [16].)

Two double-occurrence words are called equivalent if one is obtained from the other by a sequence of the following three operations: (1) (bijective) renaming of the symbols, (2) a cyclic permutation, (3) taking the reverse (e.g., the reverse of w = a₁ ⋯a_k is w^R = a_k ⋯a₁). For example, w = 123231 is equivalent to its reverse w^R = 132321 and w′ = 213132 is equivalent to w by renaming 1 with 2 and 2 with 1.

Double-occurrence words are related to graphs as follows. Let Γ be a transversely connected 4-regular rigid vertex graph. Orient the graph and pick a base point on the graph. Let α = v₀, e₀, …, v_n, e_n, v₀ be an Eulerian transversal starting at the base point and let w = v₀ ⋯v_n be the sequences of consecutive vertices in α. Each vertex appears twice in w, therefore w is a double-occurrence word over the alphabet consisting of the set of vertices, corresponding to the graph Γ. Conversely, for a given double-occurrence word containing n letters, a graph is constructed as follows. The set of vertices corresponds to the set of distinct symbols in the double-occurrence word, and each vertex is labeled by a symbol. Starting from the vertex labeled by the first symbol of the given word, connect the vertices by edges in the order of appearance of symbols of the word through a Eulerian transversal, and connect the path back to the starting vertex. In the second encounter of a vertex, corresponding to the second appearance of the symbol in the word, the path goes straight through the vertex, so that the edges added in the second visit are not neighbors at that vertex. This results in a transversely connected 4-regular rigid vertex graph.

Equivalence classes of double-occurrence words are in one-to-one correspondence with isomorphism classes of transversely connected 4-regular rigid vertex graphs [2]. In particular, if w is a double-occurrence word, we write Γ_w for a graph corresponding to w.

1.1.2 Genus of transversely connected 4-regular rigid vertex graphs

An embedding of a graph in a surface is called cellular if each component of the complement of the graph in the surface is an open disk. For a graph G, the minimum orientable genus of G, denoted g_min(G), is the smallest non-negative integer g such that G admits an embedding in a closed (compact, without boundary) orientable surface F of genus g. We recall the following fact (Proposition 3.4.1 in [17]): Every embedding of G into a minimum genus surface is cellular. The maximum orientable genus of G, denoted g_max(G), is the largest non-negative integer g such that G admits a cellular embedding in a closed orientable surface F of genus g.

An embedding of a 4-regular rigid vertex graph in a surface is an embedding of the graph such that the cyclic order of edges at each vertex agrees with those of the corresponding embedded images. In particular, neighboring edges at a vertex belong to the boundary of a common complementary region.

Definition 2

The genus range gr(Γ) of a 4-regular rigid vertex graph Γ is the set of values of genera over all orientable surfaces F into which Γ is embedded cellularly. We denote the family of all genus ranges of graphs with n vertices by 𝒢ℛ_n.

Convention

In this work, every embedding of a graph is a cellular embedding in an orientable surface.

1.2 Preliminary constructions

In this section we introduce tools to study genus ranges. We describe an explicit construction of a cellular embedding of a graph, related to rotation systems of embeddings of standard graphs [17, 15, 11], called the ribbon graph construction. We also introduce two techniques that are used to calculate genus ranges in later sections: a connection change in Section 1.2.2 and the addition and removal of a vertex in Section 1.2.3. Finally, we observe that genus ranges of graphs consist of consecutive integers in Lemma 4.

1.2.1 Ribbon graph construction

One way to obtain a cellular embedding of a graph Γ in a compact orientable surface is by constructing a surface by connecting bands (ribbons) along the graph. This construction is called a ribbon construction and is described below.

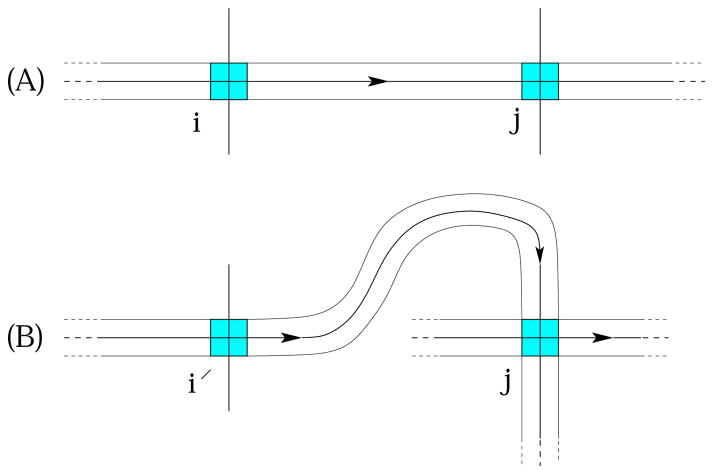
Let Γ be a graph with n vertices labeled from 1 to n, and let w be the double-occurrence word that represents Γ with respect to a transversal. To each vertex i, i = 1, …, n, we associate a square whose center axes coincide with the edges incident to the vertex as depicted in Figure 2. The bands are attached in such a way that the resulting surface is orientable. In Figure 2(A), the connection by a band is described when the vertex j immediately follows i in w, where j is the first occurrence in w. In Figure 2(B), one possibility of connecting a band to the vertex j at its second occurrence is shown. By continuing the band attachment along a transversal, one obtains a compact surface with boundary which consists of finitely many circles. The resulting surface is called a ribbon graph. The ribbon graphs have been studied in literature for general graphs (see, for example, [11]).

Figure 2.

Ribbon graph construction for w = u₁iju₂i′ju₃

By capping the boundaries of a ribbon surface with disks, one obtains a cellular embedding of Γ in an orientable, closed (without boundary) surface. On the other hand, for a given cellular embedding of a graph Γ, its neighborhood is regarded as a ribbon surface as described above. Therefore, a ribbon surface gives rise to an embedding, and any embedding of a graph in an orientable surface corresponds to a ribbon surface.

Note that there are two choices in connecting a band to a vertex j at its second occurrence, either from the top as in Figure 2(B), or from the bottom. Hence 2ⁿ ribbon graphs can be constructed, some of which may be homeomorphic. In [7, 8], the two possibilities of connecting bands are represented by signs (±), and signed Gauss codes were used to specify the two choices.

1.2.2 Connection change

The genus range of a given graph can be computed by finding genera of all surfaces constructed from the ribbon graph construction. We recall the well-known Euler characteristic formula, establishing the relation between the genus and the number of boundary components. The Euler characteristic χ(F) of a compact orientable surface F of genus g(F) and the number of boundary components b(F) are related by χ(F) = 2−2g(F)−b(F). As a complex, Γ is regarded as a 1-complex with n vertices and 2n edges, and F is homotopic to such a 1-complex (as a deformation retract). Hence χ(F) = n − 2n = −n. Thus we obtain the following well known formula, which we state as a lemma, as we use it often in this paper.

Lemma 3

Let F be a surface for a graph Γ obtained by the ribbon graph construction. Let g(F) be the genus of F, b(F) be the number of boundary components of F, and n be the number of vertices of Γ. Then we have g(F) = (1/2)(n − b(F) + 2).

Therefore the genus range of the graph Γ can be computed from the numbers of boundary components of all ribbon graphs of Γ, {b(F)|F is a ribbon graph of Γ}. Note that n and b(F) have the same parity, as genera are integers.

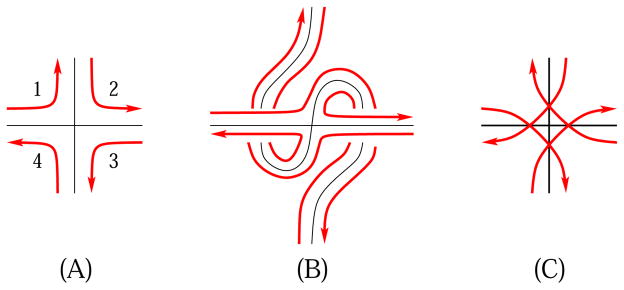
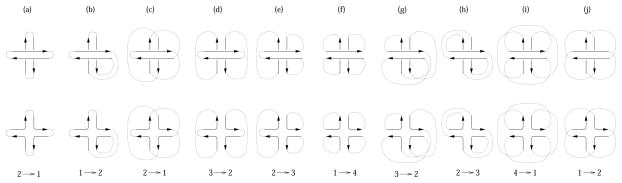
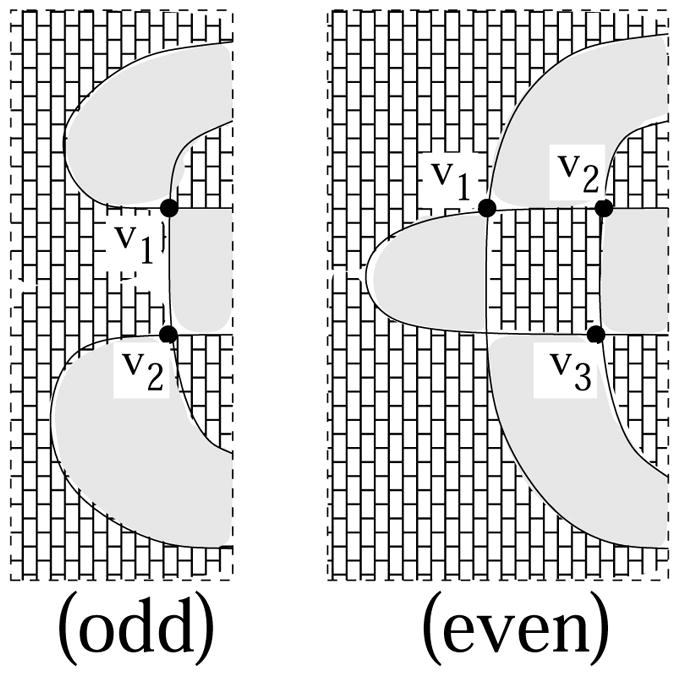
In Figure 3(A) and (B), the boundary curves of a ribbon graph of a graph, near a vertex, are indicated. The arrows of these boundary curves indicate orientations of the boundary components induced from a chosen orientation of the ribbon graph. If in Figure 2(B), the direction of entering the vertex has been changed from top to bottom (or vise versa), the ribbon graph may change. This change in the ribbon graph is illustrated in Figure 3(B). Note that the new ribbon graph is also orientable, as indicated by the arrows on the new boundary components. We use a schematic image in Figure 3(C) to indicate the changes of connections of the boundary components illustrated in Figure 3(B). We call this operation a connection change. This corresponds to changing a rotation scheme at the vertex to its reverse. Thus starting from one ribbon graph for a given graph Γ, one obtains its genus range by computing the number of boundary components for the surfaces obtained by switching connections at every vertex (2ⁿ possibilities for a graph with n vertices, for a positive integer n).

Figure 3.

Changing the connection (rotation scheme) at a vertex

The following is known for ordinary graphs, and it can be confirmed for rigid vertex graphs by observing that the number of boundary components changes by at most two by a change of connection at a vertex. Similar results have been obtained in other restricted graph embeddings as well (e.g., [18]).

Lemma 4

The genus range of any 4-regular rigid vertex graph consists of consecutive integers.

Hence, from now on the genus range {a, …, b}, for integers 0 ≤ a ≤ b, is denoted by [a, b].

1.2.3 Addition and removal of a vertex

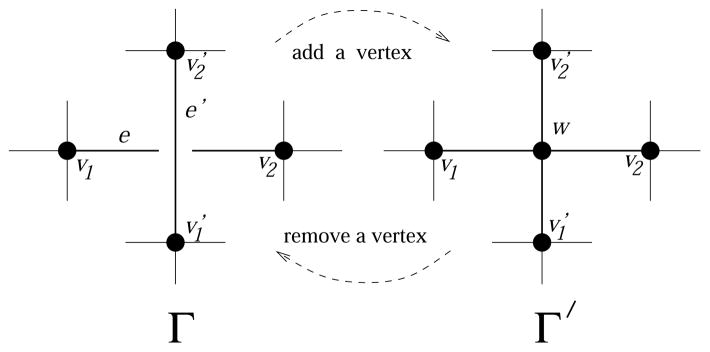
We investigate how the number of boundary components changes under a construction that generates a graph with n ± 1 vertices from one that has n vertices.

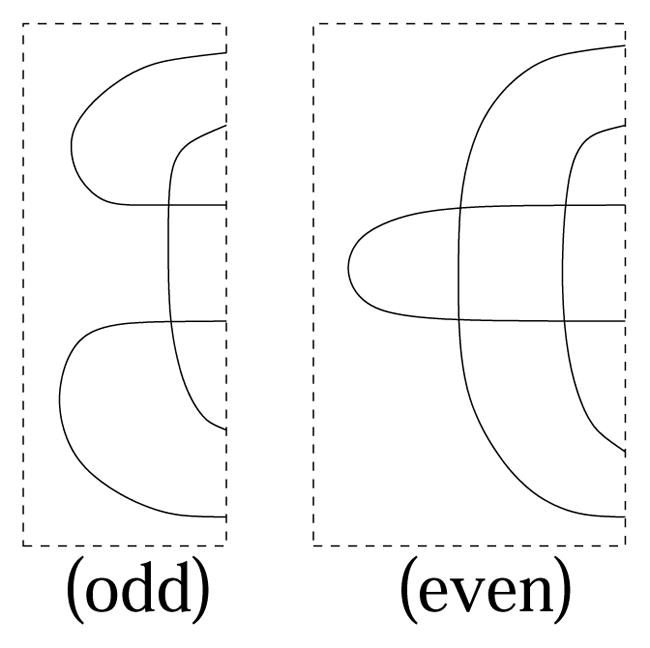
Let Γ be a graph and e, e′ be two edges in Γ with endpoints v₁, v₂ and $v_1^{\prime },v_2^{\prime }$ respectively. We say that Γ′ is obtained from Γ by addition of a vertex by crossing e, e′ and splitting e into e₁, e₂ and e′ into $e_1^{\prime },e_2^{\prime }$ in cyclic order e₁, $e_1^{\prime }$, e₂, $e_2^{\prime }$ (or simply by addition of a vertex when context allows) if Γ′ is obtained from Γ as depicted in Figure 4 and denote it by Γ′ = Γ(e, e′). In this case we also say that Γ is obtained from Γ (e, e′) by vertex removal. Note that the vertices v₁, v₂, $v_1^{\prime },v_2^{\prime }$ need not to be distinct.

Figure 4.

Addition and removal of a vertex

Let F be a ribbon graph of Γ and let Γ′ be obtained from Γ by addition of a vertex w. A ribbon graph F′ of Γ′ whose boundary connections at every vertex v ≠ w is the same as the boundary connections of F at v is denoted F (w). Since there are two possible connections of the boundary components of F (w) at the new vertex w, the notation indicates one of those two choices.

All possible changes in the global connections of boundary components of F (w) at the new vertex w relative to the boundary components of the crossing edges that add the new vertex w are depicted in Figure 5.

Figure 5.

Possibilities of connections

Definition 5

We say that the boundary component δ of a ribbon graph Γ traces the edge e of Γ if the boundary of the ribbon that contains e is a portion of δ.

There are at most two boundary components that can trace an edge, so there are at most four boundary components of a ribbon graph that trace two edges from Γ.

Lemma 6

Let Γ, Γ′ be two graphs such that Γ′ = Γ (e, e′) by crossing edges e, e′ and addition of a new vertex w. Suppose F and F (w) are ribbon graphs for Γ, Γ′ as defined above with b, b′ being the number of boundary components for F and F (w), respectively. Then we have the following:

1. If both e and e′ are traced by only one boundary component in F, then b′ = b + 1 or b′ = b + 3.

2. If both e and e′ are traced by two boundary components in F, then b′ = b + 1 or b′ = b − 1.

3. If e and e′ are traced by three boundary components in F, then b′ = b − 1.

4. If e and e′ are traced by four boundary components in F, then b′ = b − 3.

Proof

The proof follows directly from the observations shown in Figure 5.

2 Properties of Genus Ranges

In this section we investigate properties of genus ranges that are used in later sections. Although the following lemma is a special case of Lemma 12, we state it separately since its simple form is convenient to use. We recall that all graphs are transversely connected 4-regular rigid vertex graphs.

Lemma 7

For any double-occurrence word w, the genus range of Γ_w is equal to that of Γ_w′ where w′ = waa and a is a letter that does not appear in w.

Proof

The graph Γ_w′ corresponding to w′ is obtained from the graph Γ_w by adding a loop with a single vertex corresponding to the letter a. Both of the two boundary connections at the added vertex a increase the number of boundary components by one as depicted in Figure 5 (b) and (h). Hence the genus range remains unchanged.

Definition 8

A double-occurrence word v is said to be obtained from w by loop nesting if there exists a sequence of double-occurrence words w = w₀, w₁, …, w_n = v such that $w_{i+1}=w_i^{\prime }{a}_i{a}_i$ where $w_i^{\prime }$ is a cyclic permutation or reverse of w_i and a_i is a single letter that does not appear in w_i for i = 0, …, n − 1. A double-occurrence word obtained from the empty word ε by loop nesting is called loop-nested. A 4-regular rigid vertex graph corresponding to a loop-nested double-occurrence word is called a loop-nested graph.

Lemma 7 implies that loop nesting preserves the genus ranges. Specifically,

Corollary 9

If a double-occurrence word w′ is obtained from a double-occurrence word w by loop nesting, then their corresponding graphs have the same genus range.

Corollary 10

If a set A appears as the genus range in 𝒢ℛ_n for a positive integer n, then A appears as a genus range in 𝒢ℛ_m for any integer m > n.

Proof

Let w′ = wa₁a₁a₂a₂ ⋯a_ka_k where k = m − n > 0, then by Corollary 9 Γ_w′ has the same genus range as Γ_w.

Definition 11

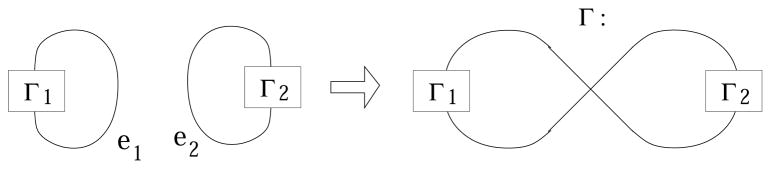
Let Γ₁ and Γ₂ be graphs and e_i be an edge in Γ_i for i = 1, 2. A graph Γ is said to be obtained from Γ₁ and Γ₂ by a cross sum with respect to e₁ and e₂ if it is formed by connecting Γ₁ and Γ₂ through a new vertex to form the figure-eight graph with e₁ and e₂, as depicted in Figure 6. The crossing at the middle in the right of Figure 6 is the newly added vertex.

Figure 6.

Cross sum

The cross sum was discussed, in relation to virtual knots, in [10]. The cross sum construction depends on the choice of edges of the two graphs to connect to the figure-eight.

Lemma 12

Let Γ₁ and Γ₂ be graphs. If Γ is obtained from Γ₁ and Γ₂ by a cross sum, then gr(Γ) = { g₁ + g₂ | g₁ ∈ gr(Γ₁), g₂ ∈ gr(Γ₂)}.

Proof

Let Γ be the graph obtained from Γ₁ and Γ₂ by cross sum through e₁ and e₂. For given ribbon graphs F₁ and F₂ of Γ₁ and Γ₂, respectively, a ribbon graph F of Γ is constructed as depicted in Figure 7. The two boundary curves tracing the edges e_i of Γ_i (i = 1, 2) belong to either one component or two in each of F₁ and F₂. In Figure 7(A), the case where the two curves belong to one component for both Γ_i, i = 1, 2, is depicted. In (B), the case when one of the two edges is traced by distinct components (Γ₂ in this figure) is depicted, and in (C), the case when the both edges are traced by distinct components of F_i, i = 1, 2, is depicted. From the figures we identify these cases (A), (B), (C) with the connection cases (a), (b) and (h), respectively, in Figure 11. We see from Figure 11 that by a connection change in all these cases, the number of boundary components does not change. Let v_i and b_i be the numbers of vertices and boundary components of F_i, i = 1, 2, respectively, and similarly v, b for F. Then for all cases (A), (B) and (C) we have v = v₁ + v₂ + 1 and b = b₁ + b₂ − 1. From Lemma 3 we compute

Figure 7.

Boundary curves of a cross sum construction

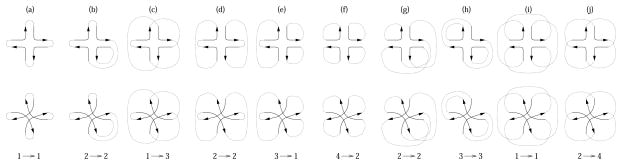
Figure 11.

Possibilities of connections

$$g(F)=\frac{1}{2}(v-b+2)=\frac{1}{2}((v_1+v_2+1)-(b_1+b_2-1)+2)=g(F_1)+g(F_2)$$

as desired.

Definition 13

Let Γ be a graph, Γ₀ be the graph corresponding to the word 1212, and Γ′ be the graph obtained by connecting an edge e of Γ with Γ₀ as depicted in Figure 8. Then Γ′ is said to have been obtained by connecting a pretzel to Γ.

Figure 8.

Connecting a pretzel

Lemma 14

Let Γ′ be obtained from Γ by connecting a pretzel. Suppose gr(Γ) = [m, n] for non-negative integers m and n (m ≤ n).

If there is a minimum genus embedding of Γ such that the two boundary curves tracing edge e belong to the same boundary component, then gr(Γ′) = [m, n + 1]. Otherwise gr(Γ′) = [m + 1, n + 1].

Proof

In Figure 9, the boundary curves corresponding to all possible connections at vertices of Γ₀ are depicted in (A) through (D). The number of boundary components are 3 for (A) and (C), and 2 for (B) and (D). In (E) and (F), the situations of how they are connected are schematically depicted, respectively. The Figure (E) represents (A) and (C), and (F) represents (B) and (D).

Figure 9.

Boundary curves for 1212

1. Suppose Γ satisfies the condition that for all ribbon graphs of Γ, the two boundary curves tracing edge e belong to two distinct boundary components. Consider a ribbon graph F for Γ with genus g ∈ gr(Γ). For each ribbon graph F₀ in (A) through (D) of Γ₀ in Figure 9, we obtain a ribbon graph F′ of Γ′ by connecting corresponding boundaries of the ribbon graphs for Γ₀ and Γ. If the connection of the boundary curves of a ribbon graph F₀ of Γ₀ is as in Figure 9(E), then the two curves tracing e become connected, and there is an additional component indicated by a small circle in the middle of (E). So the number of boundary components remains unchanged, and the number of vertices increases by 2. Hence g(F′) = g + 1, and g + 1 is an element of gr(Γ′). If the connection of the boundary curves of a ribbon graph F₀ of Γ₀ is as in Figure 9(F), then again the number of boundary curves of the ribbon graph for Γ′ remains the same as F, and the number of vertices increases by 2, so that g(F′) = g + 1, hence g + 1 is an element of gr(Γ′). Therefore gr(Γ) = [m + 1, n + 1].

2. Suppose Γ satisfies the condition that for some ribbon graphs of Γ, the two boundary curves tracing edge e belong to the same boundary component. Suppose that the connection of the boundary curves of a ribbon graph F₀ of Γ₀ is as in Figure 9(E). If the boundary component of a ribbon graph F for Γ tracing e is connected, then it becomes disconnected after connecting a pretzel and there is an additional component in F′. Therefore the number of boundary components increases by 2, and the number of vertices increases by 2. Hence g(F′) = g, and g is an element of gr(Γ′). If the boundary component of F for Γ tracing e is disconnected, then the number of boundary components remain unchanged, and the number of vertices increases by 2. Hence in this case g(F′) = g + 1.

If the connection of the boundary curves of a ribbon graph F₀ of Γ₀ is as in Figure 9(F), then the number of boundary components of the ribbon graph for Γ′ remains the same as that of F. In this case the number of vertices increases by 2, so g(F ′) = g + 1, and g + 1 is an element of gr(Γ′). Therefore gr(Γ) = [m, n + 1] or [m + 1, n + 1]. We note that the genus range of Γ′ is [m, n + 1] if and only if there exists a ribbon surface F with the minimum genus m such that e is traced by a single boundary component.

As to the condition (i) in the proof of Lemma 14, we note the following.

Lemma 15

Let Γ be a planar graph and e be an edge in Γ. Then for all ribbon graphs of Γ, there are two distinct boundary components that trace e.

Proof

Fix a planar diagram of Γ, still denoted by Γ. The closure of a topological, thin neighborhood of Γ in the plane determines a ribbon graph F. Each boundary curve of F corresponds to a region of the complement of F (a connected component of ℝ² \ F) in the plane. In this construction, the connection of boundary curves at every vertex has the form in Figure 3(A). We assign checker-board “black” and “white” coloring to these regions (there is one, see [16] for example) such that regions bordering the same edge have distinct colors. The corresponding boundary curves of F inherit this coloring. Hence every edge is traced by boundary components of two distinct colors. Let B and W be (disjoint, non-empty) families of boundary curves colored black and white, respectively. Any ribbon graph F ′ of Γ is obtained from F by changing boundary connections at some vertices. When we change the boundary connection at a vertex v, two diagonal boundary curves of the same color become connected, see Figure 3 (A) and (C). The connected curves inherit the color, each component of the boundary curves is colored black or white after the change, and every edge of Γ is traced by two boundary components, one white and one black.

3 Realizations of Genus Ranges

Guided by observations made from computer calculations (Table 1), in this section we prove general statements on the non-existence (Section 3.1) and existence (Section 3.2) of various genus ranges. We recall again that all graphs are transversely connected 4-regular rigid vertex graphs.

3.1 Genus ranges that do not arise

In what follows, all graphs refer to transversely connected 4-regular rigid vertex graphs.

Lemma 16

For any positive integer n, there is no graph with 2n − 1 vertices with genus range [0, n].

Proof

Suppose there is such a graph Γ. Since its genus range contains 0, Γ is planar. By Lemma 15, every ribbon graph of Γ has more than one boundary component, and therefore, the genus cannot be n by Lemma 3.

The lemma below uses arguments and methods similar to those in [18].

Lemma 17

For every graph there is a ribbon graph with more than one boundary component.

Proof

Let Γ be a graph with k vertices. Starting from one vertex, we enumerate the edges of Γ along the transversal from 1 to 2k. Since the transversal consists of an Eulerian path in which two consecutive edges are not neighbors, every vertex in Γ is incident to two even numbered edges and two odd numbered edges. Moreover, the odd numbered (similarly, even numbered) edges incident to a common vertex are neighbors to each other. Let G be the subgraph of Γ that is induced by the odd numbered edges. This graph consists of k vertices and k edges, so it is a collection of cycles. For any cycle c of G, there is a choice of connection such that c is a boundary component of a ribbon graph F. Since this component traces edges only in G, the ribbon graph F must contain boundary components that trace the edges not in G, hence, F has more than one component.

The lemma immediately implies the following.

Lemma 18

For any positive integer n, there is no graph with 2n − 1 vertices with genus range {n}.

3.2 Genus ranges that do arise

Proposition 19

For any integer m ≥ 0, there exists an integer n such that {m} is a genus range in 𝒢ℛ_n.

Proof

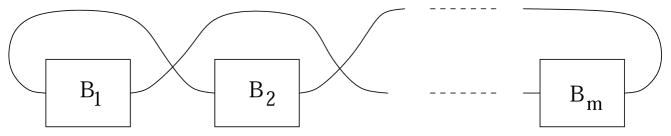
Let Γ_m be the graph obtained by connecting m copies of Γ₀ in the boxes B₁, …, B_m as depicted by solid line in Figure 10, where Γ₀ is the graph depicted in the upper half of Figure 8 that corresponds to the word 1212. This is obtained from copies of Γ₀ by repeated application of cross sum of Definition 11. Recall that Γ₀ has the genus range {1}. By Lemma 12, Γ_m has the genus range {m}.

Figure 10.

Repeating cross sum

The following provides a characterization of graphs with genus range {0}, giving an answer to Problem 1 (b) for this range.

Proposition 20

A double-occurrence word w is loop-nested if and only if gr(Γ_w) = {0}.

Proof

Corollary 9 implies that if w is loop-nested then gr(Γ_w) = {0}. The converse follows from a known characterization of signed double-occurrence words corresponding to closed normal planar curves (Theorem 1 of [7]).

In Figure 11, all possibilities of global connections of local arcs for a neighborhood of a vertex corresponding to Figure 3(A) are depicted in the top row, and in the middle row, the global connections after the change of connection as in Figure 3(C) are depicted. In the bottom row, the change of the number of boundary components associated with a connection change is listed. This list is used in the proofs below.

Proposition 21

The graph corresponding to any word obtained from w = 12 ⋯ n12 ⋯ n, for an odd integer n, by loop nesting has the genus range [0, 1].

Proof

First we show that the graph Γ_n corresponding to a word w = 12 ⋯ n12 ⋯ n has genus range {0, 1}. We start with the planar diagram depicted in Figure 12. Boundary curves of the ribbon graph obtained as a neighborhood of Γ_n are depicted by dotted lines. When the connection of one vertex (the vertex 1 in Figure 13 left) is changed, both pairs of diagonal curves are connected from two components to one (see Figure 11(f)). Hence the number of boundary components reduce by 2, and the genus increases from 0 to 1 by Lemma 3.

Figure 12.

Graphs for words of the form 12 ⋯ n12 ⋯ n

Figure 13.

Changing connections for repeat word graphs

After the change at the vertex 1, the boundary connection at every other vertex 2 through n is as depicted in Figure 11(h). Hence the number of the boundary components does not change by changing the boundary connections. After the second change of the boundary connection at the vertex i, the connection at every vertex remains the same as in Figure 11(h). This property holds for odd n. In Figure 13 middle and right, changes are made at vertices i = 2 and 3, respectively, after the change at the vertex 1.

The statement follows from Lemma 7.

Conjecture 22

Any double-occurrence word whose corresponding graph has genus range [0, 1] is obtained from the word w = 12 ⋯ n12 ⋯ n for an odd integer n by loop nesting.

Proposition 23

For any integer n > 1, there exists a graph Γ of 2n vertices with gr(Γ) = [0, n].

Proof

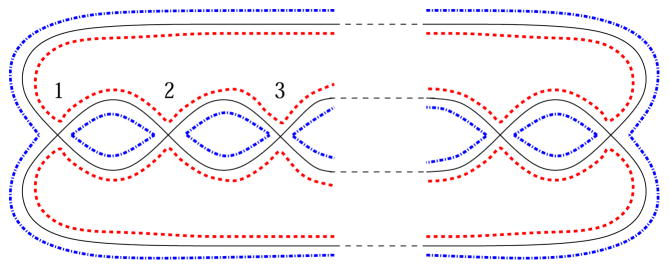
Computer calculations in Table 1 show that there is a unique graph of 4 vertices corresponding to 12314324 that has genus range {0, 1, 2}. In Figure 14, a graph P₃ is depicted that has the genus range {0, 1, 2, 3}. To show this, we start with the planar diagram as depicted. We consider the ribbon graph that is a thin neighborhood of this planar diagram. For this ribbon graph, the boundary connection at every vertex appears as type (A) in Figure 3. The genus of this ribbon graph is 0. Each region of the diagram corresponds to a boundary curve of the corresponding ribbon graph. Four of such boundary curves (out of total 8) are depicted by dotted lines in the figure, for the regions labeled by a₁, a₂, b₁, and b₂.

Figure 14.

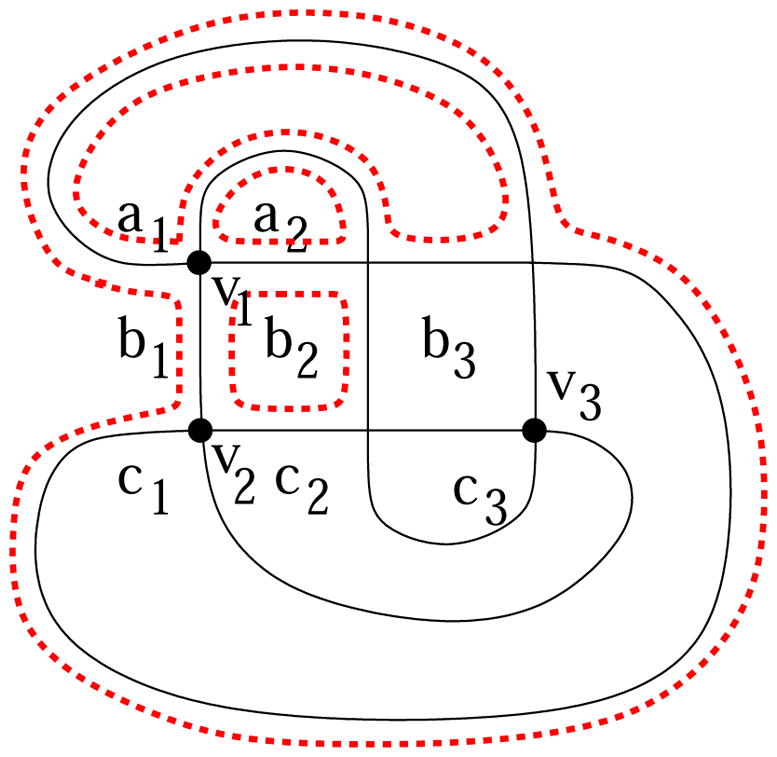
Proof for P₃

We change the boundary connection at the vertex labeled by v₁ from type (A) in Figure 3 to type (C), where the connection is as indicated in Figure 11(f). Then as Figure 11(f) indicates, the curves a₁ and b₂, a₂ and b₁, are connected, respectively, reducing the number of boundary components by 2. This causes the increase of the genus of the new ribbon graph by 1 by Lemma 3, so that the new surface has genus 1. After the connection change at v₁, the boundary connection at v₂ remains as in Figure 11(f), since the regions b₁, b₂, c₁, c₂ are bounded by distinct curves. Thus by repeating this process with vertices v₂ and v₃, we obtain ribbon graphs of genus 2 and 3, respectively. The number of boundary curves after performing the changes at v₁, v₂ and v₃ is 2. The two components can be seen as a checkerboard coloring of the regions, and the two boundary curves near every edge belong to distinct components (cf. Lemma 15). This shows that the genus range for this graph is {0, 1, 2, 3}.

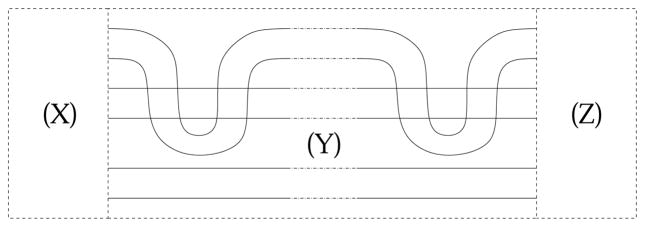
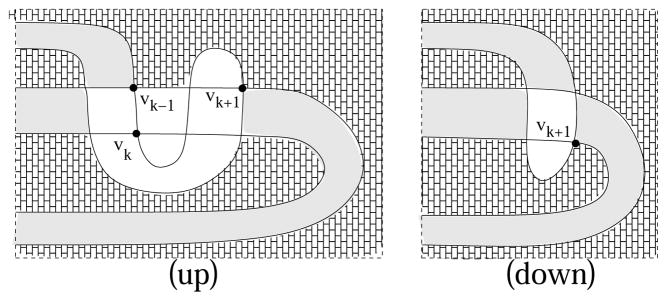
Next we describe the graph P_n for n > 3 as the combination of three subgraphs indicated in Figure 17 as follows. If n is odd, then the subgraph in the box (X) in Figure 17 is as depicted in Figure 15(odd), and if n is even, it is as depicted in Figure 15(even), respectively. The middle part in the box (Y) is as depicted in Figure 17. The subgraph in box (Z) in Figure 17 is either (down) or (up) of Figure 16, and the choice is determined by the number of vertices of P_n. Specifically, for integers k, P_n has the following patterns in boxes (X) and (Z) in Figure 17, respectively: If n = 4k, 4k+1, 4k+2, 4k+3, respectively, the box (X) and (Z) are filled with (even) and (down), (odd) and (up), (even) and (up), (odd) and (down), respectively. Examples for n = 6 (even, up) and 7 (odd, down) are depicted in Figure 18 and 19, respectively.

Figure 17.

Inductive construction of P_n

Figure 15.

Box (X)

Figure 16.

Box (Z)

Figure 18.

P₆

Figure 19.

P₇

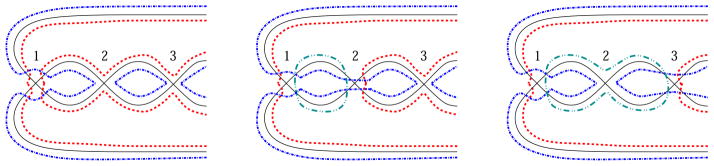
We generalize the argument for P₃ to P_n inductively. We start with the ribbon graph that is a thin neighborhood of the planar diagram as described in Figure 17, where the boundary connection at every vertex is of type (A) in Figure 3. The connection of boundary curves is as Figure 11(f) at every vertex. We successively change boundary connections from type (A) to type (C) at a subset of vertices we describe below. With every such change, the number of boundary components of the corresponding ribbon graph reduces by 2, and hence the genus increases by 1. We start by changing the boundary connections for the vertices in the subgraph in box (X). For n odd, we change the boundary connection at vertices v₁ and v₂ in Figure 20(odd), and for n even, at vertices v₁, v₂ and v₃ in Figure 20(even). The checkerboard coloring in Figure 20 indicates that the boundary curves of the regions of the same shading are connected.

Figure 20.

Shading (X)

Next we proceed to box (Y) inductively. In Figure 21, after the changes of the boundary connections at vertices v_i and v_i+1 in this order, the boundary curves are connected for the curves of the regions of the same shading in Figure 21. Note that the boundary curves of the four regions (a) through (d) in the figure belong to distinct components. Hence the connection changes at the vertices v_i+2 and v_i+3 in this order connects the curves (a) and (c), (b) and (d) to those two curves corresponding to the two shadings, respectively. Inductively, by changing boundary connections in all thickened vertices in Figure 17 box (Y), all curves bounding the regions in box (Y) are connected to two boundary components. The two components are indicated by the checkerboard shading.

Figure 21.

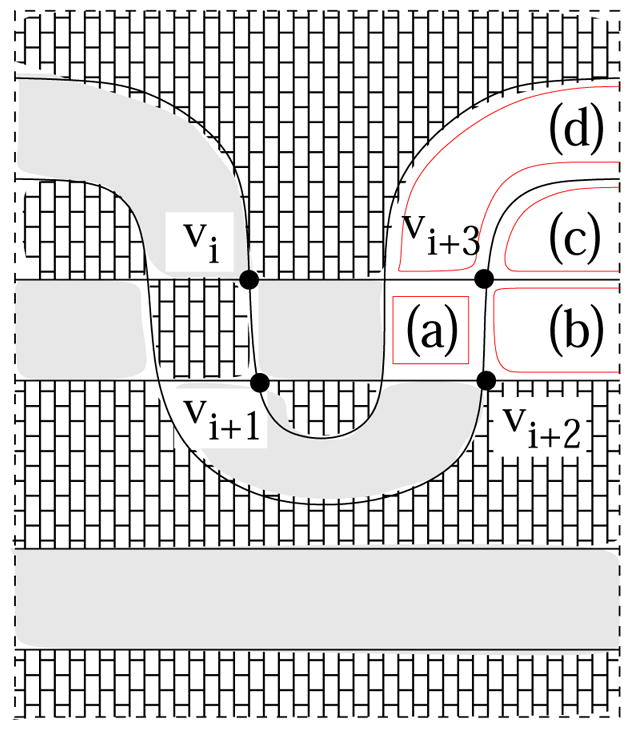
Shading (Y)

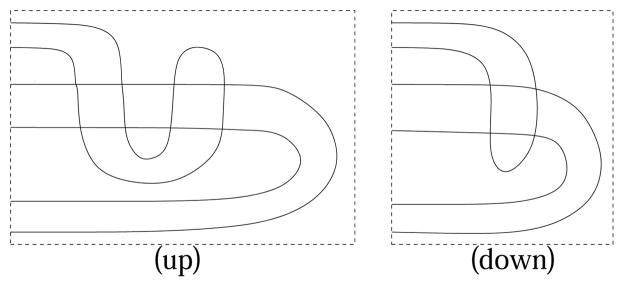
We complete the induction in box (Z) as indicated in Figure 3.2. The last sequences of vertices where the boundary connections are changed from type (A) to (C) are depicted in the figure for each case (up) and (down) of Figure 16.

Proposition 24

For any integer n > 1, there exists a graph Γ of 2n + 1 vertices with gr(Γ) = [0, n].

Proof

This follows from Proposition 23 and Lemma 10.

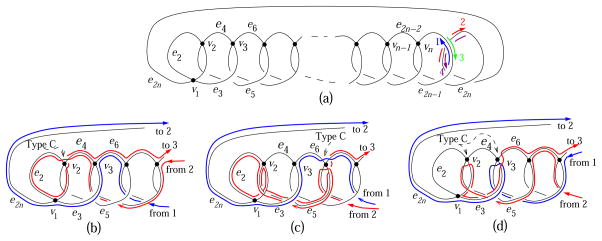
Next, we find the genus range of a family of graphs called the tangled cords. Furthermore, in view of Problem 1, we prove that for all odd n the maximum genus range $\left\{\lfloor \frac{n-1}{2}\rfloor ,\lfloor \frac{n+1}{2}\rfloor \right\}$ is achieved by the tangled cord with n vertices. The analysis of the genus range in this case uses a technique of addition and removal of a vertex, described in Section 1.2.3.

Definition 25

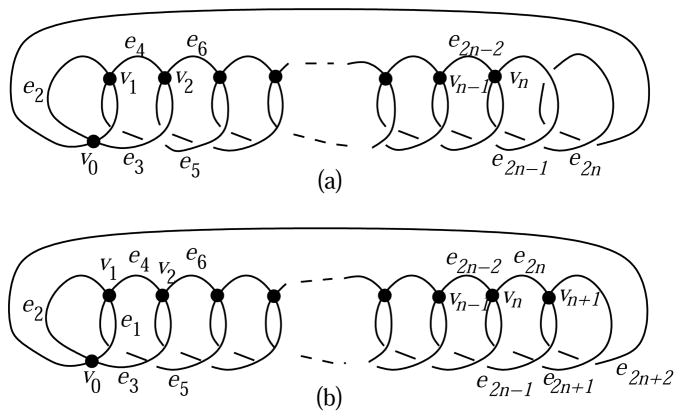
A tangled cord [6] with n vertices and 2n edges, denoted T_n, is a special type of graphs of the form illustrated in Figure 23.

Figure 23.

Tangled cord T_n

The graph T_n corresponds to the double-occurrence word

$$1213243\cdots (n-1)(n-2)n(n-1)n.$$

Specifically, T₁, T₂ and T₃ correspond to 11, 1212, and 121323 respectively, and the double-occurrence word of T_n+1 is obtained from the double-occurrence word of T_n by replacing the last letter (n) by the subword (n + 1)n(n + 1). Figure 23 shows the structure of the tangled cord. For vertices and edges of T_n, we establish the following notation for the rest of the section. The edges of T_n are enumerated as e₁, …, e_2n as they are encountered by the transverse path given by the double-occurrence word, in this order. The adjacent edges to each vertex are listed below, in the cyclic order around the vertex, as follows.

$$\begin{array}{l}{v}_1:e_1,e_3,e_{2n},e_2\\ v_2:e_1,e_5,e_2,e_4\\ v_i:e_{2(i-1)},e_{2i},e_{2(i-2)+1},e_{2i+1}\text{for}i\ne 1,2,n-1,n\\ v_{n-1}:e_{2(n-2)},e_{2n-2},e_{2(n-3)+1},e_{2n-1}\\ v_n:e_{2n},e_{2n-2},e_{2n-1},e_{2n-3}\end{array}$$

By construction, T_n+1 is obtained from T_n by addition of a vertex v_n+1 by crossing e_2n−1 and e_2n as in Figure 23, with the cyclic order e_2n+1, e_2n−1, e_2n, e_2n−2 at v_n+1.

The tangled cord T_n was introduced in [6] as a graph that provided a tight upper bound on the number of Hamiltonian polygonal paths (paths in which consecutive edges are neighbors with respect to their common incidence vertex visiting every vertex exactly once) over all graphs of the same number of vertices.

We prove that for each T_n, if F is a ribbon graph for T_n then it has either 1 or 3 boundary components (if n is odd) or it has 2 or 4 boundary components (if n is even). First we prove the following lemma:

Lemma 26

Let F be a ribbon graph for T_n (n ≥ 2) and suppose B is the set of boundary components that trace edges e_2n−1 and e_2n. Then every edge of T_n is traced by a curve in B.

Proof

We use the following notation: for any set E of edges, let B(E) be the set of boundary components of the ribbon graph F that trace at least one edge in E. So B in the statement is written as B({e_2n−1, e_2n}). Observe that B has at most four elements as there are at most four boundary components tracing two edges. Edges e_2n−1 and e_2n in T_n are not neighbors, but they are consecutive edges of the transverse path defining T_n. Hence all boundary components tracing e_2n−1 and e_2n (which are at most four) must trace their neighboring edges e_2n−2 and e_2n−3 (see Figure 3(A) or (C)). Therefore B({e_2n, e_2n−1, e_2n−2, e_2n−3}) = B. But then edges e_2n−1 and e_2n−2 are consecutive edges of the transverse path at vertex v_n−1 and so, all boundary components that trace e_2n−1 and e_2n−2 must also trace their neighboring edges at v_n−1, that is, edges e_2n−4 and e_2n−5. So B({e_2n, …, e_2n−5}) = B.

Inductively, if B({e_2n, …, e_2i, e_2i−1}) = B, then all edges incident to vertices v_n, v_n−1, …, v_i+1 (i ≥ 2) are traced with boundary components from B. The edges e_2i+1 and e_2i are not neighbors and are both incident to v_i, therefore the boundary components that trace e_2i+1 and e_2i, also trace e_2i−2 and e_2i−3. Hence B({e_2n, e_2n−1, …, e_2i−2, e_2i−3}) = B. If i = 2 we obtain that B(E) = B where E is the set of all edges of T_n.

As a consequence of Lemma 26, and the fact that the parity of the number of boundary components of the ribbon graph must match the parity of the vertices from Lemma 3, we have that if n is even then any ribbon graph of T_n has 2 or 4 boundary components, and if n is odd, then any ribbon graph of T_n has 1 or 3 boundary components. In the following we observe that all these situations appear.

Lemma 27

For every odd number n > 2 there is a ribbon graph of T_n with three boundary components.

Proof

This lemma is a corollary of Lemma 18 (and its proof) where it is observed that for every graph there is a ribbon graph with more than one boundary component.

Lemma 28

For every odd number n > 2, there is a ribbon graph F of T_n with a single boundary component tracing edges e_2n and e_2n−1 whose global connection is as in Figure 5(f).

Proof

Since n is odd, the number of boundary components are either 1 or 3. The global connection of the boundary component in Figure 5(f) implies that the four possible boundary components tracing edges e_2n and e_2n−1 (indicated in Figure 24(a) with 1 through 4) are connected such that 1 is connected to 2, 2 connected to 3. If 3 is connected to 1, there would be two boundary components, hence 3 must be connected to 4, and back to 1. Therefore we only need to show that there is a ribbon graph where 1 is connected to 2 and 2 to 3. Suppose a ribbon graph corresponding to a fixed planar diagram in Figure 24(a) has boundary curves connected as type (A) of Figure 3 at vertices v_n, v_n−1, …, v₅ and also at vertex v₁. Then following the indicated arrows in Figure 24(a) the boundary curves visit vertices:

$$v_n{v}_{n-2}{v}_{n-3}{v}_{n-5}{v}_{n-6}{v}_{n-8}{v}_{n-9}\dots \text{by}\text{following}\text{boundary}\text{curve}1$$ (*)

$$v_n{v}_{n-1}{v}_{n-3}{v}_{n-4}{v}_{n-6}{v}_{n-7}{v}_{n-9}\dots \text{by}\text{following}\text{boundary}\text{curve}2$$ (**)

Figure 24.

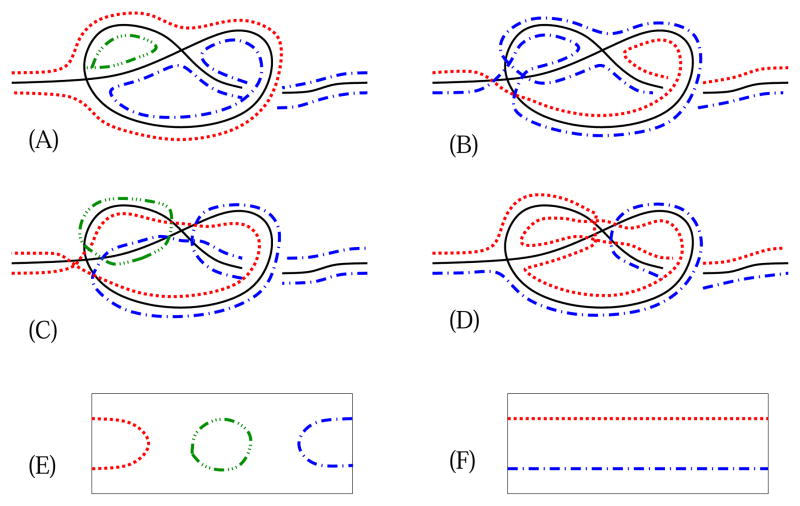
Connections of four boundary components in T_n

It follows that the two curves “meet” at every other vertex they visit (with indices changing in gaps of 3), but if the two curves “meet” at v_i, one of the curves traces edge e_2i and the other traces e_2i+1. There are three possibilities for the vertex of the smallest index (greater than 2) for (*) and (**) to “meet”: at vertex v₃, vertex v₄ and at vertex v₅ respectively. These situations are depicted in Figure 24(b–d, respectively) where the blue component indicates (*) and the red indicates (**).

The curves “meet” at vertex v₃ when n = 6k + 3 (Figure 24(b)), in which case we consider the ribbon graph where the boundary curves are connected at vertex v₂ in type (C) in Figure 3, and at all other vertices the connections are of type (A). The curves “meet” at vertex v₄ when n = 6k+1 (Figure 24(c)), in which case we consider the ribbon graph where the boundary curves are connected at vertex v₄ in type (C), and at all other vertices the connections are of type (A). The curves “meet” at vertex v₅ when n = 6k +5 (Figure 24(d)), in which case we consider the ribbon graph where the boundary curves are connected at vertex v₂ and v₃ in type (C), and at all other vertices the connections are of type (A). In all three cases we note that: (i) the (blue) boundary curve 1 that traces e₃ to v₁ and then e_2n, continues to “join” with boundary curve 2 and (ii) the (red) boundary curve 2 that traces the even edges e₆, e₈, e₁₀, …, e_2n−2, and then e_2n−1 “joins” with boundary curve 3 (Figure 24(a)). Since in all three cases situations (i) and (ii) appear, the global connection of the boundary components at edges e_2n−1 and e_2n are the same as in Figure 5(f).

The following proposition gives the final result about the genus range of T_n.

Proposition 29

Let T_n be the tangled cord with n = 2k or 2k − 1 vertices. Then gr(T_n) = [k − 1, k].

Proof

Recall that there are at most 4 boundary components by Lemma 26. By Lemmas 27, 28 for every odd n, there is a ribbon graph for T_n with one boundary component and there is a ribbon graph for T_n with three boundary components. We need to prove, for n even, that there are ribbon graphs with 2 and 4 boundary components. The graph T_n+1 is obtained from T_n by vertex addition by crossing e_2n−1 and e_2n. Suppose n ≥ 3 is odd. Then T_n has ribbon graphs with one and three components. By Lemma 6(iii) by adding vertex v_n+1 through crossing e_2n−1 and e_2n the three-component ribbon graph for T_n becomes a ribbon graph with two boundary components for T_n+1. By Lemma 28 there is a ribbon graph for T_n with a single boundary component, in which the global boundary connection traces edges e_2n−1 and e_2n as in Figure 5(f). Then after adding vertex v_n+1 by crossing e_2n−1 and e_2n, this ribbon graph becomes a ribbon graph with four boundary components for T_n+1. By Lemma 3 the result follows.

4 Towards Characterizing Genus Ranges

In this section we state and prove the main theorem on genus ranges of transversely connected 4-regular rigid vertex graphs. First we set the following notation.

Definition 30

We define the consecutive power set of {0, 1, …, n} for a positive integer n, denoted by 𝒞℘(n), to be the set of all consecutive positive integers: 𝒞℘(n) = { [a, b] | 0 ≤ a ≤ b ≤ n}.

Corollary 31

For any n ∈ ℕ, we have 𝒢ℛ_2n−1, 𝒢ℛ_2n ⊂ 𝒞℘(n).

Proof

This follows from Lemma 4, and Lemma 3 since b(F) ≥ 0.

To describe the genus ranges we can realize, we define the following integer sequence. For a positive integer n, define $K_n=\lfloor \frac{n+1}{7}\rfloor ,L_n=\lfloor \frac{n-7K_n+1}{3}\rfloor$, and ψ_n = 3K_n +L_n. For n = 100, for example, K_n = 14, L_n = 1 and ψ_n = 43. These numbers allow us to state the main theorem in the paper.

Theorem 32

1. For any n > 1, n ∈ ℕ, 𝒢ℛ_2n contains the set 𝒞℘(n) \ {[h, h] | ψ_2n < h ≤ n}.

2. For any n ∈ ℕ, 𝒢ℛ_2n−1 contains the set 𝒞℘(n) \ {[0, n], [h, h] | ψ_2n−1 < h ≤ n}.

3. For any n ∈ ℕ, [0, n], [n, n] ∉ 𝒢ℛ_2n−1.

Proof

The part (iii) is a restatement of Lemmas 16 and 18. We show (i) and (ii) by induction and constructions. Computer calculations in Table 1 show that the statements hold for n = 1, 2, 3 for 𝒢ℛ_2n−1 and n = 2, 3 for 𝒢ℛ_2n.

First we focus on sets [a, b] with a < b. Assume for induction that 𝒢ℛ_2k−1 contains all sets [a, b] ∈ 𝒞℘(k), where a < b ≤ k, excluding [0, k]. By Lemma 10, all these sets are contained in 𝒢ℛ_2k. Proposition 23 implies that [0, k] is contained in 𝒢ℛ_2k and so is in 𝒢ℛ_2k+1. Hence all sets [a, b] ∈ 𝒞℘(k), where a < b ≤ k for n ≤ k, are contained in 𝒢ℛ_2k and 𝒢ℛ_2k+1.

Assume next that 𝒢ℛ_2k contains all sets [a, b] ∈ 𝒞℘(k), where a < b ≤ k, and also that 𝒢ℛ_2k−1 contains all sets [a, b] ∈ 𝒞℘(k), where a < b ≤ k, excluding [0, k]. By Lemma 10, all [a, b] ∈ 𝒞℘(k), where a < b ≤ k, are contained in 𝒢ℛ_2k+1. We show that 𝒢ℛ_2k+1 contains all [a, b] ∈ 𝒞℘(k + 1), where a < b ≤ k + 1, excluding [0, k + 1]. Among these wanted, the following have not been covered by the induction assumption: [h, k + 1] for h = 1, …, k and [0, k]. There is a graph with 2k + 1 vertices and genus range [0, k] by Proposition 24. Thus we construct a graph Γ with |Γ| = 2k + 1 and gr(Γ) = [h, k + 1] for h = 1, …, k. Let T_2h+1 be the tangled cord of size 2h + 1, which has genus range [h, h + 1] by Proposition 29. Let F be a ribbon graph of T_2h+1 with genus h, and hence with 3 boundary components. We claim that there is an edge that is traced by a single component. Assume otherwise, that every edge is traced by distinct components. Since 4 boundary curves meet at every vertex, and there are 3 boundary components, at least two curves at each vertex belong to the same component.

In Figure 11, there are two possibilities with 3 boundary components at the top row, cases (e) and (h). Case (e) contains an edge traced by a single component, hence it is excluded by assumption. After the connection change (Figure 11 (h) bottom), the total number of boundary components stays as 3. A similar inspection shows that if both diagonal components belong to the same components (and 2 components meet at the vertex, Figure 11 (j)), then the connection change would separate these components into 4 components, which is impossible with T_2h+1 by Proposition 29. Therefore if every edge is traced by distinct components, then at every vertex the situation must be as in Figure 11 (h). But then, a connection change at any vertex does not change the number of components 3, which again contradicts Proposition 29 that the genus range of T_2h+1 is not a singleton. Hence there exists an edge e that is traced by a single component.

In Lemma 14, let Γ = T_2h+1 with the choice of an edge e that is traced by a single component for some ribbon graph F as found above. By (the proof of) Lemma 14, the genus range of the graph Γ′ obtained by connecting a pretzel along the edge e from Γ has genus range [h, h+2] and has size 2h+3. The edge connection of Γ₀ that gives rise to the genus h for Γ′ is as depicted in Figure 9(E). Hence either of the edges connecting Γ and Γ₀ is traced by a single boundary component for the ribbon graph resulted from these surfaces for Γ and Γ₀. Inductively, by taking this graph Γ′ as a new Γ, and by repeating this process (k–h) times, we obtain a graph with genus range [h, h+1+(k−h)] = [h, k+1] and size (2h + 1) + 2(k − h) = 2k + 1 as desired.

We analyze the case [a, a]. Computer calculation shows that there is a unique graph Γ₆ with genus range [3, 3] among all 6 vertex graphs. The graph Γ₆ is represented by 123245153646. Let Γ(K, L) be the graph obtained by taking cross sums of K copies of Γ₆ and L copies of Γ₀ (represented by the word 1212). Then the number of vertices of Γ(K, L) is 7K + 3L − 1. Its genus range is [ψ, ψ] where ψ = 3K + L. The number of vertices of the graph Γ(K − 1, L+ 2) is one less than that of Γ(K, L) and its genus range is [ψ−1, ψ −1]. If K = 0, the number of vertices of the graph Γ(0, L−1) is two less than that of Γ(0, L) and its genus range is [ψ−1, ψ−1]. For n < 6, the statement follows from computer calculation (Table 1). For n ≥ 6, the genus range of the graph Γ(K_n, L_n) is [ψ_n, ψ_n], and theorem follows by considering Γ(K, L) with K ≤ K_n as above and applying Corollary 10.

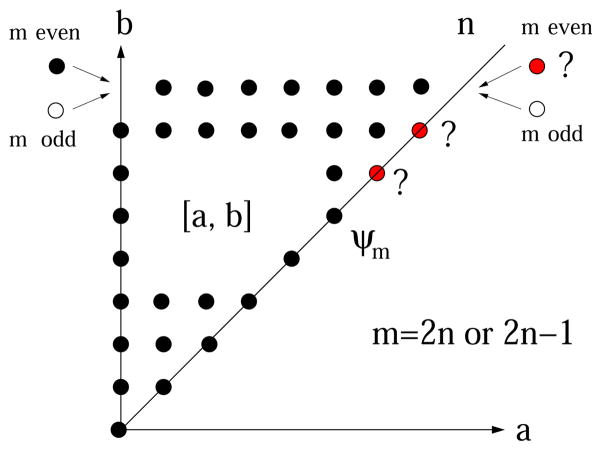
Conjecture 33

For any m ∈ ℕ, there is an integer Ψ_m ≥ ψ_m such that

$$\begin{array}{lll}\mathcal{G}{\mathcal{R}}_{2n}\hfill & =\hfill & \mathcal{C}\mathcal{P}(n)\backslash \{[h,h]\mid {\mathrm{\Psi }}_{2n}<h\le n\},\hfill \\ \mathcal{G}{\mathcal{R}}_{2n-1}\hfill & =\hfill & \mathcal{C}\mathcal{P}(n)\backslash \{[0,n],[h,h]\mid {\mathrm{\Psi }}_{2n-1}<h\le n\}.\hfill \end{array}$$

This means that there is no gap along the diagonal (see Figure 25). For small values of m ≤ 20, the conjecture holds with Ψ_m = ψ_m for m = 1, …, 7, 9, 13. At this time we are not able to determine if [5, 5] is in 𝒢ℛ_m for m = 10, 11, [6, 6] for m = 12, [7, 7] for m = 14, 15, [8, 8] for m = 16, 17, 18, and [9, 9] for m = 18, 19. The conjecture is true if there is only one unknown entry, and therefore, the conjecture holds for all m ≤ 20 except m = 18, and m = 18 is the smallest number for which we do not know if the conjecture holds. If one finds [8, 8] ∉ 𝒢ℛ₁₈ but [9, 9] ∈ 𝒢ℛ₁₈, then this will provide a counterexample. For n = 100, for example, we do not know if [h, h] ∈ 𝒢ℛ₁₀₀ for h = 43, …, 50. We know that [4, 4] is not in 𝒢ℛ₈ only by computer calculations in Table 1 searching through all graphs with 8 vertices.

Figure 25.

Diagram representing the conjecture

The situation for graphs with n vertices is depicted in Figure 25. Dots with the coordinates (a, b) represents the genus range [a, b]. The black dots represent that we have proved that there exists a graph with the corresponding genus range. Unmarked lattice points represent that there is no graph with the corresponding genus range due to the Euler characteristic formula. The white dots represent that we have proved, in this paper, that there are no graphs with such genus ranges. The red dots with question marks represent that these upper diagonal ranges remain unknown, beyond the number ψ_n we provided.

5 Concluding Remarks

For transversely connected 4-regular rigid vertex graphs, we considered the orientable genus range, that are genera of cellular embeddings. Some ranges are realized by using specific families of graphs, and others by some operations applied on graphs of smaller sizes. A few ranges are shown to be not realized as genus range. We identify particular intervals and singletons [h, h] that are unknown to be genus ranges. An interesting open question is whether these in fact can be realized.

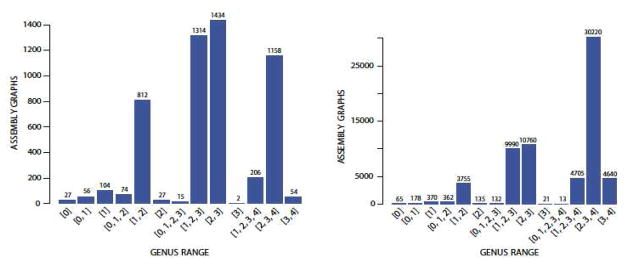
In Figure 26(right), we note that there are only 13 graphs among 65346 graphs of 8 vertices with genus range [0, 4]. In Proposition 23, we constructed graphs with 2n vertices with genus range [0, n], and these graphs seem to be very rare. Also we notice that among 7 vertex graphs, there are only 2 graphs with genus range [3, 3]. It is a curious fact that certain types of genus rages are very rare, and some are numerous. It may be of interest to determine the distributions of genus ranges.

Figure 26.

Histogram of genus range distributions for the number of graphs graphs with 7 and 8 vertices, with a given genus range

We conclude with comments on possible relations and applications to the studies on DNA assembly. A mathematical model using 4-regular rigid vertex graphs for DNA recombination processes was proposed and studied in [2, 3, 6]. The molecular structure in space at the exact moment of recombination is modeled by assembly graphs, and the assembled gene is modeled by Hamiltonian polygonal paths, paths that make “90° turn” at every rigid vertex, and visit every vertex exactly once. These polygonal paths have been also studied in graph theory as A-trails (for example, [1]). In [6], it was proved that the tangled cord, which achieves the maximal genus range for at least the graphs with odd number of vertices, has the largest number of Hamiltonian polygonal paths among all assembly graphs of the same number of vertices. If one follows a boundary curve of a ribbon graph at every vertex (see Figure 3), the consecutive edges traced by the boundary curve must be neighbors, so they form a polygonal path. Thus it is expected that smaller numbers of boundary components contribute to larger numbers of Hamiltonian polygonal paths. However, an explicit relationship between the genus range and the number of Hamiltonian polygonal paths is still unknown.

Figure 22.

Shading (Z)