Conspectus
The understanding of adsorption and reactions of (large) organic molecules at metal surfaces plays an increasingly important role in modern surface science and technology. Such hybrid inorganic/organic systems (HIOS) are relevant for many applications in catalysis, light-emitting diodes, single-molecule junctions, molecular sensors and switches, and photovoltaics. Obviously, the predictive modeling and understanding of the structure and stability of such hybrid systems is an essential prerequisite for tuning their electronic properties and functions. At present, density-functional theory (DFT) is the most promising approach to study the structure, stability, and electronic properties of complex systems, because it can be applied to both molecules and solids comprising thousands of atoms. However, state-of-the-art approximations to DFT do not provide a consistent and reliable description for HIOS, which is largely due to two issues: (i) the self-interaction of the electrons with themselves arising from the Hartree term of the total energy that is not fully compensated in approximate exchange-correlation functionals, and (ii) the lack of long-range part of the ubiquitous van der Waals (vdW) interactions. The self-interaction errors sometimes lead to incorrect description of charge transfer and electronic level alignment in HIOS, although for molecules adsorbed on metals these effects will often cancel out in total energy differences. Regarding vdW interactions, several promising vdW-inclusive DFT-based methods have been recently demonstrated to yield remarkable accuracy for intermolecular interactions in the gas phase. However, the majority of these approaches neglect the nonlocal collective electron response in the vdW energy tail, an effect that is particularly strong in condensed phases and at interfaces between different materials.
Here we show that the recently developed DFT+vdWsurf method that accurately accounts for the collective electronic response effects enables reliable modeling of structure and stability for a broad class of organic molecules adsorbed on metal surfaces. This method was demonstrated to achieve quantitative accuracy for aromatic hydrocarbons (benzene, naphthalene, anthracene, and diindenoperylene), C60, and sulfur/oxygen-containing molecules (thiophene, NTCDA, and PTCDA) on close-packed and stepped metal surfaces, leading to an overall accuracy of 0.1 Å in adsorption heights and 0.1 eV in binding energies with respect to state-of-the-art experiments. An unexpected finding is that vdW interactions contribute more to the binding of strongly bound molecules on transition-metal surfaces than for molecules physisorbed on coinage metals. The accurate inclusion of vdW interactions also significantly improves tilting angles and adsorption heights for all the studied molecules, and can qualitatively change the potential-energy surface for adsorbed molecules with flexible functional groups. Activation barriers for molecular switches and reaction precursors are modified as well.
Introduction
Adsorption of organic molecules at metal surfaces is attracting increasing research attention, owing to their potential importance in many applications, for instance, catalysis, molecular switches and sensors, photovoltaics, and energy materials.1−5 Such interfaces synergetically combine the best features of two distinct material classes, for example, the electrical conductivity of the metal and the highly tunable properties of organic molecules, resulting in new functionalities that are not possessed by either of the materials separately.6 The electronic, optical, and transport properties of such hybrid systems are very sensitive to the adsorbate structure and intermolecular interactions.7,8 Therefore, the accurate description of the bonding between adsorbates and substrates is key to understanding and controlling the functionality of such hybrid systems, and a prerequisite for designing novel nanodevices at the single-molecule level. This is a challenge for theory because the bonding in complex organic/metal systems arises from a delicate balance between covalent bonds, van der Waals (vdW) forces, hydrogen bonds, charge transfer, and Pauli repulsion.8 Indeed, until recent developments for efficiently incorporating the long-range vdW energy within state-of-the-art density-functional theory (DFT), it was not possible to determine the structure and stability for extended systems and adsorption processes.
Nowadays, a variety of electronic structure methods exist that in principle could be applied to inorganic/organic systems. It would be desirable to use quantum-chemical techniques, such as the full configuration interaction or coupled-cluster methods, which are potentially highly accurate.9,10 Unfortunately, these wave function-based calculations are computationally too expensive and presently not feasible for studying large systems. In the DFT framework, generalized gradient approximated (GGA) functionals can often properly treat Pauli repulsion, covalent, ionic, and strong hydrogen bonds.11 However, these widely used functionals fail to capture the long-range vdW interactions and suffer from severe self-interaction (SI) errors.12 Hybrid functionals, such as PBE0 and HSE, significantly reduce the SI error, but are still unable to properly account for vdW interactions.13 Because of this, the development of accurate and efficient vdW-inclusive DFT approaches has become an active field of research in the past decade. Examples of recently developed methods include DFT-D3,14 vdW-DF2,15 and vdW-DF-type functionals with modified exchange,16 BEEF-vdW functionals,17 the XDM method,18,19 and the DFT+vdW method.8,20 We refer the reader to refs (8 and 21−23) for recent reviews of these methods and their applications.
While the role of vdW interactions for the description of intermolecular and intramolecular bonding in the gas phase has been reasonably well understood, much less is known about vdW interactions in solids and adsorption. This stems from the fact that so far there is no established benchmark data set for molecular adsorption on solid surfaces, neither from high-level theoretical calculations nor from reliable measurements. Moreover, nonlocal collective electron response (or screening) effects, which are particularly important for extended systems, are not properly accounted for in most of widely used approaches. Recently, we developed a method, termed “DFT+vdWsurf”,24 to explicitly include these collective effects of an extended substrate. This method achieves quantitative results for 25 adsorption systems (from a set of 9 molecules on 8 metals), leading to an overall accuracy of 0.1 Å in adsorption heights and 0.1 eV in binding energies with respect to state-of-the-art experiments.25
In this Account, we address the state-of-the-art of modeling of organic molecules adsorbed at metal surfaces. For such systems, the SI errors of semilocal DFT functionals often cancel out when computing adsorption energies. Therefore, the SI errors, which are known to lead to spurious charge-transfer problems for ionic crystals and oxides, can be safely ignored throughout this work.26 We demonstrate that the correct inclusion of vdW interactions including collective substrate response in the DFT framework allows us to quantitatively predict adsorption geometries and energetics for certain systems. Moreover, vdW interactions can qualitatively affect adsorption processes in many applications, for example, change the potential-energy surfaces and reaction pathways of molecular switches and model catalysts. Despite the fact that successful prediction of structural and energetic properties of single molecules on metal surfaces now seems possible, many serious challenges remain in the study of complex organic/metal interfaces. We will summarize these challenges to motivate further developments toward reliable methods that can efficiently capture the full complexity of many-body exchange-correlation effects in HIOS.
Comparison between Theory and Experiment
Accurate experimental data are crucial as a benchmark for theoretical description of organic/metal systems. A number of experimental techniques provide reliable information concerning adsorption geometries and energetics for molecules at surfaces, ranging from normal incidence X-ray standing wave (NIXSW),1,27 low-energy electron diffraction (LEED), microcalorimetry measurements,28−31 and temperature-programmed desorption (TPD). Note that most of these methods probe the statistics of adsorbed molecular ensembles, which makes it sometimes difficult to directly compare with DFT calculations that are carried out for single adsorbed molecules or well-ordered monolayers. Thus, one should always ensure that the coverage and structure used in DFT calculations represents the experimental situation as closely as possible. Moreover, special attention must be paid in the interpretation of experimental adsorbate geometry, binding energy, and electronic properties. For example, adsorbed molecules, such as benzene, may decompose during heating in TPD measurements, in particular at low coverage.32 Adsorption of molecules on steps, kinks, and defects might also complicate the interpretation of experimental measurements. In addition, the recent thermodynamic analysis of Campbell and Sellers33 demonstrates that the pre-exponential factor used in the Redhead analysis of TPD experiments on organic molecules should be noticeably larger than the typically employed value of 1013 s–1.
Addressing the challenge of consistent comparison between experiment and theory, novel experimental approaches have been recently developed for direct identification of HIOS at single-molecule level. For example, by repeatedly detaching a molecule from a metal surface, Tautz’s group introduced a novel experimental method to extract the binding potential of large organic adsorbates on surfaces.34 Another promising example was reported by Schuler et al.,35 by analyzing frequency-shift curves from noncontact atomic force microscopy (NC-AFM), the adsorption height differences and tilts of the molecular plane can now be discriminated with a precision of 3 pm and 0.2°, respectively. These efforts facilitate the important reconciliation of experiments and theory at the single-molecule level.
van der Waals Interactions Inclusive DFT Methods
Many encouraging ideas and methods have been proposed in recent years for approximately including the missing long-range vdW interactions in DFT (see refs (8 and 21−23) and references therein). Loosely speaking, different available methods can be divided into two classes: (a) interatomic methods, where electronic interactions are coarse-grained into atomic fragments; and (b) nonlocal functionals that model vdW interactions as integrals over r and r′ with a given approximate interaction kernel K(r,r′). Despite significant progress in this field during the past decade, many questions still remain unanswered and further development is required before a truly universally applicable (accurate and efficient) method emerges. For example, interatomic vdW potentials are frequently employed for the modeling of molecules on surfaces,36−38 neglecting the relatively strong long-range Coulomb screening present within inorganic bulk materials. On the other hand, the popular nonlocal vdW-DF functionals15,39 use a homogeneous dielectric approximation for the polarizability, which is not expected to be accurate for inhomogeneous systems, such as molecules or surfaces. Nevertheless, the interaction energies between small organic molecules turn out to be reasonably accurate. Understanding the physical reasons of why these different approaches “work well” outside of their expected domain of applicability is important for developing more robust approximations.
The DFT+vdWsurf Method
It is obvious that accurate and efficient treatment of electronic exchange and correlation effects in HIOS demands effective and novel solutions. We recently developed the DFT+vdWsurf method,24 which extends pairwise vdW approaches to modeling of adsorbates on surfaces by a synergetic combination of the DFT+vdW method20 for intermolecular interactions with the Lifshitz–Zaremba–Kohn (LZK) theory.40,41 This method has been implemented in a variety of codes; in particular, all calculations reported here have been carried out using the all-electron atom-centered basis set code FHI-aims.42 Here we only highlight several salient features of our method, summarized in refs (24 and 43):
(1) The collective response (screening) by the substrate electrons is included in DFT+vdWsurf via the LZK theory, through the dependence of the vdW parameters on the dielectric function of the substrate. Typically, we use the experimental dielectric function.
(2) The spatial variations, or the “semi-local” interface polarization, and image-plane effects in the dielectric function close to the surface are approximately accounted for by the original DFT+vdW method, by its dependence on the self-consistent electron density of the interface.
(3) The DFT+vdWsurf method can be coupled to different DFT exchange-correlation functionals, including advanced schemes such as the range-separated hybrid functionals.44 This enables accurate description of both electronic properties and binding structures on equal footing. For the sake of consistency, here we couple the vdWsurf method to the PBE functional,45 which can be universally applied to both molecules and solids. In particular, the PBE functional is better suited for metals than hybrid functionals.
The inclusion of collective response effects in the vdWsurf method significantly changes the vdW C6 coefficients and vdW radii of transition metals in comparison to bare (unscreened) values used in many alternative interatomic vdW methods. As shown in Figure 1, the collective response is extremely sensitive to the dielectric properties of the metal substrate, reducing the C6 coefficients by merely 30% for Pd to 450% for Rh. The change in the C6 coefficients from their gas-phase values essentially reflects the effective number of delocalized electrons in different metals, since these electrons act to screen the vdW interaction. At the same time, vdW radii are also reduced for all metals. This leads to opposite effects in the vdW energy and results in a nontrivial behavior for different metals. As illustrated in our previous work,43 the combined effect of dielectric screening decreases the binding energies when benzene adsorbs on Cu(111), Ag(111), Au(111), and Rh(111) surfaces, whereas an increase in the adsorption energies is observed for benzene on Pd(111), Pt(111), and Ir(111) surfaces. In addition, the collective response effects shorten the adsorption height by 0.2 Å for benzene on coinage metal surfaces, but do not change adsorption geometries for benzene chemisorbed on the Pd(111), Pt(111), Rh(111), and Ir(111) surfaces. This is rationalized by the fact that covalent bonds largely determine the local coordination for benzene at these substrates.
Figure 1.
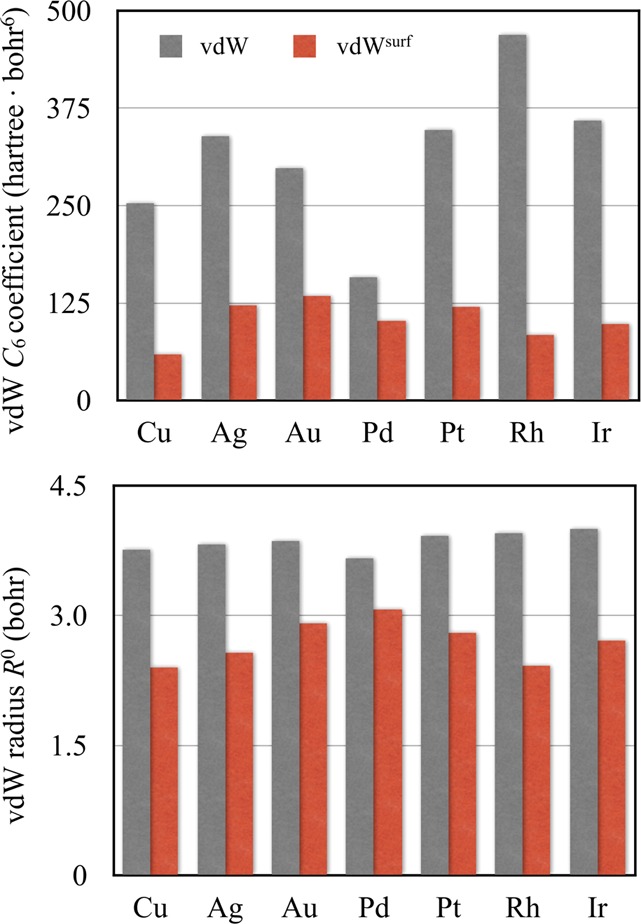
Screened van der Waals parameters as used in the PBE+vdWsurf method. For comparison, the corresponding bare (unscreened) parameters as used in the PBE+vdW method are also shown.
Vertical Adsorption Distances and Stability of Organic Molecules on Metal Surfaces
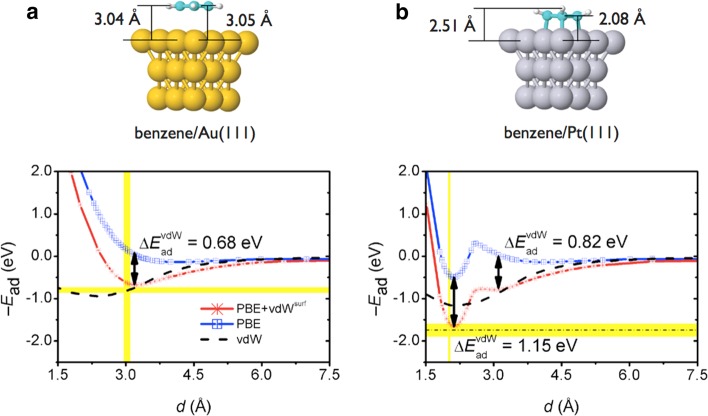
Let us start with the conceptually most simple physisorbed systems, exhibiting only weak overlap of electron orbitals between the adsorbate and the substrate surface. Prototypical examples of physisorption include noble gases adsorbed on metal surfaces,49 benzene on coinage metal surfaces,43 and graphene on the (111) surfaces of Al, Ag, Cu, Au, and Pt.50 Physisorbed systems are typically characterized by relatively weak binding energy, relatively large adsorption height, almost zero molecular distortion, and flat potential-energy surface (PES) for sliding of the adsorbed species parallel to the surface. In these cases, the vdW interactions are frequently the only force that binds the molecule to the surface. As shown in Figure 2a, the inclusion of vdW forces by the vdWsurf method on top of the PBE functional brings the benzene molecule closer to the Au(111) surface by 0.6 Å, and leads to an excellent agreement with the measured vertical position (2.95–3.10 Å), obtained from the experimental work function of benzene/Au(111), and the adsorption height of pentacene/Au(111).51−53 In contrast, the adsorption height from the standard PBE functional (3.62 Å) is considerably larger than that obtained by NIXSW.54 Figure 2a also shows the binding energy as a function of adsorption height d, from which one can observe that the PBE+vdWsurf binding energy is on top of the experimental values at 0.1 ML, determined by the most recent and thorough interpretation of TPD data by Campbell’s group (0.74 vs 0.76 eV).43
Figure 2.
Top: Adsorption structures of the benzene/Au(111) and benzene/Pt(111) systems, both at the so-called bri30° adsorption site, where 30° refers to the angle of the C–C bond relative to the close-packed metal rows. The indicated distances are obtained based on the PBE+vdWsurf optimized structures. Gray, yellow, cyan, and white spheres represent Pt, Au, C, and H atoms, respectively. Bottom: Adsorption energy −Ead as a function of the adsorption height d for benzene on the Au(111) and Pt(111) surfaces from the PBE and PBE+vdWsurf methods (all carbon atoms are located at a distance d from the top metal layer). The experimentally derived binding distances and adsorption energies are indicated by yellow intervals (from refs (28, 43, 46, and 47)). Reproduced with permission from ref (48). Copyright 2012 American Physical Society.
When comparing the relative vertical positions for benzene adsorbed on Cu, Ag, and Au in Figure 3, only the accurate inclusion of vdW interactions reproduces the experimental trend, known from NIXSW measurements, dCM(Cu) < dCM(Ag) < dCM(Au).54 This hierarchy stems from a combined effect of screened C6 coefficients and vdW radii in the vdW energy, both of which increase from Cu to Ag to Au (see Figure 1). In contrast, the bare (unscreened) values of vdW parameters do not follow this trend.
Figure 3.
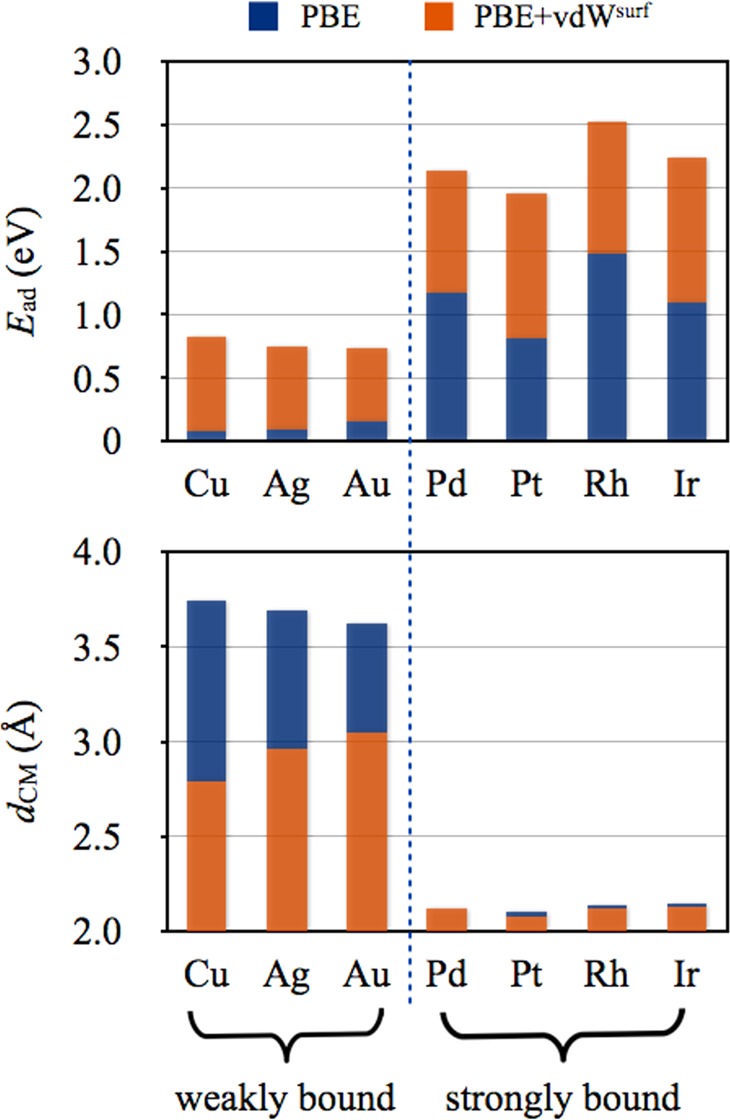
Adsorption energies Ead (in eV) and the average distance between carbon and the first metal layer dCM (in Å) for benzene on the (111) surfaces of Cu, Ag, Au, Pd, Pt, Rh, and Ir from PBE and PBE+vdWsurf methods.
Besides the PBE+vdWsurf method, a number of recently developed vdW-inclusive methods, such as the DFT-D,55 vdW-DF,39 and M06-L,56 also give results in reasonable agreement with experiments for these weakly bound systems. The general consensus between all these approaches is that the inclusion of the vdW energy significantly reduces the adsorption height and increases the binding energy.
Strongly Bound Organic/Metal Systems
By now, it is well established that vdW interactions contribute significantly to the binding in physisorbed systems. However, what is the role of vdW interactions for covalently bound molecules on metal surfaces? When molecular wave functions strongly overlap with substrate electronic bands, vdW forces are deemed to play a minor role. Because of this, standard GGA functionals are often considered to yield reasonable results for chemisorption. Nevertheless, as shown by Campbell’s group,28,30 the GGA-PW91 binding energy only accounts for half of the heat of adsorption directly measured in microcalorimetry experiments. Moreover, the binding energy difference between experiments and GGA calculations increased with molecular size (e.g., from benzene to naphthalene).30 We rationalized this disagreement between theory and experiment by adding and analyzing the role of vdW interactions.48 Other studies also clearly identified that the inclusion of vdW interactions is crucial for the correct description of covalently bound molecules on metal surfaces.57−59 Taking the benzene/Pt(111) system as an example (see Figure 2b), the relatively short adsorption height (2.08 Å), the bending of the molecule, the elongation of the C–C bonds, and the tilting of the H atoms all unambiguously suggest that the nature of bonding is strong chemisorption. However, also in this case, the PBE+vdWsurf method significantly increases the binding energy by 1.15 eV compared to standard PBE functional, and leads to agreement with the measured microcalorimetry values at 0.7 ML (1.96 vs 1.57–1.91 eV, the same coverage used in the DFT calculations). Almost the same adsorption height is found by PBE (2.10 Å) and PBE+vdWsurf (2.08 Å) methods, in agreement with LEED experiments (2.02 ± 0.02 Å).47 This suggests that chemical bonds largely determine the adsorption height for strongly bound benzene. This can be understood by comparing the steepness of the repulsive wall in Figure 2 for benzene on Au and Pt. The Pauli repulsion is much stronger for the Pt substrate, and the attractive vdW interaction only reduces the adsorption height of benzene by 0.02 Å compared to the PBE functional.
Comparison of the binding-energy curves in Figure 2 shows that the vdW energy for benzene on Pt(111) is considerably larger than that for Au(111) at respective equilibrium distances (1.15 vs 0.68 eV). At first glance, this finding is unexpected, in particular when considering that the vdW C6 coefficients and vdW radii are almost identical for Pt and Au (see Figure 1). The explanation simply stems from the rather short adsorption height of the benzene molecule on the Pt(111) surface.43 The above conclusion, that is, the greater role of the vdW energy in strongly bound systems, holds in general for benzene on many transition-metal surfaces. As shown in Figure 3, according to the binding energy and adsorption height, the seven benzene adsorption systems can be classified as either weak adsorption, including benzene on Cu(111), Ag(111), and Au(111), or strong adsorption, including benzene on Pd(111), Pt(111), Rh(111), and Ir(111). In all cases, the vdW energies for the latter group (∼1 eV) are considerably larger than those for the former (∼0.6 eV). Similar conclusion also holds for water adsorption on metals. For example, by using the optB88-vdW functional,16 Carrasco et al.60 found that the vdW contribution for water/Pt(111) is larger than that for water/Au(111) [186 vs 158 meV/H2O], since the water molecule adsorbs closer to the Pt surface than to the Au surface. We thus conclude that the stability for benzene (and other molecules) on reactive transition metals results from a concerted effort of covalent bonding and vdW interactions.
Although many vdW-inclusive methods work well for physisorption, they fail or perform poorly when used to study strongly bound systems. For example, the computed binding energies for benzene/Pt(111) using the vdW-DF functional39 and its second (improved) version (0.77 and 0.34 eV, respectively)15 are much smaller than the experimental values (1.57–1.91 eV), and even smaller than those calculated with the PBE functional (0.81 eV). We also note that the results are extremely sensitive to the choice of the exchange part in the vdW-DF-type functionals, yielding a wide range of binding energies for benzene/Pt(111) at the same coverage (0.6–2.4 eV).59 Thus, achieving the right balance between exchange and correlation is not a trivial task. Furthermore, most of the mentioned methods do not correctly account for the strong screening by the extended substrate, making their transferability questionable.
Molecular Tilting Angles and Potential-Energy Surfaces
Most organic/metal systems of importance in realistic applications exhibit nontrivial interplay of weak and strong bonding scenarios. Some representative examples include pyridine, pyrazine, thiophene, and phenol molecules adsorbed on metal surfaces.36 In these cases, covalent bonds are formed between oxygen, sulfur, or nitrogen of the molecule and metal atoms of the substrate, while vdW forces dominate the interactions of the remaining “parts” of the molecule (such as the π-conjugated carbon rings and methyl groups). Obviously, when adsorbate geometries are not parallel the surface, computational methods that can simultaneously treat covalent bonding and vdW interactions are required.
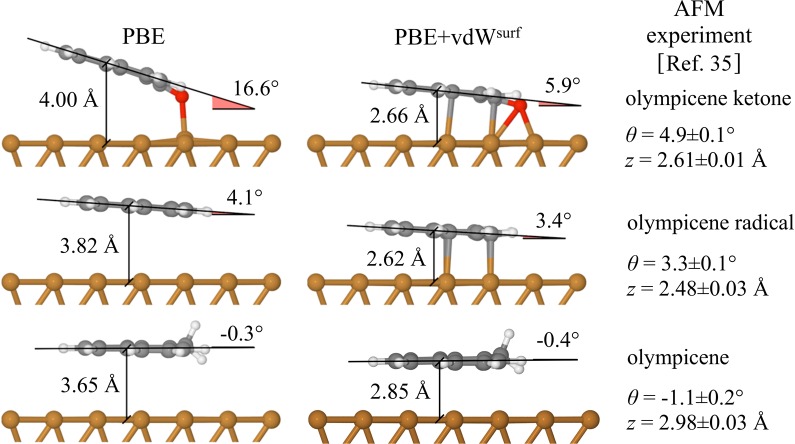
The recently synthesized olympicene-derived ketone (C19H10O) adsorbed on the Cu(111) surface is a good model for complex organic/metal systems (Figure 4; top). This molecule contains five carbon rings and a carbonyl group with a sp2-hybridized central carbon, allowing us to study the interplay of covalent bonds and vdW interactions in a single adsorption system. In experiments, the tilt of the ketone can be observed by the AFM image contrast: The darker (lighter) areas suggest stronger (weaker) contact with the substrate.35 Both the PBE and PBE+vdWsurf calculations show that the ketone is in an intermediate regime between physisorption and chemisorption: The end group of the molecule (C–O) anchors to the Cu(111) surface, forming a covalent bond between O and Cu, while the distances between carbon rings and the metal substrate are much larger. However, the tilting angle of the PBE-relaxed structure (16.6°) is significantly larger than that obtained from AFM experiments. The latter was quantitatively determined by a least-squares fitting to the spectra of three-dimensional force maps and gives 5.4° for a CO-terminated tip and 4.9 ± 0.1° for a Xe-terminated tip.35 Correspondingly, PBE dramatically overestimates the distance between the central carbon atom and the first metal layer by 1.4 Å. The vdW interactions bring the carbon rings closer to the Cu(111) surface compared to PBE, noticeably reducing the adsorption height to 2.66 Å. The calculated tilt angle of 5.9° is in excellent agreement with the AFM derived result.35
Figure 4.
Least mean square fit plane to the carbon atoms in the PBE and PBE+vdWsurf optimized adsorption structures for the olympicene ketone (top), olympicene radical (middle), and olympicene molecule (bottom) on the Cu(111) surface. Note that the effective adsorption height z* measured by AFM is translated into the absolute adsorption height z by adding a tip and bias dependent offset, which is 0.4 ± 0.05 Å for Xe-terminated tip.35
The good agreement between PBE+vdWsurf and experiments for tilting angles and adsorption heights is also found for the olympicene radical (Figure 4; middle) and the olympicene molecule (Figure 4; bottom) on Cu(111). Different from the olympicene ketone, the computed tilting angles for the olympicene and its radical are almost the same no matter whether the PBE or PBE+vdWsurf is used. Nevertheless, the radical and the olympicene are 0.8 and 1.2 Å closer to the substrate surface upon inclusion of vdW interactions in the calculations.
Role of vdW Interactions in the Adsorption of Molecules with Flexible Functional Groups
In many catalytic applications, as well as in molecular switches and molecular sensors, rather flexible molecules are employed as adsorbates. However, as shown by Nørskov and Bligaard,61 the standard electronic structure methods are frequently not sufficiently accurate with their structure prediction, thus hindering a reliable description of catalytic mechanisms. During the last decades, DFT has been extensively applied to study molecular reactions on surfaces (see refs (62−64) for detailed reviews). In these earlier studies, DFT has been extensively used to understand the adsorption of small molecules, such as CO, NO, and N2, and their reactions over various catalysts. Semilocal DFT functionals frequently yield good agreement with experimental findings, but this is not always the case (as exemplified in the famous “CO adsorption puzzle”65), which stems from severe SI errors in semilocal DFT functionals.
In the case of larger molecules adsorbed on surfaces, SI errors are typically less of an issue in relative terms, and the lack of vdW interactions is the main source of error when semilocal DFT functionals are employed. A prototypical example is the adsorption of ethanol (C2H5OH) at the Pt(111), an essential process in the steam reforming reaction to convert ethanol into H2. The standard PBE functional yields the same stability for the two structures shown in Figure 5a (0.28 eV). The vdW interactions profoundly influence the PES, contributing differently to the binding energy for the two configurations (0.45 eV for the parallel, and 0.38 eV for the perpendicular one). Therefore, the PBE+vdWsurf method predicts that the parallel orientation of the C–C bond is 70 meV more stable than the perpendicular one (0.73 vs 0.66 eV). Upon inclusion of vdW forces, the carbon atoms are found closer to the substrate, facilitating the breakage of the C–C bond in ethanol.66
Figure 5.
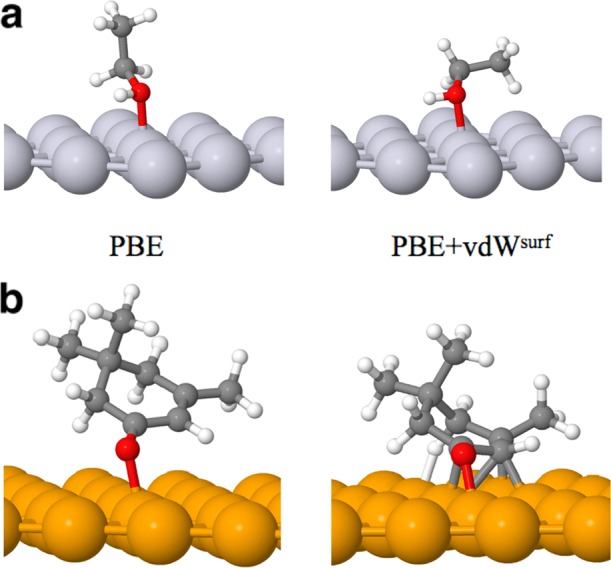
Two most stable structures of ethanol (C2H5OH) at Pt(111) (a) and of isophorone at the Pd(111) (b) relaxed by the PBE and PBE+vdWsurf methods. Gray, white, red, light gray, and yellow represent C, H, O, Pt, and Pd atoms, respectively. Reproduced with permission from ref (67). Copyright 2012 American Chemical Society.
A similar example has been reported by some of us on the low-temperature dehydrogenation of the isophorone molecule at the Pd(111) surface.67 Isophorone is an important proxy for catalysis because it contains conjugated C=C and C=O bonds that can be selectively hydrogenated. Isophorone is also a prochiral molecule that can be transformed to two enantiomers after selective hydrogenation of the olefinic double bond. For the isophorone/Pd(111) system, the experiments show that the C=C and C=O vibrational intensities do not appear in the IR spectra. This suggests parallel orientation of the two bonds relative to the metal surface due to the metal selection rule. However, without the inclusion of vdW forces one cannot easily identify the adsorption geometries consistent with experimental observations: the structure relaxed using the standard PBE functional shows that the C=O and C=C bonds are tilted (see Figure 5b). Only after correctly accounting for vdW interactions, the C=C and C=O bonds become parallel to the substrate, in agreement with the experimental IR spectra. Furthermore, the proximity of the hydrogen atoms to the metal reduces the dehydrogenation barriers for this system, a process that is also observed in TPD experiments.67
In summary, the above two examples show that, for larger molecules on metal surfaces, the vdW forces can significantly affect the orientation of functional groups and the energy hierarchy of adsorbed molecules. Thus, we expect noticeably different activation barriers and reaction pathways in catalytic applications.
Potential-Energy Surfaces of Molecular Switches
Another example of a qualitative change in the PES of molecules adsorbed on surfaces is found for molecular switches based on benzene derivatives. As shown in Figure 2b, an energy barrier exists at 2.6 Å in the PBE adsorption curve for benzene/Pt(111), corresponding to a sudden change in the occupation of frontier molecular orbitals.48 Upon inclusion of vdW interactions, the barrier to adsorption almost vanishes, and a metastable precursor state emerges just above 3 Å, a typical distance for physisorption. This physisorbed precursor state has also been observed by Ihm et al.28 in their sticking-coefficient measurements for benzene on Pt(111). Aiming at controlling the interplay between physisorption and chemisorption minima, we also studied the adsorption of benzene derivatives on metals. In the case of halogenated benzene derivatives, we demonstrated that the physisorbed state can have essentially equal stability as the chemisorbed state, with a moderate switching barrier between them.68 In contrast, without vdW interactions, the physisorbed state is completely absent in the binding curve.
Challenges and Outlook for the Accurate Description of Inorganic/Organic Systems
While this paper discussed the modeling of organic molecules adsorbed at metal surfaces, our conclusions apply to a much broader class of systems. For example, the accurate treatment of collective response by the substrate electrons is crucial for any polarizable solid, including semiconductors, ionic solids, oxides, and molecular materials. The DFT+vdWsurf method is in principle equally applicable to all these classes of materials. However, several challenges remain to be addressed for a seamless treatment of monolayer/multilayer formation on solids. First and foremost, the full treatment of collective response in the combined adsorbate/substrate system needs to be accounted for, including the screening of intermolecular interactions within the adsorbed layers. This can be achieved by seamless many-body methods, such as the random-phase approximation (RPA)69 to the correlation energy or the recently developed efficient dipole approximation to the RPA, termed DFT+MBD.70,71 While RPA can be used to study all classes of materials, the MBD method currently can only be applied to nonmetallic systems. Second, the SI error in the underlying semilocal DFT functional can affect charge transfer and electronic level alignment between the adsorbate and the substrate. This issue has not been fully solved yet, since the reduction of SI error requires the addition of a fraction of exact exchange which needs to be screened in inhomogeneous systems. The screening properties of molecules and solids are rather different, leading to distinct parameter ranges that need to be seamlessly coupled.
In summary, we have demonstrated that the inclusion of screened vdW interactions in DFT calculations leads to significant improvement in vertical adsorption heights, tilting angles, stabilities, and potential-energy surfaces of both weakly and strongly adsorbed molecules on metal surfaces. However, we stress that our understanding of the structure, stability, and electronic properties of complex adsorption systems is still in early stages of development and further major breakthroughs can be anticipated in the near future.
Acknowledgments
A.T. and W.L. acknowledge support from the European Research Council (ERC Starting Grant VDW-CMAT).
Biographies
Wei Liu obtained his Ph.D. in materials science in 2009 at the Jilin University, China. During 2011–2013, he was an Alexander von Humboldt Fellow in the Theory Department of the Fritz Haber Institute (FHI) in Berlin. He is currently a research scientist at FHI.
Alexandre Tkatchenko obtained his Ph.D. in physical chemistry in 2007 at the Universidad Autonoma Metropolitana, Mexico. During 2008–2010, he was an Alexander von Humboldt Fellow in the Theory Department at FHI, Berlin. Currently, he leads a group on Functional Materials and Intermolecular Interactions at FHI.
Matthias Scheffler obtained his Ph.D. in physics in 1978 at the Technical University of Berlin, Germany. Since 1988, he is director of the Theory Department of the FHI, Berlin.
The authors declare no competing financial interest.
References
- Tautz F. S. Structure and bonding of large aromatic molecules on noble metal surfaces: The example of PTCDA. Prog. Surf. Sci. 2007, 82, 479–520. [Google Scholar]
- Lu W.; Lieber C. M. Nanoelectronics from the bottom up. Nat. Mater. 2007, 6, 841–850. [DOI] [PubMed] [Google Scholar]
- Waser R.; Aono M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833–840. [DOI] [PubMed] [Google Scholar]
- Koch N.; Gerlach A.; Duhm S.; Glowatzki H.; Heimel G.; Vollmer A.; Sakamoto Y.; Suzuki T.; Zegenhagen J.; Rabe J. P.; Schreiber F. Adsorption-induced intramolecular dipole: Correlating molecular conformation and interface electronic structure. J. Am. Chem. Soc. 2008, 130, 7300–7304. [DOI] [PubMed] [Google Scholar]
- Morgenstern K. Switching individual molecules by light and electrons: From isomerisation to chirality flip. Prog. Surf. Sci. 2011, 86, 115–161. [Google Scholar]
- Xu Y.; Hofmann O. T.; Schlesinger R.; Winkler S.; Frisch J.; Niederhausen J.; Vollmer A.; Blumstengel S.; Henneberger F.; Koch N.; Rinke P.; Scheffler M. Space-charge transfer in hybrid inorganic/organic systems. Phys. Rev. Lett. 2013, 111, 226802. [DOI] [PubMed] [Google Scholar]
- Kronik L.; Koch N. Electronic properties of organic-based interfaces. MRS Bull. 2010, 35, 417–421. [Google Scholar]
- Tkatchenko A.; Romaner L.; Hofmann O. T.; Zojer E.; Ambrosch-Draxl C.; Scheffler M. Van der Waals interactions between organic adsorbates and at organic/inorganic interfaces. MRS Bull. 2010, 35, 435–442. [Google Scholar]
- Crawford T. D.; Schaefer H. An introduction to coupled cluster theory for computational chemists. Rev. Comput. Chem. 2000, 14, 33–136. [Google Scholar]
- Szabo A.; Ostlund N. S.. Modern quantum chemistry: Introduction to advanced electronic structure theory; Dover Publications: New York, 1996. [Google Scholar]
- Burke K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [DOI] [PubMed] [Google Scholar]
- Gross A.Theoretical surface science: A microscopic perspective, 2nd ed.; Springer-Verlag: Berlin, Heidelberg, 2009. [Google Scholar]
- Marom N.; Tkatchenko A.; Rossi M.; Gobre V. V.; Hod O.; Scheffler M.; Kronik L. Dispersion interactions with density-functional theory: Benchmarking semiempirical and interatomic pairwise corrected density functionals. J. Chem. Theory Comput. 2011, 7, 3944–3951. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [DOI] [PubMed] [Google Scholar]
- Lee K.; Murray E. D.; Kong L.; Lundqvist B. I.; Langreth D. C. Higher-accuracy van der Waals density functional. Phys. Rev. B 2010, 82, 081101. [Google Scholar]
- Klimeš J.; Bowler D. R.; Michaelides A. Chemical accuracy for the van der Waals density functional. J. Phys.: Condens. Matter 2010, 22, 022201. [DOI] [PubMed] [Google Scholar]
- Wellendorff J.; Lundgaard K. T.; Møgelhøj A.; Petzold V.; Landis D. D.; Nørskov J. K.; Bligaard T.; Jacobsen K. W. Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation. Phys. Rev. B 2012, 85, 235149. [Google Scholar]
- Kannemann F. O.; Becke A. D. van der Waals interactions in density-functional theory: Intermolecular complexes. J. Chem. Theory Comput. 2010, 6, 1081–1088. [DOI] [PubMed] [Google Scholar]
- Steinmann S. N.; Corminboeuf C. Comprehensive benchmarking of a density-dependent dispersion correction. J. Chem. Theory Comput. 2011, 7, 3567–3577. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. [DOI] [PubMed] [Google Scholar]
- Ehrlich S.; Moellmann J.; Grimme S. Dispersion-corrected density functional theory for aromatic interactions in complex systems. Acc. Chem. Res. 2012, 46, 916–926. [DOI] [PubMed] [Google Scholar]
- Cohen A. J.; Mori-Sánchez P.; Yang W. Challenges for density functional theory. Chem. Rev. 2011, 112, 289–320. [DOI] [PubMed] [Google Scholar]
- Klimeš J.; Michaelides A. Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory. J. Chem. Phys. 2012, 137, 120901. [DOI] [PubMed] [Google Scholar]
- Ruiz V. G.; Liu W.; Zojer E.; Scheffler M.; Tkatchenko A. Density-functional theory with screened van der Waals interactions for the modeling of hybrid inorganic-organic systems. Phys. Rev. Lett. 2012, 108, 146103. [DOI] [PubMed] [Google Scholar]
- Camarillo-Cisneros J.; Liu W.; Ruiz V. G.; Ferri N.; Scheffler M.; Tkatchenko A.. Benchmark database of equilibrium geometries and adsorption energies of hybrid organic/metal systems. In preparation.
- Hofmann O. T.; Atalla V.; Moll N.; Rinke P.; Scheffler M. Interface dipoles of organic molecules on Ag(111) in hybrid density-functional theory. New J. Phys. 2013, 15, 123028. [Google Scholar]
- Henze S. K. M.; Bauer O.; Lee T.-L.; Sokolowski M.; Tautz F. S. Vertical bonding distances of PTCDA on Au(111) and Ag(111): Relation to the bonding type. Surf. Sci. 2007, 601, 1566–1573. [Google Scholar]
- Ihm H.; Ajo H. M.; Gottfried J. M.; Bera P.; Campbell C. T. Calorimetric measurement of the heat of adsorption of benzene on Pt(111). J. Phys. Chem. B 2004, 108, 14627–14633. [Google Scholar]
- Ajo H.; Ihm H.; Moilanen D.; Campbell C. Calorimeter for adsorption energies of larger molecules on single crystal surfaces. Rev. Sci. Instrum. 2004, 75, 4471–4480. [Google Scholar]
- Gottfried J. M.; Vestergaard E. K.; Bera P.; Campbell C. T. Heat of adsorption of naphthalene on Pt(111) measured by adsorption calorimetry. J. Phys. Chem. B 2006, 110, 17539–17545. [DOI] [PubMed] [Google Scholar]
- Crowe M. C.; Campbell C. T. Adsorption microcalorimetry: Recent advances in instrumentation and application. Annu. Rev. Anal. Chem. 2011, 4, 41–58. [DOI] [PubMed] [Google Scholar]
- Somorjai G. A.; Li Y.. Introduction to surface chemistry and catalysis, 2nd ed.; John Wiley & Sons: New York, 2010. [Google Scholar]
- Campbell C. T.; Sellers J. R. V. The entropies of adsorbed molecules. J. Am. Chem. Soc. 2012, 134, 18109–18115. [DOI] [PubMed] [Google Scholar]
- Wagner C.; Fournier N.; Tautz F. S.; Temirov R. Measurement of the binding energies of the organic-metal perylene-teracarboxylic-dianhydride/Au(111) bonds by molecular manipulation using an atomic force microscope. Phys. Rev. Lett. 2012, 109, 076102. [DOI] [PubMed] [Google Scholar]
- Schuler B.; Liu W.; Tkatchenko A.; Moll N.; Meyer G.; Mistry A.; Fox D.; Gross L. Adsorption geometry determination of single molecules by atomic force microscopy. Phys. Rev. Lett. 2013, 111, 106103. [DOI] [PubMed] [Google Scholar]
- Atodiresei N.; Caciuc V.; Lazić P.; Blügel S. Chemical versus van der Waals interaction: The role of the heteroatom in the flat absorption of aromatic molecules C6H6, C5NH5, and C4N2H4 on the Cu(110) Surface. Phys. Rev. Lett. 2009, 102, 136809. [DOI] [PubMed] [Google Scholar]
- Busse C.; Lazić P.; Djemour R.; Coraux J.; Gerber T.; Atodiresei N.; Caciuc V.; Brako R.; N’Diaye A. T.; Blügel S.; Zegenhagen J.; Michely T. Graphene on Ir(111): Physisorption with chemical modulation. Phys. Rev. Lett. 2011, 107, 036101. [DOI] [PubMed] [Google Scholar]
- Tonigold K.; Gross A. Adsorption of small aromatic molecules on the (111) surfaces of noble metals: A density functional theory study with semiempirical corrections for dispersion effects. J. Chem. Phys. 2010, 132, 224701. [DOI] [PubMed] [Google Scholar]
- Dion M.; Rydberg H.; Schröder E.; Langreth D. C.; Lundqvist B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. [DOI] [PubMed] [Google Scholar]
- Lifshitz E. M. The theory of molecular attractive forces between solids. Sov. Phys. – JETP 1956, 2, 73–83. [Google Scholar]
- Zaremba E.; Kohn W. Van der Waals interaction between an atom and a solid surface. Phys. Rev. B 1976, 13, 2270–2285. [Google Scholar]
- Blum V.; Gehrke R.; Hanke F.; Havu P.; Havu V.; Ren X.; Reuter K.; Scheffler M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar]
- Liu W.; Ruiz V. G.; Zhang G.-X.; Santra B.; Ren X.; Scheffler M.; Tkatchenko A. Structure and energetics of benzene adsorbed on transition-metal surfaces: Density-functional theory with van der Waals interactions including collective substrate response. New J. Phys. 2013, 15, 053046. [Google Scholar]
- Agrawal P.; Tkatchenko A.; Kronik L. Pair-wise and many-body dispersive interactions coupled to an optimally tuned range-separated hybrid functional. J. Chem. Theory Comput. 2013, 9, 3473–3478. [DOI] [PubMed] [Google Scholar]
- Perdew J.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [DOI] [PubMed] [Google Scholar]
- Syomin D.; Kim J.; Koel B. E.; Ellison G. B. Identification of adsorbed phenyl (C6H5) groups on metal surfaces: Electron-induced dissociation of benzene on Au(111). J. Phys. Chem. B 2001, 105, 8387–8394. [Google Scholar]
- Wander A.; Held G.; Hwang R. Q.; Blackman G. S.; Xu M. L.; de Andres P.; Van Hove M. A.; Somorjai G. A. A diffuse LEED study of the adsorption structure of disordered benzene on Pt(111). Surf. Sci. 1991, 249, 21–34. [Google Scholar]
- Liu W.; Carrasco J.; Santra B.; Michaelides A.; Scheffler M.; Tkatchenko A. Benzene adsorbed on metals: Concerted effect of covalency and van der Waals bonding. Phys. Rev. B 2012, 86, 245405. [Google Scholar]
- Zaremba E.; Kohn W. Theory of helium adsorption on simple and noble-metal surfaces. Phys. Rev. B 1977, 15, 1769. [Google Scholar]
- Khomyakov P. A.; Giovannetti G.; Rusu P. C.; Brocks G.; Van den Brink J.; Kelly P. J. First-principles study of the interaction and charge transfer between graphene and metals. Phys. Rev. B 2009, 79, 195425. [Google Scholar]
- Toyoda K.; Nakano Y.; Hamada I.; Lee K.; Yanagisawa S.; Morikawa Y. First-principles study of benzene on noble metal surfaces: Adsorption states and vacuum level shifts. Surf. Sci. 2009, 603, 2912–2922. [Google Scholar]
- Abad E.; Ortega J.; Dappe Y. J.; Flores F. Dipoles and band alignment for benzene/Au(111) and C60/Au(111) interfaces. Appl. Phys. A: Mater. Sci. Process. 2009, 95, 119–124. [Google Scholar]
- Abad E.; Dappe Y. J.; Martnez J. I.; Flores F.; Ortega J. C6H6/Au(111): Interface dipoles, band alignment, charging energy, and van der Waals interaction. J. Chem. Phys. 2011, 134, 044701. [DOI] [PubMed] [Google Scholar]
- Tautz S. Forschungszentrum Jülich, private communication.
- Grimme S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [DOI] [PubMed] [Google Scholar]
- Zhang R.; Hensley A. J.; McEwen J.-S.; Wickert S.; Darlatt E.; Fischer K.; Schöppke M.; Denecke R.; Streber R.; Lorenz M.; Papp C.; Hans-Peter S. Integrated X-ray photoelectron spectroscopy and DFT characterization of benzene adsorption on Pt(111), Pt(355) and Pt(322) surfaces. Phys. Chem. Chem. Phys. 2013, 15, 20662–20671. [DOI] [PubMed] [Google Scholar]
- Yildirim H.; Kara A. Effect of van der Waals interactions on the adsorption of olympicene radical on Cu(111): Characteristics of weak physisorption versus strong chemisorption. J. Phys. Chem. C 2013, 117, 2893–2902. [Google Scholar]
- Yildirim H.; Greber T.; Kara A. Trends in adsorption characteristics of benzene on transition metal surfaces: Role of surface chemistry and van der Waals interactions. J. Phys. Chem. C 2013, 117, 20572–20583. [Google Scholar]
- Carrasco J.; Klimeš J.; Michaelides A. The role of van der Waals forces in water adsorption on metals. J. Chem. Phys. 2013, 138, 024708. [DOI] [PubMed] [Google Scholar]
- Nørskov J. K.; Bligaard T. The catalyst genome. Angew. Chem., Int. Ed. 2013, 52, 776–777. [DOI] [PubMed] [Google Scholar]
- Nørskov J. K.; Bligaard T.; Rossmeisl J.; Christensen C. H. Towards the computational design of solid catalysts. Nat. Chem. 2009, 1, 37–46. [DOI] [PubMed] [Google Scholar]
- Yu W.; Porosoff M. D.; Chen J. G. Review of Pt-based bimetallic catalysis: From model surfaces to supported catalysts. Chem. Rev. 2012, 112, 5780–5817. [DOI] [PubMed] [Google Scholar]
- Nørskov J. K.; Abild-Pedersen F.; Studt F.; Bligaard T. Density functional theory in surface chemistry and catalysis. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 937–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feibelman P. J.; Hammer B.; Nørskov J. K.; Wagner F.; Scheffler M.; Stumpf R.; Watwe R.; Dumesic J. The CO/Pt(111) puzzle. J. Phys. Chem. B 2001, 105, 4018–4025. [Google Scholar]
- Tereshchuk P.; Da Silva J. L. Density functional investigation of the adsorption of ethanol-water mixture on the Pt(111) surface. J. Phys. Chem. C 2013, 117, 16942–16952. [Google Scholar]
- Liu W.; Savara A.; Ren X.; Ludwig W.; Dostert K.-H.; Schauermann S.; Tkatchenko A.; Freund H.-J.; Scheffler M. Towards low-temperature dehydrogenation catalysis: Isophorone on Pd(111). J. Phys. Chem. Lett. 2012, 3, 582–586. [DOI] [PubMed] [Google Scholar]
- Liu W.; Filimonov S. N.; Carrasco J.; Tkatchenko A. Molecular switches from benzene derivatives adsorbed on metal surfaces. Nat. Commun. 2013, 4, 2569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren X.; Rinke P.; Joas C.; Scheffler M. Random-phase approximation and its applications in computational chemistry and materials science. J. Mater. Sci. 2012, 47, 7447–7471. [Google Scholar]
- Tkatchenko A.; DiStasio R. A. Jr.; Car R.; Scheffler M. Accurate and efficient method for many-body van der Waals interactions. Phys. Rev. Lett. 2012, 108, 236402. [DOI] [PubMed] [Google Scholar]
- Ambrosetti A.; Reilly A. M.; DiStasio R. A. Jr.; Tkatchenko A. Long-range correlation energy calculated from coupled atomic response functions. J. Chem. Phys. 2014, 140, 18A508. [DOI] [PubMed] [Google Scholar]