Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Nov 1.
Published in final edited form as: Neuropsychology. 2016 Jul 21;30(8):915–919. doi: 10.1037/neu0000301

Amnesic patients show superior generalization in category learning

Garret O’Connell 1,*, Catherine E Myers 2, Ramona O Hopkins 3,4, R P McLaren 5, Mark A Gluck 6, Andy J Wills 1
PMCID: PMC5088063  NIHMSID: NIHMS797619  PMID: 27442451

Abstract

OBJECTIVE

Generalization is the application of existing knowledge to novel situations. Questions remain about the precise role of the hippocampus in this facet of learning, but a connectionist model by Gluck and Myers (1993) predicts that generalization should be enhanced following hippocampal damage.

METHOD

In a two-category learning task, a group of amnesic patients (n=9) learned the training items to a similar level of accuracy as matched controls (n=9). Both groups then classified new items at various levels of distortion.

RESULTS

The amnesic group showed significantly more accurate generalization to high-distortion novel items, a difference also present when compared to a larger group of unmatched controls (n=33).

CONCLUSIONS

The model prediction of a broadening of generalization gradients in amnesia, at least for items near category boundaries, was supported by the results. Our study shows for the first time that amnesia can sometimes improve generalization.

Keywords: categorical learning, stimulus generalization, gradient, hippocampus, lesion

INTRODUCTION

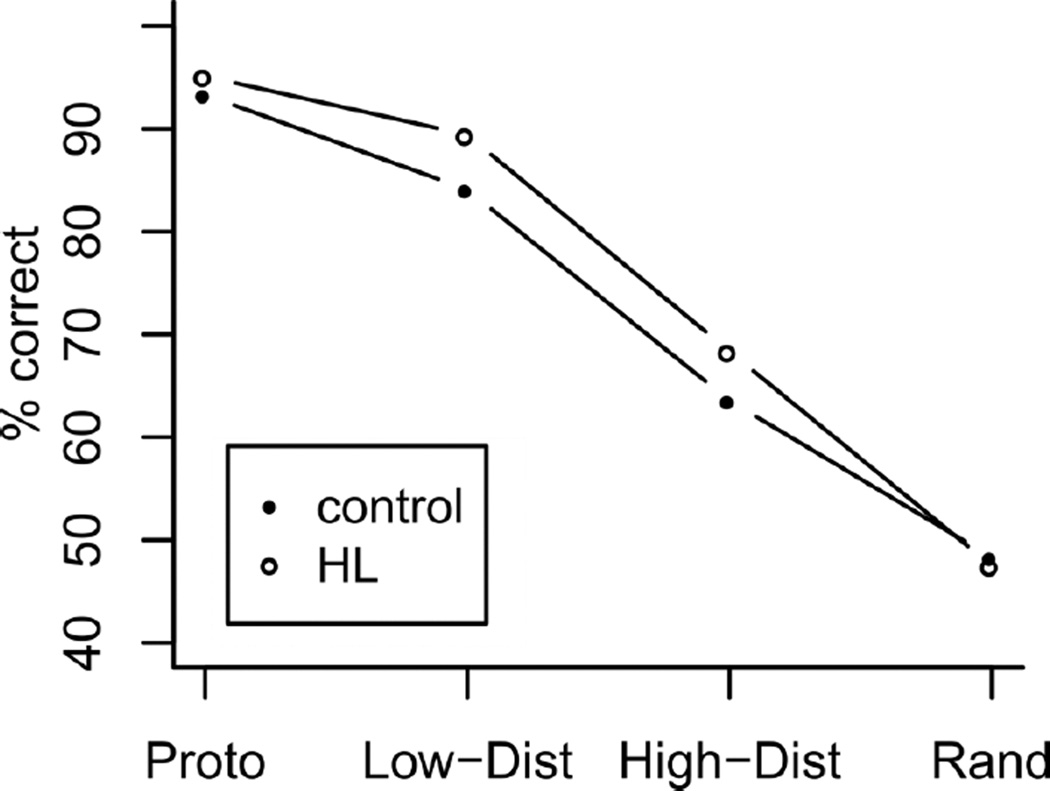
Generalization is central to the application of knowledge, because most situations we encounter are in some way novel. For example, you might identify an object as a “cup”, even if you have not seen that specific object before. The degree to which novel and less typical stimuli are perceived as belonging to a common category can be measured in terms of generalization gradients (Buss, 1950; Grice & Saltz, 1950; Wills & McLaren, 1997), such as those shown in Figure 1. A generalization gradient plots some performance measure, in this case classification accuracy, across a range of test stimuli, from stimuli similar to previously encountered examples, to quite dissimilar items.

Figure 1.

Figure 1

Open in a new tab

Predictions of the cortico-hippocampal model (Gluck & Myers, 1993). Control: Intact model. HL: model with hippocampal-region lesion. Proto: prototype, Low-Dist: low distortion, High-Dist: high distortion, Rand: random (50% accuracy expected).

Gluck and Myers (1993) predicted that a hippocampal-region lesion prior to learning would lead to broader generalization to novel items, relative to controls. Figure 1 illustrates this prediction in the context of a two-category learning task. As the average of the training items, the prototype items are maximally similar to them. Low-distortion and high-distortion items are more and less similar to the training items respectively, but both have a correct answer, as they are more similar to one of the trained categories than the other. Finally, random items are unclassifiable, being equally similar to each of the two trained categories. The striking prediction for a two-category task is that hippocampal lesions lead to superior (more accurate) generalization, relative to controls (as illustrated in Figure 1).

Gluck and Myers's prediction emerges a priori from their connectionist model of cortico-hippocampal interaction (Gluck & Myers, 1993). In fact, Figure 1 is the output of simulating a hippocampal-region lesion in their model in the context of the specific experiment reported below. Full details of the simulation, including source code, are available at [maskedlink]. In informal terms, the Gluck-Myers model makes this prediction because of two assumed functions of the hippocampal region. The first, redundancy compression, acts to increase the perceived similarity of stimuli that belong to the same category. The second, predictive differentiation, acts to decrease the perceived similarity of stimuli that belong to different categories. Both processes are considered to have a number of adaptive advantages (see Gluck & Myers, 1993, for a discussion). However, in the current case, they cause generalization to drop off more rapidly, leading to inferior performance on high-distortion test items. Hippocampal-region lesions eliminate these redundancy compression and predictive differentiation processes, leading to broader generalization gradients that, in the context of the current experiment, lead to a prediction of more accurate/superior generalization performance in amnesics, relative to controls.

Some other accounts of the effects of hippocampal damage on category learning are compatible with this prediction of the Gluck-Myers model. For example, Nosofsky and Zaki (1998) characterized the effects of amnesia on category learning through the assumption that all stimuli appear more similar to each other for amnesics than controls (instantiated in their formal model as a reduction in the sensitivity parameter for amnesics). In cases where amnesics show similar performance to controls on the training items, such an account predicts superior performance on high-distortion test items for amnesics, because these items appear more similar to the training items than is the case for controls. Of course, the high-distortion items become more similar to both the correct and the incorrect category under this account, but non-linearities in the way their model calculates similarity (an exponential decay function) means that an overall effect of improved generalization can be accommodated by the Nosofsky-Zaki account.

There is no existing data set that is well-suited to examine this prediction of the Gluck-Myers model. The majority of studies of category learning in amnesia (Kitchener & Squire, 2000; Knowlton & Squire, 1993; Reed et al, 1999; Squire & Knowlton, 1995) train only one category. It is not possible to test the prediction of superior generalization performance under amnesia in a one-category task because, in a one-category task, there are no correct or incorrect answers to novel items. Participants are exposed to a number of stimuli, all of which belong to the same category. They are then shown some novel items, which vary in similarity to the trained items. In the absence of a second contrast category any novel item, however dissimilar, could reasonably be classified as belonging to the trained category. This is not a criticism of the above studies, as they were not designed to test the Gluck-Myers prediction, but it does mean their data are not ideal to examine whether this prediction is correct. However, we note in passing there are some other problems in interpreting the results of one-category tasks (“learning-at-test” effect; Palmeri & Flanery, 1999) which are resolved through the introduction of a second contrast category (Homa et al., 2011).

Turning to experiments with more than one trained category, Kolodny (1994) compared amnesic and control performance in three-category tasks. However, no generalization gradient was reported. Zaki et al. (2003) used a two-category task, and reported a generalization gradient. However, in their study, amnesics perform substantially less well on the training items than did controls. Under such circumstances, the Gluck-Myers model does not predict superior generalization in the amnesic group. In summary, no existing data set speaks to the Gluck-Myers prediction of superior amnesic generalization in a two-category task.

In the current study, we employed the two-category task developed by Wills and associates (Wills & McLaren, 1997). This task is well-suited to examining the Gluck-Myers prediction, for two reasons. First, we know that normal adults acquire the training categories quickly and to a high level of accuracy in this task (e.g. Jones et al., 1998, Experiment 2). On this basis, we predicted that, with sufficient training, both amnesics and controls would show high and comparable accuracy on the training items. Second, the task produces orderly generalization gradients under a range of conditions (Jones, Wills & McLaren, 1998; Wills, 2002; Wills & McLaren, 1997; Wills et al., 2000) – an essential property for testing the Gluck-Myers prediction. Note that based on previous data using these task materials (Wills & McLaren, 1997), categorization accuracy of low-distortion items is expected to be close to ceiling. Group differences in generalization accuracy therefore should be more pronounced for less easy high-distortion items.

METHODS

Participants

We tested 9 patients with bilateral hippocampal damage due to hypoxic brain injury (age range = 27–57, female = 2). Structural MRI (n=7) confirmed bilateral hippocampal volume reductions compared to age-appropriate norms. We also tested 9 healthy controls (age range = 36–57, female = 5), matched for mean age, reading, and executive function. In the Rey-Osterrieth Complex Figure (ROCF) test, both groups performed equally in the copy condition, but the hippocampal-region lesion (HL) group performed worse than controls (M = 23.9) in the delayed condition (M = 13.5), t(16) = 2.99, p < .01, conforming to the characteristic explicit memory deficits of amnesia.

Materials and Procedure

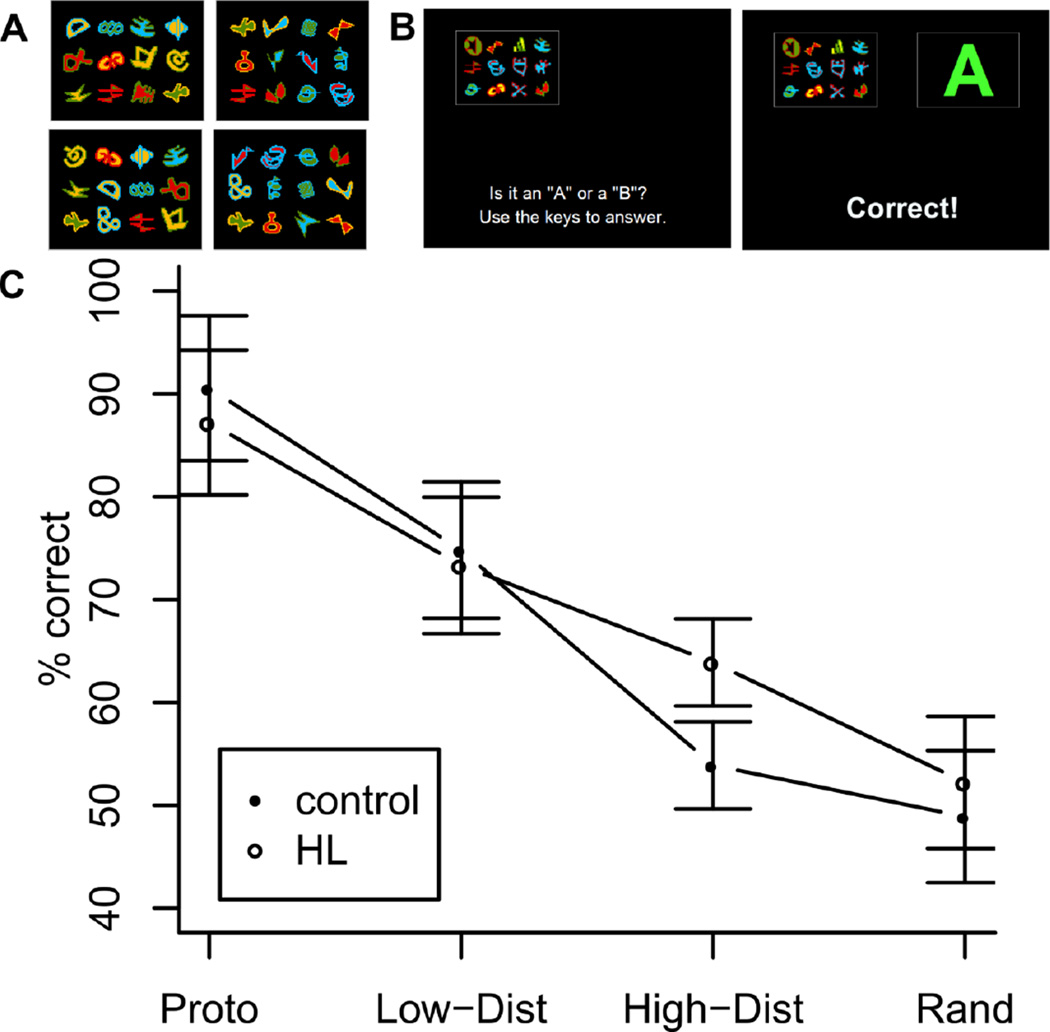
Figure 2A shows some example training items for this task. Each training item is composed of 12 different coloured icons, whose position varies randomly from trial to trial. There are 12 icons that are characteristic of category A, and 12 that are characteristic of category B. In creating a category A training item, one starts with all 12 category-A icons, and then gives each an independent 10% chance of being replaced by a category-B icon. A corresponding process is used to create category B training items. Hence, the training items have some variability, but the two categories differ substantially and thus are relatively easy to acquire. Virtually all training items contain between 9 and 12 category-characteristic icons.

Figure 2.

Figure 2

Open in a new tab

A: Example category items for a participant, two examples from each category (A on left, B on right). B: Example training trial in which a different participant (hence, different random allocation of icons to categories) correctly responds “A” and positive feedback appears. C: Generalization gradients for each group. Error bars are 95% CI, adjusted for between-subject variance (Baguley, 2012). Labels on the abscissa are as per Figure 1.

During 60 training trials (half from each category), participants were asked to categorize exemplars as A or B, with feedback provided (Figure 2B). They then received 130 test (no-feedback) trials, where they categorized novel items. There were four types of novel item: prototypes, low-distortion, high-distortion, and random. Prototypes contained all 12 icons of one category, and zero icons of the other. Prototypes are the central tendency of the trained item of a category, and hence performance is expected to be good on these items. Low-distortion items, although novel, were typical of the training items. Specifically, low-distortion items contained between 9 and 11 icons characteristic of one category, with the remainder from the other category. In contrast, high-distortion items were very atypical of the training items, containing 7 or 8 icons characteristic of one category, with again the remainder coming from the other category. Nevertheless, high-distortion items can in principle be classified correctly, because they contain more icons characteristic of one category than the other. Finally, random items contained 6 category-A icons, and 6 category-B icons. Thus, there is no correct classification of these items and, in the absence of a response bias for one category, accuracy is expected to be around 50%. Overall, the test phase comprised 130 test items: 20 prototypes, 60 low-distortion items, 40 high-distortion items, and 10 random items. The order of presentation of the test items was random. The number and distribution of test items is identical to most previous applications of this particular category-learning procedure (e.g. Jones et al., 1998: Wills 2002; Wills & McLaren, 1997).

RESULTS

No significant group difference in classification accuracy was observed during training, t(14.9) = .724, p = .480. Figure 2C shows the generalization gradients for the HL and control groups. A significant effect of distortion level (excluding random items) on categorization accuracy was found F(2,32) = 48.44, p < .001. The condition-by-group interaction was marginally significant, F(2,32) = 2.81, p = .075. Categorization accuracy for high-distortion items was significantly higher for the HL group (M = 63.9, SE = 3.09) than for controls (M = 53.9, SE = 2.54), p = .014, one-tailed, using a permutation test1. A permutation test is appropriate given the small (although not atypical) sample sizes. A one-tailed test is appropriate given the directional nature of our a priori prediction, although the result remains significant two-tailed, and also after Bonferroni corrections to accommodate the fact that Figure 1 also predicts an effect for low-distortion items, which is not observed. An ANCOVA revealed that group remained a significant predictor of between-group difference in high-distortion classification accuracy when including age as a covariate, F(1,15) = 5.79, p = .03.

In order to further test the robustness of this effect, we recruited an additional 24 unmatched controls (age range=19–34, female=18) from a younger student population. With a total of 33 control participants, the superior performance of the HL group on high-distortion test items remained marginally significant, p = .052, one-tailed permutation test. The unmatched control group showed superior training-phase accuracy relative to the HL group, t(14.4) = 2.45, p = .03. This is perhaps to be expected given younger people acquire categories faster (Krishna et al. 2012), and it makes the finding of superior generalization in the HL group relative to an unmatched control group containing many young people, all the more striking.

Data archive

Trial-level raw data for the unmatched control group are available at [maskedlink] with an MD5 checksum2 of 0783fd6357fbaccdc07a996bda15aa75. All analysis scripts are available at the same location. Data from the HL and age-matched control groups is available from the authors on request.

DISCUSSION

Overall, the current study provides some evidence for the Gluck-Myers’ model prediction that amnesics can show superior generalization in a two-category learning task, relative to controls. Nevertheless, our experiment has a few limitations, which future research may wish to address. For example, a skeptic might reasonably argue that the predictions of the Gluck-Myers model are not fully supported by the current experiment, as an effect was expected for both low- and high-distortion items, but was only observed for high-distortion items. However, it should be pointed out that that the low-distortion null effect represents an absence of evidence, not evidence of absence. It would therefore be incorrect to describe it as evidence against the model.

One explanation for this apparent deviation between model predictions and observed data is a lack of power. Performance on low-distortion items is closer to ceiling than for high-distortion items, and hence may be harder to detect. Large-scale independent replication would resolve this issue one way or the other, and we encourage others to attempt this. If future studies replicate this finding of a difference in high-, but not low-, distortion items, this might call for some revision of the model.

Another apparent discrepancy between model and data is that, compared to the Figure 1 simulation, the observed accuracy levels are somewhat lower. We advise against over-interpreting this difference. Figure 1 is an illustration of the ordinal direction of effects - the absolute accuracy scores from the simulation are dependent on the choice of parameters used in modelling. A relatively parameter-free prediction of the model is that performance on distorted items will be ordinally better for HL than for controls.

Another potential criticism of the current study is that the stimulus set we used is relatively novel and less well understood compared to, for example, the dot-pattern stimuli used in some previous research (e.g. Knowlton & Squire, 1993). There were good reasons for our choice of procedure (see Introduction); nevertheless, future researchers may wish to examine the generality of this result with other stimulus sets.

Finally, although this experiment provides evidence for an a priori prediction of the Gluck and Myers (1993) cortico-hippocampal model, it seems likely that some other competing accounts can also accommodate this result (e.g. Nosofsky & Zaki, 1998). Future research might seek to investigate further predictions of these accounts. For example, the Gluck-Myers model makes the prediction that the effect is driven by the presence of category labels. If instead an unsupervised training phase was used (i.e. exposure to the training items without feedback, see e.g. Homa & Cultice, 1984; Wills & McLaren, 1998), no such effect would be expected under the Gluck-Myers account. This is because the processes of differentiation and compression assumed by the Gluck-Myers model are driven by the presence of category labels in their account. In other words, things that have the same label are made more similar, and things that have different labels are made more different. Without the labels, this doesn’t happen. In contrast, the sort of increased memorial confusability account offered by Nosofsky and Zaki is a static representational difference between amnesics and controls that is not specifically tied to the presence of category labels.

Acknowledgments

This work was partially supported by the NIMH (R01 MH065406 and by Merit Award I01 CX000771 from the U. S. Department of Veterans Affairs Clinical Sciences Research and Development Service. The contents of this article do not necessarily represent the views of the U. S. Department of Veterans Affairs or the United States Government.

Footnotes

1

Asymptotic exact test, using the perm package (Fay & Shaw, 2010), within the R environment R Core Team, 2015).

2

Publication of an MD5 checksum allows the reader to independently confirm that the raw data in the archive is unchanged.

REFERENCES

  1. Baguley T. Calculating andg within-subject confidence intervals for ANOVA. Behavior Research Methods. 2012;44(1):158–175. doi: 10.3758/s13428-011-0123-7. [DOI] [PubMed] [Google Scholar]
  2. Buss AH. A study of concept formation as a function of reinforcement and stimulus generalization. Journal of Experimental Psychology. 1950;40(4):494–503. doi: 10.1037/h0061631. [DOI] [PubMed] [Google Scholar]
  3. Jones FW, Wills AJ, McLaren IPL. Perceptual categorization: connectionist modelling and decision rules. Quarterly Journal of Experimental Psychology B. 1998;51(1):33–58. doi: 10.1080/713932666. [DOI] [PubMed] [Google Scholar]
  4. Fay MP, Shaw PA. Exact and asymptotic weighted logrank tests for interval censored data: The interval R Package. Journal of Statistical Software. 2010;36(2):1–34. doi: 10.18637/jss.v036.i02. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gluck MA, Myers CE. Hippocampal mediation of stimulus representation: a computational theory. Hippocampus. 1993;3(4):491–516. doi: 10.1002/hipo.450030410. [DOI] [PubMed] [Google Scholar]
  6. Grice GR, Saltz E. The generalization of an instrumental response to stimuli varying in the size dimension. Journal of Experimental Psychology. 1950;40(6):702–708. doi: 10.1037/h0054435. [DOI] [PubMed] [Google Scholar]
  7. Homa D, Cultice J. Role of feedback, category size, and stimulus distortion on the acquisition and utilization of ill-defined categories. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10(1):83–94. [Google Scholar]
  8. Homa D, Hout MC, Milliken L, Milliken AM. Bogus concerns about the false prototype enhancement effect. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2011;37(2):368–377. doi: 10.1037/a0021803. [DOI] [PubMed] [Google Scholar]
  9. Kitchener EG, Squire LR. Impaired verbal category learning in amnesia. Behavioral Neuroscience. 2000;114(5):907–911. [PubMed] [Google Scholar]
  10. Knowlton BJ, Squire LR. The learning of categories: parallel brain systems for item memory and category knowledge. Science. 1993;262(5140):1747–1749. doi: 10.1126/science.8259522. [DOI] [PubMed] [Google Scholar]
  11. Kolodny JA. Memory processes in classification learning: An investigation of amnesic performance in categorization of dot patterns and artistic styles. Psychological Science. 1994;5(3):164–169. [Google Scholar]
  12. Krishna R, Moustafa AA, Eby A, Skeen LC, Myers CE. Learning and Generalization in Healthy Aging: Implication for Frontostriatal and Hippocampal Function. Cognitive and Behavioral Neurology. 2012;25(1):7–15. doi: 10.1097/WNN.0b013e318248ff1b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Nosofsky RM, Zaki SR. Dissociations between categorization and recognition in amnesic and normal individuals: an exemplar-based interpretation. Psychological Science. 1998;9(4):247–255. [Google Scholar]
  14. Palmeri TJ, Flanery MA. Learning about categories in the absence of training: Profound amnesia and the relationship between perceptual categorization and recognition memory. Psychological Science. 1999;10(6):526–530. [Google Scholar]
  15. R Core Team. R: A Language and Environment for Statistical Computing. Austria: R Foundation for Statistical Computing Vienna; 2015. http://www.R-project.org/ [Google Scholar]
  16. Reed JM, Squire LR, Patalano AL, Smith EE, Jonides J. Learning about categories that are defined by object-like stimuli despite impaired declarative memory. Behavioral Neuroscience. 1999;113(3):411–419. doi: 10.1037//0735-7044.113.3.411. [DOI] [PubMed] [Google Scholar]
  17. Squire LR, Knowlton BJ. Learning about categories in the absence of memory. Proceedings of the National Academy of Sciences USA. 1995;92(26):12470–12474. doi: 10.1073/pnas.92.26.12470. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wills AJ. Adapting to a response deadline in categorization. In: Gray WD, Schunn CD, editors. Proceedings of the 24th Annual Conference of the Cognitive Science Society; Mahwah, NJ: Lawrence Erlbaum Associates; 2002. pp. 938–943. [Google Scholar]
  19. Wills AJ, McLaren IPL. Generalization in human category learning: A connectionist account of differences in gradient after discriminative and non discriminative training. Quarterly Journal of Experimental Psychology A. 1997;50(3):607–630. [Google Scholar]
  20. Wills AJ, McLaren IPL. Perceptual learning and free classification. Quarterly Journal of Experimental Psychology B. 1998;51(3):33–58. doi: 10.1080/713932680. [DOI] [PubMed] [Google Scholar]
  21. Wills AJ, Reimers S, Stewart N, McLaren IPL. Tests of the ratio rule in categorization. Quarterly Journal of Experimental Psychology A. 2000;53(4):983–1011. doi: 10.1080/713755935. [DOI] [PubMed] [Google Scholar]
  22. Zaki SR, Nosofsky RM, Jessup NM, Unverzagt FW. Categorization and recognition performance of a memory-impaired group: Evidence for single-system models. Journal of the International Neuropsychological Society. 2003;9(3):394–406. doi: 10.1017/S1355617703930050. [DOI] [PubMed] [Google Scholar]

RESOURCES