The effect of lung deformation on the spatial distribution of pulmonary blood flow

Abstract

Key points

• Pulmonary perfusion measurement using magnetic resonance imaging combined with deformable image registration enabled us to quantify the change in the spatial distribution of pulmonary perfusion at different lung volumes.

• The current study elucidated the effects of tidal volume lung inflation [functional residual capacity (FRC) + 500 ml and FRC + 1 litre] on the change in pulmonary perfusion distribution.

• Changes in hydrostatic pressure distribution as well as transmural pressure distribution due to the change in lung height with tidal volume inflation are probably bigger contributors to the redistribution of pulmonary perfusion than the changes in pulmonary vasculature resistance caused by lung tissue stretch.

Abstract

Tidal volume lung inflation results in structural changes in the pulmonary circulation, potentially affecting pulmonary perfusion. We hypothesized that perfusion is recruited to regions receiving the greatest deformation from a tidal breath, thus ensuring ventilation–perfusion matching. Density‐normalized perfusion (DNP) magnetic resonance imaging data were obtained in healthy subjects (n = 7) in the right lung at functional residual capacity (FRC), FRC+500 ml, and FRC+1.0 l. Using deformable image registration, the displacement of a sagittal lung slice acquired at FRC to the larger volumes was calculated. Registered DNP images were normalized by the mean to estimate perfusion redistribution (nDNP). Data were evaluated across gravitational regions (dependent, middle, non‐dependent) and by lobes (upper, RUL; middle, RML; lower, RLL). Lung inflation did not alter mean DNP within the slice (P = 0.10). The greatest expansion was seen in the dependent region (P < 0.0001: dependent vs non‐dependent, P < 0.0001: dependent vs middle) and RLL (P = 0.0015: RLL vs RUL, P < 0.0001: RLL vs RML). Neither nDNP recruitment to RLL [+500 ml = −0.047(0.145), +1 litre = 0.018(0.096)] nor to dependent lung [+500 ml = −0.058(0.126), +1 litre = −0.023(0.106)] were found. Instead, redistribution was seen in decreased nDNP in the non‐dependent [+500 ml = −0.075(0.152), +1 litre = −0.137(0.167)) and increased nDNP in the gravitational middle lung [+500 ml = 0.098(0.058), +1 litre = 0.093(0.081)] (P = 0.01). However, there was no significant lobar redistribution (P < 0.89). Contrary to our hypothesis, based on the comparison between gravitational and lobar perfusion data, perfusion was not redistributed to the regions of the most inflation. This suggests that either changes in hydrostatic pressure or transmural pressure distribution in the gravitational direction are implicated in the redistribution of perfusion away from the non‐dependent lung.

Key points

• Pulmonary perfusion measurement using magnetic resonance imaging combined with deformable image registration enabled us to quantify the change in the spatial distribution of pulmonary perfusion at different lung volumes.

• The current study elucidated the effects of tidal volume lung inflation [functional residual capacity (FRC) + 500 ml and FRC + 1 litre] on the change in pulmonary perfusion distribution.

• Changes in hydrostatic pressure distribution as well as transmural pressure distribution due to the change in lung height with tidal volume inflation are probably bigger contributors to the redistribution of pulmonary perfusion than the changes in pulmonary vasculature resistance caused by lung tissue stretch.

Abbreviations

ASL

arterial spin labelling

DNP

density‐normalized perfusion

FRC

functional residual capacity

FOV

field of view

mGRE

multiple gradient echo

MRI

magnetic resonance imaging

RLL

right lower lobe

RML

right middle lobe

RUL

right upper lobe

TLC

total lung capacity

Introduction

As inspiration occurs, the extent of local tissue deformation due to breathing is associated with greater regional ventilation, as regions that deform more from the baseline condition receive more of the incoming delivery of fresh gas. Simultaneously, this lung deformation induced by normal respiratory motion also results in structural changes in the pulmonary vasculature tree that have the potential to significantly influence the spatial distribution of pulmonary blood flow. This is because the geometry of pulmonary circulation depends not only on the underlying vascular structure but also on mechanical deformation of the lung parenchymal tissue to which the vasculature structure is tethered (Hopkins et al. 2007; Prisk et al. 2007; Clark et al. 2011).

Lung inflation induces both radial and axial distensions in pulmonary vascular structure. These two types of distension potentially act in opposition to one another to alter pulmonary vasculature resistance and flow, in a complicated way, as axial elongation is expected to increase, and radial distension decrease vascular resistance (Fung & Sobin, 1972 b; Yen et al. 1980; Yen & Foppiano, 1981). Also as predicted by the zone model of pulmonary perfusion (West et al. 1964) any change in the hydrostatic pressure distribution due to changing lung dimensions may also contribute to the redistribution of pulmonary blood flow. This is because in inspiration, the vertical dimension of the lung in the direction of gravity increases, and thus changes the distribution of hydrostatic pressure gradients. If regional lung inflation is a primary mechanism of ensuring ventilation–perfusion matching, then perfusion should be redistributed to regions experiencing greater local lung inflation. This finding would imply that radial distension of pulmonary vessels would predominate in the regions with greater local inflation as this is the means whereby vascular resistance would be reduced.

The effect of normal lung inflation on the distribution of pulmonary blood flow is not well known; the debate over the changes in local haemodynamics due to negative pressure lung inflation, occurring during normal breathing, has, thus far, lasted over five decades (Burton & Patel, 1958; Peták et al. 2009). On a whole lung level, the literature suggests that a decline in pulmonary vascular resistance is seen with negative lung inflation (Burton & Patel, 1958). In the human lung, it is thought that the relatively large extra‐alveolar vessels are held open and expand as the lung inflates (Hughes et al. 1968). In excised dog lungs, Howell et al. (1961) reported that large vessels were expanded while small alveolar vessels were compressed with lung inflation, demonstrating that the different sizes of pulmonary vessels responded differently to lung inflation at a more microscopic level. These conflicting effects on the pulmonary vasculature thus have the potential to affect the overall response of pulmonary vascular resistance and flow to inflation. Further work by Thomas et al. (1961) showed that there was a ‘U‐shaped’ relationship between lung volume and vascular resistance; the lowest pulmonary vascular resistance was seen around functional residual capacity (FRC) with the resistance increasing as the volume increases to total lung capacity (TLC) and also increasing as volume decreases towards a completely collapsed lung (minimal volume).

In part, some of the controversy may stem from the difficulty in making measurements in vivo, in the absence of mechanical ventilation and with an intact chest wall. In this study, we hypothesized that regional lung inflation induces a change in the spatial distribution of pulmonary perfusion in a manner that is expected to maintain ventilation–perfusion matching. If this is the case, a lung region experiencing greater inflation and inspiratory volume would be expected to increase perfusion with inflation. On the other hand a region with little local inflation would be expected to have little to no increase in perfusion.

We used functional magnetic resonance imaging (MRI) techniques that allow changes in the spatial distribution of pulmonary blood flow in the human lung to be evaluated. A technique known as arterial spin labelling (ASL) (Mai & Berr, 1999; Mai et al. 2000; Bolar et al. 2006; Henderson et al. 2009) measures perfusion, which when combined with proton density measurements (Theilmann et al. 2009) allows the creation of a pulmonary perfusion map in units of ml(blood) min^–1 g^–1  (tissue). This enables changes in blood flow to be assessed independently of changes in the underlying tissue distribution. We previously used these techniques to show large‐scale changes in perfusion with large changes in lung volume (Hopkins et al. 2010). However, local smaller‐scale changes could not be evaluated, because of the different size and shapes of the lung images. Consequently, we developed a deformable image registration technique that enables the warping of a lung image onto another reference shape and a pulmonary perfusion map can be registered onto another perfusion map acquired at a different lung volume. The regional lung inflation that occurs between two images was also estimated by the deformation vector field computed by the deformable image registration. Following registration, the regional blood flow differences can be calculated by comparing the two images, and these techniques can thus measure the changes in local pulmonary blood flow induced by a normal tidal volume‐like negative pressure lung inflation.

To evaluate the effects of tidal volume lung inflation, pulmonary perfusion maps were obtained in supine healthy subjects within a short ∼15 s breath hold at three different lung volumes (FRC, FRC + 500 ml and FRC + 1.0 l inhalation volumes). These two inhalation volumes were chosen to approximate a normal human tidal volume ∼ 500 ml in the supine posture with larger sigh breaths of ∼ 1 l (Prisk et al. 1995; Stallinger et al. 2001; Sá et al. 2010).

Methods

Overview

The present study employed a 2D ASL technique in conjunction with a multiple gradient echo (mGRE)‐based proton density imaging technique to quantify the distribution of pulmonary perfusion. This was measured within a single representative sagittal slice in the right lung at FRC, which was designated as the measurement slice. Since with tidal volume lung inflation the measurement slice was expected to expand in both the in‐plane and the through‐plane directions, additional sagittal images were acquired laterally to form a 3D volumetric image for each level of inflation to account for any through‐plane expansion. Then, a 3D deformable image registration technique was used to warp the two inflated volumetric lung images into the FRC reference image. Thus, perfusion data from the two different inflated lung volumes were reshaped and were directly compared to the measurement slice obtained at FRC.

Subjects

This study was approved by the University of California, San Diego's Human Subjects Research Protection programme. Subjects participated after giving written, informed consent. Seven healthy subjects [3 women, 4 men: age = 27(5) years, height = 168(12) cm, and weight = 65(12) kg] participated. They were lifelong non‐smokers, with no history of pulmonary or cardiovascular disease. Each subject underwent screening for MRI safety and spirometric pulmonary function test. Subject characteristics are given in Table 1.

Table 1.

Subject characteristics and pulmonary function data for all seven subjects studied

					FEV1 (litres)	FVC (litres)	FEV1/FVC
Subject	Sex	Age (years)	Height (cm)	Weight (kg)	(% predicted)	(% predicted)	(% predicted)
1	M	28	178	77	3.80(84)	5.06(92)	0.75(91)
2	M	32	170	68	3.31(82)	4.33(88)	0.77(94)
3	M	31	185	75	5.04(105)	6.03(101)	0.84(102)
4	M	26	170	68	3.89(95)	5.25(107)	0.74(90)
5	F	30	163	57	3.18(99)	3.95(104)	0.81(94)
6	F	23	155	64	2.65(82)	3.41(92)	0.78(91)
7	F	19	152	43	2.79(95)	2.95(90)	0.95(109)
Mean		27	168	65	3.52(92)	4.43(96)	0.81(96)
SD		5	12	12	0.81(9)	1.09(8)	0.07(7)

FEV₁, forced expiratory volume in 1 s; FVC, forced vital capacity. SD, standard deviation among all seven subjects.

Lung volume control

A face mask (Hans Rudolph 7400 Oro‐Nasal Mask, Hans Rudolph Inc., Shawnee, KS, USA) equipped with a non‐rebreathing T‐valve (Hans Rudolph, 2600 Medium, Hans Rudolph Inc.) was fitted to the subject. The outlet of the T‐valve was connected to a 6 m long, large‐bore low‐resistance expiratory line, leading out of the scanner room, where expired tidal volume was simultaneously measured using a ParvoMedics Metabolic Measurement System (Sandy, UT, USA). The inspiratory end of the T‐valve was connected to a remote‐controlled three‐way pneumatic sliding valve (Hans Rudolph model 8500) and allowed rapid switching between two inspiratory ports. One end of the three‐way valve was opened to room air, allowing the subject to breathe freely during the interval between image acquisitions. The other end was connected to a 5 l Mylar bag.

Two different levels of lung inflation, FRC + 500 ml and FRC + 1 litre, were chosen to represent typical tidal volume breathing, and were obtained as follows: the predetermined volume of air was instilled into the Mylar bag using a calibrated syringe. Before the image acquisition began, the subject was asked to hold his or her breath at FRC. Then, the sliding switch at the three‐way valve was turned, allowing the subject to inhale the predetermined volume of air (500 ml or 1.0 litre) from the bag. Once the subject emptied the bag, they were instructed to breath‐hold, but cautioned not to forcibly expand the chest against the empty bag (to avoid raising intrathoracic pressure) and to maintain an open glottis during image acquisition. The breath‐holds lasted for a maximum of 15 s. Subjects were trained in the breathing manoeuvre so that they could comfortably repeat the breath‐hold at the desired level of lung inflation. Using this method to control lung volume, subjects were able to achieve negative pressure inspiratory lung inflation, similar to that occurring during normal respiration. Any inconsistency in breath‐holding was monitored by checking chest wall and diaphragm movement in the acquired MR image and the presence of expiratory flow detected using the metabolic measurement system at the end of the expiratory outlet.

MRI data collection

Data were collected with a 1.5‐T Signa HDx TwinSpeed MRI system (General Electric Medical Systems, Milwaukee, WI, USA). The subject lay in the supine posture in the scanner and MRI‐compatible ECG electrodes (Invivo ECG Quadtrodes) were placed on the left chest. Silicon reference phantoms for quantification (Breast Implant Round 150cc, Mentor, Santa Barbara, CA, USA) were placed on the anterior chest wall so as to be within the field of view (FOV) of the perfusion and lung density images. The subject lay on the posterior element of an eight‐channel torso coil, and the anterior elements were placed directly onto the subject's chest over the reference phantoms.

Measurement slice for perfusion evaluation

The primary evaluation of perfusion changes with lung deformation took place in a single sagittal slice of the right lung at FRC, which we designate as the measurement slice. The right lung was chosen to eliminate motion artifacts from the aorta and heart in the left hemithorax. The location of the measurement slice (15 mm slice thickness) was positioned in the mid‐clavicular line to capture the maximum anterior–posterior diameter of the lung, thus allowing us to capture the wide range of regional lung inflation due to gravitational dependency of regional lung tissue distribution (Hopkins et al. 2007; Theilmann et al. 2009) and specific ventilation (Sá et al. 2010).

Additional lateral slices on both sides of the measurement slice

The measurement slice, when inflated, is expected to deform not only in the in‐plane direction, which can be visualized, but also in the through‐plane direction, to an unknown extent. To account for this, additional 2D sagittal images were obtained to constitute a 3D volume. The number of image slices obtained at each lung volume for each MRI sequence is described in Table 2. Additional slice locations were progressively shifted by 5 mm in the left–right direction so that two adjacent images overlapped by 10 mm of the total slice thickness of 15 mm. Part of the right lung was covered with this overlap scheme in 3D space (Fig. 1).

Table 2.

MRI slice selection strategy; the number of slice locations and scans for ASL and proton density imaging at different lung volumes

Lung volume	ASL	Proton density	Resultant DNP	Measurement slice location
FRC	9 slices	9 slices	9 slices	The centre of 9 slices (5th slice)
	9 scans	3 scans
FRC + 500 ml & +1.0 litre	5 slices	9 slices	5 slices	Deformed within a 3D volume
	5 scans	3 scans

The number of scans corresponds to the minimum number to obtain 3D volumetric lung data at each lung volume. ASL, arterial spin Labelling. DNP, density normalized perfusion.

Figure 1. 2D sagittal slice locations shown in an axial view .

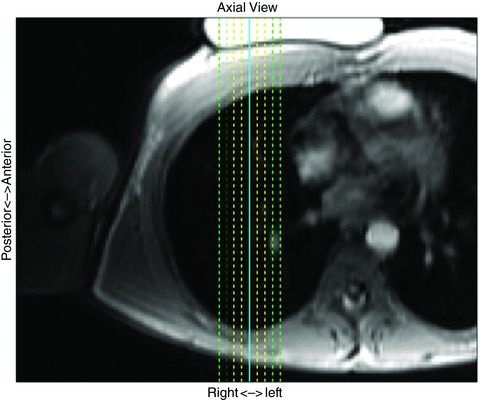
Multiple, overlapping, 15 mm thick 2D sagittal MR images were obtained at different lateral slice locations to encompass a part of the right lung in 3D space. Adjacent slice locations were shifted by 5 mm, and overlapped by 10 mm. At FRC, both proton density and perfusion–vascular structure images were obtained from nine slice locations (dashed green, yellow and solid blue lines), covering 4 cm thickness of the right lung. The solid blue line represents the measurement slice location. At the two inflated volumes, proton density images were obtained from the nine slice locations whereas perfusion–vascular structure images were obtained from five slice locations (dashed yellow and solid blue lines), covering a 2 cm thick lung region. A 3D deformable image registration technique was used to compute the deformation of the measurement slice at FRC with respect to two levels of tidal lung inflation. Table 2 describes the number of slices for each imaging scheme at different lung volumes.

At FRC a total of nine ASL‐based perfusion images and nine mGRE‐based proton density images were acquired with this overlap scheme. This 3D image stack measured at FRC is denoted as the reference FRC volume in which the measurement slice was positioned at the centre slice of the 3D image stack, i.e. the 5th slice out of nine parallel slices. The distance between the centres of the most medial and lateral slices was 4 cm.

For the two inflated lung acquisitions, only five ASL‐based perfusion images were taken while nine proton density images were taken (Table 2 and Fig. 1). Some slice locations were omitted for inflated lung volumes because the measurement slice or a part of it was not expected to be shifted or inflated more than 1 cm in either direction and because it reduced the number of breath‐holds the subjects needed to perform shortening the duration of data acquisition. The five perfusion images were collocated with 3rd to 7th slice locations of the nine proton density images (Fig. 1). The centre image (the 3rd slice out of five slice locations) was positioned at the same slice location as the centre of reference FRC volume (the 5th slice out of nine slice locations, i.e. measurement slice).

Lung proton density imaging

Regional proton density was measured using a fast gradient echo sequence (as described in detail by Theilmann et al. 2009) during a 9 s breath‐hold. Each acquisition acquires three 15 mm adjacent slices simultaneously and this was repeated three times at each lung volume to cover the 3D image stack described above. Imaging sequence parameters were TR = 10 ms, flip angle = 10 deg, receiver bandwidth = 125 kHz, the slice thickness of 15 mm, the in‐plane FOV of 40 × 40 cm and a full acquisition matrix of 64 × 64. Two echo times (TE_short = 1.1 ms and TE_long = 1.8 ms) were alternated. The regional proton density was determined by fitting a single exponential on a voxel‐by‐voxel basis for the two different echo times and extrapolating back the magnetization at time zero. This technique was previously validated using ex vivo pig lungs (Holverda et al. 2011), with excellent validity (R ² ∼0.95).

Perfusion and vascular structure images

Three images were acquired during a 15 s breath‐hold within each slice location as follows. First, two images were acquired to assess regional pulmonary perfusion using 2D ASL with a flow‐sensitive alternating inversion recovery with an extra radiofrequency pulse (FAIRER) imaging sequence and a half‐Fourier acquisition single‐shot turbo spin‐echo (HASTE) data collection scheme. ASL‐FAIRER consists of a pair of cardiac triggered MR images to yield one perfusion‐weighted image as described in detail (Bolar et al. 2006; Henderson et al. 2009). ASL sequence parameters were as follows: TR = 5 s, TI = 600–800 ms (set to 80% of the subject's R–R interval measured using the cardiac ECG), effective TE = 21.3 ms. The collected image matrix size was 256 × 128 and was reconstructed by the scanner to 256 × 256. The slice thickness and FOV were matched to the lung density sequence, 15 mm and 40 × 40 cm, respectively. Then an additional inversion recovery sequence with TI = 50 ms, optimized to highlight the vascular structure in the lung, was obtained, which was used for image registration. Since these three images (i.e. a pair of ASL images and one vascular structure image) were obtained during the same breath‐hold, they shared an identical physical coordinate system. The vascular structure image was used to determine the deformation vector field of lung inflation by comparing it with the corresponding images at different lung volumes. It also provided clear delineation between the three lobes in the right lung, since blood vessels do not cross lobar boundaries, providing a dark contrast at the fissures.

Nine perfusion–vascular structure image sets were taken at FRC to establish a reference volumetric lung, covering the exact same physical location as the lung density images with 5 mm lateral shift and 10 mm overlap between adjacent images (Fig. 1). For each lung volume (FRC + 500 ml and FRC + 1 litre), five sagittal perfusion–vascular structure images were acquired using the same spatial overlapping scheme, covering a 2 cm thick region of the right lung. In each slice, at each lung volume, image acquisition was repeated at least three times and one representative image was chosen to ensure that the 3D image stack reconstructed a continuous 3D volumetric lung. The in‐plane resolution of the volumetric lung was approximately 1.6 × 1.6 mm while the through‐plane resolution was 5 mm.

3D deformation vector field analysis

3D deformable image registration was used to warp the inflated lung onto the reference volumetric lung at FRC. The deformation vector field between the reference and inflated volumetric lungs for each subject was modelled using 3D bicubic–linear polynomial interpolation (Nielsen et al. 1991). Thus, deformation and through‐plane shift of the measurement slice was computed. In‐plane deformation was interpolated with cubic B‐spline polynomials (Yin et al. 2009) while through‐plane deformation was interpolated with a linear interpolation method, given the lower spatial sampling in this plane (Nielsen et al. 1991).

The inversion recovery vascular structure images were used for the deformation analysis. The deformation vector field was separately computed within each of the three manually segmented lobes (right lower, upper and middle lobes) to avoid potential errors induced by lobar sliding, which cannot be expressed by the polynomial B‐spline interpolation method (Ding et al. 2009).

The deformation algorithm (developed in‐house in MATLAB; Mathworks, Natick, MA, USA) follows a stepwise approach, from a relatively crude to a finer scale: a single cuboid (3D rectangular) element that encompasses each lobe is used at first. This initial low‐resolution element was then recursively refined in‐plane until the size of the refined element grid becomes approximately 8 pixels, dividing the original element into an integer number of grids. The sum of squares difference between reference FRC and warped inflated lungs was used as the cost function for the image registration. Finally, the quality of image registration was visually inspected by checking the alignment between vascular structures in reference FRC and warped lungs.

The regional lung volume change expressed as a fraction of the resultant deformed volume to original volume (V/V ₀) was computed from the Jacobian determinant of the deformation vector field (Yin et al. 2009; Choi et al. 2013). The three independently computed lobar deformation vector fields (right lower, upper and middle lobes) were reassembled to represent the whole lung volume deformation.

Perfusion measurements within the measurement slice

Quantified ASL (ml min^–1 cm^–3) and density (g cm^–3) images obtained at FRC + 500 ml and FRC + 1 litre lung volumes were warped onto the reference FRC volumetric lung based on the 3D deformation vector field computed using the vascular structure images. Therefore, these data were compared at the exact same location within the measurement slice as in the reference FRC image.

The large, conduit, vessel signal (which does not represent perfusion) was removed from the ASL images using a 35% maximum‐intensity threshold (Burrowes et al. 2012). Once the conduit vessel signals were removed, ASL maps were then smoothed with a Gaussian low pass filter [full width half maximum = 7 voxels (1.1 cm)] (Henderson et al. 2013), resulting in an effective spatial resolution of the perfusion map of approximately the size that would be associated with five acini (Haefeli‐Bleuer & Weibel, 1988). Any voxels with negative ASL flow signal were removed as they represent inherent ASL measurement errors. In addition to ASL large vessel and error correction, voxels with regional volume change of greater and less than the 95th and 5th percentiles (for each inflation volume) were also eliminated from the data to remove the occasional, probably spurious, volume changes resulting from the image registration algorithm. These occur as a result of discontinuous tissue deformation within a lobe, or local collisions of the deformation vector field, and result in voxels that show either the large scale regional volume change (V/V ₀) or lung deflation (V/V ₀ < 1). On average ∼10% of total voxels after ASL error correction were removed for each inflated lung image. As all lung data sets were combined, 82% of voxels remained in common in all three lung volumes for the data analysis. The ASL perfusion images were divided by the density images, yielding density‐normalized perfusion images (DNP: ml min^–1 g^–1), giving perfusion in millilitres per minute per gram of lung.

Scale of measurement

The smallest nominal resolution employed in this study was the voxel resolution of ASL, 1.6 × 1.6 × 15 mm. The perfusion data were smoothed using a Gaussian kernel with full width half maximum of 7 × 7 voxels. In addition, cubic B‐spline control points used for deformable image registration were separated by approximately 8 voxels in plane. Thus, the smallest spatial scale of measurement that can be distinguished in this study is expected to be approximately 10 × 10 voxels, which is 3.8 cm³.

Data analysis

Density, density‐normalized perfusion and fractional regional lung volume change (computed as the determinant of Jacobian: V/V ₀) maps were calculated for the measurement slice. Lung density inherently decreases with lung inflation, as each voxel contains more air after inflation. The density images at the increased lung volumes were corrected with the regional volume change map to capture the effects of lung inflation on the distribution of lung water, yielding the deformation‐corrected density in units of g cm^{–3 *} (i.e. density × V/V ₀; the asterisk (^*) indicates that voxel size is corrected with the local lung inflation). As this influence of voxel size change due to lung deformation is countered by the change in density, density‐normalized perfusion also corrects for regional lung deformation. It reflects the amount of perfusion per gram lung (tissue + blood volumes).

In addition to the measurement slice, the lung was divided into three lobar sections (right lower lobe, RLL; right upper lobe, RUL; and right middle lobe, RML) and three vertically gravitational regions (dependent, middle and non‐dependent; Fig. 2 B). The lung was manually segmented into three lobes based on fissures apparent on the vascular structure images. There are three lobes in the right lung: RLL, RUL and RML (Fig. 2 C). The lung was also divided into three equal vertical distance gravitational regions (anterior–posterior direction, as the subjects were supine), starting from the most posterior part of the lung and proceeding anteriorly giving dependent, middle and non‐dependent gravitational regions, respectively.

Figure 2. Lobar and gravitational segmentation of sagittal lung .

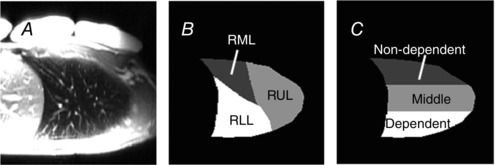
A, for each subject and lung volume a vascular structure image optimized to highlight the vascular structure in the lung was acquired, and used to delineate three lobes in the right lung. B, the lung was manually segmented into three lobes based on fissures apparent on the vascular structure images (ASL difference image, not shown). There are three lobes in the right lung; the oblique fissure separates the lower lobe from the rest of the lung and the horizontal fissure divides the upper and middle lobes (right lower lobe, RLL; right upper lobe, RUL; and right middle lobe, RML). C, the lung was also divided into three equidistant vertical gravitational regions, starting from the most posterior part of the lung and proceeding anteriorly giving dependent, middle and non‐dependent regions, respectively.

To study the effect of lung volume change on the redistribution of perfusion in the measurement slice, independent of any overall change in bulk flow, the density‐normalized perfusion maps were normalized by their own mean, yielding the nDNP map. nDNP is a dimensionless quality and the difference between nDNP maps at different lung volumes compared to FRC reflects any perfusion redistribution with lung inflation without the confounding influence of an overall mean cardiac output change. In other words, if there is no redistribution of perfusion, the difference between two nDNP maps would become zero at all spatial locations.

ANOVA (Statview 5.0, SAS Institute, Cary, NC, USA) for repeated measures was used to statistically evaluate changes in the major dependent variable over the three different lung volumes (three levels: FRC, FRC + 500 ml, FRC + 1 litre). Dependent variables for this analysis were lung density, regional lung volume change, density‐normalized perfusion and nDNP. Where overall significance occurred, post hoc testing was conducted with Student's t‐testing. All data are presented as mean(SD) over seven subjects; the null hypothesis (no effect) was rejected for P < 0.05, two‐tailed.

Results

Demographics and metabolic data

Subject demographic data are given in Table 1. Pulmonary function data were within the normal range. Tidal volume, respiratory rate and minute ventilation while the subject was in the MR scanner (excluding breath‐holds) were 0.5(0.1) litres, 11(2) min⁻¹ and 5.0(1.0) litres min^–1, respectively. Other physiological data during breath‐holding at different lung volumes are shown in Table 3. There was no overall effect (P = 0.17) on the arterial oxygen saturation measured by pulse oximetry during the measurement conditions [FRC, 97.7(1.2)%; FRC + 500 ml, 97.9(0.5)%; FRC + 1 litre, 98.4(0.5)%]. There was a borderline effect (P = 0.06) on heart rate, although the detected difference was small, approximately 3 b.p.m. between the different lung volumes [FRC, 62(15) b.p.m.; FRC + 500 ml, 61(14) b.p.m.; FRC + 1 litre, 64(15) b.p.m.].

Table 3.

Arterial oxygen saturation ($S_{\mathrm{p}{\mathrm{O}}_2}$) and heart rate at the different levels of lung volume

	Lung volume
	FRC	FRC + 500 ml	FRC + 1 litre	Main effect
$S_{\mathrm{p}{\mathrm{O}}_2}$ (%)	97.7(1.2)	97.9(0.5)	98.4(0.5)	P = 0.17
Heart rate (b.p.m.)	62(15)	61(14)	64(15)	P = 0.06

Values are mean(SD) over seven subjects. There was a borderline effect (P = 0.06) on heart rate, although the detected difference was approximately 3 b.p.m. between the different lung volumes, and therefore unlikely to be physiologically relevant.

Lung volume

Figure 3 shows the effect of lung deformation on mean regional lung volume change within the lung region of interest in the measurement slice. FRC + 500 ml and FRC + 1 litre lung inflations showed approximately 22(9) and 37(13)% increases in mean lung volume, respectively [FRC + 500 ml, 1.22(0.09); FRC + 1 litre, 1.37(0.13)]. The two increased lung volumes were significantly greater than FRC reference volume (P < 0.0001). The mean regional lung volume at FRC + 1 litre was also significantly greater than that at FRC + 500 ml (P < 0.01).

Figure 3. Effect of lung inflation on mean regional lung volume change (V/V₀) .

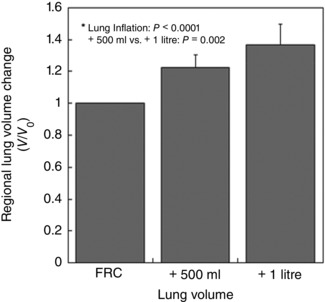
The continuous line at V/V ₀ = 1 indicates there was no net inflation or deflation of regional lung volume. FRC + 500 ml and FRC + 1 litre showed approximately 22(9) and 37(13)% increases in the mean lung volume, respectively. Both measured regional lung volumes were significantly greater than FRC (= 1: continuous line) (P < 0.0001). The mean regional lung volume at FRC + 1 litre was also greater than that at FRC + 500 ml (P < 0.01). The error bars correspond to the standard deviation over seven subjects.

Proton density

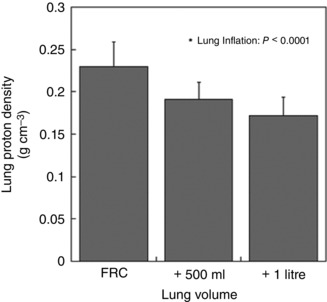
The change in mean density within the measurement slice with inflation is given in Fig. 4. As expected, mean lung density was greatest at FRC and decreased as lung volume increased [FRC, 0.23(0.03) g cm^–3; FRC + 500 ml, 0.19(0.02) g cm^–3; FRC + 1 litre, 0.17(0.02) g cm^–3; P < 0.0001]. The density at FRC + 500 ml was greater than that at FRC + 1 litre, although this was not a statistically significant difference (P = 0.11). Figure 5 shows the deformation‐corrected density, which was nearly identical between conditions [FRC, 0.23(0.03) g cm^{–3 *}; FRC + 500 ml, 0.23(0.03) g cm^{–3 *}; FRC + 1 litre, 0.24(0.03) cm^{3 *}; P = 0.86], suggesting that there was no overall change in lung water in the imaging slice with lung inflation.

Figure 4. Effect of lung deformation on mean lung density .

Mean lung density was greatest at FRC and decreased as lung volume increased (P < 0.0001). The density at FRC + 500 ml was higher than that at FRC + 1 litre, although no significant difference was found based on post hoc testing (P = 0.11). The error bars correspond to the standard deviation over seven subjects.

Figure 5. Deformation‐corrected density .

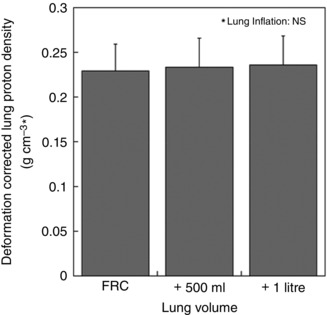
Density image at increased lung volume was corrected with the regional volume change map in order to capture the original lung density at FRC. The deformation‐corrected density is in units of g cm^{–3 *} where ^* indicates that MR voxel size, which is the denominator in the units, is corrected by the local lung deformation. Deformation‐corrected density values at different lung volumes were nearly identical (P = 0.86). The error bars correspond to the standard deviation over seven subjects.

Density‐normalized perfusion

The mean density‐normalized perfusion decreased with increased lung volume (Fig. 6), although this was of borderline statistical significance [FRC, 10.0(2.5) ml min^–1 g^–1; FRC + 500 ml, 8.4(1.5) ml min^–1 g^–1; FRC + 1 litre, 8.8(0.8) ml min^–1 g^–1; P = 0.10].

Figure 6. Effect of lung deformation on mean perfusion .

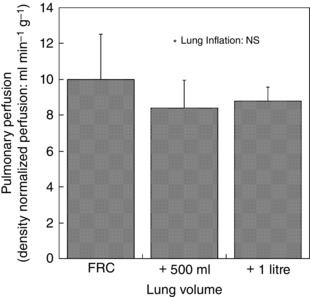
The effect of lung volume on mean density‐normalized pulmonary perfusion was not statistically significant (P = 0.10). The error bars correspond to the standard deviation over seven subjects.

Regional volume change and perfusion redistribution

Figure 7 A and B shows that the lung expands differently with respect to lobes and gravitational regions. Both types of regional data showed a strong overall significant difference (P < 0.0001). The greatest lobar expansion was seen in RLL (P = 0.0015: lower lobe vs upper lobe; P < 0.0001: lower lobe vs middle lobe), while the smallest expansion was seen in RML (P = 0.0045: upper lobe vs middle lobe). In terms of the gravitational dependency, the dependent part showed the largest expansion (P < 0.0001: dependent vs non‐dependent; P < 0.0001: dependent vs middle) while the non‐dependent part showed the smallest effect (P = 0.016: middle vs non‐dependent).

Figure 7. Lobar and gravitational dependency of regional volume change (V/V₀) .

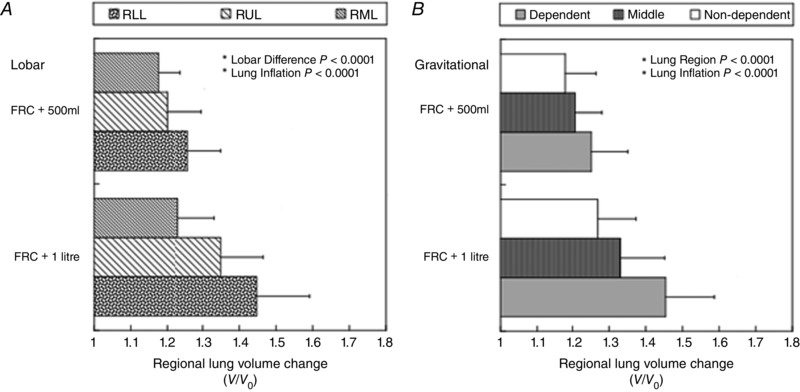
A, lobar dependency. Each lobe expanded differently with lung inflation (P < 0.0001). The right lower lobe inflated the most, while the right middle lobe inflated the least. RLL, right lower lobe; RUL, right upper lobe; RML, right middle lobe. B, gravitational dependency. The three gravitational regions (non‐dependent, middle and dependent) expanded differently with lung inflation (P < 0.0001). The non‐dependent part inflated the least, while the dependent part inflated the most. The error bars correspond to the standard deviation over seven subjects.

The redistribution of perfusion among three lobes and three gravitational regions measured by the difference between nDNP maps at the inflated lung volume and at FRC is given in Fig. 8 A and B. The nDNP redistribution data showed there was no overall significant difference in lobar nDNP redistribution (P < 0.89) with lung inflation. The gravitational nDNP redistribution data showed that there was a decrease in the gravitationally non‐dependent [+500 ml: −0.075(0.152), +1.0 litre: −0.137(0.167)] and an increase in the gravitational middle part of the lung (+500 ml: 0.098(0.058), +1.0 litre: 0.093(0.081)] with lung inflation; these differences were both statistically significant (P < 0.05) based on the post hoc testing. However, there was no statistically significant difference between +500 ml inflation and +1.0 litre inflation.

Figure 8. Lobar and gravitational redistribution of pulmonary perfusion due to lung inflation measured by nDNP change from FRC .

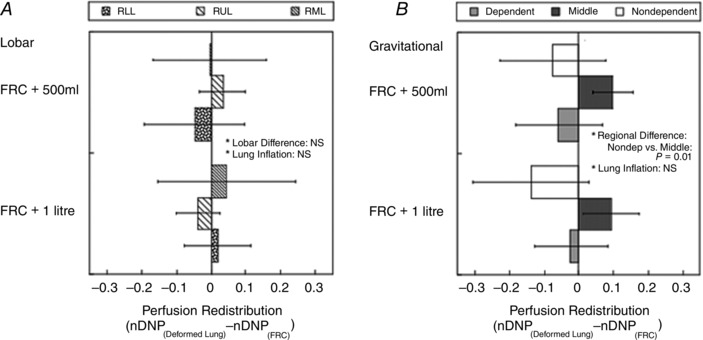
The difference between two nDNP (dimensionless quality) maps at different lung volumes reflects the perfusion redistribution without the influence of any overall mean blood flow change such as from a change in cardiac output. A, lobar redistribution. There was no overall significant difference in lobar nDNP redistribution (P = 0.89), despite the fact that each lobe expanded differently as shown in Fig. 7 A. RLL, right lower lobe; RUL, right upper lobe; RML, right middle lobe. B, gravitational redistribution. nDNP decreased in the non‐dependent and increased in the middle region of the lung with lung inflation and these differences were statistically significant (P = 0.01). The error bars correspond to the standard deviation over seven subjects.

Figure 9 shows the overall relationship between regional lung volume change and nDNP redistribution at FRC + 1 litre lung inflation at the smallest resolution of measurement (3.8 cm³) within the measurement slice for all seven subjects. The average correlation coefficient of these relationships over the seven subjects was FRC + 500 ml: 0.03(0.19) and FRC + 1.0 litre: −0.01(0.18), which was not significantly different from zero in any subject (P = 0.88). Moreover, the average slopes of these relationships over seven subjects were FRC + 500 ml = 0.08(0.54) and FRC + 1 litre = −0.06(0.32), which were also not significantly different from zero (P = 0.73).

Figure 9. The relationship between regional volume change (V/V₀) at +1 litre lung inflation and redistribution of pulmonary perfusion measured as the nDNP difference from FRC at a spatial scale of 10 × 10 voxels, 3.8 cm³ .

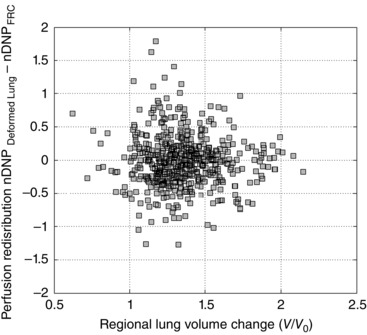
The 95th and 5th percentile cutoff was not applied to this data set. Data are from all seven subjects combined. The average slope of these relationships over the seven subjects was FRC + 1.0 litre: −0.06(0.32), which was not significantly different from zero (P = 0.73).

Finally, nDNP redistributions within the smallest 5th and largest 5th percentiles of lung inflation (data points eliminated from Figs 3, 4, 5, 6, 7, 8) were compared to demonstrate the change in lung perfusion in two extremes: FRC + 500 ml: smallest 5th percentile: −0.031(0.193) vs largest 5th percentile: 0.043(0.128) and FRC + 1.0 litre: smallest 5th percentile: 0.053(0.113) vs largest 5th percentile: −0.030(0.150) (smallest 5th percentile vs. largest 5th percentile, P = 0.95). Thus, there was no statistically significant difference between two lung inflation extremes.

Discussion

The main focus of this study was to evaluate whether local lung inflation caused by an inspiratory volume reflective of that occurring during tidal volume breathing affects regional lung perfusion on a lobar scale. The results show that lung inflation did not cause a significant change in the total amount of perfusion into the slice (Fig. 6). There was no evidence of recruitment of perfusion to regions with the greatest deformation (i.e. the gravitationally dependent and right lower lobar regions, as shown in Fig. 8). Despite differences in local lobar inflation, there was no lobar redistribution in pulmonary perfusion (Fig. 8 A) and no evidence for redistribution at a smaller spatial scale of ∼3.8 cm³. There was redistribution of flow with respect to gravity whereby perfusion decreased in the gravitationally non‐dependent region, while it was increased in the gravitational middle part of the lung (Fig. 8 B).

Zone model‐type effects

Our data suggest that tidal volume‐sized lung inflation alters the distribution of pulmonary perfusion across gravitational regions, but not between lobar boundaries, consistent with hydrostatic zone model‐type effects. The lower lobe and the dependent region, the upper lobe and the middle region, and the middle lobe and the non‐dependent region showed similar regional lung volume changes, respectively (Fig. 7 A and B). The gravitational dependency in the regional lung volume change found in the present study (Fig. 7 B) was consistent with previous findings (Hopkins et al. 2007; Prisk et al. 2007). Moreover, previous reports of lobar dependency of regional lung volume change in the supine right lung have shown that the RLL and the RML experience the largest and smallest lung volume change, respectively, with FRC to TLC lung expansion (Amelon et al. 2011; Choi et al. 2013). This is also consistent with the result of present study (Fig. 7 A).

Despite the similarity in the magnitude of gravitational and lobar lung expansions shown in Fig. 7, the redistribution of perfusion occurred differently based on the different lung segmentations. As measured by nDNP, redistribution only occurred away from the gravitationally non‐dependent region despite the fact that the non‐dependent region and the RML experienced almost the same extent of tissue deformation [FRC + 500 ml: +17.5(6.3)% vs +17.9(8.5)%, FRC + 1 litre: +23.2(9.69)% vs +26.9(10.4)%]. Therefore, these data suggest that physiological levels of lung inflation are not a primary cause of change in vascular resistance, determining the spatial distribution of pulmonary perfusion. Our data suggest that the redistribution of blood flow may be a result of changes in the hydrostatic pressure distribution in the gravitational direction as predicted by the zone model (West et al. 1964). The change in perfusion per height change becomes more pronounced with lung inflation above tidal volume. The marked reduction of pulmonary perfusion in the gravitationally non‐dependent part of the lung was previously demonstrated with total lung capacity inflation (Hughes et al. 1968; Hopkins et al. 2010). This reduction could be explained by an increase in zone 2 regions (where alveolar pressure exceeds pulmonary venous/venule pressure and the greater difference in perfusion), resulting from the increase in the anterior–posterior distance with inflation. This increases the vertical height of the lung and is expected to reduce the hydrostatic pressure in pulmonary blood vessels mainly in the non‐dependent lung. Therefore, some regions of zone 3 are converted into zone 2 regions.

Transmural pressure distribution

In addition to the changes in the hydrostatic pressure, the effects of lung inflation on transmural pressure distribution may also have an effect. Kira & Hukushima (1968) demonstrated that when the vascular transmural pressure was approximately 5 cmH₂O, a low‐pressure condition, the pulmonary vasculature resistance increased as the lung stretched. However, when the vascular pressure was high (11 cmH₂O), the transmural pressure in small vessels remained high and the vasculature cross‐sectional area remained large. Therefore, in the high transmural pressure condition, the reduction in vasculature cross‐sectional area due to axial stretch was a lesser influence and the vasculature resistance was virtually unchanged (Kira & Hukushima, 1968). Pulmonary vessels with low transmural pressures are predominantly located in the gravitationally non‐dependent region, while the high transmural vessels are located in the gravitationally dependent region of the lung. Therefore, the non‐dependent part of the lung may be more prone to a reduction in perfusion caused by lung expansion than the dependent part of the lung, highlighting its vulnerability. Consistent with this, Hopkins et al. (2010) showed that pulmonary perfusion in the non‐dependent region of the lung was significantly reduced with lung inflation to total lung capacity compared to FRC. Our data from the present study suggest that this reduction in perfusion in the non‐dependent lung occurs even with a tidal volume breath.

Local pulmonary vascular resistance

Lung deformation also has the potential to affect regional pulmonary blood via changes in local vascular resistance. Pulmonary vasculature geometry is thought to be closely associated with pulmonary circulation mechanics, owing to the distensibility of pulmonary vessel walls (Fung & Sobin, 1972 a,b; Yen et al. 1980; Yen & Foppiano, 1981; Fung et al. 1983) and to linkage of vascular driving pressures to hydrostatic pressure gradients in the lung (West et al. 1964). Differing influences of inflation on local pulmonary vascular resistance have been reported: Burton & Patel (1958) have shown that pulmonary vascular resistance monotonically decreased as the lung expands. However, Thomas et al. (1961) showed a decrease in pulmonary resistance compared to the completely collapsed lung with moderate inflation (corresponding to a pneumothorax lung and FRC, respectively). They also found the increase in the resistance on further inflation, giving a ‘U‐shaped’ change in vascular resistance with lung inflation.

The effect of lung inflation is also expected to have differing effects on vascular resistance depending on the size of the pulmonary vessels. If the classic pulmonary circulation model known as the forth power and fifth power laws (Fung & Sobin, 1972 a,b) of vascular geometry plays a major role in regulating pulmonary perfusion in the inflated lung, it is expected that radial distention would decrease pulmonary vasculature resistance by a power of four in pulmonary capillary and a power of five in pulmonary arteries and veins, resulting in an increase in blood flow, whereas axial distension would increase the resistance and decrease the flow linearly. In this study, however, neither an increase nor a decrease in perfusion was clearly seen. Although our data showed that the mean density‐normalized perfusion decreased with increased lung volume from FRC, this was of borderline statistical significance (P = 0.10). That implies either the changes in the pulmonary vessel size did not occur to a great extent or the net change in perfusion was neutralized as the two conflicting effects occurred in different levels of the pulmonary vascular tree. Howell et al. (1961) demonstrated that the different sizes of pulmonary vasculatures responded differently to lung inflation in excised dog lungs: large vessels, which are embedded within and tethered to the interstitium of the lung, were expanded with lung inflation while smaller vessels in close association with alveoli were compressed. A similar effect was also reported by Lai‐Fook (1979) in which the vessel diameters of both pulmonary arteries and veins were small at FRC and increased with lung inflation in excised dog lower lobes at any vascular pressure inside. However, note that those findings were based on positive pressure lung inflation, whereas the normal spontaneous breathing is negative pressure lung inflation.

Positive and negative lung inflation schemes are expected to affect the pulmonary vasculature resistance differently. Especially in small vessels, the transmural pressure (pulmonary blood pressure minus alveolar pressure) determines pulmonary vessel resistance via the change in vessel diameter. As positive inflation elevates the alveolar pressure, it decreases transmural pressure throughout the lung and thus increases the vessel resistance. By contrast, the transmural pressure is expected to remain the same with negative inflation. Therefore, lung geometry and structure‐related changes in pulmonary vasculature resistance are similar in both positive and negative inflations, while transmural pressure‐related changes are different between the two lung inflation schemes. Overall the above information suggests that with lung inflation, vascular resistance in large vessels decreases while that in the small vessels increases. This is also consistent with our data, which showed no overall increase in perfusion with lung inflation, suggesting that neither of the two opposing effects predominated such that the overall perfusion was not significantly changed.

Figure 5 showed the deformation‐corrected density at three lung volumes (density map × regional lung volume change map for that lung volume) was identical for all three levels, suggesting that the local lung water content and the local blood volume did not change with a tidal volume inflation. This is consistent with the perfusion data, suggesting that overall vascular resistance did not change, probably owing to the way that the opposing forces described above act on the lung.

95th and 5th percentile cutoff

Extremes in regional lung volume change were eliminated from the data analysis shown in Figs 3, 4, 5, 6, 7, 8, and our reasons for doing so was that there was a high likelihood that these represented spurious values. The reason for this is that (1) local lung deflation might not be distinguishable from algorithmic error inherent in the deformable image registration and (2) large‐scale local volume change causes the alignment error between multiple images at different lung volumes. However, one potential criticism is that these exclusion criteria could have driven the conclusions reported here. One could also argue that if these regions were real, then evidence of lung inflation‐induced perfusion redistribution could be found by comparing the perfusion changes in these two extreme regions alone. However, there was no statistically significant difference in nDNP difference between two lung inflation extremes (smallest 5th percentile vs. largest 5th percentile, P = 0.95), and when these extremes were included in the entire dataset the results were nearly identical. Thus, it is highly unlikely that excluding these extremes biased our results towards negative findings.

Study limitations

The experimental design of this study was limited by the image acquisition, which requires a breath‐hold for 15 s after inhalation of a predetermined volume of air with open glottis. Inspiratory breath‐holding with an open glottis perturbs pulmonary perfusion via a change in transpulmonary pressure and sympathetic nerve activities (Macefield, 1998; Taneja et al. 2010). Inspiration increases the right atrial filling via reduced intrapleural pressure, resulting in a brief increase in mean arterial pressure and heart rate. When the inspiration is completed, it is immediately followed by the suppression of sympathetic activity via the pulmonary stretch reflex (Looga, 1997), which causes bradycardia and reduction in mean arterial pressure. This reduction in the cardiac performance with inspiratory breath‐holding has been commonly reported in supine (Sakuma et al. 2001; Taneja et al. 2010) and upright (Ferrigno et al. 1986) postures. Because of the nature of breath‐hold, this study did not simulate the dynamic aspect of normal spontaneous breathing. However, this study was able to replicate a quasi‐static tidal volume lung inflation achieved by negative pressure lung inflation.

Another limitation related to breathing is the subject's posture; humans spend most of their active lives upright and not supine. In the upright posture, compared to supine, more regions of the lung are above the heart (Friedman et al. 1986), and Glenny et al. (1999) demonstrated in baboon lungs that the gravitational dependency of perfusion distribution was more pronounced in upright posture than supine. Lung inflation increases the vertical dimension of the upright lung as the diaphragm displaces inferiorly, and because the heart rests on the central tendon of the diaphragm it is also displaced inferiorly during inspiration (Reynolds, 1877). This will affect the hydrostatic pressure gradients in the lung to the extent that the pulmonary arteries are also displaced inferiorly. In the supine posture, the change in the relative height difference between the heart and the most non‐dependent part of the lung is smaller with lung inflation. For these reasons we expect that there may well be a greater effect on of lung inflation on regional perfusion distribution in upright posture compared to supine.

The present study was performed in a single 15 mm slice in the sagittal plane, denoted as ‘measurement slice’ in the right lung. Even though multiple sagittal images at different lateral slice locations were obtained in 5 mm slice overlapping interleaves, these extra image slices were only utilized to estimate the through‐plane deformation of the measurement slice at different lung volumes. It should also be noted that the number of acquired slice locations for ASL‐based perfusion–vascular structure images at FRC was nine whereas that at two inflated lungs was five. The number of slices was adequate to estimate the ‐lane displacement of the measurement slice as the slice did not move more than 1 cm laterally (i.e. left–right direction) with inflation. Because this measurement image plane highlights the gravitationally dependent distribution of lung tissue (Theilmann et al. 2009) and specific ventilation (Sá et al. 2010), it is suitable for testing the effects of lung tissue stretch on the distribution of pulmonary perfusion. Nonetheless, the imaging slice does not necessarily represent the whole right lung. The lung region of interest for this study was approximately 150 ml, which encompasses approximately 6% of the lung. In addition the image acquisition for ASL‐FAIRER is also limited to a single image slice at a time. For this reason the measured ASL perfusion images for different image planes were not obtained simultaneously. Therefore, it should be noted that deformation‐corrected images at the different lung volumes contain perfusion information, which is spatially and temporally interpolated between two adjacent slices at any given spatial locations.

In lung deformation analysis using the deformable image registration technique, the accuracies in displacement field and its gradient fields have to be taken into consideration in both in‐plane and through‐plane directions. The accuracy in calculating the displacement field is crucial for the anatomical comparison of the perfusion distribution at the different lung volumes. Alignments between all reference and warped image pairs were visually inspected. Since the in‐plane resolution of pulmonary perfusion was reduced to approximately 1 cm using a Gaussian low‐pass filter in this study, the in‐plane displacement error is expected to be much smaller than the measurement scale and thus negligible. As through‐plane resolution of ASL‐FAIRER measurement was 1.5 cm and adjacent sagittal slices overlapped by 1.0 cm, the displacement error should be also negligible compared to the measurement scale.

In this study we attempted to precisely control the extent of lung inflation by having the subject inspire a predetermined volume out of a Mylar bag. Further expansion of the chest against the empty bag has the potential to further decrease intrathoracic pressure and increase the lung volume, resulting in a greater volume change than 500 ml or 1 litre. However, this is unlikely as any failure and inconsistency in breath‐holding were monitored by checking chest wall and diaphragm movement in the acquired MR images and evaluating the presence of expiratory flow detected using the metabolic measurement system at the end of the expiratory outlet.

Finally, it is important to point out that the main findings from the present study refer to a spatial scale of lobar and gravitational third segments. The choice of this spatial scale is because the errors associated with registration of two types of MR images as well as deformable image registration are negligible at this scale. In addition, our data at a smaller spatial scale (3.8 cm³) support the same conclusion, although it must be interpreted with some caution because of the registration and smoothing steps necessary. Also, because of these steps, not all the segments at this spatial scale contain the same number of voxels from the original ASL images due to partial voluming from edge effects and removal of large conduit vessels.

Figure 9 shows the relationship between nDNP redistribution and regional lung volume change obtained at the spatial scale of 10 × 10 voxels, 3.8 cm³ from all seven subjects. Two types of information can be extracted from this analysis; the slope and the correlation coefficient. There was no correlation between regional lung volume change and the redistribution of nDNP at this level of spatial resolution and different levels of lung inflation. The overall slopes were not different from zero. Note that the lung inflation‐induced perfusion redistribution was not evident at the level of resolution enabled by this study. However, perfusion redistribution at a smaller spatial scale than 3.8 cm³ cannot be excluded from these data.

Conclusion

Pulmonary perfusion measurement using ASL‐FAIRER combined with deformable image registration enabled the quantification of the change in the spatial distribution of pulmonary perfusion at different lung volumes. The current study elucidated the effects of tidal volume lung inflation on the change in pulmonary perfusion distribution.

Although there was a tendency for tidal volume lung inflation to reduce overall pulmonary perfusion, the change was not statistically significant. Pulmonary perfusion was redistributed from the non‐dependent part of the lung into the gravitational middle of the lung, although there was no evidence of lobar redistribution. In conclusion, the regional changes in perfusion caused by tidal volume lung inflation were probably not caused by changes in the local perfusion resistance. Changes in hydrostatic pressure distribution as well as transmural pressure distribution due to the change in lung height with lung inflation are probably greater contributors to the pulmonary perfusion redistribution than the changes in pulmonary vasculature resistance due to changes in lung tissue stretch. We originally hypothesized that perfusion is recruited to regions receiving the greatest deformation from a tidal breath, ensuring ventilation–perfusion matching on a gross scale. However, the perfusion redistribution induced solely by lung inflation was not evident in the present study. Thus, a change in lung volume at a lobar scale does not play a direct contributing role in matching regional ventilation to perfusion.

Additional information

Competing interests

None declared.

Author contributions

T.J.A., R.J.T., R.C.S., M.T.V. and S.R.H. designed the study. T.J.A., R.J.T. and R.C.S. developed the image registration methodology. T.J.A., R.J.T., R.C.S. and M.T.V. collected the data and T.J.A., and M.T.V. performed the data analysis under the supervision of S.R.H., R.C.S. and R.J.T. T.J.A. and S.R.H. wrote the manuscript with input from R.C.S., R.J.T. and M.T.V.

Funding

This work was supported by the National Institutes of Health through grant, 1HL122753.