Optimization of b-Value Sampling for Diffusion-Weighted Imaging of the Kidney

Abstract

Diffusion-weighted imaging (DWI) involves data acquisitions at multiple b values. In this paper, we presented a method of selecting the b values that maximize estimation precision of the biexponential analysis of renal DWI data. We developed an error propagation factor for the biexponential model, and proposed to optimize the b-value samplings by minimizing the error propagation factor. A prospective study of four healthy human subjects (eight kidneys) was done to verify the feasibility of the proposed protocol and to assess the validity of predicted precision for DWI measures, followed by Monte Carlo simulations of DWI signals based on acquired data from renal lesions of 16 subjects. In healthy subjects, the proposed methods improved precision (P = 0.003) and accuracy (P < 0.001) significantly in region-of-interest based biexponential analysis. In Monte Carlo simulation of renal lesions, the b-sampling optimization lowered estimation error by at least 20–30% compared with uniformly distributed b values, and improved the differentiation between malignant and benign lesions significantly. In conclusion, the proposed method has the potential of maximizing the precision and accuracy of the biexponential analysis of renal DWI.

Diffusion-weighted magnetic resonance imaging (DWI) appears promising for the functional assessment of kidneys (1–3) and for the detection and characterization of renal lesions (4–7). An important part of the DWI acquisition protocol is the choice of diffusion encoding (b values), which for constant echo times controls the intensity of the bipolar gradient pulse and thus the degree of diffusion weighting in the acquired signal (8,9). Abdominal DWI is usually performed with a small number of b values, mostly because of time limitations related to the desire to image in a breathhold.

In tissues with strong microcirculatory flow such as the kidney, there are a least two major contributing factors to DWI signal decay—a fast (conventionally termed as pseudodiffusion) component and a slow (diffusion) component (10–14). Reflecting these two contributions, Wittsack et al. (15) found that a biexponential model described renal DWI data better than a monoexponential model. Additionally, Zhang et al. (16) showed that the use of biexponential model significantly reduces the variability of diffusion coefficients in healthy kidneys compared to use of a monoexponential model. However, precise computation of the fast component of the biexponential model remains a challenging task (13,17–21).

One of the key issues is the selection of proper b values to provide maximum precision of diffusion parameters. It has been recognized that uniformly distributed b-sampling is not optimal for estimating the biexponential model. For example, to better estimate the fast component, Eisenberger et al. (12) sampled more low b values, using b-sampling of 0, 10, 20, 50, 100, 180, 300, 420, 550, 700 s/mm². Quantitative optimization for b-value sampling, based on the minimization of an error propagation factor, has been explored for monoexponential analysis in the brain (22–24), but the same methodology has rarely been extended to biexponential model or to abdominal imaging subject to breath-hold limitations.

We present a method for optimizing b-value sampling for biexponential analysis of DWI data. Our approach is to minimize analytically derived error propagation. We hypothesized that DWI acquired at optimal b-value sampling significantly improves parameter precision and accuracy that is achieved by nonoptimized sampling, e.g., uniformly distributed b-sampling. To test the claim, DWI magnetic resonance imaging (MRI) of healthy volunteers was acquired at optimal and uniformly distributed b-value settings, and the precisions of the resulted parameter estimates were compared. As DWI has been recognized as a promising tool for characterizing renal masses, we also performed Monte Carlo simulations to assess the benefit of the optimal b values in differentiating malignant and benign renal lesions.

THEORY

The biexponential model for DWI data can be written as

$$S=S_0·[(1-F_{\mathrm{P}})·exp(-b·D_{\mathrm{T}})+F_{\mathrm{P}}·exp(-b·D_{\mathrm{P}})],$$ [1]

where S is the DWI signal, S₀ corresponds to signal intensity at b = 0, F_P is the fraction of the perfusion component, D_T is the diffusion coefficient, and D_P is the pseudodiffusion coefficient due to microcirculation effects. As F_P relates to vascular volume fraction and D_P typically is proportional to vascular velocity, their product, F_P × D_P, could potentially reflect the perfusion rate (25).

Given DWI measurements, the biexponential parameters, F_P, D_P, D_T, can be determined by minimizing the sum of squared residue between the data and the model fit,

$$R(S_0,F_{\mathrm{P}},D_{\mathrm{P}},D_{\mathrm{T}})=\sum _{i=1}^{N_{\mathrm{b}}}{[S(b_i;S_0,F_{\mathrm{P}},D_{\mathrm{P}},D_{\mathrm{T}})-S_{{\mathrm{b}}_i}]}^2$$ [2]

where N_b is the overall number of signal acquisitions and S_bi is the measured signal (with noise) at b_i.

In the process of model fitting, random noise in the DWI signal, δ, propagates into the estimates of the model parameters. We define an error propagation factor ξ as the ratio of the relative error in a model parameter to the relative input noise δ/S₀. These factors can be estimated by computing the partial derivatives (Jacobian matrix) of function S(F_P, D_P, D_T) in Eq. 2:

$$\mathrm{\xi }(n)=\frac{\mathrm{\delta }x(n)/x(n)}{\mathrm{\delta }/S_0}=\frac{S_0}{x(n)}\sqrt{\sum _{m=1}^4\sum _{p=1}^4\left[A^{-1}(n,m)·A^{-1}(n,p)·\sum _{i=1}^{N_b}\left(\frac{\partial S(b_i,x)}{\partial x(m)}·\frac{\partial S(b_i,x)}{\partial x(p)}\right)\right]},$$ [3]

In Eq. 3, x(n) (n = 1,2,3,4) represent the parameters: S₀, F_P, D_P, and D_T, δx denotes the propagated parameter error, the 4 × 4 matrix A=J^T·J, and J is Jacobian matrix of S. The derivation of partial derivative terms is shown in the Appendix.

Given a set of biexponential parameters and a set of b values, Eq. 3 allows us to predict the error propagation factor for each of the model parameters. As the expression for ξ(n) given in Eq. 3 is a function of N_b b values used for data acquisition, the b values can next be adjusted to minimize ξ(n). Any of numerical optimization techniques, (26) including the well known Levenberg method (27), can be used to solve this problem.

In clinical MRI applications, the multiple types of tissue in an image, each having a range of values for every model parameter, are imaged by the same set of b values. Hence, it is important that the selected b values minimize the error propagation over the expected ranges of parameter values for at least those types of tissue, we are interested in. Moreover, we are typically interested in using several parameters to differentiate tissue types, possibly weighted by their clinical significance. This leads to the following generalization of the problem, in which the expression for ξ(n) is replaced by the integration and linear combination of the cost function introduced:

$$\overline{\mathrm{\xi }}=\underset{D_{\mathrm{T}}^{min}}{\overset{D_{\mathrm{T}}^{max}}{\int }}\underset{D_{\mathrm{P}}^{min}}{\overset{D_{\mathrm{P}}^{max}}{\int }}\underset{F_{\mathrm{P}}^{min}}{\overset{F_{\mathrm{P}}^{max}}{\int }}(w_{F_{\mathrm{P}}}{\mathrm{\xi }}_{F_{\mathrm{P}}}+w_{D_{\mathrm{P}}}{\mathrm{\xi }}_{D_{\mathrm{P}}}+w_{D_{\mathrm{T}}}{\mathrm{\xi }}_{D_{\mathrm{T}}})\times \mathrm{d}{F}_{\mathrm{P}}\mathrm{d}{D}_{\mathrm{P}}\mathrm{d}{D}_{\mathrm{T}}.$$ [4]

In Eq. 4, w_FP, w_DP, and w_DT are positive weighting factors specified by user and X^min to X^max reflect the expected range of values for parameter X of the tissues examined. For any given clinical question, the parameter ranges can be estimated from a group of human subject data.

As the implementation of the b-value optimization requires knowledge of the typical ranges of the parameters (Eq. 4), we used data from one previous study of healthy kidneys (16): F_P [30%, 35%], D_T [1.5, 2.0] × 10⁻³ mm²/s, D_P [10, 15] × 10⁻³ mm²/s. For the optimization, the upper bound was set at b = 750 s/mm² (the maximal b value in our data below). The integration in Eq. 4 was done numerically and its minimization with regard to the b values used Levenberg’s method in MAT-LAB (Mathworks, Natick, MA). Separate optimizations were done for N_b = 4, 6, 8, 10. Using our DWI protocol described below, a scan with N_b of 4~10 can be finished with 1~2 breath holds.

MATERIALS AND METHODS

We describe a prospective study of human subjects done to verify the feasibility of the proposed protocol and to assess the validity of predicted precision for DWI measures, followed by Monte Carlo simulations of renal lesions.

Human Subject Validation

Following written consent, and according to our institutional review board-approved and health insurance portability and accountability act (HIPAA)-compatible protocol, abdominal DWI MRI was acquired on four volunteers without a history of renal disease. Data were acquired on 3T TIM Trio (Siemens, Siemens Medical Solutions, Erlangen, Germany), using single-shot echo planar free-breathing DWI sequence: coronal slice thickness 6 mm, field of view 345 × 410 mm, acquisition matrix 162 × 192, repetition time 2000 ms, echo time 80 ms, three diffusion directions, parallel imaging factor 2, and b values, from 0 to 750 at intervals of 50 s/mm² and with nine repetitions. The large dataset enabled easy sampling using different schemes (optimal or uniformly distributed) for comparison, and fitted as a whole, provided reference parameter values for such comparisons. During the scan (~14 min), the subject was asked to breathe shallowly. To correct for any in-plane translational motion artifact, the acquired DWI images were cropped and coregistered for each individual kidney using a normalized cross-correlation method (28).

For region-of-interest (ROI) analysis, cortical and medullary ROIs were delineated manually at lower, middle and upper poles in a middle coronal slice of diffusion data for each kidney. Coronal T₂-weighted half Fourier acquisition single shot turbo spin echo (HASTE) and T₁-weighted fast low angle shot (FLASH) images showing good corticomedullary differentiation were used to assist the manual segmentation of the diffusion images. Each ROI included ~30–50 voxels. Merging the three ROIs of a same tissue type in each kidney, we generated a signal versus b curve, a “full signal” curve, which contained 144 data points (16 b values and nine repetitions). Biexponential model fitting of the full-signal curve resulted in the reference values for the parameters.

The full-signal curve was desampled at N_b optimal b values (N_b = 4, 6, 8, 10) and again at uniformly distributed b values of the same N_b. All the sampled b values were rounded to the nearest b values available in the measured data (with interval of 50 s/mm²). From the full-signal curve, we obtained multiple independent “samples” of signal versus b curve for each b-sampling scheme (either optimal or uniformly distributed ones). For example, for a b-value set [0, 50, 250, 250, 250, 750] that contains three repetitions for at least one b value, three independent samples can be obtained from the full-signal curve. Availability of multiple independent samples enabled the assessment of parameter estimates’ precision and accuracy. Note that in full-signal curve, different numbers of independent “samples” can be available for optimal and uniformly distributed b-samplings of a same N_b, but we kept the “samples” numbers of the two sampling schemes the same for fair comparison. For each “sample” of signal versus b curve, biexponential model fitting was applied. With parameter estimates from all available “samples” of signal versus b curve for each kidney, the coefficient of variation (CV) and the relative deviation (RD) were calculated. For a given b-sampling scheme, CV indicates the precision and RD the accuracy of the parameter, and due to statistical error, are supposed to vary across different kidneys. Using analysis of variance (ANOVA), we evaluated if the optimized b-sampling improved precision and accuracy of the parameters when compared with uniformly distributed b values.

Parametric mapping with biexponential model was done for one kidney to confirm the benefit of b-value optimization on pixel scale. From the “full-signal” diffusion weighted images (16 b values and nine repetitions), we sampled two subsets of images: images acquired at 10 optimal b values and those at 10 uniformly distributed b values. For each subset and the full-signal data, voxelwise biexponential model fitting was computed, and for each parameter, the resulting maps were saved for visualization.

Simulations

We applied computer simulations to assess the potential benefits of b-value optimization procedure for differentiation between benign and malignant renal lesions. To calculate the optimal b values for renal lesions, we used data from a previous patient study (29), in which breathhold DWI using b values of 0, 50, 100, 150, 250, 400, 600 and 800 s/mm² was performed for 16 subjects (8 benign and 10 malignant lesions detected). The parameter ranges were estimated from the study. The optimization of b values was performed for N_b = 4, 6, 8, 10 and with the upper-bound b value at 800 s/mm².

The first simulation aimed to evaluate the precision improvement due to the optimal b values across the parameter ranges. With the fitted biexponential parameter values for each of the 18 renal masses, we generated a ‘continuous’ signal versus b curve. Each curve was then desampled in one of two ways: (1) at the optimized b values and (2) at uniformly distributed b values. Rician noise with standard deviation (SD) of 0.01S₀ was added to the desampled curves. This noise level is equivalent to that of a ROI of 30–50 voxels when the signal-to-noise ratio (SNR) of each voxel is 15–20. As the next step, the desampled curve with noise was fitted by the biexponential model to obtain parameter estimates. For each scenario, that is, for each lesion and each b-sampling, the procedure of noise addition and model fitting was repeated n_trials = 1000 times, which was sufficient for ±3% accuracy. The SD of the n_trials estimates for each scenario provides the estimation error for a b-value sampling scheme in determining the biexponential parameter value for each of the 18 lesions. The average of the SD across the 18 lesions indicates the overall performance of that b-value sampling scheme in estimating one parameter across its typical range for renal lesions. We hypothesized that the use of optimized b values would result in smaller averaged SD values than uniformly distributed b values of the same N_b.

The second simulation aimed to predict the benefit of the optimal b values in differentiating benign and malignant renal lesions. The fitted values for each biexponential parameter were averaged separately for the eight benign and for the 10 malignant renal masses. With the averaged parameter values, we generated signal versus b curves for the “ideal,” i.e., noise-free, benign, and malignant lesions. The same procedure of b-value desampling, noise addition and model fitting as in the first simulation were performed. For each b-value sampling, the n_trials estimates of a parameter (F_P, D_P, or D_T) for benign lesions and those for malignant lesions might overlap due to their respective estimation errors. To quantify such overlap, we estimated the effect size, which was computed as the difference between the mean values divided by the pooled SD across all Monte Carlo trials (30). Larger effect size corresponds to less overlap or higher degrees of differentiation. We hypothesized that the use of optimal b values would enable better differentiation between benign and malignant lesions than uniformly distributed b values.

RESULTS

Human Subject Validation

Table 1 lists the results of b-sampling optimization for renal imaging, using parameter ranges from healthy subjects (16). For this optimization, equal weights were assigned to each parameter in the calculation of error propagation. Our results show that, in each case, the optimal b values were drawn from four distinct values. As N_b increased, the error propagation ξ decreased. For each N_b, the error propagation ξ was smaller for the optimized b values than for the uniformly distributed b values. However, the difference between optimal and uniform b values diminished with increasing N_b. For 10 b values, optimal sampling reduced error propagation by 26%, from 12.7 to 9.4, compared to uniform sampling, whereas for four b values, optimal sampling reduced error propagation by 73%, from 58.2 to 15.6. We also looked at error propagation to each individual parameter for the optimized b-value sets. Generally, D_T showed the smallest (and D_P the largest) error propagation factors for a given optimized b-value set, consistent with the CV values shown in Fig. 1 and with the expected relative uncertainties in determining biexponential fit parameters.

Table 1.

Optimal b Values for Healthy Kidneys

Nb	b1 (s/mm2)	b2 (s/mm2)	b3 (s/mm2)	b4 (s/mm2)	Averaged ξ of optimal b	Averaged ξ of uniform b
4	0	52	268	750	15.6	58.2
6	0	59	2 × 286	2 × 750	12.3	20.7
8	0	2 × 60	3 × 271	2 × 750	10.5	15.0
10	0	3 × 60	3 × 272	3 × 750	9.4	12.7

The parameter ranges for b optimization were (16): F_P [30%, 35%], D_T [1.5, 2.0] × 10⁻³ mm²/s, D_P [10, 15] × 10⁻³ mm²/s. “Averaged ξ” represents the mean value of “the average error propagation factors for F_P, D_P, and D_T” across the parameter ranges.

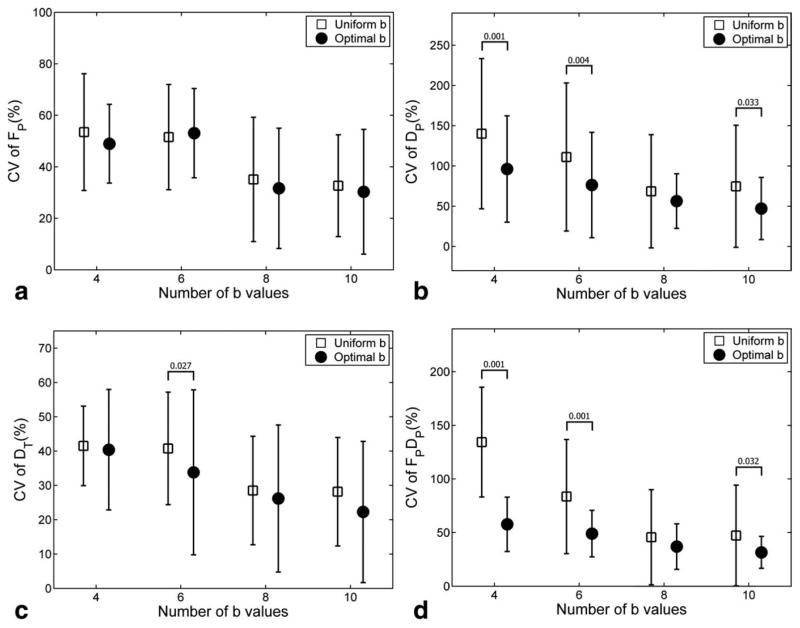
FIG. 1.

Coefficient of variation (CV) of the biexponential parameters for healthy kidneys. The error bars represent the average ± SD of the CV values across all ROIs. Significant improvement (P < 0.05) of optimized versus conventional protocol are shown with their P values.

The use of the optimal b-sampling significantly improved the precision of biexponential model estimation, compared with uniformly distributed b-sampling (analysis of variance, P = 0.003). Figure 1 plots the coefficients of variation (CV) of the parameters, averaged across all ROIs. For parameters D_P and F_P × D_P, and for N_b=4, 6, 10, the CV values obtained using the optimal b-sampling were significantly lower (P < 0.05) than those of uniformly distributed b-sampling. For other scenarios, no statistical significance was detected.

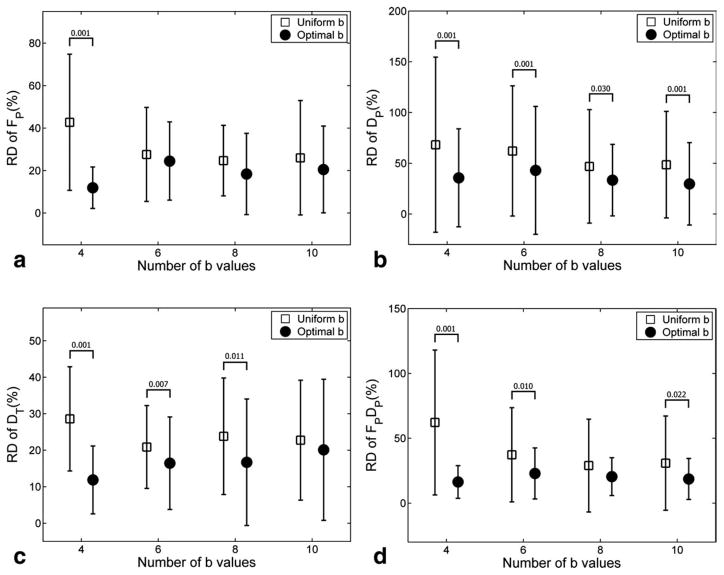
The optimal b-sampling improved the accuracy of biexponential model estimation significantly (ANOVA, P < 0.001). The RD of the parameter estimates, averaged across all ROIs, are depicted in Fig. 2. For all the four parameters, the four optimal b values provided significantly lower RD, or higher accuracy, than the four uniformly distributed b values (P < 0.001). The advantage of the optimal b values diminished with increased N_b. For parameters D_P, F_P × D_P and D_T, the optimal b significantly lowered RD as compared with uniformly distributed b in three out of four scenarios.

FIG. 2.

Relative deviation (RD) of the biexponential DWI parameters for volunteer data. The error bars represent the average ± SD of the RD values across all ROIs. P values smaller than 0.05 are shown above the error-bars.

Voxel-based parametric maps shown in Fig. 3 illustrate the improvements due to optimal b values. A smoother texture and better agreement with renal anatomy (depiction of cortex) can be observed for all parameters, especially for D_P and F_P × D_P.

FIG. 3.

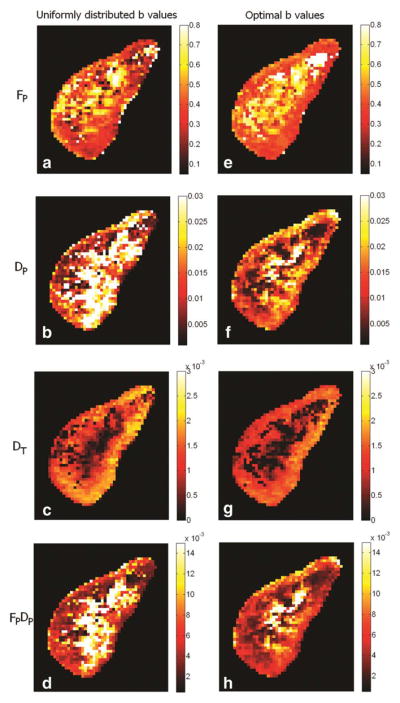
Biexponential parametric maps for a healthy kidney. Subplots (a–d): F_P, D_P, D_T, F_P × D_P by using 10 uniformly distributed b values (rounded to the nearest b values available) [0, 100, 200, 250, 350, 400, 500, 600, 650]; subplots (e–h), by 10 optimal b values (rounded to the nearest b values available) [0, 50, 50, 50, 250, 250, 250, 750, 750, 750]. Maps obtained using the optimal b values have smoother texture and better rendering of renal cortex.

Simulation for Renal Lesions

Table 2 lists the distribution of parameters F_P, D_P, and D_T from 18 renal lesions (29). Malignant tumors had higher F_P, lower D_T and slightly lower D_P than benign lesions. Based on these values, parameter ranges (X^min and X^max in Eq. 4) were defined for each of the three parameters.

Table 2.

Biexponential Parameters for Malignant and Benign Renal Lesions (29)

	Enhancing lesions (10)	Nonenhancing lesions (8)	Ranges for b optimization
FP (%)	24.8 ± 11.9	8.1 ± 11.6	[5, 30]
DT (10−3 mm2/s)	1.46 ± 0.4	2.18 ± 0.7	[1, 3]
DP (10−3 mm2/s)	11.0 ± 2.4	12.3 ± 10.9	[10,15]

Results of b value optimization for 4, 6, 8, and 10 acquisitions are shown in Table 3. The results are similar to those of healthy subjects, except that the non-zero and non-upper-bound b values are slightly different due to the different parameter ranges used in optimization.

Table 3.

Optimal b Values for Renal Lesions

Nb	b1 (s/mm2)	b2 (s/mm2)	b3 (s/mm2)	b4 (s/mm2)	Averaged ξ of optimal b	Averaged ξ of uniform b
4	0	51	259	800	40.5	194.3
6	0	58	2 × 278	2 × 800	32.2	58.2
8	0	2 × 59	3 × 261	2 × 800	27.5	39.9
10	0	3 × 59	3 × 263	3 × 800	24.5	33.2

“Averaged ξ” represents the mean value of “the average error propagation factors for F_P, D_P, and D_T” across the parameter ranges in Table 2.

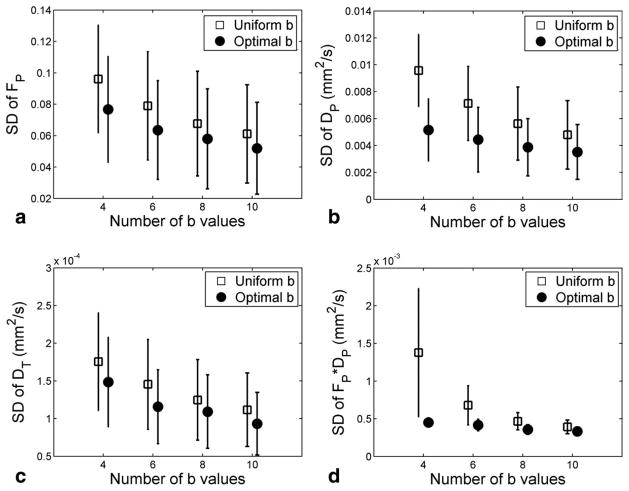
Figure 4 plots the parameter variability for the values obtained using the optimal and uniformly distributed b values for N_b of 4, 6, 8, and 10 (simulation 1). As N_b increases, SD for all the parameters decreases, indicating improved precision. For D_P and F_P × D_P, the use of the optimal b values brought a dramatic (up to 2–3 fold) increases in precision. For F_P and D_T, the precision improvements were lower (about 25%) but of practical value and consistent across N_b.

FIG. 4.

Precision of the biexponential model parameters, estimated by Monte Carlo trials (simulation 1). The error-bars are average ± standard deviation of the SD values across the 18 lesions. This simulation result shows that both increasing the number of b values and the use of b-sampling optimization improved the precision of all of the biexponential model parameters for diffusion-weighted MRI. These experimental results are consistent with human subject results in Fig. 1.

The effect sizes for differentiating between benign and malignant renal masses (simulation 2) are shown in Table 4. For F_P, the optimal b values improved the effect size by 11.5~28.4% (depending on N_b) compared to uniformly distributed b values. D_T differentiated the two types of lesion well for both b schemes (with large effect size around 1.71– 1.92). Parameter F_P × D_P achieved better differentiation between lesions than F_P or D_P. For N_b < 8, the effect size for F_P × D_P was on average 30% better when using the optimal b values than the uniformly distributed b values.

Table 4.

Simulated Effect Size for Differentiation Between Benign and Malignant Renal Lesions

Nb	FP		DT		DP		FP × DP
	Uniform	Optimal (%)	Uniform	Optimal (%)	Uniform	Optimal (%)	Uniform	Optimal (%)
4	1.07	1.30 (20.8)	1.71	1.80 (5.2)	0.13	0.40 (206.9)	1.26	1.74 (38.6)
6	1.14	1.46 (28.4)	1.79	1.88 (5.1)	0.25	0.36 (42.0)	1.46	1.77 (21.5)
8	1.33	1.59 (19.3)	1.85	1.90 (3.0)	0.50	0.47 (−6.4)	1.71	1.82 (6.3)
10	1.43	1.60 (11.5)	1.87	1.92 (2.3)	0.47	0.41 (−12.4)	1.78	1.86 (4.7)

Compared are the uniformly distributed (“uniform”) and the optimized (“optimal”) sets of b values. The percentages in parentheses express the increase of effect size due to the use of optimized b values. Large value for effect size corresponds to easy differentiation.

DISCUSSION

Because the kidney is highly vascular, DWI presents an ideal opportunity to introduce in the model a fast decaying component related to movement of water in blood vessels or other driven incoherent water motion. Resulting parameters D_P and F_P may enhance the diagnostic value of renal DWI. There is ample evidence of large contrast between the decaying coefficients of the fast and the slow decaying components in normal renal tissue [10–20 versus 1.5–2.0 mm²/ms (16)]. Besides the kidney, intravoxel incoherent motion (IVIM) effect has also been demonstrated in liver cirrhosis (31,32). There is increasing recognition of the potential importance of IVIM in abdominal organs such as kidneys and liver. However, compared with monoexponential analysis, the biexponential analysis is numerically more challenging, especially under conditions of low SNR.

We have derived an explicit analytic formula that relates the propagation of noise in DWI data to errors in fitting the parameters of the biexponential model. The minimization of a cost function based on this formula and on estimated parameter ranges can be used to determine optimal b values. Comparisons of the optimized b-value sampling were not made with the nonuniformly distributed ones empirically chosen in previous studies, because we believe that the two selection methods share the same aim of minimizing error propagation, although by different implementations (empirical selection versus quantitative calculation). Human subjects with healthy kidneys show lower errors (Figs. 1 and 2) and smoother parametric maps (Fig. 3) when optimal b values were used. While we have no direct human validation results for renal lesions, our simulations based on realistic parameter ranges indicate that the use of the optimal b values may improve the precision of biexponential parameters by 20–30%, leading to better differentiation of benign and malignant renal lesions.

One interesting finding was that the set of optimal b values consisted of multiple repetitions of essentially four distinct b values (including b of 0). We note that a similar “repeated” encoding scheme was found in previous optimization studies of monoexponential diffusion kernels. However, this pattern of repeated sampling differs from that employed in most multi-exponential (e.g. IVIM) studies in the literature to date, which employ more distributed sampling, particularly at low b-values. The latter approach is reasonable when investigating the diffusion response a novel organ or pathology and determining whether the biexponential model is justified and sufficient. Once that behavior is established, the optimization scheme presented in this work can be employed to maximize the precision of its parameter estimates. One benefit of the finding is noted: with optimal b values repeated at four distinct values, the b-optimization problem can be reduced to optimizing 6 variables (instead of N_b): three non-zero b values and the counts of repetitions at each of them (the sum of the counts is fixed at N_b). Such a scheme overcomes the well known problem associated with poor convergence rate when minimizing functions of many variables.

In principle, the proposed b-sampling optimization can be used for DWI of organs other than the kidneys. For example, biexponential analysis has been used in high b-value DWI and diffusion tensor imaging (DTI) of brain (33,34). To implement the method, we need to estimate typical ranges for the parameters of interest and N_b, which is usually determined by available scan time. As part of the optimization process, we selected equal weightings for the error propagation from each of the three DWI parameters, F_P, D_P, and D_T. However, future optimizations could be fine-tuned to emphasize a parameter that is especially relevant in answering clinical or research needs.

Our study does havemultiple limitations. First, our volunteer study included four subjects only. For each subject, nine repetitions of DWI acquisition were collected, resulting in only few independent samples for calculating CV and RD for the parameters estimates. However, the results are generally in agreement with the simulation (Fig. 4) that used many more trials. Second, with the various diagnostic tools available, simply differentiating benign and malignant renal lesions as in the simulation study may not be challenging. The biexponential analysis, with perfusion measures, may help discriminate the subtypes of malignant lesions. However, the application of the proposed method here will have to be done in future when reliable parameter ranges for these subtypes are available. Third, our image coregistration corrected for translation motion effect, but not rotational motion or deformation. However, respiratory cycle causes only a minimal rotation and deformation for the kidney (35). Fourth, parallel imaging that is often used in DWI studies (36) could alter characteristics of DWI noise and thus its propagation into biexponential parameters, and this will be investigated in future work. Finally, the optimization scheme requires estimates for the expected ranges of the measured parameters as input, which requires some foreknowledge of the system/pathology of interest. Future work may explore the dependence of the b-values chosen and the benefit obtained on the size and centroid of the parameter ranges.

In conclusion, for determination of perfusion/microcirculation and diffusion contributors to DWI signal changes, we have developed a method to choose b values for data acquisition that can maximize the precision and accuracy of the parameters of biexponential model. With improved precision, the potential utility of biexponential model in detecting and characterizing renal lesions can be more easily validated.

APPENDIX

Error Propagation in Biexponential Analysis of DWI Data

Least square regression searches for the model parameter values that minimize a sum-of-squared-deviation difference (denoted as R) between the model fit and the data. Mathematically, the optimal estimates can be obtained by solving the following equations of partial derivatives with regard to all the parameters,

$$\frac{\partial R}{\partial x(m)}=\sum _{i=1}^{N_b}\left\{2·\left[S(b_i,x)-S_{b_i}\right]·\frac{\partial S(b_i,x)}{\partial x(m)}\right\}=0,m=1,2,3,4.$$ [A1]

For simplicity in the following derivation, we use x(m) (m = 1, 2, 3, 4) to represent S₀, F_P, D_P, and D_T, respectively. In the following, we show the derivation of error propagations from signal to each parameter.

According to Taylor’s theorem, in the limit of increasing SNR, the term in the square brackets in Eq. A1 can be approximated by the first order partial derivatives,

$$\sum _{n=1}^4\left(\mathrm{\delta }x(n)\frac{\partial S(b_i,x)}{\partial x(n)}\right),$$ [A2]

where δx is the column vector of estimation errors (difference from true values) in the parameters. By replacing (A2) into (A1) and denoting the noise in the measured signals as ε, we get

$$\sum _{i=1}^{N_b}\left\{\left[\sum _{n=1}^4\left(\mathrm{\delta }x(n)·\frac{\partial S(b_i,x)}{\partial x(n)}\right)-\mathrm{\epsilon }(i)\right]·\frac{\partial S(b_i,x)}{\partial x(n)}\right\}=0,m=1,2,3,4;$$ [A3]

Rearranged and expressed in matrix form, Eq. A3 can be re-written as

$$A·\mathrm{\delta }x=B,$$ [A4]

where A = J^T·J, J is Jacobian matrix of S(x), and $B(m)={\sum }_{i=1}^{N_b}\left(\mathrm{\epsilon }(i)·\frac{\partial S(b_i,x)}{\partial x(m)}\right)$.

Assuming signal noise ε as independent and identically distributed, we obtain the variance of the model parameters as

$${[\mathrm{\delta }x(n)]}^2={\mathrm{\delta }}^2\sum _{m=1}^4\sum _{p=1}^4\left[A^{-1}(n,m)·A^{-1}(n,p)\times \sum _{i=1}^{N_b}\left(\frac{\partial S(b_i,x)}{\partial x(m)}·\frac{\partial S(b_i,x)}{\partial x(p)}\right)\right],$$ [A5]

where δ² is the variance of noise. Accordingly, the error propagation factor for each parameter can be derived by taking the ratio of relative error in the parameter and relative measurement noise,

$$\frac{\mathrm{\delta }x(n)/x(n)}{\mathrm{\delta }/S_0}=\frac{S_0}{x(n)}\sqrt{\sum _{m=1}^4\sum _{p=1}^4\left[A^{-1}(n,m)·A^{-1}(n,p)·\sum _{i=1}^{N_b}\left(\frac{\partial S(b_i,x)}{\partial x(m)}·\frac{\partial S(b_i,x)}{\partial x(p)}\right)\right]}.$$ [A6]

The partial derivatives in Eq. A6 are

$$\begin{array}{l}\partial S/\partial S_0=(1-F_{\mathrm{P}})e^{-b·D_{\mathrm{T}}}+F_{\mathrm{P}}{e}^{-b·D_{\mathrm{P}}}\\ \partial S/\partial F_{\mathrm{P}}=S_0[e^{-b·D_{\mathrm{P}}}-e^{-b·D_{\mathrm{T}}}]\\ \partial S/\partial D_{\mathrm{T}}=-S_0(1-F_{\mathrm{P}})e^{-b·D_{\mathrm{T}}}b\\ \partial S/\partial D_{\mathrm{P}}=-S_0{F}_{\mathrm{P}}{e}^{-b·D_{\mathrm{P}}}b\end{array}$$ [A7]