Entropy-driven structural transition and kinetic trapping in formamidinium lead iodide perovskite

In a photovoltaic perovskite, entropy-driven structural transition enables kinetic trapping of a desired photovoltaic phase.

Abstract

A challenge of hybrid perovskite solar cells is device instability, which calls for an understanding of the perovskite structural stability and phase transitions. Using neutron diffraction and first-principles calculations on formamidinium lead iodide (FAPbI₃), we show that the entropy contribution to the Gibbs free energy caused by isotropic rotations of the FA⁺ cation plays a crucial role in the cubic-to-hexagonal structural phase transition. Furthermore, we observe that the cubic-to-hexagonal phase transition exhibits a large thermal hysteresis. Our first-principles calculations confirm the existence of a potential barrier between the cubic and hexagonal structures, which provides an explanation for the observed thermal hysteresis. By exploiting the potential barrier, we demonstrate kinetic trapping of the cubic phase, desirable for solar cells, even at 8.2 K by thermal quenching.

INTRODUCTION

The record of solar cell efficiency based on hybrid organic-inorganic perovskites (HOIPs) has reached 22% (1–3), which rivals that of conventional silicon solar cells. Combined with their inexpensive solution-based processing and all earth-abundant compositions, HOIPs are among the most promising next-generation solar cell materials. Arguably the biggest challenge that HOIP solar cells face is their device instability. HOIPs have been shown to be susceptible to decomposition when exposed to humidity, high temperature, and extended period of light exposure (4). To avoid these issues, researchers have investigated various approaches such as encapsulation, device architecture engineering, and making alloys of different perovskites (4). A recent paper by Nagabhushana et al. (5) has claimed that, based only on enthalpy of formation measurements, HOIPs may be thermodynamically and intrinsically unstable even without any external factors such as humidity and light exposure, which will severely limit their potential for solar cell applications. However, HOIP solar cell efficiencies have been shown to maintain more than 90% of performance over at least 60 days even in the ambient air (30 to 50% relative humidity) without any encapsulation (6, 7). These seemingly contradictory observations indicate that the total free energy, including both the enthalpy and entropy contributions, should be considered for the HOIP stability.

Among HOIPs, methylammonium lead iodide (MAPbI₃) (1) and formamidinium lead iodide (FAPbI₃) (2) are currently the champion materials with ~20% record efficiencies. Although FAPbI₃ has a higher theoretical power conversion efficiency than MAPbI₃ because of its bandgap that is better matched to the solar spectrum (2, 8–10), it has been studied less compared to MAPbI₃ because of its structural phase instability. Upon cooling, FAPbI₃ exhibits abrupt suppression of photovoltaic effect as the system undergoes cubic-to-hexagonal transition (2, 3, 11–16). This transition occurs around at room temperature. However, the transition temperature and rate were found to vary widely depending on the sample environment (2, 3, 11–16). Several papers have been published, which report methods to stabilize the cubic phase at room temperature depending on the sample synthesis method and history (2, 3, 11–16). The nature of this phase transition and the precise mechanisms for the cubic phase stabilization remain elusive.

Here, using neutron diffraction and first-principles calculations on an HOIP, FAPbI₃, we provide a microscopic understanding of the structural energy landscape and show that the entropy contribution of the organic cation to the Gibbs free energy plays a crucial role in the selection of structure and stability of the HOIP. We find that in the high-temperature cubic phase, the FA⁺ cations have isotropic orientation with large entropy, which stabilizes the cubic structure. Upon cooling, the FA⁺ cations acquire strong preferential orientations in the hexagonal phase with lower entropy. Surprisingly, we find a large thermal hysteresis of the cubic-to-hexagonal phase transition that occurs at 350 K upon heating and at 290 K upon cooling. Furthermore, we demonstrate kinetic trapping of the cubic phase even at 8.2 K for an extended period of time by thermal quenching. Our experimental data indicate that the two structural states are separated by an energy barrier, which is also confirmed by our first-principles calculations.

RESULTS AND DISCUSSION

Figure 1 shows the neutron diffraction data obtained from a powder sample of FAPbI₃ in three different structural phases: the cubic phase at 390 K, a hexagonal phase at 220 K (hereafter Hex-IT), and another hexagonal phase at 15 K (Hex-LT). As shown in Fig. 1A, at 390 K, the data can be reproduced by the cubic structure with Pm$\overline{3}$m symmetry and lattice constant of a_c = b_c = c_c = 6.3855(2) Å, consistent with the results reported by Weller et al. (17). This further confirms that the black phase of FAPbI₃ is cubic Pm$\overline{3}$m (17) rather than the P3m1 trigonal phase as initially reported by x-ray studies (11, 18). The Pm$\overline{3}$m symmetry dictates that there is an O_h symmetry at the center of the unit cell. The presence of FA⁺ cations inside the unit cell will break the symmetry. However, rotation of organic cation and dynamical averaging over time will restore the O_h symmetry. The minimum rotation that restores the mirror planes involves 12 equivalent sites as suggested by Weller et al. (17). However, instead of the 12 sites, we find that the orientation of the FA⁺ cation is random, as illustrated in Fig. 1D. The inset of Fig. 1A shows the calculated neutron Bragg peak intensities at (110), (111), and (200), based on two different models of the FA⁺ cation orientations. The blue line is the calculated intensities, assuming that the cation has 12 possible sites (17). This model does not reproduce the data extremely well, and this discrepancy was seen in Fig. 1 (bottom) of the study by Weller et al. (17). On the other hand, the red line is based on our model in which the cation has 480 possible sites, which approximates random orientation. The latter fits the data significantly better than the former, indicating that the FA⁺ cations have random orientation in the cubic phase of FAPbI₃ at 390 K.

Fig. 1. Neutron diffraction patterns of HC(ND₂)₂PbI₃.

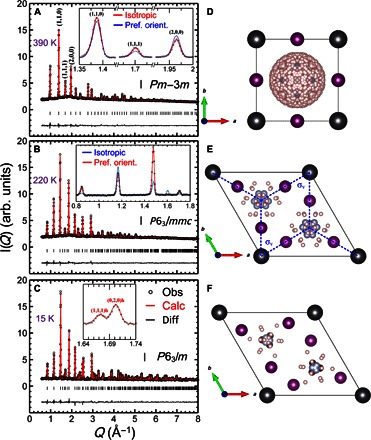
Measured at (A) 390 K, (B) 220 K, and (C) 15 K. Refined structures with the symmetry of (D) cubic Pm$\overline{3}$m for 390 K, (E) hexagonal P6₃/mmc for 220 K, and (F) hexagonal P6₃/m for 15 K. The neutron intensities are plotted in arbitrary units (arb. units). The spheres in dark gray, violet, pink, and light blue represent Pb, I, H/D, and N atoms, respectively. The view of the C atoms is blocked by the N atoms in this projection angle. The insets in (A) and (B) compare the two different models (see the main text for details). The inset of (C) shows an extra (111)_h peak at 15 K that is absent at 220 K.

Figure 1B shows the diffraction data obtained at 220 K. The Bragg peaks observed in the 390-K data disappear; instead, new peaks that cannot be indexed by the cubic structure appear. They can be indexed by a hexagonal structure (18), with P6₃/mmc space group and lattice constants of a_h = b_h = 8.6226(5) Å and c_h = 7.9458(5) Å. In the study by Stoumpos et al. (18), the P6₃mc space group was used for the Hex-IT phase. We found that the higher symmetry P6₃/mmc reproduces the neutron data equally well. The inset shows the fits of two models: one with 12 preferred FA⁺ cation orientations (red line) and the other with random orientations (blue line). The model of preferred orientations, where the FA⁺ molecular plane is perpendicular to the hexagonal ab plane (see fig. S1 for detailed analysis and Fig. 1E for illustration), reproduces the data much better than the isotropic model. This indicates that the FA⁺ cation acquires the preferred orientations as the system becomes hexagonal upon cooling. At 15 K (see Fig. 1C), the diffraction data show the appearance of additional extra peaks, such as (111)_h shown in the inset, indicating further reduction in symmetry. The Bragg peaks can be indexed with P6₃/m space group. Detailed structural parameters for all three phases are listed in tables S1 to S3.

The cubic Pm$\overline{3}$m and the hexagonal P6₃/mmc space groups are not related by a simple group/subgroup relation. This means that for the cubic-to-hexagonal transition to occur, the organic molecules, lead, and iodide atoms must undergo a complex combination of sliding and twisting, which results in breaking/forming of Pb–I bond. In the context of energy landscape, this complex transition does not occur spontaneously; thus, it must exhibit an energy barrier between the two states. To experimentally check this hypothesis, we have investigated the temperature dependence of the phase transition behaviors such as thermal hysteresis and kinetic trapping. We monitored the Bragg peaks in the Q range of 1.65 to 1.76 Å⁻¹ that covers distinctive peaks for all three phases (cubic, Hex-IT, and Hex-LT). Figure 2A shows that, at the base temperature of 8.2 K, the data exhibit both (111)_h and (020)_h peaks, indicating that the system is in the Hex-LT phase. Upon heating, the (111)_h starts to gradually decrease at about 100 K and disappears at 175(5) K. The (111)_h is allowed in the Hex-LT (P6₃/m) phase but not in the Hex-IT (P6₃/mmc) phase. This indicates that the system enters Hex-IT above 175(5) K. Upon further heating, the system undergoes a sharp first-order transition at 350(5) K into the cubic phase, where only the (111)_c peak is observed (see Fig. 2, A and C). In the Hex-LT phase, there is a considerably large diffuse scattering under the Bragg peaks, which we refer to as “Diffuse” in Fig. 2 (C and D). Upon heating, the diffuse scattering intensity decreases rapidly as the (111)_h disappears and, upon further heating, gradually decreases up to 400 K. This diffuse scattering mainly originates from the low-energy rotational motions in the system, as seen in MAPbI₃ (19).

Fig. 2. Structural thermal hysteresis.

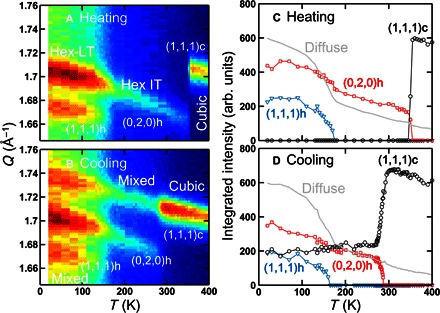
Elastic neutron scattering data obtained from FAPbI₃ at SPINS, NCNR, upon heating (A and C) and upon cooling (B and D). (A) and (B) are contour maps of the scattering intensity as a function of momentum transfer, Q, and temperature, T. Q range of 1.65 to 1.76 Å⁻¹ was covered to probe the distinctive nuclear Bragg peaks—(1,1,1)_c, (0,2,0)_h, and (1,1,1)_h—associated with the cubic, Hex-IT, and Hex-LT phases, respectively. (C) and (D) are integrated intensities of the three peaks—(1,1,1)_c (black circle), (0,2,0)_h (red square), and (1,1,1)_h (blue triangle)—as a function of temperature. The light gray line indicates the temperature-dependent diffuse scattering intensity, as explained in the text.

After this heating process, the same Q scan was performed upon cooling from 400 K to probe the existence of any thermal hysteresis and kinetic trapping. Upon cooling, the cubic–to–Hex-IT transition starts at 290 K, which is 60 K lower than the phase transition temperature observed during heating. We note that this thermal hysteresis is not an experimental artifact due to thermal nonequilibrium during the temperature change, because we have verified the thermal equilibrium during the measurements by monitoring the Bragg peak positions during the heating and cooling processes, as shown in fig. S4. This cubic–to–Hex-IT transition stops below 265 K. We note that we spent 525 min to go from 300 to 265 K. As shown in Fig. 2 (B and D), the cubic (~40%) and hexagonal (~60%) phases coexist below 265 K. Upon further cooling, below 165(5) K, only the Hex-IT phase transitions into the Hex-LT phase, whereas the cubic phase remains intact. The large thermal hysteresis observed in the cubic–to–Hex-IT transition supports our scenario of the transition involving complex atomic displacements. The data also indicate that the cubic–to–Hex-IT transition is a thermally activated process between the two structures separated by an energy barrier. As a result, if the temperature of the system gets rapidly quenched from the cubic phase to a temperature below 265 K, then the system can be kinetically trapped entirely in the cubic (or a pseudo-cubic) phase. To check for the complete trapping, we have performed a more rapid quenching experiment in which the sample was heated to 400 K and cooled to 200 K over ~80 min. No phase transition was detected, and the whole system remained cubic (see Fig. 3A). The sample was monitored for 1 hour at 200 K, and still, no phase transition was observed. The system remains in the cubic phase upon further cooling to 8.2 K and monitoring for seven additional hours (see fig. S5).

Fig. 3. Quenching and energy landscape.

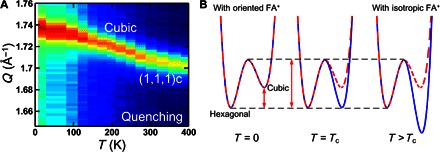
(A) The elastic neutron scattering data were taken during rapid thermal quenching. (B) The kinetically trapped cubic phase indicates the existence of a potential energy barrier between the cubic and hexagonal phases. In (B), the red dashed line represents a schematic energy landscape, the details of which are shown in Fig. 4. The blue solid line represents the free energy landscape that accounts for the entropy contribution.

To understand the structural stability of the cubic and hexagonal phases and their structural transition mechanism, we performed first-principles density functional theory (DFT) calculations (see the Supplementary Materials for computational details) (20, 21). We first confirm that the formation enthalpy of the hexagonal phase is lower by ~70 meV per formula unit than that of the cubic phase (see Fig. 4B), identifying the hexagonal phase as the most favorable configuration at zero temperature. Then, we further identify a transition pathway from the hexagonal phase to the cubic phase. It is plausible that the system goes through many different phase transition pathways. Here, we discuss one possible pathway between the experimentally determined cubic and hexagonal structures. Assuming that the Pb and I atoms translate linearly between the cubic and hexagonal phases, we interpolate their atomic coordinates and generate 42 initial transition states in the reaction coordinate. For a given transition state, we performed constrained optimization (see the Supplementary Materials) (22) to obtain its relaxed configuration and energy. Figure 4A shows some of the intermediate structures. The complex displacements along the transition pathway are illustrated by the changes in the color of I-cage polygons, representing the disappearance of an old I cage and the appearance of a new one, the shape of the purple I-I lines, and the orientations and positions of the FA⁺ cations. The lines connecting the Pb atoms illustrate the transition from the hexagonal to the cubic phase, where the two states are separated by an energy barrier with an order of hundreds of milli–electron volt in height.

Fig. 4. Transition pathway and energy barrier.

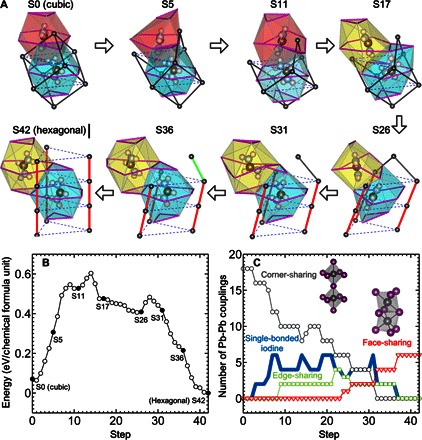
(A) Illustration of a possible transition pathway from the cubic to the hexagonal structure. The colored polygons represent the cages formed by iodine atoms located at the corners. The purple lines connecting iodine atoms, such as the hexagonal and triangle lines in the initial cubic structure, are drawn at each step to show how the iodine atoms move and the cages distort along the pathway. The eight spheres inside each polygon represent the HC(ND₂)₂⁺ (FA⁺) cation. The dark gray spheres represent lead atoms. Each lead atom is surrounded by six iodine atoms. The dark gray, green, and red solid lines connecting the lead atoms represent a pair of neighboring lead atoms that share one iodine (corner-sharing PbI₃ octahedra), two iodine atoms (edge-sharing), and three iodine atoms (face-sharing), respectively. The dark gray lines in the initial cubic structure show the cube of a unit cell. The dashed blue lines in the final hexagonal structure are connecting the lead atoms in different unit cells in the hexagonal ab plane. (B) Calculated energy of the optimized structures along the pathway. (C) Number of corner-sharing (dark gray symbol), edge-sharing (green symbol), and face-sharing (red symbol) PbI₃ octahedra and single-bonded iodine atoms (blue symbol) per six cubic unit cells along the pathway.

At nonzero temperatures, the rotation of the FA⁺ cation is activated. Our neutron diffraction results revealed the isotropic random orientations of the FA⁺ cation in the cubic phase, which is in contrast to the preferred orientations in the hexagonal phase. A finite temperature transition between the two different phases can be cast into the variation of Gibbs free energy (23); it consists of changes in the internal energy (ΔU) and vibrational/rotational Helmholtz free energy [ΔF(T) = −TS, where S is the entropy of the system] by neglecting the energy change incorporated with the change in volume at a given pressure. Because the Helmholtz free energy is dominated by soft modes (24), the prominent difference in Gibbs free energy between the two phases is mainly from the isotropic rotation of FA⁺. The entropy (S_rot) of a freely rotating FA⁺ cation is as follows

$${\mathit{S}}_{\text{rot}}=\frac{3}{2}{\mathit{k}}_{\mathrm{B}}\{1+ \text{ln}(0.4786{\mathit{k}}_{\mathrm{B}}\mathit{T}\sqrt[3]{{\mathit{I}}_1{\mathit{I}}_2{\mathit{I}}_3})\}$$

where k_B and T are the Boltzmann constant and temperature, respectively, and the principal moments of inertia (I_i) of HC(ND₂)₂⁺ (FA⁺) cations are 11.644, 60.161, and 71.806 uŲ, where the unified atomic mass unit, u, is 1.6605 × 10⁻²⁷ kg. Because the rotational entropy contribution is negligible for the hexagonal phase with the preferred orientation, the Helmholtz free energy difference between the two phases becomes ΔF(T) ~ −TS_rot; it is −273 meV at T = 300 K. Thus, this entropy contribution lowers the free energy of the cubic structure well below the hexagonal structure at high temperatures, as illustrated with the blue lines in Fig. 3B. Although the transition temperature is determined from the free energy difference, the energy barrier is relevant to the rate of phase transition. According to the Arrhenius equation, the transition rate coefficient, k, is $\mathit{k}=\mathrm{\nu }{\mathit{e}}^{-\frac{{\mathit{E}}_{\mathrm{b}}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}}$, where ν is the attempt frequency and E_b is the activation barrier (25). Typically, the attempt frequency is estimated to be similar to the phonon frequency of related modes. In this case, the attempted frequency can be assumed to be ~50 cm⁻¹ (1.5 THz) based on the characteristic frequency of the vibration modes of Pb/I cage (26). Combined with our calculated activation barrier value of ~0.6 eV, according to the Arrhenius equation, the reaction should be completed in ~67 ms at room temperature, which supports the experimentally observed fast phase transition at room temperature.

The coherent picture that emerges from our study is that the hexagonal-to-cubic phase transition in FAPbI₃ is entropy-driven, with the two states separated by an energy barrier. This picture can explain all the experimental observations in a consistent way. The energy barrier is responsible for the experimentally observed, kinetically trapped cubic phase at low temperatures shown in Fig. 3A. Furthermore, the observed thermal hysteresis can be understood by the fact that the entropy contribution to the free energy requires activation (deactivation) of the FA⁺ cation’s isotropic rotation upon heating (cooling).

CONCLUSION

Our work highlights the important role of organic cations in HOIPs. The entropy contribution due to the change in the organic cation’s rotational modes must be considered when studying the stability, phase transition, and selection of structures in HOIPs. The kinetic trapping of the cubic phase, which is highly desirable for solar cell applications, opens new opportunities for practical application of FAPbI₃-based devices. In colder environments, such as in spacecraft and aircraft, the cubic phase of FAPbI₃ can be kinetically trapped for efficient and stable solar power conversion. For terrestrial applications, the kinetic trapping may also be exploited to obtain more stable FAPbI₃ solar cells. It would be interesting to see whether other HOIP systems with different organic cations have similar properties. If so, this would call for further studies on the possibility of fine-tuning of the exact phase transition temperature and degree of kinetic trapping by chemical and device manipulations.

MATERIALS AND METHODS

Sample preparation

PbI₂ (99.999%) in a powder form and γ-butyrolactone (99%) in a liquid form were purchased from Sigma-Aldrich. Formamidinium iodide (FAI) in a powder form was purchased from Dyesol. D₂O (99.9%) was purchased from Cambridge Isotope Laboratories.

Four grams of FAI was deuterated by dissolving in 250 ml of D₂O and heating to 95°C for 4 hours under nitrogen. The liquid was then evaporated at 70°C under flowing nitrogen. The evaporation process took 8 hours, and white solid was collected and further dried at 100°C under nitrogen for 2 hours. Deuterated FAI (3.58 g), PbI₂ (9.38 g), and D₂O (3 ml) were added to γ-butyrolactone (30 ml). The solution was dissolved at 150°C under flowing nitrogen, and heating was continued for 12 hours until the solvent had evaporated and black crystals were visible. The sample was then cooled to room temperature. The yellow solid was collected and further dried in a nitrogen glove box for 2 hours at 100°C. Yellow powder (12.47 g) was collected.

Neutron diffraction at BT1 and elastic neutron scattering at SPINS

NIST NCNR BT1.

Crystal structure and structural parameters were determined by neutron powder diffraction, using the BT1 diffractometer at the NIST (National Institute of Standards and Technology) Center for Neutron Research (NCNR) located in Gaithersburg, MD. The wavelength of incident neutrons, λ = 1.5398 Å, was selected using a Cu(311) monochromator with an in-pile 60′ collimator. The scattered neutrons were collected by 32 ³He detectors over the 2θ range of 1.3° to 166.3° with 0.05° step size. FAPbI₃ (~10 g) sample was placed into a cylindrical vanadium can in a dry helium box. The vanadium can was sealed with an indium O-ring. The sample can was mounted in a closed-cycle helium refrigerator.

NIST NCNR SPINS.

Figures 2 and 3A show the elastic neutron scattering data obtained at the cold neutron triple-axis spectrometer, SPINS, at NCNR. FAPbI₃ (~10 g) sample was placed into a cylindrical aluminum can in a dry helium box. The aluminum can was sealed with a lead O-ring. The sample can was mounted in a closed-cycle helium refrigerator, and the temperature was changed in the range of 8.2 to 400 K. The energy of the neutrons was 5 meV. The collimations were open-80′-80′-open from the cold neutron guide to the monochromator to the sample to the analyzer to the detector. The higher-order neutron contaminations were eliminated by placing two liquid nitrogen–cooled beryllium filters before and after the sample.

DFT calculations

See the Supplementary Materials for details on DFT calculations.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/10/e1601650/DC1

Tables of atomic parameters for the three structural phases

Preferred orientation of FA⁺ cation in the hexagonal phase

Synchrotron x-ray diffraction measurements

Confirmation of thermal equilibrium during neutron measurement

Kinetic trapping of the cubic structure by thermal quenching

Details on DFT calculations

table S1. Refined structural parameters of FAPbI₃ for 390 K.

table S2. Refined structural parameters of FAPbI₃ for 220 K.

table S3. Refined structural parameters of FAPbI₃ for 15 K.

fig. S1. Orientation of FA⁺ cation.

fig. S2. Refined crystal structure.

fig. S3. Synchrotron x-ray powder diffraction data for FAPbI₃.

fig. S4. Check for thermal equilibrium during elastic neutron scattering measurements.

fig. S5. Temporal monitoring of the stability of the cubic phase at 8.2 K after thermal quenching.

References (27–31)