Coupled Harmonic Bases for Longitudinal Characterization of Brain Networks

Abstract

There is a great deal of interest in using large scale brain imaging studies to understand how brain connectivity evolves over time for an individual and how it varies over different levels/quantiles of cognitive function. To do so, one typically performs so-called tractography procedures on diffusion MR brain images and derives measures of brain connectivity expressed as graphs. The nodes correspond to distinct brain regions and the edges encode the strength of the connection. The scientific interest is in characterizing the evolution of these graphs over time or from healthy individuals to diseased. We pose this important question in terms of the Laplacian of the connectivity graphs derived from various longitudinal or disease time points — quantifying its progression is then expressed in terms of coupling the harmonic bases of a full set of Laplacians. We derive a coupled system of generalized eigenvalue problems (and corresponding numerical optimization schemes) whose solution helps characterize the full life cycle of brain connectivity evolution in a given dataset. Finally, we show a set of results on a diffusion MR imaging dataset of middle aged people at risk for Alzheimer’s disease (AD), who are cognitively healthy. In such asymptomatic adults, we find that a framework for characterizing brain connectivity evolution provides the ability to predict cognitive scores for individual subjects, and for estimating the progression of participant’s brain connectivity into the future.

1. Introduction

Large scale scientific initiatives such as the Human Connectome Project (HCP) are beginning to provide exquisite imaging data that may eventually enable a full structural connectivity mapping of the human brain [28]. For instance, diffusion magnetic resonance imaging (dMRI), an imaging modality central to the aforementioned studies, captures in a spatially localized (voxel-wise) manner, water diffusion properties that can be used to infer the arrangement of network pathways in the brain [23, 27]. After suitable preprocessing, e.g., via so-called tractography procedures, we obtain a unique view of the fiber bundle layout that connects distinct brain regions [10] (see Fig. 1). From an analysis perspective, once the spatial organization of these fiber bundles is expressed as a graph whose nodes represent separate brain regions and the edges denote the “strength” of connection (e.g., number) of the connecting inter-region fibers, a variety of analyses can be conducted [12, 13, 24, 34]. For example, we may ask whether a specific edge of the graph exhibits statistically different connectivity measurements across clinically disparate groups: diseased and healthy. If the results of this hypothesis test are statistically significant, we can conclude that the corresponding fiber bundle (pertaining to the edge) is possibly affected by the disease.

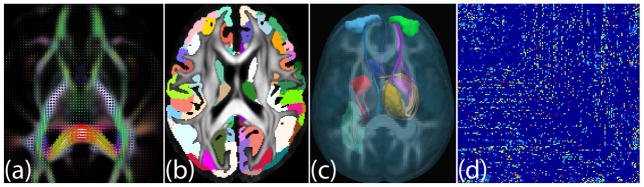
Figure 1.

(a) Diffusion tensor ellipsoids obtained from the dMRI data using non-linear estimation. (b) Anatomical regions in cortical and sub-cortical gray matter are used to define the nodes in the brain network. (c) Fiber tracts (axonal pathways between brain regions) estimated via tractography are used to define connectivity strength between various gray matter nodes in the brain. (d) The brain networks can be represented as symmetric adjacency matrices.

But more recently, there is increasing interest in identifying not just imaging based or structural connectivity based biomarkers, rather to quantitatively characterize disease progression [3, 18, 31]. For example, studies may recruit subjects for multiple visits over a period of time (which varies from months to years) and acquire diffusion imaging data at several time points. In such longitudinal datasets, each subject (or sample) corresponds to multiple images (or the corresponding brain connectivities) at different time points. The scientific goal then is to identify the entire life cycle of brain connectivity evolution — from when a middle aged participant was healthy to a stage where the individual’s cognitive function has become much worse.

The standard approach to answering the question above is to characterize change in brain connectivity at the level of individual edges in the graph. There are two problems with this proposal. First, treating individual edges as primitives neglects the local context in which the edge exists in the actual object of interest — i.e., the entire connectivity graph of the individual. But from a technical perspective, a second issue is perhaps more important. For n regions, we obtain 𝒪(n²) edges. After learning a model (e.g., association of the connection weights with age) for each edge and estimating the significance of the fit (e.g., p-values), we cannot simply report the edges with small p-values as relevant. Since the analysis is being conducted for a large number of edges, the likelihood of false positives is high, so a severe multiple comparisons correction needs to be adopted. This correction may often be too conservative, and we may end up discarding connections that are, in fact, scientifically meaningful; this is an undesirable consequence of treating the edges individually. To avoid this problem, practitioners often rely on summary measures of the connectivity graph instead, such as clustering coefficients, small-worldness, modularity and so on [2, 20]. This works well but is limited in that we cannot uncover spatially localized effects of disease (or other covariates) on connectivity.

A more attractive solution is to think of the graphs as an object and utilize a suitable parameterization of the graph. One possibility is to use the Laplacians [19, 25], either at the level of individual subjects or in terms of distinct partitions of the full cohort progressively going from healthy to diseased, i.e., the first partition is comprised of completely healthy individuals whereas the k-th partition includes diseased subjects. Then, if we look at the full set of bases of the partition-specific Laplacian we can come up with ways to characterize change in these bases as we move from the healthy to the diseased partition. Of course, such a parameterization also enables longitudinal analysis. For example, if we have data for multiple time-points for each partition, we can track how the Laplacian bases evolve over time. To achieve these goals, i.e., for analyzing changes across partitions of disease severity or partition-specific longitudinal analysis, one requirement is the ability to derive a coupled set of harmonic bases for a set of ordered Laplacians (longitudinally and cross-sectionally). This allows treating the full data holistically while preserving the ordinal nature of time and disease-induced cognitive decline. While a mature body of literature in numerical analysis provides sophisticated ways of deriving orthonormal set of bases for any self-adjoint operator, it provides little guidance on how to impose the coupling requirement, essential in this application. For example, we find that for most of the widely used eigenvalue decomposition methods [21, 32], it is non-trivial to modify the numerical scheme to satisfy the consistency requirement between consecutive set of eigen-bases. Addressing this limitation is a goal of this paper.

Key contributions

With the foregoing motivation, the core of this work deals with deriving efficient numerical optimization schemes to solve an ordinally and longitudinally coupled set of a generalized eigenvalue problems. To our knowledge, few publicly available alternatives currently exist [14, 15]. We provide (1) a novel formulation for estimating harmonic bases of brain connectivity networks that are smoothly varying in terms of both longitudinal as well as cross-sectional ordering (induced by a separate covariate such as cognitive performance). We provide an iterative numerical scheme for solving the problem using stochastic block coordinate descent based manifold optimization techniques. (2) We show that such a framework provides an exciting scientific tool in the following sense. Once the model has been estimated, we can vary a single parameter and “see” how the structural brain connectivity of an individual evolves over time or as a function of disease (see Fig. 2 for a qualitative demonstration). This yields a valuable mechanism for performing individual-level prediction. We show how our algorithm is able to provide connectivity prediction in a population of healthy controls who have some known risk factors of AD. Even though these individuals are asymptomatic, our approach is able to obtain a nominal degree of accuracy in assigning the subject to distinct cognitive quantiles. Demonstrating that we can, in fact, obtain a better than chance accuracy where the disease signal is so weak is the main contribution of this work.

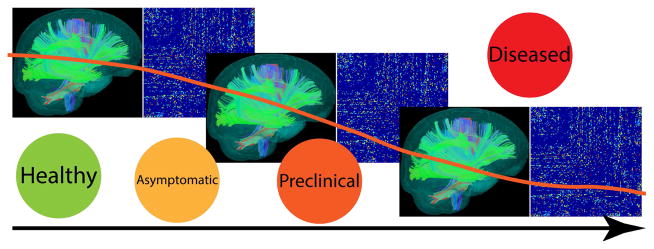
Figure 2.

Using coupled harmonic representations derived from brain connectivity networks, we can turn a “knob” and see how a network evolves as the cognitive stage changes from healthy to diseased.

2. Coupled harmonic bases for brain networks

Parameterization

Let us first describe a simple procedure for parameterizing the brain connectivity network in terms of its bases for individual subjects. Let A be a n × n weighted adjacency graph, A as in Fig. 1(d) representing a brain connectivity between n regions of the brain for a subject. We construct the Laplacian L, a commonly used tool/parameterization for representing graphs, defined as

$$L=D-A,D(i,i)=\sum _{j=1}^{n}A(i,j),$$

where D is called the degree matrix. Based on spectral graph theory, the eigenvectors corresponding to lower order eigenvalues contain the ‘low frequency’ information which reflects the latent structure of the Laplacian. The bases are estimated by minimizing the following objective function

$$\underset{V\in {ℝ}^{n\times p}}{min}\text{tr}(V^{T}LV),\text{s.t.}{V}^{T}V=I,$$ (1)

where tr(·) is the trace functional. The solution V to the above numerical optimization problem consists of the eigenvectors associated with the p smallest eigenvalues of L which we solve to express a given brain connectivity network via its Laplacian and/or its p eigenvectors/eigenvalues.

Now suppose we are given a longitudinal dMRI dataset for N subjects with T time points: this provides NT brain networks. We can parameterize all the networks simultaneously by minimizing the following objective function

$$\underset{V_{[i,j]}\in {ℝ}^{n\times p}}{min}\sum _{i=1}^N\sum _{j=1}^T\text{tr}(V_{[i,j]}^T{L}_{[i,j]}{V}_{[i,j]})\text{s.t.}{V}_{[i,j]}^T{V}_{[i,j]}=I,$$ (2)

where L_[i,j] denotes the Laplacian matrix of brain network for subject i and time point j and V_[i,j] denotes the set of p eigenvectors for L_[i,j].

However, this formulation ignores a couple of key properties of our analysis goal (conceptually shown in Fig. 3). (1) Each subject has multiple time points which means that not all networks in the population are ‘independent’. There are strong dependencies among the networks derived from a single person observed over time. (2) The subjects can, if desired, be partitioned into distinct groups if a covariate of interest for the subjects is close enough (i.e., similar cognitive scores or a measure of pathology such as amyloid protein load may have roughly similar connectivity strength [6]). This suggests that the bases that we find must also be related, or coupled, while still respecting, to the extent possible, their original Laplacians. If we consider the population of networks as a system, the recovery of the full set of bases must ensure a notion of consistency among {V_[i,j]}, governed by either the cognitive score grouping or longitudinal ordering described above.

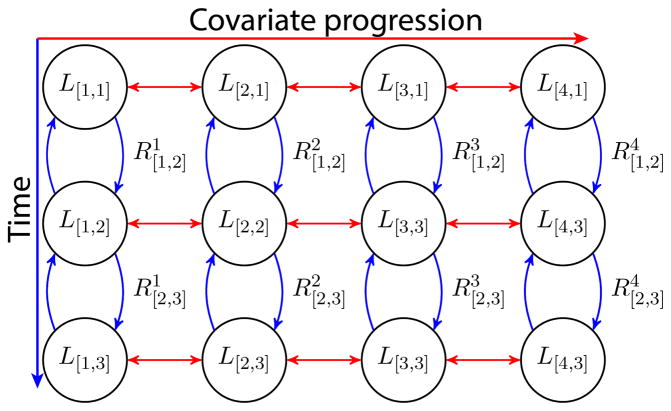
Figure 3.

The graph representation of the coupled data matrices. The nodes in each row (cross-sectional) are coupled horizontally in red while the nodes in each column (longitudinal) are coupled vertically in blue.

We now present our proposed framework for adding constraints in (2) that will ensure that the full set of Laplacians are treated jointly. Without loss of generality, we can work with the example dataset scenario presented in Fig. 3.

2.1. Longitudinal coupling

In this section, we introduce basis coupling constraints that model the relationships (blue arrows in Fig. 3) between temporally consecutive bases. Suppose we consider the bases V_[•,j] and V_[•,j+1] for two consecutive time points j and j + 1 for a specific subject. Since these are derived from the Laplacians of the same subject, we impose a homology constraint between the latent structures. In other words, we expect that V_[•,j] and V_[•,j+1] differ only by a small degree of rotation. Specifically, we impose

$$V_{[•,j+1]}=R_{[j,j+1]}^{•}{V}_{[•,j]},$$ (3)

where $R_{[j,j+1]}^{•}\in \mathbb{S}\mathbb{O}(n)$ which is a group of n × n orthogonal matrices with determinant = +1. This is, in fact, a Procrustes problem [30] of aligning the bases which provides the longitudinal evolution process of the set of bases as a sequence of rotation matrices. Note that the rotation matrix which aligns V_[•,j+1] to V_[•,j] is simply $R_{[j+1,j]}^{•}=R_{[j,j+1]}^{{•}^T}$.

Now, for eigenvectors V_[•,j] and V_[•,j+1], we see that

$$V_{[•,j]}^T{V}_{[•,j]}=V_{[•,j]}^T{R}_{[j+1,j]}^{•}{V}_{[•,j+1]}=I,$$ (4)

$$V_{[•,j+1]}^T{V}_{[•,j+1]}=V_{[•,j+1]}^T{R}_{[j,j+1]}^{•}{V}_{[•,j]}=I.$$ (5)

Multiplying the above two equations we have

$$\begin{array}{l}\left(V_{[•,j]}^T{R}_{[j+1,j]}^{•}{V}_{[•,j+1]}\right)\left(V_{[•,j+1]}^T{R}_{[j,j+1]}^{•}{V}_{[•,j]}\right)=I\\ \Rightarrow V_{[•,j]}^T\underset{M_{[j+1,j]}^{\prime }}{\underbrace{(R_{[j+1,j]}^{•}{V}_{[•,j+1]}{V}_{[•,j+1]}^T{R}_{[j+1,j]}^{{•}^T})}}{V}_{[•,j]}=I.\end{array}$$

Thus, we have now added a constraint on V_[•,j] that addresses the coupling between j and j + 1 as

$$V_{[•,j]}^T{M}_{[j+1,j]}^{\prime }{V}_{[•,j]}=I.$$ (6)

Note that for j ∉ {1, T}, each V_[•,j] is tied to V_[•,j−1] and V_[•,j+1]. Thus, the coupling matrices for those two relationships are $M_{[j-1,j]}^{\prime }$ and $M_{[j+1,j]}^{\prime }$ respectively. To account for both relations, we take the average coupling matrix as [7]:

$$M_{[•,j]}=\frac{M_{[j-1,j]}^{\prime }+M_{[j+1,j]}^{\prime }}{2}.$$ (7)

For the boundary values of j = 1 and j = T, $M_{[•,1]}=M_{[2,1]}^{\prime }$ and $M_{[•,T]}=M_{[T,T-1]}^{\prime }$ respectively. Thus, for a subject i, we derive the following optimization model for discovering longitudinally coupled bases for the brain connectivity Laplacians,

$$\underset{V_{[i,j]}\in {ℝ}^{n\times p}}{min}\text{tr}(V_{[i,j]}^T{L}_{[i,j]}{V}_{[i,j]}),\text{s.t.}{V}_{[i,j]}^T{M}_{[i,j]}{V}_{[i,j]}=I.$$ (8)

Recall that the above constraint is the so-called generalized Stiefel constraint [1] with the mass matrix M_[i,j]. This is also known as the generalized eigenvalue problem that finds the first p smallest eigenvalues and the respective eigenvectors of L_[i,j] for the mass matrix M_[i,j]. We can finally extend this implementation for all subjects as follows,

$$\underset{V_{[i,j]}\in {ℝ}^{n\times p}}{min}\sum _{i=1}^N\sum _{j=1}^T\text{tr}(V_{[i,j]}^T{L}_{[i,j]}{V}_{[i,j]})\text{s.t.}{V}_{[i,j]}^T{M}_{[i,j]}{V}_{[i,j]}=I.$$ (9)

We point out that for each i and j, the above model is equivalent to (8).

2.2. Cross-sectional coupling

In this section, we present the appropriate constraints that will encode cross-sectional dependencies among the eigenvectors {V_[i,j]}. Let us say the population can be partitioned into K distinct groups (columns in Fig. 3) where each group/column is cognitively equivalent based on some battery of tests. Such partitions may also be derived by certain measures of pathology. For each group, we first construct an average Laplacian X_[i,•] at a fixed time point. This average Laplacian serves as a representative of that specific group. In principle, we can work with individual level Laplacians L, however, since the goal is to formulate the coupling of bases with respect to the covariates, the averaging helps us reduce the individual level variability and provides a more succinct picture of the network evolution along the trajectory of that covariate (e.g., cognitive scores).

Let us consider three such average Laplacians X_[i−1,•], X_[i,•] and X_[i+1,•] from three consecutive/ordered partitions. The corresponding eigenvectors will be V_[i−1,•], V_[i,•] and V_[i+1,•]. Since these bases are derived from partitions with disjoint/distinct groups of subjects, we cannot assume a homological relationship between them. Since the coupling constraints will be added only between adjacent partitions it is nonetheless reasonable to assume that the bases will not change drastically affecting the full connectivity network. We encode this requirement as a sparsity constraint on the difference of the bases, e.g., via ℓ₀ norm. We use the relaxed ℓ₁ alternative,

$$g(V_{[i,•]})=\lambda ({\Vert V_{[i-1,•]}-V_{[i,•]}\Vert }_1+{\Vert V_{[i,•]}-V_{[i+1,•]}\Vert }_1)$$ (10)

where λ > 0 is the regularization parameter which controls only the magnitude of the cross-sectional coupling.

Intuitively, it enforces similarities in certain dimensions of the cross-sectional bases while allowing the others to vary freely. In other words, we preserve some structural consistencies across the groups while still allowing the group-wise bases to be different. Note that for i = 1 and i = K, the regularization terms will only contain the first term and the second term of (10) respectively. The cross-sectionally coupled bases (V_[i,•]) can then be estimated by minimizing the following,

$$\underset{V_{[i,•]}\in {ℝ}^{n\times p}}{min}\text{tr}(V_{[i,•]}^T{X}_{[i,•]}{V}_{[i,•]})+\lambda g(V_{[i,•]})\text{s.t.}{V}_{[i,•]}^T{M}_{[i,•]}{V}_{[i,•]}=I.$$ (11)

Putting it all together, we have the following coupled generalized eigenvalue formulation,

$$\underset{V_{[i,j]}}{min}\sum _{i=1}^K\sum _{j=1}^T\text{tr}(V_{[i,j]}^T{X}_{[i,j]}{V}_{[i,j]})+\lambda \sum _{i=1}^{K-1}\sum _{j=1}^T{\Vert V_{[i+1,j]}-V_{[i,j]}\Vert }_1\text{s.t.}{V}_{[i,j]}^T{M}_{[i,j]}{V}_{[i,j]}=I;V_{[i,j]}\in {ℝ}^{n\times p}.$$ (12)

We have now imposed both the longitudinal and cross-sectional basis coupling: for all partitions and time points.

3. Optimization scheme for coupled bases

In this section, we present an efficient numerical procedure for solving (12). Recall that the constraints involving the mass matrix form the generalized Stiefel manifold. We first present a few relevant technical details of the Stiefel manifold for completeness.

The set GF_n,p = {u ∈ ℒ(ℝⁿ, ℝ^p) : rank(u) = n} of n–frames in ℝ^p is called the Stiefel manifold. When p = n, GF_n,n := GF_n is the General Linear group or the set of n × n matrices with nonzero determinant. In other words, a Stiefel manifold is the set of n × p orthonormal matrices (with a Riemannian structure). ℒ(ℝⁿ, ℝ^p) is the vector space of linear maps form ℝⁿ to ℝ^p with the space ℝ^n×p of n × p matrices. Additional details on these topics such as tangent space, exponential map and retraction, are available in [1].

Algorithm 1.

Stochastic block coordinate descent in GF_n,p

1:	Given: f : GFn,p → ℝ, V ∈ GFn,p(M), M ∈ ℝn×n
2:	while Convergence criteria not met do
3:	𝒮 := Subproblem row indices
4:	P0 := Initial feasible submatrix (19)
5:	G := Subdifferential of f w.r.t. P0 (20)
6:	W := Descent curve in the direction of −G on GFs,p(M𝒮𝒮) at P0 (22)
7:	τ:= Step size under strong Wolfe conditions [17]
8:	P := Feasible point W(τ) of subproblem with sufficient decrease in f
9:	V′ (P) := Update new feasible point (23)
10:	end while

Our main strategy is to perform block coordinate descent over GF_n,p to solve for {V_[i,j]} for each matrix X_[i,j] given in (12). Specifically, our algorithm iteratively decreases the objective value of the problem by finding the next feasible point in a curve which lies in the generalized Stiefel manifold GF_n,p described in the constraints of (8), by adapting the scheme in [4, 9, 33]. This process is invoked as a module within our full pipeline.

Next, we show the entire framework of our algorithm which solves for all V_[i,j] of the model (12) by iteratively solving for each V_[i,j] while fixing the other decision variables V_[i′,j′], ∀i′ ≠ i&j′ ≠ j. In each iteration, we also update the mass matrix M_[i,j] using the most recent bases.

Stochastic block coordinate descent in GF_n,p

For simplicity, let us focus on a single arbitrary partition and its Laplacian X, mass matrix M and the eigenvectors V and setup the following coupled model as in (11):

$$\underset{V\in {ℝ}^{n\times p}}{min}\text{tr}(V^{T}XV)+\lambda g(V)\text{s.t.}{V}^{T}MV=I,$$ (13)

where the regularization term g(V) from (10). First, we show how to solve (13) on a subset of the dimensions. This is a very common procedure in a coordinate descent method where the dimensions can be computed nearly independently to allow parallelization and make large-scale implementation possible. Specifically, we construct a subproblem for each submatrix V_𝒮· ∈ ℝ^s×p where 𝒮 is a subset of s row indices of V. We choose this submatrix as the free variable which we ultimately solve for while fixing the complementary submatrix V_𝒮̄· for the rows 𝒮̄ called the fixed variable which we essentially treat as constants. Assuming w.l.o.g. that V_𝒮· contains the first s rows of V and its complement V_𝒮̄· contains the leftover indices, the constraint V^TMV = I in (13) can be reorganized as

$${\left[\begin{array}{c}{V}_{\mathcal{S}·}\\ V_{\overline{\mathcal{S}}·}\end{array}\right]}^T\left[\begin{array}{cc}{M}_{\mathcal{S}\mathcal{S}}& M_{\overline{\mathcal{S}}\mathcal{S}}^T\\ M_{\overline{\mathcal{S}}\mathcal{S}}& M_{\overline{\mathcal{S}}\overline{\mathcal{S}}}\end{array}\right]\left[\begin{array}{c}{V}_{\mathcal{S}·}\\ V_{\overline{\mathcal{S}}·}\end{array}\right]=I.$$ (14)

Rearranging it to move all the fixed variables on one side results in

$$V_{\mathcal{S}·}^T{M}_{\mathcal{S}\mathcal{S}}{V}_{\mathcal{S}·}+V_{\overline{\mathcal{S}}·}^T{M}_{\overline{\mathcal{S}}\mathcal{S}}{V}_{\mathcal{S}·}+V_{\mathcal{S}·}^T{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·}=:\widehat{H},$$ (15)

for a constant matrix Ĥ. With the full-rank assumption on M_𝒮𝒮, completing the square results the following:

$${\left(M_{\mathcal{S}\mathcal{S}}^{\frac{1}{2}}{V}_{\mathcal{S}·}+M_{\mathcal{S}\mathcal{S}}^{-\frac{1}{2}}{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·}\right)}^T\left(M_{\mathcal{S}\mathcal{S}}^{\frac{1}{2}}{V}_{\mathcal{S}·}+M_{\mathcal{S}\mathcal{S}}^{-\frac{1}{2}}{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·}\right)=H$$ (16)

for a new constant matrix $H=\widehat{H}+V_{\overline{\mathcal{S}}·}^T{M}_{\overline{\mathcal{S}}\mathcal{S}}{M}_{\mathcal{S}\mathcal{S}}^{-1}{M}_{\mathcal{S}\overline{\mathcal{S}}}{V}_{\overline{\mathcal{S}}·}$. Since we assume that M is positive definite, M_𝒮𝒮 is also positive definite and invertible.

Now, given an orthogonal subproblem decision matrix P, the next feasible iterate can be provided as

$$V_{\mathcal{S}·}=M_{\mathcal{S}\mathcal{S}}^{-\frac{1}{2}}P{H}^{\frac{1}{2}}-M_{\mathcal{S}\mathcal{S}}^{-1}{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·},$$ (17)

which satisfies the constraints in (14). Note that by using a retraction, we can smoothly map the tangent vectors to the manifold and preserve the key properties of the exponential function necessary to perform feasible descent on the manifold. For the Stiefel manifold, a computationally efficient retraction comes from the Cayley transform which can be extended to the generalized Stiefel manifold shown by Equation (1.2) and Lemma 4.1 of [33]. Consequently, we can eliminate the extra computation of the matrix square roots and simplify (17) to the following:

$$V_{\mathcal{S}·}=P-M_{\mathcal{S}\mathcal{S}}^{-1}{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·}.$$ (18)

If P^TM_𝒮𝒮P = H for M_𝒮𝒮 ≻ 0 and non-singular H, the above equation satisfies the subproblem constraint. Thus, given the previous V, the descent curve starts at the point:

$$P_0=V_{\mathcal{S}·}+M_{\mathcal{S}\mathcal{S}}^{-\frac{1}{2}}{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·}.$$ (19)

So far, we have shown how to setup the initial point for the line search step. Next, we describe how to compute the descent curve of the subproblem on the generalized Stiefel manifold for the line search on the manifold. The first step is to find the gradient of the objective function of (13) which is f(V) = V^TXV + λ g(V). Thus, for f(U) and V(P) where the next feasible point V as a function of P as in (18), the gradient of f ○ V(P) w.r.t. P is

$$\frac{\partial (f\circ V(P))}{\partial P}=2(X_{\mathcal{S}\mathcal{S}}{V}_{\mathcal{S}·}+X_{\mathcal{S}\overline{\mathcal{S}}}{V}_{\overline{\mathcal{S}}·})+\lambda g^{\prime }(V(P)),$$ (20)

where g′(V(P)) is the subgradient of the regularization term (10). Next, we project the descending subgradient −G′ at P₀ onto the tangent space of the manifold GF_i,p(M_𝒮𝒮) by constructing a skew-symmetric matrix:

$$Q=G{P}_0^T-P_0{G}^T,$$ (21)

which conveniently allows the Cayley transform as in [33] to smoothly map from the tangent space to the generalized Stiefel manifold to create the descent curve W as a function of τ:

$$W(\tau )={\left(I+\frac{\tau }{2}Q{M}_{\mathcal{S}\mathcal{S}}\right)}^{-1}\left(I-\frac{\tau }{2}Q{M}_{\mathcal{S}\mathcal{S}}\right)P_0.$$ (22)

We can linearly search over the descent curve to find the new point P = W(τ) for some τ which results sufficient decrease in f. Thus, the next feasible decision variable V′ ∈ ℝ^n×p as a function of P is

$$V^{\prime }(P)=\left[\begin{array}{c}P-M_{\mathcal{S}\mathcal{S}}^{-1}{M}_{\overline{\mathcal{S}}\mathcal{S}}^T{V}_{\overline{\mathcal{S}}·}\\ V_{\overline{\mathcal{S}}·}\end{array}\right]$$ (23)

so we can finally assign the current V with V′. By the construction of the coupled bases model (13), V′ is updated to minimize the objective function while it remains coupled with the other longitudinal and cross-sectional bases connected to V. The pseudo-code of the algorithm is in Alg. 1.

Algorithm 2.

Coupled bases framework using SBCD

1:	Given:
	f : GFn,p → ℝ, V[:,:] ∈ GFn,p(M[:,:]), M[:,:] ∈ ℝn×n
2:	while Convergence criteria not met do
3:	for i = 1,…, K do
4:	for j = 1,…, T do
5:	V[i,j] := Free variable
6:	V[i,j] := SBCD(V[i,j]) (Alg. 1)
7:	end for
8:	for j = 1,…, T do
9:	R[i,j] := Rotation matrix (3)
10:	end for
11:	for j = 1,…, T do
12:	M[i,j] := Mass matrix (6), (7)
13:	end for
14:	end for
15:	end while

Iterative SBCD in GF_n,p for bases coupling

With the stochastic block gradient descent (SBCD) method roughly similar to [16] as a solver for a single coupled basis, we now setup the framework to solve for all coupled bases. Specifically, given multiple matrices X_[i,j] for i = 1,…, K and j = 1,…, T, we set up grid-like iterations as shown in Alg. 2 where we iteratively pass through all possible pairs of i and j. In each iteration, we set V_[i,j] for the current pair of i and j to be the free variable and set V_[i′,j′] of the remaining i′ ≠ i and j′ ≠ j to be the fixed variables. We solve for only the free variable V_[i,j] using SBCD iteratively for all i and j.

Since (13) imposes the longitudinal coupling based on the mass matrices that are precomputed from the bases available at that iteration, they might not reflect the most accurate longitudinal relations precomputed mass matrices involving rotation matrices of the bases. Therefore, we must update the mass matrices so that they reflect the most accurate bases (encoding the naturally derived longitudinal trajectory) by recomputing the rotation matrices of the newly updated bases. Thus, the mass matrix computation step immediately follows the bases update step. We repeat these steps iteratively until convergence criteria are met.

4. Experiments

Data and scientific goal

Our dataset focuses on a cohort of middle aged individuals who are at risk for Alzheimer’s disease (AD) due to a positive family history (at least one parent with confirmed diagnosis of AD). Our data corresponds to at least three longitudinal scans of these subjects. The participants are cognitively healthy but some AD related brain changes, while subtle, have already begun. Note that in the analysis of anatomical changes in standard magnetic resonance images (not brain connectivity as we do here), numerous findings suggest that accurate quantification of brain “changes”, e.g., via tensor based morphometry, is often more sensitive than the analysis of individual images independently [8]. But in the context of AD (and for other brain disorders) most, if not all, such studies focus on data that cover the full spectrum of the disease (healthy to AD) – the disease effects of those data are much stronger and arguably easier to detect than those in the setting we consider here. We expect that estimating the longitudinal change process in connectivity accurately via the coupled harmonic bases model will enable identifying a disease signal even in the pool of healthy (but at-risk) individuals.

Workflow for deriving brain connectivity networks

There are three key steps in deriving brain connectivity networks for a given population study. (a) Coordinate system. For population level analysis of brain images, one typically needs to register all the images onto a standard coordinate system in a way that avoids any unwanted biases. We follow recommended procedures for deriving an unbiased coordinate system for the 3D+time regime as follows [11]. We first estimate a subject-specific average that is temporally unbiased. The subject specific averages are then used to generate an unbiased population level average template space, the process is summarized in Fig. 4. (b) Edges. We use tractography for deriving edges of the in vivo brain (structural) networks. The key ingredient needed for these algorithms is the orientational information of white matter fibers passing through a voxel, inferred by fitting a tissue model to the acquired MR signal from diffusion weighted imaging. Our data was acquired at a single shell diffusion weighting of b = 1000 s/mm². Although limited in its ability to resolve crossing fiber tissue, for this data the most reliable model that can be fit is the so called diffusion tensor. The principal eigenvector of the diffusion tensor in a voxel provides a proxy to the predominant orientation of the white matter fibers in that voxel. Using this information, we repeated probabilistic tractography twenty times [5]. The normalized standard deviation of the eigenvectors of the tensor (also known as fractional anisotropy) in the tracts passing between two regions serves as the edge strength between nodes in our experiments. (c) Nodes. The third key component is the node definition. For defining nodes, we relied on expert neuroanatomy groups who have carefully delineated the boundaries of regions in the brain based on their knowledge (including histological studies). We used the gray matter atlas defined on a DTI template [29] which provides 160 distinct regions in the brain.

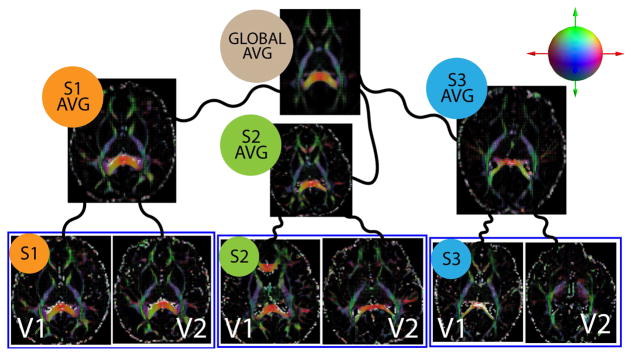
Figure 4.

Unbiased estimation of the global coordinate system for the longitudinally acquired imaging data. Visits are averaged first which are then used to estimate the global average. Each of the curved black lines represents a combination of rigid, affine and non-linear diffeomorphic transformations. These transformations and the spatial averages are estimated iteratively. Diffusion tensors are directly registered using log-Euclidean framework [35].

Covariates for creating sub-cohorts/partitions

We partition the full cohort using two key ordinal covariates: Rey Auditory Verbal Learning Test (RAVLT) [22] and Mini Mental State Exam (MMSE) [26]. These are cognitive performance scores based on tests that assess the cognitive functioning of the subjects and common in preclinical assessments of AD. Note that there is a systematic effect of age and gender on these scores. To control for these nuisance variables, we perform regression against these variables and derive z-scores for both RAVLT and MMSE. This imposes an implicit ordering of the subjects for the two measures, after the effect of age and sex has been accounted for. We derive K partitions of the z-scores to “stage” the cognitive status (and the subjects) into distinct cognitive quantiles. This implies that even within the full set of “healthy” individuals, subjects that fall within the same quantile are similar. If this staging is finer, we have fewer samples in each partition. We used K ∈ {2, 3, 4} partitions to keep the individual-level variance manageable while still allowing us to identify the general connectivity evolution patterns. Although we assume that all participants are recruited into the study concurrently (which may not be true), since they are assigned to distinct cognitive quantiles, estimating their longitudinal trajectories is reasonable (also, since the entire cohort is middle aged). In case of uneven distribution along the time axis, standard imputation strategies may be needed. Here, we only utilized data where all three time points were available to keep the presentation simple and avoid concerns related to the potential effect/bias of the specific imputation methods. Once the subjects are assigned to the appropriate partitions based on their z-scores (columns in Fig. 3), we can derive the average Laplacians, formulate the system as (12) and solve for the coupled bases.

Design

We use 68 subjects with three longitudinal time points and partition them for different K based on RAVLT and MMSE z-scores. Then, for each setting, we compute four sets of bases: (a) non-coupled (2), (b) longitudinally coupled (9), (c) cross-sectionally coupled ((12) with matrix M = I) and (d) longitudinally+cross-sectionally coupled (12). Thus, each partition now has a set of longitudinal bases (vertical direction in Fig. 3). For a novel test subject, we can calculate the corresponding connectivity graph and compare to each of the K partitions. The quantile of the closest partition is the label of this new subject. First, to measure the overall accuracy of this procedure, we use 21 ‘held out’ test subjects, which were not used to compute the four sets of bases to avoid overfitting, where each subject has three longitudinal scans available. So, we have total of 21 × 3 = 63 distinct Laplacians. We perform two classification tasks. First, we only predict the quantiles of the Laplacians at the first (or baseline) time point. Next, we predict all 63 Laplacians which is expected to be much harder since the quantiles of the subsequent time points are not used in deriving the partitions. Nonetheless, we expect that if our coupled bases are accurate, the information from the first time point should, in principle, affect subsequent time points in a way that allows our model to still predict the label correctly. We evaluated p ∈ {n/4, n/2, 3n/4} and chose p = n/4 since the residual is extremely small beyond n/2. We used |𝒮| = 40, but for larger datasets, it can be set to be larger if computationally feasible while also considering the approximation/speed trade-off. Lastly, we used λ ∈ {1, 20, 50}.

Results

We show the prediction accuracies of our algorithm in Table 1. We run the classification tasks for K ∈ {2, 3, 4} respectively. We compare the similarities of the bases of each test subject (using ℓ₂ norm) to the set of bases in each partition to locate the closest one, which is the assigned quantile label of the test subject. In Table 1, we show the accuracy results for RAVLT and MMSE using four setups (columns 2 through 5): (a) non-coupled, (b) longitudinally coupled, (c) cross-sectionally coupled and (d) both longitudinally and cross-sectionally coupled. For RAVLT, first, we discuss the simplest setting for K = 2 (R:2 in Table 1). Here, the performance estimates suggest that the first three setups are unable to identify the signal whereas our proposed coupled setup offers accuracy estimates approaching 70%. This trend of the coupled setup improving the accuracy of the non-coupled or partially coupled setup continues for K = 3 (R:3) and K = 4 (R:4). We observe a very similar trend for the MMSE quantile prediction task suggesting that capturing the full set of longitudinal data in terms of its coupled bases offers significant advantages for predicting subject-level cognitive status.

Table 1.

Prediction accuracy (%) of RAVLT (R:K ∈ {2, 3, 4} quantiles) and MMSE (M:K ∈ {2, 3, 4} quantiles) on j = 1 time point and j = {1, 2, 3}. Best results are in red.

K	Non-coupled		Longitudinal		Cross-section		Coupled
	j=1	{1, 2, 3}	1	{1, 2, 3}	1	{1, 2, 3}	1	{1, 2, 3}
R:2	33.33	34.92	42.86	42.86	66.67	60.32	71.43	71.43
R:3	38.10	33.33	52.38	36.51	57.14	44.44	57.14	55.56
R:4	28.57	28.57	23.81	30.16	30.16	23.81	47.62	34.92
M:2	42.86	41.27	28.57	30.16	57.14	39.68	76.19	71.43
M:3	42.86	38.10	47.62	49.21	47.62	46.03	47.62	50.79
M:4	34.92	28.57	23.81	14.29	19.05	12.70	47.62	28.57

Discussion

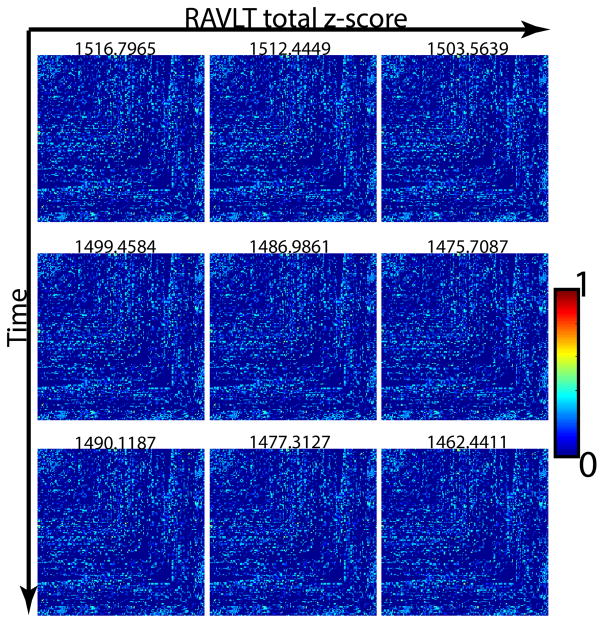
We briefly elaborate on the relevance of these findings. Recall that our dataset is preclinical, i.e., all subjects are healthy. This means that the brain connectivity changes that we seek to capture using our proposed formulation are extremely subtle. To appreciate the small effect sizes in this dataset, we show in Fig. 5 the actual brain connectivity adjacency matrices for K = 3 from the RAVLT based staging. The numbers at the top of each matrix image is the total sum of edge weights in the graph. As expected, when we move from left to right (and top to bottom), the overall connectivity progressively becomes weaker but the changes are extremely small and nearly impossible to pick up in a statistically significant way if this analysis were conducted on an edge-by-edge manner. Despite the fact that the overall changes are in the 0.5–1.0% range over the entire set of 12720 edges, our coupled harmonic bases setup is still able to offer better than chance prediction accuracy. Achieving this capability in a preclinical population is the main scientific result of our experimental evaluations.

Figure 5.

Average adjacency matrices for each of the three stages (columns) based on RAVLT total z-scores and each of the three time points (rows). The total magnitude of connectivity strengths (sum of the total edge weights) are shown in the respective titles of the matrices. Even though there is a trend of decrease in the overall connectivity strength along the cognitive staging, the effect sizes are extremely small 0.5 – 1.0%. In the case of individual edges the effects are even smaller.

Finally, we note that our model recovers disease effects at the level of individual tracts reliably: it specifically identified the top 50 fiber tracts with the most changes in connectivity strength across RAVLT progression (illustrative results are described in detail in the supplement).

5. Conclusion

The goal of this paper is to characterize the evolutionary patterns of brain connectivity networks derived from a longitudinal set of middle-aged healthy individuals who are at risk for Alzheimer’s disease. The changes in brain connectivity are extremely small during the preclinical stages and existing approaches do not seem to be sensitive enough. We presented a framework which treats the entire set of graph Laplacians of the brain connectivity networks as a system by explicitly considering the coupling between different cognitive as well as the longitudinal (temporal) stages. Our experimental results provide evidence that such a coupled bases approach can indeed provide better insights into the brain network changes across the clinical stages. While the technical development of our framework was motivated by the neuroimaging application, the resultant numerical optimization schemes can be widely applicable for incorporating relevant couplings into generalized eigenvalue problems which are pervasive in many other areas of computer vision and machine learning. The extended version of this paper, the supplement and the code are available at http://pages.cs.wisc.edu/~sjh/.