Abstract
To assess the statistical significance of associations between variants and traits, genome-wide association studies (GWAS) should employ an appropriate threshold that accounts for the massive burden of multiple testing in the study. Although most studies in the current literature commonly set a genome-wide significance threshold at the level of P=5.0 × 10−8, the adequacy of this value for respective populations has not been fully investigated. To empirically estimate thresholds for different ancestral populations, we conducted GWAS simulations using the 1000 Genomes Phase 3 data set for Africans (AFR), Europeans (EUR), Admixed Americans (AMR), East Asians (EAS) and South Asians (SAS). The estimated empirical genome-wide significance thresholds were Psig=3.24 × 10−8 (AFR), 9.26 × 10−8 (EUR), 1.83 × 10−7 (AMR), 1.61 × 10−7 (EAS) and 9.46 × 10−8 (SAS). We additionally conducted trans-ethnic meta-analyses across all populations (ALL) and all populations except for AFR (ΔAFR), which yielded Psig=3.25 × 10−8 (ALL) and 4.20 × 10−8 (ΔAFR). Our results indicate that the current threshold (P=5.0 × 10−8) is overly stringent for all ancestral populations except for Africans; however, we should employ a more stringent threshold when conducting a meta-analysis, regardless of the presence of African samples.
Introduction
Genome-wide association studies (GWAS) have successfully identified thousands of loci associated with human diseases and traits.1, 2 To assess the statistical significance of associations between tested variants and traits, GWAS should employ an appropriate threshold that accounts for the massive burden of multiple testing undertaken in the study.3, 4 Although a variety of statistical approaches have been developed to estimate this burden, including the Bonferroni correction,5, 6 Sidak correction,7 false discovery rate8 and permutation test, most GWAS commonly set a genome-wide significance threshold at the level of P=5.0 × 10−8, which is equivalent to the Bonferroni-corrected threshold (α=0.05) for 1 million independent variants (approximately the number of independent single-nucleotide polymorphisms (SNPs) estimated using the HapMap Phase II data set9).
The number of variants tested in recent GWAS, however, has increased dramatically because of the widespread use of genotype imputation using the 1000 Genomes data set as a reference10, 11, 12, 13 or whole-genome sequencing,14, 15, 16 and therefore the supposition of the above-mentioned Bonferroni correction has become untenable. Additionally, the variants tested in a study are inevitably dependent on population-specific factors, such as linkage disequilibrium (LD) pattern and minor allele frequency (MAF), suggesting that the appropriate threshold for genome-wide significance might vary for different populations.17 For example, the threshold for a population with a lower LD pattern, such as the African population, should be more stringent than a population with higher LD, as the number of independent markers tends to be greater in the former population than the latter. To address the independence of genetic markers in LD, several studies have proposed methods for estimating the effective number of independent tests Me;17, 18, 19 however, the effectiveness of these methods remains unclear. On the other hand, the current threshold, P=5.0 × 10−8, has been claimed to be overly stringent.20, 21 A previous study showed that 73% of ‘borderline' associations (5.0 × 10−8<P⩽10−7) could be replicated with the inclusion of additional data from subsequent GWAS, suggesting the potential for relaxation of the current threshold.20
We report here empirical estimation of genome-wide significance thresholds for different populations based on GWAS simulations using the 1000 Genomes Phase 3 data set, the most recently released and widely used reference panel for genotype imputation containing five major ethnic ancestries. For each ancestral population in this data set, we tested associations of the variants with the simulated phenotypes and calculated empirical genome-wide significance thresholds based on the distributions of the minimum P-value of the associations. Our empirical estimation revealed that different thresholds should be adopted for different ancestral populations or trans-ethnic meta-analyses rather than the current single genome-wide significance threshold of P=5.0 × 10−8.
Materials and methods
Samples and ancestral populations
We used the 1000 Genomes Project11, 12 (http://www.1000genomes.org/) Phase 3 data set (version 5), which comprises approximately 51 million variants (autosome and chromosome X) from 2504 individuals in 26 populations (Table 1). We split the data set into five ancestral populations: African (AFR; n=661), European (EUR; n=503), Admixed American (AMR; n=347), East Asian (EAS; n=504), and South Asian (SAS; n=489). For each ancestral population, we excluded SNPs that were monomorphic, singleton or MAF<0.5% and obtained 21 048 933, 11 980 247, 14 261 439, 10 201 713 and 12 641 702 variants for AFR, EUR, AMR, EAS and SAS, respectively.
Table 1. Overview of the 1000 Genomes Phase 3 (version 5) samples.
|
No. of samples |
||||||
|---|---|---|---|---|---|---|
| Ancestral population | Subpopulation | Code | Male | Female | Total | No. of variantsa (MAF>0.5%) |
| AFR | African Caribbeans in Barbados | ACB | 47 | 49 | 96 | 21 048 933 |
| Americans of African Ancestry in SW USA | ASW | 26 | 35 | 61 | ||
| Esan in Nigeria | ESN | 53 | 46 | 99 | ||
| Gambian in Western Divisions in the Gambia | GWD | 55 | 58 | 113 | ||
| Luhya in Webuye, Kenya | LWK | 44 | 55 | 99 | ||
| Mende in Sierra Leone | MSL | 42 | 43 | 85 | ||
| Yoruba in Ibadan, Nigeria | YRI | 52 | 56 | 108 | ||
| Subtotal | 319 | 342 | 661 | |||
| EUR | Utah Residents (CEPH) with Northern and Western European Ancestry | CEU | 49 | 50 | 99 | 11 980 247 |
| Finnish in Finland | FIN | 38 | 61 | 99 | ||
| British in England and Scotland | GBR | 46 | 45 | 91 | ||
| Iberian Population in Spain | IBS | 54 | 53 | 107 | ||
| Toscani in Italia | TSI | 53 | 54 | 107 | ||
| Subtotal | 240 | 263 | 503 | |||
| AMR | Colombians from Medellin, Colombia | CLM | 43 | 51 | 94 | 14 261 439 |
| Mexican Ancestry from Los Angeles, USA | MXL | 32 | 32 | 64 | ||
| Peruvians from Lima, Peru | PEL | 41 | 44 | 85 | ||
| Puerto Ricans from Puerto Rico | PUR | 54 | 50 | 104 | ||
| Subtotal | 170 | 177 | 347 | |||
| EAS | Chinese Dai in Xishuangbanna, China | CDX | 44 | 49 | 93 | 10 201 713 |
| Han Chinese in Beijing, China | CHB | 46 | 57 | 103 | ||
| Southern Han Chinese | CHS | 52 | 53 | 105 | ||
| Japanese in Tokyo, Japan | JPT | 56 | 48 | 104 | ||
| Kinh in Ho Chi Minh City, Vietnam | KHV | 46 | 53 | 99 | ||
| Subtotal | 244 | 260 | 504 | |||
| SAS | Bengali from Bangladesh | BEB | 42 | 44 | 86 | 12 641 702 |
| Gujarati Indian from Houston, Texas | GIH | 56 | 47 | 103 | ||
| Indian Telugu from the UK | ITU | 59 | 43 | 102 | ||
| Punjabi from Lahore, Pakistan | PJL | 48 | 48 | 96 | ||
| Sri Lankan Tamil from the UK | STU | 55 | 47 | 102 | ||
| Subtotal | 260 | 229 | 489 | |||
| Total | 1233 | 1271 | 2504 | 28 993 742 | ||
Abbreviations: AFR, African; AMR, Admixed American; EAS, East Asian; EUR, European; MAF, minor allele frequency; SAS, South Asian.
MAF was calculated within each ancestral population.
GWAS simulations
To empirically estimate appropriate genome-wide significance thresholds for different ancestral populations, we calculated empirical null distributions of the minimum P-values of the variants by randomly simulating case–control phenotypes. We conducted the simulations 100 000 times for each ancestral population using a permutation procedure. For each iteration, we randomly assigned case–control phenotypes at a ratio of 1:1 within each single subpopulation in the ancestral population. For autosomal variants, we tested associations of the variants on a logistic regression model using the PLINK 1.9 software (https://www.cog-genomics.org/plink2).22, 23 In order to account for potential population stratification, we included the top two principal components as covariates in the model; these were calculated for each ancestral population using the smartpca program in the EIGENSOFT 6.0.1 package (http://www.hsph.harvard.edu/alkes-price/software/).24 Additionally, we applied post-genomic control (GC) correction25 if the population-specific genomic inflation factor λGC was >1 in each simulation. For chromosome X variants, we first split a population into males and females and conducted separate analyses using the same procedure as described for autosomal variants. We then performed a meta-analysis across male and female subjects and integrated this into the autosomal variants' result to conduct a meta-analysis across all ancestral populations.
Meta-analysis
To simulate trans-ethnic meta-analysis, we performed a GWAS meta-analysis for a given iteration across all ancestral populations using the inverse-variance method with the assumption of a fixed-effect model.26 We included 28 993 742 variants that existed in at least one ancestral population. To prevent potential inflation from the inclusion of AFR samples, we also performed an additional meta-analysis that excluded AFR but included all other ancestries (that is, EUR, AMR, EAS and SAS).
Estimation of an empirical genome-wide significance
We measured the distributions of the minimum P-values of the variants (Pmin) for each ancestral population and meta-analysis result. We defined an empirical genome-wide significance threshold, −log10 Psig, as the 95th percentile (1−α) of −log10 Pmin at a significance level of α=0.05. We calculated −log10 Psig using the Harrell–Davis distribution-free quantile estimator27 and calculated 95% confidence interval for −log10 Psig by bootstrapping method. We also estimated the effective number of independent variants by dividing the significance level α=0.05 by Psig given the Bonferroni-corrected threshold and calculated the ratio of the effective number of independent variants to the total number of variants after quality control. All calculations were performed using the authors' scripts (http://mkanai.github.io/).
In order to confirm robustness of our approach for different MAF thresholds (0.1, 1 and 5%), different number of principal components (5, 10 and 20) or without post-GC correction, we additionally estimated empirical genome-wide significance thresholds under these different conditions. We note that we conducted the additional estimations for just 10 000 permutations each, except for the one without post-GC correction, considering their intensive computational cost.
LD pruning
Given that a population-specific LD structure significantly affects the number of independent variants in a population, we evaluated how Psig would reflect the effective number of independent variants estimated using the LD-based approach.17 We applied LD pruning with the PLINK 1.9 software,22, 23 using a 40-kb sliding window size, a 4-kb window step size and a maximum r2 threshold ranging from 0.1 to 1.0 in increments of 0.1. The number of remaining variants after LD pruning was considered as the effective number of independent variants. We calculated the LD-based genome-wide significance threshold by dividing the significance level α=0.05 by the population-specific effective number of independent variants, given the Bonferroni-corrected threshold. The effective ratio was defined as the ratio of the effective number of independent variants to the total number of variants after quality control.
Results
Empirical genome-wide significance
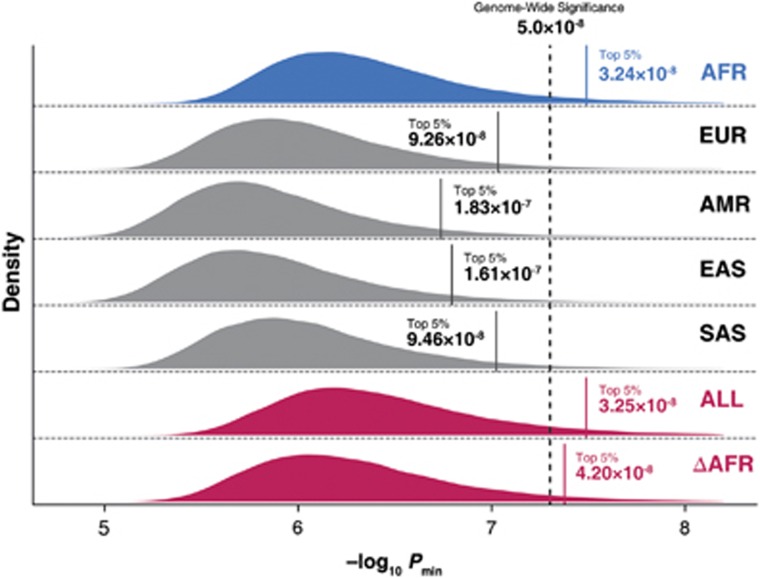
Based on the GWAS simulations for 100 000 times, we measured the −log10 Pmin distribution for each ancestral population and meta-analysis result (Figure 1). The empirical genome-wide significance thresholds for AFR, EUR, AMR, EAS and SAS were Psig=3.24 × 10−8 (95% confidence interval: 3.11–3.36 × 10−8); 9.26 × 10−8 (9.01–9.51 × 10−8); 1.83 × 10−7 (1.79–1.87 × 10−7); 1.61 × 10−7 (1.57–1.64 × 10−7) and 9.46 × 10−8 (9.20–9.69 × 10−8), respectively (Table 2). These results indicate that, with the exception of the African population, each ancestral population requires a different genome-wide significance threshold that is slightly more lenient than the current threshold of P=5.0 × 10−8.
Figure 1.
The −log10 Pmin distributions for five ancestral populations and meta-analysis results. We conducted GWAS simulations using the 1000 Genomes Phase 3 data set and measured the minimum P-value of the variants (Pmin). Each panel represents a population/meta-analysis result. Each vertical bar in the panel represents the top five percentile of −log10 Pmin (that is, the estimated empirical genome-wide significance −log10 Psig). The dotted vertical bar represents the common genome-wide significance threshold of 5.0 × 10−8. AFR, African; AMR, Admixed American; EAS, East Asian; EUR, European; SAS, South Asian; ALL, meta-analysis across all ancestral populations; ΔAFR, meta-analysis including all ancestral populations except for AFR (that is, EUR, AMR, EAS and SAS).
Table 2. Estimated genome-wide significance thresholds for ancestral populations and meta-analyses.
| Ancestry | Psig (−log10 Psig)a | 95% CIa | No. of variantsb (MAF>0.5%) | No. of effective variantsc | Ratio |
|---|---|---|---|---|---|
| AFR | 3.24 × 10−8 (7.49) | 3.11 × 10−8–3.36 × 10−8 (7.47–7.51) | 21 048 933 | 1 545 429 | 0.073 |
| EUR | 9.26 × 10−8 (7.03) | 9.01 × 10−8–9.51 × 10−8 (7.02–7.05) | 11 980 247 | 540 128 | 0.045 |
| AMR | 1.83 × 10−7 (6.74) | 1.79 × 10−7–1.87 × 10−7 (6.73–6.75) | 14 261 439 | 273 444 | 0.019 |
| EAS | 1.61 × 10−7 (6.79) | 1.57 × 10−7–1.64 × 10−7 (6.78–6.80) | 10 201 713 | 311 275 | 0.031 |
| SAS | 9.46 × 10−8 (7.02) | 9.20 × 10−8–9.69 × 10−8 (7.01–7.04) | 12 641 702 | 528 484 | 0.042 |
| ALL | 3.25 × 10−8 (7.49) | 3.16 × 10−8–3.33 × 10−8 (7.48–7.50) | 28 993 742 | 1 539 237 | 0.053 |
| ΔAFR | 4.20 × 10−8 (7.38) | 4.08 × 10−8–4.33 × 10−8 (7.37–7.39) | 19 862 732 | 1 189 822 | 0.060 |
Abbreviations: AFR, African; ALL, meta-analysis across all ancestral populations; AMR, Admixed American; CI, confidence interval; EAS, East Asian; EUR, European; MAF, minor allele frequency; SAS, South Asian; ΔAFR, meta-analysis including all ancestral populations except for AFR (that is, EUR, AMR, EAS and SAS).
The 5th percentile of Psig was calculated based on the 95th percentile of –log10 Psig.
MAF was calculated within each ancestral population.
The effective number of independent variants was calculated by dividing the significance level α=0.05 by Psig.
Trans-ethnic meta-analysis
Using the same procedure, we measured the −log10 Pmin distribution for trans-ethnic meta-analysis results (Figure 1). The estimated Psig values for ALL and ΔAFR were 3.25 × 10−8 (3.16–3.33 × 10−8) and 4.20 × 10−8 (4.08–4.33 × 10−8), respectively (Table 2). Compared with the current threshold for single-population GWAS (P=5.0 × 10−8), our estimations for both trans-ethnic meta-analyses (ALL and ΔAFR) are more stringent, regardless of whether the data set contained African samples or not.
We note that our empirical estimations remained approximately the same when using different MAF thresholds (0.1, 1 and 5%) or different number of principal components (5, 10 and 20) for calculations (Supplementary Tables S1 and S2). With regard to post-GC correction, although the empirical thresholds without the correction were slightly stringent as expected, the discrepancy was so small that it did not dismiss our conclusions (Supplementary Table S3).
Relationship between a population-specific LD structure and Psig
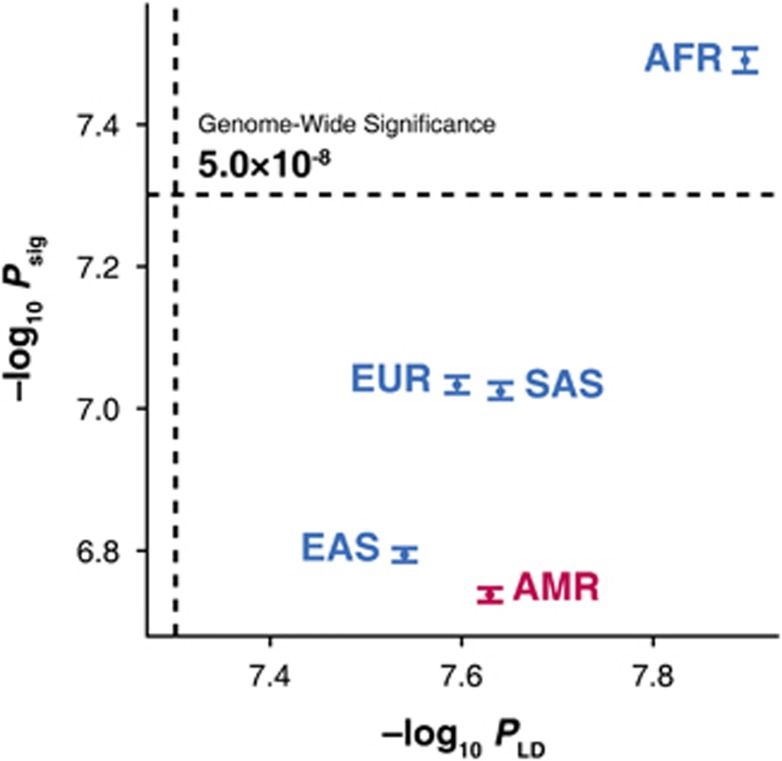
We applied LD pruning to each population using a maximum r2 threshold of 0.5 (Table 3; for a complete list, see Supplementary Tables S4 and S5). Based on the effective number of independent variants, we calculated an LD-based genome-wide significance threshold (PLD) by dividing a significance level α=0.05 given the Bonferroni-corrected threshold (Figure 2). For most ancestries (AFR, EUR, EAS and SAS), a −log10 Psig showed approximately positive correlation with −log10 PLD, suggesting that our estimation of the empirical genome-wide significance threshold clearly corresponded to the population-specific LD structure, as expected. However, we found that AMR was an outlier among the ancestral populations, with a substantial imbalance in the effective number of independent variants within the AMR population (Table 3). Although the effective numbers of independent variants for each subpopulation were well balanced in the other ancestries, the numbers for CLM (Colombians from Medellin, Colombia) and PUR (Puerto Ricans from Puerto Rico) were higher than those for the other subpopulations in AMR, leading to a potential increase in the overall effective number of independent variants for AMR.
Table 3. Estimated effective number of independent variants in the AMR subpopulations by LD pruning.
| Code | No. of variantsa (MAF>0.5%) | No. of effective variantsb | Ratio | PLD (−log10 PLD) |
|---|---|---|---|---|
| AMR | 14 261 439 | 2 129 877 | 0.149 | 2.35 × 10−8 (7.63) |
| CLM | 7 512 590 | 1 343 116 | 0.179 | 3.72 × 10−8 (7.43) |
| MXL | 7 218 484 | 985 773 | 0.137 | 5.07 × 10−8 (7.29) |
| PEL | 6 570 123 | 873 604 | 0.133 | 5.72 × 10−8 (7.24) |
| PUR | 7 735 691 | 1 542 788 | 0.199 | 3.24 × 10−8 (7.49) |
Abbreviations: AMR, Admixed American; CLM, Colombians from Medellin, Colombia; LD, linkage disequilibrium; MAF, minor allele frequency; MXL, Mexican Ancestry from Los Angeles, USA; PEL, Peruvians from Lima, Peru; PUR, Puerto Ricans from Puerto Rico.
MAF was calculated within each population.
The effective number of independent variants was estimated by LD-based pruning (sliding window size: 40 kb; window step size: 4 kb; r2<0.5).
Figure 2.
The relationship between −log10 PLD and −log10 Psig. We calculated the LD-based genome-wide significance PLD based on the effective number of independent variants, which was estimated by applying LD pruning with a maximum r2 threshold of 0.5. Whereas −log10 Psig showed approximately positive correlation with −log10 PLD for AFR, EUR, EAS and SAS (blue), AMR (red) is an outlier. The error bars represent the 95% CI for −log10 Psig. The dotted lines represent the common genome-wide significance threshold of P=5.0 × 10−8. AFR, African; AMR, Admixed American; EAS, East Asian; EUR, European; SAS, South Asian.
Discussion
In the present study, we estimated the empirical genome-wide significance thresholds for the five ancestral populations based on the GWAS simulations conducted using the 1000 Genomes Project Phase 3 data set. The results suggested that, for non-African populations, we could apply a threshold less stringent than the current level of P=5.0 × 10−8. On the other hand, the meta-analysis results revealed that more stringent thresholds should be adopted in meta-analysis study, regardless of the inclusion of African samples. Our empirical estimation based on the 1000 Genomes Project will be applicable to various studies, as most current studies conduct genotype imputation using the same data set.
To date, an increasing number of studies have conducted trans-ethnic meta-analysis to improve the power to identify susceptible loci by combining extremely large number of samples from single-population studies.28 Although these studies commonly adopted the same genome-wide significance threshold (P=5.0 × 10−8) used in a single-population GWAS, few have scrutinized the stringency of this threshold for preventing false positives. Our present study fills this gap and suggests that a more stringent threshold is needed for trans-ethnic meta-analysis even though African samples are absent from the data set.
Li et al.19 reported genome-wide significance thresholds for AFR, ASN (Asian) and EUR in the 1000 Genomes data set (released in August 2010) of 1.62 × 10−8, 3.47 × 10−8 and 3.06 × 10−8, respectively, based on the calculation of the effective number of independent markers using eigenvalues. As the number of samples and genotypes in the data set differed, we additionally applied their method to each population (AFR, EUR, AMR, EAS and SAS) in our data set, obtaining 4.94 × 10−9, 1.09 × 10−8, 9.05 × 10−9, 1.40 × 10−8 and 9.97 × 10−9, respectively. Our estimated thresholds were more lenient than both these previously reported and additionally calculated thresholds for the 1000 Genomes data set based on their method. This discrepancy arguably suggests the importance of empirical estimation, given the complex genetic backgrounds resulting from different LD structures among ancestral populations.
Considering the limited sample size (~2500) of the data set, our empirical estimation might not fully reflect the genetic backgrounds of humans. The 1000 Genomes Project estimated that their power to detect SNPs to be >95% for those with sample frequency of at least 0.5% and to be >75% with frequency of 0.1% for Europeans.11 Although it is difficult to exactly assess how far the data set of this sample size reflects the current populations, we envisage that the future panel will resolve the issue by providing new empirical estimations, given the recent efforts in the field to create much larger reference panels, such as the Haplotype Reference Consortium (http://www.haplotype-reference-consortium.org/).
Although the least stringent genome-wide significance threshold (Psig=1.83 × 10−7) was estimated for the AMR population, we note that further investigations would be required to fully assess the confounding bias resulting from complex LD structure of this recently admixed population, such as long-range LD regions.29 The observation of AMR as an outlier (Figure 2) suggests that the Psig estimated from an empirical distribution of associations does not simply reflect the population-specific LD structure but also other underlying dependencies. A recent study revealed that South American populations have different admixture history from their ancestry, which resulted in diverse proportions of African, European, Native American and Asian ancestries.30 Association studies of such complex admixed population should be carefully conducted to avoid potential false positives.
Additionally, in a typical GWAS of today, genotype imputation is commonly conducted to fine-map causal variants and increase a power,10, 13 which we should address its potential effect to our empirical estimations. Although we used whole variants in the data set that passed our quality control criteria, several variants would not be well imputed in a typical study, depending on a genotyping platform of the study. By defining imputable variants of the data set with reference to ‘SNP and indel imputability database'31 (http://www.unc.edu/~yunmli/1000G-imp/) for each combination of genotyping platforms and ancestral populations, we observed that the more variants an array has, the more stringent Psig is (Supplementary Table 6). We note that, as the database was constructed using the Phase 1 data set (version 3), we cannot simply compare the original results to those with only imputable variants. The relationship between array density and Psig supports that we could apply a more lenient threshold for current imputation-based single-population studies.
In this paper, we have presented empirically estimated genome-wide significance thresholds based on the 1000 Genomes data set. Despite the computational cost, our study illustrates the value of an empirical estimation for genetic data through calculating the empirical genome-wide significance threshold. The results indicate that we should adopt a more stringent threshold compared with the current level of P=5.0 × 10−8 in future studies of African samples or trans-ethnic meta-analyses, whereas the threshold might be relaxed for non-African studies.
Acknowledgments
This work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI grant numbers 15H05670, 15H05907, 15H05911 and 15K14429, the Japan Science and Technology Agency (JST), Mochida Memorial Foundation for Medical and Pharmaceutical Research, Takeda Science Foundation, Gout Research Foundation, the Tokyo Biochemical Research Foundation and the Japan Rheumatism Foundation.
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies the paper on Journal of Human Genetics website (http://www.nature.com/jhg)
Supplementary Material
References
- Hindorff, L. A, Sethupathy, P., Junkins, H. A, Ramos, E. M., Mehta, J. P., Collins, F. S. et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl Acad. Sci. USA 106, 9362–9367 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welter, D., MacArthur, J., Morales, J., Burdett, T., Hall, P., Junkins, H. et al. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res. 42, 1001–1006 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis, J. P. A. Non-replication and inconsistency in the genome-wide association setting. Hum. Hered. 64, 203–213 (2007). [DOI] [PubMed] [Google Scholar]
- Martin, L. J., Woo, J. G., Avery, C. L., Chen, H.-S. & North, K. E. Multiple testing in the genomics era: Findings from Genetic Analysis Workshop 15, Group 15. Genet. Epidemiol. 31, S124–S131 (2007). [DOI] [PubMed] [Google Scholar]
- Bonferroni, C. E. Teoria statistica delle classi e calcolo delle probabilità. Pubbl. R. Ist. Super. Sci. Econ. Commer. Firenze 8, 3–62 (1936). [Google Scholar]
- Bland, J. M. & Altman, D. G. Multiple significance tests: the Bonferroni method. BMJ 310, 170 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidak, Z. Rectangular confidence regions for the means of multivariate normal distributions. J. Am. Stat. Assoc. 62, 626 (1967). [Google Scholar]
- Storey, J. D. & Tibshirani, R. Statistical significance for genomewide studies. Proc. Natl Acad. Sci. USA 100, 9440–9445 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap Consortium A second generation human haplotype map of over 3.1 million SNPs. Nature 449, 851–861 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini, J. & Howie, B. Genotype imputation for genome-wide association studies. Nat. Rev. Genet. 11, 499–511 (2010). [DOI] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium A global reference for human genetic variation. Nature 526, 68–74 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudmant, P. H., Rausch, T., Gardner, E. J., Handsaker, R. E., Abyzov, A., Huddleston, J. et al. An integrated map of structural variation in 2504 human genomes. Nature 526, 75–81 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood, A. R., Perry, J. R. B., Tanaka, T., Hernandez, D. G., Zheng, H.-F., Melzer, D. et al. Imputation of variants from the 1000 Genomes Project modestly improves known associations and can identify low-frequency variant-phenotype associations undetected by HapMap based imputation. PLoS One 8, e64343 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cirulli, E. T. & Goldstein, D. B. Uncovering the roles of rare variants in common disease through whole-genome sequencing. Nat. Rev. Genet. 11, 415–425 (2010). [DOI] [PubMed] [Google Scholar]
- Gudbjartsson, D. F., Helgason, H., Gudjonsson, S. A., Zink, F., Oddson, A., Gylfason, A. et al. Large-scale whole-genome sequencing of the Icelandic population. Nat. Genet. 47, 435–444 (2015). [DOI] [PubMed] [Google Scholar]
- Cai, N., Bigdeli, T. B., Kretzschmar, W., Li, Y., Liang, J., Song, L. et al. Sparse whole-genome sequencing identifies two loci for major depressive disorder. Nature 523, 588–591 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobota, R. S., Shriner, D., Kodaman, N., Goodloe, R., Zheng, W., Gao, Y.-T. et al. Addressing population-specific multiple testing burdens in genetic association studies. Ann. Hum. Genet. 79, 136–147 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao, X., Starmer, J. & Martin, E. R. A multiple testing correction method for genetic association studies using correlated single nucleotide polymorphisms. Genet. Epidemiol. 32, 361–369 (2008). [DOI] [PubMed] [Google Scholar]
- Li, M.-X., Yeung, J. M. Y., Cherny, S. S. & Sham, P. C. Evaluating the effective numbers of independent tests and significant P-value thresholds in commercial genotyping arrays and public imputation reference datasets. Hum. Genet. 131, 747–756 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panagiotou, O. A, Ioannidis, J. P. & Genome-Wide Significance Project. What should the genome-wide significance threshold be? Empirical replication of borderline genetic associations. Int. J. Epidemiol. 41, 273–286 (2012). [DOI] [PubMed] [Google Scholar]
- Williams, S. M. & Haines, J. L. Correcting away the hidden heritability. Ann. Hum. Genet. 75, 348–350 (2011). [DOI] [PubMed] [Google Scholar]
- Purcell, S., Neale, B., Todd-Brown, K., Thomas, L., Ferreira, M. A., Bender, D. et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, C. C., Chow, C. C., Tellier, L. C., Vattikuti, S., Purcell, S. M. & Lee, J. J. Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience 4, 1–16 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A. & Reich, D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38, 904–909 (2006). [DOI] [PubMed] [Google Scholar]
- Devlin, B. & Roeder, K. Genomic control for association studies. Biometrics 55, 997–1004 (1999). [DOI] [PubMed] [Google Scholar]
- de Bakker, P. I. W., Ferreira, M. A R., Jia, X., Neale, B. M., Raychaudhuri, S. & Voight, B. F. Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum. Mol. Genet 17, R122–R128 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrell, F. E. & Davis, C. E. A new distribution-free quantile estimator. Biometrika 69, 635–640 (1982). [Google Scholar]
- Okada, Y., Wu, D., Trynka, G., Raj, T., Terao, C., Ikari, K. et al. Genetics of rheumatoid arthritis contributes to biology and drug discovery. Nature 506, 376–381 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price, A. L., Weale, M. E., Patterson, N., Myers, S. R., Need, A. C., Shianna, K. V. et al. Long-range LD can confound genome scans in admixed populations. Am. J. Hum. Genet. 83, 132–135 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homburger, J. R., Moreno-Estrada, A., Gignoux, C. R., Nelson, D., Sanchez, E., Ortiz-Tello, P. et al. Genomic insights into the ancestry and demographic history of South America. PLOS Genet. 11, e1005602 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan, Q., Liu, E. Y., Croteau-Chonka, D. C., Mohlke, K. L. & Li, Y. A comprehensive SNP and indel imputability database. Bioinformatics 29, 528–531 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.