Negative thermal expansion materials: technological key for control of thermal expansion

Abstract

Most materials expand upon heating. However, although rare, some materials contract upon heating. Such negative thermal expansion (NTE) materials have enormous industrial merit because they can control the thermal expansion of materials. Recent progress in materials research enables us to obtain materials exhibiting negative coefficients of linear thermal expansion over −30 ppm K⁻¹. Such giant NTE is opening a new phase of control of thermal expansion in composites. Specifically examining practical aspects, this review briefly summarizes materials and mechanisms of NTE as well as composites containing NTE materials, based mainly on activities of the last decade.

Introduction

Thermal expansion, the increase in volume upon heating under constant pressure, is assumed to be normal from experience in the realm of research and in daily life. Ubiquity of thermal expansion is easily understood from well-known examples: the joints of rails or bridge girders contain spaces, and precision optical instruments are placed under strict temperature control to reduce the effects of thermal expansion.

For a typical material iron, the coefficient of linear thermal expansion, α=(1/L₀)(dL/dT), is about 12 ppm K⁻¹, where L and L₀ are the lengths at temperature T and reference temperature T₀, respectively, and ppm stands for parts per million. This corresponds to a 1.2 mm elongation of a 1-m-long iron rod upon heating by 100 K. Such a small elongation is difficult to detect by the unaided eye no matter how we fix our eyes on it. However, even such a minute variation fatally degrades the performance of a device and facilities in many fields of highly advanced modern industries, as is apparent in production processes of semiconductor devices with 30 nm line width and optical system handling of light with ultrashort wavelength such as x-rays. The control of thermal expansion is also a key technology for providing high performance to fuel cells and thermoelectric converters.

Negative thermal expansion (NTE) materials, materials that contract upon heating, meet the severe requirement of tuning the overall thermal expansion of materials. Remarkable development in the field of NTE materials has been achieved over the last decade. This has opened a new field of composites using NTE materials as thermal-expansion compensators.

This review presents specific examination of the recent activities of thermal-expansion control in materials. The materials and mechanisms of NTE are explained, mainly from a practical viewpoint. Thermal-expansion adjustable composites comprising NTE materials are also introduced in the latter part of this review. General arguments on NTE are beyond the scope of this review and can be found in [1–6].

Thermal expansion of solids

A standard textbook on solid state physics shows that the anharmonicity of lattice vibrations causes thermal expansion [7]. Anharmonicity means that the springs that tie atoms together in a lattice model do not exactly and simply obey Hooke's law. The atoms are prevented from getting extremely close to each other because of the Pauli exclusion principle. Therefore, the potential energy of atomic bonds as a function of interatomic distance Δr diverges when Δr approaches zero (figure 1). Because of this asymmetry of the potential well, excursions to longer interatomic distances are easier than shorter interatomic distances. Consequently, the average interatomic distance increases concomitantly with increasing temperature. Thermal expansion caused by the natural law is apparently a destiny of solids.

Figure 1.

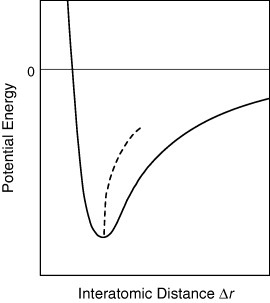
Potential energy (solid line) for a typical chemical bond as a function of interatomic distance Δr. The dashed line represents the average interatomic distance.

The coefficient of linear thermal expansion α is expressed as

assuming that the variation in the frequency of lattice vibration due to anharmonicity is proportional to minute changes in the volume V. Here, γ is Grüneisen's parameter, C_Debye is Debye specific heat and K is the bulk modulus. For simplicity, let us consider an isotropic material. In that case, the coefficient of volume thermal expansion β=(1/V₀)(dV/dT) (V₀: volume at reference temperature T₀) is simply related to α as β=3α. γ represents how the Debye temperature θ, which dominates the lattice vibration, depends on volume, which is defined as

The elastic properties can be expressed in terms of the Young's modulus E, shear modulus G and Poisson ratio ν. For isotropic materials, the independent constants are reduced to two: K=E/[3(1−2ν)] and G=E/[2(1+ν)]. Regarding inorganic materials, Poisson ratio ν is weakly dependent on the materials and in most cases can be treated as a constant in the range of 0.2–0.3. Therefore, we can estimate G and K from E, which is often easier to measure.

Usually, γ and K are weakly dependent on temperature, and thus α exhibits an almost identical temperature dependence to that of C_Debye:

Therefore, volume V depends on temperature T as

Equation (4) provides a theoretical description of thermal expansion. It is used to fit the experimental thermal expansion with refinement of relevant parameter θ, when γ and K are given. It is also useful for estimating the ideal phononic contribution to thermal expansion in a magnetic metal (see section 3.3). Functions approximating the integral in equation (4) for the convenience of analyses are available in the literature [8].

For polymers, a significant contribution to thermal expansion originates from free volume, which is related to the free motion of the constituent atoms. The concept of free volume is omitted from this review because it specifically applies to inorganic solids. The motion degree of freedom of the constituent atoms is much lower in inorganic solids than in polymers. Consequently, the contribution of free volume to thermal expansion can be ignored in inorganic solids. Thermal expansion of polymers is described in the relevant literature [9].

Negative thermal expansion

Thermal expansion is a fundamental property of solids. However, although rare, some materials contract upon heating under constant pressure. These are negative thermal expansion (NTE) materials. In fact, NTE cannot be explained by the normal scheme described above and is a subject of research in itself. It also has significant practical value because it allows the adjustment of the thermal expansion of a material to some particular value, typically zero, by forming composites. Typical NTE materials are presented in table 1. The table includes the important low-expansion material Fe-36Ni Invar, which is closely related to NTE magnetic metals in physics. The mechanisms relevant to NTE are classified into three categories, (i) flexible network, (ii) atomic radius contraction and (iii) magnetovolume effect. An outline of the mechanism and typical materials are summarized for each category in the following.

Table 1.

Coefficients of linear thermal expansion α and operating temperatures T_oper of typical negative/low thermal expansion materials.

Materials	α (ppm K−1)	Toper (K)	Category	Methoda	References
β-eucryptite	−1 to −6b	300–900	1	D	[1, 4, 15]
α-ZrW2O8	−9	<425	1	D/N	[20]
β-ZrW2O8	−6	425–1030	1	D/N	[20]
Cd(CN)2	−33.5	170–375	1	X	[27]
ReO3	−0.5	<220	1	N	[10]
ReO3	−0.7	600–680	1b	N	[10]
(HfMg)(WO4)3	−2b	Room temp. ∼1070	1	D	[11]
Sm2.75C60	−100b	<30	2	X	[29]
Bi0.95La0.05NiO3	−82b	320∼380	2	D	[35]
Invar (Fe-36Ni)	0.1–1	<500	3	D	[37, 38]
Invar (Fe3Pt)	−6 to −30	100–420	3	D	[49, 50]
Tm2Fe16Cr	−9b	340–380	3	X	[47]
CuO nano particles	−36b	<150	3b	X	[48]
Mn3Cu0.53Ge0.47N	−16	265–340	3	D	[73]
Mn3Zn0.4Sn0.6N0.85C0.15	−23	270–335	3	D	[75]
Mn3Zn0.5Sn0.5N0.85C0.1B0.05	−30	280–340	3	D	[76]

^a D, dilatometry; N, neutron diffraction; X, x-ray diffraction.

^b The thermal expansion is anisotropic and α is the averaged value.

^c Details of the mechanism are unknown. The classification is temporary (see text).

Flexible network

This category includes diverse materials, for example, silicates such as LiAlSiO₄ (β-eucryptite), tungstates such as ZrW₂O₄, and cyanides such as Cd(CN)₂, as well as ReO₃ [10] and (HfMg)(WO₄)₃ [11]. NTE materials classified into this category are characterized by strong atomic bonds, which often have large Pauling bond strength z/p (z: cation charge; p: cation coordination number) such as W–O and Si–O [12]. As bonds strengthen, the corresponding potential well becomes more symmetric and vibrations therefore become more harmonic. For very strong bonds, there might be no detectable thermal expansion. Net negative thermal expansion appears when dynamical deformation consumes open spaces in a crystal lattice under the condition that the thermal expansion of the core unit such as WO₄ is suppressed (figure 2). For this reason, most NTE oxides are free from displacive phase transitions to lower-symmetry, lower-volume structures. Structural allowance is necessary for this mechanism. The NTE oxides in this category include both rigid and soft parts in the structure. Consequently, their overall elastic moduli are suppressed as a general trend. Young's modulus of ZrW₂O₈ is, for example, 90 GPa at highest [13]. Such a structural characteristic is also considered to be the origin of the relatively low thermal conductivity of this material [14].

Figure 2.

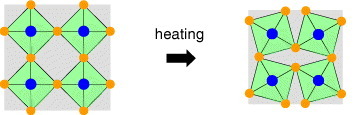
Schematic of negative thermal expansion in a flexible network. A vibrational mode consuming a space in a lattice is thermally excited, which yields thermal contraction.

Silicates

A practically important group of negative- or low-expansion materials is formed by silicates of various kinds such as LiAlSiO₄ (β-eucryptite) [15], Li₂Al₂Si_nO_4+2n (β-spodumenes) [16] and Mg₂Al₄Si₅O₁₈ (cordierite) [17]. Such silicates are sometimes distinguished from other NTE materials having flexible networks [4]. Here, they are grouped together, emphasizing their common features that non-expansive covalent bonds and thermally excited lattice deformation consuming open spaces play an essential role in NTE. These material contain two-dimensional sheets composed of ionic bonds such as Li–O and Mg–O; the sheets are connected by strong covalent bonds such as Al–O and Si–O. Because the ionic bonds lengthen with increasing temperature, expansion occurs in two dimensions within the sheets. Due to the rigidity of the covalent bonds, the sheets are forcibly pulled closer together, as shown schematically in figure 3 [18]. Consequently, significant NTE appears in one direction to the perpendicular to thermal-expansive sheets (figure 4). Although volume thermal expansion can be either positive or negative in this mechanism, many materials show net negative (although not large) volume thermal expansion. Large anisotropy in the thermal expansion restricts the practical use of these materials. For example, their performance as thermal-expansion compensators depends strongly on their morphology [1].

Figure 3.

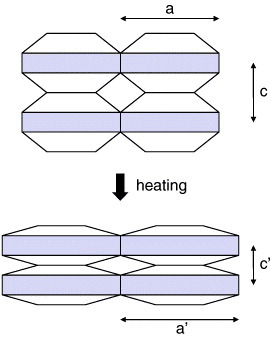
Schematic of anisotropic thermal expansion in the silicates. As the shaded layers undergo thermal expansion, they are pulled closer together in the direction perpendicular to the layers, which causes significant thermal contraction in this direction.

Figure 4.

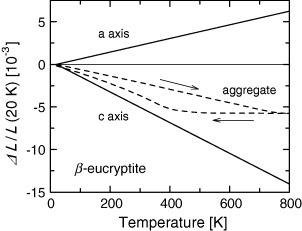
Axial and aggregate thermal expansion of β-eucryptite [15].

Zirconium tungstate

Negative thermal expansion of ZrW₂O₈ was first reported by Martinek and Hummel [19] with subsequent reporting of isotropic NTE over a wide T range T=0.3−1050 K from Sleight's group (figure 5, [20]). In fact, ZrW₂O₈ consists of ZrO₆ octahedra and WO₄ tetrahedra, which are connected via the corner O atoms. As an important exception, one O atom on each WO₄ tetrahedron is not connected to another unit and is therefore regarded as unconstrained. This O atom is located on a WO₄ vertex oriented along one of the [111] directions [21]. For ZrV₂O₇, which has a similar structure to ZrW₂O₈, three corners of a VO₄ tetrahedron are shared with ZrO₆ octahedra, but the fourth corner of each VO₄ tetrahedron is shared with another VO₄ tetrahedron and is therefore more highly constrained.

Figure 5.

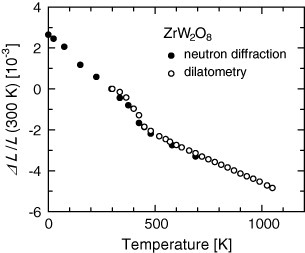
Linear thermal expansion ΔL/L of ZrW₂O₈ [20].

The ZrO₆ octahedra and the WO₄ tetrahedra themselves show negligible thermal expansion because of their strong covalent bonds. The primary origin of NTE in ZrW₂O₈ has long been attributed to the large-amplitude low-energy transverse vibration of the O atom in the middle of the W–O–Zr linkage [22]. A transverse vibration of a bridging O in a framework in which metal (M)–O bond distances remain largely unchanged will cause contraction of the M–M distance and a negative coefficient of thermal expansion (figure 6(a)).

Figure 6.

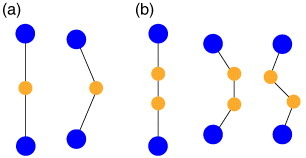
Schematic of local vibrational modes responsible for negative thermal expansion: (a) single-atom and (b) diatomic linkages. The larger (blue) circles represent heavy (usually metal) atoms, whereas the smaller (orange) circles represent light atoms such as carbon, nitrogen, or oxygen.

ZrW₂O₈ undergoes a structural phase transition at 430 K from low-Tα-phase (P2₁3) with a larger NTE (α=−9 ppm K⁻¹) to high-Tβ-phase () with a smaller NTE (α=−6 ppm K⁻¹). This phase transition is interpreted as the order–disorder transition related to the orientation of WO₄ tetrahedra [20, 23]. At low temperatures, each of the unconstrained O atoms described above is strongly bound to one W atom, leading to an asymmetric arrangement of WO₄ tetrahedra. Above the phase transition, however, the positions of both O atoms become disordered. In other words, the unconstrained O atom in the α-phase is randomly bound to both W atoms of adjacent WO₄ tetrahedra in the β-phase. Consequently, the motion of the WO₄ tetrahedra and hence that of Zr–O–W bridges are limited, thereby suppressing NTE.

Cyanides

For NTE in a flexible network, it is important that steric contraction outweighs the conventional thermal expansion of chemical bonds. To this end, strong covalent bonds are not indispensable. This point is exemplified by a series of cyanide-bridged compounds [24–27]. This class of materials exhibits the largest NTE in this category, i.e. α=−33.5 ppm K⁻¹.

The cyanide-bridged compound incorporates stiff octahedral units with strong metal–carbon and metal–nitrogen bonds joined linearly by loose cyanide bridges [25]. An increase in the average transverse displacement of the cyanide bridge with increasing temperature allows the contraction of non-nearest-neighbor M–M and M–C/N distances, despite the observed expansion of the nearest-neighbor M–C/N and C–N bond lengths. Although the generally stated mechanism of NTE in this category assumes that the positive thermal expansion (PTE) of the bond lengths is small, these systems exhibit a large PTE for the M–C/N bond length—considerably larger than the Si–O bond expansion coefficient such as β-eucryptite and greater in magnitude than the bulk NTE in ZrW₂O₈ [26]. The cyanide bridge M–C–N–M has a larger degree of freedom than the M–O–M bridge in the silicates and the tungstates; therefore, larger pull-up effects are expected (figure 6(b)). The importance of looseness in the bridge is evidenced by the fact that in the cyanide-bridged framework, NTE weakens and eventually α changes its sign from negative to positive with a decrease in the lattice constant [28].

Atomic radius contraction

The largest NTE in inorganic materials to date was achieved using the mechanism of atomic radius contraction. This type of NTE results from the variation in the atomic (ionic) radius depending on the valence. When charge transfer occurs between constituent atoms, an atom accepting electrons expands, whereas an atom donating electrons shrinks. However, this variation in the atomic radius depends strongly on the element and/or electronic configuration. Net volume contraction occurs when the expansion of an electron-accepting atom is relatively small and the contraction of an electron-donating atom is relatively large. NTE can occur when such a charge transfer is thermally induced, as reported for Sm_2.75C₆₀ [29].

Generally, the atomic radius depends not only on the valence and coordination number but also on the spin configuration [30]. For a given valence and coordination number, the high-spin state has a larger radius than the low-spin state because the Pauli exclusion principle requires the electrons to be placed in different orbitals in the case of a high-spin configuration. The concept of the 2γ model [31], which was proposed in the early stages of research as a microscopic explanation of low thermal expansion in Fe-36Ni Invar (see section s3.3), is that upon heating, the spin configuration of Fe changes gradually from the high-spin state with a larger radius to the low-spin state with a smaller radius. This was a theoretical attempt to explain magnetovolume effects from the viewpoint of atomic radius contraction. NTE arising from atomic radius contraction has been discovered recently in perovskite oxides [32–35]. Control of the spin state of magnetic atoms such as Mn, Fe and Co as well as Ce and Pr is a promising strategy for the development of new NTE materials.

Perovskite oxides

The nickel-based perovskite oxide Bi_0.95La_0.05NiO₃ [35] undergoes a first-order phase transition from the larger-volume low-T phase to the smaller-volume high-T phase. The volume change reaches 2.9%. This volume change results from charge transfer from Ni to Bi as the temperature increases. Although this change in volume results from the phase transition, it is not discontinuous but rather gradual, similarly to in relaxor ferroelectrics. This oxide has NTE of α=−82 ppm K⁻¹ at T=320–380 K (figure 7). A similar NTE was observed for LaCu₃Fe₄O₁₂ [32–34], which results from the charge transfer from Fe to Cu upon heating.

Figure 7.

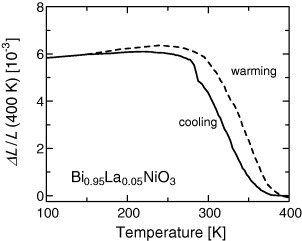
Linear thermal expansion ΔL/L of Bi_0.95La_0.05NiO₃ measured by dilatometry [35].

The huge room-temperature NTE in Bi_0.95La_0.05NiO₃ has significant practical value in compensating for thermal expansion. However, a wider range of applications of this material is hindered by the high pressures (6 GPa) required for its synthesis and the large thermal hysteresis caused by the first-order phase transition.

Magnetovolume effect

The magnetovolume effect is a change in volume due to a variation in the amplitude of the magnetic moment in a magnetic metal. It was first discovered by Guillaume in 1897 [36] in Fe-36Ni Invar: which has low thermal expansion of α=0.5–1 ppm K⁻¹ below the Curie temperature T_C=500 K (figure 8 [37]). For this discovery, Guillaume was awarded a Nobel Prize in Physics in 1920. A general explanation of NTE due to the magnetovolume effect is that a larger volume favors the appearance of a magnetic moment in a metal. The electronic theory of solids provides a microscopic picture: an increase in volume suppresses the overlap of electronic orbitals and therefore reduces the width of electronic bands. Narrowing of the bandwidth can increase the density of states ρ(∊) at the Fermi energy ∊_F, which favors magnetism. The magnetovolume effect is directly related to a longstanding problem—the origin of magnetism in metals—and has been regarded as a fundamental topic in physics [38, 39].

Figure 8.

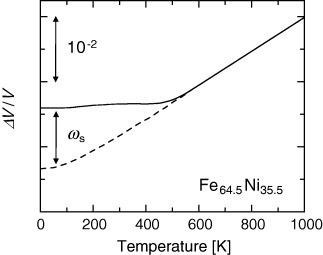
Volume thermal expansion ΔV/V of Fe_64.5Ni_35.5 (solid line) [37]. The dashed line represents the phonon contribution estimated using with equation (4). The difference between the curves corresponds to the spontaneous volume magnetostriction ω_s.

In a general concept of the magnetovolume effect based on itinerant-electron magnetism [40, 41], spontaneous volume magnetostriction ω_s, corresponding to lattice expansion caused by magnetism, is defined as

where F_m(M, T, V) is the magnetic contribution of free energy and M is the amplitude of the magnetic moment. F_m is expanded in terms of M as

The coefficients a,b,… are determined by the energy dependence of the density of states ρ(∊) near the Fermi energy ∊_F. The above-mentioned singularity in ρ(∊) characteristic to a magnetic metal affects ω_s via these coefficients and via M. Combining equations (5) and (6), we obtain the following relation as a first-order approximation:

Here, C is called the magnetovolume coupling constant, given by

Practically, ω_s is estimated by subtracting the ideal lattice thermal expansion (dashed line in figure 8) from the measured thermal expansion (solid line in figure 8). The ideal lattice expansion is determined by extrapolating the measured thermal expansion in the paramagnetic (PM) phase using equation (4)¹ [42].

The magnetovolume effect is commonly observed for magnetic metals of various kinds aside from Invar, including Laves phase intermetallics such as YMn₂ [43, 44], Th₂Zn₁₇-type intermetallics such as Tm₂Fe₁₆Cr [45, 46, 47], and manganese antiperovskites Mn₃AX (A represents transition metals or semiconducting element; X denotes C and N). Recently, large NTE related to magnetism has been discovered in CuO nanoparticles [48].

Invar alloys

Invar means the first discovered Fe–Ni alloys in a narrow sense, but now it is used as a general term for magnetic metals and alloys that exhibit thermal-expansion anomalies of magnetic origin. The magnetovolume effect itself is often called the Invar effect. For over a hundred years, Fe–36Ni has been an important general-purpose, low-expansion material. Aside from the Fe–Ni alloys, this group of materials includes materials of many kinds such as Fe–Pt Invar [49, 50] and super Invar (Fe–Ni–Co) [51]. In addition to these ferromagnetic (FM) alloys, an antiferromagnetic (AF) Cr-based Invar [52, 53] is known.

For the microscopic elucidation of these phenomena, the 2γ model described above was proposed in the early stages of research. However, the magnetovolume effect is commonly observed for magnetic metals and alloys of various kinds. The universality of these phenomena supports the above-mentioned, more general physics based on the singularity of the electronic structure, rather than the mechanism specific to Fe atoms.

Antiperovskites

Materials

An antiperovskite M₃AX is a general term for ordered alloys in which an interstitial light element occupies the body center of a Cu₃Au-type (fcc) alloy (inset of figure 9). Metal and semiconducting elements of various kinds can occupy the face center M and corner A positions, whereas the light elements H, B, C, N and O can enter the body center position X. In an antiperovskite, the positions of light elements and metals are reversed from those of a normal perovskite, in which light elements and metals respectively occupy the face center and body center positions. Aside from manganese, nickel, for example, also forms a series of antiperovskite Ni₃AX. Ni₃MgC [54] and Ni₃ZnN_1−δ [55] are known as superconductors.

Figure 9.

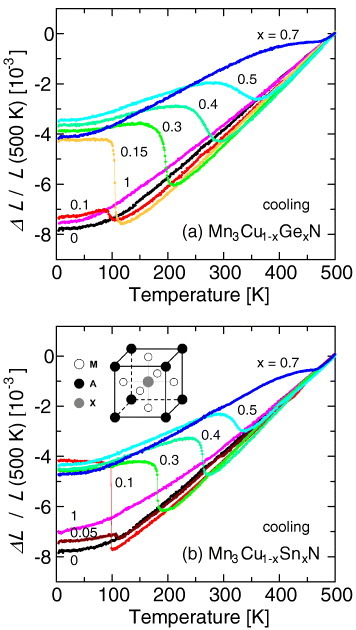
Linear thermal expansion ΔL/L of Mn₃Cu_1−xM_xN: (a) M=Ge, (b) M=Sn. The inset in (b) shows the crystal structure of the antiperovskite M₃AX.

Studies on manganese antiperovskites were initiated in the 1960s [56, 57] and are reviewed in references [58, 59]. For nitrides such as Mn₃GaN [57] and Mn₃ZnN [60] particularly, huge volume contraction occurs upon heating, retaining the cubic structure, accompanied by a first-order transition from AF to PM phases. The volume of the low-T AF phase is larger than that of the high-T PM phase. The volume change reaches 2%, which is among the largest for magnetic metals, next to 4% volume change in YMn₂ [44]. Manganese antiperovskites exhibit many other advantageous features such as magnetostriction [61–63], magnetocaloric effects [64, 65], magnetoresistance effects [66, 67], and a low temperature coefficient of resistance [68–70], and hence attract great attention as a reservoir of functionalities.

The unique physical properties of manganese antiperovskites are mainly attributable to the electronic structure near the Fermi level, which consists of a broad Mn4s band and a narrow Mn3d–X2p covalent band [71, 72]. The singularity of ρ(∊) producing the magnetovolume effect of these compounds is considered to originate from this narrow Mn3d–X2p band. The potential degeneracy of the Mn3d–X2p band arising from Mn₆X octahedra in the cubic Mn₃AX crystal structure induces lattice instabilities, which form the physical background for the characteristic magnetostructural correlations in these compounds.

Negative thermal expansion properties

The NTE in manganese antiperovskites [73–79] was achieved by doping Ge or Sn into the A site as ‘relaxant’ of the sharp volume change due to the first-order magnetic transition (figure 9). Manganese antiperovskites have several advantages over existing NTE materials. (i) The operation temperature and the coefficient of NTE are controllable in the pure form without forming composites. (ii) The negative α is tunable across widely various values. Indeed, at its largest, it can be −30 ppm K⁻¹, which is one order of magnitude larger than NTE materials commercially available to date. We should also note that the absolute magnitude of the negative α found in the antiperovskite is larger than its positive counterpart seen in ceramics such as Al₂O₃ (9 ppm K⁻¹) and typical metals such as Fe (12 ppm K⁻¹), and is comparable to those of high-expansion light metals such as Al (23 ppm K⁻¹) and Mg (25 ppm K⁻¹). This impacts on practical applications for compensation of thermal expansion. (iii) The negative thermal expansion is isotropic and shows no hysteresis. This is highly advantageous as it allows us, for example, to avoid micro-cracking during repeated thermal cycling. Free from the structural constraint that is unavoidable for flexible-network NTE materials, manganese antiperovskites exhibit large elastic moduli, for example E=300 GPa at largest [80]. Their high stiffness enables the production of components and frameworks that are lighter and smaller, and they compensate for thermal expansion more effectively than other NTE materials (see section s5).

Magnetostructural correlations

The crystal and magnetic structures of manganese antiperovskites vary greatly with temperature and composition. This can be attributed to the realization of a more stable state by lifting the degeneracy of the Mn3d–X2p band. The Γ^5g AF spin configuration and the cubic crystal structure are key ingredients for a pronounced magnetovolume effect, typically observed in Mn₃ZnN and Mn₃GaN (figure 10(a), [81]). The general picture of the magnetovolume effect described above shows the relation between the amplitude of the magnetic moment M and the spontaneous volume magnetostriction ω_s (or volume V), but it does not refer to the relation to the crystal and/or magnetic structures. Additional consideration beyond the previous arguments is necessary to elucidate the magnetovolume effect in manganese antiperovskites.

Figure 10.

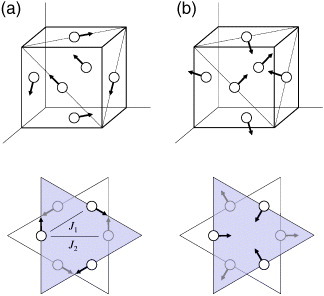
Antiferromagnetic spin structure of a Mn₆N octahedron: (a) Γ^5g, (b) Γ^4g. Upper figures: only magnetic Mn atoms (open circles) are left in the inset of figure 9. Lower figures: perspective view of the spin configuration from the [111] direction. Shaded and white triangles represent adjacent (111) planes. The Γ^5g structure is changed continuously to the Γ^4g structure by 90° rotation of the magnetic moments within the (111) plane.

Analysis of the spin structure suggests the origin of the large ω_s in the manganese antiperovskites. The Mn₆X octahedron has three-dimensional geometrical frustration when the nearest-neighbor magnetic interaction J₁ is antiferromagnetic [82]. Consequently, non-collinear long-range order such as that associated with the Γ^5g AF structure is stabilized only by a very narrow margin of energy with the assistance of a strong FM next-nearest-neighbor interaction J₂. The Γ^4g AF structure (figure 10(b)) also satisfies the ferromagnetic alignment of the next-nearest-neighbor spins, but it yields a small magnetovolume effect [83]. Some manganese antiperovskites, such as Mn₃NiN and Mn₃AgN, have the AF states resulting from the mixture of the Γ^5g and Γ^4g configurations [58]. The spontaneous volume magnetostrictions ω_s of these compounds are much smaller (ω_s∼7×10⁻³ and ∼6×10⁻³ for Mn₃NiN and Mn₃AgN, respectively) than those of compounds with the pure Γ^5g AF states such as Mn₃ZnN and Mn₃GaN (ω_s∼18×10⁻³ and ∼19×10⁻³, respectively) [76, 84]. An important difference between the two configurations is the sign of the magnetic dipole interaction of the next-nearest-neighbor moments: repulsive in the Γ^5g configuration, but attractive in the Γ^4g configuration. The magnetic dipole interaction is revisited as the origin of the crystal deformation triggered by AF ordering in CrN [85], although it had been regarded as being too small for magnetostriction.

Although the change in volume becomes gradual by the partial substitution of Ge or Sn for the A elements, the magnetic transition temperature is still defined as a kink in the magnetization-temperature curve [74]. The broad change in volume is interpreted as a sign of a second-order phase transition rather than of chemical disproportion. The reported results suggest that dopants for broadening the volume change are selective. In contrast to Ge- or Sn-doped series, Ga-doped compounds retain a sharp volume change over their entire concentration range [75]. This dissimilarity is presumably ascribed to the difference in the physical properties of the end materials. Neither Mn₃GeN nor Mn₃SnN, which both show no magnetovolume effect, has a cubic or Γ^5g magnetic structure [58]. Therefore, as doping proceeds, Mn₃Cu_1−xM_xN (M=Ge, Sn) becomes unstable against the phase transition in the crystal and magnetic structures that finally occurs in Mn₃GeN or Mn₃SnN. The relaxed volume change is regarded as a result of the above phase instability and/or phase competition. Indeed, the magnetic and structural phases of Mn₃Cu_1−xGe_xN are very busy for x>0.7 [58]. The atomic pair distribution function analysis of neutron diffraction data [86] and the x-ray absorption fine structure measurement [87] suggest that local lattice distortion is relevant to the broadening of the volume change. Theoretical investigations also highlight the peculiar magnetostructural correlations of manganese antiperovskites [88–90].

Control of thermal expansion by NTE materials

Although it is difficult to control the properties of individual pure materials, this task is greatly facilitated when such materials are combined in composites. Composites may also enable us to generate a function that is impossible in a pure form and/or to endow a material with plural functions simultaneously that are incompatible in a pure form. Recently discovered materials with a huge NTE will lead to a new phase of composite science and technology [91].

Let us consider the thermal expansion of a composite that contains particles of an isotropic thermal-expansion compensator uniformly dispersed in an isotropic matrix. Here, subscripts c, m and t, respectively, represent the composite, matrix, and thermal-expansion compensator. A bound of α_c is given, assuming that stress is uniform everywhere in a composite. This is equivalent to the assumption that the matrix and the thermal-expansion compensator exhibit their own thermal expansion independently. Consequently, the thermal expansion of a composite is given by the volume-weighted sum of the contributions from the matrix and the dispersed phase.

Here, v_m and v_t are the volume fractions of the matrix and thermal-expansion compensator, respectively, and v_m+v_t=1. This is called the rule of mixture (ROM). Another bound is given by the approximation that strain is uniform everywhere in a composite, as first proposed by Turner [92]:

In equation (10), the element with the larger elastic modulus contributes more to the thermal expansion of the composite. In the case of α_m>α_t and E_m<E_t, equation (9) gives the upper bound and equation (10) gives the lower bound for α_c. Schapery derived a more realistic estimation, in which inner stress arising from differences between α_m and α_t in a composite is determined under the condition of minimum free energy [93]:

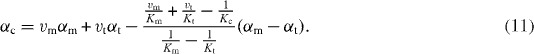When deriving this equation, it was assumed that K_m<K_t and G_m<G_t. In this scheme α_c is determined by the bulk modulus of the composite K_c. Adopting Hashin and Shtrikman's estimation of K_c [94], equation ((11)) gives the upper and lower bounds of Schapery's α_c, corresponding to the upper and lower limits of K_c, respectively. In this case, Schapery's upper limit corresponds to Kerner's estimation [95].

Within the present assumption that the thermal-expansion compensator has larger elastic moduli than the matrix, the values of α_c estimated with different models decrease in the following order: ROM, Schapery's upper limit (Kerner's estimation), Schapery's lower limit and Turner's estimation. This condition is applicable to most cases of composites containing NTE materials, but in the case of ZrW₂O₈/copper composite, for example, this condition is not valid because of the low elastic moduli of ZrW₂O₈. In such a case, the order of bounds is reversed. Turner's estimation is the highest and ROM is the lowest. More details can be found in [96].

Various composites containing an NTE material as a thermal-expansion compensator are being developed such as ZrW₂O₈/copper [97, 98], ZrW₂O₈/aluminum [99], ZrW₂O₈/phenolic resin [100], ZrW₂O₈/polyimide [101, 102], and β-eucryptite/copper [103]. In these studies, the obtained thermal expansion of the composites was analyzed using the above models. The observed discrepancies between the data and the fitting equations are not surprising given that the models assume perfect interfaces; therefore it is important to collect information on the condition of interfaces and on the amount of voids. Furthermore, the overall thermal expansion of composites depends on their morphology. A preform made using NTE materials is favorable for the suppression of thermal expansion. Indeed, in the case of a SiC/aluminum composite, the preform [104] suppresses thermal expansion more effectively than the dispersed particles [105].

Composites with an adjustable thermal expansion containing NTE manganese antiperovskites have been studied recently. The author's group fabricated a metal matrix composite (MMC) in which a molten aluminum alloy (JIS AC8A, Al–Si–Cu–Ni–Mg) is infiltrated by pressure into a preform made of Mn–Cu–Sn–N antiperovskite [106]. Control over thermal expansion was achieved in a wide range of α between −7.4 and 3.5 ppm K⁻¹. For example, the Mn₃Cu_0.5Sn_0.5N_1−δ/AC8A composite has a low expansion of α=3.5 ppm K⁻¹ at T=320–355 K (figure 11). The obtained thermal expansion is close to, or slightly smaller than, that estimated using ROM. Therefore, the effective suppression of thermal expansion attributable to the high stiffness of the manganese antiperovskite is not yet confirmed. Ding et al reported the Mn₃Cu_0.5Sn_0.5N/copper composite by powder metallurgy, which achieved low expansion of α=0.47 ppm K⁻¹ at T=290–320 K [107].

Figure 11.

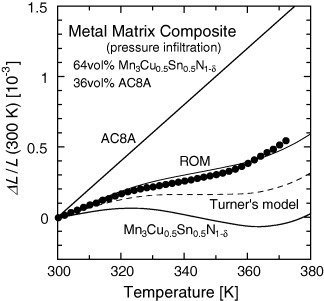
Linear thermal expansion ΔL/L of the metal matrix composite (MMC) Mn₃Cu_0.5Sn_0.5N_1−δ/aluminum alloy (JIS AC8A) fabricated by pressure infiltration [106].

The thermal expansion of composites containing ZrW₂O₈ is suppressed much less than expected because the structural transformation between the normal-pressure (α or β) phase with a larger volume and the high-pressure (γ) phase with a smaller volume is induced by inner stress [98]. Such a structural transformation is absent in the manganese antiperovskites. This class of manganese antiperovskites is classified into ordered alloys of a kind and therefore has closer affinity with metals. This affinity is favorable to form stable interfaces, but it simultaneously promotes chemical reactions between the metal matrix and NTE manganese antiperovskites in a heat-treatment process of combination. It is necessary to find optimal conditions, presumably with a narrow range of parameters, that will enable the formation of strong chemical bonds at interfaces but will minimize chemical reactions.

Concluding remarks and future prospects

New materials with NTE exceeding α=−30 ppm K⁻¹ have been discovered successively over the last decade. These giant NTE materials will expand our capability of thermal-expansion control, opening a new paradigm of materials science and technology—thermal-expansion-adjustable composites. These NTE materials are expected to produce novel functionalities. For example, a large-scale, lightweight, high-strength low-expansion, structural material would be a desirable new material, with which we can compose frames of high-precision facilities themselves as an ultimate solution for thermal-expansion control.

However, adding such a giant NTE material to a composite results in a large difference in thermal expansion between the matrix and the thermal-expansion compensator. This difference generates instabilities at interfaces and in composite functionalities. A technology allowing us to form stable interfaces is urgently needed to improve the performance of composites exhibiting adjustable thermal expansion. An alternative that overcomes problems of interfaces is to design a one-component material with zero thermal expansion. Such ambitious attempts have been pursued using manganese antiperovskites [108], zirconium vanadates [109] and hafnium tungstates [11].