Tailoring the morphology and crystallinity of poly(L-lactide acid) electrospun membranes

Abstract

Biodegradable poly(L-lactic acid) (PLLA) microfibers were prepared by electrospinning by varying the applied potential, solution flow rate and collector conditions. PLLA fibers with smoothly oriented and random morphologies were obtained and characterized by scanning electron microscopy. The optimum fiber orientation was obtained at 1000 rpm using a 20.3 cm diameter collecting drum, while for higher and lower drum rotation speeds, the rapid random motion of the jets resulted in a random fiber distribution. The deformation of the jet with rapid solidification during electrospinning often results in a metastable phase. PLLA electrospun fibers are amorphous but contain numerous crystal nuclei that rapidly grow when the sample is heated to 70–140 °C. In this way, the degree of crystallinity of the fibers can be tailored between 0 and 50% by annealing. Infrared transmission spectra revealed that the processing conditions do not affect the PLLA samples at the molecular level and that the crystallinity of the samples is related to the presence of α-crystals.

Introduction

Nanofibers can be produced by a variety of methods such as drawing, template synthesis, self-assembly, wet spinning, electrospinning and phase separation [1]. However, most of these techniques cannot be upscaled, are specific to certain polymers or cannot control the diameter and orientation of the fibers. Electrospinning has proven to be an excellent method for the synthesis of thin fibers for a wide range of polymeric materials. The electrospinning process was described by Formhals in the 1930s and was developed with the aim of commercializing textile yarns [2]. This technique is relatively versatile, simple, fast and efficient. Electrospun membranes have potential biomedical applications such as scaffolds for tissue engineering, sutures, implants and controlled drug delivery systems [1, 3, 4].

Poly(lactic acid) (PLA) is one of the most commonly used biomaterials and exhibits a low density, low processing power, elastomeric behavior, corrosion resistance and versatile fabrication [5]. The use of PLA in the medical field has increased owing to its biocompatibility, bioresorption, degradation, low toxicity and high mechanical performance.

PLA is a linear polyester that exists in the form of two stereoisomers: poly(L-lactic acid) (PLLA) and poly(D-lactic acid) (PDLA), and their racemic mixture is poly(D,L-lactic acid) (PDLLA) [6]. PLLA is mainly used in biomedical applications. PLLA and PDLA are semi-crystalline and PDLLA is an amorphous polymer [6–8]. The properties of PLA, such as mechanical strength, crystallinity and melting temperature, are determined by the polymer structure (which in turn is affected by the L to D ratio) and molecular weight [9].

The most common stereoisomer, PLLA, crystallizes, depending on the conditions, in the α-, β- or γ-form. The α-form is the most common and stable polymorph. It is characterized by a 10₃ helical chain conformation where two chains belong to an orthorhombic unit cell. The β-form is typically produced by stretching the α-form at high drawing ratios and high temperatures. The γ-form is produced by epitaxial crystallization [6, 10, 11].

Several processing parameters affect the morphology and properties of electrospun fibers. The most important ones are those corresponding to the initial polymer solution, namely the solvent (its dielectric constant, volatility, boiling point, etc), the solution concentration (which determines the viscosity) and the molecular weight of the polymer (which must take into account polymer entanglement) [3]. Other important parameters controlling the jet formation and solvent evaporation are the flow rate through the needle, the needle diameter, the distance from the tip to the collector, temperature, applied voltage and the collection procedure (static or dynamic, i.e. the use of a rotating drum collector). The rotation speed of the drum collector determines the fiber diameter and orientation [12].

Several groups have reported the effect of electrospinning processing parameters on the morphology of PLA fibers [13–16]. Tsuji et al [13] found that the fiber diameter decreases with increasing applied voltage. Tomaszewski et al [14] studied the effect of poly(L-lactide) molecular weight and the viscosity of the spinning solution on the fiber dimensions. Gu and Ren [15] investigated the effect of applied voltage and polymer concentration on fiber diameter and found that the diameter increases with increasing polymer concentration and decreases with increasing applied voltage. Zeng et al reported the effect of solution viscosity and electrical conductivity on the diameter and morphology of fibers. A decrease in the fiber diameter and the formation of beaded fibers were observed for low PLA concentrations in the spinning solution. However, an increase in the electrical conductivity of the solution reduced bead formation [16]. Despite these studies, the control of electrospinning parameters to obtain fibers with the desired morphology, crystallinity and molecular structure has yet to be achieved.

In this work, we studied the effect of the applied voltage, solution flow rate and collecting procedure on the fiber characteristics and orientation. Furthermore, we analyzed the development of microfiber crystallinity upon the annealing of PLLA electrospun samples using differential scanning calorimetry (DSC) and Fourier transform infrared (FTIR) transmission spectroscopy.

Experimental details

Materials

Purasorb PL18 PLLA, with an average molecular weight of 217.000–225.000 g mol⁻¹, was purchased from Purac and dissolved in a 3/7 vol/vol mixture of N,N-dimethylformamide (DMF, from Merck) and dichloromethane (MC, from Sigma–Aldrich) to achieve a polymer concentration of 10 wt% in the solution. The process was conducted at room temperature using a magnetic stirrer until complete polymer dissolution.

Electrospinning

The polymer solution was placed in a commercial plastic syringe (10 ml) fitted with a steel needle of 500 μm inner diameter. Electrospinning was conducted by applying a voltage between 12 and 25 kV with a PS/FC30P04 power supply from Glassman. A syringe pump (from Syringepump) fed the polymer solution into the needle tip at a rate between 1 and 8 ml h⁻¹. The electrospun fibers were collected on a grounded collecting plate (random fibers) placed 15 cm away from the needle. Oriented fibers were produced using a grounded collecting drum of 20.3 cm diameter.

Characterization

Electrospun fibers were coated with a thin gold layer using a sputter coater (Polaron, SC502) and observed with a scanning electron microscope (SEM, JSM-6300, JEOL) at an accelerating voltage of 20 kV. The mean fiber diameter and its distribution were calculated using SEM images of 40 fibers taken at 1000× magnification and Image J software [17].

Infrared transmission measurements were performed at room temperature with a Perkin-Elmer Spectrum 100 apparatus in the attenuated total reflectance mode from 4000 to 650 cm⁻¹. FTIR spectra were collected by performing 32 scans with a resolution of 4 cm⁻¹.

The stability of the electrospun fiber mats was analyzed by DSC with a Perkin Elmer Diamond setup. The samples were cut into ∼2×2 mm⁻², 6 mg pieces, from the middle region of the electrospun membranes, placed in 40 μl aluminum pans and heated between 30 and 200 °C at a heating rate of 10 °C min⁻¹. All experiments were performed under a nitrogen gas flow. The glass transition temperature (T_g), cold-crystallization temperature (T_cc), melting temperature (T_m), cold-crystallization enthalpy (ΔII_cc), melting enthalpy (ΔII_m) and degree of crystallinity (ΔX_c) of the electrospun fiber mats were evaluated.

Results and discussion

Processing parameters

Among the parameters affecting the fiber morphology and properties of electrospun PLLA membranes, this work focuses on the effects of applied voltage, flow rate and collector condition (static or rotating). The effect of applied voltage was investigated while keeping the needle diameter constant at 0.5 mm, the flow rate at 4 ml h⁻¹ and the traveling distance at 15 cm. The SEM images in figure 1 show the effect of the applied voltage on the diameter of the electrospun fibers, as well as the mean value ± standard deviation of the diameter.

Figure 1.

SEM images of PLLA mats electrospun at a traveling distance of 15 cm, a needle diameter of 0.50 mm, a flow rate of 4 ml h⁻¹ and an applied voltage of 12 kV (a), 15 kV (b), 20 kV (c) and 25 kV (d). The scale bar corresponds to 20 μm.

The diameter of the PLLA fibers ranges from 1.37 to 2.45 μm. It decreases when the voltage is raised from 12 to 20 kV (figures 1(a)–(c)) and increases at higher voltages (figure 1(d)). The increase in fiber diameter with increasing voltage between 20 and 25 kV might be related to changes in the mass flow and jet dynamics [1, 15]. The mean fiber diameters are smaller for the PLLA mats than for PLLA fibers prepared by the conventional solution-spinning (60–108 μm [18]) and melt-spinning methods (20–500 μm [19]). A porous structure with a maximum pore size of ∼60 μm is created in the PLLA electrospun mats.

Figure 2 shows SEM images of the samples obtained at 20 kV with a needle diameter of 0.50 mm. The traveling distance was 15 cm and the solution feed rate was varied between 1 and 8 ml h⁻¹. The images reveal that the average fiber diameter increases with increasing polymer feed rate from 1.03 μm at 1 ml h⁻¹ to 1.91 μm at 8 ml h⁻¹. The fibers have a smooth surface but contain numerous pores with a size larger than 30 μm.

Figure 2.

SEM images of PLLA mats electrospun at a traveling distance of 15 cm, needle diameter of 0.50 mm, applied voltage of 20 kV and a flow rate of 1 ml h⁻¹ (a), 2 ml h⁻¹ (b), 4 ml h⁻¹ (c) and 8 ml h⁻¹ (d). The scale bar corresponds to 20 μm.

The shape of the droplet on the hole of the electrode (steel needle tip) at the initial stage of the electrospinning process was affected by several processing parameters such as the electrospinning voltage. Consequently, the resulting fiber morphology could be changed from a typical cylindrical shape to a bead or string-of-pearls structure. The electric field initiates the jet. Once the electric field is applied to the droplet of polymer solution at the tip of the spinneret, the liquid surface is charged owing to the motion of the ions through the liquid. At a high field, the electric force overcomes the surface tension and a quasi-stable, straight and electrically charged jet is ejected [1, 20]. The balance between the surface tension and the electric force determines the initial cone shape of the polymer solution at the needle tip.

Fiber orientation using a rotating collector

Electrospun mats can be oriented using a rotating collector. The effect of the rotation speed on fiber diameter and orientation is presented in figure 3, where the voltage was maintained at 20 kV, the flow rate at 4 ml h⁻¹, the needle diameter at 0.50 mm and the traveling distance at 15 cm. Figure 3 shows the PLLA fiber mats obtained by electrospinning using a 20.3 cm drum collector, as well as the mean ± standard deviation of the fiber distribution.

Figure 3.

SEM images of PLLA microfibers electrospun at a traveling distance of 15 cm, a needle diameter of 0.50 mm, an applied voltage of 20 kV, flow rate of 4 ml h⁻¹ and a rotation speed of 500 rpm (a), 750 rpm (b), 1000 rpm (c) and 1500 rpm (d). The scale bar corresponds to 20 μm.

The mean fiber diameter was larger at the lowest rotating speeds (500 and 750 rpm) and the fiber orientation was partly random at these speeds. At higher rotation speeds (1000 rpm), the fibers had a minimum diameter of 0.86 μm and were aligned in one preferential direction; their pores were smaller and the structure more compact compared with other samples. The fiber orientation had poorer alignment at 2000 rpm. The physical mechanisms of electrospinning are still not well understood and some intuitive conjectures are given as follows. When the linear speed of the rotating drum surface, which serves as a fiber collector, matches that of the evaporated jet deposits, the fibers are collected at the surface of the cylinder in a circumferential manner, resulting in good alignment. Such a speed can be called the alignment speed, and it is about 1000 rpm for PLLA. Randomly oriented fibers are collected at lower surface speeds, at which the rapid chaotic motion of the jet determines the deposition (figures 3(a) and (b), 500 and 750 rpm, respectively) [21]. On the other hand, there is a limiting rotation speed above which continuous fibers cannot be collected (figure 3(d), 1500 rpm). The optimum rotation speed depends on the material used and the polymer concentration [3, 22–24].

Isothermal crystallization of electrospun mats

The thermal properties of electrospun PLLA were studied for an unoriented mat obtained at an applied voltage of 20 kV, a traveling distance of 15 cm, a needle diameter of 0.50 mm and a flow rate of 2 ml h⁻¹. However, the results and discussion can also be applied to the samples obtained under other electrospinning conditions.

The deformation of the jet with rapid solidification during electrospinning often results in a metastable phase [25]. In the case of PLLA, as it is a slowly crystallizing polymer and because its glass transition temperature is above room temperature, the dry samples collected at room temperature maintain a stable crystalline fraction.

PLLA fibers electrospun from solution usually exhibit a cold-crystallization peak in DSC heating scans [26, 27]. Figure 4 shows three DSC heating scans performed on electrospun PLLA samples. Scan 1 shows a normalized thermogram (heat flow divided by sample mass and heating rate) recorded upon heating an untreated electrospun mat at a rate of 10 °C min⁻¹. A strong endothermic peak is observed at 59 °C and corresponds to the glass transition in PLLA. This peak can be ascribed to the recovery of the enthalpy of the sample, which was stored at room temperature (approximately 30 °C), i.e. below T_g, and therefore subjected to physical ageing. The second scan was recorded after heating the sample to 65 °C (slightly above the glass transition temperature) and rapidly cooling it to 20 °C. The glass transition peak is hardly apparent in this case since physical ageing is erased by the first scan. Cold crystallization started immediately above the glass transition temperature in scans 1 and 2 and corresponds to the broad exotherm in the range of 65–120 °C with a minimum at 85 °C. Melting takes place between 120 and 160 °C. The degree of crystallinity (ΔX_c) of the electrospun mats was calculated using the following equation:

Figure 4.

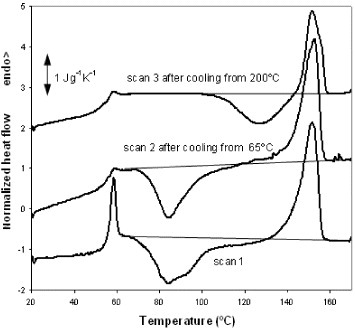
DSC normalized thermograms of a PLLA sample electrospun at a traveling distance of 15 cm, a needle diameter of 0.50 mm, an applied voltage of 20 kV and a flow rate of 2 ml h⁻¹. Scan 1 is the first heating scan, scan 2 was recorded after heating the sample to 65 °C followed by cooling at 40 °C min⁻¹ to 20 °C, and scan 3 was performed after cooling the sample at 10 °C min⁻¹ from 200 °C to 20 °C.

Here ΔH is the area under the thermogram between 65 and 160 °C (the baseline for integration is shown in figure 4) and ΔH_m⁰ is the enthalpy of melting for a fully crystallized PLLA sample (93.1 J g⁻¹ [28]). The calculation reveals that electrospun fibers are nearly amorphous because the area between the thermogram and the integration baseline is zero within the accuracy of the integration. From the area of the melting peak between 120 and 160 °C, the maximum degree of crystallinity produced in the sample during the heating scan after cool crystallization was estimated as 30%. The third heating scan, scan 3, was recorded after cooling the sample from 200 to 20 °C at a rate of 10 °C min⁻¹. As for the first scan, the total enthalpy of the exothermic and endothermic peaks is zero within the measurement accuracy, indicating that PLLA did not crystallize from the melt at the cooling rate of 10 °C min⁻¹, in agreement with previous experiments [29]. Interestingly, cold crystallization in scan 3 is shifted by more than 40 °C towards higher temperatures with respect to scans 1 and 2, and the minimum of the exothermic peak is located at approximately 130 °C. The maximum crystalline fraction produced by cold crystallization during the heating scan is 17%, as evaluated by the area under the melting peak.

The differences between the thermograms corresponding to scans 1 and 3 suggest the existence of different conformations of the polymer chains at the beginning of the scans. The temperature range of cold crystallization in scan 1, immediately above the glass transition temperature, indicates that numerous crystal nuclei were already present in the glass [29, 30]. The presence of these nuclei can be related to nonequilibrium chain conformations imposed by the electrospinning process that were frozen upon the evaporation of the solvent. The similarity between scans 1 and 2 in terms of the cold-crystallization peak shows that nucleation is not due to physical ageing, which can create crystal nuclei [29, 31]. During scan 1, PLLA crystallizes, melts and finally stabilizes at 200 °C with equilibrium chain conformations which are then preserved upon fast cooling to the glassy state. The cold crystallization of the PLLA initially in this conformation is clearly slower than that in the electrospun mat.

No significant difference was found in the value of ΔC_p=0.39 J g⁻¹ K⁻¹ between scans 2 and 3. In both cases, the sample was nearly amorphous when the glass transition occurred.

The development of crystallinity in the electrospun mats was further studied by annealing them between the glass transition temperature and 140 °C for up to 48 h. The samples were heated to the crystallization temperature in an oven, quenched to room temperature and then transferred to the DSC setup and subjected to a heating scan at 10 °C min⁻¹ from room temperature to 200 °C. Figure 5 shows the crystalline fraction of the sample measured by DSC. Samples subjected to annealing at temperatures above 90 °C or for longer than 1 h did not exhibit a significant cold-crystallization exotherm during the DSC heating scan. The crystalline fraction rapidly increases in the first few minutes of annealing, as expected from the heating scan. For instance, after only 2 min of annealing at 140 °C, crystallinity reaches 31%, whereas the maximum value for this temperature is 49%. This result indicates that numerous nucleation centers are present in the electrospun mat that grows simultaneously upon heating. This behavior is further confirmed by the fact that PLLA films, obtained by casting from the solution used for electrospinning and subjected to brief annealing at a low temperature, develop much lower crystallinity than the electrospun mats. For instance, annealing at 90 °C for 1 h yields an electrospun mat with 27% crystallinity, whereas the crystalline fraction of the films subjected to the same treatment is only 9%. The total crystalline fraction after prolonged annealing at a high temperature does not significantly differ for electrospun mats and PLLA films, whereas the distribution of crystal sizes is different since the melting peaks are broader and shifted towards low temperatures for the electrospun mat with respect to the film, as can be observed in figure 6.

Figure 5.

Crystalline fraction of electrospun samples annealed at different temperatures.

Figure 6.

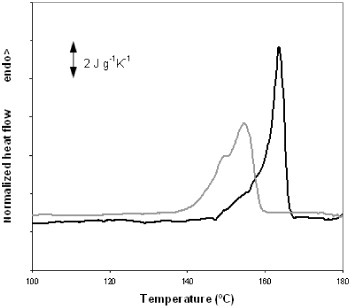
Melting peaks of a PLLA film (black line) and an electrospun mat annealed at 140 °C for 48 h.

The effect of the high crystalline fraction obtained by isothermal treatment on the properties of the electrospun fibers should be significant. Although characterization of the mechanical properties of the electrospun mats is beyond the scope of this work, SEM images taken before and after annealing (figure 7) show that highly crystalline fibers become fragile and break spontaneously during isothermal crystallization. This can be attributed to the fiber contraction induced by crystallization and the release of internal residual stresses generated during processing. Figure 7(a) shows an image of an untreated electrospun mat, in which PLLA is amorphous. No apparent change can be observed in figure 7(b), which corresponds to a sample annealed at 70 °C for 48 h with X_c=30%. On the other hand, in the sample crystallized at 140 °C (figures 7(c) and (d)) some fibers are broken and others have a rough surface.

Figure 7.

SEM images of PLLA mats electrospun at a traveling distance of 15 cm, a needle diameter of 0.50 mm, an applied voltage of 20 kV and a flow rate of 2 ml h⁻¹: as-produced (a), crystallized at 70 °C for 48 h (b) and crystallized at 140 °C for 48 h (c,d). The scale bar corresponds to 5 μm in (a–c) and to 0.5 μm in (d).

Phase content

Previous studies have identified infrared absorption bands that are characteristic of the vibrations of certain molecular groups of PLA in a given crystalline phase (table 1). Thus, the evolution of the infrared spectra can be used to monitor the development of crystallinity in this polymer. Whereas some vibration frequencies have fixed frequencies, others shift significantly between the amorphous and crystalline α and α' forms.

Table 1.

Literature review of the relevant infrared bands associated with different phases of PLLA.

IR frequency (cm−1)	Phase form	Assignment	Ref. No.
860	Amorphous		[30]
871	α		[11, 30]
908	β		[37]
921	α	Coupling of the C–C	[11, 30, 37]
		backbone stretching with
		the CH3 rocking mode
955	Amorphous		[11, 30, 37]
1044	Amorphous, α' and α	ν(C–CH3)	[38, 39]
1053	α	ν(C–CH3)	[6, 38]
1092	α' and α	νs(C–O–C)	[38]
1107	α' and α		[38]
1134	Amorphous, α' and α	rs(CH3)	[38, 39]
1183	Amorphous, α' and α	νas(C–O–C) +ras(CH3)	[38, 39]
1213	α' and α	νas(C–O–C) +ras(CH3)	[38]
1222	α	νas(C–O–C) +ras(CH3)	[6, 38]
1268	Amorphous + semicrystalline	ν(CH)+ν(COC)	[39]
1302	Amorphous	C–H stretching	[11]
1360	Semicrystalline	δ(CH), CH wagging	[39]
		(bending)
1363	Amorphous	δ(CH), CH wagging	[39]
		(bending)
1368	Semicrystalline	δ(CH), CH wagging	[39]
		(bending)
1382	α	δs(CH3)	[6, 37]
1386	α' e α	δs(CH3)	[37]
1387	Amorphous	δs(CH3)	[37]
1444	α	δas(CH3)	[30, 37]
1454	Amorphous	δas(CH3)	[30, 37]
1457	α' and α	δas(CH3)	[30, 37]
1749	α	ν(C=O)	[6, 37, 38]
1757	Amorphous	ν(C=O)	[37]
1759	α	ν(C=O)	[37]
1761	α'	ν(C=O)	[37]
2945	Amorphous	νs(CH3)	[37]
2946	α' and α	νs(CH3)	[37]
2964	α	νs(CH3)	[6, 37]
2995	Amorphous	νs(CH3)	[37]
2997	α' and α	νas(CH3)	[37]
3006	α	νas(CH3)	[6, 37]

In this work we followed the evolution of the FTIR transmission spectra after annealing between 40 and 140 °C for up to 48 h, that is the same thermal treatment as that in the DSC experiments. Figure 8 (and, in more detail, figure 9) shows the spectra after 48 h annealing at different temperatures. As can be seen in figure 5, the crystalline fraction continuously increases with increasing annealing temperature.

Figure 8.

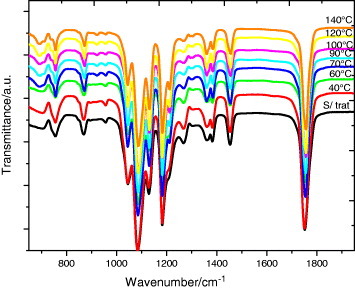
FTIR transmission spectra of PLLA electrospun scaffolds before and after annealing at the indicated temperatures for 48 h.

Figure 9.

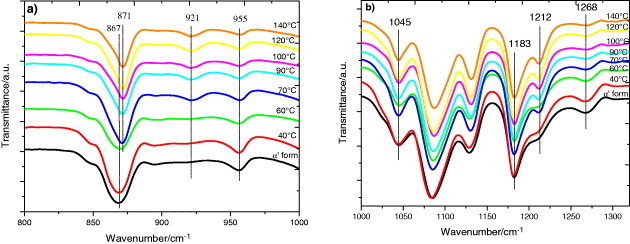
FTIR transmission spectra of PLLA electrospun scaffolds before and after annealing at the indicated temperatures for 48 h: magnification of selected spectral regions.

The FTIR spectrum of the as-produced samples does not depend significantly on the electrospinning conditions. The effect of the applied voltage, flow rate and microfiber orientation was systematically studied, and in all samples the infrared spectrum corresponds to that of amorphous PLLA, in good agreement with the DSC results. In particular, it is worth noting the absence of the absorption band at 921 cm⁻¹. PLLA crystallizes into the α-form with the distorted 10₃ helix conformation from solution or melt. Kang et al. reported that the 921 cm⁻¹ absorption band is characteristic of the α-crystals [32], associated with the transition moment perpendicular to the chain axis, to the CH₃ rocking mode combined with a minor contribution from the C–COO and O–CH stretching modes of the α-crystals [33]. The characteristic band of the PLLA β crystal at 908 cm⁻¹ is absent in our spectra [34, 35], suggesting that β PLLA does not form after electrospinning or after subsequent annealing (figure 9(a)).

As shown in figure 9(a), the increase in the crystallization degree is accompanied by a change in the shape of the absorption band between 840 and 880 cm⁻¹. The 860 and 871 cm⁻¹ bands, respectively, ascribed to the skeletal stretching and CH₃ rocking of amorphous and crystalline (α) phases, overlap in this range [36]. With increasing annealing temperature, and thus increasing degree of crystallinity, the peak shifts to higher frequencies and significantly narrows as expected for crystal formation. Similar changes occur in the region of the ν_as(C–O–C) +r_as(CH₃) modes in the amorphous phase and in the α' and α crystals (figure 9(b)), although the changes in the 955 cm⁻¹ band, corresponding to the amorphous phase are less clear.

The evolution of the infrared spectrum with annealing time follows similar trends. Figure 10(a) shows the appearance of the 921 cm⁻¹ band and the shape change of the 840 and 880 cm⁻¹ bands, which is consistent with the increasing degree of crystallinity. Figure 10(b) illustrates the changes in the region of the C=O stretching band (1800–1700 cm⁻¹), where the sift to higher frequency corresponds to the increasing crystallization. In summary, we can conclude that the crystallization of our samples is due to the presence of α-crystals in the mats.

Figure 10.

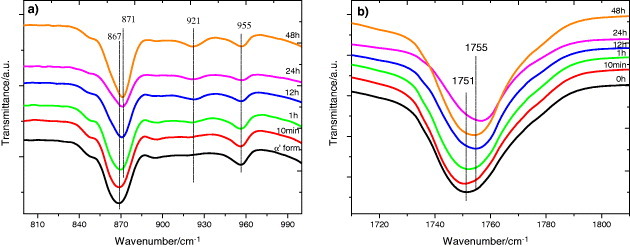
FTIR transmission spectra of PLLA electrospun scaffolds before and after annealing at 70 °C for the indicated times.

Conclusions

The fiber morphology of electrospun PLLA mats can be controlled by changing process parameters such as the applied voltage, feed rate and the collector system. Moreover, the degree of crystallinity of electrospun fibers can be easily tailored to between 50% and zero, i.e. amorphous fibers. Samples with the highest crystallinity are fragile and spontaneously break during crystallization.

Random nanofibers were obtained on a plate collector, while oriented nanofibers were collected using a 20.3 cm diameter drum. The optimum fiber alignment was observed for a rotation speed of 1000 rpm, and for higher and lower drum rotation speeds, the rapid chaotic motion of the jet resulted in randomly oriented fibers. The deformation of the jet deformation with rapid solidification during electrospinning often results in a metastable phase. PLLA electrospun scaffolds are nearly amorphous but are highly nucleated. Crystals rapidly grow when the electrospun mat is heated to 70–140 °C. Infrared transmission measurements suggest that the processing did not affect the PLLA samples at the molecular level and that the development of crystallinity in the samples after thermal annealing is due to the presence of α-crystals in the electrospun mats.