Point defects in ZnO: an approach from first principles

Abstract

Recent first-principles studies of point defects in ZnO are reviewed with a focus on native defects. Key properties of defects, such as formation energies, donor and acceptor levels, optical transition energies, migration energies and atomic and electronic structure, have been evaluated using various approaches including the local density approximation (LDA) and generalized gradient approximation (GGA) to DFT, LDA+U/GGA+U, hybrid Hartree–Fock density functionals, sX and GW approximation. Results significantly depend on the approximation to exchange correlation, the simulation models for defects and the post-processes to correct shortcomings of the approximation and models. The choice of a proper approach is, therefore, crucial for reliable theoretical predictions. First-principles studies have provided an insight into the energetics and atomic and electronic structures of native point defects and impurities and defect-induced properties of ZnO. Native defects that are relevant to the n-type conductivity and the non-stoichiometry toward the O-deficient side in reduced ZnO have been debated. It is suggested that the O vacancy is responsible for the non-stoichiometry because of its low formation energy under O-poor chemical potential conditions. However, the O vacancy is a very deep donor and cannot be a major source of carrier electrons. The Zn interstitial and anti-site are shallow donors, but these defects are unlikely to form at a high concentration in n-type ZnO under thermal equilibrium. Therefore, the n-type conductivity is attributed to other sources such as residual impurities including H impurities with several atomic configurations, a metastable shallow donor state of the O vacancy, and defect complexes involving the Zn interstitial. Among the native acceptor-type defects, the Zn vacancy is dominant. It is a deep acceptor and cannot produce a high concentration of holes. The O interstitial and anti-site are high in formation energy and/or are electrically inactive and, hence, are unlikely to play essential roles in electrical properties. Overall defect energetics suggests a preference for the native donor-type defects over acceptor-type defects in ZnO. The O vacancy, Zn interstitial and Zn anti-site have very low formation energies when the Fermi level is low. Therefore, these defects are expected to be sources of a strong hole compensation in p-type ZnO. For the n-type doping, the compensation of carrier electrons by the native acceptor-type defects can be mostly suppressed when O-poor chemical potential conditions, i.e. low O partial pressure conditions, are chosen during crystal growth and/or doping.

Introduction

Among oxide semiconductors, ZnO is a prototypical n-type system presenting several fascinating physical and chemical properties. Its traditional applications include catalysts, gas sensors and varistors [1, 2]. Recently, ZnO has attracted renewed interest owing to applications in transparent electrodes, utilizing its high n-type conductivity and optical transparency (E_g=3.44 eV [3]). In addition, optoelectronic applications such as light-emitting diodes and ultraviolet lasers have been extensively explored using its p–n and p–i–n homojunctions [4–8] and p–n heterojunctions [9, 10]. The quantum Hall effect has been observed recently in a high-mobility two-dimensional electron gas formed at ZnO/Mg_xZn_1−xO heterojunctions [11, 12].

In applications of ZnO based on such electrical and optical properties, the control and design of the point defect structure, as well as surface and interfacial structures, are keys to optimizing the device performance. The use of homojunctions requires both p- and n-type doping, but ZnO is known to show a strong n-type preference. Although difficulty in p-type doping has been overcome in several studies [7, 8, 13, 14], an efficient method of forming p-type ZnO has still been actively debated. Moreover, there exists controversy on the fundamental issues relevant to native defects and unintentional impurities, such as the sources of the n-type conductivity and non-stoichiometry of reduced ZnO. Many experiments have been devoted to the characterization of the native defects and impurities, but available knowledge is still limited. Meanwhile, first-principles studies have provided various insights into their characteristics.

In this article, we review recent first-principles approaches to point defects in ZnO. Defect energetics, atomic and electronic structures, and defect-induced properties are discussed with focus on native defects.

First-principles approaches to point defects

To address the energetics and atomic and electronic structures of point defects, approaches based on density functional theory (DFT) [15, 16] have been used in most first-principles studies. The total energy for a defect simulation model, such as a supercell and a model cluster, is obtained but taking atomic relaxation into account. With reference to total energies for the host perfect crystal and relevant phases, the formation energies are evaluated via procedures given below. However, the results significantly depend on the approximation to exchange correlation, defect simulation models and the post-processes to correct the shortcomings of the approximation and models. This section summarizes approximations employed in total energy and electronic structure calculations, models and boundary conditions in simulations of defects, and the suggested post-correction schemes. Formalisms of the defect formation energy, thermodynamic transition levels and optical transition energy are also given.

The fundamentals of the first-principles approaches to defect energetics in semiconductors are also reviewed in [17–21].

Approximations in total-energy and electronic structure calculations

The local density approximation (LDA) [16, 22, 23] and the generalized gradient approximation (GGA) [24–27] to the exchange-correlation functional are very commonly used in DFT approaches. These local and semi-local functionals reproduce structural properties of metals, semiconductors and insulators within an error of a few percent in most cases. However, the electronic structure of semiconductors and insulators is not well described, as is manifested by the underestimation of their band gaps. Furthermore, defect-induced electronic states as well as host electronic states are not treated correctly when they have localized characteristics. To remedy such shortcomings on the localized states, the Hubbard U correction, i.e. L(S)DA+U and GGA+U [28–30], has been employed. More-elaborate approaches involving hybrid Hartree–Fock (HF) density functionals, the screened exchange (sX), the self-interaction correction (SIC) and the GW approximation have also been applied to ZnO.

Simulation models and boundary conditions

The supercell approach, based on band-structure-type calculations, is widely employed for the modeling of point defects. A defect is placed in a supercell constructed by expanding the unit cell of the host system. When using standard approximations to DFT such as the LDA and GGA, the number of atoms in supercells is typically a few hundreds and can reach a few thousands in recent calculations. Since the defect is regularly repeated under three-dimensional periodic boundary conditions, electrostatic and elastic interactions occur between the defect and its periodic images. Such interactions converge very slowly with respect to the supercell size. When a dilute defect is simulated, a suitable correction to such interactions is necessary for the accurate prediction of the defect energetics, as mentioned in section 2.5.

Another choice is the cluster method. Since an isolated defect is simulated in a model cluster, it is free from the defect–defect interaction occurring in the supercell approach. However, the surface effects of the cluster should be eliminated, and, from this viewpoint, an embedded cluster hybrid quantum mechanical/molecular mechanical (QM/MM) approach is suitable for simulations of defects in solids. The cluster method has a disadvantage in the description of extended electronic states, such as those in the conduction band of metals and semiconductors.

Defect formation energy

One of the key quantities of point defects is the Gibb's free energy of defect formation, ΔG_f. It determines the equilibrium defect concentration together with configurational entropy at a given temperature, pressure and composition. Although ΔG_f cannot be evaluated directly using standard first-principles approaches, its electronic contribution, which is often noted as formation energy, ΔE_f, is obtained from the total energy of a simulation model within the employed approximation. Whereas this quantity has been considered in most first-principles studies on defect energetics in semiconductors and insulators, including ZnO, the evaluation of the Gibbs free energy or Helmholtz free energy of defect formation, in conjunction with phonon (vibration mode) calculations or molecular dynamics simulations, has also been reported, e.g. for Si [31, 32], TiO₂ [33] and In₂O₃ [34].

For dilute defects, the Gibbs free energy of defect formation can be evaluated as

where G_def denotes the Gibbs free energy of a simulation model containing a defect in charge state q; N_i and μ_i are the number and chemical potential of constituent atoms of type i, respectively (i=Zn, O for ZnO); and ε_F is the Fermi level, i.e. the electronic chemical potential.

μ_i is commonly referred to as the chemical potential in a standard state, μ_i°:

In addition, ε_F is often measured from the valence band maximum (VBM) as

where ε_VBM denotes the energy level corresponding to the VBM.

Using equations (2) and (3), equation (1) is rewritten as

Chemical potentials can vary within limits determined by phase equilibria. For ZnO, the correlation and range of Δμ_Zn and Δμ_O are given as

where ΔG_f(ZnO) denotes the formation Gibbs free energy of ZnO. The lower limit of Δμ_O, in other words the upper limit of Δμ_Zn corresponds to the O-poor (Zn-rich) limit, which is represented by

The other is the O-rich (Zn-poor) limit, which is given as

Except for the case of degenerate semiconductors, Δε_F can vary within band gap E_g as

Chemical potentials and the Fermi level should be determined at a given temperature, pressure and composition, reflecting the concentrations of native defects and impurities (dopants); the Fermi level is derived via the overall charge neutrality of constituent charged species including charged native defects, impurities and carrier electrons and holes [18, 35, 36]. In a general discussion on systems with various doping levels and compositions (degrees of non-stoichiometry), however, chemical potentials and the Fermi level are often treated as variables and defect formation energies are considered to be their functions. This is illustrated for native defects in ZnO in section 4.

In a practical procedure using first-principles calculations, the Gibbs free energy such as G_def in equation (4) is often decomposed as

where E^el denotes the electronic contribution to the total energy; E^vib and S^vib are vibrational contributions to the total energy and entropy, respectively; and T, p and V are temperature, pressure and volume, respectively. μ_i° is treated in the same manner.

Total energies obtained using first-principles calculations can be used for E^el. The vibrational contributions and the pV term are small for most crystalline solids at moderate temperatures and atmospheric pressure and, hence, may be neglected (G≈E^el). It is also noteworthy that only these changes in these contributions that are caused by the formation of a defect affect ΔG_f. Thus, defect formation energy ΔE_f is evaluated by substituting calculated total energies for G_def and also for μ_i° in equation (4) [17–19, 37, 38]. In the case of native defects in ZnO, the formation energy is given as

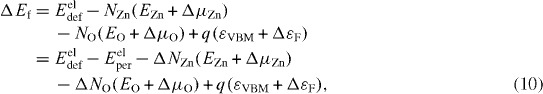where E^el_def and E^el_per, respectively, denote the total energy of the supercell containing a defect in charge state q and that of the perfect-crystal supercell. ΔN_Zn and ΔN_O are the differences in the number of Zn and O atoms between these supercells. For instance, ΔN_Zn=0 and ΔN_O=−1 for the O vacancy and ΔN_Zn=1 and ΔN_O=0 for the Zn interstitial. E_Zn and E_O are the total energies of the Zn crystal and O₂ molecule per atom, respectively. The calculated formation energy of ZnO, ΔE_f(ZnO), substitutes for ΔG_f(ZnO) in equations (5)–(7).

When the temperature and O partial pressure dependences of formation energies are of interest, a concise procedure is to consider Δμ_O in equation (10) as a function of temperature and O partial pressure, using the ideal gas model for O₂ [18, 39]. This approach can be effective for ZnO because temperature and pressure dependences for ZnO and Zn crystals are much smaller than those for the O₂ gas. More exact treatments involve vibrational contributions for solid phases via phonon calculations or molecular dynamics simulations, as mentioned above. Such approaches to point defects are computationally demanding, but are becoming feasible.

Thermodynamic transition level and optical transition energy

The thermodynamic transition level of a defect between charge states q and q′, ε(q/q′ ), corresponds to the Fermi level at which formation energies for charge states q and q′ equalize [17–19, 37]. When measured from the VBM, the thermodynamic transition level is given as

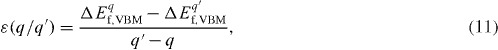where ΔE_{f, VBM}^q denotes the defect formation energy for charge state q when the Fermi level is located at the VBM (Δε_F=0). Formation energies and thermodynamic transition levels are illustrated in figure 4 with the example of the O vacancy in ZnO. The position of the thermodynamic transition level measured from the VBM, as given in equation (11), or that from the conduction band minimum (CBM) corresponds to the ionization energy of a defect, i.e. an acceptor or donor energy.

Figure 4.

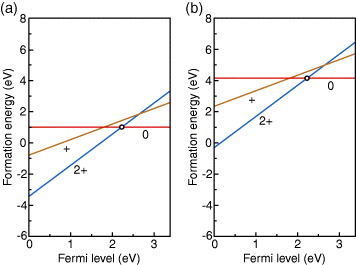
Formation energies of the O vacancy in neutral, + and 2+ charge states in ZnO as a function of the Fermi level, obtained using the HSE (a=0.375) hybrid functional in conjunction with finite cell-size corrections [44, 81]. (a) O-poor (Zn-rich) limit. (b) O-rich (Zn-poor) limit. The Fermi level at which lines of two charge states intersect corresponds to the thermodynamic transition level, as given by equation (11). Note that the + charge state is unstable for any value of the Fermi level, and, hence, only the ε(2+/0) level appears, as indicated by the open circle in each panel.

The optical (vertical) transition energy is evaluated within the Franck–Condon principle, without involving atomic relaxation [18]. By neglecting excitonic effects, it is approximately obtained using DFT total energies for two charge states relevant to the transition, in a manner similar to the evaluation of the thermodynamic transition level; however, the atomic coordinates are fixed for those of the initial states in this case. A recent study using the GW and Bethe–Salpeter equation has shown for the C vacancy in SiC that excitonic effects lead to a red shift of ∼0.2 eV [40].

Post-corrections in the supercell approach

To overcome drawbacks in the description of isolated defects due to the limitations in the approximation to exchange correlation and in simulation models, post-corrections are applied to calculated formation energies, thermodynamic transition levels and optical transition energies. In the case of the supercell approach, post-corrections concern the issues given below.

Host band structure

When the host band structure, particularly the band gap, is not well reproduced as in the case of the LDA and GGA calculations, the defect energetics also includes errors. A simple correction scheme is to shift the CBM upward so that the band gap agrees with an experimental value. Defect-induced electronic states having host conduction band-like orbital characteristics are considered to follow this shift. The formation energy of a defect with such an electronic state is corrected by mΔE_g, where m is the number of electrons at the defect state and ΔE_g denotes the difference between experimental and calculated band gaps.

For ZnO, this correction is hardly appropriate because the VBM also suffers from an error. The underbinding of the Zn-3d states leads to its overhybridization with the O-2p states and thereby to the overestimation of the VBM as mentioned in section 3. More elaborate post-corrections using a combination of the LDA and LDA+U or the GGA and GGA+U, have been proposed, in which the Zn-3d states are lowered by the +U correction [41, 42]. The post-correction scheme proposed by Janotti and Van de Walle employs an extrapolation formula based on formation energies and band gaps obtained using the LDA and LDA+U [41]. The approach proposed by Lany and Zunger takes an ε_VBM value determined using the LDA+U or GGA+U, and the CBM is then shifted upward so that the band gap agrees with an experimental value [42]. Apart from this, LDA or GGA total energies are used in the evaluation of formation energies via equation (10). As shown in section 4, the resultant defect formation energies and transition levels are markedly different between these two correction schemes.

Approaches that can describe the host band structure better, such as the hybrid HF density functional and sX [43], are more concise in view of the band gap correction. However, both hybrid functional and sX approaches may require a tuning of the parameters in the functionals depending on the system of interest [44–46]. In addition, they are computationally demanding, although defect calculations with large supercells containing a few hundreds of atoms are becoming feasible. A combined GW and DFT approach to point defects, where the atomic relaxation and the resultant energy change are estimated with the LDA/GGA or LDA+U/GGA+U, has also been suggested recently [47] and applied to ZnO [48].

Filling and emptying host bands

A correction for the occupancy of a defect-induced band is required when it shows resonance with the host conduction or valence band [18, 19, 37]. For example, if a donor state with such a characteristic is formed in a finite-sized supercell, the conduction band is artificially filled by the donated electrons. This results in an overestimation of the formation energy. This error can be fairly large when the conduction band has a large dispersion. A similar issue also concerns acceptor states showing resonance with the valence band. To correct these errors, the difference between the averaged eigenvalue for the perturbed host band and the eigenvalue at the band edge can be used [18, 19, 37].

An alternative approach is the use of a single k-point that provides the VBM and CBM in supercells. In the case of ZnO, the Γ-point can be taken as such a point for any type of supercell because ZnO has a direct band gap at the Γ-point. In the single k-point approach, large supercells containing more than a few hundred atoms may be required to avoid errors associated with insufficient k-point density. If a localized defect-induced band shows dispersion due to defect–defect interactions in a finite-sized supercell, effects of dispersion on the defect formation energy can be corrected using the difference between the averaged eigenvalue of the localized defect-induced band and the eigenvalue at the sampled single k-point [44].

Electrostatic and elastic interactions

Spurious electrostatic and elastic interactions between a defect and its periodic images can be large and converge very slowly with respect to the supercell size. To correct the electrostatic effects on the formation energies of charged defects, i.e. image charge interactions, several approaches have been proposed, such as the Madelung energy correction by Leslie and Gillan [49], a multipole expansion scheme by Makov and Payne [50], the local moment countercharge scheme by Schultz [51] and the density countercharge scheme by Dabo et al [52]. Comparative studies of the Makov–Payne and local moment countercharge schemes on the vacancy and self-interstitial in Si have revealed that the formation energies corrected using these schemes are extrapolated to nearly the same value at the dilute limit, i.e. infinite cell-size limit [53, 54].

The correction by Leslie and Gillan considers the Madelung energy for an array of point charges q in an effective medium with a static dielectric constant ε₀,

where α is the appropriate Madelung constant and L denotes the interdefect distance. The Makov–Payne approach assumes electrostatic interactions between multipoles at the periodically repeated defect sites and those between the multipoles and the charge-compensating jellium background, leading to L⁻³ and L⁻⁵ terms in addition to the L⁻¹-dependent Madelung energy term, whereas the Madelung energy term is dominant for the charged defects in ionic crystals [49, 50], the L⁻³ and L⁻⁵ terms can also be important in the case of semiconductors with covalent characteristics, e.g. for the As vacancy in GaAs [55].

In addition, recent studies have suggested that the defect-induced Madelung energy needs to be evaluated from the characteristics of defect-induced electronic states, instead of the use of the formal defect charges for q [19, 44, 56–58]. In this case, correction terms can be obtained by fitting formation energies calculated using supercells of various sizes to the multipole expansion.

In figure 1, this is exemplified for the O vacancy and Zn interstitial at the octahedral site in the neutral and 2+ charge states in ZnO [44]. For the 2+ charge states, after subtracting the L⁻¹-dependent Madelung energy contribution estimated using formal defect charges for q in equation (12), nearly linear L⁻³ dependences are left, as shown in figure 1(b). Using a linear fit of L⁻³ dependences, formation energies can be extrapolated to the infinite cell-size limit, i.e. dilute limit. Thus, the Makov–Payne approach is appropriate for these defects.

Figure 1.

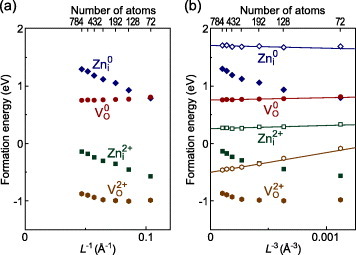
Formation energies of the O vacancy (V_O) and of the Zn interstitial at the octahedral site (Zn_i) in neutral and 2+ charge states, obtained using the GGA, as a function of (a) L^{− 1} and (b) L^{− 3} (L: average interdefect distance) [44]. The formation energies are evaluated for the O-poor limit and the Fermi level at the VBM. Filled and open symbols denote values before and after Madelung energy corrections using equation (12).

For the neutral charge state (q=0), no Madelung energy contributions, i.e. no L⁻¹ dependences, are expected. Consistent with this, the neutral O vacancy shows a very weak L⁻¹ dependence. In contrast, the formation energy of the neutral Zn interstitial has nearly the same dependence as that of the 2+ charge state. Therefore, a Madelung energy contribution similar in magnitude to the 2+ charge state is present in the neutral charge state. A Madelung energy correction for the neutral charge state, using q=2, actually leaves a linear L⁻³ dependence, as is seen in the case of the 2+ charge state. This behavior is understood from their one-electron structures [44]: Zn interstitials in neutral and 2+ charge states induce only a weak perturbation in the host CBM state, and electrons occupying this electronic state in the neutral charge state do not effectively screen the charge of the Zn²⁺ ion located at the interstitial site, resulting in an effect similar to the jellium background in the 2+ charge state.

Castleton et al have reported that the contribution of elastic interactions can also be estimated and removed by fitting formation energies obtained using various cell sizes to an appropriate function [56, 58, 59]. Hine et al have proposed a variant of the Makov–Payne approach, which is applicable to a variety of cell shapes and which eases the extrapolation to the dilute limit by choosing supercells with both positive and negative Madelung energies [60]. An efficient correction scheme explicitly evaluating the L⁻³-dependent term without empirical parameters has been proposed recently by Freysoldt et al [61]. More details on finite-size corrections concerning electrostatic and elastic interactions can be found in recent review articles by Nieminen [62] and Castleton et al [59], as well as in original articles.

VBM in charged defect supercells

The VBM in supercells with charged defects is generally different from that in the perfect-crystal cell. Therefore, they are lined up, for instance, using the average electrostatic potential in a bulk-like region far from the defect and the potential in the perfect crystal [17, 18, 37, 63, 64]. This correction is often referred to as VBM alignment or potential alignment and is applied to ε_VBM in equation (10). Although the VBM alignment is based on the fact that the total energy of charged supercells is ill-defined [65], it may double-count corrections of electrostatic interactions between defects when applied together with electrostatic interaction corrections. Therefore, the VBM alignment has not been employed in several studies that consider the electrostatic interaction corrections [44, 58, 66, 67]. In practice, the Makov–Payne approach, without the VBM alignment, works well for the O vacancy and Zn interstitial in ZnO [44]. On the other hand, the importance of the combination of the Makov–Payne scheme and VBM alignment has been demonstrated for native defects and a Te impurity in GaAs [55].

Fundamental properties of ZnO

ZnO forms a wurtzite structure with space group P6₃mc, in which both Zn and O sublattices have the hexagonal close-packed structure. The unit cell is shown in figure 2, along with views of the crystal structure from the [ ] and [0001] directions.

Figure 2.

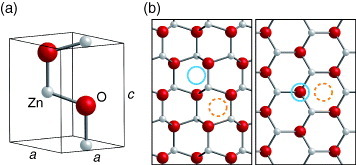
(a) Unit cell of ZnO. Smaller (light gray) and larger (red) circles denote Zn and O atoms, respectively. (b) Crystal structure of ZnO viewed from the [ ] direction (left) and from the [0001] direction (right). Octahedral and tetrahedral interstitial sites are denoted by dashed and solid circles, respectively.

Structural and electronic properties of ZnO, determined using various approximations, are summarized in table 1, along with experimental values. Theoretical approaches include the LDA in the Ceperley–Alder form [22] as parameterized by Perdew and Zunger [23], the GGA in the Perdew–Burke–Ernzerhof (PBE) form [26], LDA+U with U=4.7 eV and J=0 eV, GGA (PBE)+U with U_eff (=U−J)=5.0 and 7.5 eV, Meta-GGA in the Tao–Perdew–Staroverov–Scuseria form (TPSS) [68], HF, the B3LYP hybrid functional [69], the PBE0 hybrid functional [70–72], the HSE hybrid functional [73–75], the HSE hybrid functional with an increased amount of the Fock exchange (a=0.375) [44, 81], sX [43, 46], pseudopotentials (PP) including SIC [23, 76], G₀W₀ [77–79, 84] and self-consistent GW (scGW) with vertex corrections [80]. The electronic density of states (DOS) obtained using the HSE (a=0.375) hybrid functional is shown in figure 3 [81].

Table 1.

Structural and electronic properties of wurtzite ZnO, calculated using various approximations: lattice constants (a and c), the average position of the Zn-3d states measured from the VBM (ε_3d) and the band gap (E_g). Experimental values are also shown.

	a (Å)	c (Å)	ε3d (eV)	Eg (eV)	Reference
LDA	3.195	5.160	∼−5	0.80	[82]
GGA (PBE)	3.288	5.305	−4.9	0.73	[81]
LDA+U (U=4.7 eV, J=0 eV)	3.148	5.075	∼−6.5	1.51	[82]
GGA (PBE)+U (Ueff=5.0 eV)	3.235	5.214	−6.3	1.42	[81]
GGA (PBE)+U (Ueff=7.5 eV)	3.196	5.149	−7.2	1.81	[81]
Meta-GGA (TPSS)	3.285	5.225	−5.1	1.45	[83]
HF	–	–	−9.3	11.07	[84]
Hybrid (B3LYP)	3.278	5.287	–	3.38	[85]
Hybrid (PBE0)	3.257	5.223	−5.9	3.18	[44]
Hybrid (HSE)	3.260	5.221	−6.2	2.90	[83]
Hybrid (HSE06)	3.260	5.239	−5.9	2.46	[81]
Hybrid (HSE, a=0.375)	3.248	5.213	−6.4	3.42	[81]
sX	3.267	5.245	−7.0	3.41	[46]
SIC-PP	3.29	5.29	−8.9	3.8	[76]
G0W0 from the LDA	–	–	–	2.44	[78]
G0W0 from HSE03	–	–	−6.1	2.87	[84]
scGW with vertex corrections	–	–	−6.7	3.2	[80]
Experiment	3.242	5.188	∼−7.5	3.44	[3, 86, 87]

Figure 3.

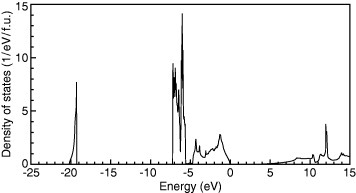
DOS for ZnO, obtained using the HSE (a=0.375) hybrid functional [81]. The zero of the energy is set at the VBM.

ZnO has a direct band gap at the Γ-point and its experimental value is 3.44 eV [3]. As shown in figure 3, the lower part of the valence band at ∼−7.5 to −5.5 eV shows narrow, sharp peaks in the DOS, which are mainly composed of the Zn-3d orbital. The upper part ∼−5 to 0 eV consists mainly of the O–2p orbital, where some hybridization of the Zn-3d, 4s, and 4p orbitals occurs. Below the valence band, the O–2s states are situated at ∼−20 eV. The conduction band is located above 3.4 eV with a small, gradually increasing DOS. Main components of the conduction band are the Zn-4s and 4p orbitals.

As shown in table 1, when the LDA and GGA are used, calculated lattice constants are not significantly different from the experimental values. Concerning the band structure, however, the underbinding of the Zn-3d states and the underestimation of the band gap are noticeable [81, 82, 88]. The underbinding of the localized Zn-3d states originates from a strong self-interaction [76, 78, 82, 89], and it causes overhybridization between the Zn-3d and O-2p states to raise the electronic states near the VBM. The severe underestimation of the band gap in ZnO is partly attributed to this effect.

To overcome drawbacks of the LDA and GGA, the Hubbard U correction scheme [28–30] has been applied to the Zn-3d states [39, 41, 42, 90–93]. This approach can lower the Zn-3d states, as shown in table 1. The position of the Zn-3d states depends on the choice of the effective U (U_eff) value, and it is well reproduced using the GGA (PBE)+U with U_eff=7.5 eV. The band gap is increased from the GGA value of 0.73 eV to 1.42 and 1.81 eV for U_eff=5.0 and 7.5 eV, respectively, but this is still far from the experimental value. The TPSS meta-GGA functional [68] also improves both the Zn-3d position and the band gap over the LDA/GGA, although a severe underestimation of the band gap is recognized. In contrast, the HF approach largely overestimates the band gap.

A hybrid HF density functional approach, which admixes the non-local Fock exchange into local or semilocal (LDA or GGA) exchange-correlation functionals, has been reported to improve the description of the electronic structure for a variety of molecules and solids [71, 72, 94–103]. For ZnO, a much better reproduction of the band structure than the LDA and GGA has been demonstrated using various hybrid functionals, e.g. B3LYP [104], B97-1 [105], PBE0 [44] and HSE [44, 83]. The way and amount of the admixture of the non-local exchange differ between hybrid functionals, and the results show some dispersion. However, improvements over the LDA and GGA are generally found for both the Zn-3d position and the band gap. The HSE functional, in which the non-local Fock-exchange with a=0.25 is admixed into the short-range part only, shows the largest underestimation of the band gap among hybrid functionals shown in table 1, but by increasing the a value to 0.375 the band gap is well reproduced. Meanwhile, lattice constants approach experimental values. Although the Zn-3d states are still underbound, the position is close to the result of a recent scGW calculation with vertex corrections [80]. An sX approach with an inverse Thomas–Fermi screening length of 2.3 Å⁻¹ [46] yields similar results with this hybrid functional. It is noteworthy that structural properties are also better reproduced with the hybrid functional and sX approaches. On the other hand, the approach using PP including SIC and self-interaction and relaxation correction [76] overshoots the Zn-3d position and the band gap.

The GW approximation with and without a vertex correction [79, 80, 106] also improves the description of the band structure of ZnO, although results strongly depend on the level of the approximation and computational details, as discussed in the literature. The GW approximation and a combined GW and DFT approach have been applied to the O vacancy in ZnO [48, 107].

Overall, structural properties of ZnO are reasonably reproduced using various levels of the approximation, whereas the band structure depends significantly on the approximation. As mentioned above, an approach that can well reproduce the band structure reduces the uncertainty in the defect energetics. For instance, formation energies obtained using hybrid functionals can be significantly different from the raw or empirically corrected LDA and GGA values because of the discrepancies in the host VBM and CBM values, in addition to discrepancies observed in the description of localized defect states [17, 37, 44, 98, 108]. Moreover, the difference in the atomic relaxation contribution can be significant [109].

Native defects in ZnO

Native defects in ZnO have been discussed in connection with its non-stoichiometry and n-type conductivity. The Zn interstitial and O vacancy were considered as such defects in early experimental and theoretical studies [110–112], but there existed controversy on which defect contributed to these properties. Later, first-principles studies have provided various insights into the energetics and the atomic and electronic structures of native defects [39, 41, 42, 44, 85, 90, 92, 93, 104, 105, 107, 109, 113–118]. Most studies conclude that the Zn interstitial has a high formation energy, although it is a shallow donor. The O vacancy has a low formation energy, but it is a deep donor that cannot produce a high concentration of carrier electrons. Therefore, neither Zn interstitial nor O vacancy is a likely source of n-type conductivity. Several other candidates have been proposed on the basis of first-principles calculations: the H impurity unintentionally incorporated into an interstitial site (OH⁻–like configuration) or into the O site [91, 119], a metastable shallow donor state of the O vacancy [42], a complex of a Zn interstitial and N impurity [120], and a Zn interstitial stabilized in the presence of a high concentration of the O vacancy [118].

Most of these conclusions are, however, based on results with the LDA, GGA or the LDA/GGA with Hubbard U corrections (LDA+U/GGA+U), none of which reproduce the band structure of ZnO well, as discussed in section 3. Several post-correction schemes have been proposed to overcome shortcomings of the LDA/GGA and LDA+U/GGA+U, as mentioned in section 2.5, but the resultant defect formation energies and levels depend even qualitatively on the correction schemes [39, 41, 42, 90, 92, 107]. Recent hybrid HF density functional and sX approaches, which reproduce the band structure of ZnO well, have clarified characteristics of native defects in this view [44, 46, 85, 104, 105, 109], as well as the combined GW and GGA+U approach [48]. In this section, we discuss the characteristics of native defects in ZnO based on the formation energies, transition levels, one-electronic states and the atomic structure calculated using an HSE (a=0.375) hybrid functional [44, 81], together with other reported results.

Vacancies, interstitials, and anti-sites of Zn and of O are considered to be the native defects in ZnO. As discussed below, the O vacancy, Zn interstitial and Zn anti-site, which are associated with O deficiency or Zn excess, are donor-type defects. The Zn vacancy, O interstitial, and O anti-site are acceptor-type defects associated with Zn deficiency or O excess. The interstitials can be located at the octahedral and tetrahedral sites, as shown in figure 2. Phonon calculations predict the Zn interstitial at the tetrahedral site to be dynamically unstable [81]. The O interstitial can form in an O₂-molecule-like configuration as a result of large atomic relaxation. Such a defect cannot be simply characterized as a point defect at the lattice and at interstitial sites.

Figures 4 and 5 show the formation energies and thermodynamic transition levels of native defects in ZnO, obtained using the HSE (a=0.375) hybrid functional in conjunction with finite cell-size corrections [44, 81]. Figure 5(c) includes the results for H impurities at two sites, i.e. an interstitial OH⁻-like configuration and substitutional O-site. The range of the Fermi level is set by the calculated VBM (Δε_F= 0 eV) and CBM (Δε_F=3.4 eV). Figures 4(a) and 5(a) show results at the O-poor (Zn-rich) limit as an extreme case of the reduced ZnO. At this limit, formation energies of defects associated with O deficiency or Zn excess, i.e. the O vacancy, Zn interstitial, and Zn anti-site, are the lowest, whereas those associated with Zn deficiency or O excess, such as the Zn vacancy, O interstitial, and O anti-site, are the highest. In the other extreme case, i.e. the O-rich (Zn-poor) limit considered in figures 4(b) and 5(b), formation energies are raised by −ΔE_f(ZnO) for the O vacancy and Zn interstitial and by −2ΔE_f(ZnO) for the Zn anti-site, as derived from equations (6), (7) and (10). In contrast, the formation energy of the Zn vacancy is lowered by −ΔE_f(ZnO). Using the HSE (a=0.375) hybrid functional, a value of ΔE_f(ZnO)=−3.1 eV has been obtained [44], whereas the experimental value of the formation enthalpy of ZnO, ΔH_f(ZnO), is −3.63 eV [121]. As for the Fermi level dependence, the slope corresponds to the charge state defined using equation (10). Defects that show positive slopes, such as the O vacancy, Zn interstitial, and Zn anti-site, can be positively charged, indicating their donor-type characteristics. Similarly, the negative slope of the Zn vacancy indicates its acceptor-type behavior.

Figure 5.

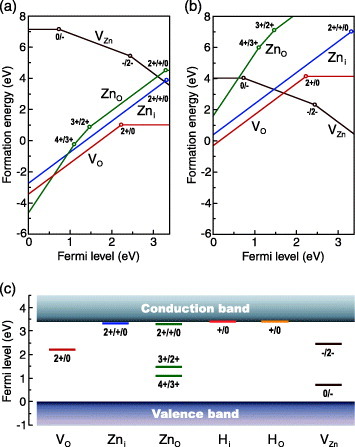
Formation energies and thermodynamic transition levels of the O vacancy (V_O), the Zn interstitial at the octahedral site (Zn_i), the Zn anti-site (Zn_O) and the Zn vacancy (V_Zn) in ZnO, obtained using the HSE (a=0.375) hybrid functional in conjunction with finite cell-size corrections [44, 81]. Formation energies as a function of the Fermi level at the (a) O-poor (Zn-rich) limit and (b) O-rich (Zn-poor) limit. The slope corresponds to the charge state. Only these charge states that are energetically the most favorable at a given Fermi level are shown for each defect. Thermodynamic transition levels are indicated by open circles. For Zn_i and Zn_O, the ε(2+/+) and ε(+/0) levels are very close to each other and are shown as ε(2+/+/0) levels. (c) Thermodynamic transition levels, corresponding to open circles in panels (a) and (b). Also shown are levels of H impurities at the interstitial site (H_i), i.e. OH⁻-like configuration and the O site (H_O).

Table 2 lists formation energies and thermodynamic transition levels reported using several approaches for the O vacancy and the Zn interstitial at the octahedral site [39, 44, 46, 48, 85, 92, 93, 105]. It is recognized that reported formation energies and thermodynamic transition levels show dispersion because of differences in the approximation and/or post-corrections. Nevertheless, several common and important insights have been obtained. Theoretically suggested characteristics of respective native defects are discussed below.

Table 2.

Formation energies (ΔE_f) and thermodynamic transition levels measured from the CBM (ε ′ (q/q′ )=E_g− ε(q/q′ )) of the O vacancy and the Zn interstitial at the octahedral site. Formation energies are obtained at the O-poor limit when the Fermi level is located at the CBM, i.e. a strong n-type condition. Values for the ε ′ (2+/0) level are listed for the O vacancy because it shows a negative U behavior, i.e. instability of the + charge state. CB denotes a transition level within the conduction band. All values are in eV.

Method	O vacancy			Zn interstitial			Reference
	ΔEf	ε ′ (2+/0)		ΔEf	ε ′ (2+/+)	ε ′ (+/0)
Extrapolation using LDA and LDA+U	3.72	1.3		6.95	CB	CB	[92]
GGA with VBM correction using GGA+U	0.8	2.2		5.2	0.6	0.2	[39]
LSDA+Ud+Us	2.0	2.5		–	–	–	[93]
Hybrid (HSE06)	0.96a	0.67a		–	–	–	[48]
Hybrid (HSE, a=0.375)	1.0	1.2		3.9	0.1	0.1	[44]
Hybrid (PBE0)	0.9	1.2		–	–	–	[44]
Hybrid (B3LYP)		1.13		–	0.09	0.16	[85]
Hybrid (B97-1), QM/MM	1.6b	–		–	–	–	[105]
sX	0.85	1.21		3.7	0.1	<0.1	[46]
GW-HSE	–	1.68a		–	–	–	[48]

^aValues calculated for the zinc-blende structure.

^bEstimated by the present authors, using the reported value for the formation energy with reference to the O₂ molecule.

O vacancy

Formation energies of the O vacancy in the neutral, + and 2+ charge states are shown in figure 4. As defined by equation (10), the formation energy depends on the Fermi level, with the slope corresponding to the charge state. When the Fermi level is low, the 2+ charge state is energetically the most preferable for the O vacancy. As the Fermi level rises, the formation energy approaches that of the neutral state, above the Fermi level of 2.2 eV, the neutral state becomes more favorable. The thermodynamic transition level of ε(2+/0) is located 2.2 eV above the VBM (1.2 eV below the CBM). The position of this level depends on the approach, as shown in table 2. Qualitatively speaking, however, it is concluded that the O vacancy has a deep donor level. In addition, the + charge state is never stable at any value of the Fermi level. In other words, the O vacancy exhibits a negative U behavior, as has been seen in most previous studies using the LDA/GGA and LDA+U/GGA+U [39, 41, 42, 90, 92, 93, 107, 113–117], hybrid functionals [44, 81, 104, 109], sX [46], and a combined GW and GGA+U approach [48] and confirmed experimentally [122].

This characteristic is related to the atomic relaxation and the one-electron structure particular to each charge state [41, 44, 92]. As shown in figure 6, the neutral O vacancy induces a deep and localized one-electron state in the band gap. In the HSE (a=0.375) case, this state exists 2.5–2.6 eV below the CBM. The formation of such an electronic state is accompanied by a large inward relaxation of the first-nearest-neighbor Zn ions by 10%. In contrast, V_O²⁺ shows an outward relaxation by 23% and no localized states in the band gap. Note that one-electron states do not directly correspond to the thermodynamic transition levels; as indicated in equation (11), thermodynamic transition levels are determined using formation energies of two charge states with respective equilibrium (relaxed) geometries.

Figure 6.

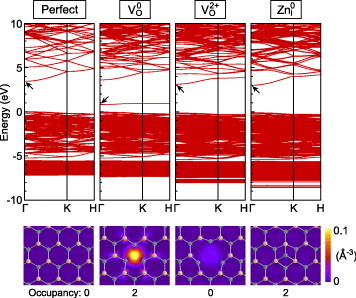
Band structures of the perfect ZnO crystal, of the O vacancy (V_O) in neutral and 2+ charge states and of the Zn interstitial at the octahedral site (Zn_i) in the neutral charge state, obtained using the HSE (a=0.375) hybrid functional and 4 × 4 × 3 supercells containing 192 atoms (and a defect) [44]. Squared wavefunctions of states designated by the arrows, and plotted in the middle of (0001) Zn and O planes adjacent to the defects, are shown below, together with projected Zn and O atom positions denoted with green and yellow circles, respectively.

The formation energy of the O vacancy is shown along with those of other defects in figures 5(a) and (b). It is recognized that the O vacancy has the lowest formation energy among the native donor-type defects at most positions of the Fermi level. In particular, under n-type conditions, where the Fermi level is close to the CBM, it is energetically much preferable to the other defects. Using the HSE (a=0.375) approach, the formation energy of the neutral O vacancy is 1.0 eV at the O-poor limit. As shown in table 2, nearly identical values are obtained using HSE06 and PBE0 hybrid functionals [44, 48] and the sX approach [46], whereas the B97-1 hybrid functional in combination with the hybrid QM/MM approach yields a slightly larger value of 1.6 eV [105].

The value of ∼1 eV is close to the raw GGA value of 0.8 eV [44] and to that obtained with a post-correction scheme proposed by Lany and Zunger [39], in which the correction is not applied to the neutral O vacancy. The formation energy of ∼1 eV is sufficiently low to account for the observed non-stoichiometry of ZnO: for instance, 190 ppm in the specimen treated at 1373 K [123]. Thus, it has been proposed that the O vacancy is a source of non-stoichiometry in ZnO. In contrast, another post-correction scheme proposed by Janotti and Van de Walle, which uses an extrapolation formula based on the LDA and LDA+U results, leads to a much higher value of 3.7 eV [92]. The thermodynamic transition level of ε(2+/0), predicted with this approach, is close to those obtained using the hybrid functionals, but the correction for the VBM using LDA+U is not sufficient, leading to the difference in absolute formation energy from the hybrid functional results [124].

Turning to p-type conditions where the Fermi level is close to the VBM, the 2+ charge state is preferred, as shown in figures 4 and 5. The formation energy is close to zero at the O-rich limit and is even negative at the O-poor limit. Therefore, a strong compensation of holes by the O vacancy is expected in p-type ZnO.

The origin of the green luminescence in ZnO has been a topic of intensive discussion on the basis of experimental results such as electron paramagnetic resonance [125, 126] and optically detected magnetic resonance [126–128] in conjunction with optical emission and absorption measurements. The O vacancy is considered as a source of the green luminescence in some studies [122, 125, 127], whereas others attribute it to the Zn vacancy [129] or residual impurities such as Cu [130, 131]. First-principles studies have predicted optical transition energies of the O vacancy on the basis of the Franck–Condon principle [41, 42, 44, 92]. As for the origin of the green luminescence, the transition between + and neutral charge states of the O vacancy [42, 107] has been proposed, whereas other studies suggest the transition between − and 2− charge states of the Zn vacancy [92, 113] and that involving the Zn vacancy in the neutral triplet state [105].

Zn interstitial

For the Zn interstitial, the octahedral site in the wurtzite structure is considered in figure 5. Another possible site, i.e. the tetrahedral site, has been reported to be energetically less favorable [44, 113–115, 117] or dynamically unstable [81, 92, 105]. In the HSE (a=0.375) result, the Zn interstitial has a thermodynamic transition level of ε(2+/+/0) in the vicinity of the CBM, where the three charge states have nearly identical formation energies (within 0.05 eV). Therefore, the Zn interstitial is suggested to be a shallow donor, in line with experimental observations, e.g. a donor energy of 30 meV as reported by Look et al [132]. As shown in figure 6, the neutral Zn interstitial only slightly perturbs one-electron states at the CBM. Similar band structures have been obtained for the + and 2+ charge states [44]. This feature in the one-electron structure is consistent with the thermodynamic transition level near the CBM. As shown in table 2, most other studies have also identified the shallow donor characteristic of the Zn interstitial.

With regard to the formation energy of the Zn interstitial, a considerably high value of ∼4 eV, under n-type conditions, is found even at the O-poor limit. Therefore, the concentration of the Zn interstitial is expected to be very low in n-type ZnO under thermal equilibrium. A recent LDA+U study by Kim and Park suggests that the Zn interstitial can be stabilized in the presence of a high concentration of the O vacancy [118], as discussed in section 5.2. Under p-type conditions, the formation energy of the Zn interstitial is as low as 0.5 eV at the O-rich limit and is even negative at the O-poor limit. Hence, Zn interstitials can compensate for holes in p-type ZnO.

The Zn interstitial has been suggested to have a low migration barrier of 0.22 eV [133] or 0.57 eV [92, 134] for the 2+ charge state. Therefore, it is expected to diffuse out easily or bind with other defects or impurities [92, 134].

Zn anti-site

The Zn anti-site, a Zn ion located at the O site, shows a transition level of ε(2+/+/0) near the CBM, as seen in the case of the Zn interstitial. It also has deep ε(4+/3+) and ε(3+/2+) levels located below the middle of the band gap. In contrast to the HSE (a=0.375) result shown in figure 5, an LDA+U-based approach predicted that the 3+ charge state is unstable [92]. However, a qualitative picture can be drawn that the electronic structure of the Zn anti-site involves both deep and shallow donor levels. This electronic structure can be understood by the fact that the Zn anti-site is regarded as a complex of an O vacancy and a Zn interstitial, having deep and shallow levels, respectively; the position of the anti-site Zn ion in the relaxed geometry is displaced by more than 1 Å from the O site [81, 92]. Under n-type conditions, the formation energy of the Zn anti-site is even higher than that of the Zn interstitial. Thus, the Zn anti-site is unlikely to form at a substantial concentration in n-type ZnO. Turning to p-type conditions, the formation energy of the Zn anti-site becomes very low because of the preference of the highly positive charge states, as is seen in the case of the O vacancy and the Zn interstitial. The Zn anti-site is also expected to compensate for holes in p-type ZnO, particularly under O-poor conditions where its formation energy can be negative.

Zn vacancy

Theoretically, the Zn vacancy has been suggested to be a dominant acceptor-type defect in ZnO [39, 42, 44, 90, 92, 105, 107, 113–117, 134]. This is consistent with positron annihilation results reported by Tuomisto et al [135]. As shown in figure 5, the Zn vacancy has two deep acceptor levels: ε(0/−) and ε(−/2−) at 0.7 and 2.4 eV above the VBM, respectively. LDA- and LDA+U-based extrapolation approach is predicted the acceptor levels of 0.18 and 0.87 eV [92], and values of 0.9 and 1.5 eV have been obtained from GGA calculations with a VBM correction using GGA+U [39]. Although reported transition levels strongly depend on the computational approach, it can be concluded that the Zn vacancy is a deep acceptor that cannot be a major source of holes. It is noted, however, that the Zn vacancy can play an important role in optical properties; as mentioned above, its relevance to the green luminescence in ZnO has been suggested [92, 113].

With regard to the formation energy of the Zn vacancy, it is lowest under the O-rich limit considered in figure 5(b), because the Zn vacancy is associated with a Zn deficiency. At the O-poor limit considered in figure 5(a), the formation energy is found to be rather high (∼4 eV) when the Fermi level is close to the CBM. Therefore, under O-poor conditions, the Zn vacancy is unlikely to form at a substantial concentration, implying the absence of significant carrier electron compensation by the acceptor-type Zn vacancy. This feature is consistent with the fact that high carrier concentrations can be attained in reduced or donor-doped ZnO, but it has not been predicted from the LDA/GGA and LDA+U/GGA+U calculations other than by applying post-corrections to the LDA/GGA as suggested in [39, 107].

O interstitial and O anti-site

O interstitials have been suggested to form in several configurations, such as that of an O ion at the octahedral interstitial site and in O₂-molecule-like configurations, which are referred to as dumbbell [136] or split [92] interstitials. The octahedral interstitial configuration has a higher formation energy than does the Zn vacancy [92, 136], and induces deep acceptor levels, ε(0/−) and ε(−/2−) at 0.72 and 1.59 eV, respectively [92]. The dumbbell (split) configuration is lower in formation energy than the octahedral configuration, except under n-type conditions. However, it is present in the neutral charge state over the whole range of the Fermi level, suggesting an electrically inactive role [92]. The O anti-site shows even higher formation energy than the O interstitials [92]. In summary, first-principles studies suggest that the O interstitial and O anti-site are very high in formation energy and/or electrically inactive. These defects are not expected to play important roles under thermal equilibrium.

Proposed source of n-type conductivity

As discussed in section 4, the O vacancy shows a low formation energy under O-poor conditions. However, it has a deep donor level of ε(2+/0) and, hence, cannot be a source of carrier electrons. In contrast, the Zn interstitial and anti-site are shallow donors but have high formation energies. Such features of the O vacancy, Zn interstitial and Zn anti-site suggest that sources other than isolated donor-type native defects should be considered for the n-type conductivity of reduced ZnO. As summarized below, several candidates have been proposed through first-principles calculations.

Metastable configuration of the O vacancy

Lany and Zunger have reported that a metastable configuration of the O vacancy has a shallow donor state, in contrast to the deep donor state of the stable configuration mentioned above [42]. Such a metastable configuration has been proposed as a cause of the persistent photoconductivity of ZnO. Its shallow donor behavior can be understood from the nature of O vacancy in 2+ charge state. As shown in figure 6, the O vacancies in the neutral and 2+ charge states are accompanied by the relaxation of neighboring Zn ions in opposite directions. The resultant one-electron structures are significantly different from each other. For the 2+ charge state, the lowest unoccupied state is similar in energy and orbital character to these of the CBM state of the perfect crystal. The metastable neutral configuration is considered to be the O vacancy in the 2+ charge state, with two additional electrons trapped at the perturbed conduction-band state. Its formation energy, however, is estimated to be at least a few eV higher than that of the stable configuration, and, hence, the metastable configuration is suggested to form by optical excitation. The reverse transition to the stable configuration is impeded by an energy barrier, which leads to persistent photoconductivity [42].

Zn interstitial stabilized by the O vacancy

Kim and Park suggested by means of LDA+U calculations that the Zn interstitial is stabilized in the presence of a high concentration of the O vacancy [118]. Several configurations of the Zn interstitial and O vacancy yield a binding energy of ∼0.4 eV, leading to multiple interactions between them. This results in a high concentration of the Zn interstitial and of carrier electrons produced by it, of the order of 10¹⁹ cm⁻³ at 900 K. This concept should be important for understanding the defect structure in heavily reduced ZnO, where the O vacancy can be present at a high concentration. It is noted, however, that this conclusion is based on LDA+U results with a band gap underestimated as 1.74 eV. The formation energy of the isolated Zn interstitial is estimated to be ∼2.5 eV, without additional band-gap corrections. If we instead take an HSE (a=0.375) value of 3.9 eV for the formation energy of the isolated Zn interstitial, then considerably lower concentrations of interstitial and carrier electrons are expected even in the presence of the interaction with the O vacancy. Thus, further consideration would be required for an accurate estimation of the carrier concentration associated with the Zn interstitial and O vacancy.

Residual impurity

Van de Walle proposed that the hydrogen impurity acts as a shallow donor in ZnO [119]. The shallow donor behavior contrasts with the role of the H impurity in other semiconductors, where it can compensate carriers [137]. Several stable/metastable sites have been suggested theoretically for the interstitial H impurity [119, 138]. The shallow donor behavior and the presence of multiple configurations have been confirmed by experiments [139–143]. In most configurations, an H impurity at an interstitial site is bonded to an O ion with a bond length similar to those in the H₂O molecule and in the OH⁻ ion. The orientation of the O–H bond varies, and the H site located between the Zn–O bond along the c-axis, is suggested to be the most energetically favorable configuration [138]. Such interstitial-like H impurities can easily diffuse, implying a trap by other defects [144].

Janotti and Van de Walle proposed that the H impurity is also located at the substitutional O site and acts as a shallow donor [91]. The formation energy and, hence, the concentration of the substitutional H impurity explicitly depend on the O chemical potential, i.e. the O partial pressure, since it can be regarded to be a complex of the O vacancy and H impurity. Under O-poor conditions, it is comparable in formation energy to interstitial-like configurations [91]. As shown in figure 5(c), the HSE (a=0.375) hybrid functional approach supports the shallow donor behavior of the H impurities in both interstitial-like and substitutional configurations. Their low formation energies, comparable to that of the O vacancy, have also been found under O-poor conditions [44]. Thus, the H impurity can be a source of the n-type conductivity of (nominally) undoped ZnO. In addition, because of the occupancy of the H impurity at the O site, the substitutional configuration can be related to the non-stoichiometry, as well as to the O vacancy. A positron annihilation and optical transmission study reported by Selim et al supports the presence of the substitutional H impurity [145].

The double shallow donor behavior of the Si impurity in ZnO and its relevance to the unintentional n-type conductivity have also been suggested through hybrid functional calculations by Lyons et al [108].

Look et al have reported that the complex of a Zn interstitial and an N impurity acts as a shallow donor [120]. The Zn interstitial is stabilized as a complex with a large binding energy of 0.9 eV, implying that in the presence of N impurities, Zn interstitials mostly form complexes at low temperature.

Summary

Recent first-principles studies of point defects in ZnO are reviewed focusing on the energetics of the native defects. Dominant defect species and their relevance to the electrical and optical properties are discussed on the basis of calculated formation energies, donor and acceptor levels, optical transition energies, and local atomic and electronic structures of the defects. Although results strongly depend on the computational method, several important conclusions can be drawn.

The O vacancy exhibits the lowest formation energy among donor-type native defects under most chemical potential conditions. It forms a deep donor level in the band gap. Therefore, the O vacancy is considered to be the dominant donor-type defect associated with non-stoichiometry toward the O-deficient side, but is unlikely to provide carrier electrons. The Zn interstitial and anti-site are both shallow donors. However, they have high formation energies in n-type ZnO and, hence, do not form at high concentration under thermal equilibrium. When the Fermi level is low, the O vacancy, Zn interstitial and Zn anti-site are energetically favorable. Therefore, these donor-type defects can compensate for holes in p-type ZnO.

The Zn vacancy is the representative acceptor-type defect. It is a deep acceptor that does not produce high hole concentrations. The Zn vacancy can compensate for carrier electrons and for non-stoichiometry toward the O-deficient side under n-type and O-rich conditions; such effects are insignificant under O-poor conditions where the Zn vacancy shows a sufficiently high formation energy. The O interstitial and anti-site are high in formation energy and/or are electrically inactive; they are hence, unlikely to play essential roles in electrical properties under thermal equilibrium. These features of the isolated native defects indicate that the n-type conductivity observed in undoped ZnO originates from other sources. Candidates have been proposed through first-principles calculations, which include the metastable configuration of the O vacancy with a shallow donor state, the Zn interstitial stabilized by a high concentration of the O vacancy, residual impurities such as H, Si, and the complex of a Zn interstitial and an N impurity. Hopefully, further theoretical and experimental studies will provide a better understanding and stronger evidence of the origin of the n-type conductivity.