Hydrothermal synthesis and properties of NiFe₂O₄@BaTiO₃ composites with well-matched interface

Abstract

NiFe₂O₄@BaTiO₃ multiferroic composite particles were produced by a simple hydrothermal method in two steps: preparing NiFe₂O₄ nanoparticles and then synthesizing core-shell nanocomposites. Multiferroic composite ceramics were sintered from these powders. X-ray diffraction, Raman scattering and energy dispersive x-ray analyses indicated that the core-shell composites with a NiFe₂O₄ core and BaTiO₃ shell were formed in the hydrothermal environment. Different types of sharp interfaces were self-assembled owing to the minimization of direct elastic energy. The saturation magnetization of the composites linearly increased with the NiFe₂O₄ content while the dielectric constant decreased. A dielectric peak appeared at around 460 °C because of the oxygen vacancies in the BaTiO₃ ceramics. It resulted in an enhancement of magnetic permeability in the composites, indicating magnetoelectric coupling that was also observed by direct magnetoelectric measurements.

1. Introduction

Multiferroic materials attract much research interest because of their fundamental physical properties and potential applications [1–6], such as magnetic probes, transducers, novel actuators and sensors. These materials simultaneously possess magnetic, electric and elastic orders and display a magnetoelectric coupling, in which the electric polarization or permittivity can be modified by an applied magnetic field, or a magnetic moment can be induced by an electric field [4–6]. However, these intriguing multiferroic properties in a single phase are observed only in a few systems, and the magnetoelectric coupling usually occurs under extreme conditions, such as very high magnetic fields and/or very low temperatures, because the ferroelectric and magnetic orders have opposite requirements to the 3d-orbital occupancy [1, 2, 7]. Alternatively, magnetoelectric composites possess relatively high magnetoelectric responses originating from the ferroelectric and magnetic phases, which individually do not exhibit multiferroic properties. These magnetoelectric responses are induced by stress mediation between the two phases according to the principles of product properties [4, 5], and therefore depend on the intrinsic properties of each phase and on the mechanical coupling between them. Materials with a high piezoelectric constant such as Pb(Zr,Ti)O₃ and BaTiO₃ are selected as the ferroelectric phase, whereas Terfenol-D, FeBSiC and ferrites with high magnetostrictive parameters are chosen as the magnetic phase [8–23]. It is easier to tailor the magnetoelectric properties in a composite than in the individual phases by adjusting the volume fractions and interactions among the components. Different connective structures have been tried to enhance the magnetoelectric coupling, including particulate composites [8–14], laminated composites [15–17, 24], multilayers [18, 25], nanofibers [23] and ferrite nanopillars embedded in a ferroelectric matrix [19–22, 26].

Most recently, researchers have turned their interest to magnetoelectric nanocomposites, such as films [17–19, 27] and nanoceramics [9–13, 28], because of the demand for high-density electronic components with high performance, multifunctionality, smaller size and low cost [29]. In nanoscience, surfaces and interfaces play a key role in modulating the effective material properties. Magnetoelectric nanocomposites with a well-matched interface between the magnetic and ferroelectric phases at the atomic scale have been prepared by physical deposition [19–22, 30, 31]. They are an interesting object to investigate the magnetic, ferroelectric, dielectric and magnetoelectric properties. However, it is difficult to prepare magnetoelectric nanocomposites with a well-matched interface between the two phases by wet chemical methods [4].

Some researchers have recently tried new methods of in situ preparation of composite powders to ensure a better microstructural control. Coprecipitation [8, 9], sol–gel [9, 32], gel-combustion [33] and sonochemical methods [12, 34] were employed to improve mixing of the ferroelectric and magnetic phases and obtain homogeneous microstructures. Multiferroic core-shell nanopowders appear to have a better connectivity between the phases, resulting in superior dielectric and magnetoelectric properties [10–12]. The nanocomposite powders exhibit a high chemical activity and can be densified at relatively low temperatures, which avoids the formation of foreign phases at the interface between the two phases during the sintering.

The ratio between piezoelectric and piezomagnetic phases was a main factor influencing the magnetoelectric coefficient [5, 15]. However, the composite ceramics synthesized by the direct mechanical mixing of powders of the two phases exhibited a weak magnetoelectric effect, partly because of the mechanical defects and low percolation threshold (about 18%) in the randomly mixed ferrite grains. The core-shell nanopowder appears to be a better solution to break through the percolation threshold of the magnetostrictive phase [4, 5]. Several core-shell multiferroic composites have been obtained, such as Ni_0.5Zn_0.5Fe₂O₄@BaTiO₃ [10], Fe₂O₃@ BaTiO₃ [11], BaTiO₃@Fe₃O₄ [12], PZT@NiFe₂O₄ [13], BaTiO₃@Fe₂O₃ [34] and SrTiO₃@BiFeO₃ [35]. The main reported magnetoelectric core-shell composites and our results are summarized in table 1. The strain caused by a core and/or shell enhances the magnetoelectric coupling because core materials are wrapped by shell materials through well-defined interfaces [12]. Since the piezoelectric component is far more electrically insulating than the magnetic one, core-shell structures are usually designed to have a ferrite core and ferroelectric shell [9, 10], preventing the ferrite particles from direct contact during sintering. It was proven rather difficult to synthesize microstructured ceramics with a perfect interface between the ferrite core and ferroelectric shell [4]. Nevertheless, a well-matched interface between ferrite and BaTiO₃ was produced with a wet chemical method by carefully controlling the experimental conditions [27, 36, 37]. Oxygen vacancies are the most common defects in perovskites and spinels, and are formed during sintering at high temperatures and low partial oxygen pressures [38]. Such defects appearing at the interface will act as charge traps, resulting in a high dielectric loss. Therefore, the sintering temperature is reduced for magnetoelectric core-shell nanopowders compared with the materials prepared by conventional solid-state reaction methods, which suppresses diffusion across the interface.

Table 1.

Summary of the composition and properties of the multiferroic core-shell nanocomposites.

Core@Shell	Core-shell preserved	Synthesis method	Interface	Measured properties
CoFe2O4@BaTiO3 [8, 9]	Maybe	Coprecipitation/	Grain boundary	Magnetization linearly increases
		sol–gel		with CoFe2O4 content.
				α33=1.48 mV (cm Oe)−1
				d33=44.6 pC N−1.
Ni0.5Zn0.5Fe2O4@BaTiO3 [10]	Maybe	Chemical	Grain boundary	Magnetization, dielectric
				constant and
				conductivity versus temperature
Fe2O3@BaTiO3 [11]	Yes	Colloidal chemistry/	Physical	Low magnetization, permittivity
		solid-state reaction
BaTiO3@Fe2O3,	Yes	Sonochemical		Magnetoresistance, magnetization,
BaTiO3@Fe3O4 [12, 34]				magnetodielectric properties;
				magnetization jumps near the BaTiO3
				structural phase transition temperatures
CoFe2O4@Pb(Zr0.52Ti0.48)O3 [23]	Core-shell	Sol–gel + electrospinning	Physical	Magnetization, piezoresponse and
	nanofiber			magnetoelectric properties
Pb(Zr0.52Ti0.48)O3@NiFe2O4 [13]	Yes	Solid-state reaction/		Magnetization, α33=190 mV (cm Oe)−1
		chemical
Ferrite@perovskite [14]	Yes	Hydrothermal + annealing	Physical	Magnetization, resistivity
NiFe2O4@BaTiO3∗	Yes	Two-step hydrothermal	Well matched	Magnetization, magnetodielectric and
				magnetoelectric properties

^∗This manuscript.

Nickel ferrites combine a wide range of useful magnetic properties with a relatively low electrical conductivity; they exhibit low eddy current loss in alternating-current applications and have numerous applications in electric devices. BaTiO₃ is one of the most useful dielectric materials in microelectronic devices because of its good chemical stability, high dielectric constant and low loss in a wide frequency range. It has a perovskite structure with lattice parameters a = 0.4006 nm and c = 0.4017 nm (powder diffraction file (PDF) No. 89-1428). Meanwhile, NiFe₂O₄ has a spinel structure with a lattice parameter a = 0.8337 nm (PDF No. 89-4927), approximately twice that of BaTiO₃, allowing the formation of a well-matched interface with BaTiO₃. In this work, we prepared NiFe₂O₄@BaTiO₃ composite powders with well-matched interfaces by a two-step hydrothermal method, and then sintered the ferroelectric–magnetic composite ceramic. The structural and functional properties were investigated in detail.

2. Experimental procedures

2.1. Synthesis of composites

The chemical reagents used for reactions were Fe(NO₃)₃·9H₂O, Ni(NO₃)₃·6H₂O, Ba(NO₃)₂, TiCl₄ and a NaOH mineralizer. All chemicals were used as received without further purification. High-quality NiFe₂O₄@BaTiO₃ nanoparticles were synthesized by a hydrothermal method in two steps: preparing NiFe₂O₄ nanoparticles and then covering them with a shell.

Fe(NO₃)₃·9H₂O and Ni(NO₃)₃·6H₂O with a molar ratio of 2:1 were dissolved in distilled water under mechanical stirring and slowly precipitated with NaOH to a final pH of 13. Then, the brown suspension was transferred into an autoclave filled up to 4/5 of its capacity for reaction at 250 °C for 1 h under mechanical stirring. After natural cooling to room temperature, the resultant powders were washed several times with distilled water until the liquid became neutral, and NiFe₂O₄ nanoparticles were recovered.

TiCl₄ was dissolved in ethanol and Ba(NO₃)₂ in distilled water under mechanical stirring, and the solutions were mixed together with a molar ratio of 1:1.8. NaOH solution was slowly added to coprecipitate metal ions and adjust the pH to 13. Then, the suspension together with the NiFe₂O₄ nanoparticles was transferred into the autoclave filled up to 4/5 of its capacity. The molar contents of NiFe₂O₄ in the composites were set to 10, 20, 30, 40 and 50%, and the corresponding samples were named as C10, C20, C30, C40 and C50, respectively. The hydrothermal treatment was performed at pH = 13 and 300 °C for 2 h under mechanical stirring to avoid NiFe₂O₄ agglomeration. Then, the composite powders were washed several times with distilled water until the liquid became neutral. We separated the NiFe₂O₄@BaTiO₃ nanopowders with a magnet from pure BaTiO₃ to ensure the presence of NiFe₂O₄ in the nanocomposites. For comparison, pure BaTiO₃ and NiFe₂O₄ powders were prepared under the same conditions.

The obtained nanocomposite powders were pressed into different shapes by applying a pressure of about 300 MPa for the electric and magnetic measurements. Tablets 1.5–2 mm in thickness and 6 mm in diameter were used for dielectric measurements. Toroids 1.5 mm in thickness, 8 mm in inner diameter and 18 mm in outer diameter were used for measuring magnetic permeability. The tablets and toroids were sintered in air at 1100 °C for 6 h to obtain xNiFe₂O₄-(1 − x) BaTiO₃ (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5 and 1) ceramics. Then, the tablets were polished to a uniform parallel surface and coated with a silver paste to form electrical contacts. Ten turns of a Cu wire were wound on the toroidal samples for measuring magnetic permeability.

2.2. Characterization

X-ray diffraction (XRD) patterns of the composite powders and ceramics were measured using a Rigaku D/Max 2550 diffractometer with a Cu Kα (λ = 1.5418 Å) source. The lattice parameters, average crystal size and phase ratios of NiFe₂O₄ and BaTiO₃ were calculated with Jade 6.5 software. The morphology of the NiFe₂O₄-BaTiO₃ nanopowders and ceramics was studied by scanning electron microscopy (SEM, FEI-Quanta 200) and transmission electron microscopy (TEM, F30) combined with energy dispersive spectroscopy (EDS). One of the C20 ceramic samples was polished and thinned for investigating the interface between NiFe₂O₄ and BaTiO₃ by high-resolution TEM (HRTEM).

The dielectric properties were measured using an Agilent 4294A complex impedance analyzer in the frequency range of 10³–10⁸ Hz. Raman measurements were performed using an ALMEGA-TM dispersive Raman spectrometer and 532 nm laser excitation. Magnetic hysteresis loops were measured with an LDJ9600 vibrating sample magnetometer (VSM). Curie temperature was determined from the change in magnetic permeability upon heating at a rate of 4 °C min⁻¹, and from the change in magnetic moment upon heating at a rate of 10 °C min⁻¹ in a magnetic field of 500 Oe. The magnetoelectric effect was measured using a dynamic method as described in [24]. The composite pellet was poled electrically and then placed in a dc magnetic field that was varied up to 3.6 kOe. An ac magnetic field δH generated by a Helmholtz coil was superimposed on the dc magnetic field, both fields being parallel to the sample plane. The charges generated from the samples were collected by a charge amplifier. Then, the magnetoelectric coefficient was calculated as α_E = δE/δH = δV/tδH = δQ/ε_rε₀SδH, where t and S are the thickness and surface area of the sample, E and V are the electric field and voltage induced by the magnetic field, respectively, and ε_r is the relative permittivity.

3. Results and discussion

3.1. Crystal structure

Figure 1(a) shows the XRD patterns of the as-prepared NiFe₂O₄, BaTiO₃ and NiFe₂O₄-BaTiO₃ powders while figure 1(b) shows the patterns of the corresponding ceramics sintered at 1100 °C. Only NiFe₂O₄ and BaTiO₃ phases are observed, indicating that no intermediate phase formed at the interface between the NiFe₂O₄ core and BaTiO₃ shell either during the hydrothermal synthesis or after sintering. BaTiO₃ exhibits a tetragonal structure because the (200), (211) and (202) diffractions are broader than the (111) peak. This means that BaTiO₃ has a polar structure in both the powders and sintered composites. However, the absence of splitting in the (002)/(200) doublet indicates that the c/a ratio of the lattice parameters is much lower in our samples than in macroscopic single crystals and coarse-grained ceramics (c/a =1.01). This is a typical feature of nanocrystalline BaTiO₃ particles and ceramics [39]. The relative intensity of the NiFe₂O₄ diffractions varies accordingly with the NiFe₂O₄ content. Figure 1(c) shows the NiFe₂O₄ content calculated by fitting the integrated XRD intensities; the values agree well with the nominal composition, implying that the reaction was well completed under the hydrothermal conditions.

Figure 1.

XRD patterns of (a) nanopowders prepared by the hydrothermal method and (b) the corresponding ceramics sintered at 1100 °C for 6 h; dependences on the nominal NiFe₂O₄ content of (c) the NiFe₂O₄ content derived from the XRD patterns, (d) lattice parameters and (e) the average crystal size of NiFe₂O₄ and BaTiO₃.

The lattice parameters calculated from the XRD patterns are shown in figure 1(d). The lattice parameters do not vary with composition in the NiFe₂O₄ and BaTiO₃ powders, and change by 1% in ceramics, which may be attributed to the strain between the two phases caused by sintering at high temperature owing to their different shrinking rates. Invariable lattice parameters imply low stress in the nanocomposites. The average crystal size of both phases obtained from the refinement of XRD patterns is plotted in figure 1(e) versus the NiFe₂O₄ content. The powder crystal size remains constant at about 70 nm for NiFe₂O₄ and 83 nm for BaTiO₃, indicating that NiFe₂O₄ crystallites remain unchanged during the second step of the synthesis of core-shell composites. It is believed that the crystallite size is a main factor affecting the crystal structure [40]. After sintering at 1100 °C, the BaTiO₃ crystal size decreases slightly, while the NiFe₂O₄ crystal size remains constant at low and increases at high NiFe₂O₄ concentrations. In the second step of the hydrothermal reaction, several BaTiO₃ crystallites may epitaxially grow on one NiFe₂O₄ nanoparticle. At low NiFe₂O₄ concentrations, NiFe₂O₄ particles are isolated homogeneously by BaTiO₃ particles that prevent the NiFe₂O₄ aggregation, whereas at higher concentrations of 40 and 50%, NiFe₂O₄ particles contact each other, resulting in the NiFe₂O₄ particle growth during sintering at high temperatures.

Raman spectroscopy is a highly sensitive technique of probing the local crystal structure in materials. Figure 2 shows the Raman spectra of nanocrystallites measured at room temperature for pure BaTiO₃ and NiFe₂O₄ and their composites. There are several Raman-active modes resulting from the tetragonal phase for the as-prepared BaTiO₃ nanocrystallites; particularly the bands at 516 and 710 cm⁻¹ correspond to the E(TO) and E(LO) modes in polar BaTiO₃, respectively [41]. The polar order of BaTiO₃ is strongly depressed as judged from the absence of the 305 cm⁻¹ peak, indicating symmetry with the TiO₆ octahedra. The 810 cm⁻¹ peak is specific for cubic BaTiO₃ [42, 43]. Its presence in figure 2 implies that the cubic phase appears in the pure BaTiO₃ particles because of their composite structure consisting of the inner tetragonal core, the cubic shell, and a gradient lattice-strain layer in between [39]. There are five Raman-active A_1g + E_g + 3T_2g modes at about 700, 320, 210, 330 and 560 cm⁻¹ in the bulk NiFe₂O₄; however, these modes are very weak in NiFe₂O₄ nanoparticles [44, 45] and are not seen in figure 2. The composite exhibits very weak Raman peaks corresponding to the BaTiO₃ phase. The weakness of the Raman peaks in the nanocomposites can be explained using the schematic in the top part of figure 2. The BaTiO₃ particles have a uniform crystal structure and a significant size of about 300 nm, and therefore exhibit strong Raman signals. The NiFe₂O₄ core in the nanocomposite effectively splits the original large uniform particle into smaller fragments wherein the signals are reduced owing to the size effects.

Figure 2.

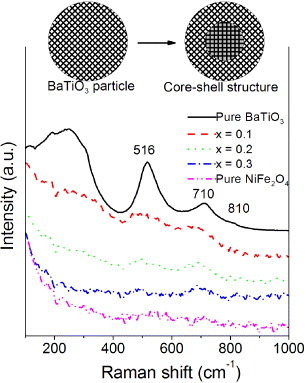
Raman spectra of BaTiO₃, NiFe₂O₄ and their composite powders. The inset shows a schematic of BaTiO₃ and core-shell particles.

3.2. Morphology and interface

Figure 3(a) shows a typical SEM image of the hydrothermally synthesized BaTiO₃ nanoparticles. The particles are spherical and mostly not aggregated. They have a narrow size distribution of 200–300 nm, similar to previous reports [40, 43, 46]. Figure 3(b) shows a typical TEM image of the precursor NiFe₂O₄ nanoparticles. Their regular morphology was achieved at pH = 13 owing to the moderate speed of nucleation and crystal growth [47, 48]. Figures 3(c)–(g) show the SEM images of the composites with x = 0.1–0.5, which consist of spherical nanoparticles with a small grain size of 100–250 nm. Even smaller particles can be discerned in sample C50. All the grains contain NiFe₂O₄ particles because they were selected by a magnet. In fact, all the particles were extracted, indicating that all the BaTiO₃ crystallites have grown on the NiFe₂O₄ particles. BaTiO₃ crystallites on NiFe₂O₄ cannot grow larger than the particles shown in figure 3(a) owing to the lattice mismatch between the two phases. We have investigated the spatial distribution of the two phases on the sample C20 (figure 3(h)). The existence of the core-shell nanostructure in this sample is well supported by the EDS analysis (figure 3(i)): Fe, Ni, Ba and Ti elements are detected in the central part whereas Ba and Ti dominate the outer region. This result confirms the successful preparation of composite powders with a NiFe₂O₄ core and BaTiO₃ shell.

Figure 3.

SEM images of (a) BaTiO₃ particles, (b) NiFe₂O₄ particles and (c–g) C10–C50 nanocomposites; (h) TEM image of sample C20 and (i) EDS spectra acquired at positions 1 and 2 on a typical NiFe₂O₄@BaTiO₃ nanoparticle.

Although perfect epitaxial orientation for the composite was obtained in thin films [19, 20, 30, 31, 37], it is difficult to observe a homogenous epitaxial relationship between NiFe₂O₄ and BaTiO₃ in composite particles for the following reasons: (i) the irregular NiFe₂O₄ surfaces hinder the formation of uniform epitaxial BaTiO₃; (ii) the BaTiO₃ crystallites grow only in one dimension for the films, whereas they grow along any direction out of the NiFe₂O₄ particle surface in our experiment, resulting in a NiFe₂O₄–BaTiO₃–BaTiO₃ triple junction as shown in figure 4(c); (iii) if there exists an epitaxial BaTiO₃ on a NiFe₂O₄ particle in the composite, it is hard to prove that by HRTEM because of the difficulty of thinning the composite ceramic along a low-index direction. Nevertheless, sharp interfaces are observed in figure 4, confirming the absence of impurity phases and defects at the NiFe₂O₄–BaTiO₃ interfaces.

Figure 4.

Typical HRTEM images of interfaces in sample C20: (a, b) two different types of interface and (c) is a triple NiFe₂O₄–BaTiO₃–BaTiO₃ interface.

The interface between two phases was characterized by HRTEM in sample C20, which was thinned to several tens of nanometers. Figure 4 shows three typical cross-sectional HRTEM images at the interface. The sharp interfaces between NiFe₂O₄ and BaTiO₃, other than a simple connection through van der Waals interaction [9–13, 28, 35], were obtained via the simple precursor hydrothermal reaction. The low mutual solid solubility between BaTiO₃ and NiFe₂O₄ is an important factor for obtaining clean interfaces. The hydrothermal reaction commonly involves two stages, i.e. nucleation and crystalline growth. At the second step, BaTiO₃ tends to grow on NiFe₂O₄ nanoparticles because this allows the nucleation energy to be saved. The similar lattice parameters of BaTiO₃ and NiFe₂O₄ allow direct deposition of BaTiO₃ on NiFe₂O₄ forming well-matched interfaces. Figures 4(a)–(c) present three typical cross-sectional HRTEM images at different locations of the interface. Figure 4(a) shows the NiFe₂O₄ (220) and BaTiO₃ (110) crystal planes that have similar interplanar distances. Their angles with the interface are, however, different, resulting in a 2% misfit. The lattice mismatch energy at the interface is relaxed through the formation of an asymmetrical interface rather than the dislocations [20, 22, 26, 49]. Figure 4(b) shows the crystal planes of NiFe₂O₄ (111) and BaTiO₃ (110), which have very different interplanar distances. The interface strain energy was relaxed by the planes marked with white lines, which have different densities at two sides of the interface. Figure 4(c) shows a triple interface among the NiFe₂O₄ (200), BaTiO₃ (200) and BaTiO₃ (110) crystal planes. The BaTiO₃ and NiFe₂O₄ sides of the interface exhibit different stripe densities that allow us to reduce the lattice strain energy and form clear interfaces. BaTiO₃ (200) and BaTiO₃ (110) planes connect together through dislocations as indicated by the black arrows in figure 4(c). BaTiO₃ (200) lattice planes traverse the dark area out of the NiFe₂O₄ corner, indicating a perfect self-assembled growth in the hydrothermal environment. Although it is difficult to grow epitaxial BaTiO₃ on the NiFe₂O₄ crystallites as discussed above, sharp interfaces between NiFe₂O₄ and BaTiO₃ with different connections were self-assembled owing to the minimization of the interface elastic energy between the two phases. The conclusion above is general and can be applied to other self-assembled nanocomposite systems.

The ceramics sintered at 1100 °C were observed by SEM. Both the BaTiO₃ and NiFe₂O₄ grains grew after sintering as shown in figures 5(a) and (b). The composites C10, C20 and C30 [figures 5(c)–(e)] maintain a homogeneous microstructure with better mixing of the two phases because the grain growth is suppressed by the very low mutual solid solubility of the phases. The ceramics show much higher density than the materials prepared by solid-state reactions [50, 51]. However, some large crystallites 1–2 μm in size appear in the sample C40 and even larger ones in C50 as shown in figures 5(f) and (e). We analyzed their composition by EDS and found Fe, Ni, Ba, Ti and O in the small grains. However, only Fe, Ni and O elements were detected in the large grains, indicating the NiFe₂O₄ grain growth. The NiFe₂O₄ molar ratio is large in these two samples because some NiFe₂O₄ particles could not be coated by the BaTiO₃ grains as shown in figures 3(h) and (g). These NiFe₂O₄ particles grew larger during the sintering process, as confirmed from the XRD results shown in figure 1(e). In the particulate composite ceramics synthesized by the direct mixing of powders of two phases, the ferrite particles have a low percolation threshold of about 18% [5, 52], over which the relative low resistance NiFe₂O₄ could degrade the insulating properties of the composite. In this work, the BaTiO₃ shell was grown on the NiFe₂O₄ core to form composite particles. Some NiFe₂O₄ particles could not be coated at high NiFe₂O₄ content. Thus, in the composite the coated particles act as insulators, and the insulating properties will be retained if the concentration of remaining uncoated NiFe₂O₄ crystallites remains below 18%. As a result, the total NiFe₂O₄ content can be higher than that in the case of direct mixing, and no significant NiFe₂O₄ agglomeration was observed up to 40% of NiFe₂O₄ in this study.

Figure 5.

SEM cross-sectional images of ceramics sintered at 1100 °C: (a) BaTiO₃, (b) NiFe₂O₄ and (c–g) C10–C50 nanocomposites; (h) and (i) show EDS spectra acquired at different positions on samples C40 and C50, respectively.

3.3. Electrical properties

We have studied the electrical and magnetic properties of the produced two-phase composites. Figure 6 shows the frequency dependences of the dielectric constant and dielectric loss in NiFe₂O₄, BaTiO₃ and composite ceramics at room temperature. These properties remain almost unchanged below 10 MHz in BaTiO₃ and composites. The composites have high dielectric constants of ∼720 for x = 0.10 and ∼530 for x = 0.20. Strong dielectric resonances appear in BaTiO₃ and composite ceramics. The dielectric resonance in NiFe₂O₄ may occur at high frequencies [53], beyond our measurement range. The resonance frequency shifts to higher frequencies with increasing NiFe₂O₄ content as shown in the top-left inset in figure 6, as in magnetodielectric composites [54–56]. The resonances observed in these ceramics are due to the activation of different piezoelectric vibration modes, which originate from particulate microstructural features and random orientation of the crystallites with respect to the applied field. The presence of the magnetic phase suppresses the piezoelectric resonance [56].

Figure 6.

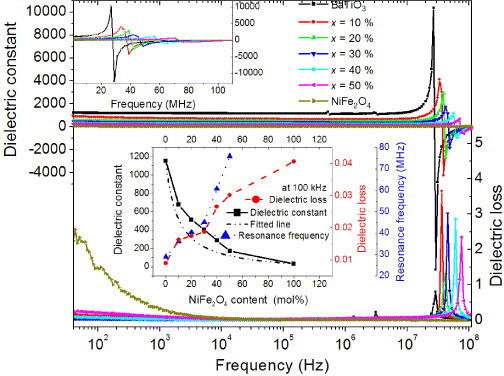
Frequency dependence of dielectric constant and dielectric loss for the samples sintered at 1100 °C. The top-left inset is a magnification of the dielectric peaks. The lower inset shows the dielectric constant, dielectric loss and resonance frequency versus NiFe₂O₄ content.

The dielectric constant decreases while dielectric loss increases with increasing NiFe₂O₄ content, as shown in the lower inset in figure 6. This tendency can be modeled using the effective medium approximation and the Maxwell–Garnett equation as follows [57, 58]:

Here ε, ε_N and ε_B are the dielectric constants of the composite, NiFe₂O₄ and BaTiO₃, respectively, and is the volume fraction of BaTiO₃. Equation (2) fits well the experimental data at 100 kHz over a wide range of compositions as shown in the lower inset in figure 6.

Figure 7 shows the variation of dielectric constant with temperature at 1 kHz, 10 kHz, 100 kHz and 1 MHz for the ceramics with x = 0–1. The dielectric properties differ for our BaTiO₃ samples and BaTiO₃ ceramics prepared with the solid-state reaction, in which the dielectric constant exhibits a λ-type transition near the Curie temperature of T_C ∼120 °C. In contrast, the dielectric constant of BaTiO₃, which was hydrothermally synthesized at 300 °C and then sintered at 1100 °C, increases slowly to a maximum at around 100 °C, followed by a decrease, indicating a phase transition. The permittivity peak at around 100 °C confirms the tetragonal structure of the sintered composites. The decrease in the transition temperature compared with that of the bulk material can be explained by the small grain size [39]. With a further increase in temperature, the electrical conductivity increases because of increasing drift mobility of thermally activated electrons. As a result, the dielectric constant and dielectric polarization increase. A new dielectric peak was observed at 460 °C and its detailed mechanism has not been clearly determined. The dielectric relaxation at high temperatures is caused by oxygen vacancies [59–61]. The short-range hopping of oxygen vacancies in the external electric field, similar to reorientation of a dipole, may result in a dielectric relaxation peak [62].

Figure 7.

Variation of dielectric constant with temperature at different frequencies.

The dielectric constant of NiFe₂O₄ shows a broad peak at 240–500 °C, which shifts towards high temperatures with increasing frequency. Above this peak, the dielectric constant continuously increases with temperature. These observations can be explained as follows. Electron hopping between nickel and iron ions of different chemical valences in the external field produces holes in the bulk of the samples. Then both n- and p-type carriers take part in the conduction. Increasing the temperature excites more charge carriers from their trapping centers. This in turn enhances their contribution to the polarization, resulting in an increase in the dielectric constant ε [63, 64]. As the frequency increases, the electrons cannot keep pace with the rapidly changing field, and thus, the polarization decreases. Consequently, a higher energy is required to restore polarization, which is provided by increasing the temperature. The higher the frequency, the higher the required temperature, and thus, the dielectric maximum shifts towards higher temperatures. The dielectric constant of the composites combines the characteristics of NiFe₂O₄ and BaTiO₃ almost as predicted by the Maxwell–Garnett equation.

The increase in dielectric constant at around 600 °C is related to the magnetic phase transition in NiFe₂O₄. The electron hopping between Ni²⁺/Ni³⁺ and Fe²⁺/Fe³⁺ ions in NiFe₂O₄ causes local displacements in the direction of the applied electric field, which affects the dielectric polarization in ferrites. Such an anomaly is predicted from the thermodynamic theory of simultaneously ferroelectrically and ferromagnetically ordered materials. It can be attributed to phase transitions as an effect of vanishing magnetic order on electric order, and hence, is a signature of magnetoelectric coupling [65]. In ferrites, magnetic ordering is responsible for the change in dielectric constant with temperature [66]. The large increase in the dielectric constant near T_C is observed owing to the temperature dependence of domain wall motion [67, 68]. At low temperatures, the mobility of domain walls is hindered, and hence, the dielectric response due to the extrinsic contribution is small. When the temperature is higher than T_C, domains disappear after the phase transition, and the dielectric response is also small. Near the magnetic–paramagnetic transition temperature, the thermal energy is comparable to the potential barrier for domain movement; hence, the domain wall motion becomes very active, resulting in a high dielectric constant.

3.4. Magnetic properties

Figure 8(a) shows the magnetic hysteresis loops of powders and nanoceramics. The magnetic characteristics of the powders and ceramics are similar, with thin loops illustrating a soft magnetic behavior. In figure 8(b), the saturation magnetization and coercivity are plotted as functions of NiFe₂O₄ content. The coercivity of the magnetic nanopowders is related to both the material intrinsic properties and grain size [69]; it remains almost constant at ∼50 Oe, indicating that the NiFe₂O₄ nanoparticles retain their small size during the BaTiO₃ hydrothermal growth. In contrast, the coercivity of the ceramics C10, C20 and C30 significantly increases to 250 Oe. Diffusion of elements may occur and enhance the interfacial interaction during high-temperature sintering. This hinders the rotation of the magnetic domain wall while the magnetic NiFe₂O₄ particles are magnetized or demagnetized in the external magnetic field, resulting in a high coercivity of the composite ceramics as shown in figure 8.

Figure 8.

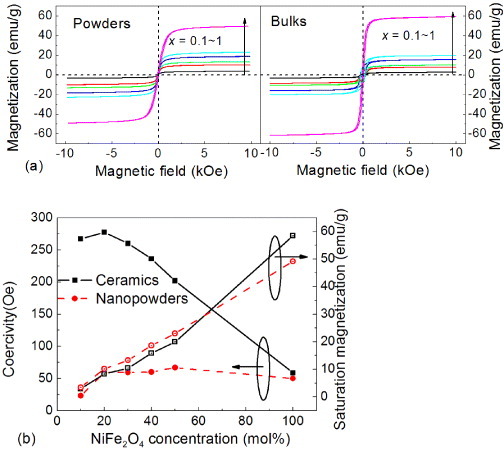
(a) Hysteresis loops of the as-prepared powders and nanocomposite ceramics sintered at 1100 °C; (b) NiFe₂O₄ concentration dependence of coercivity and saturation magnetization of the powders and ceramics.

The saturation magnetization of the nanopowders increases linearly with the NiFe₂O₄ content, suggesting that the presence of BaTiO₃ phase does not affect the magnetic interaction. The lower magnetization of the composites is due to a better isolation of the magnetic phase by the nonmagnetic part in the core-shell structure, which is consistent with the XRD result shown in figure 1(e). The saturation magnetization of the NiFe₂O₄ ceramic is higher than that of the nanopowders, which results from the larger grain size or surface effects [69] after sintering at high temperature as shown in figures 3(b) and 5(b). The saturation magnetization is smaller in the composite ceramics than in the nanopowder, which is attributed to the elemental diffusion at the interface during high-temperature sintering. Therefore, the presence of a nonmagnetic perovskite phase and the interface effects do not influence the magnetic properties in the composite powders but slightly reduce the saturation magnetization and enhance the coercivity in the composite ceramics. Although the sharp interfaces between NiFe₂O₄ and BaTiO₃ were obtained, the elemental diffusion between them is difficult to avoid during high-temperature sintering.

3.5. Magnetoelectric coupling

The temperature dependence of magnetic permeability is a convenient indicator of a phase transition. Figure 9(a) shows the temperature dependence of magnetic permeability measured at 1 MHz. The magnetic permeability falls abruptly when the magnetic state of the ferrite changes from ferromagnetic to paramagnetic around 550 °C. Physically, the thermal agitation is so violent that it reduces the alignment of the magnetic moment along a given axis to zero at T_C. The Curie temperature increases with the NiFe₂O₄ content reaching 565 °C for pure NiFe₂O₄, which was confirmed by the magnetic moment dependence on temperature as shown in figure 9(b). The decrease in the Curie temperature of the composite is attributed to the diffusion of nonmagnetic elements into the spinel lattice. The nonmagnetic elements weaken the A–B superexchange interaction as a result of the distance increase between the magnetic moments in the A and B sites in the spinel structure. The weaker superexchange interaction is more affected by the thermal motion, resulting in a decrease in the Curie temperature of the composite ceramics. Just below the Curie temperature, magnetic permeability μ_i increases with temperature to a maximum value because it relates as to the crystal anisotropy K₁, which decreases with temperature (M_S is saturation magnetization). Since the temperature dependence is stronger for the crystal anisotropy than magnetization, at the paramagnetic phase transition, the magnetic permeability approaches infinity just below T_C and then decreases [70]. This feature is called the Hopkinson peak.

Figure 9.

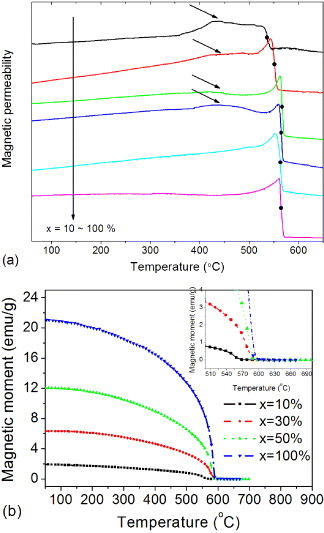
Temperature dependences of (a) magnetic permeability measured at 1 MHz, (b) magnetic moment at 500 Oe for the samples sintered at 1100 °C.

Another broad peak between 420 and 470 °C is observed in the composites C20–C50 having a high BaTiO₃ content. This peak does not appear in pure NiFe₂O₄ and the low-BaTiO₃ composite C10. We attribute it to the dielectric change of BaTiO₃ shown in figure 7(a). Phase transitions in BaTiO₃ could lead to the jump in the magnetization observed in magnetoelectric composites [12, 31, 37]. In our samples, BaTiO₃ exhibits a dielectric peak at around 460 °C attributed to oxygen vacancies. Additional free electrons generated in this temperature range should increase the magnetic superexchange interaction, resulting in an enhancement of magnetic permeability.

Figure 10 shows the variation with H_bias of magnetoelectric effects for the composites at 10 kHz. The composites share similar magnetoelectric characteristics, that is, α_E increases rapidly to a maximal value and then slowly decreases when the applied magnetic field is increased from zero to 3.6 kOe. The initial rise in magnetoelectric output is attributed to the enhancement of elastic interactions. The magnetoelectric peak indicates that the magnetostriction reaches saturation at a certain value of H_bias, which corresponds to the saturation magnetization in NiFe₂O₄. We find that the magnetoelectric output decreases with the NiFe₂O₄ content. A different behavior is observed in laminate composites where the magnetoelectric coefficient increases with increasing piezomagnetic component [15, 25].

Figure 10.

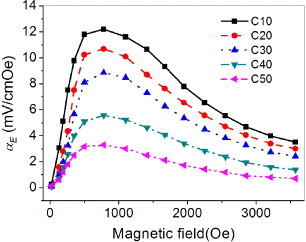
Variation of magnetoelectric coefficient α_E with applied magnetic field for the composites at 10 kHz.

4. Conclusions

Core-shell ceramics exhibiting sharp interfaces between the NiFe₂O₄ core and BaTiO₃ shell were prepared by a simple hydrothermal method, as confirmed from Raman spectra and EDS analysis. The good agreement between the measured and nominal molar contents of NiFe₂O₄ and BaTiO₃ indicated an efficient reaction. Different types of interfaces were self-assembled owing to the minimization of direct elastic interactions between the two phases. The saturation magnetization linearly increased with the NiFe₂O₄ content in the composites. Their dielectric constants combined the properties of NiFe₂O₄ and BaTiO₃ obeying the Maxwell–Garnett relationship. A peak at around 460 °C was observed in the temperature dependence of the dielectric constant and was attributed to the oxygen vacancies in BaTiO₃, which also lead to an enhancement of magnetic permeability in the composites. Such an anomaly is a signature of magnetoelectric coupling, which was confirmed by magnetoelectric measurements. Core-shell nanoparticles composed of ferroelectric and ferromagnetic materials are promising candidates for possible applications of nanosized multiferroics and magnetodielectrics.