The effect of the interlayer element on the exfoliation of layered Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) MAX phases into two-dimensional Mo₂C nanosheets

Abstract

The experimental exfoliation of layered, ternary transition-metal carbide and nitride compounds, known as MAX phases, into two-dimensional (2D) nanosheets, is a great development in the synthesis of novel low-dimensional inorganic systems. Among the MAX phases, Mo-containing ones might be considered as the source for obtaining Mo₂C nanosheets with potentially unique properties, if they could be exfoliated. Here, by using a set of first-principles calculations, we discuss the effect of the interlayer ‘A’ element on the exfoliation of Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) MAX phases into the 2D Mo₂C nanosheets. Based on the calculated exfoliation energies and the elastic constants, we propose that Mo₂InC with the lowest exfoliation energy and the highest elastic constant anisotropy between C₁₁ and C₃₃ might be a suitable compound for exfoliation into 2D Mo₂C nanosheets.

Introduction

Two-dimensional (2D) nanosheets are expected to have a significant impact on a large variety of applications, ranging from electronic and thermoelectronic to gas storage, catalysis, high-performance sensors, support membranes and coatings [1–3]. These important applications have stimulated tremendous research into the synthesis and characterization of new complex 2D systems. So as to obtain new 2D nanosheets, as a top-down approach, experimentalists have focused on the exfoliation of layered organic and inorganic materials with weak van der Waals interlayer interactions. For instance, monolayers and flakes of 2D graphene were obtained mechanically by rubbing graphite against other surfaces or by the sonication of graphite powder in various aqueous or organic solvents [4]. Similar mechanical techniques were also applied to some of the inorganic layered materials, such as boron nitrides and metal chalcogenides [5, 6]. Recently, a selective chemical etching method with hydrofluoric acid (HF) was proposed to exfoliate some members of a family of highly conductive, tough layered ceramics with strong interlayer interactions, known as the MAX phases, into 2D carbide nanosheets [7–14]. The MAX phases are compounds with the chemical formula of M_n+1AX_n(n = 1, 2 or 3) where ‘M’, ‘A’ and ‘X’ are an early transition metal, an element from groups 13–16 in the periodic table, and carbon and/or nitrogen, respectively [15]. After the removal of the interlayer ‘A’ element by HF treatment, the 2D carbide and nitride nanosheets created are called MXenes [7, 8]. By using the above method, three-dimensional particles of Ti₂AlC, Ti₃AlC₂ and Ta₃AlC₂ were successfully exfoliated into 2D-Ti₂C, -Ti₃C₂ and -Ta₄C₃ nanosheets [7, 8].

Owing to the large compositional possibilities of the MAX phases, a large number of new 2D M_n+1X_n systems is also expected to be synthesized. The first-principles calculations have shown that the 2D MXenes possess a variety of electronic structures depending on their composition and surface functionalization [16–24]. In addition, some MXenes were predicted to have peculiar properties such as large Seebeck coefficients [21]. Hence, the experimental synthesis and characterization of some of the MXenes are a priority because of their expected remarkable properties for energy-related applications. In this regard, 2D Mo₂C is one of the target systems, since it has been predicted to have unique electronic and thermoelectric properties [25]. In addition the nanostructured Mo₂C thin films are considered as an active catalyst in a wide variety of reactions: for methane aromatization, hydrodesurfurization, hydrodenitrogenation and so on [26–33].

It is expected that 2D Mo₂C nanosheets could be synthesized from the exfoliation of layered Mo₂AC powders, using an appropriate selective etchant. The models of bulk Mo₂AC and 2D Mo₂C nanosheets are presented in figure 1. At least seven possible compositions could be considered for Mo₂AC (where A = Al, Si, P, Ga, Ge, As or In) MAX phases. Among them, Mo₂GaC has already been experimentally synthesized [34, 35] and was shown to be a superconductor with the transition temperature of 3.7–4.1 K [36]. Mo₂AlC has also already been synthesized as a solid solution, (Ti_1−xMo_x)₂AlC, and used for the fabrication of a (Ti_1−xMo_x)₂AlC/10 wt% Al₂O₃ composite [37]. There is no reason that the other Mo-containing MAX phases cannot be synthesized in the near future.

Figure 1.

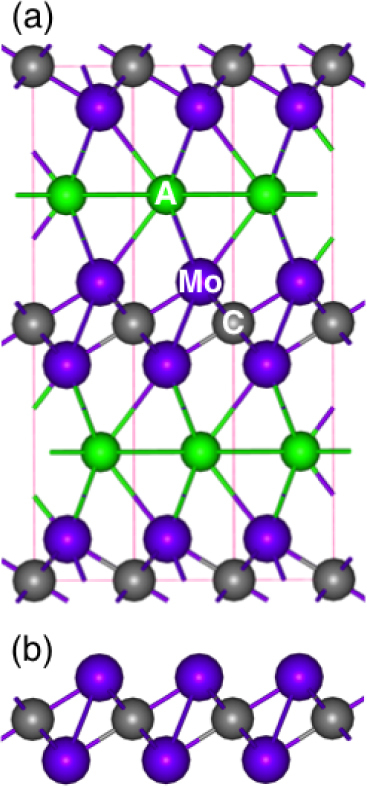
(a) Crystal structure of a Mo₂AC system and (b) side view of a 2D Mo₂C nanosheet.

Here, using a set of first-principles calculations, we investigate the exfoliation possibility of seven possible layered Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) MAX phases into 2D Mo₂C nanosheets. First, by calculating the elastic constants, it is shown that the above Mo₂AC systems are mechanically stable. Then, considering the elastic constant results and by calculating the exfoliation energies, it is concluded that Mo₂InC is the best source to realize a perfect 2D Mo₂C nanosheet.

Method of calculations

The first-principles calculations were performed within the framework of the density functional theory with the Perdew–Burke–Ernzerhof version of the generalized gradient approximation (GGA) as the exchange-correlation functional [38]. The projector augmented wave method was used for the basis. In the calculations, a plane-wave cutoff energy of 520 eV was used. The positions of atoms, cell parameters and angles were fully optimized by using the conjugate gradient method and applying the Methfessel–Paxton smearing scheme [39] with a smearing width of 0.1 eV. In the optimized structures, the magnitude of the force acting on each atom became less than 0.005 eV Å⁻¹. The total energies of the optimized structures were well converged within 10⁻⁶ eV cell⁻¹. In the structural optimizations of bulks, the Brillouin zone was sampled using a set of 12 × 12 × 4 k points [40]. The densities of states were obtained using 42 × 42 × 18 k points and using a tetrahedron technique. All of the calculations were done by VASP code [41]. We have also performed a set of spin-polarized calculations within GGA. However, all the compounds were found to be non-magnetic. The current GGA approach obtains the equilibrium lattice parameters for Mo₂GaC in good agreement with the experimental results within 2% [34, 35].

Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) with hexagonal structures adopt P6₃/mmc space group symmetry. The elastic constants are obtained by means of a Taylor expansion of the total energy of the strained crystal with respect to a small distortion parameter (α), as described in [42]. In this study, the elastic constants are derived from the total energy calculations of nine different distortions α = ± 0.02, ±0.015, ±0.01, ±0.005 and 0.0. The bulk modulus is estimated by fitting the curve of total energies to the third-order Birch–Murnaghan equation of state [43].

Results and discussion

The optimized structures for all Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) were obtained. Table 1 presents the optimization results for the lattice parameters of bulk Mo₂AC (A = Al, Si, P, Ga, Ge, As or In), and the corresponding Mo–A and Mo–C bond distances. Table 2 indicates the calculation results of the elastic constants and the bulk modulus for the studied Mo₂AC systems. Our results in tables 1 and 2 are in excellent agreement with the previous experimental and theoretical studies [34, 35, 44–47]. From table 2, it can be seen that the current results for all Mo₂AC systems satisfy the elastic stability criteria: C₁₁ > |C₁₂|,C₄₄ > 0, (C₁₁ + C₁₂)C₃₃ − 2C₁₃² > 0 [48]. Thereby, it is predicted that all above Mo₂AC systems are mechanically stable and can probably be formed in particular experimental conditions. However, it should be noted that there might be some other competing phases, which might be thermodynamically more favorable than the Mo₂AC systems [49].

Table 1.

Structural parameters and bond distances in bulk Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) with P6₃/mmc symmetry.

Mo2AC	a (Å)	c (Å)	c/a	Mo–A (Å)	Mo–C (Å)
Mo2AlC	3.029, 3.038c	13.448, 13.48c	4.440, 4.437c	2.779	2.122
Mo2SiC	3.103, 3.119c	12.401, 12.39c	3.996, 3.972c	2.643	2.133
Mo2PC	3.185, 3.200c	11.603, 11.62c	3.643, 3.612c	2.565	2.150
Mo2GaC	3.071, 3.01a,b, 3.084c	13.147, 13.18a,b, 13.16c	4.281, 4.369a, 4.267c	2.766	2.121
Mo2GeC	3.135, 3.149c	12.636, 12.64c	4.030, 4.040c	2.718	2.134
Mo2AsC	3.200, 3.225c	12.210, 12.17c	3.816, 3.774c	2.695	2.145
Mo2InC	3.132, 3.140c	13.980, 14.01c	4.463, 4.462c	2.985	2.127

^aBarsoum [34].

^bJeitschko et al [35].

^cCover et al [44].

Table 2.

Calculated elastic constants and bulk moduli of Mo₂AC (in GPa; A = Al, Si, P, Ga, Ge, As or In) systems.

Structure	C11	C12	C13	C33	C44	B
Ti2AlC	304.4, 302a, 305b, 321c	65.4, 62a, 60b, 76c	64.0, 61a, 60b, 100c	269.9, 269a, 275b, 318c	105.7, 109a, 110b, 144c	139.3, 138a, 139b, 168c
Mo2AlC	354.4, 333a	98.0, 97a	146.7, 144a	358.9, 327a	144.4, 137a	203.0, 196a
Mo2SiC	326.2, 311a	151.4, 149a	197.9, 192a	359.1, 338a	130.3, 124a	229.1, 225a
Mo2PC	266.4, 262a	139.2, 148a	228.9, 218b	331.0, 329a	106.4, 105a	190.1, 225a
Mo2GaC	312.0, 294a, 306.4d	94.05, 98a, 105.1d	163.7, 160a, 169.0d	313.9, 289a, 311.2d	128.4, 127a, 102.1d	191.5, 190a, 248.6d
Mo2GeC	307.1, 299a	152.7, 151a	180.5, 170a	311.9, 325a	100.9, 97a	214.4, 212a
Mo2AsC	286.2, 247a	139.7, 140a	206.1, 200a	325.5, 306a	56.3, 60a	220.6, 209a
Mo2InC	300.1, 270a	101.1, 94a	120.6, 127a	290.2, 286a	86.2, 85a	173.3, 169a

^aCover et al [44].

^bRosen et al [45].

^cSun et al [46].

^dShein and Ivanovskii [47].

From table 1, it is found that in Mo₂AC systems, the lattice constant a and Mo–C distances are not affected significantly by different A elements. In contrast, the lattice constant c and Mo–A bond distances are strongly affected by different A elements. These trends may indicate that Mo–C bonds are rather stronger than A–A bonds. Indeed, the A–A bond length is larger than twice the corresponding covalent radius of A element. Therefore the lattice constant a is basically determined by the chemical bonds in the Mo₂C layers. The strength of Mo–C and Mo–A bonds will be discussed on the basis of the electronic structure below.

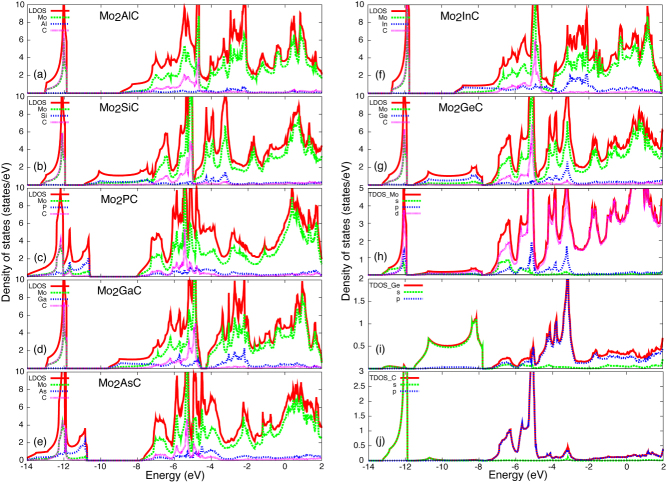
Figure 2 shows the calculated band structures of the various Mo₂AC systems. It is observed that all Mo₂AC structures are metallic, similar to many other MAX phases [50–57]. Figures 3(a)–(g) show the local density of states (LDOS) for each atom. In order to investigate the contribution of each atomic orbital in the LDOS, the projected densities of states (PDOSs), decompositions into each angular momentum channel, are also calculated. As an example, the PDOSs of Mo₂GeC are shown in figures 3(h)–(j). In general, the obtained band structure and LDOS features of Mo₂AC (A = Al, Si, P, Ga, As or In) are similar.

Figure 2.

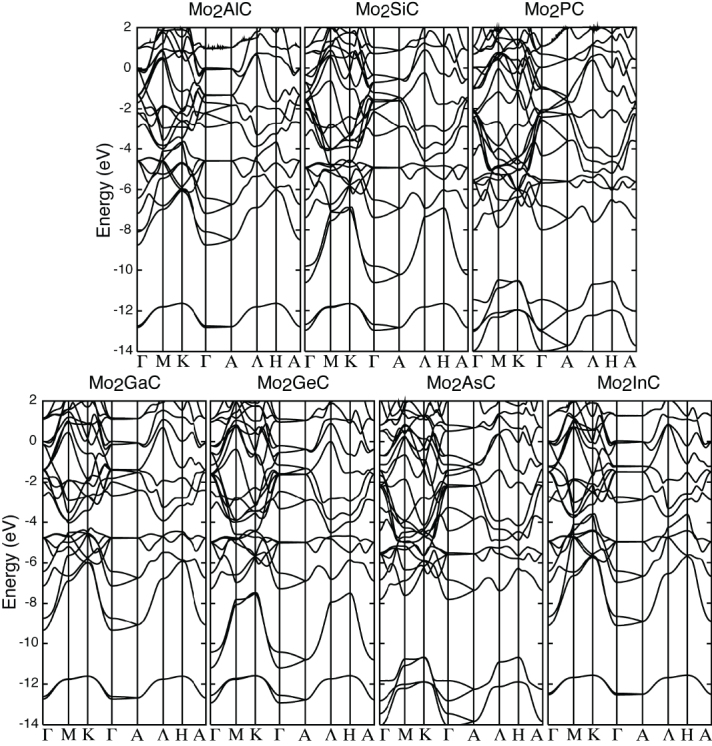
Band structures of Mo₂AC (A = Al, Si, P, Ga, Ge, As or In). Γ(0,0,0), M(1/2,0,0), K(1/3,1/3,0), A(0, 0, 1/2), Λ(1/2,0,1/2) and H(1/3,1/3,1/2) symmetry points of the Brillouin zone of a Mo₂AC. The Fermi energy is at zero.

Figure 3.

(a)–(f) LDOS for Mo₂AC (A = Al, Si, P, Ga, Ge, As or In). (g)–(j) Local projected densities of states of Mo₂GeC on different atoms and different atomic orbitals. The Fermi energy is at zero.

Metal atoms usually take part in bonding via their partially filled valence shells. Thereby, in Mo₂AC systems, C, Al, Si, P, Ga, Ge, As or In atoms are involved in the bonding states through their outmost s and p orbitals, and Mo is mainly involved through its d orbitals. Accordingly, the hybridizations of Mo-d, C-s, C-p, A-s and A-p orbitals contribute to the LDOS of Mo₂AC. As an example, let us discuss the LDOS and PDOS of Mo₂GeC in figures 3(g)–(j). In the lowest energy region, the states near −12.0 eV can be clearly assigned as bonding states between C 2s and Mo 4d orbitals. Above these bands, the Ge 4s orbitals form wider bands at energies between −12.0 and −8.0 eV from the hybridization with Mo 4d. The PDOSs of C-p and Ge-p are mainly distributed between −8.0 and −4.0 eV and between −5.0 and −2.0 eV, respectively. These states can be regarded as bonding states between the C 2p/Ge 4p and the Mo 4d orbitals. The states near the Fermi energy are mainly derived from the Mo 4d orbitals.

A strong heteropolar covalent bond is formed when the atomic levels of the paired atoms are close in energy. When the hybridizations are stronger, the bonding states will be created in the lower energies. In the LDOSs of Mo₂AC systems in figure 3, it can be seen that the centers of C-s and C-p bands do not vary significantly in the different system. This fact indicates that the strengths of Mo–C bonds in different Mo₂AC systems are relatively similar. This is the reason why the Mo–C bond distances of Mo₂AC are very similar to ∼ 2.1 Å. In contrast, the centers of the A-s and A-p bands of Mo₂AC systems differ significantly, which might imply the different strength of the Mo–A bonds in the different Mo₂AC systems. But since the atomic energy levels of A elements (Al, Si, P, Ga, As or In) are different from each other, it is not easy to compare the strength of Mo–A bonds in Mo₂AC systems from the LDOSs. However, such information might be inferred indirectly from the calculations of the elastic constants and the exfoliation energy.

Here, we discuss the calculated C₁₁ and C₃₃ elastic constants, which are listed in table 2. Basically, C₁₁ and C₃₃ elastic constants are kinds of quantities that imply the stiffness of overall chemical bonds along the ab and c directions, respectively. It is observed that in the case of Ti₂AlC, which was successfully exfoliated into 2D Ti₂C nanosheets in the experiments, C₁₁ is larger than C₃₃. Therefore, if C₃₃ is smaller than C₁₁, it might be more feasible to break the Mo–A–Mo bonds under appropriate mechanical and chemical tensions without significantly damaging the Mo–C–Mo bonds. By considering the elastic constants of Mo₂AC systems in table 2, it is seen that the C₃₃s of Mo₂PC and Mo₂AsC are larger than their C₁₁s, while for other compounds, C₃₃ and C₁₁ are similar or C₁₁ is larger than C₃₃. This indicates that in Mo₂PC and Mo₂AsC, the strength of the chemical bonds along the c lattice is stronger than that of the overall chemical bonds in the ab lattices. Therefore it is suggested that the chance for the exfoliation of Mo₂PC and Mo₂AsC into 2D Mo₂C layers is very little. In contrast, the C₃₃ of Mo₂InC is smaller than its C₁₁. This implies more chances for obtaining 2D Mo₂C nanosheets from the Mo₂InC MAX phase. In addition, from the bulk modulus calculations, it appears that Mo₂InC/Mo₂SiC is the softest/hardest among the considered Mo₂AC systems. It should be noted that the bulk modulus B in hexagonal systems is directly related to C₁₁, C₁₂, C₁₃ and C₃₃ elastic constants: B = (2C₁₁ + 2C₁₂ + 4C₁₃ + C₃₃)/9 [42].

In addition to the elastic constants, the strength of the chemical bonds between Mo and A atoms can be measured in another way by calculating the exfoliation energy of a bulk Mo₂AC system into 2D Mo₂C. In experiments, the exfoliation occurs dynamically; there are a lot of affecting parameters such as an acidic solution type, the concentration of the acid and the temperature. However, it is impossible or very difficult to simulate the details of this process using the current computational facilities. At present, static calculations are considered as the only way that we can provide some useful information on the exfoliation process. In such calculations, the exfoliation energy is defined by ΔH_f = 1/2E_tot(Mo₂AC) − E_tot(Mo₂C) − E_tot(A), where E_tot(Mo₂AC), E_tot(Mo₂C) and E_tot(A) stand for the total energies of bulk Mo₂AC, 2D Mo₂C and the ‘A’ element, respectively. The total energy of an ‘A’ element is estimated from its most stable bulk structure, as indicated in table 3 [58–64]. The results of the exfoliation energies are presented in table 4. For comparison, we have also calculated the exfoliation energy of a 2D Ti₂C nanosheet from Ti₂AlC, which was experimentally obtained. Thus, the Mo₂AC systems with a lower exfoliation energy than Ti₂AlC (− 2.668 eV) might be exfoliated into 2D Mo₂C nanosheets. Among the studied Mo₂AC systems, the exfoliation energy of Mo₂InC (− 2.543 eV) is lower than that of Ti₂AlC (− 2.668 eV). Therefore, it can be the best candidate for the exfoliation into 2D Mo₂C nanosheets.

Table 3.

Structural properties of the ‘A’ metals. The lattice distances are in Å.

‘A’ metals	Group symmetry	a	b	c
Al	Fm3m	4.039, 4.041a	4.039, 4.041a	4.039, 4.041a
Si	Fd3m	5.468 5.431b	5.468, 5.431b	5.468, 5.431b
P	P1	3.306, 3.313c	11.260, 10.408c	4.552, 4.374c
Ga	Cmca	4.579, 4.523d	7.774, 7.661d	4.594, 4.524d
Ge	Fd3m	5.783, 5.657e	5.783, 5.657e	5.783, 5.657e
As	R-3m	3.815, 3.759f	3.815, 3.759f	10.806, 10.457f
In	I4/mmm	3.328, 4.599g	3.328, 4.599g	4.977, 4.946g

^aStraumanis [58].

^bHom et al [59].

^cCartz et al [60].

^dSharma and Donohue [61].

^eSmakula and Kalnajs [62].

^fSchiferl and Barrett [63].

^gRidley [64].

Table 4.

Calculated exfoliation energies of M₂C from M₂AC (A = Al, Si, P, Ga, Ge, As, In or Ti) systems.

M2AC	Exfoliation energies (eV)
Mo2AlC	−3.247
Mo2SiC	−3.058
Mo2PC	−3.247
Mo2GaC	−3.104
Mo2GeC	−2.901
Mo2AsC	−2.818
Mo2InC	−3.544
Ti2AlC	−2.668

In the experiment, during the exfoliation process, depending on the utilized etchant, various chemical groups terminate the surfaces of MXenes. In the above exfoliation energy calculations, we discussed the suitability of Mo-containing MAX phases for possible exfoliation, irrespective of the selective etchant. This is because, for example, HF has been observed to work only for the exfoliation of Al-containing MAX-phases, and does not affect/etch the other MAX-phases. Moreover, even if we wish to discuss such issues, in the static calculation approach, since the surface termination energy of 2D Mo₂C does not depend on the ‘A’ element, it does not affect the ordering of the exfoliation energies in table 4. As examples of surface termination energies, here we report them for the Mo₂C nanosheets functionalized with F, Cl, Br and OH groups (− 7.81, −4.70, −3.90 and −6.86 eV, respectively) [25]. Such large negative energies indicate that Mo₂C nanosheets make strong bonds with the F, Cl, Br or OH groups and become more stabilized, especially by F termination.

Finally, it is worth mentioning that there might be other ways to produce 2D Mo₂C in addition to the exfoliation of the Mo₂AC MAX phases. For example, it has been shown experimentally that thin films of Mo₂C can be formed on the top of graphite surfaces resulting from MoO₃ reactions with the carbon atoms of graphite [65].

Summary

By using first-principles calculations, we have studied the electronic structures, elastic constants and exfoliation energies of Mo₂AC (A = Al, Si, P, Ga, Ge, As or In) MAX phases. On the basis of the above analyses, it is predicted that Mo₂InC has the best chance for exfoliation into 2D Mo₂C nanosheets. We hope our results would stimulate experimentalists to synthesize various Mo-containing MAX phases and investigate their selective etching and exfoliation into novel 2D Mo₂C nanosheets with potentially unique energy-related properties.